初三数学综合测试卷
初三九年级数学测试卷三
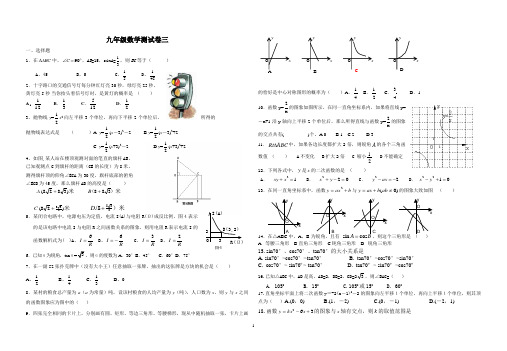
九年级数学测试卷三一、选择题1.在ABC ∆中,︒=∠90C ,AB =15,sin A =31,则BC 等于( )A 、45B 、5C 、51D 、4512.十字路口的交通信号灯每分钟红灯亮30秒,绿灯亮25秒, 黄灯亮5秒.当你抬头看信号灯时,是黄灯的概率是 ( )A .121 B .31 C .125 D .21 3.抛物线y =21x 2向左平移3个单位,再向下平移2个单位后,所得的抛物线表达式是 ( )A. y =21(x -3)2-2 B.y =21(x -3)2+2C. y =21(x +3)2-2D.y =21(x +3)2+24.如图,某人站在楼顶观测对面的笔直的旗杆AB , 已知观测点C 到旗杆的距离(CE 的长度)为8米, 测得旗杆顶的仰角∠ECA 为30度,旗杆底部的俯角 ∠ECB 为45度,那么旗杆AB 的高度是( )米)3828.(+A )米(388.+B米)28.(338+C )米(3388.+D5.某闭合电路中,电源电压为定值,电流I(A)与电阻R(Ω)成反比例,图4表示的是该电路中电流I 与电阻R 之间函数关系的图象,则用电阻R 表示电流I 的函数解析式为( )A 、R I 6=B 、R I 6-=C 、R I 3=D 、RI 2=6.已知α为锐角,tan α=3,则α的度数为A .30°B .45° C .60°D .75°7.在一副52张扑克牌中(没有大小王)任意抽取一张牌,抽出的这张牌是方块的机会是( ) A 、21 B 、41 C 、31D 、0 8.某村的粮食总产量为a (a 为常量)吨,设该村粮食的人均产量为y (吨),人口数为x ,则y 与x 之间的函数图象应为图中的( )9.四张完全相同的卡片上,分别画有圆、矩形、等边三角形、等腰梯形,现从中随机抽取一张,卡片上画的恰好是中心对称图形的概率为( )A .41 B .21 C .43D .110.函数y=x2的图象如图所示,在同一直角坐标系内,如果将直线y=-x+1沿y 轴向上平移2个单位后,那么所得直线与函数y=x2的图象的交点共有( )个。
人教版九年级数学上册 圆 几何综合单元测试卷(含答案解析)

人教版九年级数学上册 圆 几何综合单元测试卷(含答案解析)一、初三数学 圆易错题压轴题(难)1.已知圆O 的半径长为2,点A 、B 、C 为圆O 上三点,弦BC=AO ,点D 为BC 的中点,(1)如图,连接AC 、OD ,设∠OAC=α,请用α表示∠AOD ;(2)如图,当点B 为AC 的中点时,求点A 、D 之间的距离: (3)如果AD 的延长线与圆O 交于点E ,以O 为圆心,AD 为半径的圆与以BC 为直径的圆相切,求弦AE 的长. 【答案】(1)1502AOD α∠=︒-;(2)7AD =3)33133122or 【解析】【分析】(1)连接OB 、OC ,可证△OBC 是等边三角形,根据垂径定理可得∠DOC 等于30°,OA=OC 可得∠ACO=∠CAO=α,利用三角形的内角和定理即可表示出∠AOD 的值.(2)连接OB 、OC ,可证△OBC 是等边三角形,根据垂径定理可得∠DOB 等于30°,因为点D 为BC 的中点,则∠AOB=∠BOC=60°,所以∠AOD 等于90°,根据OA=OB=2,在直角三角形中用三角函数及勾股定理即可求得OD 、AD 的长.(3)分两种情况讨论:两圆外切,两圆内切.先根据两圆相切时圆心距与两圆半径的关系,求出AD 的长,再过O 点作AE 的垂线,利用勾股定理列出方程即可求解.【详解】(1)如图1:连接OB 、OC.∵BC=AO∴OB=OC=BC∴△OBC 是等边三角形∴∠BOC=60°∵点D 是BC 的中点∴∠BOD=1302BOC ∠=︒ ∵OA=OC∴OAC OCA ∠=∠=α∴∠AOD=180°-α-α-30︒=150°-2α(2)如图2:连接OB、OC、OD.由(1)可得:△OBC是等边三角形,∠BOD=130 2BOC∠=︒∵OB=2,∴OD=OB∙cos30︒=3∵B为AC的中点,∴∠AOB=∠BOC=60°∴∠AOD=90°根据勾股定理得:AD=227AO OD+=(3)①如图3.圆O与圆D相内切时:连接OB、OC,过O点作OF⊥AE∵BC是直径,D是BC的中点∴以BC为直径的圆的圆心为D点由(2)可得:3D的半径为1∴31设AF=x 在Rt △AFO 和Rt △DOF 中,2222OA AF OD DF -=-即()2222331x x -=-+- 解得:331x 4+= ∴AE=3312AF +=②如图4.圆O 与圆D 相外切时:连接OB 、OC ,过O 点作OF ⊥AE∵BC 是直径,D 是BC 的中点∴以BC 为直径的圆的圆心为D 点由(2)可得:3D 的半径为1∴31在Rt △AFO 和Rt △DOF 中,2222OA AF OD DF -=-即()2222331x x -=-解得:331x 4-= ∴AE=3312AF -=【点睛】本题主要考查圆的相关知识:垂径定理,圆与圆相切的条件,关键是能灵活运用垂径定理和勾股定理相结合思考问题,另外需注意圆相切要分内切与外切两种情况.2.已知:在△ABC中,AB=6,BC=8,AC=10,O为AB边上的一点,以O为圆心,OA长为半径作圆交AC于D点,过D作⊙O的切线交BC于E.(1)若O为AB的中点(如图1),则ED与EC的大小关系为:ED EC(填“”“”或“”)(2)若OA<3时(如图2),(1)中的关系是否还成立?为什么?(3)当⊙O过BC中点时(如图3),求CE长.【答案】(1)ED=EC;(2)成立;(3)3【解析】试题分析:(1)连接OD,根据切线的性质可得∠ODE=90°,则∠CDE+∠ADO=90°,由AB=6,BC=8,AC=10根据勾股定理的逆定理可证得∠ABC=90°,则∠A+∠C=90°,根据圆的基本性质可得∠A=∠ADO,即可得到∠CDE=∠C,从而证得结论;(2)证法同(1);(3)根据直角三角形的性质结合圆的基本性质求解即可.(1)连接OD∵DE为⊙O的切线∴∠ODE=90°∴∠CDE+∠ADO=90°∵AB=6,BC=8,AC=10∴∠ABC=90°∴∠A+∠C=90°∵AO=DO∴∠A=∠ADO∴∠CDE=∠C∴ED=EC;(2)连接OD∵DE为⊙O的切线∴∠ODE=90°∴∠CDE+∠ADO=90°∵AB=6,BC=8,AC=10∴∠ABC=90°∴∠A+∠C=90°∵AO=DO∴∠A=∠ADO∴∠CDE=∠C∴ED=EC;(3)CE=3.考点:圆的综合题点评:此类问题综合性强,难度较大,在中考中比较常见,一般作为压轴题,题目比较典型.3.如图,△ABC内接于⊙O,AB是直径,过点A作直线MN,且∠MAC=∠ABC.(1)求证:MN是⊙O的切线.(2)设D是弧AC的中点,连结BD交AC于点G,过点D作DE⊥AB于点E,交AC于点F.①求证:FD=FG.②若BC=3,AB=5,试求AE的长.【答案】(1)见解析;(2)①见解析;②AE=1【解析】【分析】(1)由AB为直径知∠ACB=90°,∠ABC+∠CAB=90°.由∠MAC=∠ABC可证得∠MAC+∠CAB=90°,则结论得证;(2)①证明∠BDE=∠DGF即可.∠BDE=90°﹣∠ABD;∠DGF=∠CGB=90°﹣∠CBD.因为D是弧AC的中点,所以∠ABD=∠CBD.则问题得证;②连接AD、CD,作DH⊥BC,交BC的延长线于H点.证明Rt△ADE≌Rt△CDH,可得AE=CH.根据AB=BH可求出答案.【详解】(1)证明:∵AB是直径,∴∠ACB=90°,∴∠CAB+∠ABC=90°;∵∠MAC=∠ABC,∴∠MAC+∠CAB=90°,即MA⊥AB,∴MN是⊙O的切线;(2)①证明:∵D是弧AC的中点,∴∠DBC=∠ABD,∵AB是直径,∴∠CBG+∠CGB=90°,∵DE⊥AB,∴∠FDG+∠ABD=90°,∵∠DBC =∠ABD ,∴∠FDG =∠CGB =∠FGD ,∴FD =FG ;②解:连接AD 、CD ,作DH ⊥BC ,交BC 的延长线于H 点.∵∠DBC =∠ABD ,DH ⊥BC ,DE ⊥AB ,∴DE =DH ,在Rt △BDE 与Rt △BDH 中,DH DE BD BD=⎧⎨=⎩, ∴Rt △BDE ≌Rt △BDH (HL ),∴BE =BH ,∵D 是弧AC 的中点,∴AD =DC ,在Rt △ADE 与Rt △CDH 中,DE DH AD CD =⎧⎨=⎩, ∴Rt △ADE ≌Rt △CDH (HL ).∴AE =CH .∴BE =AB ﹣AE =BC+CH =BH ,即5﹣AE =3+AE ,∴AE =1.【点睛】本题是圆的综合题,考查了切线的判定,圆周角定理,全等三角形的判定与性质,等腰三角形的判定,正确作出辅助线来构造全等三角形是解题的关键.4.如图,在平面直角坐标系中,O 为坐标原点,△ABC 的边BC 在y 轴的正半轴上,点A 在x 轴的正半轴上,点C 的坐标为(0,8),将△ABC 沿直线AB 折叠,点C 落在x 轴的负半轴D (−4,0)处.(1)求直线AB 的解析式;(2)点P 从点A 出发以每秒5AB 方向运动,过点P 作PQ ⊥AB ,交x 轴于点Q ,PR ∥AC 交x 轴于点R ,设点P 运动时间为t (秒),线段QR 长为d ,求d 与t 的函数关系式(不要求写出自变量t 的取值范围);(3)在(2)的条件下,点N 是射线AB 上一点,以点N 为圆心,同时经过R 、Q 两点作⊙N ,⊙N 交y 轴于点E ,F .是否存在t ,使得EF =RQ ?若存在,求出t 的值,并求出圆心N 的坐标;若不存在,说明理由.【答案】(1)132y x =-+(2)d =5t (3)故当 t =85,或815,时,QR =EF ,N (-6,6)或(2,2).【解析】 试题分析:(1)由C (0,8),D (-4,0),可求得OC ,OD 的长,然后设OB=a ,则BC=8-a ,在Rt △BOD 中,由勾股定理可得方程:(8-a )2=a 2+42,解此方程即可求得B 的坐标,然后由三角函数的求得点A 的坐标,再利用待定系数法求得直线AB 的解析式;(2)在Rt △AOB 中,由勾股定理可求得AB 的长,继而求得∠BAO 的正切与余弦,由PR//AC 与折叠的性质,易证得RQ=AR ,则可求得d 与t 的函数关系式;(3)首先过点分别作NT ⊥RQ 于T ,NS ⊥EF 于S ,易证得四边形NTOS 是正方形,然后分别从点N 在第二象限与点N 在第一象限去分析求解即可求解;试题解析:(1)∵C (0,8),D (-4,0),∴OC=8,OD=4,设OB=a ,则BC=8-a ,由折叠的性质可得:BD=BC=8-a ,在Rt △BOD 中,∠BOD=90°,DB 2=OB 2+OD 2,则(8-a )2=a 2+42, 解得:a=3,则OB=3,则B (0,3),tan ∠ODB=34OB OD = , 在Rt △AOC 中,∠AOC=90°,tan ∠ACB=34OA OC = , 则OA=6,则A (6,0),设直线AB 的解析式为:y=kx+b ,则60{3k bb+==,解得:1{23kb=-=,故直线AB的解析式为:y=-12x+3;(2)如图所示:在Rt△AOB中,∠AOB=90°,OB=3,OA=6,则22135,tan2OBOB OA BAOOA+=∠==,255OAcos BAOAB∠==,在Rt△PQA中,905APQ AP t∠=︒=,则AQ=10cosAPtBAO=∠,∵PR∥AC,∴∠APR=∠CAB,由折叠的性质得:∠BAO=∠CAB,∴∠BAO=∠APR,∴PR=AR,∵∠RAP+∠PQA=∠APR+∠QPR=90°,∴∠PQA=∠QPR,∴RP=RQ,∴RQ=AR,∴QR=12AQ=5t,即d=5t;(3)过点分别作NT⊥RQ于T,NS⊥EF于S,∵EF=QR,∴NS=NT,∴四边形NTOS是正方形,则TQ=TR=1522QR t=,∴1115151022224NT AT AQ TQ t t t==-=-=()(),分两种情况,若点N 在第二象限,则设N (n ,-n ),点N 在直线132y x =-+ 上, 则132n n -=-+ , 解得:n=-6,故N (-6,6),NT=6,即1564t = , 解得:85t = ; 若点N 在第一象限,设N (N ,N ),可得:132n n =-+ , 解得:n=2,故N (2,2),NT=2, 即1524t =, 解得:t=815∴当 t =85,或815,时,QR =EF ,N (-6,6)或(2,2)。
初三数学测试题及答案

初三数学测试题及答案一、选择题(每题3分,共30分)1. 下列哪个选项是方程x^2 - 4x + 4 = 0的解?A. x = 0B. x = 2C. x = -2D. x = 42. 函数y = 3x + 2的图象是:A. 一条直线B. 一条曲线C. 一个圆D. 一个椭圆3. 一个三角形的两边长分别为3和4,第三边长x满足:A. 1 < x < 7B. 0 < x < 7C. 1 < x < 5D. 2 < x < 74. 已知a、b、c是三角形的三边长,且a^2 + b^2 = c^2,那么这个三角形是:A. 锐角三角形B. 直角三角形C. 钝角三角形D. 等腰三角形5. 计算(3x - 2)(x + 1)的结果为:A. 3x^2 + x - 2B. 3x^2 + x + 2C. 3x^2 - x - 2D. 3x^2 - x + 26. 以下哪个选项是不等式2x - 3 > 5的解集?A. x > 4B. x > 2C. x < 4D. x < 27. 已知圆的半径为r,圆的面积S与半径r的关系是:A. S = πr^2B. S = 2πrC. S = πrD. S = 4πr^28. 函数y = 2^x的图象经过点:A. (0, 1)B. (1, 2)C. (2, 4)D. (-1, 0.5)9. 计算(2x + 3)(2x - 3)的结果为:A. 4x^2 - 6x + 9B. 4x^2 - 9C. 4x^2 + 9D. 4x^2 + 6x - 910. 一个等腰三角形的底角为45°,那么顶角的度数为:A. 45°B. 60°C. 90°D. 135°二、填空题(每题4分,共20分)11. 计算(a + b)^2 = a^2 + 2ab + b^2的结果。
12. 已知一个等差数列的首项为3,公差为2,求第5项的值。
初三数学综合测试卷

初三数学综合测试卷一、精心选一选(本大题共8小题,每小题3分,共24分) 1.已知∠A =36°58′,则∠A 的余角为( ) A .143°2′ B .143°42′ C .53°2′ D .53°42′ 2.在(1)菱形(2)梯形(3)正六边形(4)等腰三角形中,既是轴对称图形,又是中心对称图形的是( )A .(1)、(2)B .(1)、(3)C .(1)、(4)D .(3)、(4) 3.抛物线y =x 2+6x +4的顶点坐标是( ) A .(3,-5) B .(-3,-5) C .(3,5) D .(-3,5) 4.下列命题中是真命题的是( )A .两边一角对应相等的两个三角形全等B .顺次连接梯形各边中点所得的四边形是菱形C .同圆中较大的弧所对的弦也较长D .圆中过一弦所对的两弧中点的直线经过圆心 5.《中华人民共和国个人所得税法》规定:公民月工资、薪金所得不超过800元(人民币)的部分不必纳税,超过800元的部分为本月应纳税所得额,此项税款按下表分段累加计算:若某人1月份应交纳此项税款115元,则他的当月工资、薪金为( )A .1150元B .1400元C .1950元D .2200元 6.下面四个图形每个均有六个相同的小正方形组成,折叠后能围成正方体的是( )7.小红的运动服被一个铁钉划破一个呈直角三角形的洞,其中两边分别为1 cm 和2 cm ,若用同色形布将此洞全部遮盖,那么这个圆的直径最小应等于( ) A .2 cm B .3 cm C .2 cm 或3 cmD .2 cm 或5cm8.关于反比例函数y =-x3的图象,下列命题中正确的是( )A .点(3,1)在图象上B .y 随着x 的增大而减小C .图象在第二、四象限D .图象在第一、三象限二、耐心填一填(本大题共8小题,每小题3分,共24分)9.一只苍蝇腹内细菌多达2800万个,用科学记数法表示是________万个.10.一组数据-1、2、x 、3的平均数是1,则x =________.11.长为12 cm 的铁丝,围成边长为连续整数的直角三角形,则斜边上的中线为________cm .12.河堤的横断面如图1,堤高10米,迎水斜坡AB 长26米,那么斜坡AB 的坡度i 是________.图113.已知函数y =kx 与y =xk (k ≠0)的图象相交于两点A (x 1,y 1)、B (x 2,y 2),那么x 1+x 2+y 1+y 2的值等于________.14.如图2,P A 是⊙O 的切线,割线PBC 与⊙O 相交于点B 、C ,P A =6、PB =4则BC =________.ACAB 的值为________.图215.某班全体同学在“献爱心”活动中都捐了图书,捐书的情况如表:根据题目中所给的条件回答下列问题:(2)全班一共捐了________册图书. 16.在△ABC 中,a 、b 、c 分别是∠A 、∠B 、∠C 的对边,若sin A ·cos A =0且a =2c cos B ,则△ABC 的形状是________.三、用心想一想(本大题共5小题,17~19题每小题10分,20~21题每小题11分,共52分)17.已知:四边形ABCD 中,∠B =∠ADC =90°,AB =2、CD =1、∠A =60°,求:BC .图418.已知关于x的一元二次方程x2-2(m-1)x+(m2-1)=0,有两个实数根x1、x2,且x12+x22=4.求m的值.19.已知A是⊙O上的一点,⊙A与⊙O相交于点C、D,⊙O的弦AB交CD于点E,AE=2、EB=6.求:⊙A的半径长.图520.如图6,四边形ABCD内接于⊙O,AB是⊙O的直径,弦CG⊥AB(垂足为E),AD 与GC的延长线交于F.图6(1)求证:△AFC∽△ACD;(2)若CD=2、AD=3、AC=4,求:CE.21.在平面直角坐标系中,B(3+1,0),点A在第一象限内,且∠AOB=60°,∠ABO =45°.图7(1)求点A的坐标;(2)求过A、O、B三点的抛物线解析式;(3)动点P从O点出发,以每秒2个单位的速度沿OA运动到点A止,①若△POB的面积为S,写出S与时间t(秒)的函数关系;②是否存在t,使△POB的外心在x轴上,若不存在,请你说明理由;若存在,请求出t的值.参考答案一、1.C2.B3.B4.D5.D6.C7.D8.C(第5题:设此人的工资、薪金为x元,由题意可得500×5%+(x-800-500)×10%=115解之得x=2200.)二、9.2.8×10310.0511.212.5∶1213.0214.5315.4540516.等腰直角三角形三、17.解:延长BC、AD交于点E,在Rt△ABE中,∠B=90°、∠A=60°,∴∠E=30°,∴AE=2AB=2×2=4.在Rt△CDE中,∠CDE=90°、∠E=30°,∴CE=2CD=2×1=2.由勾股定理,得: BE =22AB AE -=2224-=23,∴ BC =BE -CE =23-2. 18.解:由Δ≥0,得m ≤1, 又由x 12+x 22=2m 2-8m +6=4 解之得m 1=2+3、m 2=2-3, ∵ m ≤1,∴ m =2-3. 19.解:连接AC 、AD 、DB ,∵ ∠B =∠C =∠ADC 、∠EAD =∠DAB , ∴ △EAD ∽△DAB ,∴ AD 2=AE ·AB , 即AD 2=2×8=16,∵ AD =4,即⊙A 的半径为4.20.(1)证明:连接BD ,∵ AB 是直径,CG ⊥AB , ∴ ∠ADB =∠AEF =90°、∠ABD =∠ACD =∠F , ∴ ∠F AC =∠CAD ,∴ △AFC ∽△ACD ;(2)解:由(1)得,AD AC=CD FC=ACAF ,∴ FC =38,AF =316,∵ DF ·F A =FC ·FG 、CG =2CE . ∵ (316-3)×316=×(38+2CE ) CE =1.21.解:(1)过A 作AC ⊥OB 于C ,设OC =x , 在Rt △AOC 中,AC =3x , 在Rt △ABC 中,BC =3x . ∵ OB =3+1,∴ OC +BC =OB ,∴ x +3x =3+1, ∴ x =1、AB =BC =3, ∴ 点A (1,3).(2)∵ 抛物线经过A (1,3)、O (0,0)、B (13+,0) 设y =a (x -0)(x -3-1),∴ 3=a (-3)a =-1,∴ y =-x 2+(3+1)x ,即经过A 、O 、B 三点的抛物线解析式为 y =-x 2+(3+1)x .(3)①过点P 作PD ⊥BO 于D ,OP =2t , ∴ PD =OP sin60°=2t ·23=3t ,∴ S =21OB ·PD =21(3+1)·3tS =233+t (0<t ≤1).②存在t ,使△POB 的外心在x 轴上,即△POB 的外心在OB 上, ∴ ∠OPB =90°,在Rt △OPB 中, OP =OB cos60°=21(3+1),∴ OP =2t ,∴ t =413+,当t =413+时,△POB 的外心在x 轴上.。
初三数学综合测试卷及答案

一、选择题(每题3分,共30分)1. 下列各数中,有理数是()A. √16B. √-9C. πD. 0.1010010001……2. 已知等腰三角形底边长为8cm,腰长为10cm,则其面积为()A. 32cm²B. 40cm²C. 48cm²D. 80cm²3. 下列函数中,一次函数是()A. y = 2x² - 3x + 1B. y = √x + 1C. y = 2x + 3D. y = 3/x4. 已知一元二次方程x² - 5x + 6 = 0,则其解为()A. x₁ = 2, x₂ = 3B. x₁ = 3, x₂ = 2C. x₁ = 6, x₂ = 1D. x₁ = 1, x₂ = 65. 在平面直角坐标系中,点A(2,3)关于原点的对称点是()A.(-2,-3)B.(2,-3)C.(-2,3)D.(3,-2)6. 下列各组数中,成等差数列的是()A. 1,4,7,10B. 2,5,8,11C. 3,6,9,12D. 4,7,10,137. 若直角三角形的两条直角边长分别为3cm和4cm,则斜边长为()A. 5cmB. 6cmC. 7cmD. 8cm8. 下列命题中,正确的是()A. 若a > b,则a² > b²B. 若a > b,则ac > bcC. 若a > b,则a² > b²D. 若a > b,则ac > bc9. 已知正方形的边长为a,则其对角线长为()A. aB. √2aC. 2aD. a√210. 在等腰三角形ABC中,若底边BC=8cm,腰AB=AC=10cm,则三角形ABC的周长为()A. 24cmB. 26cmC. 28cmD. 30cm二、填空题(每题4分,共40分)11. 分数 3/4 与 -1/2 的差是 ________。
初三数学综合测试题

初三数学综合测试题一、精心选一选(本大题共8小题,每小题3分,共24分)1.给出四个函数:(1)y =5x (2)y =-5x (3)y =x 2(x <-1) (4)y =-x 2(x >1)其中,y 随x 的增大而减小的函数有( ) A .1个 B .2个 C .3个 D .4个2.植物的叶子上有许多气孔,在阳光下,这些气孔一面排出氧气和蒸腾水分,一面还吸入二氧化碳,有时,一个气孔在一秒钟内能吸进25000亿个二氧化碳分子,用科学记数法表示25000亿为( )A .2.5×1012B .2.5×1011C .2.5×1010D .25×1011 3.在平面直角坐标系中,已知⊙O 的圆心坐标为(-2,-2),半径为3,则⊙O 与直线x =1的位置关系是( ) A .相离 B .相切 C .相交 D .无法确定 4.若x 1、x 2是一元二次方程3x 2+x -1=0的两个根,则11x +21x 的值是( ) A .-1 B .0 C .1 D .25.如图1,在⊙O 中,弦AB 与半径O C 相交于点M ,且OM =MC ,若AM =1.5,BM =4,则OC 的长为()图1A .26B .6C .23D .226.如图2,P A 是⊙O 的直径,PC 为⊙O 的弦,过弧AC 的中点H 作PC 的垂线交PC 的延长线于点B ,若HB =6、BC =4,则⊙O 的直径是()图2A .10B .13C .15D .207.如图3,AB 是⊙O 的直径,弦CD ⊥AB ,垂足为E ,那么下面结论中,错误的是( )图3A.CE=DE B.弧BC=弧BDC.∠BAC=∠BAD D.AC>AD8.某幼儿园准备用三种不同的多边形木板镶嵌地面,现有边长相同的正三角形和和正八边形,还要边长相同的()A.正十二边形B.正十边形C.正八边形D.正六边形二、耐心填一填(本大题共8小题,每小题4分,共32分)9.设方程x2-3x+2=0的两个根为x1、x2,则x1+x2=________;x1·x2=________.10.若点A(1,m)在函数y=x2的图象上,则点A关于原点的对称点的坐标是________.11.如图4,已知:AB是⊙O的弦,C是AB上的点,AC=4、BC=1、OC=2,则⊙O 的半径是________.图412.一次函数的函数值y随自变量x的值增大而增大,且图象经过第四象限,写出一个符合以上条件的函数式________.13.如图5,在直角坐标系中,P为x轴上一点,以P为圆心,2 cm为半径的圆与y轴相切,等边△ABC内接于圆P,且BC与x轴平行,则点A的坐标为________,点B的纵坐标为________.图514.关于x的一元二次方程(m+1)x2+x-m+1=0的根的判别式Δ=________;当-23<m <23时,这个方程的根的情况是________. 15.如图6,△ABC 内接于⊙O ,D 是劣弧AB 上一点,E 是BC 延长线上一点,AE 交⊙O 于F ,为使△ADB ∽△ACE ,应补充的一个条件是________或________.图616.某校初三(8)班第五小组9名学生的视力分别为5.2、5.2、5.2、5.0、4.8、4.4、4.3、4.3、4.2:这组数据的中位数是________;他们的平均视力是________(精确到0.1).能否用这个平均视力来估计该校学生的平均视力吗?________;为什么?________.三、用心想一想(本大题共5小题,17小题8分,18~21小题每题9分,共44分) 17.声音在空气中传播的速度y (米/秒),随着气温x (℃)的上升而增大,下表是一组测量数据:(1)写出满足上表的一个一次函数的关系式.(2)根据表中的函数关系式,如果气温x =12(℃)时,某人看到烟花燃放5秒后才听到声响,那么此人与燃放的烟花所在地约相距多远?18.请阅读下列及其证明过程,并回答所提出的问题,如图7,已知P 为⊙O 外一点,P A 、PB 为⊙O 的切线,A 和B 是切点,BC 是直径.求证:AC ∥OP .图7证明:连接AB ,交OP 于点D .∵ P A 、PB 切⊙O 于A 、B ,∴ P A =PB ,∠1=∠2; ∴ PD ⊥AB ∴ ∠3=90°;∵________,(*)∴∠4=90°∴∠3=∠4∴AC∥OP.(1)在(*)处的横线上补上应填的条件;(2)上述证明过程中用到的定理名称或定理的具体内容是(只要求写出两个).19.已知等腰三角形三边的长为a、b、c,且a=c,若关于x的一元二次方程ax2-2bx +c=0的两根之差为2,求:等腰三角形的底角度数.20.如图8,正方形ABCD中,有一直径为BC的半圆,BC=2厘米,现有两点E、F,分别从点B,点A同时出发,点E沿线段BA以1厘米/秒的速度向点A运动,点F沿折线A-D-C以2厘米/秒的速度向C运动,设点E离开B的时间为t秒.图8(1)当t为何值时,线段EF与BC平行?(2)设1<t<2,当t为何值时,EF与半圆相切?21.把边长为2 cm的正方形剪四个全等的直角三角形,请用这四个直角三角形拼成符合下列要求的图形(全部用上,互不重叠互不留空隙),并把你的拼法依照图按实际大小画在方格纸内.(1)不是正方形的菱形(一个);(2)不是正方形的矩形(一个);(3)梯形(一个);(4)不是矩形和梯形的平行四边形(一个);(5)不是梯形和平行四边形的凸四边形(一个);(6)与以上画出的图形不全等的凸四边形(画出的图形不全等,能画出几个画出几个,至少画出三个).图9 参考答案一、1.C 2.A 3.B 4.C 5.D 6.B 7.D 8.A 二、9.3 2 10.(-1,-1) 11.2212.y =x -1 13.(2,2) -114.4m 2-3 无实数根15.∠DAB =∠CAE 或∠ABD =∠E 或=或AC AD =CEBD16.4.8 4.73 不能 ∵ 样本容量太小,选取样本的范围太小三、17.解:(1)设y =kx +b ,∵ x =0时,y =331;x =5时,y =334.∴ ⎩⎨⎧=+=3345331b k b ∴ ⎪⎩⎪⎨⎧==53331k b所求函数关系式是y =53x +331; (2)当x =12时,y =53×12+331=338.2(米/秒), 338.2×5=1691(米)∴ 此人与燃放的烟花所在地约相距1691米. 18.(1)BC 是⊙O 的直径.(2)切线长定理;等腰三角形顶角的平分线垂直平分底边;直径所对的圆周角是直角;内错角相等,两直线平行.19.解:设二次方程ax 2-2bx +c =0的两实数根是x 1、x 2且x 1>x 2,则x 1-x 2=221)(x x -=21224)(1x x x x -+=24)2(2=⨯-aca b 由c =a 及3=a b ,如图,过等腰三角形的顶点B 作BD ⊥AC ,则AD =21b ,Rt △ABD 中,cos A =2321==a bAB AD ∴ ∠A =30°,即底角为30°.20.解:(1)设E 、F 出发后t 秒时,有EF ∥BC (如图甲) 则BE =t 、CF =4-2t ,∵ BE =CF ,∴ t =4-2t ,∴ t =34, 即E 、F 出发后34秒时, EF 与半圆相切(2)(如图乙)过F 作KF ∥BC 交AB 于K , 则BE =t ,在Rt △EKF 中,EF 2=EK 2+KF 2,∴ (4-t )2=(3t -4)2+22 2t 2-4t +1=0,∴ t =222±,又∵ 1<t <2,∴ t =222+ 即E 、F 出发后222+秒,EF 与半圆相切. 21.以下图形,供选择:。
2010—2011学年度初三上期末数学综合测试试卷3苏科版

(1)求证:∠ABE=∠BCE;
(2)当点P在AB的延长线上运动时,判断sin∠BCE的值是否随点P位置的变化而变化,提出你的猜想并加以证明.
25.某商店经营一种小商品,进价为2.5元,据市场调查,销售单价是13.5元时平均每天销售量是500件,而销售单价每降低1元,平均每天就可以多售出100件.
(3)劣弧比优弧短(4)菱形的四个顶点在同一个圆上
A.1个B.2个C.3个D.4个
8.如图,RtΔABC中,∠C=900,AC=6,BC=8,CD为直径的⊙O与AB相切于E,则⊙O的
半径是……………………………………………………………………………………()
A.2B.2.5C.3D.4
9.已知点(-1,y1)、(-3,y2)、(,y3)在函数y=3x2+6x+12的图象上,那么y1、y2、y3的大小
A.ODB.OAC.CDD.AB
题号
1
2
3
4
5
6
7
8
9
10
答案
二、填空题:
11.抛物线y=x2-2x+3的顶点坐标是.
12.若2是关于x的一元二次方程x2+3kx-10=0的一个根,则k=.
13.若某人沿坡度i=3∶4的斜坡前进10m,则他比原来的位置升高了_m.
14.已知⊙O1和⊙O2的半径分别为3cm和5cm,且它们相切,则圆心距O1O2等于cm.
(1)假设每件商品降低x元,商店每天销售这种小商品的利润是y元,请你写出y与x的之间的函数关系式,并注明x的取值范围;
(2)每件小商品销售价是多少元时,商店每天销售这种小商品的利润最大?最大利润是多少?(注:销售利润=销售收入-购进成本)
上海2020中考数学综合模拟测试卷2(含答案及解析)

2020上海市初中毕业模拟考试数学试题(含答案全解全析)第Ⅰ卷(选择题,共24分)一、选择题(本大题共6题,每题4分,满分24分)下列各题的四个选项中,有且只有一个选项是正确的.1.计算×的结果是( )A. B. C.2 D.32.据统计,2013年上海市全社会用于环境保护的资金投入约为60800000000元,这个数用科学记数法表示为( )A.608×108B.60.8×109C.6.08×1010D.6.08×10113.如果将抛物线y=x2向右平移1个单位,那么所得新抛物线的表达式是( )A.y=x2-1B.y=x2+1C.y=(x-1)2D.y=(x+1)24.如图,已知直线a、b被直线c所截,那么∠1的同位角是( )A.∠2B.∠3C.∠4D.∠55.某市测得上一周PM2.5的日均值(单位:微克/立方米)如下:50,40,73,50,37,50,40,这组数据的中位数和众数分别是( )A.50和50B.50和40C.40和50D.40和406.如图,已知AC、BD是菱形ABCD的对角线,那么下列结论一定正确的是( )A.△ABD与△ABC的周长相等B.△ABD与△ABC的面积相等C.菱形ABCD的周长等于两条对角线长之和的两倍D.菱形ABCD的面积等于两条对角线长之积的两倍第Ⅱ卷(非选择题,共126分)二、填空题(本大题共12题,每题4分,满分48分)7.计算:a(a+1)= .的定义域是.8.函数y=-9.不等式组-的解集是.10.某文具店二月份共销售各种水笔320支,三月份销售各种水笔的支数比二月份增长了10%,那么该文具店三月份共销售各种水笔支.11.如果关于x的方程x2-2x+k=0(k为常数)有两个不相等的实数根,那么k的取值范围是.12.已知传送带与水平面所成斜坡的坡度i=1∶2.4,如果它把物体送到离地面10米高的地方,那么物体所经过的路程为米.13.如果从初三(1)、(2)、(3)班中随机抽取一个班与初三(4)班进行一场拔河比赛,那么恰好抽到初三(1)班的概率是.14.已知反比例函数y=(k是常数,k≠0),在其图象所在的每个象限内,y的值随着x的值增大而增大,那么这个反比例函数的解析式可以是(只需写一个).15.如图,已知在平行四边形ABCD中,点E在边AB上,且AB=3EB.设=a,=b,那么= (结果用a、b表示).16.甲、乙、丙三人进行飞镖比赛,已知他们每人五次投掷的成绩如图所示,那么三人中成绩最稳定的是.17.一组数:2,1,3,x,7,y,23,…,满足“从第三个数起,前两个数依次为a、b,紧随其后的数就是2a-b”,例如这组数中的第三个数“3”是由“2×2-1”得到的,那么这组数中y表示的数为.18.如图,已知在矩形ABCD中,点E在边BC上,BE=2CE,将矩形沿着过点E的直线翻折后,点C、D分别落在边BC下方的点C'、D'处,且点C'、D'、B在同一直线上,折痕与边AD交于点F,D'F 与BE交于点G.设AB=t,那么△EFG的周长为(用含t的代数式表示).三、解答题(本大题共7题,满分78分)19.(本题满分10分)计算:--+|2-|.20.(本题满分10分)解方程:---=.21.(本题满分10分,第(1)小题满分7分,第(2)小题满分3分)已知水银体温计的读数y(℃)与水银柱的长度x(cm)之间是一次函数关系.现有一支水银体温计,其部分刻度线不清晰(如图),下表记录的是该体温计部分清晰刻度线及其对应水银柱的长度.(1)求y关于x的函数解析式(不需要写出函数定义域);(2)用该体温计测体温时,水银柱的长度为6.2cm,求此时体温计的读数.如图,已知在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,过点A作AE⊥CD,AE分别与CD、CB相交于点H、E,AH=2CH.(1)求sin B的值;(2)如果CD=,求BE的长.23.(本题满分12分,每小题满分各6分)已知:如图,梯形ABCD中,AD∥BC,AB=DC,对角线AC、BD相交于点F,点E是边BC延长线上一点,且∠CDE=∠ABD.(1)求证:四边形ACED是平行四边形;(2)连结AE,交BD于点G.求证:=.在平面直角坐标系xOy中(如图),已知抛物线y=x2+bx+c与x轴交于点A(-1,0)和点B,与y 轴交于点C(0,-2).(1)求该抛物线的表达式,并写出其对称轴;(2)点E为该抛物线的对称轴与x轴的交点,点F在对称轴上,四边形ACEF为梯形,求点F的坐标;(3)点D为该抛物线的顶点,设点P(t,0),且t>3,如果△BDP和△CDP的面积相等,求t的值.25.(本题满分14分,第(1)小题满分3分,第(2)小题满分5分,第(3)小题满分6分)如图所示,已知在平行四边形ABCD中,AB=5,BC=8,cos B=,点P是边BC上的动点,以CP为半径的圆C与边AD交于点E、F(点F在点E的右侧),射线CE与射线BA交于点G.(1)当圆C经过点A时,求CP的长;(2)连结AP,当AP∥CG时,求弦EF的长;(3)当△AGE是等腰三角形时,求圆C的半径长.答案全解全析:一、选择题1.B ×==.2.C 60800000000的整数位有11位,所以用科学记数法表示为6.08×1010.3.C 抛物线的平移规律是“左加右减,上加下减”,如当抛物线y=ax2向右平移h(h>0)个单位时,所得新抛物线的解析式为y=a(x-h)2,所以当抛物线y=x2向右平移1个单位时,所得新抛物线的解析式为y=(x-1)2.4.D ∠1在直线a的下方,且在直线c的左边,∠5在直线b的下方,也在直线c的左边,所以它们是同位角,选D.5.A 把这组数据按照从小到大的顺序排列为:37,40,40,50,50,50,73,共有七个数,中位数是50,其中50出现的次数最多,所以众数为50.故选A.6.B 解法一:由题图可知S△ABD=S菱形ABCD,S△ABC=S菱形ABCD,所以S△ABD=S△ABC.解法二:△ABC和△ABD是同底等高的两个三角形,所以S△ABC=S△ABD.二、填空题7.答案a2+a解析a(a+1)=a2+a.评析本题考查单项式与多项式的乘法.8.答案x≠1有意义,则分母x-1≠0,即x≠1.解析要使分式-评析本题考查函数的定义域.9.答案3<x<4解析解不等式x-1>2得x>3,解不等式2x<8得x<4,所以原不等式组的解集是3<x<4. 10.答案352解析根据题意列式为:320×(1+10%)=320×1.1=352(支).11.答案k<1解析因为方程有两个不相等的实数根,所以Δ>0,即(-2)2-4×1×k=4-4k>0,解得k<1.评析本题考查一元二次方程的根的判别式.12.答案26解析如图,斜坡AB的坡度i=1∶2.4=AC∶BC=10∶BC,所以BC=24米,所以AB==26米.13.答案解析初三(1)、(2)、(3)班被抽到的机会均等,共3种可能,恰好抽到初三(1)班的概率是.14.答案y=-(答案不唯一)解析因为反比例函数y=(k≠0)的图象在每个象限内y的值随着x的值增大而增大,所以k<0,即只需满足k<0即可,此题答案不唯一.15.答案a-b解析如图,过点E作EF∥AD,因为AB=3EB=3FC,所以=-b,==a,所以=+=a-b.16.答案乙解析从折线统计图可以看出,甲、丙两人成绩浮动较大,极差分别为7、6,而乙的成绩较稳定,极差为2.所以成绩最稳定的是乙.17.答案-9解析根据题意得,x=2×1-3=-1,y=2x-7=-2-7=-9.18.答案2t解析连结BD',∵点C'、D'、B在同一直线上,∴∠D=∠FD'C'=∠GD'B=90°,由翻折知,CE=C'E,∴BE=2CE=2C'E,∴∠EBC'=30°,∠BGD'=60°,∵∠BGD'=∠FGE,∴∠FGE=60°.∵AD∥BC,∴∠AFG=∠BGD'.∴∠AFG=60°,易得∠GFE=60°,∴△EFG为等边三角形.∵AB=t,∴FG=t,∴C△EFG=2t.三、解答题19.解析原式=2--2+2-=.20.解析去分母,整理得x2+x=0.解方程,得x1=-1,x2=0.经检验:x1=-1是增根,舍去;x2=0是原方程的根.所以原方程的根是x=0.评析此题考查可化为一元二次方程的分式方程的解法,易错点是忽视验根.21.解析(1)设y关于x的函数解析式为y=kx+b(k≠0).由题意,得解得所以y关于x的函数解析式为y=x+.(2)当x=6.2时,y=37.5.答:此时该体温计的读数为37.5℃.评析第(1)问考查待定系数法求一次函数解析式,第(2)问是代入自变量的值求函数值.22.解析(1)∵在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,∴AB=2CD=2BD,∴∠DCB=∠B.∵AH⊥CD,∴∠AHC=∠CAH+∠ACH=90°.又∵∠DCB+∠ACH=90°,∴∠CAH=∠DCB=∠B.∴△ABC∽△CAH.∴=.又∵AH=2CH,∴BC=2AC.可设AC=k,BC=2k,在Rt△ABC中,AB==k.∴sin B==.(2)∵AB=2CD,CD=,∴AB=2.在Rt△ABC中,AC=AB·sin B=2×=2.∴BC=2AC=4.在Rt△ACE和Rt△AHC中,tan∠CAE===.∴CE=AC=1.∴BE=BC-CE=3.23.证明(1)∵四边形ABCD是梯形,AD∥BC,AB=DC,∴∠ADC=∠DAB.∵AD∥BE,∴∠ADC=∠DCE.∴∠DAB=∠DCE.在△ABD和△CDE中,∠∠∵∠∠∴△ABD≌△CDE,∴AD=CE.又∵AD∥CE,∴四边形ACED是平行四边形.(2)∵四边形ACED是平行四边形,∴FC∥DE.∴=.∵AD∥BE,∴=.又∵AD=CE,∴=.24.解析(1)∵点A(-1,0)和点C(0,-2)在抛物线y=x2+bx+c上,∴--解得--∴该抛物线的表达式为y=x2-x-2,对称轴为直线x=1.(2)∵点E为该抛物线的对称轴与x轴的交点,∴E(1,0).∵四边形ACEF为梯形,AC与y轴交于点C,∴AC与EF不平行.∴AF∥CE.∴∠FAE=∠OEC.在Rt△AEF中,∠AEF=90°,tan∠FAE=,同理,在Rt△OEC中,tan∠OEC=,∴=.∵OC=2,OE=1,AE=2,∴EF=4,∴点F的坐标是(1,4).(3)该抛物线的顶点D的坐标是-,点B的坐标是(3,0).由点P(t,0),且t>3,得点P在点B的右侧(如图).S△BPD=×(t-3)×=t-4.S△CDP=×(1+t)×-×1×-×t×2=t+1.∵S△BPD=S△CDP,∴t-4=t+1.解得t=5.即符合条件的t的值是5.评析此题第(2)问难点是根据已知条件确定出AF∥CE.第(3)问关键是根据已知条件分别用含t的代数式表示出△BPD与△CDP的面积.考查学生灵活运用知识的能力,难度较大. 25.解析(1)过点A作AH⊥BC,垂足为点H.连结AC.在Rt△AHB中,∠AHB=90°,cos B==,AB=5,∴BH=4.∵BC=8,∴AH垂直平分BC.∴AC=AB=5.∵圆C经过点A,∴CP=AC=5.(2)过点C作CM⊥AD,垂足为点M.设圆C的半径长为x.∵四边形ABCD是平行四边形,∴AB=DC=5,AD=BC=8,∠B=∠D.又由cos B=,得DM=4,CM=3.在Rt△EMC中,∠EMC=90°,EM=-=-.又∵点F在点E的右侧,∴DE=EM+DM=-+4.∴AE=AD-DE=4--.由AD∥BC,AP∥CG,得四边形APCE是平行四边形.∴AE=CP,即4--=x.解得x=.经检验:x=是原方程的根,且符合题意.∴EM=-=.在圆C中,由CM⊥EF,得EF=2EM=.∴当AP∥CG时,弦EF的长为.(3)设圆C的半径长为x,则CE=x,又∵点F在点E的右侧,∴DE=-+4.∵四边形ABCD是平行四边形,∴AB∥DC.∴△AGE∽△DCE.由△AGE是等腰三角形,可得△DCE是等腰三角形.①若GE=GA,则CE=CD,又由(1)知CD=CA,∴CE=CA.又∵点A、E在线段AD的垂直平分线CM的同侧,∴点E与点A重合,舍去.②若AG=AE,则DC=DE,得-+4=5.解得x=±,则x=-不符合题意,舍去.∴x=.③若GE=AE,则CE=DE,得-+4=x.解得x=,不符合题意,舍去.综上所述,当△AGE是等腰三角形时,圆C的半径长为.评析此题是圆、平行四边形、锐角三角函数、等腰三角形的综合题,考查学生运用变化的观点分析问题的能力.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初三数学综合测试卷说明:1、全卷3大题,共6页,考试时刻90分钟,满分100分。
2、答题前,请在监考老师的指导下,填好试卷密封线内的姓名、校名,姓名、校名不得写在密封线以外,不得在试卷上作任何标记。
3、答选择题时,请将选项的字母代号填在答题表一内,答填空题时,请将答案填在答题表二内,做解答题时,请将解答过程写在指定的位置上。
一、选择题(本题有10小题,每题3分,共30分)答题表一每题有4个选择答案,其中只有一个是正确的,请把你认为正确答案的字母代号选填在上面的答题表一内,否则不计分。
1、下列运算正确的是()A、x3+x3=2x6B、x6÷x2=x3C、(-3x3)2=3x6D、x2·x-3=x-12、若a>0,b<-2,则点(a,b+2)应在()A、第一象限B、第二象限C、第三象限D、第四象限3、检查5个篮球的质量,把超过标准质量的克数记为正数,不足标准质量的克数记为负数,检查结果如下表:篮球编号 1 2 3 4 5与标准质量的差(克)+4 +7 -3 -8 +9质量最大的篮球比质量最小的篮球重( )A 、12克B 、15克C 、17克D 、19克4、香港于1997年7月1日成为中华人民共和国的一个专门行政区,它的区徽图案(紫荆花)如图1,那个图形( ) A 、是轴对称图形 B 、是中心对称图形 C 、既是轴对称图形,也是中心对称图形D 、既不是轴对称图形,也不是中心对称图形5、下列每张方格纸上都画有一个圆,只用不带刻度的直尺就能确定圆心位置的是( )6、某校组织学生进行社会调查,并对学生的调查报告进行了评比,分数大于或等于80分为优秀,且分数为整数,现将某年级60篇学生调查报告的成绩进行整理,分成5组画出频率分布直方图(如图2),已 知从左至右4个小组的频率分别是0.05,0.15,0.35,0.30. 那么在这次评比中被评为优秀的调查报告有( ) A 、27篇 B 、21篇 C 、18篇 D 、9篇 7、如图3所示,S 、R 、Q 在AP 上,B ,C ,D ,E 在AF 上,其中BS ,CR ,DQ ,EP 皆垂直于AF ,且AB =BC =CD =DE ,若PE =2m ,则BS +CR +DQ 的长是( )A 、23mB 、2mC 、25m D 、3m8、如图4所示,棋盘上有A 、B 、C 三个黑子与P 、Q 两个 白子,要使△ABC ∽△RPQ ,则第三个白子R 应放的位 置能够是( )A 、甲B 、乙C 、丙D 、丁9、如图5,MN 为⊙O 的切线,A 为切点,过A 点作AP ⊥MN ,交⊙O 的弦BC 于点P ,若PA =2cm ,PB =5cm ,PC =3cm ,那么⊙O 的直径等于( )A 、9cmB 、219cmC 、15cmD 、215cm10、在平面直角坐标系中,若一个点的横坐标与纵坐标互为相反数,则该点一定答题表二不在( )A 、直线y =x 上B 、直线y =-x 上C 、抛物线y =x 2上D 、双曲线y =x1上二、填空题(本题有5小题,每题3分,共15分)请把答案填在答题表二内相应的题号下,否则不计分。
11、一粒纽扣式电池能够污染60升水,某市每年报废的纽扣式电池有近10000000粒,假如废旧电池不回收,一年报废的纽扣式电池所污染的水约 升.(用科学记数法表示). 12、如图6,在菱形ABCD 中,AE ⊥BC 于E ,EC =1,cos ∠B =135, 则那个菱形的面积是 .13、如图7,AB 是⊙O 的直径,C 、D 、E 差不多上⊙O 上的点,则∠1+∠2= .14、二次函数y =x 2+bx +c 的图象如图8所示,则函数值y <0时,对应x 的取值范畴是 . 15、把正方形ABCD 沿对角线AC 的方向移动到正方形A ′B ′C ′D ′的位置,它们的重叠部分(图9中的阴影部分)的面积是正方形ABCD 面积的一半,若AC =2,则正方形移动的距离A ′A 的长是 .三、解答题(本部分共7题,其中第16、17题每题6分,第18、19、20、21题每题8分,第22题11分,共55分)16、运算:121)2(2)31(1-+︒-+---π解:原式=17、解方程组 ⎩⎨⎧=+=-12202xy x y x解:18、关于x 的方程kx 2+(k +1)x +4k=0有两个不相等的实数根.(1)求k 的取值范畴.(2)是否存在实数k ,使方程的两个实数根的倒数和等于0?若存在,求出k 的值;若不存在,说明理由. 解:19、已知:如图10,在Rt △ABC 中,∠ACB =90°, AC =BC ,D 为BC 的中点,CE ⊥AD 于E ,BF ∥AC交CE 的延长线于F .求证:AB 垂直平分DF .证明:20、商场销售某种商品,一月份销售了若干件,共获利润30000元,二月份把这种商品的单价降低了0.4元,但销售量比一月份增加了5000件,从而获得的利润比一月份多2000元,求调价前每件商品的利润是多少元?解:21、下表是小明同学填写实习报告的部分内容:已知:s解:in=.7313,cos=.68222、已知抛物线c bx ax y ++=2)0(<a 与x 轴交于A 、B 两点,点A 在x 轴的负半轴上,点B 在x 轴的正半轴上,又此抛物线交y 轴于点C ,连AC 、BC ,且满足△OAC 的面积与△OBC 的面积之差等于两线段OA 与OB 的积(即S △OAC -S △OBC =OA ·OB ). (1)求b 的值;(2)若tan ∠CAB =21,抛物线的顶点为点P ,是否存在如此的抛物线,使得△PAB 的外接圆半径为413?若存在,求出如此的抛物线的解析式;若不存在,请说明理由.解:初三数学综合测试评分参考一、选择题(每小题3分,满分共30分)1、D2、D3、C4、D5、A6、A7、D8、D9、B 10、D 二、填空题(每小题3分,满分共15分) 11、6×108; 12、)4375.2(1639或 13、90o 14、13<<-x 15、12- 三、解答题16、原式12123+++-= 3分 =5 6分17、解:⎩⎨⎧=+=-12202xy x y x由①得x y =代入②得 12222=+x x 2分 即 42=x 2±=∴x 4分 得2±=y即原方程组的解为⎩⎨⎧==22y x 或⎩⎨⎧-=-=22y x 6分18、解:(1)由题意知,k ≠0,且044)1(2>⋅-+=∆kk k 2分21->∴k ,且0≠k 4分 (2)不存在 5分 设方程的两个根是1x ,2x04121≠=x x 011212121=⋅+=+∴x x x x x x 021=+∴x x 6分kk x x 121+-=+ 01=+∴k ,即211-<-=k∴满足条件的实数k 不存在。
8分19、证明,∵∠ACB=90o ,CE ⊥AD ,∴∠CAD=∠BCF 2分 又∵BF ∥AC ,∴∠FBC=∠DCA=90o ,而AC=BC ∴△FBC ≌△DCA∴FB=CD 4分 又∵D 是BC 的中点,∴CD=DB故DB=FB ,即△DBF 为等腰三角形 6分 又由AC=BC 知 ∠CAB=∠CBABF ∥AC 知 ∠CAB=∠ABF故∠CBA=∠ABF (说明:此处学生若从 ∠CBA=∠ABF=45︒ 来论证可酌情给分 ) 即AB 为等腰三角形DBF 的顶角平分线∴AB 垂直平分DF 8分 20、解:设调价前每件商品的利润是x 元 依题意得:5000300004.020*******=--+xx 3分整理得:012452=--x x0)65)(2(=+-x x21=x 562-=x 5分经检验 21=x ,562-=x 均为方程的根562-=x 不合题意,舍去 7分答:调价前每件商品的利润为2元 8分21、解:测得三个数据:DC=5m ,∠α=45°,∠β=47°设x HG = 1分 在Rt △CHG 中47cot ⋅=x CG 3分在Rt △DHM 中545cot )5(-=⋅-=x x DM ,∵ CG DM =∴ 547cot -=⋅x x5分︒-=47cot 15x 6分0675.05=)(07.74m =答:铁塔顶端到山底的高为m 07.74 8分22、解:(1)设)0(,1x A 、)0,(2x B ,由题设可求得C 点的坐标为(0,c ),且0,021><x x ,0,0>∴<c a 由S △AOC - S △BOC =OA ·OB 得:21212121x x c x c x -=--2分 得:a ca b c =-)(21 3分得:b=–2 4分 (2)设抛物线的对称轴与x 轴交于点M ,与△PAB 的外接圆交于点N 。
∵tan ∠CAB=21, ∴OA=2·OC=2c, ∴A 点的坐标为(-2c,0) 5分 ∵A 点在抛物线上,∴ca c x ax y y c x 4520.22-=+-==-=得代入 6分 又1x 、2x 为方程022=+-c x ax 的两根, ∴a a b x x 221=-=+,即:c a x c 58222-==+- c x 522=∴ 7分∴B 点的坐标为(c 52,0) ∴顶点P 的坐标为(-c 54,59c) 8分由相交弦定理得:AM .BM=PM .MN又∵512c AB = ∴AM=BM=c 56,c PM 59=∴)59213(59)56(2c c c -= 10分∴25=c ,21-=a∴所求抛物线的函数解析式是:252212+--=x x y 11分。
