《99×99乘法表(让你的孩子更加优异-可以总结很多规律)》
九九乘法口诀表(可直接打印)-九九乘法口打印之令狐文艳创作

九九乘法口诀表令狐文艳1×1=11×2=22×2=41×3=32×3=63×3=91×4=42×4=83×4=124×4=161×5=52×5=103×5=154×5=205×5=251×6=62×6=123×6=184×6=245×6=306×6=36令狐文艳创作1×7=72×7=143×7=214×7=285×7=356×7=427×7=491×8=82×8=163×8=244×8=325×8=406×8=487×8=568×8=641×9=92×9=183×9=274×9=365×9=456×9=547×9=638×9=729×9=81九九乘法口诀表一一得一一二得二二二得四一三得三二三得六三三得九一四得四二四得八三四十二四四十六一五得五二五一十三五十五四五二十五五二十五一六得六二六十二三六十八四六二十四五六三十六六三十六令狐文艳创作一七得七二七十四三七二十一四七二十八五七三十五六七四十二七七四十九一八得八二八十六三八二十四四八三十二五八四十六八四十八七八五十六八八六十四一九得九二九十八三九二十七四九三十六五九四十五六九五十四七九六十三八九七十二九九八十一令狐文艳创作。
99乘以99的简便方法

99乘以99的简便方法
要计算99乘以99,我们可以利用一些简便的方法来快速得出结果。
下面我将介绍一种简便的方法,希望对大家有所帮助。
首先,我们知道99乘以99等于(100-1)乘以(100-1)。
这里的关键在于将99拆分成100和1的差。
这样我们就可以利用分配律来进行计算。
首先,我们计算100乘以100,结果是10000。
然后,我们计算100乘以-1,结果是-100。
接着,我们计算-1乘以100,结果也是-100。
最后,我们计算-1乘以-1,结果是1。
接下来,我们将这些结果相加,10000+(-100)+(-100)+1=9801。
所以,99乘以99的结果是9801。
通过这种简便的方法,我们可以快速得出99乘以99的结果,而不必进行繁琐的手工计算。
希望这种方法对大家有所帮助。
总结一下,我们可以利用(100-1)乘以(100-1)的形式来计算99乘以99,通过分配律和加法运算,可以快速得出结果。
希望这个简便的方法能够帮助大家更轻松地进行乘法计算。
希望本文所介绍的方法对大家有所帮助,让大家能够更轻松地进行99乘以99的计算。
祝大家数学学习进步,谢谢!。
小99乘法口诀表

小99乘法口诀表小99乘法口诀表,又称“小乘乘法表”,是一种有用的乘法计算方法,它包含 0 9 九个乘法数,每一行代表一个数的乘法。
计算结果的低位在底下,高位在上面,一目了然。
一般从把一数从1乘到9为主,通过高度有规律的乘法推算,可以做到快速计算,比如 2*3 、6*7。
“小乘乘法表”是一种智力训练的好工具,对培养孩子对数学问题的兴趣和能力有帮助。
学习这种计算方法可以让孩子更加熟练地掌握九乘九以内的数学计算,让孩子在学习中不要手忙脚乱,养成科学、规范的习惯。
小99乘法口诀表的九乘九,是由9个数,从1到9组成的,九乘九的组合形式如下:1*1=1 2*1=2 3*1=3 4*1=4 5*1=5 6*1=6 7*1=7 8*1=8 9*1=92*2=4 3*2=6 4*2=8 5*2=10 6*2=12 7*2=14 8*2=16 9*2=183*3=9 4*3=12 5*3=15 6*3=18 7*3=21 8*3=24 9*3=27 4*4=16 5*4=20 6*4=24 7*4=28 8*4=32 9*4=365*5=25 6*5=30 7*5=35 8*5=40 9*5=456*6=36 7*6=42 8*6=48 9*6=547*7=49 8*7=56 9*7=638*8=64 9*8=729*9=81小99乘法口诀表,能够帮助将来学习数学的孩子做到记忆口诀,方便快捷地掌握九乘九以内的乘法运算,为他们日后学习更复杂的数学知识打下基础。
九乘九以内的乘法,按照九乘九口诀表的推算方式:第一步,先将九乘九的每一行的加法结果都口诀出来;第二步,记住每一行的乘数,先将乘数记住;第三步,可以从第二组乘数开始,记住所有乘数,按照九乘九口诀表规律,将所有乘积都口诀出来。
举个例子:2×7=14以按照口诀表拆分成 2×6=12,加上 2×1=2,即可推出 2×7=14,让孩子们可以通过推理,自己推出这些乘法结果,而不用完全依赖于记忆。
大99X99乘法口诀表
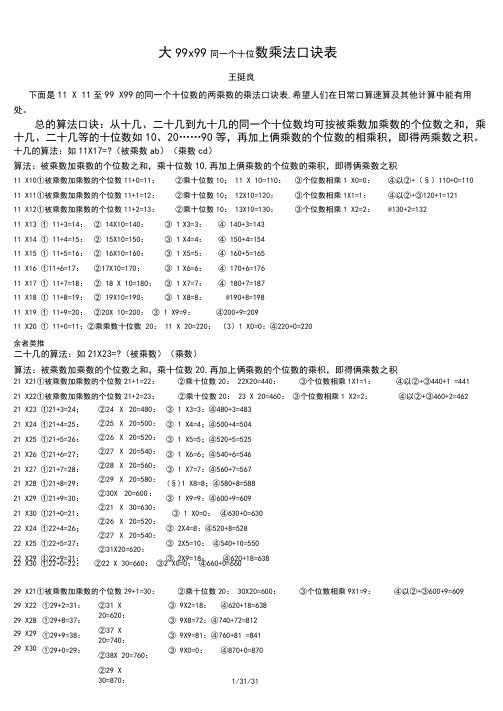
大99x99同一个十位数乘法口诀表王挺良下面是11 X 11至99 X99的同一个十位数的两乘数的乘法口诀表,希望人们在日常口算速算及其他计算中能有用处。
总的算法口诀:从十几、二十几到九十几的同一个十位数均可按被乘数加乘数的个位数之和,乘十几、二十几等的十位数如10、20……90等,再加上俩乘数的个位数的相乘积,即得两乘数之积。
十几的算法:如11X17=?(被乘数ab)(乘数cd)算法:被乘数加乘数的个位数之和,乘十位数10,再加上俩乘数的个位数的乘积,即得俩乘数之积11 X10①被乘数加乘数的个位数11+0=11:②乘十位数10; 11 X 10=110:③个位数相乘1 X0=0:④以②+(§)110+0=110 11 X11①被乘数加乘数的个位数11+1=12:②乘十位数10; 12X10=120:③个位数相乘1X1=1:④以②+③120+1=12111 X12①被乘数加乘数的个位数11+2=13:②乘十位数10: 13X10=130:③个位数相乘1 X2=2:@130+2=13211 X13 ① 11+3=14:② 14X10=140:③ 1X3=3:④ 140+3=14311 X14 ① 11+4=15:② 15X10=150:③ 1X4=4:④ 150+4=15411 X15 ① 11+5=16:② 16X10=160:③ 1X5=5:④ 160+5=16511 X16 ①11+6=17:②17X10=170:③ 1X6=6:④ 170+6=17611 X17 ① 11+7=18:② 18 X 10=180:③ 1X7=7:④ 180+7=18711 X18 ① 11+8=19:② 19X10=190:③ 1X8=8:@190+8=19811 X19 ① 11+9=20:②20X 10=200:③ 1 X9=9:④200+9=20911 X20 ① 11+0=11:②乘乘数十位数 20: 11 X 20=220:(3)1 X0=0:④220+0=220余者类推二十几的算法:如21X23=?(被乘数)(乘数)算法:被乘数加乘数的个位数之和,乘十位数20,再加上俩乘数的个位数的乘枳,即得俩乘数之积21 X21①被乘数加乘数的个位数21+1=22:②乘十位数20: 22X20=440:③个位数相乘1X1=1:④以②+③440+1 =44121 X22①被乘数加乘数的个位数21+2=23:②乘十位数20: 23 X 20=460:③个位数相乘1 X2=2:④以②+③460+2=46221 X23 ①21+3=24;21 X24 ①21+4=25:21 X25 ①21+5=26:21 X26 ①21+6=27:21 X27 ①21+7=28:21 X28 ①21+8=29:21 X29 ①21+9=30:21 X30 ①21+0=21:22 X24 ①22+4=26;22 X25 ①22+5=27:22 X29 ①22+9=31:②24 X 20=480:②25 X 20=500:②26 X 20=520:②27 X 20=540:②28 X 20=560:②29 X 20=580:②30X 20=600:②21 X 30=630:②26 X 20=520:②27 X 20=540:②31X20=620:③ 1 X3=3:④480+3=483③ 1 X4=4;④500+4=504③ 1 X5=5;④520+5=525③ 1 X6=6;④540+6=546③ 1 X7=7:④560+7=567(§)1 X8=8;④580+8=588③ 1 X9=9:④600+9=609③ 1 X0=0:④630+0=630③ 2X4=8:④520+8=528③ 2X5=10:④540+10=550③ 2X9=18:④620+18=63822 X30 ①22+0=22:②22 X 30=660:③2 X0=0:④660+0=66029 X21①被乘数加乘数的个位数29+1=30:②乘十位数20: 30X20=600:③个位数相乘9X1=9:④以②+③600+9=60929 X22 29 X28 29 X29 29 X30 ①29+2=31:①29+8=37:①29+9=38:①29+0=29:②31 X20=620:②37 X20=740:②38X 20=760:②29 X③ 9X2=18:④620+18=638③ 9X8=72:④740+72=812③ 9X9=81:④760+81 =841③ 9X0=0:④870+0=870余者类推三十几的算法:如33X36=?(被乘数)(乘数)算法:被乘数加乘数的个位数之和,乘十位数30,再加上俩乘数的个位数的乘积,即得俩乘数之积33 X39①个位相加33+9=42—@乘十位数30: 42X30=1260—加上③个位数相乘3 X9=27④等于128733 X40 ①33+0=3 J②33 X 40=1320—力口上③3 X0=0:等于 132034 X36 ①34+6=4 J②40 X30=1200—加上@4 X6=24 等于 122438 X33 ①38+3=41^)41 X30=1230—加上③8 X3=24 等于 125438 X39 ©38+9=47-^2)47 X30=1410—加上③8 X9=72 等于 148239 X39 ①39+9=48—②48 X30=1440—加上③9 X9=81 等于 1521四十几的算法:如45X46=?(被乘数)(乘数)算法:被乘数加乘数的个位数之和,乘十位数40,再加上俩乘数的个位数的乘积,即得俩乘数之积45 X46①个位相加45+6=51乘乘数十位数40: 51 X 40=2040—加上③个位数相乘5 X6=30:等于207046 X47 Q:M6+7=53^g)53 X40=2120—加上③6 X7=42 等于 216248 X49 ①48+9=57—@57 X40=2280—加上③8 X9=72 等于 235249 X49 ①49+9=5 J②58 X40=2320—加上③9 X9=81 等于 2401五十几的算法:如57X54=?(被乘数)(乘数)算法:被乘数加乘数的个位数之和,乘十位数50,再加上俩乘数的个位数的乘积,即得俩乘数之枳53 X54①个位相加53+4=57―②乘乘数十位数50: 57 X 50=2850—加上③个位数相乘3 X4=12:等于286257 X54 ①57+4=61—@61 X50=3050—加上③7 X4=28 等于 307857 X56 ①57+6=6 J②63 X50=3150—加上③7 X6=42 等于 319259 X58 ①59+8=67—@67 X50=3350—加上③9 X8=72 等于 342259 X59 ①59+9=6 J②68 X50=3400—加上③9 X9=81 等于 3481六十几的算法:如67X66=?(被乘数)(乘数)算法:被乘数加乘数的个位数之和,乘十位数60,再加上俩乘数的个位数的乘枳,即得俩乘数之积61 X64①个位相加61+4=6D乘乘数十位数60: 65 X 60=3900—加上③个位数相乘1 X4=4:等于3904 66X65①66+5=71-@71 X60=4260—加上③6 X5=30 等于 429067 X66 ① 67+6=7J②67 X60=4020—加上③ 7 X6=42 等于 406269 X69 C069+9=78-X?)78 X60=4680—加上③9 X9=81 等于 4761七十几的算法:如77X75=?(被乘数)(乘数)算法:被乘数加乘数的个位数之和,乘十位数70,再加上俩乘数的个位数的乘积,即得俩乘数之积73 X74①个位相加73+4=77—②乘乘数十位数70: 77 X 70=5390—加上③个位数相乘3 X4=12:等于540277 X75 ①77+5=82-82 X70=5740—加上③7 X5=35 等于 577577 X76 ①77+6=8 J②83 X70=5810—加上③7 X6=42 等于 585279 X78 ①79+8=87i87 X70=6090—加上③9 X8=72 等于 616279 X79 ①79+9=8 J②88X70=6160—加上③9X9=81 等于 6241八十几的算法:如87X85=?(被乘数)(乘数)算法:被乘数加乘数的个位数之和,乘十位数80,再加上俩乘数的个位数的乘积,即得俩乘数之积82 X84①个位相加82+4=86—②乘乘数十位数80: 86 X 80=6880—加上③个位数相乘2 X4=8:等于688887 X85 ①87+5=92-92 X80=7360—加上③7 X5=35 等于 739588 X86 ①88+6=94一②94 X80=7520—加上③8 X6=48 等于 756889 X89①个位相加89+9=98—②乘十位数80: 98 X80=7840—加上③个位数相乘9 X9=81等于7921九十几的算法:如94X92=?(被乘数)(乘数)算法:被乘数加乘数的个位数之和,乘十位数90,再加上俩乘数的个位数的乘积,即得俩乘数之积94 X92①个位相加94+2=96—②乘乘数十位数90: 96 X 90=8640—加上③个位数相乘4 X2=8:等于864895 X96 0)95+6=101—@101 X90=9090—力口上③5 X6=30 等于 912095 X97 ©95+7=102—02 X90=9180—加上③5 X7=35 等于 921599 X98 (099+8=107—@107 X90=9630—加上③9X8=72 等于 970299 X99 ①99+9=108一②108X90=9720—加上③9X9=81 等于 980199 X100①99+0=99—②99 X100=9900—加上③个位数相乘9 X0=0等于9900限于篇幅,余者未列入,算法完全可按上述口诀进行计算。
九九乘法口诀表(超清晰打印版

九九乘法口诀表(超清晰打印版一、概述:九九乘法口诀是初中和小学数学中最基础的内容之一,是大多数数学问题的根源和出发点。
通过记忆九九乘法口诀表,可以较为方便地计算各种数字的乘积,对于小学生、初中生以及其他学习数学的人来说都具有重要意义。
二、九九乘法口诀表:1.1×1=11×2=2 2×2=41×3=3 2×3=6 3×3=91×4=4 2×4=8 3×4=12 4×4=161×5=5 2×5=10 3×5=15 4×5=20 5×5=251×6=6 2×6=12 3×6=18 4×6=24 5×6=30 6×6=361×7=7 2×7=14 3×7=21 4×7=28 5×7=35 6×7=427×7=491×8=8 2×8=16 3×8=24 4×8=32 5×8=40 6×8=487×8=56 8×8=641×9=9 2×9=18 3×9=27 4×9=36 5×9=45 6×9=547×9=63 8×9=72 9×9=81三、九九乘法口诀的重要性:1.九九乘法口诀是数学基础。
数学是一门重要的学科,而九九乘法口诀是数学学科的基石。
如果没有掌握九九乘法口诀,学习数学将会变得困难,可能会导致整个学习计划的失败。
2.九九乘法口诀是逻辑思维的必备知识。
学会九九乘法口诀可以培养刻苦认真、耐心细致的好习惯,并能培养自己的逻辑思维能力。
3.九九乘法口诀可以帮助解决实际问题。
99乘法表 九九乘法表 99乘法表全表

九九乘法表 99乘法表全表 99乘法表1×1=11×2=2 2×2=41×3=3 2×3=6 3×3=91×4=4 2×4=8 3×4=12 4×4=161×5=5 2×5=10 3×5=15 4×5=20 5×5=251×6=6 2×6=12 3×6=18 4×6=24 5×6=30 6×6=361×7=7 2×7=14 3×7=21 4×7=28 5×7=35 6×7=42 7×7=491×8=8 2×8=16 3×8=24 4×8=32 5×8=40 6×8=48 7×8=56 8×8=641×9=9 2×9=18 3×9=27 4×9=36 5×9=45 6×9=54 7×9=63 8×9=72 9×9=81口诀表一一得一一二得二二二得四一三得三二三得六三三得九一四得四二四得八三四十二四四十六一五得五二五一十三五十五四五二十五五二十五一六得六二六十二三六十八四六二十四五六三十六六三十六一七得七二七十四三七二十一四七二十八五七三十五六七四十二七七四十九一八得八二八十六三八二十四四八三十二五八四十六八四十八七八五十六八八六十四一九得九二九十八三九二十七四九三十六五九四十五六九五十四七九六十三八九七十二九九八十。
99×99乘法表让你的孩子更加优异可以总结很多规律(完整版)

•
當然人生裡還是有很多事是無法做到的,就像
數學裡也是有許多世紀難題是還無法解決的,窮其
一生也無法解決,也不用抱著遺憾啦,因為人畢竟
ห้องสมุดไป่ตู้
是能力有限的。
•
• 98*97=(100-2)*97 • =9700-97*2 • =9700-194 • =9506
• 55*45=(50+5)*45 • =50*45+5*45 • =2250+225 • =2475
9mX9n用離100差較多的數減另一數 離100差數x100加離100兩差數積
• 像99x98,99比較接近100,而且差1,而 98是差2,所以99x98=(981)00+(1x2)=9702
• 96x92,就會是(92-4)00+(4x8)=8832
• 91x95=(91-5)00+(5x9)=8645(大數95離100 差5)
• 88x86=(8612)00+(12x14)=7400+168=7568 (大數88 離100差12)
• 當然如果你九九乘法表可以背到比較大的 數字時,你運算的範圍就會增大,不然你
• 計算101x101時先去算11x11會得121,在 從中插0進去,所以得10201
• 同樣102x102,因為12x12=144,所以答案 會是10404
掉了。整個過程我也並不是很順利啊,經過了好幾
個波折,人生亦是如此,不可能事事順利的,可怕
的不是遇到了問題,而是不去面對問題。
• 在做數學裡我常做的一件事,跟之前貼的一則笑話 很像,就是一位數學家去應徵消防員工作的。我會 把一些問題去化整為零成一些自己能應付或應付起 來得心應手的方法來做,也就是指變成自己以前解 決過解決到不想再解決的方法來做,那很多事情就 可以慢慢的去完成了。
99乘法表学习攻略:快速记忆技巧

99乘法表学习攻略:快速记忆技巧一、按顺序背诵必不可少。
这对于绝绝大部分学生来说应该不是难点。
中国人学乘法可谓是独具优势,因为发音简单,因而琅琅上口,对于文化水准欠缺的老年人尚能使用自如,更何况我们这个代见多识广的小学生呢。
二、理解口诀的意义。
在学习了乘法的意义之后,相信学生们对口诀的意义应该能有较好的理解,对于判断结果的大致范围会有一定的协助。
例如6×8,表示6个8或8个6连加,那么当学生背不出口诀时,可通过加法算出结果,或者通过它的意义估计出积的结果大约在50左右,继而排除一些不可能的结果,朝这个范围思考口诀。
三、推算出口诀的结果。
当学生能按顺序熟背口诀后,必然会有若干自己比较熟悉的口诀,例如:二五一十、九九八十一等,将这些口诀作为参照物,可使用推算的方法很快找到与之相邻的乘法口诀,比如:8×9的结果想不出,则可思考“9个9减去一个9”,也就是“81-9=72”,当然得出结论后不能写上72就算了,还应把“8×9”的口诀在心里默念一遍,那么多经历几次这样的思考后,“八九七十二”这句也将成为铭记于心的口诀了。
这样以点带面,从若干口诀辐射到所以口诀,效果应该会比较明显。
四、找寻积的特点。
我们还可通过积与因数的一些特点来协助学生记忆或判断结果的正误。
例如:1的口诀完全不需要过多的记忆,积与另一个因数相同;2的口诀结果都是双数,也就是学生常说的“2、4、6、8、10”;5的口诀末尾不是“5”就是“0”,看另一个因数,是双数则积的末尾是0,是单数积的末尾就是5。
再有就是根据两个因数来判断积的奇偶性,“双数×双数”积是双数,“双数×单数”积是双数,“单数×单数”积是单数。
当然这个判断方法对于二年级的学生来说无疑有些难度,适合思维拓展题,若仅仅是为了判断积的准确与否,也许孩子们并不愿意用。
五、在游戏中熟练。
我想这应该是该年龄段的学生乐于接受的一种记忆方式,因为纯粹的背显得很枯燥,多背一些孩子就会因为兴趣的降低而思维混乱、错误百出,老师能够在课堂中使用“补口诀比赛”或通过一些网络小游戏来协助学生提升兴趣。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例:63 * 35 = 60 * 30 + 60 * 5 + 30 * 3 + 3 * 5 = 1800 + 300 + 90 + 15 = 2205
再用上面這個方法算之前印度法算題
14 * 18 = 10 * 10 + 10 * 8 + 10 * 4 + 4 * 8 = 100 + 80 + 40 + 32 = 252 23 * 26 = 20 * 20 + 20 * 6 + 20 * 3 + 3 * 6 = 400 + 120 + 60 + 18 = 598
99x99
速算之接近100數字之乘法
数学的9*9乘法口诀表改为99*99口诀表!
• • • • • • • • •
算99x99時 我想到9x9=81,所以答案是9801 98x98的話8x8=64,所以答案是9604 97x97=9409因為7x7=49 那時算法是直接拿個位數來乘,得到的數字前面和中間 加入9和0進去 就可以得到我想要的答案了。 但這方法卻在算96x96時出錯了,因為6x6=36但96x96不 是9306而是9216 就這樣這方法一開始被我發現時只是拿來騙騙人,讓人 以為我會算大數的平方 這應該是發生在我高中的時候的事。
圖解式乘法
• 交叉線交叉點數法
】
• 【一位數 x 一位數】 • ‧左邊畫二條綠線代表2、右邊畫三條藍線 代表3 • • ‧二條線共有6個交叉點,即為答案 → 2x3=6
【一位數 x 一位數】
• 左邊畫二條綠線代表2、右邊畫三條藍線代表3 • • ‧二條線共有6個交叉點,即為答案 → 2x3=6
• • • • •
98*97 =(100-2)*97 =100*97-2*97 =9700-2*(100-3) =9700-200+6 =9506
• 55*45 • =5*11*9*5 =25*(100-1) =2500-25 =2475
• 98*97=(100-2)*97=9700-194=9506
• • • •
55*45 =5*11*9*5 =25*(100-1) =2500-25 =2475
• 另一種方法就是上面提到那種兩位數相乘的方 法的延伸 • 101x101=(101+1)00+1x1=10201 • 102x102=(102+2)00+2x2=10404 • 112x111=(112+11)00+11x12=12300+132=12432 •
• 要是事情就這樣結束了,我當然不會寫這blog 來獻醜啦。過後應該還是在高中的那段時間吧, 這兩位數乘以兩位數的算法終於被我找到的比 較正確的算法了。這想法是從平方差公式想到 的,什麼是平方差公式?a2-b2=(a+b)(a-b) • 因為在運算的都是90多的數字,所以我就 想到了把那些數變成了其中一個變成100來計 算。所以就會變成99x99=(1001)x99,98x98=(100-2)x98,可是這個方法又不怎 麼快,也就這樣不怎麼被我放在心上,繼續去 想其他的方法。
• 像要計算99x99,我的算法是99差1等於100,所以 向其中一個拿1過來,那另一個就剩98了,因為兩 個都差1,1x1=01,故99x99=9801 • 同理計算98x98,我的算法是98差2等於1பைடு நூலகம்0,所以 向其中一個拿2過來,那另一個就剩96了,因為兩 個都差2,2x2=04,故98x98=9604 • 97x97,我的算法是97差3等於100,所以向其中一 個拿3過來,那另一個就剩94了,因為兩個都差3, 3x3=09,故97x97=9409 • 所以96x96=(96-4)00+(4x4)=9216 • 95x95=(95-5)00+(5x5)=9025 • 94x94=(94-6)00+(6x6)=8836
• 計算101x101時先去算11x11會得121,在從 中插0進去,所以得10201 • 同樣102x102,因為12x12=144,所以答案 會是10404
• 最近做數學時常常會拿來和人生做比較,發現其實 做數學真的還蠻像人生的,很多思維方式都可以用 在生活上。雖然說並不是真的去運用了數學來解決 生活問題,但卻是運用了做數學的精神來解決生活 問題。難怪以前數學會是屬以哲學裡的一部份。 • 像這次從無到有的一個計算方式,不求助於人 自己慢慢的去想,偶爾拿出來想,最後還是被解決 掉了。整個過程我也並不是很順利啊,經過了好幾 個波折,人生亦是如此,不可能事事順利的,可怕 的不是遇到了問題,而是不去面對問題。
• A=10a2+a1, B=10b2+b1 A*B = (10a2+a1)*(10b2+b1) = 10a2*10b2 + a1*10b2 + 10a2*b1 + a1*b1 = 100a210b2 + 10(a1b2+a2b1) + a1b1 ... (1) 印度計法 S1 = 10a2+a1+b1 S2 = a1b1 Ans = S1*10 + S2 = 100a2+10(a1+b1)+a1b1 ... (2) 當a2 == b2 == 1 既時候 (1)先同(2)相通 所以呢個方法只適用於11<=A,B<=19
• 55*45=(50+5)(50-5)=2500-25=2475
• (a+b)(a-b)=a²-b²
• 98*97=(100-2)*(100-3) • =10000-300-200+6=9506 • 55*45 =(50+5)*(50-5)=50*50-5*5=2475
• • • • •
98*97 =(100-2)*97 =100*97-2*97 =9700-2*(100-3) =9700-200+6 =9506
=6
【二位數 x 二位數】
• • • • • • • • • • • • • • ‧左邊靠下畫二條綠線代表2,靠上畫三條淺綠線代表3
‧右邊靠上畫二條藍線代表2,靠下畫三條淺藍線代表3
‧所有線條組成的交叉點可區分為三部份,即個位、十位及百位數
‧每一部份的交叉點合計若超過10,即往前進一位 如範例的十位數部份共計有12個交叉點,於是進位後十位數就變成2 百位數部份原計有4個交叉點,再加上進位1後,百位數就變成5 於是就得到 23 x 23 的答案:529
• • • •
• • • •
98*97=(100-2)*97 =9700-97*2 =9700-194 =9506
55*45=(50+5)*45 =50*45+5*45 =2250+225 =2475
• 9X乘9X都得架#yup# 當97x98 因為100-98=2 100-97=3 所以98-3 =97-2=95 所以97x98 = 95*100 + (-2*-3) = 9506:) 最重要一開頭選咩做"100"呢個位置姐;-) (10 + p) x (10 + q) = 100 + 10p + 10q + p x q = 10 x (10 + p + q) + p x q p = 3, q = 2 -> 13 x 12 = (10 + 3) x (10 + 2) = 10 x (10 + 3 + 2) + (2 x 3) = 150 + 6 其實可以去到99X99 方法一同二照跟 99+99 9X9 最後係乘番你十位個數既十倍 即係咁 (99+99)X90+81=9801
• 總得來說呢,這種算法是 axb = [b-(100a)]x100+(100-a)(100-b),其中a>b。
• • • • • • •
999*999 =(1000-1)*(1000-1) =1000^2-2*1000*1+1^2 =1000000-2000+1 =998001 (a-b)*(c-d) =a*c-a*d-b*c+b*d
9mX9n用離100差較多的數減另一數 離100差數x100加離100兩差數積
• 像99x98,99比較接近100,而且差1,而98 是差2,所以99x98=(98-1)00+(1x2)=9702 • 96x92,就會是(92-4)00+(4x8)=8832 • 91x95=(91-5)00+(5x9)=8645(大數95離100差5) • 88x86=(86-12)00+(12x14)=7400+168=7568 (大數88離100差12) • 當然如果你九九乘法表可以背到比較大的 數字時,你運算的範圍就會增大,不然你 就需要紙筆了,就像上面那題88x86一樣。
• 14 * 18 = (14+8) * 10 + 4 * 8 = 220 + 32 = 252 23 * 26 = (23 + 6) * 20 + 3 * 6 = 598 以上是十位數相同時的算法....另外一個網友提出的算法也蠻快 的 1m x 1n= 10 x 10 + 10 x (m + n) + m x n am x an= a0 x a0 + a0 x (m + n) + m x n am x bn= a0 x b0 + a0 x n + b0 x m + m x n
• 在做數學裡我常做的一件事,跟之前貼的一則笑話 很像,就是一位數學家去應徵消防員工作的。我會 把一些問題去化整為零成一些自己能應付或應付起 來得心應手的方法來做,也就是指變成自己以前解 決過解決到不想再解決的方法來做,那很多事情就 可以慢慢的去完成了。 • 當然人生裡還是有很多事是無法做到的,就像 數學裡也是有許多世紀難題是還無法解決的,窮其 一生也無法解決,也不用抱著遺憾啦,因為人畢竟 是能力有限的。 •
