高一数学必修三模块测试题-(人教A版)

合集下载

人教A版高中数学必修三试卷高一：综合模块测试(18).docx

必修3综合模块测试18（人教A 版必修3）第I 卷（选择题，共42分）一.选择题（共14小题，每小题3分，共42分.在每小题给出的四个选项中，只有一项是符合题目要求的） 1．将两个数a=8,b=17交换,使a=17,b=8,下面语句正确一组是 ( )A . a=b ；b=aB . c=b ；b=a ；a=cC . b=a ；a=bD . a=c ；c=b ；b=a2. 给出以下四个问题，①输入一个数x ，输出它的相反数。

②求面积为6的正方形的周长。

③求三个数a,b,c 中的最大数。

④求函数1,0()2,0x x f x x x -≥⎧=⎨+<⎩的函数值. 其中不需要用条件语句来描述其算法的有( )A. 1个B. 2个C. 3个D. 4个 3.下列命题是真命题的是( ) ①必然事件的概率等于1，不可能事件的概率等于0 ②某事件的概率等于1.1 ③互斥事件一定是对立事件 ④概率是频率的稳定值，频率是概率的近似值 ⑤在适宜的条件下种下一粒种子，观察它是否发芽，这个试验为古典概型 A.①③ B. ①④ C.①③⑤ D.①④⑤ 4.用秦九韶算法计算多项式654323567983512)(x x x x x x x f ++++-+=在4-=x 时的值时,3V 的值为 ( )A.－845B.220C.－57D.345.用系统抽样法从编号160:的60辆车中随机抽出6辆进行试验，则可能选取的车的编号是（） A.5,10,15,20,25,30 B.3,13,23,33,43,53 C ．1,2,3,4,5,6 D ．2,4,8,16,32,486.某小组有2名男生和2名女生，从中任选2名同学去参加演讲比赛，那么互斥而不对立的两个事件是( )A ．“至少有1名女生”与“都是女生”B ．“至少有1名女生”与“至多1名女生”C ．“至少有1名男生”与“都是女生”D ．“恰有1名女生”与“恰有2名女生”7、我市对上下班交通情况作抽样调查，作出上下班时间各抽取12辆机动车行驶时速（单位：km/h ）的茎叶图（如下）：上班时间下班时间 8 1 6 7 9 8 7 6 1 0 2 2 5 7 8 6 5 3 2 0 3 0 0 2 6 7 0 4则上下班时间行驶时速的中位数分别为（）Ａ．28与28.5 Ｂ．29与28.5 Ｃ．28与27.5 Ｄ．29与27.5 8.甲，乙两人在相同条件下练习射击，每人打5发子弹，命中环数如下甲68998乙 10 7 7 7 9则两人射击成绩的稳定程度是（）。

人教版高中数学高一A版必修3模块综合测试

模块综合测评(时间：120分钟满分：150分)一、选择题(本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的)1．某学校高一年级有35个班，每个班的56名同学都是从1到56编的号码．为了交流学习经验，要求每班号码为14的同学留下进行交流，这里运用的是( )A ．分层抽样B ．抽签抽样C ．随机抽样D ．系统抽样2．已知函数y ＝⎩⎪⎨⎪⎧lg x ，x ＞0，2x ，x ≤0，输入自变量x 的值，输出对应函数值的算法中所用到的基本逻辑结构是( )A ．顺序结构B ．顺序结构、条件结构C ．条件结构D ．顺序结构、条件结构、循环结构3．用秦九韶算法计算当x ＝0.4时，多项式f (x )＝3x 6＋4x 5＋6x 3＋7x 2＋1的值时，需要做乘法运算的次数是( )A ．6B ．5C ．4D ．3 4．下列说法正确的是( )A ．一个人打靶，打了10发子弹，有7发子弹中靶，因此这个人中靶的概率为710B ．一个同学做掷硬币试验，掷了6次，一定有3次“正面朝上”C ．某地发行福利彩票，其回报率为47%，有个人花了100元钱买彩票，一定会有47元的回报D ．大量试验后，可以用频率近似估计概率5．如图所示，在一个边长为2的正方形中随机撒入200粒豆子，恰有120粒落在阴影区域内，则该阴影部分的面积约为( )A ．35B ．125C ．65D ．1856．如图所示是一容量为100的样本的频率分布直方图，则由图形中的数据，样本落在[15,20]内的频数为( )A ．20B ．30C ．40D ．507．某林场有树苗30 000棵，其中松树苗4 000棵．为调查树苗的生长情况，采用分层抽样的方法抽取一个容量为150的样本，则样本中松树苗的数量为( )A ．30B ．25C ．20D ．158．在面积为S 的△ABC 的边AB 上任取一点P ，则△PBC 的面积不小于S 3的概率是( )A ．23B ．13C ．34D ．149．阅读下列程序： INPUT x IF x ＜0 THEN y ＝2 *x ＋3 ELSEIF x ＞0 THEN y ＝－2 * x ＋5 ELSE y ＝0 END IF END IF PRINT y END如果输入x ＝－2，则输出结果y 为( ) A ．0 B ．－1 C ．－2 D ．910．某程序框图如图所示，该程序运行后输出的S 的值是( )A ．－3B ．－12C ．13D ．211．如图是某年青年歌手大奖赛中，七位评委为甲、乙两名选手打出的分数的茎叶图(其中m 为数字0～9中的一个)．去掉一个最高分和一个最低分后，甲、乙两名选手得分的平均数分别为a 1，a 2，则一定有( )A ．a 1＞a 2B ．a 1＜a 2C ．a 1＝a 2D ．a 1，a 2的大小与m 的值有关12．某工厂对一批产品进行了抽样检测．下图是根据抽样检测后的产品净重(单位：克)数据绘制的频率分布直方图，其中产品净重的范围是[96,106]，样本数据分组为[96,98)，[98,100)，[100,102)，[102,104)，[104,106]，已知样本中产品净重小于100克的个数是36，则样本中净重大于或等于98克并且小于104克的产品的个数是( )A．90 B．75C．60 D．45二、填空题(本大题共4小题，每小题4分，共16分．把答案填在题中的横线上)13．抛掷一枚均匀的正方体骰子，向上的点数是奇数为事件A，事件A的对立事件是__________．14．102,238的最大公约数是________．15．某服装商场为了了解毛衣的月销售量y(件)与月平均气温x(℃)之间的关系，随机统计了某4个月的月销售量与当月平均气温，其数据如下表：由表中数据算出线性回归方程y＝b x＋a中的b≈－2.气象部门预测下个月的平均气温均为6 ℃，据此估计，该商场下个月毛衣的销售量均为__________件．16．某单位200名职工的年龄分布情况如图所示，现要从中抽取40名职工作样本，用系统抽样法，将全体职工随机按1～200编号，并按编号顺序平均分为40组(1～5号，6～10号，…，196～200号)．若第5组抽出的号码为22，则第8组抽出的号码应是__________．若用分层抽样方法，则40岁以下年龄段应抽取__________人．三、解答题(本大题共6小题，共74分．解答时应写出必要的文字说明、证明过程或演算步骤)17．(本小题满分12分)有一段长为11米的木棍，现要折成两段，每段不小于3米的概率有多大？18．(本小题满分12分)某班50名同学参加数学测验，成绩的分组及各组的频数如下：[40,50),2；[50,60),3；[60,70),10；[70,80),15；[80,90),12；[90,100),8.(1)列出样本的频率分布表；(2)画出频率分布直方图．19．(本小题满分12分)对某400件元件进行寿命追踪调查，情况分布如下：寿命(h)频率[500,600)0.10[600,700)0.15[700,800)0.40[800,900)0.20[900,1 000]0.15合计 1(1)列出寿命与频数对应表；(2)计算元件寿命在[500,800) h以内的频率．20．(本小题满分12分)由世界自然基金会发起的“地球1小时”活动，已发展成为最有影响力的环保活动之一，今年的参与人数再创新高．然而也有部分公众对该活动的实际效果与负面影响提出了疑问，对此，某新闻媒体进行了网上调查，所有参与调查的人中，持“支持”、“保留”和“不支持”态度的人数如下表所示：(1)在所有参与调查的人中，用分层抽样的方法抽取n个人，已知从“支持”态度的人中抽取了45人，求n的值；(2)在持“不支持”态度的人中，用分层抽样的方法抽取5人看成一个总体，从这5人中任意选取2人，求至少有1人20岁以下的概率；(3)在接受调查的人中，有8人给这项活动打出的分数如下：9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2.把这8个人打出的分数看作一个总体，从中任取1个数，求该数与总体平均数之差的绝对值超过0.6的概率．21．(本小题满分12分)随机抽取某中学甲、乙两班各10名同学，测量他们的身高(单位：cm)，获得身高数据的茎叶图如图所示．(1)根据茎叶图判断哪个班的平均身高较高；(2)计算甲班的样本方差；(3)现从乙班这10名同学中随机抽取两名身高不低于173 cm的同学，求身高为176 cm 的同学被抽中的概率．22．(本小题满分14分)(2012·陕西高考，文19)假设甲乙两种品牌的同类产品在某地区市场上销售量相等，为了解它们的使用寿命，现从这两种品牌的产品中分别随机抽取100个进行测试，结果统计如下：甲品牌乙品牌(1)估计甲品牌产品寿命小于200小时的概率；(2)这两种品牌产品中，某个产品已使用了200小时，试估计该产品是甲品牌的概率．参考答案一、1．解析：由于分段间隔相等，是系统抽样．答案：D 2．B 3．A 4．D5．解析：阴影部分的面积约为120200×22＝125.答案：B6．解析：样本落在[15,20]内的频率是1－5(0.04＋0.1)＝0.3，则样本落在[15,20]内的频数为0.3×100＝30.答案：B7．解析：抽样比是15030 000＝1200，则样本中松树苗的数量为1200×4 000＝20.答案：C 8．答案：A解析：如图，设点P 为AB 的靠近点B 的三等分点，要使△PBC 的面积不小于3S，则点P 只能在AP 上选取，由几何概型的概率公式，得所求的概率为2233AB AP AB AB ==.9．解析：输入x ＝－2，则x ＝－2＜0成立，则y ＝2×(－2)＋3＝－1，则输出－1. 答案：B10．解析：该程序框图的运行过程是： S ＝2，i ＝1 i ＝1≤2 010成立S ＝1＋21－2＝－3 i ＝1＋1＝2 i ＝2≤2 010成立 S ＝1＋(－3)1－(－3)＝－12i ＝2＋1＝3 i ＝3≤2010成立 S ＝1＋⎝⎛⎭⎫－121－⎝⎛⎭⎫－12＝13i ＝3＋1＝4 i ＝4≤2 010成立 S ＝1＋131－13＝2i ＝4＋1＝5 ……对于判断框内i 的值，n ∈N ，当i ＝4n ＋1时，S ＝2；当i ＝4n ＋2时，S ＝－3；当i ＝4n ＋3时，S ＝－12；当i ＝4n ＋4时，S ＝13.由于2 011＝4×502＋3，则S ＝－12.该程序框图中含有当型循环结构，判断框内的条件不成立时循环终止，即i＝2 011时开始不成立，输出S ＝－12.答案：B11．解析：去掉一个最高分和一个最低分后，甲选手得分是81,85,85,84,85，则平均数是a 1＝15(81＋85＋85＋84＋85)＝84；乙选手得分是84,84,86,84,87，则平均数是a 2＝15(84＋84＋86＋84＋87)＝85＞84，所以a 1＜a 2.答案：B12．解析：设样本容量是n ，产品净重小于100克的概率为(0.050＋0.100)×2＝0.300，已知样本中产品净重小于100克的个数是36，则36n ＝0.300，所以n ＝120.净重大于或等于98克并且小于104克的产品的频率为(0.100＋0.150＋0.125)×2＝0.75.所以样本中净重大于或等于98克并且小于104克的产品的个数是120×0.75＝90. 答案：A二、13．向上的点数是偶数14．解析：利用辗转相除法或更相减损术可得最大公约数是34. 答案：3415．解析：x ＝10，y ＝38，回归直线必过点(x ，y )，则有38＝－2×10＋a ^，解得a ^＝58，所以回归方程为y ^＝－2x ＋58，当x ＝6时，y ^＝－2×6＋58＝46.答案：1616．解析：用系统抽样，由分组可知，抽样的间隔为5，又因为第5组抽出的号码为22，所以第6组抽出的号码为27，第7组抽出的号码为32，第8组抽出的号码为37. 若用分层抽样方法，40岁以下年龄段的职工数为200×0.5＝100，则应抽取的人数为40200×100＝20人．答案：37 20三、17．分析：从每一个位置折断都是一个基本事件，基本事件有无限多个，但在每一处折断的可能性相等，故是几何概型．解：记“折得两段都不小于3米”为事件A ，从木棍的两端各度量出3米，这样中间就有11－3－3＝5(米)，在中间的5米长的木棍上任何一个位置折都能满足条件，所以P (A )＝11－3－311＝511. 18．答案：解：(1)频率分布表如下：(2)频率分布直方图如图所示．19．分析：(1)频率×400＝对应寿命组的频数；(2)转化为求互斥事件的频率．解：(1)由于频率＝频数样本容量，每组的频数＝频率×400，计算得寿命与频数对应表：(2)设“元件寿命在[500,600) h 以内”为事件A ，“元件寿命在[600,700) h 以内”为事件B ，“元件寿命在[700,800) h 以内”为事件C ，“元件寿命在[500,800) h 以内”为事件D ，则事件A ，B ，C 两两互斥，且D ＝A ＋B ＋C ，由题意，得P (A )＝0.10，P (B )＝0.15，P (C )＝0.40，则P (D )＝P (A )＋P (B )＋P (C )＝0.10＋0.15＋0.40＝0.65，即元件寿命在[500,800) h 以内的频率为0.65.20．答案：解：(1)由题意得800＋10045＝800＋450＋200＋100＋150＋300n ，所以n ＝100.(2)设所选取的人中，有m 人20岁以下，则200200＋300＝m5，解得m ＝2.也就是20岁以下抽取了2人，另一部分抽取了3人，分别记作A 1，A 2；B 1，B 2，B 3，则从中任取2人的所有基本事件为(A 1，B 1)，(A 1，B 2)，(A 1，B 3)，(A 2，B 1)，(A 2，B 2)，(A 2，B 3)，(A 1，A 2)，(B 1，B 2)，(B 2，B 3)，(B 1，B 3)共10个．其中至少有1人20岁以下的基本事件有7个：(A 1，B 1)，(A 1，B 2)，(A 1，B 3)，(A 2，B 1)，(A 2，B 2)，(A 2，B 3)，(A 1，A 2)，所以从中任意抽取2人，至少有1人20岁以下的概率为710. (3)总体的平均数为x ＝18(9.4＋8.6＋9.2＋9.6＋8.7＋9.3＋9.0＋8.2)＝9，那么与总体平均数之差的绝对值超过0.6的数只有8.2，所以该数与总体平均数之差的绝对值超过0.6的概率为18. 21．分析：(1)茎叶图中的数据越集中在上部，则说明该班的平均身高较高；(2)先求出平均数，再代入方差公式即可；(3)写出所有基本事件，再统计基本事件的总数和所求事件包含的基本事件的个数，利用古典概型计算概率．解：(1)由题中茎叶图可知：甲班身高集中于160～179 cm 之间，而乙班身高集中于170～180 cm 之间，因此乙班平均身高高于甲班．(2)甲班的平均身高为 x ＝110(158＋162＋163＋168＋168＋170＋171＋179＋179＋182)＝170，甲班的样本方差为s 2＝110[(158－170)2＋(162－170)2＋(163－170)2＋(168－170)2＋(168－170)2＋(170－170)2＋(171－170)2＋(179－170)2＋(179－170)2＋(182－170)2]＝57.2.(3)设“身高为176 cm 的同学被抽中”的事件为A ，用(x ，y )表示从乙班10名同学中抽中两名身高不低于173 cm 的同学的身高，则所有的基本事件有(181,173)，(181,176)，(181,178)，(181,179)，(179,173)，(179,176)，(179,178)，(178,173)，(178,176)，(176,173)，共10个基本事件，而事件A 含有(181,176)，(179,176)，(178,176)，(176,173)，共4个基本事件，故P (A )＝410＝25. 22．答案：解：(1)甲品牌产品寿命小于200小时的频率为5＋20100＝14，用频率估计概率，所以，甲品牌产品寿命小于200小时的概率为14.(2)根据抽样结果，寿命大于200小时的产品有75＋70＝145个，其中甲品牌产品是75个，所以在样本中，寿命大于200小时的产品是甲品牌的频率是75145＝1529，用频率估计概率，所以已使用了200小时的该产品是甲品牌的概率为1529.。

人教版高中数学高一A数学必修3测试卷(一)

高中同步测试卷(一)单元检测算法与程序框图 (时间：120分钟，满分：150分)一、选择题(本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的)1．下列关于程序框图的说法正确的是( ) A ．程序框图是描述算法的图形语言B ．在程序框图中，一个判断框最多只能有两个退出点C ．程序框图虽可以描述算法，但不如用自然语言描述算法直观D ．程序框图和流程图不是一个概念 2．已知如图是算法程序框图的一部分其中含条件结构的是( )A ．①②B ．①③C ．②③D ．①②③3．在如图所示的程序框图中，若输入m ＝4，n ＝10，则输出a ，i 的值别是( ) A ．12，4 B ．16，5 C ．20，5 D ．24，6第3题图第5题图4．下列问题中，可以只用顺序结构就能解决的是( ) A ．求关于x 的方程ax 2＋bx ＋c ＝0的根B ．求函数f (x )＝⎩⎪⎨⎪⎧x 2（x ≥0）x （x <0）的值C ．求1＋4＋7＋10＋13的值D ．求一个数x 的绝对值5．按照如图所示的程序框图运行，已知输入x 的值为1＋log 23，则输出y 的值为( ) A.112 B.38 C.712 D.1124 6．如果执行如图所示的程序框图，那么输出的S 等于( ) A ．2 550 B ．－2 550 C ．2 548 D ．－2 552第6题图第7题图7．如图所示，若f (x )＝x 2，g (x )＝log 2x ，输入x ＝0.25，则输出h (x )＝( ) A ．0.25 B ．2 C ．－2 D ．－0.258．如图所示是计算12＋14＋16＋…＋120的值的一个程序框图，其中在判断框内应填入的条件是( )A ．i ≤10B ．i >10C ．i <20D ．i >20第8题图第9题图 9．执行如图所示的程序框图，输出的S 值为( ) A ．1 B ．3 C ．7 D ．1510．阅读如下程序框图，如果输出i ＝5，那么在空白矩形框中应填入的语句为( )A ．S ＝2i －2B ．S ＝2i －1C ．S ＝2iD ．S ＝2i ＋411．若如图所示的框图所给的程序运行结果为S ＝35，那么判断框中应填入的关于k 的条件是( )A ．k ＝7?B ．k ≤6?C ．k <6?D ．k >6?第11题图第12题图12．若执行如图所示的程序框图，输出S的值为4，则判断框中应填入的条件是() A．k<14? B．k<15? C．k<16? D．k<17?题号123456789101112答案二、填空题(本大题共4小题，每小题5分，共20分．把答案填在题中横线上)13．若某程序框图如图所示，则该程序运行后输出的k的值是________．14．如图所示的程序框图是变换两个变量的值并输出，则图中①处应为________．第13题图第14题图第15题图第16题图15．阅读如图所示的程序框图，若输出S＝30，则在判断框内应填入________．16．如图所示，该程序框图运行后输出的结果为________．三、解答题(本大题共6小题，共70分．解答应写出文字说明，证明过程或演算步骤)17．(本小题满分10分)阅读如图所示的程序框图，若输出y的值为0，则输入的x值是多少？18．(本小题满分12分)设计求经过任意两点P1(x1，y1)，P2(x2，y2)的直线的斜率的算法，并画出相对应的程序框图．19.(本小题满分12分)阅读右边的程序框图，运行相应的程序，试求输出i的值．20.(本小题满分12分)给出50个数1，2，4，7，11，…，其规律是：第1个数是1，第2个数比第1个数大1，第3个数比第2个数大2，第4个数比第3个数大3，…，以此类推，要求计算这50个数的和，请画出程序框图．21．(本小题满分12分)画出求满足1×3×5×7×…×n>10 000的最小自然数n的程序框图．22．(本小题满分12分)某小区每月向居民收取卫生费，计费方法是：3人和3人以下的住户，每户收取5元；超过3人的住户，每超出1人加收1.2元．设计一个算法，根据输入的人数，计算应收取的卫生费，并画出程序框图．参考答案与解析1．[导学号10390001] 解析：选A.由于存在一种多分支判断，所以一个判断框可能有多个退出点，所以B 选项是错误的；相对于自然语言，用程序框图描述算法的优点主要就是直观、形象，容易理解，在步骤表达上简单了许多，所以C 选项是错误的；程序框图就是流程图，所以D 选项也是错误的．A 选项正确．2．解析：选C.①只含顺序结构，②③均有判断框，都含有条件结构．3．解析：选C.输入m ＝4，n ＝10，i ＝1；a ＝4×1＝4，10不能整除4，i ＝1＋1＝2；a ＝4×2＝8，10不能整除8，i ＝2＋1＝3；a ＝4×3＝12，10不能整除12，i ＝3＋1＝4；a ＝4×4＝16，10不能整除16，i ＝4＋1＝5；a ＝4×5＝20，10能整除20；输出20，5，结束．故选C.4．解析：选C.A 、B 、D 项还需用到条件结构．5．[导学号10390002] 解析：选A.因为x ＝1＋log 23＜4，所以x ＝x ＋1＝2＋log 23，所以y ＝⎝⎛⎭⎫122＋log 23＝14×13＝112. 6．解析：选C.这个程序是计算－2＋0＋2＋4＋…＋100的算法，结果为2 548.故选C. 7．[导学号10390003] 解析：选C.h (x )取f (x )与g (x )中的较小值，即h (0.25)＝min{f (0.25)，g (0.25)}，g (0.25)＝log 20.25＝－2，f (0.25)＝(14)2＝116，故选C.8．解析：选A.计算的值是10个数的和．当i ≤10时成立继续循环，当i ＝11时跳出循环体，此时输出的S 就是这10个数的和． 9．解析：选C.程序框图运行如下：k ＝0<3，S ＝0＋20＝1，k ＝1<3；S ＝1＋21＝3，k ＝2<3；S ＝3＋22＝7，k ＝3.输出S ＝7. 10．解析：选C.当i ＝2时，S ＝2×2＋1＝5<10；当i ＝3时，仍然循环，排除D ；当i ＝4时，S ＝2×4＋1＝9<10；当i ＝5时，不满足S <10，即此时S ≥10，输出i ＝5.此时A 项中，S ＝2×5－2＝8，B 项中，S ＝2×5－1＝9，C 项中，S ＝2×5＝10，故C 正确．11．[导学号10390004] 解析：选D.初始值：k ＝10，S ＝1，判断条件成立； S ＝1＋10＝11，k ＝10－1＝9，判断条件成立； S ＝11＋9＝20，k ＝9－1＝8，判断条件成立； S ＝20＋8＝28，k ＝8－1＝7，判断条件成立；S ＝28＋7＝35，k ＝7－1＝6，判断条件不成立，输出S ＝35，结束算法．由此可得判断框中应填k >6？，故选D.12．解析：选C.初始条件S ＝1，k ＝2；运行第一次，S ＝1·log 23＝log 23，k ＝k ＋1＝3；运行第二次，S ＝log 23·log 34，k ＝k ＋1＝4；运行第三次，S ＝log 23·log 34·log 45，k ＝k ＋1＝5；运行第四次，S ＝log 23·log 34·log 45·log 56，k ＝k ＋1＝6；运行第五次，S ＝log 23·log 34·log 45·log 56·log 67，k ＝k ＋1＝7；…；运行第十四次，S ＝log 23·log 34·log 45·log 56·log 67…log 1516＝4，k ＝k ＋1＝16.不满足条件，停止运行，输出的S ＝4，所以判断框中应填入的条件是k <16？，故选C.13．解析：初始值：k ＝2，执行“k ＝k ＋1”得k ＝3，a ＝43＝64，b ＝34＝81，a >b 不成立； k ＝4，a ＝44＝256，b ＝44＝256，a >b 不成立；k ＝5，a ＝45＝1 024，b ＝54＝625，a >b 成立，此时输出k ＝5. 答案：514．解析：交换两个变量的值，需引入第三个量，将其中一个量的值赋给第三个量后，将第二个量的值赋给第一个量，再将第三个量的值赋给第二个量．答案：x ＝y15．[导学号10390005] 解析：由框图可知，算法结构为直到型循环结构，因为30＝12＋22＋32＋42，所以条件应为“i >4？”(或i ≥5？)．答案：i >4？(或i ≥5？)16．解析：当a ＝4时，退出循环，b ＝23＝8. 答案：817．解：由题意，⎩⎪⎨⎪⎧x >1x 2－4x ＋4＝0或⎩⎪⎨⎪⎧x <1，x ＝0，解得x ＝2或0. 18．解：算法设计如下：第一步，输入x 1，y 1，x 2，y 2.第二步，如果x 1＝x 2，输出“斜率不存在”，结束算法；否则，执行第三步．第三步，k ＝y 2－y 1x 2－x 1.第四步，输出k . 程序框图如下：19．[导学号10390006] 解：第一次循环：i ＝1，a ＝2，第二次循环：i ＝2，a ＝5，第三次循环：i ＝3，a ＝16，第四次循环：i ＝4，a ＝65>50，循环结束．所以输出i 的值为4.20．解：程序框图如图所示：21．解：程序框图如图所示：22．[导学号10390007]解：程序框图如下：。

人教A版高中数学必修三试卷高一：综合模块测试(21).docx

高中数学学习材料马鸣风萧萧*整理制作必修3综合模块测试21（人教A 版必修3）第I 卷（选择题共60分）一、选择题：本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，选择一个符合题目要求的选项.1．在下列各图中，每个图的两个变量具有相关关系的图是（）（1）（2）（3）（4）A ．（1）（2）B ．（1）（2）（3）C ．（2）（4）D ．（2）（3）2．求得459和357的最大公约数是（）A ．51B ．17C ． 9D ．33．在样本的频率分布直方图中，共有11个小长方形，若中间一个小长方形的面积等于其他10个小长方形的面积的和的41，且样本容量为160，则中间一组的频数为（） A ．40B ．0.2C ．32D ．0.254．从一批产品中取出三件，设A =“三件产品全不是次品”，B =“三件产品全是次品”，C =“三件产品不全是次品”，则下列结论正确的是（） A ．A 与C 互斥B ．B 与C 互斥C ．任两个均互斥D ．任两个均不互斥5．用秦九韵算法计算多项式15823)(35=+-+=x x x x x f 在时的值时，3V 的值为（）A ．3B ．5C ．－3D ．26．一个容量为n 的样本，分成若干组，已知某个体的频数和频率分别为40，0.125，则n 的值为( ) A.640 B.320 C.240 D.1607．把一颗骰子掷两次，观察出现的点数，并记第一次出现的点数为a ，第二次出现的点数为b ，则点),(b a 在直线5=+y x 左下方的概率为（）A ．61B ．65C ．121 D ．1211 8．如下图，图中的程序输出的结果是（）．A ．113B ．179C ．73D ．2099．如下图中的算法输出的结果是（）A ．127B ．63C ．61D ．3110．甲、乙两人约定上午7:20至8:00之间到某站乘公共汽车，在这段时间内有3班公共汽车，它们开车的时刻分别是7：40、7：50和8：00，甲、乙两人约定，见车就乘，则甲、乙同乘一车的概率为（假定甲、乙两人到达车站的时刻是互相不牵连的，且每人在7:20至8:00时的任何时刻到达车站都是等可能的）（）A ．31B ．21C ．38D ．85 第Ⅱ卷（共70分）二、填空题：本大题共4小题，每小题5分，共20分.将正确答案填在相应位置上。

人教A版高中数学必修三试卷高一：综合模块测试(23).docx

高中数学学习材料马鸣风萧萧*整理制作必修3综合模块测试23（人教A 版必修3）一、选择题(每小题3分,共36分)(选择题不用答题卡,答案写在后面的选择题答案表中) 1．简单随机抽样、系统抽样、分层抽样之间的共同点是（）A ．都是从总体中逐个抽取B ．将总体分成几部分，按事先预定的规则在各部分抽取C ．抽样过程中每个个体被抽到的可能性相等D ．抽样过程中，将总体分成几层，按比例分层抽取 2．下列各个说法正确的是（）A ．终边相同的角都相等B ．钝角是第二象限的角C ．第一象限的角是锐角D ．第四象限的角是负角 3．下列语句正确的是（）A.x+3=y-2B.d=d+2C.0=xD.x-y=5 4. 将十进制数111化为五进制数是（）A ．421（5） B. 521（5） C.423（5） D. 332（5）5. 一个单位有职工160人，其中有业务员104人，管理人员32人，后勤服务人员24人，要从中抽取一个容量为20的样本，用分层抽样的方法抽取样本，则在20人的样本中应抽取管理人员人数为（） A. 3 B. 4 C. 5 D. 6 6. 某人一次掷出两枚骰子,点数和为5的概率是（）A.41 B. 91 C. 361 D. 1817．有一个数据为50的样本,其分组以及各组的频数如下:[12.5,15.5],3; [15.5,18.5],8; [18.5,21.5],9; [21.5,24.5],11; [24.4,27.5],10; [27.5,30.5],5; [30.5,33.5],4 由以上频数,估计不超过30.5的数据大约占（）A.10%B.92%C.5%D.30%8. 某产品分甲、乙、丙三级，其中乙、丙两级均属次品.若生产中出现乙级品的概率为0.03，丙级品的概率为0.01，则对成品抽查一件抽得正品的概率为（）A ．0.99B ．0.98C ．0.97D ．0.969．把容量为100的样本拆分为10组，若前七组频率之和为0.79，而剩下的三组的频数,,a b c 满足2b ac =且互不相等，则剩下的三组频数最大的一组的频率是（）Ａ．0.16 Ｂ．0.12 Ｃ．0.16或0.12 Ｄ．以上都不对10．某种零件的次品率是1％，每6件装成一盒，每盒中恰有一件次品的概率是（）Ａ．6％Ｂ．1%6÷ Ｃ．51(99%)- Ｄ．51996()100100⋅11．一个工人在上班时间[]0,5（单位：小时）内看管两台机器．每天机器出故障的时刻是任意的，一台机器出了故障，就需要一段时间检修，在检修期间另一台机器也出了故障，称为二机器＂会面＂．如果每台机器的检修时间都是1小时，则此工人在上班时间内，二机器会面的概率是（）Ａ．1625 Ｂ．925Ｃ．15 Ｄ．4512. 一个游戏转盘上有四种颜色:红、黄、蓝、黑，并且它们所占面积的比为6：2：1：4，则指针停在红色或蓝色区域的概率为（）A. 613B.713 C ．413 D.1013选择题答案：题号 1 2 3 4 5 6 7 8 9 10 11 12 答案二、填空题(每小题4分，共16分)13. 甲、乙两名高一男生参加投篮测试，各投篮5次，一分钟内投中次数分别如下：甲：7，8，6，8，6；乙：7，8，7，7，6甲的方差是_______ ,乙的方差是________ ，说明 __________ 投篮更稳定.14. 一个路口的红绿灯,红灯的时间为30秒,黄灯的时间为5秒,绿灯的时间为40秒,当你到达路口时,看见绿灯的概率是__________ .15．终边落在阴影部分处（包括边界）的角的集合是________________________________.（用弧度制表示）4516．一个工人看管三台车床，在一个小时内车床不需要工人照管的概率分别为：第一台为0.9，第二台0.8，第三台0.7，则在一个小时内最多有一台车床需要照管的概率是．三、解答题（第17题8分，18—21题每题10分，共48分）17．设计一个程序计算二次函数2(0)y ax bx c a =++≠的最值，并根据输入的数值说明是最大值还是最小值，并求出对应的ｘ值．18. 对任意正整数n ，设计一个求Ｓ＝111123n++++的程序框图，并编写出程序.19. 假设关于某种设备的使用年限x 和支出的维修费用y （万元），有以下的统计资料：使用年限x2 3 4 5 6 维修费用y2.23.85.56.57.0（1）画出散点图；（2）求支出的维修费用y 与使用年限x 的回归方程；（3）估计使用年限为10年时，维修费用是多少？20. 设甲，乙两名射手各打10发子弹，每发子弹击中环数如下：甲：10，6，7，10，8，9，9，10，5，10；乙：8，7，9，10，9，8，7，9，8，9．试问哪一名射手的技术较好？参考答案题号 1 2 3 4 5 6 7 8 9 10 11 12 答案CBBABBBDCDBB13． 0.8; 0.4; 乙; 14.81515. |,4k k k z παπαπ⎧⎫≤≤+∈⎨⎬⎩⎭16. 0.90217.解：INPUT "请输入数值,,a b c ＂ /(2*)x b a =-(4**^2)/(4*)y a c b a =- 0IF a THEN >PRINT "当x =＂；x ；＂时＂；＂函数的最小值是＂；ｙ ELSEPRINT ＂当x =＂；x ；＂时＂；＂函数的最大值是＂；ｙ END IFEND18. IPUT “n ”;ni =1 Sum=0 WHILE i <=nSum=sum+1/i i =i +1WENDPRINT sum END19. 解:(1) 1.230.08y x ∧=+ a=0.08 b=1.23（2）维修费用=12.38开始输入n1i =sum 0=1i i =+1sum sum i=+?i n ≤是否输出sum结束20.先计算两名射手的平均环数：11067108991051010x +++++++++甲＝（）＝8.4 18791098798910x +++++++++乙＝（）＝8.4再计算两名射手的标准差：s 甲＝22222222221108.468.478.4108.488.498.498.4108.458.4108.410--------+-（－）＋（）＋（）＋（）＋（）＋（）＋（）＋（）＋（）（）＝ 1.884s 乙＝222222222218.488.478.49(8.410)(8.49)(8.48)(8.47)(8.49)(8.48)(8.49)10-+-+-+-+-+-+-+-（－）＋（）＋（－）=0.854由此可见两名射手的平均值相等，但是乙的稳定性要好，所以乙的水平比甲好．。

人教版高中数学高一必修3综合模块测试 1(人教A版必修3)

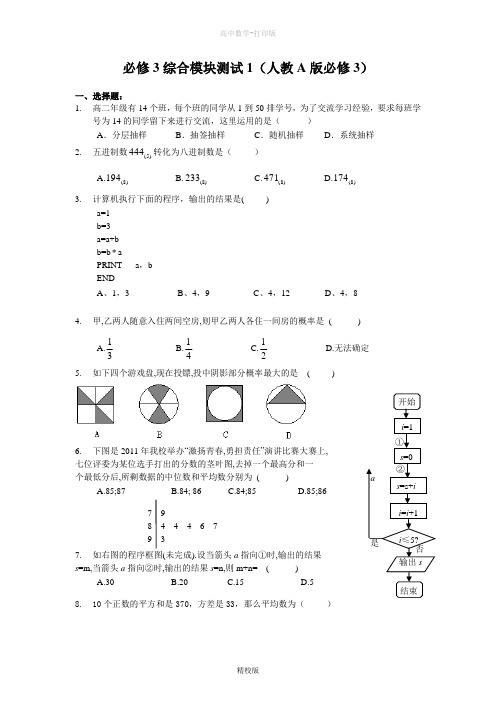
7 9 8 4 4 4 6 7 9 3 开始 i =1 s =0i =i +1s =s+ii ≤5? 输出s 结束① ②a是否必修3综合模块测试1（人教A 版必修3）一、选择题：1. 高二年级有14个班，每个班的同学从1到50排学号，为了交流学习经验，要求每班学号为14的同学留下来进行交流，这里运用的是（）A ．分层抽样B ．抽签抽样C ．随机抽样D ．系统抽样2. 五进制数(5)444转化为八进制数是（）A.(8)194B.(8)233C.(8)471D.(8)1743. 计算机执行下面的程序，输出的结果是( )a=1 b=3 a=a+bb=b a PRINT a ，b ENDA 、1，3B 、4，9C 、4，12D 、4，8 4. 甲,乙两人随意入住两间空房,则甲乙两人各住一间房的概率是 ( )A.31B.41C.21 D.无法确定 5. 如下四个游戏盘,现在投镖,投中阴影部分概率最大的是 ( )6. 下图是2011年我校举办“激扬青春,勇担责任”演讲比赛大赛上, 七位评委为某位选手打出的分数的茎叶图,去掉一个最高分和一个最低分后,所剩数据的中位数和平均数分别为 ( )A.85;87B.84; 86C.84;85D.85;867. 如右图的程序框图(未完成).设当箭头a 指向①时,输出的结果 s =m,当箭头a 指向②时,输出的结果s =n,则m+n= ( )A.30B.20C.15D.5 8. 10个正数的平方和是370，方差是33，那么平均数为（）A ．1B ．2C ．3D ．49. 读程序甲：INPUT i ＝1 乙：INPUT i ＝1000 S ＝0 S ＝0 WHILE i ＜＝1000 DOS ＝S ＋i S ＝S ＋i i ＝i ＋l i ＝i 一1 WEND LOOP UNTIL i ＜1PRINT S PRINT SEND END对甲乙两程序和输出结果判断正确的是（）A ．程序不同，结果不同B ．程序不同，结果相同C ．程序相同，结果不同D ．程序相同，结果相同 10. 已知点P 是边长为4的正方形内任一点，则P 到四个顶点的距离均大于2的概率是（）A.44π- B. 14 C. 34π- D. 1811. 甲、乙两人玩猜数字游戏,先由甲心中想一个数字,记为a ,再由乙猜甲刚才所想的数字,把乙猜的数字记为b ,其中{},1,2,3,4,5,6a b ∈,若1a b -≤,就称甲乙“心有灵犀”.现任意找两人玩这个游戏,则他们“心有灵犀”的概率为 ( ) A.19B.29C.718 D.4912. 如右的程序框图可用来估计圆周率π的值.设(1,1)CONRND -是产生随机数的函数,它能随机产生区间(1,1)-内的任何一个数,如果输入1000,输出的结果为786,则运用此方法,计算π的近似值为 ( )A.3.144B.3.141C.3.142D.3.143二、填空题：13. 语句“PRINT 37 MOD 5 ”运行的结果是＿＿＿＿. 14. 阅读右边的流程图，若0.30.322,2,log 0.8,a b c -===则输出的数是_＿___；15. 5280和2155的最大公约数是＿＿＿＿. 16. 乙两艘轮船都要停靠同一个泊位，它们可以在一昼夜（零点至24点）的任意时刻到达，设甲、乙两艘轮船停靠泊位的时间分别是3小时和5小时，则有一艘轮船停靠泊位时必须等待一段时间的概率为＿＿＿＿（用分数表示）．0.030.01频率组距三．解答题:17. （本题满分12分）设数列{}{}111,n n n n a a a a n a +=-=满足，右图是求数列30前项和的算法流程图。

人教A版高中数学必修三试卷高一：综合模块测试.docx

s=0 i=2 Do s=s+i i= i+2 Loop untilPrint sEnd 第5题高中数学学习材料马鸣风萧萧*整理制作必修3综合模块测试10（人教A 版必修3）一、选择：（共12小题，每题5分，共60分）1. 算法的三种基本结构是 ( ) A. 顺序结构、模块结构、条件结构 B. 顺序结构、循环结构、模块结构 C. 顺序结构、条件结构、循环结构 D. 模块结构、条件结构、循环结构2下列说法正确的是（） A. 任何事件的概率总是在（0，1）之间 B. 频率是客观存在的，与试验次数无关 C. 随着试验次数的增加，频率一般会越来越接近概率 D. 概率是随机的，在试验前不能确定3．用二分法求方程022=-x 的近似根的算法中要用哪种算法结构（） A ．顺序结构 B ．条件结构 C ．循环结构 D ．以上都用4．若)(B A P =1)()(=+B P A P ，则事件A 与B 的关系是（） A 互斥不对立 B 对立不互斥 C 互斥且对立 D 以上都不对 5．有下面的程序，运行该程序，要使输出的结果是30，在处应添加的条件是（） A. i>12 B. i>10 C. i=14 D. i=106．用“辗转相除法”求得459和357的最大公约数是：（） A ．3 B ．9 C ．17 D ．517．线性回归方程bx a y+=ˆ所表示的直线必经过点（） A ．（0，0） B ．（0,x ） C ．（y ,0） D ．（y x ,）8．下面有三个游戏规则，袋子中分别装有球，从袋中无放回地取球，问其中不公平的游戏是( )游戏1游戏2游戏33个黑球和一个白球一个黑球和一个白球2个黑球和2个白球取1个球，再取1个球取1个球取1个球，再取1个球取出的两个球同色→甲胜取出的球是黑球→甲胜取出的两个球同色→甲胜取出的两个球不同色→乙胜取出的球是白球→乙胜取出的两个球不同色→乙胜A ．游戏1和游戏3B ．游戏1C ．游戏2D ．游戏39．在下列各图中，每个图的两个变量具有相关关系的图是 ( )（1）（2）（3）（4） A ．（1）（2） B ．（1）（3） C ．（2）（4） D ．（2）（3）10.现有五个球分别记为A ，C ，J ，K ，S ，随机放进三个盒子，每个盒子只能放一个球，则K 或S 在盒中的概率是（） A.101 B. 53 C. 103 D. 10911．在用样本频率估计总体分布的过程中，下列说法正确的是 ( )Ａ．总体容量越大，估计越精确Ｂ．总体容量越小，估计越精确Ｃ．样本容量越大，估计越精确Ｄ．样本容量越小，估计越精确12、某初级中学有学生270人，其中一年级108人，二、三年级各81人，现要利用抽样方法取10人参加某项调查，考虑选用简单随机抽样、分层抽样和系统抽样三种方案，使用简单随机抽样和分层抽样时，将学生按一、二、三年级依次统一编号为1,2, ……,270；使用系统抽样时，将学生统一随机编号1,2, ……,270，并将整个编号依次分为10段如果抽得号码有下列四种情况：①7，34，61，88，115，142，169，196，223，250； ②5，9，100，107，111，121，180，195，200，265； ③11，38，65，92，119，146，173，200，227，254； ④30，57，84，111，138，165，192，219，246，270；关于上述样本的下列结论中，正确的是（）A 、 ②、③都不能为系统抽样B 、 ②、④都不能为分层抽样C 、 ①、④都可能为系统抽样D 、 ①、③都可能为分层抽样二填空：（共4小题，每题5分，共20分） 13．右图给出的是计算201614121++++ 的值的一个流程图，其中判断框内应填入的条件是____________ 14、数据 128,,,x x x 平均数为6，标准差为2，则数据 12826,26,,26x x x --- 的平均数为，方差为。

最新人教版高中数学必修3第三章模块测试卷a(附答案)

数学人教新课标A 版高中必修3模块测试卷A （附答案）一、选择题(每小题5分，共60分) 1．现要完成下列3项抽样调查：①从10盒酸奶中抽取3盒进行食品卫生检查；②科技报告厅有32排座位，每排有40个座位，有一次报告会恰好坐满了听众，报告会结束后，为了听取意见，需要请32名听众进行座谈；③胡集中学共有160名教职工，其中一般教师120名，行政人员16名，后勤人员24名．为了了解教职工对学校在校务公开方面的意见，拟抽取一个容量为20的样本．较为合理的抽样方法是( )．A ．①简单随机抽样，②系统抽样，③分层抽样B ．①简单随机抽样，②分层抽样，③系统抽样C ．①系统抽样，②简单随机抽样，③分层抽样D ．①分层抽样，②系统抽样，③简单随机抽样 2．以下程序运行后输出的结果是( )．A ．12,5B ．12,21C ．12,3D ．21,123．观察下列散点图，则①正相关；②负相关；③不相关．它们的排列顺序与图形相对应的是( )．A ．a —①，b —②，c —③B ．a —②，b —③，c —①C ．a —②，b —①，c —③D ．a —①，b —③，c —②4．在一次猜数字游戏中，某人猜出的数字为9.4,9.5,9.5，9.5，9.7,9.4，则下列说法正确的是( )．A ．平均数大于众数B ．平均数大于中位数C ．中位数等于平均数D ．众数大于中位数5．一只蚂蚁在如图所示的地板砖(除颜色不同外，其余全部相同)上爬来爬去，它最后随意停留在黑色地板上的概率是( )．A ．13 B ．23 C ．14 D ．186．有一农场种植一种水稻，在同一块稻田中连续8年的平均产量如下：(单位：kg) 450 430 460 440 450 440 470 460 则其方差为( )．A ．120B ．80C ．15D ．1507．(2011福建福州模拟)为了测算如图阴影部分的面积，作一个边长为6的正方形将其包含在内，并向正方形内随机投掷800个点，已知恰有200个点落在阴影部分，据此，可估计阴影部分的面积是( )．A ．12B ．9C ．8D ．68．在样本频率分布直方图中，一共有n 个小矩形，若中间一个小矩形的面积等于其余n －1个小矩形面积和的14，且样本容量为160，则中间一组的频数是( )． A ．32 B ．20 C ．40 D ．259．一个单位有职工160人，其中有业务人员104人，管理人员32人，后勤服务人员24人，要从中抽取一个容量为20的样本，用分层抽样的方法抽出样本，则在20人的样本中，应抽取管理人员( )．A ．3人B ．4人C ．12人D ．7人10．某家庭电话在家中有人时，打进的电话响第1声时被接的概率是110，响第2声时被接的概率为310，响第3声时被接的概率是25，响第4声时被接的概率是110，那么电话在响前4声内被接的概率为( )．A ．12 B ．910 C ．310 D ．4511．三位七进制的数表示的最大的十进制的数是( )． A ．322 B ．332 C ．342 D ．35212．分别以集合A ＝{2,4,6,8,11,12,13,19}中任意两个元素为分子、分母构成分数，则这种分数是可约分数的概率为( )．A ．514 B ．314 C ．12 D ．114二、填空题(每小题4分，共16分)13．阅读图示的程序框图，若输入m ＝4，n ＝6，则输出a ＝__________，i ＝__________.14．用秦九韶算法求P(x)＝x8－3x6＋5x5－2x－1当x＝2时的值为__________．15．如图所示，在半径为1的半圆内，放置一个边长为12的正方形ABCD，向半圆内任投一点，该点落在正方形内的概率为__________．16．从所有三位二进制数中随机抽取一个数，则这个数化为十进制数后比5大的概率是__________．三、解答题(共74分)17．(12分)分别用辗转相除法和更相减损术求282与470的最大公约数．18．(12分)某花木公司为了调查某种树苗的生长情况，抽取了一个容量为100的样本，测得树苗的高度(cm)数据的分组及相应频数如下：[107,109)3株；[109,111)9株；[111,113)13株；[113,115)16株；[115,117)26株；[117,119)20株；[119,121)7株；[121,123)4株；[123,125]2株．(1)列出频率分布表；(2)画出频率分布直方图；(3)据上述图表，估计数据在[109,121)范围内的可能性是百分之几？19．(12分)高三·一班有50名学生，其中走读的男生有5名．若从50名学生中任抽1名，抽到住宿男生的概率为12.求：(1)从50名学生中任抽1人，抽到走读男生的概率；(2)从50名学生中任抽1人，抽到男生的概率；(3)从50名学生中任抽1人，抽到女生的概率；(4)这个班女生有多少人？20．(12分)为了对某课题进行研究，用分层抽样方法从三所高校A，B，C的相关人员中，(1)求x，y；(2)若从高校B ，C 抽取的人中选2人作专题发言，求这二人都来自高校C 的概率． 21．(12分)(2011湖南高考)某河流上的一座水力发电站，每年六月份的发电量Y (单位：万千瓦时)与该河上游在六月份的降雨量X (单位：毫米)有关．据统计，当X ＝70时，Y ＝460；X 每增加10，Y 增加 5.已知近20年X 的值为：140,110,160,70,200,160,140,160,220,200,110,160,160,200,140,110,160,220,140,160.(1)完成如下的频率分布表：(2)假定今年六月份的降雨量与近20年六月份降雨量的分布规律相同，并将频率视为概率，求今年六月份该水力发电站的发电量低于490(万千瓦时)或超过530(万千瓦时)的概率．22．(14分)(2011广东高考)在某次测验中，有6位同学的平均成绩为75分，用x n 表示编号为n (n ＝1,2(1)求第6位同学的成绩x 6，及这6位同学成绩的标准差s ；(2)从前5位同学中，随机地选2位同学，求恰有1位同学成绩在区间(68,75)中的概率．参考答案1. 答案：A解析：①总体较少，宜用简单随机抽样；②已分段，宜用系统抽样；③各层间差距较大，宜用分层抽样．2. 答案：B解析：A ＝3＋32＝12，B ＝32＋12＝21. 3. 答案：D解析：该题考查变量相关性的定义以及图形表示，要注意点的排列规律与正、负相关的联系．4. 答案：C解析：易求得中位数、平均数、众数都是9.5. 5. 答案：A解析：由几何概型的概率公式可得，41123P ＝＝. 6. 答案：D解析：450x ＝，则s 2＝18(400＋100＋100＋100＋400＋100)＝150. 7. 答案：B解析：正方形面积为36，阴影部分面积为200369800＝.故选B 项． 8. 答案：A解析：设其余n －1个小矩形面积和为x ，则114x x ＋＝，∴45x ＝.∴中间一个小矩形的面积为15. ∴中间一组的频率为15.∴频数为1160325⨯＝. 9. 答案：B 解析：20324160⨯＝(人)． 10. 答案：B 解析：13219101051010P ＝＋＋＋＝. 11. 答案：C解析：三位七进制数最大的是666(7)，666(7)＝6×72＋6×7＋6＝342. 12. 答案：A解析：以集合A 中任意两个元素为分子、分母构成分数共有56个基本事件，是可约分数的有24，26，28，212，42，46，48，412，62，64，68，612，82，84，86，812，122，124，126，128共20个，所以所求概率为514. 13. 答案：12 3解析：要结束程序的运算，就必须通过n 整除a 的条件运算，而同时m 也整除a ，那么a 的最小值应为m 和n 的最小公倍数12，即此时有i ＝3.14. 答案：219解析：先将多项式P (x )进行改写，P (x )＝x 8－3x 6＋5x 5－2x －1＝(((((((x ＋0)x －3)x ＋5)x ＋0)x ＋0)x ＋0)x －2)x －1，将x ＝2代入由内向外逐次计算，可得P (2)＝219.15. 答案：12π解析：21124S ⎛⎫⎪⎝⎭三＝＝，21ππ122S ⨯半＝圆，由几何概型的计算公式得114π2π2S P S 正半＝＝＝圆. 16. 答案：12解析：三位二进制数共有4个，分别是111(2)，110(2)，101(2)，100(2)，其中111(2)与110(2)化为十进制数后比5大，故所求概率为2142P ＝＝.17. 解：辗转相除法： 470＝1×282＋188 282＝1×188＋94 188＝2×94∴282与470的最大公约数为94. 更相减损术：470与282分别除以2得235和141. ∴235－141＝94 141－94＝4794－47＝47∴470与282的最大公约数为47×2＝94. 18. 解：(1)(2)频率分布直方图如下：频率分布直方图(3)由上述图表可知数据落在[109,121)范围内的频率为：0.94－0.03＝0.91，即数据落在[109,121)范围内的可能性是91%.19. 解：设A 为“抽到走读男生”，B 为“抽到住宿男生”，C 为“抽到男生”，D 为“抽到女生”．(1) 51()5010P A ＝＝； (2)∵C ＝A ∪B ，且A 与B 是互斥事件，∴由概率的加法公式得P (C )＝P (A )＋P (B )＝1131025＋＝； (3)∵C 与D 是对立事件， ∴P (D )＝1－P (C )＝32155－＝.(4)这个班女生人数为250205 ＝(人)． 20. 解：(1)由题意可得，2183654x y＝＝，所以x ＝1，y ＝3.(2)记从高校B 抽取的2人为b 1，b 2，从高校C 抽取的3人为c 1，c 2，c 3，则从高校B ，C 抽取的5人中选2人作专题发言的基本事件有10种：(b 1，b 2)，(b 1，c 1)，(b 1，c 2)，(b 1，c 3)，(b 2，c 1)，(b 2，c 2)，(b 2，c 3)，(c 1，c 2)，(c 1，c 3)，(c 2，c 3)，设选中的2人都来自高校C 的事件为X ，则X 包含的基本事件有(c 1，c 2)，(c 1，c 3)，(c 2，c3)共3种，因此3()10P X＝，故选中的2人都来自高校C的概率为310.21.解：(1)在所给数据中，降雨量为110毫米的有3个，为160毫米的有7个，为200毫米的有3个．故近20年六月份降雨量频率分布表为(2)P(“发电量低于490万千瓦时或超过530万千瓦时”)＝P(Y＜490或Y＞530)＝P(X＜130或X＞210)＝P(X＝70)＋P(X＝110)＋P(X＝220)＝1323 20202010＋＋＝.故今年六月份该水力发电站的发电量低于490(万千瓦时)或超过530(万千瓦时)的概率为310.22.解：(1)x6＝6×75－(70＋76＋72＋70＋72)＝90，7s.(2)设这五位同学分别为A，B，C，D，E，其中只有B是不在(68,75)这个范围内的，从这五位同学中随机选2位同学，有以下情况：(A，B)，(A，C)，(A，D)，(A，E)，(B，C)，(B，D)，(B，E)，(C，D)，(C，E)，(D，E)共10种情况，而恰有一位同学成绩在区间(68,75)中的情况有(A，B)，(B，C)，(B，D)，(B，E)共4种情况，所以恰有1位同学成绩在区间(68,75)中的概率是2 5 .。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

省莱州一中高一数学必修三模块测试题（人教A 版）限时：120分钟1．本试卷分第I 卷（选择题）和第II 卷（非选择题）两部分，共150分，第I 卷一、选择题（每小题5分，共50分） 1．下列给出的赋值语句中正确的是：A 、3=AB 、M=—MC 、B=A=2D 、x+y=02．把89化成五进制数的末位数字为（） A 1 B 2 C 3 D 4 3．如右图,是某算法流程图的一部分，其算法的逻辑结构为（）A. 顺序结构B. 判断结构C. 条件结构D. 循环结构4．某公司在甲、乙、丙、丁四个地区分别有150个、120个、180个、150个销售点，公司为了调查产品销售的情况，需从这600个销售点中抽取一个容量为100的样本，记这项调查为(1)；在丙地区中有20个特大型销售点，要从中抽取7个调查其销售收入和售后服务情况，记这项调查为(2)。

则完成(1)、(2)这两项调查宜采用的抽样方法依次是 ( ) A 、分层抽样法，系统抽样法 B 、分层抽样法，简单随机抽样法 C 、系统抽样法，分层抽样法 D 、简单随机抽样法，分层抽样法 5．下列对一组数据的分析，不正确的说法是（） A 、数据极差越小，样本数据分布越集中、稳定 B 、数据平均数越小，样本数据分布越集中、稳定 C 、数据标准差越小，样本数据分布越集中、稳定 D 、数据方差越小，样本数据分布越集中、稳定6．有五组变量：①汽车的重量和汽车每消耗1升汽油所行驶的平均路程；②平均日学习时间和平均学习成绩； ③某人每日吸烟量和其身体健康情况； ④正方形的边长和面积； ⑤汽车的重量和百公里耗油量；其中两个变量成正相关的是（）A ．①③B ．②④C ．②⑤D ．④⑤7.计算机中常用16进制，采用数字0～9和字母A ～F 共16个计数符号与10进制得对应关系如下表：例如用16进制表示D+E ＝1B ，则A ×B=( ) A 6E B 7C C 5F D B08．从一批产品中取出三件产品，设A =“三件产品全不是次品”，B =“三件产品全是次品”，C =“三件产品至少有一件是次品”，则下列结论正确的是（） A . A 与C 互斥 B . 任何两个均互斥 C . B 与C 互斥D . 任何两个均不互斥9．从一箱产品中随机地抽取一件，设事件A=｛抽到一等品｝，事件B =｛抽到二等品｝，事件C =｛抽到三等品｝，且已知 P （A ）= 0.65 ,P(B)=0.2 ,P(C)=0.1。

则事件“抽到的不是一等品”的概率为（）A. 0.7B. 0.65C. 0.35D. 0.3 10．先后抛掷质地均匀的硬币三次,则至少一次正面朝上的概率是 ( )A.81B. 83C. 85D. 87二、填空题（每小题5分，共20分）11．计算机的程序设计语言很多，但各种程序语言都包含下列基本的算法语句：，，，，。

12．为了解某地高一年级男生的身高情况，从其中的一个学校选取容量为60的样本(60名男生的身高，单位：cm)，分组情况如下：则表中的，。

13．如右图，在正方形有一扇形（见阴影部分），扇形对应的圆心是正方形的一顶点，半径为正方形的边长。

在这个图形上随机撒一粒黄豆，它落在扇形外正方形的概率为。

（用分数表示）14．下列说法中正确的有________①平均数不受少数几个极端值的影响，中位数受样本中的每一个数据影响； ②抛掷两枚硬币，出现“两枚都是正面朝上”、“两枚都是反面朝上”、“恰好一枚硬币正面朝上”的概率一样大③用样本的频率分布估计总体分布的过程中，样本容量越大，估计越准确。

④向一个圆面随机地投一个点，如果该点落在圆任意一点都是等可能的，则该随机试验的数学模型是古典概型。

省莱州一中高一数学必修三模块测试题（人教A 版）限时：120分钟第II 卷一、选择题（每小题5分，共60分）二、填空题（每小题5分，共20分）11．，，，，。

12．=m ， =a 。

13．； 14. 。

三、解答题： 15．（12分）为了参加奥运会，对自行车运动员甲、乙两人在相同的条件下进行了6次测试，测得他们的最大速度的数据如表所示：请判断：谁参加这项重大比赛更合适，并阐述理由。

16．（13分）下面是计算应纳税所得额的算法过程，其算法如下：第一步输入工资x(注x<=5000);第二步如果x<=800,那么y=0;如果800<x<=1300,那么 y=0.05(x-800);否则 y=25+0.1(x-1300) 第三步输出税款y, 结束。

请写出该算法的程序框图和程序。

（注意：程序框图与程序必须对应）17．（13分）为了调查甲、乙两个受欢迎的程度，随机选取了14天，统计上午8：00—10：00间各自的点击量，得如下所示的统计图，根据统计图：（1）甲、乙两个点击量的极差分别是多少？（4分）（2）甲点击量在[10，40]间的频率是多少？（5分）（3）甲、乙两个哪个更受欢迎？并说明理由。

（4分）18．（本小题满分14分）在人群流量较大的街道，有一中年人吆喝“送钱”，只见他手拿一黑色小布袋，袋中有3只黄色、3只白色的乒乓球（其体积、质地完成相同），旁边立着一块小黑板写道：摸球方法：从袋中随机摸出3个球，若摸得同一颜色的3个球，摊主送给摸球者5元钱；若摸得非同一颜色的3个球，摸球者付给摊主1元钱。

（1）摸出的3个球为白球的概率是多少？（2）摸出的3个球为2个黄球1个白球的概率是多少？（3）假定一天中有100人次摸奖，试从概率的角度估算一下这个摊主一个月（按30天计）能赚多少钱？茎叶图 119．（14分）假设你家订了一份报纸，送报人可能在早上6点—8点之间把报纸送到你家，你每天离家去工作的时间在早上7点—9点之间（1）你离家前不能看到报纸（称事件A）的概率是多少？（8分，须有过程）（2）请你设计一种随机模拟的方法近似计算事件A的概率（包括手工的方法或用计算器、计算机的方法）（6分）20.（本小题满分14分）给出50个数，1，2，4，7，11，…，其规律是：第1个数是1，第2个数比第1个数大1，第3个数比第2个数大2，第4个数比第3个数大3，…，以此类推. 要求计算这50个数的和. 先将下面给出的程序框图补充完整，再根据程序框图写出程序.1. 把程序框图补充完整：Array（1）________________________ (3分)（2）________________________ (4分)2. 程序：（7分）省莱州一中高一数学必修三模块测试题（人教A 版）参考答案限时：120分钟第II 卷一、选择题（每小题5分，共60分）二、填空题（每小题5分，共20分）11．输入语句，输出语句，赋值语句，条件语句，循环语句。

12．=m 6 ， =a 0.45 。

13．44π- 14. ③ 。

解：336313537303827=+++++=甲X336362834382933=+++++=乙X （ 4分）S 甲=958.3694≈， S 乙=559.3338≈ （8分）乙甲X X =，S 甲＞S 乙（10分）乙参加更合适（12分）16．（13分）下面是计算应纳税所得额的算法过程，其算法如下：第一步输入工资x(注x<=5000);第二步如果x<=800,那么y=0;如果800<x<=1300,那么 y=0.05(x-800);茎叶图否则 y=25+0.1(x-1300) 第三步输出税款y, 结束。

请写出该算法的程序框图和程序。

（注意：程序框图与程序必须对应）解：框图7分，程序6分（不对应扣3-4分）17．（13分）为了调查甲、乙两个受欢迎的程度，随机选取了14天，统计上午8：00—10：00间各自的点击量，得如下所示的统计图，根据统计图：（1）甲、乙两个点击量的极差分别是多少？（4分）（2）甲点击量在[10，40]间的频率是多少？（5分）（3）甲、乙两个哪个更受欢迎？并说明理由。

（4分）解：（1）甲的极差为：73-8=65；（2分）乙的极差为：61-5=56 （4分）（2）甲点击量在[10，40]间的频率为4/14=2/7=0.28571 （9分）(3)甲的点击量集中在茎叶图的下方，而乙的点击量集中在茎叶图的上方。

从数据的分布情况来看，甲更受欢迎。

（13分）18．（本小题满分14分）在人群流量较大的街道，有一中年人吆喝“送钱”，只见他手拿一黑色小布袋，袋中有3只黄色、3只白色的乒乓球（其体积、质地完成相同），旁边立着一块小黑板写道：摸球方法：从袋中随机摸出3个球，若摸得同一颜色的3个球，摊主送给摸球者5元钱；若摸得非同一颜色的3个球，摸球者付给摊主1元钱。

（1）摸出的3个球为白球的概率是多少？（2）摸出的3个球为2个黄球1个白球的概率是多少？（3）假定一天中有100人次摸奖，试从概率的角度估算一下这个摊主一个月（按30天计）能赚多少钱？解：把3只黄色乒乓球标记为A、B、C，3只白色的乒乓球标记为1、2、3。

从6个球中随机摸出3个的基本事件为：ABC、AB1、AB2、AB3、AC1、AC2、AC3、A12、A13、A23、BC1、BC2、BC3、B12、B13、B23、C12、C13、C23、123，共20个（1）事件E={摸出的3个球为白球}，事件E包含的基本事件有1个，即摸出123号3个球，P（E）=1/20=0.05（2）事件F={摸出的3个球为2个黄球1个白球}，事件F包含的基本事件有9个，P （F）=9/20=0.45（3）事件G={摸出的3个球为同一颜色}={摸出的3个球为白球或摸出的3个球为黄球}，P（G）=2/20=0.1，假定一天中有100人次摸奖，由摸出的3个球为同一颜色的概率可估计事件G发生有10次，不发生90次。

则一天可赚-⨯⨯，每月可赚1200元。

90=54010119．（14分）假设你家订了一份报纸，送报人可能在早上6点—8点之间把报纸送到你家，你每天离家去工作的时间在早上7点—9点之间（1）你离家前不能看到报纸（称事件A）的概率是多少？（8分，须有过程）（2）请你设计一种随机模拟的方法近似计算事件A的概率（包括手工的方法或用计算器、计算机的方法）（6分）Array解：如图，设送报人到达的时间为X，小王离家去工作的时间为Y。

（X，Y）可以看成平面中的点，试验的全部结果所构成的区域为}9YXX，ΩY（，）{≤8=6/≤≤≤7一个正方形区域，面积为SΩ=4，事件A表示小王离家前不能看到报纸，所构成的区域为A={（X，Y）/ }≤≤≤，，即图中的阴影部≤X>7Y986YX分，面积为S A=0.5。