如何使用ASPEN软件模拟完成精馏的设计和控制马后炮
Aspen+plus精馏模拟

Aspen plus 在精馏中的应用实例教程 /teacherf/
第 3 页共 37 页
3. 精馏塔的简捷计算
·设计任务 确定理论塔板数 确定合适的回流比
·DSTWU 精馏模型简介
本例选择 DSTWU 简捷精馏计算模型. DSTWU 可对一个带有分凝器或全凝器一股进料和两种产品的蒸馏塔进行简捷精馏 计算. DSTWU 假设恒定的摩尔溢流量和恒定的相对挥发度
1)创建精馏塔模块 在模型库中选择塔设备 column 标签,如图 3.1-1.
图 3.1-1
点击该 DSTWU 模型的下拉箭头,弹出三个等效的模块,任选其一如图 3.1-2 所示.
Aspen plus 在精馏中的应用实例教程 /teacherf/
第 4 页共 37 页
·定义每个组分流量或分率(Composition) Mass-frac(质量分率):WATER: 0.632; CH3OH: 0.368.
输入数据后的窗口如图 3.5 所示.
3.6 定义单元模型
图 3.5
Aspen plus 在精馏中的应用实例教程 /teacherf/
输入回流比的实际值; 定义回流比与最小回流比的比值. 输入负号后再入数值. 在这里我们取最小回流比的 2 倍, 故输入-2.
·定义轻重关键组分的回收率(Key component recoveries) Dstwu 要求定义组分的份的回收率. 计算得到两种组分的回收率为:
轻关键组分的回收率为 0.9983 重关键组分的回收率为 0.0029
第 12 页共 37 页
3.7 模拟计算与结果查看
点击工具栏中的蓝色 N-> 图标,即可进行计算,同时进入“Control Panel”页显示运行信息, 如图 3.7-1. 该图标的作用是执行下一步操作,若数据未输入完毕自动转到待输入数据的窗口; 若数据输入完毕,则进行计算. 上面操作也可点击 Run 菜单中的 run 命令来直接
aspen 精馏模拟详细过程及探讨疑问

精馏塔设计初步介绍1.设计计算◆输入参数:●利用DSTWU模型,进行设计计算●此时输入参数为:塔板数(或回流比以及最小回流比的倍数)、冷凝器与再沸器的工作压强、轻组分与重组分的回收率(可以从产品组成估计)、冷凝器的形式◆输出参数(得到用于详细计算的数据):●实际回流比●实际塔板数(实际回流比和实际塔板数可以从Reflux Ratio Profile 中做图得到)●加料板位置(当加料浓度和此时塔板上液体浓度相当时的塔板)●蒸馏液(馏分)的流量●其他注:以上数据全部是估计得初值,需要按一定的要求进行优化(包括灵敏度以及设计规定的运用),优化主要在RadFrac模型中进行。
2.详细计算◆输入参数:●输入参数主要来自DSTWU中理论计算的数据◆输出参数:●输出的主要是设计板式塔所需要的水力学数据,尺寸数据等其他数据(主要是通过灵敏度分析以及设计规定来实现)3.疑问●在简捷计算中:回收率有时是估计值,它对得到详细计算所需的数据可靠性的影响是不是很大?●在简捷计算中:有多少个变量,又有多少个约束条件?●在简捷计算中:为什么回流比和塔板数有一定的关系?简捷计算(对塔)1.输入数据:●Reflux ratio :-1.5(估计值,一般实际回流比是最小回流比的1.2—2倍)●冷凝器与再沸器的压强:1.013 ,1.123 (压降为0.11bar)●冷凝器的形式:全冷凝(题目要求)、●轻重组分的回收率(塔顶馏出液):0.997 ,0.002 (如果没有给出,可以根据产品组成估计)●分析时,注意Calculation Option 中的设置,来确定最佳回流比以及加料板位置2.输出数据:●Reflux Ratio Profile中得到最佳的回流比与塔板数为:塔板数在45—50中选择,回流比在:0.547 —0.542●选定塔板数为:48,回流比为:0.544●把所选的塔板数回代计算,得到下列用于RadFrac模型计算的数据(见下图):●●从图中可得:实际回流比为:0.545(摩尔比);实际塔板数为:48;加料板位置:33;Distillate to feed fraction :0.578(自己认为是摩尔比,有疑问??);馏出液的流量:11673.5kg/h疑问:进料的流量是怎么确定的,肯定是大于11574kg/h,通过设计规定得到甲醇产量为:11574kg/h(分离要求),求出流量为:16584.0378kg/h。
用AspenPlus对反应精馏的模拟计算

·15·
HOAc + MeOH ←→ MeOAc + H2O 上述反应具有如下特点: ( 1) 为液相可逆反应, 转 化 率 受 化 学 平 衡 的 限 制。若通过提高反应温度增加反应速率, 则逆反应- 水解反应的速率也会随之加快。 ( 2) 反应体系存在复杂 的 共 沸 物 , 难 以 制 备 高 纯度的 MeOAc。MeOAc/H2O、MeOAc/MeOH 能够形 成共沸物( 见表 1) , 且共沸物与产品 MeOAc 的沸点 非常接近, 所以常规精馏难以直接制备纯度大于 95%的 MeOAc。
关键词 酯化反应 Aspen Plus 反应精馏 中图分类号 TQ 018
0 反应精馏技术简介
反应精馏是将化学反应与精馏相耦合的操作 技术,“反应精馏”的概念 1921 年由 Bacchau 首次提 出 [1]。 反 应 精 馏 通 过 精 馏 的 方 法 将 反 应 物 与 产 物 分 离开来, 以破坏可逆反应的平衡关系, 使反应继续向 生成产物的方向进行, 从而可提高可逆反应的转化 率、选择性和生产能力。此外, 反应精馏过程中还可 通过化学反应破坏气液平衡关系, 从而可加快传质 速率, 缩短反应时间。对于放热反应, 反应所释放出 的热量可作为精馏所需的气化热, 从而可降低能耗 和操作费用。简言之, 反应精馏具有以下优点[2]: 选择 性高; 使可逆反应收率提高; 温度易于控制, 避免出 现“热点”问题; 缩短反应时间, 强化设备生产能力; 能耗低, 操作费用低; 投资少。
aspen精馏过程模拟
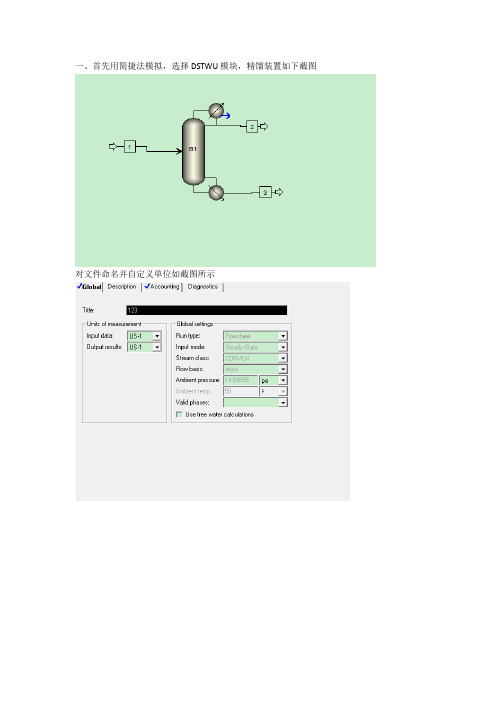
一、首先用简捷法模拟,选择DSTWU模块,精馏装置如下截图对文件命名并自定义单位如截图所示然后在计算机上输入物料的组成,如下截图所示选择一个热力学方法为SRK方法如下截图所示对1号进料物流管进行参数设定,为泡点进料,进料压力为16.5Kg/cm2,进料流量为100kmol/h。
还有物料组成及比例如下截图所示对精馏塔进行参数的设定,回流比为最小回流比的1.2倍,塔顶轻组分丙烷的含量为0.999,重组分含量丁烷为0.001,参数设定值如下截图所示参数设定完成运行软件并查看结果,计算结果如下图所示从结果可知实际的回流比为1.198,实际塔板数为38块,实际的进料板为第17块板,冷凝器的温度为44.25℃,塔釜的温度为116.88℃。
二、进行严格法计算根据简化法得到的条件进行模拟选择Radfrac模块,模拟装置图如下截图对文件命名并自定义单位如截图所示在计算机上输入物料的组成,如下截图所示选择一个热力学方法为SRK方法如下截图所示对1号进料物流管进行参数设定,为泡点进料,进料压力为16.5Kg/cm2,进料流量为100kmol/h。
还有物料组成及比例如下截图所示对塔进行参数设置,根据简化法的计算结果知,塔板数为38,实际回流比为1.198。
再根据题目设计的要求冷凝器为全回流,塔顶的采出率为80。
参数如下截图所示:根据简化法结果进料板为第十七块板进料,截图如下设置塔顶压力为16kg/cm2,冷凝器压力为15.8kg/cm2,全塔的压降为0.2kg/cm2。
设置如下截图所示参数设置完成并运行软件,查看结果不满足分离的目的,则进行自定义设定,目标值设定为0.001选择丙烷选择3号物流设置回流比的可变范围为1到100,增量为0.1运行软件查看结果满足分离的要求。
接下来进行灵敏度分析以确定最佳的进料位置参数设置完成并运行软件查看灵敏度分析的结果如下截图从结果的表中可以看出第22块板的回流比,冷凝器的热负荷,再沸器的热负荷都是最小的,从而可以知道最佳的进料位置为第22块板并对数据在plot里作出X-Y的曲线图如下截图所示从图中也可以明显的看出最佳的进料板为第22块塔板。
ASPEN_PLUS入门-培训教程=马后炮化工

路漫漫其修远兮, 吾将上下而求索
单元操作模型及其主要功能
固体处理
•RADFRAC 严格法精馏
•MULTILFRAC 严格法多 塔精馏
•EXTRAC 严格法萃取
•DSTWU 简算法精馏,设 计型
•DISTL 简算法精馏,核算 型
•SCFRAC 简算法多塔精馏
•PETROFRAC 石油炼制分 馏塔
反应器
推荐的物性方法 SOLIDS SOLIDS PR-BM,RKS-BM PR-BM,RKS-BM PR-BM,RKS-BM,BWR-LS PRWS,RKSWS,PRMHV2,,RKSMHV2,PSRK,SRPOLAR
路漫漫其修远兮, 吾将上下而求索
物性方法选择指南
路漫漫其修远兮, 吾将上下而求索
ASPEN PLUS模拟的流程
路漫漫其修远兮, 吾将上下而求索
ASPEN PLUS的优势
可以模拟固体系统
Aspen Plus在煤的气化和液化、流化床燃烧、高温冶金 和湿法
冶金,以及固体废物、聚合物、生物和食品加工业中都得到了 应用。
Aspen Plus中固体性质数据有两个来源:一是Solid数据库 ,它广泛收集了约3314种纯无机和有机物质的热化学数据 ;二是和CSIRO数据库的接口。还具有一套通用的处理固 体的单元操作模型,包括破碎机、旋风分离器、筛分、文 杜里洗涤器、静电沉淀器、过滤洗涤机和倾析器。此外, Aspen Plus中所有的单元操作都适合于处理固体,例如闪 蒸和加热器模型能计算固体的能量平衡,而反应器模型 RGIBBS可用最小GIBBS自由能来判断在平衡状态下是否 有固相存在。
路漫漫其修远兮, 吾将上下而求索
主要内容
ASPEN PLUS简介 ASPEN PLUS 安装方法及界面介绍 通过实例介绍如何建立模拟模型 模型分析工具的使用
Aspen Plus在精馏操作分析中的应用

Aspen Plus在精馏操作分析中的应用精馏是化工行业中应用很广的一种工艺操作。
影响精馏效果的因素很多,往往一个因素发生变化时,会牵扯到一些其他因素发生变化。
这使得精馏过程变得颇为灵活和复杂。
如何有效的对精馏操作进行全面详细的分析一直是技术人员的研究难点和重点。
本文简要介绍了Aspen Plus软件,并详细探讨了它在精馏操作分析中的实际应用,供大家学习交流。
标签:Aspen Plus;精馏操作;分析;应用前言精馏是化工行业中应用很广的一种工艺操作。
影响精馏效果的因素的是多方面的,主要包括分离物的组成和性质、操作过程和设备的物理参数等等。
往往一个因素发生变化时,会牵扯到一些其他因素发生变化。
由于这些影响因素多呈非线性变化,使精馏过程变得颇为灵活和复杂,如何有效的对精馏操作进行全面详细的分析一直是技术人员的研究难点和重点。
1 精馏塔的分类和原理简介精馏塔又名蒸馏塔,是一种进行蒸馏的气液塔式接触装置,主要有填料塔和板式塔两种类型,根据操作方式的不同又可以分为间隙精馏塔和连续精馏塔。
整个物料变化过程就是气相物质和液相物质相互作用的过程,首先气相从塔底进入塔内,与塔内下降的液相接触,气相中难挥发的物质源源不断的向液相转化,与此同时,液相中容易挥发的物质也会转化到气相中去,随着工序的继续,重组分在塔底积聚,轻组分流向塔顶,逐步实现轻重组分的分离。
分离出的气相进入冷凝器,液相组分一部分作为蒸馏的液体取出,另一部分继续返回塔顶进入蒸馏塔中。
塔底流出的液体,部分送入再沸器加热蒸发成气相,其它的液体作为釜残液取出。
2 Aspen Plus软件简介Aspen是由美国麻省理工学院(MIT)主持、多个部门共同参与联合开发的。
它是一款用于模拟化工生产工艺的模拟软件。
Aspen Plus拥有最完善的物性数据库,包含六千多种纯组分的物性数据。
其次,它还具有超强的热力学计算系统,以及各种单元操作模块。
Aspen Plu在整个化工工艺装置的研发、设计和安置中都发挥着巨大的作用。
ASPEN软件进行精馏塔设计

1引言1.1ASPENPLUS概述AspenPlus是大型通用流程模拟系统,源于美国能源部七十年代后期在麻省理工学院(MIT)组织的会战,开发新型第三代流程模拟软件。
该项目称为“过程工程的先进系统”(Advanc ed System for Proces s Engine ering,简称ASPE N),并于1981年底完成。
1982年为了将其商品化,成立了Asp enTec h公司,并称之为As pen Plus。
该软件经过20多年来不断地改进、扩充和提高,已先后推出了十多个版本,成为举世公认的标准大型流程模拟软件,应用案例数以百万计。
全球各大化工、石化、炼油等过程工业制造企业及著名的工程公司都是Aspen Plus 的用户。
1.2精馏塔概述精馏塔是进行精馏的一种塔式汽液接触装置,又称为蒸馏塔。
有板式塔与填料塔两种主要类型。
根据操作方式又可分为连续精馏塔与间歇精馏塔。
蒸气由塔底进入。
蒸发出的气相与下降液进行逆流接触,两相接触中,下降液中的易挥发(低沸点)组分不断地向气相中转移,气相中的难挥发(高沸点)组分不断地向下降液中转移,气相愈接近塔顶,其易挥发组分浓度愈高,而下降液愈接近塔底,其难挥发组分则愈富集,从而达到组分分离的目的。
由塔顶上升的气相进入冷凝器,冷凝的液体的一部分作为回流液返回塔顶进入精馏塔中,其余的部分则作为馏出液取出。
塔底流出的液体,其中的一部分送入再沸器,加热蒸发成气相返回塔中,另一部分液体作为釜残液取出。
1.2.1 精馏塔的分类气-液传质设备主要分为板式塔和填料塔两大类。
精馏操作既可采用板式塔,也可采用填料塔,填料塔的设计将在其他分册中作详细介绍,故本书将只介绍板式塔。
板式塔为逐级接触型气-液传质设备,其种类繁多,根据塔板上气-液接触元件的不同,可分为泡罩塔、浮阀塔、筛板塔、穿流多孔板塔、舌形塔、浮动舌形塔和浮动喷射塔等多种。
Aspen Plus 7.2 在精馏设计中的应用

Aspen Plus 7.2 在精馏设计中的应用作者:王济阳来源:《卷宗》2016年第07期摘要:精馏是化工行业中应用很广泛的一种工艺操作。
本文主要以Aspen Plus 7.2在精馏设计中的应用为例,介绍了Aspen Plus 7.2在化工设计中的步骤和方法。
关键词:Aspen Plus 7.2;精馏;化工设计精馏是化工行业中应用非常广泛的一种工艺操作,影响精馏效果的因素的方面很多。
往往一个因素发生变化时,会引起一些其他因素随之变化。
由于化工模拟软件Aspen Plus的存在,使得化工技术人员工作量减轻很多。
1 Aspen Plus的简介Aspen Plus是大型通用流程模拟系统,源于美国能源部七十年代后期在麻省理工学院(MIT)组织的会战,开发新型第三代流程模拟软件。
该项目称为“过程工程的先进系统”(Advanced System for Process Engineering,简称ASPEN),并于1981年底完成。
1982年为了将其商品化,成立了AspenTech公司,并称之为Aspen Plus。
该软件经过20多年来不断地改进、扩充和提高,已先后推出了十多个版本,成为举世公认的标准大型流程模拟软件,应用案例数以百万计。
全球各大化工、石化、炼油等过程工业制造企业及著名的工程公司都是Aspen Plus的用户。
2 Aspen Plus 7.2对甲醇精馏的模拟通过严格计算RadFrac精馏塔来分离甲醇和水的混合物。
进料组成为水63.2%(质量分数),甲醇36.2%,流率为120000 lb/hr,压力为18 psi (1 psi=6894.76 Pa),饱和液体进料(进料的汽相分率为0),精馏塔有38块塔板,进料在第23块板上。
塔顶压力为16.1 psi,每板的压力降为0.1 psi,塔顶为全凝器,蒸出流率为39885 lb/hr,回流比为1.3。
选用NRTL-RK 物性方法。
计算:1)绘制Aspen Plus的过程流程图;2)再沸器和冷凝器的热负荷。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第6 章:使用稳态计算选择控制结构Steadt-state Calculations for Control Structure Selection 在我们转入将稳态模拟转化为动态模拟细节讨论之前,要先讨论一些重要的稳态模拟计算方法。
因为经常被用于精馏设计中帮助为其选择一个实用且高效的控制结构,。
故此类讨论可能是一定意义的。
绝大部分精馏塔的设计是为了将两种关键组分分离获得指定的分离效果。
通常是两个设计自由度指定为馏出物中重关键组分的浓度和塔底产品中轻关键组分的浓度。
因此,在精馏塔的操作和控制中,“理想的”控制结构需测定两股产品的组成并操控两输入变量(如,回流流量和再沸器的输入热量),从而能够达到两股产品中关键组分的纯度要求。
然而,由于一些现实的原因,很少有精馏塔使用这种理想的控制结构。
组分检测仪通常购价昂贵且维修成本高,其可靠性对连续在线控制而言,有时略显不足。
如果使用色层法,还会在控制回路中引入死时间。
此外,不使用直接测量组分法,通常也有可能取得非常高效的控制效果。
温度测量被广泛应用于组分的推理控制。
温度传感器廉价而又可靠,在控制回路上只有很小的测量滞后。
对恒压二元体系,温度与组成是一一对应相关的。
这在多组分体系中不适用,但精馏塔中合适位置的温度通常能够相当准确地提供关于关键组分浓度的信息。
在单端控制结构中,只需控制某块塔板的温度;选择剩下的“控制自由度”时应使产品质量可变性最小。
例如,确定一定的回流比RR 或者固定回流与进料流量的比值R/F。
有时候,需要控制两个温度(双温控制系统)。
我们将在本章中讨论这些被选方案。
如果选择使用塔板温度控制,那么问题便是选择最佳一块或数块塔板,该处的温度保持恒定。
在精馏文献中,这个问题已讨论了半个世纪以上,且提出了一些可选择的方法。
我们将一一审视这些方法,并举例说明其在各个系统中的有效性。
需要重点关注的是,所有这些方法都仅使用稳态信息,因此,如Aspen Plus 之类的稳态过程模拟器可便捷地用于计算。
这些方法均要求恒定某些变量的同时将另一些变量变化。
例如,两股产品的组成或是某块塔板温度及回流流量恒定不变,而进料组成变化。
在Aspen Plus 中,“Design Spec/Vary”功能可以用来使期望的自变量恒定不变,计算所有其余应变量的值。
在一些方法中,变化的变量是进料组成。
但对于任何一种方法,均不考虑进料流量。
这是因为进料流量的扰动可以直接通过固定受控变量的流量与进料量的比值来处理。
当然,这需要假设整个塔的塔板效率固定不变。
同时,还需要假设每个塔板的压力均不变。
这很少见,因为当气液流率变化时,塔板压降及塔板持液高度也会发生变化。
但是,这些影响均小到不足以对控制系统造成很大的不利影响。
6.1 方法概要6.1.1 斜率判据满足斜率判据,关键在于选择相邻塔板之间温差最大的那块塔板。
绘制出在设计条件下的温度剖面图,研究剖面图的斜率,寻找斜率最大的那块塔板。
相邻塔板之间温度变化大,说明该区域内重要成分的组成发生了变化。
控制此位置的塔板温度不变,则应该可以维持此精馏塔的组成剖面,防止轻组分流向塔底、重组分窜入塔顶。
6.1.2 灵敏度判据满足灵敏度判据的重点在于寻找由于一个受控变量的变化引起最大温度变化的那块塔板。
改变某一个受控变量(比如,回流流量),使其发生很小的变化(设计值的0.1%)。
研究产生的塔板温度变化,观察哪块塔板的温度变化最大。
对于其他受控变量(如再沸器热量输入),重复这一过程。
塔板温度的变化值除以受控变量的变化值,就是这个塔板温度与此受控变量之间的开环稳态增益。
温度变化最大的塔板即是最“灵敏”的,故选择控制它。
增益较大,说明此塔板的温度可以由相应的受控变量有效地控制。
增益较小说明阀门饱和态易于发生,且操作区域受到限制。
6.1.3 奇异值分解判据Moore 曾详尽地研究了稳态增益矩阵中奇异值分解(Singular Value Decomposition)问题。
译者免责声明:译者已经竭尽所能地确保译文正确完整地传达原作的意旨。
然而文中所论及的方法在工程中的具体使用,其使用责任完全在于使用人员。
本文仅为在上节,我们计算了所有塔板温度和两个受控变量之间的稳态增益,从而形成了一个增益矩阵K。
它有N T 行(塔板个数)和2 列(受控变量――回流比R、再沸器热量输入Q――的个数)。
利用标准奇异值分解程序(如Matlab 中的svd 函数,svd(x,0)),将此矩阵分解为三个矩阵:K=UσV T(分解的结果:U 为N T×2 矩阵, σ为2×2 矩阵,V T 为2×2 矩阵)。
以塔盘数为座标轴,绘制两个矢量U1 值和U2 值的曲线。
对应着U 量值最大的一块或数块塔板则指出了塔中最有效的控制位置。
σ是2×2 的对角矩阵,(其对角线元素)是K 矩阵的奇异值。
(σ的对角元素中的)较大值和较小值的比值即为条件数,可以用来评估二元温度控制方案的可行性。
条件数较大(或者最小奇异的值较小)时表明该系统难以控制。
调节器就是装置增益矩阵的逆矩阵,假如奇异值为”0”则说明这是一个退化矩阵,不可转秩。
1.增益矩阵的概念:按照控制理论, 在多变量耦合控制系统中, 选择其中第 i 个受控变量, 当只有 u j 作用时, 即只改变 u j, 使其他各受控变量u k(k=1,2,3….n,k≠j)保持不变, 当u j 变化Δu j 时,所得的控制变量y i 的变化量与u j 的变化量之比,称为u j 到y i 通道的第一放大系数,Δy也有称为开路增益的, K =|(u ,k=1,2,3...,n,k≠j) 此处稳态开路增益的概念与自控常用的相对增益矩阵的概念有区别.iij Δu kj2.奇异值分解的实际例子:上述的描述过于抽象,现在按照Luyben 先生1997 年的” Essentials of Process Control”第458 页的讲述,试举例如下:某9 块塔盘的精馏塔用于分离水和异丙醇,对于其两个受控变量回流比R 及热输入Q, 各塔盘温度有如下的稳态增益:塔盘编号ΔT n/ΔR ΔT n/ΔQ9 -0.0077327 0.01347238 -0.2399404 0.23787527 -2.5041590 2.42231206 -5.9972530 5.78378005 -1.6773120 1.65816304 0.0217166 0.02594783 0.1976678 -0.15867022 0.1289912 -0.10689001 0.0646059 -0.0538632上表内各项即为该塔的稳态增益矩阵K 的各元素, K 矩阵有9 行 2 列⎡ΔT⎡9⎡⎡ΔT⎡⎡8⎡⎡=.⎡⎡⎡⎡.⎡⎡ΔT⎡⎡1⎡R⎡K⎡⎡⎡⎡Q对K 做奇异值分解,得到以下3 个矩阵: K= UΣV T⎡- Σ= 9 V T =0.0015968 - 0.0828981⎡U=⎡⎡⎡⎡.3452 0- 0.0361514 - 0.0835548⎡⎡⎡⎡⎡0.7191619⎡−0.6948426⎡−0.6948426⎡⎡−0.7191619⎡- 0.8915611 0.1473784⎡⎡⎡⎡- 0.2523673 - 0.6482796⎡⎡⎡⎡- 0.0002581 - 0.6482796⎡⎡0.0270092 - 0.4463671⎡⎡⎡0.0178741 - 0.2450451⎡⎡⎡⎡⎡0.0089766 - 0.1182182则矩阵U 的第一列中最大的元素是-0.8915611, 对应的塔盘数为6, 因此, SVD法的结论是受控变量为回流量时,可以控制第6块塔盘的温度.必须指出,一般的对于一个m×n 阶矩阵A 的奇异值分解,得到的是一个m×m 阶正交矩阵U, m×n 阶对角阵Σ和n×n 阶正交矩阵V,这时所用的MATLAB 命令是[U,S,V] = svd(X),此处所用的MATLAB 命令是[U,S,V] = svd(X,0), 即求”经济尺寸”的奇异值分解,与常规的SVD 得到的U,Σ,V 的矩阵阶数并不相同.详情请参见MATLAB 主页: /access/helpdesk/help/techdoc/ref/svd.html译者免责声明:译者已经竭尽所能地确保译文正确完整地传达原作的意旨。
然而文中所论及的方法在工程中的具体使用,其使用责任完全在于使用人员。
本文仅为学习了解所用,一切版权归于John Wiley & Sons,Inc. 请于下载后的24 小时之内将此删除,译者不承担由此引起的一切法律责任。
第 3 页共18 页3.条件数的概念: 在数值计算领域,条件数是与特定问题使用数字计算的可控制性(适定性)相关的一个度量参数.问题的 条件数较小,则称其为良态的,假如条件数较大则称为病态的. 对于矩阵的条件数而言,并没有关于良态和病态的界定数 值.在我们的讨论所涉及范围内, 由条件数的定义推导出: 矩阵的条件数 κ(A), 有:σ(A ) κ(A)=maxσ (A )min其中σmax (A)和σmin (A)分别是矩阵 A 奇异值的极大和极小值.扩展阅读资料:1. 有关奇异值分解在增益矩阵上的应用,参见:C. F. Moore, Selection of controlled and manipulated variables, in Practical Distillation Control, Van Nostrand- Reinhold, 1992, Chapter 8. 或 Luyben 的 Essentials of Process Control,(1997)第 13 章; 或 Luyben 的 Plantwide Process Control(1998) 第 6 章.2. 有关奇异值分解本身的线性代数定义、意义及其在数值计算中的作用及 MATLAB 中的基本使用,建议阅读:《数值 分析与科学计算》,第 2 章等相关内容,Jeffery J. Leader 著,清华大学出版社 2008 年 5 月第 1 版。
3.有关开路稳态增益、增益矩阵、相对增益矩阵及其解析解法的实际应用,增益值的对比和对实际控制结构选择上的 指导意义,参见《自动化仪表与过程控制,第四版》第 8 章及以下相关内容,作者:施仁、刘文江等,电子工业出版 社,2009 年 2 月第 1 版。
6.1.4 恒定温度判据判据保持塔的馏出物和塔底产品的纯度不变,我们在预期的范围里改变进料组成值。
选择其温度不随进料组成变化而变化 那块塔板。
这个方法的困难性在于,对于进料组成的所有变化,可能并不存在保持恒定温度的塔板。
