矩阵论 第二章 入-矩阵与矩阵的Jordan标准形
矩阵与矩阵的标准形

λ ( λ + 1) λ λ ≃ 2 ( λ + 1) λ ( λ + 1) ≃ λ λ − λ ( λ + 2) 1
λ ( λ + 1) 3 2 ≃ λ + 2λ + λ 0 2 − λ − 2λ 1 λ ( λ + 1) 2 ≃ λ (λ + 1) 1 1 λ ( λ + 1) ≃ 2 λ (λ + 1)
将其化为Smith标准形。 解:
0 0 −1 λ − a λ − a 0 −1 0 A( λ ) ≃ 0 λ − a −1 0 0 0 λ − a 0
−1 λ − a 0 (λ − a )2 ≃ 0 0 0 0 0 1 0 (λ − a )2 ≃ 0 0 0 0
1 0 ≃ 0 0
1 0 0 0 1 0 4 0 0 (λ − a ) 0 0 0
λ 矩阵标准形的唯一性
定 义:A( λ ) 为一个 λ 矩阵且 rank ( A( λ )) = r 对 于任意的正整数 k ,1 ≤ k ≤ r , ( λ ) 必有非零的 k A 阶子式, 阶子式,A( λ ) 的全部 k 阶子式的最大公因式 Dk ( λ ) 行列式因子。 称为 A( λ ) 的 k 阶行列式因子。
2
2 1 0 λ2 + λ − 4 ≃ λ −2 λ −1 2 2 4λ + 3λ − 7 3λ − 3 λ + 3λ − 4 2 0 1 2 λ −2 ≃ λ +λ −4 λ −1 2 2 3λ − 3 4λ + 3λ − 7 λ + 3λ − 4
2.3 矩阵的Jordan标准形

a11 (λ ) a12 (λ ) a1n (λ ) a21 (λ ) a22 (λ ) a2 n (λ ) A(λ ) = a (λ ) a (λ ) a (λ ) m1 m2 mn
6 2 2 − 6 k1 − 3k2 3 . 1 1 − 3 − k1 , 1 1 − 3 − k 2 4 设 P −1 AP = J , 1 . P = (ξ1 , ξ 2 , ξ 3 ), 1 2 2 −6
′ = ( 2, 0, 1) , ξ1 = ( −1, 1, 0) , ξ 2 = ( 3, 0, 1) ? ξ 2 T T ξ = ( 2 , 0 , 1 ) , ′ ′ ξ 2 = k1ξ1 + k2ξ 2 = ξ1 + ξ 2 = ( 2, 1, 1) , 3 k1 = k2 = 1, 第二章 λ-矩阵
λi J 1 0 其一般形状 , 其中 J i = J s 1 1 λi ki ×ki
λi
第二章
λ-矩阵
3
初等因子, Jordan形的推导
例
D3(λ) = (λ-2) , λE-A有一个2阶子式
A= 0 2 2 1 2 1 2
第二章 λ-矩阵
5
初等因子, Jordan形的推导
− 1 − 2 6 例 求矩阵A的Jordan标准形, A = − 1 0 3 . − 1 − 1 4 解 1 λ − 4 r2 − r1 1 λ +1 2 − 6 r3 − (λ + 1)r1 r1 ↔ r3 λ −3 λE − A = 1 λ −3 1 λ +1 2 − 6 1 1 − 4 λ 1 0 0 λ −4 1 c2 − c1 1 c3 − (λ − 4)c1 1− λ 1− λ 0 λ −1 0 λ −1 0 1 − λ − (λ − 1)(λ − 2) 0 1 − λ − (λ − 1)(λ − 2) 0 0 0 0 1 1 r3 + r2 c3 + c2 1− λ 0 Smith标准形. 0 λ −1 0 λ −1 2 ( −1)r3 2 0 − − − 0 ( λ 1 ) 0 0 ( λ 1 ) 1 A的初等因子: λ-1, (λ-1)2. J = 1 1 . A的Jordan标准形为: 6 1 第二章 λ-矩阵
矩阵多项式的Jordan标准形

A(λ)=[■(a_11 (λ)&a_12 (λ)&⋯&a_1n (λ)@a_21 (λ)&a_22 (λ)&⋯&a_2n (λ)@⋮&⋮&&⋮@a_m1 (λ)&a_m2 (λ)&⋯&a_mn (λ) )]
在实际应用中,我们遇到的往往不是单个矩阵,而是矩阵函数[ ]。而多项式是最简单的一类函数,因此讨论矩阵多项式的Jordan标准形是有意义的。 专家通过对矩阵方幂的Jordan标准形进行研究,已有如下结论:可逆矩阵A的任意次幂A^m与A有相同的Jordan标准形,仅把对角元λ_i换为〖λ_i〗^m。但是对于矩阵多项式f(A)的Jordan标准形的研究较少,这也是本文的难点和创新之处。
第二章,主要给出了两种经典的求Jordan标准形的方法,第一种为通过求初等因子进而得到Jordan标准形的普通方法;第二种方法通过确定矩阵A每个特征值对应的Jordan块总数和各阶Jordan块的数目,进而得到A的Jordan标准形。
第三章,利用相似矩阵具有相同的Jordan标准形,分析Jordan块J_i、Jordan多项式f(J)以及矩阵多项式f(A)的关系,对Jordan块J_i是否可逆分情况进行讨论,最后得到求矩阵多项式f(A)的Jordan标准形的方法。
虽然有些矩阵不能相似于对角阵,但任意矩阵总能相似于一个形式上比对角阵稍复杂的Jordan标准形J.下面给出Jordan块与Jordan标准形的定义。
定义1.1.5 形如
J_i=[■(λ_i&0&⋯&0&0&0@1&λ_i&⋯&0&0&0@⋮&⋮&&⋮&⋮&⋮@0&0&⋯&1&λ_i&0@0&0&⋯&0&1&λ_i )]_(s_i×s_i )
第2章矩阵与矩阵的Jordan标准形(详解)
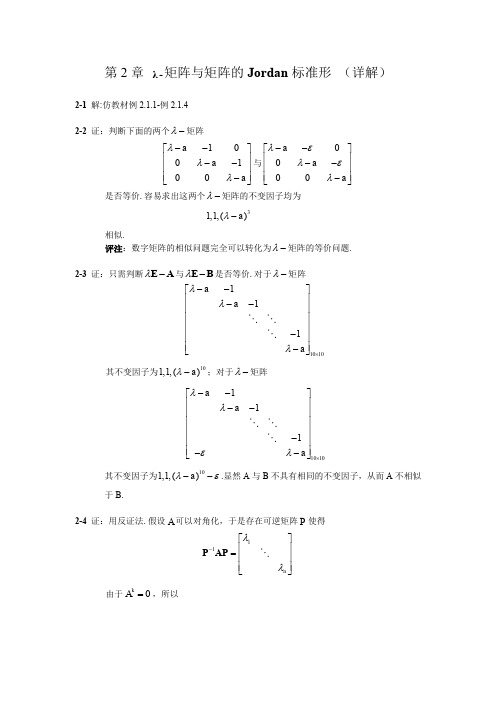
第2章 λ-矩阵与矩阵的Jordan 标准形 (详解)2-1 解:仿教材例2.1.1-例2.1.42-2 证:判断下面的两个λ-矩阵100100a a a λλλ--⎡⎤⎢⎥--⎢⎥⎢⎥-⎣⎦与0000a a a λελελ--⎡⎤⎢⎥--⎢⎥⎢⎥-⎣⎦是否等价.容易求出这两个λ-矩阵的不变因子均为31,1,()a λ-相似.评注:数字矩阵的相似问题完全可以转化为λ-矩阵的等价问题.2-3 证:只需判断λ-E A 与λ-E B 是否等价.对于λ-矩阵1010111a a a λλλ⨯--⎡⎤⎢⎥--⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥-⎣⎦ 其不变因子为101,1,()a λ-;对于λ-矩阵1010111a a a λλελ⨯--⎡⎤⎢⎥--⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥--⎣⎦ 其不变因子为101,1,()a λε--.显然A 与B 不具有相同的不变因子,从而A 不相似于B.2-4 证:用反证法.假设A 可以对角化,于是存在可逆矩阵P 使得11n λλ-⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦P AP 由于0kA =,所以11()0k k n λλ-⎡⎤⎢⎥==⎢⎥⎢⎥⎣⎦A P P 即10k k n λλ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦由此可知120n λλλ====,故100-⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦P AP 这表明0A =,这与0A ≠矛盾.2-5 证:只要证明A 的每一个Jordan 标准形为1211,1i iiii s i n n a a a ⨯⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦J J J J J 那么存在相似变换矩阵P 使得1-=P AP J .因此1k k -==J P A P E于是有111ik k ii k k iiki k k i k i a ka a ka ka a ---⎡⎤⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎣⎦J E故i J 必为一阶子块,即s n -.所以A 与对角矩阵相似.2-6证:设A 的若当标准形为11,1ii s i J J J J λλ⎛⎫⎛⎫ ⎪ ⎪ ⎪== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭1J Q AQ -=,由2A A =有2J J =,从而i J 都是一阶的,再利用矩阵的初等变换调整对角线上的元素,得证.2-7解:仿教材上的例题.2-8解:仿教材上的例题.2-9 解:用两种方法求解此题.方法一 相似变换矩阵的方法.对于任意一个可逆矩阵P ,矩阵1-PJP 均与矩阵J 相似,从而其Jordan 标准形必为J ,于是任取两个不同的可逆矩阵P ,即可得到两个矩阵A ,B .方法二 矩阵秩的方法.设A (或B )的Jordan 标准形为100021002⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦从而A (或B )的Smith 标准形为211(2)(1)λλ⎡⎤⎢⎥⎢⎥⎢⎥--⎣⎦由此可知A (或B )的行列式因子为2123()1,()1,()(2)(1)D D D λλλλλ===--这样的矩阵A (或B )有很多,取表达式较为简单的矩阵,下列任何一种矩阵都可以200100200*10,*20,*20,**2**2**12**1**2**01*,02*,020********⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦下面分析“*”处元素取何值时才能保证1为主对角元的Jordan 块只有一个,以2为主对角元的Jordan 块也只有一个.根据求矩阵Jordan 标准形的第二种方法(矩阵秩的方法),只要使(2)2r -=A E 或(2)2r -=B E即可.例如20020-1921,010001002⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦均可以.但2001-10020,021051002⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦都不可以. 2-10解(思路)设1Q JQ A -=,其中J 是A 的若当标准形,则1001100A Q J Q -=2-11解: A 的不变因子()()()()123,,133λ(λ+1)λn d d d d λλλλ=====;由A 的初等因子以及E A λ-的秩为n 写出A 的若当标准形J .2-12解:仿教材例题.2-13解: 仿教材例题.2-14 解:因为()10λ=-≠A 1()1λλλλλ--⎡⎤=⎢⎥-+⎣⎦A故 11()1λλλλλ--+⎡⎤=⎢⎥--⎣⎦A 注:n 阶λ-矩阵()λA 的秩为n ,不等价于()λA 可逆,这是与数字矩阵不相同之处.例如1()1λλλ⎡⎤=⎢⎥⎣⎦A 的秩为2,但是它不可逆. 2-15 解:()λA 的元素中有非零常数212221321222122132223221111()2222221101102220031122221111222220010214202,2c c c c c c r r r r c c λλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥←−→⎢⎥⎢⎥=+--+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥++⎣⎦⎣⎦⎡⎤-+⎢⎥⎢⎥⎢⎥-+-+-⎢⎥⎢⎥⎢⎥+---⎣⎦-++-+-+----A ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦132221222432224323243231000421012100()04214100(3)4100(21)0404003410010104003c c c r c rc c λλλλλλλλλλλλλλλλλλλλλλλ⎡⎤←−→⎢⎥-+-⎢⎥⎢⎥---⎣⎦⎡⎤⎢⎥+⎢⎥-+-⎢⎥⎢⎥-+--⎢⎥⎣⎦⎡⎤-+⎢⎥⎢⎥⎢⎥-+--⎣⎦⎡⎤⎢⎥⎢⎥⎢⎥-++⎣⎦-2-16 解:()λA 的元素有公因子λ,所以额可以用初等变换把左上角元素变成λ3223122222112223322()533515353223c c c r r λλλλλλλλλλλλλλλλλλλλλλλλλ⎡⎤⎡⎤-←−→-=⎢⎥⎢⎥++⎣⎦⎣⎦⎡⎤+⎡⎤←−→+⎢⎥⎢⎥⎢⎥--⎣⎦⎢⎥⎣⎦A然后用初等变换把公因子λ所在的行、列的其余元素均化为零.2212223122525()320(103)33(5)00(103)r r c c λλλλλλλλλλλλλλλλλλλ⎡⎤+⎡⎤+-⨯+⎢⎥⎢⎥=⎢⎥⎢⎥---⎢⎥⎢⎥⎣⎦⎣⎦-++⎡⎤⎢⎥--⎣⎦A2-17 解:()λA 的元素无公因子,也无常数元素.用初等变换把矩阵中某一个元素变成常数22212222222123221343221232432110()11100(1)0100()00r r r r r r c c λλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλ⎡⎤⎡⎤-++⎢⎥⎢⎥=--⎢⎥⎢⎥⎢⎥⎢⎥+-+-⎣⎦⎣⎦⎡⎤+-+⎢⎥--+-⎢⎥-++⎢⎥----⎣⎦⎡⎤-++⎢⎥--+-⎢⎥⎢⎥----⎣⎦A剩下的右下角的二阶矩阵有公因子λ,参照2-16用的方法.有32432233224323322223223100()0010000100000100(1)0000110010000(1)c c r r c c r r λλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλ⎡⎤⎢⎥--+-⎢⎥⎢⎥----⎣⎦⎡⎤←−→⎢⎥---+⎢⎥⎢⎥----⎣⎦⎡⎤-+⎢⎥---+⎢⎥⎢⎥--⎣⎦⎡⎤-+-+⎢⎥-⎢⎥⎢⎥--⎣⎦-⨯⎡⎤-⨯⎢⎥⎢⎥⎢⎥+⎣⎦A2-18 解:()λA 的元素中有常数.2322123212213323243243212323213(1)1()11(1)1(1)11(1)(+1)1(1)(1)0210100(1)02c c r r r r c c c c λλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλ⎡⎤+⎢⎥=+-⎢⎥⎢⎥-⎣⎦⎡⎤+←−→⎢⎥+-⎢⎥⎢⎥-⎣⎦-+⎡⎤+--+⎢⎥----+-⎢⎥⎢⎥-++-++⎣⎦-++----+A 243243210λλλλλλλλ⎡⎤⎢⎥-+-⎢⎥⎢⎥-++-++⎣⎦剩下的二阶矩阵使元素既无公因子又无常数的矩阵,参照2-17的方法可把二阶矩阵初等变换化3232432432233224323222432100()0210100021001000100c c c c λλλλλλλλλλλλλλλλλλλλλλλλλλλ⎡⎤⎢⎥----+-⎢⎥⎢⎥-++-++⎣⎦⎡⎤-+⎢⎥--+-⎢⎥⎢⎥-++⎣⎦⎡⎤++⎢⎥--+-⎢⎥⎢⎥-++⎣⎦A2324324322324324322234322432432232432100010100010100()0100(1)()100()01000(1)()c c c c c c r r λλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλ⎡⎤+⎢⎥---⎢⎥⎢⎥-++-++⎣⎦⎡⎤←−→⎢⎥---⎢⎥⎢⎥-++-++⎣⎦⎡⎤--+⎢⎥-⎢⎥⎢⎥-++--+-++⎣⎦⎡-+++--+-++⎤⎢⎥⎢⎥⎢⎥⎣⎦2-19 解:()λA 虽然是对角形,但不是Smith 标准形.2232233222(1)()(1)(1)(1)(1)00(2)0200211(1)(1)c c r r λλλλλλλλλλλλλλλλλλλλλλ+⎡⎤⎢⎥=⎢⎥⎢⎥+⎣⎦+⎡⎤+⎢⎥⎢⎥⎢⎥+⎣⎦+⎡⎤-++⎢⎥++⎢⎥⎢⎥--⎣⎦⎡⎤⎢⎥+⎢⎥⎢⎥+⎣⎦A2-20 解:首先容易求出()λA 的不变因子233342321()(1)(2)(2)()(1)()(1)()1d i i d d d λλλλλλλλλλλλ=-+-=-=-=于是()λA 的Smith 标准形为223331000000(1)0000()00(1)000000(1)(2)(2)00000000i i λλλλλλλλλ⎡⎤⎢⎥-⎢⎥⎢⎥=-⎢⎥-+-⎢⎥⎢⎥⎣⎦A对于准对角形矩阵()0()0()λλλ⎡⎤=⎢⎥⎣⎦B A C 为准对角形矩阵,则()λB 与()λC 的不变因子求得()λA 的不变因子,但是能从()λB 与()λC 的初等因子立即得到()λA 的初等因子.2-21 解:方法一 ()λA 行列式因子易得为121()()()1,()()n n n a λλλλλ-=====-D D D D于是()λA 的不变因子为121()()()1,()()n n n d d d d a λλλλλ-=====-因而初等因子只有一个方法二 对()λA 用初等变换求得不变因子为11,1,,1,()n n a λ--个故初等因子为()n a λ-2-22 解:将()λA 之第二行,第三行,,第n 行分别乘以21,,,n λλλ-都加第一行上去,得到1221000()10010()00001n n f a a a a λλλλλ--⎡⎤⎢⎥-⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥--⎢⎥⎣⎦A 其中 12121()n n n n n f a a a a λλλλλ---=+++++易得 det ()()f λλ=A 故 ()()n f λλ=D 又 1()1n λ-=D 于是 122()()()1n λλλ-====D D D所以 121()()()1,()()n n d d d d f λλλλλ-=====因此()λA 之Smith 标准形为1()1()f λλ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦A2-23 解:因为A 的初等因子乘积22(1)1λλλλλ-+是7次多项式,故A 是7阶的.2-24 解:A 是5阶矩阵,答案有如下几种情况:(1)A 的初等因子1,1,2,2,2λλλλλ++---A 的不变因子1,1,2,(1)(2),(1)(2)λλλλλ-+-+-(2)A 的初等因子21,1,2,(2)λλλλ++--A 的不变因子21,1,1,(1)(2),(1)(2)λλλλ+-+-(3)A 的初等因子21,1,(2)λλλ++-A 的不变因子31,1,1,1,(1)(2)λλλ++-(4)A 的初等因子2(1),2,2,2λλλλ+---A 的不变因子31,1,2,2,(2)(1)λλλλ---+(5)A 的初等因子22(1),2,(2)λλλ+--A 的不变因子221,1,1,2,1,(2)(1)λλλλ-+-+(6)A 的初等因子22(1),(2)λλ+-A 的不变因子231,1,1,1,(1)(2)λλ+-2-25 解:先求A 的初等因子.对()λ-E A 运用初等变换可得21261131114(1)λλλλλλ+-⎡⎤⎡⎤⎢⎥⎢⎥-=--⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦E A A 的初等因子是21,(1)λλ--故A 的Jordan 标准形是100011001⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦J2-26 解:100011001⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦AJ故存在333c ⨯∈P ,满足=AP PJ命 123(,,)=P X X X (1) 把P 代入式(1)得123123100(,,)(,,)011001⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦AX AX AX X X X (2)比较式(2)两边得1122323,,===+AX X AX X AX X X即 1232()0,()0,()-=-=-=-E A X E A X E A X X在上述每个方程组中只要依次取一个解分别为123,,X X X ,组成123(,,)=P X X X 即可.易见12,X X 是A 的特征值为1的两个线性无关的特征向量.解方程组()0-=E A X可求得两个线性无关的特征向量(1,1,0),(3,0,1)T T =-=ξη若取12,==ξX ηX ,代入32()-=-E A X X ,该方程组无解,这时不能认为P 不存在.因为A 的特征子空间是二维的,即A 的线性无关特征向量不仅是,ξη.例如,只要,S t 满足1≠St 的任意数,,++ξS ηt ξη也是A 的线性无关特征向量.因此,若取12,k ==+X ξX ξη(0)k ≠,k 只要使得方程组32()-=-E A X X 有解.不难知道当1k =时,取2(2,1,1)T=+=X ξη代入32()-=-E A X X 方程组有解为1232331(,)x x x x x =-+-为任意数取它的一个解3(2,0,1)T=X ,就可.于是122110011-⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦P容易验证有1100011001-⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦P AP从以上两例可以概括出求Jordan 标准形变换矩阵P 的过程.设A 的Jordan 标准形为J ,则12s ⎡⎤⎢⎥⎢⎥===⎢⎥⎢⎥⎣⎦J J AP PJ P J 其中111i iiii n n λλλ⨯⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦J 把变换矩阵P 按Jordan 块i J 的阶数i n 进行相应的分块,即设12(,,,)S =P P P P其中in n i C⨯∈P ,因此12121212(,,,)(,,,)(,,,)S S S s =⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦A P P P P P P J J J P P P J 故 121122(,,,)(,,,)S s S =AP AP AP J P J P J P比较上式两端得i i i =AP P J (1,2,,)i s =对i P 再按列分块12(,,,)i i n n i i i in C ⨯=∈P X X X其中12,,,i i i in X X X 是i n 个线性无关的n 维列向量,代入i i i =AP P J 可得1121221i i i i i i i i i i i n in i in λλλ-=⎧⎪=+⎪⎨⎪⎪=+⎩AX X AX X X AX XX (1,2,,)i s =由第一个方程看到,列向量1i X 是矩阵A 的特征为i λ所对的特征向量.且由1i X 继而可以求得23,,,i i i in X X X .因此,长方形矩阵i P 以至P 都可以求得.由前面例子中可以看到,特征向量1i X 的选取要保证2i X 可以求出,类似地2i X 的选取(因为2i X 的选定并不唯一,只要适当选取一个就可)也要保证3i X 可以求出,如此等等.2-27 解:两种可能性. ①初等因子321,(1),2,(2)λλλλ++--,②初等因子222(1),(1),2,(2)λλλλ++-- (Jordan标准形略).2-28 解:A.若i j λλ≠,则21()()1()2()(1)1()0()i i i i i i i i i n i i i i i h i i i i a rank n rank n rank n n rank h n λλλλ--=--=--=--=-=≥E J E J E J EJ()()(1,2,)l i j j j b rank n l λ-==E J 2()[](1)1[](2)2[]()ii i j i j i j j ii i j i j i j j ihi i j j i j c rank n n n n rank n n n n rank n h n λλλ+++⎛⎫-=-+=+-⎪⎝⎭⎛⎫-=-+=+-⎪⎝⎭⎛⎫-=≥⎪⎝⎭J E J J E J J EJ B .若i j λλ=,不妨设i j n n >,则2()()1()2()0()i j j i i j j i h i j j j a rank n rank n rank h n λλλ-=--=--=≥E J E J EJ21()[](1)(1)2[](2)(2)4[]((1))((1))2[]()()j jii i j i j i j j ii i j i j i j j in i i j i j j j i j j in i i j i j j j i j c rank n n n n rank n n n n rank n n n n n n rank n n n n n n λλλλ++-++⎛⎫-=-+-=+-⎪⎝⎭⎛⎫-=-+-=+-⎪⎝⎭⎛⎫-=--+--=-+⎪⎝⎭⎛⎫-=-+-=-⎪⎝⎭J E J J E J J E J J EJ 12[][(1)]0(1)[](2)[]0j j ij in i i j i j j i j in i i j i j j in i i j j rank n n n n rank n n rank λλλ+++++⎛⎫-=-++⎪⎝⎭=-+⎛⎫-=-+⎪⎝⎭⎛⎫-=⎪⎝⎭J E J J E J J EJ反过来,可以借助(),()kki i i i j j rank rank λλ--E J E J ,[]ik i i j j rank λ+⎛⎫-⎪⎝⎭J E J 得出,i j J J 的阶数,i j n n .由于()()k k i i rank rank λλ-=-E J E A ,因此可以借助计算()ki rank λ-E J 得到Jordan 块的个数,阶数分析,继而可得J 的形状.2-29 解: 4(1)λλ-=-E A234()3,()2()1,()0rank rank rank rank -=-=-=-=E A E A E A E A因此,Jordan 块是4阶1块,即1111111⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦A2-30 解:命 123(,,)Tx x x =X ,则方程组可写为126103114d dt --⎡⎤⎢⎥=-=⎢⎥⎢⎥--⎣⎦X X AX 其中 126103114--⎡⎤⎢⎥=-⎢⎥⎢⎥--⎣⎦A 1100011001-⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦P AP其中 122110011-⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦P 1102112113--⎡⎤⎢⎥=-⎢⎥⎢⎥--⎣⎦P令X =PY 得113322132333222()()()t t t t t t tx k e k e k t k e x k e k t k e x k e k t k e =-+++=++=++其中123,,k k k 为任意常数.2-31 解:先求A 的初等因子,然后求得A 的Jordan 标准形2124⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦J设123(,,)Tααα=P ,且1-=P AP J ,即=AP JP . 于是111211213332(2)02(2)4(4)0ααααααααααα=-==+-=-=-=A E A A E A A E A不难求得1(0,1,0)T α=211(,0,)22T α=-3(1,0,1)T α=11010102100,101111010222-⎡⎤⎡⎤-⎢⎥⎢⎥⎢⎥⎢⎥==-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦P P于是10121010210021011411010222⎡⎤⎡⎤-⎢⎥⎢⎥⎡⎤⎢⎥⎢⎥⎢⎥=-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥⎣⎦⎣⎦A10099100100100991999919999100999919999199101210020102100210114110102222202210022100222022⎡⎤⎡⎤-⎢⎥⎢⎥⎡⎤⎢⎥⎢⎥⎢⎥=-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥⎣⎦⎣⎦⎡⎤-+-+⎢⎥=-⎢⎥⎢⎥-++⎣⎦A2-32 证:由2k =A A 可知A 的特征值只可能是0,k.方法一:由2k =A A 得()0kE A -=A 故秩()A +秩()kE A -n ≤又秩()A +秩()kE A - ≥秩()kE A +-A =秩()k E =n 因此秩()A +秩()kE A -n =若秩()A r =,则A 属于特征值为0的线性无关特征俩向量有r -n 个,A 的属于特征值为k 的线性无关特征向量有n-秩()kE A -=n-[n-秩()A ]=r.所以A 共有(n-r )+r=n 个线性无关特征向量.于是A 可对角化. 方法二:设A 的Jordan 标准形为12(,,,)r diag =J J J J .于是存在可逆矩阵P ,11,--==P AP J A PJP代入2k =A A 可得22,,(1,2,,)i i k k i r ===J J J J .不难验算可知,若2i i k =J J ,i J 必须是一阶Jordan 块.因此A 的Jordan 块(1,2,,)i i r =J 全是一阶的.因此A 与对角矩阵相似.2-33 证:设A 的Jordan 标准形12(,,,)r diag =J J J J ,即存在可逆矩阵P ,满足112(,,,)r diag -==J J J J PAP于是112(,,,)()T T T T T T T r diag -==J J J J P A P这表明TT AJ ,所以如果能证明对于每一个(1,2,,)i i r =都有Ti i J J .则根据相似的传递性便知TA A .事实上,若令00101010i ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦P (i P 的阶数=i J 的阶数) 则不难验证1,T i i i i i i -==P P P J P J (证毕)2-34 解:121001011n n a a a a λλλλ-⎡⎤⎢⎥-⎢⎥⎢⎥-=-⎢⎥⎢⎥⎢⎥-+⎣⎦EC 它的不变因子为111(1)1,11,n n n n n a a a λλλ---++++个.2-35 解:2321111(1)(2)584λλλλλλ⎡⎤⎡⎤⎢⎥⎢⎥-==⎢⎥⎢⎥⎢⎥⎢⎥---+-⎣⎦⎣⎦E A100004021108002015⎡⎤⎡⎤⎢⎥⎢⎥==-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦AJ F052100031⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦P为了求Q 需先求FJ 的变换矩阵M ,即=FM MJ设123(,,)βββ=M ,代入=FM MJ 得123123100(,,)(,,)021002ββββββ⎡⎤⎢⎥==⎢⎥⎢⎥⎣⎦F比较两边得1122323,2,2βββββββ===+F F F解之得123(4,4,1),(2,3,1)(1,1,0)T T T βββ=-=-=-于是123421(,,)431110βββ-⎡⎤⎢⎥==--⎢⎥⎢⎥⎣⎦M1111110124-⎡⎤⎢⎥=--⎢⎥⎢⎥⎣⎦M故1052111318100110111031124214---⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥==--⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦Q PM2-36 解:221111(1)21λλλλλλ⎡⎤⎡⎤⎢⎥⎢⎥--=-⎢⎥⎢⎥⎢⎥⎢⎥--+⎣⎦⎣⎦E A因此100100011001001002⎡⎤⎡⎤⎢⎥⎢⎥==-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦A J F 122110011-⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦P 为了求Q 需先求F J 的变换矩阵M ,即=FM MJ 设123(,,)βββ=M ,代入=FM MJ 得123123100(,,)(,,)011001ββββββ⎡⎤⎢⎥==⎢⎥⎢⎥⎣⎦F 比较两边得1122323,,βββββββ===+F F F解之得123(1,0,0),(0,1,1)(0,1,0)T T T βββ==-=故123100(,,)011010βββ⎡⎤⎢⎥==-⎢⎥⎢⎥⎣⎦M 1100001011-⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦M 于是1122100110001011011124101012--⎡⎤⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦-⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦Q PM2-37 解:(1)A 的初等因子21,(2)λλ+-故A 的不变因子为321,1,34λλ-+ 于是A 的有理标准形为 004100013-⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦F(2)A 的初等因子21,(1)λλ-- 故A 的不变因子为21,1,(1)λλ-- 于是A 的有理标准形为100001012⎡⎤⎢⎥=-⎢⎥⎢⎥⎣⎦F。
浅谈矩阵Jordan标准形及其应用

数学写作论文题目:浅谈矩阵Jordan标准形及其应用专业代码:作者姓名:学号:单位: 级班指导教师:年月日原创性声明本人郑重声明: 所提交的学位论文是本人在导师指导下, 独立进行研究取得的成果. 除文中已经注明引用的内容外, 论文中不含其他人已经发表或撰写过的研究成果, 也不包含为获得聊城大学或其他教育机构的学位证书而使用过的材料. 对本文的研究做出重要贡献的个人和集体, 均已在文中以明确方式标明. 本人承担本声明的相应责任.学位论文作者签名: 日期指导教师签名: 日期目录第一章引言 (1)第二章基本概念 (1)2.1若尔当标准形的定义 (1)2.2若尔当标准形的性质 (3)第三章若尔当标准形的应用 (5)3.1矩阵分解论中的应用 (5)3.2解矩阵方程中的应用 (6)3.3解线性递推关系式中的应用 (7)3.4哈密顿—凯莱定理的证明 (11)第四章结束语 (13)参考文献 (14)致谢 (15)摘要矩阵在高等代数中占有举足轻重的作用.而且矩阵有很多形式,本文主要介绍Jordan标准形的定义、性质及其应用,例如:每个n级复数都与一个若尔当形矩阵相似、复数矩阵A与对角矩阵相似的充分必要条件是A的不变因子没有重根等,对于今后的高等代数的进一步研究学习有很大的帮助.关键词:若尔当标准形; 矩阵分解; 线性递推; 哈密顿—凯莱定理AbstractMatrix is very import in high level mathematic. There are many kinds of matrix. This paper describes several equivalent definitions of mathematic, and then focused on the properties of Jordan matrix and application of the Jordan matrix such as every n level plural is similar for a Jordon matrix, plural A is similar to diagonally matrix on the base of the unconverted factor without two same resultsKey words Jordan matrix; matrix resolve; analysis linearly; Hamilton-Caylay浅谈矩阵Jordan标准形及其应用第一章引言在学习与代数相关的知识中,矩阵的学习是必须的,在高等代数中矩阵是研究问题很重要的工具.在研究矩阵相似问题时,若尔当块、若尔当标准形的定义及简单性质比较容易给出,但对若尔当标准形一些具有规律性的性质研究却很少,而正是这些性质使得若尔当标准形具有极其重要的理论和应用价值.对于若尔当标准形的性质及其应用,大多都是从相似的角度提及.但在大量实际应用中不难发现,将一般矩阵的问题化为若尔当标准形来讨论,可以使问题得到简化.为此,本文将围绕若尔当标准形的应用,从四个大方面:若尔当标准形在矩阵分解论中的应用、若尔当标准形在解线性递推关系式中的应用、若尔当标准形在矩阵方程中的应用、以及用若尔当标准形证明哈密顿—凯莱(Hamilton-Caylay)定理,来对若尔当标准形的应用进行归纳总结.本文以例题的形式给出了若尔当矩阵在这四个方面的应用,通过同常规解题方法的比较,不难得出,矩阵的若尔当标准形对于我们求解某些矩阵的幂、行列式的值以及证明都是很有用的.总的来说,本文从若尔当标准形的定义及简单性质出发,对若尔当标准形的应用做了系统的梳理.第二章 Jordan标准形基本概念2.1定义形式为0 (000)1 (000)(,)00 (10)00 (01)t t J tλλλλλ⨯⎛⎫⎪⎪⎪=⎪⎪⎪⎝⎭的矩阵为若尔当(Jordan )块,其中λ是复数.由若干个若尔当块组成的准对角矩阵为若尔当形矩阵,其一般形式如12s J J J ⎛⎫ ⎪ ⎪ ⎪ ⎪⎝⎭,其中1=11i i i ii ii k k J λλλλ⨯⎛⎫ ⎪ ⎪⎪ ⎪ ⎪ ⎪⎝⎭,并且12,,......,s λλλ中有一些可以相等.特别地,一级若尔当块就是一级矩阵,因此若尔当矩阵包括对角矩阵.在复数域范围内,对任意方阵A 总存在可逆矩阵P ,使11k J P AP J -⎛⎫⎪=⎪ ⎪⎝⎭,其中11ii i J λλ⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭为若尔当块()1,2,,i k =.而1k J J ⎛⎫ ⎪ ⎪ ⎪⎝⎭称为A 的若尔当标准形.2.2性质性质1 n 级的复矩阵A 的若尔当标准形除去其中若尔当块的排列次序外是被矩阵A 唯一确定的.性质2 n 级的复矩阵A 的若尔当标准形J ,主对角线上的元素正是A 的特征多项式的全部的根,即A 的全部特征值(重根按重数计算).性质3 复数矩阵A 与对角矩阵相似的充分必要条件是,A 的若尔当标准形全由1级的若尔当块构成.性质4 设n nA C ⨯∈,()[]f x C x ∈,若12,,,nλλλ为A 的全部特征值,则()f A 的全部特征值为12(),(),,()n f f f λλλ,即11()()()n f P f A P f λλ-⎛⎫⎪=⎪ ⎪*⎝⎭.证明 设110n P AP λλ-⎛⎫⎪=⎪ ⎪⎝⎭为A 的若尔当标准形,再设10()m m f x a x a x a =+++,则111100()n n f A f P P PfP λλλλ--⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪⎪ ⎪== ⎪ ⎪⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭11110000mm m n n P a a a E Pλλλλ-⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪=+++ ⎪⎪⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭11()0()n f P P f λλ-⎛⎫ ⎪=⎪ ⎪*⎝⎭,可见()f A 的全部特征值为12(),(),,()n f f f λλλ.性质5 在复数域范围内,对任意方阵A 总存在可逆矩阵P , 使11k J P AP J -⎛⎫⎪=⎪ ⎪⎝⎭,则11K J A P P J -⎛⎫ ⎪=⎪ ⎪⎝⎭11m m m k J A P P J -⎛⎫⎪∴=⎪ ⎪⎝⎭.其中m i J111111mi m m i m mmm m m m m m i i C C C C C λλλλ----⎛⎫⎪ ⎪⎪= ⎪ ⎪ ⎪⎝⎭(1,2,,)i k =.证明 设011iii i i J E A λλλλ⎛⎫ ⎪⎪==+ ⎪ ⎪⎝⎭,0110A ⎛⎫⎪ ⎪= ⎪ ⎪⎝⎭注意到:001010i nA ⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭,200001100i n A ⎛⎫⎪ ⎪ ⎪= ⎪ ⎪ ⎪⎝⎭,,100100i i n n A -⎛⎫ ⎪ ⎪ ⎪= ⎪ ⎪⎪⎝⎭,0(0)i i nn A =.于是11110000()m m m m m m mi i i m i m i J E A E C A C A A λλλλ---=+=++++111111mi m m i m mmm m m m m m i i C C C C C λλλλ----⎛⎫⎪ ⎪⎪= ⎪ ⎪ ⎪⎝⎭第三章 若尔当标准形的应用3.1 若尔当标准形在矩阵分解论中的应用(V oss 定理)设()n n A Mat C ⨯∈,证明:A 可以分解成两个对称矩阵之积,并且其中至少有一个是可逆的.例1设()n n A Mat C ⨯∈,矩阵P 和矩阵B 都是11n n ⨯矩阵,记111()1P n ⎛⎫⎪⎪= ⎪ ⎪⎝⎭, 11111111(,)1B n λλλλλ⎛⎫⎪ ⎪ ⎪= ⎪ ⎪ ⎪⎝⎭, 则有A PB =.证明 矩阵P 和矩阵B 都是对称的11n n ⨯矩阵,且1()P n 是可逆的,并有11111(,)()(,)J n P n B n λλ=又()n n A Mat C ⨯∈,则A 相似于一个若尔当矩阵,即存在()n n C Mat C ⨯∈,使得1A CJC -=,其中1122((,),(,),,(,))s s J diag J n J n J n λλλ=取12((),(),,())T s P Cdiag P n P n P n C =111122()((,),(,),,(,))T s s B C diag B n B n B n C λλλ--=即满足B ,P 都是对称的,P 是可逆的,并且A PB =.3.2 若尔当标准形在矩阵方程中的应用我们以“设()n n A Mat C ⨯∈,求矩阵X ,使得AX XA =”为例,说明Jordan 标准形在解矩阵方程中的应用.为了描述结果,我们引进下面的记号.记(){((0,))()[]}T n n g J n g x C x ⨯=∈如果121210()n n n n g x t x t x t x t ----=++++则 01201210((0,))n n n t t t g J n t t t t t t ---⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦上面的矩阵也称为下三角形Toepliz 矩阵。
Jordan标准型

-
初等矩阵都是可逆矩阵,并且有
P (i , j ) P (i , j ), P ( j(k )) P ( j(k )),
1
1
1
P [ j(h( )), i ] P[ j( h( )), i ]
1
定义2.2.3
若
-矩阵 A( ) 经过
有限次初等变换,化成 -矩阵 B( ),
2 1 1 1 2 2 1 1 A 1 2 1 2 0 0 0 3
1 0 A 0 0
关于
-矩阵的三种初
两行(列)互换位置
⑵
⑶
某行(列)乘不等于零的数
用 的多项式 h ( ) 乘某行(列
)并加另一行列上。
三种初等变换对应三个初等矩阵,
P(i, j ), P(i(k )), P[h( ) j, i]
并且,施于行变
换时,相当左乘相应初等矩阵,施 于列变换时,相当右乘相应初等矩 阵,可以证明初等变换不改变 矩阵的秩。
第二讲 Jordan标准型
2.1
-矩阵和初等因子
2.2 行列式因子和初等因子
2.3 Jordan 标准型
2.1
-矩阵和初等因子
引入 -矩阵
a11 ( ) a12 ( ) a21 ( ) a22 ( ) A( ) a ( ) a ( ) n2 n1 a1n ( ) a2 n ( ) ann ( )
(1) 反身性:每一个 -矩阵与自己等 价。 (2) 对称性:若 A( ) 与 B( )等价,则 B( ) 与 A( )等价,这是因为初等变换具有可逆 性。
(3)传递性:若 A( )与 B ( ) 等价, ) B( 与 C ( ) 等价,则 A( )与 C ( ) 等价。
矩阵论—矩阵的Jordan标准形

( 1)n1 , ( 2 )n2 , , ( s )ns .
A的特征矩阵E A,其行列式 E A 0 所以,特征矩阵E A的秩为n.
数字矩阵A与B相似 对应的特征矩阵E A与E B等价 A与B有相同的不变因子 A与B有相同的行列式因子 A与B有相同的初等因子
(i
)
1
1
解:显然E-J
(i
)
~
的初等因子。
1
i ni ni
( i )ni nini
所以,J (i )的初等因子为( i )ni .
A1()
定理:设A()
A2 ()
At ()
则A1(),A2 (), , At ()的初等因子的全体
就是A( )的初等因子。
2 0 0
det(B)= n det(A)
所以,矩阵A与矩阵B不相似。
定理:设A C nn , A的初等因子为:
( 1)n1 , ( 2 )n2 , , ( s )ns ,
则矩阵A相似与矩阵J ,
J1(1)
J
J2 (2 )
J
s
(s
)
其中
i 1
i 1
J
(i
)
1
i ni ni
定理:由A()的不变因子可以确定A()的初等因子, 由A()的初等因子和A()的秩可以确定不变因子。
定义:矩阵A的特征矩阵E-A的初等因子称为矩阵A
的初等因子。
求矩阵A的初等因子。
1 1 0 A 4 3 0
1 0 2
1
解:
E
A
~
1
( 1)2 ( 2)
所以,A的初等因子为( 1)2,( 2)
di ()称为A()的不变因子。
矩阵论之Jordan标准型

例6:设A() diag{( 1), 2, ( 1)2, ( 1)}, 求A()的初等因子,不变因子及标准形.
解:A()的初等因子有, 1, 2,( 1)2, , 1.
将初等因子降幂排列
2, , 1, 1, 1, 1,
, 1
1, 1 1, 1
不变因子为d4 () 2 ( 1)( 1), d3() ( 1), d2 () , d1() 1.
定义:若A(λ)经过有限次初等变换化成B(λ) ,则称 A(λ) 与B(λ)等价,记为A(λ) ≌ B(λ) .
注: λ-矩阵等价则秩相同,反之不然,这与数字矩 阵有区别. 如:
A(
)
0
0
,
B()
1 1
何时等价?
定理3:设 -矩阵A( )的秩为r,则
d1()
0
A()
dr ()
1
0
A(1,2 ,
,n )=(1,2,
,n
)
.
0
n
也即Ai ii (i 1,
,
n),
这说明i是属于
的
i
特征向量,而P可逆,故1,2, ,n线性无关.
反之亦然.
1) 3), 设f () | I A | ( 1)d1 ( 2 )d2 ( m )dm ,
d1 dm n,即i的代数重数为di ,不妨设
P
0
0 4100
P1.
定理2:A可对角化 最小多项式m A()无重根.
证明:只证必要性:设有可逆阵P,使得P-1AP=diag{1, , n}. 不妨设1, , (s s n)为A的全部互异特征值, 令g()=( 1)( 2 ) ( s ), 由P-1g(A)P=g(P-1AP)=g(diag{1, , n})=diag{g(1), , g(n )}=0 可知g(A)=0.即g()使A零化,从而m A()|g(), 但A的特征值均是 m A ()的根,故m A ()=g().
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
λ
0
例2
λ ( λ + 1) λ A(λ ) = 2 ( λ + 1)
将其化成Smith标准形。 解:
λ ( λ + 1) A( λ ) = λ 2 ( λ + 1)
λ ( λ + 1) λ λ 2 ( λ + 1) λ ( λ + 1) λ λ − λ ( λ + 2) 1
2
λ λ λ −λ 2 2 λ −λ
2
1 λ 1 + λ 2
λ +λ 0 −λ λ 2 2 −λ λ
2
1 λ +λ 3 2 0 −λ − λ + λ 0 −λ 4 − λ 3 − λ
0 −λ 2 −λ
0 1 0 −λ 3 − λ 2 + λ 4 3 0 −λ − λ − λ
显然,如果 rank ( A( λ )) = r ,则行列式因子 一共有 r 个。 例1 求
1− λ A(λ ) = λ 1 + λ 2
λ λ λ −λ 2 2 λ −λ
2
的各阶行列式因子。
解:由于
(1 − λ , λ ) = 1 ,所以 D1 (λ ) = 1 。
A(λ )
容易计算上面的标准形的各阶行列式因子为
D1 (λ ) = d1 (λ ) D2 (λ ) = d1 (λ )d 2 (λ )
L
显然有:
Dr (λ ) = d1 (λ )d 2 (λ )L d r (λ )
D2 (λ ) d1 (λ ) = D1 (λ ) d 2 (λ ) = D1 (λ ) Dr (λ ) L d r (λ ) = Dr −1 (λ )
0 1 λ + 2 0 0 1 0 λ+2 (3) 0 0 λ+2 1 0 0 0 λ + 2
0 0 λ − a −1 λ − a 0 0 −1 0 0 λ − a −1 λ − a 0 0 −1
0 0 1 0 −1 ( λ − a ) 2 0 0 λ − a 0 0 0 0 1 0 0 −1 ( λ − a ) 2 3 0 0 (λ − a ) 0 0 0
λ 矩阵为 A(λ ) 的Smith标准形。 d1 (λ ), d 2 ( λ ),L , d r ( λ )称为 A( λ ) 的不变因子。
例1
1− λ A(λ ) = λ 1 + λ 2
λ λ λ −λ 2 2 λ −λ
2
将其化成Smith标准形。
解:
1− λ A( λ ) = λ 1 + λ 2
由于 A( λ ) 与上面的Smith标准形具有相同的 子为
各阶行列式因子,所以 A( λ ) 的各阶行列式因
D1 (λ ), D2 ( λ ),L , Dr ( λ )
而
d1 (λ ), d 2 (λ ),L , d r (λ )
又是由这些行列式因子唯一确定的,于是我 们得到 定理2: A( λ ) 的Smith标准形是唯一的。 定理 例1 求下列
λ ( λ + 1) 3 2 λ + 2λ + λ 0 2 − λ − 2λ 1 λ ( λ + 1) 2 λ (λ + 1) 1 1 λ ( λ + 1) 2 λ (λ + 1)
例3
3λ + 2λ − 3 2λ − 1 λ + 2λ − 3 2 2 A(λ ) = 4λ + 3λ − 5 3λ − 2 λ + 3λ − 4 λ2 + λ − 4 λ −2 λ −1
2 2
将其化为Smith标准形。 解:
A( λ )
λ +λ −4 λ−2 λ −1 2 2 3λ + 2λ − 3 2λ − 1 λ + 2λ − 3 4λ 2 + 3λ − 5 3λ − 2 λ 2 + 3λ − 4
λ 矩阵的Smith标准形。
0 0 0 λ 2 0 λ −λ 0 0 (1) 0 ( λ − 1)2 0 0 2 0 0 0 λ − λ c1 λ − a λ −a c2 (2) O O λ − a cn −1 λ − a
r +1 r
r
零矩阵的秩为0。 定义 一个 n 阶 λ 矩阵称为可逆的,如果有一个
n 阶 λ 矩阵
B ( λ ) ,满足
A( λ ) B ( λ ) = B ( λ ) A( λ ) = E 这里 E 是 n 阶单位矩阵。 B ( λ )称为 A( λ ) 矩 阵的逆矩阵,记为 A−1 ( λ ) 。
A(λ )
d1 ( λ ) d 2 (λ ) O d r (λ ) 0 O 0
其中 r ≥ 1, d i ( λ ) 是首项系数为1的多项式且
d i ( λ ) d i +1 ( λ )
称这种形式的
(i = 1, 2,L , r − 1)
L a1n ( λ ) L a2 n ( λ ) L L L amn ( λ )
矩阵。 为多项式矩阵或 λ 矩阵。 定义 如果 λ 矩阵 A( λ ) 中有一个 阶 ( r ≥ 1) 子式不为零,而所有 阶子式(如果有的话) 全为零,则称 A( λ ) 的秩为 ,记为
RankA(λ ) = r
2
1− λ λ
λ
1− λ
2
λ λ
2
2
= λ ( −λ − λ + 1) = f (λ )
2
λ +1 λ 显然 ( f ( λ ), g ( λ )) = λ 而且其余的7个2 阶 子式也都包含 λ 作为公因子,所以 D2 (λ ) = λ 3 2 3 2 另外 A( λ ) = − λ − λ ⇒ D3 ( λ ) = λ + λ
2
2 1 0 λ2 + λ − 4 λ −2 λ −1 2 2 4λ + 3λ − 7 3λ − 3 λ + 3λ − 4 2 0 1 2 λ −2 λ +λ −4 λ −1 2 2 3λ − 3 4λ + 3λ − 7 λ + 3λ − 4
P(i, j ), P(i (c )), P (i, j (ϕ ))
定理 对一个 m × n的 λ 矩阵 A( λ ) 的行作初等行变换, 相当于用相应的 m 阶初等矩阵左乘A( λ ) ,对 A( λ ) 的 列作初等列变换,相当于用相应的 n 阶初等矩阵右 乘 A( λ ) 。 定义 如果 A( λ ) 经过有限次的初等变换之后变成 B ( λ ) ,则称 A( λ ) 与 B ( λ ) 等价,记之为
2
λ +λ −4 λ −2 λ −1 2 2 4λ + 3λ − 7 3λ − 3 λ + 3λ − 4 4λ 2 + 3λ − 5 3λ − 2 λ 2 + 3λ − 4
2
λ +λ −4 λ −2 λ −1 2 2 4λ + 3λ − 7 3λ − 3 λ + 3λ − 4 2 1 0
0 0 −1 λ − a
0 0 −1 λ − a
1 0 0 0 1 0 0 0
0 1
0 0
0 ( λ − a )3 0 0 0 1 0 0
0 0 −1 λ − a 0 0
3 0 −1 ( λ − a ) 0 λ −a 0
0 −λ 2 −λ
1 0 0 1 0 0 1 0 0
0 −λ −λ 2 0 −λ 0 0
0 3 2 −λ − λ + λ −λ 4 − λ 3 − λ 3 2 −λ − λ + λ 2 −λ − λ 0 0 λ (λ + 1) 0
第二章
λ - 矩阵与矩阵的Jordan标准形 矩阵与矩阵的 标准形
j = 1, 2,L , n )
λ
矩阵的基本概念
定义: 定义:设 aij ( λ )(i = 1, 2,L , m; 上的多项式, 为数域 F 上的多项式,则称
a11 ( λ ) a12 ( λ ) a (λ ) a (λ ) 22 21 A= L L am1 ( λ ) am 2 ( λ )
1 0 0 0
1 0 0 0 1 0 4 0 0 (λ − a ) 0 0 0
λ 矩阵标准形的唯一性
定义: 定义: A( λ ) 为一个 λ 矩阵且 Rank ( A(λ )) = r 对 于任意的正整数 k ,1 ≤ k ≤ r , ( λ ) 必有非零的 k A 阶子式, 阶子式,A( λ ) 的全部 k 阶子式的最大公因式 Dk ( λ ) 行列式因子。 称为 A( λ ) 的 k 阶行列式因子。
定理 定义
一个 n 阶 λ 矩阵 A( λ ) 可逆的充要必要是 det A(λ ) 一个非零的常数。
下列各种类型的变换,叫做 λ 矩阵的初等变 换: (1) 矩阵的任二行(列)互换位置; (2) 非零常数 c 乘矩阵的某一行(列); (3) 矩阵的某一行(列)的 ϕ ( λ )倍加到另一行(列) 上去,其中ϕ ( λ ) 是 λ 的一个多项式。 对单位矩阵施行上述三种类型的初等变换便 得相应得三种 λ 矩阵称为初等矩阵
