初二几何证明经典难题.
初二几何证明高难度题目

初二几何证明高难度题目题目描述给定一个三角形ABC,其中AB = AC,角BAC = 90°。
点D 是BC边上的一个点,使得角ADC = 90°。
点E是AC边上的一个点,使得AE = AD。
证明:角BCE = 45°。
证明过程我们可以通过以下步骤来证明角BCE = 45°:1.连接BE和CD两条线段。
2.由题目给定,AC = AB,所以ACB是一个等腰直角三角形。
3.角ADC = 90°,所以ADC是一个直角三角形。
4.由于AE = AD,所以AE也等于AC,即AE = AC。
5.角EAC = 角CAE,因为AE = AC。
6.角EAC + 角CAE + 角AEC = 180°,根据三角形内角和定理。
7.角EAC + 角CAE + 90° = 180°,因为ACB是一个直角三角形。
8.角EAC + 角CAE = 90°。
9.角BEC = 角EAC + 角CAE,根据相邻角的性质。
10.角BEC = 90°,根据步骤8.11.角CBE = 180° - 角BEC - 角BCE = 180° - 90° - 角BCE。
12.角CBE = 90° - 角BCE。
13.角CBE = 角BCE,因为CBE = 45°。
14.90° - 角BCE = 角BCE,根据步骤13.15.角BCE = 45°。
结论通过以上证明过程可以得出结论:在给定的三角形ABC中,当点D是BC边上的一个点,使得角ADC = 90°,点E是AC边上的一个点,使得AE = AD时,角BCE = 45°。
初二几何证明挑战难题

初二几何证明挑战难题引言初二几何证明是中学数学的重要内容之一,是培养学生逻辑思维能力和推理能力的关键环节。
然而,有些几何证明问题对于学生来说是具有一定难度的,需要一些挑战性的问题来激发学生的研究兴趣和思考能力。
本文将介绍一些初二几何证明的挑战难题,旨在帮助学生提升自己的证明能力。
难题1:平行线性质证明题目描述给定平行线l1和l2,证明两个平行线的截线与这两条平行线的交点共线。
证明思路1.根据平行线的定义,我们知道两条平行线的截线是平行的。
2.假设截线AB与平行线l1和l2的交点分别为C和D。
3.通过截线AB,可以构造三角形ACD。
4.观察三角形ACD,可以发现AC和AD与平行线l1和l2平行。
5.根据平行线的性质,可以得出AC和AD平行。
6.根据平行线的性质,如果两条线分别与另外一条直线平行,那么这两条线也是平行的。
7.因此,AC和AD是平行的。
8.综上所述,截线AB与平行线l1和l2的交点共线。
难题2:等腰三角形性质证明题目描述给定等腰三角形ABC,证明等腰三角形的顶角的平分线与底边中点重合。
证明思路1.根据等腰三角形的定义,我们知道等腰三角形的两个底角相等。
2.设顶角A的平分线与底边BC的交点为D。
3.因为顶角A的平分线,所以∠BAD=∠CAD。
4.此外,因为等腰三角形ABC,所以∠BAC=∠ABC。
5.根据三角形内角和等于180度的性质,我们可以得知∠BAC+∠ABC+∠ACB=180度。
6.由于∠___∠ABC,所以∠BAC+∠BAC+∠ACB=180度。
7.综上所述,2∠BAC+∠ACB=180度。
8.因为∠BAC=∠CAD,所以2∠CAD+∠ACB=180度。
9.再考虑三角形ACD,我们可以得出∠CAD+∠CAD+∠ACD=180度。
10.综上所述,2∠CAD+∠ACD=180度。
11.由于2∠CAD+∠ACD=2∠CAD+∠ACB,所以2∠BAC+∠ACB=2∠CAD+∠___。
12.可以推导出∠BAC=∠CAD,即顶角A的平分线与底边BC 的交点D重合。
初二数学平面几何经典难题

初二数学平面几何经典难题
以下是初二数学平面几何的一些经典难题:
1. 直角三角形中的勾股定理:在一个直角三角形中,直角边的平方和等于斜边的平方。
这是勾股定理的基本形式,但是有许多变种和证明方法。
2. 三角形中的角度和定理:一个三角形的三个内角之和等于180度。
这个定理有许多证明方法和应用,例如在几何作图和计算面积时。
3. 平行线的性质和判定:平行线在几何中非常重要,因为它们有一些特殊的性质,例如同位角相等、内错角相等、同旁内角互补等。
同时,也有一些判定平行线的方法,例如同位角相等、内错角相等、同旁内角互补等。
4. 圆中的基本定理:圆中的基本定理包括圆心角定理、圆周角定理、弦心距定理等。
这些定理是圆的基础,并且对于解决关于圆的问题非常重要。
5. 立体几何初步:立体几何是平面几何的扩展,它研究三维空间中的图形和几何体。
立体几何有许多经典问题,例如计算几何体的表面积和体积、证明空间中的角度和距离等。
以上难题仅供参考,建议查阅数学教辅或资料书获取更多经典难题。
源于经典而高于经典的初二几何难题解答概要
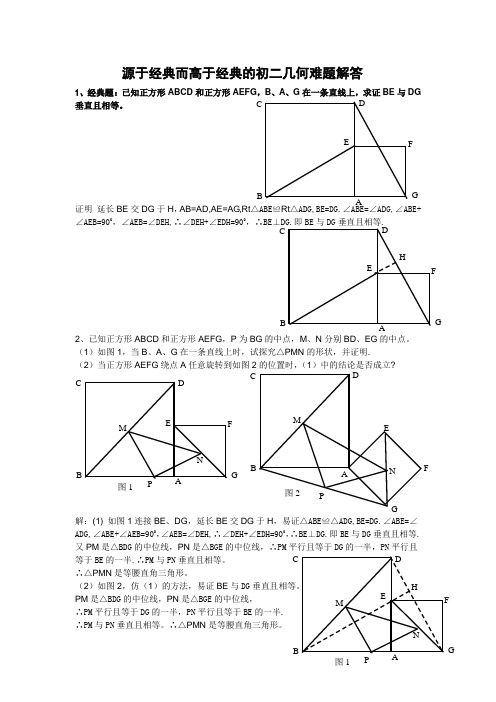
源于经典而高于经典的初二几何难题解答1、经典题:已知正方形ABCD 和正方形AEFG ,B 、A 、G 在一条直线上,求证BE 与DG垂直且相等。
证明 延长BE 交DG 于H ,AB=AD,AE=AG,Rt △ABE ≌Rt △ADG,BE=DG.∠ABE=∠ADG,∠ABE+∠AEB=900,∠AEB=∠DEH,∴∠DEH+∠EDH=900,∴BE ⊥DG.即BE 与DG 垂直且相等.2、已知正方形ABCD 和正方形AEFG ,P 为BG 的中点,M 、N 分别BD 、EG 的中点。
(1)如图1,当B 、A 、G 在一条直线上时,试探究△PMN 的形状,并证明. (2)当正方形AEFG 绕点A 任意旋转到如图2的位置时,(1)中的结论是否成立?解:(1) 如图1连接BE 、DG ,延长BE 交DG 于H ,易证△ABE ≌△ADG,BE=DG.∠ABE=∠ADG,∠ABE+∠AEB=900,∠AEB=∠DEH,∴∠DEH+∠EDH=900,∴BE ⊥DG.即BE 与DG 垂直且相等. 又PM 是△BDG 的中位线,PN 是△BGE 的中位线,∴PM 平行且等于DG 的一半,PN 平行且等于BE 的一半.∴PM 与PN 垂直且相等。
∴△PMN 是等腰直角三角形。
(2)如图2,仿(1)的方法,易证BE 与DG 垂直且相等。
PM 是△BDG 的中位线,PN 是△BGE 的中位线,∴PM 平行且等于DG 的一半,PN 平行且等于BE 的一半. ∴PM 与PN 垂直且相等。
∴△PMN 是等腰直角三角形。
N图1 D M E CPBA F G P 图2 A D M E N CB F G图1HD MEC PBAFGND E C B AF G H D E C B AF G说明:本题的第(2)小题也可看成以△ABG 边AB 、AG 向外作正方形ABCD 和 正方形AEFG 。
可得以上结论。
3、分别以任意四边形ABCD 的各边向外作正方形ABEF 、AGHD 、DIJC 、CKLB 。
【几何突破】初二证明难题汇总详细解析

【几何突破】初二证明难题汇总详细解析成才路上特级教师与奥数国家一级教练联手执教。
1、证明线段相等或角相等两条线段或两个角相等是平面几何证明中最基本也是最重要的一种相等关系。
很多其它问题最后都可化归为此类问题来证。
证明两条线段或两角相等最常用的方法是利用全等三角形的性质,其它如线段中垂线的性质、角平分线的性质、等腰三角形的判定与性质等也经常用到。
说明:利用三角形全等证明线段求角相等。
常须添辅助线,制造全等三角形,这时应注意:(1)制造的全等三角形应分别包括求证中一量;(2)添辅助线能够直接得到的两个全等三角形。
说明:当一个三角形中出现角平分线、中线或高线重合时,则此三角形必为等腰三角形。
我们也可以理解成把一个直角三角形沿一条直角边翻折(轴对称)而成一个等腰三角形。
说明:有等腰三角形条件时,作底边上的高,或作底边上中线,或作顶角平分线是常用辅助线。
证明二:如图5所示,延长ED到M,使DM=ED,连结FE,FM,BM说明:证明两直线垂直的方法如下:(1)首先分析条件,观察能否用提供垂直的定理得到,包括添常用辅助线,见本题证二。
(2)找到待证三直线所组成的三角形,证明其中两个锐角互余。
(3)证明二直线的夹角等于90°。
2. 分析:本题从已知和图形上看好象比较简单,但一时又不知如何下手,那么在证明一条线段等于两条线段之和时,我们经常采用“截长补短”的手法。
“截长”即将长的线段截成两部分,证明这两部分分别和两条短线段相等;“补短”即将一条短线段延长出另一条短线段之长,证明其和等于长的线段。
来源网络,尊重原创,如侵权则删。
本学期全部原创文章:八上第25讲十题突破八上代数重难点八上第24讲十题突破八上几何重难点八上第23讲一次函数利润,方案类问题大汇总八上第22讲一次函数行程类问题大汇总八上第21讲《一次函数》必考知识点(下)八上第20讲《一次函数》必考知识点(中)八上第19讲《函数、一次函数》必考知识点(上)八上第18讲《直角坐标系》典题大集合(下)八上第17讲《直角坐标系》典题大集合(上)八上第16讲《平面直角坐标系》全章知识点融合八上第15讲《实数近似数》必考知识点汇总八上14讲《平方根算术平方根立方根》典型易错辨析八上第13讲 4大类,9小题突破期中冲刺难点八上12讲《勾股定理》解题方法(下)——从立体到平面八上11讲《勾股定理》解题方法汇总(上)八上第10讲等腰三角形,你都掌握了吗?(下) 模型篇【期中特辑】八上考前冲刺易错题大汇总!八上第9讲等腰三角形,你都掌握了吗?(中) 方法篇八上第8讲等腰三角形,你都掌握了吗?(上)八上第7讲你必须学会的《线段、角的轴对称性》书写格式!八上第6讲你真的弄懂轴对称了吗?八上第5讲再谈全等辅助线—截长补短&半角八上第4讲全等动点问题&再谈倍长中线八上第3讲“一线三等角”型全等都在这了!八上第2讲 SAS、 ASA 、AAS 型全等典型易错分析八上第1讲怎样分割全等图形&再谈图形变化中的“对应”如何关注QQ端:将本文直接分享到微信好友聊天页面,点击蓝字即可关注.点击最右下留言,期待您的宝贵意见!您的分享和转发,是对我最大的支持!如能在文中GG位轻点一次,或者为文章点一次在看!不仅对我是莫大的鼓励,更是我长期更新的动力!最后附上成为尊贵星标用户的方法,你再也不会担心错过消息啦!笔者主编的《领跑数学二轮专题复习》,新版年后上市,敬请期待.。
初二几何经典难题集锦(含答案)

初二几何经典训练题1、如图,在直角梯形ABCD中,AB∥DC,∠ABC=90°,AB=2DC,对角线AC⊥BD,垂足为F,过点F作EF∥AB,交AD于点E,CF=4cm.⑴求证:四边形ABFE是等腰梯形;⑵求AE的长.2、如图,矩形ABCD的对角线AC、BD相交于点O,E、F分别是OA、OB的中点.(1)求证:△ADE≌△BCF;(2)若AD=4cm,AB=8cm,求CF和OF的长。
3、如图,已知直角梯形ABCD中,AD∥BC,∠B=90°,AB=12cm,BC=8cm,DC=13cm,动点P沿A→D→C线路以2cm/秒的速度向C运动,动点Q沿B→C线路以1cm/秒的速度向C运动.P、Q两点分别从A、B同时出发,当其中一点到达C点时,另一点也随之停止.设运动时间为t秒,△PQB的面积为ycm2.(1)求A D的长及t的取值范围;(2)当1.5≤t≤t0(t0为(1)中t的最大值)时,求y关于t的函数关系式;(3)请具体描述:在动点P、Q的运动过程中,△PQB的面积随着t的变化而变化的规律。
4、如图,AB与CD相交于E,AE=EB,CE=ED,D为线段FB的中点,GF与AB相交于点G,若CF=15cm,求GF 之长。
5、如图所示,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连接AE,F为AE上的一点,且∠BFE =∠C。
(1)求证:△ABF∽△EAD;(2)若AB=4,∠BAE=30°,求AE的长;(3)在(1)、(2)的条件下,若AD=3,求BF的长(计算结果可含根号)。
6、如图是一个常见铁夹的侧面示意图,OA,OB表示铁夹的两个面,C是轴,CD⊥OA于点D,已知DA =15mm,DO=24mm,DC=10mm,我们知道铁夹的侧面是轴对称图形,请求出A、B两点间的距离。
7、如图,用三个全等的菱形ABGH、BCFG、CDEF拼成平行四边形ADEH,连接AE与BG、CF分别交于P、Q,(1)若AB=6,求线段BP的长;(2)观察图形,是否有三角形与△ACQ全等?并证明你的结论.8、如图已知点E、F在△ABC的边AB所在的直线上,且AE=BF,FH∥FG∥AC,FH、EG分别交边BC所在的直线于点H、G。
(完整版)初中几何证明题五大经典(含答案)
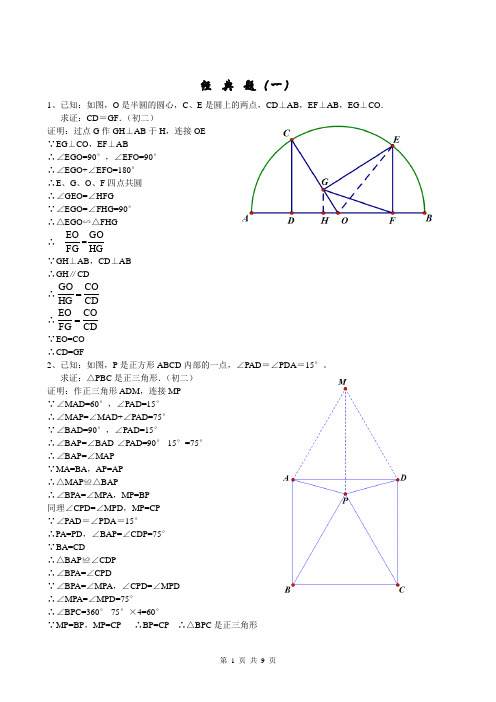
经典题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二)证明:过点G 作GH ⊥AB 于H ,连接OE ∵EG ⊥CO ,EF ⊥AB∴∠EGO=90°,∠EFO=90° ∴∠EGO+∠EFO=180° ∴E 、G 、O 、F 四点共圆 ∴∠GEO=∠HFG∵∠EGO=∠FHG=90° ∴△EGO ∽△FHG ∴FG EO =HGGO∵GH ⊥AB ,CD ⊥AB ∴GH ∥CD∴CD COHG GO =∴CDCO FG EO = ∵EO=CO ∴CD=GF2、已知:如图,P 是正方形ABCD 内部的一点,∠PAD =∠PDA =15°。
求证:△PBC 是正三角形.(初二) 证明:作正三角形ADM ,连接MP ∵∠MAD=60°,∠PAD=15° ∴∠MAP=∠MAD+∠PAD=75° ∵∠BAD=90°,∠PAD=15°∴∠BAP=∠BAD-∠PAD=90°-15°=75° ∴∠BAP=∠MAP ∵MA=BA ,AP=AP ∴△MAP ≌△BAP∴∠BPA=∠MPA ,MP=BP 同理∠CPD=∠MPD ,MP=CP ∵∠PAD =∠PDA =15°∴PA=PD ,∠BAP=∠CDP=75° ∵BA=CD∴△BAP ≌∠CDP ∴∠BPA=∠CPD∵∠BPA=∠MPA ,∠CPD=∠MPD ∴∠MPA=∠MPD=75°∴∠BPC=360°-75°×4=60°∵MP=BP ,MP=CP ∴BP=CP ∴△BPC 是正三角形3、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN于E 、F .求证:∠DEN =∠F .证明:连接AC ,取AC 的中点G ,连接NG 、MG ∵CN=DN ,CG=DG ∴GN ∥AD ,GN=21AD ∴∠DEN=∠GNM ∵AM=BM ,AG=CG ∴GM ∥BC ,GM=21BC ∴∠F=∠GMN ∵AD=BC ∴GN=GM∴∠GMN=∠GNM ∴∠DEN=∠F经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初二) 证明:(1)延长AD 交圆于F ,连接BF ,过点O 作OG ⊥AD 于G ∵OG ⊥AF ∴AG=FG ∵AB⌒ =AB ⌒ ∴∠F=∠ACB又AD ⊥BC ,BE ⊥AC ∴∠BHD+∠DBH=90° ∠ACB+∠DBH=90° ∴∠ACB=∠BHD ∴∠F=∠BHD∴BH=BF 又AD ⊥BC ∴DH=DF∴AH=AG+GH=FG+GH=GH+DH+DF+GH=2GH+2DH=2(GH+DH )=2GD 又AD ⊥BC ,OM ⊥BC ,OG ⊥AD ∴四边形OMDG 是矩形 ∴OM=GD ∴AH=2OM (2)连接OB 、OC∵∠BAC=60∴∠BOC=120° ∵OB=OC ,OM ⊥BC ∴∠BOM=21∠BOC=60°∴∠OBM=30° ∴BO=2OM由(1)知AH=2OM ∴AH=BO=AO2、设MN 是圆O 外一条直线,过O 作OA ⊥MN 于A ,自A 引圆的两条割线交圆O 于B 、C 及D 、E ,连接CD 并延长交MN 于Q ,连接EB 并延长交MN 于P. 求证:AP =AQ .证明:作点E 关于AG 的对称点F ,连接AF 、CF 、QF ∵AG ⊥PQ ∴∠PAG=∠QAG=90°又∠GAE=∠GAF ∴∠PAG+∠GAE=∠QAG+∠GAF 即∠PAE=∠QAF∵E 、F 、C 、D 四点共圆 ∴∠AEF+∠FCQ=180° ∵EF ⊥AG ,PQ ⊥AG ∴EF ∥PQ∴∠PAF=∠AFE ∵AF=AE∴∠AFE=∠AEF ∴∠AEF=∠PAF ∵∠PAF+∠QAF=180° ∴∠FCQ=∠QAF ∴F 、C 、A 、Q 四点共圆 ∴∠AFQ=∠ACQ 又∠AEP=∠ACQ ∴∠AFQ=∠AEP3、设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)证明:作OF ⊥CD 于F ,OG ⊥BE 于G ,连接OP 、OQ 、OA 、AF 、AG ∵C 、D 、B 、E 四点共圆 ∴∠B=∠D ,∠E=∠C ∴△ABE ∽△ADC ∴DFBGFD 2BG 2DC BE AD AB === ∴△ABG ∽△ADF ∴∠AGB=∠AFD ∴∠AGE=∠AFC ∵AM=AN , ∴OA ⊥MN 又OG ⊥BE ,∴∠OAQ+∠OGQ=180° ∴O 、A 、Q 、E 四点共圆 ∴∠AOQ=∠AGE 同理∠AOP=∠AFC ∴∠AOQ=∠AOP又∠OAQ=∠OAP=90°,OA=OA ∴△OAQ ≌△OAP ∴AP=AQ 在△AEP 和△AFQ 中 ∠AFQ=∠AEP AF=AE ∠QAF=∠PAE ∴△AEP ≌△AFQ ∴AP=AQ4、如图,分别以△ABC 的AB 和AC 为一边,在△ABC 的外侧作正方形ABFG 和正方形ACDE ,点O 是DF 的中点,OP ⊥BC求证:BC=2OP (初二)证明:分别过F 、A 、D 作直线BC 的垂线,垂足分别是L 、M 、N ∵OF=OD ,DN ∥OP ∥FL ∴PN=PL∴OP 是梯形DFLN 的中位线 ∴DN+FL=2OP ∵ABFG 是正方形∴∠ABM+∠FBL=90° 又∠BFL+∠FBL=90° ∴∠ABM=∠BFL又∠FLB=∠BMA=90°,BF=AB ∴△BFL ≌△ABM ∴FL=BM同理△AMC ≌△CND ∴CM=DN∴BM+CN=FL+DN ∴BC=FL+DN=2OP经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F . 求证:CE =CF .(初二)证明:连接BD 交AC 于O 。
很难证明的几何题

很难证明的几何题一、那些让人头疼的几何题。
几何题啊,真的是像一个个小怪兽,有些时候特别难搞定。
就像那种证明三角形全等或者相似的题目,条件给得模模糊糊的,你得像个侦探一样在图里找线索。
比如说有一道题,给了一个三角形,里面几条线段交叉着,然后告诉你一些线段的长度关系,让你证明这个三角形和另一个三角形相似。
那图看起来就像一团乱麻,你得先把那些线段关系捋清楚。
有时候呢,是角度的问题。
那些角度隐藏在图形的各个角落,就像调皮的小精灵,你得把它们一个个找出来。
像在多边形里,求某个内角的度数,又要用到内角和公式,又要找互补角、对顶角之类的关系,一个不小心就会掉进陷阱里。
我记得有一次考试,有个几何题是关于四边形的,它的对角线把四边形分成了好几个三角形,然后要根据这些三角形的角度关系来证明四边形的一些性质。
我当时看着那图,眼睛都花了,那些角度感觉就像在跟我捉迷藏一样。
二、圆相关的证明题——弯弯绕绕的难题。
圆的几何题也是难搞的主儿。
圆里面的切线、割线、圆周角、圆心角这些概念,单独看都还好,一旦放在一道题里,就变得超级复杂。
比如说要证明一条直线是圆的切线,你得想办法证明这条直线和圆只有一个交点,或者证明这条直线垂直于过切点的半径。
这就需要你在图里找到各种隐藏的直角三角形,利用勾股定理或者三角形的相似性来证明垂直关系。
还有那种关于圆内接四边形的题目,什么对角互补啦,外角等于内对角啦。
这些性质要在证明题里灵活运用,真的不容易。
我有个同学,他在做一道圆内接四边形的证明题时,被那些角的关系绕晕了。
他说感觉自己就像走进了一个迷宫,在那些角之间转来转去,怎么也找不到出口。
三、立体几何——从平面到空间的挑战。
立体几何就更上一层楼了,难度直接升级。
从平面图形到立体图形,多了一个维度,我们的脑袋有时候就转不过来这个弯儿。
像证明两个立体图形之间的关系,比如证明一个三棱柱和一个四棱锥的某些面平行或者垂直。
你得先把立体图形拆分成平面图形来看,找到那些关键的平面,然后再用平面几何的知识去证明。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初二几何证明经典难题
1、已知:如图,P是正方形ABCD内点,/ PAD = / PDA =150.
求证:△ PBC是正三角形.
如下图做△ DGC使与△ ADP全等,可得△ PDG为等边△,从而可得△ DGC APD CGP,得出PC=AD=DC,和/ DCG= / PCG =150 所以/ DCP=300 , 从而得出△ PBC是正三角形
2、已知:如图,在四边形ABCD中,AD =BC , M、N分别是AB、CD的中点, AD、BC
的延长线交MN于E、F .
求证:/ DEN = / F .
如下图连接AC并取其中点Q ,连接QN和QM ,所以可得/ QMF= / F , /
QNM= / DEN 和/ QMN= / QNM ,从而得出 / DEN = / F。
、如图分别以△ ABC的AC和BC为一边,在厶ABC的外侧作正方形ACDE 和正方形CBFG,点P是EF的中点.
求证:点P到边AB的距离等于AB的一半.
3. 过E,C,F点分别作AB所在直线的高EG , CI , FH。
可得PQ=
EG FH
+。
由厶EGA AIC ,可得EG=AI,由△ BFH CBI
,可得FH=BI。
从而可得PQ=
2
AI BI += 2AB
,从而得证。
3 / 4
4
、如图,四边形ABCD为正方形,DE // AC , AE =AC , AE与CD相交于F .求证:CE =CF .
顺时针旋转△ ADE ,到△ ABG ,连接CG .由于/ ABG= /
ADE=900+450=1350
从而可得B , G , D在一条直线上,可得△ AGB ◎△ CGB。
推出
AE=AG=AC=GC,可得△ AGC为等边三角形。
/ AGB=300,既得/ EAC=300,从而可得/ A EC=750。
又/ EFC=Z DFA=450+300=750.可证:CE=CF。
5、如图,四边形ABCD为正方形,DE // AC ,且CE =CA ,直线EC交DA延长
线于F .
求证:AE =AF .
连接BD作CH丄DE
由AC=CE=2GC=2CH,
可得/ CEH=300,所以/ CAE=Z CEA= / AED=150, 又/ FAE=900+450+150=1500,
从而可知道/ F=150,从而得出AE=AF
6 设P是正方形ABCD —边BC上的任一点,PF丄AP , CF平分/ DCE .求证:PA =PF .
作FG丄CD , FE丄BE ,可以得出GFEC为正方形
令AB=Y , BP=X ,CE=Z ,可得PC=Y-X。
tan / BAP=ta n/ EPF= X
Y
-+
,可得YZ=XY-X2+XZ,
即Z(Y-X=X(Y-X ,既得X=Z ,得出△ ABP PEF ,得到PA =PF 得证。
