2014年一模试卷及答案x
2014年邢台一模语文试题(扫描版)及答案
2014语文模拟试题参考答案及评分标准1.D（魔幻意象源于创作主体自身所植根的文化传统和自己的经验世界。
）2.C（原文为“其实日常生活并非是诗意的，有时需要通过文学的引领才能让我们抵达其中所蕴含的诗意”。
）3.D（原文“小说因为这些魔幻意象而生成了某种朦胧感、荒凉感和忧郁情调，并最终构成了诗性品格的艺术因素”一句中的“小说”指的是《透明的红萝卜》，并不泛指每篇小说。
）4.B（通“与”，参与。
）5.D（①是吏的行为。
⑤说的是王觌依法处置狡吏，不能表现“持正论始终”。
）6.C（“失轻重之体”是王觌为苏轼辩护的言辞，不是苏轼的罪名。
“消除了大臣中的朋党之说”文中无据。
）7.(1) 像这样的旱灾势头，百姓粮食已断绝，倾尽粮仓供给，还怕不能救济，还能以赋税督责（要求）他们吗？（廪、克、责、“尚……邪”反问句式，各1分，语句通畅1分。
）(2) 江水横贯城中为渠，因年岁久远水道堵塞而多水灾，王觌疏通治理恢复原样，百姓感激他的恩德，命名为“王公渠”。
（贯、疏、德、号，各1分，语句通畅1分。
）译文：王觌，是泰州如皋人。
考中进士，担任编修三司令式删定官。
不乐意长时间担任这一闲职，要求担任润州推官。
二浙干旱，郡守派遣官员视察禾苗受损情况，秉承监司的意图，不敢过多免除赋税。
王觌接受公文审查，感叹道：‚像这样的旱灾势头，百姓粮食已断绝，倾尽粮仓供给，还怕不能救济，还能以赋税督责他们吗？‛过了几天，全部免除。
监司愤怒，多方搜集王觌罪证。
恰逢朝廷派使臣赈济借贷，王觌求见，对使臣诉说民间利弊。
使臣感到高兴，回朝推荐王觌，被任命为司农寺主簿，转任司农寺丞，移任太常寺。
差役法重新实行，王觌认为：‚朝廷意在方便百姓，但议论的人就认为免役法无一事可用。
法无新旧之分，惟善者是从。
‛因而采集对差役法有帮助可以通行的几十条上呈。
于是论青苗法的危害，请求废除新令，而恢复常平旧法，又说：‚刑罚时轻时重。
熙宁时的大臣，认为刑罚不重，那么人无所惧惮。
【2014大连一模】辽宁省大连市2014届高三第一次模拟考试 英语试题 扫描版含答案
2014年大连市高三第一次模拟考试英语能力测试参考答案听力部分（1.5×20=30分）1 ~ 5 ACBBA 6 ~10 BBCAC 11~15 BCACB 16~20 CABAA阅读理解（2×20=40分）21~24 DBBC 25~28 CBAA 29~31 DCA 32~35 ADBC 36~40 EBFGC完形填空（1.5×20=30分）41~45 BDCAB 46~50 DCABC 51~55 AADCB 56~60 ABDCD语法填空（1.5×10=15分）61. can 62. When 63. gave 64. However 65. have been taking 66. to 67. to do 68. medicines 69. it 70. better短文改错（1×10=10分）Dear Headmaster,I am writing to talk about the canteen of our school. There are only a few stand instandsthe canteen, leading to lots of students have to line up for food. It is ∧waste of time,having aisn’t it? But at times the food is not fresh and does not taste deliciously. So it’s not And delicioussurprising that some students chose to go to the street to buy junk food which do harmchoose doesto their health. Would you think about that how to improve it? I would appreciate youitif you could take some measures. Hopefully, my opinion can be taken to account.intoJack书面表达（25分）One possible version：Looking back to the National English Speaking Competition I took several days ago, I have a lot to share with you.For a start, I feel really delighted that I’ve won the first prize in the competition, which makes me understand the true meaning of the proverb “no pains, no gains”. Furthermore, in the five‐day competition, I established a close friendship with students from all over our country, from whom I’ve learned a lot. More importantly, taking this competition has enabled me to overcome my fear of speaking in public, thus developing my self‐confidence. Additionally, I owe many thanks to my tutor and the judges, without whose proper help, I couldn’t have done such an excellent job.To sum up, I will always cherish this meaningful and memorable experience.书面表达（25分）依据高考作文评分标准。
2014年一模试题答案
22、解：设一个足球、一个篮球分别为 x、y 元，根据题意得
3x 2 y 310
x 50
2x
5y
500
，解得
y
80
，∴一个足球、一个篮球各需
50
元、80
元；
（2）设足球买 x 个，则篮球（96-x）个，根据题意得
50x+80(96-x)≤5720，解得 x≥ 65 1 ，∵x 为整数，∴x 最小取 66，∴96-x=96-66=30, 3
∴+=
=
=1，
∴无论 k 取何值， + 的值都等于同一个常数 1．
∴AP=
=．
24、解：⑴连接 BF（如图①），
∵△ABC≌△DBE，∴BC=BE，AC=DE． ∵∠ACB=∠DEB=90°，∴∠BCF=∠BEF=90°，
∵BF=BF，∴Rt△BFC≌Rt△BFE．
∴CF=EF． 又∵AF+CF=AC，∴AF+EF =DE ． ………………………………5 分
⑵画出正确图形如图②
∴最多可以买 30 个篮球
23、解（1）证明：连结 AD、OD，如图， ∵AB 是⊙O 的直径， ∴∠ADB=90°， ∵AB=AC， ∴AD 垂直平分 BC，即 DC=DB， ∴OD 为△BAC 的中位线， ∴OD∥AC， 而 DE⊥AC，
（2）解：∵OD⊥DE，DE⊥AC， ∴四边形 OAED 为矩形， 而 OD=OA， ∴四边形 OAED 为正方形， ∴AE=AO，
∴ + = + =1；
②k 取任何值时，设点 A（x1， x12﹣1），B（x2， x22﹣1），
则+=
+
=
=
，
2014年物理一模答案
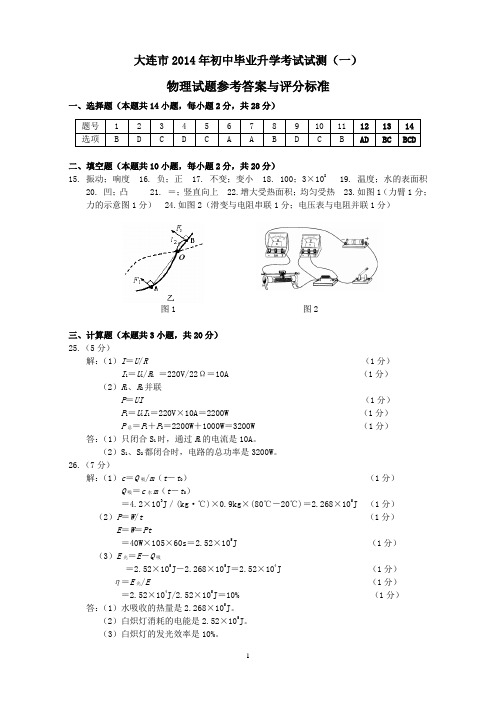
大连市2014年初中毕业升学考试试测（一）物理试题参考答案与评分标准一、选择题（本题共14小题，每小题2分，共28分）二、填空题（本题共10小题，每小题2分，共20分）15. 振动；响度 16. 负；正 17. 不变；变小 18. 100；3×10819. 温度；水的表面积20. 凹；凸 21. ＝；竖直向上 22.增大受热面积；均匀受热 23.如图1（力臂1分；力的示意图1分） 24.如图2（滑变与电阻串联1分；电压表与电阻并联1分）图1 图2三、计算题（本题共3小题，共20分） 25.（5分）解：（1）I ＝U /R （1分） I 1＝U 1/R 1 ＝220V/22Ω＝10A （1分）（2）R 1、R 2并联P ＝UI （1分）P 1＝U 1I 1＝220V ×10A ＝2200W （1分） P 总＝P 1＋P 2＝2200W ＋1000W ＝3200W （1分）答：（1）只闭合S 1时，通过R 1的电流是10A 。
（2）S 1、S 2都闭合时，电路的总功率是3200W 。
26.（7分） 解：（1）c ＝Q 吸/m （t －t 0） （1分）Q 吸＝c 水m （t －t 0）＝4.2×103J ／(kg·℃)×0.9kg ×(80℃－20℃)＝2.268×105J （1分） （2）P ＝W /t （1分）E ＝W ＝Pt＝40W ×105×60s ＝2.52×105J （1分） （3）E 光＝E －Q 吸＝2.52×105J －2.268×105J ＝2.52×104J （1分） η＝E 光/E （1分）＝2.52×104J/2.52×105J ＝10% （1分）答：（1）水吸收的热量是2.268×105J 。
（2）白炽灯消耗的电能是2.52×105J 。
2014年苏锡常镇高三数学一模试卷及参考答案(纯word版)
2014年苏、锡、常、镇四市高三教学情况调查（一）数学Ⅰ试题命题单位：常州市教育科学研究院 2014．3参考公式：柱体的体积公式：V 柱体=Sh ，其中S 是柱体的底面积，h 是高．直棱柱的侧面积公式：S 直棱柱侧=ch ，其中c 是直棱柱的底面周长，h 是高．一、填空题：本大题共14小题，每小题5分，共计70分．请把答案填写在答题卡相应位置上．．．．．．．．． 1．已知集合{}1,2,3,4A =，{},4,7B m =，若{}1,4A B =，则AB = ．2．若复数z =13i1i+-（i 为虚数单位），则 | z | = ． 3．已知双曲线2218x y m -=m 的值为 ．4．一个容量为20的样本数据分组后，分组与频数分别如下：(]10,20，2； (]20,30，3；(]30,40，4；(]40,50，5；(]50,60，4；(]60,70，2．则样本在(]10,50上的频率是 ．5．执行如图所示的算法流程图，则最后输出的y 等于 ． 6．设函数2()sin f x a x x =+，若(1)0f =，则(1)f -的值为 ．7．四棱锥P - ABCD 的底面ABCD 是边长为2的正方形，P A ⊥底面ABCD 且P A = 4， 则PC 与底面ABCD 所成角的正切值为 ．8．从甲，乙，丙，丁4个人中随机选取两人，则甲乙两人中有且只有一个被选取的概率为 ．9．已知2tan()5+=，1tan 3=，则)4tan(π+a 的值为 ． 10．设等差数列{}n a 的前n 项和为n S ，若13a =-，132k a +=，12k S =-，则正整数k = ．11．已知正数,x y 满足22x y +=，则8x yxy+的最小值为 ．12．如图，在△ABC 中，BO 为边AC 上的中线，2BG GO =，设CD ∥AG ，若15AD AB AC =+λ()∈R λ，则λ的值为 ．13．已知函数22(2)e ,0,()43,0,x x x x f x x x x ⎧-=⎨-++>⎩≤()()2g x f x k =+，若函数()g x 恰有两个不（第5题）（第12题）ABCDOG同的零点，则实数k 的取值范围为 ．14．在平面直角坐标系xOy 中，已知点(3,0)P 在圆222:24280C x y mx y m +--+-=内，动直线AB 过点P 且交圆C 于,A B 两点，若△ABC 的面积的最大值为16，则实数m 的取值范围为 ． 二、解答题：本大题共6小题，共计90分． 15．（本小题满分14分）设函数2()6cos cos f x x x x =-． （1）求()f x 的最小正周期和值域；（2）在锐角△ABC 中，角,,A B C 的对边分别为,,a b c ，若()0f B =且2b =，4cos 5A =，求a 和sin C ．16．（本小题满分14分）如图，在三棱柱111ABC A B C -中，侧面11AA B B 为菱形， 且160A AB ∠=︒，AC BC =，D 是AB 的中点．（1）求证：平面1A DC ⊥平面ABC ； （2）求证：1BC ∥平面1A DC ．17．（本小题满分14分）一个圆柱形圆木的底面半径为1m ，长为10m ，将此圆木沿轴所在的平面剖成两个部分．现要把其中111DC B AC BA （第16题）一个部分加工成直四棱柱木梁，长度保持不变，底面为等腰梯形ABCD（如图所示，其中O为圆心，,C D 在半圆上），设BOC∠=，木梁的体积为V（单位：m3），表面积为S（单位：m2）．（1）求V关于θ的函数表达式；（2）求的值，使体积V最大；（3）问当木梁的体积V最大时，其表面积S是否也最大？请说明理由．18．（本小题满分16分）如图，在平面直角坐标系xOy中，已知A，B，C是椭圆22221(0)x ya ba b+=>>上不同的三点，θD CB A O（第17题）2A，(3,3)B--，C在第三象限，线段BC的中点在直线OA上．（1）求椭圆的标准方程；（2）求点C的坐标；（3）设动点P在椭圆上（异于点A，B，C）且直线PB，PC分别交直线OA于M，N两点，证明OM ON⋅为定值并求出该定值．19．（本小题满分16分）设各项均为正数的数列{}n a的前n项和为S n，已知11a=，且11()(1)n n n nS a S aλ+++=+对一切*n∈N 都成立．（第18题）（1）若λ = 1，求数列{}n a的通项公式；（2）求λ的值，使数列{}n a是等差数列．20．（本小题满分16分）已知函数e()ln,()e xxf x mx a x mg x=--=，其中m，a均为实数．（1）求()g x的极值；（2）设1,0m a =<，若对任意的12,[3,4]x x ∈12()x x ≠，212111()()()()f x f xg x g x -<-恒成立， 求a 的最小值；（3）设2a =，若对任意给定的0(0,e]x ∈，在区间(0,e]上总存在1212,()t t t t ≠，使得120()()()f t f t g x == 成立，求m 的取值范围．数学Ⅱ（附加题）21．【选做题】在A 、B 、C 、D 四小题中只能选做两题．．．．．．，每小题10分，共计20分．请在答题卡指定区．．．．．．域．内作答，解答时应写出文字说明、证明过程或演算步骤．A．选修4—1：几何证明选讲如图，⊙O为四边形ABCD的外接圆，且AB AD=，E是CB延长线上一点，直线EA与圆O相切．求证：CD AB AB BE=．B．选修4—2：矩阵与变换已知矩阵1221⎡⎤=⎢⎥⎣⎦M，17⎡⎤=⎢⎥⎣⎦β，计算6Mβ．C．选修4—4：坐标系与参数方程在平面直角坐标系xOy中，圆的参数方程为22cos,()2sinxy=+⎧⎨=⎩为参数，以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系．求：（1）圆的直角坐标方程；（2）圆的极坐标方程．D．选修4—5：不等式选讲已知函数2()122f x x x a a=++---，若函数()f x的图象恒在x轴上方，求实数a的取值范围．【必做题】第22题、第23题，每题10分，共计20分．22．（本小题满分10分）甲乙两个同学进行定点投篮游戏，已知他们每一次投篮投中的概率均为23，且各次投篮的结果互不影E （第21-A题）响．甲同学决定投5次，乙同学决定投中1次就停止，否则就继续投下去，但投篮次数不超过5次． （1）求甲同学至少有4次投中的概率； （2）求乙同学投篮次数的分布列和数学期望．23．（本小题满分10分）设01212(1)m m n n n n n m S C C C C ---=-+-+-，*,m n ∈N 且m n <，其中当n 为偶数时，2nm =； 当n 为奇数时，12n m -=． （1）证明：当*n ∈N ，2n ≥时，11n n n S S S +-=-； （2）记01231007201420132012201110071111120142013201220111007S C C C C C =-+-+-，求S 的值．2014年苏、锡、常、镇四市高三教学情况调查（一）数学Ⅰ试题参考答案一、填空题：本大题共14小题，每小题5分，共70分．1．{}1,2,3,4,7 2 3. 4 4.710 5．63 6．2 7 8. 23 9． 9810．13 11．9 12．6513.27321,{0,22e+⎛⎫--⎪⎝⎭14. [3(327,3++--二、解答题：本大题共6小题，共计90分．解答时应写出文字说明、证明过程或演算步骤．15. 解：（1）1+cos2()622xf x x=⨯=3cos223x x+=)36x++．…………………3分所以()f x的最小正周期为22T==，…………………4分值域为[3-+．…………………6分（2）由()0f B=，得πcos(2)6B+=．B为锐角，∴ππ7π2666B<+<，π5π266B+=，∴π3B=． (9)分∵4cos5A=，(0,)A∈，∴3sin5A==．…………………10分在△ABC中，由正弦定理得32sinsinb AaB⨯===．…………………12分∴21sin sin()=sin()sin322C A B A A A=---=+=．…………………14分16．（1）证明：∵11ABB A为菱形，且160A AB∠=︒，∴△1A AB为正三角形．…………………2分D是AB的中点，∴1AB A D⊥．∵AC BC=，D是AB的中点，∴AB CD⊥．…………………4分1A D CD D=，∴AB⊥平面1A DC．…………………6分∵AB⊂平面ABC，∴平面1A DC⊥平面ABC．…………………8分（2）证明：连结1C A，设11AC AC E=，连结DE．∵三棱柱的侧面11AA C C是平行四边形，∴E为1AC中点．…………………10分在△1ABC中，又∵D是AB的中点，∴DE∥1BC．…………………12分∵DE⊂平面1A DC，1BC⊄平面1A DC，∴1BC∥平面1A DC．…………………14分17．解：（1）梯形ABCD的面积2cos 2sin 2ABCD S +=⋅=sin cos sin +，(0,)2∈． …………………2分 体积()10(sin cos sin ),(0,)2V =+∈． …………………3分（2）2()10(2cos cos 1)10(2cos 1)(cos 1)V '=+-=-+． 令()0V '=，得1cos 2=，或cos 1=-（舍）． ∵(0,)2∈，∴3=． …………………5分当(0,)3∈时，1cos 12<<，()0,()V V '>为增函数；当(,)32∈时，10cos 2<<，()0,()V V '<为减函数． …………………7分∴当3=时，体积V 最大． …………………8分（3）木梁的侧面积210S AB BC CD =++⋅侧（）=20(cos 2sin 1)2++，(0,)2∈． 2ABCD S S S =+侧=2(sin cos sin )20(cos 2sin 1)2++++，(0,)2∈．…………………10分设()cos 2sin 12g =++，(0,)2∈．∵2()2sin 2sin 222g =-++，∴当1sin22=，即3=时，()g 最大． …………………12分 又由（2）知3=时，sin cos sin +取得最大值，所以3=时，木梁的表面积S 最大． …………………13分综上，当木梁的体积V 最大时，其表面积S 也最大． …………………14分 18．解：（1）由已知，得222291821,991,a b a b ⎧⎪+=⎪⎨⎪+=⎪⎩ 解得2227,27.2a b ⎧=⎪⎨=⎪⎩ …………………2分所以椭圆的标准方程为22127272x y +=． …………………3分 （2）设点(,)C m n (0,0)m n <<，则BC 中点为33(,)22m n --． 由已知，求得直线OA 的方程为20x y -=，从而23m n =-．① 又∵点C 在椭圆上，∴22227m n +=．②由①②，解得3n =（舍），1n =-，从而5m =-． …………………5分 所以点C 的坐标为(5,1)--． …………………6分 （3）设00(,)P x y ，11(2,)M y y ，22(2,)N y y ．∵,,P B M 三点共线，∴011033233y y y x ++=++，整理，得001003()23y x y x y -=--．…………………8分 ∵,,P C N 三点共线，∴22011255y y y x ++=++，整理，得00200523y x y x y -=-+．…………………10分 ∵点C 在椭圆上，∴2200227x y +=，2200272x y =-．从而22200000001222200000003(56)3(3627)393449241822x y x y y x y y y x y x y y x y +--+===⨯=+---+． …………………14分 所以124552OM ON y y ⋅==． …………………15分 ∴OM ON ⋅为定值，定值为452． …………………16分 19．解：（1）若λ = 1，则11(1)(1)n n n n S a S a +++=+，111a S ==．又∵00n n a S >>，， ∴1111n n n nS a S a +++=+， ………………… 2分 ∴3131221212111111n n n nS S a a S a S S S a a a +++++⋅⋅⋅=⋅⋅⋅+++， 化简，得1112n n S a +++=．① ………………… 4分 ∴当2n ≥时，12n n S a +=．②② - ①，得12n n a a +=， ∴12n na a +=（2n ≥）． ………………… 6分 ∵当n = 1时， 22a =，∴n = 1时上式也成立，∴数列{a n }是首项为1，公比为2的等比数列， a n = 2n -1（*n ∈N ）． …………………8分 （2）令n = 1，得21a λ=+．令n = 2，得23(1)a λ=+． ………………… 10分要使数列{}n a 是等差数列，必须有2132a a a =+，解得λ = 0． ………………… 11分 当λ = 0时，11(1)n n n n S a S a ++=+，且211a a ==． 当n ≥2时，111()(1)()n n n n n n S S S S S S +-+-=+-， 整理，得2111n n n n n S S S S S +-++=+，1111n n n nS S S S +-+=+， ………………… 13分 从而3312412123111111n n n nS S S S S S S S S S S S +-+++⋅⋅⋅=⋅⋅⋅+++， 化简，得11n n S S ++=，所以11n a +=． ……………… 15分 综上所述，1n a =（*n ∈N ），所以λ = 0时，数列{}n a 是等差数列． ………………… 16分20．解：（1）e(1)()exx g x -'=，令()0g x '=，得x = 1． ………………… 1分 列表如下：∵g (1) = 1，∴y =()g x 的极大值为1，无极小值． …………………3分 （2）当1,0m a =<时，()ln 1f x x a x =--，(0,)x ∈+∞．∵()0x af x x -'=>在[3,4]恒成立，∴()f x 在[3,4]上为增函数． …………………4分 设1e ()()e x h x g x x ==，∵12e (1)()x x h x x --'=> 0在[3,4]恒成立， ∴()h x 在[3,4]上为增函数． …………………5分 设21x x >，则212111()()()()f x f xg x g x -<-等价于2121()()()()f x f x h x h x -<-， 即2211()()()()f x h x f x h x -<-．设1e ()()()ln 1e xu x f x h x x a x x=-=---⋅，则u (x )在[3,4]为减函数．∴21e (1)()10e x a x u x x x -'=--⋅≤在（3，4）上恒成立． …………………6分∴11e ex x a x x---+≥恒成立． 设11e ()e x x v x x x --=-+，∵112e (1)()1e x x x v x x ---'=-+=121131e [()]24x x ---+，x ∈[3，4]，∴1221133e [()]e 1244x x --+>>，∴()v x '< 0，()v x 为减函数．∴()v x 在[3，4]上的最大值为v (3) = 3 -22e 3． ………………… 8分∴a ≥3 -22e 3，∴a 的最小值为3 -22e 3． …………………9分（3）由（1）知()g x 在(0,e]上的值域为(0,1]． …………………10分 ∵()2ln f x mx x m =--，(0,)x ∈+∞，当0m =时，()2ln f x x =-在(0,e]为减函数，不合题意． ………………… 11分当0m ≠时，2()()m x m f x x-'=，由题意知()f x 在(0,e]不单调，所以20e m <<，即2em >．① …………………12分此时()f x 在2(0,)m 上递减，在2(,e)m上递增， ∴(e)1f ≥，即(e)e 21f m m =--≥，解得3e 1m -≥．② 由①②，得3e 1m -≥． …………………13分 ∵1(0,e]∈，∴2()(1)0f f m =≤成立． …………………14分下证存在2(0,]t m ∈，使得()f t ≥1．取e m t -=，先证e 2m m-<，即证2e 0m m ->．③ 设()2e x w x x =-，则()2e 10x w x '=->在3[,)e 1+∞-时恒成立． ∴()w x 在3[,)e 1+∞-时为增函数．∴3e ))01((w x w ->≥，∴③成立． 再证()e m f -≥1． ∵e e 3()1e 1m m f m m m --+=>>-≥，∴3e 1m -≥时，命题成立． 综上所述，m 的取值范围为3[,)e 1+∞-． …………………16分21、【选做题】在A 、B 、C 、D 四小题中只能选做两题．．．．．．，每小题10分，共计20分． A ．选修4—1：几何证明选讲证明：连结AC ．EA 是圆O 的切线，∴EAB ACB ∠=∠． …………………2分AB AD =，∴ACD ACB ∠=∠． ∴ACD EAB ∠=∠． …………………4分圆O 是四边形ABCD 的外接圆，∴D ABE ∠=∠． …………………6分∴CDA ∆∽ABE ∆． …………………8分 ∴CD DAAB BE=， AB AD =，∴CD ABAB BE=． …………………10分 B ．选修4—2：矩阵与变换 解：矩阵M 的特征多项式为212()2321f λλλλλ--==----．令12()031f λλλ===-，解得，，对应的一个特征向量分别为111⎡⎤=⎢⎥⎣⎦α，211⎡⎤=⎢⎥-⎣⎦α． …5分令12m n =+βαα，得4,3m n ==-．6666661212112913(43)4()3()433(1)112919⎡⎤⎡⎤⎡⎤=-=-=⨯--=⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦M βM ααM αM α．……………10分 C ．选修4—4：坐标系与参数方程解：（1）圆的直角坐标方程为22(2)4x y -+=． …………………5分 （2）把cos ,sin ,x y ρθρθ=⎧⎨=⎩代入上述方程，得圆的极坐标方程为4cos ρθ=．…………………10分D ．选修4—5：不等式选讲解：()f x 的最小值为232a a --， …………………5分由题设，得223a a -<，解得(1,3)a ∈-． …………………10分【必做题】第22题、第23题，每题10分，共计20分．22．解：（1）设甲同学在5次投篮中，有x 次投中，“至少有4次投中”的概率为P ，则(4)(5)P P x P x ==+= …………………2分=441550552222()(1)()(1)3333C C -+-=112243． …………………4分 （2）由题意1,2,3,4,5=．2(1)3P ==，122(2)339P ==⨯=，1122(3)33327P ==⨯⨯=，3122(4)3381P ⎛⎫==⨯= ⎪⎝⎭， 411(5)381P ⎛⎫=== ⎪⎝⎭．的分布表为…………………8分的数学期望22221121123453927818181E =⨯+⨯+⨯+⨯+⨯=． …………………10分23．解：（1）当n 为奇数时，1n +为偶数，1n -为偶数， ∵1101221112(1)n n n n nn S CC C+++++=-++-，110122112(1)n n n n n n S C C C---+=-++-，11012211212(1)n n n n n n S C CC------=-++-，∴1111110011222221111111222()()(1)()(1)n n n n n n n n n n n n n n S S C C C C CCC-+-++-++-++++-=---++--+-=11012212112((1))n n n n n n CCCS --------++-=-．∴当n 为奇数时，11n n n S S S +-=-成立． …………………5分 同理可证，当n 为偶数时， 11n n n S S S +-=-也成立． …………………6分 （2）由01231007201420132012201110071111120142013201220111007S C C C C C =-+-+-，得 0123100720142013201220111007201420142014201420142013201220111007S C C C C C =-+-+-=0112233100710072014201320132012201220112011100710071231007()()()()2013201220111007C C C C C C C C C -+++-++-+=0121007012100620142013201210072012201120101006()()C C C C C C C C -+----+-+=20142012S S -． …………………9分 又由11n n n S S S +-=-，得6n n S S +=， 所以20142012421S S S S -=-=-，12014S =-． …………………10分。
2014年理科数学一模答案
2014年理科一模答案1.D2.D3.C4.C5.B6.B7.A8.D9.A 10.B 11.D 12.D 13. 3 14.61 15.8 16. 23-=xy17. 1)6sin(cos 4)(-+=πx x x f1)c o s 21s i n 23(c o s 4-+=x x x…………………（1分） 1cos 2cos sin 322-+=x x xx x 2cos 2sin 3+= …………………（2分）)62sin(2π+=x…………………（3分） （1）令.,226222Z k k x k ∈+≤+≤-πππππ…………………（4分）递增区间是).(],6,3[Z k k k ∈+-ππππ …………………（5分）（2）,0π<<C ,613626πππ<+<∴C 由1)(=C f ，可得3π=C∵21cos 2222==-+C ab c a b ， …………………（7分） ∴22222c ab c b a ab -≥-+=, …………………（9分） 又∵4=c ∴.16≤ab 343sin 1621=⨯⨯=π∆ABC S…………………（11分）当且仅当4==b a 时,故△ABC 面积的最大值是34. …………………（12分）18.解：（1）乙的中间有两个数187和188，因此乙的中位数为187.5cm…………… （3分）（2）根据茎叶图知，“优秀品种”的有12株，“非优秀品种”的有18株. 用分层抽样的方法抽取，每株被抽中的概率是51306= “优秀品种”的有11226⨯=株，“非优秀品种”的有11836⨯=株. ……………（5分） 用事件A 表示“至少有一株‘优秀品种’的被选中”，则2325C 37()11,C 1010P A =-=-=因此从5株树苗中选2株，至少有一株“优秀品种”的概率是710.……………………（7分） （3）依题意，一共有12株优秀品种，其中乙种树苗有8株，甲种树苗有4株，则X 的所有可能取值为0，1，2，3，321884331212C C C 1428(0);(1);C 55C 55P X P X ======213484331212C C C 121(2);(3).C 55C 55P X P X ======………………………………………（9分）因此X 的分布列如下：X 0123P1455 2855 1255 155所以1428121()0123155555555E X =⨯+⨯+⨯+⨯=.……………………………………（12分）19.（1）由三视图可知NABB BC 1面⊥，建系)0,8,0(),0,4,4(),0,0,4(,)0,0,0(1B N A B ，,)4,8,0(),4,0,0(1C C…………………（1分）)4,4,4(),0,4,4(),0,4,4(11--=-==N C N B BN …………………（2分） 01=⋅N B BN ，01=⋅N C BN 且N N C N B =⋂11, …………………（4分）⊥∴BN 平面N B C 11 …………………（5分）（2）设平面1CNB 的法向量),,(z y x n =，则0=⋅CN n ，01=⋅CB n⎩⎨⎧=-=-+∴0480444z y z y x )2,1,1(=∴n …………………（8分）设N C 1与平面1CNB 所成的角为θ,则32sin 11=⋅=nN C n N C θ…………………（11分） ∴直线N C 1与平面1CNB 所成角的正弦值为32. …………………（12分）20.. (I) 由已知||32||MQ MP -=,即32||||=+MQ MP …………………（2分） 且32大于||PQ …………………（3分） 所以M 的轨迹是以(2,0),(2,0)-为焦点，23为长轴长的椭圆，即其方程为2213x y += …………………（5分）(II)设AB 的方程为t kx y +=代入椭圆方程得到0336)13(222=-+++t ktx x k224(933)0k t ∆=+->, 即2231k t +>① 方程有两个不同的解…………………（6分）122631kt x x k -+=+,1223231x x ktk +-=+122231y y t k +=+, …………………（7分） 1212112202y y x x k ++=-+-,化简得到2314k t += ② …………………（8分）得到04t << 又原点到直线的距离为2||1t d k =+ …………………（9分）22221224(933)||1||131k t AB k x x kk +-=+-=++ …………………（10分）222224(933)11||=||||122311AOB k t t S AB d k k k ∆+-=+++化简得到21=3(4)4AOB S t t ∆- ，所以当2t =时,即73k =±…………………（11分）AOB S ∆取得最大值32 …………………（12分）21. （1）（1）xx f 1)(=', …………………（1分） 1)1(='f , …………………（2分） 故切线方程为1-=x y ； …………………（4分）（2）)ln (2)(a x xx a x x g -+-='， …………………（5分）令a xxx a x x F -+-=ln )(，则)(x F y =在[)+∞,1上单调递增．221ln )(xa x x x F ++-='，则当1≥x 时，01ln 2≥++-a x x 恒成立， 即当1≥x 时，1ln 2-+-≥x x a 恒成立． …………………（6分）令1ln )(2-+-=x x x G ，则当1≥x 时，021)(2<-='xx x G ， 故1ln )(2-+-=x x x G 在[)+∞,1上单调递减，从而2)1()(m ax -==G x G ，…………………（7分）故2)(m ax -=≥x G a ． …………………（8分）（3）()()()x x a x x a a x a x x g 22222ln ln 22ln )(+++-=-+-=，令()x x a x x a a h 222lnln 22)(+++-=，则()2ln )(2x x a h -≥．…………………（9分）令x x x Q ln )(-=，则xx x x Q 111)(-=-='，显然)(x Q 在()1,0上单调递减，在()+∞,1上单调递增， …………………（10分） 则1)1()(m in ==Q x Q ， …………………（11分）则21)()(≥=a h x g ． …………………（12分）22. （1）证明：,,,A B C P 共圆，又ABC ∆ 为等边三角形，60QPB BAC ∴∠=∠=，…………………（1分）AB BC =PQ PB = ，QPB ∴∆为等边三角形，60Q BPA BCA ∴∠=∠=∠=…………………（2分）ABP ∴∆≌CBQ ∆ …………………（3分） CQ AP ∴=； …………………（4分）（2）设1AB =， 点P 是弧BC 的中点，AB AC =，90ABP ∴∠= ，60APB ∠= ，…………………（6分）33BP ∴=， …………………（8分） 221::1:33ABC BPQSSAB BP ∆∆=== …………………（10分） 23. (1)解:(I)由θθρcos 4sin 2=,得θρθρcos 4)sin (2=所以曲线C 的直角坐标方程为x y 42= ………………………………（4分） (2)将直线l 的参数方程代入x y 42=,得032382=--t t …………（5分） 设A 、B 两点对应的参数分别为t 1、t 2,则t 1+t 2=38,t 1t 2=32- …………（7分）()5842122121=-+=-=+∴t t t t t t PB PA …………（9分）4511=⋅+=+∴PB PA PB PA PB PA …………（10分）24. 24．（1）①⎩⎨⎧≤--<221x x φ∈⇒x …………………（1分）②⎩⎨⎧≤≤≤-2211x 11≤≤-⇒x…………………（2分）① ⎩⎨⎧≤>221x x ϕ∈⇒x…………………（3分）不等式的解集为]1,1[-…………………（4分）(2) ||3||2|||32|z y x z y x ++≤-+ …………………（7分） 359136121|=⨯+⨯+≤ …………………（9分）35|32|≤-+∴z y x …………………（10分）。
历下区2014一模及答案
224971721.doc1历下区2014年初三年级学业水平模拟考试数学试题（历下区一模 2014.4）一、选择题（本大题共15个小题，每小题3分，共45分．在每小题给出的四个选项中，只有一项是符合题目要求的．） 1下列运算正确的是（ ） A 3-= 3 B 21)21(-=-- C ()532a a = D a a a 632=⋅2如图所示几何体的左视图是（ ）3某市2014年第一季度财政收入为76.42亿元，用科学记数法（结果保留两个有效数字） 表示为( )Ａ8107.42⨯元 Ｂ.9103.4⨯元 Ｃ．9102.4⨯元 Ｄ81042⨯元 4.如图，将三角尺的直角顶点放在直尺的一边上，130250∠=∠=°，°，则3∠的度数等于（ ）A ．50°B ．30°C ．20°D ．15°5.下列函数中，自变量x 的取值范围是x ≥3的是 ( ) A ．31-=x y B.31-=x yC. 3-=x yD.3-=x y6.“泉城是我家，爱护靠大家”，为创建文明城市，我市学生更加自觉遵守交通规则某校学生小明每天骑自行车上学时都要经过一个十字路口，该十字路口有红、黄、绿三色交通信号灯，他在路口遇到红灯的概率为31，遇到黄灯的概率为91，那么他遇到绿灯的概率为 ( ) A 31 B 32 C 94 D 95 1 23第4题图224971721.doc7．不等式组 的解集在数轴上表示为（ ）A ． B．C ．D ．8.方程1)2)(1(+=-+x x x 的解是（ ）A ．2 B.3 C.－1，2 D.－1，39．如图，△ABC 是等边三角形，P 是∠ABC 的平分线BD 上一点，PE ⊥AB 于点E ，线段BP 的垂直平分线交BC 于点F ，垂足为点Q ．若BF ＝2，则PE 的长为( )A ．2B ．32C ．3D ．3 10．如图，点A 是直线l 外一点，在l 上取两点B 、C ，分别以A 、C 为圆心，BC 、AB 长为半径画弧，两弧交于点D ，分别连结AB 、AD 、CD ，则四边形ABCD 一定是（ ）A ．平行四边形B ．矩形C ．菱形D ．梯形11．已知⊙1O 的半径是5cm ,⊙2O 的半径是3cm ,21O O ＝6cm ,则⊙1O 和⊙2O 的位置关系是( )A ． 相交B ．外切C ． 外离D ．内含12某机械厂七月份生产零件50万个，第三季度生产零件196万个．设该厂八、九月份平均每月的增长率为x ，那么x 满足的方程是（ ） A ．196)1(502=+x B ．196)1(50502=++x C.196)1(50)1(50502=++++x x D ．196)21(50)1(5050=++++x x13抛物线c bx x y ++-=2的部分图象如图所示，若0>y ，则x 的取值范围是（ ）A ．14<<-x B.13<<-x C.4-<x 或1>x D.3-<x 或1>x 14．如图，A 、B 是双曲线xky =（k ＞0）上的点， A 、B 两点的横坐第10题图第13题图第9题图A D E PQ224971721.doc3标分别是a ，a 2，线段AB 的延长线交x 轴于点C ，若S △AOC =12．则k 为( ) A ．5 B ．6 C ．7 D ．815．如图，在Rt △AOB 中，OA=OB=23，⊙O 的半径为1，点P 是AB 边上的动点，过点P 作⊙O 的一条切线PQ （点Q 为切点），则线段PQ 的最小值为( ) A ．123- B ．2 C ．22 D ．23二、填空题（本大题共6个小题，每小题3分，共18分．把答案填在题中的横线上．） 16分解因式a ax 42-＝_ ．17如图，矩形ABCD 的对角线AC 和BD 相交于点O ，过 点O 的直线分别交AD 和BC 于点E 、F ，23AB BC ==，， 则图中阴影部分的面积为 ．18．如图，要制作一个母线长为8cm ，底面圆周长是12πcm 的圆锥形小漏斗，若不计损耗，则所需纸板的面积是 ______2cm ．19．如图，在一场羽毛球比赛中，站在场内M 处的运动员林丹把球从N 点击到了对方内的B 点，已知网高OA=1.52米，OB=4米，OM=5米，则林丹起跳后击球点N 离地面的距离NM= 米．20如图，边长为1的正方形ABCD 绕点A 逆时针旋转45°到正方形AB C D '''，图中重合部分的面积为_________．A B C第17题图第15题图224971721.doc421．菱形ABCD 中，AB=AC ，点E 、F 分别为边AB 、BC 上的点，且AE=BF ，连接CE 、AF 交于点H ，连接DH 交A C 于点O ．则下列结论：①△ABF≌△CAE，②∠AHC=120°，③AH+CH=DH，④DH OD AD ∙=2，正确的是___________三、解答题（本大题共7个小题，共57分．解答应写出文字说明、证明过程或演算骤．）22. (本小题满分7分)(1) 化简： 22111x x x x ++++ (2)解二元一次方程组3582 1.x y x y +=⎧⎨-=⎩，①②23(本题满分7分)（1）如图，已知AB 是⊙O 的直径，弦CD AB ⊥于E ，AC =8，CD =6,求cos ∠ABC 的值．（2）如图，在△ABC 中，∠A =30°，∠B =45°，AC =32，求AB 的长24．（本题满分8分）在创建“国家卫生城市”的活动中，济南市园林公司加大了对市区主干道两旁植“景观树”的力度，平均每天比原计划多植5棵，现在植60棵所需的时间与原计划植45棵所需的时间相同，问现在平均每天植多少棵树？45°30°C BA第图224971721.doc525（本小题满分8分）我区实施“翻转课堂”教学改革后，学生的自主学习、合作交流能力有很大提高，张老师为了解所教班级学生自主学习、合作交流的具体情况，对本班部分学生进行了为期半个月的跟踪调查，并将调查结果分成四类，A ：特别好；B ：好；C ：一般；D ：较差；并将调查结果绘制成以下两幅不完整的统计图，请你根据统计图解答下列问题：（1）本次调查中，张老师一共调查了 名同学，其中C 类女生有 名，D 类男生有 名；（2）将上面的条形统计图补充完整；（3）为了共同进步，张老师想从被调查的A 类和D 类学生中分别选取一位同学进行“一帮一”互助学习，请用列表法或画树形图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率26．(本小题满分9分) 如图，已知△ABC中，AB=10cm，AC=8cm，BC=6cm．如果点P由B出发沿BA 向点A匀速运动，同时点Q由A出发沿AC向点C匀速运动，P点速度为2cm/s，Q点速度为1cm/s，连接PQ，设运动的时间为t（单位：s）（0≤t≤5）．（1）当t为何值时，PQ∥BC．（2）设四边形PQCB的面积为S（单位：cm2），当t为何值时，S取得最小值，并求出最小值．（3）是否存在某时刻t，使线段PQ恰好把△ABC的面积平分？若存在，求出此时t的值；若不存在，请说明理由．224971721.doc 6224971721.doc727．（本小题满分9分）阅读理解：如图1，在四边形ABCD 的边AB 上任取一点E （点E 不与点A 、点B 重合），分别连接ED ，EC ，可以把四边形ABCD 分成三个三角形，如果其中有两个三角形相似，我们就把E 叫做四边形ABCD 的边AB 上的相似点；如果这三个三角形都相似，我们就把E 叫做四边形ABCD 的边AB 上的强相似点． 解决问题：（1）如图1，∠A=∠B=∠DEC=55°，试判断点E 是否是四边形ABCD 的边AB 上的相似点，并说明理由；（2）如图2，在矩形ABCD 中，AB=5，BC=2，且A ，B ，C ，D 四点均在正方形网格（网格中每个小正方形的边长为1）的格点（即每个小正方形的顶点）上，试在图2中画出矩形ABCD 的边AB 上的一个强相似点E ； 拓展探究：（3）如图3，将矩形ABCD 沿CM 折叠，使点D 落在AB 边上的点E 处．若点E 恰好是四边形ABCM的边AB 上的一个强相似点，试探究AB 和BC 的数量关系．图 3图 2图1224971721.doc828．（本小题满分9分）如图，已知抛物线y=ax 2+bx+c （a≠0）的顶点坐标为)32,4(，且与轴交于点C ，与x 轴交于A ，B 两点（点A 在点B 的左边），且A 点坐标为（2,0）． （1）求抛物线的解析式及B 点的坐标；（2）在（1）中抛物线的对称轴l 上是否存在一点P ，使AP+CP 的值最小？若存在，求AP+CP 的最小值，若不存在，请说明理由；（3）以AB 为直径的⊙M 与直线CE 相切于点E ，CE 交x 轴点D ，求直线CE 的解析式．E28备用E224971721.doc92014历下一模答案选择1-5 A D BCD 6-10 DBDCA 11-15 ACBDC填空16. a (x ＋2)(x －2) 17. 3 18. 48πcm 219.3.42 米 20.12- 21．①②③④22. (1) 化简： 22111x x x x ++++ 解：原式=2211x x x +++ …………………………..………1分2(1)1x x +=+……………………………………………………2分 1x =+………………………………………………………3分(2）解 ∵3582 1.x y x y +=⎧⎨-=⎩，①②由②得12-=x y ，③将③代入①，得8)12(53=-+x x ．解得1=x ．代入③，得1=y ．……………… 2分 ∴原方程组的解为11.x y =⎧⎨=⎩，……………………………… 4分23.(本题满分7分)（1）解：∵AB 是⊙O 的直径,CD AB ⊥ ∴CE=DE=CD 21=3，∠ACB=90°,∠AEC=90°………1分∴∠ABC=∠ACD ……..………2分∴cos ∠ABC= cos ∠ACD=83=AC CE ………3分 （2）如图，在△ABC 中，∠A =30°，∠B =45°，AC =32，求AB 的长. （2）作CD ⊥AB 于点D ，∵∠A=30°，∴AD=3……………………………………………5分45°30°C BAD第23（1）题图又∵∠B=45°∴6分∴7分24.设现在平均每天植树x棵，则原计划平均每天植树（x﹣5）棵．………1分依题意得：，………4分解得：x=20，………6分经检验，x=20是方程的解，且符合题意． (7)分答：现在平均每天植树20棵．………8分25.【答案】：（1）20，（1分） 2 ，（1分）1（1分）；（2）如图（2分，各1分）（3）选取情况如下：（列表或树形图正确2分、计算概率1分）224971721.doc 10224971721.doc 11∴所选两位同学恰好是一位男同学和一位女同学的概率2163==P .....................8分26．(本小题满分9分)解：（1）∵PQ ∥BC ，∴，..............................................1分 即810210tt =-...................................................................2分 解得t=1340，∴当t=1340s 时PQ ∥BC ．...........................................3分（2）∵AB =10cm ，AC =8cm ，BC =6cm ，∴∠C=90°...............................4分 过P 点作PD ⊥AC 于点D ．∴PD ∥BC ，∴， 即，解得PD=6﹣t ．.....................5分∴S=-⨯⨯8621×AQ×PD =24-×t×（6﹣t ）=479)25(532+-t∴当t=s 时，S 取得最小值，最小值为479cm 2．.................................6分（3）假设存在某时刻t ，使线段PQ 恰好把△ABC 的面积平分，则有S △AQP=S △ABC =12．S △AQP =12)566(21=-t t ， ∴123532=+-t t ，...............................................8分化简得：t 2﹣5t+20=0，∵△=（﹣5）2﹣4×1×20=﹣55＜0，此方程无解，∴不存在某时刻t ，使线段PQ 恰好把△ABC 的面积平分．..................................9分27.（1）点E 是四边形ABCD 的边AB 上的相似点．理由：∵∠A=55°，∴∠ADE+∠DEA=125°．.......................1分∵∠DEC=55°，∴∠BEC+∠DEA=125°．∴∠ADE=∠BEC ． ........................2分∵∠A=∠B ，D224971721.doc 12∴△ADE ∽△BEC ．∴点E 是四边形ABCD 的AB 边上的相似点．........................3分（2）作图如下：........................6分（3）∵点E 是四边形ABCM 的边AB 上的一个强相似点， ∴△AEM ∽△BCE ∽△ECM ，∴∠BCE=∠ECM=∠AEM ．由折叠可知：△ECM ≌△DCM ，........................7分∴∠ECM=∠DCM ，CE=CD ，∴∠BCE=∠BCD=30°， ........................8分∴BE=CE=AB ．在Rt △BCE 中，tan ∠BCE==tan30°，∴，∴．........................9分28.解：（1）由题意，设抛物线的解析式为y=a （x ﹣4）2+（a ≠0） ∵抛物线经过（2,0） ∴032)42(2=+-a 解得：a=61-∴y=32)4(612+--x .......................2分 当y=0时，x 2﹣x+2=0解得：x=2或x=6∴B （6，0）；.......................3分E PE 图1224971721.doc 13 （2）存在，如图2，由（1）知：抛物线的对称轴l 为x=4， 因为A 、B 两点关于l 对称，连接CB 交l 于点P ，则AP=BP ，所以AP+CP=BC 的值最小.......................4分 ∵B （6，0），C （0，2）∴OB=6，OC=2∴BC=2，∴AP+CP=BC=2 .......................6分（3）如图3，连接ME∵CE 是⊙M 的切线∴ME ⊥CE ，∠CEM=90°由题意，得OC=ME=2，∠ODC=∠MDE∵在△COD 与△MED 中∴△COD ≌△MED （AAS ），.......................7分∴OD=DE ，DC=DM设OD=x则CD=DM=OM ﹣OD=4﹣x则RT △COD 中，OD 2+OC 2=CD 2，∴x 2+22=（4﹣x ）2∴x= ∴D （，0） .......................8分设直线CE 的解析式为y=kx+b ∵直线CE 过C （0，-2），D （，0）两点，则 解得： ∴直线CE 的解析式为234-=x y .......................9分 E 图3 {2023-==+b b k {234-==b k。
2014石家庄一模试卷政治参考答案
2014年初中毕业生基础知识与能力学习评价思想品德参考答案卷Ⅰ（选择题，共50分）(非选择题，共50分)26．抵制谣言，回答问题。
（8分）（1）污染网络环境；侵害公民合法权益；引发公众恐慌，影响人们生活；扰乱社会秩序，危害社会稳定，败坏社会风气。
（每点2分，2点即可，共4分）（2）国家加强网络立法，依法打击制造和传播网络谣言的行为；社会加大宣传力度文明上网；个人提高分辨是非的能力，不信谣、不传谣、不制造谣言；发现散布谣言的行为，要及时制止或举报等。
互联网企业和手机媒体：加强行业自律，增强职业道德和法制观念，依法规范自身行为，以高度的社会责任感，为广大公民创造良好的网络环境。
（每点2分，两个角度即可，共4分）27．关注新修法律，分析说明。
（12分）（1）有法可依（2分）（2）有利于更好保障消费者的合法权益；有利于依法规范经营者的行为，维护市场正常的经济秩序；为保护消费者的合法权益提供了法律保障、法律依据；有利于进一步完善社会主义法律体系；有利于维护社会公平正义。
（每点2分，3点即可，共6分）（3）认真学习相关新修订的法律法规；宣传相关新修订的法律法规，让更多的人增强法律意识；自觉遵守相关法律法规，维护自身合法权益；同违法犯罪行为作斗争等。
积极行使监督权，为国家的法治建设献计献策。
（每点2分，2点即可，共4分）28．关注生态，共同努力。
(8分)（1）经济建设与环境保护的关系。
（2分）（2）环境污染严重；环境问题危害人类健康；制约着我国经济和社会的可持续发展。
（每点2分，2点即可，共4分）（3）宣传保护环境、改善空气质量的重要性，让更多的人树立环保意识、改善空气质量意识；从点滴小事做起，如绿色出行：劝说家人少开私家车，我们自己多坐公交车，步行或骑自行车；对污染空气的违法行为进行及时举报。
（每点1分，2点即可，共2分）29．学习榜样，分析说明。
（10分）（1）助人为乐、诚信、孝敬父母等。
（每点1分，2点即可，共2分）（2）有利于我国思想道德建设和精神文明建设；为实现中国梦提供精神动力；有利于提高人们的思想道德素质；有利于形成良好的社会风气等。
河南省六市2014届高三一模理综试题 Word版含答案
河南省六市2013—2014学年度高中毕业班第一次联考理科综合能力测试本试题卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，第Ⅰ卷1至5页，第Ⅱ卷6至16页，共300分。
注意事项：1．答题前，考生务必将自己的姓名、准考证号填写在答题卡上。
考生要认真校对答题卡上粘贴的条形码的“准考证号、姓名”与考生本人准考证号、姓名是否一致。
2．第Ⅰ卷每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号。
第Ⅱ卷用黑色墨水签字笔在答题卡上指定区域书写作答，在试题上作答，答案无效。
3．考试结束，监考员将试题卷、答题卡一并收回。
第Ⅰ卷（选择题，共126分）可能用到的相对原子质量H 1 Li 7 C 12 N 14 O 16 F 19 Na 23 Al 27 Si 28 P31 S 32 Ca 40 Ni 59一、选择题：本大题共13小题．每小题6分。
在每小题给出的四个选项中．只有一项是符合题目要求的。
1．下列有关“一定”的说法正确的是①进行光合作用的绿色植物，细胞一定均含有叶绿体②生长素对植物生长一定起促进作用③没有细胞结构的生物一定是原核生物④酶催化作用的最适温度一定是37℃⑤人体细胞有氧呼吸全过程一定在线粒体中⑥两个种群间的生殖隔离一旦形成，这两个不同种群的个体之间一定不能进行交配⑦与双缩脲试剂发生紫色反应的物质一定是蛋白质⑧将斐林试剂加入某植物组织样液，显现蓝色，说明该样液中一定不含有还原糖A．全部不正确B．有一个正确C．有两个正确D．有三个正确2．下列实验所选用的材料、试剂和实验目的正确的一组是A．利用甘蔗组织样液进行还原性糖的鉴定，加入斐林试剂并加热会出现明显的砖红色沉淀B．用高倍显微镜观察人口腔上皮细胞中的线粒体时，在洁净的载玻片中央滴一滴用0．5g健那绿和50mL蒸馏水配制的染液C．观察渗透现象时，在长颈漏斗口外封上一层玻璃纸，往漏斗内注入蔗糖溶液，然后将漏斗浸入盛有清水的烧杯中D．探究温度对酶活性的影响，向3％过氧化氢溶液中加入过氧化氢酶溶液3．下图是描述生命现象的示意图，以下相关叙述正确的是A．若甲代表种群，a为能量输入，则b、c可分别代表散失的热量和储存在ATP中的能量B．若甲代表人体下丘脑，a为血浆渗透压下降，则b、c可分别代表产生渴觉和尿液减少C．若甲代表人体B淋巴细胞，a为抗原刺激及淋巴因子的作用，则b、c可分别代表浆细胞和记忆细胞的形成D．若甲代表棉铃虫种群，a为诱捕雄虫，则b、c可分别代表性别比例失调和种群密度提高4．某校学生开展研究性学习，在搭建DNA分子模型的实验中，若有4种碱基塑料片共20个，其中4个C，6个G，3个A，7个T，脱氧核糖和磷酸之间的连接物14个，脱氧核糖塑料片40个，磷酸塑料片100个，代表氢键的连接物若干，脱氧核糖和碱基之间的连接物若干，则A．能搭建出20个脱氧核苷酸B．能搭建出410种不同的DNA分子模型C．所搭建的DNA分子片段最长为7碱基对D．能搭建出一个4碱基对的DNA分子片段5．自然界中，与花生相比，玉米更适合生长在高温、光照强烈和干旱的环境中，其利用CO2的能力也远远高于花生。
2014年越秀区数学一模含答案解析详细
第8题图BA ＇AB ＇O第6题图广州市越秀区2014届九年级下学期期中检测（一模）数学试题第一部分 选择题(共30分)一、选择题(本大题共10小题，每小题3分，满分30分.在每小题给出的四个选项中，只有一项是符合题目要求的) 1．4的平方根为（ * ）． A ．2B ．±2C ．4D ．±42. 对于样本数据1，2，3，2，2，以下判断：①平均数为5；②中位数为2；③众数为2；④极差为2．正确的有（ * ）． A ．1个B ．2个C ．3个D ．4个3.如图所示的几何体的主视图是（ * ）．4．如果代数式1-x x有意义，那么x 的取值范围是（ * ）． A ．x ≥0B ．x ≠1C ．x ＞0D ．x ≥0且x ≠15. 已知一个圆锥的底面半径为3cm ，母线长为10cm ，则这个圆锥的侧面积为（ * ）． A ．30πcm 2B ．50πcm 2C ．60πcm 2D ．391πcm 26．如图，将△AOB 绕点O 按逆时针方向旋转45°后得到△A ＇OB ＇，若∠AOB=15°，则∠AOB ＇的度数是（ * ）． A ．25° B ．30° C ．35° D ．40°7．一次函数32-=x y 的大致图像为（ * ）．A ．B ．C ．D ．8．如图，四个边长为1的小正方形拼成一个大正方形，A 、B 、O 是 小正方形顶点，⊙O 的半径为1，P 是⊙O 上的点，且位于右上方的小 正方形内，则∠APB 等于（ * ）．A ．30°B ．45°C ．60°D ．90°9．关于x的二次函数2(1)2y x =--+，下列说法正确的是（ * ）．A ．B ．C ．D ．第3题图第13题图 C O D E F A B第10题图A ．图象的开口向上B ．图象与y 轴的交点坐标为（0，2）C ．当1x >时，y 随x 的增大而减小D ．图象的顶点坐标是（-1,2）10．如图，直角三角形纸片ABC 中，AB=3，AC=4，D 为斜边BC 中点，第1次将纸片折叠，使点A 与点D 重合，折痕与AD 交与点P 1；设P 1D 的中点为D 1，第2次将纸片折叠，使点A 与点D 1重合，折痕与AD 交于点P 2；设P 2D 1的中点为D 2，第3次将纸片折叠，使点A 与点D 2重合，折痕与AD 交于点P 3；…；如此类推，则AP 6的长为（ * ）．A ．512532⨯B ．69352⨯C ．614532⨯D ．711352⨯第二部分 非选择题(共120分)二、填空题(本大题共6小题，每小题3分，满分18分)11．点A （0,3）向右平移2个单位长度后所得的点A ’的坐标为 * ．12．已知空气的单位体积质量为0.00124克/厘米3，将0.00124用科学记数法表示为 * ． 13．如图，△ABC 与△DEF 是位似图形，相似比为2∶3，已知AB ＝4，则DE 的长为 * ．14．化简：=+-+1112a a a * ． 15．如图，防水堤坝的轴截面是等腰梯形ABCD ，DA CB =，DC AB ∥，5=DA ，4=DC ，9=AB ，则斜坡DA 的坡角为 * __ 度．16．已知α ，β是关于x 的一元二次方程x 2+（2m +3）x +m 2=0的两个不相等的实数根，且满足βα11+=﹣1，则m 的值是 * ．三、解答题(本大题共9小题，满分102 分．解答应写出文字说明、证明过程或演算步骤)17．（本小题满分9分）解方程：xx 332=-．A B C D 第15题图18．（本小题满分9分）如图，已知□ABCD .（1）作图：延长BC ，并在BC 的延长线上截取线段CE ，使得CE =BC （用尺规作图法，保留作图痕迹，不要求写作法）； （2）在（1）的条件下，连结AE ，交CD 于点F ， 求证:△AFD ≌ △EFC . 19．（本小题满分10分）已知1=-b a 且2=ab ，求代数式32232ab b a b a +-的值．20．（本小题满分10分）小强对自己所在班级的48名学生平均每周参加课外活动的时间进行了调查，由调查结果绘制了频数分布直方图，根据图中信息回答下列问题： （1）求m 的值；（2）从参加课外活动时间在6～10小时的5名学生中随机选取2人，请你用列表或画树状图的方法，求其中至少有1人课外活动时间在8～10小时的概率．21．（本小题满分12分）为支持失学儿童，某中学计划用“义捐义卖”活动中筹集的部分资金用于购买A,B 两种型号的学习用品共1000件，已知A 型学习用品的单价为20元，B 型学习用品的单价为30元.（1）若购买这批学习用品用了26000元，则购买A,B 两种学习用品各多少件？ （2）若购买这批学习用品的钱不超过28000元，则最多能购买B 型学习用品多少件？ 22．（本小题满分12分）如图，在菱形ABCD 中，AB ＝23，∠BAD ＝60º，AC 交BD 于点O ，以点D 为圆心的⊙D 与边AB 相切于点E ． （1）求AC 的长；（2）求证：⊙D 与边BC 也相切．第18题图第20题图23．（本小题满分12分）如图，四边形ABCD 为正方形．点A 的坐标为（0，2），点B 的坐标为（0，﹣3），反比例函数xky =)0(≠k 的图象经过点C ．（1）求反比例函数的解析式；（2）若点P 是反比例函数图象上的一点，△P AD 的面积恰好等于正方形ABCD 的面积，求点P 的坐标．第23题图九年级数学参考答案与评分标准（一、选择题（本大题共有10小题，二、填空题（本大题共有6小题，每小题3分，共18分）11．（2,3） 12．1.24×10－3 13．6 14．a ﹣1 15．60 16．3 （说明：此题写出“3或-1”作为答案，给2分）三、解答题(本大题共9小题，满分102 分．解答应写出文字说明、证明过程或演算步骤) 17．（本小题满分9分） 解：方程两边同乘以()3-x x ，得()332-=x x ………………4分 解得9=x ．………………8分检验： 当 x = 9时，()3-x x 0≠所以x = 9是原方程的解．………………9分 18．（本小题满分9分） 解：（1）如图所示，线段CE 为所求； ………………3分 （2）证明：在□ABCD 中，A D ∥BC ，AD =BC .∴∠DAF =∠CEF ………………5分 ∵CE =BC ， ∴AD =CE , ………………7分 又∵∠DFA =∠CFE ， ………………8分 ∴△AFD ≌ △EFC . ………………9分（说明：第（2）小题的解法较多，只要过程合理，同样给满分） 19．（本小题满分10分）解法一：∵1=-b a 且2=ab∴32232ab b a b a +-)2(22b ab a ab +-=………………3分 2)(b a ab -= ………………6分212⨯=………………8分2= ………………10分解法二：由1=-b a 且2=ab解得⎩⎨⎧==12b a 或⎩⎨⎧-=-=21b a………………4分当⎩⎨⎧==12b a 时，32232ab b a b a +-2=；………………7分当⎩⎨⎧-=-=21b a 时，32232ab b a b a +-2= ………………10分（说明：解法二只算出一种情况共给5分）20. （本小题满分10分） 解：（1）m =48﹣6﹣25﹣3﹣2=12； ………………3分（2）记6～8小时的3名学生为A 1、A 2、A 3，8～10小时的两名学生为B 1、B 2，…8分（说明：列表法的评分标准与画树状图法一样） P （至少1人时间在8～10小时）=1072014=． ………………10分21．（本小题满分12分） 解：（1）解法一：设购买A 型学习用品x 件，则B 型学习用品为(1000)x -．根据题意，得2030(1000)26000x x +-=………3分解方程，得x =400 ………5分 则10001000400600x -=-=答：购买A 型学习用品400件，购买B 型学习用品600件．………6分解法二：设购买A 型学习用品x 件， B 型学习用品y 件．根据题意，得⎩⎨⎧=+=+2600030201000y x y x………3分解方程组，得⎩⎨⎧==600400y x………5分答：购买A 型学习用品400件，购买B 型学习用品600件．………6分（2）设最多购买B 型学习用品z 件，则购买A 型学习用品为)1000(z -件．根据题意，得2800030)1000(20≤+-z z ………9分 解不等式，得800≤z………11分 答：最多购买B 型学习用品800件．………12分22．（本小题满分12分）解：（1）∵四边形ABCD 是菱形，∠BAD ＝60º ∴∠BAO ＝30º，∠AOB ＝90º，AC =2AO ………3分 ∴330cos 32cos =︒⨯=∠⋅=BAO AB AO ………5分∴AC =6.………6分（说明：第（1）小题的解法较多，只要过程合理、答案正确，同样给满分） （2）证明： 连接DE ，过点D 作DF ⊥BC ，垂足为点F ………7分 ∵四边形ABCD 是菱形，∴BD 平分∠ABC ………9分∵⊙D 与边AB 相切于点E ，∴DE ⊥AB∵DF ⊥BC ∴DF =DE………11分 ∴⊙D 与边BC 也相切.………12分 23．（本小题满分12分） 解：（1）∵点A 的坐标为（0，2），点B 的坐标为（0，﹣3）， ∴AB =5， ∵四边形ABCD 为正方形， ∴点C 的坐标为（5，﹣3）． ………………2分 ∵反比例函数xky =的图象经过点C ， ∴53k=-，解得k =﹣15， ∴反比例函数的解析式为xy 15-=； ………………4分（2）设点P 到AD 的距离为h ． ∵△P AD 的面积恰好等于正方形ABCD 的面积，∴25521=⨯⨯h ，解得h =10． ………………6分① 当点P 在第二象限时，122=+=h y P ………………7分 此时，451215-=-=P x ∴点P 的坐标为（45-，12） ………………9分 ②当点P 在第四象限时，8)2(-=--=h y P ………………10分 此时，815815=--=P x ∴点P 的坐标为（815，﹣8） ………………12分综上所述，点P 的坐标为（45-，12）或（815，﹣8）． 24．（本小题满分14分）解：（1）∵点O 是圆心，OD ⊥BC ，BC =1，∴BD =12BC =12。
北京市西城区2014届高三一模试卷 语文 Word版含答案
北京市西城区2014年高三一模语文试题注意事项：1．本试卷分两部分，共1 50分，考试时间为150分钟；2．请将答案全部写在答题纸上；3．考试结束，请将试卷与答题纸一并交回。
第一部分(共40分)一、本大题共5小题，每小题3分，共15分。
阅读下面文字，按要求完成1—5题。
梁实秋在他的《清华八年》一文中，曾有过这样的描述：园里谈不到什么景致，不过非常整洁，绿草．．如荫．．，校舍十分甲（俭朴／简朴），但是一尘不染。
工字厅后面是荷花池，池畔松柏参天，厅后匾额上的“水木清华”四字确是当之无愧。
又有长联一副，颇为精彩：槛外山光，历春夏秋冬，万千变幻，都非凡境；窗中云影，任东西南北，去来澹荡，洵是仙居。
我在这个地方不知乙（消磨／消耗）了多少黄昏。
西园榛莽未除，一片芦蒿，登高西望，圆明园的断垣残石历历可见，俯仰苍茫，别饶野趣。
这一带景色宜人，是同学们常来读书游憩而流连忘返的去处……清华园中的荷花池，后因朱自清先生的一篇《荷塘月色》，更是如雷贯耳，招致莘莘学子的钦羡，使人丙（未免／不免）心生神往，希冀也能漫步在这荷花池畔，沐朝霞，送夕阳，书声与清风相应和，度过一段终生都值得回味的读书时光。
1．文中加点词语的书写或加点字的注音不正确的一项是A．绿草如荫B．槛（jiàn）外山光C．芦蒿D．应和（h色）2．依次填人甲、乙、丙三处的词语，最恰当的一项是A．俭朴消磨未免B．俭朴C．简朴消磨不免D．简朴3．文中加框的词语使用不正确的一项是A．一尘不染B．流连忘返C．如雷贯耳D．莘莘学子4．在文中第一段末句的横线上填人下列语句，衔接最恰当的一项是①土山的背后，缓缓流动着一条小河，②荷花池北岸上，可遥见一排高低起伏的土山，③两岸微风拂柳，又是一方胜境。
④山上松柏茂盛，树下花草丛生，别有一番风致。
A．④①③②B．②①③④c．④②①③D．②④①③5．文中“工字厅”的长联因情景交融而颇有韵味。
下面的对联与之有异曲同工之妙，且适合挂在书房中的一项是A．天边将满一轮月，世上还钟百岁人。
江苏2014年中考一模语文试卷及参考答案
江苏2014年中考一模语文试卷及参考答案（分值120分时间120分钟）一、积累与运用（28分）1．用诗文原句填空。
（10分）（1）窈窕淑女，。
（《诗经·关雎》）（2）春蚕到死丝方尽，。
（李商隐《无题》）（3），千树万树梨花开。
（岑参《白雪歌送武判官归京》）（4）春风又绿江南岸，？（王安石《泊船瓜洲》）（5）但愿人长久，。
(苏轼《水调歌头》)（6），勿施于人。
（《论语十则》）（7）2014年是中国农历马年，“马”在古代诗歌中随处可见：马致远有“枯藤老树昏鸦，小桥流水人家，“，弓如霹雳弦惊”；白居易有“乱花渐欲迷人眼，”。
请你再写出一句含有“马”字的诗句：2.汉字有着独特的形体之美、意韵之美。
（4分）（1）用正楷简体字，．工整、美观地把右图书法作品里的诗句抄写在方格中。
（2分）3.下列加点字注音完全正确的一项是（）（2分）A. 憧．憬chōnɡ参．差cān 风雪载．途zài 相形见绌．chùB. 扉．页fēi 妖娆ráo 叱咤．风云chà锲．而不舍qiâC. 追溯．shù馈．赠kuì锐不可当．dānɡ吹毛求疵．chīD. 璀璨．càn 哺．育bǔ惟妙惟肖．xiào 恪．尽职守kâ4.下列词语中没有．．错别字的一项是（）（2分）A. 烦躁推崇心旷神怡意想天开B. 踌躇媲美谈笑风声张皇失措C. 狡黠阴霾广袤无垠应接不暇D. 和煦缜密人才倍出眼花缭乱5.下列各句中没．有语病．．．的一项是（）（2分）A. 只要你用心品味汉字，认读汉字，就一定会发现她的神奇魅力。
B. 我们要养成爱读书，特别是读经典，读名著，让书香满园成为鼓楼教育的特色。
C. 阅读和写作是密不可分的。
是否多阅读，是提高一个人作文技能的途径之一。
D. 每年的植树节活动，旨在激发人们爱林造林的热情，提高人们对森林爱护的认识，改善生态环境。
2014年苏锡常镇一模试卷试题及参考答案（20143）
苏锡常镇四市2014届高三教学情况调研(一)政治2014．3第Ⅰ卷（选择题共66分）一、单项选择题：本大题共33小题，每小题2分，共66分。
在每题给出的四个选项中，只有一个选项是最符合题意的。
1．2014年2月，中国人民银行表示，将保持适度流动性，实现货币信贷及社会融资规模合理增长。
这意味着今后央行货币供应既不会大开闸门放水，也不会紧缩以致闹“钱荒”。
保持适度流动性A.可以避免通货膨胀的出现B.是纸币流通规律的客观要求C.会直接影响商业银行利润D.是国家运用财政政策的表现2．在不考虑其它因素的情况下，下列选项中与图1需求曲线变化相吻合的是A.汽油价格上调后，新能源汽车需求量的变化B.政府取消汽车购置税优惠后，汽车需求量的变化C.人民币汇率下降后，进口汽车需求量的变化D.政府优先发展公共交通后，汽车需求量的变化图13. 随着消费者对移动网络宽带化需求的日益迫切，第四代移动通信技术（4G）应运而生。
4G能够快速传输高质量视频图像，更好地满足用户对于无线服务的要求。
这表明①消费对生产的调整和升级起导向作用②消费是经济增长的根本动力③企业要坚持“高精尖”的战略定位④生产决定消费的质量和水平A.①②B.①④C.②③D.③④4．《中国劳动力动态调研：2013年报告》显示，有38.42%的职工在调查的上个月加过班，但其中只有45.57%拿到了加班工资。
劳动者因担心“不加班、或者要加班工资可能丢饭碗”而选择忍气吞声。
解决这一问题需要A.完善市场机制，改善就业结构B.加强劳动保护，改善劳动条件C.规范劳动制度，加强监管力度D.健全社会保障，依法维护权利5. 赵某花5万元在银行购买了一款理财产品，工作人员称收益率在5.5%，而且无风险。
产品到期后，赵某只获得300多元收益。
银行解释说，这款理财产品收益率是0.36%—5.5%。
经消协调解，银行以高于当前的银行定期利率补偿了赵某损失。
这说明①存款业务是商业银行的基础业务②诚实守信是规范市场秩序的治本之策③市场调节存在自发性的固有缺陷④银行理财产品的收益与风险是并存的A.①②B. ②③C. ②④D.③④2014年中央一号文件——《关于全面深化农村改革加快推进农业现代化的若干意见》全面定调2014年及今后一个时期农业农村工作。
2014山东省济南市一模试卷理科数学及答案
2014山东省济南市一模试卷理科数学及答案2014年山东省济南市一模试卷理科数学本试卷分为第I卷和第Ⅱ卷两部分，共4页。
考试时间120分钟，总分150分。
考试结束后，请将本试卷和答题卡一并交回。
注意事项：1.答题前，考生务必用0.5毫米黑色签字笔将自己的姓名、座号、考生号、县区和科类写在答题卡和试卷规定的位置上。
2.第I卷每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑。
如需改动，用橡皮擦干净后，再选涂其他答案标号，答案不能答在试卷上。
3.第Ⅱ卷必须用0.5毫米黑色签字笔作答，答案必须写在答题卡各题目指定区域内相应的位置，不能写在试卷上。
如需改动，先划掉原来的答案，然后再写上新的答案。
不能使用涂改液、胶带纸、修正带。
不按以上要求作答的答案无效。
4.填空题请直接填写答案，解答题应写出文字说明、证明过程或演算步骤。
参考公式：如果事件A、B互斥，那么P(A∪B)=P(A)+P(B)；如果事件A、B独立，那么P(A∩B)=P(A)×P(B)。
第I卷（共50分）一、选择题：本大题共10个小题，每小题5分，共50分。
每小题给出的四个选项中只有一项是符合题目要求的。
1) 已知复数z满足z(1+i)=1（其中i为虚数单位），则z的共轭复数z是A) 1+i (B) -i (C) -1+i (D) -1-i2) 已知集合A={x||x-1|<2}，B={x|y=lg(x+x)}，设U=R，则A∩(U-B)等于A) [3,+∞) (B) (-1,0) (C) (3,+∞) (D) [-1,0]3) 某几何体三视图如图所示，则该几何体的体积等于A) 2 (B) 4 (C) 8 (D) 124) 函数y=ln((x-sin(x))/(x+sin(x)))的图象大致是A)1B)C)D)5) 执行右面的程序框图，输出的S的值为A) 1 (B) 2 (C) 3 (D) 4sinC/5=3.b^2-a^2=ac，则cosB的值为A)1B)2C)3D)46) 在△ABC中，若sinC/5=3.b^2-a^2=ac，则cosB的值为7) 如图，设抛物线y=-x+1的顶点为A，与x轴正半轴的交点为B，设抛物线与两坐标轴正半轴围成的区域为M，随机往M内投一点P，则点P落在△AOB内的概率是A)2/5B)6/15C)3/5D)4/58) 已知4x^2-5x-2≤0，则x的取值范围是二、填空题：本大题共10个小题，每小题2分，共20分。
2014年九年级语文中考一模试卷及答案
2014年中考语文模拟试题（满分：150分，考试时间：150分钟）注意事项：1．你拿到的试卷满分为150分(其中卷面书写占5分)，考试时间为150分钟。
2．试卷包括“试题卷”和“答题卷”两部分。
请务必在“答题卷”上答题，在“试题卷”上答题是无效的。
3．答题过程中，可以随时使用你所带的《新华字典》。
4．考试结束后，请将“试题卷”和“答题卷”一并交回。
一、语文积累与综合运用 (35分)1．默写古诗文中的名句名篇。
(10分)(1)补写出下列名句中的上句或下句。
(任选其中6句)（6分）①学而不思则罔，思而不学则殆。
（《论语》）②山气日夕佳，飞鸟相与还。
（陶渊明《饮酒》）③造化钟神秀，阴阳割昏晓。
（杜甫《望岳》）④何当共剪西窗烛，却话巴山夜雨时。
（李商隐《夜雨寄北》）⑤无可奈何花落去，似曾相识燕归来。
（晏殊《浣溪沙》）⑥塞下秋来风景异，衡阳雁去无留意。
（范仲淹《渔家傲》）⑦山河破碎风飘絮，身世浮沉雨打萍。
（文天祥《过零丁洋》）⑧落红不是无情物，化作春泥更护花。
（龚自珍《已亥杂诗》）（2）默写李商隐的《无题》（相见时难别亦难）的中间四句。
（4分）春蚕到死丝方尽，蜡炬成灰泪始干。
晓镜但愁云鬓改，夜吟应觉月光寒。
2.阅读下面的文字，完成(1)～(4 )题。
(9分)人在世上走一遭，好比什么？就好比一个人独身走夜路。
路呢，并不好好地一条到底，有许多茬口，上错一条茬口，就会走到完全不同的地方。
走了一夜，天亮了，朝四周一看，一切都清楚：走的是哪一条路，到的是什么地方，在什么地方上了茬口，如果（）上这个茬口，（）上那个茬口路就好得多了，目的地也光明得多。
什么都明白了，可是已经晚了，不可以回头。
那么，有没有什么窍门呢？窍门没有，倒有两条经验：一是顺其自然，二是当机立断。
（1）上面语段中加点汉字“遭”“窍”的读音分别是 zāo 、qiào 。
（2分）(2)语段中含有一个错别字的词语是“茬口”，就改为“岔口”。
（2分）（3）请你根据语段中的意思写出“顺其自然”的近义词和“当机立断”的反义词。
2014西城高考一模数学理 (附答案)
北京市西城区2014年高三一模试卷数 学（理科） 2014．4第Ⅰ卷（选择题 共40分）一、选择题：本大题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项．1．设全集U =R ，集合2{|0}A x x =<≤，{|1}B x x =<，则集合()U A B = ð（ ） （A ）(,2]-∞ （B ）(,1]-∞ （C ）(2,)+∞ （D ）[2,)+∞2． 已知平面向量(2,1)=-a ，(1,1)=b ，(5,1)=-c ． 若()//k +a b c ，则实数k 的值为（ ） （A ）2（B ）12（C ）114（D ）114-3．在极坐标系中，过点π(2,)2且与极轴平行的直线方程是（ ） （A ）2ρ=（B ）2θπ=（C ）cos 2ρθ= （D ）sin =2ρθ4．执行如图所示的程序框图，如果输入2,2a b ==，那么输出的a 值为（ ） （A ）4 （B ）16 （C ）256 （D ）3log 165．下列函数中，对于任意x ∈R ，同时满足条件()()f x f x =-和(π)()f x f x -=的函数是（ ） （A ）()sin =f x x （C ）()cos =f x x （B ）()sin cos =f x x x （D ）22()cos sin =-f x x x6． “8m <”是“方程221108x y m m -=--表示双曲线”的（ ）（A ）充分而不必要条件 （B ）必要而不充分条件 （C ）充分必要条件 （D ）既不充分也不必要条件7．某企业为节能减排，用9万元购进一台新设备用于生产． 第一年需运营费用2万元，从第二年起，每年运营费用均比上一年增加2万元，该设备每年生产的收入均为11万元． 设该设备使用了()n n *∈N 年后，年平均盈利额达到最大值（盈利额等于收入减去成本），则n 等于（ ） （A ）3（B ）4（C ）5（D ）68． 如图，设P 为正四面体A BCD -表面（含棱）上与顶点不重合的一点，由点P 到四个顶点的距离组成的集合记为M ，如果集合M 中有且只有2个元素，那么符合条件的点P 有（ ） （A ）4个（B ）6个（C ）10个 （D ）14个第Ⅱ卷（非选择题 共110分）二、填空题：本大题共6小题，每小题5分，共30分． 9．设复数1ii 2ix y -=++，其中,x y ∈R ，则x y +=______．10． 若抛物线2:2C y px =的焦点在直线240x y +-=上，则p =_____；C 的准线方程为_____．11．已知一个正三棱柱的所有棱长均等于2，它的俯视图是一个边长为2的正三角形，那么它的侧（左）视图面积的最小值是________．12．若不等式组1,0,26,ax y x y x y ⎧⎪⎪⎨+⎪⎪+⎩≥≥≤≤表示的平面区域是一个四边形，则实数a 的取值范围是_______．13． 科技活动后，3名辅导教师和他们所指导的3名获奖学生合影留念（每名教师只指导一名学生），要求6人排成一排，且学生要与其指导教师相邻，那么不同的站法种数是______．（用数字作答）14．如图，在直角梯形ABCD 中，//AB CD ，AB BC ⊥，2AB =，1CD =，(0)BC a a =>，P 为线段AD （含端点）上一个动点，设AP xAD =，PB PC y ⋅=，对于函数()y f x =，给出以下三个结论：①当2a =时，函数()f x 的值域为[1,4]； ②(0,)a ∀∈+∞，都有(1)1f =成立；③(0,)a ∀∈+∞，函数()f x 的最大值都等于4． 其中所有正确结论的序号是_________．A BD C PBAD. P三、解答题：本大题共6小题，共80分．解答应写出必要的文字说明、证明过程或演算步骤． 15．（本小题满分13分）在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ． 已知222b c a bc +=+．（Ⅰ）求A 的大小；（Ⅱ）如果cos =B ，2b =，求△ABC 的面积．16．（本小题满分13分）在某批次的某种灯泡中，随机地抽取200个样品，并对其寿命进行追踪调查，将结果列成频率分布表如下． 根据寿命将灯泡分成优等品、正品和次品三个等级，其中寿命大于或等于500天的灯泡是优等品，寿命小于300天的灯泡是次品，其余的灯泡是正品．（Ⅱ）某人从灯泡样品中随机地购买了()*∈n n N 个，如果这n 个灯泡的等级情况恰好与按三个等级分．．．．．．层抽样．．．所得的结果相同，求n 的最小值； （Ⅲ）某人从这个批次的灯泡中随机地购买了3个进行使用，若以上述频率作为概率，用X 表示此人所购买的灯泡中次品的个数，求X 的分布列和数学期望．117．（本小题满分14分）如图，在四棱柱1111ABCD A B C D -中，底面ABCD 和侧面11BCC B 都是矩形，E 是CD 的中点，1D E CD ⊥，22AB BC ==．（Ⅰ）求证：1⊥BC D E ； （Ⅱ）求证：1BC // 平面1BED ；（Ⅲ）若平面11BCC B 与平面1BED 所成的锐二面角的大小为π3，求线段1D E 的长度．18．（本小题满分13分）已知函数2ln ,,()23,,x x x a f x x x x a >⎧⎪=⎨-+-⎪⎩≤ 其中0a ≥． （Ⅰ）当0a =时，求函数()f x 的图象在点(1,(1))f 处的切线方程；（Ⅱ）如果对于任意12,x x ∈R ，且12x x <，都有12()()f x f x <，求a 的取值范围．19．（本小题满分14分）已知椭圆2212x W y +=：，直线l 与W 相交于,M N 两点，l 与x 轴、y 轴分别相交于C 、D 两点，O为坐标原点．（Ⅰ）若直线l 的方程为210x y +-=，求OCD ∆外接圆的方程；（Ⅱ）判断是否存在直线l ，使得,C D 是线段MN 的两个三等分点，若存在，求出直线l 的方程；若不存在，说明理由．20．（本小题满分13分）在数列{}n a 中，1()n a n n*=∈N ． 从数列{}n a 中选出(3)k k ≥项并按原顺序组成的新数列记为{}n b ，并称{}n b 为数列{}n a 的k 项子列． 例如数列1111,,,2358为{}n a 的一个4项子列．（Ⅰ）试写出数列{}n a 的一个3项子列，并使其为等差数列；（Ⅱ）如果{}n b 为数列{}n a 的一个5项子列，且{}n b 为等差数列，证明：{}n b 的公差d 满足108d -<<； （Ⅲ）如果{}n c 为数列{}n a 的一个(3)m m ≥项子列，且{}n c 为等比数列，证明：1231122m m c c c c -++++-≤．北京市西城区2014年高三一模试卷参考答案及评分标准 高三数学（理科） 2014．4一、选择题：本大题共8小题，每小题5分，共40分．1．C 2．B 3．D 4．C 5．D 6．A 7．A 8．C 二、填空题：本大题共6小题，每小题5分，共30分．9．25-10．84x =-11． 12．(3,5)13．48 14．○2，○3注：第10题第一问2分，第二问3分． 第14题若有错选、多选不得分．三、解答题：本大题共6小题，共80分． 其他正确解答过程，请参照评分标准给分． 15．（本小题满分13分）（Ⅰ）解：因为 222b c a bc +=+，所以 2221cos 22b c a A bc +-==， ……………………………… 3分又因为 (0,π)∈A ，所以 π3A =． ……………………………… 5分（Ⅱ）解：因为 cos =B ，(0,π)∈B ，所以 sin 3B ==． ……………………………7分 由正弦定理sin sin =a bA B ， ………………………………9分 得 sin 3sin ==b Aa B． ……………………………10分 因为 222b c a bc +=+，所以 2250--=c c ，解得 1=c 因为 0>c ，所以 1=c ． ……………………………11分故△ABC 的面积1sin 22S bc A ==． ……………………………13分 16．（本小题满分13分）（Ⅰ）解：0.15a =，30b =． ……………………………… 2分 （Ⅱ）解：由表可知：灯泡样品中优等品有50个，正品有100个，次品有50个，所以优等品、正品和次品的比例为50:100:501:2:1=． ……………………………… 4分 所以按分层抽样法，购买灯泡数24()*=++=∈n k k k k k N ，所以n 的最小值为4． ……………………………… 6分 （Ⅲ）解：X 的所有取值为0,1,2,3． …………………………… 7分由题意，购买一个灯泡，且这个灯泡是次品的概率为0.10.150.25+=， ……………… 8分 从本批次灯泡中购买3个，可看成3次独立重复试验，所以033127(0)C (1)464P X ==⨯-=， 1231127(1)C (1)4464P X ==⨯⨯-=， 2213119(2)C ()(1)4464P X ==⨯-=，33311(3)C ()464P X ==⨯=． ……………………………… 11分 所以随机变量X 的分布列为：………………………………12分所以X 的数学期望2727913()0123646464644E X =⨯+⨯+⨯+⨯=． ………………………………13分（注：写出1(3,)4X B ，3311()C ()(1)44k k kP X k -==-，0,1,2,3k =． 请酌情给分）17．（本小题满分14分）（Ⅰ）证明：因为底面ABCD 和侧面11BCC B 是矩形，所以 BC CD ⊥，1BC CC ⊥， 又因为 1= CD CC C ，所以 BC ⊥平面11DCC D ， ………………………………2分 因为 1D E ⊂平面11DCC D ， 所以1BC D E ⊥． ………………………………4分（Ⅱ）证明：因为 1111//, BB DD BB DD =，所以四边形11D DBB 是平行四边形．连接1DB 交1D B 于点F ，连接EF ，则F 为1DB 在1∆B CD 中，因为DE CE =，1DF B F =，所以 1//EF B C ．分 又因为 1⊄B C 平面1BED ，⊂EF 平面1BED ，所以 1//BC 平面1BED ． ………………………………8分1（Ⅲ）解：由（Ⅰ）可知1BC D E ⊥， 又因为 1D E CD ⊥，BC CD C = ，所以 1D E ⊥平面ABCD ． ………………………………9分设G 为AB 的中点，以E 为原点，EG ，EC ，1ED 所在直线分别为x 轴，y 轴，z 轴 如图建立空间直角坐标系，设1D E a =，则11(0,0,0), (1,1,0), (0,0,), (0,1,0), (1,2,), (1,0,0)E B D a C B a G ． 设平面1BED 法向量为(,,)x y z =n ，因为1(1,1,0), (0,0,)EB ED a ==， 由10,0,EB ED ⎧⋅=⎪⎨⋅=⎪⎩n n 得0,0.x y z +=⎧⎨=⎩ 令1x =，得(1,1,0)=-n ． ……………………………11分 设平面11BCC B 法向量为111(,,)x y z =m ，因为 1(1,0,0), (1,1,)CB CB a ==，由10,0,CB CB ⎧⋅=⎪⎨⋅=⎪⎩ m m 得11110,0.x x y az =⎧⎨++=⎩ 令11z =，得(0,,1)a =-m ． ……………………………12分由平面11BCC B 与平面1BED 所成的锐二面角的大小为π3，得||π|cos ,|cos 3⋅<>===m n m n m n ， ………………………………13分 解得1a =． ……………………………14分18．（本小题满分13分） （Ⅰ）解：由题意，得()(ln )ln 1f x x x x ''==+，其中0x >， ……………………………… 2分所以 (1)1f '=， 又因为(1)0f =，所以函数()f x 的图象在点(1,(1))f 处的切线方程为1y x =-． ……………………………… 4分 （Ⅱ）解：先考察函数2()23g x x x =-+-，x ∈R 的图象，配方得2()(1)2g x x =---， ……………………………… 5分 所以函数()g x 在(,1)-∞上单调递增，在(1,)+∞单调递减，且max ()(1)2g x g ==-．……………………………… 6分因为对于任意12,x x ∈R ，且12x x <，都有12()()f x f x <成立，所以 1a ≤． …………………………… 8分 以下考察函数()ln h x x x =，(0,)x ∈+∞的图象，则 ()ln 1h x x '=+，令()ln 10h x x '=+=，解得1e=x ． …………………………… 9分 随着x 变化时，()h x 和()h x '的变化情况如下：即函数()h x 在1(0,)e上单调递减，在(,)e+∞上单调递增，且min 11()()e e==-h x h ． … 11分 因为对于任意12,x x ∈R ，且12x x <，都有12()()f x f x <成立，所以 1e≥a ． ……………………………… 12分因为 12e->-（即min max ()()h x g x >）， 所以a 的取值范围为1,e[1]．……………………………… 13分 19．（本小题满分14分）（Ⅰ）证明：因为直线l 的方程为210x y +-=，所以与x 轴的交点(1,0)C ，与y 轴的交点1(0,)2D ． ………………………… 1分 则线段CD 的中点11(,)24，||CD ==， …………………………… 3分 即OCD ∆外接圆的圆心为11(,)24，半径为1||24CD =， 所以OCD ∆外接圆的方程为22115()()2416x y -+-=． …………………………… 5分（Ⅱ）解：结论：存在直线l ，使得,C D 是线段MN 的两个三等分点．理由如下：由题意，设直线l 的方程为(0)y kx m km =+≠，11(,)M x y ，22(,)N x y ， 则 (,0)mC k-，(0,)D m ， ……………………………… 6分 由方程组2212y kx m x y =+⎧⎪⎨+=⎪⎩ 得222(12)4220k x kmx m +++-=， ……………………………… 7分 所以 2216880k m ∆=-+>， （*） ……………………………… 8分由韦达定理，得122412km x x k -+=+， 21222212m x x k-=+． ………………………… 9分由,C D 是线段MN 的两个三等分点，得线段MN 的中点与线段CD 的中点重合． 所以 1224120km x x k mk-+==+-， ………………………………10分解得 k = ………………………… 11分 由,C D 是线段MN 的两个三等分点，得||3||MN CD =．12|x x -= ……………………………… 12分即 12||3||m x x k-==，解得 5m =±． …………………………… 13分 验证知（*）成立．所以存在直线l ，使得,C D 是线段MN 的两个三等分点，此时直线l 的方程为2y x =25y x =-±． ……………………………… 14分20．（本小题满分13分）（Ⅰ）解：答案不唯一． 如3项子列12，13，16； ……………………………… 2分 （Ⅱ）证明：由题意，知1234510b b b b b >>>>>≥， 所以 210d b b =-<． ……………………………… 3分 若 11b = ，由{}n b 为{}n a 的一个5项子列，得212b ≤， 所以 2111122d b b =--=-≤． 因为 514b b d =+，50b >，所以 515411d b b b =-=->-，即14d >-． 这与12d -≤矛盾． 所以 11b ≠． 所以 112b ≤， ……………………………… 6分 因为 514b b d =+，50b >， 所以 51511422d b b b =-->-≥，即18d >-，综上，得108d -<<． ………………………… 7分 （Ⅲ）证明：由题意，设{}n c 的公比为q ，则 211231(1)m m c c c c c q q q -++++=++++ ．因为{}n c 为{}n a 的一个m 项子列， 所以 q 为正有理数，且1q <，111()c a a*=∈N ≤． 设 (,Kq K L L*=∈N ，且,K L 互质，2L ≥）． 当1K =时，因为 112q L =≤，所以 211231(1)m m c c c c c q q q -++++=++++211111()()222≤-++++ m ， 112()2-=-m ，所以 112312()2m m c c c c -++++- ≤．……………………………… 10分 当1K ≠时，因为 11111m m m m K c c q a L---==⨯是{}n a 中的项，且,K L 互质，所以 1*()-=⨯∈m a K M M N ，所以 211231(1)m m c c c c c q q q -++++=++++1232111111()----=++++ m m m m M K K L K L L ． 因为 2L ≥，*K M ∈N ，， 所以 21112311111()()2()2222m m m c c c c --++++++++=- ≤． 综上， 1231122m m c c c c -++++- ≤． …………………………… 13分。
2014汕头一模(含答案
汕头市2014年普通高中高三教学质量测评（一）理科综合（生物部分）本试卷共12页，36小题，满分300分。
考试用时150分钟。
注意事项：1．答卷前，考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上，并用2B 铅笔在答题卡上的相应位置填涂考生号。
用2B 铅笔将试卷类型(A)填涂在答题卡相应位置上。
2．选择题每小题选出答案后，用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试卷上。
3．非选择题必须用黑色字迹钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
4．考生必须保持答题卡的整洁。
考试结束后，将试卷和答题卡一并交回。
可能用到的相对原子质量：一、单项选择题：本大题共16小题，每小题4分。
共64分。
在每小题给出的四个选项中，只有一个选项符合题目要求，选对的得4分，选错或不答的得0分。
1． 下列各项在细胞质基质中进行的是A ．合成性激素B ．合成tRNAC ．初步分解葡萄糖D ．利用光能分解水2． 显微镜下观察到人的一个细胞中染色体已分成两组，每组23条。
那么，可以肯定每组染色体中A ．有23个DNA 分子B ．有46条染色单体C ．没有非同源染色体D ．没有同源染色体3． 玉米的PEPC 酶固定CO 2的能力较水稻的强60倍。
我国科学家正致力于将玉米的PEPC 基因导入水稻中，以提高水稻产量。
下列各项对此研究的分析中正确的是A ．核心步骤是构建玉米PEPC 基因表达载体B ．通常采用显微注射法将PEPC 基因导入水稻细胞C ．在受体细胞中检测到PEPC 酶则意味着此项研究取得成功D ．利用细胞培养技术将转基因水稻细胞培育成植株4． 下列中可以借助电子显微镜观察到的是A B C DA a5．黑藻是一种水生植物，叶片小而薄。
2014年广州一模理综(附答案)
试卷类型：A 2014年广州市普通高中毕业班综合测试（一）理科综合2014. 3 本试卷共12页，36小题，满分300分。
考试用时150分钟。
注意事项：1. 答卷前，考生务必用2B铅笔在“考生号”处填涂考生号。
用黑色字迹的钢笔或签. 字笔将自己所在的市、县/区、学校以及自己的姓名和考生号、试室号、座位号填写在答题卡上。
用2B铅笔将试卷类型（A)填涂在答题卡相应位置上。
2. 选择题每小题选出答案后，用2B铅笔把答题卡上对应题目选项的答案信息点涂黑；如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试卷上。
3. 非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液。
不按以上要求作答的答案效。
4. 考生必须保持答题卡的整洁。
考试结束后，将试卷和答题卡一并交回。
5. 本卷所用相对原子质量：H-1、C-12、N-14、0-16、K-39、I-127一、单项选择题：本题包括16小题，每小题4分，共64分。
在每小题给出的四个选项中，只有一个选项符合题目要求，选对的得4分，选错或不答的得0分。
1．下列有关细胞中化合物的叙述，正确的是A．叶肉细胞中含量最多的化合物是蛋白质B．肝细胞中含有葡萄糖和蔗糖C．脂肪是细胞中良好的储能物质D．细胞中的无机盐都以离子形式存在2．研究发现，一些癌细胞能进入“平衡”阶段，此阶段的癌细胞不易被免疫系统识别，不会恶性增殖，也不会导致机体发病。
下列有关分析不合理的是A．这种癌细胞是细胞正常分化的结果B．免疫系统不易清除这种癌细胞C．可以通过癌基因检测的手段来监测细胞是否癌变D．该发现有助于寻找治疗癌症的新方法3．在摩洛哥有一种被称为“奶树”的古老树种，成年树分泌的“乳液”有利于由其根部细胞发育而来的幼树成长。
下列有关推论合理的是A．“奶树”是通过细胞工程培育而成的B．成年树与其根部细胞发育而来的幼树的基因型不同C．分泌“乳液”的植株是雌性植株D．成年树分泌“乳液”是表现型4．右图为突触结构和功能的模式图，下列有关叙述不恰当的是A．瞬间增大轴突末端细胞膜对Ca2+的通透性会加速神经递质的释放B．过程①体现了细胞膜具有流动性C．过程②表示神经递质进入突触后膜所在的神经元D．过程⑧可避免突触后膜持续兴奋5.下列相关实验组合不正确的是A.显微镜直接计数----统计微生物数量B.预实验----摸索“探究木瓜蛋白酶最适pH”的实验条件C.对比实验----探究酵母菌的呼吸方式D.标志重捕法----调查植株上蚜虫的种群密度6．关于植物激素的叙述，正确的是A ．侧芽处的生长素浓度过低导致其生长受抑制B ．不同浓度的生长素对同种植物同一器官的作用可相同C ．赤霉素能促进果实成熟而脱落酸能抑制种子萌发D ．细胞分裂素能促进细胞分裂而乙烯能促进细胞生长 7．已知：Cu (s)+2H+ (aq)＝Cu2+(aq)+ H2 (g) △H 1 2H2O2(l)＝2H2O(l) + O2 (g) △H 2 2H2 (g) + O2 (g)＝2H2O(l) △H 3则反应 Cu (s)+H2O2(l)+2H+ (aq)＝Cu2+(aq)+ 2H2O(l) 的△H 是A ．△H ＝△H 1+12△H 2+12△H 3B ．△H ＝△H 1+12△H 2-12△H 3C ．△H ＝△H 1+2△H 2+2△H 3D ．△H ＝2△H 1+△H 2+△H 389．设nA 为阿伏加德罗常数的数值，下列说法正确的是 A ．3mol NO2与水充分反应，转移nA 个电子 B ．常温常压下，18g H2O 含有3nA 个原子 C ．1L 0.1 mol·L －1NaHCO3溶液中含有0.1nA 个HCO3－ D ．标准状况下，2.24L 乙醇含有0.1nA 个CH3CH2OH 分子 10．在恒容密闭容器中，反应CO2(g)+3H2(g) CH3OH(g)+H2O(g) △H ＜0达到平衡后，改变某一条件，下列说法正确的是A ．升高温度，正反应速率减小，逆反应速率增加，平衡逆向移动B ．升高温度，可提高CO2转化率C ．增加H2的浓度，可提高CO2转化率D ．改用高效催化剂，可增大反应的平衡常数11．某小组设计电解饱和食盐水的装置如图，通电后两极均有气泡产生，下列叙述正确的是A ．铜电极附近观察到黄绿色气体B ．石墨电极附近溶液呈红色C ．溶液中的Na+向石墨电极移动D ．铜电极上发生还原反应 12．对于常温下0.1 mol·L －1氨水和0.1 mol·L －1醋酸，下列说法正确的是 A ．0.1 mol·L －1氨水，溶液的pH=13 B ．0.1 mol·L －1氨水加水稀释，溶液中c(H+)和c(OH －)都减小C ．0.1 mol·L －1醋酸溶液中：c(H+)＝c(CH3COO －)D ．0.1 mol·L －1醋酸与0.1 mol·L －1NaOH 溶液等体积混合所得溶液中：c(Na+)＞c(CH3COO －)＞c(OH －)＞c(H+)13．用某色光照射金属表面时，有光电子从金属表面飞出，如果改用频率更大的光照射该金属表面，则A ．金属的逸出功增大B ．金属的逸出功减小C ．光电子的最大初动能增大D ．光电子的最大初动能不变14．如图是氢原子从n=3、4、5、6能级跃迁到n=2能级时辐射的四条光谱线，其中频率最大的是A．H αB ．H βC ．H γD ．H δ含酚酞的饱和食盐水15．如图是荷质比相同的a 、b 两粒子从O 点垂直匀强磁场进入正方形区域的运动轨迹，则A ．a 的质量比b 的质量大B ．a 带正电荷、b 带负电荷C ．a 在磁场中的运动速率比b 的大D ．a 在磁场中的运动时间比b 的长16．如图是悬绳对称且长度可调的自制降落伞．用该伞挂上重为Gl1<l2，匀速下降时每根悬绳的拉力大小分别为F1、F2，则A ．F1<F2B ．F1>F2C ．F1=F2<GD ．F1=F2>G二、双项选择题（本大题共9小题，每小题6分，共54分。
2014年中考语文一模试卷(含答案)
2014年杭州市中考语文一模试卷(拱墅区)考生须知：1.本试卷分试题卷和答题卷两部分。
满分120分，考试时间120分钟。
2.答题前，必须在答题卷的密封区内填写校名、姓名和学号。
3.所有答案都必须做在答题卷标定的位置上，务必注意试题序号和答题序号相对应。
4.考试结束后，上交答题卷。
试题卷一(30分)1. 下列加点字的注音全都正确的一项是（3分）A．巉．岩（chán）慰藉．（jí）百鸟啾啾（jiū）B．阴霾．（mái）荫．蔽（yīn）影影绰．绰（chuî）C．荣膺．（yīng）穷匮．（kuì）周道如砥．（dǐ）D．骸．骨（hái）窈．窕（yǎo）断壁残垣．（huán）2. 下列词语中没有别字的一项是（3分）A．锦嶂瞰望一气呵成花团锦簇B．芳馨倒坍遍稽群藉芒刺在背C．杀戮恻隐有例可援吹毛求疵D．跻身豁免睡眼惺忪通霄达旦3. 下列句子中加点的词语使用恰当的一项是（3分）A．只有经历过失败的痛苦与成功的喜悦，才能懂得生命的真正意义。
如果没有体恤．．过失败的苦涩，又怎能享受到成功的喜悦？B．静谧的夜，正襟危坐的他翻阅着已经泛黄了的老照片，心无旁骛，冥思遐想，沉湎．．在对那已经过去三十多年的童年的美好回忆中。
C．王老师的悉心指导和全力督促，仿佛医生妙手回春．．．．，使原本游泳极差的我，有了极大的提高，相信这次游泳拿满分不成问题。
D．清晨，我们登上黄山光明顶，透过晨曦放眼眺望，起伏的青山一座挨一座，鳞次栉比．．．．，延伸到远方，消失在迷茫的天际中。
4. 下列有关文学常识的表述有错的一项是（3分）A．《诗经》是我国最早的一部诗歌总集，收录了从西周到春秋时期的诗歌305篇，也称“诗三百”，这些诗歌分为“风”“雅”“颂”三个部分。
B．奥楚蔑洛夫是法国作家契诃夫所著《变色龙》中的主人公，这篇小说紧扣“变”字，刻画了沙皇忠实走狗的丑恶嘴脸，揭露了沙皇统治的黑暗腐朽。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
西城一模练习12．西周末年，幽王宠爱妃子褒姒，废掉申后及太子，以褒姒为后。
申后之父申侯联络犬戎举兵，杀了幽王。
申侯起兵的理由应该是A.君君臣臣父父子子B.得民心者得天下C.嫡庶有别长幼有序D.顺乎天而应乎人13. 西方学者称中国古代某学说为‚Neo-Confucianism‛，这是一种融儒家、佛教和道教等诸因素于一体的哲学，提供了一套维护儒家伦理秩序的形而上学体系。
该‚学说‛是指A.孔孟儒学B．董仲舒的新儒学C.程朱理学D．明末清初的儒学14．以下历史现象，出现时间最晚的是A.王大令众人曰协田B.大抵诸酒肆瓦市，不以风雨寒暑，白昼通夜C.乃作翻车，令童儿转之，而灌水自覆D.其货物均系江浙等省商民贩运来粤，转售外夷，载运回国15. ‚肇始于隋朝，行于唐世，扩于五代，而精于宋人。
‛横线处的文字是A.雕版B.造纸C.指南针D.火药16．图X可用来说明的主题有图X 19世纪六七十年代中国主要的近代企业分布①近代中国工业化的地区差异②民族资本主义企业诞生的原因③近代中国工业的合理布局④外国资本主义入侵造成的危害A．②④B．①②C．①④D．②③17．陈独秀在《新文化运动是什么》中说：‚新文化运动影响到产业上，应该令劳动者觉悟他们自己的地位，令资本家要把劳动者当做同类的‘人’看待，不要当做机器、牛马、奴隶看待。
‛该文应该发表于A. 1913年B. 1915年C. 1917年D.1920年图X 德国的未来18．观察图X ，该硬币A.发行于国共合作时期B.是中央红军在瑞金发行的C.可用来研究中国共产党的政权建设D.可用来研究中国共产党开展的土地革命19． 20世纪三、四十年代，日本在中国东北重点发展煤炭、钢铁、水泥、机械等重工业。
日本的意图是A.在东北建立完整的工业体系B.满足侵略战争的需要C.将东北变成日本的原料产地D.侵占中国的东北三省下的人是德国民众。
对此图的解释，最为全面准确的是A ．德国以王朝战争的形式完成了国家的统一B ．德国以强大的军事力量保护人民C ．德国的未来完全由军队控制D ．德国的政治走向由军国主义而非人民群众来决定22．下列有关20世纪30年代世界经济形势的叙述，正确的是①美国通过罗斯福新政建立了福利国家制度②苏联通过实施两个五年计划实现了工业化③中国民族工业受经济危机冲击而陷入萧条 ④土耳其是世界上工业增长速度最快国家之一A ．①③B ．①②C ．①④D ．②④23．结合所学分析表X ，正确的是表X ：美国、苏联、日本、中国国防开支表（单位：10亿美元）②苏联是二战后唯一能在军事上与美国相抗衡的国家③朝鲜战争和越南战争均导致美国国防开支大量增加④中国国防开支在六十年代的激增是因为经济的好转A ．①②③B ．①②④C ．①③④D ．②③④37．（34分）法律是人类文明的集中体现。
战国时期的韩非子认为人天生是自私的、是趋利避害的，施仁政在过去可能有效，但现在必须用严格的法律和官僚机构的有力惩罚来进行统治。
古希腊的亚里士多德以为，大多数人都不能完全消除兽欲，即使是最好的人也难免在执政时因情感而引起偏差。
法律恰恰是免除一切情欲影响的理智的体现。
（1）根据材料，比较两者观点的异同。
（8分）这种认识的社会背景。
（12分）清前期修订的《大清律》一直沿用到近代。
该律法的特点是以官僚机构组织法和刑法为核心。
其内容包括行刑、户律（田宅、婚姻等）、兵律（军政、邮驿等）、刑律（人命、盗贼、斗殴等）、工律（河防等）。
在施行中，由地方行政机构行使判决权。
1905年起，沈家本等人修订、编纂了《大清民律草案》、《大清商律草案》、《民事诉讼律草案》和《刑事诉讼律草案》等。
新刑律采用西方近代刑法典的体例，取消了适用刑罚上的等级制度。
民国初年，伍廷芳提出‚视一国之文明与否，需视其司法能独立与否，并其执法廉明与否。
‛他草拟的‚宪纲大旨‛包括保护基本人权等内容。
在实践中，他坚决反对上海当局不通过法律程序随意捕捉人犯的行径，并推动中国第一次实行陪审团参与审判。
他致力于普及现代法律观念，塑造司法新形象，并希望收回外国人在华的法律特权。
（3）结合所学，解读从清前期到民国初年中国法律的变化历程。
（14分）要求：提取信息充分；总结和归纳准确、完整；解释和分析逻辑清晰。
据清代史料记载，山西当地的风俗是‚重利之念，甚于重名。
子弟之俊秀者，多入贸易一途，其次宁为胥吏，至中材以下，方使之读书应试。
‛1824年，日升昌票号在山西平遥创立。
以日升昌为代表的山西票号，其组织结构为三种人：东家、掌柜、伙计。
大掌柜具有独立的经营权，东家不能插手经营活动。
掌柜和伙计可以人力入股，享有分红的权利。
票号的所有人员一律是山西人。
山西票号的血脉里渗透着传统文化的浸润，‚以义制利‛是其基本准则。
《清朝续文献通考》称：山西票号‚法至精密，人尤敦朴，信用最著‛。
近代以来，外国银行纷纷进入我国，金融市场竞争激烈。
清朝末年，政府设立户部银行，希望票号出钱出人。
晋商害怕外省人借机插手票号，予以拒绝。
个别晋商主张各大票号联合出资，成立近代银行，也遭否决。
民国初年，统治中国金融业近一个世纪的山西票号在内外交困中纷纷倒闭。
（1）根据材料，概括影响山西票号成败的因素。
（10分）英国殖民当局大力发展印度的铁路，印度铁路里程1861年为1588英里，1871年为5077英里，1881达到9891英里。
1910年，英国对印度直接投资约1.83亿英镑，其中77%投向铁路和通讯，17%投资于矿山和种植园，商业和工业所占比重为2%。
（1）根据材料，指出19世纪后半期到20世纪初英国在印度投资的重点领域。
（2分）结合所学，分析其影响。
（6分）CCDAB DCBBD DA37.（34分）（1）异：韩非子主张用法律惩罚人民，亚里士多德主张用法律限制执政者。
（或：韩非子认为法律是专制的工具，亚里士多德认为法律是理性的体现）（4分）同：二者都主张用法律来治理国家；其理论体系均建立在对人性分析的基础上。
（4分）（2）第一种划分：6-13世纪、14-17世纪早期（或17世纪早期）、17世纪晚期-18世纪。
第二种划分：6-13世纪、14-18世纪，或6-13世纪、17世纪-18世纪。
6-13世纪：自然法是上帝意志的体现（2分）。
背景：中世纪，基督教神学统治整个欧洲，影响到法律的制定；（2分）东罗马帝国为加强对域内众多民族的统治，制定适用于各民族的自然法。
（2分）14-17世纪早期（或17世纪早期）：自然法是人性的体现。
背景：文艺复兴运动把人从封建神学中解放出来，主张以人为中心，更多地关注人及人生活的世界。
（3分，本题总分不超过12分）17世纪晚期-18世纪：自然法是人类意志的体现。
（2分）背景：启蒙运动抨击天主教会的权威和迷信，要求获得人本身的进一步解放。
（2分）17-18世纪（或14-18世纪）：自然法是人性和人类意志的体现。
（2分）背景：文艺复兴运动把人从封建神学中解放出来，主张以人为中心，更多地关注人及人生活的世界。
（2分）启蒙运动抨击天主教会的权威和迷信，要求获得人本身的进一步解放。
（2分）（3）示例1：清前期，我国法律制度重视刑法和行政法，司法不独立，人们在法律面前不平等，是维护专制统治秩序的工具。
清末新政期间，清政府命沈家本等制定《大清民律草案》《大清商律草案》《刑事诉讼律草案》《民事诉讼律草案》，表明清政府已认识到民商法和司法程序的重要性；废除刑罚上的等级制度，开始接受法律面前人人平等的理念。
辛亥革命后，成立了中华民国。
伍廷芳等人主张司法独立和保障人权，重视法律程序，主张收回治外法权，反映了一个新兴的共和国想在世人面前树立一个文明、独立的资产阶级共和国形象的迫切愿望。
上述材料表明，我国法律最初带有专制统治工具的色彩；近代以来，随着西方文化在我国传播的逐渐深入，我国法律逐步接受了西方法律文化中的人人平等、司法独立、重视司法程序等观念。
示例2：我国法律制度的变化，既是西方殖民扩张的产物，也是中国社会发展的客观需要。
清前期，我国法律制度有浓厚的专制色彩，无法适应近代以来中国社会所面临的挑战。
随着西方的入侵，中国人对西方的认识不断深入，逐渐意识到西方的强大不仅在于其先进的技术，更在于其政治体制和法律制度。
八国联军侵华战争以后，清政府意识到再也不能维持原有的专制制度，开始实施新政，迈出了全面向西方学习的步伐，从法律内容、司法程序、法治意识等方面向西方学习。
辛亥革命后成立的资产阶级共和国，对内欲树立文明的形象，对外欲树立独立的形象，因此一些进步人士主张司法独立、保障人权和收回治外法权。
总体来讲，我国法律制度的变化，是在西方列强侵略不断加深的大背景下，为了实现国家的独立、文明与富强，一些进步人士主动了解西方并向西方学习的结果。
示例3：我国法律制度的变化，反映出西方法律文化在近代中国的传播由点及面、影响由弱到强。
从法律内容上看，清前期以刑法和行政法为核心，清末新政编撰了民商法，民国初年的一些进步人士主张保障人权。
从法律程序上看，清前期不重视法律程序，清末新政编撰了民事和刑事诉讼法，民国初年的一些进步人士也强调法律程序的重要性。
从法律地位来看，清朝司法附属于行政权力，民国初年的一些进步人士则将司法独立视为文明的标志。
从法律意识来看，清前期同罪不同罚，人们在法律面前不平等，清末新政则废除了刑法上的等级制度。
总体来讲，近代以来，我国法律制度经历了由传统的中华法律体系向近代西方法律体系转变的历程；由于传统习惯等因素的限制，近代中国法治进程发展曲折、缓慢。
40.（1）特点：主要投资于铁路及通讯。
（2分）影响：便于英国掠夺印度的各种资源；造成印度社会经济结构的不合理；客观上推动印度社会经济向前发展。
（6分）41.（1）成功的原因：第一、山西人重视经商，以经商为荣。
第二、组织结构合理，所有权和经营权分离；第三、重视文化的力量，讲究诚信。
失败的原因：第一、近代以来，外国银行抢占山西票号的市场。
第二、晋商在危机面前固守传统，拒绝变革。
1.提取信息充分；总结和归纳准确、完整；解释和分析逻辑清晰。
同时满足三项，可得满分。
2.提取信息不够充分；总结和归纳不够准确、完整；解释和分析不够清晰。
出现任何一项，最高不超过12分。
3.提取信息不够充分；总结和归纳不够准确、完整；解释和分析不够清晰。
出现任何二项，最高不超过10分。
4.提取信息不够充分；总结和归纳不够准确、完整；解释和分析不够清晰。
最高不超过8分。
5.脱离材料，仅作简单相关论述。
最高不超过4分。
6.仅罗列现象，没有相关论述。
最高不超过4分。
7.论述不当或错误；内容空泛或与要求不符。
不得分。