概率论第三章习题答案

合集下载

概率论~第三章习题参考答案与提示

设二维随机变量xy的概率密度为6第三章习题参考答案与提示?2121yxyxyxf?xy?其中1yx?和2yx?都是二维正态密度函数且它们对应的二维随机变量的相关系数分别为13和13它们的边缘密度函数所对应的随机变量的数学期望都是0方差都是1
第三章习题参考答案与提示
第三章随机变量的数字特征习题参考答案与提示
22．已知 X 、 Y 分别服从正态分布 N (0，32 ) 和 N (1，42 ) ，且 X 与Y 的相关系数 ρ XY = −1/ 2 ，设 Z = X / 3 + Y / 2 ，求：
（1）求数学期望 EZ ，方差 DZ ；（2）Y 与 Z 的相关系数 ρYZ ；答案与提示：本题要求熟悉数学期望、方差、协方差的性质、计算及有关正态分布的性质。
X
Y
0
1
0
0.1
0.2
1
0.3
0.4
求：（1） EX ， EY ， DX ， DY ；
（2）( X ， Y )的协方差，相关系数，协方差阵，相关阵。
答案与提示：（1） EX = 0.7 ， DX = 0.21， EY = 0.6 ， DY = 0.24 。
（2） EXY = 0.4 ； Cov ( X ,Y ) = −0.02 ， ρXY = 0.089 ；
（1） X 的概率密度；
（2）Y = 1 − 2 X 的概率密度。
答案与提示：考查服从正态分布随机变量的概率密度的一般表达形式、参数的
几何意义及正态分布随机变量的性质。
（1） f (x) = 1 e−(x−1.7)2 /6 (−∞ < x < +∞) 6π
（2） f ( y) = 1 e−( y+2.4)2 / 24 2 6π

概率论与数理统计第三章习题及答案

概率论与数理统计习题第三章多维随机变量及其分布习题3-1 盒子里装有3只黑球、2只红球、2只白球，在其中任取4只球.以X 表示取到黑球的只数，以Y 表示取到红球的只数，求X 和Y 的联合分布律.（X ，Y ）的可能取值为(i , j )，i =0，1，2，3， j =0，12，i + j ≥2，联合分布律为 P {X=0, Y=2 }=351472222=C C C P {X=1, Y=1 }=35647221213=C C C C P {X=1, Y=2 }=35647122213=C C C C P {X=2, Y=0 }=353472223=C C C P {X=2, Y=1 }=351247121223=C C C C P {X=2, Y=2 }=353472223=C C C P {X=3, Y=0 }=352471233=C C C P {X=3, Y=1 }=352471233=C C C P {X=3, Y=2 }=0习题3-2 设随机变量),(Y X 的概率密度为⎩⎨⎧<<<<--=其它,0,42,20),6(),(y x y x k y x f（1）确定常数k ；（2）求{}3,1<<Y X P （3）求{}5.1<X P ；（4）求{}4≤+Y X P . 分析：利用P {(X , Y)∈G}=⎰⎰⎰⎰⋂=oD G Gdy dx y x f dy dx y x f ),(),(再化为累次积分，其中⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧<<<<=42,20),(y x y x D o解：（1）∵⎰⎰⎰⎰+∞∞-+∞∞---==2012)6(),(1dydx y x k dy dx y x f ，∴81=k （2）83)6(81)3,1(321⎰⎰=--=<<dy y x dxY X P （3）3227)6(81),5.1()5.1(425.10=--=∞<≤=≤⎰⎰dy y x dx Y X P X P （4）32)6(81)4(4020=--=≤+⎰⎰-dy y x dxY X P x习题3-3 将一枚硬币掷3次，以X 表示前2次出现H 的次数，以Y 表示3次中出现H 的次数，求Y X ,的联合分布律以及),(Y X 的边缘分布律。

概率论练习册答案第三章

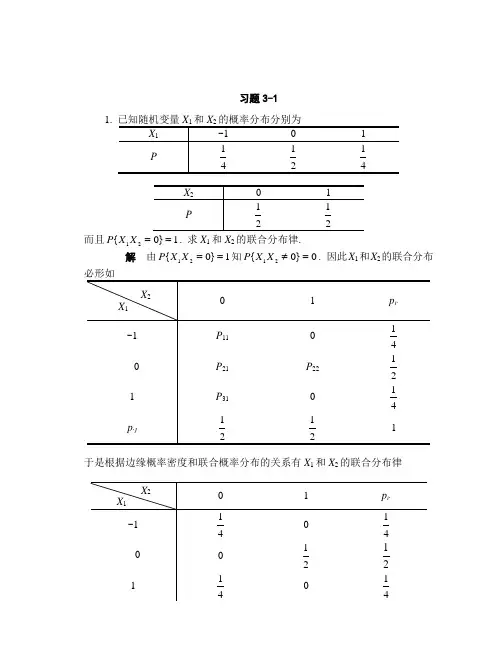
习题3-11.而且12{0}1P X X ==. 求X 1和X 2的联合分布律.解由12{0}1P X X ==知12{0}0P X X ≠=. 因此X 1和X 2的联合分布于是根据边缘概率密度和联合概率分布的关系有X 1和X 2的联合分布律(2) 注意到12{0,0}0P X X ===, 而121{0}{0}04P X P X =⋅==≠, 所以X 1和X 2不独立.2. 一盒子中有3只黑球、2只红球和2只白球, 在其中任取4只球. 以X 表示取到黑球的只数, 以Y 表示取到红球的只数. 求X 和Y 的联合分布律.解从7只球中取4球只有3547=C 种取法. 在4只球中, 黑球有i 只, 红球有j 只(余下为白球4i j --只)的取法为4322i j i j C C C --,0,1,2,3,0,1,2,i j i j ==+≤4.于是有0223221{0,2}3535P X Y C C C ====,1113226{1,1}3535P X Y C C C ====,1213226{1,2}3535P X Y C C C ====,2023223{2,0}3535P X Y C C C ====,21132212{2,1}3535P X Y C C C ====,2203223{2,2}3535P X Y C C C ====,3013222{3,0}3535P X Y C C C ====, 3103222{3,1}3535P X Y C C C ====,{0,0}{0,1}{1,0}{3,2}0P X Y P X Y P X Y P X Y ============.3. (,)(6),02,24,0,.f x y k x y x y =--<<<<⎧⎨⎩其它求: (1) 常数k ; (2) {1,3}P X Y <<; (3) { 1.5}P X <; (4) {4}P X Y +≤.解 (1) 由(,)d d 1f x y x y +∞+∞-∞-∞=⎰⎰, 得2424222204211d (6)d (6)d (10)82y k x y x k y x x y k y y k =--=--=-=⎡⎤⎢⎥⎣⎦⎰⎰⎰, 所以 18k =. (2) 3121,31{1,3}d (6)d 8(,)d d x y P X Y y x y x f x y x y <<<<==--⎰⎰⎰⎰1322011(6)d 82y x x y =--⎡⎤⎢⎥⎣⎦⎰321113()d 828y y =-=⎰. (3) 1.51.5{ 1.5}d (,)d ()d X P X x f x y y f x x +∞-∞-∞-∞<==⎰⎰⎰4 1.521d (6)d 8y x y x --=⎰⎰1.5422011(6)d 82y x x y =--⎡⎤⎢⎥⎣⎦⎰ 421633()d 882y y =-⎰ 2732=. (4) 作直线4x y +=, 并记此直线下方区域与(,)0f x y ≠的矩形区域(0,2)(0,4)⨯的交集为G . 即:02,0G x y <<<≤4x -.见图3-8. 因此{P X Y +≤4}{(,)}P X Y G =∈(,)d d Gf x y x y =⎰⎰44201d (6)d 8x y x y x -=--⎰⎰ 4422011(6)d 82xy x x y -=--⎡⎤⎢⎥⎣⎦⎰ 42211[(6)(4)(4)]d 82y y y y =----⎰ 42211[2(4)(4)]d 82y y y =-+-⎰423211(4)(4)86y y =----⎡⎤⎢⎥⎣⎦23=. 图3-8 第4题积分区域4. 二维随机变量(,)X Y 的概率密度为2(,),1,01,0,f x y kxy x y x =⎧⎨⎩≤≤≤≤其它. 试确定k , 并求2{(,)},:,01P X Y G G x y x x ∈≤≤≤≤.解由21114001(,)d d d (1)d 26x k kf x y xdy x kxy y x x x +∞+∞-∞-∞====-⎰⎰⎰⎰⎰,解得6=k .因而 2112401{(,)}d 6d 3()d 4x xP X Y G x xy y x x x x ∈==-=⎰⎰⎰. 5. 设二维随机变量(X , Y )概率密度为4.8(2),01,0,(,)0,.y x x y x f x y -=⎧⎨⎩≤≤≤≤其它求关于X 和Y 边缘概率密度.解 (,)X Y 的概率密度(,)f x y 在区域:0G ≤x ≤1,0≤y ≤x 外取零值.因而, 有24.8(2)d ,01,()(,)d 0,2.4(2),01,0,x X y x y x f x f x y y x x x +∞-∞-<<==-<<=⎧⎪⎨⎪⎩⎧⎨⎩⎰⎰其它.其它.124.8(2)d ,01,()(,)d 0,2.4(34),01,0,yY y x x y f y f x y x y y y y +∞-∞-<<==-+<<=⎧⎪⎨⎪⎩⎧⎨⎩⎰⎰其它.其它. 6. 假设随机变量U 在区间[-2, 2]上服从均匀分布, 随机变量 1,1,1,1,U X U --=>-⎧⎨⎩若≤若 1,1,1, 1.U Y U -=>⎧⎨⎩若≤若试求：(1) X 和Y 的联合概率分布；(2){P X Y +≤1}.解(2){P X Y +≤1}1{1}P X Y =-+>1{1,1}P X Y =-==12133=-=. 习题3-21. 设(X , Y )的分布律为求: (1) 在条件X =2下Y 的条件分布律;(2){22}P X Y ≥≤.解 (1) 由于6.02.01.003.0}2{=+++==X P ,所以在条件X =2下Y 的条件分布律为216.03.0}2{}1,2{}2|1{========X P Y X P X Y P ,06.00}2{}2,2{}2|2{========X P Y X P X Y P ,616.01.0}2{}3,2{}2|3{========X P Y X P X Y P ,316.02.0}2{}4,2{}2|4{========X P Y X P X Y P ,{P Y ≤2}{1}{2}P Y P Y ==+==0.10.3000.20.6++++=. 而{2,2}{2,1}{2,2}{3,1}{3,2}P X Y P X Y P X Y P X Y P X Y ===+==+==+==≥≤0.3000.20.5=+++=.因此{2,2}{22}{2}P X Y P X Y P Y =≥≤≤≥≤0.550.66==. 2. 设平面区域D 由曲线1y x=及直线20,1,e y x x ===所围成, 二维随机变量(X , Y )在区域D 上服从均匀分布, 求(X , Y )关于X 的边缘概率密度在x =2处的值.解由题设知D 的面积为22e e111d ln 2D S x x x ===⎰. 因此, (X ,Y )的密度为 1,(,),(,)20x y D f x y ∈=⎧⎪⎨⎪⎩，其它.由此可得关于X 的边缘概率密度 ()(,)d X f x f x y y +∞-∞=⎰.显然, 当x ≤1或x ≥e 2时,()0X f x =; 当21e x <<时,111()d 22x X f x y x==⎰.故(2)14X f =. 3. 设二维随机变量(X , Y )的概率密度为(,)1,01,02,0,.f x y x y x =<<<<⎧⎨⎩其它求：(1) (X , Y )的边缘概率密度(),()X Y f x f y ；(2)11{}.22P Y X ≤≤ 解 (1) 当01x <<时,20()(,)d d 2xX f x f x y y y x +∞-∞===⎰⎰;当x ≤0时或x ≥1时, ()0X f x =. 故 2,01,()0,其它.X x x f x <<=⎧⎨⎩当0<y <2时,12()(,)d d 12y Y y f y f x y x x +∞-∞===-⎰⎰;当y ≤0时或y ≥2时, ()0Y f y =.故 1,02,()20,.Y yy f y -<<=⎧⎪⎨⎪⎩其它(2) 当z ≤0时,()0Z F z =; 当z ≥2时,1)(=z F Z ;当0<z <2时, (){2Z F z P X Y =-≤2}(,)d d x y zz f x y x y -=⎰⎰≤2x12202-2d 1d d 1d zxz x zx y x y =⋅+⋅⎰⎰⎰⎰24z z =-.故 1,02,()20,.()其它Z z zz f z F z -<<'==⎧⎪⎨⎪⎩(3) {}{}11311322161122442≤，≤≤≤≤P X Y P Y X P X ===⎧⎫⎨⎬⎩⎭. 4. 设G 是由直线y =x , y =3,x =1所围成的三角形区域, 二维随机变量(,)X Y 在G 上服从二维均匀分布.求:(1) (X , Y )的联合概率密度；(2) {1}P Y X -≤；(3) 关于X 的边缘概率密度. 解 (1)由于三角形区域G 的面积等于2, 所以(,)X Y 的概率密度为⎪⎩⎪⎨⎧∉∈=.),(,0,),(,21),(G y x G y x y x f (2)记区域x y y x D -=|),{(≤}1与G 的交集为0G ,则{1}P Y X -≤0011113d d (2)22224G G x y S ===-=⎰⎰.其中0G S 为G 0的面积.(3) X 的边缘概率密度()(,)d X f x f x y y +∞-∞=⎰. 所以,当]3,1[∈x 时, 311()d (3)22X xf x y x ==-⎰. 当1<x 或3>x 时, 0)(=x f X .因此 ⎪⎩⎪⎨⎧∈-=.,0],3,1[),1(21)(其它x x x f X习题3-31. 设X 与Y 相互独立, 且分布律分别为下表:求二维随机变量(,)X Y 的分布律.解由于X 与Y 相互独立, 所以有}{}{},{j i j i y Y P x X P y Y x X P =⋅====,6,5,2,0;0,21,1=--=j i .因此可得二维随机变量(,)X Y 的联合分布律2. 设(X , Y )的分布律如下表:问,αβ为何值时X 与Y 相互独立? 解由于边缘分布满足23111,1i j i j p p ⋅⋅====∑∑, 又X , Y 相互独立的等价条件为 p ij = p i . p .j (i =1,2; j =1,2,3).故可得方程组 21,3111().939αβα++==⋅+⎧⎪⎪⎨⎪⎪⎩解得29α=,19β=.经检验, 当29α=,19β=时, 对于所有的i =1,2; j =1,2,3均有p ij = p i . p .j 成立.因此当29α=,19β=时, X 与Y 相互独立..3. 设随机变量X 与Y 的概率密度为()e (,)0,.,01,0,x y b f x y x y -+=⎧<<>⎨⎩其它(1) 试确定常数b .(2) 求边缘概率密度()X f x , ()Y f y . (3) 问X 与Y 是否相互独立？解 (1) 由11()101(,)d d e d d e d e d (1e )x y y x f x y x y b y x b y x b +∞+∞+∞+∞-+----∞-∞====-⎰⎰⎰⎰⎰⎰,得 111eb -=-.(2) ()(,)d X f x f x y y ∞-∞=⎰1e ,01,1e 0,xx --<<=-⎧⎪⎨⎪⎩其它.()(,)d Y f y f x y x ∞-∞=⎰e ,0,0,y y ->=⎧⎨⎩其它.(3) 由于(,)()()X Y f x y f x f y =⋅，所以X 与Y 相互独立.4. 设X 和Y 是两个相互独立的随机变量, X 在(0, 1)上服从均匀分布, Y 的概率密度为21e ,0,()2Y yy f y y ->=⎧⎪⎨⎪⎩，≤0.(1) 求X 和Y 的联合概率密度.(2) 设关于a 的二次方程为220a Xa Y ++=, 试求a 有实根的概率.解 (1) 由题设知X 和Y 的概率密度分别为1,01,()0,X x f x <<=⎧⎨⎩其它， 21e ,0,()20,.yY y f y ->=⎧⎪⎨⎪⎩其它因X 和Y 相互独立, 故(X , Y )的联合概率密度为21e ,01,0(,)()()20,.yX Y x y f x y f x f y -<<>==⎧⎪⎨⎪⎩其它 (2) 方程有实根的充要条件是判别式大于等于零. 即244X Y ∆=-≥20X ⇔≥Y .因此事件{方程有实根}2{X =≥}Y .下面计算2{P X ≥}Y (参见图3-3).2{P X ≥}Y 2211221(,)d d e d (1e)d 2yxx Df x y xdy x y x --===-⎰⎰⎰⎰⎰2121ed 12[(1)(0)]0.1445xx πΦΦ-=-=--≈⎰.图3-3 第6题积分区域习题3-41. 设二维随机变量(X ,Y )的概率分布为YX0 1若随机事件{X =0}与{X +Y =1}相互独立, 求常数a , b .解首先, 由题设知0.40.11a b +++=. 由此得0.5a b +=. 此外,{0}0.4P X a ==+,{1}{0,1}{1,0}0.5P X Y P X Y P X Y a b +====+===+=, {0,1}{0,1}P X X Y P X Y a =+=====. 根据题意有{0,1}{0}{1}P X X Y P X P X Y =+===+=,即(0.4)0.5a a =+⨯. 解得0.4,0.1a b ==.2. 设两个相互独立的随机变量X ,Y 的分布律分别为求随机变量Z = X + Y 的分布律. 解随机变量Z = X + Y 的可能取值为7,5,3.Z 的分布律为18.06.0.03}2,1{}3{=⨯=====Y X P Z P , {5}{1,4}{3,2}0.30.4070.60.54P Z P X Y P X Y ====+===⨯+⨯=,28.04.07.0}4,3{}7{=⨯=====Y X P Z P ,或写为3. 随机变量X 与Y 相互独立, 且均服从区间[0,3]上的均匀分布, 求{}max{,}1P X Y ≤.解由题意知, X 与Y 的概率密度均为1,03,()30x f x =⎧⎪⎨⎪⎩≤≤，其它.又由独立性, 有P {max{X +Y }≤1}=P {X ≤1,Y ≤1}= P {X ≤1} P {Y ≤1}.而 P {X ≤1}= P {Y ≤1}11011()d d 33f x x x -∞===⎰⎰, 故 P {max{X +Y }≤1}=111339⨯=.4. 设X 和Y 是两个相互独立的随机变量, 且X 服从正态分布N (μ, σ2), Y 服从均匀分布U (-a , a )( a >0), 试求随机变量和Z =X +Y 的概率密度.解已知X 和Y 的概率密度分别为22()2()e2x X f x μσπσ--=, ),(+∞-∞∈x ; ⎪⎩⎪⎨⎧-∉-∈=).,(,0),,(,21)(a a y a a y ay f Y .由于X 和Y 相互独立, 所以22()21()()()d e d 22z y aZ X Y a f z f z y f y y y a μσπσ---+∞-∞-=-=⎰⎰=1[()()]2z μa z μa ΦΦa σσ-+---. 10. 设随机变量X 和Y 的联合分布是正方形G={(x,y )|1≤x ≤3, 1≤y ≤3}上的均匀分布, 试求随机变量U=|X -Y|的概率密度f (u ).解由题设知, X 和Y 的联合概率密度为111,3,3,(,)40,.x y f x y =⎧⎪⎨⎪⎩≤≤≤≤其它记()F u 为U 的分布函数, 参见图3-7, 则有当u ≤0时,(){||F u P X Y =-≤u }=0; 当u ≥2时,()1F u =;当0< u <2时, 图3-7 第8题积分区域||(){}(,)d d x y uF u P U u f x y x y -==⎰⎰≤≤21[42(2)]412u =-⨯- 211(2)4u =--.故随机变量||U X Y =-的概率密度为1(2),02,()20,u u p u -<<=⎧⎪⎨⎪⎩其它..总习题三1. 设随机变量(X , Y )的概率密度为⎪⎩⎪⎨⎧<<<=.,0,10,||,1),(其它x x y y x f 求条件概率密度)|()|(||y x f x y f Y X X Y 和.解首先2,01,()0,.(,)其它X x x f x f x y dy +∞-∞<<==⎧⎨⎩⎰1,01,()1,10,0,(,)≤其它.Y y y f y y y f x y dx +∞-∞-<<==+-<⎧⎪⎨⎪⎩⎰图3-9第1题积分区域当01y <<时, |1,1,1(|)0,X Y y x y f x y x <<-=⎧⎪⎨⎪⎩取其它值.当1y -<≤0时, |1,1,1(|)0,X Y y x y f x y x -<<+=⎧⎪⎨⎪⎩取其它值.当10<<x 时, |1,||,(|)20,Y X y x f y x x y <=⎧⎪⎨⎪⎩取其它值.2. 设随机变量X 与Y 相互独立, 下表列出二维随机变量(,)X Y 的分布律及关于X 和关于Y 的边缘分布律中部分数值, 试将其余数值填入表中空白处 .解首先, 由于11121{}{,}{,}P Y y P X x Y y P X x Y y ====+==, 所以有11121111{,}{}{,}6824P X x Y y P Y y P X x Y y ====-===-=.在此基础上利用X 和Y 的独立性, 有11111{,}124{}1{}46P X x Y y P X x P Y y =======.于是 2113{}1{}144P X x P X x ==-==-=.再次, 利用X 和Y 的独立性, 有12211{,}18{}1{}24P X x Y y P Y y P X x =======.于是 312111{}1{}{}1623P Y y P Y y P Y y ==-=-==--=.最后, 利用X 和Y 的独立性, 有2222313{,}{}{}428P X x Y y P X x P Y y ======⨯=; 2323311{,}{}{}434P X x Y y P X x P Y y ======⨯=;1313111{,}{}{}4312P X x Y y P X x P Y y ======⨯=.因此得到下表3. (34)e (,)0,.,0,0,x y k f x y x y -+=⎧>>⎨⎩其它 (1) 求常数k ；(2) 求(X ,Y )的分布函数；(3) 计算{01,02}P X Y <<≤≤; (4) 计算(),x f x ()y f y ；(5) 问随机变量X 与Y 是否相互独立? 解 (1)由3401(,)d d e d e d 12xy kf x y x y k x y +∞+∞+∞+∞---∞-∞===⎰⎰⎰⎰,可得12=k .(2) (X ,Y )的分布函数(,)(,)d d x y F x y f u v x y -∞-∞=⎰⎰.当x <0或y <0时,有 0),(=y x F ; 当0,0x y ≥≥时, 34340(,)12e d e d (1e )(1e )x yuv x y F x y u v ----==--⎰⎰.即 34(1e )(1e ),0,0,(,)0,.x y x y F x y --⎧--≥≥=⎨⎩其它(3) {01,02}P X Y <<≤≤38(1,2)(0,0)(1e )(1e )F F --=-=--. (4) (34)012ed ,0,()(,)d 0,其它.x y X y x f x f x y y +∞-++∞-∞⎧>⎪==⎨⎪⎩⎰⎰所以 33e ,0,()0,其它.x X x f x -⎧>=⎨⎩类似地, 有44e ,0,()0,其它.y Y y f y -⎧>=⎨⎩显然2),(),()(),(R y x y f x f y x f Y X ∈∀⋅=, 故X 与Y 相互独立. 4.解已知的分布律为注意到41260}1{}1{=++====Y P X P , 而0}1,1{===Y X P ,可见P {X =1, Y =1}≠P {X =1}P {Y =1}. 因此X 与Y 不相互独立.(2) Z X Y =+的可能取值为3, 4, 5, 6, 且316161}1,2{}2,1{}3{=+===+====Y X P Y X P Z P , }1,3{}2,2{}3,1{}4{==+==+====Y X P Y X P Y X P Z P3112161121=++=, 316161}2,3{}3,2{}5{=+===+====Y X P Y X P Z P . 即Z X Y =+(3) V =21}2,2{}1,2{}2,1{}2{===+==+====Y X P Y X P Y X P V P , 21}2{1}3{==-==V P V P . 即max(,)V X Y =的分布律为(4) min{U =}3,1{}2,1{}1{==+====Y X P Y X P U P}1,2{}1,3{==+==+Y X P Y X P 21=, 21}1{1}2{==-==U P U P . 即min{,}U X Y =的分布律为(5) W U V =+31}1,2{}2,1{}2,1{}3{===+=======Y X P Y X P V U P W P ,}2,2{}3,1{}4{==+====V U P V U P W P31}2,2{}1,3{}3,1{===+==+===y X P Y X P Y X P ,31}2,3{}3,2{}3,2{}5{===+=======Y X P Y X P V U P W P .5. 2,01,01,(,)0,x y x y f x y --<<<<⎧=⎨⎩其它. (1) 求P {X >2Y }; (2) 求Z = X +Y 的概率密度f Z (z ).解 (1) 1120227{2}(,)d d d (2)d 24yx yP X Y f x y x y y x y x >>==--=⎰⎰⎰⎰. (2) 方法一: 先求Z 的分布函数:()()(,)d d Z x y zF z P X Y Z f x y x y +=+=⎰⎰≤≤.当z <0时, F Z (z )<0; 当0≤z <1时, 1()(,)d d d (2)d zz yZ D F z f x y x y y x y x -==--⎰⎰⎰⎰= z 2-13z 3; 当1≤z <2时, 2111()1(,)d d 1d (2)d Z z z yD F z f x y x y y x y x --=-=---⎰⎰⎰⎰= 1-13(2-z )3; 当z ≥2时, F Z (z ) = 1.故Z = X +Y 的概率密度为222,01,()()(2),12,0,Z Z z z z f z F z z z ⎧-<<⎪'==-<⎨⎪⎩≤其它.方法二: 利用公式()(,)d :Z f z f x z x x +∞-∞=-⎰2(),01,01,(,)0,x z x x z x f x z x ---<<<-<⎧-=⎨⎩其它 2,01,1,0,.z x x z x -<<<<+⎧=⎨⎩其它当z ≤0或z ≥2时, f Z (z ) = 0; 当0<z <1时, 0()(2)d (2);zZ f z z x z z =-=-⎰当1≤z <2时, 121()(2)d (2).Zz f z z x z -=-=-⎰故Z = X +Y 的概率密度为222,01,()(2),12,0,.Z z z z f z z z ⎧-<<⎪=-<⎨⎪⎩≤其它.6. 设随机变量(X , Y )得密度为21,01,02,(,)30,.其它x xy x y x y ϕ⎧+⎪=⎨⎪⎩≤≤≤≤试求: (1) (X , Y )的分布函数; (2) (X , Y )的两个边缘分布密度; (3) (X , Y )的两个条件密度; (4) 概率P {X +Y >1}, P {Y >X }及P {Y <12|X <12}.解 (1) 当x<0或y <0时, φ(x , y ) = 0, 所以 F (x , y ) = 0.当0≤x <1, 0≤y <2时, φ(x , y ) = x 2+13xy ,所以 201(,)(,)d d [()d ]d 3x yx yF x y u v u v u uv v u -∞-∞==+⎰⎰⎰⎰ϕ32211312x y x y =+. 当0≤x <1, 2≤y 时,2(,)(,)d d [(,)d ]d [(,)d ]d xyx y x F x y u v u v u v v u u v v u -∞-∞===⎰⎰⎰⎰⎰⎰ϕϕϕ22001[()d ]d 3xu uv v u =+⎰⎰21(21)3x x =+. 当1≤x , 0≤y <2时,1(,)(,)d d [(,)d ]d xyyF x y u v u v u v v u -∞-∞==⎰⎰⎰⎰ϕϕ12001[()d ]d 3yu uv v u =+⎰⎰1(4)12y y =+. 当1≤x , 2≤y 时,122001(,)[()d ]d 13F x y u uv v u =+=⎰⎰.综上所述, 分布函数为220,00,1(),01,02,341(,)(21),01,2,31(4),1,02,121,1, 2.x y y x y x x y F x y x x x y y y x y x y <<⎧⎪⎪+<<⎪⎪⎪=+≥⎨⎪⎪+≥⎪⎪≥≥⎪⎩或≤≤≤≤≤< (2) 当0≤x ≤1时,22202()(,)d ()d 2,33X xy x x y y x y x x ϕϕ+∞-∞==+=+⎰⎰故 222,01,()30,.其它≤≤X x x x x ϕ⎧+⎪=⎨⎪⎩当0≤y ≤2时,12011()(,)d ()d ,336Y xy y x y x x x y ϕϕ+∞-∞==+=+⎰⎰ 故 11,02,()360,.其它≤≤Y y y y ϕ⎧+⎪=⎨⎪⎩(3) 当0≤y ≤2时, X 关于Y = y 的条件概率密度为2(,)62(|).()2Y x y x xy x y y yϕϕϕ+==+当0≤x ≤1时, Y 关于X = x 的条件概率密度为(,)3(|).()62X x y x yy x y x ϕϕϕ+==+(4) 参见图3-10.图3-10 第9题积分区域图3-11 第9题积分区域1{1}(,)d d x y P X Y x y x y ϕ+>+>=⎰⎰12201165d ()d .372xx x xy y -=+=⎰⎰ 同理, 参见图3-11.{}(,)d d y xP Y X x y x y ϕ>>=⎰⎰122117d ()d .324xx x xy y =+=⎰⎰ 1111{,}(,)112222{|}1122{}()22X P X Y F P Y X P X F <<<<==<211(,)221201()534.32()d |X y x y x x xϕ+==⎰。

概率论第三章习题及答案

02
题目8
一个盒子里有100个球，其中红球有30个，蓝球有40个，黄球有20个，
绿球有10个。随机抽取一个球并记录其颜色，然后放回盒子中。连续抽
取三次，求三次抽取中抽到红球的次数的期望值。
03
题目9
一个袋子中有5个红球和5个蓝球，从中随机抽取3个球，求抽取到红球
的个数X的分布律。
02 答案部分
基础题目答案
在处理复杂事件时，应先分解为简单事件，再根据概率的加
法原则进行计算。
注意区分必然事件和不可能事件，它们在概率论中具有特殊
地位。
知识点回顾与巩固
知识点回顾概率的基本性质：概率具有非负性、规范性、有限可加性。
事件的独立性及其性质。
知识点回顾与巩固
条件概率的定义及其性质。贝叶斯公式的应用场景和推导方法。
挑战题目解题思路与技巧
总结词
综合运用知识
详细描述
对于挑战题目，需要综合运用概率论中的知识，如随机变量的分布、随机过程的性质等。要能够准确理解题目的背景和要求，构建合适的概率模型，并运用适当的数学方法进行求解。
示例
题目问的是“一个袋子中有3个红球和2个白球，每次从中随机取出1个球并放回，连续取 5次。求取出的5个球中至少有3个红球的概率。”解题时，应先计算取出的5个球中都是白球的概率，再用1减去这个概率，得出至少有3个红球的概率。
未来学习计划与展望
• 学习随机过程的基本概念和性质，了解常见的随机过程如泊松过程、马尔可夫链等。
未来学习计划与展望
展望
学习概率论与其他数学分支的交叉知识，如统计学、线性代数等。
将概率论的知识应用于实际问题和科学研究，加深对理论知识的理解和掌握。

概率论第三章习题解答

第三章习题解1 在一箱子中装有12只开关，其中2 只是次品，在其中任取两次，每次任取一只，考虑两种试验：（1）放回抽样；（2）不放回抽样。

定义随机变量X ，Y 如下：0,1X ⎧=⎨⎩若第一次取出的是正品，，若第一次取出的是次品。

0,Y 1⎧=⎨⎩若第二次取出的是正品，，若第二次取出的是次品。

试分别就（1），（2）两种情况写出X ，Y 的联合分布律。

解（1）放回抽样由于每次抽取时都是12只开关，第一次取到正品有10种可能，即第一次取到正品的概率为 105{0}126P X ===，第一次取出的是次品的概率为 21{1}126P X === 同理，第二次取到正品的概率105{0}126P Y ===第二次取到次品的概率为21{1}126P Y ===由乘法公式得X ，Y 的联合分布率为{,}{|}{}{}{}P X i Y j P Y j X i P X i P X i P Y j =========，0,1i =，0,1j =。

具体地有5525{0,0}6636P X Y ===⨯=，515{0,1}6636P X Y ===⨯=， 155{1,0}6636P X Y ===⨯=，111{1,1}6636P X Y ===⨯=用表格的形式表示为（2 5{0}6P X ==，1{1}6P X == 因为第二次抽取时，箱子里只有11只开关，当第一次抽取的是正品，则箱子中有9只正品）。

所以9{0|0}11P Y X ===， 2{1|0}11P Y X === 10{0|1}11P Y X ===， 1{1|1}11P Y X ===则5945{0,0}61166P X Y ===⨯= 5210{0,1}61166P X Y ===⨯=，11010{1,0}61166P X Y ===⨯=，111{1,1}61166P X Y ===⨯= 用表格表示为2 （14只球，以X 表示取到黑球的只数，以Y 表示取到红球的只数，求X 和Y 的联合分布律。

《概率论与随机过程》第3章习题答案

《概率论与随机过程》第三章习题答案3.2 随机过程()t X 为()()ΦωX +=t cos A t 0式中，A 具有瑞利分布，其概率密度为()02222>=-a eaa P a A ，σσ，()πΦ20，在上均匀分布，A Φ与是两个相互独立的随机变量，0ω为常数，试问X(t)是否为平稳过程。

解：由题意可得:()[]()()002121020022222002222=⇒+=*+=⎰⎰⎰⎰∞--∞φφωπσφπσφωX E πσσπd t cos da e a a dad eat cos a t a a ()()()[]()()()()()()[]()()()()()12021202120202120202221202022021012022022202010022222200201021212122112210212212121221212222222222222t t cos t t cos t t cos det t cos da e e a t t cos dea d t t cos t t cos a d ea d t cos t cos da eaadad e at cos a t cos a t t t t R a a a a a a a -=-⨯=-⨯-=-⨯⎪⎩⎪⎨⎧⎪⎭⎪⎬⎫-∞+-=-⨯-=⎩⎨⎧⎭⎬⎫+++---=++=++==-∞∞---∞∞-∞--∞⎰⎰⎰⎰⎰⎰⎰⎰⎰ωσωσωσωωφφωωπσφπφωφωσφσπφωφωX X E σσσσπσπσσπXX ）（，可见()[]t X E 与t 无关，()21t t R ，XX 与t 无关，只与()12t t -有关。

∴()t X 是平稳过程另解：()[][]0022000000[cos()][cos()][];(,)cos()cos(())cos()cos(())t E A t E A E t E A R t t E A t t E A E t t E X ωΦωΦτωΦωτΦωΦωτΦ⎡⎤=+=+=⨯=⎣⎦⎡⎤⎡⎤+=+++=+++⎣⎦⎣⎦[][][])cos()cos())cos((τωτωτωω0200022222A E t E A E =+Φ++= ∴()t X 是平稳过程3.3 设S(t) 是一个周期为T 的函数，随机变量Φ在（0，T ）上均匀分布，称X(t)=S （t+Φ）,为随相周期过程，试讨论其平稳性及各态遍历性。

概率论习题第三章答案

第三章连续型随机变量3.1设随机变量 ξ 的分布函数为F （x ），试以F （x ）表示下列概率：。

)()4();()3();()2();()1(a P a P a P a P >≥≤=ξξξξ 。

）（解：)0(1)()4();(1)()3();0()(P 2);()0()()1(+-=>-=≥+=≤-+==a F a P a F a P a F a a F a F a P ξξξξ3.2函数x211F(x)+=是否可以作为某一随机变量的分布函数，如果在其它场合恰当定义。

在其它场合恰当定义；）（,0)3(,0)2(1<<∞-∞<<∞<<∞-x x x 解：(1)F(x)在),(∞-∞内不单调，因而不可能是随机变量的分布函数； (2)F(x)在)0∞，（内单调下降，因而也不可能是随机变量的分布函数； (3)F(x)在），（－0∞内单调上升、连续且，若定义 ⎩⎨⎧≥<<∞=01)()(~x x X F x F －则)(~x F 可以是某一随机变量的分布函数。

3.3函数 sinx 是不是某个随机变量ξ的分布函数？如果ξ的取值范围为[]。

，）；（，）；（，）（⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡πππ230302201 解：(1)当⎥⎦⎤⎢⎣⎡∈2,0πx 时,sinx 0≥且1sin 20=⎰πxdx ，所以 sinx 可以是某个随机变量的分布密度； (2) 因为12sin 0≠=⎰πxdx ,所以sinx 不是随机变量的分布密度； (3) 当 ⎥⎦⎤⎢⎣⎡∈23,ππx 时,sinx<=0所以sinx 不是随机变量的分布密度。

3.4设随机变量ξ具有对称的分布函数p(x)，即p(x)=p(-x) 证明：对任意的a>0，有[][]。

－－故上式右端＝知由证：）1)(21a)P(1a)(3)P(1;-2F(a))(21)(1)1(,)(2)()()2(;)(21)()(1)(1)(1)(1)(1)()()1(.)(F 12)()3(;1)(2)()2(;(p 21)(1)()1(00000-=<=>-=-==<-=--=-=-=+=-==--=>-=<-=-=-⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰-∞-∞-∞-∞--∞-a F dxx p a F dx x p dx x p a P dx x p dx x p dx x p a F dx x p dxx p dx x p dx x p a F a a P a F a P dx x a F a F a a a a a aaaaaa ξξξξξ3.5设)(1x F 与)(2x F都是分布函数，证明F(x)=aF(x)+bF(x)也是一个分布函数，并由此讨论，分布函数是否只有离散型和连续型这两种类型？证：因为)(1x F与 )(2x F 都是分布函数，于是F(x1)＝aF1(x1)+bF2(x2)<= aF1(x1)+bF2(x2)= F(x2) 又F(x-0)= aF1(x1-0)+bF2(x2-0) = aF1(x)+bF2(x)= F(x) 所以，F(x)也是分布函数。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第三章练习题
一、单项选择题
1．设二维随机变量（X ，Y ）的分布律为
Y
X
1 2
3
1
2
101 103 102
101 102 101 则P{XY=2}=（ C ）A ．5 B ．10 C ．2 D ．5
2．设二维随机变量（X ，Y ）的概率密度为
⎩
⎨⎧≤≤≤≤=,,0;
10,10,4),(其他y x xy y x f
则当0≤y ≤1时，（X ，Y ）关于Y 的边缘概率密度为f Y ( y ) 1
=(,)4f x y dx xydx +∞
-∞
==⎰
⎰=
（ D ）
A ．x
21
B ．2x
C ．y 21
D ．2y
3．设随机变量X ，Y 相互独立，其联合分布为
1+9
α
12 1
+9
α 1+18β 116=+9918
α⎛⎫ ⎪⎝⎭ 则有（ B ）
A ．92
,91==βα B ．91,92==βαC ．32,31==βα D ．3
1,32==βα
二、填空题
1.设随机变量X ，Y 相互独立，且P{X ≤1}=21，P{Y ≤1}=3
1
，则P{X ≤1,Y ≤1}=_
1
6
__. 2.已知二维随机变量(X ,Y )的分布律为
0 2 5 0 0.1
0.1
0.3
Y
X
1 0.25 0 0.25
则P (X ≤0,Y =2)＝___0.1___.
3．设二维随机变量（X ，Y ）的分布律为
Y
X
1 2 3
1
2
61 121 81 81 41 4
1 则P{Y=2}=____
4
_______. 4．设随机变量(X,Y)的概率密度为f(x,y)=⎩
⎨⎧≤≤≤≤其他02
y 0,1x 0xy ，
则X 的边缘概率密度f x (x)=
2
(,)f x y dy xydy +∞
-∞
==⎰
⎰_____2x___________．
三、计算题
1．设二维随机变量(X ，Y )只能取下列数组中的值：(0，0)，（-1，1），（-1，3
1
），（2，0），
且取这些值的概率依次为61，31，121，12
5
.（1）写出(X ，Y )的分布律；
（2）分别求(X ，Y )关于X ，Y 的边缘分布律.
(1)
{}
{}
1351112
3
121166551212
71112
12
3
01-10
00020
1
j i X Y P Y y P X x ==
(2)
13711
12
12
3
1
X P
5
5112
6
12
10
2
Y P
-
2．设二维随机变量（X ，Y ）的概率密度为⎪⎩
⎪⎨⎧>>=+.,0;0,0,e
),()-(其他y x y x f y x
（1）分别求（X ，Y ）关于X 和Y 的边缘概率密度；
f x (x)=
()0
(,),0x y x f x y dy e dy e x +∞
∞
-+--∞
==>⎰
⎰
f Y ( y ) ()0
=
(,),0x y y f x y dx e dx e y +∞
∞
-+--∞
==>⎰
⎰
（2）问：X 与Y 是否相互独立，为什么？
()
()()(,)x y x y X Y f x y e
e e
f x f y -+--==⋅=⋅,因此相互独立
3.设二维随机变量(X ，Y )的分布律为
0.7
0.4 0.2 0.4
（1）求(X ，Y )分别关于X ,Y 的边缘分布律；(2)试问X 与Y 是否相互独立，为什么？
（1）
010.30.7X P 012
0.40.20.4
Y P
(2) {}{}{}000.200.300.4P X Y P X P Y =======，，， {}{}{}0000P X Y P X P Y ==≠=⨯=，,因此不独立
4．设随机变量（X ，Y ）的概率密度为(6),02,24;
(,)0,
.k x y x y f x y --<<<<⎧=⎨⎩其他
求：（1）k 的值。

（2）{}4P X Y +≤.
()+4
2
-2
(,)6f x y dxdy k x y dxdy ∞+∞
∞
-∞
=--⎰⎰
⎰
⎰。