不等式约束最优化的非光滑精确罚函数的一个光滑近似
约束优化问题的序列近似方法收敛性

段庆松
【摘 要】对抽象约束优化问题的序列近似方法的收敛性进行讨论,证明了在目标函数序列连续收敛和约束集合序列收敛的条件下,序列近似问题的全局最优值收敛到原问题的最优值。进一步,证明了在序列近似问题目标函数和约束集合具有某些单调性质的前提下,把目标函数序列连续收敛减弱到上图收敛,该结论仍然成立。最后,将这一结果用于分析互补约束优化问题的光滑化方法的收敛性中。%T he convergence of the sequential approximation method for abstract constrained optimization problems is discussed .It is proved that the global optimal solutions of the sequential approximation problems converge to the optimal solutions of the original problem under the continuous convergency of the objective function sequence and the convergency of the constrained set sequence .Moreover ,if the objective function sequence is assumed to be epi‐convergence instead of continuous convergence ,the conclusion still holds w hen some monotonicity property of the objective functions and the constrained sets of the sequential approximation problems is satisfied .At last ,the research result can be applied to analyze the convergence of the smoothing method in solving complementarity constraint optimization problem .
带约束的非线性优化问题解法小结

(1)带约束的非线性优化问题解法小结考虑形式如下的非线性最优化问题(NLP):min f(x)「g j (x )“ jI st 彳 g j (x)=O j L其 中, ^(x 1,x 2...x n )^ R n, f : R n > R , g j :R n > R(j I L) , I 二{1,2,…m }, L ={m 1,m 2...m p}。
上述问题(1)是非线性约束优化问题的最一般模型,它在军事、经济、工程、管理以 及生产工程自动化等方面都有重要的作用。
非线性规划作为一个独立的学科是在上世纪 50年 代才开始形成的。
到70年代,这门学科开始处于兴旺发展时期。
在国际上,这方面的专门性 研究机构、刊物以及书籍犹如雨后春笋般地出现,国际会议召开的次数大大增加。
在我国, 随着电子计算机日益广泛地应用,非线性规划的理论和方法也逐渐地引起很多部门的重视。
关于非线性规划理论和应用方面的学术交流活动也日益频繁,我国的科学工作者在这一领域 也取得了可喜的成绩。
到目前为止,还没有特别有效的方法直接得到最优解,人们普遍采用迭代的方法求解: 首先选择一个初始点,利用当前迭代点的或已产生的迭代点的信息,产生下一个迭代点,一 步一步逼近最优解,进而得到一个迭代点列,这样便构成求解( 1)的迭代算法。
利用间接法求解最优化问题的途径一般有:一是利用目标函数和约束条件构造增广目标 函数,借此将约束最优化问题转化为无约束最优化问题,然后利用求解无约束最优化问题的 方法间接求解新目标函数的局部最优解或稳定点,如人们所熟悉的惩罚函数法和乘子法;另 一种途径是在可行域内使目标函数下降的迭代点法,如可行点法。
此外,近些年来形成的序 列二次规划算法和信赖域法也引起了人们极大的关注。
在文献[1]中,提出了很多解决非线性 规划的算法。
下面将这些算法以及近年来在此基础上改进的算法简单介绍一下。
1. 序列二次规划法序列二次规划法,简称SQ 方法.亦称约束变尺度法。
最优化方法 第三章(罚函数法)

这种惩罚策略,对于在无约束的求解过程中企图违反约
束的迭代点给予很大的目标函数值,迫使无约束问题的 极小点或者无限地向可行域D靠近,或者一直保持在可 行域D内移动,直到收敛到原来约束最优化问题的极小 点。
不改变可行域局部极小值,可以将 约束域之外的局部极小值变大。
p ( x) 0, x D p ( x) 0, x D
k k
k 1
k 1
xk 1是F x, M k 1 的最优解.
k 1 k k 1 k 0 M k 1 M k p ( x ) p ( x ) p ( x ) p ( x )
M k 1 M k
(3) f ( x k 1 ) M k p( x k 1 ) F ( x k 1 , M k ) F ( x k , M k ) f ( x k ) M k p( x k )
gi ( x) gi ( x) max gi ( x), 0 = 罚函数p(x)的构造 2 m l p( x) (max gi ( x), 0) 2 h 2 j ( x)
i 1 j 1
(1) p(x)连续 (2) p( x) 0, x D (3) p( x) 0, x D
二、外点法 外点罚函数法算法步骤 1:给定初始点 x 0 ,初始罚因子M1 0 (可取M1 1 ), 精度 0, k : 1. 2:以 x k 1初始点,求解无约束优化问题
min F ( x, M k ) f ( x) M k p( x)
得到极小点 x* ( M k ),记为 x k , 其中
p( x) (max gi ( x), 0) h 2 j ( x)
2 i 1 j 1 m l
拉格朗日神经网络解决带等式和不等式约束的非光滑非凸优化问题

拉格朗日神经网络解决带等式和不等式约束的非光滑非凸优化问题喻昕;许治健;陈昭蓉;徐辰华【摘要】Nonconvex nonsmooth optimization problems are related to many fields of science and engineering applications, which are research hotspots. For the lack of neural network based on early penalty function for nonsmooth optimization problems, a recurrent neural network model is proposed using Lagrange multiplier penalty function to solve the nonconvex nonsmooth optimization problems with equality and inequality constrains. Since the penalty factor in this network model is variable, without calculating initial penalty factor value, the network can still guarantee convergence to the optimal solution, which is more convenient for network computing. Compared with the traditional Lagrange method, the network model adds an equality constraint penalty term, which can improve the convergence ability of the network. Through the detailed analysis, it is proved that the trajectory of the network model can reach the feasible region in finite time and finally converge to the critical point set. In the end, numerical experiments are given to verify the effectiveness of the theoretic results.%非凸非光滑优化问题涉及科学与工程应用的诸多领域,是目前国际上的研究热点.该文针对已有基于早期罚函数神经网络解决非光滑优化问题的不足,借鉴Lagrange乘子罚函数的思想提出一种有效解决带等式和不等式约束的非凸非光滑优化问题的递归神经网络模型.由于该网络模型的罚因子是变量,无需计算罚因子的初始值仍能保证神经网络收敛到优化问题的最优解,因此更加便于网络计算.此外,与传统Lagrange方法不同,该网络模型增加了一个等式约束惩罚项,可以提高网络的收敛能力.通过详细的分析证明了该网络模型的轨迹在有限时间内必进入可行域,且最终收敛于关键点集.最后通过数值实验验证了所提出理论的有效性.【期刊名称】《电子与信息学报》【年(卷),期】2017(039)008【总页数】6页(P1950-1955)【关键词】拉格朗日神经网络;收敛;非凸非光滑优化【作者】喻昕;许治健;陈昭蓉;徐辰华【作者单位】广西大学计算机与电子信息学院南宁 530004;广西大学计算机与电子信息学院南宁 530004;广西大学计算机与电子信息学院南宁 530004;广西大学电气工程学院南宁 530004【正文语种】中文【中图分类】TP183作为解决优化问题的并行计算模型,递归神经网络在过去的几十年里受到了极大的关注,不少神经网络模型被提出。
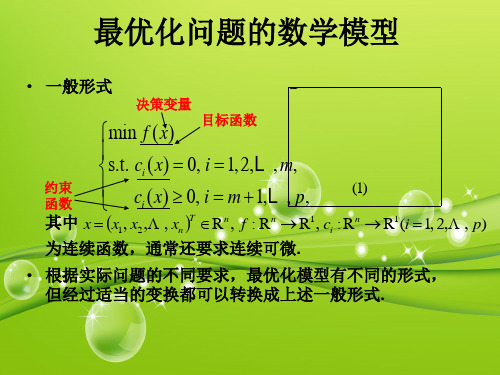
最优化问题的数学模型
为凸集.
1,
0 证明: x , y 为超球中的任意两点, 设
则有:
x 1 y
r ???
x 1 y
r r r 1
即点 x 1 y 属于超球
所以超球为凸集.
注: 常见的凸集:空集,整个欧氏空间 超平面: H
T
aR
n
和实数
,
使得: T x a
a y , x D ,
xR a x
n T
即存在超平面 H y 与凸集 D .
严格分离点
注: 点与闭凸集的分离定理。
y.
D
定理
(点与凸集的分离定理)
是非空凸集,x D, 则存在 非零向量 a R n 使成立
DR
n
目标函数
R ( i 1, 2 , , p )
1
• 根据实际问题的不同要求,最优化模型有不同的形式, 但经过适当的变换都可以转换成上述一般形式.
最优化问题的分类
最优化问题
根据约束条件 分类
m in f ( x ), x R .
n
无约束最优化问题 约束最优化问题 等式约束最优化问题 不等式约束最优化问题 混合约束优化问题
设
a xa x
T T
x D . ( D代 表 D 的 闭 包 )
_ _
定理
(两个凸集的分离定理)
n
x
x
设 D1 , D2 是
且 R 的两个非空凸集, D1 D2 ,
则存在超平面分离 D1 和 D2 , 即存在非零向量 n a R 使得 aT x aT y , x D , y D . 1 2
3不等式约束最优化问题的最优性条件.

不等式约束最优化问题
min
s.t .
f x
n
ci x 0,
3.3.1
i 1,2, m ,
n
其中f : R R,ci :R R(i 1,2 ,...,m).
不等式约束最优化问题的最优性条件
定 义
闭包:
Closure
设S R n , S的闭包定义为: clS { x | S N ( x ) , 0}.
x 处的可行方向锥 x
处的可行方向锥是全空间Rn .
D {d | d 0, 0, 使x d S , (0, )}.
注:当 x int S 时, S在
不等式约束最优化问题的最优性条件
定 下降方向(descent direction): 义设S R n , x S , d R n , d 0, 且f : S R在点x处可微,
* * 则存在非零的向量* * 0 , 1 , , m , 使得:
* * * * f x c x i i 0 0 m
* 0 i 1,2,, m * c x i i * i 0,1,2, , m i 0
2 x1 12 8 f x 2 . 2x 4 , f x 2 T T d 设 d d , d , 则 c1 x 0, d1 2d 2 0;
1 2
d T c2 x 0, 3d1 2d 2 0; d T f x 0, 8d1 2d 2 0.
x
f ( x )
S
D
不等式约束最优化问题的最优性条件
约束优化-惩罚函数法

( p) 1
,r
( p) 2
f x r G g x r H h x
( p) 1 m j 1 j ( p) 2 l k 1 k
的无约束最优化问题。
min x, r1( p ) , r2( p ) f x r1( p ) G g j x r2( p ) H hk x
k 1 l
对于每次迭代的 M ( p ),都可以求得相应的惩 罚函数最小 值和最优解X ( M ( p ) )。
当M为足够大的值时,惩罚 函数最小值将收敛于一 个有 限的极限值 *,且满足hk ( x) 0,而序列{X ( M ( p ) )}将 收敛于某一点X *。 *即为原问题f ( x)在等式约束hk ( x) 0 条件下的最小值, X *即为原问题的最优解。 即: lim M ( p ) lim M
2 另外,惩罚项形式 M h ( x ) k k 不是唯一的, k 1 l
任何仅仅当约束条件得 到满足时才等于零的 非负函数都可以当作惩 罚项,可以根据具体情 况选择。
四、惩罚函数法
将约束最优化问题 min f x f x1 , x2 , , xn s.t. g j x g j x1 , x2 , , xn 0 hk x hk x1 , x2 , , xn 0 转化为形如: min x, r ( j 1,2, , m) (k 1,2, , l )
为便于在计算机上用直 接寻优的方法进行迭代 计算, 可以构造一个新的函数 : F F Z x i 1 k 1 i k
n l 2 l F 2 x hk ( x) i 1 k 1 i n 2 2
penalty函数

penalty函数Penalty函数是一种数学变换函数,广泛应用于数学、物理和工程等领域中,作为优化算法的基础之一;它是一种特殊的非光滑函数,常常被用来惩罚表现不好的决策方案,从而使其在优化过程中趋近于最优解。
本文将介绍Penalty函数的定义、性质、应用和发展等方面的研究进展,以期为相关领域的研究提供参考和借鉴。
1. Penalty函数的定义和性质Penalty函数是一种由罚函数与约束函数组成的函数,其可表示为:P(x,ρ) = f(x) + ρ·h(x)其中,x是决策向量,f(x)是优化目标函数,h(x)是用来描述决策向量是否满足约束限制的函数,ρ是一个正常数,也叫作惩罚系数。
当决策向量满足所有的约束条件时,Penalty函数的值等于优化目标函数的值;否则,惩罚项将对优化目标函数进行惩罚,从而使得决策向量的取值趋近于约束条件的限制。
Penalty函数的惩罚项通常是由约束条件的违反程度和惩罚系数共同组成的,它可以采取线性、平方和指数等形式,以体现违反约束条件的严重程度。
例如,一个约束条件为h(x)≤0,假设决策向量x不满足该条件,当ρ>0时,Penalty函数的值可以表示为:其中,[h(x)]+表示h(x)的正部分,即当h(x)>0时,[h(x)]+=h(x),否则,[h(x)]+=0。
惩罚系数ρ的大小决定了相应的惩罚力度,ρ越大,则惩罚力度越大,决策向量越趋近于满足约束条件的限制。
Penalty函数的主要优点是简单易实现,适用于各种优化算法中,如牛顿法、共轭梯度法、遗传算法等。
同时,Penalty函数也具有一些较好的性质,如:(1)可导性:如果约束函数h(x)是可导的,则Penalty函数也是可导的;(3)非负性:Penalty函数的值通常都是非负的,但在非线性的罚函数中,可能会存在局部最小值的情况,需要格外注意。
由于Penalty函数具有一些良好的性质,因此被广泛用于一些任务中,如:(1)约束优化问题:Penalty函数通常用来处理带有约束条件的优化问题,如不等式约束优化问题、等式约束优化问题等;(2)非线性规划问题:Penalty函数常常被用来求解非线性规划问题,如非线性规划问题、混合整数规划问题等;(3)优化算法:Penalty函数作为优化算法的基础,经常被用来设计各种求解最优化问题的算法,如牛顿法、遗传算法、蚁群算法等。
