辗转相除法案例
《算法案例(辗转相除法)》

解:把98和63以大数减小数,并辗转相减
98-63=35 63-35=28 35-28=7 28-7=21 21-7=14
14-7=7 所以,98和63的最大公约数等于7
练习: 1、分别用辗转相除法、更相减损术、 求两个正数84与72的最大公约数.(对比那种方法好)
思考:求324、243、135这三个数的最大公约数。
一、进位制(课本P40)
1、什么是进位制? 2、最常见的进位制是什么? 除此之外还有哪些常见的进位制?请举例说明. 进位制是人们为了计数和运算方便而约定的记数系统。
1、我们了解十进制吗?所谓的十进制,它是如 何构成的? 十进制
第一、它有0、1、2、3、4、5、6、7、8、9十个数字;
注意: 1.最后一步商为0, 2.将上式各步所得的余数从下到上排列,得到:89=1011001(2)
练习 将下面的十进制数化为二进制数? (1)10
3、十进制转换为其它进制 例3 把89化为五进制数 解: 根据除5取余法 以5作为除数,相应的除法算式为: 5 89 5 17 5 3 0
余数
4 2 3
完整的过程
8251=6105×1+2146 6105=2146×2+1813
2146=1813×1+333 1813=333×5+148 333=148×2+37 148=37×4+0
一、辗转相除法 225=135×1+90 (欧几里得算法) P 45 练习1(2)、(3)
90=45×2 135=90×1+45
所以,110011(2)=51。
练习 将下面的二进制数化为十进制数? (1)11 (2)111
四个经典的算法案例
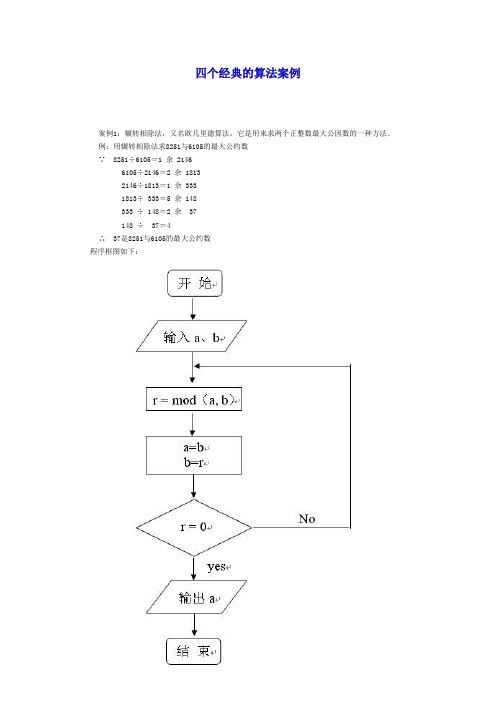
四个经典的算法案例案例1:辗转相除法,又名欧几里德算法,它是用来求两个正整数最大公因数的一种方法。
例:用辗转相除法求8251与6105的最大公约数∵ 8251÷6105=1 余 21466105÷2146=2 余 18132146÷1813=1 余 3331813÷ 333=5 余 148333 ÷ 148=2 余 37148 ÷ 37=4∴ 37是8251与6105的最大公约数程序框图如下:其中 r = mod(a, b) r表示a÷b的余数案例2:秦九韶算法,它是中国南宋时期数学家秦九韶提出的,用来解决多项式的求值问题,在西方被称作霍纳算法。
首先看一道例题:求多项式f(x)=2x5―5x4―4x3+3x2―6x+7当x=5时的值。
根据秦九韶算法:f(x)可表示为f(x)=({[(2x―5)x―4]x+3}x―6)x+7于是令 V0=5则 V1=2V0―5=2×5―5=5V2=V1X―4=5×5―4=21V3=V2X+3=21×5+3=108V4=V3X―6=108×5―6=534V5=V4X+7=534×5+7=2677∴ f(5) = 2677秦九韶算法只用到乘法、加法两个简单运算,不需要乘方运算,它是多项式求值的简化算法。
下面看程序框图,其中a0、a1、a2、a3、a4、a5是f (x) 从右向左的系数。
案例3:排序:是一种基本并且常用的算法,排序的算法很多,可以参阅课本,这里不再叙述。
案例4:进位制例:画程序框图,表示把k进制数a(共有n位),转化为十进制数b的过程框图如下:其中:t = GET a│i│ t表示a右数第i位利用上面的算法,把2进制数110011化为十进制的数即:1×20+1×21+0×22+0×23+1×24+1×25= 51以上是四个经典算法,大家可以从中体会算法的基本思想和算法的基本结构,并尝试用算法的基本语句描述它。
1.3.1算法案例(1)辗转相除法与更相减损术

63-35=28,
35-28=7, 28-7=21, 21-7=14, 14-7=7.
《九章算术》——更相减损术
算理:可半者半之,不可半者,副置分 母、子之数,以少减多,更相减损,求 其等也,以等数约之. 算法分析:
第一步、任意给定两个正整数,判断他们是否都是 偶数,若是,用2约简;若不是,执行第二步。 第二步、以较大的数减较小的数,接着把所得的差 与较小的数比较,并以大数减小数。继续这个操作, 直到所得的减数和差相等为止,则这个等数就是所 求的最大公约数.
必修③ 第一章 算法初步
1.3.1 算法案例(一)—辗转 相除法与更相减损术
咸丰一中 杨金煜
〖创设情景,揭示课题〗
[问题1]:在小学,我们已经学过求最大公约数的知
识,你能求出18与30的最大公约数吗?
30 2 18 15 3 9 3 5 ∴18和30的最大公约 数是2×3=6.
(1) 5
25 35
方法:先用两个数公有的质 因数连续去除,一直除到所得 的商是互质数为止,然后把所 有的除数连乘起来.
练习1(1)求25和35的最大公约数,(2)求49和63的最大公约数.
(2) 7 49 63
5 7 所以,25和35的最大公约数为5
7 9 所以,49和63的最大公约数为7
〖创设情景,揭示课题〗
[问题2]:我们都是利用找公约数的方法来求最 大公约数,如果公约数比较大而且根据我们的 观察又不能得到一些公约数,我们又应该怎样 求它们的最大公约数?比如求8251与6105的最 大公约数?
6,下面是求115与276的最大公约数的程序, 把程序补充完整。 a=115 b=276 DO a MOD b r=__________ a=b b=r 0 LOOP UNTIL r=____ PRINT a END
算法案例-辗转相除法与更相减损术、秦九韶算法-优质获奖精品课件 (99)

[精解详析] (1)101 111 011(2)=1×28+0×27+1×26+ 1×25+1×24+1×23+0×22+1×21+1×20=379(10). (2)235(7)=2×72+3×71+5×70=124(10). (3)
∴137(10)=345(6).
(4)53(8)=5×81+3×80=43(10). ∴53(8)=101 011(2).
[一点通]
1.k进制数化为十进制数的步骤: (1)把k进制数写成不同数位上的数字与k的幂
的乘积之和的形式. (2)按十进制数的运算规则运算出结果.
2.十进制数化为k进制数(除k取余法)的步骤:
6.二进制数101 110(2)转化为八进制数为 ( )
A.45(8)
B.56(8)
C.67(8)
D.78(8)
3.不同进位制的数照样可比较大小.但一 般要转化到同一进位制下比较大小.
[例1] 求228与1 995的最大公约数 [思路点拨] 可以考虑用辗转相除法,也可考虑用更 相减损术. [精解详析] 法一(辗转相除法) 1 995=8×228+ 171,228=1×171+57,171=3×57, 所以228与1 995的最大公约数为57.
解析:先化成十进制,再化成八进制 101 110(2)=1×25+0×24+1×23+1×22+1×2 +0=46.
∴46=56(8). 答案:B
7.下列所给的四个数中,最小的是
()
A.3 732(8)
B.5 555(7)
C.2 011
D.133 210(4)
解析:将各项都化成十进制数再比较大小.
必须从下到上排列;(3)切记在所求数的右下角标明基数.
秦九韶算法
功能 它是一种用于计算 一元n次多项式 的值的方法
算法案例.辗转相除法

在编程语言中的实现
```python def gcd(a, b) while b != 0
在编程语言中的实现
• a, b = b, a % b
在编程语言中的实现
• return a
在编程语言中的实现
```
Java实现:在Java中,可以使用以下代码实现辗转相除法
在编程语言中的实现
```java
适用范围与限制
适用范围
辗转相除法适用于求任意两个正整数 的最大公约数。
限制
辗转相除法不适用于负数、浮点数或 非整数运算。
算法的起源与历史
起源
辗转相除法最早可以追溯到古希腊数学家欧几里得(Euclid)的《几何原本》。
历史
辗转相除法在欧洲文艺复兴时期被重新发现,并被广泛用于数学研究和应用。 随着计算机科学的兴起,辗转相除法也成为计算机算法的重要基础之一,被广 泛应用于各种计算领域。
历史地位
辗转相除法是数学史上的重要成果,它最早由古希腊数学 家欧几里得在他的著作《几何原本》中提出。这一算法不 仅在数学领域有重要应用,还对计算机科学、密码学等领 域产生了深远影响。
应用价值
辗转相除法在许多领域都有广泛的应用,如计算机编程、 算法设计、密码学等。通过辗转相除法,可以快速求出任 意两个整数的最大公约数,进而实现其他数学运算和加密 算法。
减少计算量
提前结束算法
当余数小于除数时,可以提前结束算法,避免不必要 的计算。
使用更小的除数
在辗转相除法中,可以使用更小的除数来进行计算, 减少计算量。
优化循环结构
通过优化循环结构,减少循环次数,从而减少计算量。
算法的并行化实现
并行化算法设计
将辗转相除法的各个步骤分解为独立 的子任务,并分配给不同的处理器或
1.3算法案例(一)辗转相除法

练习:
• 教材48页——1
程序框图
开始 输入m,n
①
否
求m除以n的余数r
m<n? 是
m=n t=m n=r
m=n n=t
r=0? 是 输出m
否
①
结束
程序语言
INPUT m,n IF n>m THEN t=m m=n n=t END IF DO r=m MOD n m=n n=r LOOP UNTIL r=0 PRINT m END
例1、用辗转相除法 求8251与6105的最大公因数
8251=6105×1+2146 6105=2146×2+1813
2146=1813×1+333 1813=333×5+148
333=148×2+37 148=37×4 8251与6105的最大公因数是37
辗转相除法:
给定两个正数,用 较大的数 除以 较小的数 ,
1.3算法案例(一)
辗转相除法
复习提问:
小学学过的求两个数的最大公约数的方法:
先用两个数公有的 质因数 连续去除,
一直除到所得的商是 互质数 为止,
然后把所有的除数 连乘 起来.
例如:求18与30的最大公约数.
2 3 18 9 3 30 15 5
所以18与30的最大公约数是2×3=6
1、辗转相除法
求得 商 和 余数 ,若余数不为一对数继续上面
的除法,直到大数被小数除尽,这时的 较小数
就是原来两数的最大公约数。
练习:
• 教材:45页——1
2、辗转相除法计算的程序框图及程序
算法步骤: • 第一步,给定两个正整数m,n. • 第二步,比较m,n的大小,若n>m则交换 m,n,否则直接执行下一步. • 第三步,计算m除以n所得的余数r. • 第四步,m=n,n=r. • 第五步,若r=0,则m,n的最大公约数等于m; 否则,返回第三步.
1.3 算法案例1---辗转相除法与更相减损术 8

1.3 算法案例1.3 算法案例——案例1 辗转相除法与更相减损术8**学习目标**1.理解辗转相除法与更相减损术求最大公约数的方法。
2.把辗转相除法与更相减损术的方法转换成程序框图与程序语言.**要点精讲**1.辗转相除法例如,求两个正数8251和6105的最大公约数。
分析与解:8251与6105两数都比较大,而且没有明显的公约数,可以考虑用两数中较大的数除以较小的数,求得商和余数:8251=6105×1+2146显然8251与6105的公约数也必是2146的约数,同样6105与2146的公约数也必是8251的约数, 所以8251与6105的最大公约数也是6105与2146的最大公约数。
6105=2146×2+1813,2146=1813×1+333,1813=333×5+148333=148×2+37,148=37×4+0则37为37与148的最大公约数,也是148与333的最大公约数,也是333与1813的最大公约数,也是1813与2146的最大公约数,也是2146与6105的最大公约数。
所以,2146与6105的最大公约数是37。
以上我们求最大公约数的方法就是辗转相除法。
也叫欧几里德算法,它是由欧几里德在公元前300年左右首先提出的。
2.更相减损术我国早期也有解决求最大公约数问题的算法,就是更相减损术。
在《九章算术》中记载了更相减损术求最大公约数的步骤:可半者半之,不可半者,副置分母、子之数,以少减多,更相减损,求其等也,以等数约之。
翻译为:(1)任意给出两个正数;判断它们是否都是偶数。
若是,用2约简;若不是,执行第二步。
(2)以较大的数减去较小的数,接着把较小的数与所得的差比较,并以大数减小数。
继续这个操作,直到所得的数相等为止,则这个数(等数)就是所求的最大公约数。
**范例分析**例1.试分别用辗转相除法和更相减损术求840与1764、440与556的最大公约数。
算法案例—辗转相除、更相减损、秦九韶

v1=1×(-2)+5=3 v2=3×(-2)+10=4 v3=4×(-2)+10=2 v4=2×(-2)+5=1 v5=1×(-2)+1=-1
比比谁算得快!
例2 已知一个5次多项式为 f (x )
= 5x + 3.5x + 1.7x - 0.8
5ห้องสมุดไป่ตู้
3
用秦九韶算法求当x=5时,V1,V3的值及求f(5)的值做多少次乘法运算.
v1 an x an1
v2 v1 x an2
最后的一 项是什么?
v3 v2 x an3 vn vn1 x a0
最第 i 个等 式是什么?
这种将求一个n次多项式f(x)的值转化成求n个一 次多项式的值的方法,称为秦九韶算法。
特征: 对于一个n次n+1项多项式,
观察括号的特点?做几次加法,几次乘法?
an1 x
n4
a3 ) x a2 ) x a1 ) x a0
f ( x) ((an x an1 ) x an2 ) x a1 ) x a0
要求多项式的值,应该先算最内层的一次多项式的值,即 然后,由内到外逐层计算一次多项式的值,即
〖创设情景,揭示课题〗
[问题2]:我们都是利用找公约数的方法来求
最大公约数,如果两个数比较大而且根据我
们的观察又不能得到一些公约数,我们又应
该怎样求它们的最大公约数?比如求8251与
6105的最大公约数?
1.辗转相除法:
例1 求两个正数8251和6105的最大公约数。
分析:8251与6105两数都比较大,而且没 有明显的公约数,如能把它们都变小一点,根据 已有的知识即可求出最大公约数.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例3
用更相减损术求98与63的最大公约数
解:由于63不是偶数,把98和63以大数减小数,并辗转相减 98-63=35 98=63×1+35 63-35=28 63=35×1+28 35-28=7 35=28×1+7 28-7=21 21-7=21 所以,98和63的最大公约数等于7 14-7=7 辗转相除法与更相减损术的区别
m=n×q+r
算法步骤 第一步:输入两个正整数m,n(m>n). 第二步:计算m除以n所得的余数r. 第三步:m=n,n=r. 第四步:若r=0,则m,n的最大公约数等于m;否则转到第二步.
第五步:输出最大公约数m.
开始
程序框图
程 序 INPUT “m,n=“;m,n DO r = m MOD n m=n n=r LOOP UNTIL r=0 PRINT m END
长郡中学高一数学备课组
复 习回顾 1. 回顾算法的三种表述: 自然语言 程序框图 (三种逻辑结构) 程序语言 (五种基本语句)
2. 思考: 小学学过的求两个数最大公约数的方法? 先用两个公有的质因数连续去除,一直除到所得的商是 互为质数为止,然后把所有的除数连乘起来.
1、求两个正整数的最大公约数
求25ቤተ መጻሕፍቲ ባይዱ35的最大公约数
5 3 75 15 5 105 21 7
所以,75和105的最 大公约数为15
2、除了用这种方法外还有没有其它方法?
如求8251和6105的最大公约数.
案例1、辗转相除法(欧几里得算法)
例1、求8251和6105的最大公约数. 8251=6105×1+2146 6105=2146×2+1813 2146=1813×1+333 1813=333×5+148 333=148×2+37 148=37×4 所以37是8251和6105 的最大公约数
输入m,n
r=m MOD n
m=n
n=r r=0?
是 否
输出m 结束
开始 输入m,n r=1
程序框图
程 序 INPUT “m,n=“;m,n r=1 WHILE r>0 r = m MOD n m=n n=r WEND PRINT m END
n=r
m=n
求m除以n的余数r
r>0?
否 是
输出m 结束
2、更相减损术
算理:可半者半之,不可半者,副置分母、子之数,以少 减多,更相减损,求其等也,以等数约之.
第一步:任意给定两个正整数;判断他们是否都是偶 数.若是,则用2约简;若不是则执行第二步. 第二步:以较大的数减较小的数,接着把所得的差与 较小的数比较,并以大数减小数.继续这个操作,直到 所得的减数和差相等为止,则这个等数就是所求的最 大公约数.
【练习】用辗转相除法求153和119的最大公约数
153=119×1+34
119=34×3+17
34=17×2
所以17是153和1119的最大公约数
思考:从上面的两个例子可以看 出计算的规律是什么?
S1:用大数除以小数
S2:除数变成被除数,余数变成除数 S3:重复S1,直到余数为0
辗转相除法是一个反复执行直到余数等于0停止的步骤,这实际上是 一个循环结构.
(1)都是求最大公约数的方法,计算上辗转相除法以除法为主, 更相减损术以减法为主,计算次数上辗转相除法计算次数相对较 少,特别当两个数字大小区别较大时计算次数的区别较明显. (2)从结果体现形式来看,辗转相除法体现结果是以相除余数 为0而 得到,而更相减损术则以减数与差相等而得到
作业:《考一本》第8课时
