培优专题 特殊平行四边形的最值问题
特殊平行四边形中的最值问题

九年级上重难点专题突破——常考题型精选专题01 特殊平行四边形中的最值问题题型一 菱形中的最值问题1.如图,在菱形ABCD 中,10AB AC ==,对角线AC 、BD 相交于点O ,点M 在线段AC 上,且3AM =,点P 为线段BD 上的一个动点,则12MP PB +的最小值是【解答】解:如图,过点P 作PE BC ^于E ,Q 四边形ABCD 是菱形,10AB AC ==,10AB BC AC \===,ABD CBD Ð=Ð,ABC \D 是等边三角形,60ABC ACB \Ð=Ð=°,30CBD \Ð=°,PE BC ^Q ,12PE PB \=,12MP PB PM PE \+=+,\当点M ,点P ,点E 共线且ME BC ^时,PM PE +有最小值为ME ,3AM =Q ,7MC \=,sin ME ACB MC Ð==QME \=,12MP PB \+2.如图,菱形ABCD 的对角线相交于点O ,12AC =,16BD =,点P 为边BC 上一点,且P 不与写B 、C 重合.过P 作PE AC ^于E ,PF BD ^于F ,连接EF ,则EF 的最小值等于 4.8 .【解答】解:连接OP ,如图所示:Q 四边形ABCD 是菱形,12AC =,16BD =,AC BD \^,182BO BD ==,162OC AC ==,10BC \===,PE AC ^Q ,PF BD ^,AC BD ^,\四边形OEPF 是矩形,FE OP \=,Q 当OP BC ^时,OP 有最小值,此时1122OBC S OB OC BC OP D =´=´,68 4.810OP ´\==,EF \的最小值为4.8,故答案为:4.8.3.如图,在菱形ABCD 中,45B Ð=°,BC =,E ,F 分别是边CD ,BC 上的动点,连接AE ,EF ,G ,H 分别为AE ,EF 的中点,连接GH ,则GH【解答】解:连接AF ,如图所示:Q 四边形ABCD 是菱形,AB BC \==,G Q ,H 分别为AE ,EF 的中点,GH \是AEF D 的中位线,12GH AF \=,当AF BC ^时,AF 最小,GH 得到最小值,则90AFB Ð=°,45B Ð=°Q ,ABF \D 是等腰直角三角形,AF AB \===GH \=,即GH4.如图所示,四边形ABCD 中,AC BD ^于点O ,4AO CO ==,3BO DO ==,点P 为线段AC 上的一个动点.过点P 分别作PM AD ^于点M ,作PN DC ^于点N .连接PB ,在点P 运动过程中,PM PN PB ++的最小值等于 7.8 .【解答】解:4AO CO ==Q ,3BO DO ==,8AC \=,四边形ABCD 是平行四边形,AC BD ^Q 于点O ,\平行四边形ABCD 是菱形,5AD ===,5CD AD \==,连接PD ,如图所示:ADP CDP ADC S S S D D D +=Q ,\111222AD PM DC PN AC OD ×+×=×,即1115583222PM PN ´´+´´=´´,5()83PM PN \´+=´,4.8PM PN \+=,\当PB 最短时,PM PN PB ++有最小值,由垂线段最短可知:当BP AC ^时,PB 最短,\当点P 与点O 重合时,PM PN PB ++有最小值,最小值 4.837.8=+=,故答案为:7.8.5.已知菱形OABC 在平面直角坐标系的位置如图所示,顶点(5,0)A ,OB =点P 是对角线OB 上的一个动点,(0,1)D ,当CP DP +最短时,点P 的坐标为( )A.(0,0)B.1(1,)2C.6(5,3)5D.10(7,5)7【解答】解:如图连接AC,AD,分别交OB于G、P,作BK OA^于K.Q四边形OABC是菱形,AC OB\^,GC AG=,OG BG==A、C关于直线OB对称,PC PD PA PD DA \+=+=,\此时PC PD+最短,在Rt AOGD中,AG===,AC\=,12OA BK AC OB×=××Q,4BK\=,3AK==,\点B坐标(8,4),\直线OB解析式为12y x=,直线AD解析式为115y x=-+,由12115y xy xì=ïïíï=-+ïî解得10757xyì=ïïíï=ïî,\点P坐标10(7,57.故选:D.6.如图所示,在菱形ABCD中,4AB=,120BADÐ=°,AEFD为正三角形,点E、F分别在菱形的边BC、CD上滑动,且E、F不与B、C、D重合.(1)证明不论E 、F 在BC 、CD 上如何滑动,总有BE CF =;(2)当点E 、F 在BC 、CD 上滑动时,分别探讨四边形AECF 的面积和CEF D 的周长是否发生变化?如果不变,求出这个定值;如果变化,求出最小值.【解答】解:(1)如图,连接AC ,Q 四边形ABCD 为菱形,120BAD Ð=°,60BAC \Ð=°,AEF D Q 是等边三角形,60EAF \Ð=°,160EAC \Ð+Ð=°,360EAC Ð+Ð=°,13\Ð=Ð,120BAD Ð=°Q ,60ABC \Ð=°,ABC \D 和ACD D 为等边三角形,460\Ð=°,AC AB =,\在ABE D 和ACF D 中,134AB ACABC Ð=Ðìï=íïÐ=Ðî,()ABE ACF ASA \D @D .BE CF \=;(2)四边形AECF 的面积不变,CEF D的周长发生变化.理由如下:由(1)得ABE ACF D @D ,则ABE ACF S S D D =,故AEC ACF AEC ABE ABC AECF S S S S S S D D D D D =+=+=四边形,是定值,作AH BC ^于H 点,则2BH =,1122ABC AECF S S BC AH BC D ==×==四边形.CEF D 的周长CE CF EF CE BE EF BC EF BC AE=++=++=+=+由“垂线段最短”可知:当正三角形AEF 的边AE 与BC 垂直时,边AE 最短.故AEF D 的周长会随着AE 的变化而变化,且当AE 最短时,CEF D 的周长会最小44=+=+.7.如图,由两个长为8,宽为4的全等矩形叠合而得到四边形ABCD ,则四边形ABCD 面积的最大值是( )A .15B .16C .19D .20【解答】解:如图1,作AE BC ^于E ,AF CD ^于F ,,//AD BC Q ,//AB CD ,\四边形ABCD 是平行四边形,Q 两个矩形的宽都是4,4AE AF \==,ABCD S AE BC AF CD =×=×Q 四边形,BC CD \=,\平行四边形ABCD 是菱形.如图2,当菱形的一条对角线为矩形的对角线时,四边形ABCD的面积最大,,设AB BC xBE x=-,==,则8222Q,=+BC BE CE222\=-+,(8)4x x解得5x=,\四边形ABCD面积的最大值是:´=,5420故选:D.8.如图所示,在边长为1的菱形ABCD中,60DABÐ=°,M是AD上不同于A,D两点的一动点,N是+=.CD上一动点,且1AM CN(1)证明:无论M,N怎样移动,BMND总是等边三角形;(2)求BMND面积的最小值.【解答】(1)证明:如图所示,连接BD,在菱形ABCD中,60DABÐ=°,\Ð=Ð=°,60ADB NDBD是等边三角形,故ADB\=,AB BD又1+=,DN CNAM CN+=,1AM DN \=,在AMB D 和DNB D 中,60AM DN MAB NDB AB DB =ìïÐ=Ð=°íï=î,()AMB DNB SAS \D @D ,BM BN \=,MBA NBD Ð=Ð,又60MBA DBM Ð+Ð=°,60NBD DBM \Ð+Ð=°,即60MBN Ð=°,BMN \D 是等边三角形;(2)解:过点B 作BE MN ^于点E .设BM BN MN x ===,则BE x =,故212BMN S MN BE D =×=,\当BM AD ^时,x 最小,此时,min x =,1324min S ==.BMN \D.9.如图,菱形ABCD 的对角线相交于点O ,12AC =,16BD =,点P 为边BC 上一点,且P 不与B 、C 重合.过P 作PE AC ^于E ,PF BD ^于F ,连接EF ,则EF 的最小值为( )A .4B .4.8C .5D .6【解答】解:连接OP,Q 四边形ABCD 是菱形,12AC =,16BD =,AC BD \^,182BO BD ==,162OC AC ==,10BC \===,PE AC ^Q ,PF BD ^,AC BD ^,\四边形OEPF 是矩形,FE OP \=,Q 当OP BC ^时,OP 有最小值,此时1122OBC S OB OC BC OP D =´=´,68 4.810OP ´\==,EF \的最小值为4.8,故选:B .10.如图,菱形ABCD 的两条对角线长分别为6AC =,8BD =,点P 是BC 边上的一动点,则AP 的最小值为( )A .4B .4.8C .5D .5.5【解答】解:设AC 与BD 的交点为O ,Q 点P 是BC 边上的一动点,AP BC \^时,AP 有最小值,Q 四边形ABCD 是菱形,AC BD \^,132AO CO AC ===,142BO DO BD ===,5BC \===,12ABCD S AC BD BC AP =´´=´Q 菱形,24 4.85AP \==,故选:B .题型二 矩形中的最值问题1.如图,点P 是Rt ABC D 中斜边AC (不与A ,C 重合)上一动点,分别作PM AB ^于点M ,作PN BC ^于点N ,连接BP 、MN ,若6AB =,8BC =,当点P 在斜边AC 上运动时,则MN 的最小值是( )A .1.5B .2C .4.8D .2.4【解答】解:90ABC Ð=°Q ,6AB =,8BC =,10AC \===,PM AB ^Q ,PN BC ^,90C Ð=°,\四边形BNPM 是矩形,MN BP \=,由垂线段最短可得BP AC ^时,线段MN 的值最小,此时,1122ABC S BC AB AC BP D =×=×,即11861022BP ´´=´×,解得: 4.8BP =,即MN 的最小值是4.8,故选:C .2.如图,在Rt ABC D 中,90BAC Ð=°且3AB =,4AC =,点D 是斜边BC 上的一个动点,过点D 分别作DM AB ^于点M ,DN AC ^于点N ,连接MN ,则线段MN 的最小值为( )A .125B .52C .3D .4【解答】解:90BAC Ð=°Q ,且3BA =,4AC =,5BC \==,DM AB ^Q ,DN AC ^,90DMA DNA BAC \Ð=Ð=Ð=°,\四边形DMAN 是矩形,MN AD \=,\当AD BC ^时,AD 的值最小,此时,ABC D 的面积1122AB AC BC AD =´=´,125AB AC AD BC ´\==,MN \的最小值为125;故选:A .3.如图,90MON Ð=°,矩形ABCD 的顶点A 、B 分别在边OM 、ON 上,当B 在边ON 上运动时,A 随之在OM 上运动,矩形ABCD 的形状保持不变,其中6AB =,2BC =.运动过程中点D 到点O 的最大距离是 3+【解答】解:如图:取线段AB 的中点E ,连接OE ,DE ,OD ,6AB =Q ,点E 是AB 的中点,90AOB Ð=°,3AE BE OE \===,Q 四边形ABCD 是矩形,2AD BC \==,90DAB Ð=°,DE \==,OD OE DE +Q …,\当点D ,点E ,点O 共线时,OD 的长度最大.\点D 到点O 的最大距离3OE DE =+=+故答案为:34.如图,在矩形ABCD 中,2AB =,1AD =,E 为AB 的中点,F 为EC 上一动点,P 为DF 中点,连接PB ,则PB 的最小值是( )A .2B .4CD .【解答】解:如图:当点F 与点C 重合时,点P 在1P 处,11CP DP =,当点F 与点E 重合时,点P 在2P 处,22EP DP =,12//PP CE \且1212PP CE =.当点F 在EC 上除点C 、E 的位置处时,有DP FP =.由中位线定理可知:1//PP CE 且112PP CF =.\点P 的运动轨迹是线段12P P ,\当12BP PP ^时,PB 取得最小值.Q 矩形ABCD 中,2AB =,1AD =,E 为AB 的中点,CBE \D 、ADE D 、1BCP D 为等腰直角三角形,11CP =.145ADE CDE CPB \Ð=Ð=Ð=°,90DEC Ð=°.2190DP P \Ð=°.1245DPP \Ð=°.2190P PB \Ð=°,即112BP PP ^,BP \的最小值为1BP 的长.在等腰直角1BCP 中,11CP BC ==.1BP \=.PB \.故选:C .5.如图,90MON Ð=°,矩形ABCD 在MON Ð的内部,顶点A ,B 分别在射线OM ,ON 上,4AB =,2BC =,则点D 到点O 的最大距离是( )A .2-B .2+C .2-D 2+【解答】解:取AB 中点E ,连接OE 、DE 、OD ,90MON Ð=°Q ,122OE AB \==.在Rt DAE D 中,利用勾股定理可得DE =.在ODE D 中,根据三角形三边关系可知DE OE OD +>,\当O 、E 、D 三点共线时,OD 最大为2OE DE +=+.故选:B .6.如图,点E 、F 、G 、H 分别是矩形ABCD 边AB 、BC 、CD 、DA 上的点,且HG 与EF 交于点I ,连接HE 、FG ,若6AB =,5BC =,//EF AD ,//HG AB ,则HE FG +【解答】解:如图所示,连接AI ,CI ,AC ,在矩形ABCD 中,90BAD BCD B Ð=Ð=Ð=°,//AB CD ,//AD BC ,又//EF AD Q ,//HG AB ,\四边形AHIE 和四边形IFCG 为矩形,HE AI \=,FG CI =,HE FG \+的长度即为AI CI +的长度,又AI CI AC +Q …,\当A ,I ,C 三点共线时,AI CI +最小值等于AC 的长度,在Rt ABC D 中,AC ===HE FG \+.7.如图,在ABC D 中,9AC =,12AB =,15BC =,P 为BC 边上一动点,PG AC ^于点G ,PH AB ^于点H .(1)求证:四边形AGPH 是矩形;(2)在点P 的运动过程中,GH 的长度是否存在最小值?若存在,请求出最小值,若不存在,请说明理由.【解答】(1)证明91215AC AB BC ===Q ,281AC \=,2144AB =,2225BC =,222AC AB BC \+=,90A \Ð=°.PG AC ^Q ,PH AB ^,90AGP AHP \Ð=Ð=°,\四边形AGPH 是矩形;(2)存在.理由如下:连接AP .Q 四边形AGPH 是矩形,GH AP \=.Q 当AP BC ^时AP 最短.91215AP \´=×.365AP \=.8.如图,菱形EFGH 的顶点E 、G 分别在矩形ABCD 的边AD ,BC 上,顶点F ,H 在矩形ABCD 的对角线BD 上.(1)求证:BG DE =;(2)若3AB =,4BC =,则菱形EFGH 的面积最大值是 758 .【解答】(1)证明:Q 四边形ABCD 是矩形,//AD BC \,FBG HDE \Ð=Ð,Q 四边形EFGH 是菱形,FG EH \=,EFG EHG Ð=Ð,12GFH EFG Ð=Ð,12EHF EHG Ð=Ð,GFH EHG \Ð=Ð,BFG DHE \Ð=Ð,在BFG D 和DHE D 中,FBG HDE BFG DHE FG EH Ð=ÐìïÐ=Ðíï=î,()BFG DHE AAS \D @D ,BG DE \=;(2)解:当点F 与B 重合,点H 与D 重合时,菱形EFGH 的面积最大,如图所示:Q 四边形EFGH 是菱形,EG BD \^,BE DE BG ==,Q 四边形ABCD 是矩形,90BAD \Ð=°,设BE DE x ==,则4AE x =-,在Rt ABE D 中,由勾股定理得:2223(4)x x +-=,解得:258x =,257488CG AE \==-=,\菱形EFGH 的面积最大值=矩形ABCD 的面积ABE -D 的面积CDG -D 的面积177********=´-´´´=;故答案为:758.9.如图,在矩形ABCD中,3AB=,6AD=,E是AD上一点,1AE=,P是BC上一动点,连接AP,取AP的中点F,连接EF,当线段EF取得最小值时,线段PD的长度是 5 .【解答】解:过点P作//PM FE交AD于M,如图,FQ为AP的中点,//PM FE,FE\为APMD的中位线,22AM AE\==,2PM EF=,当EF取最小值时,即PM最短,当PM AD^时,PM最短,此时3PM AB==,4MD AD AM=-=Q,在Rt PMDD中,5PD==,\当线段EF取得最小值时,线段PD的长度是5,故答案为:5.10.如图,在ABCD中,90BACÐ=°,点D是BC的中点,点E、F分别是AB、AC上的动点,90EDFÐ=°,M 、N 分别是EF 、AC 的中点,连接AM 、MN ,若6AC =,5AB =,则AM MN -的最大值为 2512 .【解答】解:如图,连接DM ,DN ,由图可以得到M 的轨迹是一条线段(AD 的垂直平分线的一部分),M 在AN 上的时候最大(此时AM 最大,MN 最小),当M 在AN 上时,如图,设AM x =,则3MN x =-,DM AM x ==,1522DN AB ==,在直角三角形DMN 中,根据勾股定理,得222DM DN MN =+,222(3) 2.5x x \=-+,解得6124x =,11324x \-=,此时611125242412AM MN -=-=.AM MN \-的最大值为2512.故答案为:2512.题型三 正方形中的最值问题1.如图,正方形ABCD 中,3AB =,点E 为对角线AC 上的动点,以DE 为边作正方形DEFG .点H 是CD上一点,且23DH CD =,连接GH ,则GH【解答】解:连接CG .Q 四边形ABCD 是正方形,四边形DEFG 是正方形,DA DC \=,DE DG =,90ADC EDG Ð=Ð=°,45DAC Ð=°,ADE CDG \Ð=Ð,()ADE CDG SAS \D @D ,45DCG DAE \Ð=Ð=°,\点G 的运动轨迹是射线CG ,根据垂线段最短可知,当GH CG ^时,GH 的值最小,223DH CD ==Q ,321CH CD DH \=-=-=,\最小值sin 451CH =°==g ..2.如图,在正方形ABCD 中,AB =,E 是对角线AC 上的动点,以DE 为边作正方形DEFG ,H 是CD的中点,连接GH ,则GH【解答】解:连接CG .Q 四边形ABCD 是正方形,四边形DECG 是正方形,DA DC \=,DE DG =,90ADC EDG Ð=Ð=°,45DAC Ð=°,ADE CDG \Ð=Ð,()ADE CDG SAS \D @D ,45DCG DAE \Ð=Ð=°,\点G 的运动轨迹是射线CG ,根据垂线段最短可知,当GH CG ^时,GH 的值最小,最小值sin 45CH =°=g .3.如图,平面内三点A 、B 、C ,5AB =,4AC =,以BC 为对角线作正方形BDCE ,连接AD ,则AD 的最大值是( )A .5B .9C .D 【解答】解:如图,将BDA D 绕点D 顺时针旋转90°得到CDM D ,由旋转不变性可知:5AB CM ==,DA DM =,90ADM Ð=°,ADM \D 是等腰直角三角形,AD \=,\当AM 的值最大时,AD 的值最大,AM AC CM +Q …,9AM \…,AM \的最大值为9,AD \.故选:D .4.如图,已知正方形ABCD 的边长为4,点M 和N 分别从B 、C 同时出发,以相同的速度沿BC 、CD 向终点C 、D 运动,连接AM 、BN ,交于点P ,连接PC ,则PC 长的最小值为( )A .2B .2C .1-D .【解答】解:由题意得:BM CN =,Q 四边形ABCD 是正方形,90ABM BCN \Ð=Ð=°,4AB BC ==,在ABM D 和BCN D 中,AB BC =,ABM BCN Ð=Ð,MB CN =,()ABM BCN SAS \D @D ,BAM CBN \Ð=Ð,90ABP CBN Ð+Ð=°Q ,90ABP BAM \Ð+Ð=°,90APB \Ð=°,\点p 是以AP 为半径的圆上远动,设圆心为O ,运动路径一条弧 BG ,是这个圆的14,如图所示:连接OC交圆O于P,此时PC最小,Q,AB=4\==,2OP OB由勾股定理得:OC==,\=-=;PC OC OP2故选:A.5.如图,在边长为4的正方形ABCD中,点E、F分别是边BC、CD上的动点,且BE CF=,连接BF、+的最小值为( )DE,则BF DEA B C D【解答】解:连接AE,如图1,Q四边形ABCD是正方形,ABE BCFÐ=Ð=°.\=,90AB BC又BE CF=,\D@D.ABE BCF SAS()\=.AE BF所以BF DE +最小值等于AE DE +最小值.作点A 关于BC 的对称点H 点,如图2,连接BH ,则A 、B 、H 三点共线,连接DH ,DH 与BC 的交点即为所求的E 点.根据对称性可知AE HE =,所以AE DE DH +=.在Rt ADH D 中,DH ===,BF DE \+.故选:D .6.如图,在ABC D 中,5AB AC ==,BC =D 为边AB 上一动点(B 点除外),以CD 为一边作正方形CDEF ,连接BE ,则BDE D 面积的最大值为 8 .【解答】解:过点C 作CG BA ^于点G ,作EH AB ^于点H ,作AM BC ^于点M .5AB AC ==Q ,BC =,BM CM \==,易证AMB CGB D D ∽,\BM AB GB CB=,8GB \=,设BD x =,则8DG x =-,易证()EDH DCG AAS D @D ,8EH DG x \==-,2111(8)(4)8222BDE S BD EH x x x D \==-=--+g ,当4x =时,BDE D 面积的最大值为8.故答案为8.7.如图,在平面直角坐标系中,已知矩形OABC 的顶点A 在x 轴上,4OA =,3OC =,点D 为BC 边上一点,以AD 为一边在与点B 的同侧作正方形ADEF ,连接OE .当点D 在边BC 上运动时,OE 的长度的最小值是 【解答】解:如图所示:过点D 作DG OA ^,过点E 作HE DG ^.DG OA ^Q ,HE DG ^,90EHD DGA \Ð=Ð=°.90GDA DAG \Ð+Ð=°.Q 四边形ADEF 为正方形,DE AD \=,90HDE GDA Ð+Ð=°.HDE GAD \Ð=Ð.在HED D 和GDA D 中HDE GAD EHD DGA DE AD Ð=ÐìïÐ=Ðíï=î,HED GDA \D @D .3HE DG \==,HD AG =.设(,3)D a ,则DC a =,4DH AG a ==-.(3,7)E a a \+-.OE \==.当2a =时,OE有最小值,最小值为.故答案为:8.如图,正方形ABCD 的边长为4cm ,动点E 、F 分别从点A 、C 同时出发,以相同的速度分别沿AB 、CD 向终点B 、D 移动,当点E 到达点B 时,运动停止,过点B 作直线EF 的垂线BG ,垂足为点G ,连接AG ,则AG-.【解答】解:设正方形的中心为O ,可证EF 经过O 点.连接OB ,取OB 中点M ,连接MA ,MG ,则MA ,MG 为定长,可计算得MA =,12MG OB ==AG AM MG -=…,当A ,M ,G 三点共线时,AG 最小=-,9.如图,M 、N 是正方形ABCD 的边CD 上的两个动点,满足AM BN =,连接AC 交BN 于点E ,连接DE交AM 于点F ,连接CF ,若正方形的边长为6,则线段CF 的最小值是 3- .【解答】解:如图,在正方形ABCD 中,AD BC CD ==,ADC BCD Ð=Ð,DCE BCE Ð=Ð,在Rt ADM D 和Rt BCN D 中,AD BC AM BN =ìí=î,Rt ADM Rt BCN(HL)\D @D ,DAM CBN \Ð=Ð,在DCE D 和BCE D 中,BC CD DCE BCE CE CE =ìïÐ=Ðíï=î,()DCE BCE SAS \D @D ,CDE CBE\Ð=ÐDAM CDE \Ð=Ð,90ADF CDE ADC Ð+Ð=Ð=°Q ,90DAM ADF \Ð+Ð=°,1809090AFD \Ð=°-°=°,取AD 的中点O ,连接OF 、OC ,则132OF DO AD ===,在Rt ODC D中,OC ==根据三角形的三边关系,OF CF OC +>,\当O 、F 、C 三点共线时,CF 的长度最小,最小值3OC OF =-=.故答案为:3-.10.如图,正方形ABCD 边长为4,点O 在对角线DB 上运动(不与点B ,D 重合),连接OA ,作OP OA ^,交直线BC 于点P .(1)判断线段OA ,OP 的数量关系,并说明理由.(2)当OD =时,求CP 的长.(3)设线段DO ,OP ,PC ,CD 围成的图形面积为1S ,AOD D 的面积为2S ,求12S S -的最值.【解答】解:(1)OA OP=,理由是:如图1,过O作OG AB^于G,过O作OH BC^于H,Q四边形ABCD是正方形,=,ABO CBO\Ð=Ð,AB BC\=,OG OHQ,Ð=Ð=Ð=°90OGB GBH BHO\四边形OGBH是正方形,BG BHÐ=°,GOH\=,90Q,Ð=Ð=°90AOP GOH\Ð=Ð,AOG POH()\D@D,AGO PHO ASA\=;OA OP^于Q,过O作OH BC(2)如图2,过O作OQ CD^于H,连接OC,90\Ð=°,OQDQ,Ð=°45ODQ\D是等腰直角三角形,ODQQ,OD=\==,1OQ DQÐ=Ð,OD OD=,=Q,ADO CDOAD CD\D@D,ADO CDO SAS()\==,AO OC OPQ,OH PC^PH CH OQ\===,1\=;2PC。
专题02 特殊平行四边形中的四种最值问题(解析版)-2024年常考压轴题攻略(9年级上册人教版)
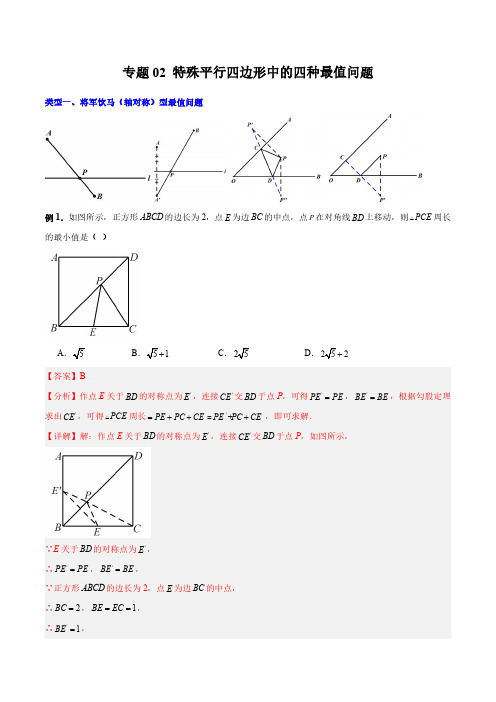
专题02特殊平行四边形中的四种最值问题类型一、将军饮马(轴对称)型最值问题A .5B .【答案】B 【分析】作点E 关于BD 的对称点为∵E 关于BD 的对称点为'E ,∴'PE PE =,'BE BE =,∵正方形ABCD 的边长为2,点A.0B.3【答案】C【分析】要使四边形APQE的周长最小,由于在BC边上确定点P、Q的位置,可在与BC交于一点即为Q点,过A点作后过G点作BC的平行线交DC的延长线于长度.∵四边形ABCD 是矩形,∴8BC AD ==,90D Ð=°,∠QCE =90°,∵2PQ =,∴6DF AD AF =-=,∵点F 点关于BC 的对称点G ,∴FG AD⊥∴90DFG ∠=︒∴四边形FGHD 是矩形,∴GH =DF =6,∠H =90°,∵点E 是CD 中点,∴CE =2,∴EH =2+4=6,∴∠GEH =45°,∴∠CEQ =45°,设BP =x ,则CQ =BC ﹣BP ﹣PQ =8﹣x ﹣2=6﹣x ,在△CQE 中,∵∠QCE =90°,∠CEQ =45°,∴CQ =EC ,∴6﹣x =2,解得x =4.故选:C .【点睛】本题考查了矩形的性质,轴对称﹣最短路线问题的应用,题目具有一定的代表性,是一道难度较大的题目,对学生提出了较高的要求.例3.如图,在矩形ABCD 中,26AB AD ==,,O 为对角线AC 的中点,点P 在AD 边上,且2AP =,点Q【答案】210【分析】①连接PO并延长交BC 明四边形APHB是矩形可得AB②过点O作关于BC的对称点PQ OQ+的最小值为PO'的长度,延长∵GO AD'⊥,点O是AC的中点,∴132AG AD==,【点睛】本题考查矩形的性质、全等三角形的判定与性质、勾股定理及轴对称识是解题的关键.【变式训练1】如图,正方形ABCD的周长为24,P为对角线AC上的一个动点,E是CD的中点,则PE PD+的最小值为()A .35B .32C .6D .5【答案】A 【详解】解:如图,连接BE ,设BE 与AC 交于点P',∵四边形ABCD 是正方形,∴点B 与D 关于AC 对称,∴P'D =P'B ,∴P'D +P'E =P'B +P'E =BE 最小.即P 在AC 与BE 的交点上时,PD +PE 最小,即为BE 的长度.∵正方形ABCD 的周长为24,∴直角△CBE 中,∠BCE =90°,BC =6,CE =12CD =3,∴226335BE =+=故选A.【变式训练2】如图,在矩形ABCD 中,AB =2,AD =3,动点P 满足S △PBC =14S 矩形ABCD ,则点P 到B ,C 两点距离之和PB +PC 的最小值为()A 10B 13C 15D .3【答案】B 【详解】解:设△PBC 中BC 边上的高是h .∵S △PBC =14S 矩形ABCD .∴12BC •h =14AB •AD ,∴h =12AB =1,∴动点P 在与BC 平行且与BC 的距离是1的直线l 上,如图,作B 关于直线l 的对称点E ,连接CE ,则CE 的长就是所求的最短距离.在Rt △BCE 中,∵BC =3,BE =BA =2,∴CE 2213+AB BC 即PB +PC 13故选:B .【变式训练3】如图,在正方形ABCD 中,4AB =,AC 与BD 交于点O ,N 是AO 的中点,点M 在BC 边上,且3BM =,P 为对角线BD 上一点,则PM PN -的最大值为_____________.【答案】1【分析】作N 关于BD 的对称点E ,连接PE ,ME ,过点M 作MQ ⊥AC ,垂足为Q ,可判定当点P ,E ,M 三点共线时,PM -PE 的值最大,为ME 的长,求出CE ,CQ ,得到EQ ,利用垂直平分线的性质得到EM =CM =1即可.【详解】解:如图:作N 关于BD 的对称点E ,连接PE ,ME ,过点M 作MQ ⊥AC ,垂足为Q ,∴PN =PE ,则PM -PN =PM -PE ,【答案】13【分析】连接CF、AF+=+,故当EF MN EF AF类型二、翻折型最值问题例1.如图,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上的一动点,将△AMN 沿MN所在直线翻折得到△A'MN,连接A'C,则A'C长度的最小值是()【变式训练1】如图,在矩形ABCD 中,3AB =,4=AD ,E 在AB 上,1BE =,F 是线段BC 上的动点,将EBF △沿EF 所在的直线折叠得到'EB F △,连接'B D ,则'B D 的最小值是()A .6B .4C .2D .1-【答案】D 【详解】解:如图,'B 的运动轨迹是以E 为圆心,以BE 的长为半径的圆.所以,当'B 点落在DE 上时,'B D 取得最小值.根据折叠的性质,△EBF ≌△EB’F ,∴E 'B ⊥'B F ,∴E 'B =EB ,∵1BE =∴E 'B =1,∵3AB =,4=AD ,∴AE =3-1=2,∴DE =D 'B =.故选:D .【变式训练2】如图,在正方形ABCD 中,AB =6,E 是CD 边上的中点,F 是线段BC 上的动点,将△ECF 沿EF 所在的直线折叠得到EC F '△,连接AC ',则的最小值是AC '_______.【答案】3【详解】解:∵四边形ABCD 是正方形,∴6CD AB AD ===,∵E 是CD 边上的中点,∴132EC CD ==∵△ECF 沿EF 所在的直线折叠得到EC F '△,∴3EC EC '==,∴当点A ,C ',E 三点共线时,AC '最小,如图,在Rt ADE △中,由勾股定理得:AE ==3AE EC '-=-,∴AC '的最小值为3.类型三、旋转型最值问题【答案】353-【分析】过点M 作MP CD ⊥,垂足为P ,连接CM ,根据正方形的性质求出CE ,证明EDC DMP △≌△股定理求出CM ,根据CN MN CM +≥即可求出CN 【详解】解:过点M 作MP CD ⊥,垂足为P ,连接由旋转可得:DE DM =,3EF MN ==,90EDM ∠=例2.如图,长方形ABCD 中,6AB =,8BC =,E 为BC 上一点,且2BE =,F 为AB 边上的一个动点,连接EF ,将EF 绕着点E 顺时针旋转30°到EG 的位置,连接FG 和CG ,则CG 的最小值为______.【答案】2+【详解】解:如图,将线段BE 绕点E 顺时针旋转30°得到线段ET ,连接GT ,过E 作EJ CG ⊥,垂足为J ,∵四边形ABCD 是矩形,∴AB =CD =6,∠B =∠BCD =90°,∵∠BET =∠FEG =30°,∴∠BEF =∠TEG ,在△EBF 和△TEG 中,EB ET BEF TEG EF EG =⎧⎪∠=∠⎨⎪=⎩,∴△EBF ≌△ETG (SAS ),∴∠B =∠ETG =90°,∴点G 的在射线TG 上运动,∴当CG ⊥TG 时,CG 的值最小,∵∠EJG =∠ETG =∠JGT =90°,∴四边形ETGJ 是矩形,∴∠JET =90°,GJ =TE =BE =2,∵∠BET =30°,∴∠JEC =180°-∠JET -∠BET =60°,∵8BC =,∴226,3,3EC BC BE EJ CJ EC EJ =-===-=,∴CG =CJ +GJ =332+.∴CG 的最小值为332+.故答案为:332.【变式训练1】如图,已知正方形ABCD 的边长为a ,点E 是AB 边上一动点,连接ED ,将ED 绕点E 顺时针旋转90︒到EF ,连接DF ,CF ,则当DF CF +之和取最小值时,DCF 的周长为______.(用含a 的代数式表示)【答案】()51a +【分析】连接BF ,过点F 作FG AB ⊥交AB 延长线于点G ,先证明AED GFE △≌△,即可得到点F 在CBG ∠的角平分线上运动,作点C 关于BF 的对称点C ',当点D ,F ,C 三点共线时,DF CF DC +='最小,根据勾股定理求出DC DF CF '=+的最小值为35,即可求出此时DCF 的周长为353+.将ED绕点E顺时针旋转90︒到EF,=,∴⊥,EF DEEF DEDEA FEG DEA ADE∴∠+∠=∠+∠=︒,90∴∠=∠,ADE FEG又90,∠=∠=︒DAE FGE(1)试猜想线段BG 和AE 的数量关系,并证明你得到的结论;(2)将正方形DEFG 绕点D 逆时针方向旋转一定角度后(旋转角度大于过观察或测量等方法判断(1)中的结论是否仍然成立?如果成立,请予以证明;如果不成立,请说明理由;(3)若2BC DE ==,在(2)的旋转过程中,①当AE 为最大值时,则AF =___________.ABC 是等腰直角三角形,AD BC ∴⊥,BD CD =,90ADB ADC ∴∠=∠=︒.四边形DEFG 是正方形,DE DG ∴=.在BDG 和ADE V 中,BD AD BDG ADE GD ED =⎧⎪∠=∠⎨⎪=⎩,(SAS)ADE BDG ∴△≌△,BG AE ∴=;(2)(1)中的结论仍然成立,BG AE =,BG AE ⊥.理由如下:如图②,连接AD ,延长EA 交BG 于K ,交DG 于O .在Rt BAC 中,D 为斜边BC 中点,AD BD ∴=,AD BC ⊥,90ADG GDB ∴∠+∠=︒.四边形EFGD 为正方形,DE DG ∴=,且90GDE ∠=︒,90ADG ADE ∴∠+∠=︒,BDG ADE ∴∠=∠.在BDG 和ADE V 中,BD AD BDG ADE GD ED =⎧⎪∠=∠⎨⎪=⎩,(SAS)BDG ADE ∴△≌△,BG AE ∴=,BGD AED ∠=∠,2,==BC DEBG∴=+=.213AE∴=.3在Rt AEF中,由勾股定理,得222=+=+3AF AE EF中,如图②中,在BDGBG∴-≤≤+,2112∴的最小值为1,此时如图④中,AE在Rt AEF中,2=AF EF【点睛】本题属于四边形综合题,考查了旋转的性质的运用,等腰直角三角形的性质的运用,勾股定理的运用,全等三角形的判定及性质的运用,正方形的性质的运用,解答时证明三角形全等是关键.类型四、PA+KPB型最值问题3A.27B.23【答案】C【分析】连接AC与EF相交于∵四边形ABCD是菱形,∠=∠,∴OAE OCFA.3B.22【答案】D【分析】连接AF,利用三角形中位线定理,可知四边形ABCD是菱形,∴==,AB BC23,H分别为AE,EF的中点,GGH∴是AEF△的中位线,【答案】51-【分析】连接BD交EF的中点,求出OB的长,得到AH AM MH>=-–51直线l平分正方形∴O是BD的中点,四边形ABCD是正方形,∴==,BD AB24【答案】26【分析】利用轴对称的性质作出如图的辅助线,在【详解】解:延长DC '''∴E F G H E '''、、、、在同一直线上时,四边形EFCH 作E K AB '⊥交AB 延长于点K ,则23EK BE CD A E AB CD '''=++=+=,E K BC '=+在△ABH中,∠AHB=90°,∠ABH过点D作DE∥AC交BC延长线于点E,作点C【点睛】本题考查了对称的性质,勾股定理,等边三角形的判定和性质,最值问题,直角三角形的性质,多边形的面积,知识点较多,难度较大,解题的关键是作出辅助线,得出当且仅当B,D,F三点共线时,BD+CD取得最小值.。
专题03特殊平行四边形中的最值、定值问题教师版

专题03特殊平行四边形中的最值、定值问题【典型例题】9.(2020·万杰朝阳学校)如图,在△ABC中,AB=6,AC=8,BC=10,P为边BC上一动点(且点P不与点B、C重合),PE⊥AB于E,PF⊥AC于F.则EF的最小值为()A.4B.4.8C.5.2D.6【解析】如图,连接P A.∵在△ABC中,AB=6,AC=8,BC=10,∴BC2=AB2+AC2,∴∠A=90°.又∵PE⊥AB于点E,PF⊥AC于点F.∴∠AEP=∠AFP=90°,∴四边形PEAF是矩形.∴AP=EF.∴当P A最小时,EF也最小,即当AP⊥CB时,P A最小,∵12AB۰AC=12BC۰AP,即AP=6810AB ACBC⋅⨯==4.8,∴线段EF长的最小值为4.8;故选B.2.(2019·余干县第二中学期末)如图,在边长为10的菱形ABCD中,对角线BD=16,对角线AC,BD 相交于点G,点O是直线BD上的动点,OE⊥AB于E,OF⊥AD于F.(1)求对角线AC的长及菱形ABCD的面积.(2)如图①,当点O在对角线BD上运动时,OE+OF的值是否发生变化?请说明理由.(3)如图②,当点O在对角线BD的延长线上时,OE+OF的值是否发生变化?若不变,请说明理由;若变化,请探究OE,OF之间的数量关系.【答案】解:(1)在菱形ABCD中,AG=CG,AC⊥BD,BG=12BD=12×16=8,由勾股定理得AG6==,所以AC=2AG=2×6=12.所以菱形ABCD的面积=12AC·BD=12×12×16=96.(2)不发生变化.理由如下:如图①,连接AO,则S△ABD=S△ABO+S△AOD,所以12BD·AG=12AB·OE+12AD·OF,即12×16×6=12×10·OE+12×10·OF.解得OE+OF=9.6,是定值,不变.(3)发生变化.如图②,连接AO,则S△ABD=S△ABO-S△AOD,所以12BD·AG=12AB·OE-12AD·OF.即12×16×6=12×10·OE-12×10·OF.解得OE-OF=9.6,是定值,不变.所以OE+OF的值发生变化,OE,OF之间的数量关系为OE-OF=9.6.【专题训练】一、选择题1.(2020·安徽和县)如图,在周长为12的菱形ABCD中,AE=1,AF=2,若P为对角线BD上一动点,则EP+FP的最小值为()A.1B.2C.3D.4【解析】作F点关于BD的对称点F′,则PF=PF′,连接EF′交BD于点P.∴EP+FP=EP+F′P.由两点之间线段最短可知:当E、P、F′在一条直线上时,EP+FP的值最小,此时EP+FP=EP+F′P=EF′.∵四边形ABCD为菱形,周长为12,∴AB=BC=CD=DA=3,AB∥CD,∵AF=2,AE=1,∴DF=AE=1,∴四边形AEF′D是平行四边形,∴EF′=AD=3.∴EP+FP的最小值为3.故选C.考点:菱形的性质;轴对称-最短路线问题2.(2020·江苏淮阴)如图,由两个长为9,宽为3的全等矩形叠合而得到四边形ABCD,则四边形ABCD 面积的最大值是()A.15B.16C.19D.20【解析】如图1,作AE⊥BC于E,AF⊥CD于F,∵AD∥BC,AB∥CD,∴四边形ABCD是平行四边形,∵两个矩形的宽都是3,∴AE=AF=3,∵S四边形ABCD=AE⋅BC=AF⋅CD,∴BC=CD,∴平行四边形ABCD是菱形.如图2,设AB =BC =x ,则BE =9−x , ∵BC 2=BE 2+CE 2,∴x 2=(9−x )2+32,解得x =5,∴四边形ABCD 面积的最大值是:5×3=15.故选A . 3.(2020·江西九江初三零模)如图,菱形ABCD 的边长为6,∠ABC =120°,M 是BC 边的一个三等分点,P 是对角线AC 上的动点,当PB +PM 的值最小时,PM 的长是( )A .2B .3C .5D 【解析】连接DP ,BD ,作DH ⊥BC 于H .∵四边形ABCD 是菱形,∴AC ⊥BD ,B 、D 关于AC 对称, ∴PB +PM =PD +PM ,∴当D 、P 、M 共线时,P ′B +P ′M =DM 的值最小,∵CM =13BC =2,∵∠ABC =120°,∴∠DBC =∠ABD =60°,∴△DBC 是等边三角形,∵BC =6,∴CM =2,HM =1,DH =在Rt △DMH 中,DM =,∵CM ∥AD ,∴''P M CM DP AD ==26=13,∴P ′M =14 DM =2.故选A . 4.(2019·全国单元测试)如图,在菱形ABCD 中,AB =4,∠A =120°,点P ,Q ,K 分别为线段BC ,CD ,BD 上的任意一点,则PK +QK 的最小值为( )A .2B .2√3C .4D .2+√32【解析】作点P关于BD的对称点P′,作P′Q⊥CD交BD于K,交CD于Q,∵AB=4,∠A=120°,∴点P′到CD的距离为4×√32=2√3,∴PK+QK的最小值为2√3,故选:B. 5.(2020·浙江锦绣育才教育科技集团有限公司初三二模)如图,在矩形ABCD中,AB=5,AD=3,动点P满足S△P AB=13S矩形ABCD,则点P到A、B两点距离之和P A+PB的最小值为()A B C.D解:设△ABP中AB边上的高是h.∵S△P AB=13S矩形ABCD,∴12AB•h=13AB•AD,∴h=23AD=2,∴动点P在与AB平行且与AB的距离是2的直线l上,如图,作A关于直线l的对称点E,连接AE,连接BE,则BE就是所求的最短距离.在Rt△ABE中,∵AB=5,AE=2+2=4,∴BE,即P A+PB D6.(2020·朝阳市英德中学初三零模)如图,点P是矩形ABCD的边上一动点,矩形两边长AB、BC长分别为15和20,那么P到矩形两条对角线AC和BD的距离之和是()A.6B.12C.24D.不能确定【解析】连接OP,如图所示:∵四边形ABCD是矩形,∴AC=BD,OA=OC=12AC,OB=OD=12BD,∠ABC=90°,S△AOD=14S矩形ABCD,∴OA=OD=12AC,∵AB=15,BC=20,∴AC 25,S △AOD =14S 矩形ABCD =14×15×20=75,∴OA =OD =252, ∴S △AOD =S △APO +S △DPO =12OA •PE +12OD •PF =12OA •(PE +PF )=12×252(PE +PF )=75, ∴PE +PF =12.∴点P 到矩形的两条对角线AC 和BD 的距离之和是12.故选B .7.(2018·常州市武进区星辰实验学校初二一模)如图,矩形ABCD 中,AB =4,BC =6,P 是CD 边上的中点,E 是BC 边上的一动点,M ,N 分别是AE 、PE 的中点,则随着点E 的运动,线段MN 长为( )A B .C .D .不确定【解析】连接AP ,∵矩形ABCD 中,AB =DC =4,P 是CD 边上的中点,∴DP =2,∴AP∵M ,N 分别是AE 、PE 的中点,∴MN 是△AEP 的中位线,∴MN =12AP .故选A . 8.(2019·沈阳市第八十五中学)如图,在矩形ABCD 中,AB =3,AD =4,点P 在AB 上,PE ⊥AC 于E ,PF ⊥BD 于F ,则PE +PF 等于( )A .75B .125C .135D .145【解析】解析:因为AB =3,AD =4,所以AC =5,1522AO AC == ,由图可知1122AOB S AO PE BO PF =⋅+⋅ ,AO =BO ,则()12AOB S AO PE PF =+ ,因此223122.55AOB S PE PF AO ⨯+=== ,故本题应选B . 9.(2020·张家界市民族中学期末)如图,在正方形ABCD 中,AB =9,点E 在CD 边上,且DE =2CE ,点P 是对角线AC 上的一个动点,则PE +PD 的最小值是( )A .B .C .9D .解:如图,连接BE ,设BE 与AC 交于点P ′,∵四边形ABCD 是正方形,∴点B 与D 关于AC 对称,∴P ′D =P ′B ,∴P ′D +P ′E =P ′B +P ′E =BE 最小.即P 在AC 与BE 的交点上时,PD +PE 最小,为BE 的长度.∵直角△CBE 中,∠BCE =90°,BC =9,CE =13CD =3,∴BE A .10.(2020·河北孟村期末)如图 ,正方形ABCD 的边长为4,M 在DC 上,且DM =1,N 是AC 上一动点,则DN +MN 的最小值为( ).A .3B .4C .5D .【解析】如图,连接BM ∵点B 和点D 关于直线AC 对称,NB =ND则BM 就是DN +MN 的最小值∵正方形ABCD 的边长是4,DM =1∴CM =CD -DM =4-1=3,在Rt △BCM 中,BM 5,故DN +MN 的最小值是5.故选C .11.(2019·山东罗庄期中)如图,正方形ABCD 的边长为8 ,E 为AB 上一点,若EF ⊥AC 于F ,EG ⊥BD 于G ,则EF +EG =( )A .4B .8C .82D .42【解析】解:如图,连接0E ,∵四边形ABCD 是正方形,边长为8,∴AC =BD =,∴OA =OB =,又∵S △ABO =S △AEO +S △EBO ,∴111222OA OB OA EF OB EG ⋅=⋅+⋅即11()22EF EG ⨯=⨯+∴EF +EG =故答案为:D 12.(2020·商丘综合实验中学初中部月考)如图,正方形ABCD 的面积为4,△ABE 是等边三角形,点E 在正方形ABCD 内,在对角线AC 上有一点P ,使PD +PE 的和最小,则这个最小值为( )A .√3B .2C .3D .2√3【解析】解:连接BD ,与AC 交于点F .∵点B 与D 关于AC 对称,∴PD =PB ,∴PD +PE =PB +PE =BE 最小.∵正方形ABCD 的面积为4,∴AB =2.又∵△ABE 是等边三角形,∴BE=AB=2.∴所求最小值为2.故选B.13.(2020·江苏海安期中)如图,E是边长为4的正方形ABCD的对角线BD上一点,且BE=BC,P为CE 上任意一点,PQ⊥BC于点Q,PR⊥BR于点R,则PQ+PR的值是()A.B.2C.D.8 3【解析】如图,连接BP,设点C到BE的距离为h,则S△BCE=S△BCP+S△BEP,即12BE⋅h=12BC⋅PQ+12BE⋅PR,∵BE=BC,∴h=PQ+PR,∵正方形ABCD的边长为4,∴h=4×2=.故答案为.二、填空题14.(2020·陕西陇县期末)如图,已知菱形ABCD的周长为16,面积为E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为______.【解析】解:如图作CE′⊥AB于E′,甲BD于P′,连接AC、AP′.首先证明E′与E重合,∵A、C关于BD对称,∴当P与P′重合时,P A′+P′E的值最小,∵菱形ABCD的周长为16,面积为AB=BC=4,AB·CE′=∴CE ′=,由此求出CE 的长=15.(2019·孟津县黄鹿山乡二中期中)如图,菱形ABCD 中,AB =4,∠B =60°,E ,F 分别是BC ,DC 上的点,∠EAF =60°,则△AEF 的面积最小值是___.【解析】试题解析:当AE ⊥BC 时,∵△ABC 是等边三角形,∴AB =AC ,∠ACB =60°,∴∠B =∠ACF =60°,∵AD ∥BC ,∴∠AEB =∠EAD =∠EAF +∠F AD =60°+∠F AD ,∠AFC =∠D +∠F AD =60°+∠F AD ,∴∠AEB =∠AFC ,在△ABE 和△ACF 中,{B ACFAEB AFC AB AC∠∠∠∠===,∴△ABE ≌△ACF (AAS ),∴AE =AF ,∵∠EAF =60°,∴△AEF 是等边三角形,∵当AE ⊥BC 时,AB =4,∴AE =∴△AEF 的面积最小值=1216.(2018·常州市武进区星辰实验学校)如图,在边长为4的菱形ABCD 中,∠A =60°,M 是AD 边的中点,点N 是AB 边上一动点,将△AMN 沿MN 所在的直线翻折得到△A ′MN ,连接A ′C ,则线段A ′C 长度的最小值是______.【解析】解:如图所示:∵MA ′是定值,A ′C 长度取最小值时,即A ′在MC 上时,过点M 作MF ⊥DC 于点F ,∵在边长为2的菱形ABCD 中,∠A =60°,M 为AD 中点,∴2MD =AD =CD =2,∠FDM =60°,∴∠FMD =30°,∴FD =12MD =1, ∴FM =DM ×cos 30°MC =A ′C =MC ﹣MA ′=2.故答案为2.17.(2020·全国课时练习)如图,菱形ABCD 中,AB =4,∠ABC =60°,点E 、F 、G 分别为线段BC ,CD ,BD 上的任意一点,则EG +FG 的最小值为________.解:作点E 关于BD 的对称点E ′,连接E ′F 与BD 的交点即为所求的点G ,如图,∵AB =4,∠ABC =60°, ∴点E ′到CD 的距离为4×2EG +FG的最小值为.故答案为: 18.(2019·辽宁昌图初三月考)如图,在边长为2的菱形ABCD 中, ∠ABC =120°, E ,F 分别为AD ,CD 上的动点,且AE +CF =2,则线段EF 长的最小值是__________.【解析】试题解析:∵四边形ABCD 是边长为2的菱形,120ABC ∠=, ∴,ABD CBD 都是边长为2的正三角形,2AE CF +=,2CF AE AD AE DE ∴=-=-=, 又2,60BD BC BDE C ==∠=∠=, 在BDE 和BCF 中,{DE DFBDE C BD BC =∠=∠=,()SAS BDE BCF ≌,∴ EBD FBC ∴∠=∠, EBD DBF FBC DBF ∴∠+∠=∠+∠,60EBF DBC ∴∠=∠=,又BE BF =, BEF ∴是正三角形,EF BE BF ∴==,当,BE AD ⊥即E 为AD 的中点时,BEEF BE =,∴EF . 19.(2020·木兰县吉兴乡吉兴中学期末)如图,在△ABC 中,AB =3,AC =4,BC =5,P 为边BC 上一动点,PE ⊥AB 于E ,PF ⊥AC 于F ,M 为EF 中点,则AM 的最小值为_____.【解析】∵在△ABC 中,AB =3,AC =4,BC =5,∴AB 2+AC 2=BC 2,即∠BAC =90°.又PE ⊥AB 于E ,PF ⊥AC 于F ,∴四边形AEPF 是矩形,∴EF =AP .∵M 是EF 的中点,∴AM =12EF =12AP . 因为AP 的最小值即为直角三角形ABC 斜边上的高,即2.4,∴AM 的最小值是1.2.20.(2020·河南洛宁期末)如图,正方形ABCD 的边长为4,E 是边BC 上的一点且BE =1,P 为对角线AC 上的一动点,连接PB ,PE ,当点P 在AC 上运动时,△PBE 周长的最小值是____.【解析】连接DE 于AC 交于点P ′,连接BP ′,则此时△BP ′E 的周长就是△PBE 周长的最小值, ∵BE =1,BC =CD =4,∴CE =3,DE =5,∴BP ′+P ′E =DE =5,∴△PBE 周长的最小值是5+1=6, 故答案为6.21.(2020·山东历下期中)如图,四边形ABCD中,∠A=90°,AB=,AD=3,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为.【解析】试题解析:∵ED=EM,MF=FN,∴EF=12DN,∴DN最大时,EF最大,∵N与B重合时DN最大,此时DN=DB6,∴EF的最大值为322.(2020·山东邹城初三其他)如图,已知正方形ABCD边长为3,点E在AB边上且BE=1,点P,Q分别是边BC,CD的动点(均不与顶点重合),当四边形AEPQ的周长取最小值时,四边形AEPQ的面积是_____.解:如图1所示,作E关于BC的对称点E′,点A关于DC的对称点A′,连接A′E′,四边形AEPQ 的周长最小,∵AD=A′D=3,BE=BE′=1,∴AA′=6,AE′=4.∵DQ∥AE′,D是AA′的中点,∴DQ是△AA′E′的中位线,∴DQ=12AE′=2;CQ=DC﹣CQ=3﹣2=1,∵BP∥AA′,∴△BE′P∽△AE′A′,∴'''BP BEAA AE=,即164BP=,BP=32,CP=BC﹣BP=332-=32,S四边形AEPQ=S正方形ABCD﹣S△ADQ﹣S△PCQ﹣S BEP=9﹣12AD•DQ﹣12CQ•CP﹣12BE•BP=9﹣12×3×2﹣12×1×3 2﹣12×1×32=92,故答案为92.三、解答题23.(2018·山东青岛经开区实验初级中学初三单元测试)如图,在边长为5的菱形ABCD中,对角线BD=8,点O是直线BD上的动点,OE⊥AB于E,OF⊥AD于F.如图,在边长为5的菱形ABCD中,对角线BD=8,点O是直线BD上的动点,OE⊥AB于E,OF⊥AD于F.(1)对角线AC的长是________,菱形ABCD的面积是________;(2)如图1,当点O在对角线BD上运动时,OE+OF的值是否发生变化?请说明理由;(3)如图2,当点O在对角线BD的延长线上时,OE+OF的值是否发生变化?若不变请说明理由,若变化,请直接写出OE、OF之间的数量关系,不用明理由.解:(1)如图,连接AC与BD相交于点G,在菱形ABCD中,AC⊥BD,BG=12BD=12×8=4,由勾股定理得,AG=3,∴AC=2AG=2×3=6,菱形ABCD的面积=12AC•BD=12×6×8=24;故答案为6;24;(2)如图1,连接AO,则S△ABD=S△ABO+S△ADO,∴12BD•AG=12AB•OE+12AD•OF,即12×8×3=12×5•OE+12×5•OF,解得OE+OF=4.8是定值,不变;(3)如图2,连接AO,则S△ABD=S△ABO-S△ADO,∴12BD•AG=12AB•OE-12AD•OF,即12×8×3=12×5•OE-12×5•OF,解得OE-OF=4.8,是定值,不变,∴OE+OF的值变化,OE、OF之间的数量关系为:OE-OF=4.8.24.(2019·广东期中)如图,在△ABC中,AC=9,AB=12,BC=15,P为BC边上一动点,PG⊥AC于点G,PH⊥AB于点H.(1)求证:四边形AGPH是矩形;(2)在点P的运动过程中,GH的长度是否存在最小值?若存在,请求出最小值,若不存在,请说明理由.【答案】(1)证明∵AC=9AB=12BC=15,∴AC2=81,AB2=144,BC2=225,∴AC2+AB2=BC2,∴∠A=90°.∵PG⊥AC,PH⊥AB,∴∠AGP=∠AHP=90°,∴四边形AGPH是矩形;(2)存在.理由如下:连结AP.∵四边形AGPH是矩形,∴GH=AP.∵当AP⊥BC时AP最短.∴9×12=15•AP.∴AP=365.【点睛】本题考查了矩形的判定与性质.解答(2)题时,注意“矩形的对角线相等”和“面积法”的正确应用.25.(2019·五华县河口中学初三月考)在矩形ABCD中,已知AD=4,AB=3,点P是直线AD上的一点,PE⊥AC,PF⊥BD,E,F分别是垂足,AG⊥BD与点G,(1) 如图①点P在线段AD上,求PE+PF的值; (2) 如图②点P在直线AD上,求PE-PF的值.【答案】解:(1)如图③,过点A作AG⊥BD于点G,连接PO,∵四边形ABCD是矩形,∴OA=OD,∠BAD=90°.在Rt△ABD中,AD=4,AB=3,由勾股定理得BD5==.∵AG⊥BD,∴S△ABD=12AB·AD=12BD·AG∴AB·AD=BD·AG∴3×4=5AG,解得AG=125.∵S△AOD=S△AOP+S△POD,∴12OD·AG=12OA·PE +12OD·PF.∵OA=OD,∴AG=PE+PF.∴PE+PF= AG=125;(2)如图④,过点A作AG⊥BD于点G,连接PO,∵S△AOD=S△AOP-S△POD,∴12OD·AG=12OA·PE-12OD·PF,∵OA=OD,∴AG=PE-PF,∴PE-PF= AG=125.。
特殊的平行四边形中动点及最值问题

特殊的平行四边形中动点及最值问题下载提示:该文档是本店铺精心编制而成的,希望大家下载后,能够帮助大家解决实际问题。
文档下载后可定制修改,请根据实际需要进行调整和使用,谢谢!本店铺为大家提供各种类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!特殊的平行四边形中动点及最值问题在数学领域,平行四边形是一种熟悉而常见的几何形状。
中考复习特殊平行四边形中最小值问题

中考复习:特殊平行四边形中最小值问题1.(2022秋•泰山区校级期末)如图,在菱形ABCD中,E,F分别是边CD,BC 上的动点,连接AE,EF,G,H分别为AE,EF的中点,连接GH.若∠B =45°,BC=2,则GH的最小值为()A.B.C.D.2.(2022秋•惠济区校级期末)如图,在Rt△ABC中,∠B=90°,BC=4,AC =5,点D在BC上,以AC为对角线的所有平行四边形ADCE中,DE的最小值是()A.3B.6C.8D.10 3.(2022秋•河西区校级期末)如图,在边长为1的正方形ABCD中,将射线AC绕点A按顺时针方向旋转α度(0<α≤360°),得到射线AE,点M是点D关于射线AE的对称点,则线段CM长度的最小值为()A.B.C.D.4.(2022秋•朝阳区校级期末)如图,在矩形ABCD中,AB=12,AD=10,点P在AD上,点Q在BC上,且AP=CQ,连结CP、QD,则PC+QD的最小值为()A.22B.24C.25D.26 5.(2021秋•保定期末)如图,已知正方形ABCD的边长为2,P是对角线BD 上一点,PE⊥BC于点E,PF⊥CD于点F,连接AP,EF.给出下列结论:①PD=EC;②四边形PECF的周长为4;③△APD一定是等腰三角形;④AP=EF;⑤EF的最小值为.其中正确结论的序号为()A.①②③④B.①②④⑤C.②④⑤D.①②④6.(2022秋•横县期中)如图,边长为6的等边三角形ABC中,E是对称轴AD 上的动点,连接EC,将线段EC绕点C逆时针旋转60°等到FC,连接DF,则在点E运动过程中,DF的最小值是()A.B.1.5C.2D.6 7.(2022秋•西山区校级期中)如图边长为5的正方形ABCD中,E为边AD上一点,且AE=2,F为边AB上一动点,将线段EF绕点F顺时针旋转90°得到线段FG,连接DG,则DG的最小值为()A.B.5C.D.8.(2022秋•启东市期中)如图,已知,在正方形ABCD中,AB=4,以点B为圆心,1为半径作⊙B,点P在⊙B上移动,连接AP.将AP绕点A逆时针旋转90°至AP',连接BP'.在点P移动过程中,BP'长度的最小值是()A.4﹣1B.4C.4D.3 9.(2022秋•常州期中)如图,在边长为2的正方形ABCD中,点M在AD边上自A至D运动,点N在BA边上自B至A运动,M,N速度相同,当N运动至A时,运动停止,连接CN,BM交于点P,则AP的最小值为()A.1B.2C.D.10.(2022春•江夏区校级月考)如图,点P是Rt△ABC中斜边AC(不与A,C 重合)上一动点,分别作PM⊥AB于点M,作PN⊥BC于点N,点O是MN 的中点,若AB=9,BC=12,当点P在AC上运动时,则BO的最小值是()A.3B.3.6C.3.75D.411.(2022春•韶关期末)如图,在边长为4的正方形ABCD中,点E、F分别是边BC、CD上的动点,且BE=CF,连接BF、DE,则BF+DE的最小值为()A.8B.4C.4D.4 12.(2022春•孝感期末)如图,菱形ABCD的两条对角线长AC=6,BD=8,点E是BC边上的动点,则AE长的最小值为()A.4B.C.5D.13.(2022春•潼南区期末)如图,正方形ABCD的对角线AC,BD相交于点O,点P是BC上任意一点,PE⊥BD于点E,PF⊥AC于点F,若AC=2,则EF的长的最小值为()A.2B.1C.D.14.(2022秋•惠阳区校级期末)如图,点E是等边三角形△ABC边AC的中点,点D是直线BC上一动点,连接ED,并绕点E逆时针旋转90°,得到线段EF,连接DF.若运动过程中AF的最小值为,则AB的值为()A.2B.C.D.4 15.(2022春•南京期末)如图,在正方形ABCD中,AB=4,E为AB边上一点,点F在BC边上,且BF=1,将点E绕着点F顺时针旋转90°得到点G,连接DG,则DG的长的最小值为()A.2B.2C.3D.16.(2023•五华县校级开学)如图,△ABC中,AB=AC=10,BC=12,D为AC边上一动点,E为平面内一点,以点B、C、D、E为顶点的四边形为平行四边形,则DE的最小值为.17.(2022秋•潜江期末)如图,在正方形ABCD中,AB=4,G是BC的中点,E是正方形内一个动点,且EG=2,连接DE,将线段DE绕点D逆时针旋转90°得到线段DF,连接CF,则线段CF长度的最小值为.18.(2022秋•南沙区校级期末)如图,在矩形ABCD中,AB=3,BC=3,点P在线段BC上运动(含B、C两点),连接AP,以点A为中心,将线段AP逆时针旋转60°到AQ,连接DQ,则线段DQ的最小值为.19.(2022秋•绿园区校级期末)如图,在Rt△ABC中,∠BAC=90°,且BA =5,AC=12,点D是斜边BC上的一个动点,过点D分别作DM⊥AB于点M,DN⊥AC于点N,连接MN,则线段MN的最小值为.20.(2022秋•大冶市期末)如图,D是等边三角形ABC外一点,连接AD,BD,CD,已知BD=8,CD=3,则当线段AD的长度最小时,①∠BDC=;②AD的最小值是.21.(2022秋•皇姑区校级期末)如图,边长为5的正方形ABCD中,点E、G 分别在射线AB、BC上,F在边AD上,ED与FG交于点M,AF=1,FG=DE,BG>AF,则MC的最小值为.22.(2022秋•任城区期末)如图,△ABC是等边三角形,且AB=4,点D在边BC上,连接AD,将线段AD绕点A顺时针旋转60°,得到线段AE,连接DE,BE.则△BED的周长最小值是.23.(2022秋•西安期末)如图,矩形ABCD中,AB=8,AD=4,E为AB的中点,F为EC上一动点,P为DF中点,连接PB,则PB的最小值是.24.(2022秋•镇平县期中)在Rt△ABC中,∠C=90°,AC=6,BC=8,点N 是BC边上一点,点M为AB边上的动点,点D、E分别为CN,MN的中点,则DE的最小值是.(培优特训)专项9.6 特殊平行四边形中最小值问题1.(2022秋•泰山区校级期末)如图,在菱形ABCD中,E,F分别是边CD,BC 上的动点,连接AE,EF,G,H分别为AE,EF的中点,连接GH.若∠B=45°,BC=2,则GH的最小值为()A.B.C.D.【答案】D【解答】解:连接AF,如图所示:∵四边形ABCD是菱形,∴,∵G,H分别为AE,EF的中点,∴GH是△AEF的中位线,∴,当AF⊥BC时,AF最小,GH得到最小值,则∠AFB=90°,∵∠B=45°,∴△ABF是等腰直角三角形,∴,∴,即GH的最小值为,故选:D.2.(2022秋•惠济区校级期末)如图,在Rt△ABC中,∠B=90°,BC=4,AC =5,点D在BC上,以AC为对角线的所有平行四边形ADCE中,DE的最小值是()A.3B.6C.8D.10【答案】A【解答】解:平行四边形ADCE的对角线的交点是AC的中点O,当OD⊥BC 时,OD最小,即DE最小.∵OD⊥BC,BC⊥AB,∴OD∥AB,∵∠B=90°,BC=4,AC=5,∴AB==3,又∵OC=OA,∴CD=DB,∴OD是△ABC的中位线,∴OD=AB=1.5,∴DE=2OD=3.故选:A.3.(2022秋•河西区校级期末)如图,在边长为1的正方形ABCD中,将射线AC绕点A按顺时针方向旋转α度(0<α≤360°),得到射线AE,点M是点D关于射线AE的对称点,则线段CM长度的最小值为()A.B.C.D.【答案】B【解答】解:如图所示:连接AM.∵四边形ABCD为正方形,∴AC===.∵点D与点M关于AE对称,∴AM=AD=1.∴点M在以A为圆心,以AD长为半径的圆上.如图所示,当点A、M、C在一条直线上时,CM有最小值.∴CM的最小值=AC﹣AM′=﹣1,故选:B.4.(2022秋•朝阳区校级期末)如图,在矩形ABCD中,AB=12,AD=10,点P在AD上,点Q在BC上,且AP=CQ,连结CP、QD,则PC+QD的最小值为()A.22B.24C.25D.26【答案】D【解答】解:如图,连接BP,在矩形ABCD中,AD∥BC,AD=BC=10,∵AP=CQ,∴AD﹣AP=BC﹣CQ,∴DP=QB,DP∥BQ,∴四边形DPBQ是平行四边形,∴PB∥DQ,PB=DQ,则PC+QD=PC+PB,则PC+QD的最小值转化为PC+PB的最小值,在BA的延长线上截取AE=AB=12,连接PE,则BE=2AB=24,∵P A⊥BE,∴P A是BE的垂直平分线,∴PB=PE,∴PC+PB=PC+PE,连接CE,则PC+QD=PC+PB=PC+PE≥CE,∴CE===26,∴PC+PB的最小值为26,即PC+QD的最小值为26,故选:D.5.(2021秋•保定期末)如图,已知正方形ABCD的边长为2,P是对角线BD 上一点,PE⊥BC于点E,PF⊥CD于点F,连接AP,EF.给出下列结论:①PD=EC;②四边形PECF的周长为4;③△APD一定是等腰三角形;④AP=EF;⑤EF的最小值为.其中正确结论的序号为()A.①②③④B.①②④⑤C.②④⑤D.①②④【答案】B【解答】解:①如图,∵四边形ABCD是正方形,∴∠DBC=45°,∠BCD=90°,∵PF⊥CD,∴∠PFD=90°,∴∠BCD=∠PFD,∴PF∥BC,∴∠DPF=∠DBC=45°,∴∠PDF=∠DPF=45°,∴PF=EC=DF,在Rt△DPF中,DP2=DF2+PF2=EC2+EC2=2EC2,∴DP=EC.故①正确;②∵PE⊥BC,PF⊥CD,∠BCD=90°,∴四边形PECF为矩形,∴四边形PECF的周长=2CE+2PE=2CE+2BE=2BC=4,故②正确;③∵点P是正方形ABCD的对角线BD上任意一点,∠ADP=45°,∴当∠P AD=45°或67.5°或90°时,△APD是等腰三角形,除此之外,△APD不是等腰三角形,故③错误;④连接PC,∵四边形PECF为矩形,∴PC=EF,由正方形为轴对称图形,∴AP=PC,∴AP=EF,故④正确;⑤由EF=PC=AP,∴当AP最小时,EF最小,则当AP⊥BD时,即AP=BD=×2=时,EF的最小值等于,故⑤正确;故选:B.6.(2022秋•横县期中)如图,边长为6的等边三角形ABC中,E是对称轴AD 上的动点,连接EC,将线段EC绕点C逆时针旋转60°等到FC,连接DF,则在点E运动过程中,DF的最小值是()A.B.1.5C.2D.6【答案】B【解答】解:取线段AC的中点G,连接EG,如图所示.∵△ABC为等边三角形,且AD为△ABC的对称轴,∴CD=CG=AB=3,∠ACD=60°,∵∠ECF=60°,∴∠FCD=∠ECG.在△FCD和△ECG中,,∴△FCD≌△ECG(SAS),∴DF=GE.当EG⊥AD时,EG最短,即DF最短.∵点G为AC的中点,∴此时EG=DF=CD=1.5.故选:B.7.(2022秋•西山区校级期中)如图边长为5的正方形ABCD中,E为边AD上一点,且AE=2,F为边AB上一动点,将线段EF绕点F顺时针旋转90°得到线段FG,连接DG,则DG的最小值为()A.B.5C.D.【答案】A【解答】解:过点G作GM⊥AB于M,作GN⊥AD于N,∵四边形ABCD是正方形,∴∠A=90°,∵GM⊥AB,GN⊥AD,∴∠FMG=∠DNG=90°,∴四边形AMGN是矩形,∴MG=AN,AM=NG,∠A=∠FMG,∵线段EF绕点F顺时针旋转90°得到线段FG,∴EF=FG,∠EFG=90°,∴∠EF A+∠GFM=90°,∵∠GFM+∠FGM=90°,∴∠EF A=∠FGM,在△AEF和△MFC中,,∴△AEF≌△MFG(AAS),∴AE=MF,AF=MG,∵AE=2,∴MF=2,设AF=x(0≤x≤5),则MG=x,AM=x+2,AN=MG=x,∴NG=x+2,∵AB=5,∴DN=5﹣x,∴DG===,∴当x=时,DG的最小值为,故选:A.8.(2022秋•启东市期中)如图,已知,在正方形ABCD中,AB=4,以点B为圆心,1为半径作⊙B,点P在⊙B上移动,连接AP.将AP绕点A逆时针旋转90°至AP',连接BP'.在点P移动过程中,BP'长度的最小值是()A.4﹣1B.4C.4D.3【答案】A【解答】解:如图,当P′在对角线BD上时,BP′最小,连接BP,由旋转得:AP=AP′,∠P AP′=90°,∴∠P AB+∠BAP′=90°,∵四边形ABCD为正方形,∴AB=AD,∠BAD=90°,∴∠BAP′+∠DAP′=90°,∴∠P AB=∠DAP′,∴△P AB≌△P′AD(SAS),∴P′D=PB=1,在Rt△ABD中,∵AB=AD=4,由勾股定理得:BD==4,∴BP′=BD﹣P′D=4﹣1,即BP′长度的最小值为(4﹣1).故选:A.9.(2022秋•常州期中)如图,在边长为2的正方形ABCD中,点M在AD边上自A至D运动,点N在BA边上自B至A运动,M,N速度相同,当N运动至A时,运动停止,连接CN,BM交于点P,则AP的最小值为()A.1B.2C.D.【答案】C【解答】解:∵四边形ABCD是正方形,∴AB=BC=CD=DA,∠A=∠ABC=90°,∴∠BCN+∠BNC=90°,又BN=AM,∴△ABM≌△BCN(SAS),∴∠ABM=∠BCN,∴∠ABM+∠BNC=90°,∴∠BPC=∠BPN=90°,∴点P的运动轨迹为以BC为直径的一段弧,如图所示,连接AO1交弧于点P,此时,AP的值最小,在Rt△ABO1中,,由勾股定理得,,∴,故选:C.10.(2022春•江夏区校级月考)如图,点P是Rt△ABC中斜边AC(不与A,C 重合)上一动点,分别作PM⊥AB于点M,作PN⊥BC于点N,点O是MN 的中点,若AB=9,BC=12,当点P在AC上运动时,则BO的最小值是()A.3B.3.6C.3.75D.4【答案】B【解答】解:连接BP,如图所示:∵∠ABC=90°,PM⊥AB于点M,PN⊥BC于点N,∴四边形BMPN是矩形,AC===15,∴BP=MN,BP与MN互相平分,∵点O是MN的中点,∴BO=MN,当BP⊥AC时,BP最小===7.2,∴MN=7.2,∴BO=MN=3.6,故选:B.11.(2022春•韶关期末)如图,在边长为4的正方形ABCD中,点E、F分别是边BC、CD上的动点,且BE=CF,连接BF、DE,则BF+DE的最小值为()A.8B.4C.4D.4【答案】D【解答】解:连接AE,如图1,∵四边形ABCD是正方形,∴AB=BC,∠ABE=∠BCF=90°.又BE=CF,∴△ABE≌△BCF(SAS).∴AE=BF.所以BF+DE最小值等于AE+DE最小值.作点A关于BC的对称点H点,如图2,连接BH,则A、B、H三点共线,连接DH,DH与BC的交点即为所求的E点.根据对称性可知AE=HE,所以AE+DE=DH.在Rt△ADH中,DH===4,∴BF+DE最小值为4.故选:D.12.(2022春•孝感期末)如图,菱形ABCD的两条对角线长AC=6,BD=8,点E是BC边上的动点,则AE长的最小值为()A.4B.C.5D.【答案】B【解答】解:∵点E是BC边上的一动点,∴AE⊥BC时,AE有最小值,∵四边形ABCD是菱形,∴AC⊥BD,AO=CO=AC=3,BO=DO=BD=4,∴BC===5,=×AC×BD=BC×AE,∵S菱形ABCD∴AE=,故AE长的最小值为,故选:B.13.(2022春•潼南区期末)如图,正方形ABCD的对角线AC,BD相交于点O,点P是BC上任意一点,PE⊥BD于点E,PF⊥AC于点F,若AC=2,则EF的长的最小值为()A.2B.1C.D.【答案】B【解答】解:如图,连接OP、EF,∵正方形ABCD的对角线AC,BD相交于点O,点P是BC上任意一点,PE⊥BD于点E,PF⊥AC于点F,∴四边形OEPF为矩形,∴EF=OP,∴EF最小时OP最小,当OP⊥BC于P的时候OP最小,而当OP⊥BC时,P为BC的中点,∴OP=BC,∵AC=2,则BC=2,∴OP=1,∴EF的长的最小值为1.故选:B.14.(2022秋•惠阳区校级期末)如图,点E是等边三角形△ABC边AC的中点,点D是直线BC上一动点,连接ED,并绕点E逆时针旋转90°,得到线段EF,连接DF.若运动过程中AF的最小值为,则AB的值为()A.2B.C.D.4【答案】D【解答】解:如图,连接BE,延长AC至N,使EN=BE,连接FN,∵△ABC是等边三角形,E是AC的中点,∴AE=EC,∠ABE=∠CBE=30°,BE⊥AC,∴∠BEN=∠DEF=90°,BE=AE,∴∠BED=∠CEF,在△BDE和△NFE中,,∴△BDE≌△NFE(SAS),∴∠N=∠CBE=30°,∴点N在与AN成30°的直线上运动,∴当AF'⊥F'N时,AF'有最小值,∴AF'=AN,∴+1=(AE+AE),∴AE=2,∴AC=4,故选:D.15.(2022春•南京期末)如图,在正方形ABCD中,AB=4,E为AB边上一点,点F在BC边上,且BF=1,将点E绕着点F顺时针旋转90°得到点G,连接DG,则DG的长的最小值为()A.2B.2C.3D.【答案】C【解答】解:过点G作GH⊥BC,垂足为H,∴∠GHF=90°,∵四边形ABCD是正方形,∴AB=CD=4,∠B=90°,∴∠B=∠GHF=90°,由旋转得:EF=FG,∠EFG=90°,∴∠EFB+∠GFH=90°,∵∠BEF+∠BFE=90°,∴∠BEF=∠GFH,∴△EBF≌△FHG(AAS),∴BF=GH=1,∴点G在与BC平行且与BC的距离为1的直线上,∴当点G在CD边上时,DG最小且DG=4﹣1=3,∴DG的最小值为3,故选:C.16.(2023•五华县校级开学)如图,△ABC中,AB=AC=10,BC=12,D为AC边上一动点,E为平面内一点,以点B、C、D、E为顶点的四边形为平行四边形,则DE的最小值为.【答案】9.6【解答】解:当DE是平行四边形BDCE的对角线,且DE⊥AC时,DE的长最小,BC和DE交于M,作BH⊥AC于H,连接AM,在平行四边形BDCE中,MB=CM,BE∥AC,∴MB=BC=6,∴AM===8,∵△ABC的面积=AC•BH=BC•AM,∴10BH=12×8,∴BH=9.6,∵四边形BEDH是矩形,∴DE=BH=9.6.∴DE长的最小值是9.6.故答案为:9.6.17.(2022秋•潜江期末)如图,在正方形ABCD中,AB=4,G是BC的中点,E是正方形内一个动点,且EG=2,连接DE,将线段DE绕点D逆时针旋转90°得到线段DF,连接CF,则线段CF长度的最小值为.【答案】【解答】解:连接DG,将DG绕点D逆时针旋转90°得DM,连接MG,CM,MF,作MH⊥CD于H,如图,∵∠EDF=∠EDG+∠GDF=90°,∠GDM=∠GDF+∠FDM=90°,∴∠EDG=∠FDM,在△EDG和△FDM中,,∴△EDG≌△FDM(SAS),∴MF=EG=2,∵MH⊥CD,∴∠HDM+∠DMH=90°,∵∠GDC+∠HDM=90°,∴∠GDC=∠DMH,在△DGC和△MDH中,,∴△DGC≌DMH(AAS),∴CG=DH=2,MH=CD=4,∴,∵CF≥CM﹣MF,∴CF的最小值为:,故答案为:.18.(2022秋•南沙区校级期末)如图,在矩形ABCD中,AB=3,BC=3,点P在线段BC上运动(含B、C两点),连接AP,以点A为中心,将线段AP逆时针旋转60°到AQ,连接DQ,则线段DQ的最小值为.【答案】【解答】解:如图,以AB为边向右作等边△ABF,作射线FQ交AD于点E,过点D作DH⊥QE于H.∵四边形ABCD是矩形,∴∠ABP=∠BAD=90°,∵△ABF,△APQ都是等边三角形,∴∠BAF=∠P AQ=60°,BA=F A,P A=QA,∴∠BAP=∠F AQ,在△BAP和△F AQ中,,∴△BAP≌△F AQ(SAS),∴∠ABP=∠AFQ=90°,∵∠F AE=90°﹣60°=30°,∴∠AEF=90°﹣30°=60°,又∵AB=AF=3,∴AF=EF,AE=2EF,∴EF=,AE=2,∴点Q在射线FE上运动,∵AD=BC=3,∴DE=AD﹣AE=,∵DH⊥EF,∠DEH=∠AEF=60°,∴EH=DE=,DH=EH=,根据垂线段最短可知,当点Q与H重合时,DQ的值最小,最小值为,故答案为:.19.(2022秋•绿园区校级期末)如图,在Rt△ABC中,∠BAC=90°,且BA =5,AC=12,点D是斜边BC上的一个动点,过点D分别作DM⊥AB于点M,DN⊥AC于点N,连接MN,则线段MN的最小值为.【答案】【解答】解:连接AD,∵∠BAC=90°,且BA=5,AC=12,∴,∵DM⊥AB,DN⊥AC,∴∠DMA=∠DNA=∠BAC=90°,∴四边形DMAN是矩形,∴MN=AD,∴当AD⊥BC时,AD的值最小,此时,△ABC的面积=,∴,∴MN的最小值为;故答案为:.20.(2022秋•大冶市期末)如图,D是等边三角形ABC外一点,连接AD,BD,CD,已知BD=8,CD=3,则当线段AD的长度最小时,①∠BDC=;②AD的最小值是.【答案】①60°;②5.【解答】解:如图所示,以BD为边向外作等边三角形BDE,连接CE,∵△BDE,△ABC均为等边三角形,∴BE=BD,AB=BC,∠ABC=∠DBE=60°,∴∠ABD=∠CBE,在△ABD和△CBE中,,∴△ABD≌△CBE(SAS),∴CE=AD,∵BE=BD=DE=8,CD=3,∴当C,D,E三点共线时,CE有最小值,∴CE=DE﹣CD=8﹣3=5,∴AD的最小值为5,此时∠BDC=60°.故答案为:①60°;②5.21.(2022秋•皇姑区校级期末)如图,边长为5的正方形ABCD中,点E、G分别在射线AB、BC上,F在边AD上,ED与FG交于点M,AF=1,FG=DE,BG>AF,则MC的最小值为.【答案】﹣2【解答】解:取FD的中点H,作FK垂直BC于点K,∵DE=FG,AD=FK,∠A=∠FKG=90°,∴△AED≌△KFG(HL),∴∠ADE=∠KFG,又∵∠FGK=∠DFM,∠KFG+∠FGK=90°,∴∠DFM+∠ADE=90°,∴∠FMD=90°,∴MH==2,所以M在以H为圆心,2为半径的圆弧上运动,∵MC≥CH﹣MH当M落在CH上时,取到等号即MC达到最小,最小值为CH﹣M′H=﹣2.22.(2022秋•任城区期末)如图,△ABC是等边三角形,且AB=4,点D在边BC上,连接AD,将线段AD绕点A顺时针旋转60°,得到线段AE,连接DE,BE.则△BED的周长最小值是.【答案】4+2【解答】解:∵△ABC是等边三角形,∴AB=AC,∠BAC=60°,∵∠DAE=60°,∴∠BAC=∠DAE,∴∠BAC﹣∠BAD=∠DAE﹣∠BAD,∴∠BAE=∠CAD,又∵AD=AE,∴△ABE≌△ACD(SAS),∴CD=BE,∴△BED的周长=BE+BD+ED=CD+BD+ED=BC+DE,∵将线段AD绕点A顺时针旋转60°,∴AD=AE,∠DAE=60°,∴△ADE是等边三角形,∴DE=AD,当AD⊥BC时,DE最小,即△BED的周长有最小值,∵AD⊥BC,BC=4,∴BD=CD=2,∴AD==2,∴△BED的周长最小值是BC+DE=4+2,故答案为:4+2.23.(2022秋•西安期末)如图,矩形ABCD中,AB=8,AD=4,E为AB的中点,F为EC上一动点,P为DF中点,连接PB,则PB的最小值是.【答案】4【解答】解:如图,取CD中点H,连接AH,BH,∵四边形ABCD是矩形,∴AB=CD=8,AD=BC=4,CD∥AB,∵点E是AB中点,点H是CD中点,∴CH=AE=DH=BE=4,∴四边形AECH是平行四边形,∴AH∥CE,∵点P是DF的中点,点H是CD的中点,∴PH∥EC,∴点P在AH上,∴当BP⊥AH时,此时点P与H重合,BP有最小值,∵AD=DH=CH=BC=4,∴∠DHA=∠DAH=∠CBH=∠CHB=45°,AH=BH=4,∴∠AHB=90°,∴BP的最小值为4,故答案为4.24.(2022秋•镇平县期中)在Rt△ABC中,∠C=90°,AC=6,BC=8,点N 是BC边上一点,点M为AB边上的动点,点D、E分别为CN,MN的中点,则DE的最小值是.【答案】【解答】解:连接CM,∵点D、E分别为CN,MN的中点,∴DE=CM,当CM⊥AB时,CM的值最小,此时DE的值也最小,由勾股定理得:AB===10,==,∵S△ABC∴CM=,∴DE==,故答案为:.。
【初中数学】特殊平行四边形中的最值问题+课件+北师大版数学九年级上册

⊥ OB ,∴∠ AOB =90°.∴∠ BON +∠ AON =90°.∴∠ AOM =
∠=∠,
∠ BON . 在△ AOM 和△ BON 中, =,
∠=∠,
∴△ AOM ≌△ BON (ASA).
∴ BE = BG ,∠ ABE =∠ CBG .
∴∠ EBG =∠ EBC +∠ CBG =∠ EBC +
∠ ABE =90°.
∵∠ EBF =45°,
∴∠ GBF =∠ EBF =45°.
答图
返回目录
数学 九年级上册 BS版
易证得△ EBF ≌△ GBF SAS .
∵ BH ⊥ EF , BC ⊥ CD ,
∴ PD + PE 的最小值为2 10 .
【点拨】两定一动,动点在直线上的最值问题就是“将军饮
马”最值问题,常常利用轴对称来解决问题.
返回目录
数学 九年级上册 BS版
1. 如图,正方形 ABCD 的边长为2,点 E 是 BC 的中点,点 P 是
AC 边上的一个动点,连接 BP , EP ,则 BP + EP 的最小值
解:如图,连接 BD 交 AC 于点 O ,连接 PB .
1
∵ 菱形 = AC ·BD ,
2
1
∴24= ×12·BD .
2
∴ BD =4.
返回目录
数学 九年级上册 BS版
∵四边形 ABCD 是菱形,
1
1
∴ OA = AC =6, OB = BD =2, AC ⊥ BD .
2
2
∴ AB = 62 +22 =2 10 .
∴ BH = BC =4.
12特殊平行四边形的最值问题(1)

12特殊平行四边形的最值问题(1) 特殊平行四边形的最值问题知识回顾:1.两点之间的线段最短。
2.点到直线的距离最短是垂线段。
3.三角形两边之和大于第三边,两边之差小于第三边。
题讲练:类型一:根据两点之间线段最短求最值1.在菱形ABCD中,AB=4,∠ABC=120°,点E是边AB的中点,P是对角线AC上的一个动点。
求PB+PE的最小值。
2.在正方形ABCD中,AB=BC=CD=DA=4,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小。
求这个最小值。
3.在矩形ABCD中,AB=4,AD=3,矩形内部有一动点P满足S△PAB=6.求点P到A,B两点的距离之和PA+PB的最小值。
类型二:根据垂线段最短求最值4.在△ABC中,AC=5,BC=12,AB=13,点E是BC边上一点,ED⊥XXX于D,DF⊥AC于点F。
求线段EF的最小值。
5.在边长为4的菱形ABCD中,BD=4,E、F分别是AD、CD上的动点(包含端点),且AE+CF=4,连接BE、EF、FB。
1)试探究BE与BF的数量关系,并证明你的结论;2)求EF的最小值。
类型三:根据三角形三边关系求最值6.在矩形ABCD中,AB=3,BC=4,P是AB上动点,PQ平行于BC交CD于Q,M是AD上动点,MN平行于XXX于N。
求PM+NQ的最小值。
7.在矩形ABCD中,AB=9,BC=6,∠MON=90°,矩形的顶点C、D分别在边ON、OM上滑动。
在滑动过程中,点A到点O的最大距离为9.求矩形的面积。
8.在正方形ABCD中,边长为4,E、F分别是边AD、DC上两个动点,满足AE=DF,连接AF,BE,它们相交于点H,连接DH。
求线段DH长度的最小值。
巩固练:1.在菱形ABCD中,AC=2,P是对角线AC上的一个动点,M、N分别是AB、BC边上的中点。
求MP+PN的最小值。
2.在菱形ABCD中,AB=2,∠A=120°,点P、Q、K分别为线段BC、CD、BD上的任意一点。
平行四边形最值问题及解决方法

平行四边形最值问题及解决方法一、边长相关的最值问题。
题目1:在平行四边形ABCD中,AB = 5,AD = 3,对角线AC和BD相交于点O,点E 是边AD上的动点,求OE的最大值。
解析:因为平行四边形的对角线互相平分,所以AO=(1)/(2)AC。
在AOD中,OE是AOD的中线,根据三角形中线的性质,OE<(1)/(2)AD。
当E点与D点重合时,OE取得最大值,此时OE=(1)/(2)AD=(3)/(2)。
题目2:已知平行四边形ABCD中,AD = 6,∠ DAB=60^∘,E是AB上的动点,连接DE,求DE的最小值。
解析:过D作DF⊥ AB于F。
在Rt ADF中,∠ DAB = 60^∘,AD=6,则DF =AD×sin60^∘=6×(√(3))/(2)=3√(3)。
因为垂线段最短,所以当E点与F点重合时,DE取得最小值3√(3)。
题目3:平行四边形ABCD中,AB = 8,BC=10,P是平行四边形ABCD内一点,求PA + PC的最小值。
解析:利用平行四边形的对称性,连接AC、BD相交于点O,PA + PC≥slant AC。
根据平行四边形的性质,AC=√(AB^2)+BC^{2- 2AB× BC×cos∠ ABC}。
因为平行四边形ABCD,AB = 8,BC = 10,设∠ ABC=θAC=√(64 + 100-2×8×10×cosθ)根据平行四边形对角线互相平分,PA+PC的最小值就是AC的长。
由平行四边形性质可知cos∠ ABC=cos∠ BAD在ABC中,AC=√(8^2)+10^{2-2×8×10×cos∠ ABC}=√(64 + 100-160×cos∠ ABC)当cos∠ ABC = 1时(∠ ABC = 0^∘,这种极限情况方便计算最小值)AC=√(64+100 - 160)=2实际上,根据平行四边形性质计算AC=√(8^2)+10^{2-2×8×10×cos∠ ABC}=√(164-160cos∠ ABC),AC的最小值为2二、面积相关的最值问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
培优专题(四) 特殊平行四边形的最值问题
【例】如图,正方形ABCD的边长为10 cm,E是AB上一点,BE=4 cm,P是对角线AC上一动点,求PB +PE的最小值.
1.如图,在周长为12的菱形ABCD中,AE=1,AF=2,若P为对角线BD上一动点,求EP+FP的最小值
2.如图,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE最小,求这个最小值
3.如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,M为斜边AB上一动点,过点M作MD⊥AC于点D,
过点M作ME⊥CB于点E,求线段DE的最小值.
4.如图,已知正方形ABCD的边长为3,点E在AB边上,且BE=1,点P,Q分别是边BC,CD上的动点(均
不与顶点重合),求四边形AEPQ的周长的最小值为.
5.如图,在平行四边形ABCD中,AB=2,AD=1,∠ADC=60°,将平行四边形ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,折痕交CD边于点E.
(1)求证:四边形BCED′是菱形;
(2)若点P是直线l上的一个动点,请计算PD′+PB的最小值.。
