高中数学 第一章 三角函数 2 弧度制练习 北师大版必修4
高一数学训练习题参考答案

数学必修(4)同步练习参考答案§1.1任意角和弧度制一、CDDCBA二、7.{x|x=k•3600+1800, k∈Z}, {x|x=k•1800+450,k∈Z} ; 8.-345°; 9. ;10.第二或第四象限, 第一或第二象限或终边在y轴的正半轴上三、11.{ α|α=k•3600+1200或α=k•3600+3000, k∈Z } -60° 120°12.由7θ=θ+k•360°,得θ=k•60°(k∈Z)∴θ=60°,120°,180°,240°,300°13.∵l=20-2r,∴S= lr= (20-2r)•r=-r2+10r=-(r-5)2+25∴当半径r=5 cm时,扇形的面积最大为25 cm2,此时,α= = =2(rad)14.A点2分钟转过2θ,且π<2θ<π,14分钟后回到原位,∴14θ=2kπ,θ= ,且 <θ< π,∴θ= π或π§1.2.1 任意角的三角函数一、CCDBCD二、7.一、三; 8. 0 ; 9. 或π; 10.二、四三、11.[2kπ, 2kπ,+ ( k∈Z)12.13.∵sinθ= - ,∴角θ终边与单位圆的交点(cosθ,sinθ)=( ,- )又∵P(-2, y)是角θ终边上一点, ∴cosθ<0,∴cosθ= - .14.略.§1.2.2同角三角函数的基本关系式一、BCDBBA二、7. ; 8.0; 9. ; 10.三、11.12.原式= - ==sinx+cosx13.左边=tan2θ-sin2θ= -sin2θ=sin2θ• =sin2θ• =sin2θ•tan2θ=右边14.(1)当m=0时, α=kπ, k∈Z ,cosα=±1, tanα=0(2)当|m|=1时, α=kπ+ , k∈Z ,cosα=0, tanα=0不存在(3)当0<|m|<1时,若α在第一或第四象限,则cosα= tanα= ;若α在第二或第三象限,则cosα=- tanα=- .§1.3 三角函数的诱导公式一、BBCCBC二、7. ; 8.1 ; 9.1 ; 10.三、11. 112. f(θ)= = =cosθ-1∴f( )=cos -1=-13.∵cos(α+β)=1, ∴α+β=2kπ, k∈Z. ∴cos(2α+β)= cos(α+α+β)= cos(π+α)=- cosα= - .14. 由已知条件得:sinα= sinβ①, cos α=- cosβ②,两式推出sinα= ,因为α∈(- , ),所以α= 或- ;回代②,注意到β∈(0,π),均解出β= ,于是存在α= ,β= 或α=- ,β= ,使两等式同时成立。
高中数学必修4全套学案含答案
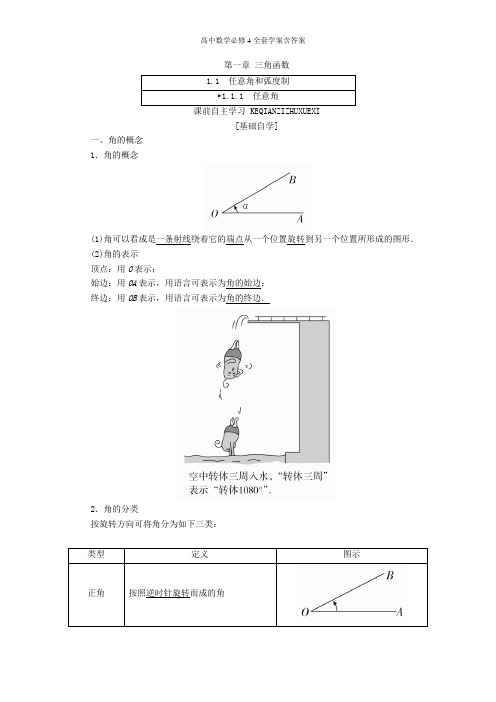
第一章三角函数1.1 任意角和弧度制►1.1.1 任意角课前自主学习 KEQIANZIZHUXUEXI[基础自学]一、角的概念1.角的概念(1)角可以看成是一条射线绕着它的端点从一个位置旋转到另一个位置所形成的图形.(2)角的表示顶点:用O表示;始边:用OA表示,用语言可表示为角的始边;终边:用OB表示,用语言可表示为角的终边.2.角的分类按旋转方向可将角分为如下三类:类型定义图示正角按照逆时针旋转而成的角负角按照顺时针旋转而成的角零角当射线没有旋转时,我们也把它看成一个角,叫做零角1.象限角:若角的顶点在原点,角的始边与x轴非负半轴重合,则角的终边在第几象限,就称这个角是第几象限角.2.轴线角:若角的终边在坐标轴上,则这个角不属于任何象限.三、终边相同的角设α表示任意角,所有与角α终边相同的角,包括α本身构成一个集合,这个集合可记为{β|β=α+k·360°,k∈Z}.[自我小测]1.判断(正确的打“√”,错误的打“×”)(1)研究终边相同的角的前提条件是角的顶点在坐标原点.( )(2)锐角是第一象限的角,但第一象限的角不一定是锐角.( )(3)象限角与终边落在坐标轴上的角表示形式是唯一的.( )提示:(1)×(2)√(3)×2.做一做(1)下列各组角中,终边不相同的是( )A.60°与-300° B.230°与950°C.1050°与-300° D.-1000°与80°答案 C(2)将-885°化为α+k·360°(0°≤α<360°,k∈Z)的形式是________.答案195°+(-3)×360°课堂合作探究 KETANGHEZUOTANJIU1终边相同的角之间有什么关系?提示:与α终边相同的角,可表示为β=k·360°+α(k∈Z),即两角相差360°的整数倍.2如何表示终边在坐标轴上的角和象限角?提示:终边在x轴非负半轴上的角:α=k·360°(k∈Z);终边在y轴上的角:α=90°+k·180°(k∈Z);第二象限角:90°+k·360°<α<180°+k·360°(k∈Z).题型一正确理解角的概念例1 下列结论:①锐角都是第一象限角;②第一象限角一定不是负角;③第二象限角是钝角;④小于180°的角是钝角、直角或锐角.其中正确的序号为________(把正确结论的序号都写上).[解析] ①锐角是大于0°且小于90°的角,终边落在第一象限,故是第一象限角,所以①正确;②-330°角是第一象限角,但它是负角,所以②不正确;③480°角是第二象限角,但它不是钝角,所以③不正确;④0°角小于180°,但它既不是钝角,也不是直角或锐角,故④不正确.[答案] ①角的概念的理解正确解答角的概念问题,关键在于正确理解象限角与锐角、直角、钝角、平角、周角等概念,另外需要掌握判断结论正确与否的技巧,判断结论正确需要证明,而判断结论不正确只需举一个反例即可.【跟踪训练1】(1)经过2个小时,钟表上的时针旋转了( )A.60° B.-60°C.30° D.-30°(2)如图∠α=__________,∠β=__________. 答案 (1)B (2)-150° 210°解析 (1)钟表的时针旋转一周是-360°,其中每小时旋转-360°12=-30°,所以经过2个小时应旋转-60°.题型二 终边相同的角的表示及象限角 例2 已知α=-1910°.(1)把α写成β+k ·360°(k ∈Z,0°≤β<360°)的形式,指出它是第几象限的角; (2)求θ,使θ与α的终边相同,且-720°<θ≤0°. [解] (1)∵-1910°÷360°=-6余250°, ∴-1910°=-6×360°+250°.相应β=250°,从而α=-6×360°+250°是第三象限的角. (2)令θ=250°+k ·360°(k ∈Z ),取k =-1,-2就得到适合-720°<θ≤0°的角: 250°-360°=-110°,250°-720°=-470°. ∴θ=-110°或θ=-470°.[变式探究] 与-1560°角终边相同的角的集合中,最小正角是________,最大负角是________.答案 240° -120°解析 与-1560°角终边相同的角的集合为{α|α=k ·360°+240°,k ∈Z },所以最小正角为240°,最大负角为-120°.怎样表示终边相同的角及象限角(1)已知终边所处的位置,写角的集合时,可先写出0°~360°范围内的角,然后再加k ·360°(k ∈Z )组成集合即可.(2)象限角的判定有两种方法:一是根据图形判定,在直角坐标系中作出角,角的终边落在第几象限,此角就是第几象限角.二是根据终边相同的角的概念.把角转化到0°~360°范围内,转化后的角在第几象限,此角就是第几象限角.【跟踪训练2】 在0°到360°范围内,找出与下列各角终边相同的角,并判定它们是第几象限的角.(1)-120°;(2)640°;(3)-950°12′.解(1)-120°=-360°+240°,∴在0°到360°范围内,与-120°终边相同的角是240°角,它是第三象限的角.(2)640°=360°+280°,∴在0°到360°范围内与640°终边相同的角是280°角,它是第四象限的角.(3)-950°12′=-3×360°+129°48′,∴在0°到360°范围内与-950°12′终边相同的角是129°48′,它是第二象限的角.题型三区域角的表示例3 写出终边落在阴影部分的角的集合.[解] 设终边落在阴影部分的角为α,角α的集合由两部分组成.①{α|k·360°+30°≤α<k·360°+105°,k∈Z}.②{α|k·360°+210°≤α<k·360°+285°,k∈Z}.∴角α的集合应当是集合①与②的并集:{α|k·360°+30°≤α<k·360°+105°,k∈Z}∪{α|k·360°+210°≤α<k·360°+285°,k∈Z}={α|2k·180°+30°≤α<2k·180°+105°,k∈Z}∪{α|(2k+1)180°+30°≤α<(2k+1)180°+105°,k∈Z}={α|2k·180°+30°≤α<2k·180°+105°或(2k+1)·180°+30°≤α<(2k+1)180°+105°,k∈Z}={α|k·180°+30°≤α<k·180°+105°,k∈Z}.[变式探究] 将例3改为下图,写出角的终边在图中阴影区域的角的集合(包括边界).解(1){α|45°+k·180°≤α≤90°+k·180°,k∈Z}.(2){α|-150°+k·360°≤α≤150°+k·360°,k∈Z}.表示区间角的三个步骤(1)先按逆时针方向找到区域的起始和终止边界.(2)由小到大分别标出起始、终止边界对应的一个角α,β,写出所有与α,β终边相同的角.(3)用不等式表示区域内的角,组成集合.【跟踪训练3】写出终边在如下图所示阴影部分内的角α的取值范围.解(1)与45°角终边相同的角的集合为{α|α=45°+k·360°,k∈Z},与30°-180°=-150°角终边相同的角的集合为{α|α=-150°+k·360°,k∈Z},因此终边在阴影部分内的角α的取值范围为{α|-150°+k·360°<α≤45°+k·360°,k∈Z}.(2)方法同(1),可得终边在阴影部分内的角α的取值范围为{α|45°+k·360°≤α≤300°+k·360°,k∈Z}.[规律小结]1.角的概念的理解(1)弄清角的始边与终边.(2)结合图形明确这个角从始边到终边转过了多少度.(3)注意逆时针旋转与顺时针旋转的区别.2.研究象限角时应注意的问题(1)前提条件:角的顶点与原点重合,角的始边与x轴的非负半轴重合;(2)并不是任何角都是象限角,如终边落在坐标轴上的角叫轴线角,轴线角的表示如下表:终边所在的位置角的集合x轴非负半轴{α|α=k·360°,k∈Z}x轴非正半轴{α|α=k·360°+180°,k∈Z}y轴非负半轴{α|α=k·360°+90°,k∈Z}y轴非正半轴{α|α=k·360°+270°,k∈Z}3.表示与α终边相同的角时应注意的问题(1)k是整数,这个条件不能漏掉;(2)α是任意角;(3)k ·360°与α之间是“+”号,如k ·360°-30°应看成k ·360°+(-30°)(k ∈Z );(4)终边相同的角不一定相等,但相等的角终边一定相同. [走出误区]易错点⊳分角所在象限及范围的确定的误区 [典例] 若α是第三象限的角,则α3是( )A.第一象限的角B.第三象限的角C.第四象限的角D.第一象限或第三象限或第四象限的角[错解档案] 因为α是第三象限的角,所以取α=210°,得到α3=70°,是第一象限的角,故选A.[误区警示] 第三象限的角α有无数个,用α=210°得到α3=70°而选择答案A ,犯了以偏概全的错误.[规范解答] 因为α是第三象限的角,所以k ·360°+180°<α<k ·360°+270°(k ∈Z ),则k ·120°+60°<α3<k ·120°+90°(k ∈Z ),取k =0,得到α3可在第一象限;取k =1,得到α3可在第三象限;取k =2,得到α3可在第四象限.故选D.矫正训练 若α为第二象限的角,则α2为第几象限角?解 若α为第二象限角,则有随堂消化吸收 SUITANGXIAOHUAXISHOU1.[2016·吉林实验高一期中]下列叙述正确的是( ) A .三角形的内角是第一象限角或第二象限角 B .钝角是第二象限角 C .第二象限角比第一象限角大 D .不相等的角终边一定不同 答案 B解析 三角形的内角是第一象限角、第二象限角或在y 轴非负半轴上的角,故A 错误;钝角是第二象限角,B 正确;象限角不能比较大小,故C 错误;不相等的角终边也可能相同,如40°和400°,故D 错误.2.[2016·山东枣庄模拟]若α是第四象限角,则180°+α是( ) A .第一象限角 B .第二象限角 C .第三象限角 D .第四象限角答案 B解析 因为α与180°+α的终边关于点(0,0)对称,所以角180°+α的终边在第二象限.3.如果将钟表拨快10分钟,则时针所转成的角度是________度,分针所转成的角度是________度.答案 -5 -60解析 将钟表拨快10分钟,则时针按顺时针方向转了10×360°12×60=5°,所转成的角度是-5°;分针按顺时针方向转了10×360°60=60°,所转成的角度是-60°.4.若α为锐角,则-α+k ·360°(k ∈Z )在第________象限. 答案 四解析 由于0°<α<90°,所以-90°<-α<0°,所以-α是第四象限角,从而-α+k ·360°(k ∈Z )在第四象限.5.[2016·大连高一检测]写出与下列各角终边相同的角的集合S ,并把S 中适合不等式-360°≤α≤720°的元素α写出来:(1)60°;(2)-21°.解 第一步:利用终边相同的角的集合公式写出: (1)S ={α|α=60°+k ·360°,k ∈Z }; (2)S ={α|α=-21°+k ·360°,k ∈Z }.第二步:在第一步的基础上,利用约束条件对其中的k 值分别采用赋值法求出元素α; (1)-300°,60°,420°;(2)-21°,339°,699°.课后课时精练 KEHOUKESHIJINGLIAN 时间:25分钟满分:60分一、选择题(每小题5分,共25分)1.已知α=-130°,则α的终边落在( )A.第一象限B.第二象限C.第三象限D.第四象限答案 C解析∵-130°=-360°+230°,而230°是第三象限角,∴α的终边落在第三象限.2.已知角α的终边落在直线y=x上,则角α的集合S=( )A.{α|α=k·360°+45°,k∈Z}B.{α|α=k·90°+45°,k∈Z}C.{α|α=k·360°+225°,k∈Z}D.{α|α=k·180°+45°,k∈Z}答案 D解析本题考查终边在特殊直线上的角以及分类讨论的数学思想.由于角α的终边落在直线y=x上,故角α在0°~360°内所对应的两个角分别为45°及225°,从而角α的集合S={α|α=k·360°+45°或α=k·360°+225°,k∈Z}={α|α=k·180°+45°,k∈Z},故选D.3.若α是钝角,则θ=k·180°+α,k∈Z是( )A.第二象限角B.第三象限角C.第二象限角或第三象限角D.第二象限角或第四象限角答案 D解析当k为偶数时,θ=k·180°+α,k∈Z是第二象限角,当k为奇数时,θ=k·180°+α,k∈Z是第四象限角.4.已知角α、β的终边互为反向延长线,则α-β的终边在( )A.x轴的非负半轴上B.y轴的非负半轴上C.x轴的非正半轴上D.y轴的非正半轴上答案 C解析由题意知β+180°应与α终边相同,即α=β+180°+k·360°(k∈Z),∴α-β=180°+k·360°.故选C.5.已知角2α的终边在x轴上方,那么α是( )A.第一象限角B.第一或第二象限角C.第一或第三象限角D.第一或第四象限角答案 C解析由条件知k·360°<2α<k·360°+180°,(k∈Z),∴k·180°<α<k·180°+90°(k∈Z),当k为偶数时,α在第一象限,当k为奇数时,α在第三象限.二、填空题(每小题5分,共15分)6.[2016·广东佛山一中期中]终边在x轴上的角β的集合是________.答案{β|β=180°·k,k∈Z}解析 本题考查终边相同的角的概念.终边在x 轴正半轴上的角的集合为{β|β=360°·k ,k ∈Z },终边在x 轴负半轴上的角的集合为{β|β=180°·(2k +1),k ∈Z },所以终边在x 轴上的角β的集合为{β|β=180°·k ,k ∈Z }.7.时钟的时针走过了1小时20分钟,则分针转过的角为________. 答案 -480°解析 时针走过了1小时20分钟,则分针转了43圈,又因顺时针旋转的角为负角,∴分针转过的角为-43×360°=-480°.8.若集合M ={x |x =k ·90°+45°,k ∈Z },N ={x |x =k ·45°+90°,k ∈Z },则M ________N .(填“”“”)答案解析 M ={x |x =k ·90°+45°,k ∈Z } ={x |x =45°·(2k +1),k ∈Z },N ={x |x =k ·45°+90°,k ∈Z }={x |x =45°·(k +2),k ∈Z },∵k ∈Z ,∴k +2∈Z ,且2k +1为奇数,∴M N . 三、解答题(每小题10分,共20分)9.如图所示,试写出终边落在阴影区域内的角的集合S (包括边界),并指出-950°12′是否是该集合中的角.解 由题图可知,终边落在阴影区域内的角的集合S ={β|120°+k ·360°≤β≤250°+k ·360°,k ∈Z }.∵-950°12′=-3×360°+129°48′,且120°<129°48′<250°,∴-950°12′是该集合中的角. 10.已知α为第二象限角,问2α,α2分别是第几象限角?解 ∵α是第二象限角,∴90°+k ·360°<α<180°+k ·360°,k ∈Z , ∴180°+2k ·360°<2α<360°+2k ·360°,k ∈Z .∴2α是第三或第四象限角,或是终边落在y 轴的非正半轴上的角.同理45°+k2·360°<α2<90°+k2·360°. 当k 为偶数时,不妨令k =2n ,n ∈Z ,则45°+n ·360°<α2<90°+n ·360°,此时,α2为第一象限角;当k 为奇数时,令k =2n +1,n ∈Z ,则225°+n ·360°<α2<270°+n ·360°,此时,α2为第三象限角.∴α2为第一或第三象限角. ►1.1.2 弧度制课前自主学习 KEQIANZIZHUXUEXI[基础自学]一、弧度的概念设扇形的半径为r ,弧长为l ,α为其圆心角,则度量单位类别α为角度制 α为弧度制 扇形的弧长 l =πr ·⎪⎪⎪⎪⎪⎪α180l =r |α| 扇形的面积S =πr 2⎪⎪⎪⎪⎪⎪α360S =12r 2|α|=12rl1.判断(正确的打“√”,错误的打“×”)(1)“度”与“弧度”是相同的,都是用来度量角的单位.( )(2)终边落在x 轴非正半轴上的角可表示为α=k ·360°+π(k ∈Z ).( ) (3)1 rad 的角和1°的角大小一样.( )(4)用圆心角所对的弧长与半径的比来度量圆心角是合理的.( ) 提示:(1)× (2)× (3)× (4)√2.做一做(1)半径为2,圆心角为π3的扇形的面积是( )A.4π3 B .π C.2π3D.π3答案 C解析 由扇形面积公式S =12r 2·|α|可得S =12×4×π3=2π3,故选C. (2)角度与弧度互化: ①7π6=________;②-75°=________. 答案 ①210° ②-5π12课堂合作探究 KETANGHEZUOTANJIU1角度制与弧度制如何换算?提示:360°=2π rad,180°=π rad,1°=π180rad ,1 rad =⎝⎛⎭⎪⎫180π°≈57.30°.2扇形的弧长与面积的计算公式是什么? 提示:l =|α|·r ,S =12l ·r =12|α|·r 2.题型一 弧度制的概念例1 下列命题中,假命题是( )A .“度”与“弧度”是度量角的两种不同的度量单位B .一度的角是周角的1360,一弧度的角是周角的12πC .1弧度是长度等于半径长的弧所对的圆心角,它是角的一种度量单位.D .不论是用角度制还是用弧度制度量角,它们均与圆的半径长短有关[解析] 根据角度和弧度的定义,可知无论是角度制还是弧度制,角的大小与圆的半径长短无关,而是与弧长与半径的比值有关,所以D 是假命题.选项A 、B 、C 均为真命题.[答案] D“度”与“弧度”的区别和联系(1)弧度制是以“弧度”为单位来度量角的单位制,角度制是以“度”为单位来度量角的单位制.(2)1弧度是长度等于半径长的弧所对的圆心角(或这条弧)的大小,而1°的角是周角的1360. (3)无论是以“弧度”还是以“度”为单位,角的大小都是一个与半径大小无关的值.【跟踪训练1】 下列命题中,真命题是( ) A .一弧度是一度的圆心角所对的弧B .一弧度是长度为半径的弧C .一弧度是一度的弧与一度的角之和D .一弧度是长度等于半径长的弧所对的圆心角的大小,它是角的一种度量单位 答案 D解析 根据一弧度的定义:我们把长度等于半径长的弧所对的圆心角叫做一弧度的角.对照各选项,可知D 为真命题.故选D.题型二 弧度和角度的换算 例2 将下列角度与弧度进行互化. (1)20°;(2)-15°;(3)7π12;(4)-115π.[解] (1)20°=20×π180=π9.(2)-15°=-15×π180=-π12.(3)712π=712π×⎝ ⎛⎭⎪⎫180π°=105°.(4)-115π=-115π×⎝ ⎛⎭⎪⎫180π°=-396°.角度制与弧度制互化的注意事项(1)用“弧度”为单位度量角时,“弧度”二字或“rad”可以省略不写.(2)用“弧度”为单位度量角时,常常把弧度数写成多少π的形式,如无特别要求,不必把π写成小数.(3)度化弧度时,应先将分、秒化成度,再化成弧度.【跟踪训练2】 (1)-450°化成弧度是________. (2)75π化成角度是________. 答案 (1)-52π (2)252°解析 (1)-450°=-450×π180=-52π.(2)75π=75π×⎝ ⎛⎭⎪⎫180π°=252°.题型三 用弧度表示角例3 (1)把下列角化为2k π+α(0≤α<2π,k ∈Z )的形式:①16π3;②-315°. (2)用弧度表示顶点在原点,终边落在阴影部分内的角的集合(不包括边界,如图所示). [解] (1)①16π3=4π+4π3.∵0≤4π3<2π,∴16π3=4π+4π3.②-315°=-315×π180=-7π4=-2π+π4.∵0≤π4<2π,∴-315°=-2π+π4.(2)330°=360°-30°=2π-π6,而60°=π3,它所表示的区域位于-π6与π3之间且跨越x 轴的正半轴.所以⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫θ⎪⎪⎪2k π-π6<θ<2k π+π3,k ∈Z.弧度制表示角的注意事项(1)用弧度表示区域角,实质是角度表示区域角在弧度制下的应用,必要时,需进行角度与弧度的换算.注意单位要统一.可以先写(-π,π)或(0,2π)内的角,再加上2k π,k ∈Z .(2)终边在同一直线上的角可以合并为{x |x =α+k π,k ∈Z };终边在相互垂直的两直线上的角可以合并为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x =α+k ·π2,k ∈Z.【跟踪训练3】 (1)把-1480°写成α+2k π(k ∈Z )的形式,其中0≤α<2π; (2)若β∈[-4π,0],且β与(1)中α终边相同,求β. 解 (1)∵-1480°=-1480π180=-74π9=-10π+16π9,又0≤16π9<2π,∴-1480°=16π9-2×5π=16π9+2×(-5)π.(2)由(1)可知α=16π9.∵β与α终边相同,∴β=2k π+16π9,k ∈Z .又∵β∈[-4π,0],令k =-1,则β=-2π9.令k =-2, 则β=-20π9,∴β的值是-2π9,-20π9.题型四 扇形的弧长与面积 例4 扇形AOB 的周长为8 cm.(1)若这个扇形的面积为3 cm 2,求圆心角的大小; (2)求该扇形的面积取得最大值时圆心角的大小和弦长AB . [解] 设这个扇形的半径为R ,弧长为l ,圆心角为α(α>0). (1)由已知,得⎩⎪⎨⎪⎧2R +l =8,12lR =3,解得⎩⎪⎨⎪⎧R =3,l =2.或⎩⎪⎨⎪⎧R =1,l =6.由|α|=l R 可得:α=23或α=6.(2)扇形的面积 S =12lR =12(8-2R )R =-(R -2)2+4(0<R <4),所以,当且仅当R =2时,S 取得最大值4. 这时,l =8-2R =4,可求出:α=lR=2. 又∵0<2<π,∴|AB |=2R ·sin α2=4sin1.[变式探究] 将例4中扇形周长改为6 cm ,面积改为2 cm 2,求圆心角的大小. 解 设扇形的半径为R ,弧长为l ,圆心角为α(α>0),则有⎩⎪⎨⎪⎧2R +l =612lR =2解得⎩⎪⎨⎪⎧R =1l =4或⎩⎪⎨⎪⎧R =2l =2,由|α|=lR得α=4或α=1.扇形周长及面积的最值(1)当扇形周长一定时,扇形的面积有最大值.其求法是把面积S 转化为关于r 的二次函数,但要注意r 的取值范围.特别注意一个扇形的弧长必须满足0<l <2πr .(2)当扇形面积一定时,扇形的周长有最小值.其求法是把扇形周长L 转化为关于r 的函数,但要注意r 的取值范围.【跟踪训练4】 已知扇形AOB 的圆心角为120°,半径长为6,求: (1) AB ︵的长; (2)弓形AOB 的面积.解 (1)∵120°=120180π=23π,∴l =6×23π=4π,∴AB ︵的长为4π.(2)∵S 扇形OAB =12lr =12×4π×6=12π,如图所示.又S △OAB =12×AB ×OD (D 为AB 中点)=12×2×6cos30°×6×sin30°=9 3. ∴S 弓形OAB =S 扇形OAB -S △OAB =12π-9 3.[规律小结]1.弧度制与角度制的区别与联系 (1)区别①单位不同.弧度制以“弧度”为度量单位,角度制以“度”为度量单位; ②定义不同. (2)联系不管以“弧度”还是以“度”为单位的角的大小都是一个与圆的半径大小无关的定值. 2.角度制与弧度制换算时应注意的问题(1)弧度制与角度制的互化是一种比例关系的变形,具体变化时,可牢记以下公式:π180=弧度角度,只要将已知数值填入相应的位置,解出未知的数值,再添上相应的单位即可; (2)如无特别要求,不必把π写成小数;(3)度化为弧度时,应先将分、秒化为度,再化为弧度; (4)同一个式子中角度和弧度不能混用. [走出误区]易错点⊳角度制与弧度制的应用误区[典例] 将-1485°化成2k π+α(0≤α<2π,k ∈Z )的形式为________. [错解档案] 因为-1485°=-4×360°-45°=-4×360°+(-360°+315°)=-5×360°+315°, 所以-1485°化为2k π+α形式应为-10π+315°.[误区警示] 只考虑了将-1485°写成了“2k π”的组合形式,而忽视了对α的要求,忽视了角度和弧度的统一,这是初学者极易犯的一个错误.[规范解答] 由-1485°=-5×360°+315°, 所以-1485°可以表示为-10π+74π.矫正训练 将17π4化成k ·360°+α(0°≤α<360°,k ∈Z )的形式为________.答案 2·360°+45° 解析 17π4=765°=720°+45°=2×360°+45°, 故17π4=2·360°+45°.随堂消化吸收 SUITANGXIAOHUAXISHOU1.1920°转化为弧度数为( ) A.163 B.323 C.16π3D.32π3答案 D解析 ∵1°=π180弧度,∴1920°=1920×π180=323π.2.若α=-3,则角α的终边在( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限答案 C解析 ∵-3≈-171.9°,∴α=-3表示的角的终边在第三象限.3.[2016·南昌市高一月考]已知扇形的半径为R ,面积为R 2,那么这个扇形中心角的弧度数是________.答案 2解析 由l =|α|·R 及S =12lR ,得S =12|α|R 2.∴|α|=2S R 2=2R2R2=2.4.用弧度制表示终边落在第二象限的角的集合为________.答案 ⎩⎨⎧α⎪⎪⎪⎭⎬⎫2k π+π2<α<2k π+π,k ∈Z解析 若角α的终边落在第二象限,则 2k π+π2<α<2k π+π,k ∈Z .5.将下列各角转化成2k π+α(k ∈Z ),且0≤α<2π的形式,并指出它们是第几象限角:(1)-1725°;(2)64π3.解 (1)∵-1725°=-5×360°+75°=-10π+5π12,∴-1725°角与角5π12的终边相同.又∵5π12是第一象限角,∴-1725°是第一象限角. (2)∵64π3=20π+4π3,∴角64π3与角4π3的终边相同.又∵4π3是第三象限角,∴64π3是第三象限角. ,课后课时精练 KEHOUKESHIJINGLIAN时间:25分钟满分:60分一、选择题(每小题5分,共25分) 1.-300°化为弧度是( ) A .-4π3B .-5π3C .-7π4D .-7π6答案 B解析 ∵1°=π180 rad ,∴-300°=-5π3 rad.2.8π5弧度化为角度是( ) A .278° B .280° C .288° D .318°答案 C 解析 ∵1 rad =⎝⎛⎭⎪⎫180π°,∴8π5=8π5×⎝ ⎛⎭⎪⎫180π°=288°.3.[2016·清华附中月考]若角α,β的终边关于y 轴对称,则α,β的关系一定是( ) A .α+β=π B .α-β=π2C .α-β=(2k +1)π(k ∈Z )D .α+β=(2k +1)π(k ∈Z ) 答案 D解析 本题考查关于y 轴对称的两个角之间的关系.角α,β的终边关于y 轴对称,则画图可知α+β=(2k +1)π(k ∈Z ),D 选项正确;也可以用特殊值方法,例如取α=π4,β=3π4或α=-π4,β=-3π4,结合选项可知D 正确.故选D. 4.[2016·兰州一中高一期末]已知扇形的圆心角的弧度数为2,扇形的弧长为4,则扇形的面积为( )A .2B .4C .8D .16答案 B解析 由S =12lR 及|α|=l R ,得S =12l 2|α|=12·422=4.5.[2016·浙江永嘉高一月考]集合⎩⎪⎨⎪⎧α⎪⎪⎪ k π+π4≤α≤k π+π2,} k ∈Z 中的角所表示的范围(阴影部分)是()答案 C解析 当k =2m ,m ∈Z 时,2m π+π4≤α≤2m π+π2,m ∈Z ;当k =2m +1,m ∈Z 时,2m π+5π4≤α≤2m π+3π2,m ∈Z ,所以选C.二、填空题(每小题5分,共15分) 6.角度制与弧度制间的互化:(1)1095°=__________rad ;(2)-94π=__________.答案 (1)7312π (2)-405°解析 (1)1095°=1095×π180=73π12.(2)-94π=-94π×⎝ ⎛⎭⎪⎫180π°=-405°. 7.若圆的半径为6 cm ,则15°的圆心角所对的弧长为________,扇形面积为________.(用π表示)答案π2 cm 32π cm 2解析 15°=15×π180=π12,l =|α|·r =π12×6=π2cm , S =12l ·r =12×π2×6=32π cm 2.8.圆的半径变为原来的3倍,而所对弧长不变,则该弧所对圆心角是原来圆弧所对圆心角的________.答案 13解析 本题考查弧长公式的应用.设原来圆的半径为r ,弧长为l ,圆心角为α,则l =αr ,设将圆的半径变为原来的3倍后圆心角为α1,则α1=l 3r =αr 3r =α3,故α1α=13.三、解答题(每小题10分,共20分) 9.已知α=-800°.(1)把α改写成β+2k π(k ∈Z,0≤β<2π)的形式,并指出α是第几象限角; (2)求角γ,使γ与角α的终边相同,且γ∈⎝⎛⎭⎪⎫-π2,π2. 解 (1)∵-800°=-3×360°+280°,280°=149π,∴α=-800°=149π+(-3)×2π.∵角α与14π9终边相同,∴角α是第四象限角.(2)∵与角α终边相同的角可写为2k π+14π9,k ∈Z 的形式,而γ与α终边相同,∴γ=2k π+14π9,k ∈Z .又γ∈⎝ ⎛⎭⎪⎫-π2,π2,∴-π2<2k π+14π9<π2,k ∈Z , 解得k =-1,∴γ=-2π+14π9=-4π9.10.已知扇形的周长为20 cm ,当它的半径和圆心角各取什么值时,才能使扇形的面积最大?最大面积是多少?解 设扇形的圆心角为α,半径为R cm ,面积为S cm 2,弧长为l cm ,则有l +2R =20,∴l =20-2R ,∴S =12lR =12(20-2R )R =-R 2+10R =-(R -5)2+25.故当半径R =5时,扇形的面积有最大值25 cm 2.此时扇形的圆心角为α=l R =20-2×55=2.[基础自学]一、三角函数的定义 1.单位圆中三角函数的定义设α是一个任意角,它的终边与单位圆交于点P (x ,y ),那么: ①y 叫做α的正弦,记作sin α,即sin α=y ; ②x 叫做α的余弦,记作cos α,即cos α=x ; ③yx 叫做α的正切,记作tan α,即tan α=y x(x ≠0). 2.任意角的三角函数的定义直角坐标系中任意大小的角α终边上一点P 的坐标(x ,y ),它到原点的距离是r (r >0),r =x 2+y 2,那么任意角的三角函数的定义:tanαyxtanα=yx⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫α⎪⎪⎪α≠kπ+π2,k∈Z记忆口诀:“一全正、二正弦、三正切、四余弦”.三、诱导公式(一)名称符号语言文字语言诱导公式(一)sin(2kπ+α)=sinα(k∈Z)cos(2kπ+α)=cosα(k∈Z)tan(2kπ+α)=tanα(k∈Z)终边相同的角的同名三角函数值相等1.判一判(正确的打“√”,错误的打“×”)(1)sinα,cosα,tanα中可以将“α”与“sin”“cos”“tan”分开.( )(2)同一个三角函数值能找到无数个角与之对应.( )(3)sin253π=sin⎝⎛⎭⎪⎫π3+8π=sinπ3=32.( )提示:(1)×(2)√(3)√2.做一做(1)若sinα<0,且tanα<0,则角α是( )A.第一象限角B.第二象限角C.第三象限角D.第四象限角答案 D解析若sinα<0,则α为第三或第四象限角.若tanα<0,则α为第二或第四象限角,故α为第四象限角,选D.(2)计算:sin180°+2cos270°的值为________.答案0解析sin180°+2cos270°=0+2×0=0.(3)tan390°的值为________.答案33解析tan390°=tan(360°+30°)=tan30°=33.课堂合作探究 KETANGHEZUOTANJIU1三角函数值在各象限的符号有什么规律吗?提示:由三角函数的定义知sin α=y r ,cos α=x r ,tan α=y x(r >0),可知角的三角函数值的符号是由角终边上任一点P (x ,y )的坐标确定的,可简记为:一全正,二正弦,三正切,四余弦.2诱导公式一的作用是什么?提示:公式一的作用:把求任意角的三角函数值转化为求0~2π(或0°~360°)角的三角函数值.题型一 求任意角的三角函数值例1 [2015·黑龙江五校联考]已知角θ的终边上有一点P (-3,m ),且sin θ=24m ,求cos θ与tan θ 的值.[解] 由已知有24m =m3+m2, 得m =0,或m =± 5.(1)当m =0时,cos θ=-1,tan θ=0; (2)当m =5时,cos θ=-64,tan θ=-153; (3)当m =-5时,cos θ=-64,tan θ=153. [变式探究] 将例1中的P 点坐标改为(3,m )再去求解. 解 ∵24m =mm 2+3,∴m =0或m =±5, 当m =0时,cos θ=1,tan θ=0; 当m =5时,cos θ=64,tan θ=153; 当m =-5时,cos θ=64,tan θ=-153.利用三角函数的定义求值的策略(1)求一个角的三角函数值,需确定三个量:角的终边上异于原点的点的横、纵坐标及其到原点的距离.(2)若终边在直线上时,因为角的终边是射线,应分两种情况处理.(3)若已知角,则需确定出角的终边与单位圆的交点坐标.【跟踪训练1】 已知角θ的顶点与原点重合,始边与x 轴的非负半轴重合,终边在直线y =2x 上,则2cos 2θ-1=( )A .-45B .-35C.35D.45答案 B解析 设P (t,2t )(t ≠0)为角θ终边上任意一点,则 cos θ=t5|t |. 当t >0时,cos θ=55;当t <0时,cos θ=-55. ∴2cos 2θ-1=25-1=-35.题型二 三角函数值的符号例2 (1)α是第四象限角,判断sin α·tan α的符号; (2)若sin α|sin α|+|cos α|cos α=0,试判断α所在象限.[解] (1)∵α是第四象限角,∴sin α<0,tan α<0,∴sin α·tan α>0. (2)由条件知,sin α与cos α异号. ∴α是第二象限角或第四象限角.[变式探究] 将例2(1)中α改为第三象限角,则sin α·tan α的符号如何? 解 ∵α是第三象限角,∴sin α<0,tan α>0,∴sin α·tan α<0.熟记各象限函数值的符号准确确定三角函数中角所在象限是基础,准确记忆三角函数在各象限的符号并牢记记忆口诀“一全正,二正弦,三正切,四余弦”是解决这类问题的关键.【跟踪训练2】 (1)若sin α=-2cos α,判断sin α·tan α的符号;(2)判断符号:sin3·cos4·tan ⎝ ⎛⎭⎪⎫-23π4.解 (1)∵sin α=-2cos α,∴sin α与cos α异号. ∴α是第二或第四象限角.当α是第二象限角时,tan α<0,sin α>0,∴sin α·tan α<0. 当α是第四象限角时,tan α<0,sin α<0,∴sin α·tan α>0.(2)∵π2<3<π,π<4<3π2,∴sin3>0,cos4<0.∵-23π4=-6π+π4,∴tan ⎝⎛⎭⎪⎫-23π4>0. ∴sin3·cos4·tan ⎝ ⎛⎭⎪⎫-234π<0.题型三 诱导公式(一)的应用 例3 计算下列各式的值:(1)sin(-1395°)cos1110°+cos(-1020°)sin750°;(2)sin ⎝⎛⎭⎪⎫-11π6+cos 12π5·tan4π. [解] (1)原式=sin(-4×360°+45°)cos(3×360°+30°)+cos(-3×360°+60°)sin(2×360°+30°)=sin45°cos30°+cos60°sin30°=22×32+12×12=64+14=1+64. (2)原式=sin ⎝ ⎛⎭⎪⎫-2π+π6+cos ⎝⎛⎭⎪⎫2π+2π5·tan(4π+0)=sin π6+cos 2π5×0=12.利用诱导公式化简(1)将已知角化为k ·360°+α(k 为整数,0°≤α<360°)或2k π+β(k 为整数,0≤β<2π)的形式.(2)将原三角函数值化为角α的同名三角函数值.(3)借助特殊角的三角函数值或任意角三角函数的定义达到化简求值的目的.【跟踪训练3】 求值: (1)cos 25π3+tan ⎝ ⎛⎭⎪⎫-154π; (2)sin810°+ta n765°+tan1125°+cos360°. 解 (1)原式=cos(8π+π3)+tan ⎝ ⎛⎭⎪⎫-4π+π4=cos π3+tan π4=12+1=32.(2)原式=sin(2×360°+90°)+tan(2×360°+45°)+tan(3×360°+45°)+cos(360°+0°)=sin90°+tan45°+tan45°+cos0°=1+1+1+1=4.[规律小结]1.对三角函数定义的理解(1)三角函数也是一种函数,它满足函数的定义,可以看成是从一个角的集合(弧度制)到一个比值的集合的对应,并且对任意一个角,在比值集合中都有唯一确定的象与之对应.三角函数的自变量是角α,比值是角α的函数.(2)三角函数是用比值来定义的,所以三角函数的定义域是使比值有意义的角的范围.如在求正切时,若点P 的横坐标x 等于0,则tan α无意义.(3)三角函数值是比值,是一个实数,这个实数的大小和点P (x ,y )在终边上的位置无关,只由角α的终边位置确定.即三角函数值的大小只与角有关.2.三角函数值在各象限内的符号(1)三角函数值的符号是根据三角函数的定义,由各象限内点的坐标的符号得出的. (2)对正弦、余弦、正切函数值的符号可用下列口诀记忆:“一全正,二正弦,三正切,四余弦”,该口诀表示:第一象限全是正值,第二象限正弦是正值,第三象限正切是正值,第四象限余弦是正值.3.诱导公式一的理解及其应用(1)公式一的实质是说终边相同的角的三角函数值相等.(2)公式一的结构特征:①左、右为同一三角函数;②公式左边的角为α+k ·2π,右边的角为α.(3)公式一的作用:把求任意角的三角函数值转化为求0~2π(或0°~360°)范围内角的三角函数值.[走出误区]易错点⊳求三角函数定义域的误区[典例] 求满足y =sin x ·tan x 的x 的取值范围. [错解档案] 由题意知,只需要sin x ·tan x ≥0.即⎩⎪⎨⎪⎧sin x ≥0tan x ≥0①或⎩⎪⎨⎪⎧sin x ≤0tan x ≤0②对①可知x 为第一象限角或终边在x 轴或y 轴上的角. 对②可知x 为第四象限角或终边在x 轴或y 轴上的角. 因此x的取值范围为⎩⎪⎨⎪⎧x ⎪⎪⎪ 2k π-π2≤x <2k π或2k π<x ≤2k π+π2或x =⎭⎬⎫k π2,k ∈Z .[误区警示] 求y =sin x ·tan x 的x 取值范围时没有考虑tan x 的条件,致使思考问题不周全而出错.[规范解答] 所求x 应满足⎩⎪⎨⎪⎧sin x ·tan x ≥0,x ≠k π+π2k ∈Z ,即⎩⎪⎨⎪⎧sin x ≥0,tan x ≥0,x ≠k π+π2k ∈Z ,或⎩⎪⎨⎪⎧sin x ≤0,tan x ≤0,x ≠k π+π2k ∈Z .根据x 所在象限情况可判断x 的取值范围是⎩⎨⎧⎭⎬⎫x 2k π-π2<x <2k π或2k π<x <2k π+π2或x =k π,k ∈Z .矫正训练 求y =cos xsin x的x 的取值范围. 解 ∵cos x ≥0∴x 为第一、四象限角或x 轴非负半轴上的角或y 轴上 又∵sin x ≠0 ∴x 不能在x 轴上∴x 为第一或第四象限角或y 轴上.x 的取值范围是⎩⎪⎨⎪⎧x ⎪⎪⎪ -π2+2k π≤x <2k π或2k π<x ≤2k π+⎭⎬⎫π2,k ∈Z。
北师大版高中数学必修4第一章第3节《弧度制》题型专题练(学生版)

《弧度制》题型一:角度与弧度互化1.225︒化为弧度是2.512π= 3.300︒-化成弧度制为 4.320-︒化为弧度是5.1500︒转化为弧度数为6.712π= 7.12π弧度制等于8.150-︒的弧度数是9.45π化成角度制的结果为 10.下列转化结果错误的是( ) A .60°化成弧度是3π B .103π-化成角度是600︒- C .150︒-化成弧度是76π- D .12π化成角度是15° 11.24︒=_________弧度;49π弧度=________.12.72°化为弧度制为__________.13.210︒-弧度数为________.14.弧度数为2的角的终边落在第______象限.15.将下列角度与弧度进行互化.(1)20°;(2)-15°;(3)712π(4)-115π.16.把下列各角的弧度数化为度数,度数化为弧度数.(1)712π;(2)136π- ; (3)1125° ;(4)-225°.17.把下列角度化成弧度:(1)36︒;(2)150︒-;(3)1095︒;(4)1440︒.18.把下列各弧度化为角度.(1)12π;(2)53π;(3)310π;(4)8π;(5)32π-;(6)56π-.题型二:用弧度制表示终边相同的角1.把-765°化成2k π+α(0≤α<2π),k ∈Z )的形式是2.把-1215°化成2k π+α(k ∈Z,)的形式是3.把02130-化为()2,02k k Z απαπ+∈≤≤的形式是___________.4.将1500︒-化成2π(02π,)k k αα+<∈Z 的形式是_________.5.已知角2025α=︒.(1)将角α改写成2k βπ+(k Z ∈,02βπ≤<)形式,并指出角α是第几象限角; (2)在区间[)5,0π-上找出与角α终边相同的角.6.已知角920α=-︒.(1)把角α写成2k πβ+(02,k Z βπ≤<∈)的形式,并确定角α所在的象限; (2)若角γ与α的终边相同,且(4,3)γππ∈--,求角γ.7.(1)把1480︒写成2()a k k π+∈Z 的形式,其中02απ≤<;(2)[4,0)βπ∈-,且β与(1)中α的终边相同,求β.题型三:扇形的弧长和面积公式1.半径为3,圆心角为150︒的扇形的弧长为2.已知扇形圆心角为6π,面积为3π,则扇形的弧长等于3.已知扇形的面积为,扇形圆心角的弧度数是,则扇形的周长为4.已知某扇形的面积为22.5cm ,若该扇形的半径r ,弧长l 满足27cm r l +=,则该扇形圆心角大小的弧度数是5.已知扇形的圆心角为23π,半径为5,则扇形的面积为______.6.已知扇形的圆心角为6π,面积为3π,则扇形的弧长等于__________.7.已知扇形的周长等于它所在圆的周长的一半,则这个扇形的圆心角是__________.8.半径为2的圆中,弧长为4的弧所对的圆心角是______弧度.9.已知扇形的周长为3cm ,扇形的圆心角的弧度数是1rad ,则半径是10.某扇形的面积为21cm ,它的周长为4cm ,那么该扇形圆心角的大小为11.已知扇形的周长是12,面积是8,则扇形的中心角的弧度数是12.已知扇形的圆心角为2弧度,其所对的弦长为2,则扇形的弧长等于13.已知一扇形的圆心角为α,半径为R ,弧长为l.(1)若α=60°,R =10 cm ,求扇形的弧长l ;(2)已知扇形的周长为10 cm ,面积是4 cm 2,求扇形的圆心角;(3)若扇形周长为20 cm ,当扇形的圆心角α为多少弧度时,这个扇形的面积最大?14.已知一扇形的圆心角为(0)αα>,所在圆的半径为R .(1)若60α︒=,10R cm =,求扇形的弧长及该弧所在的弓形的面积;(2)若扇形的周长为20 cm ,当扇形的圆心角α等于多少弧度时,这个扇形的面积最大?15.已知扇形AOB 的周长为10cm.(1)若这个扇形的面积为4cm 2,求扇形圆心角的弧度数;(2)求该扇形的面积取得最大值时圆心角的大小及弧长.。
高中数学 第一章 三角函数 1.3 弧度制自主训练 北师大版必修4(2021年整理)

高中数学第一章三角函数1.3 弧度制自主训练北师大版必修4编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(高中数学第一章三角函数1.3 弧度制自主训练北师大版必修4)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为高中数学第一章三角函数1.3 弧度制自主训练北师大版必修4的全部内容。
1.3 弧度制自主广场我夯基 我达标1.下列命题中,错误的是( )A.“度”与“弧度”是度量角的两种不同的度量单位B 。
一度的角是周角的3601,一弧度的角是周角的π21 C.根据弧度的定义,180°等于π弧度D 。
不论用角度制还是用弧度制度量角,它们与圆的半径长短有关思路解析:由角和弧度的定义,可知无论是角度制还是弧度制,角的大小与半径的长短无关,只与弧长与半径的比值有关.答案:D2.α是第三象限的角,则π+α是( )A 。
第一象限的角B 。
第二象限的角C 。
第三象限的角D 。
第四象限的角思路解析:结合图形,π+α可以看成将α按顺时针旋转π得到的,则π+α是第一象限的角. 答案:A3。
如果一扇形的圆心角为72°,半径等于20 cm ,则扇形的面积为( )A 。
40π cm 2B 。
80π cm 2C 。
40 cm 2D 。
80 cm 2思路解析:先把角度化为弧度,然后利用弧度制下的扇形面积公式即可解出.72°=52π,S=21|α|r 2=21×52π×202=80π cm 2. 答案:B4.若扇形的面积是1 cm 2,它的周长是4 cm,则扇形圆心角的弧度数为( )A.1 B 。
2 C.3 D 。
高一数学必修四第一章课后练习

4.在0°~360°范围内,找出与下列各角终边相同的角,并指出它们是第几象限角:
(1)-54°18′(2)395°8′(3)-1190°30′.
5.写出与下列各角终边相同的角的集合,并把集合中适合不等式-720°≤β<360°的元素β写出来:
1.4.1正弦函数、余弦函数的图像
练习:
1.4.2正弦函数、余弦函数的性质
练习:
2.你认为我们应当如何利用函数的1.4.3正切函数的性质与图像
练习:
1.5函数y=Asin(ωx+φ)的图像
练习:
3.作一个以5cm为单位长度的圆,然后分别作出225°,330°角的正弦线、余弦线、正切线,量出它们的长度,从而写出这些角的正弦值、余弦值、正切值.
4.你认为三角函数线对认识三角函数概念有哪些作用?
1.2.2同角三角函数的基本关系
练习:
1.3三角函数的诱导公式
练习:
4.填表:
1.4三角函数的图像与性质
5.分别用角度制、弧度制下的弧长公式,计算半径为1m的圆中,60°的圆心角所对的弧的长度(可用计算器).
6.已知半径为120mm的圆上,有一条弧的长是144mm,求该弧所对的圆心角的弧度数.
1.2.1任意角的三角函数
练习:
3.填表:
角
角 的弧度数
sin
cos
tan
练习:
1.你能从单位圆中的三角函数线出发得出三角函数的哪些性质?
第一章三角函数
1.1.1任意角
练习
1.(口答)锐角是第几象限角?第一象限角一定是锐角吗?再分别就直角、钝角来回答这两个问题.
2.(口答)今天是星期三,那么7k(k∈Z)天后的那一天是星期几?7k(k∈Z)天前的那一天是星期几?100天后的那一天是星期几?
1.1.2弧度制

o
o
1 3 67 30 ' = rad × 67 = π rad 180 2 8 3 rad化成度 化成度。 (2) 把 — π rad化成度。 5
解: 3 π rad 5
3 = × 180 5
o
π
2
= 108
o
试一试:教材 试一试:教材P9 练习 1 2
四、练习: 练习:
例1.请写出一些特殊角的弧度数 1.请写出一些特殊角的弧度数
练习1 与角-1825 的终边相同 的终边相同, 练习1:与角-1825º的终边相同,且绝对值 最小的角的度数是___,合___弧度。 最小的角的度数是___,合___弧度。 ___, 弧度 360º-25º, 解:-1825 =-5×360 -25 , :-1825º= 1825 所以与角-1825 的终边相同 的终边相同, 所以与角-1825º的终边相同,且绝对值 最小的角是-25 . 最小的角是-25º.
其中: 以角α 其中:l —— 以角α为圆心角所对的弧长 r —— α角所在圆的半径 角所在圆的半径 角所在
l α = r
这种用“弧度” 做单位来度量角的制度, 这种用“弧度” 做单位来度量角的制度, 叫做弧度制 弧度制。 叫做弧度制。
弧度数的计算公式可以用弧长与其半径的 比值来表示, 比值来表示,那么一个角的弧度数与所在的 圆的半径之间是否存在一定联系?若存在, 圆的半径之间是否存在一定联系?若存在, 请阐述是什么关系?若不存在,说明理由. 请阐述是什么关系?若不存在,说明理由. 结论:当圆心角一定时, 结论:当圆心角一定时,它所对的弧长与 半径的比值是一定的,与所在圆的半径大 半径的比值是一定的, 小无关. 小无关
任意角的三角函数及弧度制教案及练习(含答案)
第一章:三角函数第一课时教材:角的概念的推广目的:要求学生掌握用“旋转”定义角的概念,并进而理解“正角”“负角”“象限角”“终边相同的角”的含义。
过程:一、提出课题:“三角函数”回忆初中学过的“锐角三角函数”——它是利用直角三角形中两边的比值来定义的。
相对于现在,我们研究的三角函数是“任意角的三角函数”,它对我们今后的学习和研究都起着十分重要的作用,并且在各门学科技术中都有广泛应用。
二、角的概念的推广1.回忆:初中是任何定义角的?(从一个点出发引出的两条射线构成的几何图形)这种概念的优点是形象、直观、容易理解,但它的弊端在于“狭隘”2.讲解:“旋转”形成角突出“旋转”注意:“顶点”“始边”“终边”“始边”往往合于x轴正半轴3.“正角”与“负角”——这是由旋转的方向所决定的。
记法:角α或α∠可以简记成α4.由于用“旋转”定义角之后,角的范围大大地扩大了。
1︒角有正负之分如:α=210︒β=-150︒γ=-660︒2︒角可以任意大实例:体操动作:旋转2周(360︒³2=720︒) 3周(360︒³3=1080︒)3︒还有零角一条射线,没有旋转三、关于“象限角”为了研究方便,我们往往在平面直角坐标系中来讨论角角的顶点合于坐标原点,角的始边合于x轴的正半轴,这样一来,角的终边落在第几象限,我们就说这个角是第几象限的角(角的终边落在坐标轴上,则此角不属于任何一个象限)例如:30︒ 390︒-330︒是第Ⅰ象限角, 300︒-60︒是第Ⅳ象限角585︒ 1180︒是第Ⅲ象限角,-2000︒是第Ⅱ象限角等四、关于终边相同的角1.观察:390︒,-330︒角,它们的终边都与30︒角的终边相同2.终边相同的角都可以表示成一个0︒到360︒的角与)k∈个周角的和(Zk390︒=30︒+360︒)1k(=-330︒=30︒-360︒ )1(-=k 30︒=30︒+0³360︒ )0(=k 1470︒=30︒+4³360︒ )4(=k -1770︒=30︒-5³360︒ )5(-=k3.所有与α终边相同的角连同α在内可以构成一个集合 {}Z k k S ∈⋅+==,360| αββ即:任何一个与角α终边相同的角,都可以表示成角α与整数个周角的和 五、小结: 1︒ 角的概念的推广, 用“旋转”定义角,角的范围的扩大 2︒“象限角”与“终边相同的角”第二课时教材:弧度制目的:要求学生掌握弧度制的定义,学会弧度制与角度制互化,并进而建立角的集合与实数集R 一一对应关系的概念。
数学必修4第一章三角函数
第一章三角函数1.1任意角和弧度制1.1.1任意角1.B.2.C.3.C.4.-1485°=-5³360°+315°.5.{-240°,120°}.6.{α|α=k²360°-490°,k∈Z};230°;-130°;三.7.2α的终边在第一、二象限或y轴的正半轴上,α2的终边在第二、四象限.集合表示略.8.(1)M={α|α=k²360°-1840°,k∈Z}.(2)∵α∈M,且-360°≤α≤360°,∴-360°≤k²360°-1840°≤360°.∴1480°≤k²360°≤2200°,379≤k≤559.∵k∈Z,∴k=5,6,故α=-40°,或α=320°.9.与45°角的终边关于x轴对称的角的集合为{α|α=k²360°-45°,k∈Z},关于y轴对称的角的集合为{α|α=k²360°+135°,k∈Z},关于原点对称的角的集合为{α|α=k²360°+225°,k∈Z},关于y=-x对称的角的集合为{α|α=k²360°+225°,k∈Z}.10.(1){α|30°+k²180°≤α≤90°+k²180°,k∈Z}.(2){α|k²360°-45°≤α≤k²360°+45°,k∈Z}.11.∵当大链轮转过一周时,转过了48个齿,这时小链轮也必须同步转过48个齿,为4820=2.4(周),即小链轮转过2.4周.∴小链轮转过的角度为360°³2 4=864°.1.1.2弧度制1.B.2.D.3.D.4.αα=kπ+π4,k∈Z.5.-5π4.6.111km.7.π9,7π9,13π9.8.2π15,2π5,2π3,4π5.9.设扇形的圆心角是θrad,∵扇形的弧长是r θ,∴扇形的周长是2r+rθ,依题意,得2r+rθ=πr,∴θ=π-2,∴扇形的面积为S=12r2θ=12(π-2)r2.10.设扇形的半径为R,其内切圆的半径为r,由已知得l=π2R,R=2lπ.又∵2r+r=R,∴r=R2+1=(2-1)R=2(2-1)πl,∴内切圆的面积为S=πr2=4(3-22)πl2.11.设圆心为O,则R=5,d=3,OP=R2-d2=4,ω=5rad/s,l=|α|R,α=ωt=25rad,l=4³25=100(cm).1.2任意角的三角函数1.2.1任意角的三角函数(一)1.B.2.B.3.C.4.k.5.π6,56π.6.x|x≠2kπ+32π,k∈Z.7.-25.8.2kπ+π2,2kπ+π,k∈Z.9.α为第二象限角.10.y=-3|x|=-3x(x≥0),3x(x<0),若角α的终边为y=3x(x<0),即α是第三象限角,则sinα=-31010,tanα=3;若角α的终边为y=-3x(x≥0),即α是第四象限角,则sinα=-31010,tanα=-3.11.f(x)=-(x-1)2+4(0≤x≤3).当x=1时,f(x)max=f(1)=4,即m=4;当x=3时,f(x)min=f(3)=0,即n=0.∴角α的终边经过点P(4,-1),r=17,sinα+cosα=-117+417=31717.1.2.1任意角的三角函数(二)1.B.2.C.3.B.4.334.5.2.6.1.7.0.8.x|2kπ+π≤x<2kπ+32π,或x=2kπ,k∈Z.9.(1)sin100°²cos240°<0.(2)tan-11π4-cos-11π4>0.(3)sin5+tan5<0.10.(1)sin25π6=sin4π+π6=sinπ6=12.(2)cos-15π4=cos-4π+π4=cosπ4=22.(3)tan13π3=tan4π+π3=tanπ3=3.11.(1)∵cosα>0,∴α的终边在第一或第四象限,或在x轴的非负半轴上;∵tanα<0,∴α的终边在第四象限.故角α的集合为α2kπ-π2<α<2kπ,k∈Z.(2)∵2kπ-π2<α<2kπ,k∈Z,∴kπ-π4<α2<kπ,k∈Z .当k=2n(n∈Z)时,2nπ-π4<α2<2nπ,n∈Z,sinα2<0,cosα2>0,tanα2<0;当k=2n+1(n∈Z)时,2nπ+3π4<α2<2nπ+π,n∈Z,sinα2>0,cosα2<0,tanα2<0. 1.2.2同角三角函数的基本关系1.B.2.A.3.B.4.-22.5.43.6.232.7.4-22.8.α2kπ+π2<α<2kπ+3π2,或α=kπ,k∈Z.9.0.10.15.11.3+12.1.3三角函数的诱导公式(一)1.C.2.A.3.B.4.-1-a2a.5.12.6.-cos2α.7.-tanα.8.-2sinθ.9.32.10.-22+13.11.3.1.3三角函数的诱导公式(二)1.C.2.A.3.C.4.2+22.5.-33.6.13.7.-73.8.-35.9.1.10.1+a4.11.2+3.1.4三角函数的图象与性质1.4.1正弦函数、余弦函数的图象1.B.2.C.3.B.4.3;-3.5.2.6.关于x轴对称.7.(1)取(0,0),π2,1,(π,2),3π2,1,(2π,0)这五点作图.(2)取-π2,0,0,12,π2,0,π,-12,3π2,0这五点作图.8.五点法作出y=1+sinx的简图,在同一坐标系中画出直线y=32,交点有2个.9.(1)(2kπ,(2k+1)π)(k∈Z).(2)2kπ+π2,2kπ+32π(k∈Z).10.y=|sinx|=sinx(2kπ≤x≤π+2kπ,k∈Z),-sinx(π+2kπ<x<2π+2kπ,k∈Z),图象略.y=sin|x|=sinx(x≥0),-sinx(x<0),图象略.11.当x>0时,x>sinx;当x=0时,x=sinx;当x<0时,x<sinx,∴sinx=x只有一解.1.4.2正弦函数、余弦函数的性质(一)1.C.2.A.3.D.4.4π.5.12,±1.6.0或8.提示:先由sin2θ+cos2θ=1,解得m=0,或m=8.7.(1)4.(2)25π.8.(1)π.(2)π.9.32,2.10.(1)sin215π<sin425π.(2)sin15<cos5.11.342.1.4.2正弦函数、余弦函数的性质(二)1.B.2.B.3.C.4.<.5.2π.6.3,4,5,6.7.函数的最大值为43,最小值为-2.8.-5.9.偶函数.10.f(x)=log21-sin2x=log2|cosx|.(1)定义域:xx≠kπ+π2,k∈Z.(2)值域:(-∞,0]. (3)增区间:kπ-π2,kπ(k∈Z),减区间:kπ,kπ+π2(k∈Z).(4)偶函数.(5)π.11.当x<0时,-x>0,∴f(-x)=(-x)2-sin(-x)=x2+sinx.又∵f(x)是奇函数,∴f(-x)=-f(x).∴f(x)=-f(-x)=-x2-sinx.1.4.3正切函数的性质与图象1.D.2.C.3.A.4.5π.5.tan1>tan3>tan2.6.kπ2-π4,0(k∈Z).7.2kπ+6π5<x<2kπ+3π2,k∈Z .8.定义域为kπ2-π4,kπ2+π4,k∈Z,值域为R,周期是T=π2,图象略.9.(1)x=π4.(2)x=π4或54π.10.y|y≥34.11.T=2π,∴f99π5=f-π5+20π=f-π5,又f(x)-1是奇函数,∴f-π5-1=-fπ5-1 f-π5=2-fπ5=-5,∴原式=-5.1.5函数y=Asin(ωx+φ)的图象(一)1.A.2.A.3.B.4.3.5.-π2.6.向左平移π4个单位.7.y=sinx+2的图象可以看作是将y=sinx图象向上平移2个单位得到,y=sinx-1的图象可以看作是将y=sinx图象向下平移1个单位而得到.8.±5.9.∵y=sin3x-π3=sin3x-π9,∴可将y=sin3x的图象向右平移π9个单位得到.10.y=sin2x+π4的图象向左平移π2个单位,得到y=sin2x+π2+π4,故函数表达式为y=sin2x+5π4.11.y=-2sinx-π3,向左平移m(m>0)个单位,得y=-2sin(x+m)-π3,由于它关于y轴对称,则当x=0时,取得最值±2,此时m-π3=kπ±π2,k∈Z,∴m的最小正值是5π6.1.5函数y=Asin(ωx+φ)的图象(二)1.D.2.A.3.C.4.y=sin4x.5.-2a;-310a+2ka(k∈Z);-2a.6.y=3sin6x+116π.7.方法1y=sinx横坐标缩短到原来的12y=sin2x向左平移π6个单位y=sin2x+π6=y=sin2x+π3.方法2y=sinx向左平移π3个单位y=sinx+π3横坐标缩短到原来的12y=sin2x+π3.8.(1)略.(2)T=4π,A=3,φ=-π4.9.(1)ω=2,φ=π6.(2)x=12kπ+π6(k∈Z),12kπ-112π,0(k∈Z).10.(1)f(x)的单调递增区间是3kπ-5π4,3kπ+π4(k∈Z).(2)使f(x)取最小值的x的集合是x|x=7π4+3kπ,k∈Z.11.(1)M=1,m=-1,T=10|k|π.(2)由T≤2,即10|k|π≤2得|k|≥5π,∴最小正整数k 为16.1.6三角函数模型的简单应用(一)1.C.2.C.3.C.4.2sinα.5.1s.6.k²360°+212 5°(k∈Z).7.扇形圆心角为2rad时,扇形有最大面积m216.8.θ=4π7或5π7.9.(1)设振幅为A,则2A=20cm,A=10cm.设周期为T,则T2=0.5,T=1s,f=1Hz.(2)振子在1T内通过的距离为4A,故在t=5s=5T内距离s=5³4A=20A=20³10=200cm=2(m).5s末物体处在点B,所以它相对平衡位置的位移为10cm.10.(1)T=2πs.(2)12π次.11.(1)d-710=sint-1.8517.5π.(2)约为5.6秒.1.6三角函数模型的简单应用(二)1.D.2.B.3.B.4.1-22.5.1124π.6.y=sin52πx+π4.7.95.8.12sin212,1sin12+2.9.设表示该曲线的三角函数为y=Asin(ωx+φ)+b.由已知平均数量为800,最高数量与最低数量差为200,数量变化周期为12个月,所以振幅A=2002=100,ω=2π12=π6,b=800,又7月1日种群数量达最高,∴π6³6+φ=π2.∴φ=-π2.∴种群数量关于时间t的函数解析式为y=800+100sinπ6(t-3).10.由已知数据,易知y=f(t)的周期T=12,所以ω=2πT=π6.由已知,振幅A=3,b=10,所以y=3sinπ6t+10.11.(1)图略.(2)y-12.47=cos2π(x-172)365,约为19.4h.单元练习1.C.2.B.3.C.4.D.5.C.6.C.7.B.8.C.9.D.10.C.11.5π12+2kπ,13π12+2kπ(k∈Z).12.4412.13.-3,-π2∪0,π2.14.1972π.15.原式=(1+sinα)21-sin2α-(1-sinα)21-sin2α=1+sinα|cosα|-1-sinα|cosα|=2sinα|cosα|. ∵α为第三象限角,|cosα|=-cosα,∴原式=-2tanα.16.1+sinα+cosα+2sinαcosα1+sinα+cosα=sin2α+cos2α+2sinαcosα+sinα+cosα1+sinα+cosα=(sinα+cosα)2+sinα+cosα1+sinα+cosα=(sinα+cosα)·(1+sinα+cosα)1+sinα+cosα=sinα+cosα. 17.f(x)=(sin2x+cos2x)2-sin2xcos2x2-2sinxcosx-12sinxcosx+14cos2x=1-sin2xcos2x2(1-sinxcosx)-12sinxcosx+14cos2x=12+12sinxcosx-12sinxcosx+14cos2x=12+14cos2x.∴T=2π2=π,而-1≤cos2x≤1,∴f(x)max=34,f(x)min=14.18.∵Aπ3,12在递减段上,∴2π3+φ∈2kπ+π2,2kπ+3π2.∴2π3+φ=5π6,φ=π6.19.(1)周期T=π,f(x)的最大值为2+2,此时x∈x|x=kπ+π8,k∈Z;f(x)的最小值为2-2,此时x ∈x|x=kπ-38π,k∈Z;函数的单调递增区间为kπ-3π8,kπ+π8,k∈Z.(2)先将y=sinx(x∈R)的图象向左平移π4个单位,而后将所得图象上各点的横坐标缩小为原来的12,纵坐标扩大成原来的2倍,最后将所得图象向上平移2个单位.20.(1)1π.(2)5π或15.7s.(3)略.。
高中数学必修4课后练习题、习题答案优选教学课件
还有一件有趣的事也不得不提。我的前桌坐着一个很秀气的姑娘,常常梳着一个麻花辫,说起话来总是温温柔柔的,暂且起名叫她“淑女”吧!有一天早上,我惊奇地发现她纤纤的十指,涂了黑漆漆的指甲油,她迫不及待地和班上的人炫耀了她的杰作。很不巧的是第一堂课是内科,老师教的又是“叩诊”,国字脸的女老师,用严厉的目光环顾了教室一周,最后锁定了我的前座,她冷冷地说:“来,这位同学,你上黑板给大家演示一下—叩诊的方法。” “淑女”显得有些难为情,慢腾腾地起身走到在黑板前,低下头,缓慢地伸出涂着黑色指甲油的双手,给大家表演着“叩诊”。如果老师当时没问也还好,可老师偏偏问了,“你这手怎么弄的,指甲都成这样了,怎么没上医院啊?”这一问引起全班哄堂大笑,老师感到有些莫名其妙,纳闷地问:“你们都笑什么?”不料班级最捣蛋的一个男 生出卖了她,“她涂的是黑色指甲油,不是病。”从此以后,我没见她再涂过任何颜色的指甲油。
甚至不知所措。我傻傻地站在那里,也不知道是过去一个小时,还是几个小时,人才渐渐地少了,突然间我的耳朵捕获了一串数字,是住宿费的缴费窗口传出来的,我不由得摸了一下包,心里便有了主意:先把住宿费交了,其他再说。于是,我深吸了一口气,故作镇定地交了住宿费,领了被罩和盆,就忐忑不安地住进了宿舍。 宿舍共八个人,来自不同的地方,因为都是年轻人,很快都熟络了起来。我的班主任则是一个娇小的,长得很漂亮的女老师,叫李丽。医学虽然看上枯燥,但很多东西都与我们息息相关,所以学起来也没有那么难。不论解剖课的死人骷髅头,各类人骨,还是内外科的各种病理药理,以及活体的各种器官,我都学得津津有味。可是学习的高涨的热情,无法掩盖我内心的不安,我很害怕触碰到老师的目光,怕她对我说:白XX,你不知道学费没有交吗?就这样我怀着惴惴不安的心情,熬过了整整三个月。直到有一天,李丽老师气匆匆地走进教室,用鄙夷的略带愤怒的目光注视着我时,我心虚了,低下头不敢再去看她,我心跟明镜似的。她喝道:“白XX, 王校长要见你,在二楼校长室。” 走廊里我挪着步,每走一步都觉得很沉,不知道校长会怎么批评我,或者是严惩我,害怕与紧张让我在房门前不得不倒吸了一口气,接着又闭上眼睛静等五秒钟后,我才敢扣响房门,听到里面传出:进来,我才小心翼翼地推开那扇门。我径直地站在校长的办公桌前,不敢发出一点声响。看见王校长端坐在桌前书写着什么,看见我进来,便马上收起笔,他从椅子上慢慢站起来,用惊愕的眼神上下打量着我,他严肃的目光里还带着一股寒气,仿佛瞬间就能将我冰封,我连大气都不敢出。紧接着他开始发怒了,大声呵斥道:“你,你就是XXX。”我不敢说话,只是点点头。他猛然摘下眼镜,愤怒下的眼睛突出的更加厉害,手在不停地拍打着豪华的办公桌,来压抑着他内心的烦躁,他一声高过一声地责问我:“你小小年纪,也太有主意了,这么多钱没交,竟然能瞒这么久”。我羞愧地低下了头了,
高中数学必修四同步练习题库:任意角和弧度制(简答题:容易1,较易8,一般26,较难29,困难30)
任意角和弧度制(简答题:容易1,较易8,一般26,较难29,困难30)1、把下列各角用另一种度量制表示出来:;;;.2、如果角的终边经过点,试写出角的集合,并求集合中最大的负角和绝对值最小的角.3、已知扇形的中心角为,扇形所在圆的半径为,若扇形的面积值与周长值的差为,求的最小值及对应的值.4、扇形AOB的周长为8cm,它的面积为3 cm2,求圆心角的大小.5、(本小题满分13分)直角坐标系中,锐角的终边与单位圆的交点为,将绕逆时针旋转到,使,其中是与单位圆的交点,设的坐标为.(Ⅰ)若的横坐标为,求;(Ⅱ)求的取值范围.6、一个半径大于2的扇形,其周长,面积,求这个扇形的半径和圆心角的弧度数.7、一个扇形OAB的面积是1 cm2,它的周长是4 cm,求圆心角的弧度数和弦长AB.8、已知扇形OAB的圆心角α为120°,半径长为6,(1)求的弧长;(2)求弓形OAB的面积.9、写出如图所示阴影部分的角α的范围.10、如图,动点,从点出发,沿圆周运动,点按逆时针方向每秒钟转弧度,点按顺时针方向每秒钟转弧度,求,第一次相遇时所用的时间及,点各自走过的弧长.11、已知角的顶点与坐标原点重合,始边落在x轴的非负半轴上,在范围内,找出与下列各角终边相同的角,并判断它们是第几象限角.(1);(2);(3).12、已知扇形AOB的圆心角为120°,半径长为6,求:(I)弧的长;(II)扇形所含弓形的面积 (即阴影面积).13、一只红蚂蚁与一只黑蚂蚁在一个单位圆(半径为1的圆)上爬动,若两只蚂蚁均从点A(1,0)同时逆时针匀速爬动,若红蚂蚁每秒爬过α角,黑蚂蚁每秒爬过β角(其中0°<α<β<180°),如果两只蚂蚁都在第14秒时回到A点,并且在第2秒时均位于第二象限,求α,β的值.14、在角的集合{α|α=k•90°+45°,k∈Z}中:(1)有几种终边不相同的角?(2)有几个适合不等式﹣360°<α<360°的角?(3)写出其中是第二象限角的一般表示法.15、已知扇形的圆心角为,所在圆的半径为.(1)若,,求扇形的弧长.(2)若扇形的周长为24,当为多少弧度时,该扇形面积最大?并求出最大面积.16、已知一个扇形的半径为,圆心角为,求这个扇形的面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
C .{α|0≤α≤π}
D .{α|-4≤α≤-π}∪{α|0≤α≤π}
答案:D
解析:求出集合A 在[-4,4]附近区域内的x 的数值,k =0时,0≤x ≤π;k =1时,x ≥2π≥4;在k =-1时,-2π<x <-π,而-2π<-4,-π>-4,从而求出A ∩B .
6.圆弧长度等于其内接正三角形的边长,则其圆心角的弧度数为( )
A.π3
B.23
π C. 3 D .2
答案:C
解析:设圆半径为r ,则其内接正三角形的边长为3r ,∴θ=3r
r = 3.
二、填空题:(每小题5分,共5×3=15分)
7.把-1125°化为2k π+α(k ∈Z,0≤α<2π)的形式是________.
答案:-8π+7π4
8.若角α的终边在如图所示的阴影部分,则角α的取值范围是________.
答案:{α|2k π+23π≤α≤2k π+76
π,k ∈Z } 解析:该阴影部分在(0,2π)内对应的取值范围为[23π,76
π],所以该阴影部分的取值范围是{α|2k π+23π≤α≤2k π+7π6
,k ∈Z }. 9.半径为4 cm 的扇形,若它的周长等于弧所在的半圆周的长,则这个扇形的面积是
______cm 2.
答案:8π-16
解析:设扇形的圆心角的弧度数为α.
∵R =4,扇形周长等于弧所在的半圆周的长.
∴2×4+4α=4π,∴α=π-2.
∴S 扇形=12|α|R 2=12
(π-2)×42=8π-16(cm 2). 三、解答题:(共35分,11+12+12)
10.已知角α=2010°.
(1)将α改写成θ+2k π(k ∈Z,0≤θ<2π)的形式,并指出α是第几象限角;
(2)在区间[-5π,0)上找出与α终边相同的角.
解:(1)2010°=2010×π180=67π6=5×2π+7π6
. 又π<7π6<3π2,角α与角7π6
的终边相同,故α是第三象限角. (2)与α终边相同的角可以写为r =7π6
+2k π(k ∈Z ). 又-5π≤r <0,
∴k =-3,-2,-1.
当k =-3时,r =-29π6
;。
