三相异步电动机的机械特性(精)
7.6三相异步电动机的机械特性
2 R s X 2 2 2
) n f (I2 ) n f (cos 2
s R2
2 R s X 2 2 2
r1
I1
x1
rm
x2
I2
E 1 E2
r2
U1
Im
1 s r2 s
• 起动时的情况
– “起动”即是转子堵转状态。 – n＝0，s＝1； – 附加电阻为0，电路为短路状态。 – 起动电流很大，功率因素较低。
r1
I1
x1
rm
x2
I2
E 1 E2
r2
U1
Im
1 s r2 s
xm
异步电动机起动时起动电流的大小与负载轻重无关
• 发电机运行
n1
n1
n1
外转矩使转子逆着旋转磁场的 方向旋转，此时电磁转矩方向 仍和旋转磁场方向一致，但与 外转矩方向相反，电磁转矩仍 是制动性质的。
异步电动机，转速略低 于同步转速，电磁转矩 是拖动性质的。
用一外在转矩拖动异步电机， 使转速超过同步转速，此时电 磁转矩是制动性质的，异步电 机从转子轴上输入机械功率。
1、降低定子端电压的人为机械特性
异步电机磁路在额定电压下已有点饱和，故不宜再升高电压。 只能讨论降低定子端电压时的人为机械特性。
U 3 Tm ' 21 ( X1 X 2 )
' U12 R2 3 Tst ' 2 ' 2 1 ( R1 R2 ) ( X1 X 2 )
几种异步电机的典型运行情况
三相异步电机的机械特性(精)
实验报告课程名称：电机与拖动基础实验项目：三相异步电动机机械特性姓名：lmysdju一．实验目的理解三相异步电动机的机械特性，用MATLAB绘制出不同控制方法下三项异步电机的机械特性曲线。
二．实验项目1. E1/f1为常数，在不同供电频率下绘制出机械特性曲线；2. U1/f1为常数，在不同供电频率下绘制出机械特性曲线；，在不同供电频率下绘制出机械特性曲线。
三．实验内容本实验是基于MATLAB软件的，所需要的电机时参数已知的。
电机的特征如下：三相四极，定子绕组为Y接，其额定数据和毎相参数如下：1. 采用恒E1/f1控制，通过MATLAB编程，绘制出不同供电频率下三相异步电机的机械特性。
其程序如下：%Mechanical characteristic with E1/f1=Constclcclearsyms U1n Nph Poles Fe0 Nn R1 R2p X10 X20p R0 X0 Nsn Sn Zeq Z1 F1 Ns X1 X2p Xm...E1 E1n S Nrl Teml a b;U1n=380/sqrt(3);Nph=3;Poles=4;Fe0=50;Nn=1480;R1=1.03;R2p=1.02;X10=1.03;X20p=4.4;R0=7;X0=90;Nsn=120*Fe0/Poles;Sn=(Nsn-Nn)/Nsn;Zeq=(R0+j*X0)*(R2p/Sn+j*X20p)/((R0+j*X0)+(R2p/Sn+j*X20p)); Z1=R1+j*X10; E1n=abs(Zeq*U1n/(Zeq+Z1));for b=1:4if b==1F1=50;elseif b==2F1=35;elseif b==3F1=25;elseif b==4F1=10;endNs=120*F1/Poles;X1=X10*(F1/Fe0);X2p=X20p*(F1/Fe0);Xm=X0*(F1/Fe0);E1=E1n*(F1/Fe0);for a=1:2000S=a/2000;Nrl=Ns*(1-S);Teml=Nph*Poles/(4*pi)*(E1/F1)^2*F1*R2p/S/((R2p/S)^2+X2p^2);Tem(a)=Teml;Nr(a)=Nrl;plot(Teml,Nrl);hold on;endhold on;endxlabel('Torque[N.m]');ylabel('Speed[r/min]');title('Mechanical characterristic with E1/f1=const');ylim([0,1600]);xlim([0,105]);text(50,1350,'f=50Hz');text(50,900,'f=35Hz');text(50,600,'f=25Hz');text(50,150,'f=10Hz');运行结果：Mechanical characterristic with E1/f1=constSpeed[r/min]Torque[N.m]2．采用恒U1/f1控制，重新绘制出不同供电频率下三相异步电机的机械特性曲线。
第九章 三相异步电动机的机械特性及各种运转状态 第一节 三相异步电动机机械特性的三种表达式
U
2 X
(10 17)
R12
(X1
X
' 2
)
2
正号对应于电动机状态，而负号则适用于发电机状态 考虑 R1 << ( X1 + X2') ,可得：
Sm
R2'
X1
X
' 2
(10 18)
Tm
m1U
2 X
20 ( X1
X
' 2
)
(10 19)
可以看出：
4.几点规律
1)当电动机各参数及电源频率不变时， Tm 与 UX2 成正比，sm 因与 UX 无关而保持不变
二.异步电动机机械特性的参数表达式
采用参数表达式可直接建立异步电动机工作时转矩和转速关系并 进行定量分析
E
' 2
2f1W1kW1 m (10 5)
0
2f
p
(10 6)
T
m1 0
E
' 2
I
' 2
c
os
' 2
(10 7)
E
' 2
I
' 2
Z
' 2
(10 8)
R2'
c
os
' 2
PT
3I
2 2
R2 R f s
(10 44)
转子轴上机械功率为
P2 PT (1 s) (10 45)
s > 1，P2 为负值，即电动机由轴上输入机械功率 转子电路的损耗为
DP2 PT (1 s) (10 45)
DP2 数值上等于 PT 与 P2 之和，所以反接制动时能量损耗极大 3)用途 可以用于稳定下放位能性负载
三相异步电动机的机械特性
三相异步电动机的机械特性
三相异步电动机的机械特性（1）转子机械特性转子是定子绕组中通过一对或几对磁极而产生旋转磁场，在转子导条轴上装有铁芯和滑环。
由于各种原因会使转子发生振动。
为了保证起动时的正常运行，要求转子机械特性曲线应与负载所需的机械特性曲线相符合。
三相异步电动机的机械特性（2）磁路机械特性当定子绕组通以直流电后，便产生感应电势，并随着转速增大而增大，同时转子也将感应出较强的交变磁场，这个磁场称为旋转磁场，它可分解成若干个正弦波，在空间形成闭合回路，并沿转轴作切割磁力线的运动。
53三相异步电动机的转矩特性和机械特性
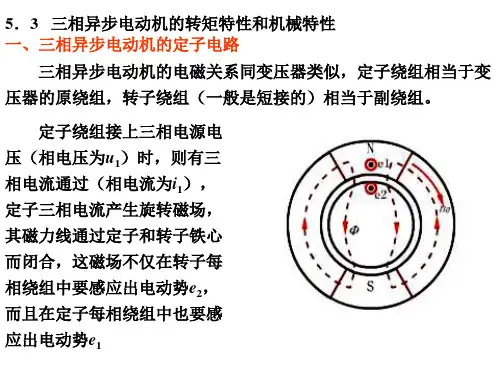
电动机也会停转
此外，电网电压下降 ，在负载不变的条件下，将使电动机转 速下降，转差率S 增大，电流增加，引起电动机发热甚至烧坏。
（2）定子电路接入电阻或电抗时的人为特性
在电动机定子电路中外串电阻或电抗后，电动机端电压为电源 电压减去定子外串电阻上或电抗上的压降，致使定子绕组相电压降 低,这种情况下的人为特性与降低电源电压时的相似.。
四．机械特性 在异步电动机中，转速 n=(1-S)n0，为了符合习惯画法，可将
曲线换成转速与转矩之间的关系曲线，即称为异步电动机的机械特 性。
1．固有机械特性
异步电动机在额定电压和额定频率下，用规定的接线方式， 定子和转子电路中不串联任何电阻或电抗时的机械特性称为固有 （自然）机械特性。
根据
T
R22
设定子和转子每相绕组的匝数分别为N1和N2，如图所示电路 图是三相异步电动机的一相电路图。
旋转磁场的磁感应强度沿定子与转子间空气隙的分布是近于按 正弦规律分布的，因此，当其旋转时，通过定子每相绕相的磁通也 是随时间按正弦规律变化的，
m sin t
定子每相绕组中产生的感应电动势为：e1
N1
d
dt
（3）改变定子电源频率时的人为特性
n0
60 f p
Sm
R2 X 20
n0 nm n0
Tmax
K
U2 2 X 20
Tst
K
R2U 2
R22
X
2 20
Tmax
注意到TN：X 20 f , K 1 f
一般变频调速采用恒转矩调速， 即希望最大转矩保持为恒值，为此在 改变频率的同时，电源电压也要作相 应的变化，使 U/f =C ，这在实质上 是使电动机气隙磁通保持不变。
三相异步电动机的电磁转矩及机械特性
电动机起动时有最大转矩，可令sk=1 ，则起动 转矩为最大转矩时转子回路所串的电阻应为：
rs xk r2
16
1、三相绕线式异步电动机转子回路串电阻后，下 列参数将如何变化？ （1）起动电流 （2）起动转矩 （3）最大转矩 （4）临界转差率
减小，增大，不变，增大
17
2、若频率为50HZ的三相异步电动机接在频率为 60Hz的电网上运行，电动机下列参数将如何变化？ （1）起动转矩； （2）最大转矩； （3）起动电流。
最大电磁转矩与电源电压平方成正比；临界转差 率与电源电压无关。
转子回路电阻越大，临界转差率越大；最大电磁 转矩与转子电阻无关。
频率越高，最大电磁转矩和临界转差率越小；漏 抗越大，最大电磁转矩和临界转差率越小。
13
3.最大电磁转矩、起动转矩、额定转矩
Tmax
pm1
1
U12
1 2 xk
注意：
（1）三相异步机的 Tmax和电压的平方成正比，所
（2）最大电磁转矩 Tmax 最大转矩:电机带动最大负载的能力。
TL Tmax，电机因带不动负载而停转。
电磁转矩
r2
T
pm1
2 f1
U12
s ( r2)2
s
xk2
令 dT 0，求出当T最大时的转差率sK。
dS
10
3.最大电磁转矩、起动转矩、额定转矩
（2）最大电磁转矩 Tmax
sk
C1r2 r12 (x1 C1x2 )2
Tmax
m1 pU12
2 f1
2C1(r1
1 r12 (x1 x2 )2 )
sk
r2 xk
C1 1 Tmax
m1 pU12
三相异步电动机的机械特性
空载时损耗占比例大，效率低；随P2增 加，增加，当负载过大，铜损耗增加快，使 效率下降，如图所示。
2023年8月26日 星期六
§4－5 三相异步电动机的机械特性
效率曲线和功率因数曲线都是在额定负载附近 达到最高，因此合理选用电动机容量时，对电动 机的寿命、功率因数和效率都有很实际的意义。 5、功率因数特性cos1=f(P2)
§4－5 三相异步电动机的机械特性
本节要点： 一、三相异步电动机的工作特性 二、机械特性：n = f ( T ) ㈠固有机械特性曲线分析 ㈡人为机械特性 三、运行性能 1、运行状态 2、启动转矩倍数
3、过载能力 4、异步电动机机械特性的结论
2023年8月26日 星期六
§4－5 三相异步电动机的机械特性
原因：是静止的转子导体与定子旋转磁 场之间的相对切割速度很大（n1）。将 产生很大的I2，使定子电流也增大。但 由于转子绕组的功率因数cosφ2很小， 由于Tst=CTφI2cosφ2，故启动转矩并不 很大。
只有当Tst达到一定值时，电动机才 能启动。
Tst>TL ，将 S = 1代入T公式，即 可得Tst 的表达式。
2023年8月26日 星期六
§4－5 三相异步电动机的机械特性
⑵额定运行点（TN、nN） TN = 9.55 PN/nN
⑶临界工作点（Tm、nm） 当S = Sm 时，电磁转矩达到最大
值。
Sm ∈( 0.04，0.14 ) ⑷同步点（0、n1）
n = n1
2023年8月26日 星期六
§4－5 三相异步电动机的机械特性
2023年8月26日 星期六
§4－5 三相异步电动机的机械特性
2、转矩特性T=f(P2) 空载时P2=0，电磁转矩T等于空载转矩 T0。随着P2的增加，已知T2=9.55P2/n， 如n基本不变，则T2为过原点的直线。 考虑到P2增加时，n稍有降低，故 T2=f(P2)随着P2增加略向上偏离直线。 在T=T0+T2式中。T0很小，且为常数。所 以T=f(P2)将比平行上移T0数值，如图所 示。
4-5 三相异步电动机的机械特性
4-6 三相笼型异步电动机的起动与控制
图4-30 XJ0l系列自耦减压起动器电路图
4-6 三相笼型异步电动机的起动与控制
（三)星一三角减压起动控制电路
•原理： 1 I I stY st 3
1 TstY Tst 3
•特点：Y-△减压起动时，起动电流和起动转矩都下降为直接 起动时的1／3。这种起动方法简便、经济，运行可靠。 Y系 列电动机采用Y-△降压起动不仅适用于轻载起动，也可适用 于中型负载下的起动。 •线路：两接触器式 ----用于13kW以下电动机的控制 三接触器式-- --用于13kW以上电动机的控制
二、减压起动与控制 （一） 定子串电阻(或电抗)减 压起动 1 •原理 t
I st I st k Tst 1 Tst 2
k
•特点：优点是起动较平稳，运 行可靠，设备简单。缺点是起 动转矩随电压的平方降低，只 适合轻载起动，同时起动时电 能损耗较大。 •线路
图4-29 时间原则自动短接电阻减压起动电路 a）自动短接电阻减压起动 b)自动与手动短 接电阻减压起动
4-5 三相异步电动机的机械特性 三相异步电动机的机械特性是指在一定条件下，电动机的 转速n与电磁转矩Tem之间的关系，即n= ƒ (Tem)，也用 Tem= ƒ (s)的形式表示。
一、固有机械特性的分析 三相异步电动机的固有机械特性是指异步电动机工作在额 定电压和额定频率下，按规定的接线方式接线，定、转子外 接电阻为零时的机械特性。整个机械特性可看作由两部分组 成： 1)H—P部分(转矩由0～Tm，转差率由0～sm)。工作部分，特 性接近于一条直线 。 2)P—A部分(转矩由Tm～Tst，转差率由sm～1)。称为机械特 性的非工作部分，曲线部分 。
图4-24 电动机单向旋转接触器控制 电路
电机机械特性的测定(精)
第五章电机机械特性的测定实验一三相异步电动机在各种运行状态下的机械特性一．实验目的了解三相绕线式异步电动机在各种运行状态下的机械特性。
二．预习要点1．如何利用现有设备测定三相绕线式异步电动机的机械2．测定各种运行状态下的机械特性应注意哪些问题。
3．如何根据所测得的数据计算被试电机在各种运行状态下的机械特性。
三．实验项目1．测定三相绕线式异步电动机在电动运行状态和再生发电制功状态下机械特性。
2．测定三相绕线式异步电动机在反接制动运行状态下的机械特性。
四．实验设备及仪器1．MEL系列电机系统教学实验台主控制屏。
2．电机导轨及测速表（MEL-13、MEL-14）3．直流电压、电流、毫安表4．三相可调电阻器900Ω（MEL-03）5．三相可调电阻器900Ω（MEL-04）6．波形测试及开关板（MEL-05）五．实验方法及步骤按实验线路图5-5接线M为三相绕线式异步电动机M09，额定电压U N=220伏，Y接法；G为直流并励电动机M03（作他励接法），其U N=220伏，P N=185WR S选用三组90Ω电阻（每组为MEL-04，90Ω电阻）R1选用675Ω电阻（MEL-03中，450Ω电阻和225Ω电阻相串联）。
R f选用3000Ω电阻（电机起动箱中，磁场调节电阻）V2、A2、mA分别为直流电压、电流、毫安表，采用MEL-06或直流在主控制屏上V1、A1、W1、W2为交流、电压、电流、功率表，含在主控制屏上S1选用MEL-05中的双刀双掷开关1．测定三相绕线式异步电机电动及再发电制动机械特性仪表量程及开关、电阻的选择：（1）V2的量程为300V档，mA的量程为200mA档，A2的量程为2A档。
实验步骤：（1）接下绿色“闭合”按钮，接通三相交流电源，调节三相交流电压输出为180V（注意观察电机转向是否符合要求），并在以后的实验中保持不变。
（2）接通直流电机励磁电源，调节R f阻值使I f=95mA并保持不变。
三相异步电动机的机械特性
三相异步电动机的机械特性是一条非线性曲线，一般情况下，以最大转矩（或临界转差率）为分界点，其线性段为稳定运行区，而非线性段为不稳定运行区。固有机械特性的线性段属于硬特性，额定工作点的转速略低于同步转速。人为机械特性曲线的形状可用参数表达式分析得出，分析时关键要抓住最大转矩、临界转差率及启动转矩这三个量随参数的变化规律。
1 三相异步电动机的机械特性文
三相异步电动机的机械特性是指电动机的转速n与电磁转矩Tem之间的关系。由于转速n与转差率S有一定的对应关系，所以机械特性也常用Tem＝f（s）的形式表示。三相异步电动机的电磁转矩表达式有三种形式，即物理表达式、参数表达式和实用表达式。物理表达式反映了异步电动机电磁转矩产生的物理本质，说明了电磁转矩是由主磁通和转子有功电流相互作用而产生的。参数表达式反映了电磁转矩与电源参数及电动机参数之间的关系，利用该式可以方便地分析参数变化对电磁转矩的影响和对各种人为特性的影响。实用表达式简单、便于记忆，是工程计算中常采用的形式。
摘 要：阐述了异步电动机结构，运行可靠、价格低、维护方便等一系列的优点，目前，异步电动机的电力拖动已被广泛地应用在各个工业电气自动化领域中。就三相异步电动机的机械特性出发，主要简述电动机的启动、制动、调速等技术问题。
关键词：三相异步电动机；电力拖动机具有结构简单、运行可靠、价格低、维护方便等一系列的优点，因此，异步电动机被广泛应用在电力拖动系统中。尤其是随着电力电子技术的发展和交流调速技术的日益成熟，使得异步电动机在调速性能方面大大提高。目前，异步电动机的电力拖动已被广泛地应用在各个工业电气自动化领域中。就三相异步电动机的机械特性出发，主要简述电动机的启动，制动、调速等技术问题。
三相异步电机的机械特性
磁路
电流 I
磁通 φ
电动势 E
磁通势 F
电压降 U=IR 磁压降
电阻 R
磁阻 Rm Hl F Rm
欧姆定律
磁路欧姆定律
I U(E) R
F(NI )
Rm
AC
涡流：线圈中通交流时，产生的磁通是交变的。因此， 不仅要在线圈中产生感应电势，而且在铁心内也要产生 感应电势和感应电流，这种感应电流就叫做“涡流”。
直流电机的用途
采用直流电源（干电池、蓄电池）的电机 输出同样的力矩，要比交流电机小得多
（生活中需要电动机，又使用电池的便携产品）
热水器水泵电机、汽车散热风扇、电脑风扇、收录机电机、USB 吸尘器、电动自行车、飞机、剔须刀、VCD、激光扫描仪、激 光打字机、电动玩具、振动功能……
大型轧钢机、大型精密机床、矿井卷扬机等严格要求线速度一致 的地方；
T
K
SR2U12R22 SX 20 2KSR2U 2
R22 SX 20 2
5.27
U,U1---定子绕组相电压，电源电压；
R2------转子每相绕组的电阻；
X20-----n=0时转子每相绕组的感抗；
K-------三相异步电动机的转矩常数。K
m1P
2f1
选择合适的电机型号
第五章 交流电动机的工原理及特性
电动机铭牌上的额定数据 型号 如Y90S-4 额定功率PN (输出的机械功率) 额定电压 UN (220/380V △/Y) 额定频率f (50HZ) 额定电流IN (10.35/5.9A △/Y) 额定转速nN (额定转差率SN) 工作方式 (定额：连续,短时重复,短时 ) 温升(或绝缘等级) 电动机重量
因此选用高速电机较为经济.如极对数P＝1或2
三相异步电动机的机械特性
1. 降低定子端电压U1的人为机械特性
2）最大转矩点
横坐标Tm ：
最大转矩Tm与定子端电压U1的 平方成正比，降低U1之后，最 大转矩Tm的值大幅度减小。
纵坐标nm： nm=n1(1-sm) =n1(1-R2/X2)
用平滑曲线连接这三个坐标 点，就得到了降低定子端电 压U1的人为机械特性。
1.降低定子端电压U1的人为机械特性
降低电压U1对电动机运行 性能的影响：
TL1 TL2
1）最大转矩Tm和启动转矩Tst 都大幅度减小，过载能力λ和 启动能力Kst都显著降低。 如果U1降低得太多，可能会因 为Tst<TL而无法启动，也可能 会因为Tm<TL而堵转。
长期欠压过载运行，电动机绕组的温升会超过允许值而损害 绕组的绝缘，甚至会烧毁绕组。
电动机的电气控制电路要设置欠电压保护：
1）电动机通常由接触器控制。接触器在其线圈电压下降到 85%UN时，会自动释放而切断电路，自带欠压保护功能。 2）低压断路器上有失压脱扣器，在低电压时会自动跳闸， 有欠压失压保护功能。 3）有时需要设置专门的欠电压继电器作欠压保护。
TL1 TL2 TL3
TL4
可采取的措施2：
电动机的固有机械特性
√ 换一台启动转矩Tst大于TL3，额定转矩TN与TL3相当的电动
机，带动TL3重新启动。
运行情况：
TN ≈ TL3，电动机会运行在额定状态附近，运行性能好。
★通过固有机械特性判断电机运行情况
参考答案4：
电动机带负载TL4不能启动， 绕组很快就会烧毁。
第1步： 从产品目录中查出电动机的外部参数值，计算出Tm和sm的 值，代入实用表达式，得到T = f ( s )。在转差率s的取值范 围内，计算出电动机若干个运行点的（s，T）坐标值。
三相异步电动机的调速方法与特性(精)
由定子绕组展开图知： 只要改变一相绕组中一半元 件的电流方向即可改变磁极 对数。当T1、T2、T3外接三 相交流电源，而T4、T5、T6 对外断开时，电动机的定子 绕组接法为△，极对数为2P， 当T4、T5、T6外接三相交流 电源，而T1、T2、T3连接在 一起时，电动机定子绕组的 接法为YY，极对数为P，从 而实现调速，其控制电路图 如所示。
5.5 三相异步电动机的调速
由 可知，若要改变异步电动机的转速，可以有 以下三种方法： （1）改变电动机的磁极对数p。 （2）改变电动机的电源频率f1。 （3）改变电动机的转差率s。 下面对各种调速方法的原理及特点做一简单 介绍。
60 f1 n n1 (1 s ) (1 s ) p
5.5.1 变极调速
△/YY变极调速控制原理图
其工作情况为：合上刀开 关QS后，当KM3闭合而KM1、 KM2断开时，电动机定子绕组 为D接法，电动机低速启动。当 KM3断开，而KM2、KM1闭合 时，电动机的定子绕组接成YY， 电动机高速运行。△/YY接法的 调速方式适用于恒功率负载， 其机械特性如图4.25所示。 由机械特性知，变极调速 时电动机的转速几乎是成倍的 变化，因此调速的平滑性差， 但是稳定性较好，特别是低速 启动转矩大。
1 1 1 N 1 1 N N
1 1
1 1
1 1
1
1
1
5.5.3 改变转差率调速
改变转差率的方法主要有三 种：定子调压调速、转子电路串电 阻调速和串级调速。下面分别介绍。 1．定子调压调速 图为定子调压的机械特性曲线， 由图可知对恒转矩负载而言，其调 速范围很窄，实用价值不大，但对 于通风机负载而言，其负载转矩TL 随转速的变化而变化，如图中虚线 所示。可见其调速范围很宽，所以 目前大多数的风扇采用此法。 但是这种调速方法在电动机转 速较低时，转子电阻上的损耗较大， 使电动机发热较严重，所以这种调 速方法一般不宜在低速下长时间运 图 行。
7.1 三相异步电动机的机械特性
R2 sm பைடு நூலகம் X1 X 2
m1 pU12 Tm ) 4πf1 ( X 1 X 2
Tm
分析可得：
1）当电动机各参数及电源频率不变时，Tm与U12成正比，sm则不变，且与U1 无关。 成反比。 2）当电源频率及电压不变时，sm与Tm近似地与 X1 X 2
成正比。 值无关， sm则与 R2 3）Tm与 R2
I2
——转子电路的功率因数 cos φ2
cos φ2 s R2 s )2 X 2 2 ( R2
R2 2 s 2 X 2 2 R2
0
cos φ2
， Tem , I 2 cos φ2
用于定性分析异步电机在各运转状态下的物理过程。
一、三相异步电动机机械特性的三种表达式
n n （ 1500 （ 1 0.036 ） 1446 r/min 1 1 s）
由上例可知，实用表达式常用于工程计算。
练习：已知一台三相异步电动机，额定功率 PN=150kW , 额定
电压380V ,额定转速nN=1460r/min，过载倍数KT ＝2.4。当转子 回路不串入电阻时，（1）求其转矩的实用表达式；（2）问电
（4）起动点D：
2Tm 2 1975 Tst 616 N m 1 0.16 1 sm 0.16 1 sm 1
二、三相异步电动机的固有和人为机械特性 2、人为机械特性
/s m1 pU12 R2 Tem 2 2 2πf1 ( R R / s ) ( X X ) 2 1 2 1
/s m1 pU12 R2 Tem 2 2 2πf1 ( R R / s ) ( X X ) 2 1 2 1
三相异步电动机的机械特性
三相异步电动机的机械特性
1.三相异步电动机的电磁转矩
三相异步电动机的转矩:
三相异步电动机的转矩是由旋转磁场的每极磁通Φ与转子电流I2相互作用而生成的。
它与Φ和I2 的乘积成正比，此外，它还与转子电路的功率因素cosφ2 有关。
转矩表达式：
式中，K——与电动机结构参数、电源频率有关的一个常数；
U1，U ——定子绕组相电压，电源相电压；
R2——转子每相绕组的电阻；
X20——电动机不动（n＝0）时转子每相绕组的感抗。
2.三相异步电动机的固有机械特性
固有机械特性：
异步电动机在额定电压和额定频率下，用规定的接线方式，定子和转子电路中的不串联任何电阻或电抗时的机械特性称为固有（自然）机械特性。
电动机的抱负空载转速：
额定转矩及额定转差率：S=(N1-N2)/N1
转矩－转差率特性的有用表达式，即规格化转矩－转差率特性。
3.三相异步电动机的人为机械特性
人为机械特性：
异步电动机的机械特性与电动机的参数有关，也与外加电源电压、电源频率有关，将关系式中的参数人为地加以转变而获得的特性称为异步电动机的人为机械特性。
电压U的变化对抱负空载转速no和临界转差率Sm不发生影响，但最大转矩Tmax与U2成正比，当降低定子电压时，no和Sm不变，而Tmax大大减小。
在同一转差率状况下，人为特性与固有特性的转矩之比等于电压的平方之比。
因此在绘制降低电压的人为特性时，是以固有特性为基础，在不同的S处，取固有特性上对应的转矩乘降低电压与额定电压比值的平方，即可作出人为特性曲线：
在电动机定子电路中外串电阻或电抗后，电动机端电压为电源电压减去定子外串电阻上或电抗上的压降，致使定子绕组相电压降低。
三相异步电动机的机械特性
起动转矩与额定转矩的比值称为起动转矩倍 数或堵转转矩倍数，用kst表示，则有：
一般异步电动机起动转矩倍数为0.8～1.2。
Tst k st TN
r1sm 2 实用表达式： r 1 T 2 r1sm sm s Tm r22 r2 r22 2 s 2 2r1 2 s r2 s s s sm m
降电压人为机械特性曲线 Tm∝U12；Tst∝U12；n1和sm与电压无关
TL1-恒转矩负载特性、TL2-风机类负载特性
（2）定子回路串入对称电阻的人为机械特性
当定子电阻r1 增大时，同步 转速n1不变， 但临界转矩Tm、 临界转差率sm、 起动转矩Tst都 变小
定子回路串入对称电阻的 接线图和人为机械特性
从产品目录查出该异步电动机的数据PN、nN、 λm应用实用公式就可方便得出机械特性表达 式。
2.固有机械特性
异步电动机的固有机 械特性是指U1=U1N， ƒ1=ƒ1N，定子三相绕 组按规定方式连接， 定子和转子电路中不 外接任何元件时测得 的机械特性n =ƒ（T） 或T=ƒ（s）曲线。 对于同一台异步电动 机有正转（曲线1） 和反转（曲线2）两 条固有机械特性。
机械特性曲线
在电压、频率及绕组参数一定的条件下，电磁转矩T 与转差率s之间的关系可用曲线表示如图所示。
异步电动机机械特性
①最大转矩Tm
最大转矩Tm是T=ƒ（s）的极值点，最大转 矩为： 3 pU 2
Tm 4f1 r1 r12 ( x1 x2 ) 2
1
最大转矩对应的临界转差率为：
三相异步电动机的机械特性
三相异步电动机的运行特性摘要：本章介绍了三相异步电动机的机械特性的三个表达式。
固有机械特性和人为机械特性，阐述了三相异步电动机的起动、调速和制动的各种方法、特点和应用5.1三相异步电动机的运行特性三相异步电动机的运行特性就是三相异步电动机的运行工作时的机械特性。
和直流电动机一样，三相异步电动机的机械特性也是指电磁转矩与转子转速之间的关系。
由于转子转速与同步转速、转差率存在下列关系，即（5.1）则三相异步电动机的机械特性用曲线表示时，习惯上纵坐标同时表示转速和转差率，横坐标表示电磁转矩。
三相异步电动机的机械特性有三种表达式，现介绍如下：5.1.1机械特性的物理表达式由上一章三相异步电动机的转矩关系知，三相异步电动机转矩的一般表达式为（5.2）式中为三相异步电动机的转矩系数，是一常数；为三相异步电动机的气隙每极磁通量；为转子电流的折算值；为转子电路的功率因数；式（5.2）表明了电磁转矩与磁通量和转子电流的有功分量的乘积成正比，它是电磁力定律在三相异步电动机的应用，它从物理特性上描述了三相异步电动机的运行特性，因此这一表达式又称为三相异步电动机的物理表达式。
仅从式（5.2）不能明显地看出电磁转矩与转差率之间的变化规律。
要从分析气隙每极磁通量，转子相电流，以及为转子功率因数与转差率之间的关系，间接地找出其变化规律。
现分析如表5.1所示。
根据表5.1中的分析，可作出曲线、和分别如图5.2、5.3、5.4所示，据此可得出图5.1所示的机械特性曲线。
曲线分为两段：当较小时(),变化不大，，电磁转矩与转子相电流成正比关系，表现为AB段近似为直线，称为直线部分；当较大时()，如，减少近一半，很小，尽管转子相电流增大，有功电流不大，使电磁转矩反而减小了，此时表现为段，段为曲线段，称为曲线部分。
由此分析知，三相异步电动机的机械特性在某转差率下，产生最大转矩，即点称为最大转矩点，相应的转矩为称为最大转矩，对应的转差率称为临界转差率。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
（3）启动点A Tst 为电动机 Tem Tst 。 电动机工作在启动点A时n=0，s=1， 的启动转矩或称堵转转矩。电动机的启动转矩必须大于电动 机所带负载的转矩，电动机才能启动，因此，堵转转矩的大 小是衡量电动机启动性能好坏的技术指标。由机械特性方程 式知： 2
Tst
（4-6） 由式可知：启动转矩 Tst 的大小与电源电压的平方成正比， 同时也受转子电阻大小的影响。为了衡量电动机的启动性能， TN Tst 我们用电动机的启动转矩 与额定转矩 之比来表示。 T K Km 即 被称之为启动转矩倍数，反映电动机的 T ， K 启动能力。一般 在 1.8 m ～2.0之间。 （4）额定点N n n P n n ,s s , T T 9 550 n n ， nN 由 电动机工作在额定点时， 铭牌可知，TN 可通过铭牌参数计算得到。额定工作点是希望的 工作点。
m1PU1
2
由此进一步可知： ① 三相异步电动机的临界转差率S m 与电源电压U1无关，只与 成正比，所以改变转子 电动机自身的参数有关，且与转子电阻 R2 的大小（如在绕线型异步电动机转子电路中串接变阻器） 电阻 R2 即可改变临界转差率 Sm 。 无关。 ② 三相异步电动机的最大电磁转矩 Tm 与转子电阻 R2 因此，电动机转子电阻的大小不会影响电动机的最大转矩，只会 影响产生最大转矩时的转差率。 ③ 最大电磁转矩 Tm 的大小与电源电压U1的平方成正比，而 临界转差率 S m 却与电源电压无关。最大电磁转矩 Tm 与额定转矩 T m 的值在电动机技术数据资料中 之比叫过载能力， 即 ， T 可查到：一般异步电动机 m 在1.6～2.5之间，特殊用途的电动机 （如起重、冶金用电动机）的 m 值在3.3～3.4之间。m 是异步电 动机的一个重要参数，反映电动机承受负载波动的能力。
由图可见整个机械特性可以分成两个部分。 （1）H-P部分 即sm>s>0范围内。在这一部分，随着 电磁转矩 Tem 的增加，转速降低。根据电力系统稳定运 行的条件，这部分为稳定运行工作部分，电动机应工作 于这一范围内。此时机械特性曲线近似为一条直线。 （2）P-A部分 即1>s>sm范围内。这一部分随着转矩 的减小，转速也减小。此区域称为不稳定运行区域，三 相异步电动机一般不能稳定地工作于这一范围。因此， 有时也将称这一部分为非工作部分。 为了进一步描述三相异步电动机机械特性的特点， 下面重点研究几个反映电动机工作的特殊点。 （1）理想空载点H 此时n=n1, s=0。因转子电流I2=0，定子电流I1=I0， 所以电磁转矩Tem=0。
（2）最大转矩点P
对于三相异步电动机而言，通过数学求导，令 dTem/ds=0 分析可知，产生最大转矩 Tm 时的临界转差率 为 Sm R2 Sm 2 2 R12 X 1 X （4-4） 进而可求得最大电磁转矩Tm为； m PU （4-5） T
m 2 2 2 4f1 R1 R1 X 1 X 1 2 1
4.1 三相异步电动机的机械特性 电动机作为一种将电能转化成机械能，从而 带动其他机械进行工作的设备，我们最关心的是 电动机的机械特性。所谓三相异步电动机的机械 特性是指在一定条件下，电动机的转速n与转矩 Tem之间的关系n=f（Tem）。三相异步电动机的转 n n s 速n与转差率s之间存在一定关系： n ，所以 三相异步电动机的机械特性也往往用Tem=f（s） 的形式表示。
1 1
4.1.1 机械特性的表达式
根据前面章节的学习，我们知道三相异步电动机的等效电路图 可以化简为如图4.1所示。 从电路的观点分析知，电磁功率为；
P em m 1I 2
2
R2 s
图4.1 三相异步电动机T型等效电路图
一、电磁转矩的物理表达式
我们把 ' cos （4-1） Tem CT 1I 2 2 式中 CT——转矩常数 上式表明电动机的电磁转矩与主磁通成正比，与转子电流 的有功分量成正比，从物理概念上反映了Tem、 I 2' cos 2 、Φ1 三者的关系，并符合左手定则。 二、电磁转矩的参数表达式 U I 转子电流折算值为 （4-2） R R X X
ห้องสมุดไป่ตู้
m1 I 2
2
2f1 p
R2 s
m1 pU12
2 R2 2 2f1 R1 X 1 X 2 s
R2 s
4.1.2 三相异步电动机的机械特性
1．固有机械特性 三相异步电动机的固有机 械特性是指电动机工作在额定 电压和额定频率下，按规定方 法接线，定子、转子外接电阻 为零时，n（或s）与Tem的关系。 对于某一台确定的电动机 而言。机械特性方程式表明， 此时只有n（或s）与Tem是变量， 其余均为确定值。因为机械特 性方程式是一个二次方程，故 Tem存在最大值。以Tem为横轴， n（或s）为纵轴，做出如图4.2 所示的三相异步电动机固有机 图4.2 三相异步电动机的 械特性曲线。 固有机械特性曲线
2 1 2
Tem
PMEC 公式进行整理（利用前面已学的公式）可得；
1
2
s
1
2
2
电磁转矩为
Tem
Pem
（4-3） 可见， （4-3）方程，它清楚地表示了异步电动机电磁转 矩、转差率与电动机各参数之间的关系，下面我们就从这个公 式出发，分析三相异步电动机的固有特性及人为机械特性。
1
由于 X1 X 2' R1 忽略Ｒ１得近似表达式；
Sm 2 2 R12 X 1 X R2
Ｘ ＋Ｘ＇
１ ２
＇ R ２
m1 pU12 Tm ' 2 2 4 f （ X X ） 1 1 2 2 4f1 R1 R1 X 1 X