2020高考数学(文科)二轮专题精讲《空间几何体》1
2020版高考数学大二轮文科通用版 教师课件:专题四 第1讲 空间几何体及三视图

其三视图如图所示.如果网格纸上小正方形的边长为1,那么该几何
体的体积为
.
解析:在正方体中还原该几何体,如图所示.
该几何体的体积 V=43-1×(2+4)×2×4=40.
2
答案:40
5.(2019天津,文12)已知四棱锥的底面是边长为 2 的正方形,侧棱长
均为 5 .若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点,另
1.旋转体的侧面积和表面积
名称 图形
表面积
圆柱
S=2π r2+2π rl =2π r(r+l)
侧面积 S 侧=2π rl
圆锥
S=π r2+π rl =π r(形 圆台 球
表面积
S=π (r'2+r2+ r'l+rl)
侧面积 S 侧=π (r+r')l
S=4π R2
2.柱体、锥体、台体、球体的体积公式
答案:(1)B (2)C
考点1 考点2 考点3 考点4
考点1 考点2 考点3 考点4
角度二 空间几何体的体积
例3(1)(2018浙江,3)某几何体的三视图如图所示(单位:cm),则该几
何体的体积(单位:cm3)是( )
A.2 B.4 C.6 D.8
(2)(2018全国Ⅱ,文16)已知圆锥的顶点为S,母线SA,SB互相垂直,SA
A.2 3 B.2 2 C.2 D. 3
考点1 考点2 考点3 考点4
解析:(1)如图,三棱锥 A-BCD 即为所求几何体,根据题设条件,知 辅助的正方体棱长为 2,CD=1,BD=2 2,BC= 5,AC=2,AB=3,AD= 5, 则最长棱为 AB,长度为 3.
2020年高考文科数学二轮复习:专题四 第一讲 空间几何体
二、填空题
13.已知一个几何体的三视图是三个全等的边长为1的正方形,如图所示,则它的体积为________.
解析:该几何体是一个单位正方体被截去了一部分,其直观图如图所示,其体积为1- × ×1×1×1= .
答案:
14.如图所示是一个几何体的三视图,则该几何体的体积为________.
解析:由题可知该几何体由两个相同的半圆柱和一个长方体拼接而成,因此该几何体的体积V=1×2×4+π×12×2=8+2π.
A.6B.3
C.2 D.3
解析:由三视图可知,该几何体是一个直三棱柱,其底面为侧视图,该侧视图是底边为2,高为 的三角形,正视图的长为三棱柱的高,故h=3,所以几何体的体积V=S·h= ×3=3 .
答案:B
2.某个几何体的三视图如图所示,其中正视图中的圆弧是半径为2的半圆,则该几何体的表面积为()
解析:由题意知,该三棱柱可以看作是长方体的一部分,且长方体同一顶点处的三条棱长分别为3、4、12,又∵三棱柱的外接球即为长方体的外接球,(2R)2=32+42+122,∴R= .故选C.
答案:C
5.一块石材表示的几何体的三视图如图所示,将该石材切削、打磨,加工成球,则能得到的最大球的半径等于()
A.1B.2
答案:B
7.如图是一个几何体的三视图,则该几何体任意两个顶点间距离的最大值是D
8.一空间几何体的三视图如图所示,则该几何体的体积为()
A.12B.6
C.4D.2
解析:该几何体为四棱锥PABCD,其中PA⊥平面ABCD,如图,
则该几何体的体积为V= ×2× ×(2+1)×2=2.
C.3D.4
解析:由三视图可知该几何体是一个直三棱柱,底面为直角三角形,高为12,如图所示,其中AC=6,BC=8,∠ACB=90°,则AB=10.要使该石材加工成的球的半径最大,只需球与直三棱柱的三个侧面都相切,则半径r等于直角三角形ABC的内切圆半径,即r= =2,故能得到的最大球的半径为2,故选B.
湖南省2020年高考数学第二轮复习 专题五 立体几何第1讲 空间几何体的三视图、表面积及体积 文
专题五立体几何第1讲空间几何体的三视图、表面积及体积真题试做1.(2020·湖南高考,文4)某几何体的正视图和侧视图均如图1所示,则该几何体的俯视图不可能是( ).图12.(2020·天津高考,文10)一个几何体的三视图如图所示(单位:m),则该几何体的体积为__________ m3.3.(2020·湖北高考,文15)已知某几何体的三视图如图所示,则该几何体的体积为______.4.(2020·湖北高考,文19)某个实心零部件的形状是如图所示的几何体,其下部是底面均是正方形,侧面是全等的等腰梯形的四棱台A1B1C1D1ABCD,上部是一个底面与四棱台的上底面重合,侧面是全等的矩形的四棱柱ABCDA2B2C2D2.(1)证明:直线B1D1⊥平面ACC2A2;(2)现需要对该零部件表面进行防腐处理.已知AB=10,A1B1=20,AA2=30,AA1=13(单位:厘米),每平方厘米的加工处理费为0.20元,需加工处理费多少元?考向分析通过对近几年高考试题的分析可看出,空间几何体的命题形式比较稳定,多为选择题或填空题,有时也出现在解答题的某一问中,题目常为中、低档题.考查的重点是直观图、三视图、面积与体积等知识,此类问题多为考查三视图的还原问题,且常与空间几何体的表面积、体积等问题交会,是每年的必考内容.预计在2020年高考中:对空间几何体的三视图的考查有难度加大的趋势,通过此类题考查考生的空间想象能力;对表面积和体积的考查,常见形式为蕴涵在两几何体的“切”或“接”形态中,或以三视图为载体进行交会考查,此块内容还要注意强化几何体的核心——截面以及补形、切割等数学思想方法的训练.热点例析热点一空间几何体的三视图与直观图【例1】(1)将长方体截去一个四棱锥,得到的几何体如下图所示,则该几何体的侧(左)视图为( ).(2)若某几何体的三视图如下图所示,则这个几何体的直观图可以是( ).规律方法 (1)三视图的正(主)视图、侧(左)视图、俯视图分别是从物体的正前方、正左方、正上方看到的物体轮廓线的正投影围成的平面图形,反映了一个几何体各个侧面的特点.正(主)视图反映物体的主要形状特征,是三视图中最重要的视图;俯视图要和正(主)视图对正,画在正(主)视图的正下方;侧(左)视图要画在正(主)视图的正右方,高度要与正(主)视图平齐;(2)要注意到在画三视图时,能看到的轮廓线画成实线,看不到的轮廓线画成虚线; (3)A .32B .16+16 2C .48 D.16+32 2(2)一个水平放置的平面图形的斜二测直观图是一个底角为45°,腰和上底长均为1的等腰梯形,则这个平面图形的面积是( ).A.12+22 B .1+22 C .1+ 2 D .2+ 2 热点二 空间几何体的表面积与体积【例2】(2020·福建高考,文20)如图,在四棱锥P ABCD 中,PA ⊥底面ABCD ,AB ⊥AD ,点E 在线段AD 上,且CE ∥AB .(1)求证:CE ⊥平面PAD ;(2)若PA =AB =1,AD =3,CD =2,∠CDA =45°,求四棱锥P ABCD 的体积.规律方法 (1)求几何体的体积问题,可以多角度、多方位地考虑.对于规则的几何体的体积,如求三棱锥的体积,采用等体积转化是常用的方法,转化的原则是其高与底面积易求;对于不规则几何体的体积常用割补法求解,即将不规则几何体转化为规则几何体,以易于求解.(2)求解几何体的表面积时要注意S 表=S 侧+S 底.(3)对于给出几何体的三视图,求其体积或表面积的题目关键在于要还原出空间几何体,并能根据三视图的有关数据和形状推断出空间几何体的线面关系及相关数据,至于体积或表面积的求解套用对应公式即可.变式训练2 已知某几何体的三视图如下图所示,其中正(主)视图中半圆的半径为1,则该几何体的体积为( ).A .24-32πB .24-13πC .24-πD .24-12π热点三 多面体与球【例3】已知正四棱锥的底面边长为a ,侧棱长为2a . (1)求它的外接球的体积; (2)求它的内切球的表面积.规律方法 (1)涉及球与棱柱、棱锥的切、接问题时,一般过球心及多面体中的特殊点或线作截面,把空间问题化归为平面问题,再利用平面几何知识寻找几何体中元素间的关系.(2)若球面四点P ,A ,B ,C 构成的线段PA ,PB ,PC 两两垂直,且PA =a ,PB =b ,PC =c ,则4R 2=a 2+b 2+c 2,把有关元素“补形”成为一个球内接正方体(或其他图形),从而显示出球的数量特征,这种方法是一种常用的好方法.变式训练3 如图所示,在四棱锥P ABCD 中,底面ABCD 是边长为a 的正方形,PD ⊥底面ABCD ,且PD =a ,PA =PC =2a .若在这个四棱锥内放一球,则此球的最大半径是__________.思想渗透立体几何中的转化与化归思想求空间几何体的体积时,常常需要对图形进行适当的构造和处理,使复杂图形简单化,非标准图形标准化,此时转化与化归思想就起到了至关重要的作用.利用转化与化归思想求空间几何体的体积主要包括割补法和等体积法,具体运用如下:(1)补法是指把不规则的(不熟悉或复杂的)几何体延伸或补成规则(熟悉的或简单的)的几何体,把不完整的图形补成完整的图形;(2)割法是指把复杂的(不规则的)几何体切割成简单的(规则的)几何体;(3)等积法的前提是几何图形(或几何体)的面积(或体积)通过已知条件转化为易求的面积(体积)问题.【典型例题】如图,在直三棱柱ABC A 1B 1C 1中,AB =AC =5,BB 1=BC =6,D ,E 分别是AA 1和B 1C 的中点.(1)求证:DE ∥平面ABC ; (2)求三棱锥E BCD 的体积.(1)证明:取BC 中点G ,连接AG ,EG .因为E 是B 1C 的中点,所以EG ∥BB 1,且EG =12BB 1.由直棱柱知,AA 1BB 1.而D 是AA 1的中点,所以EG AD ,所以四边形EGAD 是平行四边形,所以ED ∥AG . 又DE 平面ABC ,AG ⊂平面ABC , 所以DE ∥平面ABC .(2)解:因为AD ∥BB 1,所以AD ∥平面BCE , 所以V E BCD =V D BCE =V A BCE =V E ABC .由(1)知,DE ∥平面ABC ,所以V E ABC =V D ABC =13AD ·12BC ·AG =16×3×6×4=12.1.(2020·山东济南三月模拟,4)如图,正三棱柱ABC A 1B 1C 1的各棱长均为2,其正(主)视图如图所示,则此三棱柱侧(左)视图的面积为( ).A .2 2B .4 C. 3 D .2 32.(2020·安徽安庆二模,7)一空间几何体的三视图如图所示(正(主)、侧(左)视图是两全等图形,俯视图是圆及圆的内接正方形),则该几何体的表面积是( ).A .7π cm 2B .(5π+43)cm 2C .(5π+23)cm 2D .(6π+27-2)cm 23.(2020·北京丰台区三月月考,4)若某空间几何体的三视图如图所示,则该几何体的体积是( ).A .20-2πB .20-23πC .40-23πD .40-43π4.(2020·湖南株洲下学期质检,14)一个三棱锥的正(主)视图、侧(左)视图、俯视图如下,则这个三棱锥的体积为__________,其外接球的表面积为__________.5.已知正四面体的外接球半径为1,则此正四面体的体积为__________.6.正六棱锥P ABCDEF 中,G 为PB 的中点,则三棱锥D GAC 与三棱锥P GAC 体积之比为__________.7.如图,在等腰梯形ABCD 中,AB =2DC =2,∠DAB =60°,E 为AB 的中点,将△ADE 与△BEC 分别沿ED ,EC 向上折起,使A ,B 重合,求形成三棱锥的外接球的体积.参考答案命题调研·明晰考向真题试做1.C 解析:若为C 选项,则主视图为:故不可能是C 选项.2.30 解析:由几何体的三视图可知:该几何体的上部为平放的直四棱柱,底部为长、宽、高分别为4 m,3 m,2 m 的长方体.∴几何体的体积V =V 直四棱柱+V 长方体=(1+2)×12×4+4×3×2=6+24=30(m 3).3.12π 解析:该几何体是由3个圆柱构成的几何体,故体积V =2×π×22×1+π×12×4=12π.4.解:(1)因为四棱柱ABCD A 2B 2C 2D 2的侧面是全等的矩形,所以AA 2⊥AB ,AA 2⊥AD .又因为AB ∩AD =A ,所以AA 2⊥平面ABCD . 连接BD ,因为BD ⊂平面ABCD ,所以AA 2⊥BD . 因为底面ABCD 是正方形,所以AC ⊥BD .又已知平面ABCD ∥平面A 1B 1C 1D 1,且平面BB 1D 1D ∩平面ABCD =BD , 平面BB 1D 1D ∩平面A 1B 1C 1D 1=B 1D 1,所以B 1D 1∥BD .于是由AA 2⊥BD ,AC ⊥BD ,B 1D 1∥BD ,可得AA 2⊥B 1D 1,AC ⊥B 1D 1. 又因为AA 2∩AC =A ,所以B 1D 1⊥平面ACC 2A 2.(2)因为四棱柱ABCD A 2B 2C 2D 2的底面是正方形,侧面是全等的矩形,所以S 1=S 四棱柱上底面+S四棱柱侧面=(A 2B 2)2+4AB ·AA 2=102+4×10×30=1 300(cm 2).又因为四棱台A 1B 1C 1D 1ABCD 的上、下底面均是正方形,侧面是全等的等腰梯形(其高为h ),所以S 2=S 四棱台下底面+S 四棱台侧面=(A 1B 1)2+4×12(AB +A 1B 1)h=202+4×12×(10+20)132-⎣⎢⎡⎦⎥⎤12×(20-10)2=1 120(cm 2).于是该实心零部件的表面积为S =S 1+S 2=1 300+1 120=2 420(cm 2), 故所需加工处理费为0.2S =0.2×2 420=484(元). 精要例析·聚焦热点热点例析【例1】 (1)D (2)B 解析:(1)被截去的四棱锥的三条可见侧棱中有两条为正方体的面对角线,它们在右侧面上的投影与右侧面(正方形)的两条边重合,另一条为正方体的对角线,它在右侧面上的投影与右侧面的对角线重合,对照各图及对角线方向,只有选项D 符合.(2)由正(主)视图可排除A ,C ;由侧(左)视图可判断该几何体的直观图是B.【变式训练1】 (1)B (2)D 解析:(1)由三视图知原几何体是一个底面边长为4,高是2的正四棱锥.如图:∵AO =2,OB =2,∴AB =2 2.又∵S 侧=4×12×4×22=162,S 底=4×4=16,∴S 表=S 侧+S 底=16+16 2.(2)如图,设直观图为O ′A ′B ′C ′,建立如图所示的坐标系,按照斜二测画法的规则,在原来的平面图形中,OC ⊥OA ,且OC =2,BC =1,OA =1+2×22=1+2,故其面积为12×(1+1+2)×2=2+ 2.【例2】 (1)证明:因为PA ⊥平面ABCD ,CE ⊂平面ABCD ,所以PA ⊥CE .因为AB ⊥AD ,CE ∥AB ,所以CE ⊥AD . 又PA ∩AD =A ,所以CE ⊥平面PAD . (2)解:由(1)可知CE ⊥AD .在Rt△ECD 中,DE =CD ·cos 45°=1,CE =CD ·sin 45°=1. 又因为AB =CE =1,AB ∥CE , 所以四边形ABCE 为矩形.所以S 四边形ABCD =S 矩形ABCE +S △ECD =AB ·AE +12CE ·DE =1×2+12×1×1=52.又PA ⊥平面ABCD ,PA =1,所以V 四棱锥P ABCD =13S 四边形ABCD ·PA =13×52×1=56.【变式训练2】 A 解析:由三视图可知该几何体为一个长、宽、高分别为4,3,2的长方体,剖去一个半圆柱而得到的几何体,其体积为2×3×4-12π×1×3,即24-32π.【例3】 解:如图所示,△SAC 的外接圆是外接球的一个大圆,∴只要求出这个外接圆的半径即可,而内切球的球心到棱锥的各个面的距离相等,∴可由正四棱锥的体积求出其半径.(1)设外接球的半径为R ,球心为O ,则OA =OC =OS ,∴O 为△SAC 的外心,即△SAC 的外接圆半径就是球的半径. ∵AB =BC =a ,∴AC =2a .∵SA =SC =AC =2a ,∴△SAC 为正三角形.由正弦定理得2R =AC sin∠ASC =2a sin 60°=263a ,因此R =63a ,V 外接球=43πR 3=8627πa 3. (2)如图,设内切球的半径为r ,作SE ⊥底面于E ,作SF ⊥BC 于F ,连接EF , 则有SF =SB 2-BF 2=(2a )2-⎝ ⎛⎭⎪⎫a 22=72a ,S △SBC =12BC ·SF =12a ×72a =74a 2, S 棱锥全=4S △SBC +S 底=(7+1)a 2.又SE =SF 2-EF 2=⎝ ⎛⎭⎪⎫72a 2-⎝ ⎛⎭⎪⎫a 22=62a ,∴V 棱锥=13S 底·SE =13a 2×62a =66a 3,∴r =3V 棱锥S 棱锥全=3×66a 3(7+1)a 2=42-612a ,S 内切球=4πr 2=4-73πa 2. 【变式训练3】 12(2-2)a 解析:当且仅当球与四棱锥的各个面都相切时,球的半径最大.设放入的球的半径为r ,球心为O ,连接OP ,OA ,OB ,OC ,OD ,则把此四棱锥分割成四个三棱锥和一个四棱锥,这些小棱锥的高都是r ,底面分别为原四棱锥的侧面和底面,则V P ABCD =13r (S △PAB +S △PBC +S △PCD +S △PAD +S 正方形ABCD )=13r (2+2)a 2.由题意知PD ⊥底面ABCD ,∴V P ABCD =13S 正方形ABCD ·PD =13a 3.由体积相等,得13r (2+2)a 2=13a 3,解得r =12(2-2)a .创新模拟·预测演练1.D2.D 解析:据三视图可判断该几何体是由一个圆柱和一个正四棱锥组合而成的,直观图如图所示:易求得表面积为(6π+27-2)cm 2.3.B 解析:由三视图可知该几何体的直观图为一个正四棱柱,从上表面扣除半个内切球.易求出正四棱柱的底面边长为2,内切球的半径为1,故体积为2×2×5-23π=20-2π3.4.4 29π 5.827 3 解析:首先将正四面体补形为一个正方体,设正四面体棱长为a ,则其对应正方体的棱长为22a ,且由球与正方体的组合关系易知3⎝ ⎛⎭⎪⎫22a 2=(1×2)2,解得a 2=83, ∴正四面体的体积为V =⎝ ⎛⎭⎪⎫22a 3-4×13×12×⎝ ⎛⎭⎪⎫22a 3=13⎝ ⎛⎭⎪⎫22a 3=827 3.6.2∶1 解析:由正六棱锥的性质知,点P 在底面内的射影是底面的中心,也是线段AD的中点.又G 为PB 的中点,设P 点在底面内的射影为O ,则G 点在底面内的射影为OB 的中点M ,且GM ∥PO .又M 为AC 的中点,则GM ⊂平面GAC ,所以点P 到平面GAC 的距离等于点O 到平面GAC 的距离.又因为OM ⊥平面GAC ,DC ⊥平面GAC ,且DC =2OM ,则V D GAC V P GAC =13S △GAC ×DC13S △GAC ×OM =2.7.解:由已知条件知,平面图形中AE =EB =BC =CD =DA =DE =EC =1,∴折叠后得到一个棱长为1的正三棱锥(如图). 方法一:作AF ⊥平面DEC ,垂足为F , F 即为△DEC 的中心,取EC 中点G ,连接DG ,AG , 过球心O 作OH ⊥平面AEC , 则垂足H 为△AEC 的中心,∴外接球半径可利用△OHA ∽△AFG 求得. ∵AG =32,AF =1-⎝⎛⎭⎪⎫332=63,AH =33, ∴OA =AG ·AHAF =32×3363=64,∴外接球体积为43π×OA 3=43·π·6643=68π.方法二:如图,把棱长为1的正三棱锥放在正方体中,显然,棱长为1的正三棱锥的外接球就是正方体的外接球.∵正方体棱长为22, ∴外接球直径2R =3·22, ∴R =64,∴体积为43π·⎝ ⎛⎭⎪⎫643=68π.。
高考数学二轮复习考点知识与题型专题讲解31---空间几何体

高考数学二轮复习考点知识与题型专题讲解第31讲 空间几何体[考情分析] 空间几何体的结构特征是立体几何的基础,空间几何体的表面积和体积是高考的重点与热点,多以选择题、填空题的形式考查,难度中等或偏上.考点一 空间几何体的折展问题核心提炼空间几何体的侧面展开图 1.圆柱的侧面展开图是矩形. 2.圆锥的侧面展开图是扇形. 3.圆台的侧面展开图是扇环.例1 (1)“莫言下岭便无难,赚得行人空喜欢.”出自南宋诗人杨万里的作品《过松源晨炊漆公店》.如图是一座山的示意图,山大致呈圆锥形,山脚呈圆形,半径为40 km ,山高为4015 km ,B 是山坡SA 上一点,且AB =40 km.为了发展旅游业,要建设一条从A 到B 的环山观光公路,这条公路从A 出发后先上坡,后下坡,当公路长度最短时,下坡路段长为( )A .60 kmB .12 6 kmC .72 kmD .1215 km 答案 C解析 该圆锥的母线长为(4015)2+402=160, 所以圆锥的侧面展开图是圆心角为2×π×40160=π2的扇形,如图,展开圆锥的侧面,连接A ′B ,由两点之间线段最短,知观光公路为图中的A ′B ,A ′B =SA ′2+SB 2=1602+1202=200, 过点S 作A ′B 的垂线,垂足为H ,记点P 为A ′B 上任意一点,连接PS ,当上坡时,P 到山顶S 的距离PS 越来越小,当下坡时,P 到山顶S 的距离PS 越来越大, 则下坡段的公路为图中的HB , 由Rt △SA ′B ∽Rt △HSB , 得HB =SB 2A ′B =1202200=72(km).(2)(2022·深圳检测)如图,在三棱锥P -ABC 的平面展开图中,AC =3,AB =1,AD =1,AB ⊥AC ,AB ⊥AD ,∠CAE =30°,则cos ∠FCB 等于( )A.12B.13C.35D.34 答案 D解析 由题意知,AE =AD =AB =1,BC =2, 在△ACE 中,由余弦定理知, CE 2=AE 2+AC 2-2AE ·AC ·cos ∠CAE =1+3-2×1×3×32=1, ∴CE =CF =1,而BF =BD =2,BC =2,∴在△BCF 中,由余弦定理知,cos ∠FCB =BC 2+CF 2-BF 22BC ·CF =4+1-22×2×1=34.规律方法 空间几何体最短距离问题,一般是将空间几何体展开成平面图形,转化成求平面中两点间的最短距离问题,注意展开后对应的顶点和边.跟踪演练1 (1)(多选)如图是一个正方体的展开图,如果将它还原为正方体,则下列说法中正确的是( )A .C ∈GHB .CD 与EF 是共面直线C .AB ∥EFD .GH 与EF 是异面直线 答案 ABD解析 由图可知,还原正方体后,点C 与G 重合, 即C ∈GH ,又可知CD 与EF 是平行直线,即CD 与EF 是共面直线,AB 与EF 是相交直线(点B 与点F 重合),GH 与EF 是异面直线,故A ,B ,D 正确,C 错误.(2)如图,在正三棱锥P -ABC 中,∠APB =∠BPC =∠CP A =30°,P A =PB =PC =2,一只虫子从A 点出发,绕三棱锥的三个侧面爬行一周后,又回到A 点,则虫子爬行的最短距离是( )A .32B .3 3C .23D .2 2 答案 D解析 将三棱锥由P A 展开,如图所示,则∠AP A 1=90°,所求最短距离为AA 1的长度,∵P A =2, ∴由勾股定理可得 AA 1=22+22=2 2.∴虫子爬行的最短距离为2 2.考点二 表面积与体积核心提炼1.旋转体的侧面积和表面积(1)S 圆柱侧=2πrl ,S 圆柱表=2πr (r +l )(r 为底面半径,l 为母线长). (2)S 圆锥侧=πrl ,S 圆锥表=πr (r +l )(r 为底面半径,l 为母线长). (3)S 球表=4πR 2(R 为球的半径). 2.空间几何体的体积公式(1)V 柱=Sh (S 为底面面积,h 为高). (2)V 锥=13Sh (S 为底面面积,h 为高).(3)V 台=13(S 上+S 上·S 下+S 下)h (S 上,S 下为底面面积,h 为高).(4)V 球=43πR 3(R 为球的半径).例2 (1)(2022·全国甲卷)甲、乙两个圆锥的母线长相等,侧面展开图的圆心角之和为2π,侧面积分别为S 甲和S 乙,体积分别为V 甲和V 乙.若S 甲S 乙=2,则V 甲V 乙等于( )A. 5 B .2 2 C.10 D.5104答案 C解析 方法一因为甲、乙两个圆锥的母线长相等,所以结合S 甲S 乙=2,可知甲、乙两个圆锥侧面展开图的圆心角之比是2∶1.不妨设两个圆锥的母线长为l =3,甲、乙两个圆锥的底面半径分别为r 1,r 2,高分别为h 1,h 2, 则由题意知,两个圆锥的侧面展开图刚好可以拼成一个周长为6π的圆, 所以2πr 1=4π,2πr 2=2π,得r 1=2,r 2=1. 由勾股定理得,h 1=l 2-r 21=5,h 2=l 2-r 22=22,所以V 甲V 乙=13πr 21h113πr 22h 2=4522=10.方法二 设两圆锥的母线长为l ,甲、乙两圆锥的底面半径分别为r 1,r 2,高分别为h 1,h 2,侧面展开图的圆心角分别为n 1,n 2, 则由S 甲S 乙=πr 1l πr 2l =n 1πl 22πn 2πl22π=2,得r 1r 2=n 1n 2=2. 由题意知n 1+n 2=2π, 所以n 1=4π3,n 2=2π3,所以2πr 1=4π3l ,2πr 2=2π3l ,得r 1=23l ,r 2=13l .由勾股定理得,h 1=l 2-r 21=53l , h 2=l 2-r 22=223l , 所以V 甲V 乙=13πr 21h113πr 22h 2=4522=10.(2)(多选)(2022·新高考全国Ⅱ)如图,四边形ABCD 为正方形,ED ⊥平面ABCD ,FB ∥ED ,AB =ED =2FB .记三棱锥E -ACD ,F -ABC ,F -ACE 的体积分别为V 1,V 2,V 3,则( )A .V 3=2V 2B .V 3=V 1C .V 3=V 1+V 2D .2V 3=3V 1 答案 CD解析 如图,连接BD交AC 于O ,连接OE ,OF .设AB =ED =2FB =2, 则AB =BC =CD =AD =2, FB =1.因为ED ⊥平面ABCD ,FB ∥ED , 所以FB ⊥平面ABCD ,所以V 1=V E -ACD =13S △ACD ·ED =13×12AD ·CD ·ED =13×12×2×2×2=43,V 2=V F -ABC =13S △ABC ·FB =13×12AB ·BC ·FB =13×12×2×2×1=23.因为ED ⊥平面ABCD ,AC ⊂平面ABCD , 所以ED ⊥AC , 又AC ⊥BD ,且ED ∩BD =D ,ED ,BD ⊂平面BDEF ,所以AC ⊥平面BDEF . 因为OE ,OF ⊂平面BDEF , 所以AC ⊥OE ,AC ⊥OF . 易知AC =BD =2AB =22, OB =OD =12BD =2,OF =OB 2+FB 2=3, OE =OD 2+ED 2=6, EF =BD 2+(ED -FB )2 =(22)2+(2-1)2=3,所以EF 2=OE 2+OF 2,所以OF ⊥OE . 又OE ∩AC =O ,OE ,AC ⊂平面ACE , 所以OF ⊥平面ACE , 所以V 3=V F -ACE =13S △ACE ·OF=13×12AC ·OE ·OF =13×12×22×6×3=2, 所以V 3≠2V 2,V 1≠V 3,V 3=V 1+V 2,2V 3=3V 1, 所以选项A ,B 不正确,选项C ,D 正确. 规律方法 空间几何体的表面积与体积的求法(1)公式法:对于规则的几何体直接利用公式进行求解.(2)割补法:把不规则的图形分割成规则的图形,或把不规则的几何体补成规则的几何体,不熟悉的几何体补成熟悉的几何体.(3)等体积法:选择合适的底面来求体积.跟踪演练2 (1)已知圆锥的顶点为S ,母线SA ,SB 所成角的余弦值为78,SA 与圆锥底面所成角为45°,若△SAB 的面积为515,则该圆锥的侧面积为( ) A .802π B .40 C .402π D .405π 答案 C解析 由圆锥的顶点为S ,母线SA ,SB 所成角的余弦值为78,可得sin ∠ASB =1-⎝⎛⎭⎫782=158, 又△SAB 的面积为515, 可得12SA 2sin ∠ASB =515,即12SA 2×158=515,可得SA =45, 由SA 与圆锥底面所成角为45°, 可得圆锥的底面半径为22×45=210, 则该圆锥的侧面积为π×210×45=402π.(2)(2022·连云港模拟)如图是一个圆台的侧面展开图,若两个半圆的半径分别是1和2,则该圆台的体积是( )A.72π24B.73π24C.72π12D.73π12 答案 B解析 如图,设上底面的半径为r ,下底面的半径为R ,高为h ,母线长为l ,则2πr =π·1,2πR =π·2, 解得r =12,R =1,l =2-1=1, h =l 2-(R -r )2=12-⎝⎛⎭⎫122=32,上底面面积S ′=π·⎝⎛⎭⎫122=π4, 下底面面积S =π·12=π,则该圆台的体积为13(S +S ′+SS ′)h =13×⎝⎛⎭⎫π+π4+π2×32=73π24. 考点三 多面体与球核心提炼求空间多面体的外接球半径的常用方法(1)补形法:侧面为直角三角形,或正四面体,或对棱均相等的模型,可以还原到正方体或长方体中去求解;(2)定义法:到各个顶点距离均相等的点为外接球的球心,借助有特殊性底面的外接圆圆心,找其垂线,则球心一定在垂线上,再根据到其他顶点距离也是半径,列关系式求解即可.例3 (1)(2022·烟台模拟)如图,三棱锥V -ABC 中,VA ⊥底面ABC ,∠BAC =90°,AB =AC =VA =2,则该三棱锥的内切球和外接球的半径之比为( )A .(2-3)∶1B .(23-3)∶1C .(3-1)∶3D .(3-1)∶2 答案 C解析 因为VA ⊥底面ABC ,AB ,AC ⊂底面ABC , 所以VA ⊥AB ,VA ⊥AC , 又因为∠BAC =90°,所以AB ⊥AC ,而AB =AC =VA =2,所以三条互相垂直且共顶点的棱,可以看成正方体中共顶点的长、宽、高,因此该三棱锥外接球的半径R =12×22+22+22=3,设该三棱锥的内切球的半径为r , 因为∠BAC =90°,所以BC =AB 2+AC 2=22+22=22, 因为VA ⊥AB ,VA ⊥AC ,AB =AC =VA =2, 所以VB =VC =VA 2+AB 2=22+22=22, 由三棱锥的体积公式可得,3×13×12×2×2·r +13×12×22×22×32·r =13×12×2×2×2⇒r =3-33, 所以r ∶R =3-33∶3=(3-1)∶3.(2)(2022·新高考全国Ⅱ)已知正三棱台的高为1,上、下底面边长分别为33和43,其顶点都在同一球面上,则该球的表面积为( ) A .100π B .128π C .144π D .192π 答案 A解析 由题意,得正三棱台上、下底面的外接圆的半径分别为23×32×33=3,23×32×43=4.设该棱台上、下底面的外接圆的圆心分别为O 1,O 2,连接O 1O 2(图略),则O 1O 2=1,其外接球的球心O 在直线O 1O 2上.设球O 的半径为R ,当球心O 在线段O 1O 2上时,R 2=32+OO 21=42+(1-OO 1)2,解得OO 1=4(舍去);当球心O 不在线段O 1O 2上时,R 2=42+OO 22=32+(1+OO 2)2,解得OO 2=3,所以R 2=25,所以该球的表面积为4πR 2=100π. 综上,该球的表面积为100π.规律方法 (1)求锥体的外接球问题的一般方法是补形法,把锥体补成正方体、长方体等求解. (2)求锥体的内切球问题的一般方法是利用等体积法求半径.跟踪演练3 (1)(2022·全国乙卷)已知球O 的半径为1,四棱锥的顶点为O ,底面的四个顶点均在球O 的球面上,则当该四棱锥的体积最大时,其高为( ) A.13B.12 C.33D.22答案 C解析 该四棱锥的体积最大即以底面截球的圆面和顶点O 组成的圆锥体积最大. 设圆锥的高为h (0<h <1),底面半径为r , 则圆锥的体积V =13πr 2h =13π(1-h 2)h ,则V ′=13π(1-3h 2),令V ′=13π(1-3h 2)=0,得h =33,所以V =13π(1-h 2)h 在⎝⎛⎭⎫0,33上单调递增,在⎝⎛⎭⎫33,1上单调递减,所以当h =33时,四棱锥的体积最大. (2)(2022·衡水中学调研)将两个一模一样的正三棱锥共底面倒扣在一起,已知正三棱锥的侧棱长为2,若该组合体有外接球,则正三棱锥的底面边长为________,该组合体的外接球的体积为________. 答案6823π解析 如图,连接P A 交底面BCD 于点O ,则点O 就是该组合体的外接球的球心.设三棱锥的底面边长为a , 则CO =PO =R =33a , 得2×33a =2, 所以a =6,R =2, 所以V =43π·(2)3=823π.专题强化练一、单项选择题1.(2022·唐山模拟)圆柱的底面直径与高都等于球的直径,则球的表面积与圆柱的侧面积的比值为()A.1∶1 B.1∶2C.2∶1 D.2∶3答案 A解析设球的半径为r,依题意知圆柱的底面半径也是r,高是2r,圆柱的侧面积为2πr·2r=4πr2,球的表面积为4πr2,其比例为1∶1.2.(2021·新高考全国Ⅰ)已知圆锥的底面半径为2,其侧面展开图为一个半圆,则该圆锥的母线长为()A.2 B.2 2 C.4 D.4 2答案 B解析设圆锥的母线长为l,因为该圆锥的底面半径为2,所以2π×2=πl,解得l=2 2.3.某同学为表达对“新冠疫情”抗疫一线医护人员的感激之情,亲手为他们制作了一份礼物,用正方体纸盒包装,并在正方体六个面上分别写了“致敬最美逆行”六个字.该正方体纸盒水平放置的六个面分别用“前面、后面、上面、下面、左面、右面”表示.如图是该正方体的展开图.若图中“致”在正方体的后面,那么在正方体前面的字是()A.最B.美C.逆D.行答案 B解析把正方体的表面展开图再折成正方体,如图,面“致”与面“美”相对,若“致”在正方体的后面,那么在正方体前面的字是“美”.4.已知正方体ABCD -A 1B 1C 1D 1的棱长为2,则三棱锥A -B 1CD 1的体积为( ) A.43 B.83 C .4 D .6 答案 B解析 如图,三棱锥A -B 1CD 1是由正方体ABCD -A 1B 1C 1D 1截去四个小三棱锥A -A 1B 1D 1,C -B 1C 1D 1,B 1-ABC ,D 1-ACD 形成的,又1111ABCD A B C D V -=23=8,11111111A A B D C B C D B ABC D ACD V V V V ----====13×12×23=43, 所以11A B CD V -=8-4×43=83.5.(2022·河南联考)小李在课间玩耍时不慎将一个篮球投掷到一个圆台状垃圾篓中,恰好被上底口(半径较大的圆)卡住,球心到垃圾篓底部的距离为510a ,垃圾篓上底面直径为24a ,下底面直径为18a ,母线长为13a ,则该篮球的表面积为( ) A .154πa 2B.6163πa 2C .308πa 2D .616πa 2 答案 D解析 球与垃圾篓组合体的轴截面图如图所示.根据题意,设垃圾篓的高为h ,则h =(13a )2-(12a -9a )2=410a . 所以球心到上底面的距离为10a . 设篮球的半径为r , 则r 2=10a 2+(12a )2=154a 2. 故篮球的表面积为4πr 2=616πa 2.6.(2022·湖北联考)定义:24小时内降水在平地上积水厚度(mm)来判断降雨程度.其中小雨(<10 mm),中雨(10 mm ~25 mm),大雨(25 mm ~50 mm),暴雨(50 mm ~100 mm),小明用一个圆锥形容器接了24小时的雨水,如图,则这天降雨属于哪个等级()A .小雨B .中雨C .大雨D .暴雨 答案 B解析 由题意知,一个半径为2002=100(mm)的圆面内的降雨充满一个底面半径为2002×150300=50(mm),高为150(mm)的圆锥,所以积水厚度d =13π×502×150π×1002=12.5(mm),属于中雨.7.(2022·八省八校联考)如图,已知正四面体ABCD 的棱长为1,过点B 作截面α分别交侧棱AC ,AD 于E ,F 两点,且四面体ABEF 的体积为四面体ABCD 体积的13,则EF 的最小值为( )A.22 B.32 C.13 D.33答案 D解析 由题知V B -AEF =13V B -ACD ,所以S △AEF =13S △ACD =13×12×1×1×32=312,记EF =a ,AE =b ,AF =c , 则12bc sin 60°=312,即bc =13. 则a 2=b 2+c 2-2bc cos 60°≥2bc -bc =bc =13,当且仅当b =c =33时取等号, 所以a 即EF 的最小值为33. 8.(2022·新高考全国Ⅰ)已知正四棱锥的侧棱长为l ,其各顶点都在同一球面上.若该球的体积为36π,且3≤l ≤33,则该正四棱锥体积的取值范围是( ) A.⎣⎡⎦⎤18,814 B.⎣⎡⎦⎤274,814 C.⎣⎡⎦⎤274,643D .[18,27] 答案 C解析 方法一 如图,设该球的球心为O ,半径为R ,正四棱锥的底面边长为a ,高为h ,依题意,得36π=43πR 3,解得R =3.由题意及图可得⎩⎨⎧l 2=h 2+⎝⎛⎭⎫22a 2,R 2=(h -R )2+⎝⎛⎭⎫22a 2,解得⎩⎨⎧h =l 22R =l 26,a 2=2l 2-l418,所以正四棱锥的体积V =13a 2h=13⎝⎛⎭⎫2l 2-l 418·l 26=l 418⎝⎛⎭⎫2-l 218(3≤l ≤33), 所以V ′=49l 3-l 554=19l 3⎝⎛⎭⎫4-l 26(3≤l ≤33).令V ′=0,得l =26, 所以当3≤l <26时,V ′>0; 当26<l ≤33时,V ′<0,所以函数V =l 418⎝⎛⎭⎫2-l 218(3≤l ≤33)在[3,26)上单调递增,在(26,33]上单调递减,又当l =3时,V =274;当l =26时,V =643;当l =33时,V =814,所以该正四棱锥的体积的取值范围是⎣⎡⎦⎤274,643.方法二 如图,设该球的球心为O ,半径为R ,正四棱锥的底面边长为a ,高为h ,依题意,得36π=43πR 3,解得R =3.由题意及图可得⎩⎨⎧l 2=h 2+⎝⎛⎭⎫22a 2,R 2=(h -R )2+⎝⎛⎭⎫22a 2,解得⎩⎨⎧h =l 22R =l 26,a 2=2l 2-l418,又3≤l ≤33,所以该正四棱锥的体积V =13a 2h=13⎝⎛⎭⎫2l 2-l 418·l 26=l 418⎝⎛⎭⎫2-l 218 =72×l 236·l 236·⎝⎛⎭⎫2-l 218 ≤72×⎣⎢⎡⎦⎥⎤l 236+l 236+⎝⎛⎭⎫2-l 21833=643⎝⎛⎭⎫当且仅当l 236=2-l 218,即l =26时取等号, 所以正四棱锥的体积的最大值为643,排除A ,B ,D.方法三 如图,设该球的半径为R ,球心为O ,正四棱锥的底面边长为a ,高为h ,正四棱锥的侧棱与高所成的角为θ,依题意,得36π=43πR 3,解得R =3,所以正四棱锥的底面边长a =2l sin θ,高h =l cos θ. 在△OPC 中,作OE ⊥PC ,垂足为E , 则可得cos θ=l 2R =l 6∈⎣⎡⎦⎤12,32,所以l =6cos θ, 所以正四棱锥的体积 V =13a 2h =13(2l sin θ)2·l cos θ=23(6cos θ)3sin 2θcos θ=144(sin θcos 2θ)2. 设sin θ=t ,易得t ∈⎣⎡⎦⎤12,32,则y =sin θcos 2θ=t (1-t 2)=t -t 3, 则y ′=1-3t 2.令y ′=0,得t =33, 所以当12<t <33时,y ′>0;当33<t <32时,y ′<0, 所以函数y =t -t 3在⎝⎛⎭⎫12,33上单调递增,在⎝⎛⎭⎫33,32上单调递减.又当t =33时,y =239;当t =12时,y =38;当t =32时,y =38, 所以38≤y ≤239,所以274≤V ≤643. 所以该正四棱锥的体积的取值范围是⎣⎡⎦⎤274,643. 二、多项选择题9.(2022·武汉模拟)一个圆柱和一个圆锥的底面直径和它们的高都与一个球的直径2R 相等,下列结论正确的是( ) A .圆柱的侧面积为4πR 2 B .圆锥的侧面积为2πR 2C .圆柱的侧面积与球的表面积相等D .球的体积是圆锥体积的两倍 答案 ACD解析 对于A ,∵圆柱的底面直径和高都等于2R , ∴圆柱的侧面积S 1=2πR ·2R =4πR 2,故A 正确; 对于B ,∵圆锥的底面直径和高等于2R , ∴圆锥的侧面积为S 2=πR ·R 2+4R 2=5πR 2,故B 错误; 对于C ,圆柱的侧面积为S 1=4πR 2,球的表面积S 3=4πR 2,即圆柱的侧面积与球的表面积相等,故C 正确; 对于D ,球的体积为V 1=43πR 3,圆锥的体积为V 2=13πR 2·2R =23πR 3,即球的体积是圆锥体积的两倍,故D 正确.10.设一空心球是在一个大球(称为外球)的内部挖去一个有相同球心的小球(称为内球),已知内球面上的点与外球面上的点的最短距离为1,若某正方体的所有顶点均在外球面上且所有面均与内球相切,则( )A .该正方体的棱长为2B .该正方体的体对角线长为3+ 3C .空心球的内球半径为3-1D .空心球的外球表面积为(12+63)π 答案 BD解析 设内、外球半径分别为r ,R ,则正方体的棱长为2r ,体对角线长为2R ,∴R =3r , 又由题知R -r =1, ∴r =3+12,R =3+32, ∴正方体棱长为3+1,体对角线长为3+3, ∴外接球表面积为4πR 2=(12+63)π.11.如图,已知四棱台ABCD -A 1B 1C 1D 1的上、下底面均为正方形,其中AB =22,A 1B 1=2,AA 1=BB 1=CC 1=DD 1=2,则下列叙述正确的是( )A .该四棱台的高为 3B .AA 1⊥CC 1C .该四棱台的表面积为26D .该四棱台外接球的体积为32π3答案 AD解析 将四棱台补为如图所示的四棱锥P -ABCD ,分别取BC ,B 1C 1的中点E ,E 1,记四棱台ABCD -A 1B 1C 1D 1的上、下底面中心分别为O 1,O ,连接AC ,A 1C 1,BD 1,B 1D 1,A 1O ,OE ,OP ,PE ,由条件知A 1,B 1,C 1,D 1分别为四棱锥的侧棱P A ,PB ,PC ,PD 的中点, 则P A =2AA 1=4,OA =22AB =2A 1B 1=2, 所以OO 1=12PO =12P A 2-OA 2=3,故该四棱台的高为3,故A 正确;由P A =PC =4,AC =4,得△P AC 为正三角形, 则AA 1与CC 1所成角为60°,故B 错误; 四棱台的斜高h ′=12PE =12PO 2+OE 2=12(23)2+(2)2=142, 所以该四棱台的表面积为 (22)2+(2)2+4×2+222×142=10+67,故C 错误;由△P AC 为正三角形,易知OA 1=OA =OC =OC 1,OB 1=OD 1=OB =OD ,所以O 为四棱台外接球的球心,且外接球的半径为2,所以该四棱台外接球的体积为4π3×23=32π3,故D 正确.12.(2022·聊城模拟)用与母线不垂直的两个平行平面截一个圆柱,若两个截面都是椭圆形状,则称夹在这两个平行平面之间的几何体为斜圆柱.这两个截面称为斜圆柱的底面,两底面之间的距离称为斜圆柱的高,斜圆柱的体积等于底面积乘以高.椭圆的面积等于长半轴长与短半轴长乘积的π倍,已知某圆柱的底面半径为2,用与母线成45°角的两个平行平面去截该圆柱,得到一个高为6的斜圆柱,对于这个斜圆柱,下列选项正确的是( ) A .底面椭圆的离心率为22B .侧面积为242πC .在该斜圆柱内半径最大的球的表面积为36πD .底面积为42π 答案 ABD解析 不妨过斜圆柱的最高点D 和最低点B 作平行于圆柱底面的截面圆,夹在它们之间的几何体是圆柱,如图,矩形ABCD 是圆柱的轴截面,平行四边形BFDE 是斜圆柱的过底面椭圆的长轴的截面,由圆柱的性质知∠ABF =45°, 则BF =2AB ,设椭圆的长轴长为2a ,短轴长为2b , 则2a =2·2b ,即a =2b , c =a 2-b 2=a 2-⎝⎛⎭⎫22a 2=22a , 所以离心率为e =c a =22,A 正确;作EG ⊥BF ,垂足为G ,则EG =6, 易知∠EBG =45°,则BE =62, 又CE =AF =AB =4,所以斜圆柱侧面积为S =2π×2×(4+62)-2π×2×4=242π,B 正确;由于斜圆柱的两个底面的距离为6,而圆柱的底面直径为4,所以斜圆柱内半径最大的球的半径为2,球的表面积为4π×22=16π,C 错误;易知2b =4,则b =2,a =22, 所以椭圆面积为πab =42π,D 正确.三、填空题13.(2022·湘潭模拟)陀螺是中国民间的娱乐工具之一,也叫做陀罗.陀螺的形状结构如图所示,由一个同底的圆锥体和圆柱体组合而成,若圆锥体和圆柱体的高以及底面圆的半径长分别为h 1,h 2,r ,且h 1=h 2=r ,设圆锥体的侧面积和圆柱体的侧面积分别为S 1和S 2,则S 1S 2=________.答案22解析 由题意知,圆锥的母线长为l =h 21+r 2=2r ,则圆锥的侧面积为S 1=πrl =2πr 2,根据圆柱的侧面积公式,可得圆柱的侧面积为 S 2=2πrh 2=2πr 2,所以S 1S 2=22.14.(2022·福州质检)在正三棱柱ABC -A 1B 1C 1中,AB =AA 1=2,F 是线段A 1B 1上的动点,则AF +FC 1的最小值为________. 答案6+ 2解析 依题意,把正三棱柱ABC -A 1B 1C 1的上底面△A 1B 1C 1与侧面矩形ABB 1A 1放在同一平面内,连接AC 1,设AC 1交A 1B 1于点F ,如图,此时点F 可使AF +FC 1取最小值,大小为AC 1,而∠AA 1C 1=150°,则AC 1=AA 21+A 1C 21-2AA 1·A 1C 1cos ∠AA 1C 1 =22+22-23cos 150° =8+43=6+2,所以AF +FC 1的最小值为6+ 2.15.某同学在参加《通用技术》实践课时,制作了一个实心工艺品(如图所示).该工艺品可以看成是一个球体被一个棱长为4的正方体的6个面所截后剩余的部分(球心与正方体的中心重合),其中一个截面圆的周长为3π,则该球的半径为________;现给出定义:球面被平面所截得的一部分叫做球冠.截得的圆叫做球冠的底,垂直于截面的直径被截得的一段叫做球冠的高.如果球面的半径是R ,球冠的高是h ,那么球冠的表面积计算公式是S =2πRh .由此可知,该实心工艺品的表面积是________.答案5247π2解析 设截面圆半径为r ,则球心到某一截面的距离为正方体棱长的一半,即此距离为2,根据截面圆的周长可得3π=2πr ,得r =32,故R 2=r 2+22=254,得R =52,所以球的表面积S 1=25π. 如图,OA =OB =52,且OO 1=2,则球冠的高h =R -OO 1=12,得所截的一个球冠表面积S =2πRh =2π×52×12=5π2,且截面圆的面积为π×⎝⎛⎭⎫322=9π4, 所以工艺品的表面积为4πR 2-6⎝⎛⎭⎫S -9π4=25π-3π2=47π2.16.(2022·开封模拟)如图,将一块直径为23的半球形石材切割成一个正四棱柱,则正四棱柱的体积取最大值时,切割掉的废弃石材的体积为________.答案 23π-4解析 设正四棱柱的底面正方形边长为a ,高为h ,则底面正方形的外接圆半径r =22a , ∴h 2+r 2=h 2+12a 2=3,∴a 2=6-2h 2,∴正四棱柱的体积V =a 2h =(6-2h 2)h =-2h 3+6h (0<h <3), ∴V ′=-6h 2+6=-6(h +1)(h -1),∴当0<h <1时,V ′>0;当1<h <3时,V ′<0;∴V =-2h 3+6h 在(0,1)上单调递增,在(1,3)上单调递减, ∴V max =V (1)=4,又半球的体积为23π×()33=23π,∴切割掉的废弃石材的体积为23π-4.。
2020新高考文科数学二轮培优空立体几何中的热点问题考点考向考题突破(85张)

核心知识回顾
热点考向探究
真题VS押题
配套作业
(2)存在满足条件的点 M.取 CF 的中点记作 M,设 DF 的中点为 N,连接 AN,MN,则 MN 綊12CD,
又 AO 綊12CD,则 MN 綊 AO,
∴四边形 MNAO 为平行四边形, ∴OM∥AN,又 AN⊂平面 DAF,OM⊄平面 DAF, ∴OM∥平面 DAF. 即存在一点 M 为 CF 的中点,使得 OM∥平面 DAF.
核心知识回顾
热点考向探究
真题VS押题
配套作业
(1)求证:平面 PBC∥平面 EFH; (2)求三棱锥 P-EFH 的体积.
核心知识回顾
热点考向探究
真题VS押题
配套作业
解 (1)证明:因为在菱形 ABCD 中,E,H 分别为 AB,CD 的中点, 所以 BE 綊 CH,四边形 BCHE 为平行四边形,则 BC∥EH,
(1)求证:BC⊥平面 ACD;
(2)若点 F 在棱 CD 上,且满足 AD∥平面 BEF,求几何体 F-BCE 的体
积.
核心知识回顾
热点考向探究
真题VS押题
配套作业
解 (1)证明:在图 1 中,由题意,知 AC=BC=2 2,
所以 AC2+BC2=AB2,所以 AC⊥BC.
因为点 E 为 AC 的中点,如图,连接 DE,则 DE⊥AC, 又平面 ADC⊥平面 ABC, 且平面 ADC∩平面 ABC=AC,DE⊂平面 ACD,从而 ED⊥平面 ABC,
又 EH⊄平面 PBC,所以 EH∥平面 PBC.
又点 E,F 分别为 AB,AP 的中点,所以 EF∥BP,
又 EF⊄平面 PBC,所以 EF∥平面 PBC.而 EF∩EH=E, 所以平面 EFH∥平面 PBC.
高考数学第二轮立体几何复习课件 第20课时 空间几何体

2
2 3 1 3 3 3 cm3 .
答案:A
3
解答此类题目时: 1.可以从熟知的某一视图出发,想象出直观图, 再验证其他视图是否正确; 2.视图中标注的长度在直观图中代表什么,要 分辨清楚; 3.视图之间的数量关系:正俯长对正,正侧高 平齐,侧俯宽相等.
1 3
100
10
3 1000 3
3.
19
1.解题时误以为∠CAB就是线面角. 线面角的作法:在斜线上取一点(一般取 特殊点:中点,端点)作平面的垂线,垂足与 斜足的连线为斜线在平面内的射影,射影与斜 线所成的角即为线面角; 2.圆锥的母线是侧面展开图的扇形的半 径,易与圆锥底面圆半径混用,要注意分清.
12
变式2(2011 顺德一模)下图为一简单组合体,其底面 ABCD为正方形,PD 平面ABCD,EC PD,且PD AD 2EC 2.
1求四棱锥B CEPD的体积; 2求证:BE 平面PDA.
13
解析 因为PD 平面ABCD,PD 平面PDCE,
所以平面PDCE 平面ABCD.
2.要注意几何体的三视图与直观图的联系, 能将两者互相转化;要注意正视图、俯视图、 侧视图之间的数量关系.
25
3.对于能用公式求解的问题,要将空间问 题转化为平面几何问题,求出公式中所需要的 量,如高度、长度、角度等.这种转化包括: 侧面展开、将部分图画成平面图等.
4.与圆柱、圆锥、球有关的组合体问题, 主要指内接和外切,要认真研究轴截面,分析 平面图,借助相似或比例或直角三角形等找出 变量之间的关系.
4 画好后,擦去辅助线就得六边形ABCDEF 的直观图ABCDEF .请写出第 2 步.
2020高考数学(文)二轮专题课件:大题考法课立体几何
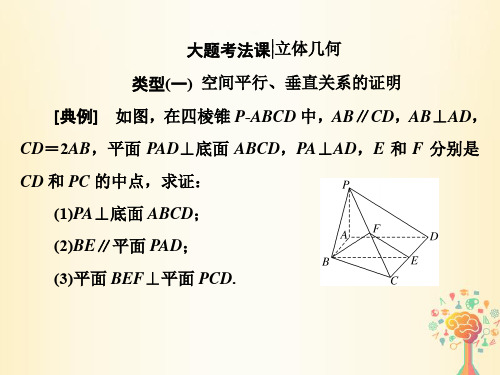
解:(1)证明:由题知,BD=AD=4 2,又 AB=8,∴AB2=AD2 +BD2,∴BD⊥AD. ∵平面 PAD⊥平面 ABCD,且两平面的交线是 AD,BD⊂平面 ABCD,BD⊥AD,∴BD⊥平面 PAD,又 BD⊂平面 MBD,∴ 平面 MBD⊥平面 PAD.
(2)过点 P 作 PO⊥AD 交 AD 于点 O,则 PO⊥平面 ABD,∴点
知 A1B1 綊 DC,可得 B1C 綊 A1D,故 ME 綊
ND,因此四边形 MNDE 为平行四边形,所以 MN∥ED.
又 MN⊄平面 C1DE,扣 1 分.
[微点提醒]
[微点提醒]
加红处若漏掉 MN⊄ 平面 C1DE,扣 1 分.
❶转化:线线平行⇒线面平行 MN∥ED⇒MN∥平面 C1DE.
(2)存在一个常数 m= 23,使得平面 PED⊥ 平面 PAB,理由如下: 要使平面 PED⊥平面 PAB,只需 AB⊥DE, 因为 AB=AD=2,∠DAB=30°, 所以 AE=ADcos 30°= 3, 又因为 PD⊥平面 ABCD,PD⊥AB,PD∩DE=D, 所以 AB⊥平面 PDE, 因为 AB⊂平面 PAB,所以平面 PDE⊥平面 PAB, 所以 m=AAEB= 23.
(2)取 CG 的中点 M,连接 EM,DM. 因为 AB∥DE,AB⊥平面 BCGE,所以 DE⊥平面 BCGE, 所以 DE⊥CG. 因为四边形 BCGE 是菱形,且∠EBC=60°, 所以 EM⊥CG, 又 DE∩EM=E,所以 CG⊥平面 DEM. 所以 DM⊥CG. 在 Rt△DEM 中,DE=1,EM= 3, 故 DM=2. 所以四边形 ACGD 的面积为 4.
[微点提醒]
[关键步骤]
加红处只作 CH⊥C1E,不进行证 明 CH⊥平面 C1DE 的扣 2 分.
2020版高考文科数学大二轮专题复习新方略讲义:5.1空间几何体 Word版含解析

的中点,当底面ABC水平放置时,先画出圆柱的直观图,根据题图的三视图可知点①1.由直观图确认三视图的方法根据空间几何体三视图的定义及画法规则和摆放规则确认.『对接训练』广东实验中学段考]正方体ABCD,E,C1的平面截去该正方体的上半部分,()的中点,过点A,E,C该平面截去正方体的上半部分后,剩余几何体的侧视图为江西八所重点中学联考]某四面体的三视图如图所示,四面体最长的棱长与最短的棱长的比值是(的正方体中还原该四面体,最长的棱为PC.因为正方体的棱长为空间几何体的表面积与体积空间几何体的几组常用公式柱体、锥体、台体的侧面积公式:本题主要考查空间几何体的结构特征与体积的计算,考查考生的空间想象能力,考查的核心素养是直观想象、数学运算.由题可得,四棱锥底面对角线的长为2,则圆柱底面的半径为由几何体的三视图可知,该几何体为半圆柱,×1×2=1.求解几何体的表面积及体积的技巧『对接训练』如图,长方体ABCD-E-BCD的体积是本题主要考查空间几何体的体积,考查考生的空间想象能力和运算求解能力,考查的核心素养是直观想象、数学运算.B C D的体积是)+2 3根据三视图可知该三棱柱的直观图如图所示,所以该三棱]+2×4=(2×EF⊥CE,所以PBBD,PD,易证ACCE=C,AC,CE,因为PA=PB=该正方体的体对角线长为6,所以三棱锥P-ABC的外接球的半径R=62,所以球O的体积V=43πR3=43π⎝⎛⎭⎪⎫623=6π,故选D.方法二设PA=PB=PC=2a,则EF=a,FC=3,∴EC2=3-a2.在△PEC中,cos∠PEC=a2+3-a2-(2a)22a3-a2.在△AEC中,cos∠AEC=a2+3-a2-42a3-a2.∵∠PEC与∠AEC互补,∴3-4a2=1,a=22,故PA=PB=PC= 2.又∵AB=BC=AC=2,∴PA⊥PB⊥PC,∴外接球的直径2R=(2)2+(2)2+(2)2=6,∴R=62,∴V=43πR3=43π×⎝⎛⎭⎪⎫623=6π.故选D.【答案】 D(1)涉及球与棱柱、棱锥的切、接问题时,一般过球心及多面体中的特殊点或线作截面,把空间问题化归为平面问题,再利用平面几何知识寻找几何体中元素间的关系.(2)球心与截面圆心的连线垂直圆面,其距离为d,常利用直角三角形建立量的关系,R2=d2+r2.『对接训练』5.[2019·河南洛阳尖子生联考]四棱锥S-ABCD的所有顶点都在同一个球面上,底面ABCD是正方形且和球心O在同一平面内,当此四棱锥的体积取得最大值时,其表面积等于8+83,则球O的体积等于()由题意得,当此四棱锥的体积取得最大值时,四棱锥为正,则球心O为AC=R,∴AB=BC2的中点为D,B1C1,则DA=DB垂直于直三棱柱的上、下底面,所以点为直三棱柱的外接球的球心22如图,四面体ABCD长方体是虚拟图形,起辅助作用)图、侧视图、俯视图分别是(用①②③④⑤⑥代表图形.①②③.③④⑤正视图是边长为3和4的矩形,其对角线左下到右上是实线,左上到右下是虚线,因此正视图是①;侧视图是边长为矩形,其对角线左上到右下是实线,左下到右上是虚线,因此侧视图.10π+4 3几何体最长的棱的长度为()该几何体是如图所示的四棱锥的组合体,由图知该几何体最长的一条棱为由三视图知,该几何体是一个底面为直角三角形的直三棱柱截去一个三棱锥后得到的,如图,该几何体的体积,故选C.视图为扇形,则该几何体的体积为()平面B1BCC1,∴为平行四边形.如图,连接42,FK=1,在RtE=42+22=2等于()该几何体为一个底面是直角梯形的四棱锥=8,∴x=4.)4π+4π由三视图可知,该几何体是一个半球和一个直四棱柱的组合体,根据图中数据可知,表面积为4×4×2D.三棱锥的四个面中,最大面的面积是()解析:如图,设该三棱锥为P-ABC,其中PA⊥底面ABC,PA =4,△ABC是边长为4的等边三角形,故PB=PC=42,所以S△ABC=12×4×23=43,S△PAB=S△PAC=12×4×4=8,S△PBC=12×4×(42)2-22=47,故四个面中最大面的面积为S△PBC=47,故选C.答案:C11.[2019·广东深圳调研]如图,在平面四边形ABCD中,AB=AD =CD=1,BD=2,BD⊥CD,将其沿对角线BD折成四面体ABCD,使平面ABD⊥平面BCD,若四面体ABCD的所有顶点在同一个球面上,则该球的体积为()A.3π2B.3πC.2π3D.2π解析:如图,取BD的中点E,BC的中点O,连接AE,OD,EO,AO.因为AB=AD,所以AE⊥BD.由于平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,所以AE⊥平面BCD.因为AB=AD=CD=1,BD=2,所以AE=22,EO=12,所以OA=32.在Rt△BDC中,OB=OC=OD=12BC=32,所以四面体ABCD的外接球的球心为O,半径为32,所以该球的体积V=43π×⎝⎛⎭⎪⎫323=3π2.答案:AR,则由4πR2=20此三棱柱为正三棱柱,故设三棱柱的底面边长为,四边形BCC1B1的中心Rt△AOO1中,OO,则绕行的最短距离是________.易知圆锥的侧面展开图是扇形,如图,=3,因为圆锥的底面半径的最短距离为所对的弦⊥平面ABC于,OF⊥BC于易知当球内切于四棱锥P-ABCD各个面均相切时,球的半径最大.作出相切时的侧视图如图所示,设内切球的半径为r,则1 2×。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
①若α∥β,则m∥n;
②若α∥β,则m∥β;
③若α∩β=l,且m⊥l,n⊥l,则α⊥β;
④若α∩β=l,且m⊥l,m⊥n,则α⊥β.
其中真命题的个数是( )
A.0
B.1
C.2
D.3
[解析] (1)若α∥β,则m∥n,这与m,n为异面直线矛盾,所以A不正确;将已 知条件转化到正方体中,易知α与β不一定垂直,但α与β的交线一定平行于l,从而排 除B、C.故选D.
(2)如图,过点C作C1E的垂线,垂足为H. 由已知可得DE⊥BC,DE⊥C1C,且BC∩C1C=C,所以DE⊥平面C1CE, 故DE⊥CH.从而CH⊥平面C1DE,故CH的长即为点C到平面C1DE的距离.
由已知可得CE=1,C1C=4,所以C1E=
17
,故CH=
4 17 17
.从而点C到平面
C1DE的距离为4
解:(1)证明:记AB的中点为D,连接PD,CD,如图.因为侧面三角形PAB是边 长为2的正三角形,所以PD⊥AB.
在正三角形ABC和正三角形PAB中得CD= 3,PD= 3.
因为PC= 6,所以PC2=PD2+CD2,所以PD⊥CD. 因为AB∩CD=D,所以PD⊥平面ABC. 因为PD⊂平面PAB,所以平面PAB⊥平面ABC.
2.设l,m,n表示不同的直线,α,β,γ表示不同的平面,给出下列四个命题:
①若m∥l,且m⊥α,则l⊥α;
②若m∥l,且m∥α,则l∥α;
③若α∩β=l,β∩γ=m,γ∩α=n,则l∥m∥n;
④若α∩β=m,β∩γ=l,γ∩α=n,且n∥β,则l∥m.
其中正确命题的个数是( )
A.1
B.2
C.3
2.(2019·合肥模拟)如图,在四棱锥 P-ABCD 中,△BCD 为等边三角形,BD= 2 3,PA= 2,AB=AD=PB=PD,∠BAD=120°.
(1)若点 E 为 PC 的中点,求证:BE∥平面 PAD; (2)求四棱锥 P-ABCD 的体积.
解:(1)证明:如图,取CD的中点为M,连接EM,BM. ∵△BCD为等边三角形, ∴BM⊥CD. ∵∠BAD=120°,AD=AB, ∴∠ADB=30°,∴∠ADC=30°+60°=90°, ∴AD⊥CD,∴BM∥AD. 又BM⊄平面PAD,AD⊂平面PAD, ∴BM∥平面PAD.
解析:选 B 如图,取 CD 的中点 F,DF 的中点 G,连接 EF,FN,MG,GB, BD,BE.
∵点 N 为正方形 ABCD 的中心, ∴点 N 在 BD 上,且为 BD 的中点. ∵△ECD 是正三角形,∴EF⊥CD. ∵平面 ECD⊥平面 ABCD, 平面 ECD∩平面 ABCD=CD, ∴EF⊥平面 ABCD.
|规 律 方 法 | 空间平行、垂直关系证明的主要思想是转化,即通过判定定理、性质定理将线线、 线面、面面之间的平行、垂直关系相互转化.
|对点训练| 1.(2019·武汉模拟)如图,在三棱锥 P-ABC 中,底面三角形 ABC 和侧面三角形 PAB 是边长为 2 的正三角形,PC= 6.
(1)求证:平面 PAB⊥平面 ABC; (2)求点 B 到平面 PAC 的距离.
考点二 空间平行、垂直关系的证明 |析典例|
【例】 (2018·全国卷Ⅲ)如图,矩形 ABCD 所在平面与半圆弧C︵D所在平面垂直, M 是C︵D上异于 C,D 的点.
(1)证明:平面 AMD⊥平面 BMC; (2)在线段 AM 上是否存在点 P,使得 MC∥平面 PBD?说明理由.
[解] (1)证明:由题设知,平面CMD⊥平面ABCD,交线为CD.因为BC⊥CD, BC⊂平面ABCD,所以BC⊥平面CMD,故BC⊥DM.因为M为 C︵D 上异于C,D的点, 且DC为直径,所以DM⊥CM.
∵FN⊂平面ABCD, ∴EF⊥FN. 不妨设AB=2,则FN=1,EF= 3, ∴EN= FN2+EF2=2. ∵EM=MD,DG=GF,∴MG∥EF,且MG=12EF, ∴MG⊥平面ABCD,∴MG⊥BG. ∵MG=12EF= 23,
BG= CG2+BC2=
322+22=52,
∴BM= MG2+BG2= 7.
【例】 (1)已知m,n为异面直线,m⊥平面α,n⊥平面β.直线l满足l⊥m,l⊥ n,l⊄α,l⊄β,则( )
A.α∥β且l∥α B.α⊥β且l⊥α C.α与β相交,且交线垂直于l D.α与β相交,且交线平行于l
(2)已知m,n是空间中两条不同的直线,α,β是两个不同的平面,且m⊂α,n⊂β.
有下列命题:
解:(1)证明:如图,连接B1C,ME.因为M,E分别为BB1,
BC的中点,所以ME∥B1C,且ME=
1 2
B1C.又因为N为A1D的中
点,所以ND=12A1D.
由题设知A1B1 DC,可得B1C A1D,故ME ND,因此四 边形MNDE为平行四边形,所以MC1DE,所以MN∥平面C1DE.
A.AG⊥平面 EFH C.HF⊥平面 AEF
B.AH⊥平面 EFH D.HG⊥平面 AEF
解析:选B 根据折叠前、后AH⊥HE,AH⊥HF不变, 得AH⊥平面EFH,∴B正确;∵过A只有一条直线与平面EFH垂直,∴A不正 确;∵AG⊥EF,EF⊥GH,AG∩GH=G,∴EF⊥平面HAG,又EF⊂平面AEF,∴ 平面HAG⊥平面AEF,过H作直线垂直于平面AEF,一定在平面HAG内,∴C不正 确;由条件证不出HG⊥平面AEF,∴D不正确.故选B.
又∠BAD=120°,BD=2 3,△PBD≌△ABD,∴AO=PO=1.
所以AB⊥BE. 在Rt△ABE中,tan ∠BAE=ABBE= 25.故选C.
6.(2019·全国卷Ⅰ)如图,直四棱柱ABCD-A1B1C1D1的底面是菱形,AA1=4, AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.
(1)证明:MN∥平面C1DE; (2)求点C到平面C1DE的距离.
∵E为PC的中点,M为CD的中点,∴EM∥PD. 又EM⊄平面PAD,PD⊂平面PAD, ∴EM∥平面PAD. ∵EM∩BM=M,∴平面BEM∥平面PAD. 又BE⊂平面BEM,∴BE∥平面PAD.
(2)如图,连接AC交BD于点O,连接PO.
∵CB=CD,AB=AD,∴AC⊥BD且O为BD的中点.
又BC∩CM=C,所以DM⊥平面BMC. 而DM⊂平面AMD,故平面AMD⊥平面BMC.
(2)当 P 为 AM 的中点时,MC∥平面 PBD. 理由如下:如图,连接 AC 交 BD 于 O.因为 ABCD 为矩形,所以 O 为 AC 中点.连 接 OP,因为 P 为 AM 中点,所以 MC∥OP. 因为 MC⊄平面 PBD,OP⊂平面 PBD,所以 MC∥平面 PBD.
∴BM≠EN.
∵BM,EN是△DBE的中线,∴BM,EN必相交.
故选B.
3.(2017·全国卷Ⅰ)如图,在下列四个正方体中,A,B为正方体的两个顶点, M,N,Q为所在棱的中点,则在这四个正方体中,直线AB与平面MNQ不平行的是 ()
解析:选A B选项中,AB∥MQ,且AB⊄平面MNQ,MQ⊂平面MNQ,则AB∥ 平面MNQ;C选项中,AB∥MQ,且AB⊄平面MNQ,MQ⊂平面MNQ,则AB∥平面 MNQ;D选项中,AB∥NQ,且AB⊄平面MNQ,NQ⊂平面MNQ,则AB∥平面MNQ.故 选A.
4.(2017·全国卷Ⅲ)在正方体ABCD-A1B1C1D1中,E为棱CD的中点,则( )
A.A1E⊥DC1
B.A1E⊥BD
C.A1E⊥BC1
D.A1E⊥AC
解析:选C ∵A1B1⊥平面BCC1B1,BC1⊂平面BCC1B1,∴A1B1⊥BC1,又BC1⊥ B1C,且B1C∩A1B1=B1,∴BC1⊥平面A1B1CD,又A1E⊂平面A1B1CD,∴BC1⊥A1E. 故选C.
(2)①若α∥β,则m∥n或m,n异面,不正确; ②若α∥β,根据平面与平面平行的性质,可得m∥β,正确; ③若α∩β=l,且m⊥l,n⊥l,则α与β不一定垂直,不正确; ④若α∩β=l,且m⊥l,m⊥n,l与n不一定相交,不能推出α⊥β,不正确. [答案] (1)D (2)B
|规 律 方 法 | 判断与空间位置关系有关的命题真假的方法 (1)借助空间线面平行、面面平行、线面垂直、面面垂直的判定定理和性质定理 进行判断. (2)借助空间几何模型,如从长方体模型、四面体模型等模型中观察线面位置关 系,结合有关定理,进行判断. (3)借助于反证法,当从正面入手较难时,可利用反证法,推出与题设或公认的 结论相矛盾的命题,进而作出判断.
D.4
解析:选B ①正确;②中也可能直线l⊂α,故错误;③中三条直线也可能相交 于一点,故错误;④正确,所以正确的命题有2个,选B.
3.如图,在正方形 ABCD 中,E,F 分别是 BC,CD 的中点,G 是 EF 的中点, 现在沿 AE,AF 及 EF 把这个正方形折成 一个空间图形,使 B,C,D 三点重合,重 合后的点记为 H,那么,在这个空间图形中必有( )
10 2.
从而
BH=2
515,即点
B
到平面
PAC
的距离为2
15 5.
解法二:由题意得S△ABC=
3,S△PAC=
15 2.
设点B到平面PAC的距离为h,因为VP-ABC=VB-PAC,所以结合(1)知13S△ABC·PD=13S
△PAC·h,所以h=2 515.所以点B到平面PAC的距离为2 515.
17 17 .
析考情
1.高考对此部分命题较为稳定,选择题、填空题多考查线面位置关系的判断, 此类试题难度中等偏下.
2.解答题的第(1)问考查空间平行关系和垂直关系的证明,而第(2)问多考查面 积、体积的计算,难度中等偏上.解答题的基本模式是“一证明二计算”.
考点一 空间位置关系的判断 |析典例|
