圆综合测试题(含详细解析及答案)
圆测试题及答案解析
圆测试题及答案解析一、选择题1. 已知圆的半径为5，圆心到直线的距离为3，那么直线与圆的位置关系是什么？A. 直线与圆相离B. 直线与圆相切C. 直线与圆相交D. 直线在圆内答案：C解析：根据圆心到直线的距离小于圆的半径，可以判断直线与圆相交。
2. 圆的周长公式是什么？A. C = 2πrB. C = πr²C. C = 2rD. C = rπ答案：A解析：圆的周长公式是C = 2πr，其中C表示周长，r表示半径。
二、填空题1. 半径为7的圆的面积是 __________。
答案：153.94解析：圆的面积公式是A = πr²，将半径7代入公式得A = π ×7² ≈ 153.94。
2. 如果一个扇形的半径为10，圆心角为30°，那么它的弧长是__________。
答案：5π解析：弧长公式是L = θ × r，其中θ为圆心角（以弧度为单位），r为半径。
将圆心角30°转换为弧度是π/6，代入公式得L = π/6× 10 = 5π/3 ≈ 5。
三、简答题1. 描述圆的切线的性质。
答案：圆的切线在圆上某一点处与圆相切，且与过该点的半径垂直。
解析：圆的切线是一条直线，它恰好在一个点上与圆接触，并且这个接触点处的切线与从圆心到接触点的半径形成90°的角。
四、计算题1. 已知圆的半径为8，求圆的面积。
答案：圆的面积为200π。
解析：根据圆的面积公式A = πr²，将半径8代入公式得A = π × 8² = 64π ≈ 200π。
2. 已知圆的直径为20，求圆的周长。
答案：圆的周长为20π。
解析：圆的周长公式是C = πd，其中d为直径。
将直径20代入公式得C = π × 20 = 20π。
人教版九年级数学上册 圆 几何综合单元测试卷(含答案解析)
人教版九年级数学上册 圆 几何综合单元测试卷（含答案解析）一、初三数学 圆易错题压轴题（难）1．已知圆O 的半径长为2，点A 、B 、C 为圆O 上三点，弦BC=AO ，点D 为BC 的中点，(1)如图，连接AC 、OD ，设∠OAC=α，请用α表示∠AOD ；(2)如图，当点B 为AC 的中点时，求点A 、D 之间的距离： (3)如果AD 的延长线与圆O 交于点E ，以O 为圆心，AD 为半径的圆与以BC 为直径的圆相切，求弦AE 的长． 【答案】（1）1502AOD α∠=︒-；（2）7AD =3）33133122or 【解析】【分析】（1）连接OB 、OC ，可证△OBC 是等边三角形，根据垂径定理可得∠DOC 等于30°，OA=OC 可得∠ACO=∠CAO=α，利用三角形的内角和定理即可表示出∠AOD 的值.（2）连接OB 、OC ，可证△OBC 是等边三角形，根据垂径定理可得∠DOB 等于30°，因为点D 为BC 的中点，则∠AOB=∠BOC=60°，所以∠AOD 等于90°，根据OA=OB=2,在直角三角形中用三角函数及勾股定理即可求得OD 、AD 的长.（3）分两种情况讨论：两圆外切，两圆内切.先根据两圆相切时圆心距与两圆半径的关系，求出AD 的长，再过O 点作AE 的垂线，利用勾股定理列出方程即可求解.【详解】(1)如图1：连接OB 、OC.∵BC=AO∴OB=OC=BC∴△OBC 是等边三角形∴∠BOC=60°∵点D 是BC 的中点∴∠BOD=1302BOC ∠=︒ ∵OA=OC∴OAC OCA ∠=∠=α∴∠AOD=180°-α-α-30︒=150°-2α(2)如图2：连接OB、OC、OD.由（1）可得：△OBC是等边三角形，∠BOD=130 2BOC∠=︒∵OB=2，∴OD=OB∙cos30︒=3∵B为AC的中点，∴∠AOB=∠BOC=60°∴∠AOD=90°根据勾股定理得：AD=227AO OD+=（3）①如图3.圆O与圆D相内切时：连接OB、OC，过O点作OF⊥AE∵BC是直径，D是BC的中点∴以BC为直径的圆的圆心为D点由（2）可得：3D的半径为1∴31设AF=x 在Rt △AFO 和Rt △DOF 中，2222OA AF OD DF -=-即()2222331x x -=-+- 解得：331x 4+= ∴AE=3312AF +=②如图4.圆O 与圆D 相外切时：连接OB 、OC ，过O 点作OF ⊥AE∵BC 是直径，D 是BC 的中点∴以BC 为直径的圆的圆心为D 点由（2）可得：3D 的半径为1∴31在Rt △AFO 和Rt △DOF 中，2222OA AF OD DF -=-即()2222331x x -=-解得：331x 4-= ∴AE=3312AF -=【点睛】本题主要考查圆的相关知识：垂径定理，圆与圆相切的条件，关键是能灵活运用垂径定理和勾股定理相结合思考问题，另外需注意圆相切要分内切与外切两种情况.2．已知：在△ABC中，AB=6，BC=8，AC=10，O为AB边上的一点，以O为圆心，OA长为半径作圆交AC于D点，过D作⊙O的切线交BC于E.（1）若O为AB的中点(如图1)，则ED与EC的大小关系为：ED EC（填“”“”或“”）（2）若OA<3时（如图2），（1）中的关系是否还成立？为什么？（3）当⊙O过BC中点时（如图3），求CE长.【答案】（1）ED=EC；（2）成立；（3）3【解析】试题分析：（1）连接OD，根据切线的性质可得∠ODE=90°，则∠CDE+∠ADO=90°，由AB=6，BC=8，AC=10根据勾股定理的逆定理可证得∠ABC=90°，则∠A+∠C=90°，根据圆的基本性质可得∠A=∠ADO，即可得到∠CDE=∠C，从而证得结论；（2）证法同（1）；（3）根据直角三角形的性质结合圆的基本性质求解即可.（1）连接OD∵DE为⊙O的切线∴∠ODE=90°∴∠CDE+∠ADO=90°∵AB=6，BC=8，AC=10∴∠ABC=90°∴∠A+∠C=90°∵AO=DO∴∠A=∠ADO∴∠CDE=∠C∴ED=EC；（2）连接OD∵DE为⊙O的切线∴∠ODE=90°∴∠CDE+∠ADO=90°∵AB=6，BC=8，AC=10∴∠ABC=90°∴∠A+∠C=90°∵AO=DO∴∠A=∠ADO∴∠CDE=∠C∴ED=EC；（3）CE=3.考点：圆的综合题点评：此类问题综合性强，难度较大，在中考中比较常见，一般作为压轴题，题目比较典型．3．如图，△ABC内接于⊙O，AB是直径，过点A作直线MN，且∠MAC＝∠ABC．（1）求证：MN是⊙O的切线．（2）设D是弧AC的中点，连结BD交AC于点G，过点D作DE⊥AB于点E，交AC于点F．①求证：FD＝FG．②若BC＝3，AB＝5，试求AE的长．【答案】（1）见解析；（2）①见解析；②AE＝1【解析】【分析】（1）由AB为直径知∠ACB＝90°，∠ABC+∠CAB＝90°．由∠MAC＝∠ABC可证得∠MAC+∠CAB＝90°，则结论得证；（2）①证明∠BDE＝∠DGF即可．∠BDE＝90°﹣∠ABD；∠DGF＝∠CGB＝90°﹣∠CBD．因为D是弧AC的中点，所以∠ABD＝∠CBD．则问题得证；②连接AD、CD，作DH⊥BC，交BC的延长线于H点．证明Rt△ADE≌Rt△CDH，可得AE＝CH．根据AB＝BH可求出答案．【详解】（1）证明：∵AB是直径，∴∠ACB＝90°，∴∠CAB+∠ABC＝90°；∵∠MAC＝∠ABC，∴∠MAC+∠CAB＝90°，即MA⊥AB，∴MN是⊙O的切线；（2）①证明：∵D是弧AC的中点，∴∠DBC＝∠ABD，∵AB是直径，∴∠CBG+∠CGB＝90°，∵DE⊥AB，∴∠FDG+∠ABD＝90°，∵∠DBC ＝∠ABD ，∴∠FDG ＝∠CGB ＝∠FGD ，∴FD ＝FG ；②解：连接AD 、CD ，作DH ⊥BC ，交BC 的延长线于H 点．∵∠DBC ＝∠ABD ，DH ⊥BC ，DE ⊥AB ，∴DE ＝DH ，在Rt △BDE 与Rt △BDH 中，DH DE BD BD=⎧⎨=⎩， ∴Rt △BDE ≌Rt △BDH （HL ），∴BE ＝BH ，∵D 是弧AC 的中点，∴AD ＝DC ，在Rt △ADE 与Rt △CDH 中，DE DH AD CD =⎧⎨=⎩， ∴Rt △ADE ≌Rt △CDH （HL ）．∴AE ＝CH ．∴BE ＝AB ﹣AE ＝BC+CH ＝BH ，即5﹣AE ＝3+AE ，∴AE ＝1．【点睛】本题是圆的综合题，考查了切线的判定，圆周角定理，全等三角形的判定与性质，等腰三角形的判定，正确作出辅助线来构造全等三角形是解题的关键．4．如图，在平面直角坐标系中，O 为坐标原点，△ABC 的边BC 在y 轴的正半轴上，点A 在x 轴的正半轴上，点C 的坐标为（0，8），将△ABC 沿直线AB 折叠，点C 落在x 轴的负半轴D （−4，0）处．（1）求直线AB 的解析式；（2）点P 从点A 出发以每秒5AB 方向运动，过点P 作PQ ⊥AB ，交x 轴于点Q ，PR ∥AC 交x 轴于点R ，设点P 运动时间为t （秒），线段QR 长为d ，求d 与t 的函数关系式（不要求写出自变量t 的取值范围）；（3）在（2）的条件下，点N 是射线AB 上一点，以点N 为圆心，同时经过R 、Q 两点作⊙N ，⊙N 交y 轴于点E ，F ．是否存在t ，使得EF =RQ ？若存在，求出t 的值，并求出圆心N 的坐标；若不存在，说明理由．【答案】（1）132y x =-+（2）d =5t （3）故当 t =85，或815，时，QR =EF ，N （-6，6）或（2，2）．【解析】 试题分析：（1）由C （0，8），D （-4，0），可求得OC ，OD 的长，然后设OB=a ，则BC=8-a ，在Rt △BOD 中，由勾股定理可得方程：（8-a ）2=a 2+42,解此方程即可求得B 的坐标，然后由三角函数的求得点A 的坐标，再利用待定系数法求得直线AB 的解析式；（2）在Rt △AOB 中，由勾股定理可求得AB 的长，继而求得∠BAO 的正切与余弦，由PR//AC 与折叠的性质，易证得RQ=AR ，则可求得d 与t 的函数关系式；（3）首先过点分别作NT ⊥RQ 于T ，NS ⊥EF 于S ，易证得四边形NTOS 是正方形，然后分别从点N 在第二象限与点N 在第一象限去分析求解即可求解;试题解析：（1）∵C （0，8），D （-4，0），∴OC=8，OD=4，设OB=a ，则BC=8-a ，由折叠的性质可得：BD=BC=8-a ，在Rt △BOD 中，∠BOD=90°，DB 2=OB 2+OD 2，则（8-a ）2=a 2+42， 解得：a=3，则OB=3，则B （0，3），tan ∠ODB=34OB OD = ， 在Rt △AOC 中，∠AOC=90°，tan ∠ACB=34OA OC = ， 则OA=6，则A （6，0），设直线AB 的解析式为：y=kx+b ，则60{3k bb+==，解得：1{23kb=-=，故直线AB的解析式为：y=-12x+3；（2）如图所示：在Rt△AOB中，∠AOB=90°，OB=3，OA=6，则22135,tan2OBOB OA BAOOA+=∠==，255OAcos BAOAB∠==，在Rt△PQA中，905APQ AP t∠=︒=，则AQ=10cosAPtBAO=∠,∵PR∥AC，∴∠APR=∠CAB，由折叠的性质得：∠BAO=∠CAB，∴∠BAO=∠APR，∴PR=AR，∵∠RAP+∠PQA=∠APR+∠QPR=90°，∴∠PQA=∠QPR，∴RP=RQ，∴RQ=AR，∴QR=12AQ=5t,即d=5t;（3）过点分别作NT⊥RQ于T，NS⊥EF于S，∵EF=QR，∴NS=NT，∴四边形NTOS是正方形，则TQ=TR=1522QR t=，∴1115151022224NT AT AQ TQ t t t==-=-=（）（），分两种情况，若点N 在第二象限，则设N （n ，-n ），点N 在直线132y x =-+ 上， 则132n n -=-+ ， 解得：n=-6，故N （-6，6），NT=6，即1564t = ， 解得：85t = ; 若点N 在第一象限，设N （N ，N ），可得：132n n =-+ , 解得：n=2，故N （2，2），NT=2， 即1524t =, 解得：t=815∴当 t =85，或815，时，QR =EF ，N （-6，6）或（2，2）。
初中圆综合试题及答案
初中圆综合试题及答案一、选择题（每题2分，共10分）1. 圆的周长公式是（）。
A. C = πdB. C = 2πrC. C = πr^2D. C = 2πd2. 圆的面积公式是（）。
A. A = πr^2B. A = 2πrC. A = πd^2D. A = πd3. 圆的直径是半径的（）倍。
A. 1B. 2C. 3D. 44. 圆的半径增加1倍，面积增加（）倍。
A. 1B. 2C. 4D. 85. 圆的半径为r，直径为d，周长为C，下列关系式正确的是（）。
A. C = 2πrB. d = 2rC. C = πdD. A和B都正确二、填空题（每题2分，共10分）1. 圆的周长公式是C = 2πr，其中r代表圆的______。
2. 圆的面积公式是A = πr^2，其中r代表圆的______。
3. 圆的直径是半径的______倍。
4. 如果圆的半径为3厘米，那么它的周长是______厘米。
5. 圆的半径增加1倍，面积增加到原来的______倍。
三、解答题（每题10分，共20分）1. 已知圆的半径为5厘米，求该圆的周长和面积。
2. 一个圆的周长为25.12厘米，求该圆的半径。
四、证明题（每题15分，共30分）1. 证明圆的周长和直径的比值是一个常数。
2. 证明圆的面积与半径的平方成正比。
答案：一、选择题1. B2. A3. B4. C5. D二、填空题1. 半径2. 半径3. 24. 31.45. 4三、解答题1. 周长：C = 2πr = 2 × 3.14 × 5 = 31.4厘米面积：A = πr^2 = 3.14 × 5^2 = 78.5平方厘米2. 半径：r = C / (2π) = 25.12 / (2 ×3.14) = 4厘米四、证明题1. 证明：设圆的直径为d，半径为r，则d = 2r。
圆的周长C = πd = 2πr，所以C/d = 2πr / 2r = π，即圆的周长和直径的比值是一个常数π。
2023年九年级中考数学高频考点专题训练 圆的综合题(含解析)
2023年中考数学高频考点专题训练--圆的综合题1．已知：△ABC内接于△O，直径AM平分△BAC．（1）如图1，求证AB＝AC；（2）如图2，弦FG分别交AB、AC于点D、E，AE＝BD，当△ADE+△DEC＝90°时，连接CD，直径AM分别交DE、CD、BC于N、H、R，若CD△AB，求证：△NDC＝△ACB；（3）在（2）的条件下，若DE长为√2，求△ACH的面积．2．在平面直角坐标系xOy中，对于点P，Q和图形G，给出如下定义：若图形G上存在一点C，使△PQC＝90°，则称点Q为点P关于图形G的一个“直角联络点”，称Rt△PCQ为其对应的“联络三角形”．如图为点P关于图形G的一个“直角联络点”及其对应的“联络三角形”的示例．（1）已知点A（4，0），B（4，4）①在点Q1（2，2），Q2（4，﹣1）中，点O关于点A的“直角联络点”是；②点E的坐标为（2，m），若点E是点O关于线段AB的“直角联络点”，直接写出m的取值范围；（2）△T的圆心为（t，0），半径为√10，直线y＝﹣x+2与x，y轴分别交于H，K两点，若在△T上存在一点P，使得点P关于△T的一个“直角联络点”在线段HK 上，且其对应的“联络三角形”是底边长为2的等腰三角形，直接写出t的取值范围．3．对于平面直角坐标系xOy中的点P和△C，给出如下定义：若△C上存在一个点M，使得PM = MC，则称点P为△C的“等径点”．已知点D (12，13)，E(0，2√3)，F (−2，0)．（1）当△O的半径为1时，①在点D，E，F中，△O的“等径点”是；②作直线EF，若直线EF上的点T（m，n）是△O的“等径点”，求m的取值范围．（2）过点E作EG△EF交x轴于点G，若△EFG上的所有点都是某个圆的“等径点”，求这个圆的半径r的取值范围．4．问题背景：如图①，在四边形ADBC中，△ACB=△ADB=90°，AD=BD，探究线段AC，BC，CD之间的数量关系．小吴同学探究此问题的思路是：将△BCD绕点D，逆时针旋转90°到△AED处，点B，C分别落在点A，E处（如图②），易证点C，A，E在同一条直线上，并且△CDE 是等腰直角三角形，所以CE= √2CD，从而得出结论：AC+BC= √2CD．简单应用：（1）在图①中，若AC= √2，BC=2 √2，则CD=．（2）如图③，AB是△O的直径，点C、D在△上，AD̂= BD̂，若AB=13，BC=12，求CD的长．拓展规律：（3）如图④，△ACB=△ADB=90°，AD=BD，若AC=m，BC=n（m＜n），求CD 的长（用含m，n的代数式表示）（4）如图⑤，△ACB=90°，AC=BC，点P为AB的中点，若点E满足AE= 1 3AC，CE=CA，点Q为AE的中点，则线段PQ与AC的数量关系是．5．如图，等边三角形ABC中，AB= 2√3，AH△BC于点H，过点B作BD△AB交线段AH的延长线于点D，连结CD. 点E为线段AD上一点(不与点A，D重合)，过点E作EF△AB交BC于点F，以EF为直径作△O. 设AE的长为x.（1）求线段CD的长度.（2）当点E在线段AH上时，用含x的代数式表示EF的长度.（3）当△O与四边形ABDC的一边所在直线相切时，求所有满足条件的x的值. 6．如图1，⊙O是ΔABC的外接圆，AB是直径，D是⊙O外一点且满足∠DCA=∠B，连接AD.（1）求证：CD是⊙O的切线；（2）若AD⊥CD，AB=8，AD=6，求AC的长；（3）如图2，当∠DAB=45°时，AD与⊙O交于E点，试写出AC、EC、BC 之间的数量关系并证明.7．问题探究（1）如图1，在△ABC中，BC=8，D为BC上一点，AD=6，则△ABC面积的最大值是。
2023年中考九年级数学高频考点提升练习--圆的综合题(含答案)
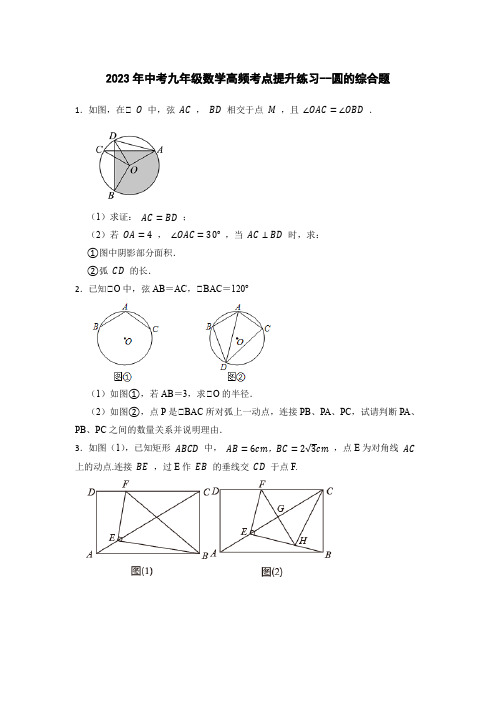
2023年中考九年级数学高频考点提升练习--圆的综合题1．如图，在⊙ O中，弦AC，BD相交于点M，且∠OAC=∠OBD．（1）求证：AC=BD；（2）若OA=4，∠OAC=30°，当AC⊥BD时，求：①图中阴影部分面积．②弧CD的长．2．已知⊙O中，弦AB＝AC，⊙BAC＝120°（1）如图①，若AB＝3，求⊙O的半径．（2）如图②，点P是⊙BAC所对弧上一动点，连接PB、PA、PC，试请判断PA、PB、PC之间的数量关系并说明理由．3．如图（1），已知矩形ABCD中，AB=6cm，BC=2√3cm，点E为对角线AC 上的动点.连接BE，过E作EB的垂线交CD于点F.（1）探索BE与EF的数量关系，并说明理由.（2）如图（2），过F作AC垂线交AC于点G，交EB于点H，连接CH.若点E从A出发沿AC方向以2√3cm/s的速度向终点C运动，设E的运动时间为ts.①是否存在t，使得H与B重合？若存在，求出t的值；若不存在，说明理由；②t为何值时，△CFH是等腰三角形；③当CG=GH时，求△CGH的面积.4．如图，AB是⊙O的直径，BC为⊙O的切线，D为⊙O上的一点，CD＝CB，延长CD交BA的延长线于点E.（1）求证：CD是⊙O的切线；（2）求证：⊙C＝2⊙DBE.（3）若EA＝AO＝2，求图中阴影部分的面积.（结果保留π）5．定义：三角形一边上的点将该边分为两条线段，且这两条线段的积等于这个点到该边所对顶点连线的平方，则称这个点为三角形该边的“好点”.如图1，⊙ABC中，点D 是BC边上一点，连结AD，若AD2=BD⋅CD，则称点D是⊙ABC中BC边上的“好点”.（1）如图2，⊙ABC的顶点是4×3网格图的格点，请仅用直尺画出AB边上的一个“好点”.（2）⊙ABC中，BC=9，tanB=43，tanC=23，点D是BC边上的“好点”，求线段BD的长.（3）如图3，⊙ABC是⊙O的内接三角形，OH⊙AB于点H，连结CH并延长交⊙O于点D.①求证：点H是⊙BCD中CD边上的“好点”.②若⊙O的半径为9，⊙ABD=90°，OH=6，请直接写出CHDH的值.6．如图，⊙O为等边⊙ABC的外接圆，半径为2，点D在劣弧上运动（不与点A，B 重合），连接DA，DB，DC.（1）求证：DC是⊙ADB的平分线；（2）设四边形ADBC的面积为S，线段DC的长为x，试用含x的代数式表示S；（3）若点M，N分别在线段CA，CB上运动（不含端点），经过探究发现，点D 运动到每一个确定的位置，⊙DMN的周长有最小值t，随着点D的运动，t的值会发生变化，求所有t值中的最大值.7．在⊙ABC中，D，E分别是⊙ABC两边的中点，如果弧DE（可以是劣弧、优弧或半圆）上的所有点都在⊙ABC的内部或边上，则称弧DE为⊙ABC的中内弧．例如，图1中弧DE是⊙ABC其中的某一条中内弧．（1）如图2，在边长为4 √3的等边⊙ABC中，D，E分别是AB，AC的中点．画出⊙ABC的最长的中内弧DE，并直接写出此时弧DE的长；（2）在平面直角坐标系中，已知点A（2 √3，6），B（0，0），C（t，0），在⊙ABC中，D，E分别是AB，AC的中点．①若t＝2 √3，求⊙ABC的中内弧DE所在圆的圆心P的纵坐标的取值范围；②请写出一个t的值，使得⊙ABC的中内弧DE所在圆的圆心P的纵坐标可以取全体实数值．8．如图，⊙O是⊙ABC的外接圆，AC是直径，过点O作OD⊙AB于点D，延长DO 交⊙O于点P，过点P作PE⊙AC于点E，作射线DE交BC的延长线于F点，连接PF．（1）若⊙POC=60°，AC=12，求劣弧PC的长；（结果保留π）（2）求证：OD=OE；（3）求证：PF是⊙O的切线．9．如图，点A和动点P在直线l上，点P关于点A的对称点为Q，以AQ为边作Rt△ABQ，使∠BAQ=90°，AQ：AB=3：4，作△ABQ的外接圆O.点C在点P右侧，PC=4，过点C作直线m⊥l，过点O作OD⊥m于点D，交AB右侧的圆弧于点E.在射线CD上取点F，使DF=32CD，以DE，DF为邻边作矩形DEGF.设AQ=3x.（1）用关于x的代数式表示BQ=，DF=.（2）当点P在点A右侧时，若矩形DEGF的面积等于90，求AP的长.（3）当点P在点A右侧时，作直线BG交⊙O于点N，若BN的弦心距为1，求AP的长.10．如图，⊙ABC中，⊙ACB=90°，D是边AB上一点，且⊙A=2⊙DCB．E是BC边上的一点，以EC为直径的⊙O经过点D．（1）求证：AB是⊙O的切线；（2）若CD的弦心距为1，BE=EO，求BD的长．11．已知：A、B两点在直线l的同一侧，线段AO，BM均是直线l的垂线段，且BM 在AO的右边，AO=2BM，将BM沿直线l向右平移，在平移过程中，始终保持⊙ABP=90°不变，BP边与直线l相交于点P．（1）当P与O重合时（如图2所示），设点C是AO的中点，连接BC．求证：四边形OCBM是正方形；（2）请利用如图1所示的情形，求证：ABPB=OMBM；（3）若AO=2 √6，且当MO=2PO时，请直接写出AB和PB的长．12．（问题情境）如图①，小区A、B位于一条笔直的道路l的同侧，为了方便A，B两个小区居民投放垃圾，现在l上建一个垃圾分类站C，使得C与A，B的距离之比为2：1.（1）（初步研究）在线段AB上作出点C，使CACB=2.如图，做法如下：第一步：过点A作射线AM，以A为圆心，任意长为半径画弧，交AM于点P1；以P1为圆心，AP1长为半径画弧，交AM于点P2；以P2为圆心，AP1长为半径画弧，交AM于点P3.第二步：连接BP3，作∠AP2C=∠AP3B，交AB于点C.则点C即为所求.请证明所作的点C满足CACB=2.（2）（深入思考）如图，点C在线段AB上，点D在直线AB外，且DADB=CACB=2.求证：DC是∠ADB的平分线.（3）（问题解决）如图，已知点A，B和直线l，点C在线段AB上，且CACB=2.用直尺和圆规完成下列作图.（保留作图痕迹，不写作法）（⊙）在直线AB上作出点E（异于点C），使EAEB=2；（⊙）在直线l上作出点F，使FAFB=2.13．在矩形ABCD中，BC=2AB，点E是对角线AC上任意一点，过点E作AD的垂线分别交AD，BC于点F，G，作FH平行AC交CD于点H．（1）证明：EF=CH．（2）连结GH交AC于点K，若AE：CK=3，求AE：EK的值．（3）作⊙FGH的外接圆⊙O，且AB=1．①若⊙O与矩形的边相切时，求CH的长．②作点E关于GH的对称点E'，当E'落在⊙O上时，直接写出⊙FGH的面积。
中考真题——圆的综合练习20题答案版
1.如图，已知在ZkABC中，ZA=90°<1)请用圆规和直尺作出G)P,使圆心P在AC边上，且与AB,BC两边都相切(保留作图痕迹，不写作法和证明).(2)若ZB=60°,AB=3,求。
P的面积•作图一复杂作图；切线的性质..(1)作/ABC的平分线交AC于P,再以P为圆心PA为半径即可作出:(2)根据角平分线的性质得到NABP=30°,根据三角函数可得萨巧，再根据圆的面积公式即可求解.解:(1)如图所示.则。
P为所求作的圆•(2) V ZB=60°,BP平分ZABC,/.ZABP=30°,VtanZABP=^,国=岛.\S or=3n.AB点本题主要考查了作图-复杂作图，角平分线的性质，即角平分线上的点到角两边的距评：离相等.同时考查了圆的面积•2.如图，己知四边形ABCD是平行四边形，AD与△ABC的外接圆恰好相切于点A,边CD与。
0相交于点E,连接AE,BE.(1)求证：AB=AC；(2)若过点A作AH1BE于H,求证：BH=CE+EH.考点：切线的性质；平行四边形的性质.分析：(1)根据弦切角定理和圆周角定理证明ZABC=ZACB,得到答案;(2)作AF±CD于F,证明△A EH^AAEF,得到EH=EF,根据△A BH丝△ACF,得到答案.解答：证明：(1)•.•AD与/\旭(；的外接圆。
0恰好相切于点A, ABENDAE,又ZEAC=ZEBC,A ZDAC=ZABC,•.•AD〃BC,A ZDAC=ZACB,A ZABC=ZACB,AAB=AC；(2)作AF±CD于F,..•四边形ABCE是圆内接四边形，二NABC二NAEF,又ZABOZACB,A ZAEF=ZACB,又ZAEB=ZACB,/.ZAEH=ZAEF,在ZkAEH和Z XAEF中，［r ZAHE=ZAE«ZAEH=ZAEF,AAAEH^AAEF,..・EH二ef,.-.CE+EH=CF,.AE二AE在△ABH和△ACF中，r ZABH=ZACF*ZAHB=ZAFC,AAABH^AACF,ABH=CF=CE+EH.、AB 二A C点评：本题考查的是切线的性质和平行四边形的性质以及全等三角形的判定和性质，运用性质证明相关的三角形全等是解题的关键，注意圆周角定理和圆内接四边形的性质的运用.3.00是的外接圆，AB是直径，过贷的中点P作00的直径PG交弦BC 于点D,连接AG、CP、PB.(1)如图1，若D是线段CP的中点，求/BAC的度数；(2)如图2,在DG上取一点K,使DK=DP,连接CK,求证：四边形AGKC是平行四边形；(3)如图3,取CP的中点E,连接ED并延长ED交AB于点H,连接PH,求证: PH±AB.分析：(1)由垂径定理得出PG1BC,CD=BD,再由三角函数求出ZB0D=60°,证出AC〃PG,得出同位角相等即可；(2)先由SAS证明△P DB^ACDK,得出CK=BP,Z0PB=ZCKD,证出AG=CK,再证明AG〃CK,即可得出结论；(3)先证出DH〃AG,得出Z0AG=Z0HD,再证0D=0H,由SAS证明△O BD^AHOP,得出Z0HP=Z0DB=90o,即可得出结论.解答：(1)解：・.•点P为证的中点，AB为00直径，・.・BP=PC,PGJ_BC,CD=BD,[AZ0DB=90°,•.・D为OP的中点，..・OD=【OP=A)B,..・cos NB0D=^=【，A ZB0D=60°,2 2 OB2•.・AB为。
圆综合测试题(含详细解析及答案).docx
《圆》的综合测试题学校: __________ 姓名：___________ 班级：___________ 考号： ___________一、选择題（題型注释）1. 用半径为3cm,圆心角是120。
的扇形鬧成一个惻锥的侧面，则这个圆锥的底面半径为（）A. 2πcm B ・ 1. 5cm C. πcmD. ICm2. 已知C ）O ］的半径为5cm, （Do2的半径为3cm,两圆的圆心距为7cm,则两圆的位置关系是（）A 外离B.外切C,内切D,相交3.如图是某公园的一角，ZAOB=90° ,弧AB 的半径OA 长是6米，C 是OA 的中点，点 D 在弧AB 上.CD 〃0B ・则图中休闲区（阴影部分）的面积是【】4.如右图，圆心角ZAOB=I00°,则ZACB 的度数为（）6.如图，肋是00的直径，弦CDLAB^点E ZCDB=3/ , 00的半径为3cm∙则圆Λ∙-∣√3C10∕r —牙 米-B.CA 、100o B. 50o C. 80o D 、45°心0到弦少的距离为（7. 圆心角为120%弧长为12π的扇形半径为（ ）A. 6B. 9C. 18D. 368. GK ）的直径AB = IOcm,弦CD 丄AB,垂足为P ・若OP ： 0B=3: 5,则CD 的长为（ ）9.如图.在△磁中，ZJ=90o ∙ AB=AC=2.以％的中点0为圆心的圆弧分别与月从 SC 相切于点八E∙则图中阴影部分的面枳是【 】A' 4Ttπ π πA. 1- —B.— C∙ 1 — _ D. 2- —44 22 ■10.如图，PA. PB 切00于A 、B 两点，CD 切C ）O 于点E,交PA, PB 于C 、D,若C ）O 的 半径为cZ∖PCD 的周长等于3“贝IJ tanZAPB 的值是（）二、填空题（题型注释）11. 母线长为4,底面圆的半径为1的圆锥的侧面枳为 _______________ ..12. 如图，AB 是半圆0的直径，点P 在AB 的延长线卜.，PC 切半圆0于点C,连接AC ・若 ZCPA=20° ,则 ZA 二 _______ 0•CA. 2 CrnB. 3 CmC. 3y∣3 CnlD. 6cmA ・ 6cm B. 4cm C. 8cmD. -∖∕9TCmD.313.如图是一个用來盛爆米花的圆锥形纸杯，纸杯开I I圆的直径EF长为IOCm・母线OE (OF)长为IOcm.在母线OF上的点A处有一块爆米花残渣，且FA=2cm, 一只蚂蚁从杯I 1的点E处沿圆锥表面爬行到A点,则此蚂蚁爬行的最短距离为_____________ cm.14. •如图，OO内切于Z∖ABC∙切点分别为D、E、E己知<B=50° , <C=60o ,连结OE. OF、DE、DFJlIJ<EDF= _______________________ 度.15.己知AB、CD是直径为10的C)O中的两条平行弦，且AB=8, CD二6.则这两条弦的距离为三、计算題(題型注释)四、解答题(题型注释)16.如图，AB足G)0的直径，AF是G)O切线，CD是垂直于AB的弦，垂足为E,过点C 作DA的平行线与AF相交于点F, CD=4√3 , BE=Z.求证：(1)四边形FADC是菱形：(2) FC是©0的切线.17.如图①，②，在平面直角坐标系Xoy中，点A的坐标为(4, 0),以点A为圆心, 4为半径的圆与X轴交于O, B两点∙OC为弦，z≤AOC = 60∖ PALX轴上的•动点，连结CP∙(1)求ZoAC的度数；(2)如图①，当CP与0A相切时，求Po的长：(3)如图②，当点P在直径OB上时，CP的延长线与0A相交于点Q ,问PO为何值时，∆OCQ是等腰三角形？18.如图，己知BQ与」Q相交于点E、F,点P是两圆连心线上的一点，分别联结PE、PF交ZIq于A、C两点，并延长交[]O∣与B、D两点。
第一单元《圆》综合达标训练提优测评卷 2022—2023北师大版六年级上册(含答案)
第一单元《圆》综合训练习题2022—2023北师大版六年级上册（含答案）一、选择题1. 下面三幅图的阴影部分的周长相比较，（）。
A．图（1）大B．图（2）大C．图（3）大2. 画一个周长是56.52厘米的圆，圆规两脚之间的距离是（）厘米。
A．3 B．6 C．9 D．123. 外圆半径为R，内圆半径为r的一个圆环的面积等于（）。
A．π（R²－r²）B．π（R－r）²C．2πR－2πr D．π（R＋r）²4. 车轮滚动一周，求所行的路程，就是求车轮的（）。
A．半径 B．直径 C．周长 D．面积5. 小明在三张边长为8厘米的正方形彩色卡纸上分别画出不同规格的圆形（如图所示），将图中的圆形剪下后，正方形彩色卡纸一定会有剩下的废料，下面说法正确的是（）。
A．甲种彩色卡纸剩下的废料多B．乙种彩色卡纸剩下的废料多C．丙种彩色卡纸剩下的废料多D．剩下的废料同样多二、填空题6. 一个周长是12.56厘米的圆，若它的直径扩大到原来的4倍，则周长扩大到原来的_________倍，面积扩大到原来的___________倍。
7. 用一根6.28dm长的铁丝弯成一个圆形铁环，这个铁环的直径是( )dm，面积是( )2dm。
8. 杂技演员表演独轮车走钢丝，车轮直径为30cm，要骑过18.84m长的钢丝，车轮要转____________周。
（ 取3.14）9. 如图,长方形和圆的面积相等，圆的周长是6.28厘米，长方形的长是( )厘米。
请你任选一种（画示意图、写文字、列算式等）方式表达：( )10. 一个车轮滚动100圈前进了188.4米，这个车轮的半径是( )米。
11. 一个钟表分针长10厘米，时针长8厘米，从2时走到3时，分针所扫过的面积是__________平方厘米，分针尖端走过的周长是__________厘米；从3时到6时，时针扫过的面积是__________平方厘米。
（ 取3.14）12. 圆周率是圆的和的比值，它是一个小数．13. 在一个直径是6米的圆形水池周围，修一条2米宽的石子路。
中考数学《圆的综合》专题训练(含有答案)
中考数学《圆的综合》专题训练(含有答案)1．如图，：AB 是O 的直径：BC 是O 弦，OD CB ⊥于点E ，交BC 于点D ．(1)请写出三个不同类型的正确结论(2)连结CD ，设BCD α∠= ABC β∠= 试找出α与β之间的一种关系式并给予证明．2．如图，，在ABC 中 AB AC = 以AB 为直径的O 交BC 于点D 交CA 的延长线于点E ．(1)求证点D 为线段BC 的中点．(2)若63BC = 3AE = 求O 的半径及阴影部分的面积．3．如图，AB 为O 的直径 点C 在O 上 延长BC 至点D 使DC CB =．延长DA 与O 的另一个交点为E 连结AC CE ，．(1)求证D E ∠=∠(2)若42AB BC AC =-=， 求CE 的长．4．请仅用无刻度的直尺完成下列作图 不写作法 保留作图痕迹(1)如图1， ABC 与ADE 是圆内接三角形 AB AD = AE AC = 画出圆的一条直径．(2)如图2 ， AB CD 是圆的两条弦 AB CD =且不相互平行 画出圆的一条直径． 5．如图，AB 是O 的直径 点D 在AB 的延长线上 点C 在O 上 ,30CA CD CDA =∠=︒．(1)求证CD 是O 的切线(2)若O 的半径为6 求点A 到CD 所在直线的距离．6．如图， 点C 在以AB 为直径的O 上 过C 作O 的切线交AB 的延长线于E AD CE ⊥于D 连接AC ．(1)求证ACD ABC ∠=∠(2)若3tan 4CAD ∠= 8AD = 求O 直径AB 的长．7．如图， 已知以Rt ABC 的直角边AC 为直径作O 交斜边AB 于点E 连接EO 并延长交BC 的延长线于点D 连接AD 点F 为BC 的中点 连接EF ．(1)求证EF 是O 的切线(2)若O 的半径为6 8CD = 求AB 的长．8．如图， AB 是半圆O 的直径 D 为半圆O 上的点(不与A B 重合) 连接AD 点C 为BD 的中点 过点C 作CF AD ⊥ 交AD 的延长线于点F 连接BF AC 交于点E ．(1)求证FC 是半圆O 的切线(2)若3AF = 23AC = 求半圆O 的半径及AE 的长．9．如图， AB 为O 的直径 C 为BA 延长线上一点 CD 是O 的切线 D 为切点 OF AD ⊥于点E 交CD 于点F ．(1)求证ADC AOF ∠=∠ (2)若53OC OB = 24BD = 求EF 的长． 10．如图，所示 AB 是O 的直径 点D 在AB 上 点C 在O 上 AD AC =CD 的延长线交O 于点E ．(1)在CD 的延长线上取一点F 使BF BC = 求证BF 是O 的切线 (2)若2AB = 2CE 求图中阴影部分的面积．11．如图， ABC 内接于O AB 为O 的直径 D 为BA 延长线上一点 连接CD 过O 作OF BC ∥交AC 于点E 交CD 于点F ACD AOF ∠=∠．(1)求证CD 为圆O 的切线 (2)若1sin 4D =10BC = 求EF 的长． 12．如图， 四边形ABCD 是O 的内接四边形 AD CD = 70BAC ∠=︒ 50∠=°ACB ．(1)求ABD ∠的度数 (2)求BAD ∠的度数．13．如图， 四边形ABCD 是O 的内接四边形 且对角线BD 为O 的直径 过点A 作AE CD ⊥ 与CD 的延长线交于点E 且DA 平分BDE ∠．(1)求证AE 是O 的切线(2)若O 的半径为5 6CD = 求DA 的长．14．如图， 在正方形ABCD 中有一点P 连接AP BP 旋转APB △到CEB 的位置．(1)若正方形的边长是8 4BP =．求阴影部分面积 (2)若4BP = 7AP = 135APB ∠=︒ 求PC 的长．15．如图， AB 是O 的直径 OD 垂直于弦AC 于点E 且交O 于点D F 是BA 延长线上一点 若CDB BFD ∠=∠．(1)求证 FD 是O 的一条切线(2)若15AB = 9BC = 求DF 的长． 16．如图，O 是ABC ∆的外接圆 AE 切O 于点A AE 与直径BD 的延长线相交于点E ．(1)如图，① 若70C ∠=︒ 求E ∠的大小 (2)如图，① 若AE AB = 求E ∠的大小．17．已知 如图， 直线MN 交O 于A B 两点 AC 是直径 AD 平分CAM ∠交O 于D 过D 作DE MN ⊥于E ．(1)求证DE 是O 的切线(2)若8cm DE = 4cm AE = 求O 的半径．18．已知四边形ABCD 内接于O C 是DBA 的中点 FC AC ⊥于C 与O 及AD 的延长线分别交于点,E F 且DE BC =．(1)求证~CBA FDC(2)如果9,4AC AB == 求tan ACB ∠的值．参考答案与解析1．(1)见解析(2)关系式为2=90αβ+︒ 证明见解析【分析】（1）AB 是O 的直径 BC 是弦 OD BC ⊥于E 本题满足垂径定理． （2）连接,CD DB 根据四边形ACDB 为圆内接四边形 可以得到290αβ+=︒． 【解析】（1）解不同类型的正确结论有 ①BE CE = ①BD CD = ①90BED ∠=︒ ①BOD A ∠=∠ ①AC OD ∥ ①AC BC ⊥ ①222OE BE OB += ①ABC S BC OE =⋅△ ①BOD 是等腰三角形 ①BOE BAC △∽△等等． （2）如图， 连接,CD DBα与β之间的关系式为290αβ+=︒证明AB 为圆O 的直径90A ABC ∴∠+∠=︒①又四边形ACDB 为圆内接四边形180A CDB ∠∠∴+=︒①∴①-①得90CDB ABC ∠∠-=︒①18021802CDB BCD α∠=︒-∠=︒- 即180290αβ︒--=︒ ①2=90αβ+︒．【点评】本题考查了圆的一些基本性质 且有一定的开放性 垂径定理 圆内接四边形的性质掌握圆的相关知识． 2．(1)见解析 (2)半径为3 39π324S =阴【分析】（1）连结AD 可得90ADB ∠=︒ 已知AB AC = 根据等腰三角形三线合一的性质即可得证点D 为线段BC 的中点（2）根据已知条件可证ABC DEC ∽△△ 得到ED ECAB BC= 22BD AB EC =⋅ 且EDC △是等腰三角形 进而得到ED DC BD == 设AB x = 则(()22333x x =+ 解方程即可求得O 的半径连接OE 可证AOE △是等边三角形 再根据AOEAOE S S S =-阴扇形即可求出阴影部分的面积【解析】（1）连结AD①AB 为O 的直径 ①90ADB ∠=︒ ①AB AC = ①BD CD =即点D 为线段BC 的中点． （2）①B E ∠=∠ C C ∠=∠ ①ABC DEC ∽△△ ①ED ECAB BC= ①AB AC = ①B C ∠=∠ ①C E ∠=∠ ①ED DC BD == ①22BD AB EC =⋅ 设AB x = 则 (()22333x x =+解得19x =-（舍去） 26x = ①O 的半径为3 连接OE ①60AOE =︒∠ ①AOE △是等边三角形 ①AE 33①AOEAOE S S S=-阴扇形260313333602π⨯⨯=-⨯ 39π324=【点评】本题主要考查等腰三角形的性质 相似三角形的判定和性质 不规则图形面积的计算 熟练掌握相关知识点是解题的关键． 3．(1)见解析 (2)CE 的长为17【分析】（1）由AB 为O 的直径得90ACB ∠=︒ 通过证明()ACD ACB ≌SAS 得到D B ∠=∠ 又由B E ∠=∠ 从而得到D E ∠=∠（2）设BC x = 则2AC x =- 在Rt ABC 中 由勾股定理可得222AC BC AB += 即()22224x x -+= 解一元二次方程得到BC 的长 由（1）知D E ∠=∠ 从而得到CD CE = 又由DC CB = 得到17CE CB ==【解析】（1）证明AB 为O 的直径90ACB ∴∠=︒180ACD ACB ∠+∠=︒90ACD ∴∠=︒在ACD 和ACB △中AC AC ACD ACB DC BC =⎧⎪∠=∠⎨⎪=⎩()ACD ACB ∴≌SASD B ∴∠=∠ BE ∠=∠D E ∴∠=∠（2）解设BC x =2BC AC -=∴2AC x =-在Rt ABC 中 由勾股定理可得222AC BC AB += 即()22224x x -+=解得117x = 217x = 17BC ∴=由（1）得D E ∠=∠ CD CE ∴= DC CB =17CE CB ∴==∴ CE 的长为17【点评】本题主要考查了圆周角定理 三角形全等的判定与性质 等腰三角形的性质 勾股定理解直角三角形 熟练掌握圆周角定理 三角形全等的判定与性质 等腰三角形的性质是解题的关键． 4．(1)见解析 (2)见解析【分析】（1）设BC DE 交于点G 连接AG 交圆于点F 即可作答（2）连接BC AD 交于点F 延长BA DC 两线交于点E 作直线EF 交圆于点M N 即可作答．【解析】（1）如图， 设BC DE 交于点G 连接AG 并延长 交圆于点F线段AF 即为所求证明如图， BC AE 交于点Q DE AC 交于点P 连接DB 交AF 于点H①AB AD = AE AC = ①C E ∠=∠ ADE ABC =∠∠ ①DAE BAC ∠=∠①DAE BAC ≌ ①BC DE = ①DAE BAC ∠=∠ ①BAE DAC ∠=∠①AB AD = ADE ABC =∠∠ ①DAP BAQ ≌ ①AQ AP = ①AE AC = ①QE PC =①QGE PGC ∠=∠ C E ∠=∠ ①QGE PGC ≌ ①QG PG =①AG AG = AQ AP = ①QAG PAG ≌ ①QAG PAG ∠=∠ ①BAE DAC ∠=∠ ①BAG DAG ∠=∠ ①AH AH = AB AD = ①BAH DAH ≌①BH DH = 90AHB AHD ∠=∠=° ①AF 垂直平分弦DB ①AF 是圆的直径（2）如图， 连接BC AD 交于点F 延长BA DC 两线交于点E 作直线EF 交圆于点M N线段MN 即为所求． 证明方法同（1）．【点评】本题主要考查了垂径定理 圆周角定理以及全等三角形的判定与性质等知识 掌握圆周角定理以及垂径定理是解答本题的关键． 5．(1)见解析 (2)9【分析】（1）已知点C 在O 上 先连接OC 由已知CA CD = 30CDA ∠=︒ 得30CAO ∠=︒ 30ACO ∠=︒ 所以得到60COD ∠=︒ 根据三角形内角和定理得90DCO ∠=︒ 即能判断直线CD 与O 的位置关系．（2）要求点A 到CD 所在直线的距离 先作AE CD ⊥ 垂足为E 由30CDA ∠=︒ 得12AE AD = 在Rt OCD △中 半径6OD = 所以212OD OC == 18AD OA OD =+= 从而求出AE ．【解析】（1）①ACD 是等腰三角形 30D ∠=︒①30CAD CDA ∠=∠=︒．连接OC①AO CO =①AOC 是等腰三角形①30CAO ACO ∠=∠=︒①60COD ∠=︒在COD △中 又①30CDO ∠=︒①90DCO ∠=︒①CD 是O 的切线 即直线CD 与O 相切．（2）过点A 作AE CD ⊥ 垂足为E ．在Rt OCD △中 ①30CDO ∠=︒①212OD OC ==61218AD AO OD =+=+=在Rt ADE △中①30EDA ∠=︒①点A 到CD 边的距离为92AD AE ==． 【点评】此题考查的知识点是切线的判定与性质 解题的关键是运用直角三角形的性质及30°角所对直角边的性质．6．(1)见解析 (2)252AB =．【分析】（1）连接OC 由DE 为O 的切线 得到OC DE ⊥ 再由AD CE ⊥ 得到AD OC ∥ 得到OCA CAD ∠=∠ 根据OA OC = 利用等边对等角得到OCA CAB ∠=∠ 等量代换得到CAD CAB ∠=∠ 由AB 为O 的直径 可知90ACB ∠=︒ 最后根据等角的余角相等可得结论 （2）在Rt CAD △中 利用锐角三角函数定义求出CD 的长 根据勾股定理求出AD 的长 由（1）易证ADC ACB 得到AD AC AC AB= 即可求出AB 的长． 【解析】（1）解连接OC由题意可知DE 与O 的相切于COC DE ∴⊥AD CE ⊥AD OC ∴∥OCA CAD ∴∠=∠OA OC =OCA CAB ∴∠=∠CAD CAB ∴∠=∠ AB 为O 的直径90ACB ∴∠=︒90CAD ACD CAB ABC ∴∠+∠=∠+∠=︒ACD ABC ∴∠=∠（2）在Rt CAD △中3tan 4CDCAD AD ∠== 8AD =364CD AD ∴==22226810AC CD AD ∴+=+=由（1）可知CAD CAB ∠=∠90D ACB ∠=∠=︒ADC ACB ∴ADACAC AB ∴=81010AB∴= 252AB ∴=【点评】此题考查了切线的性质 以及解直角三角形 熟练掌握切线的判定与性质是解本题的关键． 7．(1)证明见解析 (2)125AB =【分析】（1）连接FO 可根据三角形中位线的性质可判断OF AB ∥ 然后根据直径所对的圆周角是直角 可得CE AE ⊥ 进而知OF CE ⊥ 然后根据垂径定理可得FEC FCE ∠=∠OEC OCE ∠=∠ 再通过Rt ABC 可知90OEC FEC ∠+∠=︒ 因此可证EF 为O 的切线（2）根据题意可先在Rt OCD △中求出OD 然后在Rt EFD 中求出FC 最终在Rt ABC 中求解AB 即可．【解析】（1）证连接FO 则由题意OF 为Rt ABC 的中位线①OF AB ∥①AC 是O 的直径①CE AE ⊥①OF AB ∥①OF CE ⊥①由垂径定理知 OF 所在直线垂直平分CE①FC FE = OE OC =①FEC FCE ∠=∠ OEC OCE ∠=∠①90ACB ∠=︒即90OCE FCE ∠+∠=︒①90OEC FEC ∠+∠=︒即90FEO ∠=︒①EF 是O 的切线（2）解①O 的半径为6 8CD = 90ACB ∠=︒①OCD 为直角三角形 6OC OE == 8CD = ①2210OD OC CD += 10616ED OD OE =+=+=由（1）知 EFD △为直角三角形 且FC FE =①设FC FE x == 则8FD FC CD x =+=+①由勾股定理 222EF ED FD +=即()222168x x +=+ 解得12x =即12FC FE ==①点F 为BC 的中点①224BC FC ==①212AC OC ==①在Rt ABC 中 22125AB BC AC +①125AB =【点评】本题考查切线的证明 圆的基本性质 以及勾股定理解三角形等 掌握切线的证明方法 熟练运用圆中的基本性质是解题关键．8．(1)见解析(2)半径为2 123AE =【分析】（1）根据点C 为弧BD 的中点 得出FAC CAB ∠∠= 然后得出FAC ACO ∠∠= 根据平行线的性质得出CF OC ⊥ 进而即可求解（2）连接BC 设OC 与BF 相交于点P 证明AFC ACB ∽ 得出4AB = 证明BOP BAF ∽得出1322OP AF == 进而证明ECP EAF ∽ 根据相似三角形的性质列出比例式 进而即可求解． 【解析】（1）证明连接OC 如图，点C 为弧BD 的中点∴CD CB =FAC CAB ∠∠∴=又OA OC =CAB ACO ∠∠∴=FAC ACO ∠∠∴=∴OC AF ∥又CF AD ⊥CF OC ∴⊥FC ∴是半圆O 的切线．（2）解连接BC 如图，AB 是半圆O 的直径90ACB ∠∴=︒90AFC ACB ∠∠∴==︒又FAC CAB ∠∠=AFC ACB ∴∽ ∴AFACAC AB = 23234AB ∴=∴半圆O 的半径为2．设OC 与BF 相交于点POC AF ∥BOP BAF ∴∽ ∴12OPOB AF AB == ∴1322OP AF == ∴12PC OC OP =-=OC AF ∥ECP EAF ∴∽ ∴EC PCAE AF = 即123AC AEAE -= 2316AE-=∴123AE = 【点评】本题考查了切线的性质与判定 相似三角形的性质与判定 掌握切线的判定以及相似三角形的性质与判定是解题的关键．9．(1)见解析(2)3【分析】（1）连接DO 根据CD 是O 的切线 OF AD ⊥ 证明ADC DOF ∠∠= 利用等腰三角形三线合一性质 证明ADC AOF ∠∠=．（2） 利用平行线分线段成比例定理 计算OE 证明CFO CDB △∽△ 计算OF两线段作差即可求解．【解析】（1）如图， 连接DO CD 是O 的切线OD DF ∴⊥90ADC ADO ∠∠∴+=︒OF AD ⊥ OA OD =90DOF ADO ∠∠∴+=︒ DOF AOF ∠∠=ADC DOF ∠∠∴=ADC AOF ∠∠∴=．（2）如图， 连接DO CD 是O 的切线OD DF ∴⊥90CDO ∠∴=︒53OC OB =设5(0)CO k k => 则3DO OB AO k ===4CD k ∴=538CB CO OB k k k ∴=+=+= AB 是O 的直径 24BD =AD DB ∴⊥OF AD ⊥∴OF BD ∥ ∴AO AE OB ED = CFO CDB △∽△ ∴OF CO BD CB= AE ED ∴=5524538OF k k k ==+ ∴1122OE BD == 15OF = 3EF OF OE ∴=-=．【点评】本题考查了切线的性质 等腰三角形的三线合一性质 平行线分线段成比例定理 相似三角形的性质与判定 熟练掌握切线的性质 相似三角形的性质与判定是解题的关键．10．(1)证明过程见解析 (2)142π-【分析】（1）AB 是O 的直径 AC AD = BF BC = 可求出90FBD ∠=︒ AB BF ⊥ 由此即可求证（2）如图，所示（见解析）连接,CO EO 可得1OC OE == 可证222CO O CE += 90COE ∠=︒ 根据扇形面积的计算方法即可求解．【解析】（1）证明①AB 是O 的直径①90ACB ∠=︒①90ACD BCD ∠+∠=︒①AC AD =①ACD ADC ∠=∠①ADC BDF ∠=∠①ACD BDF ∠=∠①BC BF =①BCD F ∠=∠①90BDF F ∠+∠=︒①180()90FBD FDB F ∠=︒-∠+∠=︒①AB BF ⊥ 且OB 是O 的半径①BF 是O 的切线．（2）解如图，所示 连接,CO EO①2AB =①1OC OE == ①2CE ①222CO EO += 2222CE == ①222CO O CE +=①90COE ∠=︒ ①29011111360242ππS ⨯=-⨯⨯=-阴影 ①图中阴影部分的面积为142π-． 【点评】本题主要考查圆的基础知识 掌握圆的切线的证明方法 扇形面积的计算方法是解题的关键．11．(1)见解析(2)3【分析】（1）连接CO 根据OF BC ∥可得B AOF ∠=∠ 根据直径所对的圆周角为直角可得90B CAB ∠+∠=︒ 再根据AO CO =得出CAB ACO ∠=∠ 最后证明90ACD ACO ∠+∠=︒即可 （2）根据中位线定理得出152OE BC == 证明DBC DOF ∽ 根据相似三角形对应边成比例 即可求解．【解析】（1）证明连接CO①OF BC ∥①B AOF ∠=∠①AB 为O 的直径①90ACB ∠=︒ 则90B CAB ∠+∠=︒①90AOF CAB ∠+∠=︒①AO CO =①CAB ACO ∠=∠①ACD AOF ∠=∠①90ACD ACO ∠+∠=︒ 即OC CD ⊥①CD 为圆O 的切线（2）①AB 为O 的直径①点O 为AB 中点①OF BC ∥①OE 为ABC 中位线 ①152OE BC == ①1sin 4D = OC CD ⊥ ①4OD OC = 则5BD OD OB OC =+=①OF BC ∥①DBC DOF ∽ ①OF OF BC BD = 即4510OC OF OC = 解得8OF =①853EF OF OE =-=-=．【点评】本题主要考查了切线的判定和性质 圆周角定理 相似三角形的判定和性质以及解直角三角形 解题的关键是掌握切线的判定和性质以及相似三角形的判定和性质．12．(1)30︒(2)100︒【分析】（1）根据三角形内角和定理可得60ABC ∠=︒ 再由AD CD = 可得ABD CBD ∠=∠ 即可求解（2）根据圆周角定理可得30ABD ACD ∠∠==︒ 从而得到80BCD ∠=︒ 再由圆内接四边形的性质 即可求解．【解析】（1）解①70,50BAC ACB ∠=︒∠=︒①18060ABC BAC ACB ∠=︒-∠-∠=︒①AD CD = ①1302ABD CBD ABC ∠=∠=∠=︒ （2）解由圆周角定理得30ABD ACD ∠∠==︒①80BCD ACB ACD ∠=∠+∠=︒①四边形ABCD 是O 的内接四边形①180100BAD BCD ∠=︒-∠=︒．【点评】本题主要考查了圆内接四边形的性质 圆周角定理等知识 熟练掌握圆内接四边形的性质 圆周角定理是解题的关键．13．(1)见解析(2)AD 的长是25【分析】（1）连接OA 根据已知条件证明OA AE ⊥即可解决问题（2）作OF CD ⊥ 则四边形OAEF 是矩形 且132DF CD ==由此可求得DE 的长 在Rt OFD △中 勾股定理求出OF 即AE 的长 在Rt AED △中利用勾股定理求DA ． 【解析】（1）证明如图， 连接OA①AE CD ⊥①90DAE ADE ∠+∠=︒．①DA 平分BDE ∠①ADE ADO ∠=∠又①OA OD =①OAD ADO ∠=∠①90DAE OAD ∠+∠=︒①OA AE ⊥①AE 是O 的切线（2）解过点O 作OF CD ⊥于F ．①90OAE AEF OFE ∠︒=∠=∠=①四边形OAEF 是矩形①5EF OA AE OF ===，．①OF CD ⊥ ①132DF FC CD ===①532DE EF DF =-=-=在Rt OFD △中 2222534OF OD DF --=①4AE OF ==在Rt AED △中 22224225AD AE DE ++=①AD 的长是25【点评】本题考查了切线的判定与性质 垂径定理 圆周角定理 勾股定理 解决本题的关键是掌握切线的判定与性质．14．(1)12π(2)9【分析】(1) 根据题意 CEB APB ABC PBE S S S S S =+--阴影扇形扇形 根据公式计算即可．(2) 连接PE 根据题意 45,135,90PEB CEP PEC ∠=︒∠=︒∠=︒ 根据勾股定理计算即可．【解析】（1）如图， ①正方形ABCD 旋转APB △到CEB 的位置①APB CEB ≌ 90ABC PBE ∠=∠=︒ =CEB APB S S ①CEB APB ABC PBE S S S S S =+--阴影扇形扇形①ABC PBE S S S =-阴影扇形扇形①48BP AB ==， ①9064901612360360S πππ︒⨯⨯︒⨯⨯=-=︒︒阴影． （2）连接PE根据题意 45,135PEB APB CEP ∠=︒∠=∠=︒ AP CE =①90PEC ∠=︒①4BP = 7AP =①2227,4432CE PE ==+=①222273281PC CE PE =+=+=解得9PC =．【点评】本题考查了正方形的性质 旋转的性质 阴影面积的计算 扇形面积公式 勾股定理 熟练掌握旋转的性质 阴影面积的计算 扇形面积公式 勾股定理是解题的关键．15．(1)证明见解析(2)10DF =【分析】（1）因为CDB CAB ∠=∠ CDB BFD ∠=∠ 所以CAB BFD ∠=∠ 即可得出FD ①AC 可得得出OD FD ⊥ 进而得出结论（2）利用勾股定理先求解AC 再利用垂径定理得出AE 的长 可得OE 的长 证明AEO FDO ∽ 再利用相似三角形的判定与性质得出DF 的长．【解析】（1）①CDB CAB ∠=∠ CDB BFD ∠=∠①CAB BFD ∠=∠①FD AC ∥①OD 垂直于弦AC 于点E①OD FD ⊥①FD 是O 的一条切线（2）①AB 为O 的直径①90ACB ∠=︒①15AB = 9BC = ①2215912AC -= 7.5AO OB OD ===①DO AC ⊥①6AE CE == ①227.56 4.5OE -①AC FD ∥①AEO FDO ∽ ①AE EO FD DO = ①4.567.5FD= 解得10DF =．经检验符合题意.【点评】本题主要考查了相似三角形的判定与性质 垂径定理 圆周角定理 切线的判定 以及平行线的判定 掌握相似三角形的判定与性质 垂径定理 圆周角定理以及平行线的判定是解题的关键．16．(1)50︒(2)30︒【分析】（1）连接OA 先由切线的性质得OAE ∠的度数 求出2142AOB C ∠=∠=︒ 进而得AOE ∠ 则可求出答案（2）连接OA 根据等腰三角形的性质及切线的性质列方程求解即可．【解析】（1）连接OA ．如图，①AE 切O 于点AOA AE ∴⊥90OAE ∴∠=︒70C ∠=︒2270140AOB C ∴∠=∠=⨯︒=︒又180AOB AOE ∠+∠=︒40AOE ∴∠=︒90AOE E ∠+∠=︒904050E ∴∠=︒-︒=︒．（2）连接OA 如图，①设E x ∠=．AB AE =ABE E x ∴∠=∠=OA OB =OAB ABO x ∴∠=∠=2AOE ABO BAO x ∴∠=∠+∠=． AE 是O 的切线OA AE ∴⊥ 即90OAE ∠=︒在OAE ∆中 90AOE E ∠+∠=︒即290x x +=︒解得30x =︒30E ∴∠=︒．【点评】本题主要考查了切线的性质 等腰三角形的性质 圆周角的性质 三角形内角和的性质 用方程思想解决几何问题 关键是熟悉掌握这些性质．17．(1)见解析(2)10cm【分析】(1)连接OD 根据平行线的判定与性质可得90ODE DEM ∠=∠=︒ 又点D 在O 上 即可证得DE 是O 的切线(2)首先根据勾股定理可得AD 的长 再由ACD ADE ∽ 根据相似三角形的性质列出比例式 代入数据即可求得圆的半径．【解析】（1）证明如图，连接ODOA OD =OAD ODA ∠=∠∴ AD 平分CAM ∠OAD DAE ∴∠=∠ODA DAE ∴∠=∠DO MN ∴∥DE MN ⊥90ODE DEM ∴∠=∠=︒ 即OD DE ⊥ 又点D 在O 上 OD 为O 的半径DE ∴是O 的切线（2）解90AED ∠=︒ 8cm DE = 4cm AE =22228445AD DE AE ∴++如图，连接CDAC 是直径90ADC AED ∴∠=∠=︒CAD DAE ∠=∠ACD ADE ∴△∽△AD AC AE AD ∴= 4545=解得20AC =O ∴的半径为10cm ．【点评】本题考查圆了切线的判定；等边对等角 平行线的判定与性质 圆周角定理 勾股定理 相似三角形的判定和性质等知识 在圆中学会正确添加辅助线是解决问题的关键．18．(1)见解析 (2)49【分析】（1）欲证~CBA FDC ，只要证明两个角对应相等就可以．可以转化为证明DE BC =就可以 （2）由~CBA FDC 可得814CF = ACB F ∠=∠ 进而即可得到答案． 【解析】（1）证明①四边形ABCD 内接于O①CBA CDF ∠=∠．①DE BC =①BCA DCE ∠=∠．①~CBA FDC（2）解①C 是DBA 的中点①9CD AC ==①~CBA FDC 4AB = ①AB AC CD CF = 即499CF= ①814CF = ①~CBA FDC ①94tan tan 8194AC ACB F CF ∠=∠===．【点评】本题考查的是圆的综合题；涉及弧、弦的关系；等腰三角形的性质；相似三角形的判定与性质；锐角三角函数；掌握相似三角形的判定和性质是解答此题的关键．。
人教版九年级数学中考圆的综合专项练习及参考答案
人教版九年级数学中考圆的综合专项练习类型一 与全等结合1. 如图，⊙O 的直径AB ＝4，C 为⊙O 上一点，AC ＝2.过点C 作⊙O 的切线DC ，P 点为优弧CBA ︵上一动点(不与A 、C 重合)． (1)求∠APC 与∠ACD 的度数；(2)当点P 移动到劣弧CB ︵的中点时，求证：四边形OBPC 是菱形； (3)当PC 为⊙O 的直径时，求证：△APC 与△ABC 全等．第1题图(1)解：∵AC ＝2，OA ＝OB ＝OC ＝12AB ＝2，∴AC ＝OA ＝OC ， ∴△ACO 为等边三角形， ∴∠AOC ＝∠ACO ＝∠OAC ＝60°， ∴∠APC ＝12∠AOC ＝30°，又∵DC 与⊙O 相切于点C ， ∴OC ⊥DC ， ∴∠DCO ＝90°，∴∠ACD ＝∠DCO －∠ACO ＝90°－60°＝30°；第1题解图(2)证明：如解图，连接PB ，OP ，∵AB 为直径，∠AOC ＝60°， ∴∠COB ＝120°，当点P 移动到CB ︵的中点时，∠COP ＝∠POB ＝60°， ∴△COP 和△BOP 都为等边三角形， ∴OC ＝CP ＝OB ＝PB ， ∴四边形OBPC 为菱形；(3)证明：∵CP 与AB 都为⊙O 的直径，∴∠CAP ＝∠ACB ＝90°， 在Rt △ABC 与Rt △CPA 中，⎩⎪⎨⎪⎧AB ＝CP AC ＝AC ， ∴Rt △ABC ≌Rt △CPA (HL)．2. 如图，AB 为⊙O 的直径，CA 、CD 分别切⊙O 于点A 、D ，CO 的延长线交⊙O 于点M ，连接BD 、DM . (1)求证：AC ＝DC ； (2)求证：BD ∥CM ；(3)若sin B ＝45，求cos ∠BDM 的值．第2题图(1)证明：如解图，连接OD ，∵CA 、CD 分别与⊙O 相切于点A 、D ， ∴OA ⊥AC ，OD ⊥CD ， 在Rt △OAC 和Rt △ODC 中，⎩⎪⎨⎪⎧OA ＝OD OC ＝OC，∴Rt△OAC≌Rt△ODC(HL)，∴AC＝DC；(2)证明：由(1)知，△OAC≌△ODC，∴∠AOC＝∠DOC，∴∠AOD＝2∠AOC，∵∠AOD＝2∠OBD，∴∠AOC＝∠OBD，∴BD∥CM；(3)解：∵BD∥CM，∴∠BDM＝∠M，∠DOC＝∠ODB，∠AOC＝∠B，∵OD＝OB＝OM，∴∠ODM＝∠OMD，∠ODB＝∠B＝∠DOC，∵∠DOC＝2∠DMO，∴∠DOC＝2∠BDM，∴∠B＝2∠BDM，如解图，作OE平分∠AOC，交AC于点E，作EF⊥OC于点F，第2题解图∴EF ＝AE ，在Rt △EAO 和Rt △EFO 中，∵⎩⎪⎨⎪⎧OE ＝OE AE ＝EF ， ∴Rt △EAO ≌Rt △EFO (HL)， ∴OA ＝OF ，∠AOE ＝12∠AOC ，∴点F 在⊙O 上，又∵∠AOC ＝∠B ＝2∠BDM ， ∴∠AOE ＝∠BDM ， 设AE ＝EF ＝y ， ∵sin B ＝45，∴在Rt △AOC 中，sin ∠AOC ＝AC OC ＝45，∴设AC ＝4x ，OC ＝5x ，则OA ＝3x ，在Rt △EFC 中，EC 2＝EF 2＋CF 2， ∵EC ＝4x －y ，CF ＝5x －3x ＝2x ， ∴(4x －y )2＝y 2＋(2x )2， 解得y ＝32x ，∴在Rt △OAE 中，OE ＝OA 2＋AE 2＝（3x ）2＋（32x ）2＝352x ，∴cos ∠BDM ＝cos ∠AOE ＝OA OE ＝3x 352x＝255.3. 如图，⊙O 是△ABC 的外接圆，AC 为直径，AB ︵＝BD ︵，BE ⊥DC 交DC 的延长线于点E . (1)求证：∠1＝∠BCE ； (2)求证：BE 是⊙O 的切线； (3)若EC ＝1，CD ＝3，求cos ∠DBA .第3题图(1)证明：如解图，过点B 作BF ⊥AC 于点F ，∵AB ︵＝BD ︵， ∴AB ＝BD在△ABF 与△DBE 中， ⎩⎪⎨⎪⎧∠BAF ＝∠BDE ∠AFB ＝∠DEB AB ＝DB， ∴△ABF ≌△DBE (AAS)， ∴BF ＝BE ， ∵BE ⊥DC ，BF ⊥AC ， ∴∠1＝∠BCE ； (2)证明：如解图，连接OB ，∵AC 是⊙O 的直径，∴∠ABC ＝90°，即∠1＋∠BAC ＝90°， ∵∠BCE ＋∠EBC ＝90°，且∠1＝∠BCE ， ∴∠BAC ＝∠EBC ， ∵OA ＝OB ， ∴∠BAC ＝∠OBA ，∴∠EBC ＝∠OBA ，∴∠EBC ＋∠CBO ＝∠OBA ＋∠CBO ＝90°， ∴∠EBO ＝90°， 又∵OB 为⊙O 的半径， ∴BE 是⊙O 的切线；第3题解图(3)解：在△EBC 与△FBC 中，⎩⎪⎨⎪⎧∠BEC ＝∠CFB ，∠ECB ＝∠FCB ，BC ＝BC ，∴△EBC ≌△FBC (AAS)， ∴CE ＝CF ＝1.由(1)可知：AF ＝DE ＝1＋3＝4， ∴AC ＝CF ＋AF ＝1＋4＝5，∴cos ∠DBA ＝cos ∠DCA ＝CD CA ＝35.类型二 与相似结合4. 如图，△ABC 内接于⊙O ，AB ＝AC ，∠BAC ＝36°，过点A 作AD ∥BC ，与∠ABC 的平分线交于点D ，BD 与AC 交于点E ，与⊙O 交于点F .(1)求∠DAF 的度数； (2)求证：AE 2＝EF ·ED ； (3)求证：AD 是⊙O 的切线．第4题图(1)解：∵AB ＝AC ，∠BAC ＝36°，∴∠ABC ＝∠ACB ＝12(180°－36°)＝72°，∴∠AFB ＝∠ACB ＝72°， ∵BD 平分∠ABC ， ∴∠DBC ＝36°， ∵AD ∥BC ，∴∠D ＝∠DBC ＝36°，∴∠DAF ＝∠AFB －∠D ＝72°－36°＝36°；(2)证明：∵∠EAF ＝∠FBC ＝∠D ，∠AEF ＝∠AED ，∴△EAF ∽△EDA ，∴AE DE ＝EF EA， ∴AE 2＝EF ·ED ；(3)证明：如解图，过点A 作BC 的垂线，G 为垂足，∵AB ＝AC ， ∴AG 垂直平分BC ， ∴AG 过圆心O ， ∵AD ∥BC ， ∴AD ⊥AG ， ∴AD 是⊙O 的切线．第4题解图5. 如图，AB 为半圆的直径，O 为圆心，OC ⊥AB ，D 为BC ︵的中点，连接DA 、DB 、DC ，过点C 作DC 的垂线交DA 于点E ，DA 交OC 于点F .(1)求证：∠CED ＝45°；(2)求证：AE ＝BD ；(3)求AO OF的值．第5题图(1)证明：∵∠CDA ＝12∠COA ＝12×90°＝45°， 又∵CE ⊥DC ，∴∠DCE ＝90°，∴∠CED ＝180°－90°－45°＝45°；(2)解：如解图，连接AC ，∵D 为BC ︵的中点，∴∠BAD ＝∠CAD ＝12×45°＝22.5°， 而∠CED ＝∠CAE ＋∠ACE ＝45°，∴∠CAE ＝∠ACE ＝22.5°，∴AE ＝CE ，∵∠ECD ＝90°，∠CED ＝45°，∴CE ＝CD ，又∵CD ︵＝BD ︵，∴CD ＝BD ，∴AE ＝CE ＝CD ＝BD ，∴AE ＝BD ；第5题解图(3)解：设BD ＝CD ＝x ，∴AE ＝CE ＝x ，由勾股定理得，DE ＝2x ，则AD ＝x ＋2x ，又∵AB 是直径，则∠ADB ＝90°，∴△AOF ∽△ADB ，∴AO OF ＝AD DB ＝x ＋2x x＝1＋ 2. 6. 如图，AB 为⊙O 的直径，P 点为半径OA 上异于点O 和点A 的一个点，过P 点作与直径AB 垂直的弦CD ，连接AD ，作BE ⊥AB ，OE //AD 交BE 于E 点，连接AE 、DE ，AE 交CD 于点F .(1)求证：DE 为⊙O 的切线；(2)若⊙O 的半径为3，sin ∠ADP ＝13，求AD ； (3)请猜想PF 与FD 的数量关系，并加以证明．第6题图(1)证明：如解图，连接OD ，∵OA ＝OD ，∴∠OAD ＝∠ODA ，∵OE ∥AD ，∴∠OAD ＝∠BOE ，∠DOE ＝∠ODA ，∴∠BOE ＝∠DOE ，在△BOE 和△DOE 中，⎩⎪⎨⎪⎧OB ＝OD ∠BOE ＝∠DOE OE ＝OE，∴△BOE ≌△DOE (SAS)，∴∠ODE ＝∠OBE ，∵BE ⊥AB ，∴∠OBE ＝90°，∴∠ODE ＝90°，∵OD 为⊙O 的半径，∴DE 为⊙O 的切线；(2)解：如解图，连接BD ，∵AB 为⊙O 的直径，∴∠ADB ＝90°，∴∠ABD ＋∠BAD ＝90°，∵AB ⊥CD ，∴∠ADP ＋∠BAD ＝90°，∴∠ABD ＝∠ADP ，∴sin ∠ABD ＝AD AB ＝sin ∠ADP ＝13， ∵⊙O 的半径为3，∴AB =6，∴AD ＝13AB ＝2；第6题解图(3)解：猜想PF ＝FD ，证明：∵CD ⊥AB ，BE ⊥AB ，∴CD ∥BE ，∴△APF ∽△ABE ，∴PF BE ＝AP AB ，∴PF ＝AP ·BE AB ，在△APD 和△OBE 中，⎩⎪⎨⎪⎧∠APD ＝∠OBE∠PAD ＝∠BOE ，∴△APD ∽△OBE ，∴PD BE ＝AP OB ，∴PD ＝AP ·BE OB ，∵AB ＝2OB ，∴PF ＝12PD ， ∴PF ＝FD .7. 如图①，⊙O 是△ABC 的外接圆，AB 是⊙O 的直径，OD ∥AC ，OD 交⊙O 于点E ，且∠CBD ＝∠COD .(1)求证：BD 是⊙O 的切线；(2)若点E 为线段OD 的中点，求证：四边形OACE 是菱形．(3)如图②，作CF ⊥AB 于点F ，连接AD 交CF 于点G ，求FG FC的值．第7题图(1)证明：∵AB 是⊙O 的直径，∴∠BCA ＝90°，∴∠ABC ＋∠BAC ＝90°，∵OD ∥AC ，∴∠ACO ＝∠COD .∵OA＝OC，∴∠BAC＝∠ACO，又∵∠COD＝∠CBD，∴∠CBD＝∠BAC，∴∠ABC＋∠CBD＝90°，∴∠ABD＝90°，即OB⊥BD，又∵OB是⊙O的半径，∴BD是⊙O的切线；(2)证明：如解图，连接CE、BE，∵OE＝ED，∠OBD＝90°，∴BE＝OE＝ED，∴△OBE为等边三角形，∴∠BOE＝60°，又∵AC∥OD，∴∠OAC＝60°，又∵OA＝OC，∴△OAC为等边三角形，∴AC＝OA＝OE，∴AC∥OE且AC＝OE，∴四边形OACE是平行四边形，而OA＝OE，∴四边形OACE是菱形；第7题解图(3)解：∵CF⊥AB，∴∠AFC＝∠OBD＝90°，而AC∥OD，∴∠CAF＝∠DOB，∴Rt△AFC∽Rt△OBD，∴FCBD＝AFOB，即FC＝BD·AFOB，又∵FG∥BD，∴△AFG∽△ABD，∴FGBD＝AFAB，即FG＝BD·AFAB，∴FC FG ＝AB OB＝2， ∴FG FC ＝12. 8. 如图，AB 是⊙O 的直径，点E 为线段OB 上一点(不与O 、B 重合)，作EC ⊥OB 交⊙O 于点C ，作直径CD 过点C 的切线交DB 的延长线于点P ，作AF ⊥PC 于点F ，连接CB .(1)求证：AC 平分∠FAB ；(2)求证：BC 2＝CE ·CP ；(3)当AB ＝43且CF CP ＝34时，求劣弧BD ︵的长度．第8题图(1)证明：∵PF 切⊙O 于点C ，CD 是⊙O 的直径，∴CD ⊥PF ，又∵AF ⊥PC ，∴AF ∥CD ，∴∠OCA ＝∠CAF ，∵OA＝OC，∴∠OAC＝∠OCA，∴∠CAF＝∠OAC，∴AC平分∠FAB；(2)证明：∵AB是⊙O的直径，∴∠ACB＝90°，∵∠DCP＝90°，∴∠ACB＝∠DCP＝90°，又∵∠BAC＝∠D，∴△ACB∽△DCP，∴∠EBC＝∠P，∵CE⊥AB，∴∠BEC＝90°，∵CD是⊙O的直径，∴∠DBC＝90°，∴∠CBP＝90°，∴∠BEC＝∠CBP，∴△CBE ∽△CPB ，∴BC PC ＝CE CB， ∴BC 2＝CE ·CP ；(3)解：∵AC 平分∠FAB ，CF ⊥AF ，CE ⊥AB ，∴CF ＝CE ，∵CF CP ＝34， ∴CE CP ＝34， 设CE ＝3k ，则CP ＝4k ，∴BC 2＝3k ·4k ＝12k 2，∴BC ＝23k ，在Rt △BEC 中，∵sin ∠EBC ＝CE BC ＝3k 23k ＝32， ∴∠EBC ＝60°，∴△OBC 是等边三角形，∴∠DOB ＝120°，∴BD ︵＝120π·23180＝43π3.类型三 与全等相似结合9. 如图，四边形ABCD 内接于圆O ，∠BAD ＝90°，AC 为直径，过点A 作圆O 的切线交CB 的延长线于点E ，过AC 的三等分点F (靠近点C )作CE 的平行线交AB 于点G ，连接CG .(1)求证：AB ＝CD ；(2)求证：CD 2＝BE ·BC ；(3)当CG ＝3，BE ＝92，求CD 的长．第9题图(1)证明：∵AC 为直径，∴∠ABC ＝∠ADC ＝90°，∴∠ABC ＝∠BAD ＝90°，∴BC ∥AD ，∴∠BCA ＝∠CAD ，又∵AC＝CA，∴△ABC≌△CDA(AAS)，∴AB＝CD；(2)证明：∵AE为⊙O的切线且O为圆心，∴OA⊥AE，即CA⊥AE，∴∠EAB＋∠BAC＝90°，而∠BAC＋∠BCA＝90°，∴∠EAB＝∠BCA，而∠EBA＝∠ABC，∴△EBA∽△ABC，∴EBAB＝BABC，∴AB2＝BE·BC，由(1)知AB＝CD，∴CD2＝BE·BC；(3)解：由(2)知CD2＝BE·BC，即CD 2＝92BC ①， ∵FG ∥BC 且点F 为AC 的三等分点，∴G 为AB 的三等分点，即CD ＝AB ＝3BG ，在Rt △CBG 中，CG 2＝BG 2＋BC 2，即3＝(13CD )2＋BC 2②， 将①代入②，消去CD 得，BC 2＋12BC －3＝0， 即2BC 2＋BC －6＝0，解得BC ＝32或BC ＝－2(舍)③， 将③代入①得，CD ＝332. 10．如图，AB 为⊙O 的直径，C 为圆外一点，AC 交⊙O 于点D ，BC 2＝CD ·CA ，ED ︵＝BD ︵，BE 交AC 于点F .(1)求证：BC 为⊙O 的切线；(2)判断△BCF 的形状并说明理由；(3)已知BC ＝15，CD ＝9，∠BAC ＝36°，求BD ︵的长度(结果保留π).第10题图 (1)证明：∵BC 2＝CD ·CA ，∴BC CA ＝CD BC ，∵∠C ＝∠C ，∴△CBD ∽△CAB ，∴∠CBD ＝∠BAC ，又∵AB 为⊙O 的直径，∴∠ADB ＝90°，即∠BAC ＋∠ABD ＝90°，∴∠ABD ＋∠CBD ＝90°，即AB ⊥BC ，又∵AB 为⊙O 的直径，∴BC 为⊙O 的切线；(2)解：△BCF 为等腰三角形．证明如下：∵ED ︵＝BD ︵，∴∠DAE ＝∠BAC ，又∵△CBD ∽△CAB ，∴∠BAC ＝∠CBD ，∴∠CBD ＝∠DAE ，∵∠DAE ＝∠DBF ，∴∠DBF ＝∠CBD ，∵∠BDF ＝90°，∴∠BDC ＝∠BDF ＝90°，∵BD ＝BD ，∴△BDF ≌△BDC ，∴BF ＝BC ，∴△BCF 为等腰三角形；(3)解：由(1)知，BC 为⊙O 的切线，∴∠ABC ＝90°∵BC 2＝CD ·CA ，∴AC ＝BC 2CD ＝1529＝25，由勾股定理得AB ＝AC 2－BC 2＝252－152＝20，∴⊙O 的半径为r ＝AB 2＝10，∵∠BAC ＝36°， ∴BD ︵所对圆心角为72°.则BD ︵＝72×π×10180＝4π.。
圆的综合题附答案解析
一．选择题（共24小题）1．（2015•杭州模拟）现有两个圆，⊙O1的半径等于篮球的半径，⊙O2的半径等于一个乒）2．（2015•诸城市二模）如图，AB是⊙O的直径，D、C在⊙O上，AD∥OC，∠DAB=60°，连接AC，则∠DAC等于（）））5．（2013秋•太康县校级期中）下列说法：①直径不是弦；②相等的弦所对的弧相等；③在同圆或等圆中，优弧一定比劣弧长；④同一条弦所对的两条弧是等弧．6．（2013秋•裕华区校级月考）如图，将一个含有60°角的三角板，按图所示的方式摆放在半圆形纸片上，O为圆心，则∠ACO的度数为（）7．（2013秋•泰山区校级月考）如图，⊙O的直径AB与弦CD的延长线交于点E，若DE=OB，∠AOC=84°，则∠E等于（）8．（2013秋•昭通校级月考）如图，在以原点为圆心，2为半径的⊙O上有一点C，∠COA=45°，则C的坐标为（），，﹣），9．（2012秋•张店区校级期中）某公园计划砌一个形状如图（1）的喷水池，后来有人建议改为图（2）的形状，且外圆的直径不变，若两种方案砌各圆形水池的周边需用的材料费分别为W1和W2，则（）10．（2007•天水）如图，在Rt△ABC中，∠ACB=90度．点P是半圆弧AC的中点，连接BP交AC于点D，若半圆弧的圆心为O，点D、点E关于圆心O对称．则图中的两个阴影部分的面积S1，S2之间的关系是（）11．（2006•新疆）某公园计划砌一个形状如图（1）所示的喷水池，后来有人建议改为图（2）的形状，且外圆的直径不变，喷水池边沿的宽度、高度不变，你认为砌喷水池的边沿（）．cm14．如图，一枚半径为r的硬币沿着直线滚动一圈，圆心经过的距离是（）15．（2014•凤冈县二模）如图，弧AD是以等边三角形ABC一边AB为半径的四分之一圆周，P为弧AD上任意一点，若AC=5，则四边形ACBP周长的最大值是（）5+516．（2014春•萧山区校级月考）如图，半圆O是一个量角器，△AOB为一纸片，AB交半圆于点D，OB交半圆于点C，若点C、D、A在量角器上对应读数分别为45°，70°，160°，则∠B的度数为（）17．（2013•温州）在△ABC中，∠C为锐角，分别以AB，AC为直径作半圆，过点B，A，C作，如图所示．若AB=4，AC=2，S1﹣S2=，则S3﹣S4的值是（）．B．．D．18．（2012秋•昆山市期末）如图，将大小两块量角器的零度线对齐，且小量角器的中心O2恰好在大量角器的圆周上．设它们圆周的交点为P，且点P在小量角器上对应的刻度为75°，那么点P在大量角器上对应的刻度为（）19．（2012秋•邗江区期中）如图，在△ABC中，∠C=90°，∠B=28°，以C为圆心，CA为半径的圆交AB于点D，交BC于点E，则弧AD的度数为（）20．（2010•北仑区二模）如图，以AB为直径的半圆O上有两点D、E，ED与BA的延长线交于点C，且有DC=OE，若∠C=20°，则∠EOB的度数是（）21．（2005•内江）在一个地球仪的赤道上用铁丝打一个箍，现将铁丝箍半径增大1米，需增加m米长的铁丝，假设地球的赤道上也有一个铁箍，同样半径增大1米，需增加n米长的22．（2003•广东）如图，正方形的边长为a，以各边为直径在正方形内画半圆，所围成的图形（阴影部分）的面积为（）．πa2﹣a2D﹣π23．如图中奥迪车商标的长为34 cm，宽为10 cm，则d的值为（）24．如图，两个半径都是4cm的圆外切于点C，一只蚂蚁由点A开始依A、B、C、D、E、F、C、G、A的顺序沿着圆周上的8段长度相等的路径绕行，蚂蚁在这8段路径上不断爬行，直到行走2006πcm后才停下来，则蚂蚁停的那一个点为（）二．填空题（共5小题）25．（2015春•盐城校级期中）如图，⊙O的弦AB、半径OC延长交于点D，BD=OA．若∠AOC=120°，则∠D的度数是．26．（2013•淮北模拟）如图，AB为⊙O直径，点C、D在⊙O上，已知∠AOD=50°，AD∥OC，则∠BOC=度．27．（2013•龙马潭区校级模拟）如图，点A、B在⊙O上，且AB=BO．∠ABO的平分线与AO相交于点C，若AC=3，则⊙O的周长为．（结果保留π）28．（2012秋•高坪区校级期中）如图，AB是⊙O的直径，CD是⊙O的弦，AB、CD的延长线交于点E，已知AB=2DE，若△COD为直角三角形，则∠E的度数为°．29．（2010秋•灌云县月考）如图，AB是⊙O的直径，点C在⊙O上，CD⊥AB，垂足为D，已知CD=4，OD=3，求AB的长是．三．解答题（共1小题）30．（2011秋•江宁区校级期中）如图，BD=OD，∠AOC=114°，求∠AOD的度数．参考答案与试题解析一．选择题（共24小题）1．（2015•杭州模拟）现有两个圆，⊙O1的半径等于篮球的半径，⊙O2的半径等于一个乒）=R+，；R=，r=，．，面积增加了=R+=r+＞r+2．（2015•诸城市二模）如图，AB是⊙O的直径，D、C在⊙O上，AD∥OC，∠DAB=60°，连接AC，则∠DAC等于（）DAC=∠））5．（2013秋•太康县校级期中）下列说法：①直径不是弦；②相等的弦所对的弧相等；③在同圆或等圆中，优弧一定比劣弧长；④同一条弦所对的两条弧是等弧．6．（2013秋•裕华区校级月考）如图，将一个含有60°角的三角板，按图所示的方式摆放在半圆形纸片上，O为圆心，则∠ACO的度数为（）7．（2013秋•泰山区校级月考）如图，⊙O的直径AB与弦CD的延长线交于点E，若DE=OB，∠AOC=84°，则∠E等于（）E=∠AOC=×8．（2013秋•昭通校级月考）如图，在以原点为圆心，2为半径的⊙O上有一点C，∠COA=45°，则C的坐标为（），，﹣），，（﹣）9．（2012秋•张店区校级期中）某公园计划砌一个形状如图（1）的喷水池，后来有人建议改为图（2）的形状，且外圆的直径不变，若两种方案砌各圆形水池的周边需用的材料费分别为W1和W2，则（）π•+2+2π•=2r++）10．（2007•天水）如图，在Rt △ABC 中，∠ACB=90度．点P 是半圆弧AC 的中点，连接BP 交AC 于点D ，若半圆弧的圆心为O ，点D 、点E 关于圆心O 对称．则图中的两个阴影部分的面积S 1，S 2之间的关系是（ ）11．（2006•新疆）某公园计划砌一个形状如图（1）所示的喷水池，后来有人建议改为图（2）的形状，且外圆的直径不变，喷水池边沿的宽度、高度不变，你认为砌喷水池的边沿（ ）．cm14．如图，一枚半径为r的硬币沿着直线滚动一圈，圆心经过的距离是（）15．（2014•凤冈县二模）如图，弧AD是以等边三角形ABC一边AB为半径的四分之一圆周，P为弧AD上任意一点，若AC=5，则四边形ACBP周长的最大值是（）5+5AD=．AD=AC+BC+BD+AD=5+5+5+5=15+516．（2014春•萧山区校级月考）如图，半圆O是一个量角器，△AOB为一纸片，AB交半圆于点D，OB交半圆于点C，若点C、D、A在量角器上对应读数分别为45°，70°，160°，则∠B的度数为（）17．（2013•温州）在△ABC中，∠C为锐角，分别以AB，AC为直径作半圆，过点B，A，C作，如图所示．若AB=4，AC=2，S1﹣S2=，则S3﹣S4的值是（）．B．．D．，，ππ18．（2012秋•昆山市期末）如图，将大小两块量角器的零度线对齐，且小量角器的中心O2恰好在大量角器的圆周上．设它们圆周的交点为P，且点P在小量角器上对应的刻度为75°，那么点P在大量角器上对应的刻度为（）19．（2012秋•邗江区期中）如图，在△ABC中，∠C=90°，∠B=28°，以C为圆心，CA为半径的圆交AB于点D，交BC于点E，则弧AD的度数为（）20．（2010•北仑区二模）如图，以AB为直径的半圆O上有两点D、E，ED与BA的延长线交于点C，且有DC=OE，若∠C=20°，则∠EOB的度数是（）21．（2005•内江）在一个地球仪的赤道上用铁丝打一个箍，现将铁丝箍半径增大1米，需增加m米长的铁丝，假设地球的赤道上也有一个铁箍，同样半径增大1米，需增加n米长的22．（2003•广东）如图，正方形的边长为a，以各边为直径在正方形内画半圆，所围成的图形（阴影部分）的面积为（）．πa2﹣a2D﹣π如图所示，则4x=π，即阴影部分的面积为π23．如图中奥迪车商标的长为34 cm，宽为10 cm，则d的值为（）24．如图，两个半径都是4cm的圆外切于点C，一只蚂蚁由点A开始依A、B、C、D、E、F、C、G、A的顺序沿着圆周上的8段长度相等的路径绕行，蚂蚁在这8段路径上不断爬行，直到行走2006πcm后才停下来，则蚂蚁停的那一个点为（）二．填空题（共5小题）25．（2015春•盐城校级期中）如图，⊙O的弦AB、半径OC延长交于点D，BD=OA．若∠AOC=120°，则∠D的度数是20．26．（2013•淮北模拟）如图，AB为⊙O直径，点C、D在⊙O上，已知∠AOD=50°，AD∥OC，则∠BOC=65度．A=27．（2013•龙马潭区校级模拟）如图，点A、B在⊙O上，且AB=BO．∠ABO的平分线与AO相交于点C，若AC=3，则⊙O的周长为12π．（结果保留π）28．（2012秋•高坪区校级期中）如图，AB是⊙O的直径，CD是⊙O的弦，AB、CD的延长线交于点E，已知AB=2DE，若△COD为直角三角形，则∠E的度数为22.5°．∠∠29．（2010秋•灌云县月考）如图，AB是⊙O的直径，点C在⊙O上，CD⊥AB，垂足为D，已知CD=4，OD=3，求AB的长是10．==5三．解答题（共1小题）30．（2011秋•江宁区校级期中）如图，BD=OD，∠AOC=114°，求∠AOD的度数．。
中考数学《圆的综合题》专项练习题及答案
中考数学《圆的综合题》专项练习题及答案一、单选题1．如图，在一块正三角形飞镖游戏板上画一个正六边形（图中阴影部分），假设飞镖投中游戏板上的每一点是等可能的（若投中边界或没有投中游戏板，则重投1次），任意投掷飞镖1次，则飞镖投中阴影部分的概率为（）A．13B．49C．12D．232．如图，AB为⊙O的直径，弦DC垂直AB于点E，⊙DCB=30°，EB=3，则弦AC的长度为（）A．3 √3B．4√3C．5√3D．6√33．如图，AB是⊙O的弦，半径OC⊙AB于点D，且AB=6cm，OD=4cm。
则DC的长为（）A．cm B．1cm C．2cm D．5cm4．如图，四边形ABCD内接于⊙ O，AB为⊙ O的直径，∠ABD=20∘，则∠BCD的度数是（）A．90°B．100°C．110°D．120°5．如图，点A，B，C，D都在⊙O上，AC，BD相交于点E，则⊙ABD=（）A．⊙ACD B．⊙ADB C．⊙AED D．⊙ACB6．如图，在⊙O中，弦AB⊙CD，若⊙ABC=40°，则⊙BOD=（）A．20°B．40°C．50°D．80°7．下列判断结论正确的有（）（1）直径是圆中最大的弦．（2）长度相等的两条弧一定是等弧．（3）面积相等的两个圆是等圆．（4）同一条弦所对的两条弧一定是等弧．（5）圆上任意两点间的部分是圆的弦．A．1个B．2个C．3个D．4个8．已知如图，PA、PB切⊙O于A，B，MN切⊙O于C，交PB于N；若PA=7.5cm，则⊙PMN的周长是（）A．7.5cm B．10cm C．15cm D．12.5cm9．若小李同学掷出的铅球在场地航砸出一个直径为10厘米，深2厘米的小坑，则该铅球的直径为（）A．20厘米B．19.5厘米C．14.5厘米D．10厘米10．如图，如果从半径为9cm的圆形纸片剪去13圆周的一个扇形，将留下的扇形（阴影部分）围成一个圆锥（接缝处不重叠），那么这个圆锥的高为（）A．6cm B．5√3cm C．8cm D．3√5cm11．如图，△ABC内接于⊙O，∠B=65o，∠C=70o，若BC=2√2，则弧BC长为（）A．πB．√2πC．2πD．√2π12．如下图，点B，C，D在⊙O上，若⊙BCD＝130°，则⊙BOD的度数是（）A．96°B．98°C．102°D．100°二、填空题13．如图，在扇形AOB中，OA＝4，⊙AOB＝90°，点P是弧AB上的动点，连接OP，点C是线段OP的中点，连接BC并延长交OA于点D，则图中阴影部分面积最小值为.14．如图，在边长为√2的正方形ABCD中，分别以四个顶点为圆心，以边长为半径画弧，分别与正方形的边和对角线相交，则图中阴影部分的面积为（结果保留π）.15．如图，⊙ABC的顶点A，B，C均在⊙O上，若⊙ABC+⊙AOC=90°，则⊙AOC的大小是．16．如图：⊙O为⊙ABC的内切圆，⊙C＝90°，AO的延长线交BC于点D，AC＝4，CD＝1，则⊙O的半径为.17．如图，在正八边形ABCDEFGH中，AC、GC是两条对角线，则tan⊙ACG=．18．如图，菱形ABCD中，已知AB=2，∠DAB=60°将它绕着点A逆时针旋转得到菱形ADEF，使AB与AD重合，则点C运动的路线CE⌢的长为．三、综合题19．如图，AB是⊙O的直径，AP是⊙O的切线，A是切点，BP与⊙O交于点C，点D为AP的中点，连结AC．求证：（1）⊙P=⊙BAC（2）直线CD是⊙O的切线．20．如图，以△ABC的边AB为直径的⊙O交AC于点F，点E是BF⌢的中点，连接BE并延长交AC于点D，若∠CBD=12∠CAB．（1）求证：BC是⊙O的切线；（2）若⊙O的半径为2，cos∠BAC=25，求CD的长．21．如图，⊙O是⊙ABC的外接圆，AC是O的直径，BD＝BA＝12，BC＝5，BE⊙DC，交D的延长线于点E，BD交直径AC于点F．（1）求证：⊙BCA＝⊙BAD．（2）求证：BE是⊙O的切线．（3）若BD平分⊙ABC，交⊙O于点D，求AD的长．22．如图，⊙OAB中，OA=OB=10cm，⊙AOB=80°，以点O为圆心，半径为6cm的优弧弧MN分别交OA，OB于点M，N．（1）点P在右半弧上（⊙BOP是锐角），将OP绕点O逆时针旋转80°得OP′．求证：AP=BP′；（2）点T在左半弧上，若AT与弧相切，求A T的长．23．如图，有一直径是√2米的圆形铁皮，现从中剪出一个圆周角是90°的最大扇形ABC，则：（1）AB的长为米；（2）用该扇形铁皮围成一个圆锥，所得圆锥的底面圆的半径为米.⌢的中点，CE⊥AB于点E，BD交CE于点F．24．如图，AB是⊙O的直径，C是BD（1）求证：CF=BF；（2）若CD﹦5，AC﹦12，求⊙O的半径和CE的长．参考答案1．【答案】D2．【答案】D3．【答案】B4．【答案】C5．【答案】A6．【答案】D7．【答案】B8．【答案】C9．【答案】C10．【答案】D11．【答案】A12．【答案】D13．【答案】4π−8√3314．【答案】4-π15．【答案】60°16．【答案】0.817．【答案】118．【答案】2√33π19．【答案】（1）解：证明：∵AB是⊙O的直径∴⊙ACB=90°∴⊙ACP=90°∴⊙P+⊙CAP=90°∵AP⊙O是切线∴⊙BAP=90°即⊙CAP+⊙BAC=90°∴⊙P=⊙BAC；（2）解：∵CD是Rt⊙PAC斜边PA的中线∴CD=AD∴⊙DCA=⊙DAC连接OC∵OC=OA∴⊙OCA=⊙OAC∴⊙DCO=⊙DAO=90°∴CD是⊙O的切线．20．【答案】（1）证明：连接AE，如图所示：∵AB是⊙O的直径∴∠AEB=90°∴∠BAE+∠ABE=90°．∵点E为弧BF的中点∴EF⌢=EB⌢∴∠BAE=∠DAE=12∠CAB．又∵∠CBD=12∠CAB∴∠BAE=∠CBD∴∠CBD+∠ABE=90°∴AB⊥CB∴BC是⊙O的切线．（2）解：∵∠BAE=∠DAE，∠AED=∠AEB=90°∴∠ADE=∠ABE∴AD=AB=2×2=4．∵cos∠BAC=2 5∴在Rt△ABC中即4AC=25，得AC=10∴CD=AC−AD=10−4=6．21．【答案】（1）证明：∵BD=BA ∴∠BDA=∠BAD．∵∠BCA=∠BDA∴∠BCA=∠BAD．（2）证明：连结OB，如图∵∠BCA=∠BAD又∵∠BCE=∠BAD∴∠BCA=∠BCE∵OB=OC∴∠BCO=∠CBO∴∠BCE=∠CBO∴OB//ED．∵BE⊥ED∴EB⊥BO．∴BE是⊙O的切线．（3）解：∵AC是⊙O的直径∴∠ABC=90°∴AC=√AB2+BC2=√122+52=13．∵∠BDE=∠CAB∴△BED∽△CBA∴BDAC=DEAB，即1213=DE12∴DE=14413∴BE=√BD2−DE2=6013∴CE=√BC2−BE2=2513∴CD=DE−CE=119 13∵BD平分⊙ABC ∴∠CBD=∠ABD∴AD=CD=119 13．22．【答案】（1）证明：∵⊙AOB=⊙POP′=80°∴⊙AOB+⊙BOP=⊙POP′+⊙BOP即⊙AOP=⊙BOP′在⊙AOP 与⊙BOP′中 OA=OB ⊙AOP=⊙BOP OP=OP′∴⊙AOP⊙⊙BOP′ ∴AP=BP′（2）解：∵A T 与弧相切，连结OT ．∴OT⊙A T在Rt⊙AOT 中，根据勾股定理得，A T= √OA 2−OT 2 ∵OA=10，OT=6 ∴AT=823．【答案】（1）1 （2）1424．【答案】（1）证明：∵AB 是 ⊙O 的直径∴∠ACB =90° ∴∠A +∠ABC =90° 又∵CE ⊥AB ∴∠CEB =90° ∴∠BCE +∠ABC =90° ∴∠BCE =∠A∵C 是 BD ⌢ 的中点 ∴CD⌢=CB ⌢ ∴∠DBC =∠A ∴∠DBC =∠BCE ∴CF =BF（2）解：∵CD⌢=CB ⌢，CD =5 ∴∠DBC =∠BDC∴BC=CD=5∵∠ACB=90°∴AB=√AC2+BC2=√122+52=13∴AO=6.5∵∠BCE=∠A，∠ACB=∠CEB=90°∴△CEB⊙ △ACB∴CE=AC⋅BCAB=12×513=6013故⊙O的半径为6.5，CE的长是6013.第11页共11。
中考数学圆的综合综合经典题含详细答案
中考数学圆的综合综合经典题含详细答案一、圆的综合1．如图，⊙O是△ABC的外接圆，点E为△ABC内切圆的圆心，连接AE的延长线交BC于点F，交⊙O于点D；连接BD，过点D作直线DM，使∠BDM=∠DAC．（1）求证：直线DM是⊙O的切线；（2）若DF=2，且AF=4，求BD和DE的长．【答案】（1）证明见解析（2）23【解析】【分析】（1）根据垂径定理的推论即可得到OD⊥BC，再根据∠BDM=∠DBC，即可判定BC∥DM，进而得到OD⊥DM，据此可得直线DM是⊙O的切线；（2）根据三角形内心的定义以及圆周角定理，得到∠BED=∠EBD，即可得出DB=DE，再判定△DBF∽△DAB，即可得到DB2=DF•DA，据此解答即可．【详解】（1）如图所示，连接OD．∵点E是△ABC的内心，∴∠BAD=∠CAD，∴BD CD=，∴OD⊥BC．又∵∠BDM=∠DAC，∠DAC=∠DBC，∴∠BDM=∠DBC，∴BC∥DM，∴OD⊥DM．又∵OD为⊙O半径，∴直线DM是⊙O的切线．（2）连接BE．∵E为内心，∴∠ABE=∠CBE．∵∠BAD=∠CAD，∠DBC=∠CAD，∴∠BAD=∠DBC，∴∠BAE+∠ABE=∠CBE+∠DBC，即∠BED=∠DBE，∴BD=DE．又∵∠BDF=∠ADB（公共角），∴△DBF∽△DAB，∴DF DBDB DA=，即DB2=DF•DA．∵DF=2，AF=4，∴DA=DF+AF=6，∴DB2=DF•DA=12，∴DB=DE=23．【点睛】本题主要考查了三角形的内心与外心，圆周角定理以及垂径定理的综合应用，解题时注意：平分弦所对一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧；三角形的内心到三角形三边的距离相等；三角形的内心与三角形顶点的连线平分这个内角．2．如图，AB是⊙O的直径，弦CD⊥AB，垂足为H，连结AC，过BD上一点E作EG∥AC 交CD的延长线于点G，连结AE交CD于点F，且EG=FG，连结CE．（1）求证：∠G=∠CEF；（2）求证：EG是⊙O的切线；（3）延长AB交GE的延长线于点M，若tanG =34，AH=33，求EM的值．【答案】（1）证明见解析；（2）证明见解析；（3）253 8.【解析】试题分析：（1）由AC∥EG，推出∠G=∠ACG，由AB⊥CD推出AD AC=，推出∠CEF=∠ACD，推出∠G=∠CEF，由此即可证明；（2）欲证明EG是⊙O的切线只要证明EG⊥OE即可；（3）连接OC．设⊙O的半径为r．在Rt△OCH中，利用勾股定理求出r，证明△AHC∽△MEO，可得AH HCEM OE=，由此即可解决问题；试题解析：（1）证明：如图1．∵AC∥EG，∴∠G=∠ACG，∵AB⊥CD，∴AD AC=，∴∠CEF=∠ACD，∴∠G=∠CEF，∵∠ECF=∠ECG，∴△ECF∽△GCE．（2）证明：如图2中，连接OE．∵GF=GE，∴∠GFE=∠GEF=∠AFH，∵OA=OE，∴∠OAE=∠OEA，∵∠AFH+∠FAH=90°，∴∠GEF+∠AEO=90°，∴∠GEO=90°，∴GE⊥OE，∴EG是⊙O的切线．（3）解：如图3中，连接OC ．设⊙O 的半径为r ．在Rt △AHC 中，tan ∠ACH =tan ∠G =AH HC =34，∵AH =33，∴HC =43，在Rt △HOC 中，∵OC =r ，OH =r ﹣33，HC =43，∴222(33)(43)r r -+=，∴r =2536，∵GM ∥AC ，∴∠CAH =∠M ，∵∠OEM =∠AHC ，∴△AHC ∽△MEO ，∴AH HC EM OE =，∴33432536EM =，∴EM =2538． 点睛：本题考查圆综合题、垂径定理、相似三角形的判定和性质、锐角三角函数、勾股定理等知识，解题的关键是学会添加常用辅助线，灵活运用所学知识解决问题，正确寻找相似三角形，构建方程解决问题吗，属于中考压轴题．3．如图，AB 为O 的直径，弦//CD AB ，E 是AB 延长线上一点，CDB ADE ∠=∠． ()1DE 是O 的切线吗？请说明理由；()2求证：2AC CD BE =⋅．【答案】（1）结论：DE 是O 的切线，理由见解析；（2）证明见解析.【解析】【分析】（1）连接OD ，只要证明OD DE ⊥即可；（2）只要证明：AC BD =，CDB DBE ∽即可解决问题.【详解】()1解：结论：DE 是O 的切线．理由：连接OD ．CDB ADE ∠=∠，ADC EDB ∴∠=∠，//CD AB ，CDA DAB ∴∠=∠，OA OD =，OAD ODA ∴∠=∠，ADO EDB ∴∠=∠， AB 是直径，90ADB ∴∠=，90ADB ODE ∴∠=∠=，DE OD ∴⊥，DE ∴是O 的切线．()2//CD AB ，ADC DAB ∴∠=∠，CDB DBE ∠=∠，AC BD ∴=，AC BD ∴=，DCB DAB ∠=∠，EDB DAB ∠=∠，EDB DCB ∴∠=∠，CDB ∴∽DBE ，CD DB BD BE∴=， 2BD CD BE ∴=⋅，2AC CD BE ∴=⋅．【点睛】本题考查相似三角形的判定和性质、圆周角定理、切线的判定等知识，解题的关键是学会添加常用辅助线，准确寻找相似三角形解决问题，属于中考常考题型.4．如图，已知四边形ABCD是矩形，点P在BC边的延长线上，且PD=BC，⊙A经过点B，与AD边交于点E，连接CE .（1）求证：直线PD是⊙A的切线；（2）若PC=25，sin∠P=23，求图中阴影部份的面积（结果保留无理数）．【答案】（1）见解析；（2）20-4π.【解析】分析：（1）过点A作AH⊥PD，垂足为H，只要证明AH为半径即可.（2）分别算出Rt△CED的面积，扇形ABE的面积，矩形ABCD的面积即可.详解：（1）证明：如图，过A作AH⊥PD，垂足为H，∵四边形ABCD是矩形，∴AD=BC，AD∥BC，∠PCD=∠BCD=90°，∴∠ADH=∠P，∠AHD=∠PCD=90°，又PD=BC，∴AD=PD，∴△ADH≌△DPC，∴AH=CD，∵CD=AB，且AB是⊙A的半径，∴AH=AB,即AH是⊙A的半径，∴PD是⊙A的切线.（2）如图，在Rt△PDC中，∵sin∠P=23CDPD，5，令CD=2x，PD=3x，由由勾股定理得：（3x）2-(2x)252，解得：x=2，∴CD=4，PD=6，∴AB=AE=CD=4，AD=BC=PD=6，DE=2，∵矩形ABCD的面积为6×4=24，Rt△CED的面积为12×4×2=4，扇形ABE的面积为12π×42=4π，∴图中阴影部份的面积为24-4-4π=20-4π.点睛：本题考查了全等三角形的判定，圆的切线证明，三角形的面积，扇形的面积，矩形的面积.5．如图，已知⊙O 的半径为1，PQ 是⊙O 的直径，n 个相同的正三角形沿PQ 排成一列，所有正三角形都关于PQ 对称，其中第一个△A 1B 1C 1的顶点A 1与点P 重合，第二个△A 2B 2C 2的顶点A 2是B 1C 1与PQ 的交点，…，最后一个△A n B n C n 的顶点B n 、C n 在圆上．如图1，当n=1时，正三角形的边长a 1=_____；如图2，当n=2时，正三角形的边长a 2=_____；如图3，正三角形的边长a n =_____（用含n 的代数式表示）．38313 24313n+ 【解析】 分析：（1）设PQ 与11B C 交于点D ，连接1B O ，得出OD=1A D -O 1A ，用含1a 的代数式表示OD ，在△O 1B D 中，根据勾股定理求出正三角形的边长1a ；（2）设PQ 与2B 2C 交于点E ，连接2B O ，得出OE=1A E-O 1A ，用含2a 的代数式表示OE ，在△O 2B E 中，根据勾股定理求出正三角形的边长2a ；（3）设PQ 与n B n C 交于点F ，连接n B O ，得出OF=1A F-O 1A ，用含an 的代数式表示OF ，在△O n B F 中，根据勾股定理求出正三角形的边长an ． 本题解析：(1)易知△A 1B 1C 1的高为323 ∴a 13.(2)设△A 1B 1C 1的高为h ，则A 2O ＝1－h ，连结B 2O ，设B 2C 2与PQ 交于点F ，则有OF ＝2h －1. ∵B 2O 2＝OF 2＋B 2F 2，∴1＝(2h －1)2＋2212a ⎛⎫ ⎪⎝⎭. ∵h 32，∴1＝32－1)2＋14a 22， 解得a 283 . (3)同(2)，连结B n O ，设B n C n 与PQ 交于点F ，则有B n O 2＝OF 2＋B n F 2，即1＝(nh －1)2＋212n a ⎛⎫ ⎪⎝⎭ . ∵h ＝32 a n ，∴1＝14a n 2＋2312n na ⎛⎫- ⎪ ⎪⎝⎭， 解得a n ＝24331n n + .6．如图1，已知AB 是⊙O 的直径，AC 是⊙O 的弦，过O 点作OF ⊥AB 交⊙O 于点D ，交AC 于点E ，交BC 的延长线于点F ，点G 是EF 的中点，连接CG(1)判断CG 与⊙O 的位置关系，并说明理由；(2)求证：2OB 2＝BC •BF ；(3)如图2，当∠DCE ＝2∠F ，CE ＝3，DG ＝2.5时，求DE 的长．【答案】（1）CG 与⊙O 相切，理由见解析；（2）见解析；（3）DE ＝2【解析】【分析】（1）连接CE ，由AB 是直径知△ECF 是直角三角形，结合G 为EF 中点知∠AEO ＝∠GEC ＝∠GCE ，再由OA ＝OC 知∠OCA ＝∠OAC ，根据OF ⊥AB 可得∠OCA +∠GCE ＝90°，即OC ⊥GC ，据此即可得证；（2）证△ABC ∽△FBO 得BC AB BO BF =，结合AB ＝2BO 即可得； （3）证ECD ∽△EGC 得EC ED EG EC =，根据CE ＝3，DG ＝2.5知32.53DE DE =+，解之可得．【详解】解：（1）CG 与⊙O 相切，理由如下：如图1，连接CE ，∵AB 是⊙O 的直径，∴∠ACB ＝∠ACF ＝90°，∵点G 是EF 的中点，∴GF ＝GE ＝GC ，∴∠AEO ＝∠GEC ＝∠GCE ，∵OA ＝OC ，∴∠OCA ＝∠OAC ，∵OF ⊥AB ，∴∠OAC +∠AEO ＝90°，∴∠OCA +∠GCE ＝90°，即OC ⊥GC ，∴CG 与⊙O 相切；（2）∵∠AOE ＝∠FCE ＝90°，∠AEO ＝∠FEC ，∴∠OAE ＝∠F ，又∵∠B ＝∠B ，∴△ABC ∽△FBO ， ∴BC AB BO BF=，即BO •AB ＝BC •BF ， ∵AB ＝2BO ，∴2OB 2＝BC •BF ；（3）由（1）知GC ＝GE ＝GF ，∴∠F ＝∠GCF ，∴∠EGC ＝2∠F ，又∵∠DCE ＝2∠F ，∴∠EGC ＝∠DCE ，∵∠DEC ＝∠CEG ，∴△ECD ∽△EGC ， ∴EC ED EG EC=， ∵CE ＝3，DG ＝2.5， ∴32.53DE DE =+，整理，得：DE2+2.5DE﹣9＝0，解得：DE＝2或DE＝﹣4.5（舍），故DE＝2．【点睛】本题是圆的综合问题，解题的关键是掌握圆周角定理、切线的判定、相似三角形的判定与性质及直角三角形的性质等知识点．7．如图，△ABC内接于⊙O，∠BAC的平分线交⊙O于点D，交BC于点E（BE＞EC），且BD＝23．过点D作DF∥BC，交AB的延长线于点F．（1）求证：DF为⊙O的切线；（2）若∠BAC＝60°，DE＝7，求图中阴影部分的面积．【答案】（1）详见解析；（2）32π．【解析】【分析】（1）连结OD，根据垂径定理得到OD⊥BC，根据平行线的性质得到OD⊥DF，根据切线的判定定理证明；（2）连结OB，连结OD交BC于P，作BH⊥DF于H，证明△OBD为等边三角形，得到∠ODB=60°，3PE，证明△ABE∽△AFD，根据相似三角形的性质求出AE，根据阴影部分的面积=△BDF的面积-弓形BD的面积计算．【详解】证明：（1）连结OD，∵AD平分∠BAC交⊙O于D，∴∠BAD=∠CAD，∴BD CD，∴OD⊥BC，∵BC∥DF，∴OD⊥DF，∴DF为⊙O的切线；（2）连结OB，连结OD交BC于P，作BH⊥DF于H，∵∠BAC=60°，AD 平分∠BAC ，∴∠BAD=30°，∴∠BOD=2∠BAD=60°，∴△OBD 为等边三角形，∴∠ODB=60°，3 ，∴∠BDF=30°，∵BC ∥DF ，∴∠DBP=30°，在Rt △DBP 中，PD=123 ，3， 在Rt △DEP 中，∵37∴22(7)(3)- =2，∵OP ⊥BC ，∴BP=CP=3，∴CE=3﹣2=1，∵∠DBE=∠CAE ，∠BED=∠AEC ，∴△BDE ∽△ACE ，∴AE ：BE=CE ：DE ，即AE ：5=17 ，∴AE=577∵BE ∥DF ， ∴△ABE ∽△AFD ， ∴BE AE DF AD= ，即5757125DF = ， 解得DF=12，在Rt △BDH 中，BH=123， ∴阴影部分的面积=△BDF 的面积﹣弓形BD 的面积=△BDF 的面积﹣（扇形BOD 的面积﹣△BOD 的面积）=22160(23)3123(23)23604π⨯⨯-3﹣2π．【点睛】考查的是切线的判定，扇形面积计算，相似三角形的判定和性质，圆周角定理的应用，等边三角形的判定和性质，掌握切线的判定定理，扇形面积公式是解题的关键．8．如图，在Rt △ABC 中，90C ∠=︒，AD 平分∠BAC ，交BC 于点D ，点O 在AB 上，⊙O 经过A 、D 两点，交AC 于点E ，交AB 于点F ．（1）求证：BC 是⊙O 的切线；（2）若⊙O 的半径是2cm ，E 是弧AD 的中点，求阴影部分的面积（结果保留π和根号）【答案】（1）证明见解析 （2）233π- 【解析】【分析】 （1）连接OD ，只要证明OD ∥AC 即可解决问题；（2）连接OE ，OE 交AD 于K ．只要证明△AOE 是等边三角形即可解决问题．【详解】（1）连接OD ．∵OA =OD ，∴∠OAD =∠ODA ．∵∠OAD =∠DAC ，∴∠ODA =∠DAC ，∴OD ∥AC ，∴∠ODB =∠C =90°，∴OD ⊥BC ，∴BC 是⊙O 的切线．（2）连接OE ，OE 交AD 于K ．∵AE DE =，∴OE ⊥AD ．∵∠OAK =∠EAK ，AK =AK ，∠AKO =∠AKE =90°，∴△AKO ≌△AKE ，∴AO =AE =OE ，∴△AOE是等边三角形，∴∠AOE =60°，∴S 阴=S 扇形OAE ﹣S △AOE 260233604π⋅⋅=-⨯22233π=． 【点睛】本题考查了切线的判定、扇形的面积、等边三角形的判定和性质、平行线的判定和性质、全等三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，灵活运用所学知识解决问题，属于中考常考题型．9．如图，已知AB 是⊙O 的直径，P 是BA 延长线上一点，PC 切⊙O 于点C ，CD ⊥AB ，垂足为D ．（1）求证：∠PCA ＝∠ABC ；（2）过点A 作AE ∥PC 交⊙O 于点E ，交CD 于点F ，交BC 于点M ，若∠CAB ＝2∠B ，CF ＝3，求阴影部分的面积．【答案】（1）详见解析；（2）6334π-. 【解析】【分析】（1）如图，连接OC ，利用圆的切线的性质和直径对应的圆周角是直角可得∠PCA=∠OCB ，利用等量代换可得∠PCA=∠ABC.（2）先求出△OCA 是等边三角形，在利用三角形的等边对等角定理求出FA=FC 和CF=FM,然后分别求出AM 、AC 、MO 、CD 的值，分别求出0A E S ∆、BOE S 扇形 、ABM S ∆ 的值，利用0A E ABM BOE S S S S ∆∆=+-阴影部分扇形，然后通过计算即可解答.【详解】解：（1）证明：连接OC ，如图，∵PC 切⊙O 于点C ，∴OC ⊥PC,∴∠PCA+∠ACO=90º,∵AB 是⊙O 的直径，∴∠ACB=∠ACO+OCB=90º∴∠PCA=∠OCB,∵OC=OB,∴∠OBC=∠OCB,∴∠PCA=∠ABC ；（2）连接OE ，如图，∵△ACB 中，∠ACB ＝90º,∠CAB ＝2∠B,∴∠B ＝30º,∠CAB ＝60º,∴△OCA 是等边三角形，∵CD ⊥AB,∴∠ACD+∠CAD ＝∠CAD ＋∠ABC ＝90º,∴∠ACD ＝∠B ＝30º,∵PC ∥AE,∴∠PCA ＝∠CAE ＝30º,∴FC=FA,同理，CF ＝FM,∴AM ＝2CF=23,Rt △ACM 中，易得AC=23×32=3＝OC, ∵∠B ＝∠CAE ＝30º,∴∠AOC=∠COE=60º,∴∠EOB=60º,∴∠EAB=∠ABC=30º,∴MA=MB,连接OM,EG ⊥AB 交AB 于G 点，如图所示，∵OA=OB,∴MO ⊥AB,∴MO ＝3∵△CDO ≌△EDO(AAS)，∴332 ∴1332ABM S AB MO ∆=⨯= 同样，易求93AOE S ∆=， 260333602BOE S ππ⨯==扇形 ∴0A E ABM BOE S S S S ∆∆=+-阴影部分扇形933633332ππ-+-=. 【点睛】本题考查了切线的性质、解直角三角形、扇形面积和识图的能力，综合性较强，有一定难度，熟练掌握定理并准确识图是解题的关键.10．如图1，等腰直角△ABC 中，∠ACB=90°，AC=BC ，过点A ，C 的圆交AB 于点D ，交BC于点E ，连结DE（1）若AD=7，BD=1，分别求DE ，CE 的长（2）如图2，连结CD ，若CE=3，△ACD 的面积为10，求tan ∠BCD（3）如图3，在圆上取点P 使得∠PCD=∠BCD （点P 与点E 不重合），连结PD ，且点D 是△CPF 的内心①请你画出△CPF ，说明画图过程并求∠CDF 的度数②设PC=a ，PF=b ，PD=c ，若（a-2c ）（b-2c ）=8，求△CPF 的内切圆半径长．【答案】（1）DE=1，CE=32；（2）tan ∠BCD=14；（3）①135°；②2. 【解析】【分析】 （1）由A 、C 、E 、D 四点共圆对角互补为突破口求解；（2）找∠BDF 与∠ODA 为对顶角，在⊙O 中，∠COD=2∠CAD ，证明△OCD 为等腰直角三角形，从而得到∠EDC+∠ODA=45°，即可证明∠CDF=135°；（3）过点D 做DH CB ⊥于点H ，以D 为圆心，DH 为半径画圆，过点P 做D 切线PF 交CB 的延长线于点F ，结合圆周角定理得出∠CPD=∠CAD=45°，再根据圆的内心是三角形三个内角角平分线的交点，得出∠CPF=90°，然后根据角平分线性质得出114522DCF CFD PCF PFC ∠+∠=∠+∠=︒，最后再根据三角形内角和定理即可求解；证明∠DCF+∠CFD=45°，从而证明∠CPF 是直角，再求证四边形PKDN 是正方形，最后以△PCF 面积不变性建立等量关系，结合已知（a-2c ）（b-2c ）=8，消去字母a ，b 求出c 值，即求出△CPF 的内切圆半径长为22c ． 【详解】（1）由图可知：设BC=x ．在Rt △ABC 中，AC=BC ．由勾股定理得：AC 2+BC 2=AB 2，∵AB=AD+BD ，AD=7，BD=1，∴x 2+x 2=82，解得：x=42． ∵⊙O 内接四边形，∠ACD=90°，∴∠ADE=90°，∴∠EDB=90°，∵∠B=45°，∴△BDE 是等腰直角三形．∴DE=DB ，又∵DB=1，∴DE=1，又∵CE=BC-BE ，∴CE=42232-=．（2）如图所示：在△DCB 中过点D 作DM ⊥BE ，设BE=y ，则DM=12y ， 又∵CE=3，∴BC=3+y ，∵S △ACB =S ACD +S DCB ， ∴()1114242103y y 222⨯=+⨯+⨯， 解得：y=2或y=-11（舍去）．∴EM=1，CM=CE+ME=1+3=4，又∵∠BCD=∠MCD ，∴tan ∠BCD=tan ∠MCD ， 在Rt △DCM 中，tan ∠MCD=DM CM =14， ∴tan ∠BCD=14． （3）①如下图所示：过点D 做DH CB ⊥于点H ，以D 为圆心，DH 为半径画圆，过点P 做D 切线PF 交CB的延长线于点F ．∵∠CAD=45°，∴∠CPD=∠CAD=45°，又∵点D 是CPF ∆的内心，∴PD 、CD 、DF 都是角平分线，∴∠FPD=∠CPD =45°，∠PCD=∠DCF ，∠PFD=∠CFD∴∠CPF=90°∴∠PCF+∠PFC=90° ∴114522DCF CFD PCF PFC ∠+∠=∠+∠=︒ ∴∠CDF=180°-∠DCF-∠CFD F=90°+45°=135°，即∠CDF 的度数为135°．②如下图所示过点D 分别作DK ⊥PC ，DM ⊥CF ，DN ⊥PF 于直线PC ，CF 和PF 于点K ，M ，N 三点， 设△PCF 内切圆的半径为m ，则DN=m ，∵点D 是△PCF 的内心，∴DM=DN=DK ，又∵∠DCF+∠CFD+∠FDC=180°，∠FDC=45°，∴∠DCF+∠CFD=45°，又∵DC ，DF 分别是∠PCF 和∠PFC 的角平分线，∴∠PCF=2∠DCF ，∠PFC=2∠DFC ，∴∠PCF+∠PFC=90°，∴∠CPF=90°．在四边形PKDN 中，∠PND=∠NPK=∠PKD=90°，∴四边形PKDN 是矩形，又∵KD=ND ，∴四边形PKDN 是正方形．又∵∠MBD=∠BDM=45°，∠BDM=∠KDP ，∴∠KDP=45°．∵PC=a ，PF=b ，PD=c ，∴PN=PK=C 2，∴NF=b c 2-，CK=a c 2-， 又∵CK=CM ，FM=FN ，CF=CM+FM ，∴CF=a b +，又∵S △PCF =S △PDF +S △PDC +S △DCF ，∴1111ab a c b c (a b 222222=⨯+⨯++-）×c 2，化简得：)2a b c c +-------（Ⅰ），又∵若（c ）（c ）=8化简得：()2ab a b 2c 8++=------（Ⅱ）， 将（Ⅰ）代入（Ⅱ）得：c 2=8，解得：c =c =-∴2==， 即△CPF 的内切圆半径长为2．【点睛】本题考查圆的内接四边形性质，圆的内心，圆心角、圆周角，同弧（或等弧）之间的相互关系，同时也考查直角三角形，勾股定理，同角或等角的三角函数值相等和三角形的面积公式，正方形，对顶角和整式的运算等知识点；难点是作辅助线和利用等式求△CPF 的内切圆半径长．11．如图，已知AB 是⊙O 的直径，BC 是弦，弦BD 平分∠ABC 交AC 于F ，弦DE ⊥AB 于H ，交AC 于G ．①求证：AG ＝GD ；②当∠ABC 满足什么条件时，△DFG 是等边三角形？③若AB＝10，sin∠ABD＝35，求BC的长．【答案】（1）证明见解析；（2）当∠ABC＝60°时，△DFG是等边三角形．理由见解析；（3）BC的长为145．【解析】【分析】（1）首先连接AD，由DE⊥AB，AB是O的直径，根据垂径定理，即可得到AD AE=，然后根据在同圆或等圆中，同弧或等弧所对的圆周角相等，证得∠ADE＝∠ABD，又由弦BD平分∠ABC，可得∠DBC＝∠ABD，根据等角对等边的性质，即可证得AG=GD；（2）当∠ABC=60°时，△DFG是等边三角形，根据半圆（或直径）所对的圆周角是直角与三角形的外角的性质，易求得∠DGF=∠DFG=60°，即可证得结论；（3）利用三角函数先求出tan∠ABD34=，cos∠ABD＝45，再求出DF、BF，然后即可求出BC.【详解】（1）证明：连接AD，∵DE⊥AB，AB是⊙O的直径，∴AD AE=，∴∠ADE＝∠ABD，∵弦BD平分∠ABC，∴∠DBC＝∠ABD，∵∠DBC＝∠DAC，∴∠ADE＝∠DAC，∴AG＝GD；（2）解：当∠ABC＝60°时，△DFG是等边三角形．理由：∵弦BD平分∠ABC，∴∠DBC＝∠ABD＝30°，∵AB是⊙O的直径，∴∠ACB＝90°，∴∠CAB＝90°﹣∠ABC＝30°，∴∠DFG＝∠FAB+∠DBA＝60°，∵DE⊥AB，∴∠DGF＝∠AGH＝90°﹣∠CAB＝60°，∴△DGF 是等边三角形；（3）解：∵AB 是⊙O 的直径，∴∠ADB ＝∠ACB ＝90°，∵∠DAC ＝∠DBC ＝∠ABD ，∵AB ＝10，sin ∠ABD ＝35， ∴在Rt △ABD 中，AD ＝AB•sin ∠ABD ＝6，∴BD ＝22AB BD -＝8，∴tan ∠ABD ＝34AD BD =，cos ∠ABD ＝4=5BD AB ， 在Rt △ADF 中，DF ＝AD•tan ∠DAF ＝AD•tan ∠ABD ＝6×34＝92， ∴BF ＝BD ﹣DF ＝8﹣92＝72， ∴在Rt △BCF 中，BC ＝BF•cos ∠DBC ＝BF•cos ∠ABD ＝72×45＝145． ∴BC 的长为：145．【点睛】此题考查了圆周角定理、垂径定理、直角三角形的性质、三角函数的性质以及勾股定理等知识．此题综合性较强，难度较大，解题的关键是掌握数形结合思想与转化思想的应用，注意辅助线的作法．12．如图，AB 是O 的直径，弦CD AB ⊥于点E ，过点C 的切线交AB 的延长线于点F ，连接DF .（1）求证：DF 是O 的切线；（2）连接BC ，若30BCF ∠=︒，2BF =，求CD 的长.【答案】（1）见解析；（2）3【解析】【分析】(1) 连接OD,由垂径定理证OF为CD的垂直平分线，得CF=DF，∠CDF=∠DCF，由∠CDO=∠OCD，再证∠CDO +∠CDB=∠OCD+∠DCF=90°，可得OD⊥DF，结论成立.(2) 由∠OCF=90°, ∠BCF=30°，得∠OCB=60°，再证ΔOCB为等边三角形，得∠COB=60°，可得∠CFO=30°，所以FO=2OC=2OB，FB=OB= OC =2，在直角三角形OCE中，解直角三角形可得CE,再推出CD=2CE.【详解】（1）证明：连接OD∵CF是⊙O的切线∴∠OCF=90°∴∠OCD+∠DCF=90°∵直径AB⊥弦CD∴CE=ED，即OF为CD的垂直平分线∴CF=DF∴∠CDF=∠DCF∵OC=OD，∴∠CDO=∠OCD∴∠CDO +∠CDB=∠OCD+∠DCF=90°∴OD⊥DF∴DF是⊙O的切线（2）解：连接OD∵∠OCF=90°, ∠BCF=30°∴∠OCB=60°∵OC=OB∴ΔOCB为等边三角形，∴∠COB=60°∴∠CFO=30°∴FO=2OC=2OB∴FB=OB= OC =2在直角三角形OCE中，∠CEO=90°∠COE=60°CE3∠==sin COEOC2∴CF3==∴CD=2 CF23【点睛】本题考核知识点：垂径定理，切线，解直角三角形. 解题关键点：熟记切线的判定定理，灵活运用含有30°角的直角三角形性质，巧解直角三角形.13．如图，AB是半圆⊙O的直径，点C是半圆⊙O上的点，连接AC，BC，点E是AC的中点，点F是射线OE上一点．（1）如图1，连接FA，FC，若∠AFC＝2∠BAC，求证：FA⊥AB；（2）如图2，过点C作CD⊥AB于点D，点G是线段CD上一点（不与点C重合），连接FA，FG，FG与AC相交于点P，且AF＝FG．①试猜想∠AFG和∠B的数量关系，并证明；②连接OG，若OE＝BD，∠GOE＝90°，⊙O的半径为2，求EP的长．【答案】（1）见解析；（2）①结论：∠GFA＝2∠ABC．理由见解析；②PE＝36．【解析】【分析】（1）证明∠OFA＝∠BAC，由∠EAO+∠EOA＝90°，推出∠OFA+∠AOE＝90°，推出∠FAO＝90°即可解决问题．（2）①结论：∠GFA＝2∠ABC．连接FC．由FC＝FG＝FA，以F为圆心FC为半径作⊙F．因为AG AG，推出∠GFA＝2∠ACG，再证明∠ACG＝∠ABC．②图2﹣1中，连接AG，作FH⊥AG于H．想办法证明∠GFA＝120°，求出EF，OF，OG即可解决问题．【详解】（1）证明：连接OC．∵OA＝OC，EC＝EA，∴OF⊥AC，∴FC＝FA，∴∠OFA＝∠OFC，∵∠CFA＝2∠BAC，∴∠OFA＝∠BAC，∵∠OEA＝90°，∴∠EAO+∠EOA＝90°，∴∠OFA+∠AOE＝90°，∴∠FAO＝90°，∴AF⊥AB．（2）①解：结论：∠GFA＝2∠ABC．理由：连接FC．∵OF垂直平分线段AC，∴FG＝FA，∵FG＝FA，∴FC＝FG＝FA，以F为圆心FC为半径作⊙F．∵AG AG，∴∠GFA＝2∠ACG，∵AB是⊙O的直径，∴∠ACB＝90°，∵CD⊥AB，∴∠ABC+∠BCA＝90°，∵∠BCD+∠ACD＝90°，∴∠ABC＝∠ACG，∴∠GFA＝2∠ABC．②如图2﹣1中，连接AG，作FH⊥AG于H．∵BD＝OE，∠CDB＝∠AEO＝90°，∠B＝∠AOE，∴△CDB≌△AEO（AAS），∴CD＝AE，∵EC＝EA，∴AC＝2CD．∴∠BAC ＝30°，∠ABC ＝60°，∴∠GFA ＝120°，∵OA ＝OB ＝2，∴OE ＝1，AE ＝，BA ＝4，BD ＝OD ＝1， ∵∠GOE ＝∠AEO ＝90°，∴OG ∥AC ， 323DG OG ∴==, 22221AG DG AD ∴=+=， ∵FG ＝FA ，FH ⊥AG ，∴AH ＝HG 21∠AFH ＝60°， ∴AF ＝27sin 603AH ︒=， 在Rt △AEF 中，EF 2213AF AE -=， ∴OF ＝OE +EF ＝43 ， ∵PE ∥OG ， ∴PE EF OG 0F=， ∴134233=， ∴PE 3． 【点睛】圆综合题，考查了垂径定理，勾股定理，圆周角定理，全等三角形的判定和性质，锐角三角函数，解直角三角形等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题.14．设C 为线段AB 的中点，四边形BCDE 是以BC 为一边的正方形，以B 为圆心，BD 长为半径的⊙B 与AB 相交于F 点，延长EB 交⊙B 于G 点，连接DG 交于AB 于Q 点，连接AD ．求证：（1）AD 是⊙B 的切线；（2）AD ＝AQ ；（3）BC 2＝CF×EG ．【答案】(1)证明见解析；（2）证明见解析；（3）证明见解析.【解析】【分析】()1连接BD ，由DC AB ⊥，C 为AB 的中点，由线段垂直平分线的性质，可得AD BD =，再根据正方形的性质，可得90ADB ∠=；()2由BD BG =与//CD BE ，利用等边对等角与平行线的性质，即可求得122.52G CDG BDG BCD ∠=∠=∠=∠=，继而求得67.5ADQ AQD ∠=∠=，由等角对等边，可证得AD AQ =； ()3易求得67.5GDE GDB BDE DFE ∠=∠+∠==∠，90DCF E ∠=∠=，即可证得Rt DCF ∽Rt GED ，根据相似三角形的对应边成比例，即可证得结论．【详解】证明：()1连接BD ，四边形BCDE 是正方形，45DBA ∴∠=，90DCB ∠=，即DC AB ⊥，C 为AB 的中点，CD ∴是线段AB 的垂直平分线，AD BD ∴=，45DAB DBA ∴∠=∠=，90ADB ∴∠=，即BD AD ⊥，BD 为半径，AD ∴是B 的切线；()2BD BG =，BDG G ∴∠=∠，//CD BE ，CDG G ∴∠=∠，122.52G CDG BDG BCD ∴∠=∠=∠=∠=， 9067.5ADQ BDG ∴∠=-∠=，9067.5AQB BQG G ∠=∠=-∠=， ADQ AQD ∴∠=∠，AD AQ ∴=；()3连接DF ，在BDF 中，BD BF =，BFD BDF ∴∠=∠，又45DBF ∠=，67.5BFD BDF ∴∠=∠=，22.5GDB ∠=， 在Rt DEF 与Rt GCD 中，67.5GDE GDB BDE DFE ∠=∠+∠==∠，90DCF E ∠=∠=，Rt DCF ∴∽Rt GED ，CF CD ED EG∴=， 又CD DE BC ==，2BC CF EG ∴=⋅．【点睛】本题考查了相似三角形的判定与性质、切线的判定与性质、正方形的性质以及等腰三角形的判定与性质.解题的关键是注意掌握数形结合思想的应用，注意辅助线的作法．15．如图1，D 是⊙O 的直径BC 上的一点，过D 作DE ⊥BC 交⊙O 于E 、N ，F 是⊙O 上的一点，过F 的直线分别与CB 、DE 的延长线相交于A 、P ，连结CF 交PD 于M ，∠C ＝12∠P ． （1）求证：PA 是⊙O 的切线；（2）若∠A ＝30°，⊙O 的半径为4，DM ＝1，求PM 的长；（3）如图2，在（2）的条件下，连结BF 、BM ；在线段DN 上有一点H ，并且以H 、D 、C 为顶点的三角形与△BFM 相似，求DH 的长度．【答案】（1）证明见解析；（2）PM ＝43﹣2；（3）满足条件的DH 的值为632- 或122311+． 【解析】【分析】（1）如图1中，作PH ⊥FM 于H ．想办法证明∠PFH=∠PMH ，∠C=∠OFC ，再根据等角的余角相等即可解决问题；（2）解直角三角形求出AD ，PD 即可解决问题；（3）分两种情形①当△CDH ∽△BFM 时，DH CD FM BF =． ②当△CDH ∽△MFB 时，DH CD FB MF=，分别构建方程即可解决问题； 【详解】（1）证明：如图1中，作PH ⊥FM 于H ．∵PD ⊥AC ，∴∠PHM ＝∠CDM ＝90°，∵∠PMH ＝∠DMC ，∴∠C ＝∠MPH ，∵∠C ＝12∠FPM ，∴∠HPF ＝∠HPM ， ∵∠HFP+∠HPF ＝90°，∠HMP+∠HPM ＝90°，∴∠PFH ＝∠PMH ，∵OF ＝OC ，∴∠C ＝∠OFC ，∵∠C+∠CMD ＝∠C+∠PMF ＝∠C+∠PFH ＝90°，∴∠OFC+∠PFC ＝90°，∴∠OFP ＝90°，∴直线PA 是⊙O 的切线．（2）解：如图1中，∵∠A ＝30°，∠AFO ＝90°，∴∠AOF ＝60°，∵∠AOF ＝∠OFC+∠OCF ，∠OFC ＝∠OCF ，∴∠C ＝30°，∵⊙O 的半径为4，DM ＝1，∴OA ＝2OF ＝8，CD ＝3DM ＝3 ，∴OD ＝OC ﹣CD ＝4﹣3 ，∴AD ＝OA+OD ＝8+4﹣3 ＝12﹣3 ，在Rt △ADP 中，DP ＝AD•tan30°＝（12﹣3 ）×33 ＝43 ﹣1， ∴PM ＝PD ﹣DM ＝4 3﹣2．（3）如图2中，由（2）可知：BF ＝12BC ＝4，FM 3BF ＝3，CM ＝2DM ＝2，CD 3 ， ∴FM ＝FC ﹣CM ＝3﹣2， ①当△CDH ∽△BFM 时，DH CD FM BF = ， ∴34432=- ，∴DH ＝632 ②当△CDH ∽△MFB 时，DH CD FB MF =， ∴34432DH =-，∴DH 1223+ ， ∵DN ()22443833--=-，∴DH ＜DN ，符合题意，综上所述，满足条件的DH 的值为62- 或1211+． 【点睛】 本题考查圆综合题、切线的判定、解直角三角形、相似三角形的判定和性质等知识，解题的关键是熟练掌握基本知识，学会用分类讨论的思想思考问题.。
初中圆的综合试题及答案
初中圆的综合试题及答案一、选择题（每题3分，共30分）1. 圆的半径为r，直径为d，则d与r的关系是（）。
A. d = 2rB. d = rC. d = r/2D. d = 4r答案：A2. 圆的周长C与半径r的关系是（）。
A. C = 2πrB. C = πrC. C = 4πrD. C = 2r答案：A3. 圆的面积S与半径r的关系是（）。
A. S = πr^2B. S = 2πrC. S = πrD. S = r^2答案：A4. 圆心角为90°的扇形面积是整个圆面积的（）。
A. 1/4B. 1/2C. 3/4D. 1答案：A5. 已知圆的半径为5cm，那么圆的直径是（）。
A. 10cmB. 15cmC. 20cmD. 25cm答案：A6. 圆的切线与半径的关系是（）。
A. 垂直B. 平行C. 相交D. 重合答案：A7. 圆的内接正方形的对角线长度等于圆的（）。
A. 半径B. 直径C. 周长D. 面积答案：B8. 圆的外切正方形的边长等于圆的（）。
A. 半径B. 直径C. 周长D. 面积答案：A9. 两个半径相等的圆是（）。
A. 同心圆B. 等圆C. 相切圆D. 相交圆答案：B10. 圆的直径是半径的（）倍。
A. 1B. 2C. 4D. 8答案：B二、填空题（每题3分，共30分）11. 圆的周长公式为C=2πr，其中r代表圆的________。
答案：半径12. 圆的面积公式为S=πr^2，其中r代表圆的________。
答案：半径13. 一个圆的半径为3cm，那么它的周长是________cm。
答案：18.8414. 一个圆的半径为4cm，那么它的面积是________cm^2。
答案：50.2415. 圆的切线垂直于经过切点的________。
答案：半径16. 圆的内接正六边形的边长等于圆的________。
答案：半径17. 圆的外切正六边形的边长等于圆的________。
答案：半径18. 两个圆的半径之和等于它们圆心距的圆是________圆。
中考数学 圆的综合 综合题含答案解析
中考数学 圆的综合 综合题含答案解析一、圆的综合1．如图，AB 为⊙O 的直径，点E 在⊙O 上，过点E 的切线与AB 的延长线交于点D ，连接BE ，过点O 作BE 的平行线，交⊙O 于点F ，交切线于点C ，连接AC（1）求证：AC 是⊙O 的切线；（2）连接EF ，当∠D= °时，四边形FOBE 是菱形．【答案】（1）见解析；（2）30.【解析】【分析】（1）由等角的转换证明出OCA OCE ∆∆≌，根据圆的位置关系证得AC 是⊙O 的切线. （2）根据四边形FOBE 是菱形，得到OF=OB=BF=EF ，得证OBE ∆为等边三角形，而得出60BOE ∠=︒，根据三角形内角和即可求出答案.【详解】（1）证明：∵CD 与⊙O 相切于点E ，∴OE CD ⊥，∴90CEO ∠=︒，又∵OC BE P ，∴COE OEB ∠=∠，∠OBE=∠COA∵OE=OB ，∴OEB OBE ∠=∠，∴COE COA ∠=∠，又∵OC=OC ，OA=OE ，∴OCA OCE SAS ∆∆≌（）， ∴90CAO CEO ∠=∠=︒，又∵AB 为⊙O 的直径，∴AC 为⊙O 的切线；（2）解：∵四边形FOBE 是菱形，∴OF=OB=BF=EF ，∴OE=OB=BE ，∴OBE ∆为等边三角形，∴60BOE ∠=︒，而OE CD ⊥，∴30D ∠=︒．故答案为30．【点睛】本题主要考查与圆有关的位置关系和圆中的计算问题，熟练掌握圆的性质是本题的解题关键.2．如图，已知△ABC 中，AB=AC ，∠A=30°，AB=16，以AB 为直径的⊙O 与BC 边相交于点D ，与AC 交于点F ，过点D 作DE ⊥AC 于点E ．（1）求证：DE 是⊙O 的切线；（2）求CE 的长；（3）过点B 作BG ∥DF ，交⊙O 于点G ，求弧BG 的长．【答案】（1）证明见解析（2）33）4π【解析】【分析】（1）如图1，连接AD ，OD ，由AB 为⊙O 的直径，可得AD ⊥BC ，再根据AB=AC ，可得BD=DC ，再根据OA=OB ，则可得OD ∥AC ，继而可得DE ⊥OD ，问题得证；（2）如图2，连接BF ，根据已知可推导得出DE=12BF ，CE=EF ，根据∠A=30°，AB=16，可得BF=8，继而得DE=4，由DE 为⊙O 的切线，可得ED 2=EF•AE ，即42=CE•（16﹣CE ），继而可求得CE 长；（3）如图3，连接OG ，连接AD ，由BG ∥DF ，可得∠CBG=∠CDF=30°，再根据AB=AC ，可推导得出∠OBG=45°，由OG=OB ，可得∠OGB=45°，从而可得∠BOG=90°，根据弧长公式即可求得»BG的长度. 【详解】（1）如图1，连接AD ，OD ；∵AB 为⊙O 的直径，∴∠ADB=90°，即AD ⊥BC ，∵AB=AC ，∴BD=DC ，∵OA=OB ，∴OD ∥AC ，∵DE ⊥AC ，∴DE ⊥OD ，∴∠ODE=∠DEA=90°，∴DE 为⊙O 的切线；（2）如图2，连接BF ，∵AB 为⊙O 的直径，∴∠AFB=90°，∴BF ∥DE ，∵CD=BD ，∴DE=12BF ，CE=EF ， ∵∠A=30°，AB=16，∴BF=8，∴DE=4，∵DE 为⊙O 的切线，∴ED 2=EF•AE ， ∴42=CE•（16﹣CE ），∴CE=8﹣43，CE=8+43（不合题意舍去）；（3）如图3，连接OG ，连接AD ，∵BG ∥DF ，∴∠CBG=∠CDF=30°，∵AB=AC ，∴∠ABC=∠C=75°，∴∠OBG=75°﹣30°=45°，∵OG=OB ，∴∠OGB=∠OBG=45°，∴∠BOG=90°，∴»BG 的长度=908180π⨯⨯=4π．【点睛】本题考查了圆的综合题，涉及了切线的判定、三角形中位线定理、圆周角定理、弧长公式等，正确添加辅助线、熟练掌握相关的性质与定理是解题的关键.3．如图，AB 为⊙O 的直径，点D 为AB 下方⊙O 上一点，点C 为弧ABD 的中点，连接CD，CA．（1）求证：∠ABD=2∠BDC；（2）过点C作CH⊥AB于H，交AD于E，求证：EA=EC；（3）在（2）的条件下，若OH=5，AD=24，求线段DE的长度．【答案】（1）证明见解析；（2）见解析；（3）92 DE=.【解析】【分析】（1）连接AD，如图1，设∠BDC=α，∠ADC=β，根据圆周角定理得到∠CAB=∠BDC=α，由AB为⊙O直径，得到∠ADB=90°，根据余角的性质即可得到结论；（2）根据已知条件得到∠ACE=∠ADC，等量代换得到∠ACE=∠CAE，于是得到结论；（3）如图2，连接OC，根据圆周角定理得到∠COB=2∠CAB，等量代换得到∠COB=∠ABD，根据相似三角形的性质得到OH=5，根据勾股定理得到AB=22AD BD+=26，由相似三角形的性质即可得到结论．【详解】（1）连接AD．如图1，设∠BDC=α，∠ADC=β，则∠CAB=∠BDC=α，∵点C为弧ABD中点，∴¶AC=¶CD，∴∠ADC=∠DAC=β，∴∠DAB=β﹣α，∵AB为⊙O直径，∴∠ADB=90°，∴α+β=90°，∴β=90°﹣α，∴∠ABD=90°﹣∠DAB=90°﹣（β﹣α），∴∠ABD=2α，∴∠ABD=2∠BDC；（2）∵CH⊥AB，∴∠ACE+∠CAB=∠ADC+∠BDC=90°，∵∠CAB=∠CDB，∴∠ACE=∠ADC，∵∠CAE=∠ADC，∴∠ACE=∠CAE，∴AE=CE；（3）如图2，连接OC，∴∠COB=2∠CAB，∵∠ABD=2∠BDC，∠BDC=∠CAB，∴∠COB=∠ABD，∵∠OHC =∠ADB =90°，∴△OCH ∽△ABD ，∴12OH OC BD AB ==， ∵OH =5，∴BD =10，∴AB =22AD BD +=26，∴AO =13，∴AH =18， ∵△AHE ∽△ADB ，∴AH AE AD AB =，即1824=26AE ，∴AE =392，∴DE =92．【点睛】本题考查了垂径定理，相似三角形的判定和性质，等腰三角形的判定和性质，正确的作出辅助线是解题的关键．4．如图，已知AB 是⊙O 的直径，点C ，D 在⊙O 上，BC=6cm,AC=8cm,∠BAD=45°．点E 在⊙O 外，做直线AE ，且∠EAC=∠D ．（1）求证：直线AE 是⊙O 的切线．（2）求图中阴影部分的面积.【答案】(1)见解析;(2)25-504π. 【解析】 分析：（1）根据圆周角定理及推论证得∠BAE=90°，即可得到AE 是⊙O 的切线； （2）连接OD ，用扇形ODA 的面积减去△AOD 的面积即可.详解：证明：（1） ∵AB 是⊙O 的直径，∴∠ACB=90°，即∠BAC+∠ABC=90°，∵∠EAC=∠ADC ，∠ADC=∠ABC ，∴∠EAC=∠ABC∴∠BAC+∠EAC =90°，即∠BAE= 90°∴直线AE 是⊙O 的切线；（2）连接OD∵ BC=6 AC=8∴ 226810AB =+=∴ OA = 5又∵ OD = OA∴∠ADO =∠BAD = 45°∴∠AOD = 90°∴AOD ODA S S S ∆-阴影扇形＝=90155553602π⨯⨯-⨯⨯ 25504π-= （2cm ）点睛：此题主要考查了圆周角定理和圆的切线的判定与性质，关键是利用圆周角定理和切线的判定与性质，结合勾股定理的和弓形的面积的求法求解，注意数形结合思想的应用.5．如图，△ABC 内接于⊙O ，弦AD ⊥BC 垂足为H ，∠ABC ＝2∠CAD ．（1）如图1，求证：AB ＝BC ；（2）如图2，过点B 作BM ⊥CD 垂足为M ，BM 交⊙O 于E,连接AE 、HM ，求证：AE ∥HM; （3）如图3，在（2）的条件下，连接BD 交AE 于N ，AE 与BC 交于点F ，若NH ＝25，AD ＝11，求线段AB 的长.【答案】（1）证明见解析；（2）证明见解析；（3）AB 的长为10.【解析】分析：（1）根据题意，设∠CAD=a ，然后根据直角三角形的两锐角互余的关系，推导出∠BAC=∠ACB ，再根据等角对等边得证结论；（2）延长AD 、BM 交于点N ，连接ED.根据圆周角定理得出∠N=∠DEN=∠BAN ，进而根据等角对等边，得到DE=DN,BA=BN，再根据等腰三角形和直角三角形的性质，求得MH∥AE；（3）连接CE，根据（2）的结论，由三角形全等的判定与性质证得HF=HC，然后结合勾股定理求出AC2-AH2=CD2-DH2，解得CD=5,CH=4,AH=8，最后根据锐角三角函数的性质得到AB.详解：（1）证明：设∠CAD=a,则∠ABC=2a,∠C=90°-a,∠BAD=90°-2a,∴∠BAC=90°-2a+a=90°-a∴∠BAC=∠ACB.∴AB=BC(2）证明：延长AD、BM交于点N，连接ED.∵∠DEN=∠DAB,∠N=∠BCD,∠BCD=∠BAN∴∠N=∠DEN=∠BAN∴DE=DN,BA=BN又∵BH⊥AN,DM⊥EN∴EM=NM,HN=HA,∴MH∥AE（3）连接CE.∠BDA=∠BCA,∠BDM=∠BAC,由（1）知∠BCA=∠BAC∴∠BDA=∠BDM,∴△BDM≌△BDH,∴DH=MH,∠MBD=∠HBD,∴BD⊥MH又∵MH∥AE,∴BD⊥EF,∴△FNB≌△ENB,同理可证△AFH≌△ACH,∴HF=HC,又∵FN=NE∴NH∥EC,EC=2NH,又∵NH=25∴EC=45∠EAC=2∠AEC=2a=∠ABC,可证弧AC=弧EC,∴AC=EC=5设HD=x，AH=11-x，∵∠ADC=2∠CAD,翻折△CHD 至△CHG,可证CG=CD=AGAH=CD+DH,CD=AH-DH=11-x-x=11-2x又∵AC 2-AH 2=CD 2-DH 2,∴(45)2-(11-x)2=(11-2x)2-x 2∴x 1=3,x 2=272(舍去)∴CD=5,CH=4,AH=8. 又∵tan2AH CH a BH DH==,∴BH=6 ∴AB=22226810BM AH +=+= 点睛：此题主要考查了圆的综合，结合圆周角定理，勾股定理，全等三角形的判定与性质，解直角三角形的性质，综合性比较强，灵活添加辅助线，构造方程求解是解题关键.6．如图，已知平行四边形OABC 的三个顶点A 、B 、C 在以O 为圆心的半圆上，过点C 作CD ⊥AB ，分别交AB 、AO 的延长线于点D 、E ，AE 交半圆O 于点F ，连接CF ．（1）判断直线DE 与半圆O 的位置关系，并说明理由；（2）若半圆O 的半径为6，求¶AC 的长．【答案】（1）直线CE 与半圆O 相切（2）4π【解析】试题分析：（1）结论：DE 是⊙O 的切线．首先证明△ABO ，△BCO 都是等边三角形，再证明四边形BDCG 是矩形，即可解决问题；（2）只要证明△OCF 是等边三角形即可解决问题，求AC 即可解决问题．试题解析：（1）直线CE 与半圆O 相切，理由如下：∵四边形OABC 是平行四边形，∴AB ∥OC.∵∠D=90°，∴∠OCE=∠D=90°，即OC ⊥DE ，∴直线CE 与半圆O 相切．（2）由（1）可知：∠COF=60°，OC=OF ，∴△OCF 是等边三角形，∴∠AOC=120°∴¶AC 的长为1206180π⨯⨯=4π.7．已知：AB 是⊙0直径,C 是⊙0外一点,连接BC 交⊙0于点D ，BD=CD,连接AD 、AC ．(1)如图1,求证:∠BAD=∠CAD(2)如图2,过点C 作CF ⊥AB 于点F,交⊙0于点E,延长CF 交⊙0于点G.过点作EH ⊥AG 于点H ，交AB 于点K,求证AK=2OF ；(3)如图3,在(2)的条件下,EH 交AD 于点L,若0K=1,AC=CG,求线段AL 的长.图1 图2 图3【答案】(1)见解析(2)见解析(3)12105 【解析】试题分析：（1）由直径所对的圆周角等于90°，得到∠ADB =90°，再证明△ABD ≌△ACD 即可得到结论；（2）连接BE ．由同弧所对的圆周角相等，得到∠GAB =∠BEG ．再证△KFE ≌△BFE ，得到BF =KF =BK ．由OF =OB -BF ，AK =AB -BK ，即可得到结论． （3）连接CO 并延长交AG 于点M ，连接BG ．设∠GAB =α．先证CM 垂直平分AG ，得到AM =GM ，∠AGC +∠GCM =90°．再证∠GAF =∠GCM =α．通过证明△AGB ≌△CMG ，得到BG =GM =12AG ．再证明∠BGC =∠MCG =α．设BF =KF =a ， 可得GF =2a ，AF =4a ． 由OK =1，得到OF =a +1，AK =2（a +1），AF = 3a +2，得到3a +2=4a ，解出a 的值，得到AF ，AB ，GF ，FC 的值．由tanα=tan ∠HAK =12HK AH =， AK =6，可以求出 AH 的长．再由1tan tan 3BAD BCF ∠=∠= ，利用公式tan ∠GAD =tan tan 1tan tan GAF BAD GAF BAD∠+∠-∠⋅∠，得到∠GAD =45°，则AL =2AH ，即可得到结论．试题解析：解：（1）∵AB 为⊙O 的直径，∴∠ADB =90°，∴∠ADC =90°．∵BD =CD ，∠BDA =∠CDA ，AD =AD ，∴△ABD ≌△ACD ，∴∠BAD =∠CAD ．（2）连接BE ．∵BG =BG ，∴∠GAB =∠BEG ．∵CF ⊥AB ，∴∠KFE =90°．∵EH ⊥AG ，∴∠AHE =∠KFE =90°，∠AKH =∠EKF ，∴∠HAK =∠KEF =∠BEF ．∵FE =FE ，∠KFE =∠BFE =90°，∴△KFE ≌△BFE ，∴BF =KF =BK ．∵ OF =OB -BF ，AK =AB -BK ，∴AK =2OF ．（3）连接CO 并延长交AG 于点M ，连接BG ．设∠GAB =α．∵AC =CG ， ∴点C 在AG 的垂直平分线上．∵ OA =OG ，∴点O 在AG 的垂直平分线上， ∴CM 垂直平分AG ，∴AM =GM ，∠AGC +∠GCM =90°．∵AF ⊥CG ，∴∠AGC +∠GAF =90°，∴∠GAF =∠GCM =α．∵AB 为⊙O 的直径，∴∠AGB = 90°，∴∠AGB =∠CMG =90°．∵AB =AC =CG ，∴△AGB ≌△CMG ，∴BG =GM=12AG ． 在Rt △AGB 中， 1tan tan 2GB GAB AG α∠=== ． ∵∠AMC =∠AGB = 90°，∴BG ∥CM ， ∴∠BGC =∠MCG =α．设BF =KF =a ， 1tan tan 2BF BGF GF α∠===，∴GF =2a ，1tan tan 2GF GAF AF α∠=== ，AF =4a ．∵OK =1，∴OF =a +1，AK =2OF =2（a +1），∴AF =AK +KF =a +2（a +1）=3a +2，∴3a +2=4a ，∴a =2， AK =6，∴AF =4a =8，AB =AC =CG =10，GF =2a =4，FC =CG -GF =6． ∵tanα=tan ∠HAK =12HK AH =，设KH =m ，则AH =2m ，∴AK 22(2)m m +=6，解得：m 65，∴AH =2m 125．在Rt △BFC 中，1tan 3BF BCF FC ∠== ．∵∠BAD +∠ABD =90°， ∠FBC +∠BCF =90°，∴∠BCF =∠BAD ，1tan tan 3BAD BCF ∠=∠= ，∴tan ∠GAD =tan tan 1tan tan GAF BAD GAF BAD ∠+∠-∠⋅∠=1123111123+=-⨯，∴∠GAD=45°，∴HL=AH，AL=2AH= 1210．58．如图，AN是⊙M的直径，NB∥x轴，AB交⊙M于点C．（1）若点A（0，6），N（0，2），∠ABN=30°，求点B的坐标；（2）若D为线段NB的中点，求证：直线CD是⊙M的切线．【答案】(1) B（，2）．(2)证明见解析.【解析】试题分析：（1）在Rt△ABN中，求出AN、AB即可解决问题；（2）连接MC，NC．只要证明∠MCD=90°即可试题解析：（1）∵A的坐标为（0，6），N（0，2），∴AN=4，∵∠ABN=30°，∠ANB=90°，∴AB=2AN=8，∴由勾股定理可知：NB=，∴B（，2）．（2）连接MC，NC∵AN是⊙M的直径，∴∠ACN=90°，∴∠NCB=90°，在Rt△NCB中，D为NB的中点，∴CD=NB=ND，∴∠CND=∠NCD ， ∵MC=MN ， ∴∠MCN=∠MNC ， ∵∠MNC+∠CND=90°， ∴∠MCN+∠NCD=90°， 即MC ⊥CD ．∴直线CD 是⊙M 的切线．考点：切线的判定；坐标与图形性质．9．如图，在Rt △ABC 中，90C ∠=︒，AD 平分∠BAC ，交BC 于点D ，点O 在AB 上，⊙O 经过A 、D 两点，交AC 于点E ，交AB 于点F ． （1）求证：BC 是⊙O 的切线；（2）若⊙O 的半径是2cm ，E 是弧AD 的中点，求阴影部分的面积（结果保留π和根号）【答案】（1）证明见解析 （2）233π【解析】 【分析】（1）连接OD ，只要证明OD ∥AC 即可解决问题；（2）连接OE ，OE 交AD 于K ．只要证明△AOE 是等边三角形即可解决问题． 【详解】 （1）连接OD ．∵OA=OD，∴∠OAD=∠ODA．∵∠OAD=∠DAC，∴∠ODA=∠DAC，∴OD∥AC，∴∠ODB=∠C=90°，∴OD⊥BC，∴BC是⊙O的切线．（2）连接OE，OE交AD于K．∵¶¶AE DE=，∴OE⊥AD．∵∠OAK=∠EAK，AK=AK，∠AKO=∠AKE=90°，∴△AKO≌△AKE，∴AO=AE=OE，∴△AOE是等边三角形，∴∠AOE=60°，∴S阴=S扇形OAE﹣S△AOE26023360π⋅⋅=-⨯22233π=-．【点睛】本题考查了切线的判定、扇形的面积、等边三角形的判定和性质、平行线的判定和性质、全等三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，灵活运用所学知识解决问题，属于中考常考题型．10．如图，等边△ABC内接于⊙O，P是弧AB上任一点（点P不与A、B重合），连AP，BP，过C作CM∥BP交PA的延长线于点M，（1）求证：△PCM为等边三角形；（2）若PA＝1，PB＝2，求梯形PBCM的面积．【答案】（1）见解析；（2153 4【解析】【分析】（1）利用同弧所对的圆周角相等即可求得题目中的未知角，进而判定△PCM为等边三角形；（2）利用上题中得到的相等的角和等边三角形中相等的线段证得两三角形全等，进而利用△PCM为等边三角形，进而求得PH的长，利用梯形的面积公式计算梯形的面积即可．【详解】（1）证明：作PH⊥CM于H，∵△ABC是等边三角形，∴∠APC=∠ABC=60°， ∠BAC=∠BPC=60°， ∵CM ∥BP ， ∴∠BPC=∠PCM=60°， ∴△PCM 为等边三角形；（2）解：∵△ABC 是等边三角形，△PCM 为等边三角形， ∴∠PCA+∠ACM=∠BCP+∠PCA ， ∴∠BCP=∠ACM ， 在△BCP 和△ACM 中，BC AC BCP ACM CP CM =⎧⎪∠=∠⎨⎪=⎩， ∴△BCP ≌△ACM （SAS ）， ∴PB=AM ，∴CM=CP=PM=PA+AM=PA+PB=1+2=3， 在Rt △PMH 中，∠MPH=30°， ∴PH=332，∴S 梯形PBCM =12（PB+CM ）×PH=12×（2+3）×332=1534．【点睛】本题考查圆周角定理、等边三角形的判定、全等三角形的性质及梯形的面积计算方法，是一道比较复杂的几何综合题．11．如图，四边形为菱形，且，以为直径作，与交于点．请仅用无刻度的直尺按下列要求画图．(保留作图痕迹)(1)在如图中，过点作边上的高． (2)在如图中，过点作的切线，与交于点．【答案】(1)如图1所示．(答案不唯一),见解析；(2)如图2所示．(答案不唯一)，见解析.【解析】【分析】（1）连接AC交圆于一点F，连接PF交AB于点E,连接CE即为所求．（2）连接OF交BC于Q，连接PQ即为所求．【详解】(1)如图1所示．(答案不唯一)(2)如图2所示．(答案不唯一)【点睛】本题考查作图-复杂作图，菱形和圆的性质等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．12．如图，AB为⊙O的直径，BC为⊙O的弦，过O点作OD⊥BC，交⊙O的切线CD于点D，交⊙O于点E，连接AC、AE，且AE与BC交于点F．（1）连接BD，求证：BD是⊙O的切线；（2）若AF：EF=2：1，求tan∠CAF的值．【答案】（1）证明见解析；（2）3 3.【解析】【分析】（1）根据全等三角形的性质得到∠OBD=∠OCD=90°，根据切线的判定定理即可得到结论； （2）根据已知条件得到AC ∥DE ，设OD 与BC 交于G ，根据平行线分线段成比例定理得到AC ：EG=2：1，EG=12AC ，根据三角形的中位线的性质得到OG=12AC 于是得到AC=OE ，求得∠ABC=30°，即可得到结论． 【详解】证明：（1）∵OC=OB ，OD ⊥BC ， ∴∠COD=∠BOD ， 在△COD 与△BOD 中，OC OB COD BOD OD OD ＝＝＝⎧⎪∠∠⎨⎪⎩， ∴△COD ≌△BOD ， ∴∠OBD=∠OCD=90°， ∴BD 是⊙O 的切线；（2）解：∵AB 为⊙O 的直径，AC ⊥BC ， ∵OD ⊥CB ， ∴AC ∥DE ， 设OD 与BC 交于G ， ∵OE ∥AC ，AF ：EF=2：1， ∴AC ：EG=2：1，即EG=12AC ， ∵OG ∥AC ，OA=OB ， ∴OG=12AC ， ∵OG+GE=12AC+12AC=AC ， ∴AC=OE ，∴AC=12AB ， ∴∠ABC=30°，∴∠CAB=60°，∵¼¼CE BE=，∴∠CAF=∠EAB=12∠CAB=30°，∴tan∠CAF=tan30°=33．【点睛】本题考查了切线的判定和性质，垂径定理，全等三角形的判定与性质，三角形的中位线的性质，三角函数的定义，正确的识别图形是解题的关键．13．如图，已知△ABC，AB=2，3BC=，∠B=45°，点D在边BC上，联结AD，以点A 为圆心，AD为半径画圆，与边AC交于点E，点F在圆A上，且AF⊥AD．（1）设BD为x，点D、F之间的距离为y，求y关于x的函数解析式，并写出定义域；（2）如果E是»DF的中点，求:BD CD的值；（3）联结CF，如果四边形ADCF是梯形，求BD的长．【答案】(1) 2442y x x=-+45; (3) BD的长是11+5.【解析】【分析】（1）过点A作AH⊥BC，垂足为点H．构造直角三角形，利用解直角三角形和勾股定理求得AD的长度．联结DF，点D、F之间的距离y即为DF的长度，在Rt△ADF中，利用锐角三角形函数的定义求得DF的长度，易得函数关系式．（2）由勾股定理求得：22AH DH+．设DF与AE相交于点Q，通过解Rt△DCQ和Rt△AHC推知12DQCQ=．故设DQ=k，CQ=2k，AQ=DQ=k，所以再次利用勾股定理推知DC的长度，结合图形求得线段BD的长度，易得答案．（3）如果四边形ADCF是梯形，则需要分类讨论：①当AF∥DC、②当AD∥FC．根据相似三角形的判定与性质，结合图形解答．【详解】（1）过点A作AH⊥BC，垂足为点H．∵∠B =45°，AB 2∴·cos 1BH AH AB B ===． ∵BD 为x ，∴1DH x =-．在Rt △ADH 中，90AHD ∠=︒，∴22222AD AH DH x x =+=-+．联结DF ，点D 、F 之间的距离y 即为DF 的长度．∵点F 在圆A 上，且AF ⊥AD ，∴AD AF =，45ADF ∠=︒． 在Rt △ADF 中，90DAF ∠=︒，∴2442cos ADDF x x ADF==-+∠∴2442y x x =-+．()03x ≤≤ ;（2）∵E 是DF 的中点，∴AE DF ⊥，AE 平分DF ． ∵BC=3，∴312HC =-=．∴225AC AH HC +=．设DF 与AE 相交于点Q ，在Rt △DCQ 中，90DQC ∠=︒，tan DQDCQ CQ∠=． 在Rt △AHC 中，90AHC ∠=︒，1tan 2AH ACH HC ∠==． ∵DCQ ACH ∠=∠，∴12DQ CQ =． 设,2DQ k CQ k ==，AQ DQ k ==， ∵35k =5k =，∴2253DC DQ CQ =+=．∵43BD BC DC =-=，∴4:5BD CD =． （3）如果四边形ADCF 是梯形则①当AF ∥DC 时，45AFD FDC ∠=∠=︒．∵45ADF ∠=︒，∴AD BC ⊥，即点D 与点H 重合． ∴1BD =． ②当AD ∥FC 时，45ADF CFD ∠=∠=︒． ∵45B ∠=︒，∴B CFD ∠=∠．∵B BAD ADF FDC ∠+∠=∠+∠，∴BAD FDC ∠=∠． ∴ABD ∆∽DFC ∆．∴AB ADDF DC=． ∵2DF AD =，DC BC BD =-．∴2AD BC BD =-．即()222-23x xx +=-,整理得 210x x --=，解得 152x ±=（负数舍去）． 综上所述，如果四边形ADCF 是梯形，BD 的长是1或1+5． 【点睛】此题属于圆的综合题，涉及了平行四边形的性质、相似三角形的判定与性质、三角函数值以及勾股定理等知识，综合性较强，解答本题需要我们熟练各部分的内容，对学生的综合能力要求较高，一定要注意将所学知识贯穿起来．14．如图，AB 是O e 的直径，DF 切O e 于点D ，BF DF ⊥于F ，过点A 作AC //BF 交BD 的延长线于点C . （1）求证：ABC C ∠∠=；（2）设CA 的延长线交O e 于E BF ，交O e 于G ，若¼DG的度数等于60o ，试简要说明点D 和点E 关于直线AB 对称的理由.【答案】（1）见解析；（2）见解析. 【解析】 【分析】（1）作辅助线，连接OD ，由DF 为⊙O 的切线，可得OD ⊥DF ，又BF ⊥DF ，AC ∥BF ，所以OD ∥AC ，∠ODB=∠C ，由OB=OD 得∠ABD=∠ODB ，从而可证∠ABC=∠C ；（2）连接OG ，OD ，AD ，由BF ∥OD ，»GD =60°，可求证»BG =»»GD AD ==60°，由平行线的性质及三角形的内角和定理可求出∠OHD=90°，由垂径定理便可得出结论． 【详解】 （1）连接OD ， ∵DF 为⊙O 的切线， ∴OD ⊥DF ． ∵BF ⊥DF ，AC ∥BF ， ∴OD ∥AC ∥BF ． ∴∠ODB=∠C ． ∵OB=OD ，∴∠ABD=∠ODB．∴∠ABC=∠C．（2）连接OG，OD，AD，DE，DE交AB于H，∵BF∥OD，∴∠OBG=∠AOD，∠OGB=∠DOG，∴»»GD AD==»BG．∵»GD=60°，∴»BG=»»GD AD==60°，∴∠ABC=∠C=∠E=30°，∵OD//CE∴∠ODE=∠E=30°．在△ODH中，∠ODE=30°，∠AOD=60°，∴∠OHD=90°，∴AB⊥DE．∴点D和点E关于直线AB对称．【点睛】本题考查的是切线的性质、圆周角定理及垂径定理，解答此题的关键是作出辅助线，利用数形结合解答．15．如图，在⊙O中，直径AB垂直弦CD于E，过点A作∠DAF=∠DAB，过点D作AF的垂线，垂足为F，交AB的延长线于点P，连接CO并延长交⊙O于点G，连接EG．（1）求证：DF是⊙O的切线；（2）若AD=DP，OB=3，求»BD的长度；（3）若DE=4，AE=8，求线段EG的长．【答案】（1）证明见解析（2）π（3）213【解析】试题分析：（1）连接OD，由等腰三角形的性质得出∠DAB=∠ADO，再由已知条件得出∠ADO=∠DAF，证出OD∥AF，由已知DF⊥AF，得出DF⊥OD，即可得出结论；（2）易得∠BOD=60°，再由弧长公式求解即可；（3）连接DG，由垂径定理得出DE=CE=4，得出CD=8，由勾股定理求出DG，再由勾股定理求出EG即可．试题解析：（1）证明：连接OD，如图1所示：∵OA=OD，∴∠DAB=∠ADO，∵∠DAF=∠DAB，∴∠ADO=∠DAF，∴OD∥AF，又∵DF⊥AF，∴DF⊥OD，∴DF是⊙O的切线；（2）∵AD=DP∴∠P=∠DAF=∠DAB =x0∴∠P+∠DAF+∠DAB =3x o=90O∴x0=300∴∠BOD=60°，∴»BD的长度=（3）解：连接DG，如图2所示：∵AB⊥CD，∴DE=CE=4，∴CD=DE+CE=8，设OD=OA=x，则OE=8﹣x，在Rt△ODE中，由勾股定理得：OE2+DE2=OD2，即（8﹣x）2+42=x2，解得：x=5，∴CG=2OA=10，∵CG是⊙O的直径，∴∠CDG=90°，∴DG=2222-=-=6，108CG CD∴EG=2222+=+=213.DG DE64。
圆综合测试题(含详细解析及答案)
《圆》的综合测试题学校:___________姓名：___________班级:___________考号：___________一、选择题（题型注释）1．用半径为3cm,圆心角是120°的扇形围成一个圆锥的侧面,则这个圆锥的底面半径为（ ）A ．2cmB ．1.5cmC ．cmD ．1cm2．已知⊙1O 的半径为5cm ,⊙2O 的半径为3cm ，两圆的圆心距为7cm ，则两圆的位置关系是( ),A 外离 ,B 外切 ,C 内切 ,D 相交3．如图是某公园的一角,∠AOB=90°，弧AB 的半径OA 长是6米，C 是OA 的中点，点D 在弧AB 上,CD∥OB,则图中休闲区（阴影部分)的面积是【 】A ．91032π⎛⎫- ⎪⎝⎭米2B ．932π⎛⎫- ⎪⎝⎭米2 C ．9632π⎛⎫- ⎪⎝⎭米2 D ．()693π-米24．如右图，圆心角∠AOB=100°，则∠ACB 的度数为（ ）OA BCA 、100°B 、50°C 、80°D 、45°5．如图，⊙O 是△ABC 的外接圆,已知∠ABO=30º，则∠ACB 的大小为( ）A ．30ºB ．45ºC ．50ºD ．60º6．如图，AB 是⊙O 的直径，弦CD ⊥AB 于点E ，∠CDB ＝30°,⊙O 的半径为3cm,则圆心O 到弦CD 的距离为( )A ．错误!cmB ．3 cmC ．3错误!cmD ．6cm7．圆心角为120°，弧长为12π的扇形半径为（ ）A ．6B ．9C ．18D ．368．⊙O 的直径AB ＝10cm ，弦CD ⊥AB ，垂足为P ．若OP ：OB ＝3：5，则CD 的长为（ )A ．6cmB ．4cmC ．8cmD ．91cm 9．如图,在△ABC 中，∠A ＝90º，AB ＝AC ＝2．以BC 的中点O 为圆心的圆弧分别与AB 、AC 相切于点D 、E ，则图中阴影部分的面积是【 】A ．1－4πB ．4πC ．1－2πD ．2－2π 10．如图，PA 、PB 切⊙O 于A 、B 两点，CD 切⊙O 于点E ，交PA,PB 于C 、D ，若⊙O 的半径为r ，△PCD 的周长等于3r ，则tan ∠APB 的值是（ )A 51312．125 C 3135 D 2133二、填空题(题型注释)11．母线长为4,底面圆的半径为1的圆锥的侧面积为___________。
小学数学人教版六年级上册第六单元《圆》综合测试卷(解析版)
小学数学人教版六年级上册第六单元《圆》综合测试卷（解析版）一、单选题1．一个半圆形的半径是r，周长是（）A．兀r B．2兀r÷2C．兀r+r D．（兀+2）r2．圆形花坛的半径是2米，绕花坛走一周，长度是（）。
A．25.12米B．12.56米C．12.56平方米D．25.12平方米3．如图，从甲到乙的两条路，说法正确的是（）。
A．①号路长B．②号路长C．一样长4．（2024六上·金东期末）一个半径为r的半圆，它的周长用式子表示正确的是（）。
A．Πr B．πr+r C．πr+2r D．πr25．（2024六上·黄岩期末）下图中，三张正方形纸片边长都是36cm，分别按下面方式剪出不同规格的圆片。
下列说法正确的是（）。
A．圆①、圆②、圆③的周长比是3：2：1B．圆①的面积是圆②的4倍C．圆③的面积是圆②的23D．三张纸片中第一张的空白部分面积最大、二、判断题6．在同一个圆内，长度是直径的一半的线段叫做半径。
（）7．圆的周长是它的直径的3.14倍。
（）8．当长方形、正方形、圆的周长相等时，圆的面积最大。
（）9．大小两个圆的半径都增加1m，那么它们的周长各增加6.28m。
（）10．（2023六下·东兰期末）一个半圆的周长是20.56分米，这个半圆的面积是41.12平方分米。
（）三、填空题11．大圆的半径与小圆的直径相等，那么大小两个圆的周长比是，它们的面积比是。
12．量得一个树桩的直径是32cm，这个树桩的横截面的面积是。
13．如图，正方形的面积与圆面积的比是。
14．一个半圆形的直径是12厘米，这个半圆形的周长是厘米。
15．（2024六下·期中）一个圆的半径扩大到原来的3倍，它的周长扩大到原来的倍，面积扩大到原来的倍．16．（2024六上·平湖期末）如图，大圆与小圆的半径比是3：2，则大圆与小圆的周长比是，大圆与小圆的面积比是。
17．（2024六上·平湖期末）如图，半圆的直径AB长12厘米，AC=CD=DB。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
《圆》的综合测试题学校: __________ 姓名：___________ 班级：___________ 考号：___________一、选择題（題型注释）1.用半径为3cm,圆心角是120。
的扇形鬧成一个惻锥的侧面，则这个圆锥的底面半径为（）A. B・ 1. 5cmC.仇cmD. lcm2.已知G）O］的半径为5cm, （DO?的半径为3cm,两圆的圆心距为7cm,则两圆的位置关系是（）A外离 B.外切C,内切D,相交3.如图是某公园的一角，ZA0B=90° ,弧AB的半径0A长是6米，C是0A的中点，点D在弧AB上.CD〃0B・则图中休闲区（阴影部分）的面积是【】10/r —牙米-B.4.如右图，圆心角ZAOB=100\则ZACB的度数为（）CA、100° B. 50° C. 80° D、45°6.如图，肋是00的直径，弦CDLAB^点£ ZCDB=3/ , 00的半径为3cm•则圆心0到弦少的距离为（7.圆心角为120%弧长为12n的扇形半径为（）A. 6B. 9C. 18D. 368.。
0的直径AB = 10cm,弦CD丄AB,垂足为P・若OP： 0B=3： 5,则CD的长为（）9.如图.在△磁中，ZJ=90\ AB=AC=2.以％的中点0为圆心的圆弧分别与月从相切于点八E.则图中阴影部分的面枳是【】小 4717T71XA. 1- —B.—C. 1 — _D. 2- —4422■10.如图，PA、PB切00于A、B两点，CD切00于点E,交PA, PB于C、D,若00的半径为r, Z\PCD的周长等于3“贝lj tanZAPB的值是（）二、填空题（题型注释）11.母线长为4,底面圆的半径为1的圆锥的侧面枳为_______________ ■，12.如图，AB是半圆0的直径，点P在AB的延长线卜.，PC切半圆0于点C,连接AC・若ZCPA=20° ,则ZA二_______ ° •A. 2 CmB. 3 cmC. 3^3 cmD. 6cmA・ 6cm B. 4cm C. 8cm D. 5/9? cmD.313.如图是一个用來盛爆米花的圆锥形纸杯，纸杯开II圆的直径EF长为10cm・母线OE (OF)长为10cm.在母线OF上的点A处有一块爆米花残渣，且FA=2cm, 一只蚂蚁从杯I 1的点E处沿圆锥表面爬行到A点,则此蚂蚁爬行的最短距离为_____________ cm.14••如图，00内切于AABC.切点分别为D、E、F.己知<B=50° , <060° ,连结OE. OF、DE、DFJ1IJ<EDF= _______________________ 度.15.己知AB、CD是直径为10的00中的两条平行弦，且AB二8, CD二6.则这两条弦的距离为三、计算題(題型注释) 四、解答题(题型注释)16.如图，AB足G)0的直径，AF是00切线，CD是垂直于AB的弦，垂足为E,过点C 作DA的平行线与AF相交于点F, CD=4>/3 , BE=2.求证：(1)四边形FADC是菱形：(2) FC是O0的切线.17.如图①，②，在平面直角坐标系xOy中，点A的坐标为(4, 0),以点A为圆心, 4为半径的圆与x轴交于O, B两点• OC为弦，厶QC = 60J P足x轴上的•动点，连结CP・(1)求ZOAC的度数；(2)如图①，当CP与。
A相切时，求PO的长：(3)如图②，当点P在直径OB上时，CP的延长线与0A相交于点Q,问PO为何值时，AOCQ是等腰三角形？18.如图，己知口4与」Q相交于点E、F,点P是两圆连心线上的一点，分别联结PE、PF交3 0：于A、C两点，并延长交DO］与B、D两点。
求证：PA=PCo19.如图所示.©As Q& OCs g OE相互外离,它们的半径都是1,顺次连接五个圆心得到五边形ABCDE,则图中五个扇形（阴影）部分的面积之和是多少？20•如图，在矩形ABCD中，点0在对角线AC上，以0A长为半径的0O与血，AC分别交于点E, F, ZACB=ZDCE -请判断直线CE与。
0的位置关系，并证明你的结论；A a参考答案1. D【解析】主要考查了圆锥侧面展开扇形与底面圆之间的关系，圆锥的侧而展开图是-个扇形, 此扇形的弧长等于圆锥底面周长，扇形的半径等于圆锥的母线长.把的扇形的弧长等于圆锥底面周长作为相等关系，列方程求解.解：设此圆锥的底面半径为r,根据圆锥的侧面展开图扇形的弧长等于圆锥底面周长町得，2Tl r=120lP3180 *解得：r=lcm.故选D.2. D【解析】・・•两个圆的半径分别是3和5,圆心距是7, 5-3V7V5+3,・・・两圆的位置关系是相交.故选D.3« Co【解析】连接0D,则S）刃形=$扇形AOD - Sqoc。
•・•弧AB的半径0A长是6米.C是0A的中点.••.0C二丄0A二丄X6二3。
2 2TZAOB二90° , CD〃OB・•'•CD丄0A。
在RtAOCD 中，TOD二6. 0C二3. ；•=届==3屁又V sinZDOC = £2 = ^=2^ , ZDOC^O0。
OD 6 2：•环］形=形AOD _Sqoc = "3：o6 _ + •'• 3若=6龙一?弟（米 ~）。
故选C。
4. B【解析】试题分析：圆周角定理：同弧或等弧所对的圆周角相等，均等于所对圆心角的一半. 由图可得ZACB= -ZAOB=50°,故选B.2考点：圆周角定理点评：本题属于基础应用题，只需学生熟练学握圆周角定理，即可完成.5. D.【解析】试题分析：AAOB 中，OA二OB. ZABO=30° : A ZA0B=180°・ 2ZAB0=120° : A ZACB= - Z2A0B=60°；故选。
.考点：圆周角定理.如图,连接CB・VAB是0O的直径，弦CD丄AB于点E・・・・圆心O到弦CD的距离为OE；・・・ZCOB二2ZCDB （同弧所对的圆周角是所对的圆心角的一半），ZCDB二30。
，・•・ ZCOB 二60。
；在RtAOCE 中，OC二3cm, OE二OC・cosZCOB, AOE=|.故选A.7. C【解析】试题分析：根据弧长的公式I二匹:进行计算.180解：设该扇形的半径是根据弧长的公式1=込，180得到：12n=120 7137,180解得r=18,考点：弧长的计算& C.【解析】试题分析:连接OC： TAB二10cm, ・・・0B=5cm； V0P： 0B=3： 5,.・.OP二3cm： RtAOCP 中,0C=0B=5cm, OP二3cm：由勾股定理.得：CP= VoC2-OP2 = lcm：所以CD二2PC二8cm.故选C.9. A【解析】解：因为△磁中，ZJ=90°, AB=AC=2,那么利用三角形面枳公式町知为2,而 扇形QDE 的面积町以得到，运用间接法，△磁的面枳减公扇形的面积和三角形COE, BOD 的 面积可得。
10. B.【解析】试题分析：如答图，连接P0, A0,取AO 中点G,连接AG,过点A 作AH 丄P0于点H, •・・PA 、PB 切00于A 、B 两点，CD 切00于点E,・・・PA 二PB, CA 二CE, DB=DE. ZAP0=ZBP0, Z0AP=90°.•・.用=塑* OH = ^^r. A GH = GO-OH = —r-^^r = -^^r .1313413 52 3>/13 ATJ RtaiiZAPB = taiiZAGH =-——=—】二GH 5伍52考点：1 •切线的性质；2•切线长定理；3•勾股定理；4•相似三角形的判定和性质：5•锐角三 角函数定义：6•直角三角形斜边上中线的性质；7•转换思想的应用.••'△PCD 的周长等于3r,.*.PA=PB=-r.2VO0的半径为 •••在RtAAPO 中，由勾股定理得PO = Jr+I Z OHA= Z 0AP=90°, Z HOA= Z AOP t :. △ HOA s △ AOP.• AH OH OA• PA _ OA _ OPHPAH _ OH _ rI ZAGH=2ZAP0=ZAPB,11・ 4TT【解析】・・•圆锥的底面半径为1,母线为4,・••圆锥的侧面积=TT X1X4=4TT12.35【解析】试题分析：连接0C，V ZCPA=20° , A ZPOC=70°。
/. ZA= 1 ZPOC =35°。
13. 2 顷【解析】分析：要求蚂蚁爬行的最短距离，需将圆锥的侧面展开，进而根据“两点之间线段城短”得出结果.解答：解：因为0E二OF二EF二10 (cm),所以底面周长=10TT (cm),将圆锥侧面沿0E剪开展平得一扇形，此扇形的半径0E=10 (cm),弧长等于圆锥底面圆的周长10TT (cm)设扇形圆心角度数为n,则根据弧长公式得：101510TT 二--- ，180所以n二180° ,即展开图是-个半圆，因为F点是展开图弧的中点，所以ZEOF=90° ,连接EA,则EA就是蚂蚁爬行的最短距离，在RtAAOE中由勾股定理得，EA:=0E:+OA:=100+64=164,所以EA二2J3T (cm),即蚂蚁爬行的最短距离是2>/41 (cm14.55【解析】先由三角形的内角和定理求出/A,然后根据切线的性质和四边形的内角和求出Z EOF,最后根据圆周角定理得到ZEDF的度数.解：VZB=50° , ZC=60° ,A ZA=180° -50° -60° =70° ； 又TE, F 是切点, ••・0E 丄AB, OF 丄AC, A ZE0F=180° 一70° 二110° • A ZEDF=- X110° =55° .故填 55° .215. 1或7・【解析】TAF 是。
0 切线.•••AF 丄AB 。
TCD 丄AB, AAF/ZCDo•・・CF 〃AD,・•・四边形FADC 是平行四边形。
TAB 是00的直径，CD 丄AB,••• CE = DE = ZCD = ix4>/3=2>/3 o2 2设 0C 二X,TBE 二2, A0E=x - 2.在 RtZiOCE 中，0C :=0E :+CE\/. x 2 = (x- 2)2 +(2*73)，解得：x 二4。