具有无关项的卡诺图化简
卡诺图化简法

2.2.1 逻辑变量的最小项及其性质
1.最小项定义:
设有n个变量,若m为包含全部n个变量的乘积项(每个变量 必须而且只能以原变量或反变量的形式出现一次)则称m为该组 变量的最小项。 如:A、B、C是三个逻辑变量,有以下八个乘积项 为此三个变量的最小项
2.特点
(1)每个最小项均含有三个因子(n个变量则含n个因子) (2)每个变量均为原变量或反变量的形式在乘积项中出现一次
ABC ABC A BC
m3 m2 m1
m(1、 2、 3)
例2
L( ABC ) ( AB AB C ) AB
AB AB C AB
AB AB C AB ( AB AB) C AB ABC ABC AB(C C) ABC ABC ABC ABC
填函数的卡诺图时,只在无关项对应的格内填任意 符号“Φ”、“d”或“×”
化简方法:视化简需要可作0或1处理。
例2.2.7:
设计一位十进制数的判奇电路,当为奇数时输出为1,否则为0。 无关项:1010 ~1111
解:
列 真 值 表
N A
0 1 2 0 0 0
B
0 0 0
C
0 0 1
D
0 1 0
结论:任一个
逻辑函数都可化 成为唯一的最小 项表达式
m3 m5 m7 m6
m(3,5,7,6)
对于一个具体的逻辑问题,逻辑表达式是不唯一的
真值表
唯一 最小项表达式
卡诺图 真值表实际上是函数最小项 表达式的一种表格表示 最小项表达式的一种图形表示 ——卡诺图
如
A 0 0 0 0 1 1 1 1
第六讲 具有无关项和多输出逻辑函数卡诺图化简法

L = A D + AD
L = L = A D + AD
L = A D + AD
CD 00 AB 00 0 01 0 11 10
01 11 10
1
= A D • AD = ( A + D) • ( A + D ) = ( A + D) • ( A + D ) = A+ D+ A + D
1 1
× 0 1 × 0 0 × × 0 0 ×
L2 = AB C + BC
将两个输出函数视为一个整体, 将两个输出函数视为一个整体,其化简过程如下
BC A 00 0 0 1
01
11
1 1
1 1
BC 10 A 00 0 0 0
01
11
10
0 0
1 1
0 0
1
0
1
1
L1 = AB C + C
L2 = AB C + BC
逻辑图如 28图 逻辑图如P28图1.20,图1.21 20,
•
•
逻辑问题的描述可用真值表、函数式、逻辑图、 逻辑问题的描述可用真值表、函数式、逻辑图、卡诺 图和时序图
求其最简与或式
F = D + BC
某逻辑函数输入是8421 8421BCD码,其逻辑表达式为: 例8. 某逻辑函数输入是8421 码 其逻辑表达式为: L(A,B,C,D)=∑ (1,4,5,6,7,9)+∑d(10,11,12,13,14,15) , )=∑m(1,4,5,6,7,9)+∑d(10,11,12,13,14,15) ( 用卡诺图法化简该逻辑函数。 用卡诺图法化简该逻辑函数。 解:(1)画出4变量卡诺图。将1、4、5、6、7、9号小方格填入1; 画出4变量卡诺图。 号小方格填入1 10、11、12、13、14、15号小方格填入 号小方格填入× 将10、11、12、13、14、15号小方格填入×。 合并最小项,如图( ) 所示。注意, 方格不能漏。 ( 2 ) 合并最小项 , 如图 ( a)所示 。 注意 , 1 方格不能漏 。 × 方 格根据需要,可以圈入,也可以放弃。 格根据需要,可以圈入,也可以放弃。 写出逻辑函数的最简与—或表达式 或表达式: (3)写出逻辑函数的最简与 或表达式: 如果不考虑无关项,如图(b)所示,写出表达式为: 如果不考虑无关项,如图(b)所示,写出表达式为:
数电课件第八次课 无关项卡诺图化简法、门电路2

AB
CD 00
1 0 0 0
00 01 11 10
结论: F = G
18
第三章
§3.1 概述
门电路
§3.2 二极管及其构成的与、或门电路 §3.3 三极管及其构成的非门电路 §3.4 TTL门电路 §3.5 CMOS门电路
19
§3.1 概述
一、门电路的概念:
算的电子电路,叫逻辑门电路。实 实现基本和常用逻辑运 实现基本和常用逻辑运算的电子电路,叫逻辑门电路。实 现与运算的叫与门,实现或运算的叫或门,实现非运算的叫非 门,也叫做反相器,等等。 门电路主要有: 与门 、或门 、与非 门,也叫做反相器,等等。门电路主要有: 门电路主要有:与门 与门、 或门、 、异或门 等。 门、或非门 或非门、 异或门等。
∑
11 0 × 0 0
10 1 0 0 0
Y = B′C ′ + A′ B′D′
Y = B′(C ′ + D′) ( A′ + C ′ )
12
⎧ Y= m(1,2,8,9) ⎪ 【例 2】 试化简逻辑函数 ⎨ 为最简与或式、 ⎪ ⎩ A′ C ′D′ + A′BCD = 0
∑
或与式和与或非式。 CD 00 AB 00 × 01 11 10 × 0 1
01 0 0 0 0 11 0 0 1 0 10 0 0 0 0
AB
CD 00
1 0 0 0
00 01 11 10
16
G = ( A′ B + B′C + C ′D + D′A)′
G ′ = A′B + B′C + C ′D + D′A
A′B =
∑ C ′D = m(1,5,9,13) ∑
具有无关项的逻辑函数及其化简

具有无关项的逻辑函数及其化简1. 约束项、任意项和逻辑函数式中的无关项在分析某些具体的逻辑函数时,经常会遇到这样一种情况,即输入变量的取值不是任意的。
对输入变量取值所加的限制称为约束。
同时,把这一组变量称为具有约束的一组变量。
例如,有三个逻辑变量A、B、C,它们分别表示一台电动机的正转、反转和停止的命令,A=1表示正转,B=1表示反转,C=1表示停止。
因为电动机任何时候只能执行其中的一个命令,所以不允许两个以上的变量同时为1。
ABC 的取值只可能是001、010、100当中的某一种,而不能是000、011、101、110、111 中的任何一种。
因此,A、B、C 是一组具有约束的变量。
通常用约束条件来描述约束的内容,为方便起见采用逻辑语言表述约束条件。
由于每一组输入变量的取值都使一个、而且仅有一个最小项的值为1,所以当限制某些输入变量的取值不能出现时,可以用它们对应的最小项等于0来表示。
这样,上述例子中的约束条件可以表示为或写成:同时,把这些恒等于0的最小项叫做约束项。
有时还会遇到另外一种情况:在输入变量的某些取值下函数值是1还是0皆可,并不影响电路的功能。
在这些变量取值下,其值等于1的那些最小项称为任意项。
由于约束项和任意项都不影响函数值,所以又把两者统称为逻辑函数式中的无关项,既可以写入函数式中,也可以不写进去。
一般情况在用卡诺图表示逻辑函数时,首先将函数化为最小项之和的形式,然后在卡诺图中这些最小项对应的位置上填入1,其他位置上填入0。
既然无关项可以包含也可以不包含在函数式中,那么在卡诺图中对应的位置上填1或0都可以。
为此,规定在卡诺图中用×(或)表示无关项。
在化简逻辑函数时既可以认为它是1,也可以认为它是0。
数字逻辑基础卡诺图化简
101
0
110
0
1 2020/8/14 1 1
1
14
练习:三变量表决逻辑真值表填入卡诺图
ABC
Y
000
0
001
0
010
0
011
1
100
0
101
1
110
1
111
1
2020/8/14
15
(2)从最小项表达式画卡诺图 把表达式中所有的最小项在对应的小方块中填
入1,其余的小方块中填入0。
例4: 画出函数Y(A、B、C、D)= ∑m(0,3,5,7,9,12,15) 的卡诺图。
① 无关项的概念
对应于输入变量的某些取值下,输出函数的值可 以是任意的(随意项、任意项),或者这些输入变量的 取值根本不会(也不允许)出现(约束项),通常把这 些输入变量取值所对应的最小项称为无关项或任意项, 在卡诺图中用符号“×”表示,在标准与或表达式中用 ∑d( )表示。
例:当8421BCD码作为输入变量时,禁止码1010~ 1111这六种状态所对应的最小项就是无关项。
相邻 相邻
② 几何相邻的必须
逻辑相邻:变量的 取值按00、01、11、 10的顺序(循环码 ) 排列 。
图1-11 三变量卡诺图的画法
2020/8/14
12
不 相邻
相邻
相邻
图1-12 四变量卡诺图的画法
正确认识卡诺 图的“逻辑相邻”: 上下相邻,左右相 邻,并呈现“循环 相邻”的特性,它 类似于一个封闭的 球面,如同展开了 的世界地图一样。
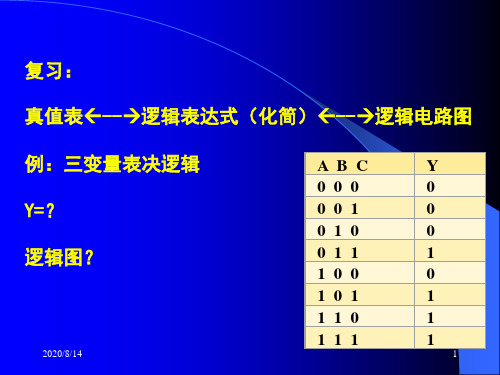
复习:
真值表--逻辑表达式(化简)--逻辑电路图
例:三变量表决逻辑 Y=? 逻辑图?
2020/8/14
卡诺图化简法PPT课件

解: 根据最小项的编号规则,得 将这四个最小项填入四变量卡诺图内
F m3 m9 m11 m13
化简得
F ACD BCD
第21页/共55页
例11 用卡诺图化简函数
F ( A, B,C, D) ABC AC D ABC D ABC
(5)按照2k个方格来组合(即圈内的1格数必须为1,2,4,8等),圈的面积越大越 好。因为圈越大,可消去的变量就越多,与项中的变量就越少。
(6)每个圈应至少包含一个新的1格,否则这个圈是多余的。 (7)用卡诺图化简所得到的最简与或式不是唯一的。
第23页/共55页
练习:判断正确与错误 例1
错误 (多画一个圈)
F C BD
正 确
F ABC ACD ABC ACD
第25页/共55页
4. 具有无关项的逻辑函数的卡诺图化简法
◆ 什么是无关项
实●际在中逻经辑常函会数遇表到达这式样中的用问题,在真值表表内示d对(无.应.关..于项..变,) 量例的如某,些取值下,函说数明的
值可最以例小是如项任:m意一2、的个dm,逻(42、或辑,4m者电,55为说路)无这的关些输项变入;量为的84取21值-B根CD本码不,会显出然现信。息中有六个变量组合
(101●0~也1用111逻)辑是表不达使式用表的示,函这数些中变的量无取关值项所,对例应如的最小项称为无关项。 如果电路正常工作,这些无关项决不会出现,那么与这些无关项所对应的电路
的量输得说出无到明●是简关无什化项关么而的A项, 定意B在也。义真就在值无于A所表所C,包或谓它含卡了的的诺,值最d图可可小中以以项用假取为A×定0无来B或为关表取1项示,1,。A。也具C可体以取假什定么为值0,。可以根据使函数尽
数字逻辑基础卡诺图化简

例5:已知 YA BA C D A B C D ,画卡诺图。
Y1 AB AB(CC)(DD)
ABCDABCDABCDABCD
m(12,13,14,15)
Y2 AC D A(B B )C D
例3: 已知Y的真值表,要求画Y的卡诺图。
表1-19 逻辑函数Y的真值表
图1-12 例3的卡诺图
ABC
Y
000
0
001
1
010
1
011
0
100
1
101
0
110
0
1 2020/7/26 1 1
1
.
14
练习:三变量表决逻辑真值表填入卡诺图
ABC
Y
000
0
001
0
010
0
011
1
100
0
101
1
110
1
或:Y(A,B,C)m3m6m7
m(3,6,7)
2020/7/26
.
8
例2: 写出三变量函数的最小项表达式。
解 利用摩根定律将函数变换为与或表达式, 然后展开成最小项之和形式。
Y ( A, B, C ) AB AB C AB
AB ABCAB
(A BA B )CA B (CC )
A B C A B C A B C A B C
2020/7/26
.
2
2.4 逻辑函数的卡诺图化简法
公式化简法评价: 优点:变量个数不受限制。 缺点:目前尚无一套完整的方法,结果是否最简 有时不易判断。
逻辑函数的卡诺图法化简

数字电路与逻辑设计
解: 直接填入
CD 00
01
00 01 11 10
0
10
0
1
11
0
11 0
11
1
10 0
00
0
电子工 程学院
School of Electronic Engineering
厚夜博学
第二章逻辑函数及其简化
例5:用卡诺图表示4变量逻辑函 数:
School of Electronic Engineering
厚饱博学
第二章逻辑函数及其简化
数字电路与逻辑设计
(2)如不是最小项表达式,应先将其先化成最小项表达式,再填入卡诺图。
例3 :用卡诺图表示4变量逻辑函数:F = ABC + ABD +
AC 解:F = ABC+ABD+AC
=ABCD + ABCD + ABCD + ABCD +
F B 00 01 11 10
C 0
Jq
0
0
0
0
0
0
1
F
IF = AC
B 00 01
11
10
C
0
0
0
0
0
0
0
1
F
B 00 01 11 10
C
0A 0
0
0
0
0
0
1
IF = BC
\ F = AB
电子工 程学院
School of Electronic Engineering
厚饱博学
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第六讲逻辑函数的卡诺图化简法(2)
课题:逻辑函数的最简式的其它形式;
具有约束的逻辑函数的化简
课时安排:2
重点:具有约束的逻辑函数的化简
难点:具有约束的逻辑函数的化简
教学目标:使同学掌握用卡诺图法求最简式的其它形式的方法,理解约束条件,掌握用约束条件化简逻辑函数的方法,了解多输出逻辑函数的化简方法。
教学过程:
一、用卡诺图法求最简式的其它形式
二、用卡诺图检验函数是否最简
三、具有约束项的逻辑函数化简法
1、约束的概念和约束的条件
2、有约束的逻辑函数的表示方法
3、具有约束的逻辑函数的化简
4、多输出逻辑函数的化简
3、具有无关项的逻辑函数的化简
无关项:
约束项:值恒为0的最小项
任意项:使函数值可以为1,也可以为0 的最小项
约束项和任意项均为无关项。
含有无关项的函数的两种表示形式:
1、L=∑m(…)+∑d(…)
2、L=∑m(…),给定约束条件为ABC+ACD=0
2.具有无关项的逻辑函数的化简
化简具有无关项的逻辑函数时,要充分利用无关项可以当0也可以当1的特点,尽量扩大卡诺圈,使逻辑函数更简。
例7.
不考虑无关项时,表达式为:
考虑无关项时,表达式为:
注意:在考虑无关项时,哪些无关项当作1,哪些无关项当作0,要以尽量扩大卡诺圈、减少圈的个数,使逻辑函数更简为原则。
