光在球面上反射和折射
第三章几何光学球面反射折射物像公式
例3.4:
一个折射率为1.6的玻璃哑铃,长20cm,两端的曲率半径为 2cm。若在 离哑铃左端5cm处的轴上有一物点,试求像的位置和性质。
[解]:两次折射成像问题。
n
P
O1
n
P’1 n` O 2
1、P为物, 对球面O1折射成像P1’
已知 : s1 5cm , r1 2cm , n 1, n ' 1.6 n n n n 由折射成像公式 ' r1 s1 s1
沿轴线段
A、凡光线与主轴交点在顶点右方者线段长度数值为正; 凡光线与主 轴交点在顶点左方者线段长度数值为负; B、物点或像点至主轴的距离在主轴上方为正,下方为负。 ② 光线的倾角均从主轴或球面法线算起,并取小于900的角度;由主轴 (或法线)转向有关光线时: A、顺时针转动,角度为正;B、逆时针转动,角度为负。 (注意:角度的正负与构成它的线段的正负无关)
2
r
2
s r
'
2
2 r s ' r cos
光程 PAP ' nl nl ' n
r 2 r s 2 2 r r s cos r
2
n
s r
'
2
2 r s r cos
1、高斯公式:
球面反射 : f ' f 1 1 2 ' s s r
六、理想成象的两个普适公式
n' n n' n 将物像公式 ' 变形为 : s s r n' n r r ' ' ' f f n n n n 1 1 ' ' s s s s
单球面反射和折射

5. 特例
(1)球面反射
n n'
1 1 2 p p' r
平行光线入射,p ,代入物像公式 1 1 2 得 pf'' 2r 2r,f ' 此时对应的像点叫焦点(fpocusp)' r 焦点到顶点的距离— 焦距(focal length)
物像公式为
11 1 p p' f '
(Gauss公式)
1.5 1.0
(8) (1)
1.2
,即成正立、放大的实像。
总的横向放大率
1
2
3
0.5 (
1) 1.2 3
为20cm和15cm,薄透镜折射率为1.5,在凸面 镀银。在球面前方40处的主轴上置一高为1cm 的物,求像的位置和成像的性质。
[解](1)P经凹球面折射成像:
p1=-40cm,n=1.0,n’=1.5,r1=-20cm,代入
n' n n'n p1' p1 r1
1
np1 ' n' p1
1 2
,
1.5 1.0 0.5 p1' 40 20
三、傍轴球面折射的物象关系式
nn'n (u(' u in)) unn('(n'('niu'))') n
p
u
i o
n' h i' c u '
p'
u h p'
r
p
p'
u h p
h
n n nn
p' p r
物像关系式
r
定义 光焦度
Φ n'n r
3-3光在球面介质上的反射、折射

3-3光在球面介质上的反射、折射 光在球面介质上的反射、 光在球面介质上的反射 球面成像的公式
第3章 几何光学 章
n′ n n′ − n − = s′ s r
物、像具有共轭关系,可逆关系. 像具有共轭关系,可逆关系 三 焦点 焦距 焦平面
n′ − n 球面成像的公式; 由球面成像的公式;令:Φ = — 球面光焦度 球面光焦度. r
n r os = f = − n′ − n
且: f ′ /
— 物空间的主焦距 物空间的主焦距 主焦距. (第一主焦距) 第一主焦距)
焦点、焦距是由介质折射率和球面半径决定 焦点、焦距是由介质折射率和球面半径决定.
f = − n′ / n
f ′=
焦距与光焦度关系: 焦距与光焦度关系:
n′ n′ → Φ = Φ f ′ n n f = → Φ = Φ f
像点在像空间无限远处! 像点在像空间无限远处!
— 像空间的主焦距 像空间的主焦距 主焦距. (第二主焦距) 第二主焦距)
n s=− r n′ − n
3-3光在球面介质上的反射、折射 光在球面介质上的反射、 光在球面介质上的反射
第3章 几何光学 章
n s=− r n′ − n
— 物空间的主焦点 (第一主焦点) 物空间的主焦点 第一主焦点) 主焦点.(
第3章 几何光学 章
n s′ s′ − r = (r − s) (− s) n′
此式表明; 只与已知量有关 具有一个像点. 只与已知量有关, 此式表明;s´只与已知量有关,具有一个像点 球面折射成像条件: ) 球面折射成像条件:1)元光束 . 2)光线近轴传播 )光线近轴传播.
s′ n 成像的公式: 成像的公式:由: s ′ − r = (r − s) (− s) n′ s′n′ rn′ rn sn ( s ′ − r ) n′ ( r − s ) n − = − = s′ s′ ( − s ) ( − s ) s′ (− s) n′ n n′ − n ∴ − = s′ s r
光在球面上的反射和折射

1 1 1 s s ( ) l l r l l
考虑近轴光线,进一步得到
它的成像规律与介质无关.
1 1 2 s s r
s:物距
s:像距
'
C
FF
o
令 令
s ,
得 得
s ,
r f f 2
凹面镜
r f ; 2 r f , 2
因此球面镜物方焦点与像方焦点重合 .
P
O n n’
A
P’
r
C
-s
s’
5 近轴光线下球面折射的物像公式
M O n n’
l s, l s
'
'
P
P’
r
C
-s
s’
n' n n'n n'n 定义光焦度(optical power) : s' s r r
r 的单位为米时,光焦度的单位称为屈光度(diopter)
n'n r
P
-u
f
-i’ C
u’
P’
Q
n’
r
s’
-s
单个折射面成像系统的笛卡尔符号规则
笛卡尔坐标规则补充
线段
纵向线段 以球面顶点 O 为原点,以入射光线进行 的方向为正方向,建立物空间坐标 s 和像空间坐标 , 物点坐标为物距,像点坐标为像距 . s 横向线段 以光轴为起点,向上为正向下为负.
n
y
• S
u
O1
R s1 ’
O2
s2 ’ s2
P’
n' n n'n s' s r
(2).
O1面:s1=-2R, r1=+R, n1=1, n1’=1.5
几何光学基本定律球面反射和折射成像

11-1-4 全反射
n1sinin2sinr
当 n1 n2 有 r i
临界角 ic :相应于折射角 为90°的入射角.
r
n2
i
ic ic
n1
全反射:当入射角 i 大于临界角时,将不会出现折射 光,入射光的能量全部反射回原来介质的现象.
sin ic
n2 n1
§11-2 平面反射和平面折射成像
i i v1 n1
n2
r v2
⑵ 入射角 i 的正弦与折射角 r 的正弦之比为一个常数
sin i sin r n 21
n21称为第二种介质对第 一种介质的相对折射率
n21
sin i sinr
v1 v2
绝对折射率:一种介质相对于真空的折射率 n c v 。
设
c n1 v1
c n2 v2
n 21
虚像
m y 1 y
像正立
例2.点光源P位于一玻璃球心点左侧25 cm处.已知玻璃球半径 是10 cm,折射率为1.5,空气折射率近似为1,求像点的位置.
解: p1 15cm
P2
R10cm
n1 1
P1
n2 1.5
n1 P p1
p 1 p2
n2
C
P2
p 2
n1 n2 n2 n1
p1 p1
R
R
2
C
P
P
R
C P
P
会聚光入射凹镜:虚物成实像
p0
p' 0
R0
f
R 2
0
发散光入射凸镜: 实物成虚像
p 0 p' 0 R0
f R 0 2
R
P
P
3.5光在球面上的反射和折射符号法则

主讲人:尹国盛 教授 河南大学物理与信息光电子学院
1
主要内容
3.1 光线的概念 3.2 费马原理 3.3 单心光束 实像和虚像 3.4 光在平面界面上的反射和折射
光学纤维 3.5 光在球面上的反射和折射 3.6 光连续在几个球面界面上的折射
如果:n1 > n2,那么 y < y ,即像点P 位于 物点 P 的上方,视深度减小。
(渔民叉鱼) 如果:n1 < n2, 那么 y > y ,即像点P 位于
物点 P 的下方,视深度增大。
20
三. 全反射 光学纤维
1.全反射:
对光线只有反射而无折射的现像。
当光从光密介质n1射向光疏介质
n2(<n1)时,i1 i2 i1 =ic
18
∵ 单心光束的波面是球面, ∴ 在平面界面上折射后,波面的形状发生 变化,不再是球面了。这样形成的互相垂直 的两小段像且不那么清晰的现像称为像散。
② 当i1=0,即当P所发出的光束几乎垂直于 界面时,有 x =0 , y = y1 = y2 = y n2 n1 。
19
这表明 y 近似地与入射角 i1 无关,则折 射光束是近似单心的,y 称为像视深度,y 为 物的实际深度。
25
例题3.1 人眼前一小物体,距人眼25cm,今 在人眼和小物体之间放置一块平行平面玻璃 板,玻璃板的折射率为1.5 ,厚度为5mm。 试问此时看小物体相对它原来的位置移动多 远?
解:利用 P162 L 3.1 的结果,
PPˊ= d ( 1-1/n )
可得:
s = 5×(1-1/1.5)= 5/3≈1.67(mm)
1. 4. 光在球面上的反射与折射
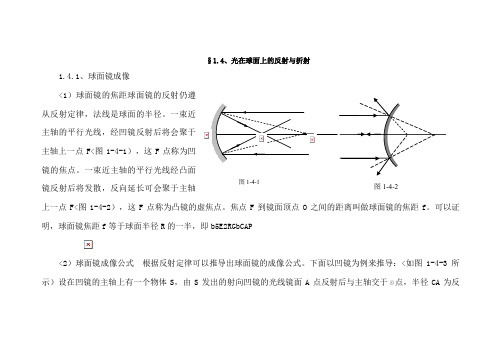
§1.4、光在球面上的反射与折射1.4.1、球面镜成像<1)球面镜的焦距球面镜的反射仍遵从反射定律,法线是球面的半径。
一束近主轴的平行光线,经凹镜反射后将会聚于主轴上一点F<图1-4-1),这F 点称为凹镜的焦点。
一束近主轴的平行光线经凸面镜反射后将发散,反向延长可会聚于主轴上一点F<图1-4-2),这F 点称为凸镜的虚焦点。
焦点F 到镜面顶点O 之间的距离叫做球面镜的焦距f 。
可以证明,球面镜焦距f 等于球面半径R 的一半,即b5E2RGbCAP<2)球面镜成像公式 根据反射定律可以推导出球面镜的成像公式。
下面以凹镜为例来推导:<如图1-4-3所示)设在凹镜的主轴上有一个物体S ,由S 发出的射向凹镜的光线镜面A 点反射后与主轴交于点,半径CA为反图1-4-1图1-4-2射的法线,即S的像。
根据反射定律,,则CA为角A的平分线,根据角平分线的性质有p1EanqFDPw①由为SA为近轴光线,所以,,①式可改写为②②式中OS叫物距u,叫像距v,设凹镜焦距为f,则代入①式化简这个公式同样适用于凸镜。
使用球面镜的成像公式时要注意:凹镜焦距f取正,凸镜焦距f取负;实物u取正,虚物u取负;实像v为正,虚像v为负。
DXDiTa9E3d上式是球面镜成像公式。
它适用于凹面镜成像和凸面镜成像,各量符号遵循“实取正,虚取负”的原则。
凸面镜的焦点是虚的,因此焦距为负值。
在成像中,像长和物长h之比为成像放大率,用m表示,RTCrpUDGiT由成像公式和放大率关系式可以讨论球面镜成像情况,对于凹镜,如表Ⅰ所列;对于凸镜,如表Ⅱ所列。
表Ⅰ 凹镜成像情况~2f表Ⅱ 凸镜成像情况~~2f同侧~<3)球面镜多次成像 球面镜多次成像原则:只要多次运用球面镜成像公式即可,但有时前一个球面镜反射的光线尚未成像便又遇上了后一个球面镜,此时就要引进虚像的概念。
5PCzVD7HxA 如图1-4-4所示,半径为R 的凸镜和凹镜主轴相互重合放置,两镜顶点O1 、 O2 相距2.6R ,现于主轴上距凹镜顶点O1为0.6R 处放一点光源S 。
光在球面上的反射和折射参考幻灯片

s'0.10m
顶点O的右边,虚像。
如右图,光线从右向
左传播,此时
A 物空间
巳知:S=0.05m, r=0.20m
Байду номын сангаас
P’
O PC
像空间
由球面镜物像公式,
11 2 s s' r
10/8/2020
1 1 2 0.05 s' 0.20
s'0.1m 0
顶点O的左边,虚像。
3.3.4 球面折射对 光束单心性的破坏
-s
考虑光线P-A-P’的光程 PA' P nln'l
n[ (r)2(rs)22(r)(rs)cos]12
n[ (r)2(s'r)22(r)(s'r)cos]12
当A点在镜面上移动时,是位置的变量。由费马原理
可得
dPA ' P 0 rss'r0
d
l
l'
由此可见,若s已知,则反射线与主轴的交点P’到O 点的距离s’随入射线的倾角u(亦即角)而变。也
由费马原理可得
d PAP' 0
d
n(rs)n'(s'r)0
l
l'
折射线与主轴的交点P’到O点的距离s’随入射线的倾角 u(亦即角)而变。
物点发出的单心光束经球面折射后,单心性也被破坏。
10/8/2020
3.3.5 近轴光线条件下球面折射的物像公式
近轴光线条件下,
角很小,在一级近似下,cos≈1,则有:l≈-s ,l’≈s’
10/8/2020 返回第3 章
3.3.1 符号法则
几何光学中的“符号”是人为规定的具有任意 性,需统一;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
F
f n f ' n'
n < n’
O
C
n n’
F’
r
-f
f’
f, f ’ 符号相反,大小不等
4 Gauss成像公式和Newton成像公式
Abbe不变式: n' n n'n s' s r
焦距公式:
f n r n n'
和
f ' n' r n'n
Gauss成像公式: f ' f 1 s' s
u
S
•
C
y
s
r s
角度
以光轴或法线为始边,沿小于 的方向旋转,顺时 针为正,逆时针为负.(顺正逆负)
图中各量的表示方法
图中只标记角度和线段的绝对值.标记点用大写字母, 标记角度和线段用小写字母.
物与像 的一一对应关系称为共轭.
n
i
y
•
S
u
O
s
n n
i
C
r s
u
笛卡尔坐标规则:
i. 假设光线从左侧进入光学系统;
ii. 线段量以光轴与介质分界面的交点为参照点, 左方负,右方正;在光轴上方为正,下方为负;
iii. 角度量以介质分界面法线或光轴为基准,按小于 90o的方向旋转,顺时针为正逆时针为负;
iv. 所有量用绝对值表示----全正表示。
-i
M
P
-u
hf
-i’ u’
S
•
y
2单个球面的反射成像
利用几何知识可以得到单球面反射系统成像公式
1 1 1 ( s s ) l l r l l
考虑近轴光线,进一步得到
1 1 2 s s r
它的成像规律与介质无关.
球面镜成像.swf
C FF o
令 s , 得 f r ;
2
令 s , 得 f r ,
s2 ' s2
r2
透镜制造者公式
r
r 的单位为米时,D的单位称为屈光度(diopter)
D n'n r
D > 0,会聚作用 F
n < n
O
C
n n’
F’
r
-f
f’
n > n
D < 0,发散作用 F’
O
CF
n n’
r
-f’ f
F’
O
n n’
-f’
f
O
F
n n’
-f
f’
F
n < n
F’ n > n
B. 焦距公式
从
n' s'
r2
2
1 s'
1 r
}
Fermat原理
M
等
r
P
O
P’
光 程
n n’ r C
-s
s’
n PM n'MP' n PO n'OP'
n {s r 2 1 1 } n'{s' r 2 1 1 } n (s) n's'
A. 用Fermat原理推导Abbe不变式:
(习题)
M
出发点: P、P为物像共轭点。
从P发出的各同心 光线都到P点
rh
P’
P
O
Q
h
C
n n’
r
-s
s’
从Fermat原理可知P点到P点的 所有成像光线有相等的光程
n PM n ' MP n PO n ' OP
PM h2 (s )2
M
MP' h2 (s')2
P
h2 r2 2
r2 h2 r 2
rh
O
Q
P’ C
n n’ r
-sபைடு நூலகம்
s’
r2
PM s2 r 2 2 s
2r
(s)2 r 2 (s)r 2
r
PM (s) 1 r 2 1 1
P’
OQ
C
n n’ r
-s s’
单个折射面成像系统的笛卡尔符号规则
线段
笛卡尔坐标规则补充
纵向线段 以球面顶点O为原点,以入射光线进行 的方向为正方向,建立物空间坐标 s 和像空间坐标 ,
物点s 坐标为物距,像点坐标为像距.
横向线段 以光轴为起点,向上为正向下为负.
n
n n
i
y
•
S
u
O
i
2
f f r 2
因此球面镜物方焦点与像方焦点重合 .
凹面镜 r 0, f f 0;
凸面镜 r 0, f f 0.
球面反射物像公式: 1 1 1 s s f
Mirror
见P173例3.3
3 单个球面的折射成像
A. Abbe不变式 B. 焦距(focal lengh) C. Gauss成像公式和 Newton成像公式
2 s r
2 s' r
n n n' n' ----- Abbe不变式 r s r s'
n n n' n'
M
r s r s'
P
O
P’
Abbe不变式的另一种形式: 成像公式
n n’ r C
-s
s’
n' n n'n s' s r
定义光焦度(optical power) :D n'n
P
n=1.5
-s1
O1
n' n n'n s' s r
O2
R
s2’
P’
s2
s1’
(2). O1面:s1=-2R, r1=+R, n1=1, n1’=1.5
s1’ =
O2面:s2= , r2= -R, n2=1.5, n2’=1
s2’ = 2R
例2. 推导薄透镜(thin lens)的焦距公式-----透镜制造者公式
3-5 光在球面上的反射和折射
光轴(optical axis) ---- 光学系统的对称轴
近轴光线(paraxial ray) ---与光轴夹角较小,并靠近光轴的光线
光轴
黄线—近轴光线 绿线—非近轴光线
1. 符号规则(sign convention) 几何光学常用的符号规则:
实正虚负规则;
笛卡尔坐标规则。
ss r
近轴光线
r << -s、r、s
PM
s
r2
2
1 s
1 r
光线PMP的光程
M
P
rh O
P’
hQ
C
n n’ r
-s
s’
同理: MP' s' r 2 1 1
2 s' r
n
{s
r2
2
1 s
1 r
}
n'{s'
f
'
(nL
1)
1 r1
1 r2
C2
O
证明: I1面: s1, s1’, r1 I2面: s2, s2’, r2
-r2
nL
I1 I2
r1 C1
薄透镜
s = s1, s’ = s2’, s2 = s1’
I 面:nL 1 nL 1
s1' s1
r1
II 面:1 nL 1 nL
n s
n'n r
s’ = 时
O
C
F
n n’
F’
r
-f f’
第一主焦距 (first focal length)或物 方主焦距:
f n r n n'
同理: 第二主焦距 (second focal length)
或像方主焦距:
f '
n'
r
n'n
f、f’、 D之间的关系:
D n'n n' n r f' f
P
F
O
P’ F’
n n’
-f -x
f’ x’
-s
s’
分别以F和F’为基准点,量度物点P和像点P’ 的位置,物距和
和像距分别用 x 和 x’ 表示:
-s = -x-f s’ = x’+f’
xx' ff '
Newton成像公式
成像规律图
以S 为横坐标, 以 S为纵坐标, 根据高斯公式作物距和像距关系曲 线. 这是一条以S=f, S=ƒ 两直线为渐近线的双曲线. 曲线上每一点 都对应光轴上一对共轭点.
P’
R
s2’
s2
s1’
解:
-s1
n' n n'n s' s r
n=1.5
O1 R
O2 P’ P1’ s2’ s2
s1’
(1). O1面:s1=-, r1=+R, n1=1, n1’=1.5 O2面:s2=R, r2= -R, n2=1.5, n2’=1
s1’ = 3R s2’ = R/2
第二象限实 物实像
s 第一象限虚 物实像
1
像放大
f
像缩小
