统计学各章计算题类型
统计学计算题复习(学生版)

统计学计算题复习(学生版)统计学复习提纲一、期末考卷题型1. 单项选择题;2. 多项选择题;3. 简答题4. 计算题二、知识点复习1. 统计学分类、指标、变量、参数、统计量等概念,以及各种统计图形;2.统计数据的相关内容,以及测量数据分布的测度的描述;平均数、中位数和众数的计算公式。
3. 调查的各种方式; 4. 组距数列的相关概念。
5. 置信区间的相关概念,以及单个总体均值、比例、方差的区间估计;6. 估计单个总体均值、比例时的样本容量的计算公式;7. 单个总体均值、比例、方差的假设检验;8. 相关系数和回归系数的相关知识;9. 一元、二元回归模型的EXCEL操作结果的解释以及模型的建立和检验;10. 时间序列的各种分类;平均速度等指标、移动平均法的概念等;平均发展水平的计算和季节指数的计算; 11.统计指数的相关概念,制作综合指数要点和原则,综合指数、平均指数的计算。
1统计学计算题复习一.平均数、中位数和众数的计算和三者之间的关系1.算术平均数。
也叫均值,是全部数据的算术平均,是集中趋势的最主要测度值。
主要适用于定距数据和定比数据,但不适用于定类数据和定序数据。
2.众数。
众数是一组数据中出现次数最多的变量值,用Mo表示。
主要用于测度定类数据的集中趋势。
组距式数列确定众数,是先根据出现次数确定众数所在组,然后利用下列公式计算众数的近似值:M?L?0f?f?1?i (f?f?1)?(f?f?1) 3.中位数。
中位数是一组数据按从小到大排序后,处于中间位置上的变量值,用Me表示。
主要用于测度定序数据的集中趋势。
分组数据计算中位数时,先根据公式N确定中位数所在的组,然后用下列公式计算2N?Sm?1中位数的近似值: M?L?2?i efm4.众数、中位数和算术平均数的关系 x?Me?Mo,数据是对称分布; x<Me<Mo,数据是左偏分布; x>Me>Mo,数据是右偏分布。
例题1:某地区有下列资料:人均月收入400以下400~500 500~600 600~700 700~800 800~900 900以上合计要求计算算术平均数、众数、中位数。
统计学基础各章习题整理

统计学基础各章习题整理第⼀章绪论⼀、单项选择题1.政治算术学派的代表⼈物是()A、康令B、威廉?配第C、凯特勒D、恩格尔2. 政治算术学派的创始⼈之⼀是( )。
A.阿亨⽡尔B.凯特勤C.约翰·格朗特D.⽪尔逊3、数理统计学的奠基⼈是:()A、威廉?配第B、阿痕⽡尔C、凯特勒D、恩格尔4、国势学派对统计学的主要贡献是:()A、采⽤了数量分析⽅法B、引⼊了⼤数法则C、提出了“统计学”这⼀名词D、证明了⼩样本理论5.“统计”⼀词的基本涵义是()A统计调查、统计整理、统计分析B统计设计、统计分组、统计计算C统计⽅法、统计分析、统计计算D统计学、统计⼯作、统计资料6.要了解某企业职⼯的⽂化⽔平情况,总体单位是()A该企业的全部职⼯; B该企业每⼀个职⼯的⽂化程度;C该企业的每⼀个职⼯; D该企业全部职⼯的平均⽂化程度。
7.以⼀、⼆、三等品来衡量产品质地的优劣,那么该产品等级是()。
A. 品质标志B. 数量标志C. 质量指标D. 数量指标8.下列标志中,属于数量标志的是()A学⽣的性别;B学⽣的年龄;C学⽣的专业;D学⽣的住址。
9.某⼯⼈⽉⼯资150元,则“⼯资”是()A数量标志;B品质标志;C质量指标;D数量指标。
10.下列变量中,属于连续变量的是()A⼤中型企业个数; B⼤中型企业的职⼯⼈数;C⼤中型企业的利润额;D⼤中型企业拥有的设备台数。
⼆、多项选择题1.对某地区⼯业⽣产进⾏调查,得到如下资料,其中,统计指标有()A某企业亏损20万元; B全地区产值3亿元; C某企业职⼯⼈数2000⼈;D全地区职⼯6万⼈; E全地区拥有各种设备6万台。
2.总体和总体单位不是固定不变的,随着研究⽬的不同()A总体单位可转化为总体; B总体可转化为总体单位; C总体和总体单位可以互相转化;D 只能是总体单位转化为总体;D只能是总体转化为总体单位。
3.下列标志中,属于数量标志的有()A性别;B⼯种;C⼯资;D民族;E年龄。
统计学各章计算题公式及解题方法

统计学各章计算题公式及解题方法第四章数据的概括性度量1.组距式数值型数据众数的计算:确定众数组后代入公式计算:下限公式:;上限公式:,其中,L为众数所在组下限,U为众数所在组上限,为众数所在组次数与前一组次数之差,为众数所在组次数与后一组次数之差,d为众数所在组组距2.中位数位置的确定:未分组数据为;组距分组数据为3.未分组数据中位数计算公式:4.单变量数列的中位数:先计算各组的累积次数(或累积频率)—根据位置公式确定中位数所在的组—对照累积次数(或累积频率)确定中位数(该公式假定中位数组的频数在该组内均匀分布)5.组距式数列的中位数计算公式:下限公式:;上限公式:,其中,为中位数所在组的频数,为中位数所在组前一组的累积频数,为中位数所在组后一组的累积频数6.四分位数位置的确定:未分组数据:;组距分组数据:7.简单均值:8.加权均值:,其中,为各组组中值统计学各章计算题公式及解题方法9.几何均值(用于计算平均发展速度):10.四分位差(用于衡量中位数的代表性):11.异众比率(用于衡量众数的代表性):12.极差:未分组数据:;组距分组数据:13.平均差(离散程度):未分组数据:;组距分组数据:14.总体方差:未分组数据:;分组数据:15.总体标准差:未分组数据:;分组数据:16.样本方差:未分组数据:;分组数据:17.样本标准差:未分组数据:;分组数据:18.标准分数:19.离散系数:第七章参数估计1.的估计值:置信水平α90%0。
1 0。
05 1。
654 95%0。
05 0.025 1。
9699%0.01 0。
005 2。
58统计学各章计算题公式及解题方法2.不同情况下总体均值的区间估计:总体分布样本量σ已知σ未知大样本(n≥30)正态分布小样本(n〈30)非正态分布大样本(n≥30)其中,查p448 ,查找时需查n—1的数值3.大样本总体比例的区间估计:4.总体方差在置信水平下的置信区间为:5.估计总体均值的样本量:,其中,E为估计误差6.重复抽样或无限总体抽样条件下的样本量:,其中π为总体比例第八章假设检验1.总体均值的检验(已知或未知的大样本)[总体服从正态分布,不服从正态分布的用正态分布近似]假设双侧检验左侧检验右侧检验假设形式已知统计量未知拒绝域值决策,拒绝2.总体均值检验(未知,小样本,总体正态分布)假设双侧检验左侧检验右侧检验假设形式统计学各章计算题公式及解题方法已知统计量未知拒绝域值决策,拒绝注:已知的拒绝域同大样本3.一个总体比例的检验(两类结果,总体服从二项分布,可用正态分布近似)(其中为假设的总体比例)假设双侧检验左侧检验右侧检验假设形式统计量拒绝域值决策,拒绝4.总体方差的检验(检验)假设双侧检验左侧检验右侧检验假设形式统计量拒绝域值决策,拒绝5.统计量的参考数值0。
统计学原理计算题复习(六种题型重点)

第三章:编制次数分配数列1.根据所给资料分组并计算出各组的频数和频率,编制次数分布表;根据整理表计算算术平均数。
例题:某单位40名职工业务考核成绩分别为: 68 89 88 84 86 87 75 73 72 68 75 82 97 58 81 54 79 76 95 76 71 60 90 65 76 72 76 85 89 92 64 57 83 81 78 77 72 61 70 81单位规定:60分以下为不及格,60─70分为及格,70─80分为中,80─90分为良,90─100分为优。
要求:(1)将参加考试的职工按考核成绩分为不及格、及格、中、良、优五组并编制一张考核成绩次数分配表;(2)指出分组标志及类型及采用的分组方法;(3)根据考核成绩次数分配表计算本单位职工业务考核平均成绩; (4)分析本单位职工业务考核情况。
解答:(1)该企业职工考核成绩次数分配表:成 绩(分) 职工人数(人) 频率(%)不及格(60以下) 3 7.5 及格 (60-70) 6 15 中 (70-80) 15 37.5 良 (80-90) 12 30 优 (90-100) 4 10 合 计 40100(2)此题分组标志是按“成绩”分组,其标志类型是“数量标志”; 分组方法是“变量分组中的组距式分组的等距分组,而且是开口式分组”;(3)根据考核成绩次数分配表计算本单位职工业务考核平均成绩。
(4)分析本单位职工考核情况。
本单位的考核成绩的分布呈两头小,中间大的“钟形分布”(即正态分布),不及格和优秀的职工人数较少,分别占总数的7.5%和10%,本单位大部分职工的考核成绩集中在70-90分之间,占了本单位的为67.5%,说明该单位的考核成绩总体良好。
)(774095485127515656553分=⨯+⨯+⨯+⨯+⨯==∑∑f xf x第四章:计算加权算术平均数、加权调和平均数(已知某年某月甲、乙两农贸市场A 、B 、C 三种农产品价格和成交量、成交额资料,试比较哪一个市场农产品的平均价格 较高?并说明原因。
统计学计算题

第三章统计整理例 1、某厂工人日产量资料如下:(单位:公斤)162 158 158 163 156 157 160 162 168 160164 152 159 159 168 159 154 157 160 159163 160 158 154 156 156 156 169 163 167试根据上述资料,编制组距式变量数列,并计算出频率。
解:将原始资料按其数值大小重新排列。
152158 159154 154 156 156 156 156 157 157 158 158 159 159 159 159 160 160 160 162 162 163 163 163 164 167168 168 169最大数=169,最小数=152,全距=169-152=17n=30, 分为 6 组例 2、某企业 50 个职工的月工资资料如下:113 125 78 115 84 135 97 105 110 130105 85 88 102 101 103 107 118 103 87116 67 106 63 115 85 121 97 117 10794 115 105 145 103 97 120 130 125 127122 88 98 131 112 94 96 115 145 143试根据上述资料,将50 个职工的工资编制成等距数列,列出累计频数和累计频率。
解:将原始资料按其数值大小重新排列。
63 97 117 118工人按日产量分组(公斤)152-154155-157158-160161-163164-166 工人数(人)361151比率(频率)(%)10.0020.0036.6016.7067 78 84 85 85 87 88 88 94 94 96 97 97 98 101 102 103 103 103 105 105 105 107 110 112 113 115 115 115 115 116 118 120 121 122 125 125 127 130 130 131 135 143 145 145按工资额分组(元)60-70 70-80 80-90频数216工人数频率( %)4212频数239向上累计频率( %)4618频数504847向下累计频率(%)1009694例 3、有 27 个工人看管机器台数如下:5 4 2 4 3 4 3 4 4 2 4 3 4 3 26 4 4 2 2 3 4 5 3 2 4 3试编制分布数列。
统计学期末复习计算题汇总

3—5
5—7 7—9 合计
30
40 30 100
4
6 8 -
120
0 120 240
3—5
5—7 7—9 合计
40
40 20 100
4
6 8 -
1.024
0.064 1.152 2.24
σ
甲
=
(x - x) f f
2
2
=
240 = 1.55 100
f σ乙 = (x - x) Σf = 2.24 = 1.5
年份 2008 2009 2010 2011
工业总产值(万元)
增长量(万元) 发展速度(%)
(
─ ─
)
(
5000 (
) (
( ) 106
) (
) ( (
)
) )
增长速度(%)
增长1%的绝对值(万元)
─
─
(
800
) (
(
)
) (
4
)
2.某企业历年工业总产值资料如下表,试填上表中所缺 的各种动态分析指标,并计算该企业工业总产值平均每 年的发展速度。 年 份 2008 2009 2010 ( 2011
9.某企业两个生产班组,各有100名工人,它们生产某 种产品的日产量资料如下表,计算有关指标,比较哪 个班组平均日产量的代表性强。
甲班组 日产量 工人数 (件) f 3—5 5—7 7—9 合计 30 40 30 100 组中值 xf x 4 6 8 — 120 240 240 600 日产量 (件) 3—5 5—7 7—9 合计 乙班组 x 生产工人 f
比重% Σf
x
f Σf
4 6 8 —
统计学复习题题目——计算题
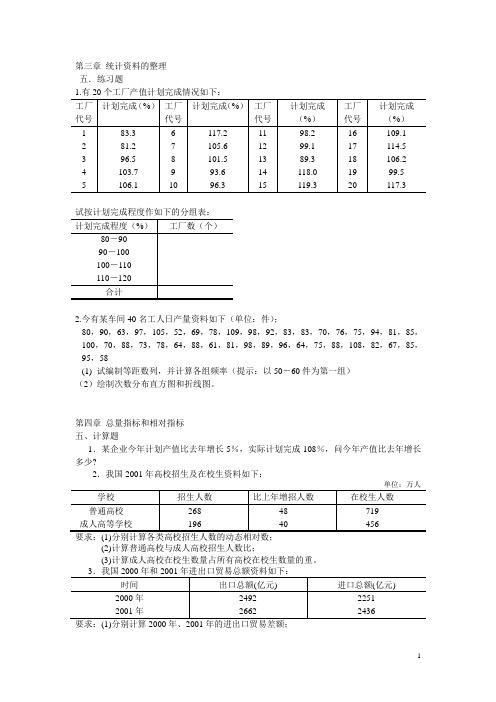
第三章 统计资料的整理 五.练习题试按计划完成程度作如下的分组表:2.今有某车间40名工人日产量资料如下(单位:件);80,90,63,97,105,52,69,78,109,98,92,83,83,70,76,75,94,81,85,100,70,88,73,78,64,88,61,81,98,89,96,64,75,88,108,82,67,85,95,58(1) 试编制等距数列,并计算各组频率(提示:以50-60件为第一组) (2)绘制次数分布直方图和折线图。
第四章总量指标和相对指标 五、计算题1.某企业今年计划产值比去年增长5%,实际计划完成108%,问今年产值比去年增长多少?2.我国2001年高校招生及在校生资料如下:(2)计算普通高校与成人高校招生人数比;(3)计算成人高校在校生数量占所有高校在校生数量的重。
(2)计算2001年进出口总额比例相对数及出口总额增长速度; (3)分析我国进出口贸易状况。
4.根据下列资料,计算强度相对数的正指标和逆指标,并根据正指标数值分析该地区5.某公司下属三个企业有关资料如下表,试根据指标之间的关系计算并填写表中所缺数第六章 动态数列习题五、计算题1.某公司某年9月末有职工250人,10月上旬的人数变动情况是:10月4日新招聘12名大学生上岗,6日有4名老职工退休离岗,8日有3名青年工人应征入伍,同日又有3名职工辞职离岗,9日招聘7名营销人员上岗。
试计算该公司10月上旬的平均在岗人数。
(2)分别计算该银行2005年第一季度、第二季度和上半年的平均现金库存额。
(2)计算该地区2001—2005年间的平均国民生产总值。
(3)计算2002—2005年间国民生产总值的平均发展速度和平均增长速度。
(2)计算该企业第四季度劳动生产率。
(2)应用最小平方法配合趋势直线,并计算各年的趋势值。
第七章统计指数习题五、计算题1.某市1999年第一季度社会商品零售额为36200万元,第四季度为35650万元,零售物价下跌0.5%,试计算该市社会商品零售额指数、零售价格指数和零售量指数,以及由于零售物价下跌居民少支出的金额。
统计学练习题(计算题)

统计学练习题(计算题)第四章----第一部分总量指标与相对指标:(1)某企业产值计划完成程度为105%,比上年增长7%,试计算计划规定比上年增长多少(2)单位产品成本上年为420元,计划规定今年成本降低5%,实际降低6%,试确定今年单位成本的计划数字和实际数字,并计算出降低成本计划完成程度指标。
(3)按计划规定,劳动生产率比上年提高10%,实际执行结果提高了12%,劳动生产率计划完成程度是多少:某市三个企业某年的下半年产值及计划执行情况如下:要求:[1]试计算并填写上表空栏,并分别说明(3)、(5)、(6)、(7)是何种相对数;[2]丙企业若能完成计划,从相对数和绝对数两方面说明该市三个企业将超额完成计划多少:我国2008年-2013年国内生产总值资料如下:单位:亿元根据上述资料,自行设计表格:(1)计算各年的第一产业、第二产业、第三产业的结构相对指标和比例相对指标;(2)计算我国国内生产总值、第一产业、第二产业、第三产业与上年对比的增长率;(3)简要说明我国经济变动情况。
:某公司下属四个企业的有关销售资料如下:根据上述资料:(1)完成上述表格中空栏数据的计算;(2)若A能完成计划,则公司的实际销售额将达到多少比计划超额完成多少(3)若每个企业的计划完成程度都达到B企业的水平,则公司的实际销售额将达到多少比计划超额完成多少第四章-----第二部分平均指标与变异指标:已知某地区各工业企业产值计划完成情况以及计划产值资料如下:要求:(1)根据上述资料计算该地区各企业产值计划的平均完成程度。
(2)如果在上表中所给资料不是计划产值而是实际产值,试计算产值计划平均完成程度。
、:已知某厂三个车间生产不同的产品,其废品率、产量和工时资料如下:计算:(1)三种产品的平均废品率;(2)假定三个车间生产的是同一产品,但独立完成,产品的平均废品率是多少;(3)假定三个车间是连续加工某一产品,产品的平均废品率是多少。
:对某车间甲、乙两工人当日产品中各抽取10件产品进行质量检查,得资料如下:试比较甲乙两工人谁生产的零件质量较稳定。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章1、某商店2003年实际销售额为1500万元,超额完成计划10%,计算2003年计划销售额。
解:计划销售额=1500/1.1=1363.64万元2、某企业2003年计划产量比上一年增长10%,实际比计划少完成5%,计算实际产量比上一年则增长多少?解:(1+10%)*(1-5%)=1.045,实际增长4.5%。
3根据以上资料计算该企业的商品周转次数的平均数。
解:次98.15099m/x m x ===∑∑4根据资料计算该企业职工工资的平均数,众数和中位数。
(保留1位小数) 解:(1)(元)2625240630000fxf x ===∑∑(2)人数最多为第三组,所以众数组为 2000-3000(元)52545100050100401004010020002110.)()()(d x m L =⨯-+--+=⨯∆+∆∆+=(3)12022402f==∑,根据向上累计,中位数组为2000-3000。
(元)2600100010060120200021=⨯-+=⨯-+=-∑d f S f x m mm Le 5、已知甲小区居民平均年龄为37岁,标准差为12岁,现对乙小区居民年龄进行抽样调根据以上资料计算:(保留1位小数) (1)计算乙小区居民的平均年龄;(2)比较甲乙两小区平均年龄的代表性大小;(1)(岁)01706464fxf x .38===∑∑ (2) 岁)(.94117037544ff )x -x (2===σ∑∑或岁)(.94183170283328x ff x 222=-=-=σ∑∑甲:%.4233712x V ==σ=甲 乙:%2.393814.9x V ==σ=乙甲乙V V >,所以甲小区的平均年龄更有代表性第四章1、某企业2009年四个季度的产值及工人数如下: 要求:(1)2009年的季平均劳动生产率。
C=a/b(2)2009工业总产值的平均增长速度。
解:(1) 人元/64.4754/)22302222152102200(4/)125.1095.9(=+++++++==b ac (2) %915.8124=-=x2、某商业企业资料如下:试计算(1)一季度的月平均商品流通费用率。
(2)二季度的月平均商品流转次数。
(1)%43.93/)196240200(3/)192120(=++++==b a c(2) 次37.23/)2666870280(3/)160160180(=+++++==b ac 要求:(1)用最小平方法配合适当的直线方程。
(2)预测2010年该地区玉米产量。
解:(1) a=83.1096659==∑n y b=61.9706732==∑∑t tyYc=109.83+9.61t(2) 2010年即t=7, y=177.1万吨4、某专业商店商品销售收入资料如下所示:(单位:万元)要求:(1)用同期平均法计算各季度销售收入的季节比率。
(2)假设已知2010年第一季度销售额为200万元,根据季节比率预测2007年第二季度的销售额。
解:(1)四季度季节比率分别为:61.5%,116.5%,150.2%,71.8% (2)x=116.5%/61.5%*200=378.86万元第五章1、某市几种主要副食品价格和销售量的资料如下:试计算:(1)各商品零售物价的个体指数;(2)四种商品物价总指数; (3)四种商品零售量总指数。
(4)对商品零售额变动进行因素分析。
(1) kp 蔬菜=p1/p0=2.2/2.0=110% kp 猪肉= p1/p0=17.8/17=104.7% kp 鲜蛋= p1/p0=9.2/5.2=176.92% kp 水产品= p1/p0=18.0/16.5=109.09% (2)价格总指数%09.10967.131636.1431011===∑∑qp q p K p∑∑=-=-万元966.1167.131636.1431011qp q p(3)销售量总指数%58.118035.11167.131001===∑∑pq p q K q∑∑=-=-万元635.20035.11167.131001p qp q(4)销售额指数%36.129035.111636.143011===∑∑pq p q K pq∑∑=-=-万元601.32035.111636.1430011p qp q相对数分析:%58.118%09.109%36.129⨯=绝对数分析:635.20966.11601.32+=2、某企业两种产品单位成本类指数及总成本资料如下:试编制这两种产品单位成本总指数,并对该企业总成本变动进行因素分析。
(1)单位成本总指数%64.822652192.1/4.807.0/6.1384.806.13811111==++==∑∑qp k q p K pp∑∑-=-=-万元4626521911111q p kq p p(2)产量总指数%5.132200265111===∑∑qp q p k K pq ∑∑=-=-万元6520026511111q p q p k p(3)总成本指数%5.10920021911===∑∑pq p q K pq ∑∑=-=-万元192002190011p qp q相对数分析:%5.132%64.82%5.109⨯= 绝对数分析:654619+-=3、试根据以下关于企业三种产品产值和产量动态资料,计算该企业的产量总指数和价格总指数。
%5.123100012353504502003504.14501.120025.100==++⨯+⨯+⨯==∑∑pq p q k K qq(2)产值总指数%5.12010001205350450200480485240011==++++==∑∑pq pq K qp(3)价格总指数%6.971235120511====∑∑pq k p q K K K qq pqp4、某企业生产甲、乙、丙三种产品,2005年和2009年的销售数据如下表所示:以上年为基期的产品价格指数如下:要求:(1)计算甲产品2005—2009年的价格平均增长率。
(2)计算该企业以2005年为基期的2009年价格总指数。
(3)计算该企业2009年比2005年的销售量增长率。
解:(1)%7.4105.106.105.103.14=-⨯⨯⨯=x (2)%4.12005.106.105.103.1=⨯⨯⨯=甲p k%8.23518.130.122.126.1=⨯⨯⨯=乙p k %7.12095.005.112.108.1=⨯⨯⨯=丙p k%1.141%7.120800%8.235700%4.12085080070085011111=++++==∑∑qp k q p K pp(3)%5.12019502350700600650800700850011==++++==∑∑pq p q K qp%4.85%1.141%5.120===ppq q K K K销售量增长率为-14.6% 第六章1、某工厂有1500名职工,用重复抽样方法从中随机抽取50名职工作为样要求:①计算样本平均数和抽样平均误差;②以95.45%的可靠性估计该厂职工的月平均工资的区间。
解: (1)(元)961f xf x ==∑∑ 元)(5.95f f )x -x (2==∑∑s5.135096.52==≈n s x μ (2)元)(275.132x =⨯==∆μt xx x x X x ∆+≤≤∆-∴ 988934≤≤X2、某家电视台为了解某项广告节目的收视率,在该地区随机电话抽样调查500户城乡居民户作为样本,调查结果是:有160户居民户收看该广告节目。
试以99.73%的概率保证程度,推断该地区收视率的可能范围。
解:p=160/500=32%%09.2500%)321(%32)1(p =-⨯=-=n p p μ %27.6%09.23t p p =⨯==∆μ因此在99.73%的概率保证程度下,该地区收视率为 [25.73%,38.27%]3、某企业为调查其生产的一批机械零件合格率。
根据过去的资料,该企业这类机械零件合格率曾有过99%、97%和95%,现要求抽样误差不超过1%,抽样估计的可靠程度为95%,问需要抽查多少个零件进行检测? 解:%1p =∆76.1824%195%)-(1%9596.1)p 1(p t n 222p 2=⨯⨯=∆-= 至少要抽取1825个零件。
4、某工厂生产一种新型灯泡5000只,随机抽取100只作耐用时间试验。
测得结果是:平均寿命为4500小时,标准差300小时,试以90%概率保证,估计该新式灯泡的平均寿命区间。
现采用重复抽样方法,若概率保证程度提高到95%,允许抽样误差缩小一半,问应抽取多少只灯泡进行测试? 解:7.29)50001001(100300)N n 1(=-=-≈n s x μ小时)(85.487.29645.1x =⨯==∆μt x在90%概率保证程度下,平均寿命的置信区间为:[4500-48.85,4500+48.85]小时5.579425.2430096.1t n 2222x 22=⨯=∆=s 因此要抽取580个灯泡。
第七章1、某企业某种产品产量与单位成本资料如下:要求:①计算相关系数,建立单位成本倚产量的直线回归方程,并解释斜率的经济含义。
②如果产量为6千件时单位成本为多少元? R=-0.909解 1)818.1)(22-=--=∑∑∑∑∑x x n x y yx n b364.57=-=x b y a回归直线方程为:x 818.1364.57y c-=斜率表示当产量每增加一千件,单位成本平均减少1.818元。
2)元456.646818.1364.57y c=⨯-=产量为6千件时单位成本为46.456元2、某市城市抽样调查队对该市居民进行调查,所得资料是:每户平均年收入为28000元,标准差为1000元,每户平均年消费支出为26500元,方差为640000,支出对于收入的回归系数b 为0.6。
要求:①计算收入与支出的相关系数; ②拟合支出对于收入的直线回归方程; ③估计收入在32000元时的消费支出额;解:1)75.080010006.0y x =⨯=⨯=σσb R2) 9700280006.026500=⨯-=-=x b y a回归直线方程为:x 6.09700y c+=3) 元28900200036.09700y c=⨯+=收入在32000元时的消费支出额为28900元3、已知x 、y 两变量的相关系数r =0.8,x =20,y =50,yσ为x σ的两倍,求y倚x 的直线回归方程。
解:1)6.128.0xy=⨯=⨯=σσr b 2)18206.150=⨯-=-=x b y a回归直线方程为:x 6.118y c+=5、设y 为因变量,x 自变量,已知89xy =∑,40x =∑,10y =∑,396x2=∑,22y 2=∑,共有5组数据。
