统计学计算题和答案精编版
统计学计算题例题(含答案)
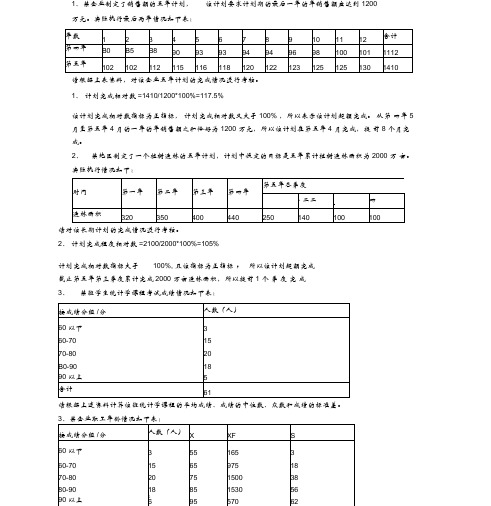
1、某企业制定了销售额的五年计划, 该计划要求计划期的最后一年的年销售额应达到 1200万元。
实际执行最后两年情况如下表:请根据上表资料,对该企业五年计划的完成情况进行考核。
1、 计划完成相对数 =1410/1200*100%=117.5%该计划完成相对数指标为正指标, 计划完成相对数又大于 100% ,所以表示该计划超额完成。
从第 四年 5 月至第五年 4 月的一年的年销售额之和恰好为 1200 万元,所以该计划在第五年 4 月完成,提 前 8 个月完成。
2、 某地区制定了一个植树造林的五年计划,计划中设定的目标是五年累计植树造林面积为 2000 万 亩。
实际执行情况如下:请对该长期计划的完成情况进行考核。
2、 计划完成程度相对数 =2100/2000*100%=105%计划完成相对数指标大于100%, 且该指标为正指标 , 所以该计划超额完成截止第五年第三季度累计完成 2000 万亩造林面积,所以提前 1 个 季 度 完 成3、某班学生统计学课程考试成绩情况如下表:请根据上述资料计算该班统计学课程的平均成绩、成绩的中位数、众数和成绩的标准差。
3、某企业职工年龄情况如下表:X 二三于=4740/62=76.45 (分)Me=70+ (62/2-18) *10/20=76.5 (分)Mo=70+(20 J5)70/[(2CM5)+(2CM8)]=77 」4 (分)G-7(55-76.45f *3 +⋯⋯+ (95^76.45f *6/62=10.45 (分)4、某学校有5000 名学生,现从中按重复抽样方法抽取250 名同学,调查其每周观看电视的小时数的情况,获得资料如下表:请根据上述资料,以95% 的概率保证程度对全校学生每周平均收看电视时间进行区间估计。
4> 样本平均数X= Sxf/Sf-l250/250-5样 ______________ __________二>/ 刀(好予f/(工f—1 )二V 1136/249 二2. 14抽样平均误差U 二s/ Vn=0.14因为 F (t) =95%, 所以日.96抽样极限误差△ 二t U 二 1. 96*0. 14=0. 27 区间下限=5-0. 27=4. 73 区间上限二5+0. 27-5. 27全校学生每周平均收看电视的吋间在( 4.73,5.27) 小时之间,概率保证程度为95%5 、某企业对全自动生产线上的产品随机抽取1000 件进行检验,发现有45 件是不合格的,设定允许的极限误差为1.32% 。
《统计学原理》计算题及答案

《统计学原理》计算题及答案第四章1、某生产车间30名工人日加工零件数(件)如下:30 26 42 41 36 44 40 37 37 25 45 29 43 31 36 36 49 34 47 33 43 38 42 32 34 38 46 43 39 35要求:(1)根据以上资料分成如下几组:25-30,30-35,35-40,40-45,45-50, 计算出各组的频数和频率,整理编制次数分布表。
(2)根据整理表计算工人生产该零件的平均日产量。
答 案:(1)40名工人日加工零件数次数分布表为:(6分)(2)平均日产量17.3830==∑=f x (件) (4分) 2、某班40名学生统计学考试成绩分别为:57 89 49 84 86 87 75 73 72 68 75 82 97 81 67 81 54 79 87 95 76 71 60 90 65 76 72 70 86 85 89 89 64 57 83 81 78 87 72 61学校规定:60分以下为不及格,60─70分为及格,70─80分为中, 80─90分为良,90─100分为优。
要求:(1)将该班学生分为不及格、及格、中、良、优五组,编制一张次数分配表。
(2)指出分组标志及类型;分组方法的类型;分析该班学生考试情况。
答 案:(1)40名学生成绩的统计分布表:(6分)2)分组标志为“成绩”,其类型是数量标志。
(1分)分组方法是变量分组中的组距分组,而且是开口式分组。
(1分)该班学生的考试成绩的分布呈两头小,中间大的“正态分布”形态。
(2分)3、 某厂三个车间一季度生产情况如下:根据以上资料计算:(1)一季度三个车间产量平均计划完成百分比。
(2)一季度三个车间平均单位产品成本。
答 案 产量平均计划完成百分比%81.10172073310.122005.13159.0198220315198==++++==∑∑x m m (5分) 平均单位成本75.1022031519822083151019815=++⨯+⨯+⨯==∑∑f xf (元/件) (5分)4、 某自行车公司下属20个企业,1999年甲种车的单位成本分组资料如下:试计算该公司1999年甲种自行车的平均单位成本。
统计学考试题及答案

统计学考试题及答案一、选择题(每题2分,共20分)1. 以下哪个不是描述性统计的范畴?A. 均值B. 中位数C. 众数D. 回归分析2. 标准差是衡量数据的:A. 集中趋势B. 离散程度C. 偏态D. 峰态3. 在正态分布中,数据的分布形态是:A. 双峰B. 单峰C. U形D. 无规律4. 以下哪个是参数估计的目的?A. 描述总体B. 描述样本C. 估计总体参数D. 进行假设检验5. 假设检验中的零假设(H0)通常表示:A. 研究者希望证明的效应B. 没有效应或效应为零C. 效应显著D. 效应不显著二、简答题(每题10分,共30分)6. 简述中心极限定理的内容及其在实际应用中的意义。
7. 解释什么是置信区间,并说明其在统计推断中的作用。
8. 描述什么是相关系数,并解释其在数据分析中的重要性。
三、计算题(每题25分,共50分)9. 给定一组数据:3, 5, 7, 9, 11, 13, 15, 17, 19, 21。
请计算: - 均值- 中位数- 众数- 方差- 标准差10. 假设某产品的质量控制数据服从正态分布,平均重量为100克,标准差为5克。
如果从这批产品中随机抽取100个样本,计算样本均值在95%置信水平下的置信区间。
统计学考试答案一、选择题1. D(回归分析属于推断统计)2. B(标准差是衡量数据离散程度的指标)3. B(正态分布是单峰分布)4. C(参数估计的目的是估计总体参数)5. B(零假设通常表示没有效应或效应为零)二、简答题6. 中心极限定理指出,大量独立同分布的随机变量之和在次数趋于无穷大时趋于正态分布,无论原始分布是什么。
这一定理在抽样调查、质量控制等领域有广泛应用。
7. 置信区间是用于估计总体参数的一个区间范围,它表示在多次抽样的情况下,有特定比例(如95%)的样本统计量会落在这个区间内。
它在统计推断中帮助我们对总体参数进行估计。
8. 相关系数是度量两个变量之间线性关系强度和方向的统计指标。
(完整版)统计学题库及题库答案

统计学题库及题库答案 题库1一、单项选择题(每题2分,共20分) 1、调查时间是指( )A 、调查资料所属的时间B 、进行调查的时间C 、调查工作的期限D 、调查资料报送的时间 2、对某城市工业企业未安装设备进行普查,总体单位是( )。
A 、工业企业全部未安装设备 B 、企业每一台未安装设备 C 、每个工业企业的未安装设备 D 、每一个工业企业3、对比分析不同性质的变量数列之间的变异程度时,应使用( )。
A 、全距B 、平均差C 、标准差D 、变异系数4、在简单随机重复抽样条件下,若要求允许误差为原来的2/3,则样本容量( )A 、扩大为原来的3倍B 、扩大为原来的2/3倍C 、扩大为原来的4/9倍D 、扩大为原来的2.25倍5、某地区组织职工家庭生活抽样调查,已知职工家庭平均每月每人生活费收入的标准差为12元,要求抽样调查的可靠程度为0.9545,极限误差为1元,在简单重复抽样条件下,应抽选( )。
A 、576户B 、144户C 、100户D 、288户 6、当一组数据属于左偏分布时,则( )A 、平均数、中位数与众数是合而为一的B 、众数在左边、平均数在右边C 、众数的数值较小,平均数的数值较大D 、众数在右边、平均数在左边7、某连续变量数列,其末组组限为500以上,又知其邻组组中值为480,则末组的组中值为( )。
A 、520B 、 510C 、 500D 、4908、用组中值代表组内变量值的一般水平有一定的假定性,即( )A 、各组的次数必须相等B 、变量值在本组内的分布是均匀的C 、组中值能取整数D 、各组必须是封闭组 9、nX X X ,,,21 是来自总体),(2σμN 的样本,样本均值X 服从( )分布 A 、),(2σμN B.、)1,0(N C.、),(2σμn n N D 、),(2n N σμ10、测定变量之间相关密切程度的指标是( )A 、估计标准误B 、两个变量的协方差C 、相关系数D 、两个变量的标准差 二、多项选择题(每题2分,共10分)1、抽样推断中,样本容量的多少取决于( )。
统计学考试计算题答案统计学试题及答案

统计学考试计算题答案统计学试题及答案一、填空题(每空1分,共10分)1.从标志与统计指标的对应关系来看,标志通常与( )相同。
2.某连续变量数列,其首组为开口组,上限为80,又知其邻组的组中值为95,则首组的组中值为( )。
3.国民收入中消费额和积累额的比例为1:0.4,这是( )相对指标。
4.在+A的公式中,A称为( )。
5.峰度是指次数分布曲线项峰的( ),是次数分布的一个重要特征。
6.用水平法求平均发展速度本质上是求( )平均数。
7.按习惯做法,采用加权调和平均形式编制的物量指标指数,其计算公式实际上是( )综合指数公式的变形。
8.对一个确定的总体,抽选的样本可能个数与( )和( )有关。
9.用来反映回归直线代表性大小和因变量估计值准确程度的指标称( )。
二、是非题(每小题1分,共10分)1.统计史上,将国势学派和图表学派统称为社会经济统计学派。
2.统计总体与总体单位在任何条件下都存在变换关系统计学原理试题及答案统计学原理试题及答案。
3.学生按身高分组,适宜采用等距分组。
4.根据组距数列计算求得的算术平均数是一个近似值。
5.基尼系数的基本公式可转化为2(S1+S2+S3)。
6.对连续时点数列求序时平均数,应采用加权算术平均方法。
7.分段平均法的数学依据是Σ(Y-YC)2=最小值。
8.平均数、指数都有静态与动态之分。
9.在不重复抽样下,从总体N中抽取容量为n的样本,则所有可能的样本个数为Nn个10.根据每对____和y的等级计算结果ΣD2=0,说明____与y之间存在完全正相关。
三、单项选择题(每小题2分,共10分)1.在综合统计指标分析^p 的基础上,对社会总体的数量特征作出归纳、推断和预测的方法是A.大量观察法B.统计分组法C.综合指标法D.模型推断法2.对同一总体选择两个或两个以上的标志分别进行简单分组,形成A.复合分组B.层叠分组C.平行分组体系D.复合分组体系3.交替标志方差的最大值为A.1B.0.5C.0.25D.04.如果采用三项移动平均修匀时间数列,那么所得修匀数列比原数列首尾各少A.一项数值B.二项数值C.三项数值D.四项数值5.可变权数是指在一个指数数列中,各个指数的A.同度量因素是变动的B.基期是变动的C.指数化因数是变动的D.时期是变动的四、多项选择题(每小题2分,共10分)1.反映以经济指标为中心的三位一体的指标总体系包括A.社会统计指标体系B.专题统计指标体系C.基层统计指标体系D.经济统计指标体系E.科技统计指标体系2.典型调查A.是一次性调查B.是专门组织的调查C.是一种深入细致的调查D.调查单位是有意识地选取的E.可用采访法取得资料3.下列指标中属于总量指标的有A.月末商品库存额B.劳动生产率C.历年产值增加额D.年末固定资金额E.某市人口净增加数4.重复抽样的特点是A.各次抽选互不影响B.各次抽选相互影响C.每次抽选时,总体单位数逐渐减少D.每次抽选时,总体单位数始终不变E.各单位被抽中的机会在各次抽选中相等5.下列关系中,相关系数小于0的现象有A.产品产量与耗电量的关系B.单位成本与产品产量的关系C.商品价格与销售量的关系D.纳税额与收入的关系E.商品流通费用率与商品销售额的关系五、计算题(每小题10分,共60分)要求:(1)写出必要的计算公式和计算过程,否则,酌情扣分。
统计学计算例题包括答案.docx

计算题例题及答案:1、某校社会学专业同学统计课成绩如下表所示。
社会学专业同学统计课成绩表学号成绩学号成绩学号成绩101023761010377510105270 101024911010387010105388 101025871010397610105493 101026781010409010105562 101027851010417610105695 101028961010428610105795 101029871010439710105866 101030861010449310105982 101031901010459210106079 101032911010468210106176 101033801010478010106276 101034811010489010106368 101035801010498810106494 101036831010507710106583要求:( 1)对考试成绩按由低到高进行排序,求出众数、中位数和平均数。
(2)考成行适当分,制数分布表,并算累数和累率。
答案:(1)考成由低到高排序:62, 66, 68, 70, 70, 75,76, 76,76, 76, 76, 77, 78, 79,80, 80, 80, 81, 82, 82,83, 83,85, 86, 86, 87, 87, 88,88, 90, 90, 90, 91, 91,92, 93,93, 94, 95, 95, 96, 97,众数: 76中位数: 83平均数:=( 62+66+⋯⋯ +96+97 )÷42=3490÷42=83.095(2)按成向上累向下累数率 (%)分数率(%)数率(%) 60-6937.14337.14342100.000 70-791126.1901433.3333992.857 80-891535.7142969.0482866.66790-991330.95242100.0001330.9522、为研究某种商品的价格(x)对其销售量(y)的影响,收集了12个地区的有关数据。
统计学原理计算题及参考答案

3.某地区历年粮食产量如下:1、某生产车间30名工人日加工零件数(件)如下: 30 26 42 41 36 44 40 37 37 25 45 29 43 31 36 36 49 34 47 33 43 38 42 32 34 38 46 43 39 35 要求:(1)根据以上资料分成如下几组:25—30,30—35,35—40,40—45,45—50,计算各组的频数和频率,编制次数分布表;(2) 根据整理表计算工人平均日产零件数。
(20分)解:(1)根据以上资料编制次数分布表如下:则工人平均劳动生产率为:17.38301145===∑∑fxf x(2)当产量为10000件时,预测单位成本为多少元?(15分)xbx a y n x b n y a x x n y x xy n b c 5.2808010703125.232105.26151441502520250512503210128353)(222-=+==+=⨯+=-=-=-=--=-⨯⨯-⨯=--=∑∑∑∑∑∑∑因为,5.2-=b ,所以产量每增加1000件时,即x 增加1单位时,单位成本的平均变动是:平均减少2.5元 (2)当产量为10000件时,即10=x 时,单位成本为55105.280=⨯-=c y 元>课程的测试,甲班平均成绩为81分,标准差为9.5分;乙班的成绩分组资料如下:计算乙班学生的平均成绩,并比较甲.乙两班哪个班的平均成绩更有代表性?解:乙班学生的平均成绩∑∑=f xf x ,所需的计算数据见下表:75554125===∑∑fxf x (比较甲.乙两班哪个班的平均成绩更有代表性,要用变异系数σν的大小比较。
)甲班%73.11815.9===xσνσ 从计算结果知道,甲班的变异系数σν小,所以甲班的平均成绩更有代表性。
%65.207549.1549.152405513200)(2======-=∑∑x ffx x σνσσ计算(1)产品产量总指数及由于产量增长而增加的总成本.(2)总成本指数及总成本增减绝对额. 解;(1)产品产量总指数为: %42.1112102342106351120605010060%10550%102100%12000==++=++⨯+⨯+⨯=∑∑qp qkp 由于产量增长而增加的总成本:∑∑=-=-242102340000qp q kp(2)总成本指数为:%62.10721022660501006046120011==++++=∑∑qp qp总成本增减绝对额:∑∑=-=-16210226011qp q p计算第二季度平均每月商品流转次数和第二季度商品流转次数. 解:商品流转次数c=商品销售额a/库存额bba c =商品销售额构成的是时期数列,所以67.23837163276240200==++==∑na a 库存额b 构成的是间隔相等的时点数列,所以33.533160327545552453224321==+++=+++=b b b b b 第二季度平均每月商品流转次数475.433.5367.238===ba c 第二季度商品流转次数3*4.475=13.425解:甲市场的平均价格为:04.123270033220027001507001080007350011009007001100137900120700105==++=++⨯+⨯+⨯==∑∑fxf x乙市场的平均价格为74.1172700317900700800120031790013795900120960001051260009590096000126000==++=++++==∑∑xM M x。
统计学专业试题及答案

统计学专业试题及答案一、选择题(每题2分,共20分)1. 以下哪项不是描述性统计学的主要任务?A. 数据收集B. 数据整理C. 数据分析D. 数据预测答案:D2. 以下哪个不是常用的统计图表?A. 条形图B. 饼图C. 散点图D. 流程图答案:D3. 在统计学中,以下哪个概念表示数据的离散程度?A. 平均数B. 中位数C. 方差D. 众数答案:C4. 以下哪个分布是正态分布?A. 泊松分布B. 均匀分布C. 指数分布D. 高斯分布答案:D5. 以下哪个概念用于描述数据的集中趋势?A. 方差B. 标准差C. 均值D. 偏度答案:C6. 以下哪个是参数估计的方法?A. 点估计B. 区间估计C. 均值检验D. 方差分析答案:A7. 以下哪个是假设检验的步骤?A. 建立假设B. 收集数据C. 计算检验统计量D. 所有选项答案:D8. 以下哪个是回归分析的基本假设?A. 线性关系B. 独立性C. 同方差性D. 所有选项答案:D9. 以下哪个是时间序列分析的特点?A. 数据具有时间顺序B. 数据具有随机性C. 数据具有周期性D. 所有选项答案:D10. 以下哪个是生存分析的应用领域?A. 医学研究B. 工程领域C. 金融领域D. 所有选项答案:A二、简答题(每题10分,共30分)1. 解释什么是中心极限定理,并说明其在实际统计分析中的重要性。
答案:中心极限定理是统计学中的一个基本定理,它指出,如果从具有相同均值和方差的总体中独立地抽取足够大的样本,那么这些样本的均值的分布将趋近于正态分布,无论原始总体的分布是什么。
这个定理在实际统计分析中非常重要,因为它允许我们使用正态分布的性质来近似任何总体的样本均值分布,从而简化了许多统计推断过程。
2. 描述什么是抽样分布,并举例说明。
答案:抽样分布是指从一个总体中抽取多个样本时,样本统计量(如样本均值、样本方差等)的分布。
例如,如果我们从一个总体中抽取多个样本,每个样本大小为n,那么这些样本均值的分布就构成了样本均值的抽样分布。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
统计学计算题和答案 GE GROUP system office room 【GEIHUA16H-GEIHUA GEIHUA8Q8-
三个企业生产的同一型号空调在甲、乙两个专卖店销售,有关资料如下:
企业型号价格(元/
台)
甲专卖店销售额
(万元)
乙专卖店销售量
(台)
A250050.0340
B3400115.6260
C4100106.6200
合计—272.2—
要求:分别计算两个专卖店空调的平均销售价格,并分析平均价格差异的原因。
答案:
2某企业甲、乙两个生产车间,甲车间平均每个工人日加工零件数为65件,标准差为11件;乙车间工人日加工零件数资料如下表。
试计算乙车间工人加工零件的平均数和标准差,并比较甲、乙两个生产车间哪个车间的平均日加工零件数更有代表性?
60以下60—7070—8080—9090—100日加工零件数
(件)
工人数(人)59121410
答案:
三、某地区2009—2014年GDP资料如下表,要求:
1、计算2009—2014年GDP的年平均增长量;
2、计算2009—2014年GDP的年平均发展水平;
3、计算2009—2014年GDP的年平均发展速度和平均增长速度。
年份200920102011201220132014
87431062711653147941580818362
GDP(亿
元)
答案:
年平均增长速度:100%100%22.9%
x-==
四,某百货公司2010—2014年的商品销售额资料如下:
试用最小平方法配合销售额的直线趋势方程,并预测2016年的销售额将达到什么水平?
答案: 2010年—2014年的数据有5项,是奇数,所以取中间为0,以1递增。
设定x为-2、-1、0、1、2、
年份/销售额(y) x xy x2
2010 320 -2 -640 4
2011 332 -1 -332 1
2012 340 0 0 0
2013 356 1 356 1
2014 380 2 760 4
合计 1728 0 144 10
b=∑xy/∑x2=144/10=14.4
a=∑y/n=1728/5=345.6
y=345.6+14.4x
预测2016年,按照设定的方法,到2016年应该是5
y=345.6+14.4*5=417.6元
五、某企业生产三种产品,2013年三种产品的总生产成本分别为20万元,45万元,35万元,2014年同2013年相比,三种产品的总生产成本分别增长8%,10%,6%,产量分别增长12%,6%,4%。
试计算:
1、三种产品的总生产成本增长的百分比及增加的绝对额;
2、三种产品的总产量增长的百分比,及由于产量增长而增加的总生产成本;
3、利用指数体系推算单位产品成本增长的百分比。
六、某商店三种商品的销售资料如下:
试计算:
1、三种商品的销售额总指数;
2、三种商品的价格总指数和销售量总指数;
3、分析销售量和价格变动对销售额的影响程度和影响绝对额。
答案:总指数:(36*2+160*2.2+100*1.6)/(30*1.8+140*1.9+100*1.5)=124.3%
:
2.某企业生产一种新的电子元件,用简单随机重复抽样方法抽取100只作耐用时间试验,测试结果,平均寿命6000小时,标准差300小时,试在95.45%的概率保证程度下,估计这种新电子元件的平均寿命区间。
假定概率保证程度提高到99.73%,允许误差缩小一半,试问应抽取多少只灯泡进行测试?
解:⑴ 6000x = 300σ= 100n =
30100
x n μ===(小时) ()95.45%F t = ∴2t =
23060x x t μ∆=⋅=⨯=(小时)
∴在95.45%的概率保证程度下,估计这种新电子元件的平均寿命区间在5940~6060小时之间
⑵ 160302
x ∆=⨯= ∴222222330030030x t n σ⨯===∆ 4.某工厂有1500个工人,用简单随机重复抽样的方法抽出50个工人作为样本,调查其月平均产量水平,得每人平均产量560件,标准差32.45
要求:(1)计算抽样平均误差(重复与不重复);
(2)以95%的概率(z=1.96)估计该厂工人的月平均产量的区间;
(3)以同样的概率估计该厂工人总产量的区间。
解: (1)
重复抽样: 59.45045.32===n x σ
μ
不重复抽样:=-=-=)1500
501(5045..32)1(22N n n x σμ (2)抽样极限误差x x z μ=∆ = 1.96×4.59 =9件
月平均产量的区间: 下限:-x △x =560-9=551件
上限:+x △x =560+9=569件
(3)总产量的区间:(551×1500 826500件; 569×1500 853500件)
5.采用简单随机重复抽样的方法,在2000件产品中抽查200件,其中合格品190件.
要求:(1)计算合格品率及其抽样平均误差
(2)以95.45%的概率保证程度(z=2)对合格品率和合格品数量进行区间估计。
(3)如果极限误差为2.31%,则其概率保证程度是多少
解:(1)样本合格率
p = n
1
/n = 190/200 = 95%
抽样平均误差
n p
p p
) 1(-
=
μ = 1.54%
(2)抽样极限误差Δ
p =zμ
p
= 2×1.54% = 3.08%
下限:-
x△p=95%-3.08% = 91.92%
上限:+
x△p=95%+3.08% = 98.08%
则:总体合格品率区间:(91.92% 98.08%)
总体合格品数量区间(91.92%×2000=1838件 98.08%×2000=1962件)
(3)当极限误差为2.31%时,则概率保证程度为86.64% (z=Δ/μ)。
