高中数学 名校学案 一课一练 人教版 《数学选修2-1》(第一章)_20
高中数学 名校学案 一课一练 人教版 《数学选修2-3》(第一章)_2
高中课标教材同步导学丛书2 ①从三个班中选一名学生会主席,有多少种不同的选法?②从(1)班㊁(2)班男生中和(3)班女生中选一名学生任学生会生活部部长,有多少种不同的选法?ʌ互动探究ɔ将题(1)中的x ,y 所满足的不等式改为不等式组2x -y ȡ0,x +y ɤ6,{则满足条件的点M (x ,y )共有多少个?ʌ规律方法ɔ用分类加法计数原理解题的一般思路分步乘法计数原理的应用ʌ典例2ɔ(1)从正方体六个面的对角线中任取两条作为一对,其中所成的角为60ʎ的共有( )(A )24对(B )30对(C )48对(D )60对(2)-2,-1,0,1,2,3这六个数字中任选3个不重复的数字作为二次函数y =a x 2+b x +c 的系数a ,b ,c,则可以组成抛物线的条数为多少.ʌ规律方法ɔ利用分步乘法计数原理解题的一般思路1.某小组有8名男生,6名女生,要从中选出一名当组长,不同的选法有( )(A )48种 (B )24种 (C )14种 (D )12种2.5本不同的语文书,4本不同的数学书,每种各取一本,不同的选法有( )(A )3种(B )9种(C )12种(D )20种3.从A 地到B 地要经过C 地和D 地,从A 地到C 地有3条路,从C 地到D 地有2条路,从D 地到B 地有4条路,则从A 地到B 地不同的走法有( )(A )3+2+4=9种(B )1种(C )3ˑ2ˑ4=24种(D )1+1+1=3种4.加工某个零件分三道工序,第一道工序有5人,第二道工序有6人,第三道工序有4人,从中选3人每人做一道工序,则选法有种.5.要安排一份5天的值班表,每天有一个人值班,共有5个人,每个人可以值多天班或不值班,但相邻两天不准由同一个人值班,此值班表共有多少种不同排法?课后巩固作业(一)一课一练,日积月累,厉兵秣马,稳固提能。
名校新学案高中数学人教A版选修2-1课后作业1.1.2四种命题及其相互关系(含答案详析)

第一章 1.1第2课时一、选择题1.命题“若p则q”的逆命题是()A.若q则p B.若¬p则¬qC.若¬q则¬p D.若p则¬q[答案] A[解析]本题考查四种命题,由逆命题定义,命题“若p则q”的逆命题为“若q则p”,选A.2.给出命题:若函数y=f(x)是幂函数,则它的图象不过第四象限,在它的逆命题、否命题、逆否命题三个命题中,真命题的个数是()A.3 B.2C.1 D.0[答案] C[解析]原命题是真命题,因为幂函数的图象不过第四象限,反过来,图象不过第四象限的函数不一定是幂函数,所以逆命题为假命题,根据等价命题的真假性相同可知,否命题为假命题,逆否命题为真命题,故选C.3.“若x2=1,则x=1”的否命题为()A.若x2≠1,则x=1 B.若x2=1,则x≠1C.若x2≠1,则x≠1 D.若x≠1,则x2≠1[答案] C[解析]“若p则q”的否命题形式为“若¬p则¬q”.4.命题“如果a、b都是奇数,则ab必为奇数”的逆否命题是()A.如果ab是奇数,则a、b都是奇数B.如果ab不是奇数,则a、b不都是奇数C.如果a、b都是奇数,则ab不是奇数D.如果a、b不都是奇数,则ab不是奇数[答案] B[解析]命题“如果a、b都是奇数,则ab必为奇数”的逆否命题是“如果ab不是奇数,则a、b不都是奇数”.5.“a2+b2≠0”的含义是()A.a、b不全为0B.a、b全不为0C.a、b至少有一个为0D.a不为0且b为0,或b不为0且a为0[答案] A[解析]若a2+b2≠0,则a≠0且b≠0,或a=0且b≠0,或a≠0且b=0,即a,b不全为0,故选A.6.原命题:“设a,b,c∈R,若a>b,则ac2>bc2”以及它的逆命题、否命题、逆否命题中,真命题共有()A.0个B.1个C.2个D.4个[答案] C[解析]当c=0时,c2=0,故原命题是假命题;若ac2>bc2,则必有c2≠0,∴c2>0,∴a>b,故逆命题为真命题,∴否命题为真,逆否命题为假,故选C.二、填空题7.“若a∈A,则a∈B”的逆否命题为________.[答案]若a∉B,则a∉A.8.给出下列命题:(1)平行四边形的对角线互相平分;(2)对角线互相平分的四边形是平行四边形;(3)若一个四边形不是平行四边形,则这个四边形的对角线不能互相平分;(4)若一个四边形的对角线不能互相平分,则这个四边形不是平行四边形.①若(1)为原命题,则(2)为(1)的________命题,(3)为(1)的________命题,(4)为(1)的________命题.②若(4)为原命题,则(1)为(4)的________命题,(2)为(4)的________命题,(3)为(4)的________命题.[答案]①逆否逆否②逆否否逆三、解答题9.设原命题为“已知a、b是实数,若a+b是无理数,则a、b都是无理数”.写出它的逆命题、否命题和逆否命题,并分别说明他们的真假.[解析]逆命题:已知a、b为实数,若a、b都是无理数,则a+b是无理数.如a=2,b=-2,a+b=0为有理数,故为假命题.否命题:已知a、b是实数,若a+b不是无理数,则a、b不都是无理数.由逆命题为假知,否命题为假.逆否命题:已知a、b是实数,若a、b不都是无理数,则a+b不是无理数.如a=2,b=2,则a+b=2+2是无理数,故逆否命题为假.10.判断命题“已知a,x为实数,如果关于x的不等式x2+(2a+1)x+a2+2≤0的解集非空,则a≥1”的逆否命题的真假.[分析]直接由原命题写出其逆否命题,然后判断逆否命题的真假.[解析]逆否命题:已知a,x为实数,如果a<1,则关于x的不等式x2+(2a+1)x+a2+2≤0的解集为空集,真命题.判断如下:抛物线y=x2+(2a+1)x+a2+2开口向上,判别式Δ=(2a+1)2-4(a2+2)=4a-7.∵a<1,∴4a-7<0,即抛物线y=x2+(2a+1)x+a2+2与x轴无交点,∴关于x的不等式x2+(2a+1)x+a2+2≤0的解集为空集,故逆否命题为真.一、选择题11.命题“若A∪B=A,则A∩B=B”的否命题是()A.若A∪B≠A,则A∩B≠B B.若A∩B=B,则A∪B=AC.若A∩B≠B,则A∪B≠A D.若A∪B≠A,则A∩B=B[答案] A[解析]否命题对命题的条件和结论都否定.12.已知命题“非空集合M中的元素都是集合P中的元素”是假命题,那么下列命题中真命题的个数为()①M中的元素都不是P的元素;②M中有不属于P的元素;③M中有属于P的元素;④M中的元素不都是P的元素.A.1 B.2C .3D .4[答案] B[解析] 由于“M ⊆P ”为假命题,故M 中至少有一个元素不属于P ,∴②④正确.M 中可能有属于P 的元素,也可能都不是P 的元素,故①③错误,选B.13.若命题p 的否命题为r ,命题r 的逆命题为s ,p 的逆命题为t ,则s 是t 的( ) A .逆否命题 B .逆命题 C .否命题 D .原命题[答案] C[解析] 特例:△ABC 中,角A 、B 、C 的对边分别为a 、b 、c . p :若∠A =∠B ,则a =b , r :若∠A ≠∠B ,则a ≠b , s :若a ≠b ,则∠A ≠∠B ,t :若a =b ,则∠A =∠B .故s 是t 的否命题.14.已知命题p :“若a >b >0,则log 12a <log 12b +1”,则命题p 及它的逆命题、否命题、逆否命题中正确命题的个数为( )A .0B .1C .2D .4 [答案] C[解析] 对于命题p ,当a >b >0时,有log 12a <log 12b ,则必有log 12a <log 12b +1,因此原命题正确,逆否命题也正确;但当log 12a <log 12b +1时,得log 12a <log 12b 2,即a >b2>0,此时不一定有a >b >0,因此逆命题不正确,则命题p 的否命题也不正确.因此一共有2个正确命题,故选C.二、填空题15.原命题:在空间中,若四点不共面,则这四个点中任何三点都不共线,其逆命题为________(真、假).[答案] 假[解析] 逆命题为:在空间中,若四个点中任何三点不共线,则这四点不共面,假命题.如:正方形ABCD 的四个顶点,任意三点不共线,但这四点共面.16.(2013·江西省临川一中月考)命题“若实数a满足a≤2,则a2<4”的否命题是________命题.(填“真”或“假”)[答案]真[解析]原命题的否命题为:若实数a满足a>2,则a2≥4,这是一个真命题.[点评]注意a2≥4的含义是a2>4或a2=4.三、解答题17.写出下列命题的逆命题、否命题、逆否命题,并分别判断其真假.(1)如果两圆外切,那么两圆心距等于两圆半径之和;(2)平面内,两条平行直线不相交.[解析](1)逆命题:如果两圆心距等于两圆半径之和,那么两圆外切,真;否命题:如果两圆不外切,那么两圆心距不等于两圆半径之和,真;逆否命题:如果两圆心距不等于两圆半径之和,那么两圆不外切,真.(2)原命题:在同一平面内,若两条直线是平行直线,则它们不相交;逆命题:在同一平面内,若两条直线不相交,则它们平行;否命题:在同一平面内,若两条直线不是平行直线,则它们相交;逆否命题:在同一平面内,若两条直线相交,则它们不平行.18.已知a,b∈R,且a2-4b>0.写出命题“若a+b+1<0,则方程x2+ax+b=0的两个实根满足x1<1<x2”的逆命题、否命题、逆否命题,并判断它们的真假.[解析]逆命题:已知a,b∈R,且a2-4b>0,若方程x2+ax+b=0的两根满足x1<1<x2,则a+b+1<0.否命题:已知a,b∈R,且a2-4b>0,若a+b+1≥0,则方程x2+ax+b=0的两个实根不满足x1<1<x2.逆否命题:已知a,b∈R,且a2-4b>0,若x2+ax+b=0的两个实根不满足x1<1<x2,则a+b+1≥0.下面对真假进行判断:(1)令f(x)=x2+ax+b.∵f(1)=a+b+1<0,f(x)的图象为开口向上的抛物线,∴x2+ax+b=0的两个实根满足x1<1<x2,故原命题为真命题.(2)∵方程x2+ax+b=0的两实根满足x1<1<x2,∴(x1-1)(x2-1)<0,x1+x2=-a,x1x2=b,∴a+b+1<0,故逆命题为真命题.由四种命题的关系可知,否命题和逆命题都是真命题.。
高中数学 名校学案 一课一练 人教版 《数学选修2-3》(第一章)_5
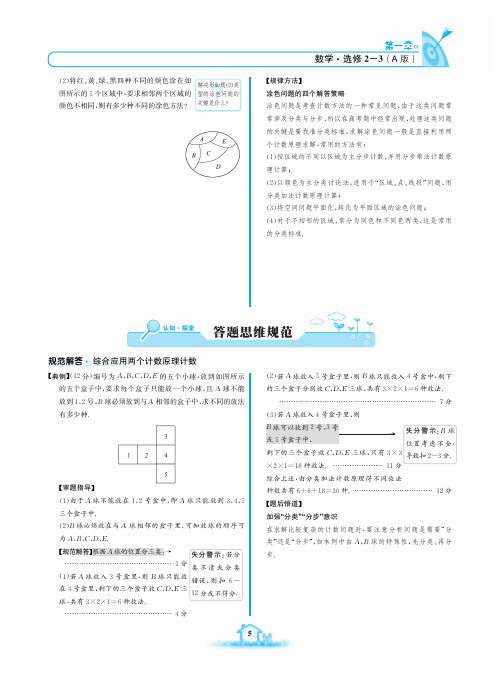
第一章数学㊃选修2-3(A 版)5解决形如题(2)类型的涂色问题的关键是什么?(2)将红㊁黄㊁绿㊁黑四种不同的颜色涂在如图所示的5个区域中,要求相邻两个区域的颜色不相同,则有多少种不同的涂色方法?ʌ规律方法ɔ涂色问题的四个解答策略涂色问题是考查计数方法的一种常见问题,由于这类问题常常涉及分类与分步,所以在高考题中经常出现,处理这类问题的关键是要找准分类标准,求解涂色问题一般是直接利用两个计数原理求解,常用的方法有:(1)按区域的不同以区域为主分步计数,并用分步乘法计数原理计算;(2)以颜色为主分类讨论法,适用于 区域㊁点㊁线段 问题,用分类加法计数原理计算;(3)将空间问题平面化,转化为平面区域的涂色问题;(4)对于不相邻的区域,常分为同色和不同色两类,这是常用的分类标准.规范解答综合应用两个计数原理计数ʌ典例ɔ(12分)编号为A ,B ,C ,D ,E 的五个小球,放到如图所示的五个盒子中,要求每个盒子只能放一个小球,且A 球不能放到1,2号,B 球必须放到与A 相邻的盒子中,求不同的放法有多少种.ʌ审题指导ɔ(1)由于A 球不能放在1,2号盒中,即A 球只能放到3,4,5三个盒子中.(2)B 球必须放在与A 球相邻的盒子里,可知放球的顺序可为A ,B ,C ,D ,E .失分警示:若分类不清或分类错误,则扣6~12分或不得分.ʌ规范解答ɔ根据A 球的位置分三类:ң1分………………………………………(1)若A 球放入3号盒里,则B 球只能放在4号盒里,剩下的三个盒子放C ,D ,E 三球,共有3ˑ2ˑ1=6种放法.4分………………………………………(2)若A 球放入5号盒子里,则B 球只能放入4号盒中,剩下的三个盒子分别放C ,D ,E 三球,共有3ˑ2ˑ1=6种放法.7分…………………………………………………………()若A 球放入号盒子里,则失分警示:B 球位置考虑不全,导致扣2~3分.剩下的三个盒子放C ,D ,E 三球,只有3ˑ3ˑ2ˑ1=18种放法.11分…………………综合上述,由分类加法计数原理得不同放法种数共有6+6+18=30种.12分……………………………ʌ题后悟道ɔ加强 分类 分步 意识在求解比较复杂的计数问题时,要注意分析问题是需要 分类 还是 分步 ,如本例中由A ,B 球的特殊性,先分类㊁再分步.。
2020版数学人教B版选修2-1学案:第一章 章末复习 Word版含解析

章末复习学习目标 1.理解全称量词、存在量词的含义,会判断全称命题、存在性命题的真假,会求含有一个量词的命题的否定.2.理解逻辑联结词的含义,会判断含有逻辑联结词的命题的真假.3.理解充分条件、必要条件的概念,掌握充分条件、必要条件的判定方法.4.理解命题及四种命题的概念,掌握四种命题间的相互关系.1.全称量词与存在量词(1)常见的全称量词有:“任意一个”“一切”“每一个”“任合”“所有的”等.(2)常见的存在量词有:“存在一个”“至少有一个”“有些”“有一个”“某个”“有的”等.(3)全称量词用符号“∀”表示;存在量词用符号“∃”表示.2.简单的逻辑联结词(1)命题中的“且”“或”“非”叫做逻辑联结词.(2)简单复合命题的真值表p q p∧q p∨q綈p真真真真假假真假真真真假假真假假假假假真3.全称命题与存在性命题(1)含有全称量词的命题叫全称命题.(2)含有存在量词的命题叫存在性命题.4.命题的否定(1)全称命题的否定是存在性命题;存在性命题的否定是全称命题.(2)p或q的否定为:非p且非q;p且q的否定为:非p或非q.5.充分条件、必要条件与充要条件(1)如果p⇒q,则p是q的充分条件,q是p的必要条件;(2)如果p⇒q,q⇒p,则p是q的充要条件.6.四种命题及其关系(1)四种命题①原命题:如果p,则q;②逆命题:如果q,则p;③否命题:如果綈p,则綈q;④逆否命题:如果綈q,则綈p.(2)四种命题间的关系(3)四种命题的真假关系①两个命题互为逆否命题,它们有相同的真假性;②两个命题互为逆命题或互为否命题,它们的真假性没有关系.1.命题“若x>0且y>0,则x+y>0”的否命题是假命题.( √ )2.“所有奇数都是质数”的否定“至少有一个奇数不是质数”是真命题.( √ ) 3.命题“若p,则q”与命题“若綈p,则綈q”的真假性一致.( × )4.已知命题p:∃x∈R,x-2>0,命题q:∀x∈R,x2>x,则命题p∨(綈q)是假命题.( × )题型一 命题及其关系例1 (1)有下列命题:①“若x+y>0,则x>0且y>0”的否命题;②“矩形的对角线相等”的否命题;③“若q≤1,则x2+2x+q=0有实根”的逆否命题;④“不等边三角形的三个内角相等”.其中是真命题的是( )A.①②③B.②③④C.①③④D.①③考点 四种命题的概念题点 判断四种命题的真假答案 D(2)设a,b,c是非零向量,已知命题p:若a·b=0,b·c=0,则a·c=0;命题q:若a∥b,b∥c,则a∥c.则下列命题中真命题是( )A.p∨q B.p∧qC.(綈p)∧(綈q) D.p∨(綈q)考点 四种命题的概念题点 四种命题定义的应用答案 A解析 由向量数量积的几何意义可知,命题p为假命题;命题q中,当b≠0时,a,c一定共线,故命题q是真命题.故p∨q为真命题.反思感悟 (1)互为逆否命题的两命题真假性相同.(2)“p 与綈p ”一真一假,“p ∨q ”一真即真,“p ∧q ”一假就假.跟踪训练1 (1)命题“若x 2>1,则x <-1或x >1”的逆否命题是( )A .若x 2>1,则-1≤x ≤1B .若-1≤x ≤1,则x 2≤1C .若-1<x <1,则x 2>1D .若x <-1或x >1,则x 2>1考点 四种命题的概念题点 四种命题定义的应用答案 B(2)已知命题p :4+2=5,命题q :3>2,则下列判断中错误的是( )A .p 或q 为真,非q 为假 B .p 或q 为真,非p 为真C .p 且q 为假,非p 为假D .p 且q 为假,p 或q 为真考点 “或”“且”“非”的综合问题题点 判断复合命题的真假答案 C解析 由p :4+2=5,可得p 是假命题,由q :3>2,可得命题q 是真命题,所以p 或q 为真,p 且q 为假,非p 为真,非q 为假,故选C.题型二 充分条件与必要条件、充要条件的探究例2 “m =”是“直线(m +2)x +3my +1=0与直线(m -2)x +(m +2)y -3=0相互垂直”12的( )A .充要条件 B .充分不必要条件C .必要不充分条件D .既不充分也不必要条件答案 B解析 当m =时,两条直线的斜率分别为-,,-×=-1,所以两条直线相互垂直;1253355335反之,若两条直线相互垂直,需分三种情况:①当m =-2时,两条直线的方程分别为-6y +1=0,-4x -3=0,显然两直线相互垂直;②当m ≠-2且m ≠0时,由-×=-1,解得m =;m +23m 2-m m +212③当m =0时,两条直线的方程分别为2x +1=0,-2x +2y -3=0,两直线不垂直.所以m =-2或.12故“m =”是“直线(m +2)x +3my +1=0与直线(m -2)x +(m +2)y -3=0相互垂直”的充分12不必要条件.反思感悟 若p ⇒q ,则p 是q 的充分条件,q 是p 的必要条件,即q 的充分条件是p ,p 的必要条件是q .如果将“必要条件”理解为“必然结果”,则可认为p 的必然结果是q ,q 是p 的必然结果.则p ⇏q 易表述为以下几种说法:p 是q 的不充分条件,q 的不充分条件是p ;q 是p 的不必要条件,p 的不必要条件是q .跟踪训练2 (1)已知命题p :对任意x ∈R ,总有2x >0;q :“x >1”是“x >2”的充分不必要条件,则下列命题为真命题的是( )A .p ∧q B .(綈p )∧(綈q )C .(綈p )∧q D .p ∧(綈q )答案 D解析 p :∀x ∈R,2x >0为真命题;q :∵x >1⇏x >2,∴“x>1”不是“x>2”的充分条件,又x>2⇒x>1,∴“x>1”是“x>2”的必要条件,∴q是假命题,∴綈q是真命题.∴p∧(綈q)为真命题.(2)“a=-1”是“函数f(x)=ax2+2x-1只有一个零点”的( )A.充要条件B.充分不必要条件C.必要不充分条件D.既不充分也不必要条件答案 B解析 ①∵a=-1⇒Δ=22-4a×(-1)=0⇒f(x)=ax2+2x-1只有一个零点,∴“a=-1”是“函数f(x)=ax2+2x-1只有一个零点”的充分条件.②f(x)=ax2+2x-1只有一个零点⇒a=-1或a=0⇏a=-1,∴“a=-1”不是“函数f(x)=ax2+2x-1只有一个零点”的必要条件.题型三 逻辑联结词与量词的综合应用例3 已知p:∃x∈R,mx2+2≤0.q:∀x∈R,x2-2mx+1>0,若p∨q为假命题,则实数m 的取值范围是( )A.[1,+∞) B.(-∞,-1]C.(-∞,-2] D.[-1,1]考点 简单逻辑联结词的综合应用题点 由含量词的复合命题的真假求参数的范围答案 A解析 因为p∨q为假命题,所以p和q都是假命题.由p:∃x∈R,mx2+2≤0为假,得∀x∈R,mx2+2>0,所以m≥0.①由q:∀x∈R,x2-2mx+1>0为假,得∃x∈R,x2-2mx+1≤0,所以Δ=(-2m)2-4≥0⇒m2≥1⇒m≤-1或m≥1.②由①和②得m≥1.反思感悟 解决此类问题首先理解逻辑联结词的含义,掌握简单命题与含有逻辑联结词的命题的真假关系.其次要善于利用等价关系,如:p真与綈p假等价,p假与綈p真等价,将问题转化,从而谋得最佳解决途径.跟踪训练3 已知m∈R,命题p:对任意x∈[0,1],不等式2x-2≥m2-3m恒成立;命题q:存在x∈[-1,1],使得m≤ax成立.(1)若p为真命题,求m的取值范围;(2)当a=1时,p且q为假命题,p或q为真命题,求m的取值范围.考点 简单逻辑联结词的综合应用题点 由含量词的复合命题的真假求参数的范围解 (1)对任意x∈[0,1],不等式2x-2≥m2-3m恒成立,令f(x)=2x-2(x∈[0,1]),则f(x)min≥m2-3m,当x∈[0,1]时,f(x)min=f(0)=-2,即m2-3m≤-2,解得1≤m≤2.因此,当p为真命题时,m的取值范围是[1,2].(2)当a=1时,若q为真命题,则存在x∈[-1,1],使得m≤x成立,所以m≤1.因此,当命题q为真时,m≤1.因为p且q为假命题,p或q为真命题,所以p ,q 中一个是真命题,一个是假命题.当p 真q 假时,由Error!得1<m ≤2;当p 假q 真时,由Error!得m <1.综上所述,m 的取值范围为(-∞,1)∪(1,2].1.设函数f (x )=x 2+mx (m ∈R ),则下列命题中的真命题是( )A .对任意m ∈R ,y =f (x )都是奇函数B .存在m ∈R ,使y =f (x )是奇函数C .对任意m ∈R ,y =f (x )都是偶函数D .存在m ∈R ,使y =f (x )是偶函数答案 D解析 存在m =0∈R ,使y =f (x )是偶函数,故选D.2.命题“如果α=,则tan α=1”的逆否命题是( )π4A .如果α≠,则tan α≠1π4B .如果α=,则tan α≠1π4C .如果tan α≠1,则α≠π4D .如果tan α≠1,则α=π4答案 C解析 命题“如果α=,则tan α=1”的逆否命题是“若tan α≠1,则α≠”,故选C.π4π43.已知α,β是两个不同的平面,直线a ⊂α,直线b ⊂β,p :a 与b 无公共点,q :α∥β,则p是q的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件答案 B解析 若α与β相交,设交线为c,若a∥c,b∥c,则a∥b,此时a与b无公共点,所以p⇏q;若α∥β,则a与b的位置关系是平行或异面,a与b无公共点,所以q⇒p.由此可知p是q 的必要不充分条件,故选B.4.已知命题p:若x>y,则-x<-y;命题q:若x>y,则x2>y2.在命题①p∧q;②p∨q;③p∧(綈q);④(綈p)∨q中,真命题是________.(填序号)答案 ②③解析 当x>y时,-x<-y,故命题p为真命题,从而綈p为假命题.当x>y时,x2>y2不一定成立,故命题q为假命题,从而綈q为真命题.由真值表知,①p∧q为假命题;②p∨q为真命题;③p∧(綈q)为真命题;④(綈p)∨q为假命题.5.分别写出由下列各组命题构成的“p或q”“p且q”“綈p”形式的复合命题,并判断它们的真假.(1)p:平行四边形的对角线相等,q:平行四边形的对角线互相平分;(2)p:方程x2-16=0的两个根的符号不同,q:方程x2-16=0的两个根的绝对值相等.考点 “或”“且”“非”的综合问题题点 判断复合命题的真假解 (1)p或q:平行四边形的对角线相等或平行四边形的对角线互相平分.p且q:平行四边形的对角线相等且平行四边形的对角线互相平分.綈p:有的平行四边形的对角线不相等.因为p假q真,所以“p或q”为真,“p且q”为假,“綈p”为真.(2)p或q:方程x2-16=0的两个根的符号不同或方程x2-16=0的两个根的绝对值相等.p且q:方程x2-16=0的两个根的符号不同且方程x2-16=0的两个根的绝对值相等.綈p:方程x2-16=0的两个根的符号相同.因为p真q真,所以“p或q”为真,“p且q”为真,“綈p”为假.1.判断复合命题真假的步骤确定复合命题的构成形式判断其中简单命题的真假⇒⇒根据真值表判断复合命题的真假2.命题p∧q,p∨q,綈p的真假判断,如下表:p q綈p p∨q p∧q真真假真真真假假真假假真真真假假假真假假3.含有一个量词的命题的否定命题命题的否定∀x∈M,p(x)∃x∈M,綈p(x)∃x∈M,p(x)∀x∈M,綈p(x)。
名校新学案高中数学人教A版选修2-1第一章反馈练习(含答案详析)

反馈练习一、选择题1.“a =2”是“直线ax +2y =0平行于直线x +y =1”的( ) A .充分而不必要条件 B .必要而不充分条件 C .充分必要条件 D .既不充分也不必要条件[答案] C[解析] 当a =2时,直线2x +2y =0,显然平行于x +y =1,若直线ax +2y =0与直线x +y =1平行,则须满足a -2=0,得a =2.2.(2013·四川文,4)设x ∈Z ,集合A 是奇数集,集合B 是偶数集.若命题p :∀x ∈A,2x ∈B ,则( )A .¬p :∃x ∈A,2x ∈B B .¬p :∃x ∉A,2x ∈BC .¬p :∃x ∈A,2x ∉BD .¬p :∀x ∉A,2x ∉B [答案] C[解析] 由命题p :∀x ∈A,2x ∈B 得¬p :∃x ∈A,2x ∉B .3.命题p :x =π是y =|sin x |的一条对称轴,q :2π是y =|sin x |的最小正周期,下列新命题:①p ∨q ;②p ∧q ;③¬p ;④¬q .其中真命题有( ) A .0个 B .1个 C .2个 D .3个[答案] C[解析] 由题意知p 真q 假,则①④为真命题,故选C.4.条件p :“直线l 在y 轴上的截距是在x 轴上截距的两倍”;条件q :“直线l 的斜率为-2”,则p 是q 的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件 [答案] B[解析] 注意当直线经过原点时,两个截距均为零,斜率值可以任意. 5.(2012·福建理,3)下列命题中,真命题是( ) A .∃x 0∈R ,e x 0≤0B .∀x ∈R,2x >x 2C .a +b =0的充要条件是ab =-1D .a >1,b >1是ab >1的充分条件 [答案] D[解析] 由指数函数的性质知,A 错误.当x =3时,23<32,知B 错误,由a =b =0时a +b =0,知C 错误,故选D. 6.与命题“若a ∈M ,则b ∉M ”等价的命题是( ) A .若a ∉M ,则b ∉M B .若b ∉M ,则a ∈M C .若a ∉M ,则b ∈M D .若b ∈M ,则a ∉M[答案] D[解析] 即原命题的逆否命题,结论的否定b ∈M 作条件,条件的否定a ∉M 作结论,故选D.7.“a >b >0”是“a 2+b 2>2ab ”成立的( ) A .必要不充分条件 B .充分不必要条件 C .充分且必要条件 D .不充分且不必要条件[答案] B[解析] ∵a >b >0,∴a 2+b 2-2ab =(a -b )2>0, ∴由a >b >0⇒a 2+b 2>2ab ,由a 2+b 2>2ab ⇒(a -b )2>0⇒/ a >b >0,故选B.8.若a ,b 均为非零向量,则“a ⊥b ”是“|a +b |=|a -b |”的( ) A .充要条件 B .必要而不充分条件 C .充分而不必要条件 D .既不充分也不必要条件[答案] A[解析] 由a ⊥b ,则如图OABC 是矩形,即可推得|OB →|=|a +b |=|a -b |=|CA →|.反之若|a +b |=|a -b |,平方得a ·b =0, 可推得a ⊥b .综上可得“a ⊥b ”是“|a +b |=|a -b |”的充要条件. 9.(2013·银川一中模拟)有下列命题:①设集合M ={x |0<x <3},N ={x |0<x <2},则“x ∈M ”是“x ∈N ”的充分而不必要条件; ②若p ∧q 是假命题,则p ,q 都是假命题;③命题P :“∃x 0∈R ,x 20-x 0-1>0”的否定¬P :“∀x ∈R ,x 2-x -1≤0”.则上述命题中为真命题的是( ) A .①②B .①③C .③D .②③[答案] C[解析] ①错误,“x ∈M ”是“x ∈N ”的必要而不充分条件;因为“且”命题满足一假即假,故p 和q 至少有一个为假命题,故②错误;由命题的否定的定义可判断③正确,综上可知只有③为真命题,故选择C.10.如果不等式|x -a |<1成立的充分非必要条件是12<x <32,则实数a 的取值范围是( )A.12<a <32B.12≤a ≤32 C .a >32或a <12D .a ≥32或a ≤12[答案] B[解析] |x -a |<1⇔a -1<x <a +1,由题意知⎝⎛⎭⎫12,32(a -1,a +1),则有⎩⎨⎧a -1≤12,a +1≥32.且等号不同时成立,解得12≤a ≤32,故选B.11.设a 、b 、c 表示三条直线,α、β表示两个平面,则下列命题中逆命题不成立的是( ) A .已知c ⊥α,若c ⊥β,则α∥βB .已知b ⊂β,c 是a 在β内的射影,若b ⊥c ,则b ⊥aC .已知b ⊂β,若b ⊥α,则β⊥αD .已知b ⊂α,c ⊄α,若c ∥α,则b ∥c [答案] C[解析] A 的逆命题是:已知c ⊥α,若α∥β,则c ⊥β,真命题;B 的逆命题是已知b ⊂β,c 是a 在β内的射影,若b ⊥a ,则b ⊥c ,是真命题;D 的逆命题是已知b ⊂α,c ⊄α,若b ∥c ,则c ∥α,是真命题.12.“θ=2π3”是“tan θ=2cos ⎝⎛⎭⎫π2+θ”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件[答案] A[解析] 解法一:∵θ=2π3为方程tan θ=2cos ⎝⎛⎭⎫π2+θ 的解,∴θ=2π3是tan θ=2cos ⎝⎛⎭⎫π2+θ成立的充分条件; 又∵θ=8π3也是方程tan θ=2cos ⎝⎛⎭⎫π2+θ的解, ∴θ=2π3不是tan θ=2cos ⎝⎛⎭⎫π2+θ的必要条件,故选A. 解法二:∵tan θ=2cos ⎝⎛⎭⎫π2+θ, ∴sin θ=0或cos θ=-12,∴方程tan θ=2cos ⎝⎛⎭⎫π2+θ的解集为A =⎩⎨⎧⎭⎬⎫θ⎪⎪θ=k π或θ=2k π±23π,k ∈Z , 显然⎩⎨⎧⎭⎬⎫2π3A ,故选A.二、填空题13.命题p :若a 、b ∈R ,则ab =0是a =0的充分条件;命题q :函数y =x -3的定义域是[3,+∞),则“p ∨q ”、“p ∧q ”、“¬p ”中是真命题的为________.[答案] p ∨q ,¬p[解析] p 为假命题,q 为真命题,故p ∨q 为真命题,¬p 为真命题. 14.已知a ,b 为两个非零向量,有以下命题:①a 2=b 2;②a ·b =b 2;③|a |=|b |且a ∥b .其中可以作为a =b 的必要不充分条件的命题是________.(将所有正确命题的序号填在题中横线上)[答案] ①②③[解析] 显然a =b 时①②③成立,即必要性成立. 当a 2=b 2时,(a +b )·(a -b )=0,不一定有a =b ; 当a ·b =b 2时,b ·(a -b )=0,不一定有a =b ;|a |=|b |且a ∥b 时,a =b 或a =-b ,即①②③都不能推出a =b .15.已知命题p :函数y =-x 2+mx +1在(-1,+∞)上单调递减;命题q :函数y =mx 2+x -1<0恒成立.若p ∨q 为真命题,p ∧q 为假命题,则m 的取值范围是________.[答案] (-2,-14)[解析] 函数y =-x 2+mx +1图象的对称轴为x =m 2,由条件m2≤-1,∴m ≤-2,即命题p :m ≤-2;∵函数y =mx 2+x -1<0恒成立,∴⎩⎨⎧m <0Δ=1+4m <0,∴m <-14,∴命题p :m <-14,∵p ∨q 为真命题,p ∧q 为假命题, ∴p 真q 假或p 假q 真,p 真q 假时,无解;p 假q 真时,-2<m <-14,∴m 的取值范围是(-2,-14).16.为激发学生的学习兴趣,老师上课时在黑板上写出三个集合:A ={x |( )x -1x <0},B ={x |x 2-3x -4≤0},C ={x |log 12x >1};然后叫甲、乙、丙三位同学到讲台上,并将“( )”中的数字告诉他们,要求他们各用一句话来描述,以便同学们能确定该数.以下是甲、乙、丙三位同学的描述:甲:此数为小于6的正整数, 乙:A 是B 成立的充分不必要条件, 丙:A 是C 成立的必要不充分条件.若老师评说三位同学都说得对,则“( )”中的数应为________. [答案] 1[解析] 集合B ={x |-1≤x ≤4},集合C ={x |0<x <12}.由甲的描述可设括号内的数为a (a >0),故集合A ={x |0<x <1a }.根据乙、丙的描述可得集合A 、B 、C 的关系是:C A B ,故1a ∈(12,4],所以a ∈[14,2).又a 为正整数,所以a =1. 三、解答题17.将下列命题改写为“若p ,则q ”的形式.并判断真假. (1)偶数能被2整除;(2)奇函数的图象关于原点对称;(3)在同圆或等圆中,同弧或等弧所对的圆周角不相等. [解析] (1)若一个数是偶数,则它能被2整除.真命题. (2)若一个函数是奇函数,则它的图象关于原点对称.真命题.(3)在同圆或等圆中,若两个角是同弧或等弧所对的圆周角,则它们不相等.假命题. 18.写出命题“x 2+x ≤0,则|2x +1|<1”的逆命题、否命题、逆否命题,并分别判断它们的真假.[解析] 逆命题:若|2x +1|<1,则x 2+x ≤0为真. 否命题:若x 2+x >0,则|2x +1|≥1为真. 逆否命题:若|2x +1|≥1,则x 2+x >0,为假.19.分别写出由下列各组命题构成的“p 或q ”、“p 且q ”、“非p ”形式的新命题,并判断新命题的真假.(1)p :正多边形有一个内切圆;q :正多边形有一个外接圆; (2)p :平行四边形的对角线相等,q :平行四边形的对角线互相平分. [解析] (1)p 或q :正多边形有一个内切圆或者有一个外接圆. p 且q :正多边形既有一个内切圆,也有一个外接圆. 非p :正多边形没有内切圆.∵p 真q 真,∴p 或q ,p 且q 为真,¬p 为假. (2)p 或q :平行四边形的对角线相等或互相平分. p 且q :平行四边形的对角线相等且互相平分. 非p :存在一个平行四边形的对角线不相等.因为p 是假命题,q 是真命题,所以“p 或q ”为真命题,“p 且q ”为假命题,“非p ”为真命题.20.已知p :x 2-8x -20>0,q :x 2-2x +1-a 2>0(a >0),若p 是q 的充分不必要条件,求实数a 的取值范围.[解析] p :A ={x |x <-2或x >10},q :B ={x |x <1-a 或x >1+a ,a >0},如图.依题意,p ⇒q ,但q ⇒/ p ,说明A B ,则有⎩⎨⎧a >01-a ≥-21+a ≤10,且等号不同时成立,解得0<a ≤3.∴实数a 的取值范围是0<a ≤3.21.设命题p :∀x ∈R ,x 2-2x >a ;命题q :∃x 0∈R ,x 20+2ax 0+2-a =0如果命题“p或q ”为真,“p 且q ”为假,求a 的取值范围.[解析] 由命题p 可知x 2-2x =(x -1)2-1>a 恒成立, ∴a <-1.由命题q 可知方程x 2+2ax +2-a =0有实数根, ∴Δ=(2a )2-4(2-a )≥0, 解得a ≤-2或a ≥1.∵p 或q 为真,p 且q 为假,∴p 与q 一真一假. 当p 真q 假时,有-2<a <-1,当p 假q 真时,有a ≥1. ∴a 的取值范围是(-2,-1)∪[1,+∞).22.已知:p :|5-3x |≤1,q :x 2+(m -3)x +2-m ≤0,若¬p 是¬q 的必要不充分条件,求实数m 的取值范围.[解析] 由|5-3x |≤1得-1≤5-3x ≤1,即43≤x ≤2.由x 2+(m -3)x +2-m ≤0知(x -1)[x -(2-m )]≤0, 当2-m =1,即m =1时,不等式x 2+(m -3)x +2-m ≤0的解集为{x |x =1}.当2-m >1,即m <1时,不等式x 2+(m -3)x +2-m ≤0的解集为{x |1≤x ≤2-m }. 当2-m <1,即m >1时,不等式x 2+(m -3)x +2-m ≤0的解集为{x |2-m ≤x ≤1}. 由题意知p 是q 的充分不必要条件,当m =1时,{x |43≤x ≤2} {x |x =1},不满足题意,故舍去.当m <1时,{x |43≤x ≤2}{x |1≤x ≤2-m }⇔2≤2-m ⇔m ≤0.所以m ≤0时符合题意.当m >1时,{x |43≤x ≤2}不可能是{x |2-m ≤x ≤1}的真子集.综上所述,m 的取值范围是m ≤0.。
高中数学 名校学案 一课一练 人教版 《数学选修2-1》(第一章)_19

(P4)
假命题.
(4)是 命 题,能 判 断 真 假,它 是 一 个 假 1.B
命题.
2.“若a>0,则a>1” “若a≤0,则a≤1”
1.2 充分条件与必要条件
1.1.2 四种命题
3.“若数列{an}中没有零项,则数列{an}为 等比数列”
第1课时 充分条件与必要条件
(P3)
基础梳理
1.(1)条件 结论 (3)互逆命题
高中课标教材同步导学丛书
(2)①逆命题:如果直线垂直于平面,那 逆否命题:若一个数是素数,则它一定不
么直线垂直于平面内的两条相交直线; 是正偶数.
1.1 命题及其关系
否命题:如果直线不垂直于平面内的两 条相交直线,那么直线不垂直于平面; 逆 否 命 题:如 果 直 线 不 垂 直 于 平 面,那
1.1.3 四种命题间的相互关系 (P5)
1.1.1 命 题
么直线 不 垂 直 于 平 面 内 的 两 条 相 交
基础梳理
(P1)
基础梳理
1.判断真假 判断为真 陈述句 符号或式子 判断为假
语言、
直线. ②逆命题:如果x>0,那么x>10; 否命题:如果x≤10,那么x≤0; 逆否命题:如果x≤0,那么x≤10.
1.①互逆 ②互否 ③互否 ④互逆 2.(1)没有关系
(P3)
1.A 2.A 3.A 4.①③ 5.【解析】(1)是命题,因为当等比数列的首
项a1<0,公比q>1时,该数列为递减数 列,因此是一个假命题. (2)不是命题,它是祈使句. (3)不是 命 题,它 是 一 个 疑 问 句,没 有 作 出判断.
否命题:若一条直线不是弦的垂直平分
(P7)
(完整word版)高中数学选修2-1课后习题答案[人教版]
![(完整word版)高中数学选修2-1课后习题答案[人教版]](https://img.taocdn.com/s3/m/10b65c4df121dd36a22d8280.png)
高中数学选修2-1 课后习题答案 [ 人教版 ]高中数学选修2-1 课后习题答案第一章常用逻辑用语1.1命题及其关系练习( P4)1、略 .2、(1)真;(2)假;(3)真;(4)真.3、(1)若一个三角形是等腰三角形,则这个三角形两边上的中线相等. 这是真命题 .(2)若一个函数是偶函数,则这个函数的图象对于y 轴对称.这是真命题.(3)若两个平面垂直于同一个平面,则这两个平面平行. 这是假命题 .练习( P6)1、抗命题:若一个整数能被 5 整除,则这个整数的末位数字是0. 这是假命题 .否命题:若一个整数的末位数字不是0,则这个整数不可以被5整除 . 这是假命题 .逆否命题:若一个整数不可以被5 整除,则这个整数的末位数字不是0. 这是真命题 .2、抗命题:若一个三角形有两个角相等,则这个三角形有两条边相等. 这是真命题 .否命题:若一个三角形有两条边不相等,这个三角形有两个角也不相等. 这是真命题 .逆否命题:若一个三角形有两个角不相等,则这个三角形有两条边也不相等.这是真命题 .3、抗命题:图象对于原点对称的函数是奇函数. 这是真命题 .否命题:不是奇函数的函数的图象不对于原点对称. 这是真命题 .逆否命题:图象不对于原点对称的函数不是奇函数. 这是真命题 .练习( P8)证明:若 a b 1,则a2b22a 4b3( a b)( a b) 2( a b) 2b3a b 2 2b3a b 10所以,原命题的逆否命题是真命题,进而原命题也是真命题.习题 1.1 A组(P8)1、(1)是;(2)是;(3)不是;(4)不是.2、(1)抗命题:若两个整数 a 与b的和a b 是偶数,则a,b都是偶数.这是假命题.否命题:若两个整数a,b 不都是偶数,则 a b 不是偶数.这是假命题.逆否命题:若两个整数 a 与b的和a b 不是偶数,则a, b不都是偶数.这是真命题.(2)抗命题:若方程 x2 x m 0 有实数根,则m 0. 这是假命题 . 否命题:若 m 0 ,则方程x2x m 0没有实数根.这是假命题.逆否命题:若方程x2x m 0 没有实数根,则m 0 .这是真命题.3、(1)命题能够改写成:若一个点在线段的垂直均分线上,则这个点到线段的两个端点的距离相等 .抗命题:若一个点到线段的两个端点的距离相等,则这个点在线段的垂直均分线上.这是真命题 .否命题:若一个点到不在线段的垂直均分线上,则这个点到线段的两个端点的距离不相等 .这是真命题.逆否命题:若一个点到线段的两个端点的距离不相等,则这个点不在线段的垂直均分线上 .这是真命题.( 2)命题能够改写成:若一个四边形是矩形,则四边形的对角线相等.抗命题:若四边形的对角线相等,则这个四边形是矩形. 这是假命题 .否命题:若一个四边形不是矩形,则四边形的对角线不相等. 这是假命题 .逆否命题:若四边形的对角线不相等,则这个四边形不是矩形. 这是真命题 .4、证明:假如一个三角形的两边所对的角相等,依据等腰三角形的判断定理,这个三角形是等腰三角形,且这两条边是等腰三角形,也就是说这两条边相等. 这就证了然原命题的逆否命题,表示原命题的逆否命题为真命题. 所以,原命题也是真命题.习题 1.1 B组(P8)证明:要证的命题能够改写成“若p ,则 q ”的形式:若圆的两条弦不是直径,则它们不能相互均分 .此命题的逆否命题是:若圆的两条订交弦相互均分,则这两条订交弦是圆的两条直径.能够先证明此逆否命题:设AB,CD 是e O的两条相互均分的订交弦,交点是 E ,若 E 和圆心 O 重合,则AB,CD是经过圆心 O 的弦,AB,CD是两条直径.若 E 和圆心 O 不重合,连结AO, BO,CO 和DO,则OE是等腰AOB , COD 的底边上中线,所以,OE AB ,OE CD .AB 和 CD 都经过点 E ,且与 OE 垂直,这是不行能的.所以, E 和 O 必定重合.即 AB 和 CD 是圆的两条直径 .原命题的逆否命题得证,由互为逆否命题的相同真假性,知原命题是真命题.1.2充足条件与必需条件练习( P10)1、(1);(2);(3);(4).2、(1).3( 1) .4、(1)真;(2)真;( 3)假;( 4)真 .练习( P12)1、(1)原命题和它的抗命题都是真命题,p 是 q 的充要条件;(2)原命题和它的抗命题都是真命题,p 是 q 的充要条件;(3)原命题是假命题,抗命题是真命题,p 是 q 的必需条件.2、(1)p是q的必需条件;(2)p是q的充足条件;( 3)p是q的充要条件;(4)p是q的充要条件.习题 1.2 A组(P12)1、略 .2、( 1)假;(2)真;(3)真.3、(1)充足条件,或充足不用要条件;(2)充要条件;(3)既不是充足条件,也不是必需条件;(4)充足条件,或充足不用要条件.4、充要条件是 a2b2r 2 .习题 1.2 B组(P13)1、(1)充足条件;(2)必需条件;(3)充要条件.2、证明:( 1)充足性:假如 a2b2c2ab ac bc ,那么 a2b2c2ab ac bc 0 .所以 (a b)2(a c)2(b c)20所以, a b 0 , a c 0 , b c0 .即 a b c ,所以,ABC 是等边三角形.(2)必需性:假如ABC是等边三角形,那么 a b c所以 (a b)2 (a c)2 (b c)2 0所以 a 所以 a 2b2c2ab ac bc 0 2b2c2ab ac bc1.3简单的逻辑联络词练习( P18)1、(1)真;(2)假 .2、(1)真;(2)假 .3、(1)225,真命题;( 2)3 不是方程 x290的根,假命题;( 3)( 1)21,真命题.习题 1.3 A组( P18)1、(1) 4{2,3}或 2 {2,3},真命题;(2) 4{2,3}且 2 {2,3} ,假命题;(3)2 是偶数或 3 不是素数,真命题;( 4) 2 是偶数且 3 不是素数,假命题 .2、(1)真命题;( 2)真命题;(3)假命题 .3、(1) 2 不是有理数,真命题;( 2)5 是 15 的约数,真命题;(3)2 3 ,假命题;(4)8715 ,真命题;(5)空集不是任何会合的真子集,真命题.习题 1.3 B组( P18)(1)真命题 . 因为p为真命题,q为真命题,所以p q为真命题;(2)真命题 . 因为p为真命题,q为真命题,所以p q为真命题;(3)假命题 . 因为p为假命题,q为假命题,所以p q为假命题;(4)假命题 . 因为p为假命题,q为假命题,所以p q为假命题 .1.4全称量词与存在量词练习( P23)1、(1)真命题;(2)假命题;(3)假命题 .2、(1)真命题;(2)真命题;(3)真命题 .练习( P26)1、(1) n0Z, n0Q ;(2)存在一个素数,它不是奇数;( 3)存在一个指数函数,它不是单一函数 .2、(1)全部三角形都不是直角三角形;(2)每个梯形都不是等腰梯形;(3)全部实数的绝对值都是正数 .习题 1.4 A 组( P26)1、(1)真命题;(2)真命题;(3)真命题;(4)假命题 .2、(1)真命题;(2)真命题;(3)真命题 .3、(1) x0N , x03x02;(2)存在一个能够被 5 整除的整数,末位数字不是0;(3) x R, x2x 10 ;(4)全部四边形的对角线不相互垂直 .习题 1.4 B组( P27)(1)假命题 . 存在一条直线,它在y轴上没有截距;(2)假命题 . 存在一个二次函数,它的图象与 x 轴不订交;(3)假命题 . 每个三角形的内角和不小于180;(4)真命题 . 每个四边形都有外接圆 .第一章复习参照题 A 组( P30)1、原命题能够写为:若一个三角形是等边三角形,则此三角形的三个内角相等.抗命题:若一个三角形的三个内角相等,则此三角形是等边三角形. 是真命题;否命题:若一个三角形不是等边三角形,则此三角形的三个内角不全相等. 是真命题;逆否命题:若一个三角形的三个内角不全相等,则此三角形不是等边三角形. 是真命题 .2、略 .3、( 1)假;(2)假;(3)假;(4)假.4、(1)真;(2)真;(3)假;(4)真;(5)真.5、(1) n N ,n20 ;(2)P { P P 在圆x2y2r 2上 } ,OP r (O 为圆心);(3)( x, y) {( x, y) x, y 是整数},2x 4y 3;( 4)x0{ x x 是无理数}, x03{ q q 是有理数} .6、(1)32,真命题;(2)5 4 ,假命题;( 3) x0R, x0 0 ,真命题;(4)存在一个正方形,它不是平行四边形,假命题.第一章复习参照题 B 组( P31)1、(1)p q;(2) ( p) (q) ,或 ( p q) .2、(1)Rt ABC,C90 ,A, B, C 的对边分别是 a, b, c ,则 c2a2b2;(2)ABC ,A,B,a b cC 的对边分别是 a, b,c ,则.sin A sin B sin C第二章 圆锥曲线与方程2.1曲线与方程练习( P37)1、是 . 简单求出等腰三角形 ABC 的 BC 上的中 AO 所在直 的方程是x 0 .2、 a32 ,b 18 .25253、解: 点 A, M 的坐 分 (t,0), ( x, y) .(1)当 t 2 ,直 CA 斜率2 02kCAt2 t2所以, k CB1 t 2k CA2由直 的点斜式方程,得直CB 的方程y 2t2( x 2) .2令 x 0 ,得 y 4 t ,即点 B 的坐 (0,4 t ) .因为点 M 是 段 AB 的中点,由中点坐 公式得 xt, y4 t .t4 t ,22由 x得 t 2x ,代入 y 22 得 y42x,即 x y 20 ⋯⋯①2( 2)当 t 2 ,可得点 A, B 的坐 分 (2,0) , (0,2)此 点 M 的坐 (1,1) ,它仍旧合适方程①由( 1)( 2)可知,方程①是点M 的 迹方程,它表示一条直.习题 2.1 A 组( P37)1、解:点 A(1, 2) 、 C (3,10) 在方程 x 2xy 2 y1 0 表示的曲 上;点 B(2, 3) 不在此曲 上2、解:当 c0 , 迹方程 xc 1;当 c 0 , 迹 整个坐 平面 .23、以两定点所在直 x , 段 AB 垂直均分 y ,成立直角坐 系,得点M 的迹方程 x 2y 2 4 .4、解法一: x 2y 2 6x 50 的 心 C , 点 C 的坐 是 (3,0) .由 意,得 CM AB , 有 k CM k AB1 .高中数学选修 2-1 课后习题答案 [ 人教版 ]yy1 (x 3, x 0)所以,3 xx化简得 x 2y 23x 0 (x 3, x 0)当 x 3 时, y 0 ,点 (3,0) 合适题意;当 x 0 时, y 0 ,点 (0,0) 不合题意 .解方程组x 2 y 23x 0, 得 x5, y2 5x 2y 26x 5 033所以,点 M 的轨迹方程是 x2y 23x 0 ,5x3.3解法二:注意到OCM 是直角三角形,利用勾股定理,得 x 2 y 2(x 3)2y 2 9 ,即 x 2y 2 3x0 . 其余同解法一 .习题 2.1 B 组( P37)1、解:由题意,设经过点P 的直线 l 的方程为xy 1.a b因为直线 l 经过点 P(3,4) ,所以341所以, ab 4a 3bab由已知点 M 的坐标为 (a,b) ,所以点 M 的轨迹方程为 xy4x 3 y 0 .2、解:如图,设动圆圆心M 的坐标为 (x, y) .y因为动圆截直线 3xy0 和 3x y 0 所得弦分别为BAB , CD ,所以, AB8 , CD 4 . 过点 M 分别CMFE作直线 3x y0 和 3x y0 的垂线,垂足分别为E ,DF ,则 AE4 , CF2 . A3xy, MF3x yME1010 .Ox连结 MA , MC ,因为 MAMC ,(第 2 题)2ME 2CF 2MF 2 则有, AE(3 x y) 2(3 x y) 210 .所以, 1610410,化简得, xy所以,动圆圆心的轨迹方程是 xy 10 .高中数学选修2-1 课后习题答案 [ 人教版 ]2.2椭圆练习( P42)1、 14. 提示:依据椭圆的定义,PF1PF220 ,因为 PF1 6 ,所以 PF22、(1)x2y2 1 ;(2) y2x21;(3) x2y21,或 y2x2 1616361636163、解:由已知,a 5, b 4 ,所以 c a2b2 3 .(1)AF1B 的周长AF1AF2BF1BF2.由椭圆的定义,得 AF1AF22a, BF1BF22a .所以, AF1B 的周长4a20.(2)假如AB不垂直于 x 轴, AF1B 的周长不变化 .这是因为①②两式仍旧成立,AF1 B 的周长20,这是定值 .4、解:设点M的坐标为 ( x, y) ,由已知,得直线 AM 的斜率y(x1)kAM;x1直线 BM 的斜率y(x1) ;kBMx1由题意,得kAM2,所以y2y( x1, y0) kBM x 1x1化简,得 x3( y0)所以,点 M 的轨迹是直线 x 3 ,并去掉点( 3,0) .练习( P48)yB2 1、以点 B2(或 B1)为圆心,以线段 OA2(或 OA1)为半径画圆,圆与 x 轴的两个交点分别为F1 , F2 .A 1F1O点 F1 , F2就是椭圆的两个焦点 .B 1这是因为,在 Rt B2OF2中,OB2 b , B2 F2OA2 a ,(第 1 题)所以, OF2 c .相同有 OF1 c .2、(1)焦点坐标为(8,0) , (8,0) ;14.1.F2 A 2x(2)焦点坐标为 (0,2) , (0, 2) .3、(1)x2y 21;(2) y2x2 1 . 363225164、(1)x2y21(2) x2y 21,或 y2x2 1. 9410064100645、(1)椭圆 9x2y236 的离心率是22 ,椭圆 x2y2 1 的离心率是 1 ,316122因为221 ,所以,椭圆x2y2 1 更圆,椭圆 9x2y236 更扁;321612(2)椭圆 x29 y236 的离心率是22 ,椭圆 x2y2 1 的离心率是10 ,36105因为2210 ,所以,椭圆x2y2 1 更圆,椭圆 x29 y 236 更扁 . 356106、(1)(3,8(2) (0,2) ;( 3)(487082 ) ;,) .7、. 537377习题 2.2 A组( P49)1、解:由点 M (x, y) 知足的关系式x2( y3)2x2( y3)210 以及椭圆的定义得,点 M 的轨迹是以F1(0,3) , F2 (0,3) 为焦点,长轴长为10 的椭圆 .它的方程是y2x21. 25162、(1)x2y 21;( 2)y2x2 1 ;(3) x2y21,或 y2x2 1. 3632259494049403、(1)不等式2x 2 , 4 y 4 表示的地区的公共部分;(2)不等式25x25 ,10y10表示的地区的公共部分 .图略 . 334、(1)长轴长2a8 ,短轴长 2b 4 ,离心率e 3 ,2焦点坐标分别是 (23,0), (23,0),极点坐标分别为 (4,0), (4,0), (0,2) , (0,2) ;(2)长轴长2a18 ,短轴长 2b 6 ,离心率e 2 2 ,3焦点坐标分别是 (0, 62),(0,62),极点坐标分别为 (0, 9) ,(0,9) , (3,0) , (3,0) .5、(1)x2y2 1 ;(2) x2y21,或 y2x2 1 ;859819(3) x2y21,或 y 2x2 1 .2592596、解:由已知,椭圆的焦距F1F2 2 .因为PF1F2的面积等于1,所以,1F1F2y P1,解得y P1. 2代入椭圆的方程,得x211,解得 x15 .P54215l所以,点 P 的坐标是(1),共有 4个 .,2QA 7、解:如图,连结 QA .由已知,得 QA QP .O所以, QO QA QO QP OP r .又因为点 A 在圆内,所以 OA OP(第 7 题)依据椭圆的定义,点 Q 的轨迹是以 O, A 为焦点, r 为长轴长的椭圆 .8、解:设这组平行线的方程为y 3 x m .2把 y 3 x m 代入椭圆方程x2y2 1 ,得 9x26mx2m218 0 .249这个方程根的鉴别式36m236(2 m 218)( 1)由0 ,得 3 2 m 3 2 .当这组直线在 y 轴上的截距的取值范围是( 32,32) 时,直线与椭圆订交 .( 2)设直线与椭圆订交获得线段AB ,并设线段 AB 的中点为M (x, y) .则 x x1x2m .23因为点 M 在直线y 3 x m 上,与 x m联立,消去 m ,得 3x 2 y0 .23这说明点 M 的轨迹是这条直线被椭圆截下的弦(不包含端点),这些弦的中点在一条直线上 .x2y29、3.5252 2.8752 1 .10、地球到太阳的最大距离 1.5288 108 km,最下距离 1.4712108 km.习题 2.2 B 组( P50)1、解:点M的坐 ( x, y) ,点P的坐 ( x0 , y0 ) ,x x0, y 3 y0 .所以 x0x , y0 2 y⋯⋯① . 23因点 P(x0, y0 ) 在上,所以 x02y02 4 ⋯⋯② .将①代入②,得点 M 的迹方程x2 4 y24,即 x2y21949所以,点 M 的迹是一个与例 2 对比可,也能够看作是由沿某个方向或拉伸获得.2、解法一:心P(x, y) ,半径R,两已知的心分O1, O2 .分将两已知的方程x2y26x 50 , x2y 26x 910配方,得 (x 3)2y2 4 ,( x3) 2y2100当 e P 与e O1:( x3)2y2 4 外切,有O1P R2⋯⋯①当 e P 与e O2:( x3)2y2100 内切,有O2P10R ⋯⋯②①②两式的两分相加,得O1P O2 P12即, ( x 3)2y2(x 3)2y212⋯⋯③化方程③ .先移,再两分平方,并整理,得 2 (x 3)2y212x ⋯⋯④将④两分平方,并整理,得3x2 4 y2 108 0 ⋯⋯⑤将常数移至方程的右,两分除以108,得x2y2 1 ⋯⋯⑥3627由方程⑥可知,心的迹是,它的和短分12, 6 3 .解法二:同解法一,得方程( x 3)2y2( x 3)2y 212⋯⋯①由方程①可知,心P(x, y) 到点 O1 ( 3,0) 和点 O2 (3,0)距离的和是常数12,所以点 P 的 迹方程是焦点 (3,0) 、 (3,0) , 等于 12 的 .而且 个 的中心与坐 原点重合,焦点在 x 上,于是可求出它的 准方程.因2c 6 , 2a 12 ,所以 c3 , a 6所以 b 2 36 927 .于是, 心的 迹方程x 2y2361.273、解: d 是点 M 到直 x8 的距离,依据 意,所求 迹就是会合PMF 1 M2d( x2)2y 2 1由此得x28将上式两 平方,并化 ,得3x24 y248 ,即x 2y 2 11612所以,点 M 的 迹是 、短 分8, 4 3 的 .4、解:如 ,由已知,得E(0, 3) , F (4,0) , G (0,3) , H (4,0) .DyGLC因 R,S,T 是 段 OF 的四均分点,R'MR , S ,T 是 段 CF 的四均分点,S' 所以, R(1,0), S(2,0), T (3,0) ;HN T'O RSTF xR (4, 9 ), S (4, 3),T (4, 3) .424直 ER 的方程是 y 3x 3 ;直 GR 的方程是 y3.AEBx 31632 , y 45 .(第 4 题)立 两个方程,解得x17 17所以,点 L 的坐 是 (32 ,45) .17 17同 ,点 M 的坐 是 (16 , 9) ,点 N 的坐 是 ( 96 ,21) .5 525 25由作 可 ,能够 的方程x 2y 21 (m 0, n 0) ⋯⋯①nm 22把点 L, M 的坐 代入方程①,并解方程 ,得11,11m 22232.4 n高中数学选修 2-1 课后习题答案 [ 人教版 ]所以经过点 L, M 的椭圆方程为x 2y 21 .16 9把点 N 的坐标代入x 2y 2 ,得 1( 96 ) 2 1 ( 21)2 1,169 16 259 25所以,点 N 在x 2y 2 1 上 . 169所以,点 L, M , N 都在椭圆x 2y 2 1 上.1692.3双曲线练习( P55)1、(1)x 2y 21 .(2) x 2y21.16 93(3)解法一:因为双曲线的焦点在y 轴上y 2x 21 ( a 0,b0)所以,可设它的标准方程为2b 2a将点 (2, 5) 代入方程,得254 1 ,即 a 2b 24a 2 25b 2 0a 2b 2又 a 2b 236解方程组a 2b 2 4a 2 25b 2 0a2b 236令 m a 2,nmn 4m 25n 0 b 2,代入方程组,得n 36m m 20 m 45 解得16,或9nn第二组不合题意,舍去,得a 2 20,b 2 16y 2x 2所求双曲线的标准方程为 120 16解法二:依据双曲线的定义,有 2a4 (5 6)24 (5 6)2 4 5 .所以, a 2 5高中数学选修2-1 课后习题答案 [ 人教版 ]又 c6,所以 b23620 16由已知,双曲线的焦点在y2x2y 轴上,所以所求双曲线的标准方程为 1 .20162、提示:依据椭圆中a2b2c2和双曲线中 a2b2c2的关系式分别求出椭圆、双曲线的焦点坐标 .3、由 (2 m)( m 1) 0 ,解得m 2 ,或 m1练习( P61)1、(1)实轴长 2a8 2 ,虚轴长2b 4 ;极点坐标为(4 2,0),(42,0);焦点坐标为 (6,0),(6,0);离心率 e3 2 .4(2)实轴长2a 6 ,虚轴长 2b18 ;极点坐标为(3,0),(3,0) ;焦点坐标为 (310,0),(310,0) ;离心率 e10 .(3)实轴长2a 4 ,虚轴长 2b 4 ;极点坐标为(0,2),(0,2);焦点坐标为 (0,22),(0,22) ;离心率 e 2 .(4)实轴长2a10,虚轴长2b14;极点坐标为(0,5),(0,5) ;焦点坐标为 (0,74),(0,74) ;离心率 e74 .52、(1)x2y 2 1 ;(2) y2x2 1.3、 x2y21169362835 4、 x2y2 1 ,渐近线方程为y x .18185、(1) (6,2),( 14,2) ;( 2) (25,3) 334习题 2.3 A组( P61)y2x21 . 因为a 8,由双曲线定义可知,点P 到两焦点距1、把方程化为标准方程,得1664离的差的绝对值等于16. 所以点P到另一焦点的距离是17.2、(1)x2y2 1 .(2) x2y2120162575高中数学选修 2-1 课后习题答案 [ 人教版 ]3、(1)焦点坐标为 F 1 ( 5,0), F 2 (5,0) ,离心率 e5 ;3 (2)焦点坐标为 F 1 (0, 5), F 2 (0,5) ,离心率 e5 ;44、(1)x 2y 21.( 2) y2x 2 1 2516916(3)解:因为 ec2 ,所以 c 22a 2 ,所以 b 2c 2 a 22a 2 a 2a 2 .a设双曲线的标准方程为x 2 y 21 ,或 y 2x 2 1.a 2 a 2a 2a 2将 ( 5,3) 代入上边的两个方程,得25 9 1 ,或 925 1 .a 2a 2 a 2a 2解得 a 216 (后一个方程无解) .所以,所求的双曲线方程为x 2 y 21 .16 165、解:连结 QA ,由已知,得 QA QP .所以, QA QO QP QO OP r .又因为点 A 在圆外,所以 OA OP .依据双曲线的定义,点Q 的轨迹是以 O, A 为焦点, r 为实轴长的双曲线 .6、 x 2 y 2 1 .8 8习题 2.3 B组( P62)1、 x 2y 2116 92、解:由声速及 A, B 两处听到爆炸声的时间差,可知A, B 两处与爆炸点的距离的差,所以爆炸点应位于以 A, B 为焦点的双曲线上 .使 A, B 两点在 x 轴上,而且原点 O 与线段 AB 的中点重合,成立直角坐标系 xOy .设爆炸点 P 的坐标为 ( x, y) ,则 PA PB 340 3 1020 .即 2a 1020 , a 510.又 AB1400,所以 2c 1400 , c 700 , b 2 c 2 a 2229900 .所以,所求双曲 的方程x 2y22601001.2299003、 x 2y 2 1a 2b 24、解: 点 A( x 1 , y 1) , B( x 2 , y 2 ) 在双曲 上,且 段 AB 的中点 M ( x, y) .点 P 的直 l 的方程 y 1 k ( x 1) ,即 y kx 1 k把 ykx1 k 代入双曲 的方程x 2y 2 1得2(2 k 2 )x 2 2k(1 k )x (1 k 2 ) 20 ( 2k 2 0 ) ⋯⋯①所以, xx 1x 2 k(1 k)22 k2由 意,得k (1k) 1,解得 k 2 .2k 2当 k2 ,方程①成 2x 2 4x 30 .根的判 式16 24 8 0 ,方程①没有 数解 .所以,不可以作一条直 l 与双曲 交于 A, B 两点,且点 P 是 段 AB 的中点 .2.4 抛物线练习( P67)1、(1) y 212x ;( 2) y 2x ;(3) y 24x, y 2 4x, x 2 4 y, x 24y .2、(1)焦点坐 F (5,0) ,准 方程 x5 ; ( 2)焦点坐 F (0, 1) ,准 方程 y1 ;88 (3)焦点坐 F (5 ,0) ,准 方程 x 5; ( 4)焦点坐 F (0, 2),准 方程 y2 ;p .883、(1) a , a( 2) (6,6 2) , (6, 6 2)2提示:由抛物 的 准方程求出准 方程. 由抛物 的定 ,点M 到准 的距离等于9,所以 x 39 , x 6, y 6 2 .yy 2= 4x练习(P72)y 2= 2x1、(1) y216 x ; ( 2) x220 y ;y 2=x52 1=(3) y 216 x ;( 4) x 232 y .yx22、 形 右, x 的系数越大,抛物 的张口越大 .Ox3、解:过点 M (2,0) 且斜率为 1 的直线 l 的方程为 yx 2与抛物线的方程 y24x 联立y x 2y24x解得x 142 3 x 24 2 3,y 1 2 2 3y 2 2 2 3设 A(x 1, y 1 ) , B(x 2 , y 2 ) ,则 AB( x 2 x 1) 2( y 2 y 1 )2( 4 3) 2( 4 3) 2 4 6 .4、解:设直线 AB 的方程为 xa ( a 0) .将 x a 代入抛物线方程 y 2 4x ,得 y 24a ,即 y 2 a .因为AB 2 y 2 2 a 4 a 4 3 , 所以, a3所以,直线 AB 的方程为 x3 .习题 2.4 A 组( P73)1、(1)焦点坐标 F (0, 1) ,准线方程 y1 ;22(2)焦点坐标 F (0,3) ,准线方程 y3 ;1616(3)焦点坐标 F ( 1 ,0) ,准线方程 x1 ;8 8 (4)焦点坐标 F ( 3 ,0) ,准线方程 x3 .222、(1) y 28x ;( 2) (4,4 2) ,或 (4, 42)3、解:由抛物线的方程 y 2 2 px ( p0) ,得它的准线方程为 xp .2依据抛物线的定义,由 MF 2 p ,可知,点 M 的准线的距离为 2 p .设点 M 的坐标为 ( x, y) ,则xp 2 p ,解得 x3p .3 p 代入 y 222将 x2 px 中,得 y3 p .2所以,点 M 的坐标为 (3 p,3 p) , (3 p,3 p) .224、(1) y 2 24 x , y 2 24x ;(2) x 212 y (图略)5、解:因为xFM 60 ,所以线段 FM 所在直线的斜率 k tan 603 .所以,直线 FM 的方程为 y3( x 1)高中数学选修2-1 课后习题答案 [ 人教版 ]与抛物 y 24xy3( x1)L L 1立,得y 24xL L 2将 1 代入 2 得, 3x210 x 3 0 ,解得, x 11, x 233把 x 11, x 23 分 代入①得y 12 3, y 2 2 333由第 5 知 (1 ,2 3) 不合 意,所以点 M 的坐 (3,2 3).33所以, FM(3 1)2 (2 3 0) 246、 明:将 y x2 代入 y 22x 中,得 ( x2) 2 2x ,化 得 x 2 6x 4 0 ,解得 x35y 3 5 2 15因 k OB1 5, k OA 1 535 35所以 k OB k OA1 5 1 5 153535 915所以 OAOB7、 条抛物 的方程是x217.5 yy8、解:成立如 所示的直角坐 系,Ox拱 抛物 的方程 x 2 2 py ,2l因 拱 离水面 2 m ,水面 4 m所以222 p( 2) , p 1所以,抛物 方程 x 2 2y4⋯⋯①(第 8 题)水面降落 1 m , y 3 ,代入①式,得 x 22 ( 3) , x6 .水面 26 m.习题 2.2 B 组( P74)1、解: 垂 段的中点坐( x, y) ,抛物 上相 点的坐(x 1, y 1 ) .依据 意, x 1x , y 1 2 y ,代入 y 122 px 1 ,得 迹方程 y21px .2由方程可知,轨迹为极点在原点、焦点坐标为( p,0) 的抛物线 .82、解:设这个等边三角形 OAB 的极点 A, B 在抛物线上,且坐标分别为( x 1 , y 1 ) , (x 2 , y 2 ) ,则 y 12 2 px 1 , y 22 2 px 2 .又 OAOB ,所以 x 12 y 12 x 22 y 22即 x 12 x 22 2 px 1 2 px 2 0, (x 12 x 22 ) 2 p( x 1 x 2 ) 0所以, ( x 1 x 2 )( x 1 x 2 2 p)因为 x 1 0, x 2 0,2 p 0 ,所以 x 1 x 2由此可得 y 1y 2 ,即线段 AB 对于 x 轴对称 .因为 x 轴垂直于 AB ,且AOx 30 ,所以y 1tan303 .x 13因为 x 1y 12 ,所以 y 1 2 3p ,所以 AB2 y 14 3 p .2 p3、解:设点 M 的坐标为 ( x, y)由已知,得 直线 AM 的斜率 k AMy ( x1) .x 1直线 BM 的斜率 k BMy ( x 1) .x 1由题意,得 k AMkBM2 ,所以,yy2( x1) ,化简,得 x 2( y 1)(x1)x 1 x 1第二章复习参照题 A 组( P80)1、解:如图,成立直角坐标系, 使点 A, B, F 2 在 x 轴上, F 2 为椭圆的右焦点 (记 F 1 为左焦点) .因为椭圆的焦点在 x 轴上,所以设它的标准方程为x 2 y 2.a2b 21(a b0)y则 a c OAOF 2 F 2 A 6371 439 6810,a c OBOF 2F 2B 6371 2384 8755 ,解得 a 7782.5 , c 8755BF 1OF 2A x所以 ba 2c 2(a c)( ac)8755 6810用计算器算得 b 7722所以, 星的 道方程是x 2y 2 1.77832772222R r 1 r 2a cR r 1 a 22、解:由 意,得,解此方程 ,得a c Rr 2r 1r 2c2所以 星 道的离心率ecr 2 r 1 .a2R r 1r 23、(1) D ; ( 2) B .4、(1)当0 ,方程表示 .(2)当 090 ,方程化成 x 2y 2 1. 方程表示焦点在 y 上的 .1cos(3)当 90 , x 21,即 x 1,方程表示平行于 y 的两条直 .(4)当 90180 ,因 cos0,所以 x 2y 2 cos1 表示双曲 ,其焦点在 x上. 而当180 ,方程表示等 双曲 .5、解:将 ykx 1代入方程 x 2y 2 4得 x 2k 2 x 2 2kx 1 4 0即 (1 k 2 ) x 2 2kx 5 0 ⋯⋯①4k 2 20(1k 2 ) 20 16k 2令0 ,解得 k5,或 k522因0 ,方程①无解,即直 与双曲 没有公共点,所以, k 的取 范 k5,或 k5226、提示: 抛物 方程y 2 2 px , 点 B 的坐 ( p, p) ,点 C 的坐 ( p, p)2 2点 P 的坐 ( x, y) , 点 Q 的坐 ( x,0) .因 , PQy2px , BC 2 p , OQ x .所以, PQ 2BC OQ ,即 PQ 是 BC 和 OQ 的比率中 .7、解: 等 三角形的此外两个 点分 是A, B ,此中点 A 在 x 上方 .高中数学选修2-1 课后习题答案 [ 人教版 ]3 p直 FA 的方程 y( x)32与 y 22 px 立,消去 x ,得 y 2 23 py p 2解方程,得 y 1 ( 3 2) p , y 2 ( 3 2) p把 y 1( 3 2) p 代入 y3( xp ) ,得 x 1(72 3) p .322把 y 2( 3 2) p 代入 y3(xp) ,得 x 2(72 3) p .322所以, 足条件的点 A 有两个 A 1((72 3) p,(3 2) p) , A 2 ((72 3) p,(3 2) p) .22依据 形的 称性,可得 足条件的点B 也有两个B 1(( 72 3) p, (3 2) p) ,2 7( 32) p)B 2 ((2 3) p,2所以,等 三角形的 是A 1B 12( 32) p ,或许 A 2 B 22(23) p .8、解: 直 l 的方程 y 2xm .把 y2x m 代入双曲 的方程 2x 23y 2 6 0 ,得 10x 2 12mx 3m 26 0 .x 1 x 26m, x 1x 23m 2 6⋯⋯①510由已知,得(1 4)[( x 1 x 2 ) 2 4x 1x 2 ] 16⋯⋯②210把①代入②,解得m3210 所以,直 l 的方程 y2x39、解: 点A 的坐 (x 1, y 1 ) ,点B 的坐 ( x 2 , y 2 ) ,点 M 的坐 (x, y) .并 点 M 的直 l 的方程 y1 k (x 2) ,即 ykx 1 2k .22y把 y kx 1 2k 代入双曲 的方程x1 ,得(2 k 2 )x 2 2k (12k )x(1 2k)2 20 (2 k 2 0) . ⋯⋯①高中数学选修 2-1 课后习题答案 [ 人教版 ]x 1 x 2 k (1 2k)所以, x22 k 2由题意,得k(12k) 2 ,解得 k42 k 2当 k4 时,方程①成为 14 x 2 56x 51根的鉴别式56 256 51 2800 ,方程①有实数解 .所以,直线 l 的方程为 y4x 7 .10、解:设点 C 的坐标为 (x, y) .由已知,得 直线 AC 的斜率 k ACy (x5)x 5直线 BC 的斜率kBCy 5 ( x 5)x 由题意,得 k AC k BCm . 所以, y y m( x5)5 x 5x化简得,x 2y 2 1(x 5)2525m当 m 0 时,点 C 的轨迹是椭圆 (m 1) ,或许圆 ( m 1) ,并除掉两点 ( 5,0),(5,0) ;当 m 0 时,点 C 的轨迹是双曲线,并除掉两点( 5,0),(5,0) ;11、解:设抛物线 y 2 4x 上的点 P 的坐标为 ( x, y) ,则 y 24x .点 P 到直线 yx 3 的距离 dx y 3y 2 4y 12 ( y 2)2824 24 2.当 y 2时, d 的最小值是2 .此时 x1,点 P 的坐标是 (1,2) .12、解:如图,在地道的横断面上,以拱y顶为原点、拱高所在直线为y 轴Ox(向上),成立直角坐标系 .抛物线设地道顶部所在抛物线的方程6 mE为 x 22 py因为点 C (4, 4) 在抛物线上DC所以 422 p( 4) 2 mFA3 m3 m2 p 4B解得高中数学选修2-1 课后习题答案 [ 人教版 ]x 24 y .EFh 0.5. F (3, h 5.5)把点 F 的坐 代入方程 x 24y ,解得 h3.25 .答: 通 地道的限制高度3.2 m.第二章复习参照题 B 组( P81)1、SPF 1F 224 3 .2、解:由 意,得 PF 1x .把 xc 代入 方程,解得yb 2 . 所以,点 P 的坐 是 ( c, b 2)aa直 OP 的斜率 k 1b 2 .直 AB 的斜率 k 2b .aca由 意,得b 2b,所以, bc , a2c .aca由已知及 F 1A a c ,得 ac 105所以 (1 2) c 105 ,解得 c5所以, a10 , b5所以, 的方程x 2y 2 1.1053、解: 点 A 的坐 (x 1, y 1 ) ,点 B 的坐 ( x 2 , y 2 ) .由 OA OB ,得 x 1x 2y 1y 2 0 .由已知,得直 AB 的方程 y2x 5 .有 y 1 y 25( y 1 y 2 ) 25 0 ⋯⋯①由 y2x 5 与 y 22px 消去 x ,得 y 2py 5 p0 ⋯⋯②y 1y 2p , y 1 y 25 p ⋯⋯③把③代入①,解得p54高中数学选修2-1 课后习题答案 [ 人教版 ]当 p5时,方程②成为 4 y 25y 25 0 ,明显此方程有实数根 .所以, p5444、解:如图,以连结 F 1 , F 2 的直线为 x 轴,线段 F 1 F 2 的中点为原点,成立直角坐标系 .对于抛物线,有p1763 529 2292 ,2所以, p4584 , 2 p 9168 .对于双曲线,有c a 2080c a 529解此方程组,得 a 775.5, c 1304.5所以, b 2 c 2 a 2 1100320 .(第 4 题)所以,所求双曲线的方程是x 2y 2 601400.31 ( x 775.5) .1100320因为抛物线的极点横坐标是 (1763 a)(1763 775.5)987.5所以,所求抛物线的方程是y 2 9168( x987.5)答:抛物线的方程为 y 29168( x 987.5) ,双曲线的方程是x 2y 21 ( x 775.5) .601400.311003205、解:设点 M 的坐标为 ( x, y)由已知,得 直线 AM 的斜率 k AMy ( x 1)x 1直线 BM 的斜率 k BMy ( x 1)x1由题意,得 kAMk2 ,所以y y 2( x1),化简,得 xy x 2 1(x1)BMx1 x 1所以,点 M 轨迹方程是 xy x 21(x1) .6、解:(1)当 m 1时,方程表示 x 轴;( 2)当m3 时,方程表示 y 轴;(3)当 m1,m 3 时,把方程写成x 2 y23 mm 1.1①当 1 m 3, m 2 时,方程表示椭圆;② m 2 时,方程表示圆;③当 m 1,或 m3时,方程表示双曲线 .7、以 AB 为直径的圆与抛物线的准线 l 相切 .高中数学选修2-1 课后习题答案 [ 人教版 ]垂线,垂足分别为 D , E .由抛物线的定义,得AD AF , BE BF .所以, AB AF BF AD BE .设 AB 的中点为 M ,且过点 M 作抛物线y22px ( p0) 的准线l的垂线,垂足为C .明显 MC ∥x轴,所以, MC 是直角梯形 ADEB 的中位线.于是, MC 1( AD BE )1AB .所以,点 C 在以 AB 为直径的圆上.22又 MC l ,所以,以 AB 为直径的圆与抛物线的准线l 相切.近似地,能够证明:对于椭圆,以经过焦点的弦为直径的圆与相应的准线相离;对于双曲线,以经过焦点的弦为直径的圆与相应的准线订交.高中数学选修 2-1 课后习题答案 [ 人教版 ]第三章空间向量与立体几何3.1空间向量及其运算练习( P86)1、略 .2、略 .uuuur uuuruuur uuur uuuur uuur uuur uuur uuuur uuur uuur uuur 3、 A C ABAD AA , BD AB AD AA , DB AA AB AD .练习( P89)uuuruuuruuuur1、(1) AD ; (2) AG ;(3) MG .2、(1) x 1; (2) x y1; (3) x y1 .3、如图 .22A CPB QRSO(第 3 题)练习( P92)1、 B .uuuur uuur uuuruuur2、解:因为 ACABADAA ,uuuur2uuur uuur uuur 所以 AC( AB AD AA )2uuur 2 uuur 2 uuur 2uuur uuur uuur uuur uuur uuurABADAA2( AB AD AB AA AD AA )uuuur 42 32 52 2 (0 10 7.5)8585所以 AC3、解:因为 AC所以 AC BD , AC AB ,又知 BD AB .uuur uuur uuur uuur 0uuur uuur 0 .所以 AC BD 0 , AC AB ,又知 BD AB uuur 2 uuur uuur CD CD CDuuur uuur uuuruuur uuuruuur(CA AB BD ) (CA ABBD )uuur 2 uuur 2uuur2CAAB BDa 2b 2c 2所以 CDa 2b 2c 2 .高中数学选修 2-1 课后习题答案 [ 人教版 ]r r r r rr r r r r 1、向量 c 与 a b , a b 必定组成空间的一个基底 . 不然 c 与 ab , a b 共面,r r r2、共面于是 c 与 a , b 共面,这与已知矛盾 .uuur uuuruuur uuur uuur uuur uuur uuur uuuur r r r 2、(1)解: OB OBBB OA AB BB OA OC OO a b c ;uuur uuur uuur uuur uuuur r rBA BABBOC OOc buuur uuur uuur uuur uuur uuuur r r rCA CA AA OA OC OO a bcuuur uuur uuuruuur1 uuur r 1 rr 1rr1r(2) OGOC CGOCCBb (ac)ab2 c .222练习( P97)1、(1) ( 2,7,4) ; (2) ( 10,1,16); (3) ( 18,12,30) ; ( 4)2.2、略 .3、解:分别以 DA ,DC , DD 1 所在的直线为 x 轴、 y 轴、 z 轴,成立空间直角坐标系 .则 D (0,0,0) , B 1 (1,1,1), M (1,1,0) , C(0,1,0) 2uuuur uuuur 1所以, DB 1 (1,1,1), CM (1, ,0) .2uuuur uuuur 1 1uuuur uuuurDB 1 CM 015所以, cos2.DB 1, CMuuuur uuuur 1 15DB 1 CM31D'4C'习题 3.1 A 组( P97)A'B' Muuuruuur uuur D GC1、解:如图,(1) ABBC AC ;uuur uuur uuuruuur uuur uuur uuuur uuuur(2) AB AD AAACAA AC CC AC ;A(第 1 题) Buuur uuur1 uuuur uuur uuuuruuuur(3)设点 M 是线段 CC 的中点,则 ABADCCACCMAM ;1 uuur 21 uuuur(4)设点 G 是线段 AC 的三均分点,则uuur uuuruuur ( AB AD AA ) AC AG .uuur uuuur uuuur uuur33向量 AC , AC , AM , AG 如下图 .2、 A .uuuur 2 uuur uuur uuur3、解: AC ( AB AD AA )2高中数学选修2-1 课后习题答案 [ 人教版 ]uuur 2 uuur 2 uuur 2 uuur uuur uuur uuur uuur uuurAB AD AA 2( AB AD AB AA AD AA ) 52 32 722(5 3 1 5 72 3 7 2 )2 2298 56 2所以, AC13.3 .uuur uuuruuur uuur 1a2;4、(1) AB ACAB AC cos60uuur uuuruuur uuur21a 2;(2) AD DBAD DB cos120uuur uuur uuur uuur 2 uuur uuur1 a2 1 1(3) GF AC GF AC cos180 2 ( GF AC a) ;2 2 uuur uuur uuur uuur 1 a 2 uuur 1 uuur 1(4) EF BC EF BC cos60 4 ( EF 2 BD a) ; uuur uuur uuur uuur uuur uuur 21 2 1 1; (5) FG BA FG BA cos120 a ( FG2 AC a)4 2uuur uuur uuur uuur 1 uuur 1 uuur(6) GE GF(GCCB2 BA)CA21 uuuruuur1 uuur 1 uuur( DCCB2 BA)2 CA21 uuur uuur 1 uuur uuur 1 uuur uuur4 DC CA 2 CB CA 4 BA CA1 uuur uuur 1 uuur uuur 1 uuur uuur4 DC CA cos120 2 CB CA cos604 BA CA cos601 a 245、(1) 60 ; (2)略 .r rr6、向量 a 的横坐标不为 0,其余均为 0;向量 b 的纵坐标不为 0,其余均为 0;向量 c 的竖坐标不为 0,其余均为 0.7、(1)9; (2) (14, 3,3) .rr r r 0 ,即 82 3x0 ,解得 x10 . 8、解:因为 ab ,所以 a buuuruuur3(5,1, 10)9、解: AB ( 5, 1,10) , BAuuuur1 uuur uuur1 9 2) ,设 AB 的中点为 M , OM2(OAOB )( , ,uuur 2 2所以,点 M 的坐标为 (1 , 9 ,( 5)2( 1)21021262) , AB2 210、解:以 DA , DC , DD 1 分别作为 x 轴、 y 轴、 z 轴成立空间直角坐标系 O xyz .高中数学选修 2-1 课后习题答案 [ 人教版 ]则 C ,M , D 1 , N 的坐标分别为: C (0,1,0) , M (1,0, 1D 1(0,0,1)1.) , , N (1,1, )uuuur1 uuuur 1 22CM (1, 1, ) , D 1 N (1,1, )2 2uuuur 12 ( 1)2 ( 1) 2 uuuur 12 12 1)2所以 CM 3 , D 1 N ( 32 2 2 2uuuur uuuur1 1 11cos CM , D 1N9 4 94因为异面直线 CM 和 D 1N 所成的角的范围是 [0,]2所以, CM 和 D 1 N 所成的角的余弦值为 1.31911、 ( , ,3)2 2习题 3.1 B组( P99)1、证明:由已知可知, uuuruuur uuur uuurOA BC , OB ACuuur uuuruuur uuuruuur uuur uuur uuur uuur uuur0 .∴ OA BC0 , OB AC 0 ,所以 OA (OC OB ) 0 , OB (OC OA)uuur uuur uuur uuur uuur uuur uuur uuur∴ OA OC OA OB , OB OC OB OA .uuur uuur uuur uuur uuur uuur uuur 0 uuur uuur 0 .∴ OA OC OB OC 0 , (OA OB) OC , BA OC∴ OC AB .2、证明:∵点 E, F ,G , H 分别是 OA,OB, BC ,CA 的中点 . uuur1 uuuruuur1 uuuruuuruuur∴ EFAB , HGAB ,所以 EFHG22∴四边形 EFGH 是平行四边形 .uuur uuur 1 uuur 1 uuur 1 uuur uuur uuur 1 uuur uuuruuur uuurEFEHABOC4 (OBOA) OC4(OB OCOA OC )2 2∵ OA OB , CA CB (已知), OC OC .∴ BOC ≌ AOC ( SSS )∴ BOC AOCuuur uuur uuur uuur∴ OB OC OA OCuuur uuur ∴ EF EH 0uuur uuur ∴ EF EH∴ 平行四边形 □ EFGH 是矩形 .。
名校新学案高中数学人教A版选修2-1课后作业1.2.2充要条件习题课(含答案详析)

第一章 1.2 第2课时一、选择题1.“a =1”是“直线x +y =0和直线x -ay =0互相垂直”的( ) A .充分而不必要条件 B .必要而不充分条件 C .充要条件 D .既不充分也不必要条件[答案] C[解析] 当a =1时,直线x -ay =0化为直线x -y =0,∴直线x +y =0与直线x -y =0垂直;当直线x +y =0和直线x -ay =0互相垂直时,有1-a =0,∴a =1,故选C. 2.m =3是直线3x -y +m =0与圆x 2+y 2-2x -2=0相切的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件 [答案] A[解析] 由圆心(1,0)到直线3x -y +m =0距离d =|3+m |2=3得,m =3或-33,故选A.3.设集合A ={x ∈R |x -2>0},B ={x ∈R |x <0},C ={x ∈R |x (x -2)>0},则“x ∈A ∪B ”是“x ∈C ”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件 [答案] C[解析] 因为A ∪B =C ,故“x ∈A ∪B ”是“x ∈C ”的充要条件. 4.“a +c >b +d ”是“a >b 且c >d ”的( ) A .必要不充分条件 B .充分不必要条件 C .充分必要条件 D .既不充分也不必要条件 [答案] A[解析] 如a =1,c =3,b =2,d =1时,a +c >b +d , 但a <b ,故由“a +c >b +d ”⇒/ “a >b 且c >d ”, 由不等式的性质可知,若a >b 且c >d ,则a +c >b +d ,∴“a +c >b +d ”是“a >b 且c >d ”的必要不充分条件.5.设命题甲为:0<x <5,命题乙为:|x -2|<3,那么甲是乙的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件[答案] A[解析] 解不等式|x -2|<3得-1<x <5, ∵0<x <5⇒-1<x <5但-1<x <5⇒/ 0<x <5, ∴甲是乙的充分不必要条件,故选A.6.(2014·南昌市高二期中)设l ,m ,n 均为直线,其中m ,n 在平面α内,则“l ⊥α”是“l ⊥m 且l ⊥n ”的( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件 [答案] A[解析] ∵l ⊥α,m ⊂α,n ⊂α,∵l ⊥m 且l ⊥n ,故充分性成立;又l ⊥m 且l ⊥n 时,m 、n ⊂α,不一定有m 与n 相交,∴l ⊥α不一定成立,∴必要性不成立,故选A.二、填空题7.平面向量a 、b 都是非零向量,a ·b <0是a 与b 夹角为钝角的________条件. [答案] 必要不充分[解析] 若a 与b 夹角为钝角,则a ·b <0,反之a ·b <0时,如果a 与b 方向相反,则a 与b 夹角不是钝角.8.已知三条直线l 1:x -y =0,l 2:x +y -2=0,l 3:5x -ky -15=0,则l 1、l 2、l 3构不成三角形的充要条件是k ∈集合________.[答案] {-5,5,-10}[解析] ①l 1∥l 3时,k =5;②l 2∥l 3时,k =-5; ③l 1、l 2、l 3相交于同一点时,k =-10. 三、解答题9.方程mx 2+(2m +3)x +1-m =0有一个正根和一个负根的充要条件是什么?[解析] 由题意知⎩⎨⎧(2m +3)2-4m (1-m )>0,1-mm <0.∴m >1或m <0,即所求充要条件是m >1或m <0.10.已知数列{a n }的前n 项和S n =p n +q (p ≠0且p ≠1),求证:数列{a n }为等比数列的充要条件为q =-1.[证明] 充分性:当q =-1时,a 1=p -1,当n ≥2时,a n =S n -S n -1=p n -1(p -1),当n =1时也成立. 于是a n +1a n=p n (p -1)p n -1(p -1)=p ,即数列{a n }为等比数列.必要性:当n =1时,a 1=S 1=p +q . 当n ≥2时,a n =S n -S n -1=p n -1(p -1), ∵p ≠0且p ≠1,∴a n +1a n =p n (p -1)p n -1(p -1)=p ,∵{a n }为等比数列,∴a 2a 1=a n +1a n=p ,即p (p -1)p +q =p , ∴p -1=p +q ,∴q =-1.综上所述,q =-1是数列{a n }为等比数列的充要条件.一、选择题11.设{a n }是等比数列,则“a 1<a 2<a 3”是“数列{a n }是递增数列”的( ) A .充分而不必要条件 B .必要而不充分条件 C .充要条件 D .既不充分也不必要条件[答案] C[解析] 若a 1<a 2<a 3,则a 1<a 1q <a 1q 2,若a 1>0,则q >1,此时为递增数列,若a 1<0,则0<q <1,同样为递增数列,故充分性成立,必要性显然成立.12.(2013·安徽理)“a ≤0”是“函数f (x )=|(ax -1)x |在区间(0,+∞)内单调递增”的 ( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件[答案] C[解析] 本题考查了函数单调性与充分必要条件的判断.若a =0,则f (x )=|x |在(0,+∞)内单调递增,若“a <0”,则f (x )=|(ax -1)x |=|ax 2-x |其图象如图所示,在(0,+∞)内递增;反之,若f (x )=|(ax -1)x |在(0,+∞)内递增,从图中可知a ≤0,故选C. 13.下列命题中的真命题有( )①两直线平行的充要条件是两直线的斜率相等;②△ABC 中,AB →·BC →<0是△ABC 为钝角三角形的充要条件; ③2b =a +c 是数列a 、b 、c 为等差数列的充要条件;④△ABC 中,tan A tan B >1是△ABC 为锐角三角形的充要条件. A .1个 B .2个 C .3个 D .4个[答案] B[解析] 两直线平行不一定有斜率,①假.由AB →·BC →<0只能说明∠ABC 为锐角,当△ABC 为钝角三角形时,AB →·BC →的符号也不能确定,因为A 、B 、C 哪一个为钝角未告诉,∴②假;③显然为真.由tan A tan B >1,知A 、B 为锐角,∴sin A sin B >cos A cos B , ∴cos(A +B )<0,即cos C >0.∴角C 为锐角, ∴△ABC 为锐角三角形.反之若△ABC 为锐角三角形,则A +B >π2,∴cos(A +B )<0,∴cos A cos B <sin A sin B , ∵cos A >0,cos B >0,∴tan A tan B >1,故④真.14.设a 、b 是两条直线,α、β是两个平面,则a ⊥b 的一个充分条件是( ) A .a ⊥α,b ∥β,α⊥βB .a ⊥α,b ⊥β,α∥βC.a⊂α,b⊥β,α∥βD.a⊂α,b∥β,α⊥β[答案] C[解析]对选项A如图①所示,由图可知a∥b,故排除A;对选项B如图②所示,由图可知a∥b,故排除B;对选项D如图③所示,其中a∥l,b∥l,由图可知a∥b,故排除D.二、填空题15.函数f(x)的定义域为I,p:“对任意x∈I,都有f(x)≤M”.q:“M为函数f(x)的最大值”,则p是q的________条件.[答案]必要不充分[解析]只有当(1)对于任意x∈I,都有f(x)≤M,(2)存在x0∈I,使f(x0)=M,同时成立时,M才是f(x)的最大值,故p⇒/ q,q⇒p,∴p是q的必要不充分条件.16.f(x)=|x|·(x-b)在[0,2]上是减函数的充要条件是______________________.[答案]b≥4[解析] f (x )=⎩⎪⎨⎪⎧x (x -b ) x ≥0,-x (x -b ) x <0.若b ≤0,则f (x )在[0,2]上为增函数,∴b >0, ∵f (x )在[0,2]上为减函数,∴b2≥2,∴b ≥4.三、解答题17.求关于x 的方程ax 2+2x +1=0至少有一个负的实根的充要条件. [解析] ①a =0时适合.②当a ≠0时,显然方程没有零根,若方程有两异号的实根,则a <0;若方程有两个负的实根,则必须满足⎩⎨⎧1a>0-2a<0Δ=4-4a ≥0,解得0<a ≤1.综上可知,若方程至少有一个负的实根,则a ≤1;反之,若a ≤1,则方程至少有一个负的实根,因此,关于x 的方程ax 2+2x +1=0至少有一个负的实根的充要条件是a ≤1.[点评] ①a =0的情况不要忽视;②若令f (x )=ax 2+2x +1,由于f (0)=1≠0,从而排除了方程有一个负根,另一个根为零的情况.18.已知p :x +210-x ≥0,q :x 2-2x +1-m 2≤0(m <0),且p 是q 的必要条件,求实数m的取值范围.[解析] 由x +210-x ≥0,解得-2≤x <10,令A ={x |-2≤x <10}.由x 2-2x +1-m 2≤0可得[x -(1-m )].[x -(1+m )]≤0,而m <0,∴1+m ≤x ≤1-m ,令B ={x |1+m ≤x ≤1-m }.∵p 是q 的必要条件,∴q ⇒p 成立,即B ⊆A .则⎩⎨⎧1+m ≥-21-m <10m <0,解得-3≤m <0.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
答案解析 数学㊃选修2-1(A 版)
-103 -要条件 为真命题.②因为M ={-1,m 2},N ={2,4},M ɘN ={4},所以m 2=4,即m =ʃ2,所以命题 若集合M ={-1,m 2},集合N ={2,4},则 m =2 是 M ɘN ={4} 的必要不充分条件 是假命题.③因为x 2-x <0,所以0<x <1,即M ={x |0<x <1}.又因为|x |<2,所以-2<x <2,即N ={x |-2<x <2},所以M ⫋N ,所以p 是q 的充分不必要条件,即命题为真命题.
④因为,所以p 是q 的充分条件.所以命题为真命题.ʌ典例2ɔ(1)-1(2)不等式x 2-8x -20>0的解集为A ={x |x >10或x <-2};不等式x 2-2x +1-a 2>0的解集为B ={x |x >1+a 或x <1-a ,a >0}.依题意p ⇒q ,所以A ⊆B .于是有a >0,1+a ɤ10,1-a ȡ-2,{解得0<a ɤ3.所以正实数a 的取值范围是(0,3].ʌ互动探究ɔʌ解析ɔ因为x 2>1⇒x <-1或x >1,又 x 2>1 是 x >a 的必要不充分条件,所以a ȡ1,所以a 的最小值为1.(P 9)1.A 2.B 3.必要 4.充分5.ʌ解析ɔ由题意知,Q ={x |1<x <3},Q ⇒P ,所以a -4ɤ1,a +4ȡ3
,{解得-1ɤa ɤ5.所以实数a 的取值范围是[-1,5].第2课时 充要条件的应用
(P 9)基础梳理
充要条件 充分必要条件 互为充要条件
(P 10)ʌ典例1ɔ(1)A (2)C (3)①易知,p :x +y =8,q :x =2且y =
6,显然q ⇒p ,但p ⇒/q ,即q 是p 的充分不必要条件,根据原命题与其逆否命题的等价性知,p 是q 的充分不必要条件.②显然x ɪA ɣB 不一定有x ɪB ,但x ɪB 一定有x ɪA ɣB ,所以p 是q 的必要不充分条件.ʌ典例2ɔ(1)B (2)不是.设x 2+a x +1=0的两实根分别为x 1,x 2,则平方和大于3的等价条件是Δ=a 2-4ȡ0,x 21+x 22=(x 1+x 2)2-2x 1x 2 =(-a )2-2>3,{即|a |>5.又{a ||a |>5}⫋{a ||a |>3},所以|a |>3这个条件是其必要不充分条件.ʌ互动探究ɔʌ解析ɔ因为|x |ɤ4⇔-4ɤx ɤ4,所以A ={x |-4ɤx ɤ4}.又A ⊆B ⇔a <-4,所以 A ⊆B 是 a >5 的既不充分也不必要条件.ʌ典例3ɔ(1)A (2)充分性:当0<a <45时,判别式Δ=a 2-4a (1-a )=5a 2-4a =a (5a -4)<0,则a x 2-a x +1-a >0对一切实数x 都成立.而当a =0时,不等式a x 2-a x +1-a =1>0.显然当a =0时,不等式a x 2-a x +1-a >0对一切实数x 都成立.必要性:因为a x 2-a x +1-a >0对一
切实数x 都成立,所以a =0或a >0,Δ=a 2-4a 1-a ()<0,{解得0ɤa <45.故0ɤa <45是不等式a x 2-a x +1-a >0对一切实数x 都成立的充要条件.(P 11)1.A 2.B 3.充要4.1<x <25.ʌ解析ɔ由二次函数的图象可知当-b 2a ɤ1,即b ȡ-2a 时,函数y =a x 2+b x +c (a >0)在[1,+ɕ)上单调递增. 1.3 简单的逻辑联结词 (P 12)基础梳理1.p 且q p 或q 非p p 的否定2.(1)p ɡq 是真命题 p ɡq 是假命题(2)p ᶱq 是真命题 p ᶱq 是假命题(3)p 必是假命题 p 必是真命题(P 12)ʌ典例1ɔ(1)且 p ɡq (2)①p 或q :5是有理数或5是整数;p 且q :5是有理数且5是整数;非p :5不是有理数.②p 或q :不等式x 2-2x -3>0的解集是(-ɕ,-1)或不等式x 2-2x -3>0的解集是(3,+ɕ);p 且q :不等式x 2-2x -3>0的解集是(-ɕ,-1)且不等式x 2-2x -3>0的解集是(3,+ɕ);非p :不等式x 2-2x -3>0的解集不是(-ɕ,-1).ʌ典例2ɔ(1)B (2)①这个命题是 p ɡq 的形式,其中p :48是16的倍数,是真命题;q :48是12的倍数,是真命题,所以 48是16与12的公倍数 是真命题.②这个命题是 p 的形式,其中p :方程x 2+x +3=0有实数根,是假命题,所以命题 方程x 2+x +3=0没有实数根 是真命题.③这个命题是 p ᶱq 的形式.其中p :相似三角形的周长相等,是假命题;q :相似三角形的对应角相等,是真命题,所以 相似三角形的周长相等或对应角相等 是真命题.ʌ典例3ɔ(1)C (2)解题流程:ʌ互动探究ɔʌ解析ɔ由条件 p ɡq 为假命题 可得到三种情况(1)p 真,q 假;(2)p 假,q 真;(3)p 假,q 假.前两种情况的解法同第(2)题解法,当p 假时,0<a ɤ1;当q 假时,a ȡ2,所以当p 假q 假时,a ɪ⌀,综上0<a ɤ1或a ȡ2.(P 14)1.C 2.C 3.B 4.①④⑤⑥5.ʌ解析ɔ(1)因为p 为假命题,q 为真命题,所以p ɡq 为假命题,p ᶱq 为真命题,p 为真命题.(2)因为p 为假命题,q 为假命题,所以p ɡq 为假命题,p ᶱq 为假命题,p 为真命题. 1.4 全称量词与存在量词 1.4.1 全称量词 1.4.2 存在量词(P 14)基础梳理1.(1)对所有的 对任意一个(2)全称量词 ∀x ɪM ,p (x ) 对任意x 属于M ,有p (x )成立2.(1)存在一个 至少有一个(2)存在量词 ∃x 0ɪM ,p (x 0) 存在一个x 0属于M ,使p (x 0)成立(P 15)ʌ典例1ɔ(1)C (2)B ʌ变式训练ɔ①可以改写为 所有的凸多边形的外角和等于360ʎ ,是全称命题.②含有存在量词 有些 ,故是特称命题.③含有全称量词 任意 ,故是全称命题.④含有存在量词 有一个 ,是特称命题.ʌ典例2ɔ(1)①真命题.因为x 2-x +1-12=x -12()2+14ȡ14>0.所以x 2-x +1>12恒成立.②真命题.例如α0=π4,β0=π2,符合题意.。
