沉降计算(JGC5)CT-2
常用的地基沉降计算方法

6.3 常用的地基沉降计算方法这里所讲的地基沉降量是指地基最终沉降量,目前常用的计算方法有:弹性力学法、分层总和法、应力面积法和考虑应力历史影响的沉降计算法。
所谓最终沉降量是地基在荷载作用下沉降完全稳定后的沉降量,要达到这一沉降量的时间取决于地基排水条件。
对于砂土,施工结束后就可以完成;对于粘性土,少则几年,多则十几年、几十年乃至更长时间。
6.3.1 计算地基最终沉降量的弹性力学方法地基最终沉降量的弹性力学计算方法是以Boussinesq 课题的位移解为依据的。
在弹性半空间表面作用着一个竖向集中力P 时,见图6-5,表面位移w (x, y, o )就是地基表面的沉降量s :E r P s 21μπ-⋅= (6-8)式中 μ—地基土的泊松比;E —地基土的弹性模量(或变形模量E 0);r —为地基表面任意点到集中力P 作用点的距离,22y x r +=。
对于局部荷载下的地基沉降,则可利用上式,根据叠加原理求得。
如图6-6所示,设荷载面积A 内N (ξ,η)点处的分布荷载为p 0(ξ,η),则该点微面积上的分布荷载可为集中力P= p 0(ξ,η)d ξd η代替。
于是,地面上与N 点距离r =22)()(ηξ-+-y x 的M (x, y )点的沉降s (x, y ),可由式(6-8)积分求得:⎰⎰-+--=Ay x d d p E y x s 22002)()(),(1),(ηξηξηξμ (6-9)从式(6-9)可以看出,如果知道了应力分布就可以求得沉降;反过来,若沉降已知又可以反算出应力分布。
对均布矩形荷载p 0(ξ,η)= p 0=常数,其角点C 的沉降按上式积分的结果为:图6-5 集中力作用下地基表面的沉降曲线 图6-6 局部荷载下的地面沉降(a )任意荷载面;(b )矩形荷载面021bp E s c ωμ-= (6-10)式中 c ω—角点沉降影响系数,由下式确定:⎪⎪⎭⎫ ⎝⎛+++++=)1ln()11ln(122m m mm m c πω (6-11)式中 m=l/b 。
常用的地基沉降计算方法

6.3 常用的地基沉降计算方法这里所讲的地基沉降量是指地基最终沉降量,目前常用的计算方法有:弹性力学法、分层总和法、应力面积法和考虑应力历史影响的沉降计算法。
所谓最终沉降量是地基在荷载作用下沉降完全稳定后的沉降量,要达到这一沉降量的时间取决于地基排水条件。
对于砂土,施工结束后就可以完成;对于粘性土,少则几年,多则十几年、几十年乃至更长时间。
6.3.1 计算地基最终沉降量的弹性力学方法地基最终沉降量的弹性力学计算方法是以Boussinesq 课题的位移解为依据的。
在弹性半空间表面作用着一个竖向集中力P 时,见图6-5,表面位移w (x, y,o )就是地基表面的沉降量s :E r P s 21μπ-⋅= (6-8)式中 μ—地基土的泊松比;E —地基土的弹性模量(或变形模量E 0);r —为地基表面任意点到集中力P 作用点的距离,22y x r +=。
对于局部荷载下的地基沉降,则可利用上式,根据叠加原理求得。
如图6-6所示,设荷载面积A 内N (ξ,η)点处的分布荷载为p 0(ξ,η),则该点微面积上的分布荷载可为集中力P= p 0(ξ,η)d ξd η代替。
于是,地面上与N点距离r =22)()(ηξ-+-y x 的M (x, y )点的沉降s (x, y ),可由式(6-8)积分求得:⎰⎰-+--=Ay x d d p E y x s 22002)()(),(1),(ηξηξηξμ (6-9)从式(6-9)可以看出,如果知道了应力分布就可以求得沉降;反过来,若沉降已知又可以反算出应力分布。
对均布矩形荷载p 0(ξ,η)= p 0=常数,其角点C 的沉降按上式积分的结果为:021bp E s c ωμ-= (6-10)式中 c ω—角点沉降影响系数,由下式确定:⎪⎪⎭⎫ ⎝⎛+++++=)1ln()11ln(122m m mm m c πω (6-11)式中 m=l/b 。
利用式(6-10),以角点法易求得均布矩形荷载下地基表面任意点的沉降。
2021年地基沉降量计算

地基沉降量计算欧阳光明(2021.03.07)地基变形在其表面形成的垂直变形量称为建筑物的沉降量。
在外荷载作用下地基土层被压缩达到稳定时基础底面的沉降量称为地基最终沉降量。
一、分层总和法计算地基最终沉降量计算地基的最终沉降量,目前最常用的就是分层总和法。
(一)基本原理该方法只考虑地基的垂向变形,没有考虑侧向变形,地基的变形同室内侧限压缩试验中的情况基本一致,属一维压缩问题。
地基的最终沉降量可用室内压缩试验确定的参数(e i、E s、a)进行计算,有:变换后得:或式中:S--地基最终沉降量(mm);e1--地基受荷前(自重应力作用下)的孔隙比;e2--地基受荷(自重与附加应力作用下)沉降稳定后的孔隙比;H--土层的厚度。
计算沉降量时,在地基可能受荷变形的压缩层范围内,根据土的特性、应力状态以及地下水位进行分层。
然后按式(4-9)或(4-10)计算各分层的沉降量S i。
最后将各分层的沉降量总和起来即为地基的最终沉降量:(二)计算步骤1)划分土层如图4-7所示,各天然土层界面和地下水位必须作为分层界面;各分层厚度必须满足H i≤0.4B(B为基底宽度)。
2)计算基底附加压力p03)计算各分层界面的自重应力σsz和附加应力σz;并绘制应力分布曲线。
4)确定压缩层厚度满足σz=0.2σsz的深度点可作为压缩层的下限;对于软土则应满足σz=0.1σsz;对一般建筑物可按下式计算z n=B(2.5-0.4ln B)。
5)计算各分层加载前后的平均垂直应力p1=σsz; p2=σsz+σz6)按各分层的p1和p2在e-p曲线上查取相应的孔隙比或确定a、E s等其它压缩性指标7)根据不同的压缩性指标,选用公式(4-9)、(4-10)计算各分层的沉降量S i8)按公式(4-11)计算总沉降量S。
分层总和法的具体计算过程可参例题4-1。
例题4-1已知柱下单独方形基础,基础底面尺寸为2.5×2.5m,埋深2m,作用于基础上(设计地面标高处)的轴向荷载N=1250kN,有关地基勘察资料与基础剖面详见下图。
沉降计算程序

沉降计算程序的理论依据为《建筑地基基础设计规范GB 50007-2011》采用的分层总和法。
即在地基沉降压缩层深度范围内划分出若干分层, 计算出各分层压缩量, 然后求其总和。
计算时, 根据基础类型及各土层有关指标, 求出土中附加应力分布。
现将分层总和法计算沉降的基本理论简述如下:1 基本原理计算地基变形时,地基内的应力分布,可采用各向同性均质线性变形体理论。
其最终变形量可按下式进行计算:s——地基最终变形量(mm);s’——按分层总和法计算出的地基变形量(mm);Ψs——沉降计算经验系数,根据地区沉降观测资料及经验确定,无地区经验时可根据变形计算深度范围内压缩模量的当量值()、基底附加压力按表5.3.5 取值;n ——地基变形计算深度范围内所划分的土层数(图5.3.5);p——相应于作用的准永久组合时基础底面处的附加压力(kPa);Esi——基础底面下第i 层土的压缩模量(MPa),应取土的自重压力至土的自重压力与附加压力之和的压力段计算;Z i 、Zi-1——基础底面至第i 层土、第i-1 层土底面的距离(m);——基础底面计算点至第i 层土、第i-1 层土底面范围内平均附加应力系数,可按本规范附录K 采用。
2 计算步骤1)选择基础类型;变电所一般采用矩形基础类型,其中长度用l表示,宽度用b表示。
2)选择沉降计算点的位置:选择沉降计算剖面,在每一个剖面上选择若干计算点。
在计算基底压力和地基中附加应力时,根据基础的尺寸及所受荷载的性质(中心受压、偏心或倾斜等),求出基底压力的大小和分布;再结合地基土层的性状,选择沉降计算点的位置。
矩形基础一般取中心点。
3)地基变形计算深度Zn确定。
根绝规范5.3.7条和5.3.8条。
4)地基分层。
在分层时天然土层的交界面和地下水位面应为分层面,同时在同一类土层中分层的厚度不宜过大。
一般取分层厚h i≤0.4b或h i=1~2m,b 为基础宽度。
5)附加应力系数的计算。
沉降计算Word版

&2垂直荷载地基应力σp(一)计算图式如图[1]1.空心桩外荷载P=40547(KN )i.50m T 梁支座反力 P 1=36960(KN ) ii.长16.60m 冒 梁 P 2=2291 (KN ) iii. φ2.30m 双桥墩柱 P 3=1296 (KN )2.空心桩自重G 桩=31490(KN )G 1=15 4×2=308×[25KN/方]=7700(KN )G 2=6 8 ×2=136×[25KN/方]=3400(KN )G 3=62.7×4=250×[25KN/方]=6270(KN )G 4=50.1×4=200×[25KN/方]=5000(KN )G 5=9 5 ×4=380×[24KN/方]=9120(KN )3.桩底垂直荷载(恒载)总和∑G 0=P+G=40547+31490=72037(KN )(二)按土壤扩散角计算桩底应力1.如图4-2 土坡扩散角θ=4ϕ=154︒=3.75° 桩长16m 扩散角锥体底面直径如下:D=d+h ·tan θ=11+(16×0.0655) ×2=11+(1.05×2=2.10)=16.10(m )A D =16.102×4π =204(m 2)2.地层不同深度的允许应力(JTGD63-2007)[f a ]=[ f a 0]+k 1r 1(b-2)+ k 2r 2(h-3) --(3.3.4)粉粘土承载力基本容许值[ f a 0]=0.20(MPa )=200(KN/m 2)宽度修正系数k 1=0 深度修正系数k 2=1.5基底埋置深度h=16(m )[ f a h ]=0.200+1.5×1.97×(16-3)=0.200+0.38=0.58(MPa )=580(KN/m 2)3.挖孔桩外形体积∑V g =1957(方)V 1=φ1 4 ×2=154×2=308(方)V 2=φ13.5×2=143×2=286(方)V 3=φ1 3 ×4=133×4=531(方)V 4=φ1 2 ×4=113×4=452(方)V 5=φ1 1 ×4=9 5×4=380(方)4.桩长h=16m 中锥体体积V 0=141615420416286422φφ++=⨯=(方)土的体积V 土= V 0-V g =2864-1957=907(方)土重G 土=907 ×[19.7t/方]=17868(KN)5.桩端水平线上桩自重,垂直重量在直线D=16.10(m )中的应力∑Q g =G 桩+ G 土=31490+17868=49358(KN)应力σg =gDQA ∑=49358204=242(KN/m 2)6.考虑桥墩及上部构造恒载后应力∑Q p = ∑Q g + P=49358+40547=89905(KN)σp = p D Q A ∑= 89905204=441(KN/m 2) <[580 KN/m 2]故安全。
地基沉降的计算方法

地基沉降的计算方法地基在荷载作用下,沉降将随时间发展,其发展规律可以通过土体固结原理进行数值分析来估算。
但是由于固结理论的假定条件和确定计算指标的试验技术上的问题,使得实测地基沉降过程数据在某种意义上较理论计算更为重要。
通过大量的沉降观测资料的积累,可以找出地基沉降过程的具有一定实际应用价值的变形规律,还可以根据路基施工时的实测沉降资料和已取得的经验进行估算,是工程中最为常用的方法。
根据经验沉降预测一般要经过3~6个月恒载(或预压)的观测才能建立。
曲线回归法法是变形预测最常用的方法,德国无碴轨道的经验,认为当曲线回归的相关系数不低于0.92时,所确定的沉降变形趋势是可靠的;当预测的6个月以后的沉降与实际沉降的偏差小于8mm 时,说明预测是稳定的,但要达到准确的预测还要求最终建立沉降预测的时间t 应满足下列条件s(t)/s(t=∞)≥75%式中:s(t): t 时间的沉降观测值; s(t=∞): 预测的总沉降。
通常利用沉降资料进行预测路堤沉降随时间发展的常用方法有以下几种: 1 双曲线法 双曲线方程为:bt a tS S t ++=0 (3.3.2-1)bS S f 10+= (3.3.2-2)式中:t S ——时间t 时的沉降量;f S ——最终沉降量(t =∞);S 0——初期沉降量(t =0);a、b——将荷载不再变化后的3组早期实测数据代入上式组成方程组求得的系数。
沉降计算的具体顺序:(1)确定起点时间(t=0),可取填方施工结束日为t=0;(2)就各实测计算t/(S t-S0),见图3.3.2-1;(3)绘制t与t/(S t-S0)的关系图,并确定系数a,b见图3.3.2-2;(4)计算S t;(5)由双曲线关系推算出沉降S~时间t曲线。
图3.3.2-1用实测值推算最终沉降的方法图3.3.2-2求a,b方法双曲线法是假定下沉平均速率以双曲线形式减少的经验推导法,要求恒载开始实测沉降时间至少半年以上。
沉降计算
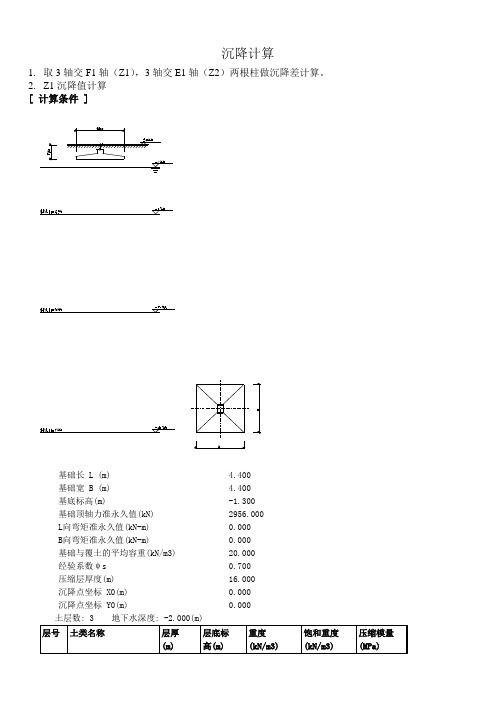
沉降计算1.取3轴交F1轴(Z1),3轴交E1轴(Z2)两根柱做沉降差计算。
2.Z1沉降值计算[ 计算条件 ]基础长 L (m) 4.400基础宽 B (m) 4.400基底标高(m) -1.300基础顶轴力准永久值(kN) 2956.000L向弯矩准永久值(kN-m) 0.000B向弯矩准永久值(kN-m) 0.000基础与覆土的平均容重(kN/m3) 20.000经验系数ψs 0.700压缩层厚度(m) 16.000沉降点坐标 X0(m) 0.000沉降点坐标 Y0(m) 0.000土层数: 3 地下水深度: -2.000(m)计算依据:建筑地基基础设计规范 GB50007-2002底板净反力 (kPa):最大= 155.29 最小=155.29 平均= 155.29角点 q1 = 155.29 q2 = 155.29 q3 = 155.29 q4 = 155.29总沉降量 = 0.700*79.13 = 55.39(mm)压缩模量的当量值: 8.58(MPa)按地基规范GB5007-2002表5.3.5 的沉降计算经验系数 = 0.882(P0≥fak) 和 0.641(P0≤0.75fak) 3.Z2沉降值计算[ 计算条件 ]基础长 L (m) 3.700 基础宽 B (m) 3.700 基底标高(m) -1.300 基础顶轴力准永久值(kN) 2134.000 L向弯矩准永久值(kN-m) 0.000 B向弯矩准永久值(kN-m) 0.000 基础与覆土的平均容重(kN/m3) 20.000 经验系数ψs 0.700 压缩层厚度(m) 16.000 沉降点坐标 X0(m) 0.000 沉降点坐标 Y0(m) 0.000 土层数: 3 地下水深度: -2.000(m)计算依据:建筑地基基础设计规范 GB50007-2002底板净反力 (kPa):最大= 158.48 最小=158.48 平均= 158.48角点 q1 = 158.48 q2 = 158.48 q3 = 158.48 q4 = 158.48各层土的压缩情况:总沉降量 = 0.700*69.47 = 48.63(mm)压缩模量的当量值: 8.57(MPa)按地基规范GB5007-2002表5.3.5 的沉降计算经验系数 = 0.882(P0≥fak) 和 0.641(P0≤0.75fak) 4.沉降值差计算沉降值差=79.13-69.47=9.66mm0.002L=0.002X5700=11.4mm9.66mm<11.4mm,满足要求。
土力学沉降量计算ppt课件

未知参数, 是表示误差的随机变量,一般可认为 ~ N(0, 2 ) , 0 。
n 对 x1, x2 ,, xm , y 进行 次观测,得到观测值:
(xi 1, xi 2 , , xi m , yi ) , i 1, 2,, n 。
之间究竟着存在这怎样的关系,这种关系如何体现在变化规律上面 的。
例如:下面是经回归分析确定的某水坝坝顶一点温度影响沉降的 数学模型
E(t)0.287s5in 3t()8.470c9o4 st)(1.101s8in 2 (t)0.004c2o2 2 s(t)
该式子反映了时间 t 与水坝坝顶沉降 E(t) 的关系
2021/5/29
;
三.回归分析和曲线拟合的方法 原理简介
为找到变形量的变化 规律,我们将观测到的 变形结果拟合成成一些 曲线,并进行回归分析, 以帮助我们确定变形的 趋势,也可以利用拟合 的曲线对所得结果进行 外推等趋势分析。
2021/5/29
;
一般地,称由 y 0 1x 确定的模型为一元线性回归模型,
b,bint,stats a=polyfit(x,Y,2)
2021/5/29
;
a=
0.0000 -0.0151 -0.2496
所以我y们 知道0 该.0 曲线1方x程5 为1 0:.2496
z=polyval(a,x);
plot(x,Y,'k+',x,z,'r')
2021/5/29
;
2021/5/29
;
2021/5/29
;
以此类推我们进行了以后的5阶,6阶,7阶 的拟合将只将拟结果给出,其过程与前面相 同。
