初三中考数学第一次模拟考试
2024年中考数学第一次模拟试卷(无锡卷)(全解全析)

2024年中考第一次模拟考试(无锡卷)数学·全解全析(考试时间:120分钟试卷满分:140分)注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答第Ⅰ卷时,选出每小题答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
写在本试卷上无效。
3.回答第Ⅱ卷时,将答案写在答题卡上。
写在本试卷上无效。
4.考试结束后,将本试卷和答题卡一并交回。
一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,恰有一项是符合题目要求的)1.下列各组数中,互为相反数的组是()A .2023-和2023-B .2023和12023C .2023-和2023D .2023-和12023【答案】A【解析】解:A .20232023-=和2023-互为相反数,故A 选项符合题意;B .2023和12023互为倒数,故B 选项不符合题意;C .20232023-=和2023不互为相反数,故C 选项不符合题意;D .2023-和12023不互为相反数,故D 选项不符合题意;故选:A .2.已知114A a =-+,下列结论正确的是()A .当5a =-时,A 的值是0B .当4a >-时,A 的最小值为1C .若A 的值等于1,则4a =-D .若A 的值等于2,则5a =-【答案】D【解析】解:当5a =-时,1111254A =-=+=-+,A 选项错误;当4a >-时,40a +>,104a >+,104a -<+,1114a -<+,即A 的最小值小于1,B 选项错误;当1A =时,1114a =-+,解得4a =-,此时分式无意义,故不合题意,C 选项错误;当2A =时,1214a =-+,解得5a =-,D 选项正确,故选:D .3.光线在不同介质中的传播速度是不同的,因此当光线从水中射向空气时,要发生折射,由于折射率相同,所以在水中平行的光线,在空气中也是平行的.如图,1122,2∠=︒∠的度数为()A .32︒B .58︒C .68︒D .78︒【答案】B【解析】解:如图,根据题意得:a b ,c d ∥,∴13180∠+∠=︒,32∠=∠,∵1122∠=︒,∴258∠=︒.故选:B .4.下列计算错误的是()A .()21x x x x -=-B .325x x x ×=C .()236x x =D .()2224a a -=-【答案】D【解析】解:A 中()21x x x x -=-,正确,故不符合要求;B 中325x x x ×=,正确,故不符合要求;C 中()236x x =,正确,故不符合要求;D()2222444a a a a -=-+≠-,错误,故符合要求;故选:D .5.若点()()()112233A x y B x y C x y ,、,、,是反比例函数11y x=-图象上的点,且1230x x x <<<,则123y y y 、、的大小关系是()A .123y y y <<B .321y y y <<C .231y y y <<D .312y y y <<【答案】D【解析】解:根据题意画出函数图象得,可知,312y y y <<.故选:D .6.随着城际交通的快速发展,某次动车平均提速60km /h ,动车提速后行驶480km 与提速前行驶360km 所用的时间相同.设动车提速后的平均速度为x km /h ,则下列方程正确的是()A .36048060x x =+B .36048060x x =-C .36048060x x =-D .36048060x x=+【答案】B【解析】解:根据题意,得36048060x x=-.故选:B .7.将抛物线()215y x =-+通过平移后,得到抛物线的解析式为223y x x =++,则平移的方向和距离是()A .向右平移2个单位长度,再向上平移3个单位长度B .向右平移2个单位长度,再向下平移3个单位长度C .向左平移2个单位长度,再向上平移3个单位长度D .向左平移2个单位长度,再向下平移3个单位长度【答案】D【解析】解:抛物线()215y x =-+的顶点坐标为15(,),抛物线()222312y x x x =++=++的顶点坐标为()12-,,而点()15,向左平移2个,再向下平移3个单位可得到()12-,,所以抛物线()215y x =-+向左平移2个,再向下平移3个单位得到抛物线y=x 2+2x+3.故选:D .8.如图,正方形ABCD 和正方形AEFG ,当正方形AEFG 绕点A 逆时针旋转45︒时,如图,连接DG 、BE ,并延长BE 交DG 于点.H 若AE =228AB =,时,则线段BH 的长为()A 16105B 14105C .5210+D .610+【答案】A【解析】解:连结GE 交AD 于点N ,连结DE ,如图,正方形AEFG 绕点A 逆时针旋转45︒,AF ∴与EG 互相垂直平分,且AF 在AD 上,2AE = 22AN GN ∴==,826DN ∴=-=,在Rt DNG 中,DG =22DN GN +2=10;由题意可得:ABE 相当于逆时针旋转90°得到AGD ,2DG BE ∴==10,DEG S = 12GE ND ⋅=12DG HE ⋅,HE ∴=10=6105BH BE HE ∴=+=6101021055+=故选:A .9.如图,AB 是O 的一条弦,点C 是O 上一动点,且ACB θ∠=,点E ,F 分别是,AC BC 的中点,直线EF 与O 交于G ,H 两点,若O 的半径是r ,则GE FH +的最大值是()A .()2sin r θ-B .()2sin r θ+C .()2cos r θ-D .()2cos r θ+【答案】A【解析】解:作直径AP ,连接BP ,90ABP ∴∠=︒,,2P C PA r θ∠=∠== ,sin sin AB P APθ∴∠==,2sin AB r θ∴=⋅,∵E ,F 分别是,AC BC 的中点,EF ∴是ABC 的中位线,1sin 2EF AB r θ∴==⋅,GE FH GH EF +=- ,∴当GH 长最大时,GE FH +有最大值,∴当GH 是圆直径时,GH 最大.∴GE FH +最大值是()2sin 2sin r r r θθ-=-.故选:A .10.如图,在矩形ABCD 中,E 为AB 中点,以AE 为边向上作正方形AEFG ,边EF 交CD 于点H ,在边AE 上取点M 使AM AD =,作MN AG ∥交CD 于点L ,交FG 于点N ,记AE a =,EM b =,欧几里得在《几何原本》中利用该图解释了()()22a b a b a b +-=-.现以BM 为直径作半圆O ,恰好经过点H ,交CD 另一点于P ,记HPB △的面积为1S ,DLF △的面积为2S ,若1b =,则12S S -的值为()A .12B .22C .1D 2【答案】A【解析】解:依题意得:四边形AEFG AMLD ,均为为正方形,四边形AMNG MEFN MEHL MBCL EBCH ,,,,均为矩形,∵AE a EM b ==,,点E 为AB 的中点,∴EB AE CH a ===,AD AM DL EH BC a b =====-,DG LN HF ME HL b =====,ML EH BC ==,∴()211•22S DL HF a b b ==-,连接MH ,∵HC ME ∥,∴ MHBP =,∴MH BP =,在Rt MHL △和Rt BPC △中,ML BC MH BP=⎧⎨=⎩,∴()Rt Rt HL MHL BPC ≌△△,∴HL PC b ==,∴HP CH PC a b =-=-,∴()211122S HP BC a b =⨯=-,∵MB 为直径,∴90MHB ∠=︒,即90MHE BHE ∠+∠=︒,∵90MEH HEB ∠=∠=︒,∴90HME MHE ∠+∠=︒,∴HME BHE ∠=∠,∴HME BHE ∽,∴EH EB EM EH =::,∴2EH BE EM =⨯,即:()2a b ab -=,∴()211122S a b ab =-=,∴()212111222S S ab a b b b -=--=,∵1b =,∴1212S S -=.故选:A .二、填空题(本大题共8小题,每小题3分,共24分.)11.化学元素钉()Ru 是除铁()Fe 、钻()Co 和镍()NIi 以外,在室温下具有独特磁性的第四个元素.钉()Ru 的原子半径约0.000 000 000 189m .将0.000 000 000 189用科学记数法表示为.【答案】101.8910-⨯【解析】解:100.000 000 000 189 1.8910-=⨯,故答案为:101.8910-⨯12.若2a +与3b -互为相反数,则22a b =.2【解析】解:∵2a +与3b -互为相反数,∴230a b ++-=,即1a b +=,∴)2222a b a b =+=213.不等式组32122x x x x ≥-⎧⎪⎨+≥⎪⎩的解集是.【答案】113x -≤≤【解析】解:32122x x x x ≥-⎧⎪⎨+≥⎪⎩①②解不等式①得:1x ≥-解不等式②得:13x ≤,∴不等式组的解集为:113x -≤≤,故答案为:113x -≤≤.14.写出一个图象是曲线且过点()1,2的函数的解析式:.【答案】2y x=(答案不唯一)【解析】解:设反比例函数解析式为k y x=,依题意,2k =∴一个图象是曲线且过点()1,2的函数的解析式是:2y x=,故答案为:2y x=(答案不唯一).15.如图,某品牌扫地机器人的形状是“莱洛三角形”,它的三“边”分别是以等边三角形的三个顶点为圆心,边长为半径的三段圆弧.若该等边三角形的边长为3,则这个“莱洛三角形”的周长是.【答案】3π根据正三角形的有关计算求出弧的半径和圆心角,根据弧长的计算公式求解即可.【解析】解:如图:∵ABC 是正三角形,∴60BAC ∠=︒,∴ BC的长为:603180ππ⨯=,∴“莱洛三角形”的周长=33ππ⨯=.故答案为:3π.16.如图,已知平行四边形ABCD 中,E 为BC 边上一点,连接AE DE 、,若AD DE =,AE DC =,4BE =,tan 3B ∠=,则EC 的长为.【答案】6【解析】解:作,AF BE DG AE ⊥⊥,如图所示:∵,AE DC AB DC==∴,AB AE B AEB =∠=∠∵AD BC ∥∴AEB DAE ∠=∠∴B AEB DAE ∠=∠=∠∵4BE =∴2BF EF ==∵tan 3AFB BF∠==∴226,210AF AB AE AF BF ===+=∵AD DE =,DG AE ⊥∴10AG EG ==∵tan tan tan 3DAE AEB B ∠=∠=∠=∴22310,10DG AD DG AG ==+=∴10BC AD ==∵4BE =∴6EC BC BE =-=故答案为:617.我国魏晋时期的数学家刘徽(263年左右)首创“割圆术”,所谓“割圆术”就是利用圆内接正多边形无限逼近圆来确定圆周率,刘徽计算出圆周率 3.14π≈.刘徽从正六边形开始分割圆,每次边数成倍增加,依次可得圆内接正十二边形,圆内接正二十四边形,⋯,割得越细,正多边形就越接近圆.设圆的半径为R ,圆内接正六边形的周长66P R =,计算632P πR ≈=;圆内接正十二边形的周长1224sin15P R =︒,计算12 3.102PπR≈=;那么分割到圆内接正二十四边形后,通过计算可以得到圆周率π≈.(参考数据:sin150.258︒≈,sin 7.50.130)︒≈【答案】3.12【解析】解:圆内接正二十四边形的周长2448sin 7.5P R =⋅⋅︒,则48sin 7.5480.130 3.1222R R π⋅︒⨯≈≈≈,故答案为3.1218.如图,点A 是双曲线y=8x在第一象限上的一动点,连接AO 并延长交另一分支于点B ,以AB 为斜边作等腰Rt △ABC ,点C 在第二象限,随着点A 的运动,点C 的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为.【答案】y=﹣8x .【解析】解:如图,连结OC ,作CD ⊥x 轴于D ,AE ⊥x 轴于E ,∵A 点、B 点是正比例函数图象与双曲线y=8x 的交点,∴点A 与点B 关于原点对称,∴OA=OB ,∵△ABC 为等腰直角三角形,∴OC=OA ,OC ⊥OA ,∴∠DOC+∠AOE=90°,∵∠DOC+∠DCO=90°,∴∠DCO=∠AOE ,∵在△COD 和△OAE 中,CDO OEA DCO EOA CO OA ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△COD ≌△OAE (AAS ),设A 点坐标为(a ,8a ),则OD=AE=8a ,CD=OE=a ,∴C 点坐标为(﹣8a,a ),∵﹣8a a ∙=﹣8,∴点C 在反比例函数y=﹣8x图象上.故答案为:y=﹣8x .三、解答题(本大题共10小题,共86分.解答时应写出文字说明、证明过程或演算步骤)19.(1)计算:()103127123π2-⎛⎫-+- ⎪⎝⎭;(2)用配方法解方程:24210x x --=.【解析】(1)解:原式()23211=--+23211=+-+52=(2)解:24210x x --=2421x x -=244214x x -+=+()2225x -=25x ∴-=±17x ∴=,23x =-20.计算:(1)()()22a b b a b -+-;(2)21241121x x x x +⎛⎫+÷ ⎪+++⎝⎭【解析】(1)解:()()22a b b a b -+-22222a ab b ab b =-++-2a =;(2)解:21241121x x x x +⎛⎫+÷ ⎪+++⎝⎭()21212(2)x x x x ++=⨯++12x +=21.如图,在ABC 中,过A 点作AD BC ∥,交ABC ∠的平分线于点D ,点E 在BC 上,DE AB ∥.(1)求证:四边形ABED 是菱形;(2)当6BC =,4AB =时,求DF 的长.【解析】(1)证明:∵AD BC ∥,DE AB ∥,∴四边形ABED 是平行四边形,∵AD BC ∥,∴ADB CBD ∠=∠,∵BD 平分ABC ∠,∴ABD CBD ∠=∠,∴ADB ABD ∠=∠,∴AD AB =,∴四边形ABED 是菱形;(2)解:∵四边形ABED 是菱形,4AB =,∴4DE BE AD AB ====,AD BC ∥,∴ADF CEF ∠=∠,∵AFD CFE ∠=∠,∴CEF ADF ∽△△,∴ADDFCE EF =,∵6BC =,∴2CE BC BE =-=,∴42DF EF=,∴2DF EF =,∴23DF DE =,∴83DF =.22.现有三张正面印有2023年杭州亚运会吉祥物琮琮、宸宸和莲莲的不透明卡片A ,B ,C ,卡片除正面图案不同外,其余均相同,(1)若将三类卡片各10张,共30张,正面向下洗匀,从中随机抽取一张卡片,则抽出的卡片图案是琮琮的概率是___________.(2)现将三类卡片各一张,放入不透明箱子,小明随机抽取一张,看后,放回,再由小充随机抽取一张.请用树状图或列表的方法列出所有等可能的结果,并求恰好摸到相同卡片的概率.【解析】(1)解;∵一共有30张卡片,其中琮琮的卡片有10张,且每张卡片被抽到的概率相同,∴从中随机抽取一张卡片,则抽出的卡片图案是琮琮的概率是101303=,故答案为:13.(2)解:画树状图如下:由树状图可知,一共有9种等可能性的结果数,其中恰好摸到相同卡片的结果数有3种,∴恰好摸到相同卡片的概率为3193=.23.某校初三物理组为激发学生学习物理的热情,组织初三500名学生进行“水火箭”制作和演示飞行活动.为了解该年级学生自制水火箭的飞行情况,现随机抽取40名学生进行水火箭飞行测试,并将测试成绩(百分制)作为样本数据进行整理、描述和分析,下面给出了部分信息.①将样本数据分成5组:5060,6070,7080,8090,90100x x x x x ≤<≤<≤<≤<≤<,并制作了如图所示的不完整的频数分布直方图;②在8090x ≤<这一组的成绩分别是:80,81,83,83,84,85,86,86,86,87,8.8,89,根据以上信息,解答下列问题:(1)补全频数分布直方图;(2)抽取的40名学生成绩的中位数是____________;(3)如果测试成绩达到80分及以上为优秀,试估计该年级500名学生中水火箭飞行测试为优秀的学生约有多少人?【解析】(1)解:在7080x ≤<这组的人数为:404612108----=(人),补全频数分布直方图如下:(2)中位数应为40个数据由小到大排列中第20,21个数据的平均数,∵数据处于较小的三组中有46818++=(个)数据,∴中位数应是8090x ≤<这一组第2,3个数据的平均数,∴中位数为:8183822+=(分),故答案为:82分;(3)∵样本中优秀的百分比为:1210100%55%40+⨯=,∴可以估计该校500名学生中对安全知识掌握程度为优秀的学生约有:55%500275⨯=(人),答:估计该校500名学生中对安全知识掌握程度为优秀的学生约有275人.24.如图,在四边形ABCD 中,90A C ∠=∠=︒.(1)经过点A 、B 、D 三点作O ;(2)O 是否经过点C ?请说明理由.【解析】(1)解:如图所示,O 即为所求;(2)O 经过点C ,理由如下:连接OC ,∵90BCD ∠=︒,点O 为BD 的中点,∴12CO BC OD OB ===,∴点C 在O 上.25.最佳视点如图1,设墙壁上的展品最高处点P 距底面a 米,最低处的点Q 距底面b 米,站在何处观赏最理想?所谓观赏理想是指看展品的视角最大,问题转化为在水平视线EF 上求使视角最大的点.如图2,当过P Q E ,,三点的圆与过点E 的水平线相切于点E 时,视角PEQ ∠最大,站在此处观赏最理想,小明同学想这是为什么呢?他在过点E 的水平线HM 上任取异于点E 的点E ',连接PE '交O 于点F ,连接QF ,…任务一:请按照小明的思路,说明在点E 时视角最大;任务二:若3 1.8a b ==,,观察者的眼睛距地面的距离为1.5米,最大视角为30︒,求观察者应该站在距离多远的地方最理想(结果精确到0.013 1.73≈).【解析】任务一:过点E 的水平线HM 上任取异于点E 的点E ',连接PE '交O 于点F ,连接QF ,∵PFQ ∠是QFE ' 的外角,∴PFQ PE Q '∠>∠,又∵PFQ ∠与PEQ ∠都是弧PQ 所对的圆周角,∴PFQ PEQ ∠=∠,∴PEQ PE Q '∠>∠,∴在点E 时视角最大.任务二:∵30PEQ ∠=︒,∴60POQ ∠=︒,又∵OP OQ =,∴OPQ △是等边三角形,OP OQ PQ ==.如图2,连接OE ,∵HE 是O 的切线,∴90OEH ∠=︒,∵90PHE ∠=︒,∴180OEH PHE ∠+∠=︒,∴//PQ OE ,又∵PQ OP OE ==,∴四边形PQOE 是平行四边形,∴30OPE PEQ ∠=∠=︒,∴603030EPH OPQ OPE ∠=∠-∠=︒-︒=︒.由题意得,3 1.5 1.5PH =-=(米),在Rt PHE △中,3•tan 1.50.873HE PH EPH =∠=⨯(米).答:观察者应该站在距离0.87米的地方最理想.26.在2024年元旦即将到来之际,学校准备开展“冬日情暖,喜迎元旦”活动,小星同学对会场进行装饰.如图1所示,他在会场的两墙AB 、CD 之间悬挂一条近似抛物线2435y ax x =-+的彩带,如图2所示,已知墙AB 与CD 等高,且AB 、CD 之间的水平距离BD 为8米.(1)如图2,两墙AB ,CD 的高度是米,抛物线的顶点坐标为;(2)为了使彩带的造型美观,小星把彩带从点M 处用一根细线吊在天花板上,如图3所示,使得点M 到墙AB 距离为3米,使抛物线1F 的最低点距墙AB 的距离为2米,离地面2米,求点M 到地面的距离;(3)为了尽量避免人的头部接触到彩带,小星现将M 到地面的距离提升为3米,通过适当调整M 的位置,使抛物线2F 对应的二次函数的二次项系数始终为15,若设点M 距墙AB 的距离为m 米,抛物线2F 的最低点到地面的距离为n 米,探究n 与m 的关系式,当924n ≤≤时,求m 的取值范围.【解析】(1)解:由题意得,抛物线的对称轴为4x =,则45422b x a a==-=-,解得:0.1a =;∴抛物线的表达式为0.10.83y x x =-+,则点(0,3)A ,即3AB CD ==(米),当4x =时,0.10.83 1.4y x x =-+=,即顶点坐标为(4,1.4),故答案为:3,(4,1.4);(2)解:设抛物线的表达式为2(2)2y a x ='-+,将点A 的坐标代入上式得23(02)2a ='-+,解得14a '=,∴抛物线的表达式为21(2)24y x =-+,当3x =时,21(2)2 2.254y x =-+=(米),∴点M 到地面的距离为2.25米;(3)解:由题意知,点M 、C 纵坐标均为4,则右侧抛物线关于M 、C 对称,∴抛物线的顶点的横坐标为11(8)422m m +=+,则抛物线的表达式为211(4)52y x m n =--+,将点C 的坐标代入上式得2113(84)52m n =--+,整理得21412055n m m =-+-;当2n =时,即214122055m m =-+-,解得85m =-;当9n 4=时,同理可得86m =故m 的取值范围为:8685m ≤≤27.定义:对多边形进行折叠,若翻折后的图形恰能拼成一个无缝隙、无重叠的四边形,则这样的四边形称为镶嵌四边形.(1)如图1,将ABC 纸片沿中位线EH 折叠,使点A 落在BC 边上的D 处,再将纸片分别沿EF ,HG 折叠,使点B 和点C 都与点D 重合,得到双层四边形EFGH ,则双层四边形EFGH 为______形.(2)ABCD Y 纸片按图2的方式折叠,折成双层四边形EFGH 为矩形,若5EF =,12EH =,求AD 的长.(3)如图3,四边形ABCD 纸片满足AD BC ∥,AD BC <,AB BC ⊥,8AB =,10CD =.把该纸片折叠,得到双层四边形为正方形.请你画出一种折叠的示意图,并直接写出此时BC 的长.【解析】(1)双层四边形EFGH 为矩形,理由如下:由折叠的性质可得AEH HED ∠=∠,BEF DEF ∠=∠,180AEH HED BEF DEF ∠+∠+∠+∠=︒ ,90HED DEF ∴∠+∠=︒,90HEF ∴∠=︒,同理可得90EHG EFD ∠=∠=︒,∴四边形EFGH 是矩形,故答案为:矩;(2) 四边形EFGH 为矩形,90FEH ∴∠=︒,EH FG =,EH FG ∥,222251213FH EF EH ∴=+=+=,EHM GFN ∠=∠,又ABCD 为平行四边形,A C ∴∠=∠,AD BC =,由折叠得A EMH ∠=∠,C GNF ∠=∠,EMH GNF ∴∠=∠,在EHM 与GFN 中,EH FGEHM GFN EMH GNF=⎧⎪∠=∠⎨⎪∠=∠⎩,(AAS)EHM GFN ∴ ≌,MH NF ∴=,由折叠得AH MH =,CF FN =,AH CF ∴=,又AD BC = ,DH BF FM ∴==,又AD AH DH =+ ,HF MH MF =+,13AD HF ∴==.(3)有以下三种基本折法:折法1中,如图所示:由折叠的性质得:AD BG =,142AE BE AB ===,152CF DF CD ===,GM CM =,90FMC ∠=︒, 四边形EFMB 是叠合正方形,4BM FM ∴==,2225163GM CM CF FM ∴=-=-=,1AD BG BM GM ∴==-=,7BC BM CM =+=;折法2中,如图所示:由折叠的性质得:四边形EMHG 的面积12=梯形ABCD 的面积,142AE BE AB ===,DG NG =,NH CH =,BM FM =,MN MC =,125GH CD ∴==, 四边形EMHG 是叠合正方形,5EM GH ∴==,正方形EMHG 的面积2525==,90B ∠=︒ ,2225163FM BM EM BE ∴=-=-=,设AD x =,则3MN FM FN x =+=+,梯形ABCD 的面积1()82252AD BC =+⨯=⨯,252AD BC ∴+=,252BC x ∴=-,2532MC BC BM x ∴=-=--,MN MC = ,25332x x ∴+=--,解得:134x =,134AD ∴=,251337244BC =-=.折法3中,如图所示,作GM BC ⊥于M ,则E ,G 分别为AB ,CD 的中点,则4AH AE BE BF ====,152CG CD ==,正方形的边长42EF GF ==4GM FM ==,2225163CM CG GM --=,11BC BF FM CM ∴=++=.综上所述:7BC =或11或374.28.如图所示,抛物线与x 轴交于A 、B 两点,与y 轴交于点C ,且1OA =,4OB OC ==.(1)求抛物线的解析式;(2)若连接AC 、BC .动点D 从点A 出发,在线段AB 上以每秒1个单位长度向点B 做匀速运动;同时,动点E 从点B 出发,在线段BC 2个单位长度向点C 做匀速运动,当其中一点到达终点时,另一点随之停止运动,连接DE ,设运动时间为t 秒.在D 、E 运动的过程中,当t 为何值时,四边形ADEC 的面积最小,最小值为多少?(3)点M 是抛物线上位于x 轴上方的一点,点N 在x 轴上,是否存在以点M 为直角顶点的等腰直角三角形CMN ?若存在,求出点M 的坐标,若不存在,请说明理由.【解析】(1)解:∵4OB OC ==,1OA =,则()0,4C ,()4,0B ,()0,1A -∴抛物线解析式为2(1)(4)34y x x x x =-+-=-++;(2)解:∵4OB OC ==,∴OBC △是等腰直角三角形,由点的运动可知:2BE t =,过点E 作EF x ⊥轴,垂足为F ,∴22tBE BF t t ==,又∵()0,1A -,则5AB =,∴ADEC ABC BDES S S =- 1145(5)22t t=⨯⨯-⨯-⨯21555(228t =-+,∵当其中一点到达终点时,另一点随之停止运动,∴224442AC =+=5AB =,∴04t ≤≤,当52t =时,四边形ADEC 的面积最小,即为558;(3)解:存在,(15,15)M +或(222,222)M -,当点M 在CN 的右侧时,如图所示,过点M 作y 轴的平行线PQ ,交x 轴于点Q ,过点C 作CP PQ ⊥,∵CMN 是以M 为直角为直角顶点的等腰直角三角形,∴CM MN =,90CMN ∠=︒,∴90PCM PMC NMQ ∠=︒-∠=∠,又90CPM MQN ∠=∠=︒∴CPM MQN ≌,∴CP MQ =,设2(,34)M m m m -++,∴234m m m -++=,解得:51m =或15m =∴(15,15)M ;当点M 在CN 的右侧时,同理可得234m m m -++=-,解得:222m =-22m =(舍去)∴(222,222)M -,综上所述,(15,15)M 或(22,22)M -.。
2024年中考数学第一次模拟考试(山东济南卷)(全解全析)

2024年中考第一次模拟考试(山东济南卷)数学·全解全析第Ⅰ卷一、选择题(本大题共10个小题,每小题4分,共40分.在每个小题给出的四个选项中,只有一项符合题目要求,请选出并在答题卡上将该项涂黑)1.图1所示的正五棱柱,其俯视图是()A .B .C .D .【答案】A【分析】找到从上面看所得到的图形即可,注意看见的棱用实线表示.【详解】解:从上面看,是一个矩形,矩形的中间有一条纵向的实线,两条纵向的虚线.故选:A .【点睛】本题考查了三视图的知识,俯视图是从物体的上面看得到的视图.2.2023年10月18日,第三届“一带一路”国际合作高峰论坛在北京举行.国家主席习近平在主旨演讲中声明:“本届高峰论坛期间举行的企业家大会达成了972亿美元的项目合作协议.”将972亿美元用科学记数法表示成元,正确的是()A .29.7210 B .99.7210 C .109.7210 D .119.7210 【答案】C【分析】本题考查了科学记数法:把一个绝对值大于等于10的数表示成10n a 的形式(a 大于或等于1且小于10,n 是正整数);n 的值为小数点向左移动的位数.根据科学记数法的定义,即可求解.【详解】解:972亿10972000000009.7210 ,故选:C .3.如图,直线m n ∥,点A 在直线n 上,点B 在直线m 上,连接AB ,过点A 作AC AB ,交直线m 于点C .若150 ,则2 的度数为().B.C..【答案】B【分析】本题考查了轴对称图形和中心对称图形的识别.根据轴对称图形和中心对称图形的定义判断即可.如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形.把一个图形绕某一点旋转180 ,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形.【详解】解:A、是轴对称图形,不是中心对称图形,本选项不符合题意;、是轴对称图形,也是中心对称图形,本选项符合题意;、不是轴对称图形,是中心对称图形,本选项不符合题意;、不是轴对称图形,是中心对称图形,本选项不符合题意;.三张图片除画面不同外无其他差别,将它们从中间剪断得到三张上部图片和三张下部图片,把三张上部图片放入一个布袋,把三张下部图片放入另一个布袋,再分别从两个布袋中各随机摸取一张,则这两张小A .(13)(23)10B .(31)(32)1C .(13)(23)36D .(13)(23)10④BH 的最小值为5.A .1B 【答案】C 【分析】根据勾股定理求出90ACB ∵,AC BC ,ACB 是等腰直角三角形,2AB AC ,90,CBN ACDN BCN,90∵垂直AD,CE,90BCN HDC抛物线 23y ax b a x b 与x 轴的另一个交点为 1,0,关于x 的方程2ax bx ax b 有两个根14x ,21x ,故③正确;④当0a ,当41x 时,12y y ,故④错误;故选:B .【点睛】本题考查了二次函数的基本性质,二次函数与一次函数交点,二次函数与不等式等,理解性质,掌握解法是解题的关键.第Ⅱ卷二、填空题(本大题共6个小题,每小题4分,共24分)【答案】53 82【分析】连接OF,由勾股定理可计算得正方形角形COD的面积为12,扇形【详解】解:连接OF,则OF【点睛】本题考查扇形面积的计算,勾股定理,正方形的性质;构造直角三角形运用勾股定理是解题的关键.15.如图,在菱形ABCD中,边长为若将EBF△沿着EF折叠,使得点【答案】2或3/3或2【分析】过点M作MF 直线l 在坐标轴上的对称点,过点M平行可得45OPA,即可证明中点坐标公式可求出MF和ME,与直线 平行,∵直线l与直线y x设直线l解析式为y x b,轴于点D,则过点M作MD x,∵直线l的解析式为y x b,OPD45,45OFE OEF均为等腰直角三角形,MDE与OEF,12bb ,解得:3点P坐标为(0,3),t .3点M关于l的对称点,当2t 时,落在y轴上,当3t 时,落在x轴上.故答案为:2或3.【点睛】本题考查了一次函数的图象与几何变换.注意在x轴、y轴上均有点M的对称点,不要漏解;其次注意点E、F坐标以及线段中点坐标的求法.三、解答题(本大题共10个小题,共86分.解答应写出文字说明,证明过程或演算步骤),(1)求证:AE DF ;(2)若120A ,83BF 【答案】(1)见详解.由(1)知AB AF ,且BAF ∴60BAH ,12BH BF∵30ABH ,(1)如图2,求遮阳棚前端B 到墙面AD 的距离;(2)如图3,某一时刻,太阳光线与地面夹角60CFG ,求遮阳棚在地面上的遮挡宽度确到1cm ).(参考数据:sin 720.951,cos 720.309,tan 72 3.078,3 1.732 【答案】(1)遮阳棚前端B 到墙面AD 的距离约为190.2cm(2)遮阳棚在地面上的遮挡宽度DF 的长约为69cm∴四边形BEHC ,四边形由(1)得190.2cm BE ∴190.2cm DK HC BE 在Rt ABE △中,cos ∴cos72200AE【点睛】本题考查了解直角三角形的应用,矩形的判定和性质,作出合适的辅助线,构造出直角三角形,“滴滴”网约车司机收入频数分布表:月收入4千元5千元9千元人数(个)342根据以上信息,分析数据如表:平均月收入/千元中位数(1)求证:BF 是O 的切线;(2)若6EF ,cos ABC ①求BF 的长;②求O 的半径.)利用圆周角定理,等腰三角形的性质和圆的切线的判定定理解答即可;交于点思考问题:(1)设1,P a a ,1,R b b,求直线OM 的函数解析式(用含a ,b 的代数式表示),并说明Q 点在直线(2)证明:13MOB AOB .(3)如图2,若直线y x 与反比例函数 40y x x 交于点C ,D 为反比例函数 40y x x 第一象限上的一个动点,使得30COD .求用材料中的方法求出满足条件D 点坐标.由题意得四边形PQRM 是矩形,∴PR QM ,12SP PR,∴SP SM ,∴12 ,【点睛】此题在考查三等分角的作法时,综合考查了待定系数法求函数解析式的方法、矩形的性质以及三角形外角的性质等,综合性较强.y x25.如图1,在平面直角坐标系xOy中,二次函数2顶点为M.矩形ABCD的顶点D与原点O重合,顶点A,当点G 在点Q 的下方时, 22224QG t t t t 52(在03t 的范围内).或52.【点睛】本题考查了二次函数图象上点的坐标特点、矩形的性质以及三角形的面积等知识,熟练掌握二次函数的图象与性质、灵活应用数形结合思想是解题的关键.(1)如图1,调整菱形ABCD ,使90A ,当点M 在菱形ABCD 外时,在射线在Rt CEM △中,CME 12CE CM ,设MD x ,MF CD ∵,45CDM ,DFM 为等腰直角三角形,22DF MF x ,∵四边形ABCD 是菱形,, ,120BCD设MD y ,同①可得:DF 26626DF CF y y ,9236y ,9236MD ,综上所述,MD 的长度为9【点睛】本题主要考查了三角形全等的判定与性质、等腰直角三角形的判定与性质、菱形的性质、正方形。
2024年中考数学第一次模拟试卷(陕西卷)(考试版A4)

2024年中考第一次模拟考试(陕西卷)数学(考试时间:120分钟试卷满分:120分)注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答第Ⅰ卷时,选出每小题答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
写在本试卷上无效。
3.回答第Ⅱ卷时,将答案写在答题卡上。
写在本试卷上无效。
4.考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷一、选择题(本大题共8个小题,每小题3分,共24分.在每个小题给出的四个选项中,只有一项符合题目要求,请选出并在答题卡上将该项涂黑)1.-2024的绝对值是()A .B .-C .-2024D .20242.下列不是三棱柱展开图的是()A .B .C .D .3.如图,在ABC 中,90C ∠=︒,点D 在AC 上,//DE AB ,若160CDE ∠=︒,则B Ð的度数为()A .40︒B .50︒C .60︒D .70︒4.下列计算正确的是()A .2m m m +=B .()22m n m n-=-C .222(2)4m n m n +=+D .2(3)(3)9m m m +-=-5.已知112233()()()x y x y x y ,,,,,为直线23y x =-+上的三个点,且123x x x <<,则以下判断正确的是()A .若120x x >,则130y y >B .若130x x <,则120y y >C .若230x x >,则130y y >D .若230x x <,则120y y >6.如图,ABC 与111A B C △位似,位似中心是点O ,若1:1:2OA OA =,则ABC 与111A B C △的周长比是()A .1:2B .1:3C .1:4D .7.如图,ABC 的内切圆О与,,AB BC AC 分别相切于点D ,E ,F ,连接OE ,OF ,90C ∠=︒,6AC =,8BC =,则阴影部分的面积为()A .122π-B .142π-C .4π-D .114π-8.如图是函数y =x 2﹣2x ﹣3(0≤x≤4)的图象,直线l ∥x 轴且过点(0,m ),将该函数在直线l 上方的图象沿直线l 向下翻折,在直线1下方的图象保持不变,得到一个新图象.若新图象对应的函数的最大值与最小值之差不大于5,则m 的取值范围是()A .m≥1B .m≤0C .0≤m≤1D .m≥1或m≤0第Ⅱ卷二、填空题(本大题共5个小题,每小题3分,共15分)9.比较大小:22-_______________03.(选填>,=,<)10.已知一个正多边形的内角和为1440°,则它的一个外角的度数为度.11.如图,▱ABCD 的顶点C 在等边△BEF 的边BF 上,点E 在AB 的延长线上,G 为DE 的中点,连接CG .若AD =3,AB =CF =2,则CG 的长为.12.如图,在平面直角坐标系中,矩形ABCD 的顶点A ,C 分别在x 轴,y 轴的正半轴上,点D (﹣2,3),AD =5,若反比例函数y xk=(k >0,x >0)的图象经过点B ,则k 的值为______13.如图,ABC 是等边三角形,6AB =,N 是AB 的中点,AD 是BC 边上的中线,M 是AD 上的一个动点,连接,BM MN ,则BM MN +的最小值是________.三、解答题(本大题共13个小题,共81分.解答应写出文字说明,证明过程或演算步骤)14.(5分)计算:22012(3π-⎛⎫-++-+ ⎪⎝⎭15.(5分)化简:22311(1).m m m m m-+-+÷16.(5分)解不等式组:5431212x x x +<⎧⎪⎨+≥-⎪⎩.17.(5分)如图,点O 是正方形,ABCD的中心.用直尺和圆规在正方形内部作一点E (异于点O ),使得;EB EC =(保留作图痕迹,不写作法)18.(5分)如图,点A ,D ,B ,E 在一条直线上AD BE =,AC DF =,//AC DF .求证:BC EF =.19.(5分)如图,在平面直角坐标系中,△ABC 的顶点A (0,1),B (2,0),C (4,4)均在正方形网格的格点上.(1)画出△ABC 关于x 轴对称的图形△A 1B 1C 1,并写出顶点C 1关于y 轴的对称点的坐标;(2)已知P 为y 轴上一点,若△ABP 的面积是△ABC 面积的,求点P 的坐标.20.(5分)从一副普通的扑克牌中取出四张牌,它们的牌面数字分别为2,3,3,6.(1)将这四张扑克牌背面朝上,洗匀,从中随机抽取一张;(2)将这四张扑克牌背面朝上,洗匀.从中随机抽取一张,不放回,求抽取的这两张牌的牌面数字恰好相同的概率.21.(6分)避雷针是用来保护建筑物、高大树木等避免雷击的装置.如图,小陶同学要测量垂直于地面的大楼BC 顶部避雷针CD 的长度(B ,C ,D 三点共线),在水平地面A 点测得53CAB ∠=︒,58DAB ∠=︒,A 点与大楼底部B 点的距离20m AB =,求避雷针CD 的长度.(结果精确到0.1m .参考数据:sin 580.85︒≈,cos 580.53︒≈,tan 58 1.60︒≈,sin 530.80︒≈,cos 530.60︒≈,tan 53 1.33︒≈)22.(7分)一个深为6米的水池积存着少量水,现在打开水阀进水,下表记录了2小时内5个时刻的水位高度,其中x 表示进水用时(单位:小时),y 表示水位高度(单位:米).x 00.51 1.52y11.522.53为了描述水池水位高度与进水用时的关系,现有以下三种函数模型供选择:y kx b =+(0k ≠),y =ax 2+bx +c(0a ≠),ky x=(0k ≠).(1)在平面直角坐标系中描出表中数据对应的点,再选出最符合实际的函数模型,求出相应的函数表达式,并画出这个函数的图象.(2)当水位高度达到5米时,求进水用时x .23.(7分)今年9月,第十四届全国运动会将在陕西省举行.本届全运会主场馆在西安,开幕式、闭幕式均在西安举行.某校气象兴趣小组的同学们想预估一下西安市今年9月份日平均气温状况.他们收集了西安市近五年9月份每天的日平均气温,并绘制成如下统计图:根据以上信息,回答下列问题:(1)这60天的日平均气温的中位数为,众数为;(2)求这60天的日平均气温的平均数;(3)若日平均气温在18℃~21℃的范围内(包含18℃和21℃)为“舒适温度”.请预估西安市今年9月份日平均气温为“舒适温度”的天数.24.(8分)如图,在中,∠ACB=90°,D 是边上一点,以为直径的与相切于点E ,连接并延长交的延长线于点F.(1)求证:BF=BD ;(2)若CF=1,tan ∠EBD=2,求直径.25.(8分)在平面直角坐标系xoy 中,已知抛物线y =-x 2+bx +c 经过点A (-1,0)和点B (0,3),顶点为C ,点D 在其对称轴上,且位于点C 下方,将线段DC 绕点D 按顺时针方向旋转90°,点C 落在抛物线上的点P处.(1)求抛物线的解析式;(2)将抛物线平移,使其顶点落在原点O ,这时点P 落在点E 的位置,在y 轴上是否存在点M ,使得MP +ME 的值最小,若存在,求出点M 的坐标;若不存在,请说明理由.26.(10)【感知】如图①,在四边形ABCD 中,∠C =∠D =90°,点E 在边CD 上,∠AEB =90°.求证:AE DEEB CB=.【探究】如图②,在四边形ABCD 中,∠C =∠D =90°,点E 在边CD 上,当点F 在AD 延长线上,∠FEG =∠AEB =90°,且FE AEEG EB=,连接BG 交CD 于点H .求证:BH =GH .【拓展】如图③,点E 在四边形ABCD 内,∠AEB +∠DEC =180°,且AE DEEB EC=,过E 作EF 交AD 于点F ,使∠EFA =∠AEB ,延长FE 交BC 于点G ,求证:BG =CG .ABCDEABC D EFGH GFEDCB A。
2024年浙江省宁波市镇海区九年级中考一模数学试题(解析版)

镇海区2024年初三模拟考试试卷数学 学科考生须知:1.全卷共三个大题,24个小题.满分为120分,考试时间为120分钟.2.请将学校、姓名、班级填写在答题卡的规定位置上.3.请在答题卡的规定区域作答,在试卷上作答或超出答题卡的规定区域作答无效.试题卷Ⅰ一、选择题(每小题3分,共30分,在每小题给出的四个选项中,只有一项符合题目要求)1. 在实数,中,最小的数是( )A. B. C. D. 【答案】D【解析】【分析】本题考查了实数的大小比较,根据负数小于0,0小于正数,即可求解.【详解】解:∴最小,故选:D .2. 据统计,2024年春节期间,国内旅游出行474000000人次,其中数474000000用科学记数法表示为( )A. B. C. D. 【答案】C【解析】【分析】此题考查科学记数法表示较大的数的方法.科学记数法的表示形式为的形式,其中,为整数.确定的值时,要看把原数变成时,小数点移动了多少位,的绝对值与小数点移动的位数相同.【详解】解:数474000000用科学记数法表示为.故选:C .3. 下列计算正确的是( )102-102-201-<<<2-74.7410⨯747.410⨯84.7410⨯90.47410⨯10n a ⨯1||10a ≤<n n a n 84.7410⨯A. B. C. D. 【答案】C【解析】【分析】本题考查整式的运算.利用合并同类项法则,同底数幂乘法法则,幂的乘方法则,平方差公式逐项判断即可.【详解】解:与不是同类项,无法合并,则选项A 不符合题意;,则选项B 不符合题意;,则选项C 符合题意;,则选项D 不符合题意;故选:C .4. 一城市准备选购一千株高度大约为2m 的某种风景树来进行街道绿化, 有四个苗圃生产基地投标(单株树的价格都一样). 采购小组从四个苗圃中都任意抽查了20株树苗的高度,得到的数据如下:树苗平均高度(单位:m )标准差甲苗圃1.8 0.2乙苗圃1.8 0.6丙苗圃2.0 0.6丁苗圃2.0 0.2请你帮采购小组出谋划策,应选购( )A. 甲苗圃的树苗B. 乙苗圃的树苗;C. 丙苗圃的树苗D. 丁苗圃的树苗【答案】D【解析】【分析】根据标准差和方差可以反映数据的波动大小,选出合适苗圃的树苗;再比较它们的高度,进而确32a a a-=326a a a ⋅=()236a a =()()2212121a a a +-=-3a 2a 3256a a a a ⋅=≠()236a a =()()2221214121a a a a +-=-≠-定选购哪家的树苗.【详解】由于标准差和方差可以反映数据的波动大小,所以甲苗圃与丁苗圃比较合适;又因为丁苗圃树苗平均高度大于甲苗圃,所以应选丁苗圃的树苗.故选D .【点睛】考查了标准差,标准差也均称方差,方差是反映一组数据波动大小的特征数,方差越大,数据的波动性越大;方差越小,稳定性越好.5. 若点是第二象限的点,则a 的取值范围是( )A. B. C. D. 或【答案】A【解析】【分析】本题考查了象限内点的坐标特征,解不等式方程组,掌握第二象限内点的坐标特征是解题关键.根据第二象限内的点横坐标小于0,纵坐标大于0,列不等式组求解即可.【详解】解:点是第二象限的点,,解得:,故选:A .6. 如图是一架人字梯,已知米,AC 与地面BC 的夹角为,则两梯脚之间的距离BC 为( )A. 米B. 米C. 米D. 米【答案】A【解析】(),2G a a -a<02a <02a <<a<02a > (),2G a a -020a a <⎧∴⎨->⎩a<02AB AC ==α4cos α4sin α4tan α4cos α【分析】根据等腰三角形的性质得到,根据余弦的定义即可,得到答案.【详解】过点A 作,如图所示:∵,,∴,∵,∴,∴,故选:A .【点睛】本题考查的是解直角三角形的应用,明确等腰三角形的性质是解题的关键.7. 一次数学课上,老师让大家在一张长12cm ,宽5cm 的矩形纸片内,折出一个菱形;甲同学按照取两组对边中点的方法折出菱形见方案一,乙同学沿矩形的对角线AC 折出,的方法得到菱形见方案二,请你通过计算,比较这两种折法中,菱形面积较大的是( ).A. 甲B. 乙C. 甲乙相等D. 无法判断【答案】B【解析】【分析】方案一中,通过图可知四个小直角三角形全等,用矩形面积减去4个小直角三角形的面积,即可得菱形面积;方案二中,两个小直角三角形全等,设菱形边长为x ,在直角三角形中利用勾股定理可求x ,再利用底高可求菱形面积然后比较两者面积大小.12BD DC BC ==AD BC ⊥AB AC =AD BC ⊥BD DC =DC co ACα=cos 2cos DC AC αα=⋅=24cos BC DC α==(EFGH )CAE DAC ∠=∠ACF ACB ∠=∠(AECF )⨯.【详解】解:方案一中,、F 、G 、H 都是矩形ABCD 的中点,≌≌≌,,,,;方案二中,设,则,,,,≌,在中,,,,由勾股定理得,解得,,,,,,故甲乙.E HAE ∴ HDG △△FCG FBE 11111111551222222222HAE S AE AH AB AD =⋅=⨯⨯=⨯⨯⨯⨯= 4HAE ABCD EFGH S S S =- 矩形菱形1512542=⨯-⨯30=BE x =12CE AE x ==-AF EC = AB CD =AE CF =ABE ∴ CDF Rt ABE 5AB =BE x =12AE x =-222(12)5x x -=+11924x =111195955222448ABE S BE AB =⋅=⨯⨯= 2ABE ABCD EFGH S S S =- 矩形菱形595125248=⨯-⨯6025≈-3530=><故选B .【点睛】本题考查菱形的性质、勾股定理以及矩形的性质.注意掌握数形结合思想与方程思想的应用.8. 甲乙两人练习跑步,如果乙先跑10米,甲跑5秒就可追上乙;如果乙先跑2秒,甲跑4秒就可追上乙.设甲速度为x 米/秒,乙的速度为y 米/秒,则可列出的方程组为( )A. B. C. D. 【答案】B【解析】【分析】根据题意,确定等量关系即甲行驶路程等于乙的两次行驶路程的和,列出方程即可,本题考查了二元一次方程组的应用,熟练掌握方程组的应用是解题的关键.【详解】根据题意,得,故选B .9. 二次函数的图象如图所示.下列结论:①;②;③;④若图象上有两点,且,则.其中正确结论的个数为( )A. 1个B. 2个C. 3个D. 4个【答案】C【解析】【分析】本题主要考查了二次函数的图象与性质.依据题意,由抛物线开口向下,从而,又抛物线为,故,再结合抛物线与轴交于负半轴,可得,进而可以判断①;又,从而可以判断②;又当时,,又,故,进而可以判断的551046x y y x =+⎧⎨=⎩551046x y x y=+⎧⎨=⎩510546x y x y+=⎧⎨=⎩551046y x y x=+⎧⎨=⎩551046x y x y =+⎧⎨=⎩2(0)y ax bx c a =++≠0abc >40b a +=0b c +>()11,x y ()22,x y 1204x x <<<12y y <a<022b x a=-=40b a =->y 0c <4b a =-1x =0y a b c =++>a<00b c a +>->③;由抛物线的对称轴是直线,从而当时与当时函数值相等,进而可得当,则,故可以判断④.【详解】解:由题意,抛物线开口向下,.又抛物线为..抛物线与轴交于负半轴,.,故①正确.又,,故②正确.由题意,当时,.又,,故③正确.抛物线的对称轴是直线,当时与当时函数值相等.当,则,故④错误.综上,正确的有:①②③.故选:C .10. 如图,点E 、F 分别是正方形的边、上的点,将正方形沿折叠,使得点B 的对应点恰好落在边上,则的周长等于( )A B. C. D. 【答案】A【解析】.2x =0x =4x =1204x x <<<12y y > <0a ∴22b x a=-=40b a ∴=-> y 0c ∴<0abc ∴>4b a =-40b a ∴+=1x =0y a b c =++>a<00b c a ∴+>-> 2x =∴0x =4x =∴1204x x <<<12y y >ABCD AD BC ABCD EF B 'CD DGB '△2AB ABBF+【分析】本题考查正方形的性质,全等三角形的判定与性质,如图,作,连接,,可证,,根据全等三角形的性质可得,,等量代换即可求解.【详解】解:如图,作,连接,,∵四边形是正方形,∴,由折叠可得,∴,∵ ∴,∴,∴,在和中,∴∴,,在和中,BH A B ''⊥BG BB 'BB C BB H ''≌ BHG BAG ≌ HB CB ''=GH AG =BH A B ''⊥BG BB 'ABCD 90ABC C A ∠=∠=∠=︒BF B F '=90FB A ABC ''∠=∠=︒23∠∠=BHG ∠=90FB A ''∠=︒BH FB ∥24∠∠=3=4∠∠BCB 'V BHB ' 9034BHB C BB BB ∠=∠=︒⎧⎪∠==''∠⎨'⎪⎩()AAS BB C BB H ''≌ BC BH =HB CB ''=Rt BAG Rt BHG BG BG BH AB=⎧⎨=⎩∴,∴,∴,故选:A .试题卷Ⅱ二、填空题(每小题4分,共24分)11. 若分式的值为0,则x 的值是______.【答案】2【解析】【分析】根据分式的值为0,即分母不为0,分子为0得到x-2=0,且x+3≠0,求出x 即可.【详解】解:∵分式的值为0,∴x-2=0,且x+3≠0,∴x=2.故答案为:2.【点睛】本题考查了分式的值为0的条件:分式的值为0,要满足分母不为0,分子为0.也考查了解方程和不等式.12. 分解因式:_____.【答案】【解析】【分析】此题主要考查了提取公因式法以及公式法分解因式,首先提取公因式,进而利用平方差公式分解因式即可,正确应用平方差公式是解题关键.【详解】解:,,故答案为:.13. 在平行四边形中,,的平分线交边于点E ,则的长为______.()HL BHG BAG ≌ GH AG =2DGB C DG GH B H B D AD CD AD '''=+++=+= 23x x -+23x x -+24mx m -=()()22m x x +-m ()2244mx m m x -=-()()22m x x =+-()()22m x x +-ABCD 58AB BC ==,B ∠BE AD DE【答案】3【解析】【分析】本题考查平行四边形的性质、等腰三角形的判定和性质.根据平行四边形的性质可得,则,再由角平分线的定义可得,从而求得,则,从而求得结果.【详解】解:∵四边形是平行四边形,∴,∴,∵的平分线交于点E ,∴,∴,∴,∵,∴,故答案为:3.14. 一个圆锥的高为4,母线长为6,则这个圆锥的侧面积是______.【答案】【解析】【分析】本题考查了圆锥的计算.先利用勾股定理计算出这个圆锥的底面圆的半径,然后根据圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和扇形的面积公式计算即可.【详解】解:这个圆锥的底面圆的半径,所以这个圆锥的侧面积.故答案为:.15. 有三面镜子如图放置,其中镜子和相交所成的角,已知入射光线经反射后,反射光线与入射光线平行,若,则镜子和相交所成的角AD BC ∥AEB CBE ∠=∠ABE CBE ∠=∠AEB ABE ∠=∠AE AB =ABCD AD BC ∥AEB CBE ∠=∠B ∠BE AD ABE CBE ∠=∠AEB ABE ∠=∠AE AB =58AB BC ==,853DE AD AE BC AB =-=-=-===1262π=⨯⨯=AB BC 110ABC ∠=︒EF ,,AB BC CD EF AEF α∠=BC CD______.(结果用含的代数式表示)【答案】【解析】【分析】本题考查了入射角和反射角、平行线以及三角形内角和等知识,解题的关键在于正确画出辅助线【详解】根据入射光线画出反射光线,交于点,同理根据入射光线画出反射光线,交于点,根据入射光线画出反射光线,过点作的平行线,使得.入射角等于反射角入射角等于反射角根据入射角等于反射角,可知:的BCD ∠=α90α︒+FE EG BC G EG GH CD H GH HK G EF GP EF HK BEG AEF α∴∠=∠=1802GEF α∴∠=︒-110ABC ∠=︒18011070BGE αα∴∠=︒-︒-=︒- 70HGC BGE α∴∠=∠=︒-()180270402EGH αα∴∠=︒-⨯︒-=︒+GP EF HK180,180GEF EGP PGH GHK ∴∠+∠=︒∠+∠=︒402EGP PGH EGH α∠+∠=∠=︒+ 360GEF EGH GHK ∴∠+∠+∠=︒()()3601802402140GHK αα∴∠=︒-︒--︒+=︒()1180140202GHC KHD ∠=∠=︒-︒=︒18090BCD CGH GHC α∴∠=︒-∠-∠=︒+故答案为:.16. 如图,已知矩形,过点A 作交的延长线于点E ,若,则______.【解析】【分析】利用矩形的性质,证明,,,变形计算,结合勾股定理,解方程,正切函数解答即可.【详解】∵矩形,∴,∴,,∵,∴,∴,,∴,∴,∴,∴,90α︒+ABCD AE AC ⊥CB AED ACB ∠=∠2tan BAE ∠=1-ADF CEF △∽△ADE FEC ∽BAE BCA △△∽ABCD ,,90,AD BC AB CD ABC BCD AD BC ==∠=∠=︒ ADF CEF △∽△ADE CEF ∠=∠AED ACB ∠=∠ADE FEC ∽AD DF EC EF=EF EC AD ED =AD ED EF EC EF-=ED EC EF AD EC =+ ()·ED EC EC AD AD EC ED=+22ED AD AD EC =+根据勾股定理,得,∴,∴,∴,∴,∵,∴,∵,∴,∴,∴,∴,解得,解得(舍去),∵∴,.【点睛】本题考查了矩形的性质,三角形相似的判定和性质,勾股定理,正切函数,直角三角形的性质,解方程,熟练掌握三角形相似的判定和性质,正切函数,勾股定理,解方程是解题的关键.三、解答题(第17-19题每小题6分,第20、21题每小题8分,第22、23题每小题10分,第24题12分,共66分)17. 计算:(1)222ED CD EC =+222CD EC AD AD EC +=+ ()()222·AB EB BC BC BC EB BC ++=++222222AB EB EB BC BC BC EB BC BC +++=++ 2220AB EB EB BC BC ++-= AE AC ⊥90BAE AEB BCA ∠︒-∠=∠=90ABE CBA ∠∠=︒=BAE BCA △△∽AB BE BC AB=2AB BE BC = 2220EB EB BC BC +-= (1EB BC ==-±1,1EB EB BC BC=-=tan BE BAE AB ∠=2222tan 1BE BE BE BAE AB BE BC BC ∠====- 102212024(3)33-+-⨯--(2)先化简,再求值:,其中【答案】(1) (2),2【解析】【分析】本题主要考查了实数的运算,整式的化简求值,对于(1),根据,,,,再根据有理数运算法则计算;对于(2),先根据整式的乘法法则及公式化简,再代入求值即可.【小问1详解】;【小问2详解】原式.当时,原式.18. 某校为了解本校九年级男生“引体向上”项目的训练情况,随机抽取该年级部分男生进行了一次测试(满分10分,成绩均记为整数分),并按测试成绩m (单位:分)分成四类:类,类,类,类,绘制出如图两幅不完整的统计图,请根据图中信息,解答下列问题:(1)本次抽样调查的人数为______,并补全条形统计图:(1)(1)(2)x x x x +-++12x =5312x +020241=2(93)-=2139-=1133-=02212024(3)33-+-⨯--111993=+⨯-213=+53=2212x x x=-++12x =+12x =11222=+⨯=A (10)m =B (79)m ≤≤C (46)m ≤≤D (3)m ≤(2)扇形统计图中A 类所对的圆心角是______°,测试成绩的中位数落在______类;(3)若该校九年级男生有500名,请估计该校九年级男生“引体向上”项目成绩为A 类或B 类的共有多少名?【答案】(1)50人,图见解析(2)72,B (3)估计该校九年级男生“引体向上”项目成绩为类或类的约有320名.【解析】【分析】本题考查条形统计图,扇形统计图,用样本估计总体,中位数;通过统计图之间的联系求出样本容量是解题的关键.(1)由统计图之间的联系求出样本容量,进一步求出组人数,补齐图形;(2)由组的占比求出对应圆心角;根据中位数定义,可知第25,26个数在组,故中位数在组;(3)由样本占比估计总本的人数.【小问1详解】解:本次抽样调查的人数为(人),组人数为(人),补全的条形统计图如图;故答案为:50人;【小问2详解】解:类所对的圆心角是;样本量为50,可知数据从大到小排列,第25,26个数在组,故中位数在类;故答案为:72,;小问3详解】解:类或类的共有(名),答:估计该校九年级男生“引体向上”项目成绩为类或类的共有320名.19. 如图,直线与双曲线相交于点.【A B C A B B 1020%50÷=C 501022315---=A 36020%72︒⨯=︒B B B A B 500(20%44%)320⨯+=A B y kx b =+(0)m y x x=>()()2,6,1A n B(1)求直线及双曲线对应的函数表达式;(2)直接写出关于x 的不等式的解集;(3)求的面积.【答案】(1)直线:,双曲线: (2)(3)8【解析】【分析】本题主要考查了一次函数,反比例函数的交点坐标,将点的坐标代入函数关系式是确定函数关系式的常用方法,理解交点坐标与不等式解集之间的关系是解本题的关键.(1)将代入到反比例函数解析式可得其解析式;先根据反比例函数解析式求得点的坐标,再由,坐标可得直线解析式;(2)根据图象得出不等式的解集即可;(3)设一次函数的图象与坐标轴交于,两点,分别过,两点作轴于,作轴于,根据题意可得,,从而求出,和,进而求出的值.【小问1详解】把代入,得:,∴反比例函数的解析式为;把代入,得:,∴,(0)m kx b x x +>>ABO 142y x =-+6(0)y x x =>26x <<()6,1B ()2,3A A B (0)m kx b x x+>>C D A B AE y ⊥E BF x ⊥F 2,1AE BF ==48OC OD ==,AOC S BOD S COD S △AOB S ()6,1B m y x=6m =6y x=()2,A n 6y x =3n =()2,3A把、代入,得:,解得:,∴一次函数的解析式为;故答案为:;.【小问2详解】由图象可知当时,,∴不等式的解集是,【小问3详解】设一次函数的图象与坐标轴交于,两点,分别过,两点作轴于,作轴于,∵、,∴,∵一次函数的解析式为,当时,,当当时,,解得,,∴点C 的坐标是,点D 的坐标是∴.∴,,()2,3A ()6,1B y kx b =+2361k b k b +=⎧⎨+=⎩124k b ⎧=-⎪⎨⎪=⎩142y x =-+5y x =-+4y x =26x <<(0)m kx b x x+>>(0)m kx b x x+>>26x <<C D A B AE y ⊥E BF x ⊥F ()2,3A ()6,1B 2,1AE BF ==142y x =-+0x =4y =0y =1042x =-+8x =()0,4()8,048OC OD ==,114,422AOC BOD S OC AE S OD BF =⋅==⋅= 1162COD S OC OD =⋅=△∴.20. 如图,已知和均是等边三角形,F 点在上,延长交于点D ,连接.(1)求证:四边形是平行四边形;(2)当点D 在线段上什么位置时,四边形是矩形?请说明理由.【答案】(1)见解析(2)当点D 在中点时,四边形是矩形,见解析【解析】【分析】本题考查了等边三角形的性质,平行四边形的判定与性质,矩形的判定等知识.熟练掌握等边三角形的性质,平行四边形的判定与性质,矩形的判定是解题的关键.(1)由和均是等边三角形,可得,则,进而可证四边形是平行四边形;(2)由,点D 在中点,可得,则,可证四边形是平行四边形,由,可证四边形是矩形.【小问1详解】证明:∵和均是等边三角形,∴,∴,∴四边形是平行四边形;【小问2详解】解:当点D 在中点时,四边形是矩形,理由如下;∵,点D 在中点,∴,∵四边形是平行四边形,∴,∴,∵,16448AOB COD AOC BOD S S S S =--=--= ABC AEF △AC EF BC AD CE ,ABDE BC ADCE BC ADCE ABC AEF △6060BAC AFE ACB FAE ∠=∠=︒∠=∠=︒,AB DE AE BD ∥,∥ABDE AB AC =BC AD BC BD CD ⊥=,AE CD =ADCE AD BC ⊥ADCE ABC AEF △6060BAC AFE ACB FAE ∠=∠=︒∠=∠=︒,AB DE AE BD ∥,∥ABDE BC ADCE AB AC =BC AD BC BD CD ⊥=,ABDE AE BD =AE CD =AE CD ∥∴四边形是平行四边形,∵,∴四边形是矩形.21. 如图的正方形网格中,每个小正方形的边长均为,的各个顶点都在格点上.(1)在边上作一点,使得的面积是,并求出的值;(2)作出边上的高,并求出高的长.(说明:只能使用没有刻度尺的直尺进行作图,并保留画图痕迹)【答案】(1)画图见解析,; (2)见解析,.【解析】【分析】()根据网格特征作即可;()根据网格特征作即可,本题考查了无刻度尺的直尺作图—作垂线,熟练掌握无刻度尺的直尺作图的方法是解题的关键.【小问1详解】如图,由网格的特征可知:,∴,∴,∴面积为,∴即为所求;ADCE AD BC ⊥ADCE 1ABC BC M ABM 83BM CMAC BD BD 12BM CM =165BD =112BM CM =2BD AC ⊥BG CH ∥CHM BGM ∽12BG BM CH CM ==ABM 1118443323ABC S =⨯⨯⨯= ABM【小问2详解】如图,根据网格作垂线的方法即可,∴即为所求,由网格的特征可知:,∴,∴.22. 星期日上午,小明从家里出发步行前往离家的镇海书城参加读书会活动,他以的速度步行了后发现忘带入场券,于是他停下来.打电话给家里的爸爸寻求帮助,爸爸骑着自行车从家里出发,沿着同一路线以的速度行进,同一时刻小明继续按原速步行赶往目的地.爸爸追上小明后载上他以相同的车速前往书城(停车载人时间忽略不计),到达书城后爸爸原速返回家.爸爸和小明离家的路程与小明所用时间的函数关系如图所示.(1)求爸爸在到达镇海书城前,他离开家的路程s 关于t 的函数表达式及a 的值.(2)爸爸出发后多长时间追上小明?此时距离镇海书城还有多远?【答案】(1),(2)爸爸出发3分钟后追上小明,此时距离镇海书城1275米【解析】【分析】本题考查一次函数的应用以及路程、速度、时间之间关系的应用,关键是用待定系数法求出函数解析式.(1)根据爸爸行驶的路程和爸爸的速度,求出爸爸到达书城所用时间,再根据待定系数法求函数解析式,再求出的值;BD 5AC ==1144522ABC S BD =⨯⨯=⨯⨯ 165BD =9:00 2.4km 75m/min 12min 9:15375m/min ()m s ()min t 3755625s t =-27.8a =a(2)设爸爸出发后分钟追上小明,根据两人路程相等列出方程,解方程求出,并求出距离书城的距离.【小问1详解】解:爸爸到达达镇海书城所用时间为,设爸爸在到达镇海书城前,他离开家的路程关于的函数表达式为,把,代入,得:,解得,爸爸在到达镇海书城前,他离开家的路程关于的函数表达式为;爸爸的速度不变,他返回家的时间和到达书城的时间均为,;【小问2详解】设爸爸出发后分钟追上小明,则,解得,此时,,答:爸爸出发后3分钟追上小明,此时距离镇海书城还有1275米.23. 根据以下素材,探索完成任务.设计跳长绳方案素材1:某校组织跳长绳比赛,要求如下:(1)每班需报名跳绳同学9人,摇绳同学2人;(2)跳绳同学需站成一路纵队,原地起跳,如图1.素材2:某班进行赛前训练,发现:(1)当绳子摇至最高处或最低处时,可近似看作两条对称分布的抛物线.已知摇绳同学之间水平距离为,绳子最高点为,摇绳同学的出手高度均为,如图x x 2400 6.4(min)375=s t s kt b =+(15,0)(21.4,2400)s kt b =+15021.42400k b k b +=⎧⎨+=⎩3755625k b =⎧⎨=-⎩∴s t 3755625s t =- ∴ 6.4min 152 6.427.8a ∴=+⨯=x 37575(12)x x =+3x =240037531275(m)-⨯=6m 2m 1m2;(2)9名跳绳同学身高如右表.【答案】任务1:;任务2:当绳子在最高点时,长绳不会触碰到位于最边侧的同学;任务3:方案可行【解析】【分析】本题考查了二次函数的应用,任务1:建立平面直角坐标系,待定系数法求解析式,即可求解;任务2,得出最右侧同学横坐标为代入解析式,结合按照排列方式可知最右(左)侧同学屈膝后身高即可求解;任务3,求得平移后的抛物线解析式,进而将代入,结合题意,即可求解.【详解】解:任务1:以两个摇绳人的中点所在直线与地面的交点为原点,地面所在直线为轴,建立直角坐标系,如图:由已知可得,在抛物线上,且抛物线顶点的坐标为,设抛物线解析式为,∴,解得:,∴抛物线的函数解析式为:任务2:∵抛物线的对称轴为直线,名同学,以轴为对称轴,分布在对称轴两侧,将同学按“中间高,两边低”的方式对称排列,同时保持的间距,则最右边侧的同学的坐标为即,当时,的21129y x =-+()1.8,1.7 1.8x =x ()()3,1,3,1-()0,222y ax =+192a =+19a =-21129y x =-+3x =9y 0.45m ()0.454,1.70⨯()1.8,1.71.8x =211.82 1.649y =-⨯+=按照排列方式可知最右(左)侧同学屈膝后身高:∴当绳子在最高点时,长绳不会触碰到位于最边侧的同学;任务3:∵当绳子摇至最高处或最低处时,可近似看作两条对称分布的抛物线.设开口向上的抛物线解析式为,对称轴为直线,则的顶点坐标为,∵,的开口大小不变,开口方向相反,∴当绳子摇至最低处时,抛物线的解析式为:∵将出手高度降低至.∴抛物线向下平移∴改变方案后的抛物线解析式为将,代入因此,方案可行24. 如图1,已知四边形内接于,且为直径.作交于点E ,交于点F .(1)证明:;(2)若,,求半径r ;(3)如图2,连接并延长交于点G ,交于点H .若,.①求;②连接,设,用含x 的式子表示的长.(直接写出答案)【答案】(1)见解析 (2) (3)①;②191.70 1.615 1.6420⨯=<2y1y =2y ()0,01y 2y 2219y x =-0.85m 10.850.15-=2310.159y x =--1.8x =223110.15 1.80.150.210.2599y x =-=⨯-=<ABCD O BD AF BC ∥CD O AF CD ⊥4cos 5DAF ∠=4AC =BE DF O AF CD =AEB BDC ∠=∠tan BDC ∠OE OE x =GH 52r =1tan 2BDC ∠=GH x =【解析】【分析】(1)根据圆周角定理得出,根据平行线的得出,即可证明结论;(2)证明,得出,根据,得出,根据,求出结果即可;(3)①过点O 作于点P ,于点Q ,证明矩形是正方形,设,,得出,,证明,得出,求出,得出;②连接,证明,得出,即,求出,证明,得出,根据,得出,证明,得出,证明,得出【小问1详解】证明:∵为直径,∴,∵,∴,即.【小问2详解】解:∵,∴,又∵,∴,90BCD ∠=︒90AED BCD ∠=∠=︒AEC DAB ∽ AC AE BD AD =4cos 5AE DAF AD ∠==45AC BD =4AC =OP DC ⊥OQ AF ⊥OPEQ OP a PE ==CE b =2BC a =()22CD PC a b ==+BEC DBC ∽ 2BC CE CD =⋅1b a =1tan 2OP a BDC DP a b ∠===+HF ODP MDE ∽OP DP ME DE ==ME x =AMN CBN ∽ 37AN AC x ==ODP MDE ∽CEB CBD ∠∠=DEG DAN ∽ AN AD EG DE ==EG AN ==ABE HFE ∽ EH AE ==BD 90BCD ∠=︒AF BC ∥90AED BCD ∠=∠=︒AF CD ⊥AF BC ∥EAC ACB ∠=∠ACB ADB Ð=ÐEAC ADB ∠=∠∵,∴,∴,∴,∴,∵,∴,即.【小问3详解】①如图2,过点O 作于点P ,于点Q ,如图所示:∵,∴四边形是矩形,∵,∴,∴矩形是正方形设,,∵,∴,∵,90AEC BAD ∠=∠=︒AEC DAB ∽ AC AE BD AD=4cos 5AE DAF AD ∠==45AC BD =4AC =5BD =52r =OP DC ⊥OQ AF ⊥90OPE PEQ OQE ∠=∠=∠=︒OPEQ AF CD =OP OQ =OPEQ OP a PE ==CE b =OP CD ⊥DP CP =DO OB =∴,,∵,∴,∵,∴,∵,∴,∴,∴,即:,解得:,∴;②如图,连接,由(3)①得,四边形为正方形,2BC a =()22CD PC a b ==+AF BC ∥AEB EBC ∠=∠AEB BDC ∠=∠EBC BDC ∠=∠BCE BCD ∠=∠BEC DBC ∽ BC EC DC BC=2BC CE CD =⋅()()222a b a b =⋅+1b a=1tan 2OP a BDC DP a b ∠===+HF OPEQ∵,∴,由,得,∴,∴,,∵,,∴为等腰直角三角形,∴,,∴,∵,,∴,∴,,解得:,∴,∵,∴,∴,∴,OE x =OP PE QE x ===1tan 2BDC ∠=DP =CP DP ==CE CP EP x =-=CD =AF CD =AF CD ⊥ADE V x AE DE ==EF CE x ==AC ==90OPD DEM ∠=∠=︒ODP MDE ∠=∠ODP MDE ∽OP DP ME DE==ME x =AM AE ME x x x =-==AF BC ∥AMN CBN ∽ 34AN AM NC BC ===37AN AC x ==∵,∴,∵,∴,∵,∴,∵,∴,∵,∴,∵,∴,∴,∴,∴∴,∵,∴,∵,∴,∴∴,∴.【点睛】本题主要考查了相似三角形的判定和性质,勾股定理,圆周角定理,等腰三角形的判定和性质,ODP MDE ∽CEB CBD∠∠= CDCD =CBD CAD ∠=∠CEB DEG ∠=∠DAN DEG ∠=∠ CFCF =EDG CAE ∠=∠AF BC ∥CAE ACB ∠=∠ AB AB =ADN ACB ∠=∠ADN EDG ∠=∠DEG DAN ∽ AN AD EG DE==EG AN x == BFBF =EAB EHF ∠=∠AEB HEF ∠=∠ABE HFE ∽ EH EF AE BE ==EH AE ==GH EH EG x =-=解题的关键是熟练掌握相关的判定和性质,数形结合,作出辅助线.。
中考数学第一次模拟考试题含答案
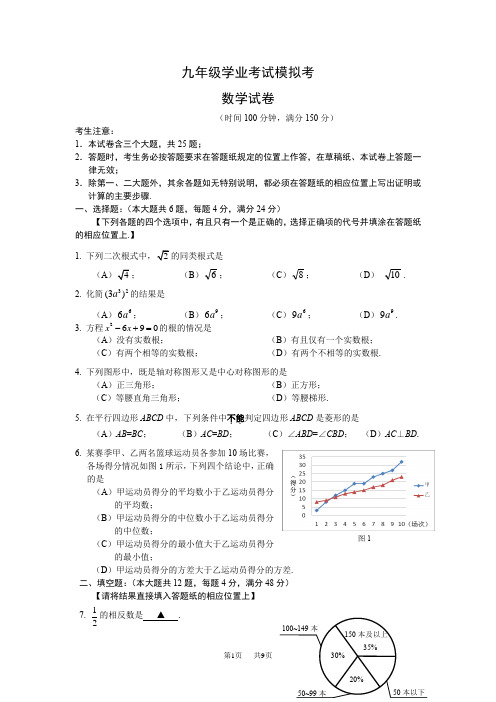
九年级学业考试模拟考数学试卷(时间100分钟,满分150分)考生注意:1.本试卷含三个大题,共25题;2.答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效;3.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤. 一、选择题:(本大题共6题,每题4分,满分24分) 【下列各题的四个选项中,有且只有一个是正确的,选择正确项的代号并填涂在答题纸的相应位置上.】1. 下列二次根式中,2的同类根式是(A )4; (B )6;(C )8;(D )10.2. 化简32(3)a 的结果是(A )66a ; (B )96a ; (C )69a ; (D )99a . 3. 方程2690x x -+=的根的情况是(A )没有实数根; (B )有且仅有一个实数根; (C )有两个相等的实数根; (D )有两个不相等的实数根. 4. 下列图形中,既是轴对称图形又是中心对称图形的是 (A )正三角形; (B )正方形;(C )等腰直角三角形; (D )等腰梯形. 5. 在平行四边形ABCD 中,下列条件中不能..判定四边形ABCD 是菱形的是 (A )AB =BC ; (B )AC =BD ; (C )∠ABD =∠CBD ; (D )AC ⊥BD . 6. 某赛季甲、乙两名篮球运动员各参加10场比赛,各场得分情况如图1所示,下列四个结论中,正确的是(A )甲运动员得分的平均数小于乙运动员得分的平均数;(B )甲运动员得分的中位数小于乙运动员得分的中位数;(C )甲运动员得分的最小值大于乙运动员得分的最小值;(D )甲运动员得分的方差大于乙运动员得分的方差. 二、填空题:(本大题共12题,每题4分,满分48分) 【请将结果直接填入答题纸的相应位置上】 7.12的相反数是 ▲ . 100~149本150本及以上 图18. 因式分解:24x y y -= ▲ . 9. 不等式组36210x x ->-⎧⎨+>⎩的解集是 ▲ .10. 方程2x x +=的根是 ▲ .11. 若反比例函数13ky x-=的图像经过第一、三象限,则 k 的取值范围是 ▲ . 12. 某校对部分学生家庭进行图书量调查,调查情况如图2所示,若本次调查中,有50本以下图书的学生家庭有24户,则参加本次调查的学生家庭数有 ▲ 户.13. 布袋中有1个黑球和1个白球,这两个球除颜色外其他都相同,如果从布袋中先摸出一个球,放回摇匀后,再摸出一个球,那么两次都摸到白球的概率是 ▲ . 14. 将抛物线2y x x =+向右平移1个单位后,所得新抛物线的表达式是 ▲ . 15. 如图3,AB ∥CD ,直线MN 分别与AB 、CD 交于点E 、F ,FG 是∠NFD 的平分线,若∠MEB=80°,则∠GFD 的度数为 ▲ . 16. 如图4,△ABC 中,D 为边AC 的中点,设BD =a ,BC =b ,那么CA 用a 、b 可表示为▲ .17. 当两个圆有两个公共点,且其中一个圆的圆心在另一圆的圆内时,我们称此两圆的位置关系为“内相交”.如果⊙1O 、⊙2O 半径分别3和1,且两圆“内相交”,那么两圆的圆心距d 的取值范围是 ▲ .18. 如图5,在△ABC 中,AB =AC =5,BC =4,D 为边AC 上一点,且AD =3,如果△ABD 绕点A 逆时针旋转,使点B 与点C 重合,点D 旋转至D ',那么线段D D '的长为 ▲ .三、解答题:(本大题共7题,满分78分) 19. (本题满分10分)计算:()1122cot 302323(31)-︒+⨯--+-.20. (本题满分10分)图5ABC D 图4 A B CD图3 E M F G N D C B AFED CBA解方程:31131x x-=+-.21. (本题满分10分,第(1)、(2)小题满分各5分) 如图6,D 是⊙O 弦BC 的中点,A 是 上一点,OA 与BC 交于点E ,已知AO =8,BC =12.(1)求线段OD 的长;(2)当EO =2BE 时,求∠DEO 的余弦值.22. (本题满分10分,第(1)、(2)小题满分各5分)已知弹簧在其弹性限度内,它的长度y (厘米)与所挂重物质量x (千克)的关系可表示为y kx b =+的形式,其中k 称为弹力系数,测得弹簧A 的长度与所挂重物(不超过弹性限度)的关系如图7-1所示.(1)求弹簧A 的弹力系数; (2)假设在其它条件不变的情况下,弹簧的弹力系数k 与弹簧的直径d (如图7-2所示)成正比例.已知弹簧B 的直径是弹簧A 的1.5倍,且其它条件均与弹簧A 相同(包括不挂重物时的长度).当弹簧B 挂一重物后,测得此时弹簧长度为9厘米,求该重物的质量.23. (本题满分12分,第(1)、(2)小题满分各6分)如图8,Rt △ABC 中,∠ACB=90°,D 是边BC 上一点,点E 、F 分别是线段AB 、AD 中点,联结CE 、CF 、EF .(1)求证:△CEF ≌△AEF ;(2)联结DE ,当BD=2CD 时,求证:DE=AF .EA DCBO 图6y (厘米) x (千克) 8 104 8 O 图7-1 d图7-224. (本题满分12分,第(1)小题满分3分,第(2)小题满分4分,第(3)小题满分5分)在平面直角坐标系xOy中,已知顶点为P(0, 2)的二次函数图像与x轴交于A、B两点,A点坐标为(2, 0).(1)求该二次函数的解析式,并写出点B坐标;(2)点C在该二次函数的图像上,且在第四象限,当△ABC的面积为12时,求点C坐标;(3)在(2)的条件下,点D在y轴上,且△APD与△ABC相似,求点D坐标.25. (本题满分14分,第(1)小题满分4分,第(2)、(3)小题满分各5分)如图9,在平行四边形ABCD中,AB=4,BC=2,∠A=60°.(1)求证:BD⊥BC;(2)延长CB至G,使BG=BC,E是边AB上一点,F是线段CG上一点,且∠EDF=60°,设AE=x,CF=y.①当点F在线段BC上时(点F不与点B、C重合),求y关于x的函数解析式,并写出定义域;②当以AE为半径的⊙E与以CF为半径的⊙F相切时,求x的值.黄浦区九年级学业考试模拟考数学参考答案与评分标准一、选择题:(本大题共6题,每题4分,满分24分)1. C;2.C;3.C;4. B;5. B;6.D.二、填空题:(本大题共12题,每题4分,满分48分)7.12-;8.(2)(2)y x x+-;9.122x-<<;10.2x=;11.图9BDCA图813k <; 12. 160; 13.14; 14. 2y x x =-; 15. 50°; 16. 22a b -; 17. 23d <<; 18.125. 三、解答题:(本大题共7题,满分78分)19. 解:原式(2(4+- …………………………………………(8分)24- ………………………………………………(1分) =2 ………………………………………………………………………(1分) 20. 解:去分母得3(1)(3)(1)(3)x x x x --+=-+. ………………………………………(3分)整理得 2230x x --=. ………………………………………………………(3分)(1)(3)0x x +-=. ………………………………………………………(1分)解得 11x =-,13x =. …………………………………………………………(2分)经检验11x =-,13x =都是原方程的根. ………………………………………………(1分) 21. 解:(1)联结OB . …………………………………………………………………………(1分)∵OD 过圆心,且D 是弦BC 中点,∴OD ⊥BC ,12BD BC =. ………………………………………………………………(2分)在Rt △BOD 中,222OD BD BO +=. ……………………………………………………(1分)∵BO =AO =8,6BD =.∴OD =. ……………………………………………………………………………(1分)(2)在Rt △EOD 中,222OD ED EO +=.设BE x =,则EO ,6ED x =-.222(6))x +-=.……………………………………………………………(2分)解得 116x =-(舍), 24x =.………………………………………………………(1分)∴ED =2,EO= 在Rt △EOD中,cos DEO ∠=………………………………………………………(2分)22. 解:(1)把(4,8),(8,10)代入y kx b =+得84108k bk b=+⎧⎨=+⎩ ………………………………………………………(2分)解得126k b ⎧=⎪⎨⎪=⎩ ………………………………………………………(2分)∴ 弹簧A 的弹力系数为12. ………………………………………………………(1分)(2)设弹簧B 弹力系数为b k ,弹簧A 的直径为A d ,则弹簧B 的直径为32A d . 由题意得32b A A k kd d =. ∴ 3324b k k ==. ………………………………………………………(2分)又∵弹簧B 与弹簧A 不挂重物时的长度相同, ∴弹簧B 长度与所挂重物质量的关系可表示为364y x =+. ……………………………(1分)把9y =代入364y x =+得 4x =. …………………………………………………(2分)∴此时所挂重物质量为4千克.23. 证明:(1)∵∠ACB=90°,且E 线段AB 中点,∴CE =12AB =AE . ………………………………………………………………………(2分)同理CF =AF . ……………………………………………………………………………(1分)又∵EF =EF ,……………………………………………………………………………(1分) ∴△CEF ≌△AEF . ……………………………………………………………………(2分)(2) ∵点E 、F 分别是线段AB 、AD 中点,∴12EF BD =,EF ∥BC . ………………………………………………………………(2分)∵BD=2CD , ∴EF CD =.又∵EF ∥BC ,∴四边形CEFD 是平行四边形. ……………………………………(2分)∴DE =CF . …………………………………………………………………………………(1分)∵CF =AF ,∴DE =AF . ……………………………………………………………………(1分) 24. 解:(1)设抛物线表达式为22y ax =+.把(2, 0)代入解析式,解得12a =-.…………………(1分)∴抛物线表达式为2122y x =-+………………………(1分)∴B (-2, 0). ……………………………………………(1分)(2)过点C 作CH ⊥x 轴,垂足为H .设点C 横坐标为m ,则2122CH m =-.…………………………………………(1分)由题意得211[2(2)](2)1222m ⋅--⋅-=…………………(1分)解得4m =±. …………………………………………(1分) ∵点C 在第四象限,∴4m =. ∴C (4, -6). ……(1分)(3)∵PO =AO =2,∠POA=90°,∴∠APO=45°. ………………………………………(1分)∵BH =CH =6,∠CHB=90°,∴∠CBA=45°. ∵∠BAC <135°,∴点D 应在点P 下方,∴在△APD 与△ABC 中,∠APD=∠CBA . ………………………………………………(1分) 由勾股定理得P A =22,BC =62.1°当PD PA AB BC =时,22462PD =.解得43PD =.∴12(0,)3D ……………………………(1H PA CB O xy分)2°当PD PABC AB =.解得6PD =.∴2(0,4)D -…………………………(1分)综上所述,点D 坐标为2(0,)3或(0,4)-……………………………………………………(1分)25. 解:(1)过点D 作DH ⊥AB ,垂足为H . …………………………………………………(1分)在Rt △AHD 中,cos cos 1AH AD A BC A =⋅∠=⋅∠=.∵12AH AD =,12BC CD =,∴AH BCAD CD=,即AH AD BC CD =. 又∵∠C =∠A =60°,∴△AHD ∽△CBD . …………………………………………………(2分)∴∠CBD =∠AHD =90°. ∴BD ⊥BC . ……………………………………………………(1分)(2)①∵AD ∥BC ,∴∠ADB =90°,∵∠BDH +∠HDA =90°,∠A +∠HDA =90°. ∴∠BDH =∠A =60°.∵∠EDF =60°,∴∠BDH =∠EDF , 即∠EDH +∠BDE =∠FDB +∠BDE .∴∠EDH =∠FDB . ………………………………………………………………………(2分)又∵∠EHD =∠CBD =90°,∴△EHD ∽△FBD . ………………………………………(1分)∴DH EHBD BF =12x y-=-. ∴42y x =-(12)x <<.……………………………(2分)②联结EF .1°当点F 在线段BC (点F 不与点B 、C 重合)上时,∵△EHD ∽△FBD ,∴DH DE BD DF =. 即DH BDDE DF=. 又∵∠BDH =∠EDF ,∴△BDH ∽△FDE . ∴∠DEF=90°.在Rt △EDH 中,DE ==∴tan 60EF DE DE =⋅︒==…………………………………………(1分)i) 当⊙E 与⊙F 内切时,(42)x x --.解得,1x =(舍),2x =(舍). ………………………………………(1分)ii)当⊙E 与⊙F 外切时,(42)x x +-解得11x =(舍),22x =-(舍). …………………………………………………………(1分)2°点F 与点B 重合时,即 x =1 时,两圆外切. 3°当点F 在线段BG (点F 不与点B 重合)上时,易得42CF x =-,且△BDH ∽△FDE 仍然成立. ∴EF =.由1°计算可知96x =时两圆内切. ………………………………………………(1分)综上所述,当 x =1 时,两圆外切,当x (1分)。
中考第一次模拟考试数学试题含答案解析

九年级班学业水平质量抽测数 学(试卷满分:150分 考试时间:120分钟)准考证号姓名 座位号注意事项:1.全卷三大题,27小题,试卷共4页,另有答题卡. 2.答案必须写在答题卡上,否则不能得分. 3.可以直接使用2B 铅笔作图.一、选择题(本大题有10小题,每小题4分,共40分.每小题都有四个选项,其中有且只有一个选项正确)1.如图,数轴上有A ,B ,C ,D 四个点,其中表示互为相反数的点是A .点A 与点 DB .点A 与点C C .点B 与点D D .点B 与点C 2.我国第一艘航母“辽宁舰”最大排水量为67500吨,这个数据用科学记数法可表示为 A .6.75×102 B . 67.5×103 C .6.75×104 D .6.75×105 3.在相同条件下重复试验,若事件A 发生的概率是1007.下列陈述中,正确的是 A .事件A 发生的频率是1007B .反复大量做这种试验,事件A 只发生了7次C .做100次这种试验,事件A 一定发生7次D .做100次这种试验,事件A 可能发生7次 4.计算()23-a 的结果是A .92-aB .92+aC .962+-a aD .962++a a5.小明骑自行车上学,开始以正常速度匀速行驶,但行至中途自行车出了故障,只好停下来修车.车修好后,因怕耽误上课,加快了骑车速度,则下面表示小明到学校剩下的路程s 关于时间t 的函数图象大致是A .B .C .D .6.在Rt ABC ∆中∠A =90°, BC =10,D 为BC 的中点.当⊙A 半径为6时,则D 点与⊙A 位置关系为 A .圆上 B .圆内 C .圆外 D .以上三种都有可能7.如图,在平面直角坐标系xoy 中,点B ,C ,E 在y 轴上,Rt △ABC 经过变 换得到Rt △ODE .若点C 的坐标为(0,1),AC =2,则这种变换可以是 A .△ABC 绕点C 顺时针旋转90°,再向下平移3 B .△ABC 绕点C 顺时针旋转90°,再向下平移1第1题O ACB y xC .△ABC 绕点C 逆时针旋转90°,再向下平移1D .△ABC 绕点C 逆时针旋转90°,再向下平移3 8.点A 是反比例函数x y 3=(x>0)的图象上任意一点,AB ∥y 轴交反比例函数xy 2-=的图象于点B ,以AB 为边作□ABCD ,其中点C ,D 都在y 轴上,则S □ABCD 为 A . 2 B . 3 C .5 D . 不确定9.如图,锐角三角形ABC 中,直线l 为BC 的垂直平分线,射线m 平分 ∠ABC ,l 与m 相交于P 点.若∠A =60°,∠ACP =24°,则∠ABP 等于 A .24° B .30°C .32°D .42°10.某次列车平均提速v km/h ,用相同的时间,列车提速前行驶s km ,提速后比提速前多行驶50 km .设提速前列车行驶的速度是x km/h ,则下面方程符合题意的是 A .x s v x s 50+=+ B .v x s x s ++=50 C .v x s x s -+=50 D .xs v x s 50+=-二、填空题(本大题有6小题,每小题4分,共24分)11.已知∠1=40°,则∠1的余角度数是 .12.一只蚂蚁在如图所示的树上寻觅昆虫作为食物.假定蚂蚁在每个岔路口都会随机选择一条路径,那么它获得食物的概率是 . 13.计算:1212---a aa =_______. 14.如图,在⊙O 中,AC ∥OB ,∠ ABO =20°,则∠BOC 的度数为 . 15.抛物线p x x y +-=2与x 轴相交,其中一个交点坐标是(p ,0). 那么该抛物线的顶点坐标是________. 16.()325732201720162015b a +=⨯⨯+⨯⨯且1610≤≤a ,则b 的最小值_______.三、解答题(本大题有11小题,共86分) 17.(本题满分7分)解不等式组31,213 3.x x x +≤⎧⎨->-⎩18.(本题满分7分)如图,已知CA =CD ,⊙1=⊙2,BC =EC . 求证:⊙ABC ≌△DEC . 19.(本题满分7分)mlP CBA第9题OCBA第14题第18题21E CDBAA第12题如图,已知⊙ABC ,∠C=90°,AC <BC ,D 为BC 上一点,且到 A ,B 两点的距离相等.用直尺和圆规,作出点D 的位置. (不写作法, 保留作图痕迹)20.(本题满分7分)已知等腰三角形的周长是12.请写出底边长y 关于腰长x 的 函数关系式,并在直角坐标系中,画出函数的图象. 21.(本题满分7分)如图,已知菱形ABCD 的周长20,sin ∠ABD =35,求菱形ABCD的面积.22. (本题满分7分)水龙头关闭不严会造成漏水,通过一次调查发现漏水量与漏水时间的关系如下表:时间 (分钟) 0 5 10 15 20 25 30水量 (毫升)0 21 41 59 79 101 121漏水量与漏水时间近似于正比例函数关系,以表中每间隔5分钟漏水量的众数为依据,来估算这种漏水状态下一天该水龙头的漏水量.23.(本题满分7分)如图,锐角⊙ABC 是⊙O 内接三角形,弦AE ⊥BC ,垂足为D . 在AD 上取点F ,使FD DE ,连接CF ,并延长交AB 于点G . 求证:CG ⊥AB .24. (本题满分7分)一个对角线的长比边长多1cm 的正方形,它的边长增加3cm 时,面积增加392cm 可以吗?请说明理由.25.(本题满分7分)当某一面积S 关于某一线段x 是一次函数时,则称S 是关于x 的奇特面积.如图,∠BAC =45°,点D 在AC 边上,且DA =2.点P ,Q 同时从D 点出发,分别沿射线DC 、射线DA 运动, P 点的运行速度是Q 点的2倍,当点Q 到达A 时,点P ,Q 同时停止运动.过点Q 作AC 的垂线段QR ,使QR =PQ ,连接PR .设QD =x ,△PQR 和∠BAC 重叠部分的面积为S ,请问S 是否存在关于x 的奇特面积?若存在,求奇特面积S 关于x 的函数关系式;若不存在,请说明理由.26.(本题满分11分)第21题DCBA第25题RAB第23题DGF CBAO已知抛物线的解析式为2y mx =()0>m 和点104F ⎛⎫⎪⎝⎭,,A 为抛物线上不同于原点的任意一点,过点A的直线l 交抛物线于另一点B ,交y 轴于点D (点D 在F 点上方),且有FA FD =.当⊙ADF 为正三角形时,1AF =. (1)求m 的值;(2)当直线l //l 1且与抛物线仅交于一点E 时,小明通过研究发现直线AE 可能过定点,请你说明直线AE 可能过定点的猜想过程,并写出猜得的定点坐标.27.(本题满分12分)如图,在四边形ABCD 中,∠ABC =90°,点,,,E F M N 分别在,,,AB AD DC CB 边上,连接,,,EF EN NM FM ,若////EF BD NM ,1EN EFAC BD+=. (1)求证:Rt ABC ∆∽Rt EBN ∆;(2)当BD EF EN =+且四边形ABCD 的面积为S 时,判断四边形EFMN 面积最大时的形状.同安区届初中毕业班学业水平质量抽测数学参考答案一、选择题(本大题共10小题,每小题4分,共40分)题号 1 2 3 4 5 6 7 8 9 10 选项ACDCDBACCB二、填空题(本大题共6小题,每题4分,共24分) 11.50° 12.3113. 2- 14. 40° 15. ⎪⎭⎫⎝⎛-4121, 16.三、解答题(本大题共9小题,共86分) 17.(本题满分7分) 解:解不等式①得2-≤x ………………………………………….3分 解不等式②得42->-x第27题M N FE DC B A2<∴x …………………………………………………6分2-≤∴x 原不等式组的解集为:……………………..7分18.(本题满分7分)证明:21∠=∠ACE ACE ∠+∠=∠+∠∴21DCE ACB ∠=∠即……………………………………………………….2分 EC BC CD CA ==, ………………………………………………… 4分DEC ABC ∆≅∆∴………………………………………………………..7分19.(本题满分7分)正确画图得6分,下结论1分(画弧1分、两弧交点2分、连线1分、点D 标出2分) 20.(本题满分7分) 解:根据题意得122=+y xx y 212-=∴(含自变量取值范围 正确画出直角坐标系 正确画出图形3分(画直线扣221.(本题满分7分) 解:连接AC 交BD 于点四边形 ABCD ⊥∴AC BD AC ,=∠∆AOB ,ABO Rt 中在90°53==∠∴AB AD ABD sin …………………………….2分355353=⨯==∴AB AD ………………………….4分4352222=-=-=∴AO AB BO ………….5分824632=⨯==⨯=∴BD ,AC …………………6分24862121=⨯⨯=⋅=∴BD AC S ABCD 菱形…………7分22.(本题满分7分)解:由表可知每间隔5分钟的漏水量分别为:21、20、18、20、22、20 .........................................................................................1分20众数是:∴ …………………………………………………………………….3分DBCAODCBA20=246057605∴⨯⨯=一天漏水量……………………………………………….6分 答:这种漏水状态下一天该水龙头的漏水量是5760毫升……………………….7分23. (本题满分7分 解:连接CE∵AD 是BC 边上的高 ∴CD⊥EF ∵FD DE = ∴CE=CF∴∠E=∠CFE…………………………2分 在⊙O 中,∠E=∠B ...............................3分 ∵∠CFE=∠A FG∴∠B =∠A FG ……………………………5分 ∵在Rt △ABD 中,∠B +∠B AD=90° ∴∠A FG +∠B AD =90 ∴∠AGF =90°∴CG ⊥AB……………………………………….7分 24.(本题满分7分) 解: 法一:设正方形的边长是acm∵()22339a a +-=……………………………………………………….2分 ∴5a =……………………………………………………………………..3分∴正方形的对角线长为:2a =5251≠+……………………………6分 ∴不存在符合要求的正方形………………………………………………7分 法二:设正方形的边长是xcm∵正方形的对角线长比边长多1cm∴2x =1x +………………………………………………………………….2分 ∴21x =+………………………………………………………………….3分当正方形的边长增加3cm 时,面积增加的部分是:22(213)(21)++-+=1562+39≠………………………………6分∴不存在符合要求的正方形……………………………………………….7分25.(本题满分7分)解: QD =x ,P 点的运行速度是Q 点运行速度2倍 ∴P D =2x………………………………………………………..1分PQ QR =第25题RB当等腰Rt △PQR 顶点R 落在∠B AC 内部时,S=()222x x +是二次函数,不符合奇特面积……………………2分当等腰Rt △PQR 顶点R 落在∠B AC 的边AB 上时, RQ =QA =PQx x x 22+=-∴22-=∴x …………………………………………………………3分当等腰Rt △PQR 顶点R 落在∠B AC 的外部时,()()22221422x x S --+=()122-+=x ()222<<-x ………………6分(含自变量得取值范围1分,也可取等号)∴当222<<-x 时,s 与x 是一次函数关系,符合奇特面积。
九年级数学中考第一次模拟考卷

九年级数学中考第一次模拟考卷一、选择题(每题4分,共40分)1. 下列选项中,既是奇数又是合数的是()A. 21B. 39C. 51D. 632. 已知a、b为实数,且a≠b,则下列等式中成立的是()A. (a+b)² = a² + b²B. (ab)² = a² b²C. (a+b)² = a² + 2ab + b²D. (ab)² = a² 2ab b²3. 下列函数中,是正比例函数的是()A. y = 2x²B. y = 3x 1C. y = x + 3D. y = 5/x4. 在三角形ABC中,a=8,b=10,cosA=3/5,则三角形ABC的面积是()A. 24B. 30C. 36D. 405. 下列关于x的不等式中,有解的是()A. x² < 0B. x² = 1C. x² > 0D. x² = 06. 已知一组数据的方差是9,那么这组数据每个数都加5后,方差是()A. 4B. 9C. 14D. 187. 下列关于圆的说法,正确的是()A. 圆的半径相等,则圆心距相等B. 圆心角相等,则弧长相等C. 弧长相等,则圆心角相等D. 圆的半径相等,则面积相等8. 下列关于概率的说法,错误的是()A. 概率的取值范围是0到1B. 必然事件的概率是1C. 不可能事件的概率是0D. 随机事件的概率大于19. 已知平行四边形ABCD的对角线交于点E,若BE=4,CE=6,则平行四边形ABCD的面积是()A. 24B. 36C. 48D. 6010. 下列关于二次函数的说法,正确的是()A. 二次函数的图像一定经过原点B. 二次函数的图像一定有最小值C. 二次函数的图像一定有最大值D. 二次函数的图像一定是一条直线二、填空题(每题4分,共40分)11. 已知等差数列的前5项和为35,第5项为15,则首项为______。
九年级第一次中考数学模拟考试试题(含参考答案及评分标准)

空,每空 2 分 .把答案写在题中横线上)
17.计 算 : a2 b 2 的 结 果 是
.
2a 2b
18.如图 8,长 4m 的楼梯 AB 的倾斜角∠ ABD 为 60°,为了改善
楼梯的安全性能,准备重新建造楼梯,使其倾斜角∠
ACD 为
45°,则调整后的楼梯 AC 的长为
米.
图8
19. 如图 9,在平面直角坐标系 xOy 中,点 A1, A2, A3,……
B. a6 a a 5
2
D. 3 2 7
5.已知方程 kx+b=0 的解是 x=3,则函数 y=kx+b 的图象可能是(
)
A .
B.
C.
D.
6.如果式子 2x 6 有意义,那么 x 的取值范围在数轴上表示出来,正确的
是(
)
A
B
C
D
7. 如图 1,一个正方体切去一个三棱锥后所得几何体的俯视图是(
)
A
1
C.
3
1
D.
2
10.某学校为绿化环境, 计划种植 600 棵树, 实际劳动中每小时植树的数量比
原计划多 20%,结果提前 2 小时完成任务 .设原计划每小时植树 x 棵,则列
出的方程为(
)
A. 600
600
2
x (1 20%) x
C. 600 600 2 x 20% x
11.如图 3,阴影部分是两个半径为
中,是轴对称图形的是(
)
A
B
C
D
3.唐山是中国第一个承办世界园艺博览会的地市级城市,绿化总面积
140 万平方米,数据 140 万用科学记数法表示为(
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初三数学第一次模拟考试
一、选择题(共36分)
1.下列计算不正确的是( ).
A.31222-+=-
B.2
11
39
⎛⎫-= ⎪⎝⎭ C.33-= D.1223=
2.下列汽车标志中既是轴对称又是中心对称图形的是( ).
大众 本田 欧宝 奥迪
A .
B .
C .
D . 3、下列运算中,正确的是( )
A .2222+=
B .632
x x x ÷= C .122-=- D. a 3
×(-a 2
)=-a 5
4.据《沈阳日报》报道,今年前四个月辽宁省进出口贸易总值达165亿美元.164亿美元用科学记数法可以表示为(保留2个有效数字)( )
A .16.5×109亿美元
B .1.65×1010亿美元
C .1.7×109亿美元
D .1.7×1010亿美元 5.下列函数中,自变量x 的取值范围是3x ≥的是( ) A .1
3
y x =
- B .3
y x =- C .3y x =- D .3y x =- 6.一次函数y =ax +1
2的图象过一、二、四象限,点A (x 1,-2)、B (x 2,4)、C (x 3,5)为反比例函数y =
a -1
x
图象上的三点,则下列结论正确的是( ). A .x 1>x 2>x 3 B .x 1>x 3>x 2 C .x 3>x 1>x 2 D .x 2>x 3>x 1 7. 如图,已知P A 、PB 是⊙O 的切线,A 、B 为切点,AC 是⊙O 的直径, 若∠P =40°,则∠C 度数是( )
A .40°
B .50°
C .60°
D .70°
8.有四张形状、大小和质地完全相同的卡片,每张卡片的正面写有一个算式.将
这四张卡片背面向上洗匀,从中随机抽取一张(不放回),接着再随机抽取一张,则抽取的两张卡片上的算式都正确的概率是( ).
A .1
2 B .1
4 C .1
6 D .1
8
第15题图
第11题图
第18题图
9.如图⑴是一个小正方体的表面展开图,小正方体从图⑵所示位置依次翻转到第1格、第2格、第3格,这时小正方体朝上一面的字是( )。
A. 腾
B. 飞
C. 燕
D. 山
10、如图5,一块三角板与圆片重合,直角边AB=AC=2,使AB 与圆片直径重合,则阴影部分的面积为( )
A .1+
4π B 、2-4
π
C .2
D .1 11.如图,为了测量某建筑物AB 的高度,在平地上C 处测得建筑物顶端A 的仰角为30°,沿CB 方向前进12m 到达D 处,在D 处测得建筑物 项端A 的仰角为45°,则建筑物AB 的高度等于( ).
A .6(3+1)m
B .6(3-1)m
C .12(3+1)m
D .12(3-1)m
12、如图,四边形ABCD 中,AB =BC ,∠ABC =∠CDA =90°,BE ⊥AD 于点E ,且四边形ABCD 的面积为8,则BE =( ) A .2 B .3
C .22
D .23
二:填空题(共18分)
13.分解因式:4a 2-b 2+6a -3b =______________________________. 14.分式方程
21
3
2=+-x x 的根是_________________. 15.如图,已知菱形ABCD 的一个内角∠BAD =80º,对角线AC 、BD 相交于点
O ,点E 在AB 上,且BE =BO ,则∠EOA =_______. 16.已知一元二次方程0562=--x x 的两根为a 、b ,则
b
a 1
1+的值是____________.
17.方程组 的解 ____________.
18.如图,直线y =
3
3
x ,点A 1坐标为(1,0),过点A 1作x 轴的垂线交直线于点B 1,以原点O 为圆心,OB 1长为半径画弧交x 轴于点A 2;再
过点A 2作x 轴的垂线交直线于点B 2,以原点O 为圆心,OB 2长为半径画弧交x 轴于点A 3,……,按此做法进行下去,点A 4的坐标为(_____,
⎩⎨⎧=-=-7
4143y x y x
图 1 图2 ____);点A n (_______,_____). 19.(本题满分10分)
甲、乙两支篮球队在集训期内进行了五场比赛,将比赛成绩进行统计后,绘制成
如图1、图2的统计图.
(1)在图2中画出折线表示乙队在集训期内这五场比赛成绩的变化情况;
(2)已知甲队五场比赛成绩的平均分甲x =90分,请你计算乙队五场比赛成绩的平均分乙x ; (3)就这五场比赛,分别计算两队成绩中位数、极差;
(4)如果从甲、乙两队中选派一支球队参加篮球锦标赛,根据上述统计情况,试从平均分、折线的走势、获胜场数和极差四个方面分别进行简要分析,你认为选派哪支球队参赛更能取得好成绩?
20.(本题满分10分)
如图,某防洪指挥部发现长江边一处长500米,高10米,背水坡的坡角为45°的防洪大堤(横断面为梯形ABCD )急需加固.经调查论证,防洪指挥部专家组制定的加固方案是:沿背水坡面用土石进行加固,并使上底加宽3米,加固后背水坡EF 的坡比i =1∶ 3. (1)求加固后坝底增加的宽度AF ;
(2)求完成这项工程需要土石多少立方米?(结果保留根号)
O N B P
C
A
M
21.(本题11分)如图,矩形ABCD 中,AB =3,BC =4,M 为CD 中点,点E 在线段MC 上运动,FG 垂直平分AE ,垂足为O ,分别交AD 、BC 于F 、G . (1)求
FG
AE
的值; (2)设x CE ,四边形AGEF 的面积为y .
①求y 关于x 的函数关系式;
②当y 取最大值时,判断四边形AGEF 的形状,并说明理由.
22、(本题11分)某食品加工厂,准备研制加工两种口味的核桃巧克力,即原味核桃巧克力和益智核桃巧克力.现有主要原料可可粉410克,核桃粉520克.计划利用这两种主要原料,研制加工上述两种口味的巧克力共50块.加工一块原味核桃巧克力需可可粉13克,需核桃粉4克;加工一块益智核桃巧克力需可可粉5克,需核桃粉14克.加工一块原味核桃巧克力的成本是1.2元,加工一块益智核桃巧克力的成本是2元.设这次研制加工的原味核桃巧克力x 块.
(1)求该工厂加工这两种口味的巧克力有哪几种方案?
(2)设加工两种巧克力的总成本为y 元,求y 与x 的函数关系式,并说明哪种加工方案使总成本最低?总成本最低是多少元?
23(本题满分12分)
如图,已知AB 是⊙O 的直径,点C 在⊙O 上,过点C 的直线与AB 的延长线
E
·
交于点P ,AC =PC ,∠COB =2∠PCB . (1)求证:PC 是⊙O 的切线; (2)求证:BC = 1
2 AB ;
(3)点M 是 AB ⌒的中点,CM 交AB 于点N ,若AB =4,求MN ·MC 的值. 24.(本题满分12分) 已知二次函数213
42
y x x =-
+的图象如图. (1)求它的对称轴与x 轴交点D 的坐标;
(2)将该抛物线沿它的对称轴向上平移,设平移后的抛物线与x 轴,y 轴的交点分别为A 、B 、C 三点,若∠ACB =90°,求此时抛物线的解析式;
(3)设(2)中平移后的抛物线的顶点为M ,以AB 为直径,D 为圆心作⊙D ,试判断直
线CM与⊙D的位置关系,并说明理由.。
