100以内的勾股数
100以内的勾股数规律整理
1
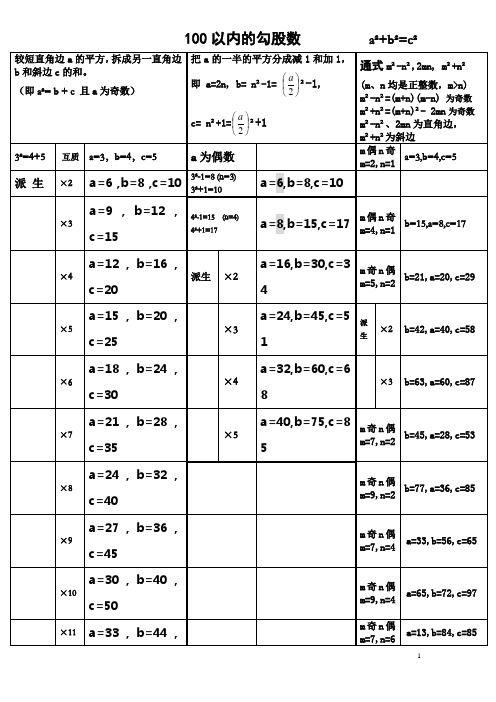
的平方, 较短直角边 a 的平方,拆成另一直角边 把 a 的一半的平方分成减 1 和加 1,
通式 m²-n²,2mn, m²+n² m²
的和。 (即 b 和斜边 c 的和。 即 a²= b + c 且 a 为 ( 奇数) ) 奇数)
a c= n²+1= ²+1 n²+1= 2
a=2n, 即 a=2n,
×2
8²-1=63 (n=8) 1=63 +1=65 8²+1=65
9²=40+41
互质
派 生
11² 11²=60+61
×2
9²-1=80 (n=9) 1=80 +1=82 9²+1=82 10² 10²-1=99 (n=10) 10² 10²+1=101
a=18,b=80,c=82 a=18,b=80,c=82 18,b=80,c= a=20,b=99,c=101 a=20,b=99,c=101 m 偶 n 奇 a=11,b=60,c=61 20,b=99,c= a=11 b=60,c=61 11, 60,c=
生
a=32,b=60, a=32,b=60,c=68 32,b=60 a=40,b=75, a=40,b=75,c=85 40,b=75
m奇n偶 b=45,a=28,c=53 45,a=28,c= b=45,a=28,c=53 m=7,n=2 m奇n偶 77,a=36,c= ,a=36,c=85 b=77,a=36,c=85 m=9,n=2 m奇n偶 a=33,b=56,c=65 33,b=56,c= a=33,b=56,c=65 m=7,n=4 m奇n偶 a=65,b=72,c=97 65,b=72,c= a=65,b=72,c=97 m=9,n=4 m奇n偶 a=13,b=84,c=85 13,b=84,c= a=13,b=84,c=85 m=7,n=6 奇数±奇数= ∵奇数±奇数=偶数 偶数±偶数= 偶数±偶数=偶数 奇数±偶数= 奇数±偶数=奇数 奇数×偶数= 奇数×偶数=偶数 奇数×奇数= 奇数×奇数=奇数 又∵ =(m+n)² 斜边 m²+n²=(m+n)²- 2mn 直角边 2mn 为偶数 =(m+n)(m直角边 m²-n²=(m+n)(m-n) 三边不能同偶 同偶基本勾 同偶, 三边不能 同偶 , 同偶基本勾 股数就不互质了 就不互质了, 股数就不互质了, m+n≠ 即 m+n≠偶数 不能同奇数、不能同偶 ∴m、n 不能同奇数、不能同偶 ∴m、n 为一奇一偶
100以内的勾股数

100以内的勾股数: i=3 j=4 k=5 i=5 j=12 k=13 i=6 j=8 k=10 i=7 j=24 k=25 i=8 j=15 k=17 i=9 j=12 k=15 i=9 j=40 k=41 i=10 j=24 k=26 i=11 j=60 k=61 i=12 j=16 k=20 i=12 j=35 k=37 i=13 j=84 k=85 i=14 j=48 k=50 i=15 j=20 k=25 i=15 j=36 k=39 i=16 j=30 k=34 i=16 j=63 k=65 i=18 j=24 k=30 i=18 j=80 k=82 i=20 j=21 k=29 i=20 j=48 k=52
i=48 j=55 k=73 i=48 j=64 k=80 i=51 j=68 k=85 i=54 j=72 k=90 i=57 j=76 k=95 i=60 j=63 k=87 i=65 j=72 k=97 勾股数的常用套路 所谓勾股数,一般是指能够构成直角三角形三条边的三个正整数( a,b,c)。 即 a^2+b^2=c^2,a,b,c∈N2 又由于,任何一个勾股数组(a,b,c)内的三个数同时乘以一个整数 n 得到的新数组(na,nb,nc)仍然是勾股数,所以一般我们想找的是 a,b ,c互质的勾股数组。 关于这样的数组,比较常用也比较实用的套路有 以下两种: 1、当 a 为大于 1 的奇数 2n+1时,b=2*n^2+2*n, c=2*n^2+2*n+1。 实际上就是把 a 的平方数拆成两个连续自然数,例 如: n=1时(a,b,c)=(3,4,5)
100以内的勾股数例举及例析

100以内的勾股数例举及例析i=3 j=4 k=5i=5 j=12 k=13i=6 j=8 k=10i=7 j=24 k=25i=8 j=15 k=17i=9 j=12 k=15i=9 j=40 k=41i=10 j=24 k=26i=11 j=60 k=61i=12 j=16 k=20i=12 j=35 k=37i=13 j=84 k=85i=14 j=48 k=50i=15 j=20 k=25i=15 j=36 k=39i=16 j=30 k=34i=16 j=63 k=65i=18 j=24 k=30i=18 j=80 k=82i=20 j=21 k=29i=20 j=48 k=52i=21 j=28 k=35i=21 j=72 k=75i=24 j=32 k=40i=24 j=45 k=51i=24 j=70 k=74i=25 j=60 k=65i=27 j=36 k=45i=28 j=45 k=53i=30 j=40 k=50i=30 j=72 k=78i=32 j=60 k=68i=33 j=44 k=55i=33 j=56 k=65i=35 j=84 k=91i=36 j=48 k=60i=36 j=77 k=85i=39 j=52 k=65i=39 j=80 k=89i=40 j=42 k=58i=40 j=75 k=85i=42 j=56 k=70i=45 j=60 k=75i=48 j=55 k=73i=48 j=64 k=80i=51 j=68 k=85i=54 j=72 k=90i=57 j=76 k=95i=60 j=63 k=87i=65 j=72 k=97勾股数的常用套路所谓勾股数,一般是指能够构成直角三角形三条边的三个正整数(a,b,c)。
即a^2+b^2=c^2,a,b,c∈N又由于,任何一个勾股数组(a,b,c)内的三个数同时乘以一个整数n得到的新数组(na,nb,nc)仍然是勾股数,所以一般我们想找的是a,b,c互质的勾股数组。
100以内的勾股数1

100以内的勾股数:i=3 j=4 k=5i=5 j=12 k=13i=6 j=8 k=10i=7 j=24 k=25i=8 j=15 k=17i=9 j=12 k=15i=9 j=40 k=41i=10 j=24 k=26i=11 j=60 k=61i=12 j=16 k=20i=12 j=35 k=37i=13 j=84 k=85i=14 j=48 k=50i=15 j=20 k=25i=15 j=36 k=39i=16 j=30 k=34i=16 j=63 k=65i=18 j=24 k=30i=18 j=80 k=82i=20 j=21 k=29i=20 j=48 k=52i=21 j=28 k=35i=21 j=72 k=75i=24 j=32 k=40i=24 j=45 k=51i=24 j=70 k=74i=25 j=60 k=65i=27 j=36 k=45i=28 j=45 k=53i=30 j=40 k=50i=30 j=72 k=78i=32 j=60 k=68i=33 j=44 k=55i=33 j=56 k=65i=35 j=84 k=91i=36 j=48 k=60i=36 j=77 k=85i=39 j=52 k=65i=39 j=80 k=89i=40 j=42 k=58i=40 j=75 k=85i=42 j=56 k=70i=45 j=60 k=75i=48 j=55 k=73i=48 j=64 k=80i=51 j=68 k=85i=54 j=72 k=90i=57 j=76 k=95i=60 j=63 k=87i=65 j=72 k=97勾股数的常用套路所谓勾股数,一般是指能够构成直角三角形三条边的三个正整数(a,b,c)。
即a^2+b^2=c^2,a,b,c∈N又由于,任何一个勾股数组(a,b,c)内的三个数同时乘以一个整数n得到的新数组(na,nb,nc)仍然是勾股数,所以一般我们想找的是a,b,c互质的勾股数组。
100以内的勾股数

n=9时(a,b,c)=(9,24,25)or (9,12,15)3* (3,4,5)
n=12时(a,b,c)= (12,35,37)or(12,16,20) 4*(3,4,5)
=========ShangJingbo补充=======
i=60 j=63 k=87
i=65 j=72 k=97
勾股数的常用套路
所谓勾股数,一般是指能够构成直角三角形三条边的三个正整数(a,b,c)。即a^2+b^2=c^2,a,b,c∈N2
又由于,任何一个勾股数组(a,b,c)内的三个数同时乘以一个整数n得到的新数组(na,nb,nc)仍然是勾股数,所以一般我们想找的是a,b,c互质的勾股数组。关于这样的数组,比较常用也比较实用的套路有以下 两种:
长度是13,求这个直角三角形的周长是多少?
用特点1解:设这个直角三角形三边分别为13、x、x+1,则有:1
69+x2=(x+1)2,解得x=84,此三角形周长=13+84+85=182。
用特点2解:此直角三角形是以奇数为边构成的直角三角形,因
此周长=169+13=182
常用勾股数口诀记忆
3,4,5:三四五
所以如果你只想得到互质的数组,这条可以改成,对于a=4n (n>=2), b=4*n^2-1, c=4*n^2+1,例如:
n=2时(a,b,c)=(8,15,17)
n=3时(a,b,c)=(12,35,37)
n=4时(a,b,c)=(16,63,65)
========Edward补充========
i=39 j=52 k=65
i=39 j=80 k=89
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
100以内的
勾股数
i=3j=4k=5 i=5j=12k=13
i=6j=8k=10 i=7j=24k=25 i=8j=15k=17 i=9j=12k=15 i=9j=40k=41 i=10j=24k=26 i=11j=60k=61 i=12j=16k=20 i=12j=35k=37 i=13j=84k=85 i=14j=48k=50 i=15j=20k=25 i=15j=36k=39 i=16j=30k=34 i=16j=63k=65
i=18j=24k=30 i=18j=80k=82
i=65j=72k=97勾股数的常用套路 所谓勾股数, 条边的三个正整数
(a,b,c)o 即 a A 2+b A 2=c A 2,a,b,c € N
又由于,任何一个勾股数组(a,b,c)内的三个数同时乘以一个整数 n 得到的新
数组(n a, nb,nc)仍然是勾股数,所以一般我们想找的是a,b,c 互质的勾股数组。
i=20j=21k=29 i=24j=45k=51 i=30j=40k=50 i=35j=84k=91 i=40j=42k=58 i=40j=75k=85 i=42j=56k=70 i=45j=60k=75 i=48j=55k=73 i=48j=64k=80 i=51j=68k=85 i=54j=72k=90 i=57j=76k=95 i=60j=63k=87 i=20j=48k=52 i=24j=70k=74 i=30j=72k=78 i=36j=48k=60 i=21j=28k=35 i=25j=60k=65 i=32j=60k=68 i=36j=77k=85 i=21j=72k=75 i=27j=36k=45 i=33j=44k=55 i=39j=52k=65 i=24j=32k=40 i=28j=45k=53 i=33j=56k=65 i=39j=80k=89
一般是指能够构成直角三角形三
关于这样的数组,比较常用也比较实用的套路有以下两种:
1、当a为大于1的奇数2n+1时,匕=2*门八2+2*皿=2*门八2+2勺+1。
实际上就是把a的平方数拆成两个连续自然数,例如:
n=1 时(a,b,c)=(3,4,5)
n=2 时(a,b,c)=(5,12,13)
n=3 时(a,b,c)=(7,24,25)
这是最经典的一个套路,而且由于两个连续自然数必然互质,所以用这个套路
得到的勾股数组全部都是互质的。
2、当a为大于4的偶数2n时,b=n A2-1,c= n A2+1
也就是把a的一半的平方分别减1和加1,例如:
n=3 时(a,b,c)=(6,8,10)
n=4 时(a,b,c)=(8,15,17)
n=5 时(a,b,c)=(10,24,26)
n=6 时(a,b,c)=(12,35,37)
这是次经典的套路,当n为奇数时由于(a,b,c)是三个偶数,所以该勾股数组必然不是互质的;而n为偶数时由于b、c是两个连续奇数必然互质,所以该勾股数组互质。
所以如果你只想得到互质的数组,这条可以改成,对于
a=4 n(n >=2),b=4* n A2-1 ,c=4* n A2+1,例如:
n=2 时(a,b,c)=(8315,17)
n=3 时(a,b,c)=(12,35,37)
n=4 时(a,b,c)=(16,63,65)
========Edward 补充========
对于N为质因数比较多的和数时还可以参照其质因数进行取相应的勾股数补充,即1个N会有多对的勾股数,例如:
门=9 时(a,b,c) =( 9,24,25)or(9,12,15) .... 3*(3,4,5)
n=12 时(a,b,c) =(12,35,37)or(12,16,20)……4*( 3,4,5)
=========Sha ngJin gb 补充=======
还有诸如此类的勾股数,20、21、29;
119、120、169;
696、697、985;
4059、4060、5741 ;
23660V 23661、33461;
137903137904195025
8037608037611136689
468465946846606625109 常见的几种通式:
(1) (3, 4, 5) , (6, 8, 10)……3n,4n,5n(n是正整数)。
