最新小学奥数圆面积的典型题和解法
小学奥数圆面积的典型题和解法

圆面积的典范题息争法一、半径r 2替代法 题的特色:一般将正方形,三角形和圆放到一路,一般已知前提是正方形或三角形面积,求圆的面积.解法:一般设法求出r,或者求出r 2,★留意:园内直角三角形一般为等腰直角三角形,两腰等长,斜边是斜边上高的2倍.例1:已知下图暗影部分面积为8平方米,解:由已知前提可得r 2=8, 是以,圆的面积为:814.32⨯=r π 例2:ABCD 为正方形,已知AC 长6m,求暗影部分面积:解:△ACD 为等腰直角三角形,则S △ACD=6*3/2=9㎡AD=DC=rAD*DC/2=9是以,r 2 =18, 扇形DAC 的面积为:4/1814.34/2⨯=r π是以,暗影部分面积为:18-4/1814.34/2⨯=r π例3:求圆与圆内最大正方形的面积比值.解:△ABC 为等腰直角三角形,则S △ABC=22/2rr r =⨯正方形的面积是两个三角形面积和,为:22r圆的面积为:2r π,则圆与圆内最大正方形的比为:2/π演习题:1.已知下图暗影部分面积为5平方米,求圆的面积:2:.在右图扇形中,正方形面积为30平方米,求暗影部分面积:3:求正方形与正方形内最大圆的面积比值.二、图像平移弥补法题的特色:一般圆内由多个暗影部分面积组成,暗影由弧线和弧线组成,或者由弧线和直线组成.解法:留意不雅察面积雷同的部分,将雷同的部分移动调换,若碰到轴对称图形可测验测验扭转图形,记住罕有的面积平移图例.,例1:求暗影部分的面积:解:正方形外三角形底为6,和正方形内三角形底雷同,因为顶角雷同,所以两个三角形可以交换.暗影部分面积则为:正方形面积-1/4圆的面积例2:求暗影部分的面积:解:平移得到下图:则暗影部分面积为扇形面积-三角形面积例3:求暗影部分的面积:解:留意不雅察,:暗影部分面积为:1*1-1*1/2=1/2演习题:求暗影部分面积:三、图像联系关系扩大法题的特色:图有好几个部分组合而成,各部分之间消失着必定的关系.解法:留意不雅察图形,将图形离开或者结合起来斟酌问题.可以测验测验弥补图形或者删减图形.例1:甲比乙的面积大6cm2,求暗影部分面积.解:甲和乙单独斟酌难解决问题,将甲.乙和直角梯形放到一路斟酌甲=乙+6,甲+直角梯形面积=乙+直角梯形面积+6.可得,S长方形ABEF=S三角形BDF+6S长方形ABEF=4*6=24 所以S△BDF=18BF*DF/2=18 DF=6BF=DF 所以S△BDF为直角等腰三角形S扇形DFG=3.14*6*6/8暗影部分面积为:S△BDF-S扇形DFG例2:正方形边长为10cm,求暗影部分面积.解:直接难以求解,可测验测验将图形分化开解决问题,如下图:可以看小正方形两块空白区域相等.是以,大正方形外部空白区域和内部空白区域相等空白区域的面积:(10*10-3.14*5*5)*2暗影部分面积:10*10-(10*10-3.14*5*5)*2 例3.求暗影部分面积解:不雅察,暗影部分面积须要用两个小半圆面积-两个空白圆弧面积.两个空白圆弧面积=空白半圆的面积-三角形面积.2/2- 3*4/2暗影部分面积=3.14*22/2+2/2-两个空白圆弧面积演习题:1、△ABC为直角三角形,1比2小28cm2,AB长40cm,BC长若干?的度数.2.扇形ABC的面积是半圆ADB面积的4/3倍,求CAB3.求暗影部分面积:。
奥数专题平面图形之圆的面积

奥数专题平⾯图形之圆的⾯积平⾯图形⾯积————圆的⾯积专题简析:在进⾏组合图形的⾯积计算时,要仔细观察,认真思考,看清组合图形是由⼏个基本单位组成的,还要找出图中的隐蔽条件与已知条件和要求的问题间的关系。
并且同学们应该牢记⼏个常见的圆与正⽅形的关系量:在正⽅形⾥的最⼤圆的⾯积占所在正⽅形的⾯积的3.144,⽽在圆内的最⼤正⽅形占所在圆的⾯积的23.14,这些知识点都应该常记于⼼,并牢牢掌握!例题1。
求图中阴影部分的⾯积(单位:厘⽶)。
【分析】如图所⽰的特点,阴影部分的⾯积可以拼成1/4圆的⾯积。
62×3.14×1/4=28.26(平⽅厘⽶)练习11.求下⾯各个图形中阴影部分的⾯积(单位:厘⽶)。
2.求下⾯各个图形中阴影部分的⾯积(单位:厘⽶)。
答例题2。
求图中阴影部分的⾯积(单位:厘⽶)。
【分析】阴影部分通过翻折移动位置后,构成了⼀个新的图形(如图所⽰)。
从图中可以看出阴影部分的⾯积等于⼤扇形的⾯积减去⼤三⾓形⾯积的⼀半。
3.14×42×1/4-4×4÷2÷2=8.56(平⽅厘⽶)练习21、计算下⾯图形中阴影部分的⾯积(单位:厘⽶,正⽅形边长4)。
答2、计算下⾯图形中阴影部分的⾯积(单位:厘⽶,正⽅形边长4)。
答1 2例题3。
如图19-10所⽰,两圆半径都是1厘⽶,且图中两个阴影部分的⾯积相等。
求长⽅形ABO1O的⾯积。
【分析】因为两圆的半径相等,所以两个扇形中的空⽩部分相等。
⼜因为图中两个阴影部分的⾯积相等,所以扇形的⾯积等于长⽅形⾯积的⼀半(如图19-10右图所⽰)。
所以3.14×12×1/4×2=1.57(平⽅厘⽶)练习31、如图所⽰,圆的周长为12.56厘⽶,AC两点把圆分成相等的两段弧,阴影部分(1)的⾯积与阴影部分(2)的⾯积相等,求平⾏四边形ABCD的⾯积。
答2、如图所⽰,AB=BC=8厘⽶,求阴影部分的⾯积。
六年级奥数专题圆的面积
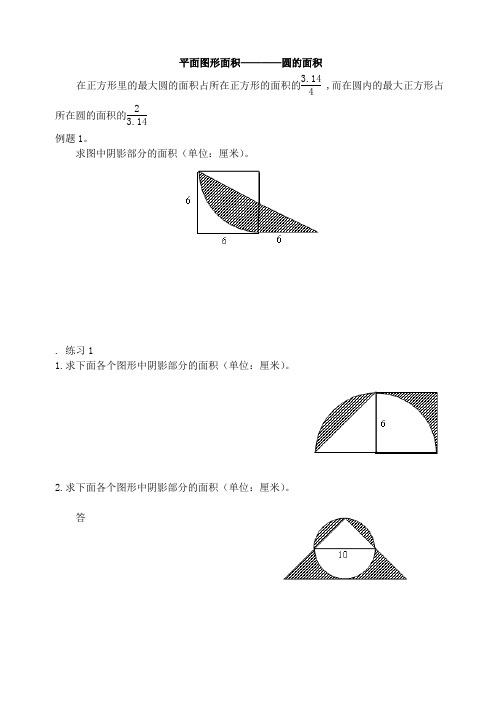
平面图形面积————圆的面积在正方形里的最大圆的面积占所在正方形的面积的3.144 ,而在圆内的最大正方形占所在圆的面积的23.14例题1。
求图中阴影部分的面积(单位:厘米)。
. 练习11.求下面各个图形中阴影部分的面积(单位:厘米)。
2.求下面各个图形中阴影部分的面积(单位:厘米)。
答1、计算下面图形中阴影部分的面积(单位:厘米,正方形边长4)。
答2、计算下面图形中阴影部分的面积(单位:厘米,正方形边长4)。
答1 2. 练习41、如图所示,三角形ABC是直角三角形,AC长4厘米,BC长2厘米。
以AC、BC为直径画半圆,两个半圆的交点在AB边上。
求图中阴影部分的面积。
答例题5。
在图中,正方形的边长是10厘米,求图中阴影部分的面积。
.1、求下面各图形中阴影部分的面积(单位:厘米)。
答2、求右面各图形中阴影部分的面积(单位:厘米)。
答3、求右面各图形中阴影部分的面积(单位:厘米)。
答.例题6。
在图的扇形中,正方形的面积是30平方厘米。
求阴影部分的面积。
练习61、如图所示,平行四边形的面积是100平方厘米,求阴影部分的面积。
答圆的面积与组合圆积专题训练一、填空题1.算出下面圆内正方形的面积为 .2.右下图是一个直角等腰三角形,直角边长2厘米,图中阴影部分面积是平方厘米.3.一个扇形圆心角120,以扇形的半径为边长画一个正方形,这个正方形的面积是120平方厘米.这个扇形面积是 .4.如图所示,以B 、C 为圆心的两个半圆的直径都是2厘米,则阴影部分的周长是 厘米.(保留两位小数)5.左下图三角形ABC 是直角三角形,阴影部分①的面积比阴影部分②的面积小28平方厘米. AB 长40厘米, BC 长 厘米6.如右下图,阴影部分的面积为2平方厘米,7.157平方厘米,这个扇形的圆心角是 .度。
8.图中扇形的半径OA=OB=6厘米.45=∠AOB , AC 垂直OB 于C,那么图中阴影部分的面积是 平方厘米.)14.3(=π9.在右图中(单位:厘米),两个阴影部分面积的和是 平方厘米.10.大圆的半径比小圆的半径长6厘米,且大圆半径是小圆半径的4倍.大圆的面积比小圆的面积大 平方厘米.11.左下图在一个半径是4.5厘米的圆中挖去两个直径都是2厘米的圆.剩下的图形的面积是 平方厘米.(π取3.14,结果精确到1平方厘米)12.右上图中三角形是等腰直角三角形,阴影部分的面积是 (平方厘米).13.如左下图所示,圆的周长是16.4厘米,圆的面积与长方形的面积正好相等.图中阴影部分的周长是 厘米.)14.3(=π14.如右下图,151=∠的圆的周长为62.8厘米,平行四边形的面积为100平方厘米.阴影部分的面积是 .15. 如左下图已知:ABCD 是正方形, ED=DA=AF=2厘米,阴影部分的面积是 .16.右下图中,扇形BAC 的面积是半圆ADB 的面积的311倍,那么,CAB 是 度.。
六年级上册奥数题圆的面积

小学六年级奥数教材课程圆的周长和面积一条线段绕着它固定的一端在平面内旋转一周,它的另一端在平面内画出一条封闭的曲线,这条封闭的曲线就是圆。
画圆时,固定的一点叫做圆心,从圆心到圆上任意一点的线段叫做圆的半径,在同一个圆中,所有的半径都相等。
通过圆心,并且两端在圆上的线段叫做直径。
在同一个圆中,所有的直径都相等,且等于半径的2倍。
圆心决定圆的位置,半径决定圆的大小。
任意一个圆,它的周长除以直径的商总是一个固定的数,这个数叫圆周率。
如果用C 表示圆周的长度,d 表示这个圆的直径,r 表示它的半径,π表示圆周率,就有C dπ=或2C r。
π是一个无限不循环小数,π=3.14159265358979323846…。
圆的周长:C=2πr 或C=πd,圆的面积:S=πr 2。
圆的周长和面积计算的基本方法是仔细观察,发现特点,找出内在的联系,常常通过对图形的割补、旋转、平移、等积变形等方法加以解决。
需要精巧的构思和恰当的设计,把形象思维和抽象思维结合起来。
(本讲π均取 3.14)例1、上海外滩海关大钟钟面的直径是5.8米,钟面的面积是多少平方米?时针长2.7米,时针绕一圈时针尖端走过途径的长度是多少米?(得数保留一位小数)分析与解法:钟面的直径是5.8米这个条件是直接的,时针长指的是半径。
解:钟面的面积是:3.14×(5.8×2)2≈26.4(平方米)。
时针绕一圈时针尖端走过途径的长度是:2×3.14×2.7≈17.0(米)。
例2、如图所示,试比较大圆的面积与阴影部分的面积、大圆的周长与阴影部分的周长。
图图(1)分析与解法:本题有两问,一是比较阴影部分面积与大圆的面积;二是比较阴影部分周长与大圆的周长。
为了考虑问题方便,我们把图经过割补成图(1),在图(1)中更容易看出大圆与小圆阴影部分的关系。
学习目标总结重点AOB解:先比较大圆面积与阴影部分的面积。
设大圆半径为r,则小圆半径为r,大圆面积为S 1=πr 2。
二年级奥数(圆形)-附答案

二年级奥数(圆形)-附答案题目一:计算圆的周长问题:一个圆形的周长是16厘米,求该圆的半径和面积。
答案:根据圆的周长公式可知,周长等于2πr(其中r为圆的半径),所以可以得到以下方程式:16 = 2πr求解上述方程式,解得r = 8/π 厘米。
接着,我们可以使用圆的面积公式计算圆的面积。
根据公式,圆的面积等于πr²,将半径代入计算可得:面积= π * (8/π)² = 64/π 平方厘米。
所以该圆的半径为8/π 厘米,面积为64/π 平方厘米。
题目二:计算扇形的面积问题:一个扇形的半径为10米,弧长为5米,求该扇形的面积。
答案:扇形的面积可以通过使用扇形面积公式来计算。
根据公式,扇形的面积等于弧长除以圆的周长乘以圆的面积。
首先,我们需要计算圆的周长,可以使用圆的周长公式计算:周长= 2πr = 2π * 10 = 20π 米。
然后,我们可以计算扇形的面积,将已知的半径和弧长代入公式:面积= (5 / 20π) * π * 10² = 10 平方米。
所以该扇形的面积为 10 平方米。
题目三:计算圆环的面积问题:一个圆环的外半径为12厘米,内半径为8厘米,求该圆环的面积。
答案:圆环的面积可以通过使用圆环面积公式来计算。
根据公式,圆环的面积等于外圆面积减去内圆面积。
首先,我们可以计算外圆的面积和内圆的面积,使用圆的面积公式:外圆面积= π * (12²) = 144π 平方厘米。
内圆面积= π * (8²) = 64π 平方厘米。
然后,我们可以计算圆环的面积,将已知的外圆面积和内圆面积相减:面积= 144π - 64π = 80π 平方厘米。
所以该圆环的面积为80π 平方厘米。
以上是二年级奥数圆形相关问题的答案。
希望对您有帮助!。
小学圆的面积奥数题100道及答案(完整版)

小学圆的面积奥数题100道及答案(完整版)题目1一个圆的半径是3 厘米,它的面积是多少平方厘米?答案:圆的面积= π×半径×半径,即3.14×3×3 = 28.26(平方厘米)题目2圆的直径是8 分米,求面积。
答案:半径= 8÷2 = 4 分米,面积= 3.14×4×4 = 50.24(平方分米)题目3一个圆的周长是18.84 米,求其面积。
答案:周长= 2×π×半径,所以半径= 18.84÷(2×3.14)= 3 米,面积= 3.14×3×3 = 28.26(平方米)题目4圆的面积是12.56 平方厘米,求半径。
答案:3.14×半径×半径= 12.56,半径×半径= 4,半径= 2 厘米题目5直径为10 厘米的圆,面积比半径为6 厘米的圆的面积小多少?答案:直径10 厘米的圆半径为5 厘米,面积为 3.14×5×5 = 78.5 平方厘米;半径6 厘米的圆面积为3.14×6×6 = 113.04 平方厘米,小113.04 - 78.5 = 34.54 平方厘米题目6一个圆的半径扩大3 倍,面积扩大多少倍?答案:原来面积= π×半径×半径,半径扩大3 倍后,面积= π×(3×半径)×(3×半径)= 9×π×半径×半径,面积扩大9 倍题目7两个圆的半径分别是2 厘米和3 厘米,它们面积的和是多少?答案:面积分别为3.14×2×2 = 12.56 平方厘米,3.14×3×3 = 28.26 平方厘米,和为12.56 + 28.26 = 40.82 平方厘米题目8一个圆的面积是50.24 平方分米,在里面画一个最大的正方形,正方形的面积是多少?答案:圆的半径= √(50.24÷3.14)= 4 分米,正方形的对角线是圆的直径为8 分米,正方形面积= 对角线×对角线÷2 = 8×8÷2 = 32 平方分米题目9圆的半径由4 厘米增加到6 厘米,面积增加了多少平方厘米?答案:原来面积= 3.14×4×4 = 50.24 平方厘米,新面积= 3.14×6×6 = 113.04 平方厘米,增加了113.04 - 50.24 = 62.8 平方厘米题目10在一个边长为8 厘米的正方形中画一个最大的圆,圆的面积是多少?答案:圆的直径= 8 厘米,半径= 4 厘米,面积= 3.14×4×4 = 50.24 平方厘米题目11已知圆的面积是28.26 平方米,求周长。
重点小学奥数圆面积的典型题和解法
精心整理页脚内容 圆面积的典型题和解法一、半径r 2替代法题的特点:一般将正方形,三角形和圆放到一起,一般已知条件是正方形或三角形面积,求圆的面积。
解法:一般设法求出r ,或者求出r 2,★注意:园内直角三角形一般为等腰直角三角形,两腰等长,斜边是斜边上高的2倍。
例1:已知下图阴影部分面积为8平方米,求圆的面积:解:由已知条件可得r 2=8,因此,圆的面积为:814.32⨯=r π例2:ABCD 为正方形,已知AC 长6m ,求阴影部分面积:解:△ACD 为等腰直角三角形,则S △ACD=6*3/2=9㎡AD=DC=rAD*DC/2=9因此,r 2=18,扇形DAC 的面积为:4/1814.34/2⨯=rπ 因此,阴影部分面积为:18-4/1814.34/2⨯=r π例3:求圆与圆内最大正方形的面积比值。
解:△ABC 为等腰直角三角形,则S △ABC=22/2r r r =⨯正方形的面积是两个三角形面积和,为:22r圆的面积为:2r π,则圆与圆内最大正方形的比为:2/π练习题:1、已知下图阴影部分面积为5平方米,求圆的面积:2:、在右图扇形中,正方形面积为30平方米,求阴影部分面积:3:求正方形与正方形内最大圆的面积比值。
二、图像平移填补法题的特点:一般圆内由多个阴影部分面积构成,阴影由弧线和弧线构成,或者由弧线和直线构成。
解法:注意观察面积相同的部分,将相同的部分移动替换,若遇到轴对称图形可尝试旋转图形,记住常见的面积平移图例。
,例1:求阴影部分的面积:解:正方形外三角形底为6,和正方形内三角形底相同,由于顶角相同,所以两个三角形可以互换。
阴影部分面积则为:正方形面积-1/4圆的面积例2:求阴影部分的面积:解:平移得到下图:则阴影部分面积为扇形面积-三角形面积例3:求阴影部分的面积:精心整理页脚内容 解:注意观察,:阴影部分面积为:1*1-1*1/2=1/2练习题:求阴影部分面积:三、图像关联扩张法题的特点:图有好几个部分组合而成,各部分之间存在着一定的关系。
六年级圆的面积题目10题
六年级圆的面积题目10题1. 一个圆的半径是3厘米,求这个圆的面积。
- 解析:根据圆的面积公式S = π r^2(其中S表示圆的面积,r表示圆的半径,π通常取3.14)。
已知半径r = 3厘米,那么这个圆的面积S=3.14×3^2=3.14×9 = 28.26平方厘米。
2. 已知圆的直径为8分米,求圆的面积。
- 解析:首先由直径d = 8分米求出半径r=(d)/(2)=(8)/(2)=4分米。
再根据面积公式S=π r^2,可得S = 3.14×4^2=3.14×16 = 50.24平方分米。
3. 圆的半径是5米,它的面积是多少平方米?(π取3.14)- 解析:根据圆的面积公式S=π r^2,这里r = 5米,π = 3.14,则S=3.14×5^2=3.14×25 = 78.5平方米。
4. 一个圆的周长是18.84厘米,求这个圆的面积。
- 解析:先根据圆的周长公式C = 2π r(C表示周长)求出半径r。
已知C=18.84厘米,18.84 = 2×3.14× r,解得r=(18.84)/(2×3.14)=3厘米。
再根据面积公式S=π r^2,可得S = 3.14×3^2=28.26平方厘米。
5. 有一个圆,半径扩大到原来的2倍,原来圆的半径为4厘米,求扩大后的圆的面积比原来圆的面积多多少平方厘米?- 解析:原来圆的半径r = 4厘米,原来圆的面积S_1=π r^2=3.14×4^2=3.14×16 = 50.24平方厘米。
半径扩大到原来的2倍后,新半径R = 2r=2×4 = 8厘米,新圆的面积S_2=π R^2=3.14×8^2=3.14×64 = 200.96平方厘米。
则面积增加了S_2-S_1=200.96 - 50.24=150.72平方厘米。
小学奥数 圆的周长和面积
第七章圆的周长和面积
一、典型例题
1、一个半径10米的圆形花坛,它的占地面积是多少?在它的一周围一圈篱笆,篱笆长多少米?
思路点拨:圆的面积公式:S=πr2,圆的周长公式:C=2πr,根据公式可以做出来。
解答:
S=π102C=2πr
=3.14×100 =2×3.14×10
=314(平方米) =62.8(米)
答:它的占地面积是314平方米,篱笆长62.8米。
二、知识运用
1、一根长5米的绳子系着一只羊,栓在草地中央的树桩上,羊吃草的面积最多是多少平方米?
2、一种麦田的自动旋转喷灌器的射程是10米,它能喷灌的面积多少平方米?
3、求右图阴影部分面积:(单位:厘米)
4、一元硬币的半径是1.2厘米,求它的周长和面积。
5、用一块边长6分米的正方形纸剪一个最大的圆,圆的面积是多少?
6、用26米长的篱笆围成一个圆形苗圃,篱笆接头处用去0.88米。
苗圃的面积多少?
7、在长6分米,宽4分米的长方形中画一个最大的圆,圆的周长和面积各是多少?
8、求各图的周长和面积:(单位:米)。
奥数训练——圆的周长和面积附答案
奥数训练 圆的周长和面积附答案 A m 阪文 第4题 O A A 第5题 图中阴影部分 的面积等于 平方厘 米 平 16平方厘平方厘米(取 C 第8题 C 点•那么 20厘米为直径画一个半圆,阴影部分①的面积比②的面积小 厘米,其中,圆弧BD 的圆心是 6 .两个半径为2厘米的二圆如右图摆放 第2题 则阴影部分的面积是 其中四边形 OABC 是正方形,图中阴影部分的面积是 如果圆的半径为1厘米,那么,阴影部分的面积是 5 •如图,ABCD 是正方形,边长是 a 厘米 10•如图,以直角三角形的直角边长 米.BC= ___________ . B 点移动到B'点,则阴影 第3题 _____ 平方厘米 3•如图,ABCD 是边长为10厘米的正方形,且AB 是半圆的直径,则阴影部分的面积是 取 3.14 ) 4.如图是半径为6厘米的半圆,让这个半圆绕 A 点按顺时针方向旋转 30°,此时 部分的面积是 _______________________ 平方厘米. 2.如图是 第1题 个边长为 4厘米的正方形 ,吟 n =3). 7.如右图,正方形DEOF 在四分之一圆中 方厘米.(n 取3.14 .) &如图,ABC 是等腰直角三角形,D 是半圆周的中点,BC 是半圆的直径•已知 AB=BC=10厘米,那么阴影部分 的面积是 _______________ 平方厘米.(n 的值取3.14 ) 9.如图,其中AB=10厘米,C 点是半圆的中点.那么,阴影部分的面积是 平方厘米.(n 取3.14 ) 平方厘米.(n 其中 P 点是半圆的中点,点 Q 是正方形一 (取 n =3.14) (共 11小题) 10厘米的正方形和直径是 10厘米的半圆组成如图所示 则阴影部分的面积为 __________________ 平方厘米 一.填空题 1 .边长是 边的中点, A I c 第6题 B E 9 第7题第9题 第10题第11题 11 •如图,阴影部分的面积是 _ _ 平方厘米. 二•解答题(共7小题)12•如图是一个圆心为 0,半径是10厘米的圆•以C 为圆心,CA 为半径画一圆弧,求阴影部分的面积.13•求下列各图中阴影部分的周长.(1) 图1中,两个小半圆的半径均为 3厘米.(2)图2中,四边形为平行四边形圆弧形对的圆心角为 60°,半径为6厘米.(3)图3中,正方形内有一个以正方形的边长为半径的 二圆弧和两个以正方形边长为直径的 二圆弧,已知正 4 215・如图,有一只狗被缚在一建筑物的墙角上,这个建筑物是边长都等于6米的等边三角形,绳长是 8米•求绳被狗拉紧时,狗运动后所围成的总面积. 方形边长为4厘米.(4)图4中,在半径为14•下面是由一个平行四边形和一个半圆形组成的图形,已知半圆的半径是 10厘米,计算图中阴影部分的面16.左图正方形边长为2厘米.以顶点A为圆心边长AB为半径作二圆弧,再分别以ABAC为直径作半圆弧.求阴影部分面积.17•如图三角形ABC是直角三角形,阴影部分①的面积比阴影部分②的面积小14.88平方厘米,直径AB长8厘米,BC长多少厘米?18•如图所示,正方形ABCD等腰三角形ADE及半圆CAE若AB=2厘米,则阴影部分的面积是多少平方厘米?B A10x - 314* 2=16, x=17.3 ;答: 10x -157=16, BC 的长度是17.3厘米.故答案为: 10x=173 17.3厘米. 参考答案与试题解析一•填空题(共11小题)一 2 解:正方形和半圆的面积之和:10X 10+3.14 X ( 10*2) -2, =100+39.25=139.25 (平方厘米),三 角形PAB 的面积是:10X 15*2=75 (平方厘米),三角形PBQ 的面积是5X 5*2=12.5 (平方厘米), 则阴影部分的面积是:139.25 - 75 - 12.5=51.75 (平方厘米);答:阴影部分的面积是51.75平方厘米. 故答案为:51.75 . 此题考查了三角形、正方形和圆的面积公式的综合应用;连接 BP,找出这两个白色三角形的高,求出 空白部分的面积是解决本题的关键. 解:如图,4X 4X 1+3.14 X ( % 2*2=4X 4x2+3.14 X2 2*2=4+6.28=10.28 (平方厘米), 4 図 4 答:阴影部分的面积是 10.28平方厘米;故答案为:10.28 . 2 解:连接BE,如图:半圆面积:3.14 x ( 10*2) *2=39.25 (平方厘米), 2 三角形ABE 面积:10 *2*2=25 (平方厘米),月牙面积:(39.25 - 25)* 2=7.125 (平方厘米), 阴影面积: 25 - 7.125=17.875 (平方厘米).故答案为:17.875 . 解: S 阴影=S 扇形ABB'+S 半圆ADB'- S 半圆ADB',又S 半圆ACB=S^圆ADB', 所以S 阴影=S 扇形ABB'.扇形部分应该半径为 6X 2=12 (厘米),二X 3.14 X22-二x 2X 上x 2, =3.14 - 2=1.14 (平方厘米), 4 2 2 答:阴影部分的面积是 1.14平方厘米.故答案为:1.14 . 解:如图,正方形的面积=对角线x 对角线x 弊1U (平方厘米)四分之一圆的面积 -X 3.14 XI 2=0.785 (平方厘米)阴影部分的面积 =0.785 - -=0.285 (平方厘米)故填 0.285 . 4 2 =25 (平方厘米),SAFDB 梯形ABEF 的面积+半圆BDE 的面积, 梯形ABEF 的面积=(10* 2+10)X ( 10* 2)* 2= (平方厘米),半圆BDE 的面积=扌/哼冗 阴影部分的面积=AFDB 的面积-三角形 AFD 的面积,=(—+二n )- 25, =32.125 (平方厘米). 答:阴影部分的面积是 32.125平方厘米.故答案为:32.125 . 解: : 3.14 X 102 - 10X 」*2,=二X 3.14 X 100- 10X 5*2, =39.25 - 25, =14.25 (平方厘米) 360 2 S 答:阴影部分的面积是 14.25 (平方厘米).故答案为:14.25 . 1 九? 解: BC 的长度为 x 厘米,-X 20X x -3.14 X *2=16 2 1.解答:点评:2.解答:3.解答:4.解答:5.解答:6.解答:7.解答:8.解答:9.解答:10.解答: 即: 解: 360 1 2 5a x 3a 2+a x 卫 360 -2(吩a ) =37.68 (平方厘米).故答案为:37.68 . (平方厘米). 答: 图中阴影部分的面积等于 0.45a 平方厘米.故答案为: 2 0.45a . 解:阴影部分的面积是: 2 Xnr 解:因为 AFD=X 10x ( 10*2) 10x - 3.14 X 100* 2=16, a= 2 2 a =0.45aX 3.14 X2 2 - 2X 2-2, =3.14 - 2 , =1.14 (平方厘米);阴影部分的面积是 1.14平方厘米•故答案为:1.14 . (共 7小题)2 三角形 ABC 的面积为:所以 AC -2=ABK OO2=10X 2X 10*2=100 (平方厘米),2由上面计算可得: AC=100X 2=200,所以阴影部分的面积是:3.14 X 10X 10-2-( -X 3.14 X 200- 100) =157-( 157 - 100),4=157 - 57, =100 (平方厘米),答:阴影部分的面积是 100平方厘米.13. 解答:解:(1)大半圆的圆弧长:2X 3.14 X ( 3+3)* 2=18.84 (厘米);小半圆的圆弧长:2X 3.14 X 3-2=9.42 (厘米);阴影部分周长:18.84+9.42 X 2=37.68 (厘米).(2) 圆弧长:2X 3.14 X 6X 一=6.28 (厘米);平行四边形周长:6X 4=24 (厘米);360 阴影部分周长:6.28+24=30.28 (厘米).(3) 一个以正方形的边长为半径的丄圆弧长:2X 3.14 X 4X 二=6.28 (厘米); 4 4 两个以正方形边长为直径的丄圆弧长:3.14 X 4=12.56 (厘米);阴影部分周长:6.28+12.56=18.84 (厘米).(4) 阴影部分周长:2X 3.14 X 4=25.12 (厘米). 14. 解:如图,解答:把半圆内的阴影部分从左边割下补到左边,阴影部分即成为一个底为半圆半径的2倍,高是半圆半径-X 10X 2X 10=100(平方厘米);答:图中阴影部分的面积是 100平方厘米 215. 解:根据图可知:解答:大扇形的圆心角为:360 - 60=300 (度), 小扇形的圆心角为:180 - 60=120 (度),故总面积为: ^ . (平方米),360 360 答:狗运动后所围成的总面积为 175.84平方米.点评:此题考查如何求扇形的面积,还要注意圆心角度数的求法.11解: •解答: 答: •解答题 12.解答: 解:16. 左图正方形边长为2厘米.以顶点A为圆心边长AB为半径作一圆弧,再分别以AB AC为直径作半圆弧.求考点:组合图形的面积.专题:压轴题;平面图形的认识与计算.分析:如图所示,作出辅助线,则4个小弓形的面积相等,将①、②经过旋转、平移到③、④的位置,贝V阴影部分的面积=以正方形的边长为半径的丄乙的面积-三角形ABC的面积,代入数据即可求解.解答•丹2解答解:3.14 X2 X 2X 2-2,4=3.14 - 2,=1.14 (平方厘米);答:阴影部分的面积是1.14平方厘米.点评:此题主要考查了正方形的性质以及旋转的性质,难度适中,关键是将所求的阴影部分的面积转化为与圆和正方形的面积有关的图形的面积.17•如图三角形ABC是直角三角形,阴影部分①的面积比阴影部分②的面积小14.88平方厘米,直径AB长8厘米,BC长多少厘米?考占: P 八、、•组合图形的面积.专题:平面图形的认识与计算.分析:从图中可以看出阴影部分①加上空白部分的面积是半圆的面积,阴影部分②加上空白部分的面积是三角形ABC的面积.又已知①的面积比②的面积小14.88平方厘米,故半圆面积比三角形ABC的面积小14.88平方厘米•求出半圆面积,再加上14.88即为三角形的面积,再根据三角形的面积公式解答即可.阴影部分面积.解答:2解:半圆面积为3.14 X(8—2)*2=25.12 (平方厘米),三角形ABC的面积为:25.12+14.88=40 (平方厘米).BC的长为:40X 2* 8=10 (厘米).答:BC长10厘米.点评:此题考查了学生三角形以及圆的面积公式及其应用,同时考查了学生观察图形的能力.18. 如图所示,正方形ABCD等腰三角形ADE及半圆CAE若AB=2厘米,贝V阴影部分的面积是多少平方厘米?考占: p 八、、•组合图形的面积.专题:平面图形的认识与计算.分析:把原图ADE以及圆弧AE移补到ADC以及圆弧AC,那么阴影部分的面积就是正方形的面积的一半,然后再进一步解答.解答:解:正方形的面积:2X 2=4 (平方厘米);阴影部分的面积:4-2=2 (平方厘米). 答:阴影部分的面积是2平方厘米.点评:分析图形,根据图形特点进行割补,寻求问题突破点.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
圆面积的典型题和解法
一、半径r 2替代法
题的特点:一般将正方形,三角形和圆放到一起,一般已知条件是正方形或三角形面积,求圆的面积。
解法:一般设法求出r ,或者求出r 2,
★注意:园内直角三角形一般为等腰直角三角形,两腰等长,斜边是斜边上高的2倍。
例1:已知下图阴影部分面积为8平方米,求圆的面积:
解:由已知条件可得r 2 =8,
因此,圆的面积为:814.32⨯=r π
例2:ABCD 为正方形,已知AC 长6m ,求阴影部分面积:
解:△ACD 为等腰直角三角形,则S △ACD=6*3/2=9㎡
AD=DC=r
AD*DC/2=9
因此,r 2 =18, 扇形DAC 的面积为:4/1814.34/2⨯=r π
因此,阴影部分面积为:18-4/1814.34/2⨯=r π
例3:求圆与圆内最大正方形的面积比值。
解:△ABC 为等腰直角三角形,则S △ABC=22/2r r r =⨯
正方形的面积是两个三角形面积和,为:22r
圆的面积为:2r π,则圆与圆内最大正方形的比为:2/π
练习题:
1、已知下图阴影部分面积为5平方米,求圆的面积:
2:、在右图扇形中,正方形面积为30平方米,求阴影部分面积:
3:求正方形与正方形内最大圆的面积比值。
题的特点:一般圆内由多个阴影部分面积构成,阴影由弧线和弧线构成,或者由弧线和直线构成。
解法:注意观察面积相同的部分,将相同的部分移动替换,
若遇到轴对称图形可尝试旋转图形,记住常见的面积平移图例。
,
例1:求阴影部分的面积:
解:正方形外三角形底为6,和正方形内三角形底相同,
由于顶角相同,所以两个三角形可以互换。
阴影部分面积则为:正方形面积-1/4圆的面积
例2:求阴影部分的面积:
解:平移得到下图:
则阴影部分面积为扇形面积-三角形面积
256
2
π
=
-
⨯
4/
4cm
2/2
.8
4
例3:求阴影部分的面积:
解:注意观察,:
阴影部分面积为:1*1-1*1/2=1/2
练习题:求阴影部分面积:
题的特点:图有好几个部分组合而成,各部分之间存在着一定的关系。
解法:注意观察图形,将图形分开或者联合起来考虑问题。
可以尝试补充图形或者删减图形。
例1:甲比乙的面积大6cm2,求阴影部分面积。
解:甲和乙单独考虑难解决问题,将甲、乙和直角梯形放到一起考虑
甲=乙+6,甲+直角梯形面积=乙+直角梯形面积+6。
可得,S长方形ABEF=S三角形BDF+6
S长方形ABEF=4*6=24 所以S△BDF=18
BF*DF/2=18 DF=6
BF=DF 所以S△BDF为直角等腰三角形
S扇形DFG=3.14*6*6/8
阴影部分面积为:S△BDF-S扇形DFG
例2:正方形边长为10cm,求阴影部分面积。
解:直接难以求解,可尝试将图形分解开解决问题,如下图:
可以看小正方形两块空白区域相等。
因此,大正方形外部空白区域和内部空白区域相等
空白区域的面积:(10*10-3.14*5*5)*2
阴影部分面积:10*10-(10*10-3.14*5*5)*2
例3、求阴影部分面积
解:观察,阴影部分面积需要用两个小半圆面积-两个空白圆弧面积。
两个空白圆弧面积=空白半圆的面积-三角形面积。
因此:两个空白圆弧面积=3.14*2.52/2- 3*4/2
阴影部分面积=3.14*22/2+3.14*1.52/2-两个空白圆弧面积
练习题:
1、△ABC为直角三角形,1比2小28cm2,AB长40cm,BC长多少?
的度数。
2、扇形ABC的面积是半圆ADB面积的4/3倍,求CAB
3、求阴影部分面积:
第I卷(共95分)
I.听力测试。
(共30分)
第一节(每小题1.5分,共9分)
听一遍。
根据你所听到的句子,从A、B、C三个选项中选出最恰当的答语,并把答题卡上对应题目的答案标号涂黑。
1、A.Nice to meet you, too. B. Thank you. C. Goodbye.
2、A.Don’t worry! B. Good idea! C.Hurry up!
3、A. You’re welcome. B. It doesn’t matter. C. Take your time.
4、A.That’s right. B.Take it easy. C. With pleasure.
5、A.Sorry, I won’t. B. Well done. C. Here you are.
6、A.Never mind! B. What a pity! C. Have a good time!
第二节(每小题1.5分,共9分)
听一遍。
根据你所听到的对话和问题,从A、B、C三个选项中选出正确答案,并把答题卡上对应题目的答案标号涂黑。
7、A. By bike. B. By bus. C. On foot.
8、A. Grace. B. Alice. C. Paul.
9、A.In the library. B. In the museum. C. In the classroom.
10、A. Math. B. Chinese. C. Science.。
