坡度、坡角
合集下载
沪科九年级数学上册第23章2 第4课时 坡角、坡度问题
2m .
(3)若斜坡AB的坡度 i = 1∶2.5，l = 5 m，则 h =
B
h
C
l
A
知识回顾
利用解直角三角形的知识解决实际问题的一般过程：
(1)将实际问题抽象为数学问题；(画出平面图形，转
化为解直角三角形的问题)
(2)根据条件的特点，适当选用锐角三角函数等去解直
角三角形；
(3)得到数学问题的答案；
k
x2 x1
α
O
x
1.如图，直线y=2x+1向上的方向与x轴的正方向所夹的锐角为α.那么
(1)tan α=
2
；(2) sin α=
2 5
5 ；(3) cos α=
y
α
O
x
5
5
.
2. 在 平 面 直 角 坐 标 系 的 第 一 象 限 中 ， 有 一 点 P(x ， y) ， 记
r=|OP|= ² + ².
要计算斜坡AB的坡角α，其中坡度与坡角之间的关系是tan α=i=1：3；
要计算AD，又有AD=AE+EF+FD，EF=BC=6 m，只要再分别求出AE和FD即可；
还要计算AB，在Rt△ABE中求解即可.
α
β
E F
A
23
6
B C
D
解：分别过点B、C作垂线，交AD于E、F点，垂足分别为E点、F点，则有
D
2.如图，水库大坝的横断面是四边形ABCD，BC∥AD，坝顶宽为6 m，
坝高为23 m，斜坡AB的坡度i=1∶3，斜坡CD的坡度i'=1∶2.5，求：
(1)斜坡AB的坡角α的值(精确到1°)；
(2)坝底宽AD和斜坡AB的值(精确到0.1 m).
(3)若斜坡AB的坡度 i = 1∶2.5，l = 5 m，则 h =
B
h
C
l
A
知识回顾
利用解直角三角形的知识解决实际问题的一般过程：
(1)将实际问题抽象为数学问题；(画出平面图形，转
化为解直角三角形的问题)
(2)根据条件的特点，适当选用锐角三角函数等去解直
角三角形；
(3)得到数学问题的答案；
k
x2 x1
α
O
x
1.如图，直线y=2x+1向上的方向与x轴的正方向所夹的锐角为α.那么
(1)tan α=
2
；(2) sin α=
2 5
5 ；(3) cos α=
y
α
O
x
5
5
.
2. 在 平 面 直 角 坐 标 系 的 第 一 象 限 中 ， 有 一 点 P(x ， y) ， 记
r=|OP|= ² + ².
要计算斜坡AB的坡角α，其中坡度与坡角之间的关系是tan α=i=1：3；
要计算AD，又有AD=AE+EF+FD，EF=BC=6 m，只要再分别求出AE和FD即可；
还要计算AB，在Rt△ABE中求解即可.
α
β
E F
A
23
6
B C
D
解：分别过点B、C作垂线，交AD于E、F点，垂足分别为E点、F点，则有
D
2.如图，水库大坝的横断面是四边形ABCD，BC∥AD，坝顶宽为6 m，
坝高为23 m，斜坡AB的坡度i=1∶3，斜坡CD的坡度i'=1∶2.5，求：
(1)斜坡AB的坡角α的值(精确到1°)；
(2)坝底宽AD和斜坡AB的值(精确到0.1 m).
坡度与坡角解析
第二步：利用正弦，通过坡角、斜边求对边
Pα
M
牛刀小试
1、某水坝的坡度为i = 1∶ 3 ，则坡角为 30°。
2、已知 ABC 中，∠C = 90°, ∠A的坡度i=1∶1, 则
∠A= 45° 。 第一二题：利用正切，通过坡度求坡角
3、如图，高2米的某地下车库的入口处有斜坡AB，其坡度
i=1∶2，则AB的长为 2 5 米。 B 第一步：利用正切，通过坡度
P
lM
查表可求得 ∠α 约为29°3′ ；第一步：利用正切，通过坡度求坡角
在直角三角形PMN中， ∠M=90°∠P= 29°3′ 。 PN=240m.由于NM是∠P的对边，PN是斜边，因此，
sin
α
=
NM PN
=
NM 240
.
即MN=
240·sinα
；可求
N
得 NM 240sin 293 116.5m.. 240米
坡度越大，山坡越陡．
(1)
(2)
自学指导
例６．一山坡的坡度i＝1:1.8，小刚从山坡脚下点P上 坡走了240m到达点N，他上升了多少米（精确到 0.1m）？这座山坡的坡角是多少度（精确到1'）？
分析
N
已知坡度i = 1:1.8，用α 表示坡角的大小，
h
由于 tan α =
1 1.8
0.5556.
。
5、斜坡的坡度是1：3，斜坡长=100米，求斜坡高为
_______米。
如果桃源水库某大坝的横断为等腰梯形，
大坝的顶宽(即等腰梯形的上底长)为11.6m，
巩固练习
大坝的坡度i=1:1.6，等腰梯形的高为12m.你能 求出坝基的底宽AB和坡角α吗？
坡度 坡角分析
B
2.8米
C
A
D
一段河坝的断面为梯形ABCD，BC=4.5米， 。 4米，试根据图中的数据，求出坝底宽 高为 AD。
B i=1：2 A F C
i=1：3
E
D
ቤተ መጻሕፍቲ ባይዱ 、
达标测试
1、斜坡的坡比是1: 3 ， 则坡角α=______度。 2、如图，梯形 ABCD是拦水坝的横断面图（图中的i 1 : 3是指坡面 的铅垂高度DE与水平宽度CE的比），B 60° ， AB 6，AD 4， 求拦水坝的横断面 ABCD 的面积。
解直角三角形（2）
---------坡度 坡角
学习目标：
1、理解坡度（坡比）、坡角的概念。 2、会运用解直角三角形有关知识解决与坡度、 坡角有关的实际问题。
理解概念
坡面的铅垂高度（ h）和水平长度（l ）的比值。 坡度（坡比）：
记作i
h 即i = l
坡角： 坡面与水平面的夹角，记作α ，
h i tan l
α
L
h
1、斜坡的坡比是1:1 ，则坡角α=______度。
2、斜坡的坡角是600 ，则坡比是 _______。 3、传送带和地面所成的斜坡的坡比为1：2，把物体 从地面送到离地面9米高的地方，则物体通过的路 程为 _______米。
一段铁路路基的横断面为等腰梯形ABCD，路基顶宽 BC为2.8米，路基高为1.2米，斜坡AB的坡度i=1：1.6 , 求(1)路基的下底宽 （2）坡角；
A D
i 1: 3
B
C
F E (2题图)
本节课你有什么收获？ 课堂小结：
（1）内容总结：
坡角和坡度的概念: 坡角与坡度之间的关系是：
h i tan l
2.8米
C
A
D
一段河坝的断面为梯形ABCD，BC=4.5米， 。 4米，试根据图中的数据，求出坝底宽 高为 AD。
B i=1：2 A F C
i=1：3
E
D
ቤተ መጻሕፍቲ ባይዱ 、
达标测试
1、斜坡的坡比是1: 3 ， 则坡角α=______度。 2、如图，梯形 ABCD是拦水坝的横断面图（图中的i 1 : 3是指坡面 的铅垂高度DE与水平宽度CE的比），B 60° ， AB 6，AD 4， 求拦水坝的横断面 ABCD 的面积。
解直角三角形（2）
---------坡度 坡角
学习目标：
1、理解坡度（坡比）、坡角的概念。 2、会运用解直角三角形有关知识解决与坡度、 坡角有关的实际问题。
理解概念
坡面的铅垂高度（ h）和水平长度（l ）的比值。 坡度（坡比）：
记作i
h 即i = l
坡角： 坡面与水平面的夹角，记作α ，
h i tan l
α
L
h
1、斜坡的坡比是1:1 ，则坡角α=______度。
2、斜坡的坡角是600 ，则坡比是 _______。 3、传送带和地面所成的斜坡的坡比为1：2，把物体 从地面送到离地面9米高的地方，则物体通过的路 程为 _______米。
一段铁路路基的横断面为等腰梯形ABCD，路基顶宽 BC为2.8米，路基高为1.2米，斜坡AB的坡度i=1：1.6 , 求(1)路基的下底宽 （2）坡角；
A D
i 1: 3
B
C
F E (2题图)
本节课你有什么收获？ 课堂小结：
（1）内容总结：
坡角和坡度的概念: 坡角与坡度之间的关系是：
h i tan l
28.2 应用举例 方位角、坡度、坡角
解:设 BC=x 米,在 Rt△ABC 中,∠CAB=180°-∠EAC=50°,所以 AB= BC ≈ BC = 5 x(米), tan 50 1.20 6
因为在 Rt△EBD 中,i=DB∶EB=1∶1, 所以 BD=EB,所以 CD+BC=AE+AB, 即 2+x=4+ 5 x,解得 x=12,所以 BC=12 米.
上,则船C到海岸线l的距离是
km. 3
4.(2017海南)为做好防汛工作,防汛指挥部决定对某水库的水坝进行加高加固,专家提供 的方案是水坝加高2米(即CD=2米),背水坡DE的坡度i=1∶1(即DB∶EB=1∶1),如图所示,已 知AE=4米,∠EAC=130°,求水坝原来的高度BC.(参考数据:sin 50°≈0.77, cos 50°≈0.64,tan 50°≈1.20)
探究点二:坡度与坡角问题 【例2】 如图,水坝的横断面为梯形ABCD,已知上底长CB=5米,迎水面坡度为1∶ 面坡度为1∶1,坝高为4米,求:坝底AD和迎水面CD的长及坡角α 和β .
,背3 水
【导学探究】 1.作CE⊥AD,BF⊥AD,由坡度可得,CE∶ DE =1∶ 2.由坡度是坡角的 正切 值可得坡角.
第2课时 方位角、坡度、坡角
一、方位角 1.平面测量时,经常以正北、正南方向为基准描述物体运动的方向,这种表示方向的角叫 做方位角. 2.如图,射线OA,OB,OC,OD分别表示北偏东30°,南偏东70°,南偏西50°,北偏西35°.
二、坡度、坡角 1.坡度:坡面的铅直高度(h)与水平宽度(l)的比叫做坡面的坡度(或坡比),记作 i,即 i= h .
在 Rt△BCD 中,∠CBD=30°,tan 30°= CD = 3 ,所以 CD= 3 BD≈115(km),
因为在 Rt△EBD 中,i=DB∶EB=1∶1, 所以 BD=EB,所以 CD+BC=AE+AB, 即 2+x=4+ 5 x,解得 x=12,所以 BC=12 米.
上,则船C到海岸线l的距离是
km. 3
4.(2017海南)为做好防汛工作,防汛指挥部决定对某水库的水坝进行加高加固,专家提供 的方案是水坝加高2米(即CD=2米),背水坡DE的坡度i=1∶1(即DB∶EB=1∶1),如图所示,已 知AE=4米,∠EAC=130°,求水坝原来的高度BC.(参考数据:sin 50°≈0.77, cos 50°≈0.64,tan 50°≈1.20)
探究点二:坡度与坡角问题 【例2】 如图,水坝的横断面为梯形ABCD,已知上底长CB=5米,迎水面坡度为1∶ 面坡度为1∶1,坝高为4米,求:坝底AD和迎水面CD的长及坡角α 和β .
,背3 水
【导学探究】 1.作CE⊥AD,BF⊥AD,由坡度可得,CE∶ DE =1∶ 2.由坡度是坡角的 正切 值可得坡角.
第2课时 方位角、坡度、坡角
一、方位角 1.平面测量时,经常以正北、正南方向为基准描述物体运动的方向,这种表示方向的角叫 做方位角. 2.如图,射线OA,OB,OC,OD分别表示北偏东30°,南偏东70°,南偏西50°,北偏西35°.
二、坡度、坡角 1.坡度:坡面的铅直高度(h)与水平宽度(l)的比叫做坡面的坡度(或坡比),记作 i,即 i= h .
在 Rt△BCD 中,∠CBD=30°,tan 30°= CD = 3 ,所以 CD= 3 BD≈115(km),
坡度和坡角
D
4.2米 A
32 °
12.51米
C
28 ° B
9
D
12.51米
C
4.2米 A
32 ° E
∟
∟
28 °
F
B
解：作DE AB,CF AB,垂足分别为E、F .由题意可知
DE CF 4.（2 米），CD EF 12.5（1 米）.
在Rt△ADE中， i DE 4.2 tan 32 , AE AE
α
A
EF
D
=184′，AD=132.5 m，AB=23 10 m
3
问题探究
4
如图，坡面的铅锤高度（ h）和水平长度（ l） 的比叫做坡面坡度（或坡比）,记作 i ,即 i h .
l 坡度通常写成 1 : m 的形式，如 i 1 : 6
坡面与水平面的夹角叫做坡角，记作 .
i h:l h
l
5
7
④堤坝横断面是等腰梯形，（如图所示）
若AB=10,CD=4,高h=4,则坡度i=__43___,AD=
____5___;
若AB=10，CD=4，i= 1
5
3
,则h=___5___.
D
C
h
i
∟
∟
AE
F
B
8
例1：如图，一段路基的横断面是梯形，高为4.2 米，上底的宽是12.51米，路基的坡面与地面的倾角 分别是32°和28°.求路基下底的宽.（精确到0.1米）
完成该工程需要多少土方？
ED C
α FA
B
11
解：作DG AB于G,作EH AB于H . CD∥AB, EH DG 5米.
ED C
DG 1 , AG 6米. AG 1.2
解直角三角形的应用——坡度、坡角
3.坡度与坡角的关系：
i=h:l=tanα
坡度越大，坡角就越 大 ，坡面 就越陡
自学检测：
知识点一 坡度与坡角
1.以下对坡度的描述正确的是（ B ）
A.坡度是指斜坡与水平线夹角的度数
B.斜坡是指斜坡的铅垂高度与水平宽度的比
C.斜坡式指斜坡的水平宽度与铅垂高度的比
D.坡度是指倾斜角度的度数
2、若斜坡的坡角为 5 6 ∘ 1 9 、，坡度i=3:2，则（ C ）
x- 2
AF =
=
°=
ta n ∠ D A F
ta n 3 0
3 (x - 2 )
AF=BE=BC+CE
即 3 (x - 2） = 2 3 &6.
DE=6米
物体通过的路程为 3 5 .
再试牛刀:
知识点二 坡度、坡角及实际问题
1. 如图，河堤横切面迎水坡AB的坡比是1：
，堤
3
高BC=10m,则坡面AB的长度是（ C ）
A.15m
B. m 2 0 3
C.20m
D. 1 0 3 m
2、如图是拦水坝的横切面，斜坡AB的水平宽度为
12m,斜面坡度为1:2，则斜坡AB的长为（ B ）
拓展提升:
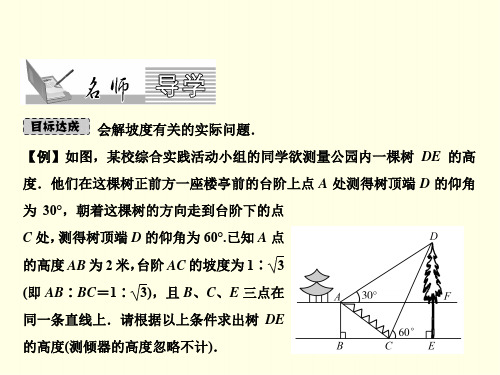
如图，某校综合实践活动小组的同学欲测量公园内 一颗树DE的高度，他们在这棵树正前方一座楼亭前 的台阶上A点处测得树顶端D的仰角为30度，朝着这 棵树的方向走到台阶下的点C处，测得树顶端D的仰 角为60，已知A点的高度AB为2米，台阶AC的坡度为 1: 3 ,且B、C、E三点在同一条直线上，请根据以上 条件求出树DE的高度（测角器的高度忽略不计）
A. 4 3 m
B.6 5 m
C. 1 2 5 m
初三上数学课件(华东师大)-坡度与坡角
h
坡度 (或坡比)，记作 i，即 i＝ l .坡度一般写成 1∶m 的形式．坡面
与水平面的夹角叫做 坡角 ，记作 α，有 i＝hl ＝ tanα α 就 越大 ，坡面就 越陡 ．
.坡度越大，坡角
1．下列对坡度的描述正确的是( B )
A．坡度是指斜坡与水平线夹角的度数
B．坡度是指斜坡的铅垂高度与水平宽度的比
解：(1)∵FD∥CG，∴∠BDF＝∠BAC＝45°，∵斜坡 AB 长 60 2米，D 是 AB 的中点，∴BD＝30 2米，∴DF＝BD·cos∠BDF＝30 2× 22＝30(米)， BF＝DF＝30 米．∵斜坡 BE 的坡比为 3∶1，∴BEFF＝ 13，∴EF＝10 3米， ∴DE＝DF－EF＝(30－10 3)米，∴休闲平台 DE 的长是(30－10 3)米； (2)设 GH＝x 米，则 MH＝GH－GM＝(x－30)米，DM＝AG＋AP＝33＋30 ＝63(米)，在 Rt△DMH 中，tan30°＝MDMH，即x－6330＝ 33，解得 x＝30＋21 3， ∴建筑物 GH 的高为(30＋21 3)米．
11．为邓小平诞辰 110 周年献礼，广安市政府 对城市建设进行了整改．如图，斜坡 AB 长 60 2 米，坡角(即∠BAC)为 45°，BC⊥AC，现计划 在斜坡中点 D 处挖去部分斜坡，修建一个平行 于水平线 CA 的休闲平台 DE 和一条新的斜坡 BE(下面两个小题结果都保留根号)． (1)若修建的斜坡 BE 的坡比为 3∶1，求休闲平台 DE 的长； (2)一座建筑物 GH 距离 A 点 33 米远(即 AG＝33 米)，小亮在 D 点测得建筑 物顶部 H 的仰角(即∠HDM)为 30°.点 B、C、A、G、H 在同一个平面内， 点 C、A、G 在同一条直线上，且 HG⊥CG，问建筑物 GH 高为多少米？
坡度坡角问题
1、斜坡的坡度为1：3 ，则坡角a=_____. 2、斜坡的坡角为60°，则坡比为______.
3、斜坡的坡长为10米，坡高为5米，则坡比为___， 坡角为______. 4、斜坡的坡度为1:3，斜坡长为100米，则斜坡的 高为______米。
【例1】如图所示，一段路基的横断面是梯形，高 为4.2米，上底的宽是12.51米，路基的坡面与地面 的倾角分别是32°、28°，求路基下底的宽.(精确 到0.1米) 参考数据：tan32°≈0.6249， tan28°≈0.5317
D C
A
32 °
28 °
B
【例2】某商场为方便顾客使用购物车，准备将 滚动电梯的坡面坡度由1：1.8改为1：2.4（如图）． 如果改动后电梯的坡面长为13米，求改动后电梯 水平宽度增加部分BC的长．
பைடு நூலகம்
【例3】如图，某防洪指挥部发现长江边一处长 500米，高10米，背水坡的坡角为45°的防洪大堤 （横断面为梯形ABCD）急需加固．经调查论证， 防洪指挥部专家组制定的加固方案是：背水坡面用 土石进行加固，并使上底加宽3米，加固后背水坡 EF的坡比i=1： 3 . （1）求加固后坝底增加的宽度AF； （2）求完成这项工程需要土石多少立方米？ （结果保留根号）
学习目标：
1、理解“坡角、坡比（坡度）”意义,掌握坡角、 坡比（坡度）间的关系 2、能根据直角三角形的知识解决与坡角、坡比 （坡度）有关的实际问题；
3、能够借助辅助线解决实际问题，掌握数形结合、 抽象归纳的思想方法.
坡度、坡角
坡面的铅垂高度h和水平宽度的比叫做坡 度（或叫做坡比），一般用i表示．把坡面与 水平面的夹角α叫做坡角．
【2011•随州】如图，防洪大堤的横断面是梯形， 背水坡AB的坡比i=1： 3 ），且AB=20m．身高为 1.7m的小明站在大堤A点，测得髙压电线杆顶端点 D的仰角为30°．已知地面CB宽30m，求髙压电线杆 CD的髙度（结果保留三个有效数字， 3 ≈1.732）
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
h L α课题： 解直角三角形的应用三
学习目标：
1、 知道坡角、坡比（坡度）的意义.
2、能将有关实际问题转化为解直角三角形的问题
自学自探：
认真看课本第115页到第116页，注意理解坡角、坡度的意义及它们的关系，例题的解题格式。
自学检测：
1、坡面的铅垂高度（h ）与水平宽度（L ）的比叫做 （或 ），记作,i 即L h i =. 坡度通常写成 的形式.
2、坡面与水平面的夹角叫做 ,记作α.
3、坡度与坡角的关系：
根据定义，你能用坡度来刻画斜坡的倾斜、即陡的程度吗？
答：
4、斜坡的坡度是
，则坡角α=______度
5、斜坡的坡角是450 ，则坡度是 _______
6、斜坡长是12米，坡高6米，则坡度是_______
7、某人沿坡度为i=120m ，则该人升高了 8、水库拦水坝的横断面为梯形ABCD ，背水坡CD 的坡比i=1，•已知背水坡的坡长CD=24m ，求背水坡的坡角α及拦水坝的高度．
教师点拨：
理解坡度坡角的概念，在复杂图形中求解时要结合图形，理解题意，运用所学知识通过构造直角三角形求解。
3:1
当堂检测
1、如图，沿倾斜角为30°的山坡植树，•要求相邻两棵树间的水平距离AC为2m，那么
相邻两棵树的斜坡距离AB约为_______m（•≈1.73）2、如图，防洪大堤的横断面是梯形，坝高AC=6米，背水坡AB的坡度i=1：2，则斜坡
AB的长为_______米．
3.如图，某登山运动员从营地A沿坡角为30°的斜坡AB到达山顶B，如果AB=2000米，则他实际上升了米．
4.（2015•四川广安）数学活动课上，老师和学生一起去测量学校升旗台上旗杆AB的高度，如图，老师测得升旗台前斜坡FC的坡比为i FC=1：10（即EF：CE=1：10），学生小明站在离升旗台水平距离为35m（即CE=35m）处的C点，测得旗杆顶端B的仰角为α，已知tanα=，升旗台高AF=1m，小明身高CD=1.6m，请帮小明计算出旗杆AB的高度．。