《电工与电子技术》毕淑娥主编第三章课后参考答案
电工与电子技术基础第3章答案

习题3.1 某三相同步发电机,三相绕组连接成星形时的线电压为10.5kV,若将它连接成三角形,则线电压是多少?若连接成星形时,B 相绕组的首末端接反了,则3 个线电压的有效值UAB、UBC、UCA 各是多少?解:三相绕组连接成星形时U L = 线电压为10.5kV,则每相绕组的电压为6.06kV,3U P ,若连接成三角形U L = U P ,则线电压为6.06kV。
若连接成星形时,B 相绕组的首末端接反了,则 B 相相电压的相位与原来的相差1800,根据相量计算可得UAB=6.06 kV、UBC=6.06 kV、UCA=10.5 kV。
3.2 题3.2 图所示的三相对称电路,线电压UL=380V,每相负载Z= 6+j8Ω,试求相电压、相电流和线电流,并画出电压和电流的相量图。
解:由题意:负载作星接U l = 3U p因U l = 380 V,则Ua = Ub = Uc =设U a = 220 / 0°(V)380 3= 220 (V)因相电流即线电流,其大小为:IA =..220 / 0° = 22/ − 53° (A) 6 + j8I B = 22 / − 173ο (A) I C = 22/ 67° (A)此时的相量图略。
3.3 有一电源和负载都是星形连接的对称三相电路,已知电源相电压为220V,负载每相阻抗Z = 10Ω ,试求负载的相电流和线电流。
解:负载的相电压等于电源的相电压:U p = 220 (V).Il = I p =U P 220 = = 22 (A) 10 Z3.4 有一电源和负载都是三角形连接的对称三相电路,已知电源相电压为220V,负载每相阻抗Z = 10Ω ,试求负载的相电流和线电流。
解:负载的相电压等于电源的相电压:U p = 220 (V)Ip =U P 220 = = 22 (A) Z 10I l = 3I p = 22 3 = 38 (A)第3章三相交流电路习题解答773.5有一电源为三角形连接,而负载为星形连接的对称三相电路,已知电源相电压为220V,每相负载的阻抗为10Ω,求负载的相电流和线电流。
电工电子学第三章习题答案 (2)

第三章交流电路3-1 试写出表示u A =)120314sin(2220,314sin 22200-==t u tV u B A 和V t u C )120314sin(22200+=的,并画出相量图。
解:V U V U V U C B A 0.00120220,120220,0220∠=-∠=∠=•••3-2 如图所示的是时间t=0时电压和电流的相量图,并已知U=220V ,I 1=10A ,I 2=52A ,试分别用三角函数式和复数式表示各正弦量。
3-3已知正弦电流i 1=22sin(100πt+60°)A, i 2=32sin(100πt+30°)A,试用相量法求i=i 1+i 2。
解A tg j j j j I I I 010000210.4284.4)598.3232.3(3914.23232.3598.3)213232(23321230sin 330cos 360sin 260cos 2∠=∠=+=⨯+⨯+⨯+⨯=+++=+=-•••i= 4.842 sin (100πt+42.00) A3-4在图示电路中,已知R=100Ω,L=31.8mH ,C=318uF 。
求电源的频率和电压分别为50Hz 、100V 和1000Hz 、100V 的两种情况下,开关S 合向a 、b 、c 位置时电流表的读数,并计算各元件中的有功功率和 无功功率.解:当F=50HZ 、U=100V 时,S 接到a ,Ia=)(1100100A =;有功功率为:P=UIa=100WS 接到b ,Ib=)(1099.9100108.312501003A LV ==⨯⨯⨯=-πω 无功功率为:Q=UIb=1000Var S 接到c ,)(10100103182506A C V Ic =⨯⨯⨯⨯==-πω。
无功功率为:q=UIc=-1000Var当F=1000HZ 、U=100V 时S 接到a ,Ia=)(1100100A =;有功功率为:P=UIa=100WS 接到b ,Ib=)(5.08.199100108.31210001003A L V ==⨯⨯⨯=-πω 无功功率为:Qb=UIb=50Var S 接到c ,)(8.19910010318210006A C V Ic=⨯⨯⨯⨯==-πω。
电路与电子技术基础第3章习题参考答案
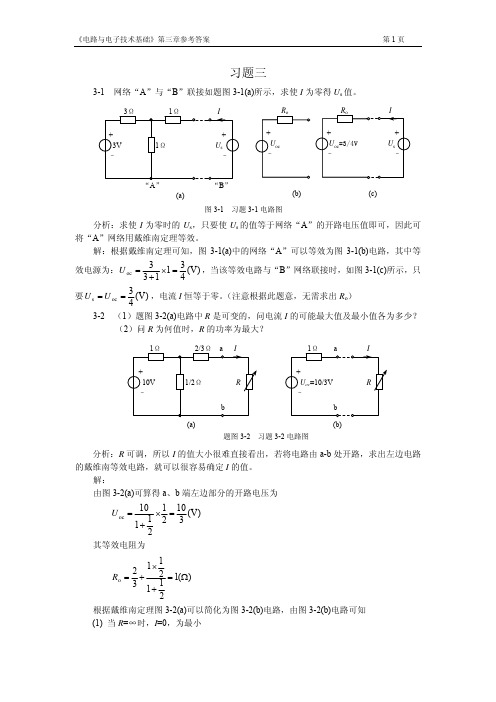
Ro1 = 20 // 30 // 60 = 10(kΩ)
对于右边电路由弥尔曼定理有
U oc2
Ro2 = 60 // 60 // 40 =
120 (kΩ) 7
所以图 3-3(a)可以简化为图 3-3(b)电路,由图 3-3(b)得
240 + 20 380 × 3 U= 7 ×3= ≈ 5.4(V ) 120 211 3 + 10 + 7
3-4 试求题图 3-4(a)所示的桥式电路中,流过 5Ω电阻的电流。 分析:欲求流过 55Ω电阻的电流,如果将该支路断开,电路就变成一个简单电路,很 容易求出开路电压,当然在求等效内阻时,尽管不是简单电路,但可以通过 Y—Δ转换,也 容易求出等效内阻。所以我们采用戴维南定理对此题进行分析。 解:用戴维南定理求解,为此将 5Ω支路断开,则图 3-4(a)可化简为图 3-4(b)电路,由 图 3-4(b),利用弥尔曼定理可计算出
′ + U ab ′′ = sin t + 0.2e −t V U ab = U ab
3-8 如题图 3-8 所示电路图,已知网络 N 为线性网络,当电压源 Us2 不变,电流源 Is 和电 当电 压源 Us1 反向时,电压 Uab 是原来的 0.5 倍; 压源 Us1 不变,电流源 Is 和电压源 Us2 反向时, 电压 Uab 是原来的 0.3 倍。问:当 Us1 和 Us2 均不 变,仅 Is 反向,电压 Uab 为原来的几倍? 分析: 此题是根据已知的 3 个电源变化导致
1Ω 3U 1Ω + 2V – – b (a) 题图 3-5 (b) 习题 3-5 电路图 2Ω 2Ω I a + U 4/15V + –b + U –8/15Ω I a + 2V – 1Ω + 2V – (d) 2Ω –6Uoc + I + 2Ω (c) 2Ω 2Ω Isc Uoc –
电工与电子技术课后习题答案习题

习题3(电工部分)3-1 有日光灯120只,每只功率W 40=NP ,额定电压V 220=NU。
若接在电压为V 220V/380的三相四线制电源上,问日光灯应如何连接?当全部灯都点亮时,其线电流与相电流是多少?解:由于日光灯的额定电压与电源的相电压相同,故应将日光灯平均分成三份,每份接在相线与零线之间以星形形式接在三相电源上当全部灯点亮时,每只灯的电阻为4022022==P U R W=1210每相负载为401210===C B A R R R W=25.30由于负载为星形联结,线电流与相电流相等,故A27.725.30220====A Pp l R U I I 3-2 三相对称负载的额定电压V 380=NU,每相负载的复数阻抗W +=87.26j 87.26Z ,三相四线制电源,其相电压V )30sin(2220°-=t u A w 。
①此三相负载应如何接入三相电源中?②计算负载的相电流和线电流;③画出相量图。
解:①根据负载的额定电压可知,三相负载应以三角形的形式接入三相电源。
如题3-2图所示。
②三相电源的线电压为V38032203=´==P l U U 负载为三角形联结时,其相电压等于电源的线电压,故负载的相电流为40盏40盏40盏AB C N题3-1图2287.2687.26380+==ZUI lP A 10= 线电流为A 32.171033=´==P l I I ③ 电压与电流的相量图如题3-2图(a )3-3 三相交流电路如题3-3图所示。
电源线电压V )30sin(2380°+=t u AB w ,三相负载W =10A Z ,W -=8j 6B Z ,W +=5j 66.8C Z ,计算线电流A I、B I 、C I 、中线电流N I 及三相负载的有功功率,并画出相量图。
解:线电压AB u 的相量为V 30380°Ð=AB U,则相电压A u 的相量为 V 022030303380°Ð=°-°Ð=A U根据对称性可得其它两相电压为V 120220°-Ð=B UV 120220°Ð=C U 则所求的电流为A 022100220°Ð=°Ð==A A A Z U IA UAB I A IAB UBC ICA IB IC I题3-2图(a)AB UBC UCA U ABCZZZ题3-2图B IA IC IAB IBC I CA IA 87.662213.53101202208j 6120220°-Ð=°-а-Ð=-°-Ð==B B BZ U IA902230101202205j 66.8120220°Ð=°Ð°=+°Ð==CC CZ U I°Ð+°-Ð+°Ð=++=902287.6622022C B A N I I I IA 31.369.3077.1j 64.3022j 23.20j 64.822°Ð=+=+-+= C C CB B B A A A I U I U I U P j j j c o s c o s c o s ++=°´´+°-´+°´=30cos 22220)13.53cos(222200cos 22220 KW 94.11=或 66.8226221022222222´+´+´=++=C CB BA AR I R I R I P KW 94.11=3-4 三相交流电路如题3-4图所示,电源线电压V 380=l U 。
电工与电子技术之电工技术第三章课后题解

第3章 正弦交流电路的稳态分析本章的主要任务是学习正弦量、正弦交流电路和相量法的基本概念、正弦交流电路的稳态分析与计算、正弦交流电路功率的概念和计算。
在此基础上理解和掌握功率因数提高的意义,和谐振的概念。
本章基本要求(1) 正确理解正弦量和正弦交流电路概念; (2) 正确理解相量法引入的意义;(3) 正确理解有功功率和功率因数的概念; (4) 掌握相量法;(5) 掌握电路定律的相量形式和元件约束方程的相量形式; (6) 分析计算正弦稳态电路; (7) 了解功率因数提高的意义; (8) 了解谐振的概念。
本章习题解析3-1 已知正弦电压和电流的三角函数式,试用有效值相量表示它们,并画出它们的相量图。
(1))20sin(210 +=t i ωA ,)60sin(2150 +=t u ωV (2))20sin(28 -=t i ωA ,)45sin(2120 -=t u ωV (3))30sin(25 +=t i ωA ,)90sin(2100 +=t u ωV解 (1)︒∠=2010IA ,︒∠=60150U V ,相量图如图3-1(a )所示。
(2))20(10︒-∠=IA ,)45(120︒-∠=U V ,相量图如图3-1(b )所示 (3)︒∠=305IA ,︒∠=90100U V ,相量图如图3-1(c )所示3-2 已知电压、电流的相量表示式,试分别用三角函数式、波形图及相量1+j (a )1+(b )1+j(c )图3-1图表示它们。
(1)4030j U+= V ,43j I += A (2)100=UV ,43j I -= A (3)V 10045 j e U=,A 44j I +=解 (1))13.53(504030︒∠=+=j U=︒+︒13.53sin 5013.53cos 50j ,V )13.53(543︒∠=+=j I=︒+︒13.53sin 513.53cos 5j ,A 波形图相量图如图3-2(a )所示。
电工与电子技术(课后答案)

电工与电子技术(课后答案) 习题 1—5 习题 1…………………………….P 2/55 习题 2…………………………….P 18/55 习题 3…………………………….P 34/55 习题 4…………………………….P 41/55 习题 5…………………………….P 52/55
E1 4V
R2
5
取顺 定律可列方程
5
题1-4图(a)
时针为循行方向, 则由基尔霍夫电压
I ( R1 R2 ) U1 E1
代入数值可得
I
U 1 E1 10 4 1A R1 R2 24
对于右边的开口电路,由于 I 0 ,故 R3 上的压降为零,则还是取顺时针为循行方向,由基尔霍夫电压定律
故 2A 电流源两端的电压为
故是发出功率,是电源元件。
E=10V I=-2A (a) U=10V I=-2A (b) 题1-2 图
I=-1A 元件 U=-1V (c)
I=-1A 元件 U=1V (d)
;②计算图 b 中 I 、 US 、 1-3 题 1-3 为某些电路的一部分,①计算图 a 中的 I x 、 I x 、 I x 及R 。
I1 I 3 I 5 I I I 2 5 4 I1R1 I 3 R3 E1 I R I R I R 0 4 4 5 5 3 3 I 2 R2 I 4 R4 E2
代入数值:
I 1 I 3 I 5 I I I 2 5 4 5 I1 20 I 3 45 20 I 42 I 2 I 0 3 4 5 3I 2 42 I 4 48
/fuyi_fly
4 / 55
/fuyi_fly
《电工与电子技术》习题册习题解答
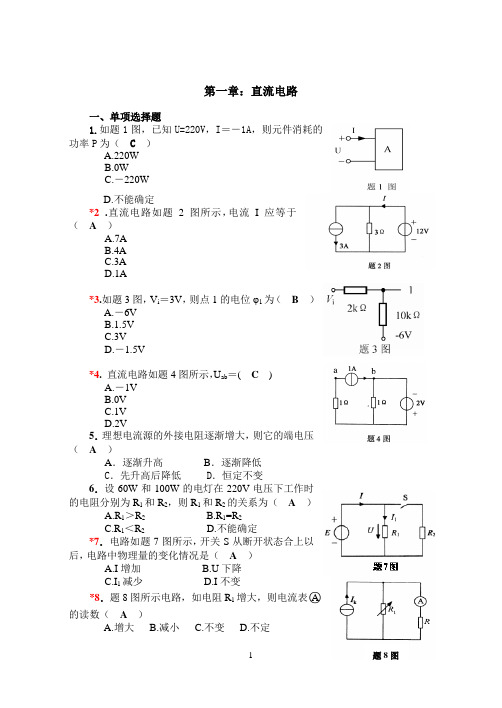
第一章:直流电路一、单项选择题1.如题1图,已知U=220V,I=-1A,则元件消耗的功率P为(C)A.220WB.0WC.-220WD.不能确定*2.直流电路如题2图所示,电流I应等于(A)A.7AB.4AC.3AD.1A*3.如题3图,V i=3V,则点1的电位φ1为(B)A.-6VB.1.5VC.3VD.-1.5V*4. 直流电路如题4图所示,U ab=( C)A.-1VB.0VC.1VD.2V5.理想电流源的外接电阻逐渐增大,则它的端电压(A)A.逐渐升高B.逐渐降低C.先升高后降低D.恒定不变6.设60W和100W的电灯在220V电压下工作时的电阻分别为R1和R2,则R1和R2的关系为(A)A.R1>R2B.R1=R2C.R1<R2D.不能确定*7.电路如题7图所示,开关S从断开状态合上以后,电路中物理量的变化情况是(A)A.I增加B.U下降C.I1减少D.I不变*8.题8图所示电路,如电阻R1增大,则电流表○A 的读数(A)A.增大B.减小C.不变D.不定*9.一个由线性电阻构成的电器,从220V 的电源吸取1000W 的功率,若将此电器接到110V 的电源上,则吸取的功率为( A )A.250WB.500WC.1000WD.2000W10.题10图示电路中,A 、B 端电压 U =( A )A.-2VB.-1VC.2VD.3V11.题11图中电流I 为 ( C )A.1AB.2AC.-1AD.-2A*12.直流电路如题12图所示,U ab 等于( C )A .-2VB .-1VC .1VD .2V13.把题13图1所示的电路用题13图2所示的等效电压源代替,该等效电压源的参数为( B )。
A.E 0=1V, R 0=2ΩB.E 0=2V, R 0=1ΩC.E 0=2V, R 0=0.5ΩD.E 0=1V, R 0=1Ω14.将题14图电路化简为一个电压源U S和电阻R S 串联的最简等效电路,其中U S 和R S 分别为 ( D )A.U S =2V ,R S =1ΩB.U S =1V ,R S =2ΩC.U S =2V ,R S =0.5ΩD.U S =1V ,R S =0.5Ω15.在题15图示电路中,已知:E=9V ,I k =6mA ,当电压源E 单独作用时,题10图 题11图题15图题13图通过R L 的电流是1mA ,那么当电压源E 和电流源I k 共同作用时,通过电阻R L 的电流I L 是( A )。
电子技术第三章课后习题答案
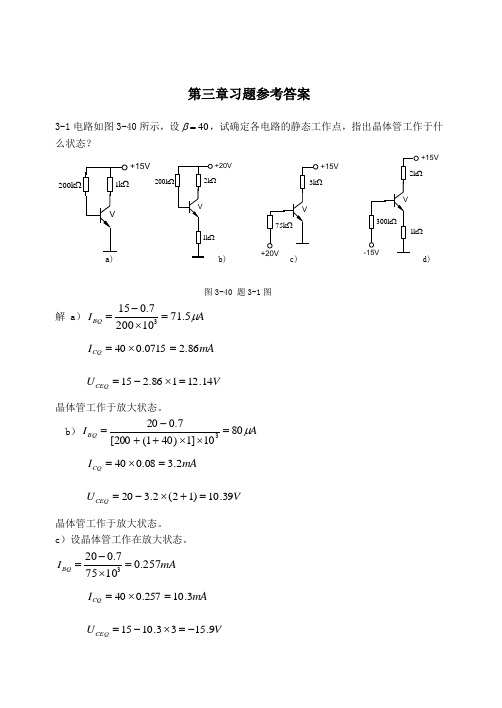
第三章习题参考答案3-1 电路如图3-40所示,设40=β,试确定各电路的静态工作点,指出晶体管工作于什么状态?b) d)图3-40 题3-1图解 a)AIBQμ5.71102007.0153=⨯-=mAICQ86.20715.040=⨯=VUCEQ14.12186.215=⨯-=晶体管工作于放大状态。
b)AIBQμ8010]1)401(200[7.0203=⨯⨯++-=mAICQ2.308.040=⨯=VUCEQ39.10)12(2.320=+⨯-=晶体管工作于放大状态。
c)设晶体管工作在放大状态。
mAIBQ257.010757.0203=⨯-=mAICQ3.10257.040=⨯=VUCEQ9.1533.1015-=⨯-=+15Vk200+15V+15V+20Vk200说明晶体管已经深度饱和。
d) 由于发射结反偏,晶体管工作于截止状态。
3-2 试判断图3-41中各电路能否放大交流信号,为什么?a ) b) c)d) e) f) 图3-41 题3-2图解 a) 晶体管的发射结正偏,集电结反偏,故可以放大交流信号。
b) 缺少直流负载电阻C R ,故不能放大交流信号。
c) 晶体管为PNP 型,偏置电压极性应为负,故不能放大交流信号。
d) 电容C1、C2的极性接反,故不能放大交流信号。
e) 缺少基极偏置电阻B R ,故不能放大交流信号。
f) 缺少直流电源CC V ,故不能放大交流信号。
3-3 在图3-42中晶体管是PNP 锗管,(1)在图上标出CC V 和21,C C 的极性;(2)设V 12-=CC V ,k Ω3=C R ,75=β,如果静态值mA 5.1=C I ,B R 应调到多大?(3)在图3-42 题3-3图调整静态工作点时,如果不慎将B R 调到零,对晶体管有无影响?为什么?通常采取何种措施来防止这种情况发生?(4)如果静态工作点调整合适后,保持B R 固定不变, 当温度变化时,静态工作点将如何变化?这种电路能否稳定静态工作点? 解 1)CC V 和21,C C 的极性如题3-3解图所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习题33-1 已知某正弦电流的瞬时值表达式为A t siin i )306280(10+=。
(1)画出i 的波形图;(2)试求i 的有效值、角频率、频率及初相位;(3)试求s t 05.0=时的i 。
解:(2)有效值:A I 25210==角频率:s rad /6280=ω 频率:Hz f 100= 初相位:30=ψ(3)s t 05.0=时,A siin i 5)3005.06280(10=+⨯=3-2 已知,)120314sin(22201V t u -=,)30314sin(22202V t u +=试求(2)他们的有效值、频率和周期。
(3)写出他们的相量式,画出相量图,计算相位差。
解:(2)V U 2201=,V U 2202=,Hz f 501=,Hz f 502=,s T T 02.021==(3)V U o1202201-∠=∙,V U o302202∠=∙,o 15021-=-=ψψϕ3-3 将虾类相量式化成指数形式或极坐标形式或代数形式。
(1)V eV V j U oj o3715375)34(-∙=-∠=-=(2)A e A A j I oj o1351210135210)1010(-∙=-∠=--=(3)V j V V e U o j o)535(301010302+=∠==∙(4)A j A A eI o j o)2424(135881352+-=-∠==-∙(5)V j V e V U oj o)86(105310533-==-∠=-∙(6)A j A eA I oj o)1216(203720373+==∠=∙3-4 用相量法求题图3-4所示电路中的各未知电表的度数。
L5A(a) (b)解:对a 图,设电流为参考相量,电感和电容上的电压大小相等,相位相反。
所以V 表的示数即为电阻上的电压10V对b 图。
设电压为参考相量,电感和电容上的电流大小相等,相位相反。
所以A 表的示数为0.U L U CII3-5在RL 串联电路中,已知,314sin 2220tV u =Ω=30R ,mH L 191=。
试求:(1)电感的感抗。
(2)电路的总电流∙I ;(3)用相量法求∙R U 和∙L U . 解:(1)电感的感抗:Ω=Ω⨯⨯==-60101913143L X L ω(2)电路总电压:V U o0220∠=∙电路的总阻抗:Ω∠=Ω+=+=o L j jX R Z 4.6308.67)6030(电路的总电流:A Z U I o 4.6327.34.6308.670220-∠=∠∠==∙∙(3)V R I U oR 4.631.98304.6327.3-∠=⨯-∠==∙∙V j jX I U o L L 6.262.196604.6327.3)(∠=∠⨯-∠==∙∙3-6 电路的相量模型如图3-6所示,已知V U 1001=∙,A I 102=∙。
试求∙U 和∙I 。
CjX -2∙I题图3-6解:设V U o01001∠=∙,则A I o90102∠=∙A j U I ooo 45210452501005511-∠=∠∠=+=∙∙A I I I 1090104521021=∠+-∠=+=∙∙∙V j U j I U 4521000100901000100)10(10)10(1-∠=∠+-∠=∠+-⨯=+-=∙∙∙3-7 在题图3-7所示电路中,已知Ω====5,200,210,10132R V U A I A I ,L R ω=2.试求1I 、C X 、L X 和2R 。
+-∙∙jX -题图3-7解:设V U U o022∠=∙,则A I90102∠=∙,A I452103-∠=∙,A I I I 010901045210321∠=∠+-∠=+=∙∙∙所以22021=+U R I ,所以V U 1502=Ω===151015022I U X C 21015022232=+=R X I U L 所以Ω==5.72L X R 3-83-9 在题图3-9中,已知1210I I A ==。
试求I ∙和S U ∙。
U ∙∙题图3-9解:设A I o0101∠=∙,则A I o90102∠=∙,A I I I4521021∠=+=∙∙∙V j I j I U S 10090104521010010)10(1=∠⨯∠+=⨯+=∙∙∙3-10 在题图3-10中,已知1(34)Z j =-Ω,2(43)Z j =+Ω,电压表的读数为U=100V 。
试求电流表的读数。
∙题图3-10解:A j I o o1.53201.53501004301001∠=-∠∠=-∠=∙A j I oo9.36209.36501003401002-∠=∠∠=+∠=∙A I I I 1.822021∠=+=∙∙∙所以,A1的示数为20A 。
A2的示数为20A 。
A 的示数为28.28A 。
3-11 在题图3-11所示电路中,已知220U V =,22R =Ω,22L X =Ω,11C X =Ω。
试求R I 、L I 、C I 及I 。
∙题图3-11解:设V U o0220∠=∙则:A R U I oR 010220220∠=∠==∙∙A jX U I o L L901090220220-∠=∠∠==∙∙A jX U I oC C902090110220∠=-∠∠=-=∙∙A I I I I C L R 4521090209010010∠=∠+-∠+∠=++=∙∙∙∙3-14有一感性负载的功率P=10KW ,功率因数cos 0.6ϕ=,电压为220V ,频率为50Hz 。
若要将电路的功率因数提高到0.9.,需要并联多大的补偿电容。
并联电容前后电路的总电流为多少?解:F U P C μϕϕω559)48.033.1(2203141010))9.0tan(arccos )6.0s (tan(arcco 2203141010)tan (tan 232312=-⨯⨯=-⨯⨯=-= 并联电容前电路总电流A U P I 76.756.02201010cos 311=⨯⨯==φ并联电容后电路总电流A U P I 5.509.02201010cos 3=⨯⨯==φ3-15 电路如图3-15所示,已知交流电源电压,314sin 2220tV u =白炽灯的功率为60W ,日光灯的功率为40W ,功率因数cos L φ=0.5。
试求:(1)等效负载的功率因数'cos L φ;(2)若将电路的功率因数提高到0.92,需并联多大的电容?C题图3-15解:(1)V P Q 3.69340)5.0(arccos 40tan ==⨯==ϕ 等效负载的功率因数:82.03.691006040cos 2222'=++=++=QP P P L 白日ϕ(2)需要并联电容值:F U P C μϕϕω79.1)264.0698.0(220314010))29.0tan(arccos )82.0s (tan(arcco 2203141010)tan (tan 22312=-⨯=-⨯⨯=-=3-16 电路如图3-16所示,已知10U V =,50f Hz =,1210R R R ===Ω,31.8L mH =,318C F μ=试计算:(1)电路中并联部分的电压ab U ;(2)电路的功率因数cos ϕ;(3)电路的P 、Q 、S 。
C题图3-16解:(1)Ω=Ω⨯⨯==-01108.313143L X L ωΩ=⨯⨯==-0110318314116C X C ω Ω=+++=10jX )jX )(jX (L1C 2L 1ab R R R Z设V U010∠=∙A Z R U I oab 5.01010010=+∠=+=∙∙V IZ U ab ab 5105.0=⨯==∙∙(2)U 与I 同相,10cos cos ==oϕ (3)A X R U I Lab 4221052211==+=2I A == W R I R I R I P P P P R R R 5222212121=++=++= 02221=-=-=C L C L X I X I Q Q QVA Q P S 522=+=3-18 在题图3-18所示电路中,u tV =,0.159L H =,500R =Ω,0.318C F μ=。
试求电路的有功功率,无功功率,视在功率和功率因数。
C题图3-18解:31400.159500L X L ω==⨯Ω=Ω611100031400.31810C X C ω-===Ω⨯⨯L I A = 1001100010ab C C U I A X === 1221150010RP P I R W ===⨯= 220L C L L C C Q Q Q I X I X =-=-=10S VA =。
