必修二平面解析几何初步知识点及练习带答案
高中数学 第二章 解析几何初步 1.2.2 直线方程的两点式和一般式练习(含解析)北师大版必修2-北
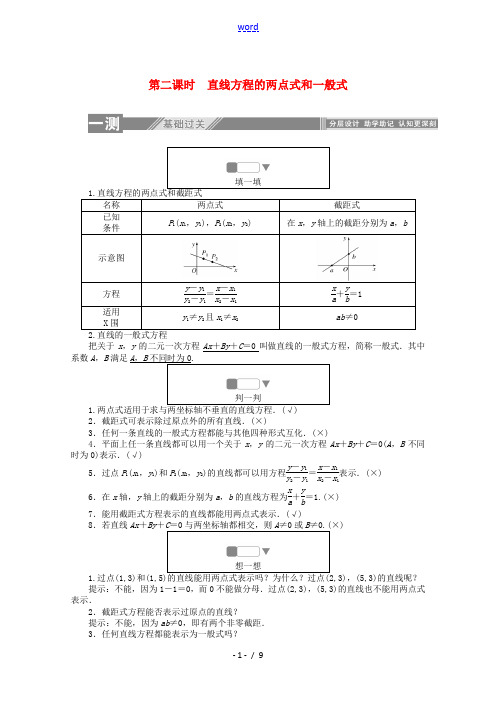
第二课时 直线方程的两点式和一般式填一填1.直线方程的两点式和截距式名称 两点式 截距式已知条件 P 1(x 1,y 1),P 2(x 2,y 2)在x ,y 轴上的截距分别为a ,b示意图方程y -y 1y 2-y 1=x -x 1x 2-x 1 x a +y b=1 适用X 围y 1≠y 2且x 1≠x 2 ab ≠02.直线的一般式方程把关于x ,y 的二元一次方程Ax +By +C =0叫做直线的一般式方程,简称一般式.其中系数A ,B 满足A ,B 不同时为0.判一判1.两点式适用于求与两坐标轴不垂直的直线方程.(√) 2.截距式可表示除过原点外的所有直线.(×)3.任何一条直线的一般式方程都能与其他四种形式互化.(×)4.平面上任一条直线都可以用一个关于x ,y 的二元一次方程Ax +By +C =0(A ,B 不同时为0)表示.(√)5.过点P 1(x 1,y 1)和P 2(x 2,y 2)的直线都可以用方程y -y 1y 2-y 1=x -x 1x 2-x 1表示.(×)6.在x 轴,y 轴上的截距分别为a ,b 的直线方程为x a +y b=1.(×) 7.能用截距式方程表示的直线都能用两点式表示.(√)8.若直线Ax +By +想一想1.过点(1,3)和,(5,3)的直线呢? 提示:不能,因为1-1=0,而0不能做分母.过点(2,3),(5,3)的直线也不能用两点式表示.2.截距式方程能否表示过原点的直线?提示:不能,因为ab ≠0,即有两个非零截距. 3.任何直线方程都能表示为一般式吗?提示:能.因为平面上任意一条直线都可以用一个关于x ,y 的二元一次方程表示. 4.当A ,B 同时为零时,方程Ax +By +C =0表示什么?提示:当C =0时,方程对任意的x ,y 都成立,故方程表示整个坐标平面; 当C ≠0时,方程无解,方程不表示任何图像.故方程Ax +By +C =0,不一定代表直线,只有当A ,B 不同时为零时,即A 2+B 2≠0时才代表直线.思考感悟:练一练1.直线x a +y b=1(ab <0)的图像可能是( )答案:C2.过两点(2018,2019),(2018,2020)的直线方程是( ) A .x =2018 B .x =2019 C .y =2018 D .x +y =2020 答案:A3.直线x -y +5=0的倾斜角为( ) A .45° B.60° C .120° D.135° 答案:A4.在x 轴、y 轴上的截距分别是5,-3的直线的截距式方程为( ) A.x 5+y 3=1 B.x 5-y 3=1 C.y 3-x5=1 D.x 5+y3=0 答案:B5.直线2x +3y -6=0与坐标轴围成的三角形面积为________. 答案:3知识点一 直线的两点式方程1.已知直线l 经过点A (1,-2),B (-3,2),则直线l 的方程为( ) A .x +y +1=0 B .x -y +1=0 C .x +2y +1=0 D .x +2y -1=0解析:由两点式得直线l 的方程为y +22--2=x -1-3-1,即y +2=-(x -1).故选A.答案:A2.过两点(-1,1)和(3,9)的直线在x 轴上的截距为( )A .-32B .-23C.25D .2 解析:由直线的两点式方程可得直线方程为y -19-1=x +13+1,即2x -y +3=0,令y =0得x=-32.故选A.答案:A知识点二 直线的截距式方程3.过点A (4,1)且在两坐标轴上截距相等的直线方程为( ) A .x +y =5 B .x -y =5C .x +y =5或x -4y =0D .x -y =5或x -4y =0解析:当直线过点(0,0)时,直线方程为y =14x ,即x -4y =0;当直线不过点(0,0)时,可设直线方程为x a +y a=1(a ≠0),把(4,1)代入,解得a =5,∴直线方程为x +y =5.综上可知,直线方程为x +y =5或x -4y =0.选C. 答案:C4.两条直线l 1:x a -y b =1和l 2:x b -y a=1在同一平面直角坐标系中的图像可以是( )解析:将两直线方程化成截距式为l 1:x a +y -b =1,l 2:x b +y-a=1,则l 1与x 轴交于(a,0),与y 轴交于(0,-b ),l 2与x 轴交于(b,0),与y 轴交于(0,-a ).结合各选项,先假定l 1的位置,判断出a ,b 的正负,然后确定l 2的位置,知A 项符合.选A.答案:A知识点三直线的一般式方程5.已知直线l 的方程为x -3y +2=0,则直线l 的倾斜角为( ) A .30° B.45° C .60° D .150°解析:设直线l 的倾斜角为θ,则tan θ=13,则θ=30°.答案:A6.设直线l 的方程为(a +1)x +y +2-a =0(a ∈R ),若l 不经过第二象限,则实数a 的取值X 围是________.解析:将直线l 的方程化为y =-(a +1)x +a -2. 则⎩⎪⎨⎪⎧ -a +1>0,a -2≤0或⎩⎪⎨⎪⎧-a +1=0,a -2≤0,∴a ≤-1. 答案:(知识点四 直线方程的应用7.(1)求证:不论a 为何值,直线l 总经过第一象限; (2)为使直线不经过第二象限,求a 的取值X 围.解析:(1)证明:方法一 将直线l 的方程整理为 y -35=a ⎝ ⎛⎭⎪⎫x -15, ∴l 的斜率为a ,且过定点A ⎝ ⎛⎭⎪⎫15,35,而点A ⎝ ⎛⎭⎪⎫15,35在第一象限,故不论a 为何值,l 恒过第一象限.方法二 直线l 的方程可化为(5x -1)a +(3-5y )=0. 当定点为(x ,y )时,上式对任意的a 总成立,必有⎩⎪⎨⎪⎧5x -1=0,3-5y =0,即⎩⎪⎨⎪⎧x =15,y =35,即l 过定点A ⎝ ⎛⎭⎪⎫15,35.以下同方法一.(2)如图,直线OA 的斜率为 k =35-015-0=3. 要使l 不经过第二象限,需它在y 轴上的截距不大于零,即令x =0时,y =-a -35≤0,∴a ≥3.8.已知直线l :y =kx +2k +1.(1)求证:对于任意的实数k ,直线l 恒过一个定点;(2)当-3<x <3时,直线l 上的点都在x 轴的上方,某某数k 的取值X 围. 解析:(1)由y =kx +2k +1, 得y -1=k (x +2).由直线的点斜式方程,可知直线l 恒过定点(-2,1). (2)设函数f (x )=kx +2k +1.若-3<x <3时,直线l 上的点都在x 轴的上方,则⎩⎪⎨⎪⎧f -3≥0,f 3≥0,即⎩⎪⎨⎪⎧-3k +2k +1≥0,3k +2k +1≥0,解得-15≤k ≤1.所以实数k 的取值X 围是⎣⎢⎡⎦⎥⎤-1,1. 综合知识 直线的方程9.(1)经过点(-1,3),且斜率为-3; (2)经过两点A (0,4)和B (4,0);(3)经过点(2,-4)且与直线3x -4y +5=0平行; (4)经过点(3,2),且垂直于直线6x -8y +3=0.解析:(1)根据条件,写出该直线的点斜式方程为 y -3=-3(x +1),即y -3=-3x -3, 整理得其一般式为3x +y =0.(2)根据条件,写出该直线的截距式为x 4+y4=1,整理得其一般式为x +y -4=0.(3)设与直线3x -4y +5=0平行的直线为3x -4y +c =0,将点 (2,-4)代入得6+16+c =0,所以c =-22.故所求直线的一般式为3x -4y -22=0.(4)设与直线6x -8y +3=0垂直的直线为8x +6y +c =0,代入点(3,2)得24+12+c =0,c =-36.从而得8x +6y -36=0,即所求直线的一般式为4x +3y -18=0.10.已知△ABC 的三个顶点为A (0,3),B (1,5),C (3,-5). (1)求边AB 所在的直线方程; (2)求中线AD 所在直线的方程.解析:(1)设边AB 所在的直线的斜率为k ,则k =5-31-0=2.它在y 轴上的截距为3.所以,由斜截式得边AB 所在的直线的方程为y =2x +3.(2)B (1,5)、C (3,-5),1+32=2,5+-52=0,所以BC 的中点D (2,0).由截距式得中线AD 所在的直线的方程为x 2+y3=1.基础达标一、选择题1.下列四个命题中的真命题是( )A .经过定点P 0(x 0,y 0)的直线都可以用方程y -y 0=k (x -x 0)表示B .经过任意两个不同点P 1(x 1,y 1)、P 2(x 2,y 2)的直线都可以用方程(y -y 1)(x 2-x 1)=(x -x 1)(y 2-y 1)表示C .不经过原点的直线都可以用方程x a +yb=1表示D .经过定点A (0,b )的直线都可以用方程y =kx +b 表示解析:当直线与y 轴平行或重合时,斜率不存在,直线方程不能用点斜式、斜截式,选项A 、D 不正确;当直线垂直于x 轴或y 轴时,直线方程不能用截距式表示,选项C 不正确;选项B 正确.故选B.答案:B2.已知直线l :ax +y -2-a =0在x 轴和y 轴上的截距相等,则a 的值是( ) A .1 B .-1 C .-2或-1 D .-2或1解析:①当a =0时,y =2不合题意.②当a ≠0时,令x =0,得y =2+a ,令y =0,得x =a +2a ,则a +2a=a +2,得a =1或a =-2.故选D.答案:D3.直线l 过点P (1,3),且与x ,y 轴正半轴围成的三角形的面积等于6的直线方程是( ) A .3x +y -6=0 B .x +3y -10=0 C .3x -y =0 D .x -3y +8=0 解析:设所求的直线方程为x a +yb=1. 所以⎩⎪⎨⎪⎧1a +3b =1,12|ab |=6,解得a =2,b =6.故所求的直线方程为3x +y -6=0.故选A.答案:A4.如果AB <0,且BC <0,那么直线Ax +By +C =0不通过( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限解析:因为直线Ax +By +C =0可化为y =-A B x -C B ,又AB <0,BC <0,所以-A B >0,-C B>0,所以直线过第一、二、三象限,不过第四象限.故选D. 答案:D5.已知m ≠0,则过点(1,-1)的直线ax +3my +2a =0的斜率为( ) A .3 B .-3 C.13 D .-13解析:由题意,得a -3m +2a =0,所以a =m ,又因为m ≠0,所以直线ax +3my +2a =0的斜率k =-a 3m =-13.故选D.答案:D6.已知两条直线的方程分别为l 1:x +ay +b =0,l 2:x +cy +d =0,它们在坐标系中的位置如图所示,则( )A .b >0,d <0,a <cB .b >0,d <0,a >cC .b <0,d >0,a >cD .b <0,d >0,a <c解析:由题图可知,直线l 1的斜率-1a >0,在y 轴上的截距-ba<0,因此a <0,b <0;直线l 2的斜率-1c >0,在y 轴上的截距-d c >0,因此c <0,d >0.且l 1的斜率大于l 2的斜率,即-1a >-1c,因此a >c ,故选C.答案:C7.若方程(2m 2+m -3)x +(m 2-m )y -4m +1=0表示一条直线,则实数m 满足( )A .m ≠0 B.m ≠-32C .m ≠1 D.m ≠1且m ≠-32且m ≠0解析:∵当2m 2+m -3=0时,m =1或m =-32;当m 2-m =0时,m =0或m =1,要使方程(2m 2+m -3)x +(m 2-m )y -4m +1=0表示一条直线,则2m 2+m -3,m 2-m 不能同时为0,∴m ≠1,故选C.答案:C 二、填空题 8.经过A (1,3)和B (a,4)的直线方程为________________________________________________________________________.解析:当a =1时,直线AB 的斜率不存在,所求直线的方程为x =1;当a ≠1时,由两点式,得y -34-3=x -1a -1,即x -(a -1)y +3a -4=0.这个方程中,对a =1时方程为x =1也满足. 所以,所求的直线方程为x -(a -1)y +3a -4=0. 答案:x -(a -1)y +3a -4=09.过点(5,2),且在x 轴上的截距是在y 轴上的截距的2倍的直线方程是________________。
高中数学必修2(人教B版)第二章平面解析几何初步2.3知识点总结含同步练习题及答案

4 时,直线与圆相切; 3 4 当 d < 2,即 m > 0 或 m < − 时,直线与圆相交; 3 4 当 d > 2,即 − < m < 0 时,直线与圆相离. 3
法二:(代数法) 将 y = mx − m − 1 代入圆的方程,化简并整理,得
(1 + m 2 )x2 − 2(m 2 + 2m + 2)x + m 2 + 4m + 4 = 0.
1. 当D 2 + E 2 − 4F > 0 时,比较方程②和圆的标准方程,可以看出②表示以(− 圆心,
1 − − − − − − − − − − − − √D 2 + E 2 − 4F 为半径长的圆; 2 D E 2. 当D 2 + E 2 − 4F = 0 时,方程②只有实数解x = − ,y = − ,它表示一个点 2 2 D E (− , − ); 2 2 3. 当D 2 + E 2 − 4F < 0 时,方程②没有实数解,它不表示任何图形.
− − − − − − − − − −− − − − −
(x − a)2 + (y − b)2 = r2 ⋯ ⋯ ①,若点M (x, y)在圆上,有上述可知,点M 的坐标适合方程 ①;反之,若点M (x, y)的坐标适合方程①,这说明点M 与圆心A 的距离为r ,即点M 在圆心为 A 半径为 r 的圆上.我们把方程①称为以A(a, b)为圆心,以 r 为半径的圆的标准方程(standard
所以 △ABC 的外接圆方程为 x 2 + y 2 − 4x − 2y − 20 = 0 . 光线从点 A(−1, 1) 发出,经过 x 轴反射到圆 C :(x − 2)2 + (y − 3)2 = 1 上,则光线经过的 最短路程是______. 解:4 . 点 A(−1, 1) 关于 x 轴的对称点为 A ′ (−1, −1) ,圆 C :(x − 2)2 + (y − 3)2 = 1 的圆心为 C (2, 3) ,半径为 1 ,所以光线经过的最短路程为
平面解析几何经典题(含答案)

平面解析几何一、直线的倾斜角与斜率1、直线的倾斜角与斜率、直线的倾斜角与斜率(1)倾斜角a 的范围000180a £<(2)经过两点的直线的斜率公式是(3)每条直线都有倾斜角,但并不是每条直线都有斜率2.两条直线平行与垂直的判定(1)两条直线平行对于两条不重合的直线12,l l ,其斜率分别为12,k k ,则有1212//l l k k Û=。
特别地,当直线12,l l 的斜率都不存在时,12l l 与的关系为平行。
的关系为平行。
(2)两条直线垂直如果两条直线12,l l 斜率存在,设为12,k k ,则12121l l k k ^Û=-注:两条直线12,l l 垂直的充要条件是斜率之积为-1,这句话不正确;由两直线的斜率之积为-1,可以得出两直线垂直,反过来,两直线垂直,斜率之积不一定为-1。
如果12,l l 中有一条直线的斜率不存在,另一条直线的斜率为0时,12l l 与互相垂直。
互相垂直。
二、直线的方程1、直线方程的几种形式名称名称方程的形式方程的形式 已知条件已知条件 局限性局限性 点斜式点斜式为直线上一定点,k 为斜率为斜率 不包括垂直于x 轴的直线轴的直线 斜截式斜截式k 为斜率,b 是直线在y 轴上的截距轴上的截距 不包括垂直于x 轴的直线轴的直线 两点式两点式是直线上两定点是直线上两定点 不包括垂直于x 轴和y 轴的直线直线截距式截距式a 是直线在x 轴上的非零截距,b 是直不包括垂直于x 轴和y 轴或线在y 轴上的非零截距轴上的非零截距过原点的直线过原点的直线 一般式一般式A ,B ,C 为系数为系数 无限制,可表示任何位置的直线直线 三、直线的交点坐标与距离公式三、直线的交点坐标与距离公式1.两条直线的交点设两条直线的方程是,两条直线的交点坐标就是方程组的解,若方程组有唯一解,则这两条直线相交,此解就是交点的坐标;若方程组无解,则两条直线无公共点,此时两条直线平行;反之,亦成立。
2019_2020学年高中数学第二章解析几何初步1.5平面直角坐标系中的距离公式练习(含解析)北师大版必修2

1.5 平面直角坐标系中的距离公式填一填1.两点间的距离公式 (1)数轴上:一般地,数轴上两点A ,B 对应的实数分别是x A ,x B ,则|AB |=|x B -x A |. (2)平面直角坐标系中:一般地,若两点A ,B 对应的坐标分别为A (x 1,y 1),B (x 2,y 2),则|AB |=x 2-x 12+y 2-y 12. 2.点到直线的距离点P (x 0,y 0)到直线Ax +By +C =0的距离记为d ,则d =|Ax 0+By 0+C |A 2+B2. 3.两平行线间的距离两条平行直线的方程分别为l 1:Ax +By +C 1=0,l 2:Ax +By +C 2=0,两条直线间的距离记为d ,即d =|C 2-C 1|A 2+B2.判一判1.原点O 到点P (x ,y )的距离为|OP |=x 2+y 2.(√) 23.平面内任意两点间的距离均可使用两点间的距离公式.(√)4.直线l 1:Ax +By +C 1=0与l 2:Ax +By +C 2=0的距离是|C 1-C 2|.(×)5.原点到直线Ax +By +C =0的距离公式是|C |A 2+B2.(√)6.平行线间的距离是两平行线上两点间距离的最小值.(√) 7.连接两条平行直线上两点,即得两平行线间的距离.(×)8想一想1. 提示:点到直线的距离公式只适用直线方程的一般式.2.两条平行直线间的距离公式写成d =|C 1-C 2|A 2+B 2时对两条直线应有什么要求?提示:两条平行直线的方程都是一般式,并且x ,y 的系数分别对应相等. 3.两条平行直线间距离有哪几种求法? 提示:(1)直接利用两平行线间的距离公式.(2)在一条直线上任意选取一点利用点到直线的距离公式求解(一般要选特殊的点,如直线与坐标轴的交点、坐标为整数的点).(3)当两直线都与x 轴(或y 轴)垂直时,可利用数形结合来解决. ①当两直线都与x 轴垂直时,l 1:x =x 1,l 2:x =x 2,则d =|x 2-x 1|; ②当两直线都与y 轴垂直时,l 1:y =y 1,l 2:y =y 2,则d =|y 2-y 1|. 4.距离公式综合应用的常见类型有哪些? 提示:(1)最值问题.①利用对称转化为两点之间的距离问题.②利用所求式子的几何意义转化为点到直线的距离.③利用距离公式将问题转化为一元二次函数的最值问题,通过配方求最值. (2)求参数问题.利用距离公式建立关于参数的方程或方程组,通过解方程或方程组求值. (3)求方程的问题.立足确定直线的几何要素——点和方向,利用直线方程的各种形式,结合直线的位置关系(平行直线系、垂直直线系及过交点的直线系),巧设直线方程,在此基础上借助三种距离公式求解.思考感悟:练一练1.已知A (3,7),B A .5 B. 5 C .3 D .29 答案:B2.已知直线上两点A (a ,b ),B (c ,d ),且a 2+b 2-c 2+d 2=0,则( ) A .原点一定是线段AB 的中点 B .A ,B 一定都与原点重合C .原点一定在线段AB 上,但不是线段AB 的中点D .原点一定在线段AB 的垂直平分线上 答案:D3.点(1,-1)到直线x -y +1=0的距离是( )A .3 2 B.22C .3 D.322答案:D4.点(5,-3)到直线x +2=0的距离等于( ) A .7 B .5 C .3 D .2 答案:A5.直线l 1:x +y =0与直线l 2:2x +2y +1=0间的距离是________.答案:24知识点一两点间距离公式的应用1.已知点A (2,m )与点B (m,1)间的距离是13,则实数m =( )A .-1B .4C .-1或4D .-4或1 解析:∵|AB |=m -22+1-m 2=13,∴m 2-3m -4=0,解得m =-1或m =4. 答案:C2.已知点A (2,1),B (-2,3),C (0,1),则△ABC 中,BC 边上的中线长为________. 解析:BC 中点为(-1,2),所以BC 边上中线长为2+12+1-22=10. 答案:10知识点二 求点到直线的距离3.已知点(a,1)到直线x -y +1=0的距离为1,则a 的值为( ) A .1 B .-1 C. 2 D .± 2解析:由题意,得|a -1+1|12+-12=1,即|a |=2, 所以a =± 2.故选D. 答案:D4.点P (x ,y )在直线x +y -4=0上,O 是原点,则|OP |的最小值是( ) A.10 B .2 2 C. 6 D .2解析:由题意可知|OP |的最小值即原点(0,0)到直线x +y -4=0的距离d =|-4|2=2 2.知识点三 两条平行直线间的距离5.12b +c 等于( )A .-12B .48C .36D .-12或48解析:将l 1:3x +4y +5=0改写为6x +8y +10=0, 因为两条直线平行,所以b =8. 由|10-c |62+82=3,解得c =-20或c =40.所以b +c =-12或48.故选D. 答案:D6.已知直线3x +2y -3=0和6x +my +1=0互相平行,则它们之间的距离是( )A .4 B.21313C.51326 D.71326解析:由两直线平行可知36=2m ≠-31,故m =4.又方程6x +4y +1=0可化简为3x +2y +12=0,∴平行线间的距离为|12--3|22+32=71326.故选D. 答案:D知识点四 对称问题7.直线y =3xA .y =3x -10B .y =3x -18C .y =3x +4D .y =4x +3解析:在直线上任取两点A (1,-1),B (0,-4),则其关于点P 的对称点A ′,B ′可由中点坐标公式求得为A ′(3,-1),B ′(4,2),由两点式可求得方程为y =3x -10.答案:A8.直线2x +3y -6=0关于点(1,-1)对称的直线的方程是( ) A .3x -2y +2=0 B .2x +3y +7=0 C .3x -2y -12=0 D .2x +3y +8=0解析:由平面几何知识易知所求直线与已知直线2x +3y -6=0平行,则可设所求直线的方程为2x +3y +C =0(C ≠-6).在直线2x +3y -6=0上任取一点(3,0),其关于点(1,-1)对称的点为(-1,-2),则点(-1,-2)必在所求直线上,∴2×(-1)+3×(-2)+C =0,解得C =8. 故所求直线的方程为2x +3y +8=0. 答案:D综合知识 距离公式的综合应用9.已知△ABC 中,A (2,-1),B (4,3),C (3,-2). (1)求BC 边上的高所在直线方程的一般式; (2)求△ABC 的面积.解析:(1)因为k BC =3--24-3=5,所以BC 边上的高AD 所在直线斜率k =-15.所以AD 所在直线方程为y +1=-15(x -2).即x +5y +3=0.(2)BC 的直线方程为:y +2=5(x -3). 即5x -y -17=0,点A 到直线BC 的距离为|2×5--1-17|52+-12=626. 又因为|BC |=3-42+-2-32=26,所以△ABC 的面积S =12×626×26=3.10.已知直线l 1经过点A (0,1),直线l 2经过点B (5,0),且直线l 1∥l 2,l 1与l 2间的距离为5,求直线l 1,l 2的方程.解析:∵直线l 1∥l 2,∴当直线l 1,l 2垂直于x 轴时,直线l 1的方程为x =0,直线l 2的方程为x =5, 这时直线l 1,l 2之间的距离等于5,符合题意. 当直线l 1,l 2不垂直于x 轴时,可设其斜率为k , 依题意得,直线l 1的方程为y =kx +1,即kx -y +1=0,直线l 2的方程为y =k (x -5), 即kx -y -5k =0.由两条平行直线间的距离公式,得|1+5k |1+k2=5, 解得k =125.∴直线l 1的方程为12x -5y +5=0,直线l 2的方程为12x -5y -60=0.综上,符合题意的直线l 1,l 2的方程有两组:l 1:x =0,l 2:x =5或l 1:12x -5y +5=0,l 2:12x -5y -60=0.基础达标一、选择题1.点P (1,-1)到直线l :3y =2的距离是( )A .3 B.53C .1 D.22解析:点P (1,-1)到直线l 的距离d =|3×-1-2|02+32=53,选B. 答案:B2.已知点M (1,4)到直线l :mx +y -1=0的距离为3,则实数m =( )A .0 B.34C .3D .0或34解析:点M 到直线l 的距离d =|m +4-1|m 2+1=|m +3|m 2+1,所以|m +3|m 2+1=3,解得m =0或m =34,选D.答案:D3.两条平行直线3x +4y -12=0与ax +8y +11=0间的距离为( ) A.1310 B.135 C.72 D.235解析:直线3x +4y -12=0,即直线6x +8y -24=0,根据直线3x +4y -12=0与ax +8y +11=0平行,可得a =6,故两条平行直线3x +4y -12=0与ax +8y +11=0间的距离为|-24-11|36+64=72. 答案:C4.已知点A (1,3),B (3,1),C (-1,0),则△ABC 的面积等于( ) A .3 B .4 C .5 D .6解析:设AB 边上的高为h ,则S △ABC =12|AB |·h .|AB |=3-12+1-32=22,AB 边上的高h 就是点C 到直线AB 的距离.AB 边所在的直线方程为y -31-3=x -13-1,即x +y -4=0.点C 到直线x +y -4=0的距离为|-1+0-4|2=52,因此,S △ABC =12×22×52=5.答案:C5.直线l 垂直于直线y =x +1,原点O 到l 的距离为1,且l 与y 轴正半轴有交点.则直线l 的方程是( )A .x +y -2=0B .x +y +1=0C .x +y -1=0D .x +y +2=0解析:因为直线l 与直线y =x +1垂直,所以设直线l 的方程为y =-x +b .又l 与y 轴正半轴有交点,知b >0,即x +y -b =0(b >0),原点O (0,0)到直线x +y -b =0(b >0)的距离为|0+0-b |12+12=1,解得b =2(b =-2舍去),所以所求直线l 的方程为x +y -2=0. 答案:A6.已知△ABC 的三个顶点是A (-a,0),B (a,0)和C ⎝ ⎛⎭⎪⎫a2,32a ,则△ABC 的形状是( )A .等腰三角形B .等边三角形C .直角三角形D .斜三角形解析:因为k AC =32a a 2+a =33,k BC =32a a2-a=-3,k AC ·k BC =-1,所以AC ⊥BC ,又|AC |=⎝ ⎛⎭⎪⎫a 2+a 2+⎝ ⎛⎭⎪⎫32a 2=3|a |. |BC |=⎝ ⎛⎭⎪⎫a 2-a 2+⎝ ⎛⎭⎪⎫32a -02=|a |,|AC |≠|BC |. 所以△ABC 为直角三角形.答案:C7.若动点A (x 1,y 1),B (x 2,y 2)分别在直线l 1:x +y -7=0和l 2:x +y -5=0上移动,则AB 的中点M 到原点距离的最小值为( )A .3 2B .2 C. 2 D .4解析:由题意,知点M 在直线l 1与l 2之间且与两直线距离相等的直线上,设该直线方程为x +y +c =0,则|c +7|2=|c +5|2,即c =-6,∴点M 在直线x +y -6=0上,∴点M 到原点的距离的最小值就是原点到直线x +y -6=0的距离,即|-6|2=3 2.答案:A 二、填空题8.已知点A (-1,2),B (3,b )的距离是5,则b =________.解析:根据两点间的距离公式,可得3+12+b -22=5,解得b =5或b =-1. 答案:5或-19.若点(2,k )到直线5x -12y +6=0的距离是4,则k 的值是________.解析:∵|5×2-12k +6|52+122=4, ∴|16-12k |=52,∴k =-3,或k =173.答案:-3或17310.两直线3x +y -3=0与6x +my +n =0平行且距离为10,则m +n =________. 解析:因为两直线平行,所以m =2, 由两平行线的距离公式知⎪⎪⎪⎪⎪⎪-3-n 232+12=10, 解得n =14或n =-26.所以m +n =16或m +n =-24. 答案:16或-2411.已知直线l 过点P (3,4)且与点A (-2,2),B (4,-2)等距离,则直线l 的方程为________________________________________________________________________.解析:显然直线l 的斜率不存在时,不满足题意; 设所求直线方程为y -4=k (x -3), 即kx -y +4-3k =0,由已知,得|-2k -2+4-3k |1+k 2=|4k +2+4-3k |1+k 2, 所以k =2或k =-23.所以所求直线l 的方程为2x -y -2=0或2x +3y -18=0. 答案:2x -y -2=0或2x +3y -18=012.已知实数x ,y 满足2x +y +5=0,那么x 2+y 2的最小值为________.解析:求x 2+y 2的最小值,就是求2x +y +5=0上的点到原点的距离的最小值,转化为坐标原点到直线2x +y +5=0的距离d =522+12= 5. 答案: 5 三、解答题13.已知点P (2,-1).(1)求过P 点且与原点距离为2的直线l 的方程;(2)求过P 点且与原点距离最大的直线l 的方程,最大距离是多少?(3)是否存在过P 点且与原点距离为6的直线?若存在,求出方程;若不存在,请说明理由.解析:(1)过P 点的直线l 与原点距离为2,而P 点坐标为(2,-1),可见,过P 点垂直于x 轴的直线满足条件,此时直线l 的斜率不存在,其方程为x =2.若直线l 的斜率存在,设其方程为y +1=k (x -2),即kx -y -2k -1=0.由已知,得|-2k -1|k 2+1=2,解得k =34,此时l 的方程为3x -4y -10=0.综上,直线l 的方程为x =2或3x -4y -10=0.(2)过P 点且与原点O 距离最大的直线是过P 点且与OP 垂直的直线.由l ⊥OP ,得k l k OP=-1,所以k l =-1k OP=2.由直线方程的点斜式得y +1=2(x -2),即2x -y -5=0.即直线2x -y -5=0是过P 点且与原点O 距离最大的直线,最大距离为|-5|5= 5.(3)由(2)可知,存在过点P 且到原点距离最大为5的直线,因此不存在过点P 到原点距离为6的直线.14.已知直线l 1:x +3y -3m 2=0和直线l 2:2x +y -m 2-5m =0相交于点P (m ∈R ). (1)用m 表示直线l 1与l 2的交点P 的坐标;(2)当m 为何值时,点P 到直线x +y +3=0的距离最短?并求出最短距离.解析:(1)解方程组⎩⎪⎨⎪⎧x +3y -3m 2=0,2x +y -m 2-5m =0,得x =3m ,y =m 2-m ,∴直线l 1与l 2的交点P 的坐标为(3m ,m 2-m ).(2)设点P 到直线x +y +3=0的距离为d ,d =|3m +m 2-m +3|2=|m 2+2m +3|2=|m +12+2|2=m +12+22,∴当m =-1时,即P 点坐标为(-3,2)时,点P 到直线x +y +3=0的距离最短,最短距离为 2.能力提升15.已知两点A (2,3),B (4,1),直线l :x +2y -2=0,在直线l 上求一点P . (1)使|PA |+|PB |最小; (2)使||PA |-|PB ||最大.解析:(1)可判断A ,B 在直线l 的同侧,设A 点关于l 的对称点A 1的坐标为(x 1,y 1), 则有⎩⎪⎨⎪⎧x 1+22+2·y 1+32-2=0,y 1-3x 1-2·⎝ ⎛⎭⎪⎫-12=-1,解得⎩⎪⎨⎪⎧x 1=-25,y 1=-95.由直线的两点式方程得直线A 1B 的方程为y -1-95-1=x -4-25-4,即y =711(x -4)+1,由⎩⎪⎨⎪⎧x +2y -2=0,y =711x -4+1得直线A 1B 与l 的交点为P ⎝⎛⎭⎪⎫5625,-325,由平面几何知识可知,此时|PA |+|PB |最小.(2)由直线的两点式方程求得直线AB 的方程为y -31-3=x -24-2,即x +y -5=0.由⎩⎪⎨⎪⎧x +2y -2=0,x +y -5=0得直线AB 与l 的交点为P (8,-3),此时||PA |-|PB ||最大.16.已知三条直线l 1:mx -y +m =0,l 2:x +my -m (m +1)=0,l 3:(m +1)x -y +(m +1)=0,它们围成△ABC .(1)求证:不论m 取何值时,△ABC 中总有一个顶点为定点; (2)当m 取何值时,△ABC 的面积取最值?并求出最值. 解析:(1)证明:设直线l 1与直线l 3的交点为A .由⎩⎪⎨⎪⎧mx -y +m =0,m +1x -y +m +1=0,解得⎩⎪⎨⎪⎧x =-1,y =0,∴点A 的坐标为(-1,0),∴不论m 取何值,△ABC 中总有一个顶点A (-1,0)为定点.(2)由⎩⎪⎨⎪⎧ x +my -m m +1=0,m +1x -y +m +1=0,解得⎩⎪⎨⎪⎧x =0,y =m +1,即l 2与l 3交点为B (0,m +1).再由⎩⎪⎨⎪⎧mx -y +m =0,x +my -m m +1=0,解得⎩⎪⎨⎪⎧x =m m 2+1,y =m 3+m 2+mm 2+1,即l 1与l 2交点为C ⎝ ⎛⎭⎪⎫mm 2+1,m 3+m 2+m m 2+1.设边AB 上的高为h , ∴S △ABC =12|AB |·h =12·1+m +12·⎪⎪⎪⎪⎪⎪m m +1m 2+1-m 3+m 2+m m 2+1+m +1m +12+1=12·|m 2+m +1|m 2+1=12·m 2+m +1m 2+1=12⎝ ⎛⎭⎪⎫1+m m 2+1.当m =0时,S =12;当m ≠0时,S =12⎝⎛⎭⎪⎪⎫1+1m +1m . ∵函数f (x )=x +1x的值域为[2,+∞)∪(-∞,-2].∴-12≤1m +1m <0或0<1m +1m≤12,∴14≤S <12或12<S ≤34. 当m =1时,△ABC 的面积的最大值为34,当m =-1时,△ABC 的面积的最小值为14.。
高中数学必修二平面解析几何

高中数学必修二平面解析几何
本文从知识点梳理、圆的方程、两个经典的解题和圆的方程的解释过程三个方面,分享了高中数学必修课《二平面解析几何》中圆的方程的介绍。
一、知识梳理
1.圆的定义及方程
2.点与圆的位置关系
二、平面解析几何——圆的方程两个易误点
三、经典考题
1、求圆的方程
(1)(2016·高考天津卷)已知圆C的圆心在x轴的正半轴上,点M(0,)在圆C上,且圆心到直线2x-y=0的距离为,则圆C的方程为________.
(2)(2016·高考浙江卷)已知a∈R,方程a2x2+(a+2)y2+4x +8y+5a=0表示圆,则圆心坐标是________,半径是
________.
解题方法:求圆的方程的两种方法
2、与圆有关的最值问题
已知实数x,y满足方程x2+y2-4x+1=0.
(1)求的最大值和最小值;
(2)求y-x的最大值和最小值.
与圆有关的最值问题解题方法
3、与圆有关的轨迹问题
(2015·高考广东卷节选)已知过原点的动直线l与圆C1:x2+y2-6x+5=0相交于不同的两点A,B.
(1)求圆C1的圆心坐标;
(2)求线段AB的中点M的轨迹C的方程.
求与圆有关的轨迹方程的方法
(2017·湖南箴言中学三模)已知方程x2+y2-2x-4y+m=0.
(1)若此方程表示圆,求实数m的取值范围;
(2)若(1)中的圆与直线x+2y-4=0相交于M,N两点,且OM⊥ON(O为坐标原点),求m的值;
(3)在(2)的条件下,求以MN为直径的圆的方程.。
人教B版高中数学必修2习题 第二章 平面解析几何初步 2.2.1 Word版含解析

第二章 2.2 2.2.1一、选择题1.有下列命题:①若直线的斜率存在,则必有倾斜角与之对应;②若直线的倾斜角存在,则必有斜率与之对应;③坐标平面上所有的直线都有倾斜角;④坐标平面上所有的直线都有斜率.其中错误的是( )A .①②B .③④C .①③D .②④[答案] D[解析] 当直线的倾斜角为90°时,其斜率不存在,故②、④错.2.若直线经过点(1,2)、(4,2+3),则此直线的倾斜角是( )A .150°B .120°C .60°D .30°[答案] D[解析] 直线的斜率k =2+3-24-1=33,∴直线的倾斜角是30°.3.若A (-2,3)、B (3,-2)、C (12,m )三点共线,则m 的值为( ) A .12 B .-12C .-2D .2[答案] A[解析] 由已知得,k AB =k AC , ∴-2-33-(-2)=m -312-(-2),解得m =12.4.直线y =kx +b ,当k >0,b <0时,此直线不经过的象限是( )A .第一象限B .第二象限C .第三象限D .以上都不是[答案] B[解析] 由k >0知,直线的倾斜角为锐角,由b <0知,直线过y 轴负半轴上点(0,b ),∴直线不经过第二象限.5.已知直线l 1、l 2、l 3的斜率分别为k 1、k 2、k 3,如右图所示,则( )A .k1<k 2<k 3B .k 3<k 1<k 2C .k 3<k 2<k 1D .k 1<k 3<k 2[答案] D[解析] 由图可知直线l 1的倾斜角为钝角,所以k 1<0;直线l 2与直线l 3倾斜角均为锐角,且直线l 2的倾斜角较大,所以k 2>k 3>0.∴k 2>k 3>k 1.∴应选D.6.(2015·陕西西安市一中高一期末测试)已知点A (1,3),B (-2,-1),若直线l :y =k (x -2)+1与线段AB 相交,则k 的取值范围是( )A .(-∞,-2)B .(-∞,-2]C .(-∞,-2]∪[12,+∞) D .[-2,12] [答案] D[解析] 直线y =k (x -2)+1过定点P (2,1),如图所示,k P A =3-11-2=-2, k PB =1-(-1)2-(-2)=12,故所求k 的取值范围为[-2,12]. 二、填空题7.(2015·甘肃张掖二中高一期末测试)三点(2,-3)、(4,3)及(5,k 2)在同一条直线上,则k 的值等于________.[答案] 12[解析] 由题意得3-(-3)4-2=k 2-35-4,∴k =12. 8.已知点A 的坐标为(3,4),在坐标轴上有一点B ,若k AB =2,则B 点的坐标为________.[答案] (1,0)或(0,-2)[解析] 设B (x,0)或(0,y ),k AB =43-x 或4-y 3, ∴43-x=2或4-y 3=2,∴x =1,y =-2. 三、解答题9.求经过下列两点直线的斜率,并判断其倾斜角是锐角还是钝角.(1)(1,1)、(2,4);(2)(-3,5)、(0,2);(3)(4,4)、(4,5);(4)(10,2)、(-10,2).[解析] (1)k =4-12-1=3>0,∴倾斜角是锐角. (2)k =2-50-(-3)=-1<0,∴倾斜角是钝角. (3)倾斜角是90°.(4)k =2-2-10-10=0,倾斜角为0°. 10.已知点A (2,-3)、B (-3,-2),直线l 过点P (1,1)且与线段AB 相交,求直线l 的斜率的取值范围.[解析] 如图,直线l 与线段AB 相交,只需直线l 绕点P 按逆时针从PB 转到P A ,即为直线l 的范围.因为k PB =34,k P A =-4,但过P 点且垂直于x 轴的直线的斜率是不存在的,所以旋转过程中,l 的斜率由k PB 变化到无穷大,此时倾斜角在增大.当倾斜角转过90°时,斜率又由无穷小到k P A ,所以直线l 的斜率的取值范围是(-∞,-4]∪[34,+∞).一、选择题1.斜率为2的直线过(3,5)、(a,7)、(-1,b )三点,则a +b 等于( )A .4B .-7C .1D .-1[答案] C[解析] 由题意,得2=7-5a -3=b -5-1-3, ∴a =4,b =-3,∴a +b =1.2.直线l 过点A (2,1)、B (3,m 2)(m ∈R ),则直线l 斜率的取值范围为( )A .[-1,+∞)B .(-1,+∞)C .(-∞,-1)D .(-∞,-1] [答案] A[解析] 直线l 的斜率k =m 2-13-2=m 2-1, ∵m ∈R ,∴m 2-1≥-1,故选A .二、填空题3.如图所示,直线l 1、l 2、l 3、l 4的斜率分别为k 1、k 2、k 3、k 4,从小到大的关系是____________.[答案] k 1<k 3<k 4<k 2[解析] 由倾斜角和斜率的关系可知k 1<k 3<k 4<k 2.4.若过点P (1-a,1+a )与Q (3,2a )的直线的倾斜角为钝角,则实数a 的取值范围是________.[答案] (-2,1)[解析] k =2a -(1+a )3-(1-a )=a -1a +2.∵倾斜角为钝角,∴a -1a +2<0,即(a -1)(a +2)<0,∴-2<a <1. 三、解答题5.(1)当且仅当m 为何值时,经过两点A (-m,6)、B (1,3m )的直线的斜率为12?(2)当且仅当m 为何值时,经过两点A (m,2)、B (-m,2m -1)的直线的倾斜角是45°?[解析] (1)由题意,得3m -61-(-m )=12,解得m =-2.(2)由题意,得(2m -1)-2-m -m =1,解得m =34.6.已知A (1,1)、B (3,5)、C (a,7)、D (-1,b )四点共线,求直线方程y =ax +b .[解析] ∵A 、B 、C 、D 四点共线,∴直线AB 、AC 、AD 的斜率相等,即k AB =5-13-1=2,k AC =7-1a -1,k AD =b -1-1-1,∴2=6a -1=b -1-2.解得a =4,b =-3.∴所求直线方程为y =4x -3.7.已知实数x 、y 满足y =-2x +8,且2≤x ≤3,求y x 的最大值和最小值.[解析] 如图,由已知,点P (x ,y )在线段AB 上运动,其中A (2,4),B (3,2),而y x =y -0x -0,其几何意义为直线OP 的斜率.由图可知k OB ≤k OP ≤k OA ,而k OB =23,k OA =2.故所求的y x 的最大值为2,最小值为23.。
高中数学平面解析几何初步全章总结新人教B版必修2
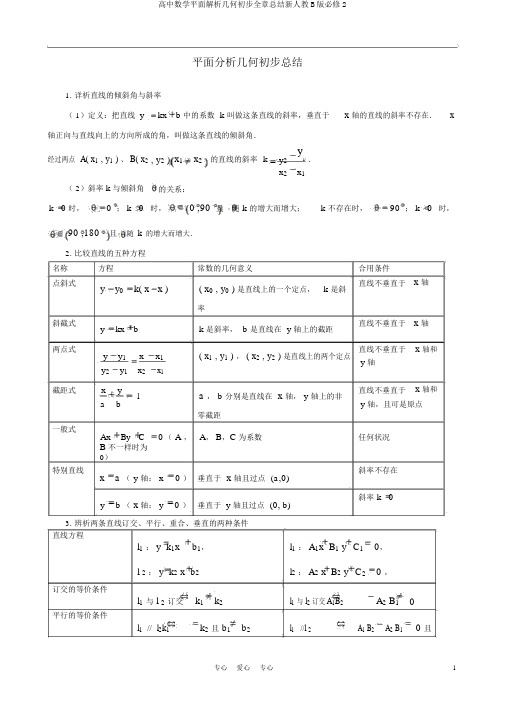
平面分析几何初步总结1.详析直线的倾斜角与斜率( 1)定义:把直线y kx b 中的系数 k 叫做这条直线的斜率,垂直于x 轴的直线的斜率不存在.x 轴正向与直线向上的方向所成的角,叫做这条直线的倾斜角.经过两点 A( x1 , y1 ) 、 B( x2, y2 )x1 x2的直线的斜率k y2y 1 .x2x1( 2)斜率k与倾斜角的关系:k 0 时,0 ; k 0时,0 ,90 且随k的增大而增大;k 不存在时,90 ; k 0时,90 ,180且随k的增大而增大.2.比较直线的五种方程名称方程常数的几何意义合用条件点斜式y y0k( x x )( x0 , y0 ) 是直线上的一个定点,k 是斜直线不垂直于x 轴率斜截式y kx b k 是斜率, b 是直线在 y 轴上的截距直线不垂直于x 轴两点式y y1x x1( x1 , y1 ) , ( x2 , y2 ) 是直线上的两个定点直线不垂直于x 轴和y 轴y2y1x2x1截距式x y1 a ,b分别是直线在 x 轴,y轴上的非直线不垂直于x 轴和a b y 轴,且可是原点零截距一般式Ax By C0( A ,A, B,C为系数任何状况B 不一样时为0)特别直线x a (y轴:x0 )垂直于 x 轴且过点(a,0)斜率不存在y b (x轴: y0 )垂直于 y 轴且过点 (0, b)斜率 k 03.辨析两条直线订交、平行、重合、垂直的两种条件直线方程b1,l1: A1x B1 y C1 0,l1: y k1xl 2: y k2 x b2l2: A2 x B2 y C20 ,订交的等价条件k1 k2l1与 l2订交A1B2A2 B10l1与 l 2订交平行的等价条件k2且 b1 b2l1//l 2A1 B2A2 B10 且l1// l2k1B 1C 2 B 2 C 1 0重合的等价条件l 1 与 l 2 重合 k 1 k 2 且 b 1 b 2 l 1 与 l 2 重 合 A 1 B 2 A 2 B 1 0 且B 1C 2 B 2 C 1 0垂直的等价条件l 1 l 2k 1 k 2 1 l 1 l 2 A 1A 2 B 1 B 2 0说明: 两直线的交点坐标即为对应方程构成的方程组的解.方程组有一组解,则两直线有一个交点;方程组无解,则两直线平行.4. 依据直线地点关系妙设直线方程( 1)与直线 Ax By C 0平行的直线方程可设为Ax Bym 0 ( m 为参数,且 m C );与直线 AxBy C 0 垂直的直线方程可设为 Bx Ay m 0 ( m 为参数).( 2)与直线 ykx m 平行的直线方程可设为y kx b (bm) ;与直线 y kxm 垂直的直线方程可设为 y1x b .k(3) 过 直 线A 1 xB 1 y 1C0 与 A 2 x B 2 yC 2 0 的 交 点 的 直 线 方 程 可 设 为A 1 xB 1 y1CA 2 xB 2 y2C0 ( 为参数).注意此方程中不包含直线A 2 xB 2 yC 2 0,在解题时要考证该直线能否切合题意.特别地,直线过定点问题,一般将直线方程整理为A 1 xB 1 yC 1A 2 xB 2 yC 20 的形式,将定点转变成直线A 1xB 1 yC 1 0与 A 2x B 2 y C 20 的交点.5. 记忆重要公式,重视坐标法思想( 1)四个距离公式和中点坐标公式种类 已知条件公式中点坐标A x 1 , y 1 ,B x 2 , y 2x 0x 1 x 2, y 0 y 1 y 222 数轴上的点A x 1 , B(x 2 )| AB | | x 2 x 1 |两点间的距离A x 1 , y 1 ,B x 2 , y 2|AB|(x 2 x 1 )2( y 2 y 1 )2点到直线的距离P x 0 , y 0 , l : Ax By C 0| Ax 0By 0 C |dA2B2两平行直线的距离l 1 : Ax By C 10 ,| C 2 C 1 |dA2B2l 2 :Ax By C 20 ,( A ,B 不一样时为零)( 2)坐标法思想:即依据图形特色,成立适合的直角坐标系,用坐标表示有关量,利用坐标间的代6.明确圆的两种方程,掌握待定系数法( 1)圆的标准方程:( x a) 2( y b)2r 2,此中,圆心是 C (a, b) ,半径是r.圆的一般方程: x2y2Dx Ey F0 ( Dx Ey F0) .此中圆心是 ( D,E) ,半径是122 D 2 E 24F .2注意:二元二次方程表示圆的条件是x2和y2项的系数相等且不为零;没有xy 项.( 2)圆的标准方程和一般方程中都含有三个参变量(a,b, r 或 D , E, F),求圆的方程时,由题意得到三个独立的条件,利用待定系数法求出三个参变量的值即可.7.点击圆的有关地点关系( 1)点与圆的地点关系点与圆的地点关系有三种:点在圆上、点在圆内、点在圆外,可经过点到圆心的距离与半径的大小关系来判断.( 2)直线与圆的地点关系直线圆的地点关系有三种:订交、相离、相切,其判断方法有两种:代数法(经过解直线方程与圆的方程构成的方程组,依据解得个数来判断)、几何法(由圆心到直线的距离 d 与半径r的大小关系来判断).(3)圆与圆的地点关系圆与圆的地点关系有五种:外离、外切、订交、内切、内含,其判断方法有两种:代数法(依据两圆方程联立的方程组解的状况判断)、几何法(依据两圆的圆心距 d 与两圆半径r1, r2之间的关系判断).8.切记圆的切线求法,细解弦长问题( 1)圆的切线求法:①设切线斜率,获得切线方程,与圆联立化为一元二次方程,依照鉴别式为0求解;②设切线斜率,获得切线方程,利用圆心到切线的距离等于圆的半径求解.解题时,注意切线斜率不存在的状况.(2)当直线与圆订交时,圆的半径、弦心距、弦长的一半构成直角三角形.(3)求订交两圆的公共弦长时,可经过两圆方程相减求出两圆公共先所在的直线方程,从而求出此中一圆心到直线的距离及该圆的半径,利用勾股定理求出弦长的一半,从而求得弦长.9.清晰空间直角坐标系的成立法例,直击距离公式( 1)建林的空间直角坐标系要按照右手法例.222( 2)空间中P1( x1, y1, z1),P2( x2, y2, z2)之间的距离| PP12|x2 x1y2 y1z2 z1.专题概括研究专题一巧设直线方程解题在本章中,常常要用直线方程解决问题,但好多时候直线方程并不是已知,而是要设出方程从而解决问题,这时,怎样选择方程形式将决定解题过程中的好坏简繁.典例 1直线l过点P(8,6),且与两坐标轴围成等腰直角三角形,求直线l 的方程.研析由题意知,直线l 在两坐标轴上的截距的绝对值相等且不为0.方法一设直线 l 的方程为xy 1 或x y 1 (a0).当直线 l 的方程为xya a a a1时,a a∵点 P(8,6) 在 l 上,∴86 1 ,解得 a14 ,a a∴直线 l 的方程为 x y140 ;当直线 l 的方程为xy 1 时,a a∵点 P(8,6) 在 l 上,∴861,解得 a 2 ,a a∴直线 l 的方程为 x y 2 0 .综上所述,所求直线l 的方程为 x y20或 x y140 .方法二设直线 l 的方程为 y kx b(k0, b0) .令 x0 ,得 y b;令 y 0 ,得 x b.kb|,∵ b由题意,得 | b | |0 ,∴ k1.k当 k 1 时,直线 l 的方程为 y x b ,∵点 P(8,6) 在 l 上,∴ 68 b ,b2,∴直线 l 的方程为 y x 2 ,即 x y20 ;当 k 1 时,直线 l 的方程为 y x b,∵点 P(8,6) 在 l 上,∴ 68 b , b14 ,∴直线 l 的方程为 x y140.综上所述,所求直线l 的方程为x y20或 x y140 .方法研究凡波及直线与坐标轴所围成三角形的面积或周长等与截距有关的问题,用截距式较简单,但要注意截距式应用的前提是截距存在且不为零.典例 2已知直线 l 过点 P(1,2) ,且点 A(4,1) , B(2,5) 到直线 l 的距离相等,求直线l 的方程.研析设直线 l 的方程为m( y2) x 1,即 x my2 m 1 0.由点到直线的距离公式可得| 4 m2m 1|| 2 5m2m 1|,解得 m0 或 m3.m21m212故直线 l 的方程为 x10 或 2x3y80 .方法研究设直线方程为 x x0m( y y0 ) ,防止了遗漏斜率不存在的状况(斜率不存在即m0 ).典例 3已知圆 C : x2y26x8y210 ,求过点(1,1)的圆 C 的切线方程.研析设所求切线的方程为m( y1)x 1 ,即 x my m 1 0 .圆的圆心坐标为 (3, 4) ,半径r1( 6)2( 8)24212.2由题意可知| 3 m4 m 1 |2 ,解得 m 0 或 m20,故所求直线方程为 z 1 或1m22121x20 y410 .方法研究过圆上一点 ( x0 , y0 ) 求圆的切线方程,都可能存在切线斜率不存在的情况.为了防止议论斜率和判断点与圆的地点关系,可直接设切线方程为m( y y0 ) x x0.专题二商讨两类圆方程的求解方法1.求过直线与圆的交点的圆的方程解此类问题的方法是:联立直线与圆的方程,求出交点坐标,依据点在圆上及其余条件求圆的方程.典例 1求经过直线 x y0 与圆x2y22x 4y 80 的交点,且经过点P( 1,2) 的圆的方程.研析x y0,x1,x 4,A(1, 1) 和点解方程组y22x 4 y 8 0.得或即直线与圆交于点x2y 1.y 4.B(4,4).设所求圆的方程为 x2y2Dx Ey F 0 ,分别将A,B,P的坐标代入,得方程组11D E F0,D3,16164D4E F 0,解得E3, ∴所求圆的方程为x2y23x 3 y 8 0 .14D2E F0.F8.2.求过两圆交点的圆的方程求过两圆交点的圆的方程,一般先求出两圆的交点坐标,在利用圆的几何性质确立所求圆的圆心坐标和半径;也可由题意设出所求圆的方程,再依据条件成立方程组求参即可.典例 2 求圆心在直线x y40 上,且经过两圆x2y24x60 和 x2y24y 60 的交点的圆的方程.研析方法一x2y2 4 x 6 0,x11,或x23,由22解得y 1.y2 3.x y 4 y60.1故两圆 x2y24x60 和 x2y2 4 y 60 的交点分别为A(1,1) , B(3,3) .线段 AB 的垂直均分线的方程为y 1( xy 1 ( x 1),x 3,1) ,由y4 0. 解得y1.x∴所求圆的圆心坐标为(3, 1) ,半径为(3 3)2(3 1)24 ,∴所求圆的方程为 ( x 3)2 ( y1)2 16 .方法二同方法一求得 A( 1, 1) , B(3,3) ,设所求圆的方程为 ( xa)2 ( y b)2 r 2 (r 0) ,由a b 4 0,a 3,( 1 a)2(1 b)2r 2 ,解得 b 1, (3 a) 2 (3 b)2r 2 .r 216.∴所求圆的方程为 ( x 3)2( y1)2 16 .接下来介绍利用过两圆交点的曲线方程来解决上述问题的方法.这里谈的过两圆交点的曲线方程是指过两圆交点的圆的方程及它的特例—直线的方程.经过两点的圆有无数个,这些圆有一共同的性质:圆心都在已知两点连线的垂直均分线上,构成了一个圆的会合,记这个会合为M .我们把拥有某一共同性质的全部的圆的会合成为圆系,它的方程叫做圆系方程.( 1)设圆 C 过圆 C 1 :x 2y 2 D 1x E 1 y F 1 0 与圆 C 2 :x 2 y 2 D 2xE 2 yF 2 0的交点 P ,Q ,则与圆 C 齐心的圆系方程为 x 2y 2 D 1x E 1 y F 1x 2 y 2 D 2 x E 2 yF 2①,此中为参数且1.该圆系方程不包含圆C 2 .方程①的特例:当1 时,方程①变成 ( D1D )x (EE ) yF F② ,21212若圆 C 与圆 C 2 相切,这时点P , Q 重合为一点,则方程②表示两圆公切线的方程(切点为P ).1( 2)若直线 l : Ax By C 0与圆 C : x 2y 2 Dx Ey F 0 订交于不一样的两点 P ,Q ,则 过 P , Q 两点的圆系方程为x 2y 2 Dx Ey F( Ax By C) 0 ( 为参数).典例 3求圆心在直线x y0上,且过两圆x 2y 2 2x10y 24 0 ,x 2 y 22x 2 y 8 0交点的圆的方程.研析设所求圆的方程为x 2 y 2 2x10y 24x 2 y 2 2 x 2 y 80 (1) ,即 x2y 22(1) 2 5y8(3 )0,可知圆心坐标为(1, 5) .11111由于圆心在直线 xy 0 上,因此15 0 ,解得2 .11将2 代入所设方程并化简,可得所求圆的方程为x 2 y 2 6x 6 y 8 0 .。
高中数学必修2解析几何初步测试题及答案详解

解析几何初步测试题及答案详解(时间:120分钟 满分:150分)一、选择题(本大题共12小题,每小题5分,共60分) 1.下列叙述中不正确的是( )A .若直线的斜率存在,则必有倾斜角与之对应B .每一条直线都有唯一对应的倾斜角C .与坐标轴垂直的直线的倾斜角为0°或90°D .若直线的倾斜角为α,则直线的斜率为tan α2.如果直线ax +2y +2=0与直线3x -y -2=0平行,则系数a 为( )A .-3B .-6C .-32D .233.在同一直角坐标系中,表示直线y =ax 与直线y =x +a 的图象(如图所示)正确的是( )4.若三点A (3,1),B (-2,b ),C (8,11)在同一直线上,则实数b 等于( ) A .2 B .3 C .9 D .-95.过点(3,-4)且在两坐标轴上的截距相等的直线的方程是( ) A .x +y +1=0 B .4x -3y =0 C .4x +3y =0D .4x +3y =0或x +y +1=0 6.已知点A (x,5)关于点(1,y )的对称点为(-2,-3),则点P (x ,y )到原点的距离是( ) A .4 B .13 C .15 D .177.已知直线l 1:ax +4y -2=0与直线l 2:2x -5y +b =0互相垂直,垂足为(1,c ),则a +b +c 的值为( )A .-4B .20C .0D .24 8.圆(x +2)2+y 2=5关于y 轴对称的圆的方程为( ) A .(x -2)2+y 2=5 B .x 2+(y -2)2=5C .(x +2)2+(y +2)2=5D .x 2+(y +2)2=59.以点P (2,-3)为圆心,并且与y 轴相切的圆的方程是( ) A .(x +2)2+(y -3)2=4 B .(x +2)2+(y -3)2=9 C .(x -2)2+(y +3)2=4 D .(x -2)2+(y +3)2=910.已知圆C :x 2+y 2-4x -5=0,则过点P (1,2)的最短弦所在直线l 的方程是( )A .3x +2y -7=0B .2x +y -4=0C .x -2y -3=0D .x -2y +3=011.若直线y =kx +1与圆x 2+y 2+kx -y -9=0的两个交点恰好关于y 轴对称,则k 等于( )A .0B .1C .2D .312.已知圆O :x 2+y 2=5和点A (1,2),则过A 且与圆O 相切的直线与两坐标轴围成的三角形的面积为( )A .5B .10C .252D .254二、填空题(本大题共4小题,每小题5分,共20分)13.在空间直角坐标系Oxyz 中,点B 是点A (1,2,3)在坐标平面yOz 内的正射影,则|OB |=______.14.如果A (1,3)关于直线l 的对称点为B (-5,1),则直线l 的方程是________________. 15.已知直线l 与直线y =1,x -y -7=0分别相交于P 、Q 两点,线段PQ 的中点坐标为(1,-1),那么直线l 的斜率为________.16.若x ∈R ,y 有意义且满足x 2+y 2-4x +1=0,则yx的最大值为________.三、解答题(本大题共6小题,共70分)17.(10分)平行四边形的两邻边所在直线的方程为x +y +1=0及3x -4=0,其对角线的交点是D (3,3),求另两边所在的直线的方程.18.(12分)已知△ABC 的两条高线所在直线方程为2x -3y +1=0和x +y =0,顶点A (1,2). 求(1)BC 边所在的直线方程; (2)△ABC 的面积.19.(12分)已知一个圆和直线l :x +2y -3=0相切于点P (1,1),且半径为5,求这个圆的方程.20.(12分)设圆上的点A(2,3)关于直线x+2y=0的对称点仍在圆上,且与直线x-y+1=0相交的弦长为22,求圆的方程.21.(12分) 如图所示,某县相邻两镇在一平面直角坐标系下的坐标为A(1,2),B(4,0),一条河所在的直线方程为l:x+2y-10=0,若在河边l上建一座供水站P,使之到A,B两镇的管道最省,那么供水站P应建在什么地方?并说明理由.22.(12分)已知坐标平面上点M(x,y)与两个定点M1(26,1),M2(2,1)的距离之比等于5.(1)求点M的轨迹方程,并说明轨迹是什么图形;(2)记(1)中的轨迹为C,过点M(-2,3)的直线l被C所截得的线段的长为8,求直线l的方程.答案详解1.D[α=90°时,斜率不存在.∴选D.]2.B[当两直线平行时有关系a3=2-1≠2-2,可求得a=-6.]3.C4.D[由k AB=k AC得b=-9.]5.D [当截距均为0时,设方程为y =kx ,将点(3,-4)代入得k =-43;当截距不为0时,设方程为x a +ya=1,将(3,-4)代入得a =-1.]6.D7.A [垂足(1,c)是两直线的交点,且l 1⊥l 2,故-a 4×25=-1,∴a =10.l :10x +4y-2=0.将(1,c)代入,得c =-2;将(1,-2)代入l 2:得b =-12.则a +b +c =10+(-12)+(-2)=-4.]8.A [(x ,y)关于y 轴的对称点坐标(-x ,y),则得(-x +2)2+y 2=5.] 9.C [圆心为(2,-3),半径为2,故方程为(x -2)2+(y +3)2=4.]10.D [化成标准方程(x -2)2+y 2=9,过点P(1,2)的最短弦所在直线l 应与PC 垂直,故有k l ·k PC =-1,由k PC =-2得k l =12,进而得直线l 的方程为x -2y +3=0.]11.A [将两方程联立消去y 后得(k 2+1)x 2+2kx -9=0,由题意此方程两根之和为0,故k =0.]12.D [因为点A(1,2)在圆x 2+y 2=5上,故过点A 的圆的切线方程为x +2y =5,令x=0得y =52.令y =0得x =5,故S △=12×52×5=254.]13.13解析 易知点B 坐标为(0,2,3),故OB =13. 14.3x +y +4=015.-23解析 设P(x,1)则Q(2-x ,-3),将Q 坐标代入x -y -7=0得,2-x +3-7=0.∴x =-2,∴P(-2,1),∴k l =-23.16. 3解析 x 2+y 2-4x +1=0(y ≥0)表示的图形是位于x 轴上方的半圆,而yx 的最大值是半圆上的点和原点连线斜率的最大值,结合图形易求得最大值为3.17.解 由题意得⎩⎪⎨⎪⎧x +y +1=0,3x -y +4=0,解得⎩⎨⎧x =-54,y =14,即平行四边形给定两邻边的顶点为⎝⎛⎭⎫-54,14. 又对角线交点为D(3,3),则此对角线上另一顶点为⎝⎛⎭⎫294,234.∵另两边所在直线分别与直线x +y +1=0及3x -y +4=0平行,∴它们的斜率分别为-1及3,即它们的方程为y -234=-⎝⎛⎭⎫x -294 及y -234=3⎝⎛⎭⎫x -294, ∴另外两边所在直线方程分别为x +y -13=0和3x -y -16=0.18.解 (1)∵A 点不在两条高线上,由两条直线垂直的条件可设k AB =-32,k AC =1.∴AB 、AC 边所在的直线方程为3x +2y -7=0, x -y +1=0.由⎩⎪⎨⎪⎧ 3x +2y -7=0x +y =0得B(7,-7). 由⎩⎪⎨⎪⎧x -y +1=02x -3y +1=0得C(-2,-1). ∴BC 边所在的直线方程2x +3y +7=0. (2)∵|BC|=117, A 点到BC 边的距离d =1513, ∴S △ABC =12×d ×|BC|=12×1513×117=452. 19.解 设圆心坐标为C(a ,b), 则圆的方程为(x -a)2+(y -b)2=25. ∵点P(1,1)在圆上, ∴(1-a)2+(1-b)2=25. 又∵CP ⊥l ,∴b -1a -1=2,即b -1=2(a -1).解方程组⎩⎪⎨⎪⎧b -1=2(a -1),(a -1)2+(b -1)2=25,得⎩⎪⎨⎪⎧a =1+5,b =1+25,或⎩⎪⎨⎪⎧a =1-5,b =1-2 5.故所求圆的方程是(x -1-5)2+(y -1-25)2=25或(x -1+5)2+(y -1+25)2=25. 20.解 设圆的方程为(x -a)2+(y -b)2=r 2,∵圆上的点A(2,3)关于x +2y =0的对称点仍在圆上,∴圆心(a ,b)在直线x +2y =0上, 即a +2b =0. ① 圆被直线x -y +1=0截得的弦长为22, ∴⎝⎛⎭⎪⎫|a -b +1|22+(2)2=r 2. ② 由点A(2,3)在圆上得(2-a)2+(3-b)2=r 2. ③由①②③解得⎩⎪⎨⎪⎧ a =6,b =-3,r 2=52或⎩⎪⎨⎪⎧a =14,b =-7,r 2=244.∴圆的方程为(x -6)2+(y +3)2=52或(x -14)2+(y +7)2=244.21.解如图所示,过A 作直线l 的对称点A ′,连接A ′B 交l 于P ,若P ′(异于P)在直线上, 则|AP ′|+|BP ′|=|A ′P ′|+|BP ′|>|A ′B|.因此,供水站只有在P 点处,才能取得最小值,设A ′(a ,b),则AA ′的中点在l 上,且AA ′⊥l ,即⎩⎨⎧a +12+2×b +22-10=0,b -2a -1·⎝⎛⎭⎫-12=-1,解得⎩⎪⎨⎪⎧a =3,b =6,即A ′(3,6).所以直线A ′B 的方程为6x +y -24=0,解方程组⎩⎪⎨⎪⎧6x +y -24=0,x +2y -10=0,得⎩⎨⎧x =3811,y =3611,所以P 点的坐标为⎝⎛⎭⎫3811,3611. 故供水站应建在点P ⎝⎛⎭⎫3811,3611处. 22.解 (1)由题意,得|M 1M||M 2M|=5.(x -26)2+(y -1)2(x -2)2+(y -1)2=5,化简,得x 2+y 2-2x -2y -23=0. 即(x -1)2+(y -1)2=25.∴点M 的轨迹方程是(x -1)2+(y -1)2=25, 轨迹是以(1,1)为圆心,以5为半径的圆. (2)当直线l 的斜率不存在时,l :x =-2, 此时所截得的线段的长为252-32=8,∴l :x =-2符合题意.当直线l 的斜率存在时,设l 的方程为 y -3=k(x +2),即kx -y +2k +3=0, 圆心到l 的距离d =|3k +2|k 2+1,由题意,得⎝⎛⎭⎪⎪⎫|3k +2|k 2+12+42=52, 解得k =512.∴直线l 的方程为512x -y +236=0.即5x -12y +46=0. 综上,直线l 的方程为x =-2,或5x -12y +46=0.。
