苏教版必修二第2章平面解析几何初步作业题及答案解析
高中数学(苏教版,必修二) 第二章平面解析几何初步 2.1.2(二) 课时作业(含答案)
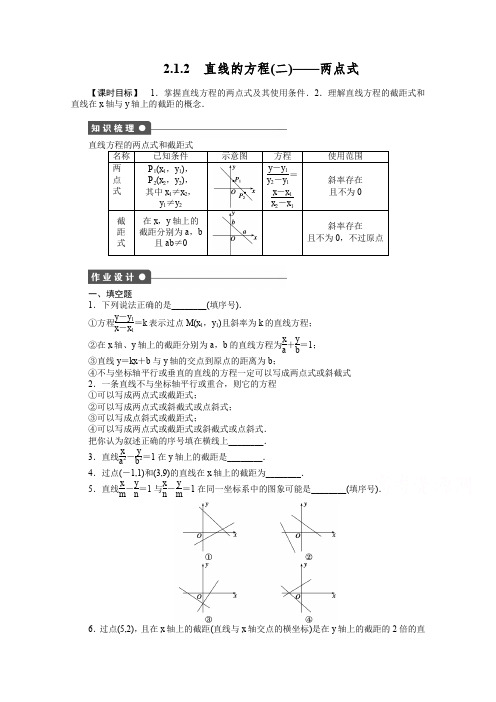
2.1.2 直线的方程(二)——两点式【课时目标】 1.掌握直线方程的两点式及其使用条件.2.理解直线方程的截距式和直线在x 轴与y 轴上的截距的概念.一、填空题1.下列说法正确的是________(填序号).①方程y -y 1x -x 1=k 表示过点M (x 1,y 1)且斜率为k 的直线方程;②在x 轴、y 轴上的截距分别为a ,b 的直线方程为x a +yb=1;③直线y =kx +b 与y 轴的交点到原点的距离为b ;④不与坐标轴平行或垂直的直线的方程一定可以写成两点式或斜截式 2.一条直线不与坐标轴平行或重合,则它的方程 ①可以写成两点式或截距式;②可以写成两点式或斜截式或点斜式; ③可以写成点斜式或截距式;④可以写成两点式或截距式或斜截式或点斜式. 把你认为叙述正确的序号填在横线上________.3.直线x a 2-yb2=1在y 轴上的截距是________.4.过点(-1,1)和(3,9)的直线在x 轴上的截距为________.5.直线x m -y n =1与x n -ym=1在同一坐标系中的图象可能是________(填序号).6.过点(5,2),且在x 轴上的截距(直线与x 轴交点的横坐标)是在y 轴上的截距的2倍的直线方程是__________.7.点(1 005,y )在过点(-1,-1)和(2,5)的直线l 上,则y 的值为________.8.过点P (6,-2),且在x 轴上的截距比在y 轴上的截距大1的直线方程是________________.9.设a ,b 是参数,c 是常数,且a ,b ,c 均不等于0,1a +1b =1c , 则直线x a +yb=1必过一定点________.二、解答题10.已知直线l 的斜率为6,且被两坐标轴所截得的线段长为37,求直线l 的方程.11.一条光线从点A (3,2)发出,经x 轴反射后,通过点B (-1,6),求入射光线和反射光线所在的直线方程.能力提升12.已知点A (2,5)与点B (4,-7),点P 在y 轴上,若P A +PB 的值最小,则点P 的坐标是________.13.已知直线l 经过点(7,1)且在两坐标轴上的截距之和为零,求直线l 的方程.1.直线方程的几种形式,都可以用来求直线的方程,但各有自己的限制条件,应用时要全面考虑.(1)点斜式应注意过P (x 0,y 0)且斜率不存在的情况.(2)斜截式,要注意斜率不存在的情况.(3)两点式要考虑直线平行于x 轴和垂直于x 轴的情况.(4)截距式要注意截距都存在的条件.2.直线方程的几种特殊形式都有明显的几何意义,在求直线方程时,应抓住这些几何特征,求直线方程.3.强调两个问题:(1)截距并非距离,另外截距相等包括截距均为零的情况,但此时不能用截距式方程表示,而应用y =kx 表示.不是每条直线都有横截距和纵截距,如直线y =1没有横截距,x =2没有纵截距.(2)方程y -y 1=y 2-y 1x 2-x 1(x -x 1)(x 1≠x 2)与y -y 1y 2-y 1=x -x 1x 2-x 1(x 1≠x 2,y 1≠y 2)以及(y -y 1)(x 2-x 1)=(x -x 1)(y 2-y 1)代表的直线范围不同(想一想,为什么?).2.1.2 直线的方程(二)——两点式 答案知识梳理 x a +y b=1 作业设计 1.① 2.② 3.-b 2解析 令x =0得,y =-b 2.4.-32解析 由两点式y -19-1=x +13+1,得y =2x +3,令y =0,有x =-32,即为在x 轴上的截距为-32.5.②解析 两直线的方程分别化为斜截式:y =nmx -n ,y =mnx -m ,易知两直线的斜率的符号相同,四个图象中仅有图象②的两直线的斜率符号相同.6.x +2y -9=0或2x -5y =0解析 当y 轴上截距b =0时,方程设为y =kx ,将(5,2)代入得,y =25x ,即2x -5y =0;当b ≠0时,方程设为x 2b +y b =1,求得b =92.7.2 007解析 过(-1,-1)和(2,5)两点的直线为y =2x +1,代入点(1 005,y )得y =2 011.8.x 3+y 2=1或x2+y =1 解析 设直线方程的截距式为x a +1+y a =1,则6a +1+-2a=1,解得a =2或a =1,则直线的方程是x 2+1+y 2=1或x 1+1+y 1=1,即x 3+y 2=1或x2+y =1.9.(c ,c )10.解 方法一 设所求直线l 的方程为y =kx +b . ∵k =6,∴方程为y =6x +b .令x =0,∴y =b ,与y 轴的交点为(0,b );令y =0,∴x =-b6,与x 轴的交点为⎝⎛⎭⎫-b 6,0. 根据勾股定理得⎝⎛⎭⎫-b62+b 2=37, ∴b =±6.因此直线l 的方程为y =6x ±6.方法二 设所求直线为x a +yb=1,则与x 轴、y 轴的交点分别为(a,0)、(0,b ).由勾股定理知a 2+b 2=37.又k =-ba =6,∴⎩⎪⎨⎪⎧a 2+b 2=37,-b a=6.解此方程组可得⎩⎪⎨⎪⎧ a =1,b =-6或⎩⎪⎨⎪⎧a =-1,b =6. 因此所求直线l 的方程为x +y -6=1或-x +y6=1.即6x -y ±6=0.11.解 ∵点A (3,2)关于x 轴的对称点为A ′(3,-2), ∴由两点式得直线A ′B 的方程为 y -6-2-6=x +13+1,即2x +y -4=0. 同理,点B 关于x 轴的对称点B ′(-1,-6), 由两点式可得直线AB ′的方程为 y -2-6-2=x -3-1-3, 即2x -y -4=0.∴入射光线所在直线方程为2x -y -4=0, 反射光线所在直线方程为2x +y -4=0. 12.(0,1)解析 要使P A +PB 的值最小,先求点A 关于y 轴的对称点A ′(-2,5),连结A ′B ,直线A ′B 与y 轴的交点P 即为所求点.13.解 当直线l 经过原点时,直线l 在两坐标轴上截距均等于0,故直线l 的斜率为17,∴所求直线方程为y =17x ,即x -7y =0.当直线l 不过原点时,设其方程x a +yb=1,由题意可得a +b =0,①又l 经过点(7,1),有7a +1b=1,②由①②得a =6,b =-6,则l 的方程为x 6+y-6=1,故所求直线l 的方程为x -7y =0或x -y -6=0.。
苏教版高中数学必修2单元测试第二章平面解析几何初步一

必修2解析几何初步检测题2一 、填空题1、过两点A (4,y ),B (2,-3)的直线的倾斜角是1350,则y=_______-52、直线122=-by a x 在y 轴上的截距是 2b - 3、过点(1,3)-且平行于直线032=+-y x 的直线方程为072=+-y x4、若直线210ax y +-=与210x y +-=垂直,则a =_____-1_____5、已知点)1,6(),5,4(---B A ,则以线段AB 为直径的圆的方程__(x-1)2+(y+3)2=296、圆034222=++-+y x y x 的圆心到直线x-y-1=0的距离为___________27、已知圆心为C (6,5),且过点B (3,6)的圆的方程为 22(6)(5)10x y -+-=8、平行于直线012=+-y x 且与圆522=+y x 相切的直线的方程是_____ 2x -y+5=0或2x -y -5=0 _。
9、已知圆:C ()()4222=-+-y a x ()0>a 及直线03:=+-y x l ,当直线l 被圆C 截得的弦长为32时,=a _____12-10、若(x P ,)y 在圆()3222=+-y x 上运动,则4-x y 11、直线0323=-+y x 截圆422=+y x 所得的劣弧所对的圆心角为 60° 。
12、已知点P (0,-1),点Q 在直线01=+-y x 上,若直线PQ 垂直于直线052=-+y x , 则点Q 的坐标是________(2,3)13、已知直线 024=-+y mx 与 052=+-n y x 互相垂直,垂足为 (1,)p 则 =+-p n m _________20___。
14、在平面直角坐标系中,设三角形ABC 的顶点分别为A(0,a),B(b,0),C (c,0) ,点P (0,p )在线段AO 上(异于端点),设a,b,c, p 均为非零实数,直线BP,CP 分别交AC , AB 于点E ,F ,一同学已正确算的OE 的方程:11110x y c b p a ⎛⎫⎛⎫-+-= ⎪ ⎪⎝⎭⎝⎭,请你求OF 的方程: ( )110x y p a ⎛⎫+-= ⎪⎝⎭. 11b c - 本小题考查直线方程的求法。
2019-2020学年高中数学(苏教版,必修二)第二章平面解析几何初步2.3.2课时作业(含答案)

2019-2020学年苏教版数学精品资料2.3.2空间两点间的距离【课时目标】1.掌握空间两点间的距离公式.2.能够用空间两点间距离公式解决简单的问题.1.在空间直角坐标系中,给定两点P1(x1,y1,z1),P2(x2,y2,z2),则P1P2=_________________________________________________________________.特别地:设点A(x,y,z),则A点到原点的距离为:OA=________________.2.若点P1(x1,y1,0),P2(x2,y2,0),则P1P2=__________________________________________________________________.3.若点P1(x1,0,0),P2(x2,0,0),则P1P2=________________.一、填空题1.若A(1,3,-2)、B(-2,3,2),则A、B两点间的距离为________.2.在长方体ABCD-A1B1C1D1中,若D(0,0,0)、A(4,0,0)、B(4,2,0)、A1(4,0,3),则对角线AC1的长为________.3.到点A(-1,-1,-1),B(1,1,1)的距离相等的点C(x,y,z)的坐标满足的关系式为____________.4.已知A(2,1,1),B(1,1,2),C(2,0,1),则△ABC的形状为____________三角形.5.已知A(x,5-x,2x-1),B(1,x+2,2-x),当AB取最小值时,x的值为________.6.点P(x,y,z)满足x-12+y-12+z+12=2,则点P的集合为____________________________.7.在空间直角坐标系中,正方体ABCD-A1B1C1D1的顶点A(3,-1,2),其中心M的坐标为(0,1,2),则该正方体的棱长为________.8.已知P 32,52,z到直线AB中点的距离为3,其中A(3,5,-7),B(-2,4,3),则z=________.9.在空间直角坐标系中,已知点A(1,0,2),B(1,-3,1),点M在y轴上,且M到A与到B的距离相等,则M的坐标是________.二、解答题10.在xOy平面内的直线x+y=1上确定一点M,使它到点N(6,5,1)的距离最小.11.如图所示,BC=4,原点O是BC的中点,点A的坐标为(32,12,0),点D在平面yOz上,且∠BDC=90°,∠DCB=30°,求AD的长度.能力提升12.已知正方形ABCD、ABEF的边长都是1,且平面ABCD⊥平面ABEF,点M在AC 上移动,点N在BF上移动,若CM=BN=a(0<a<2).(1)求MN的长;(2)当a为何值时,MN的长最小.13.在长方体ABCD—A1B1C1D1中,AB=AD=3,AA1=2,点M在A1C1上,MC1=2A1M,N在D1C上且为D1C中点,求M、N两点间的距离.空间中两点的距离公式,是数轴上和平面上两点间距离公式的进一步推广,反之,它可以适用于平面和数轴上两点间的距离的求解.设P1(x1,y1,z1),P2(x2,y2,z2),则d(P1,P2)=x2-x12+y2-y12+z2-z12,当P1,P2两点落在了坐标平面内或与坐标平面平行的平面内时,此公式可转化为平面直角坐标系中的两点间距离公式,当两点落在坐标轴上时,则公式转化为数轴上两点间距离公式.2.3.2空间两点间的距离答案知识梳理1.x1-x22+y1-y22+z1-z22x2+y2+z22.x1-x22+y1-y223.|x1-x2|作业设计1.5解析AB=1+22+3-32+-2-22=5.2.29解析由已知求得C1(0,2,3),∴AC1=29.3.x+y+z=0解析AC=BC?(x+1)2+(y+1)2+(z+1)2=(x-1)2+(y-1)2+(z-1)2.即x+y+z=0.4.直角解析AB=2,BC=3,AC=1,∴AB2+AC2=BC2.故构成直角三角形.5.8 7解析AB=x-12+3-2x2+3x-32=14x2-32x+19,∴当x=--322×14=87时,AB最小.6.以点(1,1,-1)为球心,以2为半径的球面7.239 38.0或-4解析利用中点坐标公式,则AB中点C 12,92,-2,PC=3,即32-122+52-922+[z--2]2=3,解得z=0或z=-4.9.(0,-1,0)解析设M的坐标为(0,y,0),由MA=MB得(0-1)2+(y-0)2+(0-2)2=(0-1)2+(y+3)2+(0-1)2,整理得6y+6=0,∴y=-1,即点M的坐标为(0,-1,0).10.解∵点M在直线x+y=1(xOy平面内)上,∴可设M(x,1-x,0).∴MN=x-62+1-x-52+0-12=2x-12+51≥51,当且仅当x=1时取等号,∴当点M坐标为(1,0,0)时,(MN)min=51.11.解由题意得B(0,-2,0),C(0,2,0),设D(0,y,z),则在Rt△BDC中,∠DCB=30°,∴BD=2,CD=23,z=3,y=-1.∴D(0,-1,3).又∵A(32,12,0),∴AD=322+12+12+32=6.12.解∵平面ABCD⊥平面ABEF,平面ABCD∩平面ABEF=AB,AB⊥BE,∴BE⊥平面ABCD,∴AB、BC、BE两两垂直.过点M作MG⊥AB,MH⊥BC,垂足分别为G、H,连结NG,易证NG⊥AB.∵CM=BN=a,∴CH=MH=BG=GN=22a,∴以B为原点,以AB、BE、BC所在的直线为x轴、y轴、z轴,建立如图所示的空间直角坐标系B—xyz,则M22a,0,1-22a,N22a,22a,0.(1)MN=22a-22a2+0-22a2+1-22a-02=a2-2a+1=a-222+12,(2)由(1)得,当a=22时,MN最短,最短为22,这时M、N恰好为AC、BF的中点.13.解如图分别以AB、AD、AA1所在的直线为x轴、y轴、z轴建立空间直角坐标系.由题意可知C(3,3,0),D(0,3,0),∵DD1=CC1=2,∴C1(3,3,2),D1(0,3,2),∵N为CD1的中点,∴N 32,3,1.M是A1C1的三分之一分点且靠近A1点,∴M(1,1,2).由两点间距离公式,得MN=32-12+3-12+1-22=212.。
-2019年高中数学苏教版《必修二》《第二章平面解析几何初步

-2019年高中数学苏教版《必修二》《第二章平面解析几何初步2022年-2022年高中数学苏教版《必修二》《第二章平面解析几何初步》《2.3 空间直角坐标系》课后练习试卷含答案考点及解析班级:___________ 姓名:___________ 分数:___________1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上一、选择题1.某几何体的三视图如右图,(其中侧视图中的圆弧是半圆),则该几何体的表面积为A.92+14πB.82+14πC.92+24πD.82+24πA试题分析:由三视图可知,该几何体下方为一个长方体,长宽高分别为,上方接一个沿旋转轴切掉的半圆柱,底面半径为,高为,所以表面积为.故选.考点:三视图、组合体的表面积.2.在中,,,,若把绕直线旋转一周,则所形成的几何体的体积是()A.B.C.D.B试题分析:依题意可知,旋转体是一个大圆锥去掉一个小圆锥,如图所以,,所以旋转体的体积为==,故选B .考点:旋转体的性质与体积.3.若直线不平行于平面,则下列结论成立的是()A .内的所有直线都与直线异面B .内不存在与平行的直线C .内的直线都与相交D .直线与平面有公共点D试题分析:直线不平行于平面,则与平面相交或,所以D 正确. 考点:直线与平面的位置关系.4.已知点P(a,b)(ab≠0)是圆x 2+y 2=r 2内的一点,直线m 是以P 为中点的弦所在的直线,直线l 的方程为ax+by=r 2,那么( )A .m ∥l,且l 与圆相交B .m ⊥l,且l 与圆相切C .m ∥l,且l 与圆相离D .m ⊥l,且l 与圆相离C直线m 的方程为y-b=-(x-a),即ax+by-a 2-b 2=0,∵P 在圆内,∴a 2+b 2r 2,∴m ∥l,∵圆心到直线l 的距离d=r, ∴直线l 与圆相离.5.若动点A(x 1,y 1),B(x 2,y 2)分别在直线l 1:x+y-7=0和l 2:x+y-5=0上移动,则线段AB 的中点M 到原点的距离的最小值为( )A .2B .3C .3D .4 C由题意知,M 点的轨迹为平行于l 1,l 2且到l 1,l 2距离相等的直线l,其方程为x+y-6=0,∴M 到原点的距离的最小值d==3.6.对于平面与共面的直线m ,n ,下列命题为真命题的是( )A .若m ,n 与所成的角相等,则m//nB .若m//,n//,则m//nC .若,,则//D .若m ,n//,则m//nD试题分析:根据题意,由于若m ,n 与所成的角相等,则m//n ,或者相交,错误,对于B ,由于平行于同一平面的直线有三种位置关系,故错误,对于C,由于直线n 可能在平面内,故错误就,答案为D.考点:空间中线线与线面的位置关系点评:主要是考查了线面平行以及线线平行的判定定理的运用,属于基础题。
【名师点睛】苏教版高中数学必修2第二章《平面解析几何初步》课时作业16

一、填空题1.(2013·南通检测)与直线x+2y+7=0垂直的一条直线的斜率k=____________.【解析】直线x+2y+7=0的斜率k=-12,故与其垂直的一条直线的斜率k=2.【答案】 22.(2013·内蒙古检测)已知直线方程:l1:2x-4y+7=0,l2:x-2y+5=0,则l1与l2的关系是__________.【解析】直线l1:2x-4y+7=0可化为x-2y+72=0,故l1,l2两直线的斜率相等,在y轴上的截距不相等.所以l1∥l2.【答案】平行3.(2013·威海检测)过点(-1,2)且与直线2x-3y+4=0垂直的直线方程为________________.【解析】设与直线2x-3y+4=0垂直的直线方程为3x+2y+m=0.对点(-1,2),故-3+4+m=0,m=-1.所以所求直线的方程为3x+2y-1=0.【答案】3x+2y-1=04.若点A(0,1),B(3,4)在直线l1上,直线l1⊥l2,则l2的倾斜角为________.【解析】由题意可知k AB=4-13-0= 3.又l1⊥l2,从而l2的斜率为-33.由tan α=-33得,α=150°. 【答案】150°5.若直线ax +2y -1=0与2x +y -1=0垂直,则a =________. 【解析】 由题意可知-a2×(-2)=-1,∴a =-1. 【答案】 -16.已知直线l 1的倾斜角为45°,直线l 2过点A (1,2),B (-5,-4),则l 1与l 2的位置关系是__________.【解析】 k AB =2-(-4)1-(-5)=1,l 1的斜率kl 1=tan 45°=1,k AB =kl 1,∴l 1与l 2的位置关系是平行或重合. 【答案】 平行或重合7.已知A (-1,3),B (3,1),点C 在坐标轴上,若∠ACB =90°,则点C 的坐标是__________.【解析】 (1)设C (x,0),则由k AC ·k BC =-1,得-3x +1·13-x=-1, ∴x =0或x =2,即C 为(0,0)或(2,0).(2)设C (0,y ),则由k AC ·k BC =-1,得3-y -1·1-y 3=-1,∴y =0或y =4.即C 为(0,0)或(0,4). 【答案】 (0,0)或(0,4)或(2,0)8.由三条直线l 1:2x -y +2=0,l 2:x -3y -3=0,l 3:6x +2y +5=0所围成的三角形是________三角形.【解析】 由l 2⊥l 3可知三角形为直角三角形. 【答案】 直角 二、解答题9.(2013·南京检测)在平面直角坐标系xOy 中,已知点A (-2,1),直线l :2x -y -3=0.(1)若直线m 过点A ,且与直线l 垂直,求直线m 的方程;(2)若直线n 与直线l 平行,且在x 轴、y 轴上的截距之和为3,求直线n 的方程.【解】(1)由题意,直线l的斜率为2,所以直线m的斜率为-12,所以直线m的方程为y-1=-12(x+2),即x+2y=0.(2)由题意,直线l的斜率为2,所以直线n的斜率为2,设直线n的方程为y=2x+b.令x=0,得y=b;令y=0,得x=-b2.由题知b-b2=3,解得b=6.所以直线n的方程为y=2x+6,即2x-y+6=0.图2-1-710.(2013·泉州检测)如图2-1-7,在平行四边形OABC中,点C(1,3),A(3,0)(1)求AB所在直线方程;(2)过点C做CD⊥AB于点D,求CD所在直线的方程.【解】(1)点O(0,0),点C(1,3),∴OC直线的斜率为k OC=3-01-0=3.AB∥OC,k AB=3,AB所在直线方程为y=3x-9 (2)在▱OABC中,AB∥OC,∵CD⊥AB,∴CD⊥OC.∴CD所在直线的斜率为k CD=-13.∴CD所在直线方程为y-3=-13(x-1),即x+3y-10=0.11.已知A(1,-a+13),B(0,-13),C(2-2a,1),D(-a,0)四点.当a为何值时,直线AB和直线CD(1)平行?(2)垂直?【解】k AB=-13+a+130-1=-a3,k CD=0-1-a-2+2a=12-a(a≠2).(1)k AB=k CD,∴-a3=12-a,即a2-2a-3=0.∴a=3或a=-1.当a=3时,k AB=-1,k BD=0+13-3=-19≠k AB,∴AB与CD平行不重合.当a=-1时,k AB=13,k BC=1+134=13,∴AB与CD重合.当a=2时,k AB=-23,k CD不存在.∴AB和CD不平行.∴a=3时,直线AB和直线CD平行.(2)由-a3·12-a=-1,解得a=32.当a=2时,k AB=-23,直线CD的斜率不存在.∴直线AB与CD不垂直.∴a=3时,直线AB与CD垂直.2。
【名师点睛】苏教版高中数学必修2第二章《平面解析几何初步》课时作业12

一、填空题1.(2013·中山检测)已知A (1,1),B (2,4),则直线AB 的斜率为________.【解析】 由题意可知,k AB =4-12-1=3.【答案】 32.(2013·无锡检测)过点P (2,3)和Q (-1,6)的直线PQ 的倾斜角为________.【解析】 ∵k PQ =6-3-1-2=-1,设直线PQ 的倾斜角为α,由tan α=-1,可知α=135°.【答案】 135°3.(2013·泰兴检测)已知两点A (1,-1),B (3,3),点C (5,a )在直线AB 上,则a =________.【解析】 由题意可知k AB =k AC ,即3-(-1)3-1=a -(-1)5-1,解得a =7. 【答案】 74.下列说法中正确的是__________.①倾斜角为0°的直线只有一条;②一条直线的倾斜角是-30°;③平面直角坐标系内,每一条直线都有惟一的倾斜角;④直线倾斜角α的集合{α|0°≤α<180°}与直线集合建立了一一对应关系.【解析】 ①与x 轴平行或重合的直线的倾斜角都为0°,这样的直线有无数条,①错误;②直线的倾斜角的取值范围是0°≤α<180°,②错误;③平面直角坐标系内,每一条直线都有惟一的倾斜角,③正确;④一条直线的倾斜角确定时,直线位置不能确定,直线倾斜角α集合{α|0°≤α<180°}与直线集合不能建立一一对应的关系,④错误.【答案】③图2-1-15.如图2-1-1,已知直线l1,l2,l3的斜率分别为k1,k2,k3,则k1,k2,k3的大小关系是________.【解析】由图可知,直线l3比直线l2的倾斜度大,故k3>k2>0,又k1<0,所以k3>k2>k1.【答案】k3>k2>k16.过点P(-2,m)和Q(m,4)的直线斜率不存在,则m的值等于________.【解析】由题意可知,点P和Q的横坐标相同,即m=-2.【答案】-27.若直线l沿x轴负方向平移3个单位,再沿y轴正方向平移1个单位后,又回到原来位置,那么直线l的斜率是________.【解析】设P(a,b)为l上任一点,经过平移后,点P到达点Q(a-3,b+1),此时直线PQ与l重合.故l的斜率k=k PQ=(b+1)-b(a-3)-a=-13.【答案】-1 38.已知A(3,4),在坐标轴上有一点B,使直线AB的斜率为2,则B点坐标为________.【解析】设B(x,y),则2=y-4x-3,若x=0,则y=-2;若y=0,则x=1.故B为(0,-2)或(1,0).【答案】(0,-2)或(1,0)二、解答题图2-1-29.如图2-1-2所示,直线l1的倾斜角α1=30°,直线l1⊥l2,求l1、l2的斜率.【解】l1的斜率:k1=tan α1=tan 30°=3 3.∵l2的倾斜角α2=90°+30°=120°,∴l2的斜率k2=tan 120°=tan(180°-60°)=-tan 60°=- 3.10.求经过下列两点的直线的斜率,并判断其倾斜角是锐角还是钝角.(1)(-3,5),(0,2);(2)(4,4),(4,5);(3)(10,2),(-10,2).【解】(1)k=2-50-(-3)=-1<0,∴倾斜角是钝角.(2)倾斜角是90°,斜率不存在.(3)k=2-2-10-10=0,∴倾斜角是0°.11.若直线l的斜率为函数f(a)=a2+4a+3(a∈R)的最小值,求直线l的倾斜角α.【解】f(a)=a2+4a+3=(a+2)2-1,∴f(a)的最小值为-1,∴k l=-1=tan α.又0°≤α<180°,∴α=135°.。
新苏教版高中数学必修二同步练习:第2章《平面解析几何初步复习与小结》(含答案)
随堂练习:平面解析几何(习题课)1.已知两点A(-2,0),B(1,0),如果动点P满足PA=2PB,则点P的轨迹所包围的图形的面积等于________.2.如果实数满足(x+2)2+y2=3,则yx的最大值为________3.已知两点A(-2,0),B(0,2),点C是圆x2+y2-2x=0上任意一点,则△ABC面积的最小值是________.4.在平面直角坐标系xOy中,已知圆x2+y2=4上有且只有四个点到直线12x-5y+c=0的距离为1,则实数c的取值范围是________.5.已知点A(-1,1)和圆C:(x-5)2+(y-7)2=4,一束光线从A经x轴反射到圆C上的最短路程是________.6.已知圆x2+y2=9的弦PQ的中点为M(1,2),则弦PQ的长为________.7.已知集合M={(x,y)|y=9-x2,y≠0},N={(x,y)|y=x+b},若M∩N≠∅,则实数b 的取值范围是________.8.已知圆x2+y2+x-6y+m=0与直线x+2y-3=0相交于P,Q两点,O为原点,若OP⊥OQ,求实数m的值.9.有一种商品,A、B两地均有售且价格相同,但某居住地的居民从两地往回运时,每单位距离A地的运费是B地运费的3倍.已知A、B相距10 km,问这个居民应如何选择A地或B地购买此种商品最合算?(仅从运费的多少来考虑)答案1.4π 2. 3 3.3- 2 4.(-13,13) 5.8 6.4 7.(-3,32]8.解 设P ,Q 两点坐标为(x 1,y 1)和(x 2,y 2),由OP ⊥OQ 可得x 1x 2+y 1y 2=0,由⎩⎪⎨⎪⎧x 2+y 2+x -6y +m =0,x +2y -3=0, 可得5y 2-20y +12+m =0.①所以y 1y 2=12+m 5,y 1+y 2=4.又x 1x 2=(3-2y 1)(3-2y 2) =9-6(y 1+y 2)+4y 1y 2 =9-24+45(12+m),所以x 1x 2+y 1y 2=9-24+45(12+m)+12+m 5=0,解得m =3.将m =3代入方程①,可得Δ=202-4×5×15=100>0,可知m =3满足题意,即3为所求m 的值.9.解 以AB 所在的直线为x 轴,AB 的中点为原点建立直角坐标系.AB =10,所以A(-5,0),B(5,0),设P(x ,y)是区域分界线上的任一 点,并设从B 地运往P 地的单位距离运费为a ,即从B 地运往P 地 的运费为PB·a ,则A 地的运费为PA·3a ,当运费相等时,就是PB·a =3a·PA , 即3+2+y 2=-2+y 2,整理得(x +254)2+y 2=(154)2.①所以在①表示的圆周上的居民可任意选择在A 地或B 地购买,在圆内的居民应选择在A 地购买,在圆外的居民应选择在B 地购买.。
【名师点睛】苏教版高中数学必修2第二章《平面解析几何初步》课时作业17
一、填空题1.下列直线中,能够与直线x +3y +4=0相交的直线是________. ①x +3y =1;②3x +y =0;③x 2+y 3=1;④y =-13x +4.【解析】 ①与已知直线平行,④与已知直线平行,②、③与已知直线相交. 【答案】 ②③2.直线l 1:x +by =1与直线l 2:x -y =a 的交点坐标为(0,2)则a =________,b =________.【解析】 将(0,2)代入x +by =1,得b =12, 将(0,2)代入x -y =a ,得a =-2. 【答案】 -2 123.两条直线2x +3y -k =0和x -ky +12=0的交点在y 轴上,那么k 的值是________.【解析】 两直线的交点在y 轴上,可设交点的坐标为(0,y 0), ⎩⎪⎨⎪⎧3y 0-k =0 ①-ky 0+12=0 ②则有由①可得y 0=k 3,将其代入②得-k 23+12=0, ∴k 2=36,即k =±6. 【答案】 ±64.(2013·中山检测)若三直线2x +3y +8=0,x -y -1=0和x +ky =0相交于一点,则k =________.【解析】 由⎩⎪⎨⎪⎧ 2x +3y +8=0,x -y -1=0,得⎩⎪⎨⎪⎧x =-1,y =-2.∴点(-1,-2)在x +ky =0上, 即-1-2k =0,∴k =-12. 【答案】 -125.(2013·湖南师大附中检测)无论m 为何值,直线l :(2m +1)x +(m +1)y -7m -4=0恒过一定点P ,则点P 的坐标为________.【解析】 直线l :(2m +1)x +(m +1)y -7m -4=0可变形为m (2x +y -7)+x +y -4=0,由⎩⎪⎨⎪⎧ 2x +y -7=0,x +y -4=0,得⎩⎪⎨⎪⎧x =3,y =1. 故点P 的坐标为(3,1). 【答案】 (3,1)6.直线5x +4y =2a +1与直线2x +3y =a 的交点位于第四象限,则a 的取值范围为__________.【解析】 由⎩⎪⎨⎪⎧5x +4y =2a +1,2x +3y =a ,得⎩⎨⎧x =2a +37,y =a -27.∵点(2a +37,a -27)在第四象限, ∴⎩⎨⎧a -27<0,2a +37>0,解得-32<a <2.【答案】 -32<a <27.已知直线ax +2ay +1=0与(a -1)x -(a +1)y -1=0垂直,则垂足的坐标是________.【解析】 因为直线ax +2ay +1=0与(a -1)x -(a +1)y -1=0垂直,所以a (a -1)+2a (-a -1)=0,a 2+3a =0,所以a =0或a =-3,在直线ax +2ay +1=0中,a ≠0,故a =-3,所以垂足是(-215,730).【答案】 (-215,730)8.直线ax +by +16=0与x -2y =0平行,并过直线4x +3y -10=0和2x -y -10=0的交点,则a =________,b =________.【解析】 ∵直线ax +by +16=0与直线x -2y =0平行,∴a =-b2.① 由⎩⎪⎨⎪⎧ 4x +3y -10=0,2x -y -10=0,可得⎩⎪⎨⎪⎧x =4,y =-2.∵点(4,-2)在直线ax +by +16=0上,∴4a -2b +16=0.②由①②可解得a =-2,b =4. 【答案】 -2 4 二、解答题9.(2013·广州检测)已知两直线l 1:2x -y +7=0,l 2:x +y -1=0,A (m ,n )是l 1和l 2的交点,(1)求m ,n 的值;(2)求过点A 且垂直于直线l 1的直线l 3的方程;(3)求过点A 且平行于直线l :2x -3y -1=0的直线l 4的方程. 【解】 (1)因为A (m ,n )是l 1和l 2的交点, 所以⎩⎪⎨⎪⎧2m -n +7=0,m +n -1=0,解得⎩⎪⎨⎪⎧m =-2,n =3.(2)由(1)得A (-2,3).因为kl 1=2,l 3⊥l 1,所以kl 3=-12,由点斜式得,l 3:y -3=-12(x +2),即l 3:x +2y -4=0. (3)因为l 4∥l ,所以kl 4=k l =23,由点斜式得,l 4:y -3=23(x +2),即2x -3y +13=0.10.(2013·扬州检测)已知直线l 1:(a +3)x +4y =5-3a 与l 2:2x +(a +5)y =8,则当实数a 为何值时,直线l 1与l 2:(1)平行?(2)垂直?【解】 (1)由⎩⎪⎨⎪⎧(a +3)(a +5)-8=08(a +3)-2(5-3a )≠0,得a =-7(2)由2(a +3)+4(a +5)=0得a =-13311.是否存在实数a ,使三条直线l 1:ax +y +1=0,l 2:x +ay +1=0,l 3:x +y +a =0能围成一个三角形?并说明理由.【解】 要使三条直线能围成一个三角形,则它们中的任意两条都不平行,且三条不相交于同一点.当a =0时,l 1,l 2,l 3显然能构成三角形. 当a ≠0时,分情况讨论如下: ①当l 1∥l 2时,-a =-1a ,即a =±1. ②当l 1∥l 3时,-a =-1,即a =1. ③当l 2∥l 3时,-1a =-1,即a =1.④当l 1与l 2,l 3相交于同一点时,由⎩⎪⎨⎪⎧x +ay +1=0,x +y +a =0,得交点(-1-a,1),将其代入ax +y +1=0,得a =-2或a =1.故当a≠1且a≠-1且a≠-2时,这三条直线能围成一个三角形.。
2018-2019学年苏教版必修2 第2章 平面解析几何初步 单元测试
2018-2019学年苏教版必修2 第2章 平面解析几何初步 单元测试1.直线分别与轴,轴交于,两点,点在圆上,则ABP △面积的取值范围是 A .B .C .D .【答案】A【解析】直线20x y ++=分别与x 轴,y 轴交于A ,B 两点,()()2,0,0,2A B ∴--,则AB =,点P 在圆上,圆心为(2,0),则圆心到直线距离, 故点P 到直线20x y ++=的距离的取值范围为则,故选A.2.圆2228130x y x y +--+=的圆心到直线10ax y +-=的距离为1,则a= A .43-B .34-C D .2【答案】A3.直线经过定点,则点为 A .B .C .D .【答案】D【解析】直线的方程可化为,当,时方程恒成立,直线过定点.故选.【名师点睛】本题考查的知识点是恒过定点的直线,解答的关键是将参数分离,化为的形式,令,即可解得答案.4.若直线()1:110l ax a y -++=与直线2:210l x ay --=垂直,则实数a = A .3 B .0 C .3-D .03-或【答案】D5.数学家欧拉在1765年提出,任意三角形的外心、重心、垂心位于同一条直线上,后人称这条直线为欧拉线.已知△ABC 的顶点A (2,0),B (0,4),若其欧拉线的方程为x -y +2=0,则顶点C 的坐标为 A .(-4,0) B .(-3,-1) C .(-5,0)D .(-4,-2)【答案】A【解析】设C (m ,n ),由重心公式,可得△ABC 的重心为,代入欧拉直线有:,整理得m -n +4=0 ①.AB 的中点为(1,2),k AB ==-2,AB 的中垂线方程为y -2=(x -1),即x -2y +3=0,联立可得:,所以△ABC 的外心为(-1,1),外心与点B 的距离:,外心与点B 的距离与外心与点C 的距离相等,则:(m +1)2+(n -1)2=10,整理得m 2+n 2+2m -2n =8 ②, 联立①②,可得m =-4,n =0或m =0,n =4.当m =0,n =4时,B ,C 两点重合,舍去, 当m =-4,n =0时满足题意. 所以点C 的坐标为(-4,0). 故选A. 6.已知点是曲线上任意一点,记直线(为坐标系原点)的斜率为,则 A .至少存在两个点使得 B .对于任意点都有C .对于任意点都有D .存在点使得【答案】C即至少存在两解,恒成立,所以至多存在一解,所以A 不成立.综合以上分析可得选项C 正确. 故选C .【名师点睛】本题难度较大,考查内容较多,解题时要抓住的几何特征,通过对曲线上点的坐标的分析,得到的大小关系,进而得到的取值范围.同时在解题中还应注意不等式放缩、导数与单调性的运用,逐步达到解题的目的.7.在ABC △中,若sin sin sin 0a A b B c C +-=,则圆22:1C x y +=与直线:0l ax by c ++=的位置关系是A .相切B .相交C .相离D .不确定【答案】A【解析】因为sin sin sin 0a A b B c C +-=,所以2220a b c +-=. 故圆心()0,0C 到直线:0l ax by c ++=的距离1d r ===,故圆22:1C x y +=与直线:0l ax by c ++=相切,故选A .8.若P 是圆()()22:331C x y ++-=上任一点,则点P 到直线距离的最大值是A .B . C.1D .【答案】B(本题也可以由数形结合直接得出)9.已知点()1,Q m -,P 是圆C :()()22244x a y a -+-+=上任意一点,若线段PQ 的中点M 的轨迹方程为()2211x y +-=,则m 的值为A .1B .2C .3D .4【答案】D【解析】设(),P x y ,PQ 的中点为()00,M x y因为点()00,M x y 在圆()2211x y +-=上,所以2211122x y m -+⎛⎫⎛⎫+-= ⎪⎪⎝⎭⎝⎭, 即()()22124x y m -++-=. 将此方程与方程()()22244x a y a -+-+=比较可得()1242a a m =⎧⎪⎨-=--⎪⎩,解得4m =.故选D. 10.过直线:1l y x =+上的点P 作圆C :()()22162x y -+-=的两条切线1l 、2l ,当直线1l 、2l 关于直线:1l y x =+对称时,PC =A .3B .C .1+D .2【答案】B【名师点睛】解答本题的难点是如何理解两条切线12,l l 关于直线:1l y x =+对称,从而将问题转化为CP l ⊥,最终求得点()1,6C 到直线:1l y x =+的距离,即d =,从而使得问题获解.11.已知圆:224430x y x y ++--=,动点在圆:224120x y x +--=上,则12PC C △面积的最大值为 A . B .C .D .【答案】B【解析】因为,所以1C =当时,12PC C △的面积最大,其最大值为max 142S =⨯=,应选B. 12.(2018天津卷)在平面直角坐标系中,经过三点(0,0),(1,1),(2,0)的圆的方程为 .【答案】【名师点睛】求圆的方程,主要有两种方法:(1)几何法:具体过程中要用到初中有关圆的一些常用性质和定理.如:①圆心在过切点且与切线垂直的直线上;②圆心在任意弦的中垂线上;③两圆相切时,切点与两圆心三点共线.(2)待定系数法:根据条件设出圆的方程,再由题目给出的条件,列出等式,求出相关量.一般地,与圆心和半径有关,选择标准式,否则,选择一般式.不论是哪种形式,都要确定三个独立参数,所以应该有三个独立等式. 13.(2018新课标I 卷)直线与圆交于两点,则.【答案】【解析】根据题意,圆的方程可化为,所以圆的圆心为,且半径是2,根据点到直线的距离公式可以求得, 结合圆中的特殊三角形,可知,故答案为.【名师点睛】该题考查的是有关直线被圆截得的弦长问题,在解题的过程中,熟练应用圆中的特殊三角形半弦长、弦心距和圆的半径构成的直角三角形,借助于勾股定理求得结果. 14.若直线与直线之间的距离是,则.【答案】0 【解析】直线与直线之间的距离是,,解得,(负值舍去)则.故答案为.15.(2017江苏)在平面直角坐标系xOy 中,(12,0),(0,6),A B -点P 在圆22:50O x y +=上,若20PA PB ⋅≤,则点P 的横坐标的取值范围是 .【答案】[-【名师点睛】对于线性规划问题,首先明确可行域对应的是封闭区域还是开放区域、分界线是实线还是虚线,其次确定目标函数的几何意义,是求横坐标或纵坐标、直线的截距、两点间距离的平方、直线的斜率、还是点到直线的距离等,最后结合图形确定目标函数的最值或取值范围. 16.设抛物线的焦点为F ,准线为l .已知点C 在l 上,以C 为圆心的圆与y 轴的正半轴相切于点A .若,则圆的方程为 .【答案】【解析】设圆心坐标为,则,焦点,,,,由于圆与轴得正半轴相切,则取,所求圆的圆心为,半径为1,所求圆的方程为.【名师点睛】待定系数法求圆的标准方程,先根据圆心的位置巧设圆心可以起到减元的作用,减轻解方程组的负担,根据题目的要求列出方程组解出圆心坐标和半径.直线和圆的位置关系问题是高考常见题,要学会利用圆心到直线的距离去解决直线与圆有关问题.17.(2018新课标II 理)设抛物线24C y x =:的焦点为F ,过F 且斜率为(0)k k >的直线l 与C 交于A ,B两点,||8AB =. (1)求l 的方程;(2)求过点A ,B 且与C 的准线相切的圆的方程.【答案】(1)1y x =-;(2)22(3)(2)16x y -+-=或22(11)(6)144x y -++=. 【解析】(1)由题意得(1,0)F ,l 的方程为(1)(0)y k x k =->. 设1221(,),(,)A y x y x B ,由2(1),4y k x y x =-⎧⎨=⎩得2222(24)0k x k x k -++=. 216160k ∆=+>,故122224kx k x ++=. 所以122244||||||(1)(1)x k AB AF BF k x +=+=+++=.由题设知22448k k+=,解得1k =-(舍去),1k =. 因此l 的方程为1y x =-.18.(2017新课标III 理)已知抛物线C :22y x =,过点(2,0)的直线l 交C 于A ,B 两点,圆M 是以线段AB 为直径的圆.(1)证明:坐标原点O 在圆M 上;(2)设圆M 过点()4,2P -,求直线l 与圆M 的方程.【答案】(1)见解析;(2)直线l 的方程为20x y --=,圆M 的方程为()()223110x y -+-=;或直线l 的方程为240x y +-=,圆M 的方程为2291854216x y ⎛⎫⎛⎫-++= ⎪ ⎪⎝⎭⎝⎭.(2)由(1)可得()21212122,424y y m x x m y y m +=+=++=+.故圆心M 的坐标为()22,m m +,圆M 的半径r =.由于圆M 过点()4,2P -,因此0AP BP ⋅=,故()()()()121244220x x y y --+++=,即()()1212121242200x x x x y y y y -+++++=, 由(1)可得12124,4y y x x =-=. 所以2210m m --=,解得1m =或12m =-.当1m =时,直线l 的方程为20x y --=,圆心M 的坐标为()3,1,圆M M 的方程为()()223110x y -+-=.当12m =-时,直线l 的方程为240x y +-=,圆心M 的坐标为91,42⎛⎫- ⎪⎝⎭,圆M ,圆M 的方程为2291854216x y ⎛⎫⎛⎫-++=⎪ ⎪⎝⎭⎝⎭.【名师点睛】直线与抛物线的位置关系和直线与椭圆、双曲线的位置关系类似,一般要用到根与系数的关系;在解决直线与抛物线的位置关系时,要特别注意直线与抛物线的对称轴平行的特殊情况.中点弦问题,可以利用“点差法”,但不要忘记验证0∆>或说明中点在曲线内部.(1)设出点的坐标,联立直线与抛物线的方程,由斜率之积为1-可得OA OB ⊥,即得结论; (2)结合(1)的结论求得实数m 的值,分类讨论即可求得直线l 的方程和圆M 的方程. 19.已知点,圆:,过点的动直线与圆交于两点,线段的中点为,为坐标原点.(1)求的轨迹方程; (2)当时,求的方程及的面积 【答案】(1)(2)(2)由(1)可知的轨迹是以点为圆心,为半径的圆,由于,故在线段的垂直平分线上,又在圆上,从而,因为的斜率为3,所以的斜率为, 所以的方程为, 又,到的距离为,所以的面积为.【名师点睛】求轨迹方程的常用方法:(1)直接法:直接利用条件建立, 之间的关系;(2)待定系数法:已知所求曲线的类型,求曲线方程;(3)定义法:先根据条件得出动点的轨迹是某种已知曲线,再由曲线的定义直接写出动点的轨迹方程;(4)代入(相关点)法:动点依赖于另一动点的变化而运动,常利用代入法求动点的轨迹方程.。
高中数学 第2章 平面解析几何初步单元测试 苏教版必修2
第2章 平面解析几何初步(时间:120分钟,满分:160分)一、填空题(本大题共14小题,每小题5分,共70分,请把答案填在题中横线上) 1.已知点A (1,3),B (-1,33),则直线AB 的倾斜角是________.解析:直线AB 的斜率为33-3-1-1=-3,则直线AB 的倾斜角是120°. 答案:120°2.两条平行线l 1:3x +4y -2=0,l 2:ax +6y =5间的距离为________.解析:由l 1∥l 2得a 3=64,a =92,所以l 2的方程为3x +4y -103=0.l 1、l 2间的距离d =|-2+103|5=415. 答案:4153.若方程(2m 2+m -3)x +(m 2-m )y -4m +1=0表示一条直线,则实数m 满足________.解析:2m 2+m -3,m 2-m 不能同时为0,得m ≠1.答案:m ≠14.直线l 经过l 1:x +y -2=0与l 2:x -y -4=0的交点P ,且过线段AB 的中点Q ,其中A (-1,3),B (5,1),则直线l 的方程是________.解析:法一:解方程组⎩⎪⎨⎪⎧x +y -2=0,x -y -4=0,得点P (3,-1),又线段AB 的中点Q (2,2),则直线l 的方程为:y --12--1=x -32-3,即为3x +y -8=0. 法二:设直线l 的方程为x +y -2+λ(x -y -4)=0,又线段AB 的中点Q (2,2),代入所设方程得2-4λ=0,解得λ=12,所以直线l 的方程为x +y -2+12(x -y -4)=0,即3x +y -8=0.答案:3x +y -8=05.设集合M ={(x ,y )|x 2+y 2≤4},N ={(x ,y )|(x -1)2+(y -1)2≤r 2(r >0)},若M ∩N =N ,则实数r 的取值范围是________.解析:由题意得N ⊆M ,则圆(x -1)2+(y -1)2=r 2内切于圆x 2+y 2=4,或者内含于圆x 2+y2=4,由圆心距与半径长的关系可得1+1≤2-r ,解得r ≤2- 2.又r >0,所以实数r 的取值范围是(0,2-2].答案:(0,2-2]6.对于任意实数λ,直线(λ+2)x -(1+λ)y -2=0与点(-2,-2)的距离为d ,则d 的取值范围为________.解析:无论λ取何值,直线都过定点(2,2),而点(2,2)与点(-2,-2)的距离为42,又点(-2,-2)不在已知直线上,故d >0,所以0<d ≤4 2.答案:0<d ≤4 27.圆x 2+y 2-2x -3=0与直线y =ax +1交点的个数为________.解析:直线y =ax +1恒过定点(0,1),而02+12-2×0-3<0,即点在圆内,所以直线与圆相交,有两个交点.答案:28.过点A (4,1)的圆C 与直线x -y -1=0相切于点B (2,1),则圆C 的方程为________. 解析:由题意知A 、B 两点在圆上,∴直线AB 的垂直平分线x =3过圆心.又圆C 与直线y =x -1相切于点B (2,1),∴k BC =-1.∴直线BC 的方程为y -1=-(x -2),即y =-x +3.y =-x +3与x =3联立得圆心C 的坐标为(3,0), ∴r =BC =3-22+0-12= 2.∴圆C 的方程为(x -3)2+y 2=2.答案:(x -3)2+y 2=29.等腰直角三角形ABC 中,∠C =90°,若点A 、C 的坐标分别为(0,4),(3,3),则点B 的坐标是________.解析:设B (x ,y ),根据题意可得⎩⎪⎨⎪⎧k AC ·k BC =-1BC =AC , 即⎩⎪⎨⎪⎧ 3-43-0·y -3x -3=-1x -32+y -32=0-32+4-32. 解得⎩⎪⎨⎪⎧ x =2y =0或⎩⎪⎨⎪⎧ x =4y =6,∴B (2,0)或B (4,6).答案:(2,0)或(4,6)10.在平面直角坐标系xOy 中,若曲线x =4-y 2与直线x =m 有且只有一个公共点,则实数m 等于________.解析:∵曲线x =4-y 2,即为x 2+y 2=4(x ≥0).其图形是如图所示的半圆.∴直线x =m 与半圆有且只有一个公共点时m =2.答案:211.直线x -y +1=0与2x -2y -1=0是圆的两条切线,则该圆的面积是________.解析:∵两平行直线间的距离即为圆的直径.∴2R =|1+12|2=324, ∴R =328, ∴S 圆=πR 2=932π. 答案:932π 12.已知点A (4,-3)与B (2,-1)关于直线l 对称,在l 上有一点P ,使点P 到直线4x +3y -2=0的距离等于2,则点P 的坐标是________.解析:由题意知线段AB 的中点C (3,-2),k AB =-1,故直线l 的方程为y +2=x -3,即y=x -5. 设P (x ,x -5),则2=|4x +3x -17|42+32, 解得x =1或x =277. 即点P 的坐标是(1,-4)或(277,-87). 答案:(1,-4)或(277,-87)13.若圆(x -1)2+(y +1)2=R 2上有且仅有两个点到直线4x +3y =11的距离等于1,则半径R 的取值范围是________.解析:圆心到直线的距离为2,又圆(x -1)2+(y +1)2=R 2上有且仅有两个点到直线4x +3y=11的距离等于1,结合图形可知,半径R 的取值范围是1<R <3.答案:(1,3)14.函数f (x )=(x -2 012)(x +2 013)的图象与x 轴、y 轴有三个交点,有一个圆恰好通过这三个交点,则此圆与坐标轴的另一交点坐标是________.解析:依题意得,函数f (x )=(x -2 012)(x +2 013)的图象与x 轴、y 轴的交点分别是A (-2 013,0)、B (2 012,0)、C (0,-2 012×2 013).设过A 、B 、C 三点的圆与y 轴的另一交点为D (0,y 0),圆的方程是x 2+y 2+Dx +Ey +F =0.令y =0,得x 2+Dx +F =0,此方程的两根即为A 、B 两点的横坐标,∴F =-2 013×2 012.又令x =0,得y 2+Ey -2 013×2 012=0,此方程的二根就是C 、D 两点的纵坐标,∴y 0×(-2 012×2 013)=-2 013×2 012,所以y 0=1,即经过A 、B 、C 三点的圆与y 轴的另一个交点D 的坐标是(0,1).答案:(0,1)二、解答题(本大题共6小题,共90分,解答时应写出文字说明、证明过程或演算步骤)15.(本小题满分14分)(2014·绍兴检测)已知直线l 的倾斜角为135°,且经过点P (1,1).(1)求直线l 的方程;(2)求点A (3,4)关于直线l 的对称点A ′的坐标.解:(1)∵k =tan 135°=-1,∴l :y -1=-(x -1),即x +y -2=0.(2)设A ′(a ,b ), 则⎩⎪⎨⎪⎧ b -4a -3×-1=-1,a +32+b +42-2=0,解得a =-2,b =-1,∴A ′的坐标为(-2,-1).16.(本小题满分14分)(2014·高安高一检测)过圆x 2+y 2=4外一点P (2,1)引圆的切线,求切线方程.解:当切线斜率存在时,设切线的方程为y -1=k (x -2)即:kx -y -2k +1=0, ∵圆心(0,0)到切线的距离是2,∴|-2k +1|1+k2=2,解得k =-34, ∴切线方程为-34x -y +32+1=0, 即3x +4y -10=0.当切线斜率不存在时,又x =2与圆也相切,所以所求切线方程为3x +4y -10=0和x =2.17.(本小题满分14分)已知圆C 1:x 2+y 2-2mx +4y +m 2-5=0与圆C 2:x 2+y 2+2x -2my +m 2-3=0,若圆C 1与圆C 2相切,求实数m 的值.解:对于圆C 1与圆C 2的方程配方,得圆C 1:(x -m )2+(y +2)2=9,圆C 2:(x +1)2+(y -m )2=4,则C 1(m ,-2),r 1=3,C 2(-1,m ),r 2=2,圆C 1与圆C 2相切包括两种情况:两圆外切与两圆内切.(1)当圆C 1与圆C 2相外切时,有C 1C 2=r 1+r 2,即m +12+m +22=5,整理,得m 2+3m -10=0,解得m =-5或m =2;(2)当圆C 1与圆C 2相内切时,有C 1C 2=|r 1-r 2|,即m +12+m +22=1,整理,得m 2+3m +2=0,解得m =-1或m =-2.综上所述,当m =-5或m =-1或m =±2时,圆C 1与圆C 2相切.18.(本小题满分16分)已知圆C :x 2+y 2-2x -4y +m =0,(1)求实数m 的取值范围;(2)若直线l :x +2y -4=0与圆C 相交于M ,N 两点,且OM ⊥ON ,求m 的值.解:(1)由x 2+y 2-2x -4y +m =0得(x -1)2+(y -2)2=5-m ,故5-m >0,即m <5.(2)设M (x 1,y 1),N (x 2,y 2).直线OM ,ON 的斜率显然都存在,由OM ⊥ON ,得y 1x 1·y 2x 2=-1, 即x 1x 2+y 1y 2=0.①由⎩⎪⎨⎪⎧ x +2y -4=0,x 2+y 2-2x -4y +m =0,得5y 2-16y +m +8=0.又因直线l 与圆C 交于M ,N 两点,所以Δ=162-20(m +8)>0,得m <245,且y 1+y 2=165,y 1y 2=m +85,所以x 1x 2=(4-2y 1)(4-2y 2)=16-8(y 1+y 2)+4y 1y 2=4m -165.代入①,得m =85,满足m <245. 所以m =85. 19.(本小题满分16分)已知圆C 经过两点P (-1,-3),Q (2,6),且圆心在直线x +2y -4=0上,直线l 的方程为(k -1)x +2y +5-3k =0.(1)求圆C 的方程;(2)证明:直线l 与圆C 恒相交;(3)求直线l 被圆C 截得的最短弦长.解:(1)设圆C 的方程为x 2+y 2+Dx +Ey +F =0.由条件,得⎩⎪⎨⎪⎧ 1+9-D -3E +F =04+36+2D +6E +F =0-D 2+2×-E 2-4=0,解得⎩⎪⎨⎪⎧D =-4E =-2F =-20, ∴圆C 的方程为x 2+y 2-4x -2y -20=0.(2)证明:由(k -1)x +2y +5-3k =0,得k (x -3)-(x -2y -5)=0,令⎩⎪⎨⎪⎧ x -3=0x -2y -5=0,得⎩⎪⎨⎪⎧x =3y =-1,即直线l 过定点(3,-1), 由32+(-1)2-4×3-2×(-1)-20<0,知点(3,-1)在圆内,∴直线l 与圆C 恒相交.(3)圆心C (2,1),半径为5,由题意知,直线l 被圆C 截得的最短弦长为252-[2-32+1+12]=4 5.20.(本小题满分16分)如图,圆x 2+y 2=8内有一点P (-1,2),AB 为过点P 且倾斜角为α的弦.(1)当α=135°时,求AB ;(2)当弦AB 被点P 平分时,求直线AB 的方程;(3)设过P 点的弦的中点为M ,求点M 的坐标所满足的关系式.解:(1)如图所示,过点O 做OG ⊥AB 于G ,连结OA ,当α=135°时,直线AB 的斜率为-1,故直线AB 的方程为x +y -1=0,∴OG =|0+0-1|2=22. 又∵r =22,∴GA = 8-12=152=302, ∴AB =2GA =30.(2)当弦AB 被点P 平分时,OP ⊥AB ,此时k OP =-2,∴AB 的点斜式方程为y -2=12(x +1), 即x -2y +5=0.(3)设AB 的中点为M (x ,y ),当AB 的斜率存在时,设为k ,OM ⊥AB ,则⎩⎪⎨⎪⎧ y -2=k x +1,y =-1k x , 消去k ,得x 2+y 2-2y +x =0,当AB 的斜率k 不存在时也成立,故过点P 的弦的中点M 的轨迹方程为x 2+y 2-2y +x =0.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习题课
【课时目标】 熟练掌握直线的位置关系(平行、垂直)及距离公式,能灵活应用它们解决有关的综合问题.
1.
三个距离公式⎩⎪⎨⎪⎧
(1
)两点P 1(x 1,y 1),P 2(x 2,y 2)的距离
P 1P 2
= .(2)点P (x 0
,y 0)到直线l :Ax +By +C =0 的距离d = .
(3)平行线l 1
:Ax +By +C 1
=0与l 2
:Ax + By +C 2
=0间的距离d = .
2.三种常见的对称问题 (1)点关于点的对称
点P (x 0,y 0)关于点M (a ,b )的对称点为P ′____________________________________. (2)点关于直线的对称
若两点P 1(x 1,y 1)与P 2(x 2,y 2)关于直线l :Ax +By +C =0对称,则由方程组⎩⎪⎨⎪⎧
A ·x 1+x 22+
B ·y 1+y 22+
C =0,
可得点P 1关于l 对称的点P 2的坐标(x 2,y 2)(其中A ≠0,x 1≠x 2).
(3)线关于点、线的对称
线是点构成的集合,直线的方程是直线上任一点P (x ,y )的坐标x ,y 满足的表达式,故求直线关于点、线的对称,可转化为求该直线上任一点关于点、线的对称.
一、填空题
1.点(3,9)关于直线x +3y -10=0的对称点为__________.
2.和直线3x -4y +5=0关于x 轴对称的直线方程为____________.
3.在直线3x -4y -27=0上到点P (2,1)距离最近的点的坐标是____________. 4.过点(1,3)且与原点的距离为1的直线共有________条.
5.若点(5,b )在两条平行直线6x -8y +1=0与3x -4y +5=0之间,则整数b 的值为________.
6.已知实数x ,y 满足5x +12y =60,
则x 2+y 2-2x -4y +5的最小值是________.
7.点A (4,5)关于直线l 的对称点为B (-2,7),则l 的方程为________________.
8.如图所示,已知△ABC 的顶点是A (-1,-1),B (3,1),C (1,6),直线l 平行于AB ,
且分别交AC 、BC 于E 、F ,△CEF 的面积是△CAB 面积的1
4
,则直线l 的方程为________.
9.设点A (-3,5)和B (2,15),在直线l :3x -4y +4=0上找一点
P,使P A+PB为最小,则这个最小值为________.
二、解答题
10.一条直线被直线l1:4x+y+6=0和l2:3x-5y-6=0截得的线段的中点恰好是坐标原点,求这条直线的方程.
11.已知直线l的方程为3x+4y-12=0,求满足下列条件的直线l′的方程.
(1)l′与l平行且过点(-1,3);
(2)l′与l垂直且l′与两坐标轴围成的三角形面积为4;
(3)l′是l绕原点旋转180°而得到的直线.
能力提升
12.直线2x-y-4=0上有一点P,求它与两定点A(4,-1),B(3,4)的距离之差的最大值.
13.已知M(1,0)、N(-1,0),点P为直线2x-y-1=0上的动点,求PM2+PN2的最小值及取最小值时点P的坐标.
1.在平面解析几何中,用代数知识解决几何问题时应首先挖掘出几何图形的几何条件,把它们进一步转化为代数方程之间的关系求解.
2.关于对称问题,要充分利用“垂直平分”这个基本条件,“垂直”是指两个对称点的连线与已知直线垂直,“平分”是指:两对称点连成线段的中点在已知直线上,可通过这两个条件列方程组求解.
3.涉及直线斜率问题时,应从斜率存在与不存在两方面考虑,防止漏掉情况.
习题课 答案
知识梳理
1.(1)(x 2-x 1)2+(y 2-y 1)2 (2)|Ax 0+By 0+C |
A 2+
B 2
(3)|C 2-C 1|A 2+B 2
2.(1)(2a -x 0,2b -y 0) (2)y 1-y 2x 1-x 2=B
A
作业设计
1.(-1,-3)
解析 设对称点为(x 0,y 0), 则由⎩⎪⎨
⎪⎧
y 0-9x 0-3=3,x 0
+32+3·y 0
+92
-10=0,得⎩
⎪⎨⎪⎧
x 0=-1,
y 0=-3. 2.3x +4y +5=0
解析 直线3x -4y +5=0与x 轴交点为⎝⎛⎭⎫-5
3,0,由对称直线的特征知,所求直线斜率为k =-3
4
.
∴y =-3
4⎝⎛⎭
⎫x +53,即3x +4y +5=0. 3.(5,-3)
解析 当PQ 与已知直线垂直时,垂足Q 即为所求. 4.2
解析 当直线斜率不存在时,直线方程为x =1,原点到直线距离为1,满足题意.当直线斜率存在时,设直线方程为y -3=k (x -1)即kx -y +3-k =0.由已知
|3-k |k 2+1
=1,
解得k =4
3
,满足题意.故共存在2条直线.
5.4
解析 把x =5代入6x -8y +1=0得y =31
8,
把x =5代入3x -4y +5=0得y =5,∴31
8<b <5.
又∵b 为整数,∴b =4. 6.3113 解析 x 2+y 2-2x -4y +5 =
(x -1)2+(y -2)2,
它表示点(x ,y )与(1,2)之间的距离,
两点距离的最小值即为点(1,2)到直线5x +12y =60的距离,
∴d =|1×5+2×12-60|13=3113
.
7.3x -y +3=0 8.x -2y +5=0
解析 由已知,直线AB 的斜率k =1
2,
∵EF ∥AB ,∴直线EF 的斜率为k =1
2.
∵△CEF 的面积是△CAB 面积的1
4
,
∴E 是CA 的中点,∴点E 的坐标⎝⎛⎭
⎫0,52, 直线EF 的方程是y -52=1
2
x ,即x -2y +5=0.
9.513
解析 设点A 关于直线l 的对称点A ′的坐标为(a ,b ),则由AA ′⊥l 且AA ′被l 平分, 得⎩⎪⎨
⎪⎧
b -5a +3×34=-1,3×a -32-4×b +52+4=0.
解之得a =3,b =-3.∴点A ′的坐标为(3,-3),
∴(P A +PB )min =A ′B =
(3-2)2+(-3-15)2=513.
10.解 设所求直线与直线l 1交于A (x 0,y 0),它关于原点的对称点为B (-x 0,-y 0),
且B 在直线l 2上,由⎩
⎪⎨⎪⎧
4x 0+y 0+6=0,-3x 0+5y 0-6=0,
解得⎩⎨⎧
x 0=-36
23,
y 0
=6
23,
∴所求直线方程为y =6
23-3623x =-1
6x ,
即x +6y =0.
11.解 (1)直线l :3x +4y -12=0,k l =-3
4
,
又∵l ′∥l ,∴k l ′=k l =-3
4.
∴直线l ′:y =-3
4(x +1)+3,即3x +4y -9=0.
(2)∵l ′⊥l ,∴k l ′=4
3
.
设l ′与x 轴截距为b ,则l ′与y 轴截距为-4
3
b ,
由题意可知,S =12|b |·
⎪⎪⎪
⎪
-43b =4,
∴b =±6.
∴直线l ′:y =43(x +6)或y =4
3(x -6).
(3)∵l ′是l 绕原点旋转180°而得到的直线, ∴l ′与l 关于原点对称.
任取点(x 0,y 0)在l 上,则在l ′上对称点为(x ,y ). x =-x 0,y =-y 0,则-3x -4y -12=0. ∴l ′为3x +4y +12=0.
12.解 找A 关于l 的对称点A ′,A ′B 与直线l 的交点即为所求的P 点. 设A ′(a ,b ),
则⎩⎪⎨
⎪⎧
b +1a -4×2=-1
2×4+a 2-b -12-4=0
.解得⎩
⎪⎨⎪⎧
a =0
b =1,
所以A ′B =(4-1)2+(3-0)2=32.
13.解 ∵P 为直线2x -y -1=0上的点,∴可设P 的坐标为(m,2m -1),由两点的距离公式得
PM 2+PN 2=(m -1)2+(2m -1)2+(m +1)2+(2m -1)2=10m 2-8m +4.(m ∈R ) 令f (m )=10m 2-8m +4
=10⎝⎛⎭⎫m -252+125≥125
, ∴当m =2
5
时,PM 2+PN 2取最小值,此时P ⎝⎛⎭⎫25,-15.。
