二次根式经典复习资料
二次根式知识点及典型例题(含答案)

4、不会比较根式的大小5、不会利用二次根式的非负性6、对最简二次根式的条件掌握不牢八、经典例题例1、求下列各数的平方根与算术平方根( )A.36B.81121 C.2-(5) D.41【答案】A.2=36±(6)∴36的平方根为6±,即6± ∴36的算术平方根为6,即B.2981=11121±()∴81121的平方根为911±,即911±∴81121的算术平方根为911,即911 C.25=25±()∴2-(5)的平方根为5±,即5± ∴2-(5)的算术平方根为5,即D.()241=41±∴41的平方根为 ∴41【解析】一个正数的平方根有两个,它们互为相反数,解答本题注意解题步骤的规范书写,不是完全平方数的正数,它的平方根只能用含有根号的形式表示.练习1、计算:(1 (2)【答案】(1)211=121(2)20.9=0.810.9±表示121的算术平方根,表示0.81的平方根,、的意义是解答本题的关键例2、如果一个正数的平方根为3a-5和2a-10,求这个正数【答案】由题意得,3a-5+2a-10=0得a=3∴3a-5=4∴这个数为24=16【解析】一个正数的平方根有两个,它们互为相反数,而互为相反数的两个数相加为0,故(3a-5)+(2a-10)=0.求出a后,可知3a-5与2a-10的值,在考虑哪个正数的平方根是3a-5,2a-10的值即可。
练习1、x为何值时,下列各式有意义。
【答案】解:A.10x-≥,即1x≥有意义B.10x-≥且0x≥,即01x≤≤有意义C.10x+>,即1x>-D.230x+≥,即x都有意义【解析】a≥例3、【答案】解252736<<<<即56<<的整数部分是5【解析】处在哪两个完全平方数之间.例4、:x y【答案】解:33y-1和互为相反数3y-1∴和1-2x互为相反数3y-1+1-2x=0∴:=3:2x y∴互为相反数,则a和b互为相反数,所以本题中3y-1与1-2x 互为相反数例5、实数0.5的算术平方根等于().D.1 2【答案】C【解析】理解算术平方根的意义,把二次根式化成最简形式是解答本题的关键.例6、的算术平方根是()A. 4±B. 4C. 2±D. 2【答案】D【解析】4的算术平方根,4的算术平方根为2.例7、根据下列运算正确的是()3=2 C. (x+2y)2=x2+2xy+4y2 D. A.x6+x2=x3 B.√−8√18−√8=√2【答案】解:A、本选项不能合并,错误;3=-2,本选项错误;B、√-8C、((x+2y)2=x2+2xy+4y2,本选项错误;D、√18-√8=3√2-2√2=√2,本选项正确.故选D【解析】此题考查了完全平方公式,合并同类项,以及负指数幂,幂的乘方,熟练掌握公式及法则是解本题的关键.例8、)【答案】B综合练习简单1. 式子在实数范围内有意义,则x的取值范围是()A.<1 B.≥1 C.≤-1 D.<-1【答案】B【解析】由二次根式的意义,知:x-1≥0,所以x≥1.2.如果代数式有意义,那么x的取值范围是()A.x≥0 B.x≠1 C.x>0 D.x≥0且x≠1【答案】D解:根据题意得:x≥0且x﹣1≠0.解得:x≥0且x≠1.故选D.【解析】代数式√x有意义的条件为:x﹣1≠0,x≥0.即可求得x的范围.x-13.要使式子2-x有意义,则x的取值范围是()A.x>0 B.x≥﹣2 C.x≥2 D.x≤2【答案】D解:根据题意得,2﹣x≥0,解得x≤2.【解析】根据被开方数大于等于0列式计算即可得解.4. 下列计算正确的是()=√2 D.3+2√2=5√2 A.4√3-3√3=1 B.√2+√3=√5 C.2√12【答案】C【解析】 A、4√3-3√3=√3,原式计算错误,故本选项错误;B、√2与√3不是同类二次根式,不能直接合并,故本选项错误;=√2,计算正确,故本选项正确;C、2√12D、3+2√2≠5√2,原式计算错误,故本选项错误;根据二次根式的化简及同类二次根式的合并,分别进行各选项的判断即可.5. 若,则=【答案】6【解析】原方程变为:,所以,,由得:=3,两边平方,得:=7,所以,原式=7-1=6中等题1.结果是。
二次根式复习

第十六章 二次根式考点一:二次根式的概念与性质:1a ≥0)的式子叫做二次根式。
其中a 为被开方数,为非负数。
“”为二次根号。
2、二次根式的性质:①双重非负性:__________________ ②())0__(__________2≥=a a③⎪⎩⎪⎨⎧==____________________________________2a 例题1:(利用被开方数的非负性求字母的范围或值。
)x 取何值时,下列式子有意义?①2)1(--x ②x x -+-44 ③358-x x ④112-+x x变式:①象限。
)在第(有意义,则若式子_____,1b a P aba +-②若x ,y 为实数,且y+x +y 的值。
例题2:(利用二次根式的性质进行化简求值) ①4124)2(22+-+-x x x 化简②的取值范围。
求若x x x x ,03962=+-+-2210b b -+=,则221||a b a +-=______________.变式:b a c c b a ABC c b a ---+-∆2,,2)(的三边长,化简为已知:考点2:二次根式的乘除次根式。
计算结果要化成最简二反之:则二次根式的除法:若成立,则反之:若,则二次根式的乘法:若⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧>≥==≥≥≥⋅==⋅≥≥)0,0(,0__,00,0______,0,0b a b a b a b a b a b a b a b a ab b a b a 最简二次根式:①_______________________________________________________________. ②_______________________________________________________________.例题3:计算与化简61211÷① yx x y 233⋅② ③)0,0(96223≥≥++b a ab b a a )(ab b a ab ÷④ ⑤yx x 327 ⑥⎪⎭⎫⎝⎛⨯÷-5431821834变式:化简:①a a 1- ②a a 1- ③5116 ④23b a -变式:比较5334与的大小。
二次根式 基础知识详解+基本典型例题解析

【基本典型例题】(2) 类型一、二次根式的乘除
1. 计算:(1)(2014 秋•闵行区校级期中) ×(﹣2 )÷
.
(2)(2014 春·高安市期中) a 8a 2 a 2 1 2a 2a a
【答案与解析】 解:(1) ×(﹣2 )÷
举一反三: 【变式】下列式子中二次根式的个数有( ).
(1)
1 ;(2) 3
3 ;(3)
x2 1 ;(4)3 8 ;(5)
( 1)2 ;(6) 1 x( x 1 ) 3
A.2 B.3 C.4 D.5 【答案】B.
2. (2016•贵港)式子
在实数范围内有意义,则 x 的取值范围是( )
= ×(﹣2 )×
=﹣
=﹣
=﹣ .
(2)原式= a 8a2 a2 1 2a 2a a
2 2a2 a2 2 2a 2a 2a a
2
2a2
2a a2
2a a
4 2.
【总结升华】根据二次根式的乘除法则灵活运算,注意最终结果要化简.
举一反三:
【变式】 2
a2 b2 6x2
即原式= a b c a c b b c a = a b c
【总结升华】重点考查二次根式的性质:
的同时,复习了
三角形三边的性质.
二、二次根式的乘除基础知识讲解+基本典型例题解析
【学习目标】 1、 掌握二次根式的乘除法法则和化简二次根式的常用方法,熟练进行二次根式的 乘除运算. 2、 了解最简二次根式的概念,能运用二次根式的有关性质进行化简.
.
初中数学二次根式基础知识点(共6篇)

初中数学二次根式根底知识点〔共6篇〕篇1:初中数学二次根式根底知识点 1.二次根式概念:式子a(a≥0)叫做二次根式。
2.最简二次根式:必须同时满足以下条件:3.同类二次根式:二次根式化成最简二次根式后,假设被开方数一样,那么这几个二次根式就是同类二次根式。
4.二次根式的_质:a(a0)22(1)(a)=a(a≥0);(2)aa0(a=0);5.二次根式的运算:a(a0)(1)因式的外移和内移:假如被开方数中有的因式可以开得尽方,那么,就可以用它的算术根代替而移到根号外面;假如被开方数是代数和的形式,那么先解因式,变形为积的形式,再移因式到根号外面,反之也可以将根号外面的正因式平方后移到根号里面.(2)二次根式的加减法:先把二次根式化成最简二次根式再合并同类二次根式.(3)二次根式的乘除法:二次根式相乘(除),将被开方数相乘(除),所得的积(商)仍作积(商)的被开方数并将运算结果化为最简二次根式单项式和多项式统称为整式。
1.单项式:1)数与字母的乘积这样的代数式叫做单项式。
单独的一个数或字母(可以是两个数字或字母相乘)也是单项式。
2)单项式的系数:单项式中的数字因数及_质符号叫做单项式的系数。
3)单项式的次数:一个单项式中,所有字母的指数的和叫做这个单项式的次数。
2.多项式:1)几个单项式的和叫做多项式。
在多项式中,每个单项式叫做多项式的项,其中不含字母的项叫做常数项。
一个多项式有几项就叫做几项式。
2)多项式的次数:多项式中,次数最高的项的次数,就是这个多项式的次数。
3.多项式的排列:1).把一个多项式按某一个字母的指数从大到小的顺序排列起来,叫做把多项式按这个字母降幂排列。
2).把一个多项式按某一个字母的指数从小到大的顺序排列起来,叫做把多项式按这个字母升幂排列。
由于单项式的项,包括它前面的_质符号,因此在排列时,仍需把每一项的_质符号看作是这一项的一局部,一起挪动初中数学一元二次方程常见考法1.考察一元二次方程的根与系数的关系(韦达定理):这类题目有着解题规律性强的特点,题目设置会很灵敏,所以一直很吸引命题者。
二次根式知识点总复习附解析

二次根式知识点总复习附解析一、选择题1.下列各式中,运算正确的是( )A .632a a a ÷=B .325()a a =C .=D =【答案】D【解析】【分析】利用同底数幂的除法、幂的乘方、二次根式的加法和二次根式的除法法则计算.【详解】解:A 、a 6÷a 3=a 3,故不对;B 、(a 3)2=a 6,故不对;C 、和不是同类二次根式,因而不能合并;D 、符合二次根式的除法法则,正确.故选D .2.下列各式计算正确的是( )A 1082==-= B .()()236==-⨯-=C 115236==+=D .54==- 【答案】D【解析】【分析】根据二次根式的性质对A 、C 、D 进行判断;根据二次根式的乘法法则对B 进行判断.【详解】解:A 、原式,所以A 选项错误;B 、原式,所以B 选项错误;C 、原式C 选项错误;D 、原式54==-,所以D 选项正确. 故选:D .【点睛】本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.3.已知352x x -+-=的结果是( ) A .4B .62x -C .4-D .26x - 【答案】A【解析】由352x x -+-=可得30{50x x -≥-≤ ,∴3≤x ≤5=x-1+5-x=4,故选A.4.当3x =-时,二次根m 等于( )A B C D 【答案】B【解析】解:把x =﹣3代入二次根式得,原式=,依题意得:=.故选B .5.下列计算中,正确的是( )A .=B 1b =(a >0,b >0)C =D .=【答案】B【解析】 【分析】a≥0,b≥0a≥0,b >0)进行计算即可. 【详解】A 、B 1b (a >0,b >0),故原题计算正确;C ,故原题计算错误;D 32故选:B .【点睛】此题主要考查了二次根式的乘除法,关键是掌握计算法则.6.已知n 是整数,则n 的最小值是( ).A .3B .5C .15D .25 【答案】C【解析】【分析】 【详解】解:=Q 也是整数,∴n 的最小正整数值是15,故选C .7.下列各式计算正确的是( )A .2+b =2bB =C .(2a 2)3=8a 5D .a 6÷ a 4=a 2 【答案】D【解析】解:A .2与b 不是同类项,不能合并,故错误;B 不是同类二次根式,不能合并,故错误;C .(2a 2)3=8a 6,故错误;D .正确.故选D .8.下列计算结果正确的是( )A 3B ±6CD .3+=【答案】A【解析】【分析】原式各项计算得到结果,即可做出判断.【详解】A、原式=|-3|=3,正确;B、原式=6,错误;C、原式不能合并,错误;D、原式不能合并,错误.故选A.【点睛】考查了实数的运算,熟练掌握运算法则是解本题的关键.9.a的值为()A.2 B.3 C.4 D.5【答案】D【解析】【分析】根据两最简二次根式能合并,得到被开方数相同,然后列一元一次方程求解即可.【详解】根据题意得,3a-8=17-2a,移项合并,得5a=25,系数化为1,得a=5.故选:D.【点睛】本题考查了最简二次根式,利用好最简二次根式的被开方数相同是解题的关键.10.+在实数范围内有意义的整数x有()A.5个B.3个C.4个D.2个【答案】C【解析】∴30430xx+>⎧⎨-≥⎩,解得:433x-<≤,又∵x要取整数值,∴x的值为:-2、-1、0、1.即符合条件的x的值有4个.故选C.11.下列二次根式中是最简二次根式的是()DA B C【答案】B【解析】【分析】根据最简二次根式的定义(被开方数不含有能开的尽方的因式或因数,被开方数不含有分数),判断即可.【详解】解:A,故本选项错误;BCD,故本选项错误.故选:B.【点睛】本题考查对最简二次根式的理解,能熟练地运用定义进行判断是解此题的关键.12.下列计算正确的是()A6=B=C.2=D5=-【答案】B【解析】【分析】根据二次根式的混合运算顺序和运算法则逐一计算可得.【详解】A====C.=,此选项计算错误;5=,此选项计算错误;故选:B.【点睛】本题主要考查二次根式的混合运算,解题的关键是熟练掌握二次根式的混合运算顺序和运算法则.13.1x =-,那么x 的取值范围是( )A .x≥1B .x>1C .x≤1D .x<16【答案】A【解析】【分析】根据等式的左边为算术平方根,结果为非负数,即x-1≥0求解即可.【详解】由于二次根式的结果为非负数可知:x-1≥0,解得,x≥1,故选A.【点睛】本题利用了二次根式的结果为非负数求x 的取值范围.14.a 的取值范围为()n nA .0a >B .0a <C .0a =D .不存在【答案】C【解析】试题解析:根据二次根式的性质,被开方数大于等于0,可知:a≥0,且-a≥0. 所以a=0.故选C .15.a 的取值范围是( )A .a >1B .a ≥1C .a =1D .a ≤1 【答案】B【解析】【分析】根据二次根式有意义的条件可得a ﹣1≥0,再解不等式即可.【详解】由题意得:a ﹣1≥0,解得:a≥1,故选:B .【点睛】此题主要考查了二次根式有意义的条件,关键是掌握二次根式中的被开方数是非负数.16.婴儿游泳是供婴儿进行室内或室外游泳的场所,婴儿游泳池的样式多种多样,现已知积为( )A .B .C .D . 【答案】D【解析】【分析】 根据底面积=体积÷高列出算式,再利用二次根式的除法法则计算可得.【详解】故选:D .【点睛】考核知识点:二次根式除法.理解题意,掌握二次根式除法法则是关键.17.已知1a b ==+,a b 的关系是( ) A .a b =B .1ab =-C .1a b =D .=-a b 【答案】D【解析】【分析】根据a 和b 的值去计算各式是否正确即可.【详解】A. 1a b -===B. 1ab =≠-,错误;C. 1ab =≠,错误;D. 10a b +++=,正确; 故答案为:D .【点睛】本题考查了实数的运算问题,掌握实数运算法则是解题的关键.18.若x2+在实数范围内有意义,则x的取值范围在数轴上表示正确的是()A.B.C.D.【答案】D【解析】【分析】根据二次根式有意义的条件:被开方数为非负数可得x+2≥0,再解不等式即可.【详解】2x+∴被开方数x+2为非负数,∴x+2≥0,解得:x≥-2.故答案选D.【点睛】本题考查了二次根式有意义的条件,解题的关键是熟练的掌握二次根式有意义的条件.19.2x-有意义的x的取值范围()A.x>2 B.x≥2C.x>3 D.x≥2且x≠3【答案】D【解析】试题分析:分式有意义:分母不为0;二次根式有意义,被开方数是非负数.根据题意,得20{30xx-≥-≠解得,x≥2且x≠3.考点:(1)、二次根式有意义的条件;(2)、分式有意义的条件20.5130.5a22a b-22x y+( )A.2个B.3个C.4个D.5个【答案】A【解析】51 333,不是最简二次根式;,不是最简二次根式;2-,不是最简二次根式;是最简二次根式.共有2个最简二次根式.故选A.点睛:最简二次根式必须满足两个条件:(1)被开方数不含分母;(2)被开方数不含能开得尽方的因数或因式.。
二次根式复习

二次根式(一)(1)注:二次根式的双重非负性是指:⎩⎨⎧____________________________________(2)注:分母有理化的两种类型⎩⎨⎧____________________________________(3)几个二次根式 ,则称他们为同类二次根式。
判断同类二次根式的过程是: (4)二次根式的性质①20,a ≥=若则;③= (0,0)a b ≥≥()()a a a⎧==⎨-⎩0,0)a b =≥ (5)二次根式的运算①加减法:先化为 ,在合并同类二次根式;②乘法:应用公式; ③除法:应用公式④二次根式的运算仍满足运算律,也可以用多项式的乘法公式来简化运算。
(二)1.那么x 取值范围是() A 、x ≤2 B. x <2 C. x ≥2 D. x >2 2. 下列各式属于最简二次根式的是( ) A3.) A .①和③ B .②和③ C .①和④ D .③和④ 4. x 为何值时,下列各式在实数范围内有意义 (1; (2(33.判别下列二次根式中,哪些是同类二次根式:0),3b - 4. 化简与计算2)x7)2m -⑤22-;⑥(1. 若式子12--x x 有意义,则x 的取值范围为( ) A .x ≤2 B .x ≤2且x ≠1 C .x ≥2 D .x ≥1 2. 若,则x-y 的值为( )A .-1 B .1 C .2D .33. 如果代数式mnm 1+-有意义,那么,直角坐标系中点P (m ,n )的位置在()A .第一象限B .第二象限C .第三象限D .第四象限 4. 如果等式(x+1)0=1和()x x 32232-=-同时成立,那么需要的条件是( )A .x ≠-1B .x <32且x ≠-1 C .x ≤32或x ≠1 D .x ≤32且x ≠-1 5. 若x <2,化简()x x -+-322的正确结果是()A .-1B .1C .2x-5D .5-2x6. 如果表示a ,b 两个实数的点在数轴上的位置如图所示,那么化简()b a b a -++2的结果等于()A .-2bB .2bC .-2aD .2a7. 下列根式xy 2、8、2ab 、53xy 、y x +、21中,最简二次根式的个数是()A .2个B .3个C .6个D .5个 8. 若624m -与432-m 可以合并,则m 的值不可以是( )A .1320B .2651 C .813 D .479. 下面有四对二次根式:y x 58和xy 2,xy 2和224yx ,xy 2和y x 321,2xy 和yx xy +,其中同类二次根式共有( )A .0对 B .1对 C .2对 D .3对10. 在下列各式中,二次根式b a -的有理化因式是() A .b a +B .b a + C .b a - D .b a -11. 已知a=12+,b=121-,则a 与b 的关系是()A .a=bB .ab=1C .a=-bD .ab=-112计算:()()()02013201222323232----+⋅- ()()1211612220133121-+⨯-+++⎪⎭⎫⎝⎛- 13. 先化简,再求值:242122+-÷⎪⎭⎫ ⎝⎛+--x x x x (x−2−,其中x =−4+3.11+-÷x 15. 如图所示的Rt △ABC 中,∠B=90°,点P 从点B 开始沿BA 边以1厘米/秒的速度向点A 移动;同时,点Q 也从点B 开始沿BC 边以2厘米/秒的速度向点C 移动.问:几秒后△PBQ的面积为35平方厘米?PQ 的距离是多少厘米?(结果用最简二次根式表示)。
2024年中考数学复习专题讲义:二次根式(含答案)

2024年中考数学复习专题讲义:二次根式知识点讲解1、二次根式的定义 一般地,形如a (a ≥0)的式子叫做二次根式。
2、二次根式的基本性质①2a =(a ≥0); a = (a ≥0); a = (a 取全体实数)。
3、二次根式的乘除(1)二次根式的乘法:①ab b a =⋅; ②b a ab ⋅= (a ≥0, b ≥0)。
(2)二次根式的除法:= = (a ≥0, b >0)。
4、最简二次根式 最简二次根式满足的条件:①被开方数不含分母;②被开方数中不含能开得尽方的因数或因式。
5、二次根式的加减二次根式加减时,可以先将二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并。
专题练习一、选择题1.下列二次根式中,是最简二次根式的是( )A .√12B .√8C .√13D .√0.22.若二次根式√x +2有意义,则x 的取值范围是( ).A .x >−2B .x ≥−2C .x <−2D .x ≥23.化简√(−3)2的结果是( )A .−3B .±3C .3D .94.估计(√27−√6)÷√3的值应在( )A .0到1之间B .1到2之间C .2到3之间D .3到4之间5.下列计算错误的是( )A .3√2−√2=3B .√60÷√5=2√3C .√25a +√9a =8√aD .√14×√7=7√26.若 x =√m −√n,y =√m +√n ,则 xy 的值是( ).A .2√mB .m −nC .m +nD .2√n 7.计算:√12×√13−√8÷√2的结果是( ) A .2 B .0 C .-2 D .−√28.用四张大小一样的长方形纸片拼成一个正方形 ABCD (如图),它的面积是 48, 已知长方形的一边长 AE =3√3, 图中空白部分是一个正方形,则这个小正方形的周长为( )A .2√3B .4√3C .8√3D .16√3二、填空题9.化简√3= 10.若√a +√3=3√3,则a = . 11.计算(2√2+1)(2√2−1)的结果等于 .12.若二次根式√x+3x 有意义,则x 的取值范围为 .13.当m = 时,二次根式√m −2取到最小值.三、解答题14.计算 (1)√16÷√2−√13×√6; (2)32√4x +2√x 9−x √1x +4√x4.15.已知2x =+2y =(1)试求22x y +的值; (2)试求x y y x-的值. 16.某居民小区有一块形状为长方形ABCD 的绿地,长方形绿地的长BC 为√162m ,宽AB 为√128m (即图中阴影部分),长方形花坛的长为(√13+1)m ,宽为(√13−1)m ,(1)长方形ABCD 的周长是多少?(结果化为最简二次根式)(2)除去修建花坛的地方.其他地方全修建成通道,通道上要铺上造价为50元每平方米的地砖,若铺完整个通道,则购买地砖需要花费多少元?17.已知x=2−√3,y=2+√3.(1)求x2+y2−xy的值;(2)若x的小数部分是a,y的整数部分是b,求ax−by的值.参考答案1.C2.B3.C4.B5.A6.B7.B8.C9.√33 10.1211.712.x ≥−3且x ≠013.214.解:(1)原式=√16÷2−√13×6=2√2−√2=√2;(2)原式=3√x +23√x −√x +2√x=143√x .15.(1)解:∵2x =, 2y =∴x+y=22+,xy=(22+=1 ∴()2222242114x y x y xy +=+-=-⨯= ;(2)解:∵2x =+,2y =-∴x+y=22+,x-y=((2222--=+=xy=(22=1∴()()22x y x yx y x yy x xy xy+---====16.(1)解:长方形ABCD的周长=2(√162+√128)=2(9√2+8√2)=34√2(m),答:长方形ABCD的周长是34√2m;(2)解:购买地砖需要花费=50[9√2×8√2−(√13+1)(√13−1)]=50(144−13+1)=50×132=6600(元)答:购买地砖需要花费6600元.17.(1)解:∵x=2−√3,y=2+√3,∴xy=(2−√3)(2+√3)=4−3=1,(x−y)2=(2−√3−2−√3)2=(−2√3)2=12,∴x2+y2−xy=(x−y)2+xy=12+1=13;(2)解:∵1<3<4,∴1<√3<2,∴3<2+√3<4,∴2+√3的整数部分是3,∴b=3,∵1<√3<2,∴−2<−√3<−1,∴0<2−√3<1,∴2−√3的整数部分是0,小数部分=2−√3−0=2−√3,∴a=2−√3,∴ax−by=(2−√3)(2−√3)−3(2+√3)=7−4√3+6−3√3=13−7√3,∴ax−by的值为13−7√3.)解:①(30x -2)x -②0020x x -22))(2)x -,又232x -+30x -+代数式当2x =时,代数式。
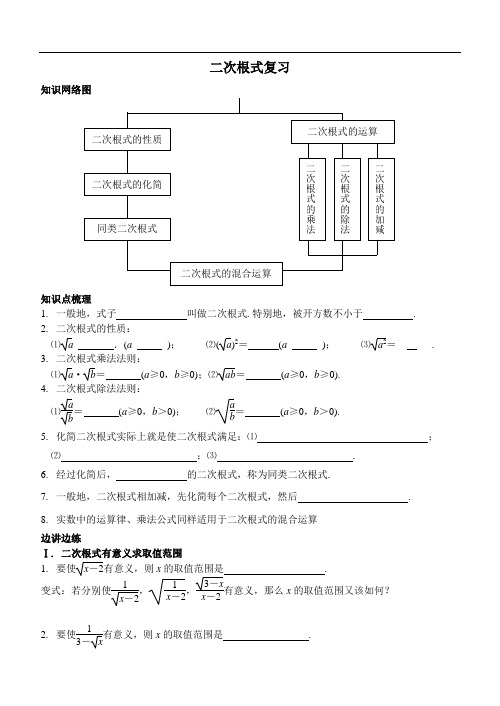
八年级上册数学-二次根式复习
二次根式复习知识网络图知识点梳理1. 一般地,式子 叫做二次根式.特别地,被开方数不小于 .2. 二次根式的性质:⑴a .(a ); ⑵(a )2= (a ); ⑶a 2=__ ___. 3. 二次根式乘法法则:⑴a ·b = (a ≥0,b ≥0);⑵ab = (a ≥0,b ≥0). 4. 二次根式除法法则: ⑴ab= (a ≥0,b >0); ⑵ab= (a ≥0,b >0). 5. 化简二次根式实际上就是使二次根式满足:⑴ ; ⑵ ;⑶ . 6. 经过化简后, 的二次根式,称为同类二次根式.7. 一般地,二次根式相加减,先化简每个二次根式,然后 . 8. 实数中的运算律、乘法公式同样适用于二次根式的混合运算 边讲边练Ⅰ. 二次根式有意义求取值范围1. 要使x -2有意义,则x变式:若分别使1x -2,1x -2,2. 要使13-x有意义,则x 的取值范围是 .3. 使x +1,1x,(x -3)0三个式子都有意义的x 的取值范围是 . 4. 使x +1·x -1=x 2-1成立的条件 ; 1-xx -2 =1-x x -2成立的条件是 .5. 若y =2x -5+5-2x -3. 则2xy = .Ⅱ. 二次根式的非负性求值1. 已知a +2+||b -1=0,那么(a +b )2017= .2. 已知x ,y 是实数,且3x +4+y 2-6y +9=0,则xy = .3. 若||4x -8+x -y -m =0,当y >0时,则m 的取值范围 .4. 若a -3与2-b 互为相反数,那么代数式-1a +6b的值为 . 5. 已知△ABC 的三边a 、b 、c 满足a 2+b +||c -1-2=10a +2b -4-22,则△ABC 为 . Ⅲ. 利用公式a 2=||a 化简1. (-7)2= ;(2)(3-π)2= ; (3) 62=2. 已知x <1,则化简x 2-2x +1的结果= ; 若a <0,化简||a -3-a 2= .3. 当a =2时,代数式a +1-2a +a 2= ; 化简(a -1)11-a= . 5. (a -3)2=3-a 成立,则a 的取值范围是______.6. 若x 3+4x 2=-x x +4,则x 的取值范围是 .7. 若||x -1=12,则代数式1x -x 2-2+1x2的值为 .8. 已知实数a 、b 、c 在数轴上的位置如图所示,试化简(a +c )2-||b -c .9. │+(x +3)2 +x 2-10x +25.Ⅳ. 最简与同类二次根式1. 下列各式中,不能再化简的二次根式是 ( )A .3a 2B .23C .24D .302. 下列各式中,是最简二次根式是 ( )A .8B .70C .99D .1x3. 下列是同类二次根式的一组是 ( )A .12,-32,18B .5,75,1245C .4x 3,22xD .a 1a,a 3b 2c5. 化简后,根式b -a3b 和2b -a +2 是同类根式,那么a =_____,b =______.Ⅴ.二次根式的运算 1. 化简:⑴312= ;⑵15+16= ;⑶18a= . 2. 计算:212-613+8= . 3. 计算12(2-3)= .4. 计算⑴(2+3)(2-3)= ; ⑵(5-2)2017( 5+2)2017= .5.下列各式①33+3=63;②177=1;③2+6=8=22;④243=22,其中错误的有( )A .3个B .2个C .1个D .0个6.下列各式计算正确的是 ( ) A .2+3= 5 B .2+2=2 2 C .33-2=2 2 D .12-102=6- 5 7. 计算: ⑴32-212-13-62⑵239x +6x4-2x 1x⑶(48-413)-(313-40.5) ⑷(218-18)-(12+2-213)⑸23x 18x +12x x 8-x 22x 3⑹(32-45)2 ⑺(3-22)(22-3)⑻(1-23)(1+23)-(1+3)2 ⑼(3+2-5)(3―2―5)(101-︒-+ (11)38x -2x x 2+4550x(12)当81.0,41==y x 时,求31441y yx y x x ---的值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第七讲 二次根式的运算式子a (a ≥0)叫二次根式,二次根式的运算是以下列运算法则为基础. (1)c b a c b c a )(±=± (c ≥0); (2)ab b a =⋅ (0,0≥≥b a ); (3)ba b a =(0,0>≥b a );(4)22)(a a =(≥a 0).同类二次根式,有理化是二次根式中重要概念,它们贯穿于二次根式运算的始终,因为二次根式的加减实质就是合并同类二次根式,二次根式除法、混合运算常用到有理化概念.二次根式的运算是在有理式(整式、分式)运算的基础上发展起来的,常常用到有理式运算的方法与技巧,如换元、字母化、拆项相消、分解相约等. 例题求解 【例1】 已知254245222+-----=xx x x y ,则22y x += . (重庆市竞赛题)思路点拨 因一个等式中含两个未知量,初看似乎条件不足,不妨从二次根式的定义入手. 注: 二次根式有如下重要性质:(1)0≥a ,说明了a 与a 、n a 2一样都是非负数;(2) a a =2)( (≥a 0),解二次根式问题的途径——通过平方,去掉根号有理化; (3) a a =2)(,揭示了与绝对值的内在一致性.著名数学教育家玻利亚曾说,“回到定义中去”,当我们面对条件较少的问题时,记住玻利亚的忠告,充分运用概念解题.提示:22222205420,262045x x x y x y x x⎧-≥⎪⎪-→-==→+=⎨-⎪≥⎪-⎩ 【例2】 化简22)1(111+++n n ,所得的结果为( )(武汉市选拔赛试题)A .1111+++n nB .1111++-n nC .1111+-+n nD .1111+--n n思路点拔 待选项不再含根号,从而可预见被开方数通过配方运算后必为完全平方式形式.提示:原式111n n n +==-+ (C )【例3】计算: (1))23)(36(23346++++; (2(3)4947474917557153351331++++++++ ;(4思路点拨 若一开始就把分母有理化,则使计算复杂化,观察每题中分子与分母的数字特点,通过分拆、分解、一般化、配方等方法寻找它们的联系,以此为解题的突破口.(1)原式===+(2)原式=(55==--=(3==12===原式11113(()2217747=+++=-=(4====【例4】 (1)化简324324-++; (北京市竞赛题)(2)计算223810++ (“希望杯”邀请赛试题)(3) 计算1212--+-+a a a a . (湖北省孝感市“英才杯”竞赛题) 思路点拨 (1)把4+23万与4—23分别化成一个平方数化简,原式11=+=由于4+23与4—23是互为有理化因式,因此原式平方后是一个正整数,我们还可以运用这一特点求解;原式3423=-21612==-==(2)原式==242(2)4+=+(3)通过配方可以简化一重根号,本题的关键是就a 的取值情况讨论,解决含根号、绝对值符号的综合问题.原式=2112a a ⎧≤≤≤⎪=+-=⎨>⎪⎩ 1,即12时,即时 【例5】 已知521332412---=----+c c b a b a ,求c b a ++的值.(山东省竞赛题)思路点拨 已知条件是一个含三个未知量的等式,三个未知量,一个等式怎样才能确定未知量的值呢?考虑从配方的角度试一试.原式可化为:2222211]2212][(3)2339]2a c c -+--+=----+即22211)2)]3)02++=,10=,得2a =20=,得6b =;30=,得12c =。
故261220a b c ++=++=。
学历训练1.如果22332+-+-=x x y ,那么4x y -=.2.已知3=xy,那么yxyx y x +的值为. (成都市中考题)提示:原式()x y x y x y x y ⎧⎪==+⎨-⎪⎩、均为正、均为负3.计算2001)13(2)13(2)13(199920002001++-+-+= .(天津市选拔赛试题) 原式199********)1)1)13]20011)11)3]20012001=-+-+=--+=4.若 ab≠0,则等式ab b b a -=--351成立的条件是.(淄博市中考题)==故33b b =-,因此0b <,∵ 0ab ->,∴0a > 5.如果式子2)1(2-+-x x 化简的结果为32-x ,则x 的取值范围是( B )A .x≤1B .x≥2C .1≤x≤2D .x >0 (徐州市中考题) 6.如果式子aa ---11)1( 根号外的因式移入根号内,化简的结果为( C )A .a -1B .1-aC .1--aD .a --1 7.已知)0,0(02>>=+-y x y xy x ,则yxy x y xy x 4353-++-的值为( D )A .31B .21 C .32 D .438.已知321+=a ,那么a a a a a a -+--+-2221211的值等于( )A .)321(+-B .1-C .32-D .3 9.计算:(1)12002200120001999+⨯⨯⨯; (2)7221756215422133021120291227625223-+-+-+-+-+-+-+-;(3)4266777647511+++++;(4))19992001()19972001(2001)20011999)(19971999(1999)20011997)(19991997(1997--+--+--(“希望杯”邀请赛试题)10.(1)已知139+与139-的小数部分分别是a 和b ,求ab -3a+4b+8的值; (2)设nn n n x ++-+=11,nn n n y -+++=11,n 为自然数,如果199********=++y xy x 成立,求n .11.如图,某货船以20海里/时的速度将一批重要物资由A 处运往正西方向的B 处,经16小时的航行到达,到达后必须立即卸货.此时,接到气象部门通知,一台风中心正以40海里/时的速度由A 向北偏西60°方向移动,距台风中心200海里的圆形区域(包括边界)均会受到影响. (1)问:B 处是否会受到台风的影响?请说明理由; (2)为避免受到台风的影响,该船应在多少小时内卸完货物? (供选用数据:4.12≈,7.13≈) (贵阳市中考题) 12.已知2323+-=x ,2323-+=y ,那么22y x x y += .(杯全国初中数学联赛题)13.若有理数x 、y 、z 满足)(2121z y x z y x ++=-+-+,则3()x yz -=.(北京市竞赛题)14.设b a +=-21027,其中a 为正整数,b 在0,1之间,则ba ba -+= .15.正数m 、n 满足34424=+--+n n m mn m ,则2002282++-+n m n m = .(北京市竞赛题)16.化简212172232-+-等于( )A .5—42B .42一1C . 5D .1 (全国初中数学联赛题) 17.若x x +=-11,则2)1(-x 等于( ) (2004年武汉市选拔赛试题) A 1-x B .x -1 C .1 D .-118.若b a b a b a -≠、、,都是有理数,那么a 和b ( ) (“希望杯”邀请赛试题) A .都是有理数 B .一个是有理数,另一个是无理数C .都是无理数D .有理数还是无理数不能确定 19.下列三个命题:①若α,β是互不相等的无理数,则αβ+α-β是无理数; ②若α,β是互不相等的无理数,则βαβα+-是无理数; ③若α,β是互不相等的无理数,则3βα+是无理数. 其中正确命题的个数是( )A . 0B .1C .2D .3 (全国初中数学联赛试题) 提示:①(21)(21)[(21)(21)]123+-++--=+=是有理数;答案A ②22221322232-==+是有理数; ③336622220+-=-=是有理数。
20.计算: (1)3426302352+--+; (2)2356101528-+--+;(3)100999910013223121121++++++ ;(4) )1552326(2+--; (5)223152525--+-++.提示:(1)原式253253626526326226(532)26+-+-====-+-+;(2)原式2(52153)2(53)(53)2(53)532532++-++-+==+-+-(53)(532)532++-=+-53=+;(3)先看通项(1)11(1)n n n n n n n n =++++++111(1)(1)11n n n n n n n n n n n n n n +-+-===-++++-++故原式19(1)()()1101022399100=-+-++-=-= (4)原式124345215435223225215=--+=++--+2(235)235352=--=--=+-; (5)原式25252(52)(51)(52)(51)2221(21)5151(51)(51)(51)(51)+-+---=+--+=+--+++-+- 552535235735(21)(21)515144+--++-=+--=+----1)1)==1)1)3)1)1=+-=+-=21.(1)求证11)1(12222+-+=+++ababaababa;(2)计算200012000199919991222-++.(“祖冲之杯”邀请赛试题)提示:(1)因为2111222()221111a a a a ab aaab b ab ab b ab b b++=+==++++,所以原式左边=1b ab===+右边(2)设1999a=,则原式1111a a==++1111a a==-++1111a a=-=++21111999111a aaa a a++=-=-==+++22.(1)323232121121)(+-+-+++=xxxxxxf,求(1)(3)(999)f f f+++的值;(2)设x、y都是正整数,且使yxx=++-100116,求y的最大值.(上海市竞赛题)提示:(1)注意到2222331()()a b a ba ab b a ab b a b a b--==++++--,原()f x可化为:()f x==12==故(1)(3)(999)f f f+++=31(10002=+++1110522===(2)设2222116216()()2108454100x mn m n m n mx n⎧-=⎪→=-→+-=⨯=⨯⎨+=⎪⎩,108y m n=+=23.试将实数)71)(51(211+++改写成三个正整数的算术根之和.(2001年第2届全澳门校际初中数学竞赛题)提示:题目的意思是:2112(1()ab c+++=++,因此配方使112(1+++=2112(1175(1=++=++++故1=24.求比6)56(+大的最小整数.(西安交通大学少年班入学试题)提示:设x=,y=x y+=1xy=那么2222()2222x y x y xy+=+-=-=,3322()()1)x y x y x xy y+=+-+=-=,66332332()2210582x y x y x y+=+-=-=即6610582+=,由于01<,故61<<60105821<-<,同减10582,得61058210581-<-<-,同乘1-得61058210581>>,即61058110582<<故比6)56(+大的最小整数为10582。
