七年级数学上册难点突破12整式的加减_去括号与添括号试题含解析新版北师大版
(完整版)北师大数学七年级第三章整式的加减(二)—去括号与添括号(提高)

整式的加减(二)—去括号与添括号(提高)知识讲解 【学习目标】1.掌握去括号与添括号法则,注意变号法则的应用;2. 熟练运用整式的加减运算法则,并进行整式的化简与求值.【要点梳理】要点一、去括号法则如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同;如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反.要点诠释:(1)去括号法则实际上是根据乘法分配律得到的结论:当括号前为“+”号时,可以看作+1与括号内的各项相乘;当括号前为“-”号时,可以看作-1与括号内的各项相乘.(2)去括号时,首先要弄清括号前面是“+”号,还是“-”号,然后再根据法则去掉括号及前面的符号.(3)对于多重括号,去括号时可以先去小括号,再去中括号,也可以先去中括号.再去小括号.但是一定要注意括号前的符号.(4)去括号只是改变式子形式,不改变式子的值,它属于多项式的恒等变形.要点二、添括号法则添括号后,括号前面是“+”号,括到括号里的各项都不变符号;添括号后,括号前面是“-”号,括到括号里的各项都要改变符号.要点诠释:(1)添括号是添上括号和括号前面的符号,也就是说,添括号时,括号前面的“+”号或“-”号也是新添的,不是原多项式某一项的符号“移”出来得到的.(2)去括号和添括号的关系如下:如:()a b c a b c +-+-垐垐垎噲垐垐添括号去括号, ()a b c a b c -+--垐垐垎噲垐垐添括号去括号要点三、整式的加减运算法则一般地,几个整式相加减,如果有括号就先去括号,然后再合并同类项.要点诠释:(1)整式加减的一般步骤是:①先去括号;②再合并同类项.(2)两个整式相减时,减数一定先要用括号括起来.(3)整式加减的最后结果的要求:①不能含有同类项,即要合并到不能再合并为止;②一般按照某一字母的降幂或升幂排列;③不能出现带分数,带分数要化成假分数.【典型例题】类型一、去括号1.(2015•泰安模拟)化简m ﹣n ﹣(m+n )的结果是( )A . 0B . 2mC . ﹣2nD . 2m ﹣2n【答案】C【解析】解:原式=m ﹣n ﹣m ﹣n=﹣2n .故选C .【总结升华】解决此类题目的关键是熟记去括号法则,及熟练运用合并同类项的法则,其是各地中考的常考点.注意去括号法则为:﹣﹣得+,﹣+得﹣,++得+,+﹣得﹣.类型二、添括号2.按要求把多项式321a b c -+-添上括号:(1)把含a 、b 的项放到前面带有“+”号的括号里,不含a 、b 的项放到前面带有“-”号的括号里;(2)把项的符号为正的放到前面带有“+”号的括号里,项的符号为负的放到前面带有“-”号的括号里.【答案与解析】解:(1)321(32)(1)a b c a b c -+-=---+;(2)321(3)(21)a b c a c b -+-=+-+.【总结升华】在括号里填上适当的项,要特别注意括号前面的符号,考虑是否要变号.举一反三:【变式】添括号:(1)22()101025()10()25x y x y x y +--+=+-+.(2)()()[(_______)][(_______)]a b c d a b c d a a -+-+-+=-+.【答案】(1)x y +; (2),b c d b c d -+-+ .类型三、整式的加减3. 3243245348x x x x x x -+--+-一个多项式加上得,求这个多项式.【答案与解析】解:在解答此题时应先根据题意列出代数式,注意把加式、和式看作一个整体,用括号括起来,然后再进行计算,在计算过程中找同类项,可以用不同的记号标出各同类项,减少运算的错误.43232(348)(45)x x x x x x --+---+ 4323243348453813.x x x x x x x x x =--+--+-=-+-答:所求多项式为433813x x x -+-.【总结升华】整式加减的一般步骤是:①先去括号;②再合并同类项.举一反三:【变式】化简:(1)15+3(1-x)-(1-x+x 2)+(1-x+x 2-x 3).(2)3x 2y-[2x 2z-(2xyz-x 2z+4x 2y)].(3)-3[(a 2+1)-16(2a 2+a)+13(a-5)]. (4)ab-{4a 2b-[3a 2b-(2ab-a 2b)+3ab]}.【答案】解: (1) 15+3(1-x)-(1-x+x 2)+(1-x+x 2-x 3)=15+3(1-x)-(1-x+x 2)+(1-x+x 2)-x 3=18-3x-x 3.. ……整体合并,巧去括号(2) 3x 2y-[2x 2z-(2xyz-x 2z+4x 2y)]=3x 2y-2x 2z+(2xy-x 2z+4x 2y) ……由外向里,巧去括号=3x 2y-2x 2z+2xyz-x 2z+4x 2y=7x 2y-3x 2z+2xyz. (3) 22113[(1)(2)(5)]63a a a a -+-++- 2213(1)(2)(5)2a a a a =-+++-- 2213352a a a a =--++-+ 21222a a =--+. (4)ab-{4a 2b-[3a 2b-(2ab-a 2b)+3ab]}=ab-4a 2b+3a 2b-2ab+a 2b+3ab ……一举多得,括号全脱=2ab.类型四、化简求值4.(2016春•盐城校级月考)先化简,再求值:3x 2y ﹣[2x 2﹣(xy 2﹣3x 2y )﹣4xy 2],其中|x|=2,y=,且xy <0.【思路点拨】原式去括号合并得到最简结果,利用绝对值的代数意义求出x 的值,代入原式计算即可得到结果.【答案与解析】 解:原式=3x 2y ﹣2x 2+xy 2﹣3x 2y+4xy 2=5xy 2﹣2x 2,∵|x|=2,y=,且xy <0,∴x=﹣2,y=,则原式=﹣﹣8=﹣. 【总结升华】化简求值题一般采用“一化二代三计算”,此类题最后结果的书写格式一般为:当x=…时,原式=….举一反三:【变式】(2015春•万州区期末)先化简,再求值:﹣2x 2﹣[3y 2﹣2(x 2﹣y 2)+6],其中x=﹣1,y=﹣.【答案】解:原式=﹣2x 2﹣y 2+x 2﹣y 2﹣3=﹣x 2﹣y 2﹣3,当x=﹣1,y=﹣时,原式=﹣1﹣﹣3=﹣4.5. 已知3a 2-4b 2=5,2a 2+3b 2=10.求:(1)-15a 2+3b 2的值;(2)2a 2-14b 2的值.【答案与解析】显然,由条件不能求出a 、b 的值.此时,应采用技巧求值,先进行拆项变形.解:(1)-15a 2+3b 2=-3(5a 2-b 2)=-3[(3a 2+2a 2)+(-4b 2+3b 2)]=-3[(3a 2-4b 2)+(2a 2+3b 2)]=-3×(5+10)=-45;(2)2a 2-14b 2=2(a 2-7b 2)=2[(3a 2-2a 2)+(-4b 2-3b 2)]=2×[(3a 2-4b 2)-(2a 2+3b 2)]=2×(5-10)=-10.【总结升华】求整式的值,一般先化简后求值,但当题目中含未知数的部分可以看成一个整体时,要用整体代入法,即把“整体”当成一个新的字母,求关于这个新的字母的代数式的值,这样会使运算更简便. 举一反三:【变式】当2m π=时,多项式31am bm ++的值是0,则多项式3145_____2a b ππ++=. 【答案】∵ 3(2)210a b ππ++=g, ∴ 338212(4)10a b a b ππππ++=++=,即3142a b ππ+=-. ∴31114555222a b ππ++=-+=. 6. 已知多项式2x ax y b +-+与2363bx x y -+-的差的值与字母x 无关,求代数式:22223(2)(4)a ab b a ab b ---++的值.【答案与解析】解:222(363)(1)(3)7(3)x ax y b bx x y b x a x y b +-+--+-=-++-++.由于多项式2x ax y b +-+与2363bx x y -+-的差的值与字母x 无关,可知: 10b -=,30a +=,即有1,3b a ==-.又2222223(2)(4)74a ab b a ab b a ab b ---++=---Q ,将1,3b a ==-代入可得:22(3)7(3)1418---⨯-⨯-⨯=.【总结升华】本例解题的关键是多项式的值与字母x 无关.“无关”意味着合并同类项后,其结果不含“x ”的项,所以合并同类项后,让含x 的项的系数为0即可.类型五、整式加减运算的应用7.有一种石棉瓦(如图所示),每块宽60厘米,用于铺盖屋顶时,每相邻两块重叠部分的宽都为10厘米,那么n(n 为正整数)块石棉瓦覆盖的宽度为 ( ) .A .60n 厘米B .50n 厘米C .(50n+10)厘米D .(60n-10)厘米【答案】C.【解析】观察上图,可知n 块石棉瓦重叠的部分有(n-1)处,则n 块石棉瓦覆盖的宽度为:60n-10(n-1)=(50n+10)厘米.【总结升华】求解本题时一定要注意每相邻两块重叠部分的宽都为10厘米这一已知条件,一不小心就可能弄错.举一反三:【变式】如图所示,长方形内有两个相邻的正方形,面积分别为9和a 2(a >0).那么阴影部分的面积为________.【答案】3a-a 2提示:由图形可知阴影部分面积=长方形面积29a --,而长方形的长为3+a ,宽为3,从而使问题获解.【巩固练习】一、选择题1.(2014•新泰市校级模拟)下列各式中去括号正确的是( ).A. a 2﹣(2a ﹣b 2+b )=a 2﹣2a ﹣b 2+bB. ﹣(2x+y )﹣(﹣x 2+y 2)=﹣2x+y+x 2﹣y 2C. 2x 2﹣3(x ﹣5)=2x 2﹣3x+5D. ﹣a 3﹣[﹣4a 2+(1﹣3a )]=﹣a 3+4a 2﹣1+3a2. 已知一个多项式与3x 2+9x 的和等于3x 2+4x-1,则这个多项式是( ) .A .-5x-1B .5x+1C .-13x-1D .13x+13.代数式2332333{10(63)}672x y x x y x y x y x ---+-+-的值( ).A .与x ,y 都无关B .只与x 有关C .只与y 有关D .与x 、y 都有关4.如果210x x +-=,那么代数式3227x x +-的值为( ).A. 6B.8C. -6D. -85.化简5(2x ﹣3)﹣4(3﹣2x )之后,可得下列哪一个结果( ).A. 2x ﹣27B. 8x ﹣15C. 12x ﹣15D. 18x ﹣276. 已知有理数,,a b c 在数轴上的位置如图所示,且a b =,则代数式a c a c b b --+---的值为( ).A. 2c - B . 0 C. 2c D.222a b c -+7.(2016春•钦州期末)﹣[x ﹣(y ﹣z )]去括号后应得( )A .﹣x+y ﹣zB .﹣x ﹣y+zC .﹣x ﹣y ﹣zD .﹣x+y+z8.如果对于某一个特定范围内x 的任意允许值,1213...19110P x x x x =-+-++-+-的值恒为一个常数,则此值为 ( ).A. 2 B. 3 C. 4 D. 5二、填空题9.()()1 a b c d a -+-=-; ()()22 ;x y z +-=-()()()()()22222223 ;4 a b a b a b a b a b a a -+-=-+---=--. 10. 如图所示是一组有规律的图案,第1个图案由4个基础图形组成,第2个图案由7个基础图形组成,…,第n(n 是正整数)个图案中由________个基础图形组成.11.(2014•阜宁县模拟)计算:2(a ﹣b )+3b= .12. 当2=x 时,代数式13+-bx ax 的值等于-17,那么当1-=x 时,代数式53123--bx ax 的值等于 . 13. 有理数a,-b 在数轴上的位置如图所示,化简a b b 322231-++--= .01a -3-2-12-b14. 任意一个三位数,减去它的三个数字之和所得的差一定能被______整除.三、解答题:15.(2016春•顺义区期末)计算:(2mn ﹣m 2+n 2)+(m 2﹣n 2+mn ).16.已知:ax 2+2xy-x 与2x 2-3bxy+3y 的差中不含2次项,求a 2-15ab+9b 2的值.17.(2015•宝应县校级模拟)先化简,再求值:(﹣4x 2+2x ﹣8y )﹣(﹣x ﹣2y ),其中x=,y=2012. 【答案与解析】一、选择题1.【答案】D.【解析】A 、a 2﹣(2a ﹣b 2+b )=a 2﹣2a+b 2﹣b ,故本选项错误;B 、﹣(2x+y )﹣(﹣x 2+y 2)=﹣2x ﹣y+x 2﹣y 2,故本选项错误;C 、2x 2﹣3(x ﹣5)=2x 2﹣3x+15,故本选项错误;D 、﹣a 3﹣[﹣4a 2+(1﹣3a )]=﹣a 3﹣[﹣4a 2+1﹣3a]=﹣a 3+4a 2﹣1+3a ,故本选项正确.2.【答案】A【解析】(3x 2+4x-1)-(3x 2+9x)=3x 2+4x-1-3x 2-9x =-5x-1.3.【答案】B【解析】合并同类项后的结果为332x --,故它的值只与x 有关.4.【答案】C【解析】21x x +=,3222227()77176x x x x x x x x +-=++-=+-=-=-.5. 【答案】D【解析】5(2x ﹣3)﹣4(3﹣2x )=5(2x ﹣3)+4(2x ﹣3)=9(2x ﹣3)=18x ﹣27.6.【答案】A【解析】由图可知:0a c b <<<,所以()()2a c a c b b a c a b c b c --+---=---+--=-.7.【答案】A【解析】解:﹣[x ﹣(y ﹣z )]=﹣(x ﹣y+z )=﹣x+y ﹣z .故选:A .8.【答案】B【解析】P 值恒为一常数,说明原式去绝对值后不含x 项,进而可得下图:由此得:P =(12)(13)...(17)(81)(91)(101)3x x x x x x -+-++-+-+-+-=.二、填空题9. 【答案】2;2;;b c d x y z a b b b -+--+-+10. 【答案】3n+1【解析】第1个图形由3×1+1=4个基础图形组成;第2个图形由3×2+1=7个基础图形组成;第3个图形由3×3+1=10个基础图形组成,故第n 个图形由(3n+1)个基础图形组成.11. 【答案】2a+b【解析】原式=2a ﹣2b+3b=2a+b.12.【答案】 22【解析】由题意可得:82117a b -+=-,即有49a b -=-.又因为12353(4)53(9)522a b a b -+-=---=-⨯--=.13.【答案】7a 3b -+【解析】3,3b b -<->,所以原式=312(2)(32)37b b a b a --++-=+-.14.【答案】9【解析】设任意一个的三位数为a ×102+b ×10+c.其中a 是1~9的正整数,b,c 分别是0~9的自然数.∵(a ×102+b ×10+c)-(a+b+c)=99a+9b=9(11a+b)=9m. (用m 表示整数11a+b) .∴任意一个三位数,减去它的三个数字之和所得的差一定能被9整除.三、解答题15.【解析】解:原式=2mn ﹣m 2+n 2+m 2﹣n 2+mn=3mn .16. 【解析】解: (ax 2+2xy-x)-(2x 2-3bxy+3y)=ax 2+2xy-x-2x 2+3bxy-3y=(a-2)x 2+(2+3b)xy-x-3y.∵此差中不含二次项, 20,230.a b -=⎧⎨+=⎩ 解得:2,3 2.a b =⎧⎨=-⎩当a=2且3b= -2时,a 2-15ab+9b 2=a 2-5a(3b)+(3b)2=22-5×2×(-2)+(-2)2=4+20+4=28.17.【解析】解:原式=﹣x 2+x ﹣2y+x+2y=﹣x 2+x ,当x=,y=2012时,原式=﹣+ = .。
初一整式的加减所有知识点总结和常考题提高难题压轴题练习(含答案解析)

初一整式的加减所有知识点总结和常考题提高难题压轴题练习(含答案解析)初一整式的加减知识点总结和常考题知识点:1.单项式:表示数字或字母乘积的式子,单独的一个数字或字母也叫单项式。
2.单项式系数:单项式中不为零的数字因数,叫单项式数字系数,简称单项式的系数。
3.单项式的次数:单项式中所有字母的指数的和,叫单项式的次数。
4.多项式:几个单项式的和叫做多项式。
5.多项式的项与项数:多项式中每个单项式叫多项式的项;不含字母的项叫做常数项。
多项式里所含单项式的个数就是多项式的项数。
6.多项式的次数:多项式里,次数最高项的次数叫多项式的次数;常数项的次数为0.注意:若a、b、c、p、q是常数,则ax+bx+c和x+px+q是常见的两个二次三项式。
7.多项式的升幂排列:把一个多项式的各项按某个字母的指数从小到大排列起来,叫做按这个字母的升幂排列。
多项式的降幂排列:把一个多项式的各项按某个字母的指数从大到小排列起来,叫做按这个字母的降幂排列。
(注意:多项式计算的最后结果一般应该进行升幂或降幂排列。
)8.整式:单项式和多项式统称为整式,即凡不含有除法运算,或虽含有除法运算但除式中不含字母的代数式叫整式。
9.整式分类:整式分为单项式和多项式。
(注意:分母上含有字母的不是整式。
)10.同类项:所含字母相同,并且相同字母的指数也相同的单项式是同类项。
11.合并同类项法:各同类项系数相加,所得结果作为系数,字母和字母指数不变。
12.去括号的法则:(原理:乘法分配律)(1)括号前面是“+”号,把括号和它前面的“+”号去掉,括号里各项的符号都不变;(2)括号前面是“—”号,把括号和它前面的“—”号去掉,括号里各项的符号都要改变。
13.添括号的法则:(1)若括号前边是“+”号,括号里的各项都不变号;(2)若括号前边是“-”号,括号里的各项都要变号。
14.整式的加减:进行整式的加减运算时,如果有括号先去括号,再合并同类项;整式的加减,实际上是在去括号的基础上,把多项式的同类项合并。
北师大版初中数学七年级上册知识讲解,巩固练习:第11讲 整式的加减(二)——去括号和添括号

整式的加减(二)—去括号与添括号【学习目标】 1.掌握去括号与添括号法则,充分注意变号法则的应用;2. 会用整式的加减运算法则,熟练进行整式的化简及求值.【要点梳理】要点一、去括号法则如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同;如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反.要点诠释:(1)去括号法则实际上是根据乘法分配律推出的:当括号前为“+”号时,可以看作+1与括号内的各项相乘;当括号前为“-”号时,可以看作-1与括号内的各项相乘.(2)去括号时,首先要弄清括号前面是“+”号,还是“-”号,然后再根据法则去掉括号及前面的符号.(3)对于多重括号,去括号时可以先去小括号,再去中括号,也可以先去中括号.再去小括号.但是一定要注意括号前的符号.(4)去括号只是改变式子形式,但不改变式子的值,它属于多项式的恒等变形.要点二、添括号法则添括号后,括号前面是“+”号,括到括号里的各项都不变符号;添括号后,括号前面是“-”号,括到括号里的各项都要改变符号.要点诠释:(1)添括号是添上括号和括号前面的符号,也就是说,添括号时,括号前面的“+”号或“-”号也是新添的,不是原多项式某一项的符号“移”出来得到的.(2)去括号和添括号是两种相反的变形,因此可以相互检验正误:如:,要点三、整式的加减运算法则一般地,几个整式相加减,如果有括号就先去括号,然后再合并同类项.要点诠释:()a b c a b c +-+-添括号去括号()a b c a b c -+--添括号去括号(1)整式加减的一般步骤是:①先去括号;②再合并同类项.(2)两个整式相加减时,减数一定先要用括号括起来.(3)整式加减的最后结果中:①不能含有同类项,即要合并到不能再合并为止;②一般按照某一字母的降幂或升幂排列;③不能出现带分数,带分数要化成假分数.【典型例题】类型一、去括号1.去括号:(1)d-2(3a-2b+3c);(2)-(-xy-1)+(-x+y).【答案与解析】(1)d-2(3a-2b+3c)=d-(6a-4b+6c)=d-6a+4b-6c ;(2)-(-xy-1)+(-x+y)=xy+1-x+y .【总结升华】去括号时.若括号前有数字因数,应先把它与括号内各项相乘,再去括号.举一反三【变式1】去掉下列各式中的括号:(1). 8m-(3n+5); (2). n-4(3-2m);(3). 2(a-2b)-3(2m-n).【答案】(1). 8m-(3n+5)=8m-3n-5.(2). n-4(3-2m)=n-(12-8m)=n-12+8m.(3). 2(a-2b)-3(2m-n)=2a-4b-(6m-3n)=2a-4b-6m+3n.【变式2】(2018•济宁)化简﹣16(x ﹣0.5)的结果是( )A . ﹣16x ﹣0.5B . ﹣16x+0.5C . 16x ﹣8D . ﹣16x+8【答案】D类型二、添括号2.在各式的括号中填上适当的项,使等式成立.(1). ; (2). . 2345()()x y z t +-+=-=+2()x =-23()x y =+-23452()2()x y z t x x -+-=+=-23()45()x y z t =--=--【答案】(1),,,.(2),,,.【解析】(1);(2).【总结升华】在括号里填上适当的项,要特别注意括号前面的符号,考虑是否要变号.举一反三【变式】.【答案】;;;. 类型三、整式的加减3.(2019•邢台二模)设A ,B ,C 均为多项式,小方同学在计算“A﹣B”时,误将符号抄错而计算成了“A +B”,得到结果是C ,其中A=x 2+x ﹣1,C=x 2+2x ,那么A ﹣B=( )A .x 2﹣2xB .x 2+2xC .﹣2D .﹣2x【思路点拨】根据题意得到B=C ﹣A ,代入A ﹣B 中,去括号合并即可得到结果.【答案】C .【解析】解:根据题意得:A ﹣B=A ﹣(C ﹣A )=A ﹣C+A=2A ﹣C=2(x 2+x ﹣1)﹣(x 2+2x )=x 2+2x ﹣2﹣x 2﹣2x=﹣2, 故选C.【总结升华】整式加减的一般步骤是:①先去括号;②再合并同类项.2345x y z t --+-2345x y z t +-+345y z t -+-45z t -345y z t -+-345y z t -+45z t -+23x y -+2345x y z t +-+(2345)x y z t =---+-(2345)x y z t =++-+2(345)x y z t =--+-23(45)x y z t =+--2345x y z t -+-2(345)x y z t =+-+-2(345)x y z t =--+23(45)x y z t =---+45(23)z t x y =---+()()1 a b c d a -+-=-;()()22 ;x y z +-=-()()()()()22222223 ;4 a b a b a b a b a b a a -+-=-+---=--b c d -+2x y z --+a b -2b b +类型四、化简求值4. 先化简,再求各式的值:【答案与解析】原式=, 当时,原式=. 【总结升华】化简求值题一般采用“一化二代三计算”,此类题的书写格式一般为:当……时,原式=? 举一反三【变式1】先化简再求值:(-x 2+5x+4)+(5x-4+2x 2),其中x =-2.【答案】 (-x 2+5x+4)+(5x-4+2x 2)=-x 2+5x+4+5x-4+2x 2=x 2+10x.当x =-2,原式=(-2)2+10×(-2)=-16.【变式2】先化简,再求值:,其中化为相反数. 【答案】因为互为相反数,所以所以5. 已知,,求整式的值.【答案与解析】由,很难求出,的值,可以先把整式化简,然后把,分别作为一个整体代入求出整式的值.原式22131222,2,;22333x x y x y x y ⎛⎫⎛⎫+-+--=-= ⎪ ⎪⎝⎭⎝⎭其中2221312232233x x y x y x y -+-+=-+22,3x y =-=22443(2)()66399-⨯-+=+=3(2)[3()]2y x x x y x +----,x y 3(2)[3()]236322()y x x x y x y x x x y x x y +----=+-+--=+,x y 0x y +=3(2)[3()]22()200y x x x y x x y +----=+=⨯=2xy =-3x y +=(310)[5(223)]xy y x xy y x ++-+-2xy =-3x y +=x y xy x y +310(5223)xy y x xy y x =++--+.把,代入得,原式.【总结升华】求整式的值,一般先化简后求值,但当题目中含未知数的部分可以看成一个整体时,要用整体代入法,即把“整体”当成一个新的字母,求关于这个新的字母的代数式的值,这样会使运算更简便. 举一反三【变式】已知代数式的值为8,求的值. 【答案】∵ ,∴ . 当时,原式=. 6. 如果关于x 的多项式的值与x 无关.你知道a 应该取什么值吗?试试看.【答案与解析】所谓多项式的值与字母x 无关,就是合并同类项,结果不含有“x ”的项,所以合并同类项后,让含x 的项的系数为0即可.注意这里的a 是一个确定的数.(8x 2+6ax+14)-(8x 2+6x+5)=8x 2+6ax+14-8x 2-6x-5=6ax-6x+9=(6a-6)x+9由于多项式(8x 2+6ax+14)-(8x 2+6x+5)的值与x 无关,可知x 的系数6a-6=0.解得a =1.3105223xy y x xy y x =++--+5310232x x y y xy xy =++-+-88x y xy =++8()x y xy =++2xy =-3x y +=83(2)24222=⨯+-=-=2326y y -+2312y y -+23268y y -+=2322y y -=2322y y -=211(32)121222y y -+=⨯+=22(8614)(865)x ax x x ++-++【总结升华】本例解题的题眼是多项式的值与字母x 无关.“无关”意味着合并同类项后,其结果不含“x ”的项.【巩固练习】一、选择题1.(2018•江西模拟)计算:a ﹣2(1﹣3a )的结果为( )A.7a ﹣2B.﹣2﹣5aC.4a ﹣2D.2a ﹣22.(2019•黄陂区模拟)下列式子正确的是( )A .x ﹣(y ﹣z )=x ﹣y ﹣zB .﹣(x ﹣y+z )=﹣x ﹣y ﹣zC .x+2y ﹣2z=x ﹣2(z+y )D .﹣a+c+d+b=﹣(a ﹣b )﹣(﹣c ﹣d )3.计算-(a-b)+(2a+b)的最后结果为( ).A .aB .a+bC .a+2bD .以上都不对4. (2010·山西)已知一个多项式与3x 2+9x 的和等于3x 2+4x-1,则这个多项式是( )A .-5x-1B .5x+1C .-13x-1D .13x+15.代数式的值( ).A .与x ,y 都无关B .只与x 有关C .只与y 有关D .与x 、y 都有关6.如图所示,阴影部分的面积是( ).A .B .C .6xyD .3xy 二、填空题7.添括号:2332333103(2)(672)x y x x y x y x y x --++--+112xy 132xy(1)..(2)..8.(2018•镇江一模)化简:5(x ﹣2y )﹣4(x ﹣2y )=________.9.若则的值是________.10.(2019•河北)若mn=m+3,则2mn+3m ﹣5mn+10= .11.已知a =-(-2)2,b =-(-3)3,c =-(-42),则-[a-(b-c)]的值是________.12.如图所示是一组有规律的图案,第1个图案由4个基础图形组成,第2个图案由7个基础图形组成,…,第n(n 是正整数)个图案中由________个基础图形组成.三、解答题13. 化简 (1).(2018•宝应县校级模拟)2(3x 2﹣2xy )﹣4(2x 2﹣xy ﹣1)(2). (3).(4).(5).(6).14.化简求值:(1). 已知:,求的值. 331(___________)3(_______)p q q -+-=+=-()()[(_______)][(_______)]a b c d a b c d a a -+-+-+=-+221m m -=2242008m m -+22222323xy xy y x y x -++-m n mn m n mn mn n m 222238.0563--+--)45(2)2(32222ab b a ab b a ---2010=a )443()842()33(232332-+++-++-+--a a a a a a a a a(2). ,其中a = -1, b = -3, c = 1. (3). 已知的值是6,求代数式 的值.15. 有一道题目:当a=2,b=-2时,求多项式:3a 3b 3-2a 2b+b-(4a 3b 3-a 2b-b 2)+(a 3b 3+a 2b)-2b 2+3的值.甲同学做题时把a=2错抄成a=-2,乙同学没抄错题,但他们做出的结果恰好一样。
北师大版七年级数学上整式的加减.docx

初中数学试卷 桑水出品整式的加减知识点1:整式的加减1.化简:(3m -2n )-(2m -3n )=_________;(x 2+y 2)-3(x 2-2y 2)=___________.2.化简(x +14)-(2x -12)的结果是( ) A .-x -14 B .-x +34C .3x -14D .x +343.计算6a 2-2ab -2(3a 2+12ab )的结果是( ) A .-3ab B .-ab C .3a 2 D .9a 24.计算:(1)6x 2-[-3x 2-(x -1)];(2)(5a 2-3b 2)+[-(a 2-2ab -b 2)-(5a 2+2ab +3b 2)].5.已知x +4y =-1,xy =5,求(6xy +7y )+[8x -(5xy -y +6x )]的值.知识点2:整式的加减的实际应用6.一根铁丝的长为5a +4b ,剪下一部分围成一个长为a ,宽为b 的长方形,则这根铁丝还剩下_________.7.某商场一月份的销售额为a 元,二月份比一月份销售额多b 元,三月份比二月份减少10%,第一季度的销售额总计为________元;当a =2万元,b =5000元时,第一季度的总销售额为_______元.8.某校组织若干师生到活动基地进行社会实践活动.若学校租用45座的客车x 辆,则余下20人无座位;若租用60座的客车,则可少租用2辆,且最后一辆还没坐满,则乘坐最后一辆60座客车的人数是( )A .200-60xB .140-15xC .200-15xD .140-60x9.某市要建一条高速公路,其中一段经过公开招标,由某建筑公司中标.在建筑过程中,该公司为了保质保量提前完工,投入了甲、乙、丙三个工程队进行同时施工,经过一段时间后,甲工程队筑路a km ,乙工程队所筑的路比甲工程队的23多18 km ,丙工程队所筑的路比甲工程队的2倍少3 km ,请问甲、乙、丙三个工程队共筑路多少千米?若该段高速公路长为1200 km ,当a =300时,他们完成任务了吗?10.当x =2时,(x 2-x )-2(x 2-x -1)的值等于( )A .4B .-4C .1D .011.减去-3a 后等于5a 2-3a -5的代数式是( )A .5a 2-5B .5a 2-6a -5C .-5a 2-6a +5D .-5a 2+512.今天数学课上,老师讲了多项式的加减,放学后,小明回到家拿出课堂笔记,认真地复习老师课上讲的内容,他突然发现一道题:(-x 2+3xy -12y 2)-(-12x 2+4xy -32y 2)=-12x 2_______+y 2,空格的地方被墨水弄污了,请你帮他补上.13.三个连续偶数,若中间的一个记为2n -2,则这三个偶数的和为________.14.三角形的周长为48,第一边长为4a +3b ,第二边比第一边的2倍少2a -b ,则第三边长为______________.15.已知a 2+2ab =-10,b 2+2ab =16,则a 2+4ab +b 2=____,a 2-b 2=______.16.先化简,再求值:(1)-(3a 2-4)-(a 2-3a +5)+(4a -a 2),其中a =-3;(2)12(x 2y -13xy 2)+5(xy 2-x 2y )-2x 2y ,其中x =15,y =-5.17.已知小明的年龄是m 岁,小红的年龄比小明的年龄的2倍少4岁,小华的年龄比小红年龄的12还多1岁,求这三名同学的年龄之和是多少?18.一位同学做一道题:“已知两个多项式A ,B ,计算2A +B ”.他误将“2A +B ”看成“A +2B ”,求得的结果为9x 2-2x +7.已知B =x 2+3x -2,请求出正确答案.19.有理数a ,b ,c 在数轴上的位置如图所示,化简|b |+b +2-|c |+|a -1|+|c -a |.。
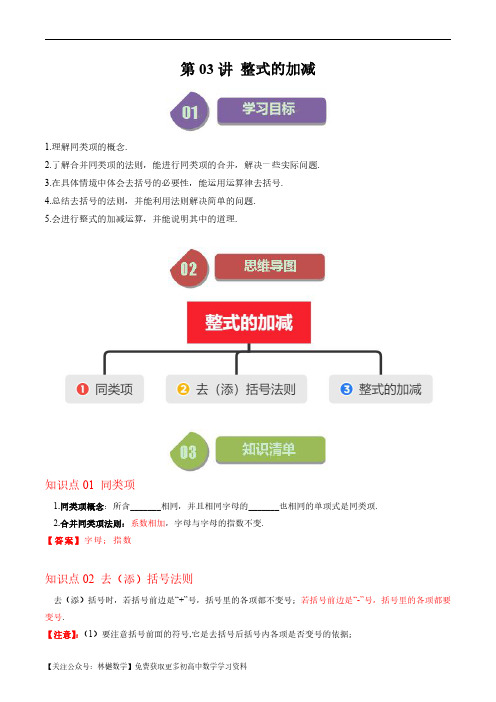
第03讲 整式的加减(9类热点题型讲练)(解析版)--初中数学北师大版7年级上册
第03讲整式的加减1.理解同类项的概念.2.了解合并同类项的法则,能进行同类项的合并,解决一些实际问题.3.在具体情境中体会去括号的必要性,能运用运算律去括号.4.总结去括号的法则,并能利用法则解决简单的问题.5.会进行整式的加减运算,并能说明其中的道理.知识点01同类项1.同类项概念:所含_______相同,并且相同字母的_______也相同的单项式是同类项.2.合并同类项法则:系数相加,字母与字母的指数不变.【答案】字母;指数知识点02去(添)括号法则去(添)括号时,若括号前边是“+”号,括号里的各项都不变号;若括号前边是“-”号,括号里的各项都要变号.【注意】:(1)要注意括号前面的符号,它是去括号后括号内各项是否变号的依据;(2)去括号时应将括号前的符号连同括号一起去掉;(3)括号前面是“-”时,去掉括号后,括号内的各项均要改变符号,不能只改变括号内第一项或前几项的符号,而忘记改变其余的符号;(4)括号前是数字因数时,要将数与括号内的各项分别相乘,不能只乘括号里的第一项;(5)遇到多层括号一般由里到外,逐层去括号.知识点3整式的加减1.整式的加减(1)几个整式相加减,通常用括号把每一个整式括起来,再用加、减连接,然后进行运算.几个整式相加减,通常用括号把每一个整式括起来,再用加、减连接,然后进行运算.(2)几个整式相加减,通常用括号把每一个整式括起来,再用加、减连接,然后进行运算.(3)运算结果,常将多项式的某个字母的降幂(升幂)排列.2.整式加减的一般步骤(1)如果有括号,那么先去括号;(2)观察有无同类项;(3)利用加法的交换律和结合律,分组同类项;(4)合并同类项.题型01同类型的判断【典例1】(2023秋·全国·七年级专题练习)下列各组单项式中,是同类项的是()A .423x y 与244x y -B .258m n -与528n mC .325a b c 与329a b -D .27m n 与62mn -【答案】B【分析】根据同类项的定义即可求解,所含字母相同,且相同字母的指数也相同的两个单项式是同类项.【详解】解:A 、423x y 与244x y -,字母相同,但对应字母的次数不同,不是同类项,故该选项不符合题意;B 、258m n -与528n m 是同类项,故该选项符合题意;C 、325a b c 与329a b -,所含字母不尽相同,不是同类项,故该选项不符合题意;D 、27m n 与62mn -,字母相同,但对应字母的次数不同,不是同类项,故该选项不符合题意.故选:B .【点睛】本题考查了同类项的定义,掌握同类项的定义是解题的关键.【变式1】(2023秋·甘肃白银·七年级统考期末)下列单项式中,与3a b 是同类项的是()题型02已知同类型求指数中字母或代数式的值题型03合并同类型题型04去括号题型05添括号【典例5】(2023春·浙江绍兴·七年级统考期末)下列多项式的变形中,正确的是()A .()y x x y -=--B .()x y x y --=--C .()x y x y -+=-+D .()y x x y +=-+【答案】A【分析】提取负号添括号时,每一项都需要变号.【详解】解:A :()()y x y x x y -=--+=--,A 选项正确;B :()x y x y --=-+,B 选项错误;C :()x y x y -+=--,C 选项错误;D :()y x x y +=--+-,D 选项错误.故选D【点睛】本题考查添括号.括号前面是负号,则括号里面每一项都需要变号.这是解决本题的关键.【变式1】(2023秋·湖北武汉·八年级统考期末)等式() a b c a -+=-,括号内应填上的项为()A .b c +B .b c-C .b c-+D .b c--【答案】B【分析】根据填括号的法则解答即可.【详解】根据填括号的法则可知,原式()a b c =--题型06整式的加减运算题型07整式的加减中化简求值【典例7】(2023春·甘肃定西·七年级统考期末)先化简,再求值:222342565x x x x x +---+-,其中2x =-.题型08整式的加减的应用【典例8】(2023秋·河南漯河·七年级校考期末)某公园里一块草坪的形状如图中的阴影部分(长度单位:m ).(1)用整式表示草坪的面积;(2)若4a =,求草坪的面积.【答案】(1)110a 平方米(2)440平方米【分析】(1)根据题意和图形中的数据可以用代数式表示出草坪的面积;(2)将4a =代入(1)中的代数式,即可解答本题.【详解】(1)解:由题意可得,草坪的面积是:(7.512.5)(222)12.5212.5216050110a a a a a a a a a a +++++-⨯-⨯=-=(平方米),答:草坪的面积是110a 平方米;(2)当4a =时,1101104440a =⨯=(平方米),∴草坪的面积是440平方米.【点睛】本题考查列代数式、代数式求值,解答本题的关键是明确题意,列出相应的代数式、求出相应的代数式的值,利用数形结合的思想解答.【变式1】(2023秋·广东韶关·七年级统考期末)今年暑假小明家买了一套经济适用房,他准备将地面铺上地砖,这套住宅的建筑平面图(由四个长方形组成)如图所示(图中长度单位:米).(1)求出用含x 、y 的代数式表示这套房的总面积是多少平方米?(2)当3x =, 1.5y =时,若铺1平方米地砖平均费用120元,求这套住宅铺地砖总费用.【答案】(1)()6218x y ++平方米(2)4680元【分析】(1)根据图形和题意可以求出这套房子的总面积;(2)根据面积,从而可以求出这套住宅铺地砖的总费用.【详解】(1)解:这套房的总面积是()()()322226366218y x x y ⨯+++⨯-+=++平方米;(2)当3x =, 1.5y =时,铺1平方米地砖平均费用120元,这套住宅铺地砖总费用()120632 1.5184680=⨯⨯+⨯+=(元).【点睛】此题考查了整式加减的应用,列代数式,已知字母的值求代数式的值,解题的关键是明确题意,求出住宅的总面积和总费用,利用数形结合的思想解答.【变式2】(2023秋·广西南宁·七年级校考期末)如图,用三种大小不同的5个正方形和1个长方形(阴影部分)拼成长方形ABCD ,其中3EF =,最小的正方形的边长为x .(1)FG =________,DG =__________;(用含x 的代数式表示)(2)用含x 的代数式表示长方形ABCD 的周长;(3)当4x =时,求长方形ABCD 的周长.【答案】(1)3x +,33x -(2)166x +(3)54【分析】(1)根据图形可得结合线段的和差、正方形的性质即可解答;(2)分别表示出AB 和BC ,然后再表示出周长即可;(3)把4x =代入(2)所求结果中进行求解即可.【详解】(1)解:由图可知:3FG x =+,()4333DG AB GC x x x =-=-+=-;故答案为:3x +,33x -;(2)解:长方形ABCD 的宽为:3334DG CG DG FG x x x +=+=-++=;长为:33343x FG x x x +=++=+,∴长方形ABCD 的周长为:()4432166x x x ++⨯=+;(3)当3x =时,166163654x +=⨯+=.【点睛】本题主要考查了列代数式和代数式求值,理解各个图形的边长之间的数量关系是解答本题的关键.题型09整式的加减中的无关型问题一、单选题1.(2023秋·广西南宁·七年级统考期中)下列各组属于同类项的是()A .23x y -与2xyB .2x y 与2x zC .2mn 与3nm -D .0.5ab -与0.5abc-【答案】C【分析】根据同类项的定义(所含字母相同,并且相同字母的指数也分别相等的项,叫同类项)判断即可.【详解】解:A 、23x y -与2xy 不是同类项,故本选项错误;B 、2x y 与2x z 不是同类项,故本选项错误;C 、2mn 与3nm -是同类项,故本选项正确;D 、0.5ab -与0.5abc -不是同类项,故本选项错误.故选:C .【点睛】本题考查了对同类项的定义的应用,注意:同类项是指:所含字母相同,并且相同字母的指数也分别相等的项.2.(2023秋·四川眉山·七年级统考期末)下列计算正确的是()A .325a b ab +=B .532y y -=C .277a a a +=D .22232x y yx x y-=【答案】D【分析】根据合并同类项的运算法则:字母和字母指数不变,只把系数相加减,逐个进行判断即可.【详解】解:A 、32a b +,不是同类项,不能合并,故A 不正确,不符合题意;B 、532y y y -=,故B 不正确,不符合题意;C 、78a a a +=,故C 不正确,不符合题意;D 、22232x y yx x y -=,故D 正确,符合题意;故选:D .【点睛】本题主要考查了合并同类项,解题的关键是掌握:合并同类项的运算法则:字母和字母指数不变,只把系数相加减.3.(2023春·河南周口·七年级统考期中)若3a b x y +-与2a b x y +是同类项,则a b -的值为()A .1B .2C .3D .4【答案】C【分析】如果两个单项式,他们所含的字母相同,并且相同字母的指数也分别相同,那么就称这两个单项式为同类项.【详解】解:由题意得:231a b a b +=⎧⎨+=⎩解得21a b =⎧⎨=-⎩所以3a b -=故选:C【点睛】本题考查了同类项的定义.熟记相关结论是解题关键.4.(2023秋·全国·七年级专题练习)下列变形中错误的是()A .()2222m m n p m m n p---+-=+B .()m n p q m n p q -+-=-+-C .()()35123521m n p m n p --+=-----⎡⎤⎣⎦D .()()11m n p n m p +--+=----+【答案】B【分析】根据去括号和添括号法则,进行计算后,判断即可.【详解】解:A 、()2222m m n p m m n p ---+-=+,故正确;B 、()m n p q m n p q -+-=--+,故错误;C 、()()35123521m n p m n p --+=-----⎡⎤⎣⎦,故正确;D 、()()111m n p m n p n m p +--+=++-=----+,故正确.故选:B .【点睛】本题考查去括号和添括号,熟练掌握去括号法则和添括号法则,是解题的关键.5.(2023春·浙江杭州·七年级校考期中)在矩形ABCD 内,将一张边长为a 和两张边长为()b a b >的正方形纸片按图1,图2两种方式放留,矩形中未被这三张正方形纸片覆盖的部分用阴影表示,若要知道图2中阴影部分的周长与图1中阴影部分的周长的差,只要测量图中哪条线段的长()A .AB B .ADC .aD .b【答案】A【分析】根据平移的知识和周长的定义,列出算式周长差244(224)AD b AB AD AB b =-+-+-,再去括号,合并同类项即可求解.【详解】解:图1中阴影部分的周长224AD AB b =+-,图2中阴影部分的周长2242AD b AB b =-+-,周长差244(224)2442242AD b AB AD AB b AD b AB AD AB b AB =-+-+-=-+--+=.故若要知道周长差,只要测量图中线段AB 的长.故选:A .【点睛】本题考查了整式的加减,周长的定义,关键是得到图2中阴影部分的周长与图1中阴影部分的周长.二、填空题(1)设AP x =,求阴影部分的面积(2)当13AP a =时,阴影部分面积为【答案】(1)222x ax-+(2)12S S <【分析】(1)依据题意,由AP。
整式的加减运算-化解求值(解析版) 2020-2021年七年级数学上册期末综合复习提优训练(北师大版

2020-2021学年七年级数学上册期末综合复习专题提优训练(北师大版)专题03 整式的加减运算-化解求值【典型例题】1.化简:(1)225223a a a a -+- (2)1(43)3(2)2a ab a b +--- 【答案】解:(1)225223a a a a -+-=()()25223a a +-+=275a a -(2)1(43)3(2)2a a b a b +---=32362a a b a b +--+=92b 【点睛】此题考查的是整式的加减,掌握去括号法则和合并同类项法则是解题关键.2.(2020·湖北武汉·七年级期中)先化简,再求值()221131122323x x y x y ⎛⎫⎛⎫--+-+ ⎪ ⎪⎝⎭⎝⎭,其中22,3x y =-= ()222221235262ab a b ab ab a b ⎡⎤⎛⎫-+-++ ⎪⎢⎥⎝⎭⎣⎦,其中1,32a b =-= 【答案】(1)解:原式22123122323x x y x y =-+-+23x y =-+, 当22,3x y =-=时, 原式()()22323⎛⎫=-⨯-+ ⎪⎝⎭469=;(2)解:原式22222135262ab a b ab ab a b ⎛⎫=----+ ⎪⎝⎭ 2222235216ab a b ab ab a b =--+-+21a b =+, 当1,32a b =-=时, 原式21312⎛⎫=-⨯+ ⎪⎝⎭74=. 【点睛】本题考查了整式的加减运算和代数式求值,属于基础题目,熟练掌握运算法则是解题的关键.【专题训练】一、选择题1.(2020·江苏七年级期中)如果单项式232n x y -与37m x y 是同类项,则m n -的值是( )A .3B .2C .1D .1- 【答案】C2.(2020·山东临沂·七年级期中)下列各式的计算,正确的是( )A .2a a a +=B .3265x x x -=C .235325x x x +=D .22234-=-a b ba a b。
北师大版七年级上册整式的加减-去括号课件
解:原式=x2-y2-8x2+12y2 =-7x2+11y2.
(3)3(2x2-y2)-2(3y2-2x2);
解:原式=6x2-3y2-6y2+4x2
=10x2-9y2. (4)(8xy-x2+y2)-3(-x2+y2+5xy). 解:原式=8xy-x2+y2+3x2-3y2-15xy
=2x2-2y2-7xy.
仔细视察每个等式前后各项符号有什么特点?请勇敢的说 出来!
仔细的视察、总结,勇敢地说出你的 结论!!!
去括号法则:
“( )”前是“ +”去掉“ +( 符号 都不变 ;
)”,括号内各项的
“( )” 前是“ -”去掉“ -( )”, 括号内各项 的符号 都改变;
正去不变,负去全变
用字母表示为:
a + (b + c) = a + b + c ;
(2)原式=a+5a-3b-a+2b =5a-b.
(3)原式=6xy-3y-2xy =4xy-3y.
(4)原式=5x-y-(2x-2y) =5x-y-2x+2y
=3x+y.
归纳总结 去括号法则注意事项
(1)去括号时,不仅要去掉括号,还要连同括号前面的符号一起去掉. (2)去括号时,第一要弄清括号前是“+”号还是“-”号. (3)注意法则中的“都”字,变号时,各项都变号;不变号时,各项都 不变号. (4)当括号前有数字因数时,应运用乘法分配律运算,切勿漏乘. (5)出现多层括号时,一般是由里向外逐层去括号.
核心知识点二: 去括号步骤
视察下列式子,并从中归纳去括号步骤:
第一种:直接去括号(括号前系数为±1)
(1)4a - a - 3b
解:原式 4a - a 3b 3a 3b
(完整版)北师大数学七年级第三章整式的加减(二)—去括号与添括号(基础)
去 括 号去 括 号【学习目标】整式的加减(二)—去括号与添括号(基础)1. 掌握去括号与添括号法则,充分注意变号法则的应用;2. 会用整式的加减运算法则,熟练进行整式的化简及求值. 【要点梳理】要点一、去括号法则如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同; 如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反.要点诠释:(1)去括号法则实际上是根据乘法分配律推出的:当括号前为“+”号时,可以看作+1 与括号内的各项相乘;当括号前为“-”号时,可以看作-1 与括号内的各项相乘.(2)去括号时,首先要弄清括号前面是“+”号,还是“-”号,然后再根据法则去掉括号及前面的符号.(3)对于多重括号,去括号时可以先去小括号,再去中括号,也可以先去中括号.再去小括号.但是一定要注意括号前的符号. (4) 去括号只是改变式子形式,但不改变式子的值,它属于多项式的恒等变形. 要点二、添括号法则添括号后,括号前面是“+”号,括到括号里的各项都不变符号; 添括号后,括号前面是“-”号,括到括号里的各项都要改变符号.要点诠释:(1) 添括号是添上括号和括号前面的符号,也就是说,添括号时,括号前面的“+”号或“-”号也是新添的,不是原多项式某一项的符号“移”出来得到的.(2) 去括号和添括号是两种相反的变形,因此可以相互检验正误:如: a + b - c 添 括 号 要点三、整式的加减运算法则a + (b -c ) , a - b + c 添 括 号a - (b -c )一般地,几个整式相加减,如果有括号就先去括号,然后再合并同类项.要点诠释: (1) 整式加减的一般步骤是:①先去括号;②再合并同类项. (2) 两个整式相加减时,减数一定先要用括号括起来.(3) 整式加减的最后结果中:①不能含有同类项,即要合并到不能再合并为止;②一般按照某一字母的降幂或升幂排列;③不能出现带分数,带分数要化成假分数.【典型例题】 类型一、去括号1.去括号:(1)d-2(3a-2b+3c);(2)-(-xy-1)+(-x+y).【答案与解析】(1)d-2(3a-2b+3c)=d-(6a-4b+6c)=d-6a+4b-6c ;(2)-(-xy-1)+(-x+y)=xy+1-x+y .【总结升华】去括号时.若括号前有数字因数,应先把它与括号内各项相乘,再去括号. 举一反三【变式 1】去掉下列各式中的括号: (1). 8m-(3n+5); (2). n-4(3-2m);(3). 2(a-2b)-3(2m-n). 【答案】(1). 8m-(3n+5)=8m-3n-5.(2). n-4(3-2m)=n-(12-8m)=n-12+8m.(3). 2(a-2b)-3(2m-n)=2a-4b-(6m-3n)=2a-4b-6m+3n.【变式2】(2015•济宁)化简﹣16(x﹣0.5)的结果是()A.﹣16x﹣0.5 B.﹣16x+0.5 C. 16x﹣8 D.﹣16x+8【答案】D类型二、添括号2.在各式的括号中填上适当的项,使等式成立.(1). 2x + 3y - 4z + 5t =-( ) =+( ) = 2x - ( ) = 2x + 3y - ( ) ;(2). 2x - 3y + 4z - 5t = 2x + ( ) = 2x - ( ) = 2x - 3y - ( ) = 4z - 5t - ( ) .【答案】(1)-2x - 3y + 4z - 5t ,2x + 3y - 4z + 5t ,-3y + 4z - 5t ,4z - 5t .(2)-3y + 4z - 5t ,3y - 4z + 5t ,-4z + 5t ,-2x + 3y .【解析】(1) 2x + 3y - 4z + 5t =-(-2x - 3y + 4z - 5t) =+(2x + 3y - 4z + 5t)= 2x - (-3y + 4z - 5t) = 2x + 3y - (4z - 5t) ;(2) 2x - 3y + 4z - 5t = 2x + (-3y + 4z - 5t) = 2x - (3y - 4z + 5t)= 2x - 3y - (-4z + 5t) = 4z - 5t - (-2x + 3y) .【总结升华】在括号里填上适当的项,要特别注意括号前面的符号,考虑是否要变号.举一反三【变式】(1)a-b+c-d=a-();(2)x+2y-z=-();(4)a2-b2-a -b =a2-a -().(3)a2-b2+a -b =(a2-b2)+();【答案】b -c +d ;-x - 2 y +z ;a -b ;b2+b .类型三、整式的加减3.(2016•邢台二模)设A,B,C 均为多项式,小方同学在计算“A﹣B”时,误将符号抄错而计算成了“A+B”,得到结果是C,其中A=x2+x﹣1,C=x2+2x,那么A﹣B=()A.x2﹣2x B.x2+2x C.﹣2 D.﹣2x【思路点拨】根据题意得到 B=C﹣A,代入 A﹣B 中,去括号合并即可得到结果.【答案】C.【解析】解:根据题意得:A﹣B=A﹣(C﹣A)=A﹣C+A=2A﹣C=2(x2+x﹣1)﹣(x2+2x)=x2+2x﹣2﹣x2﹣2x=﹣2,故选 C.【总结升华】整式加减的一般步骤是:①先去括号;②再合并同类项.2类型四、化简求值4. 先化简,再求各式的值:;⎭ 【答案与解析】原式= 1 x - 3 x + 1 y 2 - 2x + 2y 2 = -3x + y 2 ,2 23 3当 x = -2, y = 时,原式= -3⨯(-2) + ( 2)2 = 6 + 4 = 6 4.3 3 9 9【总结升华】化简求值题一般采用“一化二代三计算”,此类题的书写格式一般为:当……时,原式=? 举一反三【变式 1】先化简再求值:(-x 2+5x+4)+(5x-4+2x 2),其中 x =-2.【答案】 (-x 2+5x+4)+(5x-4+2x 2)=-x 2+5x+4+5x-4+2x 2=x 2+10x.当 x =-2,原式=(-2)2+10×(-2)=-16.【变式 2】先化简,再求值: 3( y + 2x ) -[3x - (x - y )] - 2x ,其中 x , y 化为相反数.【答案】3( y + 2x ) -[3x - (x - y )] - 2x = 3y + 6x - 3x + x - y - 2x = 2(x + y )因为 x , y 互为相反数,所以 x + y = 0所以3( y + 2x ) -[3x - (x - y )] - 2x = 2(x + y ) = 2 ⨯ 0 = 05. 已知 xy = -2 , x + y = 3 ,求整式(3xy +10 y ) +[5x - (2xy + 2 y - 3x )] 的值.【答案与解析】由 xy = -2 , x + y = 3 很难求出 x , y 的值,可以先把整式化简,然后把 xy , x + y 分别作为一个整体代入求出整式的值. 原式= 3xy +10 y + (5x - 2xy - 2 y + 3x )= 3xy +10 y + 5x - 2xy - 2 y + 3x= 5x + 3x +10 y - 2 y + 3xy - 2xy= 8x + 8 y + xy= 8(x + y ) + xy .把 xy = -2 , x + y = 3 代入得,原式= 8⨯ 3 + (-2) = 24 - 2 = 22 .【总结升华】求整式的值,一般先化简后求值,但当题目中含未知数的部分可以看成一个整体时,要用整体代入法,即把“整体”当成一个新的字母,求关于这个新的字母的代数式的值,这样会使运算更简便.1 x + ⎛ - 3 x + 1 y2 ⎫ - ⎛ 2x - 2 y 2 ⎫ , 其中x = -2, y = 2 2 ⎝ 23 ⎪ ⎭ ⎝ 3 ⎪ 3举一反三【变式】已知代数式3y2- 2 y + 6 的值为 8,求3y2-y +1的值.2【答案】∵3y2- 2 y + 6 = 8 ,∴3y2- 2 y = 2 .当3y2- 2 y = 2 时,原式=1(3y2- 2 y) +1 =1⨯ 2 +1 = 2 .2 26. 如果关于 x 的多项式(8x2+ 6ax +14) - (8x2+ 6x + 5) 的值与 x 无关.你知道 a 应该取什么值吗?试试看.【答案与解析】所谓多项式的值与字母 x 无关,就是合并同类项,结果不含有“x”的项,所以合并同类项后,让含 x 的项的系数为 0 即可.注意这里的 a 是一个确定的数. (8x2+6ax+14)-(8x2+6x+5)=8x2+6ax+14-8x2-6x-5=6ax-6x+9=(6a-6)x+9由于多项式(8x2+6ax+14)-(8x2+6x+5)的值与 x 无关,可知 x 的系数 6a-6=0.解得 a=1.【总结升华】本例解题的题眼是多项式的值与字母 x 无关.“无关”意味着合并同类项后,其结果不含“x”的项.【巩固练习】一、选择题1.(2015•江西模拟)计算:a﹣2(1﹣3a)的结果为()A.7a﹣2B.﹣2﹣5aC.4a﹣2D.2a﹣22.(2016•黄陂区模拟)下列式子正确的是()A.x﹣(y﹣z)=x﹣y﹣z B.﹣(x﹣y+z)=﹣x﹣y﹣z C.x+2y﹣2z=x﹣2(z+y)D.﹣a+c+d+b=﹣(a﹣b)﹣(﹣c﹣d)3.计算-(a-b)+(2a+b)的最后结果为( ).A.a B.a+b C.a+2b D.以上都不对4.(2010·山西)已知一个多项式与3x2+9x 的和等于3x2+4x-1,则这个多项式是( )A.-5x-1 B.5x+1 C.-13x-1 D.13x+15.代数式-3x2y -10x3+ 3(2x3y +x2y) - (6x3y - 7x3+ 2) 的值( ).A.与x,y 都无关B.只与x 有关C.只与y 有关D.与x、y 都有关6.如图所示,阴影部分的面积是( ).A.11xy B.132 2xy C.6xy D.3xy二、填空题7.添括号:(1). -3 p + 3q -1 =+( ) = 3q - ( ) .(2). (a -b +c -d )(a +b -c +d ) = [a - ( )][a + ( )].8.(2015•镇江一模)化简:5(x﹣2y)﹣4(x﹣2y)= .9.若m2- 2m =1 则2m2- 4m + 2008 的值是.10.(2016•河北)若mn=m+3,则2mn+3m﹣5mn+10=.11.已知a=-(-2)2,b=-(-3)3,c=-(-42),则-[a-(b-c)]的值是.12.如图所示是一组有规律的图案,第 1 个图案由 4 个基础图形组成,第 2 个图案由 7 个基础图形组成,…,第n(n 是正整数)个图案中由个基础图形组成.三、解答题13. 化简 (1).(2015•宝应县校级模拟)2(3x2﹣2xy)﹣4(2x2﹣xy﹣1)(2). - 3x 2y + 2x 2y + 3xy 2- 2xy 2(3). 3m 2n -mn 2-6mn +n 2m - 0.8mn - 3n 2m 5(4). 3(2a2b-ab2 )-2(5a2b-4ab2 )(5).(6).14.化简求值:(1). 已知:a = 2010 ,求(a 2- 3 - 3a +a3 ) - (2a3+ 4a 2+a - 8) + (a3+ 3a 2+ 4a - 4) 的值.(2). -1a2b -⎡ 3a2b - 3⎛abc -1a2c⎫- 4a2c⎤- 3abc ,其中a = -1, b = -3, c = 1. 2⎢23 ⎪⎥⎣⎝⎭⎦(3). 已知3x + 5 y 2+ 3 的值是 6,求代数式- 3x - 4 y 2+ 9x + 14 y 2- 7 的值.15. 有一道题目:当 a=2,b=-2 时,求多项式:3a3b3-2a2b+b-(4a3b3-a2b-b2)+(a3b3+a2b)-2b2+3 的值.甲同学做题时把 a=2 错抄成 a=-2,乙同学没抄错题,但他们做出的结果恰好一样。
强化训练-北师大版七年级数学上册第三章整式及其加减难点解析试题(含答案及解析)
七年级数学上册第三章整式及其加减难点解析考试时间:90分钟;命题人:数学教研组考生注意:1、本卷分第I 卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I 卷(选择题 30分)一、单选题(10小题,每小题3分,共计30分)1、代数式3x 2y-4x 3y 2-5xy 3-1按x 的升幂排列,正确的是( )A .-4x 3y 2+3x 2y-5xy 3-1B .-5xy 3+3x 2y-4x 3y 2-1C .-1+3x 2y-4x 3y 2-5xy 3D .-1-5xy 3+3x 2y-4x 3y 2 2、已知135x a b +与51712y a b +的和是单项式,则3x y +等于( ) A .10- B .10 C .12 D .153、整式()()()22241332xyz xy xy z yx xyz xy +-+-+--+的值( ).A .与x 、y 、z 的值都有关B .只与x 的值有关C .只与x 、y 的值有关D .与x 、y 、z 的值都无关4、当1x =时,代数式31px qx ++的值为2021,则当1x =-时,代数式31px qx ++的值为( )A .2020B .-2020C .2019D .-20195、下列是按一定规律排列的多项式:﹣x +y ,x 2+2y ,﹣x 3+3y ,x 4+4y ,﹣x 5+5y ,x 6+6y ,…,则第n 个多项式是( )A .(﹣1)nxn +nyB .﹣1nxn +nyC .(﹣1)n +1xn +nyD .(﹣1)nxn +(﹣1)nny6、已知221a a +=,则代数式()2221a a +-的值为( )A .0B .1C .1-D .2-7、下列变形正确的是( )A .(2)2a a -+=-B .1(21)212a a --=-+ C .1(1)a a -+=--D .1(1)a a -=-+8、化简()a b c ---的结果是( )A .a b c --B .a b c ---C .a b c -+-D .a b c -++9、下列代数式中是二次三项式的是( )A .232x x x +-B .222x xy y ++C .()22m mn -D .3221a a +- 10、已知a +b =4,则代数式122ab ++的值为( )A .3B .1C .0D .-1第Ⅱ卷(非选择题 70分)二、填空题(5小题,每小题4分,共计20分)1、已知多项式4(1)25n m x x x --+-是三次三项式,则(m +1)n =___.2、若x 2+2x 的值是6,则2x 2+4x ﹣7的值是__________.3、观察:第1个等式21321⨯=-,第2个等式23541⨯=-,第3个等式25761⨯=-,第4个等式27981⨯=-…猜想:第n 个等式是________.4、若单项式33m x y 与512n x y +-是同类项,则()m n -=________.5、某商品原价为a 元,如果按原价的八折销售,那么售价是_____元.(用含字母a 的代数式表示).三、解答题(5小题,每小题10分,共计50分)1、化简并求值:22111122222x x y x y ⎛⎫⎛⎫--+-+ ⎪ ⎪⎝⎭⎝⎭,其中2x =-,23y =. 2、探究规律题:按照规律填上所缺的单项式并回答问题:(1)a ,﹣2a 2,3a 3,﹣4a 4, , ;(2)试写出第2017个和第2018个单项式;(3)试写出第n 个单项式;(4)当a =﹣1时,求代数式a +2a 2+3a 3+4a 4+…+99a 99+100a 100+101a 101的值.3、若2,1a b a c -=-=,求22(2)()a b c c b --+-的值.4、代数式2323(324)(3)a a a a a a +---里的“”是“+,-,×,÷”中某一种运算符号.(1)如果“”是“+”,化简:2323(324)(3)a a a a a a +---;(2)当1a =-时,2323(324)(3)a a a a a a +---2=-,请推算“”所代表的运算符号.5、在数的学习过程中,我们总会对其中一些具有某种特性的数充满好奇,如学习自然数时,我们发现一种特殊的自然数——“好数”.定义:对于三位自然数n ,各位数字都不为0,且百位数字与十位数字之和恰好能被个位数字整除,则称这个自然数n 为“好数”.例如:426是“好数”,因为4,2,6都不为0,且4+2=6,6能被6整除;643不是“好数”,因为6+4=10,10不能被3整除.(1)判断312,675是否是“好数”?并说明理由;(2)求出百位数字比十位数字大5的所有“好数”的个数,并说明理由.-参考答案-一、单选题1、D【解析】【分析】先分清多项式的各项,然后按多项式升幂排列的定义排列.【详解】解:3x 2y-4x 3y 2-5xy 3-1的项是3x 2y 、-4x 3y 2、-5xy 3、-1,按x 的升幂排列为-1-5xy 3+3x 2y-4x 3y 2,故D 正确;故选D .【考点】考查了多项式,我们把一个多项式的各项按照某个字母的指数从大到小或从小到大的顺序排列,称为按这个字母的降幂或升幂排列.要注意,在排列多项式各项时,要保持其原有的符号.2、B【解析】【分析】由同类项的含义可得:15,13x y +=+=,再求解,x y ,再代入代数式求值即可得到答案.【详解】解:因为135x a b +与51712y a b +的和是单项式,所以它们是同类项, 所以15,13x y +=+=,解得4,2x y ==.所以343210x y +=+⨯=.故选:.B【考点】本题考查的是同类项的含义,一元一次方程组的解法,代数式的值,掌握同类项的概念是解题的关键.3、D【解析】【分析】原式去括号合并得到最简结果,判断即可.【详解】解:原式=xyz 2+4yx -1-3xy +z 2yx -3-2xyz 2-xy =-4,则代数式的值与x 、y 、z 的取值都无关.故选D .【考点】本题主要考查了整式的加减,解决本题的关键是要熟练掌握运算法则是解本题的关键.4、D【解析】【分析】先将x=1代入代数式31px qx ++中,得到p 、q 的关系式,再将x=-1代入即可解答.【详解】将x=1代入代数式31px qx ++中,得:12021p q ++=,将x=-1代入代数式31px qx ++中,得:31px qx ++=1(1)2202122019p q p q --+=-+++=-+=-,故答案为:D .【考点】本题考查的是代数式求值,会将所得关系式适当变形是解答的关键.5、A【解析】【分析】从三方面(符号、系数的绝对值、指数)总结规律,再根据规律进行解答便可.【详解】解:按一定规律排列的多项式:﹣x +y ,x 2+2y ,﹣x 3+3y ,x 4+4y ,﹣x 5+5y ,x 6+6y ,…,则第n 个多项式是:(﹣1)nxn +ny ,故选:A .【考点】本题考查的是整式中的多项式的规律探究,掌握探究的方法是解题的关键.6、B【解析】【分析】把221a a +=代入代数式()2221a a +-,求出算式的值为多少即可.【详解】解:∵221a a +=,∴()2221a a +-211=1=⨯-故选B .【考点】本题考查了代数式的求值:求代数式的值可以直接代入、计算.如果给出的代数式可以化简,要先化简再求值.7、C【解析】【分析】根据去括号和添括号法则解答.【详解】A 、原式=−a −2,故本选项变形错误.B 、原式=−a +12,故本选项变形错误.C 、原式=−(a −1),故本选项变形正确.D 、原式=−(a −1),故本选项变形错误.故选:C .【考点】本题主要考查了去括号与添括号,①去括号法则是根据乘法分配律推出的;②去括号时改变了式子的形式,但并没有改变式子的值;③添括号时,如果括号前面是正号,括到括号里的各项都不变号,如果括号前面是负号,括号里的各项都改变符号.添括号与去括号可互相检验.8、D【解析】【分析】根据去括号的方法计算即可.【详解】解:−(a −b −c )=−a +b +c .故选D .【考点】本题考查去括号的方法:去括号时,运用乘法的分配律,先把括号前的数字与括号里各项相乘,再运用括号前是“+”,去括号后,括号里的各项都不改变符号;括号前是“−”,去括号后,括号里的各项都改变符号.运用这一法则去掉括号.9、B【解析】【分析】根据多项式的次数和项数的概念,逐一判断即可.【详解】解:A. 232x x x +-是三次三项式,不符合题意,B. 222x xy y ++是二次三项式,符合题意,C. ()22m mn -是二次二项式,不符合题意,D. 3221a a +-是三次三项式,不符合题意,故选B .【考点】本题主要考查多项式的次数和项数,掌握多项式的次数是多项式的最高次项的次数,是解题的关键.10、A【解析】【分析】通过将所求代数式进行变形,然后将已知代数式代入即可得解.【详解】由题意,得411132222a b a b +++=+=+= 故选:A.【考点】此题主要考查已知代数式求代数式的值,熟练掌握,即可解题.二、填空题1、8【解析】【分析】根据多项式的项、次数的定义可得这个多项式中不含4(1)m x -,且n x -的次数为3,由此可得出,m n 的值,再代入计算即可得.【详解】解:由题意得:10,3m n -==,即1,3m n ==,则3(1)(11)8n m +=+=,故答案为:8.【考点】本题考查了多项式的项和次数,掌握理解定义是解题关键. 2、5【解析】【分析】把x2+2x当做一个整体代入所求即可求解.【详解】∵x2+2x=6∴2x2+4x﹣7=2(x2+2x)﹣7=2×6-7=5故填:5.【考点】此题主要考查代数式求值,解题的关键是熟知整体代入的方法.3、(2n-1)(2n+1)=(2n)2-1【解析】【分析】根据题目所给示例总结出相应的规律即可;【详解】解:第1个等式2⨯=-,1321第2个等式2⨯=-,3541第3个等式2⨯=-,5761第4个等式27981⨯=-,第n个等式(2n-1)(2n+1)=(2n)2-1;故答案为:(2n-1)(2n+1)=(2n)2-1.【考点】本题主要考查整式的应用,根据示例总结出相关规律是解题的关键.-4、32【分析】利用同类项的定义求出m ,n 的值,再代入求值即可.【详解】解:∵单项式3xmy 3与﹣2x 5yn +1是同类项,∴m =5,3=n +1,即m =5,n =2,∴(﹣n )m =(﹣2)5=﹣32,故答案为:﹣32.【考点】本题主要考查了同类项,解题的关键是熟记同类项的定义.5、0.8a【解析】【详解】【分析】根据实际售价=原价×10折扣数即可得. 【详解】实际售价=原价×10折扣数, 某商品原价为a 元,按原价的八折销售则售价为0.8a 元,故答案为0.8a .【考点】本题考查了销售问题、列代数式,弄清题意,列出符合题意的代数式是解题的关键.三、解答题1、2322x y -+;143【分析】先去括号,然后根据整式的加减计算法则化简,最后代值计算即可.【详解】 解:原式221112222x x y x y =-+-+ 221112222x x x y y =--++ 2322x y =-+, 当2x =-,23y =时,原式()2322142242333⎛⎫=-⨯-+⨯=+= ⎪⎝⎭. 【考点】本题主要考查了整式的化简求值,熟知相关计算法则是解题的关键.2、(1)55a ,66a -;(2)20172017a ,20182018a -;(3)1(1)n n a +-;(4)51-【解析】【分析】(1)根据规律找出系数和次数的规律即可;(2)根据(1)的规律即可求得第2017个和第2018个单项式;(3)根据(1)的规律写出第n 个单项式;(4)将1a =-代入求值即可【详解】(1)根据规律第5个单项式为55a ,第6个单项式为66a -故答案为:55a ,66a -(2)第2017个和第2018个单项式分别为20172017a ,20182018a -(3)系数的规律:第n 个对应的系数是1(1)n n +-⨯,指数的规律:第n 个对应的指数是n ,∴第n 个单项式是1(1)n n a +-,(4)当a =﹣1时,a +2a 2+3a 3+4a 4+…+99a 99+100a 100+101a 1011234100101=-+-+-+-……()()()123499100101=-++-+++-+-……50101=-51=-【考点】此题考查单项式的规律探索,分别找出单项式的系数和指数的规律是解决此类问题的关键. 3、10【解析】【分析】先把原代数式化为:22[()()][()()]a b a c a b a c -+-+---,再整体代入求值即可.【详解】 解: 2,1a b a c -=-=∴ 原式=22[()()][()()]a b a c a b a c -+-+---22(21)(21)10=++-=【考点】本题考查的是求解代数式的值,添括号的应用,掌握“整体代入法求解代数式的值”是解本题的关键.4、(1)322a a a -++;(2)-.【解析】【分析】(1)把“+”代入原式,去括号合并即可得到结果;(2)原式去括号后,把1a =-代入计算即可求出所求.【详解】解:(1)原式23233243a a a a a a =+---+322a a a =-++.(2)由题意得,2323(324)(3)2a a a a a a +---=-2323324()32a a a a a a +--+=-23232()2a a a a a +--=-当1a =-时,代入上式得321[1(1)]2-++--=-,即[1(1)]2-=,∵1(1)2--=, ∴“”所表示的运算符号是“-”.【考点】此题考查了整式的加减,以及有理数的混合运算,熟练掌握运算法则是解本题的关键.5、(1)312是“好数”,675不是“好数”,理由见解析;(2)611,617,721,723,729,831,941.理由见解析.【解析】【分析】(1)根据“好数”的定义进行判断即可;(2)设十位数字为x,个位数字为y,则百位数字为(x+5).根据题意判断出x、y取值,根据“好数”定义逐一判断即可.【详解】(1)∵3,1,2都不为0,且3+1=4,4能被2整除,∴312是“好数”.∵6,7,5都不为0,且6+7=13,13不能被5整除,∴675不是“好数”;(2)设十位数字为x,个位数字为y,则百位数字为(x+5).其中x,y都是正整数,且1≤x≤4,1≤y≤9.十位数字与个位数字的和为:2x+5.当x=1时,2x+5=7,此时y=1或7,“好数”有:611,617当x=2时,2x+5=9,此时y=1或3或9,“好数”有:721,723,729当x=3时,2x+5=11,此时y=1,“好数”有:831当x=4时,2x+5=13,此时y=1,“好数”有:941所以百位数字比十位数字大5的所有“好数”的个数是7.【考点】本题为“新定义”问题,理解好“新定义”,并根据已有数学知识和隐含条件进行分析,转化为所学数学问题是解题关键.。
七年级数学上册难点突破13整式的加减全章复习与巩固试题含解析新版北师大版
七年级数学上册难点突破:专题13 整式的加减全章复习与巩固【专题说明】1.理解并掌握单项式与多项式的相关概念;2.理解整式加减的基础是去括号和合并同类项,并会用整式的加减运算法则,熟练进行整式的加减运算、求值;3.深刻体会本章体现的主要的数学思想----整体思想.【知识点总结】一、整式的相关概念1.单项式:由数字或字母的积组成的代数式叫做单项式,单独的一个数或一个字母也是单项式.要点诠释:(1)单项式的系数是指单项式中的数字因数.(2)单项式的次数是指单项式中所有字母的指数和.2.多项式:几个单项式的和叫做多项式.在多项式中,每个单项式叫做多项式的项.要点诠释:(1)在多项式中,不含字母的项叫做常数项.(2)多项式中次数最高的项的次数,就是这个多项式的次数.(3)多项式的次数是n次,有m个单项式,我们就把这个多项式称为n次m项式.3. 多项式的降幂与升幂排列:把一个多项式按某一个字母的指数从大到小的顺序排列起来,叫做把这个多项式按这个字母降幂排列.另外,把一个多项式按某一个字母的指数从小到大的顺序排列起来,叫做把这个多项式按这个字母升幂排列.要点诠释:(1)利用加法交换律重新排列时,各项应带着它的符号一起移动位置;(2)含有多个字母时,只按给定的字母进行降幂或升幂排列.4.整式:单项式和多项式统称为整式.二、整式的加减1.同类项:所含字母相同,并且相同字母的指数也相同的项叫做同类项.所有的常数项都是同类项.要点诠释:辨别同类项要把准“两相同,两无关”:(1)“两相同”是指:①所含字母相同;②相同字母的指数相同;(2)“两无关”是指:①与系数无关;②与字母的排列顺序无关.2.合并同类项:把多项式中的同类项合并成一项,叫做合并同类项.要点诠释:合并同类项时,只是系数相加减,所得结果作为系数,字母及字母的指数保持不变.3.去括号法则:括号前面是“+”,把括号和它前面的“+”去掉后,原括号里各项的符号都不改变;括号前面是“-”,把括号和它前面的“-”号去掉后,原括号里各项的符号都要改变.4.添括号法则:添括号后,括号前面是“+”,括号内各项的符号都不改变;添括号后,括号前面是“-”,括号内各项的符号都要改变.5.整式的加减运算法则:几个整式相加减,通常用括号把每一个整式括起来,再用加、减号连接,然后去括号,合并同类项.【精典例题】一、整式的相关概念1、指出下列各式中的整式、单项式和多项式,是单项式的请指出系数和次数,是多项式的请说出是几次几项式.(1)3a - (2)5 (3)2b a - (4)2x y - (5)3xy (6)x π (7)5m n + (8)1+a % (9)1()2a b h + 【答案与解析】解:整式:(1)、(2)、(4)、(5)、(6)、(7)、(8)、(9)单项式:(2)、(5)、(6),其中:5的系数是5,次数是0;3xy 的系数是3,次数是2;x π的系数是1π,次数是1. 多项式:(1)、(4)、(7)、(8)、(9),其中:3a -是一次二项式;2x y -是一次二项式;5m n +是一次二项式;1+a %是一次二项式; 1()2a b h +是二次二项式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题12 整式的加减-去括号与添括号 【专题说明】1.掌握去括号与添括号法则,充分注意变号法则的应用;2. 会用整式的加减运算法则,熟练进行整式的化简及求值.【知识点总结】一、去括号法则如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同;如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反.要点诠释:(1)去括号法则实际上是根据乘法分配律推出的:当括号前为“+”号时,可以看作+1与括号内的各项相乘;当括号前为“-”号时,可以看作-1与括号内的各项相乘.(2)去括号时,首先要弄清括号前面是“+”号,还是“-”号,然后再根据法则去掉括号及前面的符号.(3)对于多重括号,去括号时可以先去小括号,再去中括号,也可以先去中括号.再去小括号.但是一定要注意括号前的符号.(4)去括号只是改变式子形式,但不改变式子的值,它属于多项式的恒等变形.二、添括号法则添括号后,括号前面是“+”号,括到括号里的各项都不变符号;添括号后,括号前面是“-”号,括到括号里的各项都要改变符号.要点诠释:(1)添括号是添上括号和括号前面的符号,也就是说,添括号时,括号前面的“+”号或“-”号也是新添的,不是原多项式某一项的符号“移”出来得到的.(2)去括号和添括号是两种相反的变形,因此可以相互检验正误:如:()a b c a b c +-+-添括号去括号, ()a b c a b c -+--添括号去括号三、整式的加减运算法则一般地,几个整式相加减,如果有括号就先去括号,然后再合并同类项.要点诠释:(1)整式加减的一般步骤是:①先去括号;②再合并同类项. (2)两个整式相加减时,减数一定先要用括号括起来.(3)整式加减的最后结果中:①不能含有同类项,即要合并到不能再合并为止;②一般按照某一字母的降幂或升幂排列;③不能出现带分数,带分数要化成假分数.【精典例题】一、去括号1、去括号:(1)d -2(3a -2b +3c );(2)-(-xy -1)+(-x +y ).【答案与解析】(1)d -2(3a -2b +3c )=d -(6a -4b +6c )=d -6a +4b -6c ;(2)-(-xy -1)+(-x +y )=xy +1-x +y .【总结升华】去括号时.若括号前有数字因数,应先把它与括号内各项相乘,再去括号.2、a b c --+的相反数是( ).A .a b c ++B .a b c -+C .a b c +-D .c a b +-【答案】C【解析】求a b c --+的相反数实质是求()a b c ---+,去括号,得()a b c a b c ---+=+-.【总结升华】去括号时.若括号前有数字因数,应先把它与括号内各项相乘,再去括号.二、添括号1、在各式的括号中填上适当的项,使等式成立.(1). 2345()()x y z t +-+=-=+2()x =-23()x y =+-; (2). 23452()2()x y z t x x -+-=+=-23()45()x y z t =--=--.【答案】(1). 2345x y z t --+-,2345x y z t +-+,345y z t -+-,45z t -.(2). 345y z t -+-,345y z t -+,45z t -+,23x y -+.【解析】(1)2345x y z t +-+ (2345)x y z t =---+-(2345)x y z t =++-+2(345)x y z t =--+-23(45)x y z t =+--;(2)2345x y z t -+-2(345)x y z t =+-+-2(345)x y z t =--+23(45)x y z t =---+45(23)z t x y =---+.【总结升华】在括号里填上适当的项,要特别注意括号前面的符号,考虑是否要变号.2、按要求把多项式321a b c -+-添上括号:(1)把含a 、b 的项放到前面带有“+”号的括号里,不含a 、b 的项放到前面带有“-”号的括号里;(2)把项的符号为正的放到前面带有“+”号的括号里,项的符号为负的放到前面带有“-”号的括号里.【答案与解析】(1)321(32)(1)a b c a b c -+-=---+;(2)321(3)(21)a b c a c b -+-=+-+.【总结升华】在括号里填上适当的项,要特别注意括号前面的符号,考虑是否要变号.三、整式的加减1、()()222232,23,1.;2.23.M x xy y N x xy y M N M N =-+=+---已知求: 【答案与解析】(1)2222(32)(23)M N x xy y x xy y -=-+-+- 222222223223(32)(21)(13)34x xy y x xy y x xy y x xy y =-+--+=--+++=-+ (2)2222232(32)3(23)M N x xy y x xy y -=-+-+- 2222(642)(639)x xy y x xy y =-+-+-2222222642639(66)(43)(29)711x xy y x xy y x xy y xy y =-+--+=--+++=-+【总结升华】整式加减的一般步骤是:①先去括号;②再合并同类项.2、3243245348x x x x x x -+--+-一个多项式加上得,求这个多项式. 【答案与解析】在解答此题时应先根据题意列出代数式,注意把加式,和式看作一个整体,用括号括起来,然后再进行计算,在计算过程中找同类项,可以用不同的记号标出各同类项,减少运算的错误.43232(348)(45)x x x x x x --+---+ 4323243348453813x x x x x x x x x =--+--+-=-+-答:所求多项式为433813x x x -+-.【总结升华】整式加减的一般步骤是:①先去括号;②再合并同类项.3、化简:(1)15+3(1-x )-(1-x +x 2)+(1-x +x 2-x 3).(2)3x 2y -[2x 2z -(2xyz -x 2z +4x 2y )].(3)-3[(a 2+1)-16(2a 2+a )+13(a -5)]. (4)ab -{4a 2b -[3a 2b -(2ab -a 2b )+3ab ]}.【答案】 (1)15+3(1-x )-(1-x +x 2)+(1-x +x 2-x 3)=15+3(1-x )-(1-x +x 2)+(1-x +x 2)-x 3=18-3x -x 3.. ……整体合并,巧去括号(2)3x 2y -[2x 2z -(2xyz -x 2z +4x 2y )]=3x 2y -2x 2z +(2xy -x 2z +4x 2y ) ……由外向里,巧去括号=3x 2y -2x 2z +2xyz -x 2z +4x 2y=7x 2y -3x 2z +2xyz .(3)22113[(1)(2)(5)]63a a a a -+-++- 2213(1)(2)(5)2a a a a =-+++-- 2213352a a a a =--++-+ 21222a a =--+. (4)ab -{4a 2b -[3a 2b -(2ab -a 2b )+3ab ]}=ab -4a 2b +3a 2b -2ab +a 2b +3ab ……一举多得,括号全脱=2ab .四、化简求值1、先化简,再求各式的值:22131222,2,;22333x x y x y x y ⎛⎫⎛⎫+-+--=-= ⎪ ⎪⎝⎭⎝⎭其中 【答案与解析】原式=2221312232233x x y x y x y -+-+=-+, 当22,3x y =-=时,原式=22443(2)()66399-⨯-+=+=. 【总结升华】化简求值题一般采用“一化二代三计算”,此类题的书写格式一般为:当……时,原式=?2、已知2xy =-,3x y +=,求整式(310)[5(223)]xy y x xy y x ++-+-的值.【答案与解析】由2xy =-,3x y +=很难求出x ,y 的值,可以先把整式化简,然后把xy ,x y +分别作为一个整体代入求出整式的值.原式310(5223)xy y x xy y x =++--+3105223xy y x xy y x =++--+5310232x x y y xy xy =++-+-88x y xy =++8()x y xy =++.把2xy =-,3x y +=代入得,原式83(2)24222=⨯+-=-=.【总结升华】求整式的值,一般先化简后求值,但当题目中含未知数的部分可以看成一个整体时,要用整体代入法,即把“整体”当成一个新的字母,求关于这个新的字母的代数式的值,这样会使运算更简便.3、如果关于x 的多项式22(8614)(865)x ax x x ++-++的值与x 无关.你知道a 应该取什么值吗?试试看.【答案与解析】所谓多项式的值与字母x 无关,就是合并同类项,结果不含有“x ”的项,所以合并同类项后,让含x 的项的系数为0即可.注意这里的a 是一个确定的数.(8x 2+6ax +14)-(8x 2+6x +5)=8x 2+6ax +14-8x 2-6x -5=6ax -6x +9=(6a -6)x +9由于多项式(8x 2+6ax +14)-(8x 2+6x +5)的值与x 无关,可知x 的系数6a -6=0.解得a =1.【总结升华】本例解题的题眼是多项式的值与字母x 无关.“无关”意味着合并同类项后,其结果不含“x ”的项.4、先化简,再求各式的值:(){}123225,,12x y x x y x y x y --+-++==-⎡⎤⎣⎦其中. 【答案与解析】原式[2(3245)][2(3)]x y x x y x y x y x x y =--+--+=--+-+(23)(43)43444()x y x x y x y x x y x x y x y =---+=--=-+=-=- 将1,12x y ==-代入,得:134[(1)]4622--=⨯=. 【总结升华】化简求值题一般采用“一化二代三计算”,此类题最后结果的书写格式一般为:当……时,原式=?5、已知3a 2-4b 2=5,2a 2+3b 2=10.求:(1)-15a 2+3b 2的值;(2)2a 2-14b 2的值.【答案与解析】显然,由条件不能求出a 、b 的值.此时,应采用技巧求值,先进行拆项变形.解:(1)-15a 2+3b 2=-3(5a 2-b 2)=-3[(3a 2+2a 2)+(-4b 2+3b 2)]=-3[(3a 2-4b 2)+(2a 2+3b 2)]=-3×(5+10)=-45;(2)2a 2-14b 2=2(a 2-7b 2)=2[(3a 2-2a 2)+(-4b 2-3b 2)]=2×[(3a 2-4b 2)-(2a 2+3b 2)]=2×(5-10)=-10.【总结升华】求整式的值,一般先化简后求值,但当题目中含未知数的部分可以看成一个整体时,要用整体代入法,即把“整体”当成一个新的字母,求关于这个新的字母的代数式的值,这样会使运算更简便.6、已知多项式2x ax y b +-+与2363bx x y -+-的差的值与字母x 无关,求代数式: 22223(2)(4)a ab b a ab b ---++的值.【答案与解析】222(363)(1)(3)7(3)x ax y b bx x y b x a x y b +-+--+-=-++-++由于多项式2x ax y b +-+与2363bx x y -+-的差的值与字母x 无关,可知: 10b -=,30a +=,即有1,3b a ==-又2222223(2)(4)74a ab b a ab b a ab b ---++=---,将1,3b a ==-代入可得:22(3)7(3)1418---⨯-⨯-⨯=.【总结升华】本例解题的题眼是多项式的值与字母x 无关.“无关”意味着合并同类项后,其结果不含“x ”的项,所以合并同类项后,让含x 的项的系数为0即可.五、整式加减运算的应用1、有一种石棉瓦(如图所示),每块宽60厘米,用于铺盖屋顶时,每相邻两块重叠部分的宽都为10厘米,那么n (n 为正整数)块石棉瓦覆盖的宽度为 ( ) .A .60n 厘米B .50n 厘米C .(50n +10)厘米D .(60n -10)厘米【答案】C .【解析】观察上图,可知n 块石棉瓦重叠的部分有(n -1)处,则n 块石棉瓦覆盖的宽度为:60n -10(n -1)=50n +10(厘米).【总结升华】求解本题时一定要注意每相邻两块重叠部分的宽都为10厘米这一已知条件,一不小心就可能弄错.。
