广东中考数学压轴题
2022中考数学压轴题-广东卷

2022中考数学压轴题-广东卷第22题12分,是道送分的几何题,这最后一道压轴题看着也没有太大的难度,12分,压轴题比较难的地区的同学们,扎心了。
(1)常规求解析式的问题,简单计算一下,就不多解释了;根据A坐标(1,0),以及AB=4可知B(-3,0)由两根之和可知b=2,两根之积可知c=-3则解析式y=x²+2x-3(2)△PCQ中没有一条边是横平竖直的,所以我们要找准三角形的底和高;毕竟有个PQ//BC,那么这个PQ可以当做底,当然如果用AQ当做底其实也行,我们这里选择PQ吧;既然有平行,就有线段比例,所以PQ还是可以用式子来表示的;若PQ为底,则高其实就是BC和PQ之间的距离,计算距离,这里平行线间的距离也就是垂线段,在垂直关系当中,可以想到的方法有勾股定理和三角函数,而这里BC是固定的,那么∠ABC也是固定的,所以借助三角函数还是比较容易想到的。
顶点C(-1,-4)我们假设AP长度为m,则BP=4-m由B和C坐标可知BC=2√5∴PQ/BC=AP/AB=m/4则PQ=√5/2·m而PQ和BC的距离可由BP长度以及∠ABC的三角函数来搞定不难知道tan∠ABC=2则sin∠ABC=2√5/5∴PQ和BC之间的距离h=BP·sin∠ABC=2√5/5·(4-m)则△PCQ的面积=PQ·h/2=√5/2·m·2√5/5·(4-m)·1/2=m(4-m)/2=-0.5(m²-4m)=-0.5(m-2)²+2∴当m=2时,△PCQ面积最大为2此时AP=2,P在AB之间,符合∴P坐标(-1,0),对应△PCQ面积最大值2;。
2024广东中考数学压轴题

2024广东中考数学压轴题一、在直角坐标系中,抛物线y = ax2 + bx + c与x轴交于点A(-3,0)和B(1,0),且与y 轴交于点C(0,3)。
下列说法正确的是:A. a > 0B. b < 0C. c = 0D. 抛物线的对称轴是直线x = -1(答案:D)二、已知三角形ABC的三边长为a,b,c,且满足a2 + b2 + c2 = 10a + 6b + 8c - 50。
则下列判断三角形ABC的形状中,正确的是:A. 等腰三角形B. 等边三角形C. 直角三角形D. 等腰直角三角形(答案:D)三、函数y = (x - 1)/(x + 2)中,当x的值增大时,y的值会:A. 一直增大B. 一直减小C. 在某个区间内增大,在另一个区间内减小D. 保持不变(答案:C)四、已知四边形ABCD是平行四边形,且AB = 6,BC = 8,对角线AC与BD相交于点O,则下列关于O点到AB和BC的距离d1和d2的说法正确的是:A. d1 + d2 = 14B. d1 × d2 = 24C. d1/d2 = AB/BCD. d12 + d22 = AB2 + BC2(答案:B)五、圆O的半径为5,点P在圆O外,且OP = 8。
过点P作圆O的两条切线,分别与圆O 相切于点A和B。
则弦AB的长度为:A. 6B. 4√3C. 5√2D. 2√15(答案:A)六、在数轴上,点A表示的数为-2,点B表示的数为3。
若点C表示的数为x,且满足AC + BC = 8,则x的值为:A. -3或4B. -4或3C. -3或-1D. 2或-5(答案:B)七、已知二次函数y = ax2 + bx + c的图像经过点(1,0),(2,0)和(3,4)。
下列说法正确的是:A. a > 0B. b < 0C. c = 0D. 函数的顶点在x轴上(答案:A)八、正方形ABCD的边长为4,点E在边AB上,且AE = 1。
广东省历年中考数学压轴题

广东省历年中考数学压轴题(1) 姓名:1.(2010年)阅读下列材料:)210321(3121⨯⨯-⨯⨯=⨯,)321432(3132⨯⨯-⨯⨯=⨯,)432543(3143⨯⨯-⨯⨯=⨯,由以上三个等式相加,可得2054331433221=⨯⨯=⨯+⨯+⨯.读完以上材料,请你计算下各题:(1)1110433221⨯++⨯+⨯+⨯ (写出过程); (2)=+⨯++⨯+⨯+⨯)1(433221n n ;(3)=⨯⨯++⨯⨯+⨯⨯+⨯⨯987543432321 .2.(2009年9分)小明用下面的方法求出方程032=-x 的解,请你仿照他的方法求出下面两个方程的解,并把你的解答过程填写在下面的表格,3.(2010年9分)某学校组织340名师生进行长途考察活动,带有行礼170件,计划租用甲、乙两种型号的汽车共有10辆.经了解,甲车每辆最多能载40人和16件行李,乙车每辆最多能载30人和20件行李.⑴请你帮助学校设计所有可行的租车方案;⑵如果甲车的租金为每辆2000元,乙车的租金为每辆1800元,问哪种可行方案使租车费用最省?A 2A A 1 BB 1B 2 B 3 B 4 B 5 B 6 B 7A 3A 4A 5 A 6A 7 O广东省历年中考数学压轴题(2) 姓名:4.(2007年9分)已知等边OAB ∆的边长为a ,以AB 边上的高1OA 为边,按逆时针方向作等边11B OA ∆,11B A 与OB 相交于点2A .(1)求线段2OA 的长;(2)若再以2OA 为边按逆时针方向作等边22B OA ∆,22B A 与1OB 相交于点3A ,按此作法进行下去,得到33B OA ∆,44B OA ∆,…,n n B OA ∆ (如图)。
求66B OA ∆的周长.5.(2005年9分)如图,已知半圆O的直径AB=4,将一个三角板的直角顶点固定在圆心O上,当三角板绕点O转动时,三角板的两条直角边与半圆圆周分别交于C、D两点,连接AD、BC交于点E。
广东中考数学2023压轴题

广东中考数学2023压轴题
题目
一辆汽车以每小时60公里的速度行驶,行驶了3小时后,又以每小时80公里的速度行驶了2小时。
求这段行程的平均速度是多少?
一个长方形花坛的长是12米,宽是8米。
现在要在花坛四周围上一圈砖,每块砖的边长是0.5米。
问需要多少块砖?
一条绳子长120米,现在要将其分成3段,第一段比第二段长10米,第二段比第三段长20米。
求每段绳子的长度。
甲、乙两个水果摊位上的苹果和橙子的价格比例是3:2。
现在甲摊位上苹果的价格是每斤6元,乙摊位上橙子的价格是每斤4元。
问甲、乙两个摊位上苹果和橙子的价格分别是多少?
一个三角形的两边长分别是5厘米和8厘米,夹角的正弦值是0.6。
求这个三角形的面积。
挑战压轴题解答题(真题汇编压轴特训)-2024年中考数学冲刺 挑战压轴题专题汇编(广州卷)(原卷版)

03挑战压轴题(解答题一)(1)尺规作图:将法);(2)在(1)所作的图中,连接V①求证:ABD②若tan BAC∠2.(2022·广东广州·统考中考真题)某数学活动小组利用太阳光线下物体的影子和标杆测量旗杆的高度.如图,在某一时刻,旗杆的AB的影子为BC,与此同时在C处立一根标杆CD,标杆CD的影子为CE,CD = 1.6m,BC =5CD.(1)求BC的长;(2)从条件①、条件②这两个条件中选择一个作为已知,求旗杆AB的高度.条件①:CE = 1.0m;条件②:从D处看旗杆顶部A的仰角α为54.46°.注:如果选择条件①和条件②分别作答,按第一个解答计分.参考数据:sin54.46°≈0.81,cos54.46°≈0.58,tan54.46°≈1.40.(1)求A 、B 两点的坐标;(2)设PAO V 的面积为S ,求S 关于x 的函数解析式:并写出x 的取值范围;(3)作PAO V 的外接圆C e ,延长PC 交C e 于点Q ,当POQ △的面积最小时,求C e 的半径.(1)沿AC BC 、剪下ABC V ,则ABC V 是_______三角形(填“锐角______.(2)分别取半圆弧上的点E 、F 和直径AB 上的点G 、H .已知剪下的由这四个点顺次连接构成的四边形是一个边长为6cm 的菱形.请用直尺和圆规在图中作出一个符合条件的菱形(保留作图痕迹,不要求写作法);2.(2022上·陕西西安·九年级校考期中)如图,在等边ABC V 中,点D 是AB 边上的一个动点(不与点A ,B 重合),以CD 为边作等边EDC △,AC 与DE 交于点F ,连接AE .(1)求证:ADF BCD △∽△;(2)若:5:2AB BD =,且20AB =,求ADF △的面积.3.(2022·安徽合肥·统考一模)如图,在正方形ABCD 中,9AB =,E 为AC 上一点,以AE 为直角边构造等腰直角AEF △(点F 在AB 左侧),分别延长FB ,DE 交于点H ,DH 交线段BC 于点M ,AB 与EF 交于点G ,连结BE .(1)求证:AFB AED≅V V (2)当62AE =时,求sin MBH ∠的值.(3)若BEH △与DEC V 的面积相等,记△(1)当点D 与圆心O 重合时,如图2所示,求DE 的长.(2)当CEF △与ABC V 相似时,求cos BDE ∠的值.6.(2023下·安徽蚌埠·九年级校考开学考试)如图,矩形ABCD 中,8AB =厘米,12BC =厘米,P 、Q 分别是AB 、BC 上运动的两点,若点P 从点A 出发,以1厘米/秒的速度沿AB 方向运动,同时,点Q 从点B 出发以2厘米/秒的速度沿BC 方向运动,设点P ,Q 运动的时间为x 秒.(1)设PBQ V 的面积为y ,求y 与x 之间的函数关系式及自变量x 的取值范围;(2)当x 为何值时,以P ,B ,Q 为顶点的三角形与BDC V 相似?7.(2021下·湖北随州·七年级统考期末)阅读材料:在平面直角坐标系中,二元一次方程0x y -=的一个解11x y =⎧⎨=⎩可以用一个点(1,1)表示,二元一次方程有无数个解,以方程0x y -=的解为坐标的点的全体叫作方程0x y -=的图象.一般地,在平面直角坐标系中,任何一个二元一次方程的图象都是一条直线,我们可以把方程0x y -=的图象称为直线0x y -=.直线x -y =0把坐标平面分成直线上方区域,直线上,直线下方区域三部分,如果点M (x 0,y 0)的坐标满足不等式x -y ≤0,那么点M (x 0,y 0)就在直线x -y =0的上方区域内。
广东中考数学压轴题
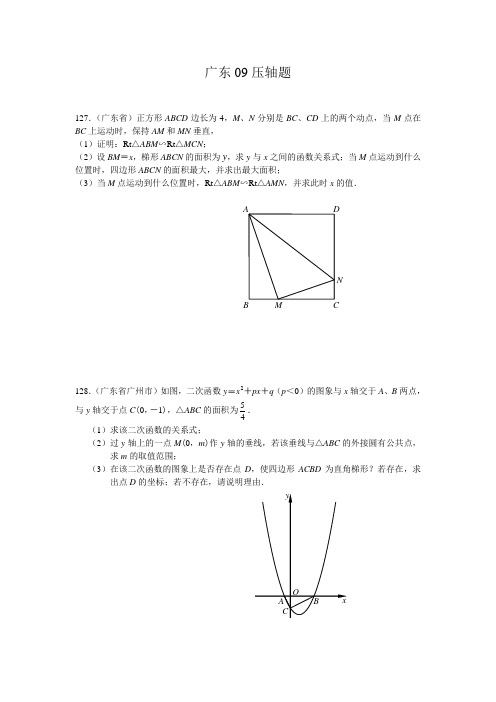
广东09压轴题127.(广东省)正方形ABCD 边长为4,M 、N 分别是BC 、CD 上的两个动点,当M 点在BC 上运动时,保持AM 和MN 垂直, (1)证明:Rt △ABM ∽Rt △MCN ;(2)设BM =x ,梯形ABCN 的面积为y ,求y 与x 之间的函数关系式;当M 点运动到什么位置时,四边形ABCN 的面积最大,并求出最大面积;(3)当M 点运动到什么位置时,Rt △ABM ∽Rt △AMN ,并求此时x 的值.128.(广东省广州市)如图,二次函数y =x2+px +q (p <0)的图象与x 轴交于A 、B 两点,与y 轴交于点C (0,-1),△ABC 的面积为45. (1)求该二次函数的关系式;(2)过y 轴上的一点M (0,m )作y 轴的垂线,若该垂线与△ABC 的外接圆有公共点,求m 的取值范围;(3)在该二次函数的图象上是否存在点D ,使四边形ACBD 为直角梯形?若存在,求出点D 的坐标;若不存在,请说明理由.M B CND A129.(广东省深圳市)如图,在直角坐标系中,点A的坐标为(-2,0),连结OA,将线段OA绕原点O顺时针旋转120°,得到线段OB.(1)求点B的坐标;(2)求经过A、O、B三点的抛物线的解析式;(3)在(2)中抛物线的对称轴上是否存在点C,使△BOC的周长最小?若存在,求出点C的坐标;若不存在,请说明理由.(4)如果点P是(2)中的抛物线上的动点,且在x轴的下方,那么△P AB是否有最大面积?若有,求出此时P点的坐标及△P AB的最大面积;若没有,请说明理由.130.(广东省深圳市)如图,在平面直角坐标系中,直线l:y=-2x-8分别与x轴,y轴相交于A,B两点,点P(0,k)是y轴的负半轴上的一个动点,以P为圆心,3为半径作⊙P.(1)连结P A,若P A=PB,试判断⊙P与x轴的位置关系,并说明理由;(2)当k为何值时,以⊙P与直线l的两个交点和圆心P为顶点的三角形是正三角形?备用图131.(广东省深圳市)已知:Rt △ABC 的斜边长为5,斜边上的高为2,将这个直角三角形放置在平面直角坐标系中,使其斜边AB 与x 轴重合(其中OA <OB ),直角顶点C 落在y 轴正半轴上(如图1).(1)求线段OA 、OB 的长和经过点A 、B 、C 的抛物线的关系式. (2)如图2,点D 的坐标为(2,0),点P (m ,n )是该抛物线上的一个动点(其中m >0,n >0),连接DP 交BC 于点E .①当△BDE 是等腰三角形时,直接写出....此时点E 的坐标. ②又连接CD 、CP (如图3),△CDP 是否有最大面积?若有,求出△CDP 的最大面积和此时点P 的坐标;若没有,请说明理由.132.(广东省珠海市)已知抛物线y =x2-32mx 与x 轴相交于点A 、B ,抛物线的顶点为C .(1)试用含m 的代数式表示AB 的长度; (2)当△ABC 为等边三角形时,求点C 的坐标; (3)在(2)的条件下,如何平移抛物线,使AC =213AB ?133.(广东省佛山市)如图1,一个长方体形的木柜放在墙角处(与墙面和地面均没有缝隙),有一只蚂蚁从柜角A 处沿着木柜表面爬到柜角C 1处. (1)请你画出蚂蚁能够最快到达目的地的可能路径;(2)当AB =4,BC =4,CC 1=5时,求蚂蚁爬过的最短路径的长; (3)求点B 1到最短路径的距离. A Bxy O 图1C A B x y O PD E图2 C A BPxy O D E 图3 C 备用图 图1134.(广东省茂名市)已知:如图,直线l :y =31x +b ,经过点M (0,41),一组抛物线的顶点B 1(1,y 1),B 2(2,y 2),B 3(3,y 3),…,B n (n ,y n )(n 为正整数)依次是直线l 上的点,这组抛物线与x 轴正半轴的交点依次是:A 1(x 1,0),A 2(x 2,0),A 3(x 3,0),…,A n +1(x n +1,0)(n 为正整数),设x 1=d (0<d <1). (1)求b 的值;(2)求经过点A 1、B 1、A 2的抛物线的解析式(用含d 的代数式表示)(3)定义:若抛物线的顶点与x 轴的两个交点构成的三角形是直角三角形,则这种抛物线就称为“美丽抛物线”.探究:当d (0<d <1)的大小变化时,这组抛物线中是否存在美丽抛物线?若存在,请你求出相应的d 的值.135.(广东省湛江市)已知矩形纸片OABC 的长为4,宽为3,以长OA 所在的直线为x 轴,O 为坐标原点建立平面直角坐标系;点P 是OA 边上的动点(与点OA 不重合),现将△POC 沿PC 翻折得到△PEC ,再在AB 边上选取适当的点D ,将△P AD 沿PD 翻折,得到△PFD ,使得直线PE 、PF 重合.(1)若点E 落在BC 边上,如图①,求点P 、C 、D 的坐标,并求过此三点的抛物线的函数关系式;(2)若点E 落在矩形纸片OABC 的内部,如图②,设OP =x ,AD =y ,当x 为何值时,y 取得最大值?(3)在(1)的情况下,过点P 、C 、D 三点的抛物线上是否存在点Q ,使△PDQ 是以PD为直角边的直角三角形?若不存在,说明理由;若存在,求出点Q 的坐标.136.(广东省肇庆市)如图,⊙O 的直径AB =2,AM 和BN 是它的两条切线,DE 切⊙O 于E ,交AM 于D ,交BN 于C .设AD =x ,BC =y . (1)求证:AM ∥BN ;(2)求y 关于x 的关系式;(3)求四边形ABCD 的面积S ,并证明:S≥2.137.(广东省清远市)如图,已知一个三角形纸片ABC ,BC 边的长为8,BC 边上的高为6,∠B 和∠C 都为锐角,M 为AB 上一动点(点M 与点A 、B 不重合),过点M 作MN ∥BC ,交AC 于点N ,在△AMN 中,设MN 的长为x ,MN 上的高为h . (1)请你用含x 的代数式表示h .(2)将△AMN 沿MN 折叠,使△AMN 落在四边形BCNM 所在平面,设点A 落在平面的点为A 1,△A 1MN 与四边形BCNM 重叠部分的面积为y ,当x 为何值时,y 最大,最大值为多少?138.(广东省梅州市)如图,矩形ABCD 中,AB =5,AD =3.点E 是CD 上的动点,以AE 为直径的⊙O 与AB 交于点F ,过点F 作FG ⊥BE 于点G . (1)当E 是CD 的中点时:①tan ∠EAB 的值为______________; ②证明:FG 是⊙O 的切线;(2)试探究:BE 能否与⊙O 相切?若能,求出此时DE 的长; 若不能,请说明理由.NB C N M A139.(广东省梅州市)如图,已知直线L过点A(0,1)和B(1,0),P是x轴正半轴上的动点,OP的垂直平分线交L于点Q,交x轴于点M.(1)直接写出直线L的解析式;(2)设OP=t,△OPQ的面积为S,求S关于t的函数关系式;并求出当0<t<2时,S的最大值;(3)直线L1过点A且与x轴平行,问在L1上是否存在点C,使得△CPQ是以Q为直角顶点的等腰直角三角形?若存在,求出点C的坐标,并证明;若不存在,请说明理由.1。
(完整版)广东中考数学省卷压轴题汇总
广东省卷压轴题汇总选择题(2009·广东)如图所示的矩形纸片,先沿虑线按箭头方向向右对折,接着将对折后的纸片沿虑线剪下一个小圆和一个小三角形,然后将纸片打开是下列图中的哪一个( )(2010广东5) 左下图为主视方向的几何体,它的俯视图是( )(2015·广东)如图,已知正△ABC 的边长为2,E 、F 、G 分别是AB 、BC 、CA 上的点,且AE=BF=CG ,设△EFG 的面积为y ,AE 的长为x ,则y 关于x 的函数图象大致是( )A .B .C .D .C .D . A . B .(2016·广东)如图,在正方形ABCD中,点P从点A出发,沿着正方形的边顺时针方向运动一周,则△APC的面积y与点P运动的路程x之间形成的函数关系图象大致是()A.B.C.D.(2017·广东)如图,已知正方形ABCD,点E是BC边的中点,DE与AC相交于点F,连接BF,下列结论:①S△ABF=S△ADF;②S△CDF=4S△CEF;③S△ADF=2S△CEF;④S△ADF=2S△CDF,其中正确的是()A.①③ B.②③ C.①④ D.②④(2018·广东)如图,点P是菱形ABCD边上的一动点,它从点A出发沿在A→B→C→D路径匀速运动到点D,设△PAD的面积为y,P点的运动时间为x,则y关于x的函数图象大致为()A.B.C.D.填空题(2009)用同样规格的黑白两种颜色的正方形瓷砖,按下图的方式铺地板,则第(3)个图形中有黑色瓷砖 __________块,第n个图形中需要黑色瓷砖__________块(用含n的代数式表示).……(1)(2)(3)第10题图(2010广东10)如图(1),已知小正方形ABCD 的面积为1,把它的各边延长一倍得到新正方形A 1B 1C 1D 1;把正方形A 1B 1C 1D 1边长按原法延长一倍得到新正方形A 2B 2C 2D 2(如图(2));以此下去…, 则正方形A 4B 4C 4D 4的面积为 .(2011广东10)如图(1),将一个正六边形各边延长,构成一个正六角星形AFBDCE ,它的面积为1;取△ABC 和△DEF 各边中点,连接成正六角星形A 1F 1B 1D 1C 1E 1,如图(2)中阴影部分;取△A 1B 1C 1和△D 1E 1F 1各边中点,连接成正六角星形A 2F 2B 2D 2C 2E 2,如图(3)中阴影部分;如此下去…,则正六角星形A 4F 4B 4D 4C 4E 4的面积为_________________.(2012•广东)如图,在▱ABCD 中,AD=2,AB=4,∠A=30°,以点A 为圆心,AD 的长为半径画弧交AB 于点E ,连接CE ,则阴影部分的面积是 _________ (结果保留π).题10图(1)A 1BCD AFEBCD A FEB CD A FEB 1C 1F 1 D 1 E 1 A 1B 1C 1F 1 D 1 E 1 A 2B 2C 2F 2 D 2E 2 题10图(2)题10图(3)(2013•广东)如图,三个小正方形的边长都为1,则图中阴影部分面积的和是_________ (结果保留π).(2014•广东)如图,ABC∠=︒,∆绕点A顺时针旋转45︒得到△AB C'',若90BAC==,则图中阴影部分的面积等于.AB AC(2015.广东)如图,△ABC三边的中线AD、BE、CF的公共点为G,若S△ABC=12,则图中阴影部分的面积是.(2016·广东)如图,点P是四边形ABCD外接圆上任意一点,且不与四边形顶点重合,若AD是⊙O的直径,AB=BC=CD.连接PA、PB、PC,若PA=a,则点A到PB和PC的距离之和AE+AF= .(2017·广东)如图,矩形纸片ABCD中,AB=5,BC=3,先按图(2)操作:将矩形纸片ABCD 沿过点A的直线折叠,使点D落在边AB上的点E处,折痕为AF;再按图(3)操作,沿过点F的直线折叠,使点C落在EF上的点H处,折痕为FG,则A、H两点间的距离为.(2018·广东)如图,已知等边△OA1B1,顶点A1在双曲线y=(x>0)上,点B1的坐标为(2,0).过B1作B1A2∥OA1交双曲线于点A2,过A2作A2B2∥A1B1交x轴于点B2,得到第二个等边△B1A2B2;过B2作B2A3∥B1A2交双曲线于点A3,过A3作A3B3∥A2B2交x轴于点B3,得到第三个等边△B2A3B3;以此类推,…,则点B6的坐标为.解答题(2009.广东)正方形ABCD 边长为4,M 、N 分别是BC 、CD 上的两个动点, 当M 点在BC 上运动时,保持AM 和MN 垂直, (1)证明:Rt Rt ABM MCN △∽△;(2)设BM x ,梯形ABCN 的面积为y ,求y 与x 之间的函数关系式;当M 点运动到什么位置时,四边形ABCN 面积最大,并求出最大面积;(3)当M 点运动到什么位置时Rt Rt ABM AMN △∽△,求此时x 的值.DM AB C第22题图N(2010广东20)已知两个全等的直角三角形纸片ABC、DEF,如图(1)放置,点B、D重合,点F在BC上,AB与EF交于点G.∠C=∠EFB=90°,∠E=∠ABC=30°,AB=DE=4.∆是等腰三角形;(1)求证:EGB∆绕点F逆时针旋转最小____度时,四边形ACDE成为以(2)若纸片DEF不动,问ABCED为底的梯形(如图(2)).求此梯形的高.(2011广东22)如图,抛物线1417452++-=x x y 与y 轴交于A 点,过点A 的直线与抛物线交于另一点B ,过点B 作BC ⊥x 轴,垂足为点C (3,0).(1)求直线AB 的函数关系式;(2)动点P 在线段OC 上从原点出发以每秒一个单位的速度向C 移动,过点P 作PN ⊥x 轴,交直线AB 于点M ,交抛物线于点N . 设点P 移动的时间为t 秒,MN 的长度为s 个单位,求s 与t 的函数关系式,并写出t 的取值范围;(3)设在(2)的条件下(不考虑点P 与点O ,点C 重合的情况),连接C M ,BN ,当t 为何值时,四边形BCMN 为平行四边形?问对于所求的t 值,平行四边形BCMN 是否菱形?请说明理由.(2012•广东21)如图,在矩形纸片ABCD中,AB=6,BC=8.把△BCD沿对角线BD折叠,使点C落在C′处,BC′交AD于点G;E、F分别是C′D和BD上的点,线段EF交AD于点H,把△FDE沿EF折叠,使点D落在D′处,点D′恰好与点A重合.(1)求证:△ABG≌△C′DG;(2)求tan∠ABG的值;(3)求EF的长.(2012•广东22)如图,抛物线y=x2﹣x﹣9与x轴交于A、B两点,与y轴交于点C,连接BC、AC.(1)求AB和OC的长;(2)点E从点A出发,沿x轴向点B运动(点E与点A、B不重合),过点E作直线l平行BC,交AC于点D.设AE的长为m,△ADE的面积为s,求s关于m的函数关系式,并写出自变量m的取值范围;(3)在(2)的条件下,连接CE,求△CDE面积的最大值;此时,求出以点E为圆心,与BC相切的圆的面积(结果保留π).(2013•广东24)如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,弦BD=BA,AB=12,BC=5,BE⊥DC交DC的延长线于点E.(1)求证:∠BCA=∠BAD;(2)求DE的长;(3)求证:BE是⊙O的切线.(2013•广东25)有一副直角三角板,在三角板ABC中,∠BAC=90°,AB=AC=6,在三角板DEF中,∠FDE=90°,DF=4,DE=.将这副直角三角板按如图1所示位置摆放,点B与点F重合,直角边BA与FD在同一条直线上.现固定三角板ABC,将三角板DEF沿射线BA 方向平行移动,当点F运动到点A时停止运动.(1)如图2,当三角板DEF运动到点D到点A重合时,设EF与BC交于点M,则∠EMC= _________ 度;(2)如图3,当三角板DEF运动过程中,当EF经过点C时,求FC的长;(3)在三角板DEF运动过程中,设BF=x,两块三角板重叠部分的面积为y,求y与x的函数解析式,并求出对应的x取值范围.(2014•广东24)如图,O是ABC⊥于点D,∆的外接圆,AC是直径,过点O作OD AB延长DO交O于点P,过点P作PE AC⊥于点E,作射线DE交BC的延长线于F点,连接PF.π(1)若60AC=,求劣弧PC的长;(结果保留)POC∠=︒,12(2)求证:OD OE=;(3)求证:PF是O的切线.(2014•广东25)如图,在ABC=,8=.点AD cmBC cm⊥于点D,10∆中,AB AC=,AD BCP从点B出发,在线段BC上以每秒3cm的速度向点C匀速运动,与此同时,垂直于AD的直线m从底边BC出发,以每秒2cm的速度沿DA方向匀速平移,分别交AB、AC、AD于E、F、H,当点P到达点C时,点P与直线m同时停止运动,设运动时间为t秒(0)t>.(1)当2t=时,连接DE、DF,求证:四边形AEDF为菱形;(2)在整个运动过程中,所形成的PEF∆的面积最大时,求∆的面积存在最大值,当PEF 线段BP的长;(3)是否存在某一时刻t,使PEF∆为直角三角形?若存在,请求出此时刻t的值;若不存在,请说明理由.(2015•广东24)⊙O是△ABC的外接圆,AB是直径,过的中点P作⊙O的直径PG交弦BC于点D,连接AG、CP、PB.(1)如图1,若D是线段OP的中点,求∠BAC的度数;(2)如图2,在DG上取一点K,使DK=DP,连接CK,求证:四边形AGKC是平行四边形;(3)如图3,取CP的中点E,连接ED并延长ED交AB于点H,连接PH,求证:PH⊥AB.(2015•广东25)如图,在同一平面上,两块斜边相等的直角三角板Rt△ABC和Rt△ADC拼在一起,使斜边AC完全重合,且顶点B,D分别在AC的两旁,∠ABC=∠ADC=90°,∠CAD=30°,AB=BC=4cm(1)填空:AD= (cm),DC= (cm)(2)点M,N分别从A点,C点同时以每秒1cm的速度等速出发,且分别在AD,CB上沿A →D,C→B方向运动,当N点运动到B点时,M、N两点同时停止运动,连接MN,求当M、N 点运动了x秒时,点N到AD的距离(用含x的式子表示)(3)在(2)的条件下,取DC中点P,连接MP,NP,设△PMN的面积为y(cm2),在整个运动过程中,△PMN的面积y存在最大值,请求出y的最大值.(参考数据sin75°=,sin15°=)(2016·广东24)如图,⊙O是△ABC的外接圆,BC是⊙O的直径,∠ABC=30°,过点B作⊙O的切线BD,与CA的延长线交于点D,与半径AO的延长线交于点E,过点A作⊙O的切线AF,与直径BC的延长线交于点F.(1)求证:△ACF∽△DAE;(2)若S△AOC=,求DE的长;(3)连接EF,求证:EF是⊙O的切线.(2016·广东25)如图,BD是正方形ABCD的对角线,BC=2,边BC在其所在的直线上平移,将通过平移得到的线段记为PQ,连接PA、QD,并过点Q作QO⊥BD,垂足为O,连接OA、OP.(1)请直接写出线段BC在平移过程中,四边形APQD是什么四边形?(2)请判断OA、OP之间的数量关系和位置关系,并加以证明;(3)在平移变换过程中,设y=S△OPB,BP=x(0≤x≤2),求y与x之间的函数关系式,并求出y的最大值.(2017·广东24)如图,AB是⊙O的直径,AB=4,点E为线段OB上一点(不与O,B重合),作CE⊥OB,交⊙O于点C,垂足为点E,作直径CD,过点C的切线交DB的延长线于点P,AF⊥PC于点F,连接CB.(1)求证:CB是∠ECP的平分线;(2)求证:CF=CE;(3)当=时,求劣弧的长度(结果保留π)(2017·广东25)如图,在平面直角坐标系中,O为原点,四边形ABCO是矩形,点A,C 的坐标分别是A(0,2)和C(2,0),点D是对角线AC上一动点(不与A,C重合),连结BD,作DE⊥DB,交x轴于点E,以线段DE,DB为邻边作矩形BDEF.(1)填空:点B的坐标为;(2)是否存在这样的点D,使得△DEC是等腰三角形?若存在,请求出AD的长度;若不存在,请说明理由;(3)①求证:=;②设AD=x,矩形BDEF的面积为y,求y关于x的函数关系式(可利用①的结论),并求出y 的最小值.(2018·广东24)如图,四边形ABCD中,AB=AD=CD,以AB为直径的⊙O经过点C,连接AC、OD交于点E.(1)证明:OD∥BC;(2)若tan∠ABC=2,证明:DA与⊙O相切;(3)在(2)条件下,连接BD交⊙O于点F,连接EF,若BC=1,求EF的长.(2018·广东24)已知Rt△OAB,∠OAB=90°,∠ABO=30°,斜边OB=4,将Rt△OAB绕点O 顺时针旋转60°,如图1,连接BC.(1)填空:∠OBC= °;(2)如图1,连接AC,作OP⊥AC,垂足为P,求OP的长度;(3)如图2,点M,N同时从点O出发,在△OCB边上运动,M沿O→C→B路径匀速运动,N 沿O→B→C路径匀速运动,当两点相遇时运动停止,已知点M的运动速度为1.5单位/秒,点N的运动速度为1单位/秒,设运动时间为x秒,△OMN的面积为y,求当x为何值时y 取得最大值?最大值为多少?。
2020年广东中考数学压轴题:动点
2020年广东省中考数学压轴题:动点问题如图1,抛物线经过点A (4,0)、B (1,0)、C (0,-2)三点.(1)求此抛物线的解析式;(2)P 是抛物线上的一个动点,过P 作PM ⊥x 轴,垂足为M ,是否存在点P ,使得以A 、P 、M 为顶点的三角形与△OAC 相似?若存在,请求出符合条件的 点P 的坐标;若不存在,请说明理由;(3)在直线AC 上方的抛物线是有一点D ,使得△DCA 的面积最大,求出点D 的坐标.,图1 满分解答(1)因为抛物线与x 轴交于A (4,0)、B (1,0)两点,设抛物线的解析式为)4)(1(--=x x a y ,代入点C 的 坐标(0,-2),解得21-=a .所以抛物线的解析式为22521)4)(1(212-+-=---=x x x x y . (2)设点P 的坐标为))4)(1(21,(---x x x . ①如图2,当点P 在x 轴上方时,1<x <4,)4)(1(21---=x x PM ,x AM -=4. 如果2==CO AO PM AM ,那么24)4)(1(21=----xx x .解得5=x 不合题意. 如果21==CO AO PM AM ,那么214)4)(1(21=----x x x .解得2=x . 此时点P 的坐标为(2,1).②如图3,当点P 在点A 的右侧时,x >4,)4)(1(21--=x x PM ,4-=x AM . 解方程24)4)(1(21=---x x x ,得5=x .此时点P 的坐标为)2,5(-. 解方程214)4)(1(21=---x x x ,得2=x 不合题意.③如图4,当点P 在点B 的左侧时,x <1,)4)(1(21--=x x PM ,x AM -=4. 解方程24)4)(1(21=---xx x ,得3-=x .此时点P 的坐标为)14,3(--. 解方程214)4)(1(21=---x x x ,得0=x .此时点P 与点O 重合,不合题意. 综上所述,符合条件的 点P 的坐标为(2,1)或)14,3(--或)2,5(-.图2 图3 图4(3)如图5,过点D 作x 轴的垂线交AC 于E .直线AC 的解析式为221-=x y . 设点D 的横坐标为m )41(<<m ,那么点D 的坐标为)22521,(2-+-m m m ,点E 的坐标为)221,(-m m .所以)221()22521(2---+-=m m m DE m m 2212+-=. 因此4)221(212⨯+-=∆m m S DAC m m 42+-=4)2(2+--=m . 当2=m 时,△DCA 的面积最大,此时点D 的坐标为(2,1).图5 图6。
中考数学临考题号押广东卷14~15题(简单几何与函数或二次方程)(解析版)
押广东卷第14—15题简单几何与函数或二次方程广东中考对第14~15题主要考查的内容注重基础知识的运算,对知识掌握的要求不高。
近几年主要考查主要考查以下两个方面:一是多边形的内角和,外角和计算;二是平行线的相关性质,三角形垂直平分线,角平分线,平行四边形,三角函数的运用,函数的图形平移等。
一般放在填空题中第12~15题进行考查,一般难度不大。
在完成这些题型时,要求考生熟练掌握几何相关概念与性质,图形变化,解三角形,二次方程根的判别式,函数的基础知识.1.(2021广东)若一元二次方程20x bx c ++=(b ,c 为常数)的两根12,x x 满足1231,13x x -<<-<<,则符合条件的一个方程为_____.【分析】设2y x bx c =++与0y =交点为12,x x ,根据题意1231,13x x -<<-<<关于y轴对称和二次函数的对称性,可找到12x x 、的值(12x x ,只需满足互为相反数且满足1||3x <<即可)即可写出一个符合条件的方程【详解】设2y x bx c =++与0y =交点为12,x x ,根据题意1231,13x x -<<-<<则1||3x <<2y x bx c =++的对称轴为0x =故设122,2x x =-=则方程为:240x -=故答案为:240x -=2.(2021广东)把抛物线221y x =+向左平移1个单位长度,再向下平移3个单位长度,得到的抛物线的解析式为___.【分析】直接根据“上加下减,左加右减”进行计算即可.【详解】解:抛物线221y x =+向左平移1个单位长度,再向下平移3个单位长度,得到的抛物线的解析式为:22(1)13y x =++-,即:224y x x =+故答案为:224y x x =+.3.(2020广东)如图,在ABCD 中,45,12,sin 5AD AB A ===.过点D 作DE AB ⊥,垂足为E ,则sin BCE ∠=______.【分析】首先根据题目中的sin A ,求出ED 的长度,再用勾股定理求出AE ,即可求出EB ,利用平行四边形的性质,求出CD ,在Rt △DEC 中,用勾股定理求出EC ,再作BF ⊥CE ,在△BEC 中,利用等面积法求出BF 的长,即可求出sin BCE ∠.【详解】∵DE AB ⊥, ∴△ADE 为直角三角形,又∵45,sin 5AD A ==, ∴4sin 55DE DE A AD, 解得DE =4,在Rt △ADE 中,由勾股定理得:2222543AE AD DE =-=-=,又∵AB =12,∴1239BE AB AE ,又∵四边形ABCD 为平行四边形,∴CD =AB =12,AD =BC =5在Rt △DEC 中,由勾股定理得: 2222124410EC CD DE , 过点B 作BF ⊥CE ,垂足为F ,如图在△EBC 中:S △EBC =11941822EB DE ;又∵S △EBC11410=21022CE BF BF BF ∴21018BF, 解得91010BF , 在Rt △BFC 中,910910sin 51050BF BCFBC , 故填:91050. 4.(2020广东)如题15图,在菱形ABCD 中,∠A=30°,取大于21AB 的长为半径,分别以点A 、B 为圆心作弧相交于两点,过此两点的直线交AD 边于点E (作图痕迹如图所示),连接BE 、BD ,则∠EBD 的度数为___________.【分析】垂直平分线的性质、菱形的性质,菱形的对角线平分对角,可知∠ABC=150°,∠ABD=75°【解答】菱形ABCD 中,∠A=30°∴∠ABC=150°,∠ABD=75°∵AE=BE∴∠A=∠ABE=30°∴∠EBD=∠ABD-∠ABE=45°故答案为:45°5.(2019广东)一个多边形的内角和是1080°,这个多边形的边数是.【分析】根据多边形内角和定理:(n﹣2)•180 (n≥3)可得方程180(x﹣2)=1080,再解方程即可.【解答】解:设多边形边数有x条,由题意得:180(x﹣2)=1080,解得:x=8,故答案为:8.6.(2019•广东)如图,某校教学楼AC与实验楼BD的水平间距CD=15米,在实验楼顶部B点测得教学楼顶部A点的仰角是30°,底部C点的俯角是45°,则教学楼AC的高度是米(结果保留根号).【分析】首先分析图形:根据题意构造直角三角形.本题涉及到两个直角三角形△BEC、△ABE,进而可解即可求出答案.【解答】解:过点B作BE⊥AB于点E,在Rt△BEC中,∠CBE=45°,BE=15;可得CE=BE×tan45°=15米.在Rt△ABE中,∠ABE=30°,BE=15,可得AE=BE×tan30°=15米.故教学楼AC的高度是AC=15米.答:教学楼AC的高度是(15)米.1.(2022年广东省佛山市禅城区中考一模)如图,矩形ABCD 中,AD =2,AB =5,P 是CD 边上的一个动点,当ADP △与BCP 相似,但不全等时,DP 的长度是 _____.【分析】需要分类讨论:△APD ∽△PBC 和△P AD ∽△PBC ,根据相似三角形的对应边成比例求得DP 的长度,舍去不合题意的情况即可.【详解】解:①当△APD ∽△PBC 时,AD PD PC BC =,即252PD PD =-, 解得:PD =1或PD =4;②当△P AD ∽△PBC 时,AD PD BC PC =,即225PD PD =-, 解得:DP =2.5,∴PC =2.5,即DP =PC ,∵∠D =∠C ,AD =BC ,∴△P AD ≌△PBC ,此情况舍去;综上所述,DP 的长度是1或4.故答案为:1或4.2.(2022年广东省中山市九年级下学期第一次模拟)在平面直角坐标系中,点(3,﹣2)到原点的距离是 _____.【分析】根据两点的距离公式计算求解即可.【详解】解:由题意知点(3,﹣2()()22302013-+--= 133.(2022年广东省梅州市中考数学模拟)如图,四边形ABCD 与四边形EFGH 位似,其位似中心为点O ,且54OE EA =,则FG BC =________.【分析】利用位似的性质得到FG OF OEBC OB OA==,然后根据比例的性质求解.【详解】解:∵四边形ABCD与四边形EFGH位似,其位似中心点O,∴FG OF OE BC OB OA==,∵54 OEEA=,∴55549 FGBC==+,故答案为:59.4.(广东省韶关市南雄市第一次质检数学试题)如果点A(﹣3,2m+1)关于原点对称的点在第一象限,则m的取值范围是______.【分析】根据关于原点对称的点的横坐标与纵坐标互为相反数判断出2m+1<0,然后解不等式即可.【详解】解:∵点A(﹣3,2m+1)关于原点的对称点在第一象限,∴点A(﹣3,2m+1)在第三象限,∴2m+1<0,解得m<﹣12.故答案为:m<﹣12.5.(广东省韶关市南雄市第一次质检数学试题)如图,点A是反比例函数kyx=图象上的一点,过点A作AC⊥x轴,垂足为点C,D为AC的中点,若△AOD的面积为1,则k的值为______.【分析】根据题意可知△AOC 的面积为2,然后根据反比例函数系数k 的几何意义即可求得k 的值.【详解】解:∵AC ⊥x 轴,垂足为点C ,D 为AC 的中点,若△AOD 的面积为1, ∴△AOC 的面积为2,∵S △AOC =12|k |=2,且反比例函数y =k x 图象在第一象限, ∴k =4,故答案为:4.6.(2022年广东省梅州市中考数学模拟)如图,在ABC 中,点D 、E 分别为边BC 、AC 上的点,连接DE ,将CDE △沿DE 翻折得到C DE ',使C D AB '∥.若75A ∠=︒,45C ∠=︒,则C EA '∠的大小为______︒.【分析】由C D AB '∥ 得出75DGE A ∠=∠=︒,由折叠性质可知,45C C '∠=∠=︒,再根据三角形外角性质求出754530C EA DGE C ''∠=∠-∠=︒-︒=︒.【详解】解:如图,设C D ' 交AC 于点G ,∵C D AB '∥,75DGE A ∴∠=∠=︒,由折叠性质可知,45C C '∠=∠=︒,754530C EA DGE C ''∴∠=∠-∠=︒-︒=︒.故答案为:307.(2022年广东省中山市九年级下学期第一次模拟)如图,把△ABC 绕点C 顺时针旋转得到△A ′B ′C ,此时A ′B ′⊥AC 于点D ,已知∠A =50°,则∠B ′CB 的度数是 _____.【分析】由旋转的性质可得∠A =∠A '=50°,∠BCB '=∠ACA ',由直角三角形的性质可求∠ACA '=40°=∠B ′CB .【详解】解:∵把△ABC 绕点C 顺时针旋转得到△A 'B 'C ,∴∠A =∠A '=50°,∠BCB '=∠ACA ',∵A 'B '⊥AC ,∴∠A '+∠ACA '=90°,∴∠ACA '=40°,∴∠B ′CB =40°,故答案为:40°.8.(2022年广东省中山市九年级下学期第一次模拟)小强推铅球时,铅球的高度y (m )与水平行进的距离x (m )之间的关系为y 112=-(x ﹣4)2+3,则小强推铅球的成绩是 _____m . 【分析】根据铅球落地时,高度y =0,把实际问题理解为当y =0时,求x 的值即可.【详解】解:铅球落地时,高度y =0, 令函数式()214312y x =--+中y =0,即()2143012x --+=, 解得:x 1=10,x 2=−2(舍去),即小强推铅球的成绩是10m ,故答案为:10.9.(2021深圳市光明区二模)如图,将△ABC 绕边AC 的中点O 顺时针旋转180°,旋转后的△CDA 与△ABC 构成四边形ABCD ,作ON ∥AB 交AD 于点N ,若∠BAC =∠BCA ,四边形ABCD 的周长为24,则ON = .【分析】由旋转的性质和等腰三角形的判定证得四边形ABCD是菱形,再根据平行线等分线段定理和三角形的中位线定理证得ON=CD即可求得ON.【解答】解:∵将△ABC绕边AC的中点O顺时针旋转180°得到△CDA,∴AB=CD,BC=AD,∵∠BAC=∠BCA,∴AB=BC,∴AB=CD=BC=AD,∴四边形ABCD是菱形,∴AB∥CD,∵四边形ABCD的周长为24,∴CD=6,∵ON∥AB,∴ON∥CD,∵点O是AC的中点,∴N是AD的中点,∴ON=CD=3,故答案为:3.10.(2021惠州市一模)如图,从甲楼底部A处测得乙楼顶部C处的仰角是30︒,从甲楼顶部B处测得乙楼底部D处的俯角是45︒,已知乙楼的高CD是45m,则甲楼的高AB是m(结果保留根号);【分析】利用等腰直角三角形的性质得出AB AD=,再利用锐角三角函数关系得出答案.【解答】解:由题意可得:45BDA∠=︒,则AB AD=,又30∠=︒,CAD∴在Rt ADC ∆中,45CD m =. 3tan tan303CD CDA AD ∠=︒==,即4533AD =, 解得:453()AD m =,453AB m ∴=.故答案为:453.11.(2021佛山市禅城区一模)一个多边形的内角和为900°,则这个多边形的边数为 .【分析】本题根据多边形的内角和定理和多边形的内角和等于900°,列出方程,解出即可.【解答】解:设这个多边形的边数为n ,则有(n ﹣2)×180°=900°,解得:n =7,∴这个多边形的边数为7.故答案为:7.12.(2021佛山市禅城区一模)如图,创新小组要测量公园内一棵树的高度AB ,其中一名小组成员站在距离树10米的点E 处,测得树顶A 的仰角为54°.已知测角仪的架高CE =1.5米,则这棵树的高度为 米.(结果保留一位小数,参考数据:sin54°≈0.8090,cos54°≈0.5878,tan54°≈1.3764)【分析】在Rt △ACD 中,求出AD ,再利用矩形的性质得到BD =CE =1.5,由此即可解决问题.【解答】解:如图,过点C 作CD ⊥AB ,垂足为D .则四边形CEBD 是矩形,BD =CE =1.5m ,在Rt △ACD 中,CD =EB =10m ,∠ACD =54°,∵tan ∠ACE =,∴AD =CD •tan ∠ACD ≈10×1.38=13.8m .∴AB =AD +BD =13.8+1.5=15.3m .答:树的高度AB 约为15.3m .故答案为:15.3.13.(2021深圳市南山区一模)如图,在Rt△ABC中,∠C=90°,BE,AF分别是∠ABC,∠CAB平分线,BE,AF交于点O,OM⊥AB,AB=10,AC=8,则OM=.【分析】过O作OG⊥AC于G,OH⊥BC于H,根据角平分线的性质和三角形的面积公式即可得到结论.【解答】解:过O作OG⊥AC于G,OH⊥BC于H,连接OC,∵AF平分∠CAB,BE平分∠ABC,∴OG=OH=OM,∵∠C=90°,AB=10,AC=8,∴BC==6∴S△ABC=AC•BC=×AB•OM+AC•OG+BC•OH,∴×8×6=+×8×OG+,∴OM=2,故答案为:2.14.(2021汕头市金平区一模)一个正n边形的一个外角等于72°,则n的值等于.【分析】可以利用多边形的外角和定理求解.【解答】解:∵正n边形的一个外角为72°,∴n的值为360°÷72°=5.故答案为:51.(2021深圳市南山区一模)如图,航拍无人机从A处测得一幢建筑物顶部B的仰角为30°,测得底部C的俯角为60°,此时航拍无人机与该建筑物的水平距离AD为60米,那么该建筑物的高度BC约为80米.【分析】分别利用锐角三角函数关系得出BD,DC的长,进而求出该建筑物的高度.【解答】解:由题意可得:tan30°===,解得:BD=20(米),tan60°===,解得:DC=60(米),故该建筑物的高度为:BC=BD+DC=80(米)故答案为80.2.(2022·广东·江门市新会东方红中学模拟预测)如图,在Rt△ABC,∠B=90°,∠ACB=50°.将Rt△ABC在平面内绕点A逆时针旋转到△AB′C′的位置,连接CC′.若AB∥CC′,则旋转角的度数为_____°.【答案】100【解析】由AB CC '∥,可得ACC CAB '∠=∠,90CAB ACB ∠=︒-∠,由旋转的性质可得AC AC '=,AC A C C C ∠='∠',由三角形内角和定理得180CAC ACC AC C '''∠=︒-∠-∠,计算求解即可.【详解】解:∵AB CC '∥∴ACC CAB '∠=∠∴9040CAB ACB ∠=︒-∠=︒由旋转的性质可得AC AC '=∴40AC A C C C ∠=∠=''︒∴180100CA AC A C C C C '''∠=︒-∠-∠=︒故答案为:100.3.(2022·广东·模拟预测)若点A (-m ,n -5)与点B (-1,-2m )关于原点对称,则-mn =________.【答案】1【解析】【分析】根据关于原点的对称点,横纵坐标都变成相反数,可得答案.【详解】解:点A (-m ,n -5)与点B (-1,-2m )关于原点对称,得-m =-(-1)=1,n -5=2m , ∴m =-1,n =3.∴-mn =-(-1)3=1,故答案为:1.4.(2022·广东·模拟预测)抛物线23(1)8y x =-+的顶点坐标为______________________________.【答案】(1,8)【解析】【分析】根据题意可知,本题考察二次函数的性质,根据二次函数的顶点式,进行求解.【详解】解:由二次函数性质可知,()2y a x h k =-+的顶点坐标为(h ,k )∴23(1)8y x =-+的顶点坐标为(1,8)故答案为:(1,8)5.(2022·广东·模拟预测)近来房地产市场进入寒冬期,某楼盘原价为每平方米10000元,连续两次降价后售价为8100元,则平均每次降价的百分率是______.【答案】10%【分析】设平均每次降价的百分率为x,根据该楼盘的原价及经过两次降价后的价格,即可得出关于x的一元二次方程,解之取其符合题意的值即可得出结论.【详解】解:设平均每次降价的百分率为x,依题意得:10000(1-x)2=8100,解得:x1=0.1=10%,x2=1.9(不合题意,舍去).故答案为:10%.6.(2022·广东清远·模拟预测)在△ABC中,已知AB=5,AC=8,∠A=60°,则△ABC中BC边长=_____.【答案】7【解析】【分析】过点B作BD⊥AC于D,利用锐角三角函数可得532.5,2AD BD==,从而得到DC=112,再由勾股定理,即可求解.【详解】解:过点B作BD⊥AC于D,如图所示:∴∠ADB=90°,∵∠A=60°,AB=5,∴1353 cos5 2.5,sin52AD AB A BD AB A=⨯=⨯==⨯==∵AC=8,∴DC=112,由勾股定理可得:BC22225311722BD DC⎛⎫⎛⎫++⎪ ⎪⎪⎝⎭⎝⎭.故答案为:7.7.(2022·广东·模拟预测)若一个正多边形的外角和等于内角和的一半,则该正多边形的边数是______.【答案】6【解析】【分析】根据正多边形内角和公式及外角和为360︒,列方程即可求得.【详解】解:设这个正多边形的边数为n , 根据题意得:1(2)1803602n -⨯⨯=, 解得6n =.故答案为:6.8.(2022·广东清远·模拟预测)关于x 的方程(a 2﹣3)x 2+ax +1=0是一元二次方程的条件是_____.【答案】a【解析】【分析】根据一元二次方程必须满足两个条件:①未知数的最高次数是2;②二次项系数不为0;由这两个条件得到相应的关系式,求解即可.【详解】∵关于x 的方程22(3)10a x ax ++=﹣是一元二次方程, ∴230a -≠,∴a ≠故答案为:a ≠9.(2022·广东惠州·模拟预测)请你写出一个图象过点(2,0),且y 随x 增大而减小的一次函数的解析式__________.【答案】y =-x +2【解析】【分析】将点(2,0)代入一次函数解析式为y =kx +b ,得到2k +b =0,又因为y 随x 的增大而减小,可得出k 小于0,取k =-1,可得出b =2,确定出满足题意的一次函数解析式,本题答案不唯一.【详解】解:设一次函数的解析式为y =kx +b ,将x =2,y =0代入得:2k +b =0,又此一次函数y 随x 的增大而减小,∴k <0,若k =-1,可得出b =2,则一次函数为y =-x +2.故答案为y =-x +2.10.(2022·广东广州·一模)如果一个正多边形的一个内角是162°,则这个正多边形是正_____边形.【答案】二十【解析】【分析】首先根据求出外角度数,再利用外角和定理求出边数.【详解】解:∵正多边形的一个内角是162°,∴它的外角是:180°﹣162°=18°,边数n =360°÷18°=20. 故答案为:二十.11.(2022·广东广州·一模)如图,若//AB CD ,点E 在直线AB 的上方,连接AE CE ,,延长EA 交CD 于点F ,已知99DCE ∠=︒,35CEF ∠=︒,则EAB ∠=_________°.【答案】134【解析】【分析】根据外角性质可得∠EFD ,根据平行线的性质可得∠EAB =∠EFD .【详解】∵9935DCE CEF ∠=︒∠=︒,,∴9935134EFD DCE CEF ∠=∠+∠=︒+︒=︒,∴//AB CD ,∴134EAB EFD ∠=∠=︒.故答案为134.12.(2022·广东·模拟预测)如图,直线a∥b,三角板的直角顶点A落在直线a上,两条直线分别交直线b于B、C两点.若∠1=42°,则∠2的度数是_____.【答案】48°.【解析】【详解】试题分析:已知∠BAC=90°,∠1=42°,根据平角的定义可得∠3=180°﹣90°﹣∠1=90°﹣42°=48°.再由平行线的性质即可得∠2=∠3=48°.13.(2022·广东惠州·模拟预测)如图,已知CD平分∠ACB,DE∥AC,∠1=30°,则∠2=___________度.【答案】60【解析】【详解】已知CD平分∠ACB,DE∥AC,可推出∠ACB=∠2,易求解.解:∵CD平分∠ACB,∴∠ACB=2∠1;∵DE∥AC,∴∠ACB=∠2;又∵∠1=30°,∴∠2=60°.14.(2021·广东·雷州市第八中学一模)如图,在平面直角坐标系中,函数y=2x(x>0)的图象经过矩形OABC的边BC的中点D,且与边AB相交于点E,则四边形ODBE的面积为____【答案】2【解析】【分析】由矩形的性质求出S△OAB=S△OBC,反比例函数系数k的几何意义△OAE和△OCD的面积各为1,根据等底同高,面积和差求出四边形OEBD的面积为2.【详解】解:连接OB,如图所示:∵OB是矩形OABC的对角线,∴S△OAB=S△OBC,又∵点D、E在反比例函数y=2x的图象上,∴1212OAE OCDS S==⨯=,又∵CD=BD,OC是△OCD和△OBD的高,∴S△OCD=S△ODB=1,又∵S△OBC=S△OCD+S△OBD,∴S△OAB=S△OBC=2,又∵S△OBE=S△OAB−S△OAE,∴S△OBE=2−1=1,又∵S四边形OEBD=S△ODB+S△OBE,∴S四边形OEBD=1+1=2,故答案为2.15.(2021·广东·佛冈县汤塘中学二模)已知关于x 的一元二次方程()21210m x x --+=有两个不相等的实数根,则m 的取值范围是_______.【答案】2m <且1m ≠【解析】【分析】由一元二次方程2x 的系数不能为0可得10m -≠,再根据一元二次方程有两个不相等的实数根对应240b ac ∆=->,代值解不等式即可得出答案.【详解】 解: ()21210m x x --+=是一元二次方程,10m ∴-≠,即1m ≠,关于x 的一元二次方程()21210m x x --+=有两个不相等的实数根,∴()()()22424114410b ac m m ∆=-=---⨯=-->,解这个不等式得2m <,∴m 的取值范围是2m <且1m ≠,故答案为2m <且1m ≠.16.(2021·广东汕头·一模)如图,在ABC ∆中,点D 、E 分别在边AB 、AC 上,∥DE BC ,如果32AE EC =,10BC =,那么DE 的长是__.【答案】6【解析】【分析】 根据32AE EC =可求得35AE AC = ,再根据平行线分线段成比例定理得到AE DE AB BC= ,即可求得DE 的长.【详解】 解:32AE EC =,AE EC AC +=, ∴35AE AC =, DE BC ∥,35DEAE BC AC , 10BC =, 6DE ∴=, 故答案为:6.。
2024年广东省中考数学填空题压轴题专题:几何变换(翻折、平移、旋转)课件
∵△ABC为等边三角形, ∴∠A=∠B=60°. ∴∠BDP=180°-∠B-∠BPD=90°.
∵∠BPD=30°, ∴BD=12BP,即 2t=12(6-2t). ∴t=1.
∠AQP=180°-∠APQ-∠A=30°.
故答案为:1.
∵∠BDP=∠APQ=90°,DP=PQ,∠BPD=∠AQP=30°,
123=25
.
又HF=AB=6, 在Rt△FHE中, EF= HF2+HE2=2 13. 故答案为:2 13.
9.如图,在△ABC中,AB=4 cm,BC=2 cm,∠ABC=30°,把△ABC绕
点B逆时针旋转,使点C旋转到AB边的延长线上的点C′处,那么AC边扫过的
图形(图中阴影部分)的面积是__5_π__cm2. 【解析】∵∠ABC=∠A′BC′=30°,
【解析】过点F作FH⊥AD于点H.
易证Rt△AD′E≌Rt△ABF,
四边形ABFH为矩形.
∵四边形ABCD是矩形,
∴AB=CD=6,BC=AD=9.
答图
设AE=x,由折叠可知ED′=ED=(9-x).
在Rt△AD′E中,由勾股定理,得62+(9-x)2=x2,
解得x=123 .
∴AH=BF=D′E=ED=9- ∴HE=123-25=4.
答图1
14.(2023辽宁)如图,在三角形纸片ABC中,AB=AC,∠B=20°,点D
是 边 BC 上 的 动 点 , 将 三 角 形 纸 片 沿 AD 对 折 , 使 点 B 落 在 点 B′ 处 , 当 B′D⊥BC时,∠BAD的度数为__2_5_°__或__1_1_5_°__.
②如图2,当点B′在直线BC的上方时, ∵B′D⊥BC, ∴∠BDB′=90°. 由折叠得∠ADB′=∠ADB=×90°=45°. ∴∠BAD=180°-∠B-∠ADB= 180°-20°-45°=115°. 故答案为:25°或115°.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
广东09压轴题
127.(广东省)正方形ABCD 边长为4,M 、N 分别是BC 、CD 上的两个动点,当M 点在BC 上运动时,保持AM 和MN 垂直, (1)证明:Rt △ABM ∽Rt △MCN ;
(2)设BM =x ,梯形ABCN 的面积为y ,求y 与x 之间的函数关系式;当M 点运动到什么位置时,四边形ABCN 的面积最大,并求出最大面积;
(3)当M 点运动到什么位置时,Rt △ABM ∽Rt △AMN ,并求此时x 的值.
128.(广东省广州市)如图,二次函数y =x
2+px +q (p <0)的图象与x 轴交于A 、B 两点,
与y 轴交于点C (0,-1),△ABC 的面积为
4
5
. (1)求该二次函数的关系式;
(2)过y 轴上的一点M (0,m )作y 轴的垂线,若该垂线与△ABC 的外接圆有公共点,
求m 的取值范围;
(3)在该二次函数的图象上是否存在点D ,使四边形ACBD 为直角梯形?若存在,求
出点D 的坐标;若不存在,请说明理由.
M B C
N
D A
129.(广东省深圳市)如图,在直角坐标系中,点A的坐标为(-2,0),连结OA,将线段OA绕原点O顺时针旋转120°,得到线段OB.
(1)求点B的坐标;
(2)求经过A、O、B三点的抛物线的解析式;
(3)在(2)中抛物线的对称轴上是否存在点C,使△BOC的周长最小?若存在,求出点C的坐标;若不存在,请说明理由.
(4)如果点P是(2)中的抛物线上的动点,且在x轴的下方,那么△P AB是否有最大面积?若有,求出此时P点的坐标及△P AB的最大面积;若没有,请说明理由.
130.(广东省深圳市)如图,在平面直角坐标系中,直线l:y=-2x-8分别与x轴,y轴相交于A,B两点,点P(0,k)是y轴的负半轴上的一个动点,以P为圆心,3为半径作⊙P.
(1)连结P A,若P A=PB,试判断⊙P与x轴的位置关系,并说明理由;
(2)当k为何值时,以⊙P与直线l的两个交点和圆心P为顶点的三角形是正三角形?
备用图
131.(广东省深圳市)已知:Rt △ABC 的斜边长为5,斜边上的高为2,将这个直角三角形放置在平面直角坐标系中,使其斜边AB 与x 轴重合(其中OA <OB ),直角顶点C 落在y 轴正半轴上(如图1).
(1)求线段OA 、OB 的长和经过点A 、B 、C 的抛物线的关系式. (2)如图2,点D 的坐标为(2,0),点P (m ,n )是该抛物线上的一个动点(其中m >0,n >0),连接DP 交BC 于点E .
①当△BDE 是等腰三角形时,直接写出....此时点E 的坐标. ②又连接CD 、CP (如图3),△CDP 是否有最大面积?若有,求出△CDP 的最大面积和此时点P 的坐标;若没有,请说明理由.
132.(广东省珠海市)已知抛物线y =x
2-32mx 与x 轴相交于点A 、B ,抛物线的顶点为
C .
(1)试用含m 的代数式表示AB 的长度; (2)当△ABC 为等边三角形时,求点C 的坐标; (3)在(2)的条件下,如何平移抛物线,使AC =
2
13
AB ?
133.(广东省佛山市)如图1,一个长方体形的木柜放在墙角处(与墙面和地面均没有缝隙),有一只蚂蚁从柜角A 处沿着木柜表面爬到柜角C 1处. (1)请你画出蚂蚁能够最快到达目的地的可能路径;
(2)当AB =4,BC =4,CC 1=5时,求蚂蚁爬过的最短路径的长; (3)求点B 1到最短路径的距离. A B
x
y O 图1
C A B x y O P
D E
图2 C A B
P
x
y O D E 图3 C 备用图 图1
134.(广东省茂名市)已知:如图,直线l :y =31x +b ,经过点M (0,4
1
),一组抛物线的
顶点B 1(1,y 1),B 2(2,y 2),B 3(3,y 3),…,B n (n ,y n )(n 为正整数)依次是直线l 上的点,这组抛物线与x 轴正半轴的交点依次是:A 1(x 1,0),A 2(x 2,0),A 3(x 3,0),…,A n +1(x n +1,0)(n 为正整数),设x 1=d (0<d <1). (1)求b 的值;
(2)求经过点A 1、B 1、A 2的抛物线的解析式(用含d 的代数式表示)
(3)定义:若抛物线的顶点与x 轴的两个交点构成的三角形是直角三角形,则这种抛物
线就称为“美丽抛物线”.
探究:当d (0<d <1)的大小变化时,这组抛物线中是否存在美丽抛物线?若存
在,请你求出相应的d 的值.
135.(广东省湛江市)已知矩形纸片OABC 的长为4,宽为3,以长OA 所在的直线为x 轴,O 为坐标原点建立平面直角坐标系;点P 是OA 边上的动点(与点OA 不重合),现将△POC 沿PC 翻折得到△PEC ,再在AB 边上选取适当的点D ,将△P AD 沿PD 翻折,得到△PFD ,使得直线PE 、PF 重合.
(1)若点E 落在BC 边上,如图①,求点P 、C 、D 的坐标,并求过此三点的抛物线的函数关系式;
(2)若点E 落在矩形纸片OABC 的内部,如图②,设OP =x ,AD =y ,当x 为何值时,y 取得最大值?
(3)在(1)的情况下,过点P 、C 、D 三点的抛物线上是否存在点Q ,使△PDQ 是以PD
为直角边的直角三角形?若不存在,说明理由;若存在,求出点Q 的坐标.
136.(广东省肇庆市)如图,⊙O 的直径AB =2,AM 和BN 是它的两条切线,DE 切⊙O 于E ,交AM 于D ,交BN 于C .设AD =x ,BC =y . (1)求证:AM ∥BN ;
(2)求y 关于x 的关系式;
(3)求四边形ABCD 的面积S ,并证明:S
≥2.
137.(广东省清远市)如图,已知一个三角形纸片ABC ,BC 边的长为8,BC 边上的高为6,∠B 和∠C 都为锐角,M 为AB 上一动点(点M 与点A 、B 不重合),过点M 作MN ∥BC ,交AC 于点N ,在△AMN 中,设MN 的长为x ,MN 上的高为h . (1)请你用含x 的代数式表示h .
(2)将△AMN 沿MN 折叠,使△AMN 落在四边形BCNM 所在平面,设点A 落在平面的点为A 1,△A 1MN 与四边形BCNM 重叠部分的面积为y ,当x 为何值时,y 最大,最大值为多少?
138.(广东省梅州市)如图,矩形ABCD 中,AB =5,AD =3.点E 是CD 上的动点,以AE 为直径的⊙O 与AB 交于点F ,过点F 作FG ⊥BE 于点G . (1)当E 是CD 的中点时:
①tan ∠EAB 的值为______________; ②证明:FG 是⊙O 的切线;
(2)试探究:BE 能否与⊙O 相切?若能,求出此时DE 的长; 若不能,请说明理由.
N
B C N M A
139.(广东省梅州市)如图,已知直线L过点A(0,1)和B(1,0),P是x轴正半轴上的动
点,OP的垂直平分线交L于点Q,交x轴于点M.
(1)直接写出直线L的解析式;
(2)设OP=t,△OPQ的面积为S,求S关于t的函数关系式;
并求出当0<t<2时,S的最大值;
(3)直线L1过点A且与x轴平行,问在L1上是否存在点C,使得△CPQ是以Q为直角顶点的等腰直角三角形?若存在,求出点C的坐标,并证明;若不存在,请说明理由.
1。
