八年级数学(下册)各单元知识结构图
合集下载
初中数学各章节知识图解思维导图(共9张PPT)

y轴的对称点
表
示
轴
对
解决几何中的
称
极值问题
基本图形
一条直线
翻折后与 两部分重 合
对称轴 定义
轴对称图形 静
基本图形 方向 距离
前.后图形全等
要素 特征
平移
静
轴对称
轴对称变换
要
动
素
旋转中心
旋转方向 旋转角 对应点到旋转中心的距离相等
图形的旋转
旋转前.后的图形全等
特
对应点与旋转中心所连线段的夹角=
征
旋转角
图形的 全等变 换
旋转角=1800
中心对称图 形
旋转
意义
单项式
字母指数和
次数
系数
数字因 数
不改变 分式的值
公因式
通分化成同分 母
分母不变 分子相 加减
通分
子积为子母积为母
注:分子、 分母为多 项式时先 分解因式
化除法为乘法
基本性质
分式
运算 分式方程
乘除 乘方
a
n
b
an bn
n为整数
an
1 an
n为整数
解法
应用
二次根式
运算
加减
代
数
性质
乘除
定义
式 (1) aa0双非负
k<0
到三边的距离相等在三角形内
点到两点 的距离相等k>0
k<0
二次函数与 两图形相似
一元二次方程
对应图顶象点的连线交于一点对应关边系平行
x1= x2 =
K同号时, 有两交点。 K异号时, 有两个、一个 或无交点
图象 性质
分母不变 分子相加减 实际问题,图象在第一象性限质
沪教版(上海)-初中数学七年级、八年级、九年级数学全册章节知识点结构思维导图集
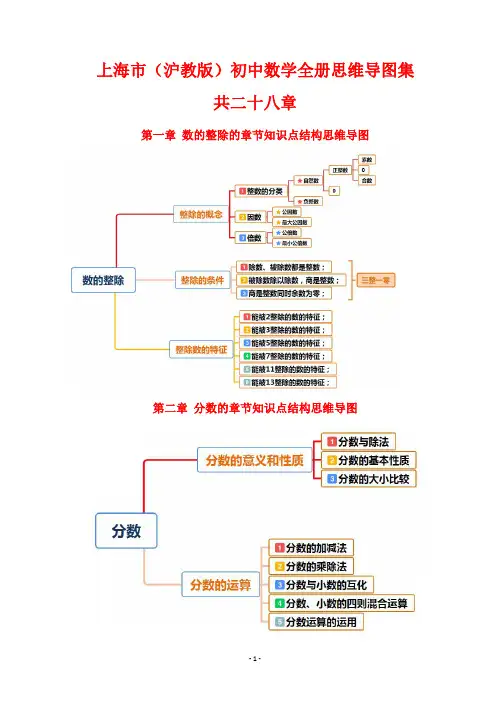
第二十五章 锐角三角比的章节知识点结构思维导图
- 14 -
第二十六章 二次函数的章节知识点结构思维导图 第二十七章 圆与正多边形的章节知识点结构思维导图
- 15 -
第二十八章 统计初步的章节知识点结构思维导图
- 16 -
-7-
第十四章 三角形的章节知识点结构思维导图 第十五章 平面直角坐标系的章节知识点结构思维导图
-8-
上海市(沪教版)八年级数学全册章节思维导图 共八个章节
第十六章 二次根式的章节知识点结构思维导图
-9-
第十七章 一元二次方程的章节知识点结构思维导图
- 10 -
第十八章 正比例函数和反比例函数的章节知识点结构思维导图 第十九章 几何证明的章节知识点结构思维导图
-3-
第七章 线段与角的画法的章节知识点结构思维导图 第八章 长方体的再认识的章节知识点结构思维导图
-4-
上海市(沪教版)七年级数学全册章节思维导图 共七章
第九章 整式的章节知识点结构思维导图
-5-
第十章 分式的章节知识点结构思维导图 第十一章 图形的运动的章节知识点结构思维导图
-6-
第十二章 实数的章节知识点结构思维导图 第十三章 相交线 平行线的章节知识点结构思维导图
- 11 -
第二十章 一次函数的章节知识点结构思维导图 第二十一章 代数方程的章节知识点结构思维导图
- 12 -
第二十二章 四边形的章节知识点结构思维导图 第二十三章 概率初步的章节知识点结构思维导图
- 13 -
上海市(沪教版)ቤተ መጻሕፍቲ ባይዱ年级数学全册章节思维导图 共五章
第二十四章 相似三角形的章节知识点结构思维导图
上海市(沪教版)初中数学全册思维导图集 共二十八章
- 14 -
第二十六章 二次函数的章节知识点结构思维导图 第二十七章 圆与正多边形的章节知识点结构思维导图
- 15 -
第二十八章 统计初步的章节知识点结构思维导图
- 16 -
-7-
第十四章 三角形的章节知识点结构思维导图 第十五章 平面直角坐标系的章节知识点结构思维导图
-8-
上海市(沪教版)八年级数学全册章节思维导图 共八个章节
第十六章 二次根式的章节知识点结构思维导图
-9-
第十七章 一元二次方程的章节知识点结构思维导图
- 10 -
第十八章 正比例函数和反比例函数的章节知识点结构思维导图 第十九章 几何证明的章节知识点结构思维导图
-3-
第七章 线段与角的画法的章节知识点结构思维导图 第八章 长方体的再认识的章节知识点结构思维导图
-4-
上海市(沪教版)七年级数学全册章节思维导图 共七章
第九章 整式的章节知识点结构思维导图
-5-
第十章 分式的章节知识点结构思维导图 第十一章 图形的运动的章节知识点结构思维导图
-6-
第十二章 实数的章节知识点结构思维导图 第十三章 相交线 平行线的章节知识点结构思维导图
- 11 -
第二十章 一次函数的章节知识点结构思维导图 第二十一章 代数方程的章节知识点结构思维导图
- 12 -
第二十二章 四边形的章节知识点结构思维导图 第二十三章 概率初步的章节知识点结构思维导图
- 13 -
上海市(沪教版)ቤተ መጻሕፍቲ ባይዱ年级数学全册章节思维导图 共五章
第二十四章 相似三角形的章节知识点结构思维导图
上海市(沪教版)初中数学全册思维导图集 共二十八章
人教版八年级(初二)数学下册 16.1 二次根式 第一课时 PPT教学课件

际问题.
5.培养观察、发现、分析问题的能力,增强学生科学研究的意识.
学习重难点
学习重点:二次根式的概念.
学习难点:二次根式有意义的条件.
回顾复习
1.平方根与算术平方根的概念.
2.若正方形的面积为S,则正方形的边长为
S .
探究新知
学生活动一 【自主探究】
认真阅读教材第2页至第3页的内容,完成下面练习并体验知识
当3为腰长时,三角形的边长分别为3,3,4,符合三角形的
三边关系,此时三角形的周长为3+3+4=10;
当4为腰长时,三角形的边长分别为4,4,3,符合三角形的
三边关系, 此时三角形的周长为4+4+3=11.
∴ 此三角形的周长为10或11.
课后作业
1.教材P5习题16.1复习巩固第1,3题,综合运用
它的长、宽各应取多少?
3
解:设长方形的宽为x m,则长方形的长为 x m,
2
3
3
∴ x∙x=18,解得x=2 3, x=3 3.
2
2
∴长方形的长为3 3 m,宽为2 3 m.
拓展应用
2.当a是怎样的实数时,下列各式在实数范围内有意义?
(1) a − ;
解:由题意,得a-1≥0,解得a≥1,
∴当a≥1时, a − 在实数范围内有意义.
x−2≠0,
∴当x≤3,且x≠2时,
3−x
在实数范围内有意义.
x−2
探究新知
(3)
x+5
.
x
解:由题意,得ቊ
x+5≥0,
解得x≥-5且x≠0.
x≠0,
∴当x≥-5且x≠0时,
x+5
5.培养观察、发现、分析问题的能力,增强学生科学研究的意识.
学习重难点
学习重点:二次根式的概念.
学习难点:二次根式有意义的条件.
回顾复习
1.平方根与算术平方根的概念.
2.若正方形的面积为S,则正方形的边长为
S .
探究新知
学生活动一 【自主探究】
认真阅读教材第2页至第3页的内容,完成下面练习并体验知识
当3为腰长时,三角形的边长分别为3,3,4,符合三角形的
三边关系,此时三角形的周长为3+3+4=10;
当4为腰长时,三角形的边长分别为4,4,3,符合三角形的
三边关系, 此时三角形的周长为4+4+3=11.
∴ 此三角形的周长为10或11.
课后作业
1.教材P5习题16.1复习巩固第1,3题,综合运用
它的长、宽各应取多少?
3
解:设长方形的宽为x m,则长方形的长为 x m,
2
3
3
∴ x∙x=18,解得x=2 3, x=3 3.
2
2
∴长方形的长为3 3 m,宽为2 3 m.
拓展应用
2.当a是怎样的实数时,下列各式在实数范围内有意义?
(1) a − ;
解:由题意,得a-1≥0,解得a≥1,
∴当a≥1时, a − 在实数范围内有意义.
x−2≠0,
∴当x≤3,且x≠2时,
3−x
在实数范围内有意义.
x−2
探究新知
(3)
x+5
.
x
解:由题意,得ቊ
x+5≥0,
解得x≥-5且x≠0.
x≠0,
∴当x≥-5且x≠0时,
x+5
初中数学各章节知识图解思维导图ppt课件
对邻
垂
顶补
直
角角
画法
同位角相等
角的度量 图形认识初步
借助角研究平面内两条直 线的位置关系
相交线
关系
相交线.平行线
断定
条件
内错角相等 同旁内角互补
平行线
平行公理.推论
性质
同位角相等 内错角相等
直线.射线.线段
同旁内角互补
多姿多彩的图形
立体图形
平面图形
图形认识初 步 相交线
平行线
命题
分类 构造
识别 展开图
对应线段 平行且相等
动
运用
利用平移制作图 案
平移过程 对应点坐标 的变化规律
(x,y〕平移后 〔x±a,y±b)
右加左减
上加下减
图案设计
用平移.轴对称和旋转的组合设计图 案
关于中心对称
两图形全等
关于原点对称
旋转1800后与 另一图形 重合
用坐标表示 旋转
对称点的坐标符号 相反
到角两边距离相等的 点
解法 运用
传播问题 行程问题 效率问题
与y轴交点位置 c>0.在正
开口方上向a<. 0.向a下>0.向对称轴在y轴的位半 在轴 负半c=轴0.在原点 置 左同右异
c<0.
解析
二次函数 与 一元二
次方程
定义
面积问题
y=ax2+bx+c (a.b.c为常数a≠0)
y axh2 k yaxx1xx2
(a 0)
性质
ac bd
对应角相等, 周长的比=相似比 方
对应边成比例, 面积的比=相似比的平
正方形
旋转 不变性 轴对称性
外心:是三边垂直平 分线的交
八年级数学下册第一章回顾与思考

本章知识结构图
实际背景
不等式
一元一次不等式 一元一次不等式组
ห้องสมุดไป่ตู้
不等式的基本性质 解不等式
解法
解法
解集 数轴表示 解集 数轴表示 解集 数轴表示
实际应用
如果a=b,那么a±c=b±c 如果a=b,那么ac=bc,a÷c=b÷c(c≠0)
如果a>b,那么a+c>b+c(或 a-c>b-c).
如果a<b,那么a+c<b+c(或 a-c<b-c).
如果a<b,且c>0,那么ac<bc 如果a>b,且c>0,那么ac>bc
如果a<b,且c<0,那么ac>bc 如果a>b,且c<0,那么ac<bc
例1.
解一元一次方程 解一元一次不等式
解法 (1)去分母; 步骤 (2)去括号;
(3)移项; (4)合并同类项
;
(5)系数化成1
(1)去分母; (2)去括号; (3)移项; (4)合并同类项; (5)系数化成1 在步骤(1)和(5)
中,要注意不等式 号方向是否改变
解的 一元一次方程只有 一元一次不等式的解
情况 一个解
集含有无限多个数
例2.
.
例3.
A
例4.
例5 .
实际背景
不等式
一元一次不等式 一元一次不等式组
ห้องสมุดไป่ตู้
不等式的基本性质 解不等式
解法
解法
解集 数轴表示 解集 数轴表示 解集 数轴表示
实际应用
如果a=b,那么a±c=b±c 如果a=b,那么ac=bc,a÷c=b÷c(c≠0)
如果a>b,那么a+c>b+c(或 a-c>b-c).
如果a<b,那么a+c<b+c(或 a-c<b-c).
如果a<b,且c>0,那么ac<bc 如果a>b,且c>0,那么ac>bc
如果a<b,且c<0,那么ac>bc 如果a>b,且c<0,那么ac<bc
例1.
解一元一次方程 解一元一次不等式
解法 (1)去分母; 步骤 (2)去括号;
(3)移项; (4)合并同类项
;
(5)系数化成1
(1)去分母; (2)去括号; (3)移项; (4)合并同类项; (5)系数化成1 在步骤(1)和(5)
中,要注意不等式 号方向是否改变
解的 一元一次方程只有 一元一次不等式的解
情况 一个解
集含有无限多个数
例2.
.
例3.
A
例4.
例5 .
