母线平行于坐标轴的柱面方程
第三节 曲面及其方程8-3

解 设M( x, y, z)是曲面上任一点,
根据题意有 | MO | 1 , | MM0 | 2
x2 y2 z2
1,
x 22 y 32 z 42 2
所求方程为
x
22
y
12
z
42
116 .
3
3 9
第八章 第三节
都可通过配方研究它的图形. 其图形可能是 一个球面 , 或点 , 或虚轨迹.
第八章 第三节
8
以上几例表明研究空间曲面有两个基本问题: (1)已知曲面作为点的轨迹时,求曲面方程.
(讨论旋转曲面)
(2)已知坐标间的关系式,研究曲面形状. (讨论柱面、二次曲面)
第八章 第三节
9
二、旋转曲面
定义 以一条平面 曲线绕其平面上的 一条直线旋转一周 所成的曲面称为旋 转曲面. 这条定直线叫旋转 曲面的轴.
第八章 第三节
10
二、旋转曲面
定义 以一条平面 曲线绕其平面上的 一条直线旋转一周 所成的曲面称为旋 转曲面. 这条定直线叫旋转 曲面的轴.
第八章 第三节
11
二、旋转曲面
定义 以一条平面 曲线绕其平面上的 一条直线旋转一周 所成的曲面称为旋 转曲面. 这条定直线叫旋转 曲面的轴.
第八章 第三节
12
5
例 3 已知A(1,2,3),B(2,1,4),求线段AB 的
垂直平分面的方程.
解 设M( x, y, z)是所求平面上任一点, 根据题意有 | MA || MB |,
x 12 y 22 z 32
x 22 y 12 z 42 ,
4.1柱面

《解析几何》-Chapter 4§1 柱面cylinderContents一、柱面的概念二、柱面的方程三、柱面的判定定理四、空间曲线的射影柱面平面v222x y a+=zxy o圆柱面v那族平行直线中的每一条直线,都叫做柱面的母线.定义4.1.1在空间,由平行于定方向且与一条定曲线相交的一族平行直线所生成的曲面叫做柱面(cylinder ),定方向叫做柱面的方向,定曲线叫做柱面的准线(directrix ),v准线准线母线v说明:柱面的准线不是惟一的,每一条与柱面的母线都相交的曲线都可以作为柱面的准线.一、柱面的概念x zy 0准线母线准线v注:一般柱面的准线不惟一,可用一张不平行于母线的平面与柱面相交得到的交线为准线.1 柱面的一般方程Ⅰ 准线方程()()12,,0,,0F x y z C F x y z =⎧⎪⎨=⎪⎩:Ⅱ 母线l 的方向数:,,X Y Z普通方法1M vCl设M 1(x 1, y 1, z 1)为准线上任意一点,①写出母线族方程:111x x y y z z X Y Z---==②写出参数x 1, y 1, z 1的约束条件:(,,),(,,).1111211100F x y z F x y z =⎧⎨=⎩(,,)0F x y z =③消去参数x 1, y 1, z 1得一个三元方程:1 柱面的一般方程()()12,,0,,0F x Xt y Yt z Zt F x Xt y Yt z Zt ---=⎧⎪⇒⎨---=⎪⎩Ⅰ 准线方程()()12,,0,,0F x y z C F x y z =⎧⎪⎨=⎪⎩:Ⅱ 母线l 的方向数:,,X Y Z()()11112111,,0,,0F x y z F x y z =⎧⎪⇔=⎨⎪⎩分析:()1111 ,,M x y z C ∈∀11M CM l∈⎧⇔⎨∈⎩t=(),,0F x y z ⇒=1M vCl母线方程111x x y y z z X Y Z---==例1柱面的准线方程为,而母线的方向数是,求这柱面的方程.2222221222⎧++=⎪⎨++=⎪⎩x y z x y z ,1,0,1-解:设M 1(x 1, y 1, z 1)为准线上任意一点,111101x x y y z z ---==-(x 1, y 1, z 1为参数)且22211122211111222⎧++=⎪⎨++=⎪⎩,(),x y z x y z 为消参数x 1, y 1, z 1,可设111101x x t y y z z ---===-则111,,=+==-x x t y y z z t 代入(1)式得2222221222⎧+++-=⎪⎨+++-=⎪⎩()(),()(),x t y z t x t y z t 消去参数t ,并化简得所求柱面方程:22()1++=x z y 222210.+++-=x y z xz 即约束方程例2:已知圆柱面的轴为点(1,-2,1)在此圆柱面的方程.11,122x y z -+==--v 轴0(0,1,1)M -1(1,2,1)M -分析普通方法:关键:求圆柱面的准线(圆)方程.{,,},=--122v (,,)-0011M 圆柱面的轴:以M 0为球心, M 0M 1为半径的球面球面:平面:过点M 1为与轴垂直的平面()()()--+--=122210x y z ()()+-++=2221114x y z 圆柱面的准线方程:()()⎧+-++=2221114x y z =0114M M例1柱面的准线方程为,而母线的方向数是,求这柱面的方程.2222221222x y z x y z ⎧++=⎪⎨++=⎪⎩,1,0,1-例2已知圆柱面的轴为,点在此圆柱面上,求这个圆柱面的方程.11122x y z -+==--()1,2,1P -二、柱面的方程还有其它方法吗?vMr 轴圆柱面:设圆柱面的轴线为000---==x x y y z z X Y Z0000(,,)M x y z 其中:0000(,,)M x y z 为轴线上的定点,{,,}=v X Y Z 为轴线方向向量.(,,)M x y z 是圆柱面上任意点①0⨯⇔= M M vvr ①已知轴线及半径②已知轴线及柱面上一定点M 1②010M M v v v vM M ⨯⨯⇔==1111(,,)M x y z解:圆柱面的轴的方向向量:{1,2,2},v --=0(0,1,1)M -为轴上定点.(,,)M x y z 设是圆柱面上任意点,且点M 1(1,-2,1)在此圆柱面上,则点M 与点M 1在到轴的距离相等,即:001M M M M v vv v⨯⨯=010 M M M v v M ⇒⨯=⨯ kj i 1 1x y z -+1 -2 -2⇒k j i 1 3 2-1 -2 -2=⇒例2已知圆柱面的轴为,点在此圆柱面上,求这个圆柱面的方程.11122x y z -+==--()11,2,1M -12222=+by a x zxyo 椭圆柱面(直角坐标系)方程的形式与柱面的图形特征之间有联系吗?三、柱面的判定定理三、柱面的判定定理定理4.1.1在空间直角坐标系中,只含有两个元(坐标)的三元方程所表示的曲面是一个柱面,它的母线平行于所缺元(坐标)的同名坐标轴。
解析几何-吕林根-课后习题解答一到五
第一章矢量与坐标§1.1 矢量的概念1.下列情形中的矢量终点各构成什么图形?(1)把空间中一切单位矢量归结到共同的始点;(2)把平行于某一平面的一切单位矢量归结到共同的始点;(3)把平行于某一直线的一切矢量归结到共同的始点;(4)把平行于某一直线的一切单位矢量归结到共同的始点.解:2. 设点O是正六边形ABCDEF的中心,在矢量OA、OB、OC、OD、OE、OF、AB、BC、CD、DE、EF和FA中,哪些矢量是相等的?[解]:图1-13. 设在平面上给了一个四边形ABCD,点K、L、M、N分别是边AB、BC、CD、DA的中点,求证:KL=NM. 当ABCD是空间四边形时,这等式是否也成立?[证明]:.4. 如图1-3,设ABCD-EFGH是一个平行六面体,在下列各对矢量中,找出相等的矢量和互为相反矢量的矢量:(1) AB、CD; (2) AE、CG; (3) AC、EG;(4) AD、GF; (5) BE、CH.解:§1.2 矢量的加法1.要使下列各式成立,矢量b a ,应满足什么条件? (1=+ (2+=+ (3-=+ (4+=- (5= 解:§1.3 数量乘矢量1 试解下列各题.⑴ 化简)()()()(→→→→-⋅+--⋅-b a y x b a y x .⑵ 已知→→→→-+=3212e e e a ,→→→→+-=321223e e e b ,求→→+b a ,→→-b a 和→→+b a 23.⑶ 从矢量方程组⎪⎩⎪⎨⎧=-=+→→→→→→by x ay x 3243,解出矢量→x ,→y .解:2 已知四边形ABCD 中,→→→-=c a AB 2,→→→→-+=c b a CD 865,对角线→AC 、→BD 的中点分别为E 、F ,求→EF . 解:3 设→→→+=b a AB 5,→→→+-=b a BC 82,)(3→→→-=b a CD ,证明:A 、B 、D 三点共线. 解:4 在四边形ABCD中,→→→+=baAB2,→→→--=baBC4,→→→--=baCD35,证明ABCD为梯形.解:6. 设L、M、N分别是ΔABC的三边BC、CA、AB的中点,证明:三中线矢量AL, BM, CN可以构成一个三角形.7. 设L、M、N是△ABC的三边的中点,O是任意一点,证明OBOA++OC=OL+OM+ON.解:8. 如图1-5,设M是平行四边形ABCD的中心,O是任意一点,证明OA+OB+OC+OD=4OM.解:9在平行六面体ABCDEFGH(参看第一节第4题图)中,证明→→→→=++AGAHAFAC2.证明:.10.用矢量法证明梯形两腰中点连续平行于上、下两底边且等于它们长度和的一半.解11. 用矢量法证明,平行四边行的对角线互相平分.解12. 设点O 是平面上正多边形A 1A 2…A n 的中心,证明: 1OA +2OA +…+n OA =0.解,13.在12题的条件下,设P 是任意点,证明 证明:§1.4 矢量的线性关系与矢量的分解1.在平行四边形ABCD 中,(1)设对角线,,b BD a AZ ==求.,,,DA CD BC AB 解(2)设边BC 和CD 的中点M 和N ,且q AN P AM ==,求CD BC ,。
解析几何-柱面

y 2 2 px z 2 准线 : 2 抛物柱面 : y 2 px (4) z 0 母线 // z轴
一般地,若一曲面方程中仅含有两个变量,则此 曲面一定是柱面,它的母线平行于和缺少的那个变 量同名的坐标轴.
如: 8 x 2 25 y 2 4 xy 20 x 10 y 0 为母线平行于 z轴的柱面 .
x x 1 y y1 z z1 1 1 0 2 2 (1)
三.母线平行于坐标轴的柱面 母线 0
S
y
f ( x, y, z)=0 z=0
x 准线
N (x, y, 0)
点N满足方程,故点M满足方程
f ( x, y, z ) 0 设柱面的准线是 xoy 坐标面上曲线 : z 0 母线平行于 z轴 , 则柱面的方程为 f ( x , y ) 0. 证 由题设 , 母线方向为 v 0,0,1 设 M 1为准线上任一点 , 则过 M 1的母线方程为 :
§3.3
柱面
一.定义 平行于定直线并沿定曲线c移动的直线l 所形成的曲面称为柱面. 这条定曲线c 叫柱面的准线, 动直线l叫柱面 的母线.
准线
c
l
柱面是直纹面
母线
二.柱面的方程
F1 ( x , y , z ) 0 已知准线方程为 : F2 ( x , y , z ) 0 母线的方向为 : l , m , n 设 M 1为准线上任一点 , 则过 M 1的母线方程为 : F1 ( x1 , y1 , z1 ) 0 ( 2 ) 又 M 1在准线上 , 故 F2 ( x1 , y1 , z1 ) 0 ( 3 ) 联立 (1)( 2 )( 3 )消去 x1 , y1 , z1 , 得柱面方程为 : F ( x, y, z ) 0
柱面方程的一点注记

柱面方程的一点注记何国庆(安徽师范大学数计学院,芜湖,241000)摘要:本文对母线方向为}{,,v l m n =的柱面讨论其方程,得到一个定理.并举例说明了此定理的应用.关键词:柱面,母线方向,方程柱面是日常生活中常见的一种曲面,它有很明显的几何特征,是教学的重点内容.所谓的[]1柱面,指的是动直线l 平行于定方向v 且与定曲线C 相交而产生的曲面.每一条动直线称为柱面的直母线,定曲线C 称为柱面的准线,v 称为柱面的母线方向.显然,柱面被它的准线及母线方向完全确定.但对于一个柱面,它的准线并不是唯一的,每一条和所有直母线均相交的曲线都可当准线.许多教材都给出求柱面方程的一般方法,但对柱面方程的特征讨论的较少.本文给出了母线方向为}{,,v l m n =的柱面方程的几种形式.有 定理:在空间直角坐标系中,设柱面S 的母线方向}{,,v l m n =,则S 的方程一定可写为(,)0l m f x z y z n n --=,或0),(=--y m n z y m l x g ,或(,)0m n h y x z x l l--=;反之,若一个曲面的方程可改写为上述三种方程之一,则它一定是柱面,其母线方向为}{,,v l m n =. 证明:由于柱面S 的母线方向}{,,0v l m n =≠,故S 一定与某个坐标面相交.如0n ≠,则S 的母线与xoy 面相交,取其交线(,)0:0f x y C z =⎧⎨=⎩为柱面S 的准线.在准线C 上任取1111(,,)P x y z ,则过1P 的母线方程为111x x lt y y mt z z nt =+⎧⎪=+⎨⎪=+⎩又1P C ∈,则111(,)00f x y z =⎧⎨=⎩ 由(1)(2)消去111,,x y z ,得(,)0l m f x z y z n n --=收稿日期:2011年9月作者简介:何国庆(1979—),女,安徽巢湖,讲师,研究方向:微分几何. E-mail:wh_hgq@(1) (2) (3)则方程(3)就是母线方向为}{,,(0)v l m n n =≠的柱面S 的方程. 同理可证:当0m ≠时,柱面S 方程为0),(=--y mn z y m l x g 当0l ≠时,柱面S 方程为(,)0m n h y x z x l l --= 反之,设曲面S 的方程可改写为(,)0l m f x z y z n n --=,则它与以曲线(,)00f x y z =⎧⎨=⎩为准线,母线方向平行于}{,,v l m n =的柱面有相同方程,故曲面S 表示一个柱面,其母线方向为}{,,v l m n =. 推论:若一个柱面的母线平行于z 轴(或x 轴,或y 轴),则它的方程不含z 项(或x 项,或y 项);反之,一个三元方程中如果不含z 项(或x 轴,或y 轴),则这个三元方程一定表示一个母线平行于z 轴(或x 轴,或y 轴)的柱面.注:此推论为文[2]中的定理.下面举例说明定理及推论的应用.例1[]1试说明方程()()2x y y z x y z ++=++表示柱面. 解:将已知方程改写为()()()()x y z y x y z y ++=+++.由定理知此曲面是以曲线0xz x z y =+⎧⎨=⎩为准线,母线方向平行于}{1,1,1v =-的柱面 注:此题也可有其他证法,如文[1]中的证法.例2[]2空间直角坐标系中,方程22221x y a b +=,22221x y a b-=,22y px =都表示母线平行于z 轴的柱面,分别称为椭圆柱面,双曲柱面,抛物柱面,统称为二次柱面.参考文献:[1]宋卫东.《解析几何》[M].北京:高等教育出版社,2003:144-147[2]杨文茂.李全英.《空间解析几何》[M].武汉:武汉大学出版社,2000:94-97A NOTE ON THE EQUA TION OF CYLINEDERHe Guoqing(College of Maththetics and Computer Science,Anhui Normal University,WUHU 241000)Abstract:The paper discusses the equation of cylineder which element parallels the vector }{,,v l m n =,and a gives theorem.Then there are some examples which use the theorem. Key words: Cylineder,The direction of element,Equation。
2.3-2.4:母线平行于坐标轴的柱面和空间曲线方程

b, 在空间建立坐标系使Oz轴重合与轴线.
取时间t为参数, 设P是轨迹上任意一点. 设动点从A(a, 0, 0 )点出发,经过t时间, 运动到P(x, y, z)点.
z
P在 xoy 面的投影 Q(x, y, 0),
容易看出
x OQ cos t a cos t y OQ sin t a sin t z QP vt bt
它的方程是
x y z R
2 2 2
2
xOy面的方程为
z=0
所以所求圆的一般方程为:
x2 y 2 z 2 R2 z 0
z a2 x2 y2 例4 方程组 a 2 a 2 表示怎样的曲线? 22 y2
注意可以将方程(1)看作F(x, y)+0z=0
这说明整个直线L在曲面上. 注意到Q点的任意性, 所以
曲面至少包含沿曲线移动而平行于z轴的所有直线.
曲面至少包含沿曲线移动而平行于z轴的所有直线. 除了这些直线外,曲面 还包含其它点吗? L P y
没有其它类型的点!
证明: 设P(x1, y1, z1)是 O
z
S1
S2
o
C
y
x
x y 1 例1 方程组 表示怎样的曲线? 2 x 3 y 3z 6
2 2
解
x 2 y 2 1 表示圆柱面,
2 x 3 y 3 z 6 表示平面,
x2 y2 1 2 x 3 y 3z 6
交线为椭圆.
例2 写出Oz轴的方程 Oz轴可以看作是两个坐标面yoz和xoz面的交线.
o
x
A
y
动画圆柱螺线
圆柱面 x 2 y 2 a 2
曲面方程的概念
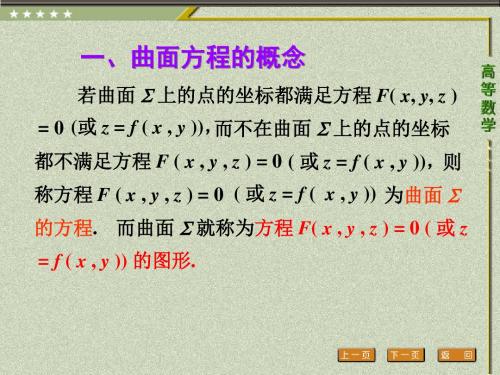
3 2 5 2 17 即 ( x ) ( y ) , 2 2 2 它是曲线 关于x y 坐标面的投 影柱面 - 圆柱面的方程, 在 x y 坐标面上投影曲线是圆. 32 5 2 17 ( x ) ( y ) , 2 2 2 z 0 .
x x ( t ), y y ( t ), z z(t ) .
形如上的方程组称为曲线 的参数方程, t 为参数.
例 4 设质点在圆柱面 x 2 y 2 R 2上以均匀的 角速度 绕 z 轴旋转, 同时又以均匀的线速度 v 向平行于 z 轴的方向上升. 运动开始,即 t = 0 时, 质点在 P0(R, 0, 0) 处, 求质点的运动方程. z 解 设时间 t 时,质点的位置为 P( x, y, z ),由 P 作 x y 坐标面的垂线 垂足为 Q (x, y , 0) 则从 P0 到 P 所转 过的角 = t, 上升的高度 QP = vt , 即质点的运动方程为:
表示的曲面称为圆锥面, 点 O 称为圆锥的顶点.
(2) y z 坐标面上的抛物线 z = ay2 绕 z 轴旋转所 得的曲面方程为
z a( x y ),
2 2
z
该曲面称为旋转抛物面. 其特征是: 当 a < 0 时,旋转 抛物面的开口向下. 一般地,
方程
x y z 2 2 a b
2
2
设空间曲线 的方程为
消去 z ,得
F1 ( x , y, z ) 0, F2 ( x, y, z ) 0,
G( x , y )= 0.
可知满足曲线 的方程一定满足方程 G( x, y) = 0 , 而 G(x , y)= 0 是母线平行于 z 轴的柱面方程, 因此,柱面 G( x , y ) = 0 就是曲线 关于 x y 坐标 面的投影柱面. 而
09-13全国大学生高等数学竞赛真题及答案(非数学类)-无答案

一、填空题(每小题 5 分,共 20分)
(x y) ln(1 y )
1.计算 D
x dxdy ____________,其中区域 D 由直线 x y 1 与 1x y
两坐标轴所围成三角形区域.
2.设 f (x) 是连续函数,且满足 f (x) 3x2 2 f (x)dx 2 , 则 f (x) ____________. 0
3.曲面 z x22 y 2 2 平行平面 2x 2 y z 0 的切平面方程是__________.
4.设函数 y y(x) 由方程 xe f ( y) d2 y ________________. dx 2
ey ln 29确定,其中 f 具有二阶导数,且 f
1 ,则
二、(5 分)求极限 lim( ex e2x
2.证明广义积分
0
sin x
x
dx
不是绝对收敛的
3.设函数 y y x 由 x3 3x2 y 2 y3 2 确定,求 y x 的极值。
4.过曲线 y 3 x x 0 上的点 A 作切线,使该切线与曲线及 x 轴所围成的平面图形 3
的面积为 4 ,求点 A 的坐标。
二、(满分 12)计算定积分 I
x sin x arctan ex dx 1 cos2 x
三 、( 满 分 12 分 ) 设 f x 在 x 0 处 存 在 二 阶 导 数 f 0 , 且
lim f x x0 x
0 。证明 :级数 f 1 收敛。
n1
n
四 、( 满 分 12 分 ) 设 f x
b
sin f x dx
2
a
m
,f x
0a x b,证 明
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
25 2.3母线平行于坐标轴的柱面方程平行与固定方向且沿一条定曲线移动的动直线的轨迹叫柱面.定曲线叫柱面的准线动直线中的每一条都叫柱面的直母线在空间直角坐标系下给定不含变量z的方程Fxy 0 2.31在xOy平面上这方程表示一条曲线cc上的任一点QxOyOO的坐标满足这方程.过Q作xOy平面的垂线L则L上任意一点PxOyOk也满足这方程因而在曲面2.31上从而直线L上的所有点均在2.31所表示的曲面上.由于直线L的任意性可知曲面2.31是由始终与z轴平行的直线L沿着c移动而形成的因而表示一个母线平行于z轴的柱面.同理方程Fyz 0表示一个母线平行于x轴的柱面.而方程xyzOQPxyOkxyOOOO Fzx 0表示一个母线平行于y轴的柱面.例在空间直角坐标系下圆柱面222Ryx双曲柱面12222byax平面1zy和抛物柱面022ppxy的图形如下26作业P90习题对本次作业进行讲评以增强对学生的空间想象能力的训练.27。
