三角函数图像和性质习题课(含答案)(可编辑修改word版)
(精校版)必修4三角函数的图像与性质1.41.6(含答案)

6
2
6
所以函数 f (x) 的解析式为 f (x) 3sin(2x π ) 2 6 分 6
(2)将函数 y f (x) 的图像向左平移 π 个单位后得到的函数解析式为 y 3sin[2(x π ) π ] 2
12
12 6
,即 y 3sin(2x π ) 2 ,再将图像上各点的横坐标扩大为原来的 4 倍,得 g(x) 3sin(1 x π ) 2
11.已知函数 f (x) cos(2x ) 2sin(x ) sin(x ) .
3
4
4
(1)求函数 f (x) 的最小正周期和图像的对称轴方程;
(2)求函数
f
(x) 在区间[
,
] 上的值域。
12 2
【答案】(1)T 2π π , x kπ π (k Z) ;(2)[ 3 ,1]
长到原来的 2 倍(纵坐标不变)得到函数 f(x)的图象,则 f(-π)等于( )
A. 3
B。 3
C. 1
2
2
2
【答案】D
D.- 1 2
【解析】
试题分析:因为将函数 y sin x 的图像上所有的点向右平行移动 π 个单位长度,得到的函数解析 3
式为 y sin(x ) 。再把函数 y sin(x ) 各点的横坐标伸长到原来的 2 倍(纵坐标不变)得到
(直打版)必修 4 三角函数的图像与性质 1.4-1.6(含答案)(word 版可编辑修改)
(直打版)必修 4 三角函数的图像与性质 1.4-1.6(含答案)(word 版可编辑修改) 编辑整理:
尊敬的读者朋友们: 这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对 文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((直打版)必修 4 三角函数的图 像与性质 1.4-1.6(含答案)(word 版可编辑修改))的内容能够给您的工作和学习带来便利。同时也 真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。 本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快 业绩进步,以 下为(直打版)必修 4 三角函数的图像与性质 1.4-1.6(含答案)(word 版可编辑修改)的全部内容。
三角函数图像和性质练习题(附答案)

三角函数的图像与性质【1】一、选择题1.已知函数f(x)=2sin ϖx(ϖ>0)在区间[3π-,4π]上的最小值是-2,则ϖ的最小值等于( )A.32 B.23C.2D.3 2.若函数cos()3y x πω=+(0)ω>的图象相邻两条对称轴间距离为2π,则ω等于. A .12B .12C .2D .43.将函数sin()()6yx x R π=+∈的图象上所有的点向左平行移动4π个单位长度,再把图象上各点的横坐标扩大到原来的2倍(纵坐标不变),则所得到的图象的解析式为A .5sin(2)()12y x x R π=+∈ B .5sin()()212x y x R π=+∈ C .sin()()212x y x R π=-∈ D .5sin()()224x y x R π=+∈4.函数2)62cos(-+=πx y 的图像F 按向量a 平移到F /,F /的解析式y=f(x),当y=f(x)为奇函数时,向量a 可以等于A.)2,6(-π B.)2,6(π C.)2,6(--π D.)2,6(π-5.将函数sin y x =的图象向左平移(02)ϕϕπ≤≤个单位后,得到函数sin()6yx π=-的图象,则ϕ等于( )A .6πB .76πC .116πD .56π6.函数x x y 2cos 32sin -=)66(ππ≤≤-x 的值域为A.[]2,2- B. []0,2- C. []2,0 D. ]0,3[-7.将函数的图象上所有点的横坐标伸长到原来的倍(纵坐标不变),再将所得的图象向左平移个单位,得到的图象对应的解析式是 ( )A .B .C.D.8.函数f(θ ) =sin θ-1cos θ-2的最大值和最小值分别是()(A) 最大值 43 和最小值0(B)最大值不存在和最小值 34(C) 最大值 -43 和最小值0(D) 最大值不存在和最小值-349.ααcos sin +=t且αα33cos sin +<0,则t 的取值范围是( )A. [)0,2-B. []2,2-C. ()(]2,10,1 -D. ()()+∞-,30,310.把函数)(x f y =的图象沿着直线0=+y x 的方向向右下方平移22个单位,得到函数x y 3sin =的图象,则()A 、2)23sin(--=x yB 、2)63sin(--=x yC 、2)23sin(++=x yD 、2)63sin(++=x y二、填空题11.设函数).0)(3cos()(πϕϕ<<+=x x f 若)()(x f x f '+是奇函数,则ϕ=. 12.方程2cos()14x π-=在区间(0,)π内的解是.13.函数]),0[)(26sin(2ππ∈-=x x y 为增函数的区间14.已知x R ∈,则函数sin cos ()max sin ,cos ,2x x f x x x +⎧⎫=⎨⎬⎩⎭的最大值与最小值的和等于。
5.4 三角函数的图象与性质(精讲)(原卷版附答案).docx
5.4 三角函数的图象与性质考点一 五点画图【例1】(1)(2020·全国高一课时练习)用五点法作出函数1cos (02)y x x π=-≤≤的简图.(2)(2020·全国高一课时练习)利用正弦或余弦函数图象作出3sin 2y x π⎛⎫=+⎪⎝⎭的图象.【一隅三反】1.(2020·全国高一课时练习)利用“五点法”作出函数y =1-sin x (0≤x ≤2π)的简图.2.(2020·全国高一课时练习)利用正弦曲线,求满足1sin 22x <≤的x 的集合.3.(2020·武功县普集高级中学高一月考)用五点法作出函数32cos y x =+在[]0,2π内的图像.考点二 周期【例2】(1)(2020·福建高二学业考试)函数cos y x =的最小正周期为( ) A .2πB .πC .32π D .2π(2)(2020年广东潮州)下列函数中,不是周期函数的是( ) A.y =|cos x | B .y =cos|x |C .y =|sin x | D .y =sin|x |【一隅三反】1.(2020·全国高一课时练习)下列函数中,最小正周期为π的是( ) A .sin y x = B .cos y x =C .sin 2y x =D .1cos2y x =2.(2019·云南高二期末)函数 ()2sin 36f x x π⎛⎫=-⎪⎝⎭的最小正周期为__________.考点三 对称性【例3】(2020·辽宁大连·高一期末)函数()cos 26f x x π⎛⎫=+⎪⎝⎭的图像的一条对称轴方程为() A .6x π=B .512x π=C .23x π=D .23x π=-【一隅三反】1.(2020·永昌县第四中学高一期末)函数y =12sin 3x π⎛⎫- ⎪⎝⎭的图象的一条对称轴是( )A .x =-2π B .x =2π C .x =-6π D .x =6π2.(2020·山西省长治市第二中学校高一期末(理))下列函数中,最小正周期为π,且图象关于直线3x π=对称的函数是( )A .2sin 23y x π⎛⎫=+⎪⎝⎭B .2sin 26y x π⎛⎫=-⎪⎝⎭C .2sin 23x y π⎛⎫=+⎪⎝⎭ D .2sin 23y x π⎛⎫=-⎪⎝⎭3.(2020·河南平顶山·高一期末)如果函数()sin 2y x ϕ=+的图象关于直线πx =对称,那么ϕ取最小值时ϕ的值为( )A .3π±B .π3C .π2-D .2π±考点四 单调性【例4】(1)(2020·吉林扶余市第一中学高一期中)函数()1πsin 223f x x ⎛⎫=+ ⎪⎝⎭的单调递增区间为( ) A .5πππ,π1212k k ⎡⎤-+⎢⎥⎣⎦,k Z ∈ B .π3ππ,π44k k ⎡⎤++⎢⎥⎣⎦,k Z ∈ C .2πππ,π36k k ⎡⎤--⎢⎥⎣⎦,k Z ∈ D .πππ,π44k k ⎡⎤++⎢⎥⎣⎦,k Z ∈ (2)(2020·吉林扶余市第一中学高一期中)已知函数()()sin 2f x x ϕ=+在π0,6⎡⎤⎢⎥⎣⎦上单调递减,则实数ϕ的一个值是( ). A .3π2B .π2-C .πD .2π【一隅三反】1.(2020·湖南益阳·高一期末)函数()cos 26f x x π⎛⎫=+⎪⎝⎭的单调递增区间为( )A .()7,1212k k k Z ππππ⎡⎤--∈⎢⎥⎣⎦B .()72,266k k k Z ππππ⎡⎤--∈⎢⎥⎣⎦C .()5,1212k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦D .()52,266k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦2.(2020·全国高三其他(理))已知函数()()sin 06f x x πωω⎛⎫=+> ⎪⎝⎭,对任意x ∈R ,都有()3f x f π⎛⎫≤⎪⎝⎭,并且()f x 在区间,63ππ⎡⎤-⎢⎥⎣⎦上不单调,则ω的最小值是( ) A .1 B .3C .5D .73.(2020·全国高三其他(理))函数()()cos f x x θ=+在[]0,π上为增函数,则θ的值可以是( )A .0B .2πC .πD .32π考点五 奇偶性【例5】(2020·上海黄浦·高一期末)下列函数中,周期是π的偶函数为( ). A .cos 2xy = B .sin 2y x = C .|sin |y x = D .sin ||y x =【一隅三反】1.(2019·贵州高三月考(文))函数sin 2y x =是( )A .最小正周期为2π的奇函数 B .最小正周期为π的奇函数C .最小正周期为2π的偶函数 D .最小正周期为π的偶函数2.(2020·辽宁辽阳·高一期末)下列函数中,周期为π的奇函数是( ) A .cos2xy π+=B .sin(23)y x π=+C .cos(2)y x π=+D .cos 2y x π⎛⎫=-⎪⎝⎭3.(2020·昆明市官渡区第一中学高一开学考试)已知函数()3()sin 42f x x x R π⎛⎫=-∈ ⎪⎝⎭,下面结论错误的是( )A .函数()f x 的最小正周期为2π B .函数()f x 在区间0,16π⎡⎤⎢⎥⎣⎦上是增函数 C .函数()f x 的图象关于直线4x π=对称 D .函数()f x 是偶函数考点六 定义域【例6】(1)(2020·宁县第二中学高一期中)函数y =的定义域是________.(2)(2020·宁县第二中学高一期中)函数y =__________.【一隅三反】1(2020·辽宁沈阳·高一期中)函数1tan 24y x π⎛⎫=+⎪⎝⎭的定义域是( )A .4,2xx k k Z ππ⎧⎫≠-+∈⎨⎬⎩⎭∣ B .2,2xx k k Z ππ⎧⎫≠+∈⎨⎬⎩⎭∣ C .32,2xx k k Z ππ⎧⎫≠+∈⎨⎬⎩⎭∣ D .,2xx k k Z ππ⎧⎫≠+∈⎨⎬⎩⎭∣2.(2020·湖南高一月考)函数()=ln(sin f x x 的定义域为( ) A .2(,)()33k k k Z ππππ++∈ B .5(,)()66k k k Z ππππ++∈ C .2(2,2)()33k k k Z ππππ++∈ D .5(2,2)()66k k k Z ππππ++∈3.(2020·吉林公主岭·高一期末(理))函数()f x =的定义域为( )A .0,3π⎡⎤⎢⎥⎣⎦B .,43ππ⎡⎤⎢⎥⎣⎦C .(,]43ππD .5,44ππ⎡⎤⎢⎥⎣⎦考点七 值域【例7】(1)(2019·福建高三学业考试)函数2sin y x =的最小值是 。
高中数学精品讲义第四章第三节三角函数的图象与性质Word版含答案

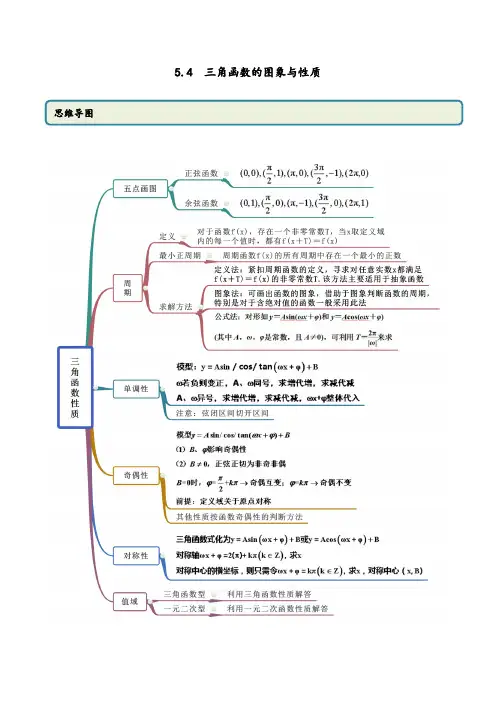
第三节三角函数的图象与性质1.用五点法作正弦函数和余弦函数的简图❶在正弦函数y =sin x ,x ∈[0,2π]的图象上,五个关键点是:(0,0),⎝⎛⎭⎫π2,1,(π,0),⎝⎛⎭⎫3π2,-1,(2π,0).在余弦函数y =cos x ,x ∈[0,2π]的图象上,五个关键点是:(0,1),⎝⎛⎭⎫π2,0,(π,-1),⎝⎛⎭⎫3π2,0,(2π,1).2.正弦、余弦、正切函数的图象与性质函数y =sin xy =cos xy =tan x五点法作图有三步:列表、描点、连线(注意光滑).正切函数的图象是由直线x=kπ+π2(k∈Z)隔开的无穷多支曲线组成的.判断三角函数的奇偶性,应首先判断函数定义域是否关于原点对称.求函数y=A sin(ωx+φ)的单调区间时,应注意ω的符号,只有当ω>0时,才能把ωx+φ看作一个整体,代入y=sin t的相应单调区间求解,否则将出现错误.写单调区间时,不要忘记k∈Z.(1)y=tan x无单调递减区间;(2)y=tan x在整个定义域内不单调.函数y=A sin(ωx+φ)和y=A cos(ωx+φ)的最小正周期都是2π|ω|,y=A tan(ωx+φ)的最小正周期是π|ω|.[熟记常用结论]1.对称与周期(1)正弦曲线、余弦曲线相邻两对称中心、相邻两对称轴之间的距离是半个周期,相邻的对称中心与对称轴之间的距离是14个周期.(2)正切曲线相邻两对称中心之间的距离是半个周期.2.奇偶性若f(x)=A sin(ωx+φ)(A≠0,ω≠0),则:(1)f(x)为偶函数的充要条件是φ=π2+kπ(k∈Z);(2)f (x )为奇函数的充要条件是φ=k π(k ∈Z).[小题查验基础]一、判断题(对的打“√”,错的打“×”) (1)y =sin x 在第一、第四象限是增函数.( ) (2)余弦函数y =cos x 的对称轴是y 轴.( ) (3)正切函数y =tan x 在定义域内是增函数.( ) (4)y =sin|x |是偶函数.( ) 答案:(1)× (2)× (3)× (4)√ 二、选填题1.函数y =tan 3x 的定义域为( ) A.⎩⎨⎧⎭⎬⎫x | x ≠3π2+3k π,k ∈ZB.⎩⎨⎧⎭⎬⎫x |x ≠π6+k π,k ∈ZC.⎩⎨⎧⎭⎬⎫x |x ≠-π6+k π,k ∈Z D.⎩⎨⎧⎭⎬⎫x |x ≠π6+k π3,k ∈Z解析:选D 由3x ≠π2+k π(k ∈Z),得x ≠π6+k π3,k ∈Z.2.函数y =2-cos x3(x ∈R)的最大值和最小正周期分别是( )A .2,3πB .1,6πC .3,6πD .3,3π解析:选C 由y =2-cos x 3知,y max =2-(-1)=3,最小正周期T =2π13=6π.3.下列函数中最小正周期为π且图象关于直线x =π3对称的是( )A .y =2sin ⎝⎛⎭⎫2x +π3B .y =2sin ⎝⎛⎭⎫2x -π6 C .y =2sin ⎝⎛⎭⎫x 2+π3D .y =2sin ⎝⎛⎭⎫2x -π3 解析:选B 函数y =2sin ⎝⎛⎭⎫2x -π6的最小正周期T =2π2=π, ∵sin ⎝⎛⎭⎫2×π3-π6=1, ∴函数y =2sin ⎝⎛⎭⎫2x -π6的图象关于直线x =π3对称. 4.函数y =sin ⎝⎛⎭⎫x -π4的图象的对称轴为______________,对称中心为________________. 解析:由x -π4=π2+k π,k ∈Z ,得x =3π4+k π,k ∈Z ;由x -π4=k π,k ∈Z ,得x =π4+k π,k ∈Z ,故函数y =sin ⎝⎛⎭⎫x -π4的图象的对称轴为x =3π4+k π,k ∈Z ,对称中心为⎝⎛⎭⎫π4+k π,0,k ∈Z.答案:x =3π4+k π,k ∈Z ⎝⎛⎭⎫π4+k π,0,k ∈Z 5.函数f (x )=32cos x -12sin x ()x ∈[0,π]的单调递增区间为________. 解析:f (x )=32cos x -12sin x =cos ⎝⎛⎭⎫x +π6,由2k π-π≤x +π6≤2k π(k ∈Z),得2k π-7π6≤x ≤2k π-π6(k ∈Z).∵x ∈[0,π],∴f (x )在⎣⎡⎦⎤5π6,π上单调递增. 答案:⎣⎡⎦⎤5π6,π6.函数f (x )=sin ⎝⎛⎭⎫2x -π4在区间⎣⎡⎦⎤0,π2上的最小值为________. 解析:由x ∈⎣⎡⎦⎤0,π2,得2x -π4∈⎣⎡⎦⎤-π4,3π4, 所以sin ⎝⎛⎭⎫2x -π4∈⎣⎡⎦⎤-22,1,故函数f (x )=sin ⎝⎛⎭⎫2x -π4在区间⎣⎡⎦⎤0,π2上的最小值为-22. 答案:-22考点一三角函数的定义域[基础自学过关][题组练透]1.函数f (x )=-2tan ⎝⎛⎭⎫2x +π6的定义域是( ) A.⎩⎨⎧⎭⎬⎫x | x ≠π6B.⎩⎨⎧⎭⎬⎫x |x ≠-π12C.⎩⎨⎧⎭⎬⎫x |x ≠k π+π6,k ∈ZD.⎩⎨⎧⎭⎬⎫x |x ≠k π2+π6,k ∈Z解析:选D 由正切函数的定义域,得2x +π6≠k π+π2(k ∈Z),即x ≠k π2+π6(k ∈Z),故选D.2.函数y =sin x -cos x 的定义域为________.解析:法一:要使函数有意义,必须使sin x -cos x ≥0.利用图象,在同一坐标系中画出[0,2π]上函数y =sin x 和函数y =cos x 的图象,如图所示.在[0,2π]内,满足sin x =cos x 的x 为π4,5π4,再结合正弦、余弦函数的周期性,所以原函数的定义域为⎩⎨⎧⎭⎬⎫x | 2k π+π4≤x ≤2k π+5π4,k ∈Z .法二:利用三角函数线,画出满足条件的终边范围(如图阴影部分所示).所以定义域为⎩⎨⎧⎭⎬⎫x |2k π+π4≤x ≤2k π+5π4,k ∈Z .答案:⎣⎡⎦⎤2k π+π4,2k π+5π4(k ∈Z) 3.函数y =lg(sin 2x )+9-x 2的定义域为________.解析:由⎩⎪⎨⎪⎧sin 2x >0,9-x 2≥0,得⎩⎪⎨⎪⎧k π<x <k π+π2,k ∈Z ,-3≤x ≤3.∴-3≤x <-π2或0<x <π2.∴函数y =lg(sin 2x )+9-x 2的定义域为⎣⎡⎭⎫-3,-π2∪⎝⎛⎭⎫0,π2. 答案:⎣⎡⎭⎫-3,-π2∪⎝⎛⎭⎫0,π2 [名师微点]求三角函数定义域实际上是构造简单的三角不等式(组),常借助三角函数线或三角函数图象来求解.考点二三角函数的值域(最值) [师生共研过关][典例精析](1)函数f (x )=3sin ⎝⎛⎭⎫2x -π6在区间⎣⎡⎦⎤0,π2上的值域为________. (2)(2017·全国卷Ⅱ)函数f (x )=sin 2x +3cos x -34⎝⎛⎭⎫x ∈⎣⎡⎦⎤0,π2的最大值是________. (3)函数y =sin x -cos x +sin x cos x 的值域为_________________________________. [解析] (1)当x ∈⎣⎡⎦⎤0,π2时,2x -π6∈⎣⎡⎦⎤-π6,5π6, ∴sin ⎝⎛⎭⎫2x -π6∈⎣⎡⎦⎤-12,1, 故3sin ⎝⎛⎭⎫2x -π6∈⎣⎡⎦⎤-32,3, ∴函数f (x )在区间⎣⎡⎦⎤0,π2上的值域为⎣⎡⎦⎤-32,3. (2)依题意,f (x )=sin 2x +3cos x -34=-cos 2x +3cos x +14=-⎝⎛⎭⎫cos x -322+1,因为x ∈⎣⎡⎦⎤0,π2,所以cos x ∈[0,1], 因此当cos x =32时,f (x )max =1. (3)设t =sin x -cos x ,则-2≤t ≤2,t 2=sin 2x +cos 2x -2sin x cos x ,则sin x cos x =1-t 22,∴y =-t 22+t +12=-12(t -1)2+1.当t =1时,y max =1;当t =-2时,y min =-12- 2.∴函数的值域为⎣⎡⎦⎤-12-2,1.[答案] (1)⎣⎡⎦⎤-32,3 (2)1 (3)⎣⎡⎦⎤-12-2,1 [解题技法]求三角函数的值域(最值)的3种类型及解法思路(1)形如y =a sin x +b cos x +c 的三角函数化为y =A sin(ωx +φ)+k 的形式,再求值域(最值);(2)形如y =a sin 2x +b sin x +c 的三角函数,可先设sin x =t ,化为关于t 的二次函数求值域(最值);(3)形如y =a sin x cos x +b (sin x ±cos x )+c 的三角函数,可先设t =sin x ±cos x ,化为关于t 的二次函数求值域(最值).[过关训练]1.若函数f (x )=(1+3tan x )cos x ,-π3≤x ≤π6,则f (x )的最大值为( )A .1B .2 C. 3D.3+1解析:选C f (x )=(1+3tan x )cos x =cos x +3sin x =2sin ⎝⎛⎭⎫x +π6.因为-π3≤x ≤π6,所以-π6≤x +π6≤π3,故当x =π6时,f (x )取最大值为3,故选C. 2.(2018·北京高考)已知函数f (x )=sin 2x +3sin x cos x . (1)求f (x )的最小正周期;(2)若f (x )在区间⎣⎡⎦⎤-π3,m 上的最大值为32,求m 的最小值. 解:(1)因为f (x )=sin 2x +3sin x cos x =12-12cos 2x +32sin 2x =sin ⎝⎛⎭⎫2x -π6+12, 所以f (x )的最小正周期为T =2π2=π. (2)由(1)知f (x )=sin ⎝⎛⎭⎫2x -π6+12. 由题意知-π3≤x ≤m ,所以-5π6≤2x -π6≤2m -π6. 要使f (x )在区间⎣⎡⎦⎤-π3,m 上的最大值为32,即sin ⎝⎛⎭⎫2x -π6在区间⎣⎡⎦⎤-π3,m 上的最大值为1. 所以2m -π6≥π2,即m ≥π3.所以m 的最小值为π3.考点三三角函数的单调性[全析考法过关][考法全析]考法(一) 求三角函数的单调区间[例1] (1)函数y =sin ⎝⎛⎭⎫π3-2x 的单调递减区间为________________. (2)函数y =|tan x |的单调递增区间为______________,单调递减区间为________________. [解析] (1)函数y =sin ⎝⎛⎭⎫π3-2x =-sin ⎝⎛⎭⎫2x -π3的单调递减区间是函数y =sin ⎝⎛⎭⎫2x -π3的单调递增区间.由2k π-π2≤2x -π3≤2k π+π2,k ∈Z ,得k π-π12≤x ≤k π+5π12,k ∈Z.故所给函数的单调递减区间为⎣⎡⎦⎤k π-π12,k π+5π12,k ∈Z. (2)作出函数y =|tan x |的图象,如图.观察图象可知,函数y =|tan x |的单调递增区间为⎣⎡⎭⎫k π,k π+π2,k ∈Z ;单调递减区间为⎝⎛⎦⎤k π-π2,k π,k ∈Z.[答案] (1)⎣⎡⎦⎤k π-π12,k π+5π12,k ∈Z(2)⎣⎡⎭⎫k π,k π+π2,k ∈Z ⎝⎛⎦⎤k π-π2,k π,k ∈Z 考法(二) 已知三角函数的单调性求参数[例2] (2018·全国卷Ⅱ)若f (x )=cos x -sin x 在[-a ,a ]是减函数,则a 的最大值是( ) A.π4 B.π2 C.3π4D .π[解析] f (x )=cos x -sin x =-2sin ⎝⎛⎭⎫x -π4, 当x ∈⎣⎡⎦⎤-π4,3π4,即x -π4∈⎣⎡⎦⎤-π2,π2时, 函数y =sin ⎝⎛⎭⎫x -π4单调递增, 则函数f (x )=-2sin ⎝⎛⎭⎫x -π4单调递减. ∵函数f (x )在[-a ,a ]是减函数, ∴[-a ,a ]⊆⎣⎡⎦⎤-π4,3π4,∴0<a ≤π4, ∴a 的最大值为π4.[答案] A[规律探求]1.设函数f (x )=sin ⎝⎛⎭⎫2x -π3,x ∈⎣⎡⎦⎤-π2,π,则以下结论正确的是( ) A .函数f (x )在⎣⎡⎦⎤-π2,0上单调递减 B .函数f (x )在⎣⎡⎦⎤0,π2上单调递增 C .函数f (x )在⎣⎡⎦⎤π2,5π6上单调递减 D .函数f (x )在⎣⎡⎦⎤5π6,π上单调递增解析:选C 由x ∈⎣⎡⎦⎤-π2,0,得2x -π3∈⎣⎡⎦⎤-4π3,-π3,所以函数f (x )先减后增;由x ∈⎣⎡⎦⎤0,π2,得2x -π3∈⎣⎡⎦⎤-π3,2π3,所以函数f (x )先增后减;由x ∈⎣⎡⎦⎤π2,5π6,得2x -π3∈⎣⎡⎦⎤2π3,4π3,所以函数f (x )单调递减;由x ∈⎣⎡⎦⎤5π6,π,得2x -π3∈⎣⎡⎦⎤4π3,5π3,所以函数f (x )先减后增.故选C.2.若函数f (x )=sin ωx (ω>0)在区间⎣⎡⎦⎤0,π3上单调递增,在区间⎣⎡⎦⎤π3,π2上单调递减,则ω=________.解析:∵f (x )=sin ωx (ω>0)过原点,∴当0≤ωx ≤π2,即0≤x ≤π2ω时,y =sin ωx 是增函数;当π2≤ωx ≤3π2,即π2ω≤x ≤3π2ω时,y =sin ωx 是减函数. 由f (x )=sin ωx (ω>0)在⎣⎡⎦⎤0,π3上单调递增, 在⎣⎡⎦⎤π3,π2上单调递减,知π2ω=π3,∴ω=32. 答案:323.若函数y =12sin ωx 在区间⎣⎡⎦⎤-π8,π12上单调递减,则ω的取值范围是________. 解析:因为函数y =12sin ωx 在区间⎣⎡⎦⎤-π8,π12上单调递减,所以ω<0且函数y =12sin(-ωx )在区间⎣⎡⎦⎤-π12,π8上单调递增,则⎩⎨⎧ω<0,-ω·⎝⎛⎭⎫-π12≥2k π-π2,k ∈Z ,-ω·π8≤2k π+π2,k ∈Z ,即⎩⎪⎨⎪⎧ω<0,ω≥24k -6,k ∈Z ,ω≥-16k -4,k ∈Z ,解得-4≤ω<0.答案:[-4,0)考点四三角函数的周期性、奇偶性、对称性[全析考法过关][考法全析]考法(一) 三角函数的周期性[例1] 在函数①y =cos|2x |,②y =|cos x |,③y =cos ⎝⎛⎭⎫2x +π6,④y =tan ⎝⎛⎭⎫2x -π4中,最小正周期为π的所有函数为( )A .①②③B .①③④C .②④D .①③[解析] ①y =cos|2x |=cos 2x ,最小正周期为π; ②由图象知y =|cos x |的最小正周期为π; ③y =cos ⎝⎛⎭⎫2x +π6的最小正周期T =2π2=π; ④y =tan ⎝⎛⎭⎫2x -π4的最小正周期T =π2,故选A. [答案] A考法(二) 三角函数的奇偶性[例2] (2019·抚顺调研)已知函数f (x )=2sin ⎝⎛⎭⎫x +θ+π3⎝⎛⎭⎫θ∈⎣⎡⎦⎤-π2,π2是偶函数,则θ的值为________.[解析] ∵函数f (x )为偶函数,∴θ+π3=k π+π2(k ∈Z).又θ∈⎣⎡⎦⎤-π2,π2,∴θ+π3=π2,解得θ=π6,经检验符合题意.[答案]π6考法(三) 三角函数的对称性[例3] (1)已知函数f (x )=2sin ⎝⎛⎭⎫ωx +π6(ω>0)的最小正周期为4π,则该函数的图象( )A .关于点⎝⎛⎭⎫π3,0对称 B .关于点⎝⎛⎭⎫5π3,0对称 C .关于直线x =π3对称D .关于直线x =5π3对称 (2)(2018·江苏高考)已知函数y =sin(2x +φ)⎝⎛⎭⎫-π2<φ<π2的图象关于直线x =π3对称,则φ的值为________.[解析] (1)因为函数f (x )=2sin ⎝⎛⎭⎫ωx +π6(ω>0)的最小正周期为4π,而T =2πω=4π,所以ω=12,即f (x )=2sin ⎝⎛⎭⎫x 2+π6.令x 2+π6=π2+k π(k ∈Z),解得x =2π3+2k π(k ∈Z), 故f (x )的对称轴为x =2π3+2k π(k ∈Z).令x 2+π6=k π(k ∈Z),解得x =-π3+2k π(k ∈Z), 故f (x )的对称中心为⎝⎛⎭⎫-π3+2k π,0(k ∈Z),对比选项可知B 正确. (2)由题意得f ⎝⎛⎭⎫π3=sin ⎝⎛⎭⎫2π3+φ=±1, ∴2π3+φ=k π+π2(k ∈Z),∴φ=k π-π6(k ∈Z). ∵φ∈⎝⎛⎭⎫-π2,π2,∴φ=-π6. [答案] (1)B (2)-π6[规律探求]只需令ωx +φ=π2+k π(k ∈Z),求x 即可;如果求f (x )的对称中心的横坐标,只需令ωx +φ=k π(k ∈Z),求x 即可.(2)对于可化为f (x )=A cos(ωx +φ)(ω>0)形式的函数,如果求f (x )的对称轴,只需令ωx +φ=k π(k ∈Z),求x 即可;如果求f (x )的对称中心的横坐标,只需令ωx +φ=π2+k π(k ∈Z),求x 即可找共性这类问题解题的关键是把原三角函数关系式统一角,统一名,即“一角一函数”,其解题思维流程是:[过关训练]1.若函数f (x )=3sin(2x +θ)+cos(2x +θ)(0<θ<π)的图象关于⎝⎛⎭⎫π2,0中心对称,则函数f (x )在⎣⎡⎦⎤-π4,π6上的最小值是________. 解析:f (x )=2sin ⎝⎛⎭⎫2x +θ+π6,又图象关于⎝⎛⎭⎫π2,0中心对称,所以2×π2+θ+π6=k π(k ∈Z), 所以θ=k π-7π6(k ∈Z),又0<θ<π,所以θ=5π6,所以f (x )=-2sin 2x ,因为x ∈⎣⎡⎦⎤-π4,π6, 所以2x ∈⎣⎡⎦⎤-π2,π3,f (x )∈[-3,2], 所以f (x )的最小值是- 3. 答案:- 32.若x =π8是函数f (x )=2sin ⎝⎛⎭⎫ωx -π4,x ∈R 的一个零点,且0<ω<10,则函数f (x )的最小正周期为________.解析:依题意知,f ⎝⎛⎭⎫π8=2sin ⎝⎛⎭⎫ωπ8-π4=0, 即ωπ8-π4=k π,k ∈Z ,整理得ω=8k +2,k ∈Z. 又因为0<ω<10,所以0<8k +2<10,得-14<k <1,而k ∈Z ,所以k =0,ω=2,所以f (x )=2sin ⎝⎛⎭⎫2x -π4,f (x )的最小正周期为π. 答案:π。
三角函数的图像和性质(含答案)

.三角函数的图像和性质1.函数)62sin(21π+=x y 的单增区间是___________. 【答案】Z k k k ∈⎥⎦⎤⎢⎣⎡+-6,3ππππ2.函数y =cos 24x π⎛⎫-⎪⎝⎭的单调递增区间是________. 【答案】388k k ππππ⎡⎤⎢⎥⎣⎦-+,+(k∈Z)3.函数3sin(2)3y x π=+图象的对称中心是_______.【答案】(,0)32k ππ-+4.若函数f(x)=sin(ωx+6π)(ω>0)的最小正周期是5π,则ω=_________。
【答案】105.函数)4tan()(π+=x x f 单调增区间为( )A .Z k k k ∈+-),2,2(ππππ B .Z k k k ∈+),,(πππC .Z k k k ∈+-),4,43(ππππD .Z k k k ∈+-),43,4(ππππ 【答案】C6.下列函数中周期为π且为偶函数的是 ( ) A .)22sin(π-=x y B. )22cos(π-=x y C. )2sin(π+=x y D. )2cos(π+=x y【答案】A7.设函数()sin(2)3f x x π=+,则下列结论正确的是A .()f x 的图像关于直线3x π=对称 B .()f x 的图像关于点(,0)4π对称C .()f x 的最小正周期为2πD .()f x 在[0,]12π上为增函数【答案】D8.如果函数)4cos(ax y +=π的图象关于直线π=x 对称,则正实数a 的最小值是( )A .41=a B .21=a C .43=a D .1=a【答案】C9.已知ω>0,0<φ<π,直线x =4π和x =54π是函数f (x )=sin(ωx +φ)图像的两条相邻的对称轴,则φ=( )(A )4π (B )3π (C )2π(D )34π【答案】A【解析】试题分析:函数f (x )=sin(ωx +φ)图像的两条相邻的对称轴间的距离等于半个周期,所以2,1T πω==.由sin()14πϕ+=得4πϕ=满足0ϕπ<<,故选A.考点:三角函数的图象及其性质. 10.若当4x π=时,函数()sin()(0)f x A x A ϕ=+>取得最小值,则函数()4y f x π=-是( )A.奇函数且图像关于点(,0)2π对称 B.偶函数且图像关于直线2x π=对称C.奇函数且图像关于直线2x π=对称 D.偶函数且图像关于点(,0)2π对称【答案】D【解析】由题意知sin()14πϕ+=-,即324k πϕπ=-; 函数3()sin(2)cos 444y f x A x k A x ππππ=-=-+-=-,所以是偶函数且图像关于点(,0)2π对称.11.函数()sin 24f x x π⎛⎫=-⎪⎝⎭在区间[0,]2π上的最小值是A .-l B.2 C.2- D .0 【答案】C【解析】因为[0,]2x π∈,所以32[,],444x πππ⎛⎫-∈- ⎪⎝⎭因此()sin 2[4f x x π⎛⎫=-∈ ⎪⎝⎭即函数最小值是2-.12.函数y =2sinx 263x ππ⎛⎫≤≤ ⎪⎝⎭的值域是________.【答案】[1,2]【解析】根据正弦函数图象,可知x =6π时,函数取到最小值1;x =2π时,函数取到最大值2. 13.当7,66x ππ⎡⎤∈⎢⎥⎣⎦时,函数23sin 2cos y x x =--的最小值是_______,最大值是________。
三角函数图像及性质习题含答案
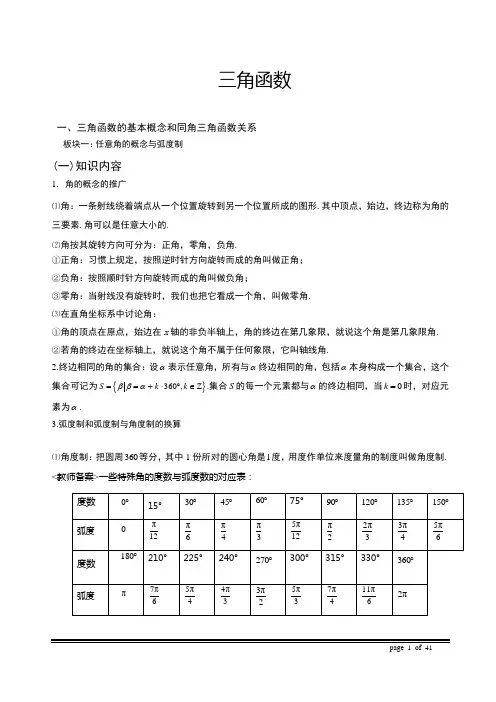
三角函数一、三角函数的基本概念和同角三角函数关系(一)知识内容1. 角的概念的推广⑴角:一条射线绕着端点从一个位置旋转到另一个位置所成的图形.其中顶点,始边,终边称为角的三要素.角可以是任意大小的.⑵角按其旋转方向可分为:正角,零角,负角.①正角:习惯上规定,按照逆时针方向旋转而成的角叫做正角; ②负角:按照顺时针方向旋转而成的角叫做负角;③零角:当射线没有旋转时,我们也把它看成一个角,叫做零角. ⑶在直角坐标系中讨论角:①角的顶点在原点,始边在x 轴的非负半轴上,角的终边在第几象限,就说这个角是第几象限角. ②若角的终边在坐标轴上,就说这个角不属于任何象限,它叫轴线角.2.终边相同的角的集合:设α表示任意角,所有与α终边相同的角,包括α本身构成一个集合,这个集合可记为{}360,Z S k k ββα==+⋅︒∈.集合S 的每一个元素都与α的终边相同,当0k =时,对应元素为α.3.弧度制和弧度制与角度制的换算⑴角度制:把圆周360等分,其中1份所对的圆心角是1度,用度作单位来度量角的制度叫做角度制.<教师备案>一些特殊角的度数与弧度数的对应表:板块一:任意角的概念与弧度制⑵1弧度的角:长度等于半径长的圆弧所对的圆心角叫做1弧度的角.规定:正角的弧度数为正数,负角的弧度数为负数,零角的弧度数为零.任一已知角α的弧度数的绝对值lrα=,这种以“弧度”作为单位来度量角的制度叫做弧度制.⑶弧度与角度的换算:180πrad=,1801rad57.305718π︒⎛⎫'=≈︒=︒⎪⎝⎭板块二:任意角的三角函数(一)知识内容1.三角函数定义在直角坐标系中,设α是一个任意角,α终边上任意一点P(除了原点)的坐标为(,)x y,它与原点的距离为(0)r r>,那么⑴比值yr叫做α的正弦,记作sinα,即sinyrα=;⑵比值xr叫做α的余弦,记作cosα,即cosxrα=;⑶比值yx叫做α的正切,记作tanα,即tanyxα=;⑷比值xy叫做α的余切,记作cotα,即cotxyα=;⑷比值rx叫做α的正割,记作secα,即secrxα=;⑸比值ry叫做α的余割,记作cscα,即cscryα=.2.三角函数的定义域、值域3.由三角函数的定义,以及各象限内点的坐标的符号,我们可以得知: ⑴正弦值yr对于第一、二象限为正(0,0y r >>),对于第三、四象限为负(0,0y r <>); ⑵余弦值xr对于第一、四象限为正(0,0x r >>),对于第二、三象限为负(0,0x r <>); ⑶正切值yx对于第一、三象限为正(,x y 同号),对于第二、四象限为负(,x y 异号). 可以用下图表示:说明:若终边落在轴线上,则可用定义求出三角函数值.4.同角三角函数的基本关系式:平方关系:22sin cos 1x x +=,22sec tan 1x x -=,22csc cot 1x x -= 商数关系:sin tan cos x x x =,cos cot sin xx x= 倒数关系:111sec ,csc ,tan cos cos cot x x x x x x=== 6.诱导公式:⑴角α与2π()k k α+⋅∈Z 的三角函数间的关系;sin(2π)sin k αα+=,cos(2π)cos k αα+=,tan(2π)=tan k αα+;⑵角α与α-的三角函数间的关系;sin()sin αα-=-,cos()cos αα-=,tan()tan αα-=-;⑶角α与(21)π()k k α++∈Z 的三角函数间的关系;[]sin (21)πsin k αα++=-,[]cos (21)πcos k αα++=-,[]tan (21)πtan k αα++=;⑷角α与πα+的三角函数间的关系.πsin cos 2αα⎛⎫+= ⎪⎝⎭,πcos sin 2αα⎛⎫+=- ⎪⎝⎭,πtan cot 2αα⎛⎫+=- ⎪⎝⎭.4.三角函数式的化简与三角恒等式的证明是个难点,需要学生熟悉并灵活运用所学的公式与知识,一般情况下,化简的基本思路是:减少角的种数,减少三角函数的种数,适当配凑和拆分,统一切割化弦等等.二、三角函数的图象与性质(一)知识内容⑴单位圆:半径等于单位长的圆叫做单位圆.设单位圆的圆心与坐标原点重合,则单位圆与x 轴交点分别为(1,0)A ,(1,0)A '-,而与y 轴的交点分别为(0,1)B ,(0,1)B '-.由三角函数的定义可知,点P 的坐标为(cos ,sin )αα,即(cos ,sin )P αα.其中cos OM α=,sin ON α=.α)这就是说,角α的余弦和正弦分别等于角α终边与单位圆交点的横坐标和纵坐标.过点(1,0)A 作单位圆的切线,它与角α的终边或其反向延长线交与点T (或T '),则tan AT α=(或AT '). ⑵有向线段:坐标轴是规定了方向的直线,那么与之平行的线段亦可规定方向.具有方向的线段叫做有向线段.规定:与坐标轴方向一致时为正,与坐标方向相反时为负. ⑶三角函数线的定义:板块一:任意角的概念与弧度制设任意角α的顶点在原点O ,始边与x 轴非负半轴重合,终边与单位圆相交于点P (,)x y ,过P 作x 轴的垂线,垂足为M ;过点(1,0)A 作单位圆的切线,它与角α的终边或其反向延长线交与点T .我们就分别称有向线段MP ,OM ,AT 为正弦线、余弦线、正切线.(一) 知识内容1.2.函数()()sin 0,0,y A x A x ωϕω=+>>∈R 的图象的作法――五点法①确定函数的最小正周期2πT ω=;②令x ωϕ+=0、π2、π、3π2、2π,得x ϕω=-、1π()2ϕω-、1(π)ϕω-、13π()2ϕω-、1(2π)ϕω-,于是得到五个关键点(,0)ϕω-、1π((),1)2ϕω-、1((π),0)ϕω-、13π((),1)2ϕω--、1((2π),0)ϕω-;③描点作图,先作出函数在一个周期内的图象,然后根据函数的周期性,把函数在一个周期内的图象向左、右扩展,得到函数()()sin 0,0,y A x A x ωϕω=+>>∈R 的图象.3.()()sin 0,0,y A x A x ωϕω=+>>∈R 的图象函数()()sin 0,0,y A x A x R ωϕω=+>>∈的图象可以用下面的方法得到:先把sin y x =的图象上所有点向左(0)ϕ>或向右(0)ϕ<平行移动||ϕ个单位;再把所得各点的横坐标缩短(1)ω>或伸长(01)ω<<到原来的1ω倍(纵坐标不变);再把所得的各点的纵坐标伸长(1)A >或缩短板块一:三角函数的图象(01)A <<到原来的A 倍(横坐标不变),从而得到sin()y A x ωϕ=+的图象.当函数sin()y A x ωϕ=+表示一个振动量时:A 叫做振幅;T 叫做周期;1T叫做频率;x ωϕ+叫做相位,ϕ叫做初相.上面是一种函数的平移缩放的过程,可以用这种方法来把一种三角函数转换成另外一种三角函数.下面把这个过程分解一下: (1)相位变换要得到函数sin()(0)y x ϕϕ=+≠的图象,可以令x x ϕ=+,也就是原来的x 变成了现在的x ϕ+,相当于x 减小了(0)ϕϕ<,即可以看做是把sin y x =的图象上的各点向左(0)ϕ>或向右(0)ϕ<平行移动||ϕ个单位而得到的.这种由sin y x =的图象变换为sin()y x ϕ=+的图象的变换,使相位由x 变为x ϕ+,我们称它为相位变换.它实质上是一种左右平移变换. (2)周期变换要得到函数sin (0,1)y x ωωω=>≠的图象,令x x ω=,即现在的x 缩小到了原来的ω倍,就可以看做是把sin y x =的图象上的各点的横坐标缩短(1)ω>或伸长(01)ω<<到原来的1ω倍(纵坐标不变)得到,由sin y x =的图象变换为sin y x ω=的图象,其周期由2π变为2πω,这种变换叫周期变换.周期变换是一种横向的伸缩. (3)振幅变换要得到sin (0,1)y A x A A =>≠且的图象,令yy A=,即相当于y 变为原来的A 倍,也就是把sin y x =的图象上的各点的纵坐标伸长(1)A >或缩短(01)A <<到原来的A 倍(横坐标不变)而得到的.这种变换叫做振幅变换.振幅变换是一种纵向的伸缩.(一)知识内容<教师备案>1.函数图象平移基本结论小结如下:(0)()()a a y f x y f x a >=−−−−−−→=+左移个单位板块二:三角函数图象变换(0)()()a a y f x y f x a >=−−−−−−→=-右移个单位(0)()()a a y f x y a f x >=−−−−−−→-=上移个单位(0)()()a a y f x y a f x >=−−−−−−→+=下移个单位1()()y f x y f x ωω=−−−−−−−−→=各点横坐标变成原来的倍()()y f x Ay f x =−−−−−−−−→=1各点纵坐标变成原来的倍A()()x y f x y f x =−−−−→-=绕轴翻折这些新的解析式可以由图象上任意一点变换后的对应关系得出,以左移a 个单位的解析式变化为例:设00(,)P x y 为()y f x =左移a 个单位后所得图象上的任意一点,则将P右移a 个单位得到的00'(,)P x a y +必在()y f x =的图象上,故00()y f x a =+,又00(,)P x y 点任意,故()y f x =的图象左移a 个单位得到的新的函数的解析式为:()y f x a =+.函数变换可以用下图表示:()()y f x y f x =−−−−→=-绕y 轴翻折板块三:三角函数的性质1.三角函数的性质][(22π,[2π,(21)π]()k k k k +∈Z 在2.sin y x =与sin y x =的性质(数学4必修)第一章 三角函数(上) [基础训练A 组]一、选择题1.设α角属于第二象限,且2cos2cosαα-=,则2α角属于( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限2.给出下列各函数值:①)1000sin(0-;②)2200cos(0-;③)10tan(-;④917tancos 107sinπππ.其中符号为负的有( )A .①B .②C .③D .④ 3.02120sin 等于( )A .23±B .23C .23-D .21 4.已知4sin 5α=,并且α是第二象限的角,那么 tan α的值等于( )A .43-B .34- C .43 D .345.若α是第四象限的角,则πα-是( )A .第一象限的角 B.第二象限的角 C.第三象限的角 D.第四象限的角6.4tan 3cos 2sin 的值( )A .小于0B .大于0C .等于0D .不存在二、填空题1.设θ分别是第二、三、四象限角,则点)cos ,(sin θθP 分别在第___、___、___象限.2.设MP 和OM 分别是角1817π的正弦线和余弦线,则给出的以下不等式: ①0<<OM MP ;②0OM MP <<; ③0<<MP OM ;④OM MP <<0,其中正确的是_____________________________。
三角函数的图象及性质(含答案)
三角函数的图象及性质一、单选题(共10道,每道10分)1.的值( )A.大于0B.小于0C.等于0D.不确定答案:A解题思路:试题难度:三颗星知识点:三角函数值的符号2.已知,若为第二象限角,则下列结论正确的是( )A. B.a=1C. D.答案:D解题思路:试题难度:三颗星知识点:同角三角函数间的基本关系3.若A,B是锐角三角形ABC的两个内角,则点位于( )A.第一象限B.第二象限C.第三象限D.第四象限答案:D解题思路:试题难度:三颗星知识点:三角函数的诱导公式4.已知点在第二象限,则α的一个变化区间是( )A. B.C. D.答案:C解题思路:试题难度:三颗星知识点:三角函数值的符号5.已知定义在上的奇函数f(x)在区间(0,﹢∞)上单调递增,若,△ABC内角A满足,则A的取值范围是( )A. B.C. D.答案:D解题思路:试题难度:三颗星知识点:三角函数的图象6.已知a是实数,则函数的图象可能是( )A. B.C. D.答案:C解题思路:试题难度:三颗星知识点:三角函数的图象7.函数,对任意x都有,则的值是( )A.2或0B.﹣2或2C.1或0D.﹣1或1答案:B解题思路:试题难度:三颗星知识点:余弦函数的对称性8.已知的值是( )A.﹣26B.﹣18C.﹣10D.10答案:A解题思路:试题难度:三颗星知识点:正弦函数的奇偶性9.关于函数,下列判断正确的是( )A.定义域是B.是奇函数C.值域是D.在上单调递减答案:C解题思路:试题难度:三颗星知识点:余弦函数定义域和值域10.函数在区间(0,10π)上可找到n个不同的数,使得,则n的最大值等于( )A.8B.9C.10D.11答案:C解题思路:试题难度:三颗星知识点:正弦函数的图象。
(13)三角函数的图像与性质 Word版含答案
寒假作业(13)三角函数的图像与性质1、若()sin f x x ω=满足(2)(2)f x f x +=-,则()f x 有( )A.最小正周期为4B.()f x 关于2x =对称C.()f x 不是周期函数D.12ω=2、cos ,[0,2π]y x x =-∈的大致图象为( )A. B. C. D.3、用“五点法”作函数cos3,R y x x =∈的图象时,首先应描出的五个点的横坐标是() A.π3π0,,π,,2π22 B.ππ3π0,,,,π424C.0,π,2π,3π,4πD.πππ2π0,,,,63234、下列函数,在π[,π]2上是增函数的是( )A.sin y x =B.cos y x =C.sin 2y x =D.cos 2y x =5、若函数()sin ([0,2π])3x f x ϕϕ+=∈是偶函数,则ϕ= ( ) A.π2 B.2π3 C.3π2 D.5π36、sin y x =,[0,2π]x ∈的图象与13y =的交点个数为( )A.0B.1C.2D.37、tan 1,x x ≥-取值范围为( ) A.,42ππ⎛⎫- ⎪⎝⎭ B.,42ππ⎡⎫-⎪⎢⎣⎭ C.,,Z 42k k k ππ⎡⎫π-π+∈⎪⎢⎣⎭ D.2,2,Z 42k k k ππ⎡⎫π-π+∈⎪⎢⎣⎭8、函数sin ()cos xf x x =在区间[],-ππ内的大致图象是( )A. B.C. D.9、()tan (0)f x x ωω=>的图象相邻两支截直线1y =所得线段长为4π,则12f π⎛⎫= ⎪⎝⎭( )A.0B.3 C.1 10、函数sin y x =的定义域为[,]a b ,值域为1[1,]2--,则b a -的最大值与最小值之和为( ) A.4π3 B.8π3 C.2π D.4π11、函数cos 1y a x =+的最大值为5,则a=____________. 12、函数3tan(),46y x x ππ=π+-<≤的值域为______________. 13、函数1tan 24y x π⎛⎫=-+ ⎪⎝⎭的单调递减区间是_______________. 14、函数()sin 2|sin |f x x x =+,[0,2π]x ∈的图象与直线y k =有且仅有两个不同的交点,则k 的取值范围是______________.15、比较1cos 0,cos,cos30,cos1,cos π2︒的大小为__________________________.答案以及解析1答案及解析:答案:A解析:令2x t -=,则(4)(),()f t f t f x +=的最小正周期为4.故选A.2答案及解析:答案:B解析:0x =时,1y =- ,故选B.3答案及解析:答案:D 解析:令π3π30,,π,22x =和2π得πππ2π0,,,,6323x =.故选D.4答案及解析:答案:D 解析:因为π[,π]2x ∈,所以2[π,2π]x ∈,所以cos 2y x =在π[,π]2上为增函数.5答案及解析:答案:C 解析:因为()f x 是偶函数,所以0ππ(Z)32k k ϕ+=+∈. 所以3π3π(Z)2k k ϕ=+∈,又[0,2π]ϕ∈,所以3π2ϕ=.6答案及解析:答案:C解析:在同一直角坐标系中,作出sin y x =,[0,2π]x ∈及13y =的函数图象(图略),可知13y =与sin ([0,2π])y x x =∈有两个交点.故选C.7答案及解析:答案:C 解析:因为tan 1,,22x x ππ⎛⎫≥-∈- ⎪⎝⎭时,可得42x ππ-≤<,所以,Z 42k x k k πππ-≤<π+∈.故选C.8答案及解析:答案:B解析:tan ,,2tan ,,02()tan ,0,2tan ,,2x x x x f x x x x x ⎧π⎡⎫-∈-π-⎪⎪⎢⎣⎭⎪⎪π⎡⎫∈-⎪⎪⎢⎪⎣⎭=⎨π⎡⎫⎪∈⎪⎢⎪⎣⎭⎪π⎡⎤⎪-∈π⎢⎥⎪⎣⎦⎩9答案及解析:答案:D 解析:由题意4T π=,又T ωπ=,所以4ω=,所以()tan 4,tan 123f x x f ππ⎛⎫===⎪⎝⎭故选D.10答案及解析:答案:C 解析:如图,当1[,]x a b ∈时,值域为1[1,]2--,且b a -最大.当2[,]x a b ∈时,值域为1[1,]2--,且b a -最大.所以最大值与最小值之和为1212()()2()b a b a b a a -+-=-+ππ7π22π626=⨯++=.11答案及解析:答案:4±解析:||15a +=,所以4a =±.12答案及解析:答案:(- 解析:函数3tan()3tan y x x =π+=,且在,46ππ⎛⎤- ⎥⎝⎦上是增函数,所以3y -<≤(-.13答案及解析: 答案:32,2,Z 22k k k π⎛⎫π-π+π∈ ⎪⎝⎭解析:11tan tan 2424y x x ππ⎛⎫⎛⎫=-+=-- ⎪ ⎪⎝⎭⎝⎭, 由1(Z)2242k x k k ππππ-<-<π+∈, 得322,Z 22k x k k πππ-<<π+∈, 所以函数1tan 24y x π⎛⎫=-+ ⎪⎝⎭的单调递减区间是32,2,Z 22k k k π⎛⎫π-π+π∈ ⎪⎝⎭.14答案及解析:答案:(1,3)解析:因为3sin ,[0,π),()sin ,[π,2π],x x f x x x ∈⎧=⎨-∈⎩ 所以()y f x =的图象如图所示.从图象上可以看出,若()y f x =与y k =的图象有且仅有两个不同的交点,则k 的范围为13k <<.15答案及解析: 答案:1cos 0coscos30cos1cos π2>>︒>> 解析:因为1π01π26<<<<,而cos y x =在区间[0,π]上是减函数,所以1cos0cos cos30cos1cos π2>>︒>>.。
高中数学:复习课(二) 三角函数的图象与性质 Word版含答案
(1) (2)①解正弦、余弦函数值问题时,应注意正弦、余弦函数的有界性,即 -1≤sin x ≤1,-1≤cos x ≤1.②解正切函数问题时,应注意正切函数的定义域,即⎩⎨⎧⎭⎬⎫x ⎪⎪x ≠kπ+π 2,k ∈Z [典例] (2017·山东高考)设函数f (x )=sin ⎝⎛⎭⎫ωx -π6+sin ⎝⎛⎭⎫ωx -π2,其中0<ω<3.已知f ⎝⎛⎭⎫π6=0.(1)求ω;(2)将函数y =f (x )的图象上各点的横坐标伸长为原来的2倍(纵坐标不变),再将得到的图象向左平移π4个单位,得到函数y =g (x )的图象,求g (x )在⎣⎡⎦⎤-π4,3π4上的最小值. [解] (1)因为f (x )=sin ⎝⎛⎭⎫ωx -π6+sin ⎝⎛⎭⎫ωx -π2, 所以f (x )=32sin ωx -12cos ωx -cos ωx =32sin ωx -32cos ωx =3⎝⎛⎭⎫12sin ωx -32cos ωx=3sin ⎝⎛⎭⎫ωx -π3. 因为f ⎝⎛⎭⎫π6=0, 所以ωπ6-π3=k π,k ∈Z.故ω=6k +2,k ∈Z. 又0<ω<3,所以ω=2.(2)由(1)得f (x )=3sin ⎝⎛⎭⎫2x -π3,所以g (x )=3sin ⎝⎛⎭⎫x +π4-π3=3sin ⎝⎛⎭⎫x -π12. 因为x ∈⎣⎡⎦⎤-π4,3π4, 所以x -π12∈⎣⎡⎦⎤-π3,2π3, 当x -π12=-π3,即x =-π4时,g (x )取得最小值-32.[类题通法]求三角函数式的值域与最值的两种形式(1)将所给三角函数式转化为y =A sin(ωx +φ)或y =A cos(ωx +φ)的形式,然后结合角x 的范围求解.(2)形如y =a sin 2x +b cos x +c 或y =a cos 2x +b sin x +c 的函数,可以先转化成同名函数,然后结合二次函数的性质求解,在转化过程中要注意sin x 或cos x 的有界性.[题组训练]1.函数y =3tan x +3的定义域为__________________________________________. 解析:3tan x +3≥0,即tan x ≥-33. ∴k π-π6≤x <k π+π2,k ∈Z ,∴函数 y =3tan x +3的定义域为⎣⎡⎭⎫k π-π6,k π+π2,k ∈Z. ★答案★:⎣⎡⎭⎫k π-π6,k π+π2,k ∈Z 2.已知|x |≤π4,则函数ƒ(x )=cos 2 x +sin x 的最小值为________.解析:ƒ(x )=cos 2x +sin x =-sin 2x +sin x +1. 令t =sin x ,∵|x |≤π4,∴-22≤sin x ≤22,即t ∈⎣⎡⎦⎤-22,22.又∵y =-t 2+t +1=-⎝⎛⎭⎫t -122+54, ∴当t =-22,即x =-π4时,y 取最小值, 即y min =-⎝⎛⎭⎫-22-122+54=1-22.★答案★:1-22(1)ωx +φ)(A >0,ω>0)图象的平移和伸缩变换以及根据图象确定A ,ω,φ的值等.考查识图、用图能力以及利用三角公式进行恒等变换的能力.(2)函数y =A sin(ωx +φ)的图象 (1)“五点法”作图设z =ωx +φ,令z =0,π2,π,3π2,2π,求出x 的值与相应的y 的值,描点、连线可得.(2)图象变换y =sin x ―――――――――→向左(φ>0)或向右(φ<0)平移|φ|个单位y =sin(x +φ) ――――――――――――→横坐标变为原来的1ω (ω>0)倍纵坐标不变 y =sin(ωx +φ)―――――――――――→纵坐标变为原来的A (A >0)倍横坐标不变y =A sin(ωx +φ). [典例] 某同学用“五点法”画函数f (x )=A sin(ωx +φ)⎝⎛⎭⎫ω>0,|φ|<π2在某一个周期内的图象时,列表并填入了部分数据,如下表:(1)请将上表数据补充完整,并直接写出函数f (x )的解析式;(2)将y =f (x )图象上所有点向左平行移动π6个单位长度,得到y =g (x )的图象,求y =g (x )的图象离原点O 最近的对称中心.[解] (1)根据表中已知数据,解得A =5,ω=2,φ=-π6,数据补全如下表:ωx +φ 0 π2 π 3π2 2π x π12 π3 7π12 5π6 13π12 A sin(ωx +φ)5-5且函数解析式为f (x )=5sin ⎝⎛⎭⎫2x -π6. (2)由(1)知f (x )=5sin ⎝⎛⎭⎫2x -π6, 因此g (x )=5sin ⎣⎡⎦⎤2⎝⎛⎭⎫x +π6-π6=5sin ⎝⎛⎭⎫2x +π6. 因为y =sin x 的对称中心为(k π,0),k ∈Z , 令2x +π6=k π,k ∈Z ,解得x =k π2-π12,k ∈Z ,即y =g (x )图象的对称中心为⎝⎛⎭⎫k π2-π12,0,k ∈Z , 其中离原点O 最近的对称中心为⎝⎛⎭⎫-π12,0. [类题通法](1)已知函数y =A sin(ωx +φ)(A >0,ω>0)的图象求解析式时,常利用待定系数法,由图中的最高点、最低点求A ;由函数的周期确定ω;由图象上的关键点确定φ.(2)由图象上的关键点确定φ时,若选取的是图象与x 轴的交点,则要弄清这个点属于“五点法”中的哪一个点.“第一点”(即图象上升时与x 轴的交点)为ωx 0+φ=2k π(k ∈Z),其他依次类推即可.[题组训练]1.由函数y =5sin ⎝⎛⎭⎫2x +π6的图象得到函数y =5sin 2x 的图象的平移变换为( ) A .向右平移π6个单位长度B .向左平移π6个单位长度C .向右平移π12个单位长度D .向左平移π12个单位长度解析:选C 函数y =5sin ⎝⎛⎭⎫2x +π6=5sin2x +π12向右平移π12个单位长度,即得y =5sin 2x ,故选C.2.如图是函数y =A sin(ωx +φ)+2(A >0,ω>0,|φ|<π)的图象的一部分,则它的振幅、周期、初相分别是( )A .A =3,T =4π3,φ=-π6B .A =1,T =4π3,φ=3π4C .A =1,T =4π3,φ=-3π4D .A =1,T =4π3,φ=-π6解析:选C 由图象,知A =3-12=1,T 2=5π6-π6=2π3,则T =4π3,ω=2πT =2π4π3=32.由5π6×32+φ=π2+2k π,k ∈Z ,得φ=-3π4+2k π,k ∈Z.令k =0,得φ=-3π4. 3.已知函数f (x )=a sin ⎝⎛⎭⎫ωx +π3,g (x )=b tan ⎝⎛⎭⎫ωx -π3,其中ω>0,它们的最小正周期之和为3π2,且f ⎝⎛⎭⎫π2=g ⎝⎛⎭⎫π2,f ⎝⎛⎭⎫π4=-3g ⎝⎛⎭⎫π4+1,求a ,b ,ω的值. 解:∵f (x )的最小正周期为2πω,g (x )的最小正周期为πω,∴2πω+πω=3π2,∴ω=2. ∴函数f (x )=a sin ⎝⎛⎭⎫2x +π3,g (x )=b tan ⎝⎛⎭⎫2x -π3. 由已知,得⎩⎨⎧a sin ⎝⎛⎭⎫π+π3=b tan ⎝⎛⎭⎫π-π3,a sin ⎝⎛⎭⎫π2+π3=-3b tan ⎝⎛⎭⎫π2-π3+1,即⎩⎨⎧-32a =-3b ,a2=-b +1,解得⎩⎪⎨⎪⎧a =1,b =12.∴a =1,b =12,ω=2.(1)数的周期性、奇偶性、单调性、对称性、最值等问题.(2)三角函数的性质,重点应掌握y =sin x ,y =cos x ,y =tan x 的定义域、值域、单调性、奇偶性、对称性等有关性质,在此基础上掌握函数y =A sin(ωx +φ),y =A cos(ωx +φ)及y =A tan(ωx +φ)的相关性质.在研究其相关性质时,将ωx +φ看成一个整体,利用整体代换思想解题是常见的技巧.[典例] 已知函数f (x )=sin π2-x sin x -3cos 2x .(1)求f (x )的最小正周期和最大值; (2)讨论f (x )在⎣⎡⎦⎤π6,2π3上的单调性. [解] (1)f (x )=sin ⎝⎛⎭⎫π2-x sin x -3cos 2x =cos x sin x -32(1+cos 2x ) =12sin 2x -32cos 2x -32 =sin ⎝⎛⎭⎫2x -π3-32, 因此f (x )的最小正周期为π,最大值为2-32.(2)当x ∈⎣⎡⎦⎤π6,2π3时,0≤2x -π3≤π,从而 当0≤2x -π3≤π2,即π6≤x ≤5π12时,f (x )单调递增,当π2≤2x -π3≤π,即5π12≤x ≤2π3时,f (x )单调递减. 综上可知,f (x )在⎣⎡⎦⎤π6,5π12上单调递增,在⎣⎡⎦⎤5π12,2π3上单调递减. [类题通法]1.三角函数的两性质(1)周期性:函数y =A sin(ωx +φ)和y =A cos(ωx +φ)的最小正周期为2π|ω|,y =tan(ωx +φ)的最小正周期为π|ω|.(2)奇偶性:三角函数中奇函数一般可化为y =A sin ωx 或y =A tan ωx ,而偶函数一般可化为y =A cos ωx +B 的形式.2.求三角函数的单调区间求形如y =A sin(ωx +φ)或y =A cos(ωx +φ)(A >0,ω>0)的函数的单调区间可以通过解不等式方法去解答,即把ωx +φ视为一个“整体”,分别与正弦函数y =sin x ,余弦函数y =cos x 的单调递增(减)区间对应解出x ,即得所求的单调递增(减)区间.[题组训练]1.同时具有性质:①最小正周期为π;②图象关于直线x =π3对称;③在⎝⎛⎭⎫π3,5π6上是减函数的一个函数是( )A .y =32sin x 2+12cos x2B .y =12sin x 2+32cos x2C .y =32sin 2x +12cos 2x D .y =32sin 2x -12cos 2x 解析:选D y =32sin 2x -12cos 2x =sin ⎝⎛⎭⎫2x -π6的最小正周期为T =2π2=π;当x =π3时,sin ⎝⎛⎭⎫2×π3-π6=sin π2=1,所以y =32sin 2x -12cos 2x 的图象关于直线x =π3对称;当x ∈⎝⎛⎭⎫π3,5π6时,2x -π6∈⎝⎛⎭⎫π2,3π2,所以函数y =sin ⎝⎛⎭⎫2x -π6在⎝⎛⎭⎫π3,5π6上单调递减.故选D.2.关于f (x )=4sin ⎝⎛⎭⎫2x +π3(x ∈R)有下列结论: ①函数的最小正周期为π;②表达式可改写为f (x )=4cos ⎝⎛⎭⎫2x -π6; ③函数的图象关于点⎝⎛⎭⎫-π6,0对称; ④函数的图象关于直线x =-π6对称.其中正确结论的序号为________.解析:显然函数f (x )的最小正周期T =2π2=π,①正确;f (x )=4sin ⎝⎛⎭⎫2x +π3=4cos ⎣⎡⎦⎤π2-⎝⎛⎭⎫2x +π3=4cos ⎝⎛⎭⎫-2x +π6=4cos ⎝⎛⎭⎫2x -π6,②正确;当x =-π6时,sin ⎝⎛⎭⎫-π3+π3=sin 0=0,③正确,④不正确.★答案★:①②③3.已知函数ƒ(x )=cos ⎝⎛⎭⎫π3+x cos ⎝⎛⎭⎫π3-x -sin x cos x +14. (1)求函数ƒ(x )的最小正周期和最大值; (2)求函数ƒ(x )在[0,π]上的单调递减区间. 解:(1)因为ƒ(x )=cos ⎝⎛⎭⎫π3+x cos ⎝⎛⎭⎫π3-x -12sin 2x +14=12cos x -32sin x 12cos x +32sin x -12sin 2x +14 =14cos 2 x -34sin 2 x -12sin 2x +14 =1+cos 2x 8-3-3cos 2x 8-12sin 2x +14=12(cos 2x -sin 2x )=22cos ⎝⎛⎭⎫2x +π4, 所以函数ƒ(x )的最小正周期为π,最大值为22. (2)由2k π≤2x +π4≤2k π+π,k ∈Z ,得k π-π8≤x ≤k π+3π8,k ∈Z ,函数ƒ(x )的单调递减区间为⎣⎡⎦⎤k π-π8,k π+3π8,k ∈Z. 又因为x ∈[0,π],则ƒ(x )在[0,π]上的单调递减区间为⎣⎡⎦⎤0,3π8,⎣⎡⎦⎤7π8,π.。
(21)三角函数的图像与性质 Word版含答案
同步卷(21)三角函数的图像与性质1、下列函数中,最小正周期为2π的奇函数的是( )A.cos4y x =B.sin 4y x =C.sin 2x y =D.cos 2xy =2、下列函数中,在0,2π⎛⎫⎪⎝⎭上为增函数的是( ) A.sin 22y x π⎛⎫=+ ⎪⎝⎭ B.cos 22y x π⎛⎫=+ ⎪⎝⎭ C.cos 2y x π⎛⎫=+ ⎪⎝⎭ D.sin 22y x π⎛⎫=- ⎪⎝⎭3、下列函数中,周期为,且在,42ππ⎡⎤⎢⎥⎣⎦上为减函数的是( ) A.sin 22y x π⎛⎫=+ ⎪⎝⎭ B.cos 22y x π⎛⎫=+ ⎪⎝⎭ C.sin 2y x π⎛⎫=+ ⎪⎝⎭ D.cos 2y x π⎛⎫=+ ⎪⎝⎭4、函数24y x π⎛⎫=- ⎪⎝⎭的单调增区间为( ) A.3,,Z 88k k k π⎡⎤π-π+π∈⎢⎥⎣⎦ B.372,2,Z 88k k k ⎡⎤π+ππ+π∈⎢⎥⎣⎦ C.37,,Z 88k k k ⎡⎤π+ππ+π∈⎢⎥⎣⎦ D.32,2,Z 88k k k π⎡⎤π-π+π∈⎢⎥⎣⎦5、将函数πsin(2)5y x =+的图象向右平移π10个单位长度,所得图象对应的函数() A.在区间3π5π[,]44上单调递增 B.在区间3π[,π]4上单调递减C.在区间5π3π[,]42上单调递增 D.在区间3π[,2π]2上单调递减6、函数5sin 22y x π⎛⎫=+ ⎪⎝⎭图象的一个对称中心是( ) A.,08π⎛⎫ ⎪⎝⎭ B.,04π⎛⎫⎪⎝⎭ C.,03π⎛⎫- ⎪⎝⎭ D.3,08π⎛⎫⎪⎝⎭7、(多选)已知函数()sin f x x =,下列说法中正确的是( )A.()f x 既是偶函数,又是周期函数B.()f xC.()y f x =的图象关于直线2x π=对称D.()y f x =的图象关于(,0)π中心对称8、对于余弦函数cos y x =的图象,有以下三项描述:①向左向右无限延伸;②与x 轴有无数多个交点;③与sin y x =的图象形状一样,只是位置不同.其中正确的有( )A.0个B.1个C.2个D.3个 9、函数3cos tan 022y x x x x ππ⎛⎫=⋅≤<≠ ⎪⎝⎭且的图象是( ) A. B.C. D.10、若点,2M m π⎛⎫- ⎪⎝⎭在函数sin y x =的图象上,则m 等于( ) A.0B.1C.-1D.2 11、设定义在区间0,2π⎛⎫ ⎪⎝⎭上的函数cos y x =与tan y x =的图象交于点P ,过点P 作x 轴的垂线,垂足为1P,直线1PP 与函数sin y x =的图象交于点2P ,则线段12P P 的长为___________. 12、已知函数()tan (0)f x x ωω=>的图象的相邻两支截直线4y π=所得线段长为4π,则4f π⎛⎫ ⎪⎝⎭的值为___________. 13、已知函数sin(2)22y x ϕϕππ⎛⎫=+-<< ⎪⎝⎭的图象关于直线3x π=对称,则ϕ的值为_________. 14、函数()sin 4f x x π⎛⎫=- ⎪⎝⎭的图象的对称轴方程是__________. 15、函数1sin y x =+,[]0,2x ∈π的图象与直线32y =的交点的个数是_________. 16、函数[]2cos ,0,2y x x =∈π的图象和直线2y =围成的一个封闭的平面图形的面积是_________.答案以及解析1答案及解析:答案:B解析:A,D 选项为偶函数,不符合题意,sin2x y =的最小正周期为4π,故C 选项不符合题意.故选B.2答案及解析:答案:D解析:sin 2cos 2,0,22y x x x ππ⎛⎫⎛⎫=-=-∈ ⎪ ⎪⎝⎭⎝⎭时,2(0,)x ∈π,所以函数sin 22y x π⎛⎫=- ⎪⎝⎭在0,2π⎛⎫ ⎪⎝⎭内是增函数,故选D.3答案及解析:答案:A解析:因为函数的周期为,所以排除C,D. 又cos 2sin 22y x x π⎛⎫=+=- ⎪⎝⎭在,42ππ⎡⎤⎢⎥⎣⎦上为增函数,故B 不符合题意. 只有函数sin 2cos 22y x x π⎛⎫=+= ⎪⎝⎭的周期为,且在,42ππ⎡⎤⎢⎥⎣⎦上为减函数.4答案及解析:答案:C 解析:2244y x x ππ⎛⎫⎛⎫=-=- ⎪ ⎪⎝⎭⎝⎭,故增区间为337222,22224244k x k k x k πππππ+π≤-≤+π+π≤≤+π,37(Z)88k x k k π+π≤≤π+π∈,故选C.5答案及解析:答案:A 解析:函数sin 25y x π⎛⎫=+ ⎪⎝⎭的图象向右平移10π个单位长度后的解析式为sin 2sin 2105y x x ⎡ππ⎤⎛⎫=-+= ⎪⎢⎥⎝⎭⎣⎦,则函数sin 2y x =的一个单调增区间为35,44ππ⎡⎤⎢⎥⎣⎦,一个单调减区间为57,44ππ⎡⎤⎢⎥⎣⎦.由此可判断选项A 正确.6答案及解析:答案:B解析:对称中心为曲线与x 轴的交点,将四个点代入验证,只有,04π⎛⎫ ⎪⎝⎭符合要求.7答案及解析:答案:ACD 解析:()sin()sin ()f x x x f x -=-==,所以()f x 是偶函数.()()f x f x +π=,所以()f x 是周期函数,A 选项正确.()f x 的最大值为1,B 选项错误.作出函数()f x 的图象,如图所示.观察图象,可知C,D 选项正确.8答案及解析:答案:D解析:作出cos y x =的图象,如图,可知三项描述均正确.9答案及解析:答案:C 解析:当02x π≤<时,cos tan sin y x x x =⋅=; 当2x π<≤π时,cos tan sin y x x x =⋅=-; 当32x ππ<<时,cos tan sin y x x x =⋅=,故其图象为C.10答案及解析:答案:C解析:由题意,得sin2m π-=,∴1m -=,∴1m =-.11答案及解析: 51-解析:不妨设1P 坐标为0(,0)x ,则12P P 的长为0sin x . ∵cos y x =与tan y x =的图象交于点P , 即00000sin cos tan ,cos cos x x x x x ==. 解得051sin x -=,则线段12P P 51-12答案及解析:答案:0解析:∵()f x 的图象的相邻两支截直线4y π=所得线段的长度即为()tan f x x ω=的一个周期,∴,44ωωππ==,因此tan 4tan 044f ππ⎛⎫⎛⎫=⨯=π= ⎪ ⎪⎝⎭⎝⎭.13答案及解析: 答案:6π- 解析:由题意得2sin 133f ϕπ⎛⎫⎛⎫=π+=± ⎪ ⎪⎝⎭⎝⎭, ∴232k ϕππ+=π+, ∴,Z 6k k ϕπ=π-∈. ∵,22ϕππ⎛⎫∈- ⎪⎝⎭, ∴取0k =得6ϕπ=-.14答案及解析: 答案:3,Z 4x k k π=π+∈ 解析:因为函数sin y x =图象的对称轴方程为(Z)2x k k π=π+∈,令42x k ππ-=π+,得3(Z)4x k k π=π+∈,所以函数()sin 4f x x π⎛⎫=- ⎪⎝⎭的图象的对称轴为方程3,Z 4x k k π=π+∈.15答案及解析:答案:2解析:由[]sin ,0,2y x x =∈π的图象向上平移1个单位长度,得[]1sin ,0,2y x x =+∈π的图象与直线32y =的交点的个数是2.16答案及解析:答案:4π解析:将余弦函数的图象在x 轴下方的部分补到x 轴上方,可得一个矩形,其面积为224π⨯=π.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
( )1
t- ∴y=4 2 2-2 (-1≤ห้องสมุดไป่ตู้≤1)
1
π
5π
∴当 t=2,即 x=6+2kπ 或 x= 6 +2kπ(k∈Z)时,ymin=-2;
3π
当 t=-1,即 x= 2 +2kπ (k∈Z)时,ymax=7.
( ) [ ] π
19
x+
-,
6.函数 y=asin 6 +b 的值域为 2 2 ,求 a 的值,以及原函数的单调递
π 3.将正弦曲线 y=sin x 上各点向左平移3个单位,再把横坐标伸长到原来的 2
倍,纵坐标不变,则所得图象解析式为______________.
( ) π
π
x+
解析 由 y=sin x 向左平移3得 y=sin 3 ,再把横坐标伸长到原来的 2 倍,
( )x π + 得 y=sin 2 3 .
( ) 1 π x- 1.函数 y= 3sin 2 4 的周期是________,振幅是________,当
x=________时,ymax=________;当 x=________时,ymin=________.
3
π
答案 4π 3 4kπ+2π (k∈Z) 3 4kπ-2(k∈Z) - 3
x+a≤ 4 ,即 a≤sin2x-sin
x+ 4 和
( ) 17
1
sin x-
a≥sin2x-sin x+1 对 k∈R 恒成立.由 sin2x-sin x+ 4 =
2 2+4≥4,得 a≤4.由
( )1 3
sin x-
sin2x-sin x+1=
2 2+4≤3,得 a≥3.
故 3≤a≤4.
练习:
[ ]π π
-, 例 4.设 ω>0 为常数,函数 y=2sin ωx 在 3 4 上单调递增,则实数 ω 的取
3
值范围是__________. 答案 0<ω≤2
( )π
2x+ 例 5.关于 f(x)=4sin 3 (x∈R),有下列命题
(1)由 f(x1)=f(x2)=0 可得 x1-x2 是 π 的整数倍;
[ ] 3-sin x
1
,2
4.函数 y=3+sin x的值域为____________. 答案 2
5.求函数 y=3-4sin x-4cos2x 的最大值和最小值,并写出函数取最值时对应
的 x 的值.
解 y=3-4sin x-4cos2x=4sin2x-4sin x-1
( )1
sin x-
=4
2 2-2,令 t=sin x,则-1≤t≤1,
kπ
π
∴x=2π-6(k∈Z),∴x1-x2 是2的整数倍,∴①错;对于②,f(x)=4sin
( ) [ ( )] ( ) π
π
π
π
2x+
- 2x+
2x-
3 利用公式得:f(x)=4cos 2
3 =4cos 6 . ∴②对;
( )π
π
2x+
对于③,f(x)=4sin 3 的对称中心满足 2x+3=kπ(k∈Z),
增区间.
( ) 5
5
π
x+
解 (1)当 a>0 时,Error!∴a=2,b=2,∴y=2sin 6 +2.
π
ππ
2π
π
又∵-2+2kπ≤x+6≤2+2kπ,k∈Z.∴- 3 +2kπ≤x≤3+2kπ,k∈Z.
[ ] 2
π
- π+2kπ, +2kπ
∴原函数的单调递增区间为 3
3
,k∈Z.
( ) 5
5
三角函数的图像和性质习题课
例 1.若函数 y=Asin(ωx+φ)(A>0,ω>0)是偶函数,则 φ 满足的条件是
______.
解析 y=Asin(ωx+φ)是偶函数,即关于 y 轴对称
π ∴sin φ=±1,∴φ=kπ+2(k∈Z).
例 2.函数 y=sin 2x 的图象向右平移 φ 个单位(φ>0)得到的图象恰好关于 x=
( )π
x+ 2.把函数 y=sin 4 的图象向
__
__ ____,可以得到函数
( )π
x- y=sin 6 的图象.
( ) ( ) π
π
5π π
x+
x-
解析 由 y=sin 4 , 而 y=sin 6 =sin(x-12+4),
( ) ( ) π
5π
π
x+
x-
即将 y=sin 4 向右平移12个单位,得 y=sin 6 .
( ) k π
π
- ,0
∴x=2π-6(k∈Z),∴ 6 是函数 y=f(x)的一个对称中心.∴③对;
对于
④,
ππ
π kπ
函数 y=f(x)的对称轴满足 2x+3=2+kπ(k∈Z),∴x=12+ 2 (k∈Z).∴④
错.
例 6.(创新拓展)已知 f(x)=-sin2x+sin x+a,
(1)当 f(x)=0 有实数解时,求 a 的取值范围;
( )π
2x+ y=sin 5 的图象,则 θ 的值为________.
( ) [ ( ) ] ( ) π
π
π
x+
2 x+ +θ
2x+ +θ
解析 设 f(x)=sin (2x+θ),则 f 4 =sin
4 =sin 2 .
( ) ( ) π
ππ π
3π
x+
2x+
由已知,f 4 =sin 5 .∴2+θ=5,∴θ=-10.
π
6对称,则 φ 的最小值为________.
π
解析 y=sin 2x 向右平移 φ 个单位得 y=sin(2x-2φ)x=6是一条对称轴,
π
π
kπ π
5π
则 2×6-2φ=kπ+2(k∈Z∴φ= 2 -12(k∈Z),∴φ 的最小值为12.
( )π
π
|θ| <
例 3.将函数 y=sin(2x+θ) 2 的图象向左平移4个单位长度,得到函数
17 (2)当 x∈R,有 1≤f(x)≤ 4 ,求 a 的取值范围.
( )1 1
sin x-
解 (1)由 f(x)=0,有 a=sin2x-sin x=
2 2-4.
[ ] 1
1
1
- ,2
当 sin x=-1 时,amax=2;当 sin x=2时,amin=-4.∴a∈ 4 .
17
17
17
(2)由 1≤f(x)≤ 4 有 1≤-sin2x+sin
( )π
2x- (2)y=f(x)的表达式可改写成 y=4cos 6 ;
( )π
π
- ,0
(3)y=f(x)图象关于 6 对称; (4)y=f(x)图象关于 x=-6,对称.
其中正确命题的序号为________.(将你认为正确的都填上)
π 解析 对于①,由 f(x)=0,可得 2x+3=kπ(k∈Z).
π
x+
(2)当 a<0 时,Error!∴a=-2,b=2.∴y=-2sin 6 +2.
π
π3
π
4
又∵2+2kπ≤x+6≤2π+2kπ,k∈Z.∴3+2kπ≤x≤3π+2kπ,k∈Z.
