数学:8.4《分式的乘除》(第1课时)学案(苏科版八年级下)
苏科版数学八年级下册教学设计10.4 分式的乘除(1)

苏科版数学八年级下册教学设计10.4 分式的乘除(1)一. 教材分析本节课的教学内容是苏科版数学八年级下册的10.4分式的乘除(1),这部分内容是学生在学习了分式的概念、分式的减法和加法的基础上进行学习的。
本节课的主要内容有:分式的乘法、分式的除法。
通过这部分的学习,学生可以进一步理解和掌握分式的运算方法,为后续的学习打下基础。
二. 学情分析学生在学习本节课之前,已经学习了分式的概念、分式的减法和加法,对于分式的运算已经有了一定的了解。
但是,学生对于分式的乘法和除法的运算规则可能还不够熟练,需要通过本节课的学习来进一步掌握。
同时,学生可能对于分式运算中的符号变换和运算顺序还有一些困惑,这也是本节课需要重点解决的问题。
三. 教学目标1.理解分式的乘法和除法的运算规则。
2.能够熟练地进行分式的乘法和除法的运算。
3.能够理解分式运算中的符号变换和运算顺序。
四. 教学重难点1.分式的乘法和除法的运算规则。
2.分式运算中的符号变换和运算顺序。
五. 教学方法采用讲解法、示例法、练习法、讨论法等教学方法。
通过讲解法,使学生理解分式的乘法和除法的运算规则;通过示例法,让学生直观地看到分式的乘法和除法的运算过程;通过练习法,让学生在实践中掌握分式的乘法和除法的运算;通过讨论法,让学生在讨论中理解分式运算中的符号变换和运算顺序。
六. 教学准备1.教学PPT。
2.练习题。
3.黑板、粉笔。
七. 教学过程1.导入(5分钟)通过复习分式的概念、分式的减法和加法,引出本节课的内容——分式的乘法和除法。
2.呈现(15分钟)讲解分式的乘法和除法的运算规则,并通过示例进行演示。
示例1:分式的乘法讲解分式的乘法的运算规则,并给出示例:a b ×cd=a×cb×d示例2:分式的除法讲解分式的除法的运算规则,并给出示例:a b ÷cd=ab×dc=a×db×c3.操练(15分钟)让学生进行分式的乘法和除法的运算练习,教师巡回指导。
校八年级数学下册 10.4分式的乘除教案 (新版)苏科版-(新版)苏科版初中八年级下册数学教案

2、等式( )k= 成立吗?为什么?
3、计算( )3的结果是( )A. ;B. ;C. ;D. 。
4、计算(1) ÷6xy4; (2) ÷ ;
(3)( )3÷( )4
二、新课
(一)情境创设
1、如何计算: · 与 ÷
2、观察下列运算:
× =, × = ,
分式的乘除
教学目标
1、理解并掌握分式的乘除法则,运用法则进行运算,能解决一些与分式有关的实际问题。
2、经历探索分式的乘除运算法则的过程,并能结合具体情境说明其合理性。
重 难 点
掌握分式的乘除运算。分子、分母为多项式的分式乘除法运算。
学习过程
旁注与纠错
一、课前预习与导学得分
1、你还记得分数的乘除法吗?请你用类似于分数的乘除法法则计算下列各式:(1) · ;(2) ÷ 。
÷ = × = ÷ = × =
二、探索活动:
1、猜一猜与 × =? ÷ =?同伴交流。
2、你能验证分式乘、除运算法则是合理、正确的吗?
3、归纳:
(1)分式的乘法法则:分式乘以分式,用分子的积做积的分子,分母的积做积的分母。 × = 。
(2)分式的除法法则:分式除以分式,把除式的分子、分母颠倒位置后,与被除式相乘。 ÷ = × = 。
(3)分式的乘方法则:分式乘方是把分子、分母各自乘方。( )n=
三、例题教学:
例1、计算:(1) ·(- );(2)( )2
例2、计算:
(1) · ; (2) ÷ 。
例3、计算:
(1)( )2· (- )3;(2)( )3÷( )4。
五、中考
已知 = , = , = ,求代数式 的值。
8.4 分式的乘除(2)教案 (苏科版八年级下)doc

8.4 分式的乘除(第2课时)教学目标:1. 使学生理解并掌握分式的乘除法则,运用法则进行运算,能解决一些与分式有关的实际问题.2.经历探索分式的乘除运算法则的过程,并能结合具体情境说明其合理性3.渗透类比转化的思想,让学生在学知识的同时学到方法,受到思维训练.教学重点:掌握分式的乘除运算教学难点:分子、分母为多项式的分式乘除法运算.教学过程:一、预习导学:1、在计算b b a 1.÷时,小明: b b a 1.÷=a ÷1=a小丽:b b a 1.÷=a .b 1 .b 1=2b a 你怎样判断是小明的做法对,还是小丽的做法正确?2.你会计算pq q p m n .÷吗?3.怎样进行分式的乘,除混合运算?分式的加,减,乘,除混合运算吗?二、交流成果三、合作探究:1.先化简,再求值:2222222222)(2)(.ba cb a b a abc b a ab a ac ab a ---÷++----+。
其中3,2,1-=-==c b a (与分数混合运算类似,分式的加,减,乘,除混合运算的顺序是:先乘除,后加减。
如有括号,则先进行括号内的运算。
)2.计算:1aa a a a 21122+-÷-- 3. 计算:23--x x ÷(x+2-25-x )4.已知.0732≠==c b a 求分式a c b a +-的值。
5.已知:)0(022,0≠=+-=-+c c b a c b a ,求c b a c b a 235523+-+-的值。
四、达标测试:一. 选择题:1.化简x y x x 1.÷,其结果为( )A. 1 B.xy C.xy D.y x 2.化简112---a a ,其结果为( )A .1+a B. 1-a C .a -1 D. 1--a 3.计算:(1)2222.2)(x y x xy y xy x x xy -+-÷- (2)x x x x x x x x -÷+----+4)44122(224.化简求值:22121-÷--a a a ,其中2=a .五、课时小结:1、分式混合运算的顺序2、分式求值的解题步骤。
数学初二下苏科版8.4分式的乘除(第1课时)教案

数学初二下苏科版8.4分式的乘除(第1课时)教案学习目标 1、理解并掌握分式的乘除法那么,运用法那么进行运算,能解决一些与分式有关的实际问题。
2、经历探究分式的乘除运算法那么的过程,并能结合具体情境说明其合理性。
学习重点 掌握分式的乘除运算学习难点 分子、分母为多项式的分式乘除法运算 教学流程预习导航 1、观看以下运算: ,43524532543297259275,53425432⨯⨯=⨯=÷⨯⨯=⨯⨯⨯=⨯, .279529759275⨯⨯=⨯=÷ 猜一猜??=÷=⨯cd a b c d b a 与同伴交流。
2、你会计算b ac 34.3229ac b =bac 34÷3229ac b = 合作探究一、 新知探究:1、猜一猜??=÷=⨯c d a b c d b a 与同伴交流。
2、你能验证分式乘、除运算法那么是合理、正确的吗?3、归纳:〔1〕分式的乘法法那么:分式乘以分式,用分子的积做积的分子,分母的积做积的分母。
b a ·d c =bdac 〔2〕分式的除法法那么:分式除以分式,把除式的分子、分母颠倒位置后,与被除式相乘。
b a ÷d c =bcad 〔3〕分式乘方法那么:分式乘方是把分子、分母各自乘方〔ba 〕n =n nb a 。
二、 例题分析:例1、计算:〔1〕b a a 2284-·6312-a ab ;〔2〕24⎪⎭⎫ ⎝⎛+c b a 例2、计算〔1〕22316xx y ÷ 〔2〕124124419622+-÷+++-a a aa a a 分析:依据分式除法的法那么,把除法转化为乘法,可先约分,再运算,在运算过程中要留意符号。
小结:分式的除法运算,需转化为乘法运算;依照乘法法那么,应先把分子、分母分别相乘,化成一个分式后再进行约分,但在实际演算时,如此做显得较繁琐,因此,可依照情况先约分,再相乘,如此做有时简单易行,又不易出错。
八年级数学下册 10.4 分式的乘除教案1 (新版)苏科版-(新版)苏科版初中八年级下册数学教案

课题
10.4 分式的乘除(1)
课型
新授课
教学目标
1、理解并掌握分式的乘除法则,运用法则进行运算,能解决一些与分式有关的实际问题。
2、经历探索分式的乘除运算法则的过程,并能结合具体情境说明其合理性。
重点
掌握分式的乘除运算
难点
分子、分母为多项式的分式乘除法运算
教法及教具
教
学
过
程
教 学 内 容
个案调整
教师主导活动
学生主体活动
一.预习指导
1、观察下 = =
新授
归纳:
(1)分式的乘法法则:分式乘以分式,用分子的积做积的分子,分母的积做积的分母。 · =
(2)分式的除法法则:分式除以分式,把除式的分子、分母颠倒位置后,与被除式相乘。 =
(3)分式乘方法则:分式乘方是把分子、分母各自乘方( )n= 。
三.例题分析
算
(1) (2)
教
学
过
程
教 学 内 容
个案调整
教师主导活动
学生主体活动
(1) (2)
三.课堂练习
1、计算 ; ;
2.
3.
4.若代数式 有意义,则x的取值X围是__________.
5、
四.小结
板书设计
(用案人完成)
作业布置
教学札记
【新苏科版】八年级下册10.4分式的乘除(1)-教案设计
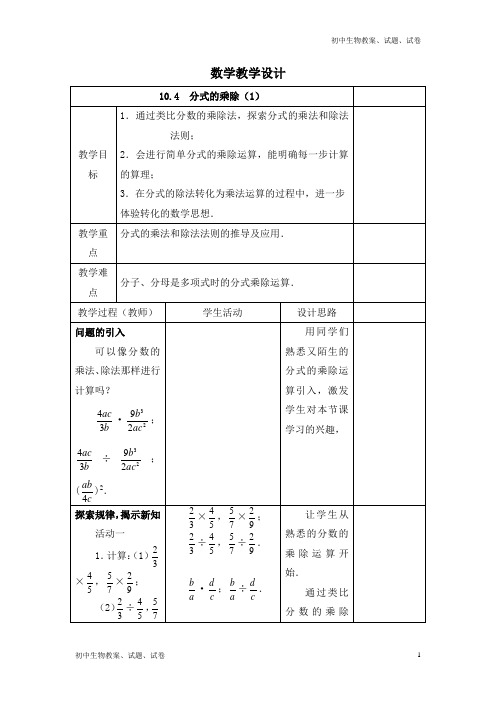
数学教学设计10.4 分式的乘除(1)教学目标1.通过类比分数的乘除法,探索分式的乘法和除法法则;2.会进行简单分式的乘除运算,能明确每一步计算的算理;3.在分式的除法转化为乘法运算的过程中,进一步体验转化的数学思想.教学重点 分式的乘法和除法法则的推导及应用.教学难点分子、分母是多项式时的分式乘除运算.教学过程(教师) 学生活动设计思路问题的引入可以像分数的乘法、除法那样进行计算吗?43ac b ·3292b ac ;43ac b÷3292b ac ;(4ab c)2.用同学们熟悉又陌生的分式的乘除运算引入,激发学生对本节课学习的兴趣,探索规律,揭示新知活动一1.计算:(1)23×45,57×29; (2)23÷45,5723×45,57×29; 23÷45,57÷29.b a ·dc ;b a ÷d c. 让学生从熟悉的分数的乘除运算开始.通过类比分数的乘除÷29.问题1:上面运算的根据是什么?问题2:你能回忆并说出分数的乘法和除法法则吗?2.问题3:你能“类比”分数的运算,计算完成下面的式子吗?b a ·dc;ba÷dc.3.问题4:再举几个这样的例子试一试.与同伴交流你的想法.问题5:请你“类比”分数的乘除法则,用语言描述出分式的乘除法则(小组内交流得出结论).分式的乘法法则:分式乘分式,用分子的积做积的分子,分母的积做积的分母.分式的除法法则:分式除以分式,把除式的分子、分母法,引导学生尝试去进行分式的乘除.让学生再举这样的例子,认识到一般规律,此时学生通过小组交流合作,通过不完全归纳探究总结分式的乘除法法则.颠倒位置后,与被除式相乘.用字母表示为:b a ·dc=bd ac ;b a ÷dc =b a ×cd =bc ad. 活动二 试一试: (1)43ac b ·3292b ac; (2)43acb÷3292bac. 注意:运用分式的乘除法运算法则进行分式的乘法和除法时,能约分的要约分.43acb·3292b ac =3322249366326⋅⋅==ac b ab c b b ac abc c;43acb÷3292b ac =43ac b ·2233428927=ac a c b b. 在学生探究出分式的乘除法法则后,通过两个简单问题的尝试,进一步熟悉运算法则.通过计算,认识到分式运算时,能约分的先约分,结果最后要化成最简.尝试反馈,领悟新知例 1 计算: (1)226cb a ·2243-ca b ; (2)(4ab c)2. 例 2 计算: (1)226xay÷例1 可由学生自己来完成,同学们互相改正错误.例2 由学生小组合作完成.在熟悉分式的乘除法法则后,例1的设计让学生尝试解决问题,巩固所学知识.例2的设计让学生应用。
八年级数学下册 10.4 分式的乘除(第1课时)学案(新版)苏科版
动
探
究
试一试 :
(1) · ;
(2) ÷ .
目
标பைடு நூலகம்
检
测
检测
1计 算:
(1) · (2)( )2.
(3) ÷ ;(4) ÷ .
2、下 面的计算对吗?如果不对,应该怎样更正?
(1) · = ;
(2) ÷ = .
教学心得
10.4分式的乘除
课题
10.4分式的乘除(1)
学习目标
学习重难点
分式的乘法和除法法则的推导及应用.
学习过程
环节
学习 内容
教师活动
学生活动
自学指导
自学检测
一、情境创设
可以像分数的乘法、除法那样进行计算吗?
· ; ÷ ;( )2.
二、探索活动
活动一1.计算:(1) × , × ;
(2) ÷ , ÷ .
问题1:上面运算的根据是什么?
问题2:你能回忆并说出分数的乘 法和除法法则吗?
2.问题3:你能“类比”分数的运算,计算完成下面的式子吗? · ; ÷ .
问题4:请你“类比”分数的乘除法则,用语言描述出分式的乘除法则 (小 组内交流得出结论).
分式的乘法法则:分式乘分式,用分子的积做积的分子,分母的积做积的分母.
分式的除法法则:分式除以分式,把除式的分子、分母颠倒位置后,与被除式相乘.
数学:8.4《分式的乘除(1)》学案(苏科版八年级下)

8.4分式的乘除(1)班级 姓名 学号学习目标:(一)知识与技能目标使学生理解并掌握分式的乘除法则,运用法则进行运算,能解决一些与分式有关的实际问题. (二)过程与方法目标经历探索分式的乘除运算法则的过程,并能结合具体情境说明其合理性 (三)情感与价值目标渗透类比转化的思想,让学生在学知识的同时学到方法,受到思维训练. 学习重点:掌握分式的乘除运算。
学习难点:分子、分母为多项式的分式乘除法运算。
教学过程 一、情境引入:你还记得分数的乘除法法则吗?你能用类似于分数的乘除法法则计算下面两题吗?(1)b ac 34·3229ac b = (2)bac34÷3229ac b =二、探究学习:(1)你能说出前面两道题的计算结果吗?(2)你能验证分式乘.除运算法则是合理的.正确的吗?(3)类比分数的乘除法则,你能从计算中总结出怎样进行分式的乘除法运算吗? 归纳小结:(1)分式的乘法法则:分式乘以分式,用分子的积做积的分子,分母的积做积的分母。
即: a b ×c d =acbd。
(2)分式的除法法则:分式除以分式,把除式的分子、分母颠倒位置后,与被除式相乘。
即:ab ÷c d =a b ×d c =ad bc。
(3)分式的乘方法则:分式乘方是把分子、分母各自乘方。
即:( a b )n =anb n三、典型例题:例1、计算:1. b a a 2284-.6312-a ab 2。
(c b a 4+)2例2、计算、1.x y 62÷231x 2.2244196aa a a +++-÷12412+-a a 归纳小结:分式的乘法运算,先把分子、分母分别相乘,然后再进行约分;进行分式除法运算,需转化为乘法运算;根据乘法法则,应先把分子、分母分别相乘,化成一个分式后再进行约分,但在实际演算时,这样做显得较繁琐,因此,可根据情况先约分,再相乘,这样做有时简单易行,又不易出错.四、反馈练习:(1) xy z y x z 54232÷- (2) b a b a 22+-.2222b a b a -+ (3) (a-4).1681622+--a a a (4) 2222)1()1()1(--+x x x ÷1)1(22--x x 五、探究交流: (1)在夏季你是怎么挑选西瓜的呢?(2)你认为买大西瓜合算还是买小西瓜合算?七、课堂小结:1、分式的分子、分母都是几个因式的积的形式,约去分子、分母中相同因式的最低次幂,注意系数也要约分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
8.4 分式的乘除(1)
教学目标:
(一)知识与技能目标
使学生理解并掌握分式的乘除法则,运用法则进行运算,能解决一些与分式有关的实际问题.
(二)过程与方法目标
经历探索分式的乘除运算法则的过程,并能结合具体情境说明其合理性
(三)情感与价值目标
渗透类比转化的思想,让学生在学知识的同时学到方法,受到思维训练.
教学重点:
掌握分式的乘除运算
教学难点:
分子、分母为多项式的分式乘除法运算.
教学过程:
一、预习导学
1、观察下列运算:
,43524532543297259275,5
3425432⨯⨯=⨯=÷⨯⨯=⨯⨯⨯=⨯, .27952
9759275⨯⨯=⨯=÷得分数乘除法的法则: 2、猜一猜??
=÷=⨯c d a b c d b a 与同伴交流。
3、如何计算b ac 34。
3229ac b = b
ac 34÷3229ac b = 4、分式乘除法则:
分式乘分式,用分子的 做积的分子,分母的积做 。
即
B A .D
C = . 分式除以分式,把除式的分子.分母 后,与被除式相 。
即B A ÷
D C = 5、分解因式:
(1)、2a -4= (2)、2
a -6a +9=
(3)、1+4a a 4+2= (4)、x 4-y
4 二、交流成果
三.合作探究; 计算:1、 b a a 2284-.6
312-a ab 2、(c b a 4+)2 3、x y 62÷231x 4、2244196a
a a a +++-÷12412+-a a
5、(a-4).16
81622
+--a a a 6.3412-+-a a a ÷a
a a 3122--
7、.44422+-+m m m ).4(2-m 16
424--m m 8、n m n m mn n m m mn m n -+÷+-÷-22222
四.课时小结:
①分式的分子、分母都是几个因式的积的形式,所以约去分子、分母中相同因式的最低次幂,注意系数也要约分
②当分式的分子、分母为多项式时,先要进行因式分解,才能够依据分式的基本性质进行约分.
五、达标测试:
1.计算:
(1)(-a c b 32).2229bc a (2)b a b a 22+-.2
22
2b a b a -+ (3) xy z y x z 54232÷- (4) 2222)
1()1()1(--+x x x ÷1)1(22
--x x
2.已知x=-2,求
x x x x x x x +-÷++223122的值。
