竖向荷载
土木工程毕业设计 第六章 竖向荷载(恒载 活载)作用下框架内力计算讲解
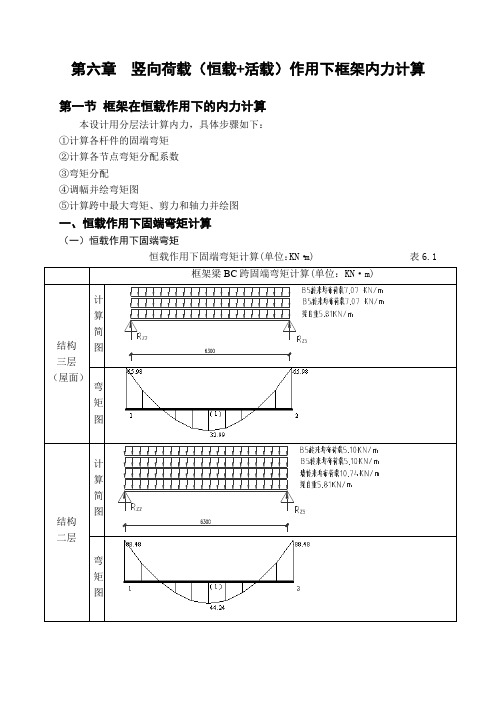
第六章竖向荷载(恒载+活载)作用下框架内力计算第一节框架在恒载作用下的内力计算本设计用分层法计算内力,具体步骤如下:①计算各杆件的固端弯矩②计算各节点弯矩分配系数③弯矩分配④调幅并绘弯矩图⑤计算跨中最大弯矩、剪力和轴力并绘图一、恒载作用下固端弯矩计算(一)恒载作用下固端弯矩恒载作用下固端弯矩计算(单位:KN·m) 表6.1弯矩图恒载作用下梁固端弯矩计算统计表6.2(二)计算各节点弯矩分配系数用分层法计算竖向荷载,假定结构无侧移,计算时采用力矩分配法,其计算要点是:①计算各层梁上竖向荷载值和梁的固端弯矩。
②将框架分层,各层梁跨度及柱高与原结构相同,柱端假定为固端。
③计算梁、柱线刚度。
对于柱,假定分层后中间各层柱柱端固定与实际不符,因而,除底层外,上层柱各层线刚度均乘以0.9修正。
有现浇楼面的梁,宜考虑楼板的作用。
每侧可取板厚的6倍作为楼板的有效作用宽度。
设计中,可近似按下式计算梁的截面惯性矩:一边有楼板:I=1.5Ir两边有楼板:I=2.0Ir④计算和确定梁、柱弯矩分配系数和传递系数。
按修正后的刚度计算各结点周围杆件的杆端分配系数。
所有上层柱的传递系数取1/3,底层柱的传递系数取1/2。
⑤按力矩分配法计算单层梁、柱弯矩。
⑥将分层计算得到的、但属于同一层柱的柱端弯矩叠加得到柱的弯矩。
(1)计算梁、柱相对线刚度图6.1 修正后梁柱相对线刚度(2)计算弯矩分配系数结构三层=5.37÷(5.37+1.18)=0.820①梁μB3C3μ=5.37÷(5.37+3.52+1.18)=0.533C3B3=3.52÷(5.37+3.52+1.18)=0.350μC3D3=3.52÷(3.52+1.18)=0.749μD3C3=1.18÷(5.37+1.18)=0.180②柱μB3B2=1.18÷(5.37+3.52+1.18)=0.117μC3C2=1.18÷(3.52+1.18)=0.251μD3D2结构二层①梁μ=5.37÷(1.18+1.18+5.37)=0.695B2C2=5.37÷(1.18+1.18+5.37+3.52)=0.477μC2B2μ=3.52÷(1.18+1.18+5.37+3.52)=0.313 C2D2=3.52÷(1.18+1.18+3.52)=0.5986 μD2C2=1.18÷(1.18+1.18+5.37)=0.1525②柱μB2B3μ=1.18÷(1.18+1.18+5.37)=0.1525B2B1=1.18÷(1.18+1.18+5.37+3.52)=0.105 μC2C3μ=1.18÷(1.18+1.18+5.37+3.52)=0.105 C2C1=1.18÷(1.18+1.18+3.52)=0.2007 μD2D3μ=1.18÷(1.18+1.18+3.52)=0.2007D2D1结构一层=5.37÷(1.18+1+5.37)=0.711①梁μB1C1=5.37÷(1.18+1+5.37+3.52)=0.485 μC1B1=3.52÷(1.18+1+5.37+3.52)=0.318 μC1D1=3.52÷(1.18+1+3.52)=0.618μD1C1=1.18÷(1.18+1+5.37)=0.156②柱μB1B2=1÷(1.18+1+5.37)=0.133μB1B0=1.18÷(1.18+1+5.37+3.52)=0.107μC1C2=1÷(1.18+1+5.37+3.52)=0.090μC1C0μ=1.18÷(1.18+1+3.52)=0.207D1D2μ=1÷(1.18+1+3.52)=0.175D1D0(三)分层法算恒载作用下弯矩恒载作用下结构三层弯矩分配表6.3B C D上柱偏心弯矩分配系数0固端弯矩分配传递分配传递分配传递分配传递分配传递分配传递分配传递合计一次分配14.650 -13.883 226.915 20.861 -251.346 84.509 -112.810 二次分配14.512 -14.512 228.818 21.278 -250.096 105.707 -105.707恒载作用下结构二层弯矩分配表6.40.768 12.717 -28.301↑↑↑B C D偏心弯矩分配系数固端弯矩分配传递分配传递分配传递分配传递分配传递分配传递分配传递合计一次分配 6.931 4.431 -4.607 308.811 46.295 47.232 -385.113 169.804 -113.072 -92.837二次分配 5.901 3.401 -9.302 300.595 44.486 45.423 -390.504 191.416 -105.826 -85.591恒载作用下结构一层弯矩分配表6.52.127 9.081 -7.935↑↑↑B C D偏心弯矩分配系数固端弯矩分配传递分配传递分配传递分配传递分配传递分配传递分配传递合计一次二次7.030 5.338 -12.368 267.469 35.352 22.097 -324.919 357.349 -46.247 -15.172 -295.930图6.2 弯矩再分配后恒载作用下弯矩图(KN·m)(四)框架梁弯矩塑性调幅为了减少钢筋混凝土框架梁支座处的配筋数量,在竖向荷载作用下可以考虑竖向内力重分布,主要是降低支座负弯矩,以减小支座处的配筋,跨中则应相应增大弯矩。
简述一般建筑结构中竖向荷载传递路线

简述一般建筑结构中竖向荷载传递路线一般建筑结构中竖向荷载传递路线是指从上部荷载到下部基础的荷载传递路径。
竖向荷载通常包括重力荷载、风荷载、地震荷载等。
在一般建筑结构中,竖向荷载的传递路线通常是由结构系统中的各个构件组成的。
以下是一般建筑结构中竖向荷载传递的几个重要路径:
1.垂直荷载传递路径:
垂直荷载主要通过柱子传递到基础。
从楼板传来的垂直荷载首先由梁承载,然后再由柱子传递到地基上。
柱子是将楼板垂直荷载传递给基础的主要构件。
2.水平荷载传递路径:
水平荷载主要通过楼板和墙体传递到基础。
从外部风荷载传来的水平力通过楼板传递到墙体上,然后再由墙体传递到地基上。
墙体是将水平荷载传递给基础的主要构件。
3.腹板承力结构:
腹板承力结构是指将竖向荷载传递给基础的一种常见的结构形式。
在这种结构中,墙体作为腹板起到承载竖向荷载的作用,将荷载传递到地基上。
腹板通常由砖墙、混凝土墙等构成。
4.框架结构:
框架结构是一种将竖向荷载传递到地基的重要结构形式。
在框架结构中,竖向荷载首先通过梁传递到柱子上,然后再由柱子传递到地基上。
梁和柱子是框架结构中的主要承载构件。
总之,一般建筑结构中竖向荷载传递路线是一个复杂的传递过程,涉及到楼板、梁、柱子、墙体等多个构件。
这些构件通过各自的承载能力和连接方式,将竖向荷载传递到基础上。
正确设计和施工竖向荷载传递路线对于保证建筑结构的稳定性和安全性至关重要。
竖向荷载的计算方法

竖向荷载的计算方法竖向荷载呢,简单说就是垂直方向作用在结构上的力。
在建筑结构里,这可是个很重要的事儿。
那咱们先来说说恒载的计算。
恒载就是那些固定不变的重量,像建筑物的自重啦。
比如说楼板,你就可以根据楼板的厚度、材料的密度来算出它的重量。
如果是混凝土楼板,混凝土的密度大概是一个固定的值,你量出楼板的面积和厚度,一乘就大概能知道这楼板自身的重量啦。
这就像是一个人本身的体重,稳稳地压在结构上,不会变来变去的。
墙的重量计算也类似哦,根据墙的类型,是砖墙还是混凝土墙,然后算出每立方米的重量,再乘以墙的体积就妥了。
再说说活载的计算。
活载可就调皮一些啦,它是可变的荷载。
像咱们人在建筑物里走来走去,家具的摆放啥的。
不同的建筑功能,活载取值可不一样呢。
比如说住宅里,按照规范呢,每平方米的活载取值有个大概的范围。
但是你要是在商场里,那活载取值就要大很多啦,毕竟商场里人多,而且可能还会有一些较重的货物临时堆放啥的。
计算活载的时候,就是用规定的活载取值乘以相应的面积。
就好像是根据不同的活动场景,预估会有多少“活动的重量”压在结构上。
还有雪荷载呢。
这雪荷载就看老天爷的心情啦。
不同地区的雪荷载标准值不一样哦。
在北方那些经常下雪的地方,雪荷载可能就比较大。
计算雪荷载的时候,也是根据当地的雪荷载标准值和屋面的面积来计算。
这就像是大自然偶尔给建筑物戴上的一顶“雪帽子”,不过这“帽子”的重量可得算清楚,不然结构可能就会被压得“喘不过气”啦。
总的来说,竖向荷载的计算虽然有点小复杂,但是只要咱们把各个部分的荷载计算清楚,再把它们加起来,就能知道结构到底承受了多少竖向的压力啦。
宝子们,是不是感觉也没有那么难呢?。
高层建筑结构的荷载和地震作用31竖向荷载ss=

第3章 高层建筑结构的荷载和地震作用高层建筑结构主要承受竖向荷载和和水平荷载。
恒荷载 风荷载 1) 竖向荷载 2)水平荷载活荷载 地震作用 本章主要内容z 竖向荷载(简介) z 风荷载(重点)z 地震作用(工程结构抗震课介绍此部分内容) 与多层建筑结构有所不同,高层建筑结构:z 竖向荷载效应远大于多层建筑结构;z 水平荷载的影响显著增加,成为其设计的主要因素; z 对高层建筑结构尚应考虑竖向地震的作用。
3.1 竖向荷载3.1.1 恒荷载1)恒荷载是指各种结构构件自重和找平层、保温层、防水层、装修材料层、隔墙、幕墙及其附件、固定设备及其管道等重量,其标准值可按构件尺寸、和材料密度(单位体积或面积的自重)计算确定。
2)材料容重可从《荷载规范》查取;固定设备由相关专业提供。
3.1.2 活荷载 1. 楼面活载1)高层建筑楼面均布活荷载的标准值及其组合值、频遇值和准永久值系数,可按《荷载规范》的规定取用。
2)在荷载汇集及内力计算中,应按未经折减的活荷载标准值进行计算,楼面活荷载的折减可在构件内力组合时进行。
2. 屋面活载1)屋面均布活荷载的标准值及其组合值、频遇值和准永久值系数,可按《荷载规范》的规定取用。
2)有些情况下,应考虑屋面直升机平台的活荷载:(优于五星级酒店的是,七星级酒店将提供秘书式的“管家服务”,辟有直升机停机坪,用直升机和“大奔”接送客人。
)3. 屋面雪荷载1)屋面水平投影面上的雪荷载标准值k s ,应按下式计算:0r k s s μ= (3.1.1)式中:0s 为基本雪压,系以当地一般空旷平坦地面上统计所得50年一遇最大积雪的自重确定,按《荷载规范》取用;μr为屋面积雪分布系数,屋面坡度α≤25°时,μr取1.0,其它情况可按《荷载规范》取用。
2)雪荷载的组合值系数可取0.7;频遇值系数可取0.6;准永久值系数按雪荷载分区Ⅰ、Ⅱ和Ⅲ的不同,分别取0.5、0.2和0。
3)雪荷载不应与屋面均布活荷载同时组合。
竖向极限承载力标准值

竖向极限承载力标准值竖向极限承载力标准值是指在竖向荷载作用下,材料或结构体所能承受的最大力量。
这一数值对于工程设计和结构安全至关重要,因此在工程实践中,需要对竖向极限承载力标准值进行准确的计算和评估。
首先,竖向极限承载力标准值的计算需要考虑材料的强度和稳定性。
材料的强度是指材料在受力作用下的抗压、抗拉等能力,而稳定性则是指材料在受力作用下的变形和破坏情况。
在计算竖向极限承载力标准值时,需要综合考虑材料的强度和稳定性,确保结构在受力作用下不会发生失稳和破坏。
其次,竖向极限承载力标准值的计算还需要考虑结构的几何形状和支座条件。
不同形状和支座条件的结构,在受到相同荷载作用下,其竖向极限承载力标准值会有所不同。
因此,在进行计算时,需要充分考虑结构的几何形状和支座条件,确保计算结果的准确性和可靠性。
另外,竖向极限承载力标准值的计算还需要考虑结构的荷载组合和荷载效应。
在实际工程中,结构往往同时受到多种不同方向和大小的荷载作用,因此在计算竖向极限承载力标准值时,需要综合考虑不同荷载的组合和效应,确保结构在受到复合荷载作用下的安全性和稳定性。
最后,竖向极限承载力标准值的计算需要遵循相关的设计规范和标准。
不同的材料和结构,在计算竖向极限承载力标准值时,需要遵循不同的设计规范和标准,确保计算结果符合国家和行业的要求。
因此,在进行计算时,需要充分了解和掌握相关的设计规范和标准,确保计算结果的准确性和合理性。
综上所述,竖向极限承载力标准值的计算是一个复杂而又重要的工作,需要综合考虑材料的强度和稳定性、结构的几何形状和支座条件、荷载组合和荷载效应,以及相关的设计规范和标准。
只有在充分考虑以上因素的基础上进行计算,才能得到准确可靠的竖向极限承载力标准值,确保工程设计和结构安全的可靠性和稳定性。
设计竖向荷载

设计竖向荷载1. 竖向荷载的定义竖向荷载是指作用在建筑结构垂直方向上的力,包括重力荷载、活荷载和附加荷载等。
在建筑设计中,竖向荷载的计算和设计是非常重要的,因为它能够决定建筑结构的安全性和稳定性。
2. 重力荷载的计算和设计重力荷载是由于自重和受重物的作用而产生的竖向荷载。
在设计建筑结构时,需要计算和设计重力荷载,以确保结构的稳定性和安全性。
重力荷载的计算包括以下步骤:2.1 确定重力荷载大小首先需要确定各个构件(如梁、柱、墙等)的自重,并根据设计要求计算出所承受的重力荷载。
2.2 确定重力荷载的作用位置确定重力荷载的作用位置可以根据建筑结构的布置和荷载的分布情况进行计算。
通常情况下,重力荷载作用位置可以取构件的重心位置。
2.3 确定重力荷载的作用方向确定重力荷载的作用方向有利于计算结构的受力情况和变形情况。
通常情况下,重力荷载的作用方向为竖直向下的方向。
2.4 计算结构的承载能力根据结构的材料和形状等参数,计算结构的承载能力,以确定结构是否满足要求的安全性和稳定性。
3. 活荷载和附加荷载的计算和设计除了重力荷载外,还需要考虑活荷载和附加荷载对建筑结构的影响。
活荷载包括人员荷载、设备荷载和雪荷载等;附加荷载包括风荷载、地震荷载和温度荷载等。
活荷载和附加荷载的计算和设计需要根据具体的建筑结构和使用要求进行。
通常情况下,可以根据相关规范和设计标准来确定活荷载和附加荷载的计算方法和设计要求。
4. 竖向荷载的设计原则在进行竖向荷载的设计时,需要遵循一些基本原则,以确保建筑结构的安全可靠。
4.1 安全性原则在设计竖向荷载时,需要确保结构能够承受荷载的作用,不产生过大的应力和变形,以保证结构的安全性。
4.2 经济性原则在设计竖向荷载时,需要尽量减少结构的重量和材料的使用量,以保证结构的经济性。
同时还需要考虑结构的施工难度和成本等因素。
4.3 实用性原则在设计竖向荷载时,需要考虑结构的使用要求和功能,以满足建筑的实际需要。
塔机吊装竖向荷载计算公式

塔机吊装竖向荷载计算公式在建筑施工中,塔机是一种常用的起重设备,用于吊装各种建筑材料和构件。
在塔机吊装过程中,对于吊装的物体,需要计算其竖向荷载以确保塔机的安全运行。
本文将介绍塔机吊装竖向荷载的计算公式,以及相关的计算方法和注意事项。
塔机吊装竖向荷载计算公式如下:F = mg。
其中,F为竖向荷载,m为吊装物体的质量,g为重力加速度(通常取9.8m/s^2)。
在实际应用中,塔机吊装竖向荷载的计算通常需要考虑吊装物体的重量、重心位置、风荷载、地面承载能力等因素。
下面将分别介绍这些因素在竖向荷载计算中的影响和计算方法。
1. 吊装物体的重量。
吊装物体的重量是影响竖向荷载的主要因素之一。
在实际应用中,通常需要通过称重或者查阅相关资料来确定吊装物体的重量。
一般来说,吊装物体的重量越大,竖向荷载也就越大。
2. 吊装物体的重心位置。
吊装物体的重心位置对竖向荷载也有较大的影响。
当吊装物体的重心偏离塔机的竖直线时,会产生倾覆力矩,导致竖向荷载增大。
因此,在计算竖向荷载时,需要考虑吊装物体的重心位置,并进行相应的修正计算。
3. 风荷载。
在室外施工中,风荷载也是影响塔机竖向荷载的重要因素之一。
风的作用会使吊装物体产生侧向位移,从而增大竖向荷载。
因此,在计算竖向荷载时,需要考虑风荷载的影响,并根据实际情况进行修正计算。
4. 地面承载能力。
塔机的安装地基的承载能力也会对竖向荷载产生影响。
如果地基的承载能力不足,可能导致塔机的倾覆或者地基沉降,从而影响塔机的安全运行。
因此,在实际应用中,需要对塔机的安装地基进行承载能力计算,并根据计算结果进行相应的调整。
在实际应用中,对于塔机吊装竖向荷载的计算,通常需要综合考虑以上因素,并根据实际情况进行修正计算。
此外,还需要注意以下几点:1. 在进行竖向荷载计算时,需要确保吊装物体的重量和重心位置的准确性,以免产生计算误差。
2. 在考虑风荷载的影响时,需要根据当地的气象条件和实际风速进行合理的修正计算。
竖向荷载计算(弯矩二次分配法)实例

05
结论
竖向荷载计算的重要性
确保结构安全
竖向荷载计算是结构设计中的重要环节,准确计 算竖向荷载对于保证结构安全至关重要。
提高结构性能
合理的竖向荷载计算有助于优化结构设计,提高 结构的承载能力、稳定性和抗震性能。
降低成本
竖向荷载计算的误差可能导致结构加固或重建, 准确计算可降低不必要的成本。
弯矩二次分配法的限制条件
01
假定楼板为刚性,不考虑楼板的变形和位移。
ቤተ መጻሕፍቲ ባይዱ02
仅适用于规则的结构,对于不规则的结构需要进行 特殊处理。
03
对于节点平衡条件,仅考虑节点左右两侧的平衡, 不考虑上下平衡。
弯矩二次分配法的优化建议
01 考虑楼板的变形和位移,采用有限元法或其他数 值方法进行计算。
02 对于不规则的结构,采用特殊处理方法,如引入 弹性支座或采用有限元模型进行模拟。
弯矩二次分配法的优势与局限性
优势
局限性
弯矩二次分配法计算过程较为复杂,需要耗费较多 时间和计算资源,对于大型复杂结构可能不适用。
弯矩二次分配法能够考虑各杆件之间的相互 作用和影响,计算结果相对准确,适用于多 种结构形式。
适用范围
弯矩二次分配法适用于梁、柱等杆系结构, 但对于板、壳等连续介质,需要采用其他方 法进行计算。
03
竖向荷载计算实例
实例一:简单框架结构
总结词
简单框架结构适用于跨度较小、层数较少的建筑,其竖向荷载计算相对简单。
详细描述
简单框架结构通常由梁和柱组成,竖向荷载通过梁传递至柱,再由柱传递至基 础。弯矩二次分配法在此类结构中应用广泛,能够快速准确地计算出各构件的 弯矩值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
理想的情况,此时各截面内只有均匀分布的正应力,拱处于轴心受压状态,如果
在拱的设计中能获得上述结果,拱的经济效果将最好。
§5-3
拱的合理轴线
在固定荷载作用下,使拱处于无弯矩状态的轴线称为合理 轴线。由上述可知,按照压力曲线设计的拱轴线就是合理轴线。 从结构优化设计观点出发,寻找合理轴线即拱结构的优化选型。
M M Hy 在本例的座标系中可表达为:
qc
x
x
shx chx
ex chx shx
dx
而 q x qc y , 即
y
H
d y 1 qc y 2 dx H
特征方程为:
y
qc , H
2
H
0
x
N 2 Q2 sin 2 H cos 2 11 2 3 0.555
2 33 41,sin 2 0.555,cos 2 0.832
7.5 0.832 9.015 k N
绘制内力图
0
y
13.300 10.958 9.015 7.749 7.500 7.433 3.325 6.796 11.235 11.665 11.700 1.421 3.331 1.060 0.600 1.000 0.472 0.003 0.354
0.600
0.000
A
1
1.125 1.500 1.125
2
y2
q=2kN .m
6m x
0.000 0.375 4.500
3
2
4 5
6m
6
0.375
7 B 8
P=8kN
0.000
M图 kN.m
N图 kN
Q图 kN
§5-2
三铰拱的压力线
拱与受弯结构不同,在竖向荷载作用下,它不仅产生弯矩
和剪力,还产生轴力。经过合理设计可使其成为以受压为主的 结构体系。 因此拱结构可采用受压性能良好而受拉性能较差的脆性材 料(如砖石、素砼)建造,以保证其良好的经济性。 下面我们研究拱截面的受力情况。
c
VA
f l1
x
VB
VA
二、内力计算 以截面D为例
P1
Qo
x-a1 M
截面内弯矩要和竖向力及水平力对D点构成 的力矩相平衡,设使下面的纤维受拉为正。
H
y
D H x
MD 0
M VA x P x a1 H y 1
Qo
VA
M M H y
H
H
y C1e
H
C2 e
x
H H q y a , 代入原方程,a c 设其特解 q y x A ch x B sh x c H H q x 0, y 0 A c 设 x 0, y 0 B 0 q y c ch x 1 悬链线 H
q qC y 。
q qc y
y f y
y*
因事先
M 得不到,故改用q(x)和y(x)表示:
d2y 1 d2 M 2 dx H dx 2
对简支梁来说, d M q x 2
2
e
2
qc+.f
M M H y M H f y 0 M y f H
VA VA
M C 11 6 2 6 3 H 7.5kN f 4
(2)内力计算
y2
以截面2为例
4f 44 x l x 312 3 3m 2 2 l 12
dy dx
x 3
M 2 M 2 Hy2 11 3 2 3 15 7.5 3 .
q 8f 4f y x x l x 2 2 x l x 2 ql l
例2、设三铰拱承受均匀分布的水压力,试证明其合理轴线是园弧曲线。
[证明] 设拱在静水压力作用下处于无弯矩状态,然后由平衡条件推导轴线方程。
q
D
E
dS R d
M0 0 N D R N E R dR 0 ND NE N
第五章
三 铰 拱
拱的实例 三铰拱的特点
P1
H
l
三铰拱的类型、基本参数
P2
f H
VA
VB
f 1 10 l
曲线形状:抛物线、园、悬链线……..
§5-1
三铰拱的支座反力和内力
一、支座反力 与同跨度同荷载对应简支梁比较
a1
d P1 a2
D
b1
c
f l2 l
b2
P2
HB
MA 0
VB
1 Pa1 P2a2 1 l
q y C q B l/2 B x A
A
l/2
f
M x [解] 由式 y x H
ql 2
x
ql 2
先列出简支梁的弯矩方程
q M x x l x 2
拱的推力为:
M C ql 2 H f 8f
注意
*合理轴线对应的是
一组固定荷载; *合理轴线是一组。
所以拱的合理轴线方程为:
Q
o
P1
Mo
Q Q cos H sin N Q sin H cos
H
V
A
三、受力特点 (1)在竖向荷载作用下有水平反力 H; (2)由拱截面弯矩计算式可见,比相应简支梁小得多; (3)拱内有较大的轴向压力N.
q=2kN .m y
2 1 0 A 3 4 5 6
15kN m .
tg 2 4 f 2x 1 l l
x 3
4 4 2 3 1 12 12
Q2 Q2 cos 2 H sin 2 11 2 3 0.832
0.667
7.5 0.555 0.0025kN 0.003kN
VB VB
VA VA
HA
y
MB 0
VA
x
VA
1 Pb1 P2b2 1 l
l1
x 0
VB
H A HB H
P1 d
P1
P2
c
H
MC 0
VA l1 P d H f 0 1
MC MC H f 0 H f
P=8kN
例 1、三铰拱及其所受荷载如
图所示拱的轴线为抛物线方程
7 8
2 y2 x
f=4m
B
7.5kN
x2=3m VA 11kN 3m 6m 6m
H 7.5kN VB 9kN
4f y 2 x l x l 制内力图。
计算反力并绘
(1)计算支座反力
269 83 11kN 12 2 6 38 9 VB VB 9 kN 12
对拱结构而言,任意截面上弯矩计算式子为:
M M Hy
它是由两项组成,第一项是简支梁的弯矩,而后一项与拱轴形状 有关。令
M M Hy 0
M x yx H
在竖向荷载作用下,三铰拱的合理轴线的纵标值与简支梁 的弯矩纵标值成比例。
例1、设三铰拱承受沿水平方向均匀分布的竖向荷载,求其合理轴线。
RA
大小和方向 o
RA
D
23
P1
M D R12 rD
N D R12 cos D
RB
索多边形 合力多边形 压力多边形 压力线
P2 QD R12 sin D
P3
如果是分布荷载,压力线
呈曲线,称为压力曲线;如果
RB
是集中荷载,压力线呈多边形,
称压力多边形。
压力线可以描述拱的工作状况。各截面合力R若都沿拱轴切线方向作用是最
y x A ch
x B sh
x
Q
M
N
R
e
拱截面一般承受三种内力:M、Q、N。 若用合力 R 代替截面所有内力,则其偏心距为e = M/N, 显然我们可以求出各个截面的合力大小、方向和作用点。
P1
作用线
P2
G
rD
P3
H
F
A
(1)确定各截面合力的 大小和方向: 数解 RA RB
绘力多边形
k1
D
k2 C
k3
B
射线
(2)确定各截面合 力的作用线
这表明拱在法向均布荷载作用下处于无弯矩状态时,截面的轴力为一常数。
y0
q dS 2 N sin
d 0 2 N qR来自q Rd N d 0
R
N q
因N为一常数,q也为一常数,所以任一点的曲率半径R也是常数,即拱轴为园弧。
例3、设三铰拱上承受填土荷载,填土表面为一水平面,试求拱的合理轴线,设 填土的容重为,拱所受的分布荷载为 [解]由拱截面弯矩计算式
