6-3无交互作用双因素方差分析
双因素试验的方差分析
i 1
j 1
要判断因素A，B及交互作用AB对试验结果是否 有显著影响，即为检验如下假设是否成立：
H01 :1 2 a 0
H02 : 1 2 b 0
H03 : ij 0 i 1, 2, , a; j 1, 2, ,b
➢ 总离差平方和的分解定理 仿单因素方差分析的方法，考察总离差平方和
a
Ti.2
b,
i1
p T 2 ab ,
DB
b
T.
2 j
a,
j1
ab
R
X
2 ij
i1 j1
例1 设甲、乙、丙、丁四个工人操作机器Ⅰ、Ⅱ、Ⅲ各一天， 其产品产量如下表，问工人和机器对产品产量是否有显著 影响？
机器 B 工人 A
ⅠⅡ
Ⅲ
甲
50 63 52
乙
47 54 42
丙
47 57 41
F值
F 值临介值
因素A 因素B
SS A SSB
df A
MS A
SS A df A
FA
MS A MSE
df B
MSB
Байду номын сангаас
SSB df B
FB
MSB MSE
F (a 1 ,
ab n 1) F (b 1 ,
ab n 1)
A B
误差 总和
SS AB
SSE SST
df AB df E dfT
MS AB SS AB
F0.01 3,6 9.78 F0.05 3,6 4.76 F0.01 2,6 10.92
FB F0.01 2,6
结论：工人对产品的产量有显著影响， 机器对产品的产量有极显著影响。
补充：双因素方差分析
2. 各个总体的方差必须相同 对于各组观察数据，是从具有相同方差的总体中抽
取的
3. 观察值是独立的
无交互作用的双因素方差分析 (无重复双因素分析)
【例】有4个品牌的彩电在5个地区销售，为分析彩电的品牌( 品牌因素)和销售地区 (地区因素)对销售量的影响，对每显著 个品牌在各地区的销售量取得以下数据。试分析品牌和销售 地区对彩电的销售量是否有显著影响？(=0.05)
结论：
SS 13004.6 2011.7 2872.7 17889
df 3 4 12 19
MS
F
P-value
F crit 3.2592
4334.85 18.1078 9.46E-05 3.4903 502.925 2.10085 0.14367 239.392
FR＝18.10777>F＝3.4903，拒绝原假设H0，说明彩
SSR SSC
SSRC SSE SST
k-1 r-1
MSR MSC
FR FC
FRC
列因素
交互作用 误差 总和
(k-1)(r-1) MSRC kr(m-1)
MSE
m为样本的行数
n-1Biblioteka 练习：一家管理咨询公司为不同的客户进行人力资源管理讲座。 每次讲座的内容基本上是一样的，但听课者有时是高级管理者， 有时是中级管理者，有时是低级管理者。取水平0.05，检验管 理者的水平不同是否会导致评分的显著性差异。
电的品牌对销售量有显著影响
FC＝2.100846< F＝3.2592，不拒绝原假设H0，无证
据表明销售地区对彩电的销售量有显著影响
有交互作用的双因素方差分析
(可重复双因素分析)
无交互影响的双因素方差分析
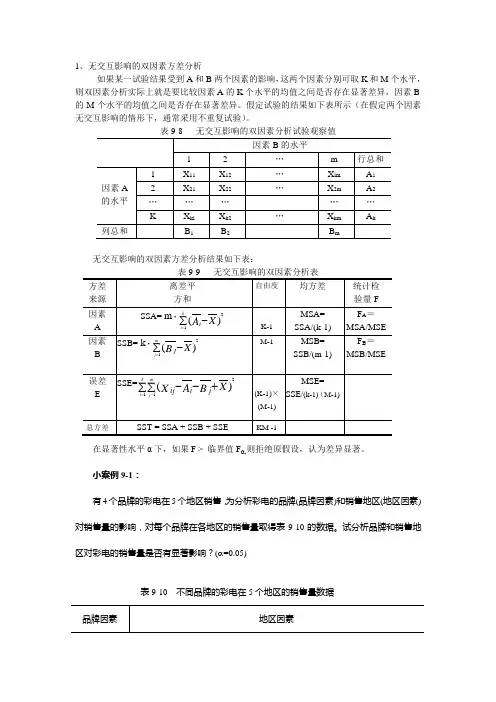
1、无交互影响的双因素方差分析如果某一试验结果受到A和B两个因素的影响，这两个因素分别可取K和M个水平，则双因素分析实际上就是要比较因素A的K个水平的均值之间是否存在显著差异，因素B 的M个水平的均值之间是否存在显著差异。
假定试验的结果如下表所示（在假定两个因素无交互影响的情形下，通常采用不重复试验）。
表9-8 无交互影响的双因素分析试验观察值无交互影响的双因素方差分析结果如下表：表9-9 无交互影响的双因素分析表在显著性水平α下，如果F > 临界值Fα,则拒绝原假设，认为差异显著。
小案例9-1：有4个品牌的彩电在5个地区销售，为分析彩电的品牌(品牌因素)和销售地区(地区因素)对销售量的影响，对每个品牌在各地区的销售量取得表9-10的数据。
试分析品牌和销售地区对彩电的销售量是否有显著影响？(α=0.05)表9-10 不同品牌的彩电在5个地区的销售量数据提出假设：对品牌因素提出的假设为：H0：m1=m2=m3=m4 (品牌对销售量无显著影响)H1：mi (i =1,2, …, 4) 不全相等(有显著影响)对地区因素提出的假设为：H0：m1=m2=m3=m4=m5 (地区对销售量无显著影响)H1：mj (j =1,2,…,5) 不全相等(有显著影响)表9-11 方差分析表结论：F品牌＝18.10777>Fα＝3.4903，拒绝原假设H0，说明彩电的品牌对销售量有显著影响。
F地区＝2.100846<Fα＝3.2592，不拒绝原假设H0，无证据表明销售地区对彩电的销售量有显著影响。
资料来源：贾俊平、何晓群、金勇进，《统计学》[M].北京: 中国人民大学出版社,2004.10第2版。
交互作用双因子方差分析
若H01 成立，即1 2 r 0 ，那么，虽然 不能苛求做为诸i 的估计值之平方和的若干倍的S A2
rst
r
（ xi•• x 2 st xi•• x 2 ）恰好等于零，
i1 j1 k 1
i 1
但相对于SE 2
来说一定不应太大，倘若S A2 SE2
超过某个界
限值k1 ，我们就有理由拒绝H01 ，故
后的剩余部分，称为水平组合 Ai , B j 的交互效应。
第7页/共35页
于是 X ij ~ N uij , 2 可以等价的表示为：
X ij uij ij u i j ij ij
ij ~ N 0, 2
， i 1,2,, r; j 1,2,, s
这表明，在因素 A, B 的不同水平组合下，试验结果的相对差异
1 rs
r i1
s
uij ——理论总均值
j 1
记：ui•
1 s
s
uij —因素A在i水平下的理论平均
j 1
记：u• j
1 r
r i 1
uij —因素B在j水平下的理论平均
第6页/共35页
显然
uij u ui• u u• j u uij ui• u• j u 记：i =ui• u
SE2 就基本上刻划了整个试验中随机因素作用的强 度，以它为尺度来比较各种效应的大小应该说是合理
的。
第15页/共35页
从矩估计的角度看， x 、xi•• 、x• j• 、 xij• 分别是 u 、ui• 、u• j 、uij 的估计值，因此， xi•• x 可作为i ui• u 的估计值； x• j• x 可作为 j u• j u 的估计值； xij• xi•• x• j• x 可作为rij uij ui• u• j u 的 估计值。
(整理)53双因素方差分析.
§5.3 双因素方差分析I 无交互作用的双因素方差分析(1) 数学模型 现在考虑影响试验指标的因素有两个：A, B 。
因素A 有水平r 个；有水平s 个；因素A, B 的各种组合水平均只作一次试验；两因素之间无交互作用。
数据结构表假设：(1*) {:1;1}ij Y i r j s ≤≤≤≤独立；(2*) 2~(,)ij ij Y N μσ，即具有相同的方差；(3*)ij ij ij Y e μ=+，其中 2~(0,)ij e N σ，且{}ij e 独立； 数学模型： i j i j ij i jY e μαβγ=++++ ， 其中：111()r s ij i j rs μμ-===∑∑—总平均值； 11si i j j s μμ-⋅==∑;11rj iji r μμ-⋅==∑;i i αμμ⋅=-—因素A 在水平Ai 下对试验指标的效应值；j j βμμ⋅=-—因素B 在水平Bj 下对试验指标的效应值；10r i i α==∑; 10s j j β==∑;rA1212s s r r rs Y Y Y Yr Y ⋅12..s Y Y Y ⋅⋅⋅i j i j i i γμμαβ=---—因素A, B 的交互效应值；{}ij e —随机部分，假定：独立同正态分布；注： “无交互作用”等价于：0ij γ=，即ij i i μμαβ=++；(2) 方差分析(i) 假设检验问题 两种因素分别进行检验：0112:0r H ααα====即因素A 对试验指标影响不显著；0212:0s H βββ====即因素B 对试验指标影响不显著；注：当01H 和02H 成立时，,(1;1)ij i r j s μμ=≤≤≤≤.(ii) 构造F-统计量及否定域 设()111r siji j Y rs Y-===∑∑；11si ij j Y s Y -⋅==∑；11rj ij i Y r Y -⋅==∑；2211()rsT ij i j S Y Y ===-∑∑；221()rA i i S s Y Y ⋅==-∑；221()sB j j S r Y Y ⋅==-∑；2211()rsE ij i j i j S Y Y Y Y ⋅⋅===--+∑∑；注：注意，2211()rsE ij i j i j S Y Y Y Y ⋅⋅===--+∑∑211()r sij ij i i j j i j e e e e μμμμ⋅⋅⋅⋅===+----++∑∑ 211[()()]rsij i j ij i j i j e e e e μμμμ⋅⋅⋅⋅===--++--+∑∑211()rsij i j i j e e e e ⋅⋅===--+∑∑.这里利用了“无交互效应”的假设条件：0i j i j i jγμμμμ⋅⋅=--+=.由此可见，2E S 与α⋅及β⋅无关，即与假设01H 和02H 是否成立无关。
交互作用双因子方差分析
H 03 的 拒 绝 域 为
W 03
S A SE
B 2
2
k3
（6.35）
为 了 确 定 界 限 值 k1 、k 2 、k3 ， 按 照 显 著 性 检 验 的 一 般
步骤，我们需要知道当相应的原假设成立时各检验统
计量的分布，
可以证明，
在 H 01 成 立 时
S A 2 r 1 ~ F r 1, rs t 1 S E 2 rs t 1
后的剩余部分，称为水平组合
Ai,Bj 的交互效应。
于 是 X ij ~ N u ij , 2 可 以 等 价 的 表 示 为 ：
X ij u ij ij u i j ij ij
ij ~ N 0, 2
，
i 1,2, , r ; j 1,2, , s
这 表 明 ， 在 因 素 A, B 的 不 同 水 平 组 合 下 ， 试 验 结 果 的 相 对 差 异 u ij u （ 视 为 总 效 应 ） 是 由 如 下 四 部 分 组 成 ：
i 1 j 1 k 1
S
2 A
r
s
t
x i•• x 2
A
称为因素 的主效应偏差平方和。
i 1 j 1 k 1
S
2 B
r
s
t
x • j• x 2
B
称为因素 的主效应偏差平方和。
i 1 j 1 k 1
S 2 A B
rst
A B
x ij • x i • • x • j • x 2 称 为
的交互效应
i1 j1 k 1
偏差平方和。
则得到总变差平方和的分解式：
ST 2
SE2
SA2
SB2
商务统计学 8.6 无交互作用双因素方差分析问题描述
无交互作用双因素方差分析应用实例
【例】企业订单的多少直接反映了企业生产的产品畅销程度，因此 企业订单数目的增减是企业经营者所关心的。一家企业经营者为了研 究产品的销售地区及外观设计对月订单数目的影响，记录了一月中不 同外观设计的一种产品在不同地区的订单数据。以此为基础，该经营 者想检验下这种产品的销售地区与外观设计是否对订单的数量有所影 响？
bj j
k
ai 0
i 1
j 1, 2,..., r
r
bj 0
j 1
无交互作用双因素方差分析问题描述
定义 ij ai bj (ij i j )
i 1, 2,..., k
水平 Ai 和水平 Bj 的交互效应
j 1, 2,..., r
(ab)ij ij i j
无交互作用双因素方差分析应用实例
因素
表 不同外观设计的产品在不同地区的订单数 （张）
外观设计 销售地区
北京 上海 深圳 西安 成都 兰州
设计方案I 700 597 697 543 600 618
设计方案II 516 450 357 552 302 389
设计方案III 720 567 515 560 420 502
无交互作用双因素方差分析问题描述
1.无交互作用双因素方差分析应用实例 2.无交互作用双因素方差分析问题描述
双因素方差分析
双因素方差分析（Two-way Analysis of Variance） 用来研究两个因素对因变量取值是否会产生显著影响。
6-3无交互作用双因素方差分析-精选文档
F值 Fcale
4.34 0.36
F临界值 Fcrif
6.94 6.94
11
6）查F0.05(2,4)对应的F分布表，得Fcrit=6.94
7）比较FA和Fcrit，因为FA<Fcrit，因此无法拒绝零假设H0； 比较FB和Fcrit，因为FB<Fcrit，因此无法拒绝零假设H0；
射出压力不同水平设置对应的成形品尺寸均值无 显著差异，模腔温度不同水平设置对应的成形品 尺寸均值无显著差异。 8)计算各因素及残差对输出的影响-----贡献率分析 通过计算各因素及残差对因变量y的影响，可以 更直观理解因素对输出影响的重要度
7
1、将实际问题转化为统计问题。 转化的统计问题为：射出压力不同设置水平 时成形品尺寸是否相同：模腔温度不同水平设置对 成形品尺寸均值是否相同。 2、建立假设。 H0：μA1=μA2=μA3；μB1=μB2=μB3 Hα：至少有一个μAi与其它不等；至少一个μBi 与其他不等 3、确定可接受的α风险系数 α=0.05 4、进行方差分析 根据本节所讲的双因素无交互作用方差公 式，我们首先需计算SST、SSA、SSB、SSe， 然后用方差分析表进行分析即可。
12
SS SS A B R ( ) 100% 64.7% R ( ) 100% 5.4% A B SS SS T T SS e R ( ) 100% 64.7% e SS T R 为 A, B 因素和残差占总体平方 和的比率
13
2）将影响作饼图表示如下： 更能直观的观察各个因素及残差对输出的影响。
r s
2 SS ( x x ) 1 . 051 ij T i 1j 1
10
4）计算SSe。
SSe=SST-SSA-SSB=0.314
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
12
SS A SS B RA ( ) 100% 64.7% R B ( ) 100% 5.4% SS T SS T SS e Re ( ) 100% 64.7% SS T R 为 A,B因素和残差占总体平方 和的比率
13
2）将影响作饼图表示如下： 更能直观的观察各个因素及残差对输出的影响。
6
4.双因素无交互作用方差分析案例 在注塑成形过程中，成形品尺寸与射出压力和模 腔温度有关，某工程师根据不同水平设置的射出 压力和模腔温度式样得出某成形品的关键尺寸如 下表，用方差分析两个因素对成形品关键尺寸是 否存在重要影响。
因素A：射出压力 水平1 水平2 水平3 水平1 30.51 30.47 30.84 因素B 水平2 30.97 30.29 30.79 模腔温度 水平3 30.99 29.86 30.62
SS T (x ij x) 2 1.051
i 1 j1
r
s
10
4）计算SSe。
SSe=SST-SSA-SSB=0.314
5）讲计算结果填入方差分析表格。
方差来源 SOV
A因素影响 B因素影响 误差影响 总和
平方和 自由度 均方和 SS df MS
0.681 0.057 0.314 1.052 2 2 4 8 0.34 0.028 0.078
7.3.1 无交互作用双因素方差分析
1
1.数据结构
如果知道因素A 与因素B不存在交互作用，或交互 作用不明显，可以忽略不计，此时仅仅分析因素A 与因素B各自对试验的影响是否显著 安排在试验时，对因素A与因素B的每一种水平组 合，就只需要安排一次试验，这样就可以大大减 少试验的次数，相应的数据结构如下：
16
2
3
在无交互作用的双因素方差分析模型中因 变量的取值受四个因素的影响：总体的平 均值；因素A导致的差异；因素B导致的差 异；以及误差项。写成模型的形式就是：
ìï x = m+ a + b + e (可加性假定) ïï ij i j ij ïï r s ï bj = 0 (约束条件) í 邋a i = 0 , ïï i= 1 j= 1 ïï ïï eij N (0, s 2 ) i = 1,2,, r; j = 1,2,, s (独立性、正态性、方差齐性假定) ïî
因素A 因素B 残差
14
小结 (1)
1、方差分析（ANOVA），一般用来分析一个定 量因变量与一个或几个定性自变量（因素）之间 的关系，它可以同时对多个总体的均值是否相等 进行整体检验。 2、根据研究所涉及的因素的多少，方差分析可分 为单因素方差分析和多因素方差分析（包括双因 素方差分析）。
2 i= 1 r s
r
s
2
( xj - x) + 邋 ( xij i= 1 j = 1
2
r
s
xi - x j + x) xi - x j + x)
2
j= 1 2 s 2
= s 邋( xi - x) + r
i= 1
r
( xj - x) + 邋 ( xij i= 1 j = 1
4
2.离差平方和的分解 SS = 邋 ( x - x )
r s 2 T ij i= 1 j = 1
= 邋 轾i - x) + ( x j - x) + ( xij - xi - x j + x) (x 犏 臌 i= 1 j = 1 = s 邋( xi - x) + r
F值 Fcale
4.34 0.36
F临界值 Fcrif
6.94 6.94
11
6）查F0.05(2,4)对应的F分布表，得Fcrit=6.94
7）比较FA和Fcrit，因为FA<Fcrit，因此无法拒绝零假设H0； 比较FB和Fcrit，因为FB<Fcrit，因此无法拒绝零假设H0；
射出压力不同水平设置对应的成形品尺寸均值无 显著差异，模腔温度不同水平设置对应的成形品 尺寸均值无显著差异。 8)计算各因素及残差对输出的影响-----贡献率分析 通过计算各因素及残差对因变量y的影响，可以 更直观理解因素对输出影响的重要度
r
s
2
j= 1
= SSA + SSB + SSE
SSA SSB SST SSE
5
3.无交互作用的双因素方差分析表
变差 来源 A因素 B因素 误 差 离差平方 和 SS SSA SSB SSE 自由度 df 均方 MS F值
合 计
SST
MSA=S FA=MSA/MS r-1 SA/(r-1) E MSB=S FB=MSB/MS s-1 SB/(s-1) E MSE=S (r-1)(s-1) SE/(r1)(s-1) rs-1
8
1）计算SSA。SSB
SS A Q1 s ( x i x)
i 1 r 2
SS B r ( x j x) 2
j1
s
x 总平均值
r 因素 A 的水平数
s 因素 B的水平数
本例中：s 3；r 3；x 30.59 x i 计算如下：
A因素水平 xi Xi平均值 1 2 3 B因素水平 Yj Yj=平均值 1 2 3
7
1、将实际问题转化为统计问题。 转化的统计问题为：射出压力不同设置水平 时成形品尺寸是否相同：模腔温度不同水平设置对 成形品尺寸均值是否相同。 2、建立假设。 H0：μA1=μA2=μA3；μB1=μB2=μB3 Hα：至少有一个μAi与其它不等；至少一个μBi 与其他不等 3、确定可接受的α风险系数 α=0.05 4、进行方差分析 根据本节所讲的双因素无交互作用方差公 式，我们首先需计算SST、SSA、SSB、SSe， 然后用方差分析表进行分析即可。
30.51 30.47 30.84
30.97 30.29 30.79 30.99 29.86 30.62 30.82 30.21 30.75
30.51 30.97 30.99
30.47 30.29 29.86 30.84 30.79 30.62 30.61 30.68 30.49
9
1）代入SSA计算式，得 SSA=3*[(30.82-30.59)2+ (30.2130.59)2+ (30.75-30.59)2]=0.681 2）计算SSB。 SSB= 3*[(30.61-30.59)2+ (30.68-30.59)2+ (30.49-30.59)2]=0.057 3）计算SST。
3、方差分析中的基本假设是，来自各个总体的数 据都服从正态分布，相互独立，且有相同的方差。
15
小结 (2)
4、方差分析的基本思想是，将观察值之间的总变 差分解为由所研究的因素引起的变差和由随机误差 项引起的变差，通过对这两类变差的比较做出接受 或拒绝原假设的判断的。 5、方差分析的主要步骤包括：建立假设；计算F检 验值；根据实际值与临界值的比较做出决策。 6、在方差分析中，当拒绝H0时表示至少有两个均 值有显著差异。但要知道哪些均值之间有显著差异 还需要借助于多重比较的方法，例如LSD方法。