CH7数学物理定解问题
合集下载
数学物理方法 7 数学物理方程的定解问题

q xdx
y
dy
负号表示扩散方向与浓度梯度方向相反
( x, y, z ) dx
x
q q d x d y d z , dxdydz 同理沿y 和沿z方向净流入量 y z 单位时间内向V的净流入量 q dxdydz q dxdydz q dxdydz x y z u 单位时间内V内粒子数的增加量 dxdydz t
泊松方程
3 u 0
2019/2/26
拉普拉斯方程
18
例1 热传导
热传导现象:当导热介质中各点的温度分布不均匀时,有 热量从高温处流向低温处。 数学建模: 所要研究的物理量: 温度
u( x, y, z, t )
设定: 温度不均匀: 用温度梯度u 表示;
传热的强弱即热流强度:用单位时间内通过单 位面积的热量 q 表示;
三、定解问题
特殊性,即个性。
泛定方程:不带有边界和初始条件的方程称为泛定方程。
2019/2/26 5
它反映了问题的共性。
5
具体问题求解的一般过程:
1、根据系统的内在规律列出泛定方程——客观规律. 2、根据已知系统的边界状况和初始状况列出边界条件和 初始条件——求解所必须的已知条件.
6
3、求解方法 —— 行波法、分离变量法、积分变换法、格林 函数法和变分法
物理规律:采用傅里叶实验定律
傅里叶定律:
q k u
热传导系数
u ˆ n 沿曲面法向流出热量:qn k n
2019/2/26 19
处理方法:在温度不均匀的无源空间,划出任一封闭曲面S包 围的体积元V(如图)。 ①在S 上选取任一足够小的微面元dS,在此 面元范围内热流强度近似为常量。
T2 cos 2 T1 cos 1
数值分析Ch7

2
f (xi , yi )
0
言
Numerical Analysis
M. H. Xu
二 理论基础 定理 7. 1 若f (x, y )在区 域 D = {(x, y )|a ≤ x ≤ b, |y | < ∞} 内连 续, 关于 y 满足 Lipschitz条件 , 即 存在 常数 L > 0, 对 任意 y1 , y2 , 不 等 式 |f (x, y1 ) − f (x, y2 )| ≤ L|y1 − y2 | 对所 有的 x ∈ [a, b]成立 , 则 初值 问题 dy = f (x, y ), a ≤ x ≤ b dx y (a) = y
Numerical Analysis
M. H. Xu
§7. 2 Euler方法与梯 形方 法 一 方法导出 由微分方程知 y (xi ) = f (xi , y (xi )), 用差商
y0 y yi y=y(x) yi+1 yn
y (xi+1 ) − y (xi ) h 近似 导数 y (xi )可 得 y (xi+1 ) ≈ y (xi ) + hf (xi , y (xi ))
0
在区 间[a, b]上有 唯 一解 y (x), 并且 y (x)为 连续 可微 的, 解函 数y (x) 连续 地依 赖于 初值 及f (x, y ).
Numerical Analysis
M. H. Xu
三 数值解法的基本步骤 第一 步: 把区 间[a, b]进行 划分 , 通 常进 行n等 分, 节点 xi = a + ih, i = 0, 1, 2 · · · , n, 其中 h = (b − a)/n; 第二 步: 求y (x)在节 点xi 处 函数 值y (xi )的近 似值 yi , 得 一列 表 函数 ; 第三 步: 根据 需要 可由 插值 方法求得 函数 y (x)在 x处的 近似 值, 或 由 列表 函数 求得 y = y (x)的近 似函 数. 说明 : 数值 解法 的关 键在 于如 何由 y0 得到y (x1 )的近 似值 y1 , 一 般地 , 如何 由y (xi )的近 似值 yi 得到y (xi+1 )的近 似值 yi+1 .
f (xi , yi )
0
言
Numerical Analysis
M. H. Xu
二 理论基础 定理 7. 1 若f (x, y )在区 域 D = {(x, y )|a ≤ x ≤ b, |y | < ∞} 内连 续, 关于 y 满足 Lipschitz条件 , 即 存在 常数 L > 0, 对 任意 y1 , y2 , 不 等 式 |f (x, y1 ) − f (x, y2 )| ≤ L|y1 − y2 | 对所 有的 x ∈ [a, b]成立 , 则 初值 问题 dy = f (x, y ), a ≤ x ≤ b dx y (a) = y
Numerical Analysis
M. H. Xu
§7. 2 Euler方法与梯 形方 法 一 方法导出 由微分方程知 y (xi ) = f (xi , y (xi )), 用差商
y0 y yi y=y(x) yi+1 yn
y (xi+1 ) − y (xi ) h 近似 导数 y (xi )可 得 y (xi+1 ) ≈ y (xi ) + hf (xi , y (xi ))
0
在区 间[a, b]上有 唯 一解 y (x), 并且 y (x)为 连续 可微 的, 解函 数y (x) 连续 地依 赖于 初值 及f (x, y ).
Numerical Analysis
M. H. Xu
三 数值解法的基本步骤 第一 步: 把区 间[a, b]进行 划分 , 通 常进 行n等 分, 节点 xi = a + ih, i = 0, 1, 2 · · · , n, 其中 h = (b − a)/n; 第二 步: 求y (x)在节 点xi 处 函数 值y (xi )的近 似值 yi , 得 一列 表 函数 ; 第三 步: 根据 需要 可由 插值 方法求得 函数 y (x)在 x处的 近似 值, 或 由 列表 函数 求得 y = y (x)的近 似函 数. 说明 : 数值 解法 的关 键在 于如 何由 y0 得到y (x1 )的近 似值 y1 , 一 般地 , 如何 由y (xi )的近 似值 yi 得到y (xi+1 )的近 似值 yi+1 .
数学物理方法-第七章 数学物理方程的定解问题-文档资料
u dxdydz t
二者相等得连续性方程
u (uv x ) 0 t x
q u dxdydz dxdydz x t
表示物质的总量守恒
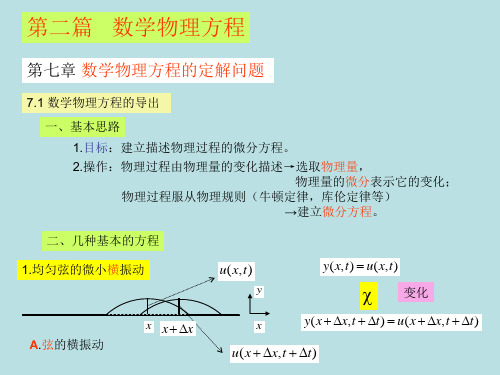
3.流体力学与声学方程 A.连续介质性质: 当振动在液体和气体中传播时,液体和气体就成为传播振动 的连续介质。在其中取一个小的立方体,可以定义介质在此 的密度 ρ,速度 v 和压强 P。 振动引起密度的疏密变化。
d2y f m 2 m ytt m utt dt
T2 sin 2 T1 sin 1 ( dx)utt
小振动:
1 0, 2 0, cos1 1, cos 2 1.
sin 1 tan 1 u x
x
ux
x
sin 2 tan2 ux
不含时的解满足方程
( )u 0 u
此为拉普拉斯方程。即稳定的浓度分布和温度分布,其浓度和温度满足 拉普拉斯方程。
8.真空静电场 高斯定理
D dS dV
S V
D 0 E
V
1 E dV
0 V
dV
1 E
又 真空还有 最后: 9.薛定谔方程
p p0 (
) p0 (1 s) p0 (1 s) 0
p vt 0 s
1 vt p
0
p p0 (1 s)
0
p vt 0 s
0
st v 0
stt a 22 s 0
a2
系统的温度
能量守恒,满足连续性方程 傅立叶定律:
q ku
q 热流强度 :单位时间通过单位面积的热量。
图的基本概念 无向图及有向图

d (v4)=4
d (v5)=2
31
最大(出/入)度,最小(出/入)度
在无向图G中, 最大度: Δ(G) = max{ dG(v) | v∈V(G) } 最小度: δ(G) = min{ dG(v) | v∈V(G) } 在有向图D中, 最大出度: Δ+(D) = max{ dD+(v) | v∈V(D) } 最小出度: δ+(D) = min{ dD+(v) | v∈V(D) } 最大入度: Δ-(D) = max{ dD-(v) | v∈V(D) } 最小入度: δ-(D) = min{ dD-(v) | v∈V(D) } + + - 简记为Δ, δ, Δ , δ , Δ , δ
i 1
i
证明 必要性。由握手定理显然得证。 充分性。由已知条件可知,d中有偶数个奇数 度点。 奇数度点两两之间连一边,剩余度用环来实现。
5 3
3
1
例7.1: 1. (3, 3, 2, 3), (5, 2, 3, 1, 4)能成为图的度 数序列吗?为什么? 2. 已知图G中有10条边,4个3度顶点,其余顶点的 度数均小于等于2,问G中至少有多少个顶点?为 什么? 解: 1.由于这两个序列中,奇数度顶点个数均为奇数, 由握手定理的推论可知,它们都不能成为图的度 数序列。 2.显然,图G中的其余顶点度数均为2时G图的顶点 数最少. 设G图至少有x个顶点. 由握手定理可知, 3×4+2×(x-4)=2 ×10 解得: x=8 所以G至少有8个顶点。
度数列举例
按顶点的标定顺序,度数列为 4,4,2,1,3。
度数列举例
按字母顺序, 度数列:5,3,3,3 出度列:4,0,2,1
CH7数学物理定解问题

• u
u
-----此即泊松方程 若所讨论区域无电荷,则为
u 0 -----laplace方程
四、方程的分类
11
1.数学物理方程的一般形式 a11u xx 2a12u xy a22u yy b1u x b2u y cu f 0
其中 a11 , a12 , a22 , b1 , b2 ,c,f 只是 x,y 的函数
描写微观粒子运动的 Schrodinger 方程和 Dirac 方程
等等 2
第七章 数学物理定解问题
重点
1、定解问题的概念 2、系统的边界条件和初始条件的写法; 3、行波法研究一维波动方程解的方法和解的表示
形式、以及解的物理意义。
3
第七章 数学物理定解问题
一、数学物理方程
数学物理方程是从物理问题中导出的反映客观物理量在各 个地点、各个时刻之间相互制约关系的数学方程。换言之, 是物理过程的数学表达。如 牛顿定律、热传导定律、热量守 恒定律、电荷守恒定律、高斯定律、电磁感应定律、胡克定 律。
以热传导方程(或输运方程)为代表的方程
ut a2u f
它主要描述扩散过程和热传导以及物质传输过程所满足的规律
14
双曲型方程和抛物型方程都是随时间变化(或发展)的, 有时也称为发展方程
3)椭圆型方程(Elliptic Equation.)
以泊松方程为代表的方程
u f (x, y, z)
当 f (x, y, z) 0, 即退化为拉普拉斯方程
有一个初始条件
二阶含时偏微分方程
ut a2u 0
有两个初始条件
u( x, y, z) |t0 f ( x, y, z)
16
utt a 2uxx 0 u( x, y, z, t) |t0 f1( x, y, z) ut ( x, y, z, t) |t0 f2 ( x, y, z)
数学物理方法姚端正CH7作业解答

uΙ =
1 x+t sin αdα = sin x sin t 2 ∫x − t 1 t 2 ∫0
t 0
由无界纯强迫振动解的公式,得
u ΙΙ =
∫
x + ( t −τ )
x − ( t −τ )
τ sin αdαdτ =
1 t {cos[ x − (t − τ )] − cos[ x + (t − τ )]}τdτ 2 ∫0
t 0
= ∫ sin x sin( t − τ )τdτ = sin x ∫ sin( t − τ )τdτ = t sin x − sin x sin t
(上式最后一步用了分部积分法) 则 u = u + u = t sin x
Ι ΙΙ
3
utt − a 2u xx = x (3) u ( x,0) = 0 u ( x,0) = 3 t
① ② ③
① 即 f1 ( x) − f 2 ( x) = −ϕ ( x) ②
解:方程 utt = u xx 的通解为: u ( x, t ) = f1 ( x + t ) + f 2 ( x − t ) 将④式代入定解条件②得: f1 (0) + f 2 (2 x) = ϕ ( x )
④
⑤
1
将④式代入定解条件③得:
2
u xx − u yy = 8 (2) u ( x,0) = 0 u ( x,0) = 0 y 解:由冲量原理,原定解问题可转化为以下定解问题: v yy − vxx = 0 v( x,τ ) = 0 v ( x,τ ) = −8 y 由 D ' Alembert 公式,该问题的解为: v( x, y;τ ) = 1 x + a ( y −τ ) − 8dα =8τ − 8 y 2 ∫x − a ( y −τ )
07_定解问题
叠加原理:如果泛定方程和定解条件都是线性的,可以把定 解问题的解看作几个部分的线性叠加,只要这些部分各自所 满足的泛定方程和定解条件的相应的线性叠加正好是原来的 泛定方程和定解条件即可。 I 2 I
例:下面的定解问题
utt a u xx f ( x, t ) I u |x 0 0; u I |x l 0 u I | 0; u I | 0 t t 0 t 0
2
sin 1 tan 1 ux ( x0 0, t ) sin 2 tan 2 ux ( x0 0, t )
h
x0
0
x
u( x0 0, t ) u( x0 0, t )
衔接条件
Tux ( x0 0, t ) Tux ( x0 0, t ) F (t )
kun |xa h u |xa u |media (u Hun ) |xa u |media
左端点x=0,(u Hux ) |x0 u |media .
( 右端点x=a, u Hux ) |xl u |media .
例2:纵振动杆,端点x=a处与弹性体连接到固定物上
u u , t n
(1) 第一类边界条件 例:弦两端固定
u( x, t ) x0 u( x, t ) xl 0
u( x, t ) xa f (t )
细杆导热,x=a端温度为f(t)
一维杂质浓度扩散,x=0, l端浓度保持为N0
1 B1u B2u Cu F . u 2 A12
i Re ( ) / 2 , or . i Im ( ) / 2i
CH7 图的基本概念 1 无向图及有向图
关联与关联次数、环、孤立点
设D=<V,E>为有向图,ek=<vi,vj>∈E, 称vi,vj为ek的端点。 若vi=vj,则称ek为D中的环。 无论在无向图中还是在有向图中,无边关 联的顶点均称为孤立点。
相邻与邻接
设无向图G=<V,E>,vi,vj∈V,ek,el∈E。 若et∈E,使得et=(vi,vj),则称vi与vj是彼此相 邻的 若ek与el至少有一个公共端点,则称ek与el是彼此 相邻的。 设有向图D=<V,E>,vi,vj∈V,ek,el∈E。 若et∈E,使得et=<vi,vj>,则称vi为et的始点, vj为et的终点,并称vi邻接到vj,vj邻接于vi。 若ek的终点为el的始点,则称ek与el相邻。
握手定理
定理7.2 设有向图D=<V,E>, V = {v1, v2,…, vn},,|E|=m,则
d v d v m
i 1 i i 1 i
n
n
35
度数列
设G=<V,E>为一个n阶无向图,V={v1,v2,…,vn},称 d(v1),d(v2),…,d(vn)为G的度数列。 对于顶点标定的无向图,它的度数列是唯一的。 反之,对于给定的非负整数列d={d1,d2,…,dn},若存在V ={v1,v2,…,vn}为顶点集的n阶无向图G,使得d(vi)=di ,则称d是可图化的。 特别地,若所得图是简单图,则称d是可简单图化的。 类似地,设D=<V,E>为一个n阶有向图,V= {v1,v2,…,vn},称d(v1),d(v2),…,d(vn)为D的度数列 ,另外称d+(v1),d+(v2),…,d+(vn)与d-(v1),d-(v2), …,d-(vn)分别为D的出度列和入度列。
(完整版)经济数学CH7动态最优化:最大值原理
为了求解这个最优化问题,建立现值汉密尔顿函数: H(c,k,t,μ)=e-ρtlog(c)+μ(kα-c-δk)
2020/8/20
10
最优化的一阶条件为:
(1)Hc e-t (1/ c)-=0和(2)Hk ( k1 ) 横截性条件为:lim[(t)k(t)] 0
t
取式(1)的对数然后对时间求导,得到:
如果令ρ=0.06,δ=0且α=0.3,那么这个系统就是以前研
2020/8/20 究过的非线性系统。
11
四、多变量的动态最优化
❖ 现在考虑一个具有n个控制变量和m个状态变量的 更一般的动态问题。选择控制变量最大化:
T 0
u[k1
(t
),
...,
km
(t
);
c1
(t
),
...,
cn
(t
);
t
]dt,
2020/8/20
6
充分条件
如果函数f(k,c,t)和g(k,c,t)是凹函数,那么 满足上述四个条件的(k*,c*)和λ*>0,是最 优化问题的极大值。
如果是凸函数,则是极小值。 经济学中的生产函数和效用函数都是严格凹函
数,因此满足充分条件。
2020/8/20
7
三、现值和当期汉密尔顿函数
❖ 1、现值汉密尔顿函数
2020/8/20
当一国的资本发展变成了一 种赌博活动的副产品时,这项 活动可能是错误的。
—— 凯恩斯
1
导论
❖ 古典数学家使用的动态问题的解法是变分法。
❖ 这种方法从两条途径得以一般化: ❖ 第一条是美国数学家贝尔曼在20世纪50年代所
发展的动态规划方法。主要适用于离散时间和 随机模型。 ❖ 第二条是俄罗斯数学家庞特里亚金在50年代所 发展的最优控制的极大值原理。
随机过程Ch7 平稳过程的谱分析
2T
=
1 2
lim
4 T
1
T→∞ 2 T
|Fx(ω,T)|2dω
显然上式左边可以看做是x(t)消耗在1Ω电阻上的平均功 率,相应地,称右边的被积函数 lim |Fx(ω,T)|2 T→∞ 2 T 为功率密度. 以上讨论的是普通时间的实质函数的频谱分析,对于随 机过程{X(t),-≦<t<≦}可以作类似的分析.
T→∞ 2 T
E[X2(t)]dt T
T
=lim
T→∞
1 2T
[
T T
a
2
-
a
2
=
a
2
2
sin(2ω0t)]dt
.
2
以上讨论了平稳过程的谱密度,对于平稳随机序列的谱 分析,我们类似地给出以下结果.
平稳过程的谱密度
设{Xn,n=0,±1,±2,…}为平稳随机序列,均值为零.若 τ只取离散值,且相关函数RX(τ)满足 |RX(n)|<≦.当 n ω在[-π,π]上取值时,若 sx(ω)= RX(n)e-inω (△) n 绝对一致收敛,则sx(ω)是[-π,π]上的连续函数, 且对 上式取绝对值再积分,有 |sx(ω)|dω≤ |RX(n)| |e-inω|dω<≦, 故 sx(ω)einωdω存在.于是(△)是以 1 RX(n)= sx(ω)einωdω, n=0,±1,±2,…(△)
T→∞ 2 T
T
1
T
=RX(0). (◇) 由(◇)式和(◇)式看出,平稳过程的平均功率等于该过程 的均方值,或等于它的谱密度在频域上的积分,即 2= 1 S (ω)dω. ψ X
该式是平稳过程X(t)的平均功率的频谱展开式,sX(ω)描 述了各种频率成分所具有的能量大小. 例7.1 设有随机过程X(t)=acos(ω0t+Θ), a,ω0为常数,
=
1 2
lim
4 T
1
T→∞ 2 T
|Fx(ω,T)|2dω
显然上式左边可以看做是x(t)消耗在1Ω电阻上的平均功 率,相应地,称右边的被积函数 lim |Fx(ω,T)|2 T→∞ 2 T 为功率密度. 以上讨论的是普通时间的实质函数的频谱分析,对于随 机过程{X(t),-≦<t<≦}可以作类似的分析.
T→∞ 2 T
E[X2(t)]dt T
T
=lim
T→∞
1 2T
[
T T
a
2
-
a
2
=
a
2
2
sin(2ω0t)]dt
.
2
以上讨论了平稳过程的谱密度,对于平稳随机序列的谱 分析,我们类似地给出以下结果.
平稳过程的谱密度
设{Xn,n=0,±1,±2,…}为平稳随机序列,均值为零.若 τ只取离散值,且相关函数RX(τ)满足 |RX(n)|<≦.当 n ω在[-π,π]上取值时,若 sx(ω)= RX(n)e-inω (△) n 绝对一致收敛,则sx(ω)是[-π,π]上的连续函数, 且对 上式取绝对值再积分,有 |sx(ω)|dω≤ |RX(n)| |e-inω|dω<≦, 故 sx(ω)einωdω存在.于是(△)是以 1 RX(n)= sx(ω)einωdω, n=0,±1,±2,…(△)
T→∞ 2 T
T
1
T
=RX(0). (◇) 由(◇)式和(◇)式看出,平稳过程的平均功率等于该过程 的均方值,或等于它的谱密度在频域上的积分,即 2= 1 S (ω)dω. ψ X
该式是平稳过程X(t)的平均功率的频谱展开式,sX(ω)描 述了各种频率成分所具有的能量大小. 例7.1 设有随机过程X(t)=acos(ω0t+Θ), a,ω0为常数,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1)第一类边界条件:
直接给出系统边界上物理量的函数形式 u x , y , z f1 ( x0 , y0 , z0 , t )
0 0 0
对于一维:
u( x, t ) | x0 f1 (t )
比如:弦的两端固定 u( x, t ) | x 0 u( x, t ) | x l 0 若弦两端按某规律运动
s
1
d E d
9
所以
E
E u
u
u
-----此即泊松方程 若所讨论区域无电荷,则为
u 0
对于扩散方程
-----laplace方程
2
ut a u 0
当时间足够长,ut=0达到稳定状态,即浓度的稳定分布方程。
1、定义:由于某种原因,物理量在某些点上发生突变,则使 系统分为两部分或多部分,使偏微分方程为两部分或多部分。 每个部分都满足同样的偏微分方程,但在这点(或区域上) 对方程来说,相当于边界而又无法给出边界条件。
如右图的弦 ①连续性 u( x0 0, t ) =
u( x0 0, t )
1
F
t
3.三种典型方程的用途
12
1) 双曲型方程(Hyperbolic Equation)
以波动方程为代表的方程
utt a u、振动过程,或声波、 电磁波的传播规律. 2) 抛物型方程(Parabolic Equation): 以热传导方程(或输运方程)为代表的方程
u qx k x
u q x | xa k | xa 0 x u | xa 0 u x | xa 0 所以 x
x 热流
x
x+dx
19
例3、弦振动中,在x=a端为自由端。
u
T1
a1
自由端说明弦在x=a 处的受力
无垂直于x方向分量
x
B
a2
T2
x+dx
x
u | xa 0 F=T x u | xa 0 x
20
33)、第三类边界条件: (
u ( u+ h ) | x0 , y 0 , z 0 = f 3 ( x 0 , y 0 , z 0 , t ) n
例4:热传导的杆在x=a端自由冷却,自由冷却的意思是:
界面法向方向上的热流与杆端温度和环境的温差成正比
u u 和 的线性关系。 给出系统在边界上 u n
注意问题: (1)、衔接条件只是时间的函数 (2)、衔接条件常常由物理规律给出。
25
§7、4
达朗贝尔公式
定解问题
一 、达朗贝尔公式 1.问题的提出: 对于常微分方程我们常来用先求出通解,然后利用附 加条件给出通解中所含的常数,能否利用此方称来求 解偏微分方程呢?--针对特定的边界形状联合方程和 边界条件(分离变量法) 2. 将方程变为通过积分可得通解的形式 —针对无限大空间中波的初值问题(行波法) 若我们可将关于u(x,y)的偏微分 方程化为形式,
一、波动方程的导出
8
泊松方程 在充满了介电常数为ε的电解质,电荷的体密度为ρ(x,y,z), 研究该区域的静电场。 1.势函数u(x,y,z)是根本量,;
2.在所研究的区域中,任作一闭合曲面s,围出一空间τ, 由高斯定理:
E d s
s
1
d
因为 所以
E d E d s
5
定解条件:边界条件和初始条件的总体。它反映了问题的 特殊性,即个性。
泛定方程:不带有边界他条件的方程称为泛定方程。
它反映了问题的共性。 具体的问题的求解的一般过程: 1、根据系统的内在规律列出泛定方程
——客观规律
2、根据已知系统的边界状况和初始状况列出边界条件和
初始条件
——求解所必须用的
6
3、求解方法 —— 行波法、分离变量法、积分变 换法、格林函数法、保角变换法
u( x, t ) f1 ( x at ) f 2 ( x at )
2、通解的物理意义: 若 f 2 ( x) 是波在t=0时的波形。选定坐标系,以速度a沿x 正向移动,
, 即退化为拉普拉斯方程
它是描述物理现象中稳定过程规律的偏微分方程.在物理 现象中,它很好地描述了重力场、静电场、静磁场、稳恒流 的速度势等规律.
14
§7、2 定解条件
一 初始条件 :
1.定义: 是对所研究系统的在开始计时时刻的系统状态初 始分布
2.初始条件的特征: 偏微分方程的阶数对应于初始条件中的数目: 一阶含时偏微分方程 有一个初始条件 二阶含时偏微分方程
ut a 2 u 0
u( x, y, z) |t 0 f ( x, y, z)
15
有两个初始条件
utt a 2 uxx 0
u( x, y, z, t ) |t 0 f1 ( x, y, z )
ut ( x, y, z, t ) |t 0 f 2 ( x, y, z )
t x 2 ( a ) t x t x
27
为了书写方便 ,作代换
1 x ( ) 2 t 1 ( ) 2a
x at x at
2 u 2 4a 0
3 、注意问题: 1)初始条件给出系统在初始状态下物理量的分布,而不 是一点处的情况。
16
研究具体的物理系统,还必须考虑研究对象所处的特定“环 境”,而周围环境的影响常体现为边界上的物理状况,即边 界条件.
二 边界条件 : 1.定义: 系统的物理量始终在边界上具有的情况。 2.分类: 常见的线性边界条件分为三类: 第一类边界条件:直接给出了所研究的物理量在边界上的数值; 第二类边界条件:给出了所研究的物理量在边界外法线方向 上方向导数的数值; 第三类边界条件:给出了所研究的物理量及其外法向导数的 线性组合在边界上的数值. 17
ku n | x a h(u | x a ) ( 环境为度)
可写为 (u+H u m ) | x a
h
f 3 (t )
21
例5 : 如图一个弹簧所施加的力F(t)=-ku(l,t),如图所示,其 中k是弹簧的劲度系数.给出边界条件.
u YS | x l ku(l , t ) 0 x YS u | x 0 0 x
第二篇
数学物理方程
1
数学物理方程常常来自于物理学、其它自然科学、技 术科学中,许多实际研究对象所涉及到的变量不仅仅是一 个变量问题,可能会涉及到很多变量,这些多变量函数所 满足的方程称为偏微分方程,有时也包括与此有关的积分 方程、微分积分方程。如: 描写电磁场运动的Maxwell方程组 波传播满足的波动方程 热传导满足的传导方程 粒子扩散满足的扩散方程 电流、电压满足的电报方程
定律。
同一问题不同环境下,其方程形式相同,即方程反映的 是物理过程变化的规律。 本篇介绍物理学中常见的三类偏微分方程及有关的定解 问题和这些问题的几种常见解法。
4
二、边界问题----边界条件 对于具体的系统,要解出满足该系统所处条件下的方 程,必须考虑到系统周围的环境,不同系统,其周围环境 不同,即边界的区别。即使它们的满足同样的方程,但它 们的解不应该相同。因此,需要知道系统周围环境所处的 状态。体现边界状态的数学方程称为边界条件。 三、历史问题----初始条件 历史上的扰动对以后的状态会有很大的影响。比如: 分别用薄的物体和厚的物体敲击同一弦,研究其后的振动。 虽然,它们满足相同的数学方程,但初始情况不同,方程 的解不应该相同。要求解方程必须知道初始扰动的情况。 体现历史状态的数学方程称为初始条件。
u( x, t ) | x 0 f (t ) u( x, t ) | x l g(t )
18
(2)、第二类边界条件: 规定了系统边界上物理量法向方向上的方向导数的 函数形式。
u | n
x0 , y0 , z0
f 2 ( x0 , y0 , z0 , t )
例2:杆在x=a处绝热。
dinger 方程和 Dirac 方程 o 描写微观粒子运动的 Schr
等等
2
第七章 数学物理定解问题
重点
1、定解问题的概念 2、系统的边界条件和初始条件的写法;
3、行波法研究一维波动方程解的方法和解的表示
形式、以及解的物理意义。
3
第七章 一、数学物理方程
数学物理定解问题
数学物理方程是从物理问题中导出的反映客观物理量在 各个地点、各个时刻之间相互制约关系的数学方程。换言之, 是物理过程的数学表达。如 牛顿定律、热传导定律、热量 守恒定律、电荷守恒定律、高斯定律、电磁感应定律、胡克
四、方程的分类
10
1.数学物理方程的一般形式
a11u xx 2 a12 u xy a 22 u yy b1u x b2 u y cu f 0
其中 a11 , a12 , a22 , b1 , b2 ,c,f 只是 x,y 的函数
2.方程的分类;
a12、a 22 组成了一个判别式 二阶偏微商项的三个系数 a11、
2 a12 a11a12
按其符号,将方程化为三种类型;
11
2 (1)、 a12 a11a22 0双曲型
( 2) 、 a12 a11a22 0抛物型
2
(3) a12 a11a22 0椭圆型
2
由判别式式知;
utt a 2u xx 0双曲型 2 u a u xx 0抛物型 t u 0 椭圆型
波动方程为: 则有:
2u 0
28
积分求通解: 对 积分一次 再积分一次
