能被某某数整除的特征
整除的性质和特征

整除的性质和特征整除是数论中的一个重要概念,它描述了一个整数能够被另一个整数整除,也就是除法运算的结果是整数。
整除有着许多重要的性质和特征,下面将详细介绍。
1.定义:整数a能够被整数b整除,即b是a的因数,记作b,a,当且仅当存在一个整数c,使得a=b·c。
其中,c称为a除以b的商,b称为a的约数,a称为b的倍数。
2.可加性:如果c是a的一个约数,那么c也是a的倍数。
换句话说,如果一个整数能够整除a,那么它也能够整除a的倍数。
3.可乘性:如果b,a且c,a,那么b·c也,a。
换句话说,如果一个整数能够整除a和b,那么它也能够整除a与b的乘积。
4.整除的传递性:如果b,a且c,b,那么c,a。
换句话说,如果一个整数能够整除a和b,那么它也能够整除a。
5.算术基本定理:任意一个大于1的整数,都可以表达为多个质数的积。
这意味着,如果一个整数可以整除另一个整数,那么它必然可以整除这个整数的所有质因数。
6. 两个非零整数的最大公约数和最小公倍数:两个非零整数a和b的最大公约数(记作gcd(a,b))是能够同时整除a和b的最大正整数。
两个非零整数a和b的最小公倍数(记作lcm(a,b))是能够同时被a和b整除的最小正整数。
于是有gcd(a,b)·lcm(a,b)=a·b。
7.唯一分解定理:任何一个整数都能够唯一地分解为几个质数的乘积。
这个定理也说明了一个数的因数有限,不会无限增多。
8. 整除与除法的关系:一个整数a能够被b整除,相当于a除以b 的余数为0。
对于任意的整数a和b,总能够找到唯一的两个整数商q和余数r,使得a=bq+r,其中r满足0≤r<,b。
9. 整除与模运算的关系:一个整数a能够被b整除,等价于a除以b的余数为0,即a mod b = 0。
在模运算中,a mod b表示a除以b的余数。
10. 除法的消去律:如果一个整数a能够被b整除,那么对于任意的整数c,ac也能够被bc整除。
能被2、3、5、7、11、13、17、19整除的数的特征

【数学】能被2、3、5、7、11、13、17、19整除的数的特征★★能被2整除的数的特征是个位上是偶数,能被3整除的数的特征是所有位数的和是3的倍数(例如:315能被3整除,因为3+1+5=9是3的倍感)能被5整除的数个位上的数为0或5,能被7整除的数的特征若一个整数的个位数字去掉,再从余下的数中,减去个位数的2倍,如果差是7的倍数,则原数能被7整除。
如果数字仍然太大不能直接观察出来,就重复此过程。
能被11整除的数的特征把一个数由右边向左边数,将奇位上的数字与偶位上的数字分别加起来,再求它们的差,如果这个差是11的倍数(包括0),那么,原来这个数就一定能被11整除。
例如:判断491678能不能被11整除。
—→奇位数字的和9+6+8=23—→偶位数位的和4+1+7=1223-12=11因此,491678能被11整除。
这种方法叫“奇偶位差法”。
能被13整除的数的特征把一个整数的个位数字去掉,再从余下的数中,加上个位数的4倍,如果和是13的倍数,则原数能被13整除。
如果数字仍然太大不能直接观察出来,就重复此过程。
如:判断1284322能不能被13整除。
128432+2×4=12844012844+0×4=128441284+4×4=13001300÷13=100所以,1284322能被13整除。
能被17整除的数的特征把一个整数的个位数字去掉,再从余下的数中,减去个位数的5倍,如果差是17的倍数,则原数能被17整除。
如果数字仍然太大不能直接观察出来,就重复此过程。
例如:判断1675282能不能被17整除。
167528-2×5=16751816751-8×5=167111671-1×5=1666166-6×5=136到这里如果你仍然观察不出来,就继续……6×5=30,现在个位×5=30>剩下的13,就用大数减去小数,30-13=17,17÷17=1;所以1675282能被17整除。
整除规则(原理,性质)

整除规则(原理,性质)各种被整除的数的特征(放在这里以备以后查阅方便)(1)被2整除的数的特征:一个整数的末位是偶数(0、2、4、6、8)的数能被2整除。
(2)被3整除的数的特征:一个整数的数字和能被3整除,则这个数能被3整除。
(3)被4整除的数的特征:一个整数的末尾两位数能被4整除则这个数能被4整除。
可以这样快速判断:最后两位数,要是十位是单数,个位就是2或6,要是十位是双数,个位就是0、4、8。
(4)被5整除的数的特征:一个整数的末位是0或者5的数能被5整除。
(5)被6整除的数的特征:一个整数能被2和3整除,则这个数能被6整除。
(6)被7整除的数的特征:“割减法”。
若一个整数的个位数字截去,再从余下的数中,减去个位数的2倍,这样,一次次下去,直到能清楚判断为止,如果差是7的倍数(包括0),则这个数能被7整除。
过程为:截尾、倍大、相减、验差。
例如,判断133是否7的倍数的过程如下:13-3×2=7,所以133是7的倍数;又例如判断6139是否7的倍数的过程如下:613-9×2=595 , 59-5×2=49,所以6139是7的倍数,余类推。
(7)被8整除的数的特征:一个整数的未尾三位数能被8整除,则这个数能被8整除。
(8)被9整除的数的特征:一个整数的数字和能被9整除,则这个数能被9整除。
(9)被10整除的数的特征:一个整数的末位是0,则这个数能被10整除。
(10)被11整除的数的特征:“奇偶位差法”。
一个整数的奇位数字之和与偶位数字之和的差是11的倍数(包括0),则这个数能被11整除。
(隔位和相减)例如,判断491678能不能被11整除的过程如下:奇位数字的和9+6+8=23,偶位数位的和4+1+7=12。
23-12=11。
因此491678能被11整除。
(11)被12整除的数的特征:一个整数能被3和4整除,则这个数能被12整除。
(12)被13整除的数的特征:若一个整数的个位数字截去,再从余下的数中,加上个位数的4倍,这样,一次次下去,直到能清楚判断为止,如果是13的倍数(包括0),则这个数能被13整除。
能被2、3、5、7、9、11、13、17、19整除的数的特征

能被2、3、5、7、9、11、13、17、19整除的数的特征能被2整除的数的特征是个位上是偶数,能被3整除的数的特征是所有位数的和是3的倍数(例如:315能被3整除,因为3+1+5=9是3的倍数)能被4(或25)整除的数的特征:末两位数能被4(或25)整除。
能被8(或125)整除的数的特征:末三位数能被8(或125)整除。
能被5整除的数个位上的数为0或5,能被7整除的数的特征若一个整数的个位数字去掉,再从余下的数中,减去个位数的2倍,如果差是7的倍数,则原数能被7整除。
如果数字仍然太大不能直接观察出来,就重复此过程。
能被9整除的数的特征是所有位数的和是9的倍数能被11整除的数的特征把一个数由右边向左边数,将奇位上的数字与偶位上的数字分别加起来,再求它们的差,如果这个差是11的倍数(包括0),那么,原来这个数就一定能被11整除。
例如:判断491678能不能被11整除。
奇位数字的和9+6+8=23偶位数位的和4+1+7=1223-12=11因此,491678能被11整除。
这种方法叫“奇偶位差法”。
能被13整除的数的特征把一个整数的个位数字去掉,再从余下的数中,加上个位数的4倍,如果和是13的倍数,则原数能被13整除。
如果数字仍然太大不能直接观察出来,就重复此过程。
如:判断1284322能不能被13整除。
128432+2×4=12844012844+0×4=128441284+4×4=13001300÷13=100所以,1284322能被13整除。
【其它方法:能被7(11或13)整除的数的特征:一个整数的末三位数与末三位以前的数字所组成的数之差(以大减小)能被7(11或13)整除。
】例1:判断1059282是否是7的倍数?例2:判断3546725能否被13整除?能被17整除的数的特征把一个整数的个位数字去掉,再从余下的数中,减去个位数的5倍,如果差是17的倍数,则原数能被17整除。
能被2、3、4、5、6、7、8、9等数整除的数的特征

能被2、3、4、5、6、7、8、9等数整除的数的特征性质1:如果数a、b都能被c整除,那么它们的和(a+b)或差(a-b)也能被c 整除。
性质2:几个数相乘,如果其中有一个因数能被某一个数整除,那么它们的积也能被这个数整除。
能被2整除的数,个位上的数能被2整除(偶数都能被2整除),那么这个数能被2整除能被3整除的数,各个数位上的数字和能被3整除,那么这个数能被3整除能被4整除的数,个位和十位所组成的两位数能被4整除,那么这个数能被4整除能被5整除的数,个位上的数都能被5整除(即个位为0或5)那么这个数能被5整除能被6整除的数,如果一个数既能被2整除又能被3整除,那么这个数能被6整除能被7整除的数,若一个整数的个位数字截去,再从余下的数中,减去个位数的2倍,如果差是7的倍数,则原数能被7整除。
如果差太大或心算不易看出是否7的倍数,就需要继续上述「截尾、倍大、相减、验差」的过程,直到能清楚判断为止。
例如,判断133是否7的倍数的过程如下:13-3×2=7,所以133是7的倍数;又例如判断6139是否7的倍数的过程如下:613-9×2=595,59-5×2=49,所以6139是7的倍数,余类推。
能被8整除的数,百位、十位和个位所组成的三位数能被8整除,那么这个数能被8整除能被9整除的数,各个数位上的数字和能被9整除,那么这个数能被9整除能被10整除的数,如果一个数既能被2整除又能被5整除,那么这个数能被10整除(即个位数为零)能被11整除的数,奇数位(从左往右数)上的数字和与偶数位上的数字和之差(大数减小数)能被11整除,则该数就能被11整除。
11的倍数检验法也可用上述检查7的「割尾法」处理!过程唯一不同的是:倍数不是2而是1!能被12整除的数,若一个整数能被3和4整除,则这个数能被12整除能被13整除的数,若一个整数的个位数字截去,再从余下的数中,加上个位数的4倍,如果差是13的倍数,则原数能被13整除。
能被整除的数的特征

能被整除的数的特征 Revised by BLUE on the afternoon of December 12,2020.能被2、3、5、7、9、11、13、17、19整除的数的特征能被2整除的数的特征是个位上是偶数,能被3整除的数的特征是所有位数的和是3的倍数(例如:315能被3整除,因为3+1+5=9是3的倍数)能被4(或25)整除的数的特征:末两位数能被4(或25)整除。
能被8(或125)整除的数的特征:末三位数能被8(或125)整除。
能被5整除的数个位上的数为0或5,能被7整除的数的特征若一个整数的个位数字去掉,再从余下的数中,减去个位数的2倍,如果差是7的倍数,则原数能被7整除。
如果数字仍然太大不能直接观察出来,就重复此过程。
能被9整除的数的特征是所有位数的和是9的倍数能被11整除的数的特征把一个数由右边向左边数,将奇位上的数字与偶位上的数字分别加起来,再求它们的差,如果这个差是11的倍数(包括0),那么,原来这个数就一定能被11整除。
例如:判断491678能不能被11整除。
奇位数字的和9+6+8=23偶位数位的和4+1+7=1223-12=11因此,491678能被11整除。
这种方法叫“奇偶位差法”。
能被13整除的数的特征把一个整数的个位数字去掉,再从余下的数中,加上个位数的4倍,如果和是13的倍数,则原数能被13整除。
如果数字仍然太大不能直接观察出来,就重复此过程。
如:判断1284322能不能被13整除。
128432+2×4=12844012844+0×4=128441284+4×4=13001300÷13=100所以,1284322能被13整除。
【其它方法:能被7(11或13)整除的数的特征:一个整数的末三位数与末三位以前的数字所组成的数之差(以大减小)能被7(11或13)整除。
】例1:判断1059282是否是7的倍数例2:判断3546725能否被13整除能被17整除的数的特征把一个整数的个位数字去掉,再从余下的数中,减去个位数的5倍,如果差是17的倍数,则原数能被17整除。
数的整除特征特点

数的整除特征特点 It was last revised on January 2, 2021
数的整除特征特点
一、尾数判断法:
(1) 能被 2、 5整除的数的特征:个位数字能被2或5整除。
(2) 能被4、25 整除的数的特征:末两位能被4或25整除。
(3) 能被8、125整除的数的特征:末三位能被8或125整除。
二、数字求和法
(1)能被3、9整除的数的特征:各位数字之和能被3或9整除。
三、奇偶位求差法
(1)能被11整除的数的特征:“奇位和”与“偶位和”的差能被11整除。
四、三位截断法
(1)能被7、11、13整除的数的特征:“末三位数字组成的数”与“末三位以前的数字组成的数”之差能被7或11或13整除。
整除特征:
7:个位数字去掉,再从余下的数中,减去个位数的2倍,如果差是7的倍数,则原数能被7整除。
(如果数字太大仍然不能直接观察出来,就重复此过程。
)
13:个位数字去掉,再从余下的数中,加上个位数的4倍,如果和是13的倍数,则原数能被13整除。
17:个位数字去掉,再从余下的数中,减去个位数的5倍,如果差是17的倍数,则原数能被17整除。
19:个位数字去掉,再从余下的数中,加上个位数的2倍,如果和是19的倍数,则原数能被19整除。
五年级整除的特征
整除的特征一、性质1、如果整数A、B都能被C整除,那么他们的和A+B或差A-B也能被C整除。
例如:8整除64,8整除24,那么8整除64+24或64-242、如果A能被B整除,B能被C整除,那么A能被C整除。
例如:30能被15整除,15能被5整除,那么30能被5整除。
二、数的整除特征能被2整除的数的特征:个位数字是0、2、4、6、8。
能被3整除的数的特征:各位数字之和是3的倍数。
能被4(或25)整除的数的特征:末两位数能被4(或25)整除。
能被5整除的数的特征:个位数字是0或5。
能被8(或125)整除的数的特征:末三位数能被8(或125)整除。
能被9整除的数的特征:各位数字之和是9的倍数。
能被11整除的数的特征:奇数位上的数字之和与偶数位上的数字之和的差能被11整除。
能被7、11、13整除的数的特征:末三位数与末三位数以前的数所组成的数之差能被7、11、13整除。
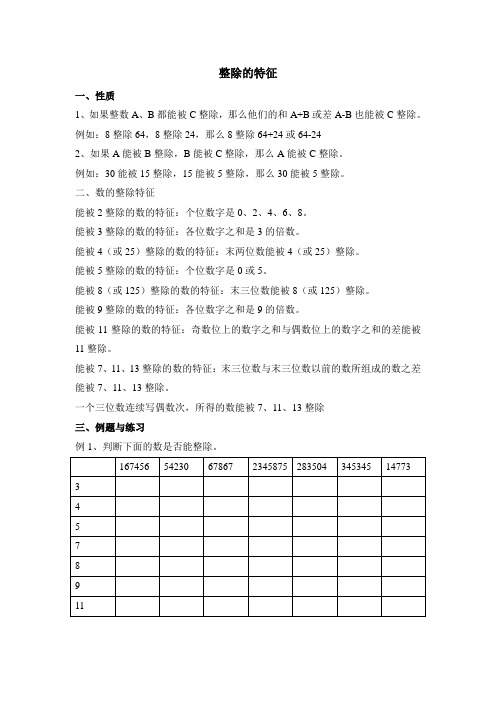
一个三位数连续写偶数次,所得的数能被7、11、13整除三、例题与练习例1、判断下面的数是否能整除。
例2、判断下面的数是否能整除。
例题3、四位数2□2□能同时被8、9整除,那么这个四位数是多少?练习1、在3□2□的方框里填入合适的数字,使这个四位数能被15整除,这样的四位数中最大的是多少?例题4、将1、2、3、4这四个数任意排列,可组成若干个四位数,在这些四位数中,能被11整除的数最小是多少?能被4整除的数最小是多少?练习3、由1、2、3这三个数任意排列,可组成若干个三位数,在这些三位数中,能被11整除的数有哪些?练习4、从0、3、5、7这四个数中选择三个数,排成一个三位数,使它能同时被2、3、5整除,这样的三位数最大的是哪个?练习5、在568后面补上三个数字,组成一个六位数,使它能被3、4、5整除,这个六位数最小是多少?例5、某个七位数1993口口口能同时被2、3、4、5、6、7、8、9整除,那么它的最后三位数字依次是多少?**例6、已知数022983298329832983个 n 能被18整除,那么n 的最小值是多少?**例7、三位数的百位、十位和个位的数字分别是5,a 和b ,将它连续重复写99次成为:abab ab ab 5个99555。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
能被特殊数整除的特征
—己巳贡生1、能被2 整除的数的特征。
如果一个数能被2 整除,那么这个数末尾上的数为偶数,“0”、“2”、“4”、“6”、“8”。
2、能被3 整除的数的特征。
如果一个数能被3整除,那么这个数所有数位上数字的和是 3 的倍数。
例如:225能被3 整除,因为2+2+5=9,9 是3 的倍数,所以225 能被3 整除。
3、能被4 整除的数的特征。
如果一个数的末尾两位能被4 整除,这个数就能被4整除。
例如:15692512 能不能被4 整除呢?因为15692512 的末尾两位12,能被4整除,所以15692512 能被4整除。
4、能被5 整除的数的特征。
若一个数的末尾是0 或5,则这个数能被5 整除。
5、能被7 整除的数的特征。
方法一:若一个整数的个位数字截去,再从余下的数中,减去个位数的2 倍,如果差是
7 的倍数,则原数能被7 整除。
如果差太大或心算不易看出是否是7 的倍数,就需要继续上述「截尾、倍大、相减、验差」的过程,直到能清楚判断为止。
例如,判断133 是否是7 的倍数的过程如下:13 —3X 2= 7,所以133是7的倍数;又例如判断6139是否7的倍数的过程如下:613 —9X 2= 595 , 59 —5X 2= 49,所以6139是7的倍数,以此类推。
方法二:如果一个多位数的末三位数与末三位以前的数字所组成的数的差, 是7 的倍数, 那么这个数就能被7 整除。
例如:280678 末三位数是678,末三位以前数字所组成的数是
280,679-280=399,399 能被7 整除,因此280679 也能被7 整除。
方法三:首位缩小法,减少7 的倍数。
例如, 判断452669 能不能被7 整除, 452669-420000=32669 ,只要32669 能被7 整除即可。
可对32669 继续, 32669-28000=4669,4669-4200=469,469-420=49,49 当然被7 整除所以452669 能被7 整除。
6、能被8 整除的数的特征。
若一个整数的未尾三位数能被8 整除,则这个数能被8整除。
7、能被9 整除的数的特征。
若一个数的数位上的数字的和能被9 整除,则这个整数能被9 整除。
例如:111111111 能不能被9整除呢?因为1+1+1+1+1+1+1+1+1=9,9 是9的倍数,所以111111111 能被9整除。
8、能被11 整除的数的特征。
方法一:若一个整数的奇位数字之和与偶位数字之和(从右往左数)的差能被11 整除,
则这个数能被11 整除。
例如,判断491678 能不能被11 整除。
奇位数字之和8+6+9=23;偶位数字之和7+1+4=12;23-12=11,11 能被11 整除,所以491678 能被11 整除。
这种方法叫作“奇偶位差法”。
方法二:11 的倍数检验法也可用上述检查7 的「割尾法」处理!过程唯一不同的是:倍数不是2 而是1!例如:判断491678 能不能被11 整除,49167-8=49159,4915-9=4906 ,490-
6=484,48-4=44 。
44能被11整除,所以得491678能被11整除。
方法三:还可以根据7 的方法二判断。
例如:283679 的末三位数是679,末三位以前数所组成的数是283,679-283=396,396 能被11 整除,因此283679 就一定能被11 整除。
9、能被13 整除的数的特征。
方法一:若一个整数的个位数字截去,再从余下的数中,加上个位数的4 倍,如果和是13 的倍数,则原数能被13 整除。
如果和太大或心算不易看出是否13 的倍数,就需要继续上述「截尾、倍大、相加、验和」的过程,直到能清楚判断为止。
例如,判断1284322 能不能被13 整除。
128432+2 X 4=128440,12844+0 X 4=12844 ,
1284+4 X 4=1300,1300 - 13=100。
所以1284322 能被13 整除。
方法二:前面7的方法二,也适用判定13。
例如:判定1284322能不能被13整除,128432 的末尾三位数是322,末尾以前的数字所组成的数是1284,322-1284=-962。
962十13=74。
所以1284322 能被13整除。
10、能被17 整除的数的特征。
方法一:若一个整数的个位数字截去,再从余下的数中,减去个位数的5 倍,如果差是17的倍数,则原数能被17整除。
如果差太大或心算不易看出是否1 7的倍数,就需要继续上述「截尾、倍大、相减、验差」的过程,直到能清楚判断为止。
例如,判断1675282能不能被17整除,167528-2X5=167518,16751-8 X5=16711,1671-1 X5=1666,166-6 X5=136, 136- 17=8,所以1675282 能被17 整除。
方法二:若一个整数的末三位与3倍的前面的隔出数的差能被17整除,则这个数能被17整除。
例如,判断1675282能不能被17整除,1675282的末三位是282,前面的数是1675,282-1675 X 3=-4743,4743 - 17=279,所以1675282 能被17 整除。
11、能被19 整除的数的特征。
方法一:若一个整数的末三位与7倍的前面的隔出数的差能被19整除,则这个数能被19整除。
例如,判断234555能不能被19整除,234555末尾三位数是555 ,前面三位是234,555-234 X 7=-1083,1083 - 19=57,所以234555 能被19 整除。
方法二:若一个整数的个位数字截去,再从余下的数中,加上个位数的2倍,如果和是19的倍数,则原数能被19整除。
如果和太大或心算不易看出是否19的倍数,就需要继续上述「截尾、倍大、相加、验和」的过程,直到能清楚判断为止。
12、能被23 整除的数的特征。
若一个整数的末四位与前面5 倍的隔出数的差能被23(或29)整除,则这个数能被23 整除。
13、能被25 整除的数的特征。
如果一个数的末尾两位能被25 整除,则这个数能被
14、能被125 整除的数的特征。
如果一个数的末尾三位能被
25 整除。
125 整除,则这个数能被
125 整除。
