2016年全国考研数学三试题解析超详细版.doc

合集下载

2016年全国硕士研究生入学统一考试数学三考研真题答案凯程首发

2016年全国硕士研究生入学统一考试数学三考研真题答案凯程首发下面凯程老师把2016年的真题答案全面展示给大家，供大家估分使用，以及2017年考研的同学使用，本试题凯程首发，转载注明出处。

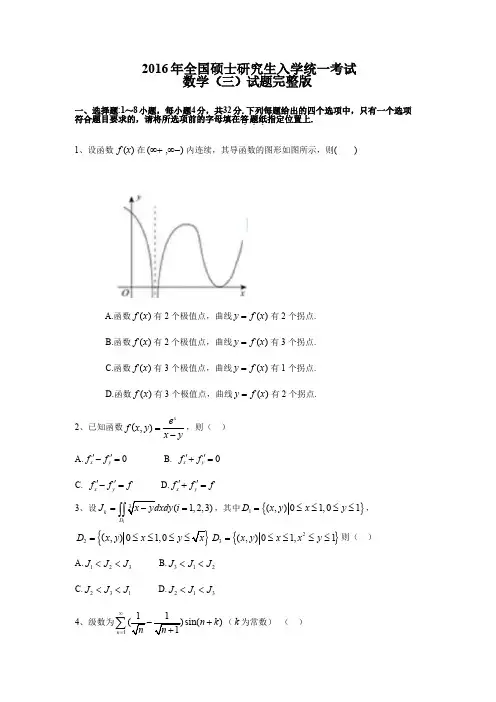
一、选择题：1～8小题，每小题4分，共32分，下列每小题给出的四个选项中，只有一项符合题目要求的，请将所选项前的字母填在答题纸．．．指定位置上. （1）设函数()y f x =在(,)-∞+∞内连续，其导数如图所示，则（）（A ）函数有2个极值点，曲线()y f x =有2个拐点（B ）函数有2个极值点，曲线()y f x =有3个拐点（C ）函数有3个极值点，曲线()y f x =有1个拐点（D ）函数有3个极值点，曲线()y f x =有2个拐点【答案】（B ）xy【解析】【解析】由图像易知选B2、已知函数(,)x e f x y x y=-，则（A ）''0x y f f -= （B ）''0x y f f += （C ）''x y f f f -= （D ）''x y f f f += 【答案】（D ）【解析】()2(1)'x x e x y f x y --=- ()2'xy e f x y =-，所以''x y f f f +=（3）设(i ,,)ii D T x y d x d y =-=⎰⎰3123，其中{}(,),D x y x y =≤≤≤≤10101，{}{}(,),,(,),D x y x y x D x y x x y =≤≤≤≤=≤≤≤≤223010011，则（A ）T T T <<123 （B ）T T T <<312 （C ）T T T <<231 （D ）T T T <<213【答案】B【解析】由积分区域的性质易知选B. （4）级数为sin()n n k n n ∞=⎛⎫-+ ⎪+⎝⎭∑1111，（K 为常数）（A ）绝对收敛（B ）条件收敛（C ）发散（D ）收敛性与K 有关【答案】A【解析】由题目可得，sin()sin()sin()()n n n n n n k n k n k n n n n n n n n ∞∞∞===+-+⎛⎫-+=+= ⎪+++++⎝⎭∑∑∑1111111111 因为sin()()()n k n n n n n n n n n n+≤≤++++++111111，由正项级数的比较判别法得，该级数绝对收敛。

2016-2017年考研数学真题及答案解析(三)

A. AT 与 BT 相似
B. A1 与 B1 相似
C. A AT 与 B BT 相似
D. A A1 与 B B1 相似
（6）设二次型 f (x1, x2 , x3 ) a( x12 x22 x32 ) 2x1x2 2x2 x3 2x1x3 的正负惯性指数分别为 1,2，则（）
A. J1 J2 J3
B. J3 J1 J2
C. J2 J3 J1
D. J2 J1 J3
（4）级数 ( 1 1 ) sin(n k) （ k 为常数）（） n1 n n 1
A.绝对收敛
B.条件收敛
C.发散
D.收敛性与 k 有关
（5）设 A, B 是可逆矩阵，且 A 与 B 相似，则下列结论错误的是（）
1, x 上服从均匀分布，令U 0,
X Y. X Y.
（ I ）写出 ( X ,Y ) 的概率密度；
（ II ）问U 与 X 是否相互独立？并说明理由；（ III ）求 Z U X 的分布函数 F (z) .
（23）（本题满分 11 分）
设总体
X
的概率密度
f
(x; )
3x 2 3
,0
x
,
0, 其他，
（Ⅰ）求需求函数的表达式；
（Ⅱ）求 p 100 万元时的边际效益，并说明其经济意义。
（17）设函数 f (x)
1
|
t
2
x2
|
dt ( x
0), 求f
( x), 并求f
( x)的最小值。
0
（18）（本题满分 10 分）
设函数 f (x) 连续，且满足
x
f (x t)dt
x
(x

2016年全国硕士研究生入学考试数学3真题完整版(可打印)

2016 年全国硕士研究生入学统一考试数学（三）试题完整版一、选择题:1～8 小题，每小题 4 分，共 32 分.下列每题给出的四个选项中，只有一个选项符合题目要求的，请将所选项前的字母填在答．题．纸．指定位置上.1、设函数 f (x ) 在(∞+ ,∞−) 内连续，其导函数的图形如图所示，则()A.函数()f x 有2个极值点，曲线()y f x =有2个拐点.B.函数()f x 有2个极值点，曲线()y f x =有3个拐点.C.函数()f x 有3个极值点，曲线()y f x =有1个拐点.D.函数()f x 有3个极值点，曲线()y f x =有2个拐点.2、已知函数(,)xe f x y x y=-，则（）A.0x y f f ''-= B.0x y f f ''+=C.x y f f f''-= D.x y f f f ''+=3、设3(1,2,3)i k D J x ydxdy i =-=⎰⎰，其中{}1(,)01,01D x y x y =≤≤≤≤，{}2(,)01,0D x y x y x =≤≤≤≤{}23(,)01,1D x y x x y =≤≤≤≤则（）A.123J J J << B.312J J J <<C.231J J J << D.213J J J <<4、级数为111()sin()1n n k n n ∞=-++∑（k 为常数）（）A.绝对收敛B.条件收敛C.发散D.收敛性与k 有关5、设,A B 是可逆矩阵，且A 与B 相似，则下列结论错误的是（）A.T A 与T B 相似B.1A -与1B -相似C.T A A +与T B B +相似D.1A A -+与1B B -+相似6、设二次型222123123122313(,,)()222f x x x a x x x x x x x x x =+++++的正负惯性指数分别为1,2，则（）A.1a >B.2a <-C.21a -<< D.1a =或2a =-7、设,A B 为两个随机事件，且0()1,0()1P A P B <<<<，如果()1P A B =，则（）A.()1P B A = B.()0P A B =C.()1P A B ⋃= D.()1P B A =8、设随机变量X 与Y 相互独立，且~(1,2),~(1,4)X N Y N ，则()D XY =（）A.6 B.8 C.14 D.15二、填空题：9～14小题,每小题4分,共24分.请将答案写在答题纸．．．指定位置上.9、已知函数()f x 满足301()sin 21lim 21x x f x x e →+-=-，则0l im ()x f x →=__________.10、极限2112lim (sin 2sin sin )n n n n n n n→∞+++= ___________.11、设函数(,)f u v 可微，(,)z z x y =由方程22(1)(,)x z y x f x z y +-=-确定，则(0,1)|dz =__________.12、设{(,)|||1,11}D x y x y x =≤≤-≤≤，则22y D x e dxdy -=⎰⎰___________.13、行列式1000100014321λλλλ--=-+_________.14、设袋中有红、白、黑球各1个，从中有放回地取球，每次取1个，直到三种颜色的球都取到时停止，则取球次数恰好为4的概率为__________.三、解答题：15～23小题,共94分.请将解答写在答题纸．．．指定位置上.解答应写出文字说明、证明过程或演算步骤.15、（本题满分10分）求极限410l im(cos 22sin 1)x x x x x →+-。

2016考研数学三真题及答案解析

（C） A + AT 与 B + BT 相似. 解析：∵ A 与 B 相似 ∴存在可逆矩阵 P ，使得 B P1AP
（D） A A1 与 B B1 相似.
故 BT PT AT (P1)T (PT )1 1 AT (PT )1 ∴ AT 与 BT 相似（A）正确
又 B1 P1 A1P ，故 B1 与 A1 相似，（B）正确
则（）
（A） T1 T2 T3
（B） T3 T1 T2
（C） T2 T3 T1
（D） T2 T1 T3 解析：如图所示，
D1 D4 D5 D6 ， D2 D5 D6 ， D3 D4 D5 ，由于被积函数 3 x y 在 D1 上为
正，所以 T2 T1 ，T3 T1 ，又因为 3 x y 在 D4 上显然大于 D6 上对应 x 处的值，所以 T2 T3 ，
x
f
y
ex (x y) ex (x y)2
ex
ex x y
f
应选（D）.
（3）设 Ti 3 x ydxdy (i 1, 2, 3) 其中 D1 ( x, y) 0 x 1, 0 y 1
Di
D2 (x, y) 0 x 1, 0 y x
D3 ( x, y) 0 x 1, x2 y 1
解析：因 P( A | B) 1 ，则 p( AB) 1 ，则 P(B) P( AB) 0 ，则 P(B A) 0 . 从而 P(B)
P(B | A) 0 .
又 P(B | A) P(B | A) 1 ，则 P(B | A) 1 ，故选 A.
（8）设随机变量 X 与Y 相互独立，且 X ~ N (1, 2),Y ~ N (1, 4) ，则 D( XY ) =( )

2016考研数学三真题及答案解析

故 T2 T3 T1 ，应选(C).
（4）级数为 n1
1 n
1 n
1
sin(n
k
)
（
k
为常数）（
）
（A）绝对收敛（B）条件收敛（C）发散
（D）收敛性 k 有关
解析： 1 1 sin(n k) 1 1 ，
n n1
n n1
而 Sn
1 1
1 2
1 2
1 3
1 n
边际收益函数为 R ' p 20P 1200
当 P=100 时，边际收益为-800 万元经济意义为：当价格为 100 万元时，收益亏损 800 万元.
（17）（本题满分 10 分）
设函数 f (x)
1| t2
0
x2
|
dt ( x
0),
求
f
(x) ，并求
f
(x)
的最小值.
解析：
当 0 x 1时, f (x) x (t2 x2 )dt 1(x2 t2 )dt 4x3 x2 1 ,
极值的怀疑点为： a,b,c, d
①
当x 当x
a时, a时,
f f
(x) (x)
0
0
a
为极大值点
当x b时, f (x) 0 ②当x b时, f (x) 0 a 不是极值点
③
当x 当x
c时, c时,
f f
(x) (x)
0 0
c
为极小值点
④当 x d 和 x d 时， f (x) 0 故 x d 不是极值点 ∴有 2 个极值点排除 C，D.
lim
ex0
4 x3
e1 2
lim

数学三2016年真题及答案

第 2 页共 12 页
2 2 2
为 1, 2 ，则（
）
（A） a 1 （B） a 2 （C） 2 a 1 （D） a 1 或 a 2 【答案】（C）【解析】考虑特殊值法，当 a 0 时， f ( x1 , x2 , x3 ) 2 x1 x2 2 x2 x3 2 x1 x3 ，
n sin n
i 1
i
i
0
x sin xdx sin 1 cos 1
(11)设函数 f ( u, v ) 可微， z z ( x, y ) 有方程 ( x 1) z y 2 x 2 f ( x z , y ) 确定，则
dz
0 ,1
____ ．
【答案】 dz 0,1 dx 2dy 【解析】 ( x 1) x y 2 x 2 f ( x z , y ) 两边分别关于 x , y 求导得
x 0 1 1
【解析】 lim cos 2 x 2 x sin x x 4
x 0
lim e
x 0
cos 2 x 2 x sin x 1 x4
1
lim e
x 0
x3 4 x 2 24 x 4 2 x x 1o( x 4 ) 3! 2 4! x4
x
x 0
2
t 2 dt t 2 x 2 dt
x

1

x
1 0
2
t 2 dt x 2 x 1 1 x 0 0 x 1 x 1

1 3
4 3 1 x x2 3 3
2 1 x 3 4 x 3 x 2 1 3 3 则 f x 4 x3 x 2 1 3 3 1 x2 3 2 x 2 4 x 2 x f ' x 2 4 x 2 x 2 x

2016年考研数学三真题解析

2016年考研数学（三）真题解析一、填空题（本题共6小题，每小题4分，满分24分. 把答案填在题中横线上） (1) 若5)(cos sin lim0=--→b x ae xx x ，则a =1，b =4-.【分析】本题属于已知极限求参数的反问题. 【详解】因为5)(cos sin lim0=--→b x a e xx x ，且0)(cos sin lim 0=-⋅→b x x x ，所以 0)(lim 0=-→a e x x ，得a = 1. 极限化为51)(cos lim )(cos sin lim00=-=-=--→→b b x x xb x a e x x x x ，得b = -4.因此，a = 1，b = -4. 【评注】一般地，已知)()(limx g x f ＝ A ， (1) 若g (x ) → 0，则f (x ) → 0；(2) 若f (x ) → 0，且A ≠ 0，则g (x ) → 0.(2) 设函数f (u , v )由关系式f [xg (y ) , y ] = x + g (y )确定，其中函数g (y )可微，且g (y ) ≠ 0，则)()(22v g v g vu f'-=∂∂∂.【分析】令u = xg (y )，v = y ，可得到f (u , v )的表达式，再求偏导数即可. 【详解】令u = xg (y )，v = y ，则f (u , v ) =)()(v g v g u+，所以，)(1v g u f =∂∂，)()(22v g v g v u f '-=∂∂∂. (3) 设⎪⎩⎪⎨⎧≥-<≤-=21,12121,)(2x x xe x f x ，则21)1(221-=-⎰dx x f .【分析】本题属于求分段函数的定积分，先换元：x - 1 = t ，再利用对称区间上奇偶函数的积分性质即可.【详解】令x - 1 = t ，⎰⎰⎰--==-121121221)()()1(dt x f dt t f dx x f＝21)21(0)1(12121212-=-+=-+⎰⎰-dx dx xe x .【评注】一般地，对于分段函数的定积分，按分界点划分积分区间进行求解.(4) 二次型2132********)()()(),,(x x x x x x x x x f ++-++=的秩为 2 .【分析】二次型的秩即对应的矩阵的秩, 亦即标准型中平方项的项数, 于是利用初等变换或配方法均可得到答案.【详解一】因为2132********)()()(),,(x x x x x x x x x f ++-++=323121232221222222x x x x x x x x x -++++=于是二次型的矩阵为 ⎪⎪⎪⎭⎫ ⎝⎛--=211121112A ,由初等变换得 ⎪⎪⎪⎭⎫ ⎝⎛--→⎪⎪⎪⎭⎫ ⎝⎛---→000330211330330211A ,从而 2)(=A r , 即二次型的秩为2.【详解二】因为2132********)()()(),,(x x x x x x x x x f ++-++=323121232221222222x x x x x x x x x -++++= 2322321)(23)2121(2x x x x x -+++= 2221232y y +=,其中 ,21213211x x x y ++= 322x x y -=.所以二次型的秩为2.(5) 设随机变量X 服从参数为λ的指数分布, 则=>}{DX X Pe1. 【分析】根据指数分布的分布函数和方差立即得正确答案. 【详解】由于21λDX =, X 的分布函数为 ⎩⎨⎧≤>-=-.0,0,0,1)(x x e x F x λ故=>}{DX X P =≤-}{1DX X P =≤-}1{1λX P )1(1λF -e1=.【评注】本题是对重要分布, 即指数分布的考查, 属基本题型.(6) 设总体X 服从正态分布),(21σμN , 总体Y 服从正态分布),(22σμN ,1,,21n X X X Λ和 2,,21n Y Y Y Λ分别是来自总体X 和Y 的简单随机样本, 则22121212)()(21σn n Y Y X X En j j n i i =⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡-+-+-∑∑==.【分析】利用正态总体下常用统计量的数字特征即可得答案.【详解】因为 2121])(11[1σX X n E n i i =--∑=, 2122])(11[2σY Y n E n j j =--∑=, 故应填 2σ.【评注】本题是对常用统计量的数字特征的考查.二、选择题（本题共6小题，每小题4分，满分24分. 每小题给出的四个选项中，只有一项符合题目要求，把所选项前的字母填在题后的括号内） (7) 函数2)2)(1()2sin(||)(---=x x x x x x f 在下列哪个区间内有界.(A) (-1 , 0).(B) (0 , 1).(C) (1 , 2).(D) (2 , 3). [ A ]【分析】如f (x )在(a , b )内连续，且极限)(lim x f a x +→与)(lim x f b x -→存在，则函数f (x )在(a , b )内有界.【详解】当x ≠ 0 , 1 , 2时，f (x )连续，而183sin )(lim1-=+-→x f x ，42sin )(lim 0-=-→x f x ，42sin )(lim 0=+→x f x ，∞=→)(lim 1x f x ，∞=→)(lim 2x f x ，所以，函数f (x )在(-1 , 0)内有界，故选(A).【评注】一般地，如函数f (x )在闭区间[a , b ]上连续，则f (x )在闭区间[a , b ]上有界；如函数f (x )在开区间(a , b )内连续，且极限)(lim x f a x +→与)(lim x f b x -→存在，则函数f (x )在开区间(a , b )内有界.(8) 设f (x )在(-∞ , +∞)内有定义，且a x f x =∞→)(lim ，⎪⎩⎪⎨⎧=≠=0,00,)1()(x x xf xg ，则 (A) x = 0必是g (x )的第一类间断点. (B) x = 0必是g (x )的第二类间断点.(C) x = 0必是g (x )的连续点.(D) g (x )在点x = 0处的连续性与a 的取值有关. [ D ] 【分析】考查极限)(lim 0x g x →是否存在，如存在，是否等于g (0)即可，通过换元xu 1=，可将极限)(lim 0x g x →转化为)(lim x f x ∞→.【详解】因为)(lim )1(lim )(lim 0u f x f x g u x x ∞→→→=== a (令xu 1=)，又g (0) = 0，所以，当a = 0时，)0()(lim 0g x g x =→，即g (x )在点x = 0处连续，当a ≠ 0时，)0()(lim 0g x g x ≠→，即x = 0是g (x )的第一类间断点，因此，g (x )在点x = 0处的连续性与a 的取值有关，故选(D).【评注】本题属于基本题型，主要考查分段函数在分界点处的连续性. (9) 设f (x ) = |x (1 - x )|，则(A) x = 0是f (x )的极值点，但(0 , 0)不是曲线y = f (x )的拐点. (B) x = 0不是f (x )的极值点，但(0 , 0)是曲线y = f (x )的拐点. (C) x = 0是f (x )的极值点，且(0 , 0)是曲线y = f (x )的拐点.(D) x = 0不是f (x )的极值点，(0 , 0)也不是曲线y = f (x )的拐点. [ C ] 【分析】由于f (x )在x = 0处的一、二阶导数不存在，可利用定义判断极值情况，考查f (x )在x = 0的左、右两侧的二阶导数的符号，判断拐点情况.【详解】设0 < δ < 1，当x ∈ (-δ , 0) ⋃ (0 , δ)时，f (x ) > 0，而f (0) = 0，所以x = 0是f (x )的极小值点. 显然，x = 0是f (x )的不可导点. 当x ∈ (-δ , 0)时，f (x ) = -x (1 - x )，02)(>=''x f ，当x ∈ (0 , δ)时，f (x ) = x (1 - x )，02)(<-=''x f ，所以(0 , 0)是曲线y = f (x )的拐点.故选(C).【评注】对于极值情况，也可考查f (x )在x = 0的某空心邻域内的一阶导数的符号来判断. (10) 设有下列命题：(1) 若∑∞=-+1212)(n n n u u 收敛，则∑∞=1n n u 收敛.(2) 若∑∞=1n n u 收敛，则∑∞=+11000n n u 收敛.(3) 若1lim1>+∞→nn n u u ，则∑∞=1n n u 发散.(4) 若∑∞=+1)(n n n v u 收敛，则∑∞=1n n u ，∑∞=1n n v 都收敛.则以上命题中正确的是 (A) (1) (2). (B) (2) (3).(C) (3) (4).(D) (1) (4).[ B ]【分析】可以通过举反例及级数的性质来说明4个命题的正确性. 【详解】(1)是错误的，如令nn u )1(-=，显然，∑∞=1n n u 分散，而∑∞=-+1212)(n n n u u 收敛.(2)是正确的，因为改变、增加或减少级数的有限项，不改变级数的收敛性.(3)是正确的，因为由1lim1>+∞→nn n u u 可得到n u 不趋向于零(n → ∞)，所以∑∞=1n n u 发散. (4)是错误的，如令n v n u n n 1,1-==，显然，∑∞=1n n u ，∑∞=1n n v 都发散，而∑∞=+1)(n n n v u 收敛. 故选(B).【评注】本题主要考查级数的性质与收敛性的判别法，属于基本题型.(11) 设)(x f '在[a , b]上连续，且0)(,0)(<'>'b f a f ，则下列结论中错误的是 (A) 至少存在一点),(0b a x ∈，使得)(0x f > f (a ). (B) 至少存在一点),(0b a x ∈，使得)(0x f > f (b ). (C) 至少存在一点),(0b a x ∈，使得0)(0='x f .(D) 至少存在一点),(0b a x ∈，使得)(0x f = 0.[ D ]【分析】利用介值定理与极限的保号性可得到三个正确的选项，由排除法可选出错误选项. 【详解】首先，由已知)(x f '在[a , b]上连续，且0)(,0)(<'>'b f a f ，则由介值定理，至少存在一点),(0b a x ∈，使得0)(0='x f ；另外，0)()(lim)(>--='+→ax a f x f a f a x ，由极限的保号性，至少存在一点),(0b a x ∈使得0)()(00>--ax a f x f ，即)()(0a f x f >. 同理，至少存在一点),(0b a x ∈使得)()(0b f x f >. 所以，(A) (B) (C)都正确，故选(D).【评注】本题综合考查了介值定理与极限的保号性，有一定的难度.(12) 设n 阶矩阵A 与B 等价, 则必有(A) 当)0(||≠=a a A 时, a B =||. (B) 当)0(||≠=a a A 时, a B -=||. (C) 当0||≠A 时, 0||=B . (D) 当0||=A 时, 0||=B . [ D ] 【分析】利用矩阵A 与B 等价的充要条件: )()(B r A r =立即可得.【详解】因为当0||=A 时, n A r <)(, 又 A 与B 等价, 故n B r <)(, 即0||=B , 故选(D). 【评注】本题是对矩阵等价、行列式的考查, 属基本题型.(13) 设n 阶矩阵A 的伴随矩阵,0*≠A 若4321,,,ξξξξ是非齐次线性方程组 b Ax =的互不相等的解，则对应的齐次线性方程组0=Ax 的基础解系(A) 不存在. (B) 仅含一个非零解向量.(C) 含有两个线性无关的解向量. (D) 含有三个线性无关的解向量. [ B ] 【分析】要确定基础解系含向量的个数, 实际上只要确定未知数的个数和系数矩阵的秩. 【详解】因为基础解系含向量的个数=)(A r n -, 而且⎪⎩⎪⎨⎧-<-===.1)(,0,1)(,1,)(,)(*n A r n A r n A r n A r根据已知条件,0*≠A 于是)(A r 等于n 或1-n . 又b Ax =有互不相等的解, 即解不惟一, 故1)(-=n A r . 从而基础解系仅含一个解向量, 即选(B).【评注】本题是对矩阵A 与其伴随矩阵*A 的秩之间的关系、线性方程组解的结构等多个知识点的综合考查.(14) 设随机变量X 服从正态分布)1,0(N , 对给定的)1,0(∈α, 数αu 满足αu X P α=>}{,若αx X P =<}|{|, 则x 等于 (A) 2αu . (B) 21αu-. (C) 21αu -. (D) αu -1. [ C ]【分析】利用标准正态分布密度曲线的对称性和几何意义即得. 【详解】由αx X P =<}|{|, 以及标准正态分布密度曲线的对称性可得21}{αx X P -=>. 故正确答案为(C). 【评注】本题是对标准正态分布的性质, 严格地说它的上分位数概念的考查.三、解答题(本题共9小题，满分94分. 解答应写出文字说明、证明过程或演算步骤.) (15) (本题满分8分)求)cos sin 1(lim 2220xxx x -→. 【分析】先通分化为“”型极限，再利用等价无穷小与罗必达法则求解即可. 【详解】xx xx x x x x x x 2222202220sin cos sin lim )cos sin 1(lim -=-→→ =346)4(21lim 64cos 1lim 44sin 212lim 2sin 41lim 22020304220==-=-=-→→→→x x x x x x x x x x x x x x . 【评注】本题属于求未定式极限的基本题型，对于“0”型极限，应充分利用等价无穷小替换来简化计算. (16) (本题满分8分) 求⎰⎰++Dd y y x σ)(22，其中D 是由圆422=+y x 和1)1(22=++y x 所围成的平面区域(如图).【分析】首先，将积分区域D 分为大圆}4|),{(221≤+=y x y x D 减去小圆}1)1(|),{(222≤++=y x y x D ，再利用对称性与极坐标计算即可.【详解】令}1)1(|),{(},4|),{(222221≤++=≤+=y x y x D y x y x D ，由对称性，0=⎰⎰Dyd σ.⎰⎰⎰⎰⎰⎰+-+=+21222222D D Dd y x d y x d y x σσσ⎰⎰⎰⎰--=θπππθθcos 20223220220dr r d dr r d .)23(916932316-=-=ππ所以，)23(916)(22-=++⎰⎰πσDd y y x . 【评注】本题属于在极坐标系下计算二重积分的基本题型，对于二重积分，经常利用对称性及将一个复杂区域划分为两个或三个简单区域来简化计算. (17) (本题满分8分) 设f (x ) , g (x )在[a , b ]上连续，且满足⎰⎰≥x axadt t g dt t f )()(，x ∈ [a , b )，⎰⎰=bab adt t g dt t f )()(.证明：⎰⎰≤ba b a dx x xg dx x xf )()(.【分析】令F (x ) = f (x ) - g (x )，⎰=xa dt t F x G )()(，将积分不等式转化为函数不等式即可. 【详解】令F (x ) = f (x ) - g (x )，⎰=x a dt t F x G )()(，由题设G (x ) ≥ 0，x ∈ [a , b ]，G (a ) = G (b ) = 0，)()(x F x G ='.从而⎰⎰⎰⎰-=-==bab aba babadx x G dx x G x xG x xdG dx x xF )()()()()(，由于 G (x ) ≥ 0，x ∈ [a , b ]，故有 0)(≤-⎰badx x G ，即0)(≤⎰ba dx x xF .因此⎰⎰≤babadx x xg dx x xf )()(.【评注】引入变限积分转化为函数等式或不等式是证明积分等式或不等式的常用的方法. (18) (本题满分9分) 设某商品的需求函数为Q = 100 - 5P ，其中价格P ∈ (0 , 20)，Q 为需求量. (I) 求需求量对价格的弹性d E (d E > 0)；(II) 推导)1(d E Q dPdR-=(其中R 为收益)，并用弹性d E 说明价格在何范围内变化时，降低价格反而使收益增加. 【分析】由于d E > 0，所以dP dQ Q P E d =；由Q = PQ 及dPdQQ P E d =可推导 )1(d E Q dPdR-=. 【详解】(I) PPdP dQ Q P E d -==20. (II) 由R = PQ ，得)1()1(d E Q dPdQ Q P Q dP dQ P Q dP dR -=+=+=. 又由120=-=PPE d ，得P = 10.当10 < P < 20时，d E > 1，于是0<dPdR，故当10 < P < 20时，降低价格反而使收益增加.【评注】当d E > 0时，需求量对价格的弹性公式为dPdQQ P dP dQ Q P E d -==. 利用需求弹性分析收益的变化情况有以下四个常用的公式：Qdp E dR d )1(-=，Q E dpdRd )1(-=，p E dQ dR d )11(-=， d E EpER-=1(收益对价格的弹性). (19) (本题满分9分) 设级数)(864264242864+∞<<-∞+⋅⋅⋅+⋅⋅+⋅x x x x Λ的和函数为S (x ). 求：(I) S (x )所满足的一阶微分方程； (II) S (x )的表达式.【分析】对S (x )进行求导，可得到S (x )所满足的一阶微分方程，解方程可得S (x )的表达式.【详解】(I) Λ+⋅⋅⋅+⋅⋅+⋅=864264242)(864x x x x S ，易见 S (0) = 0，Λ+⋅⋅+⋅+='642422)(753x x x x S)642422(642Λ+⋅⋅+⋅+=x x x x)](2[2x S x x +=.因此S (x )是初值问题0)0(,23=+='y x xy y 的解.(II) 方程23x xy y +='的通解为]2[3C dx e x e y xdx xdx +⎰⎰=⎰-22212x Ce x +--=，由初始条件y(0) = 0，得C = 1.故12222-+-=x e x y ，因此和函数12)(222-+-=x e x x S .【评注】本题综合了级数求和问题与微分方程问题，2002年考过类似的题. (20)(本题满分13分)设T α)0,2,1(1=, T ααα)3,2,1(2-+=, T b αb α)2,2,1(3+---=, Tβ)3,3,1(-=,试讨论当b a ,为何值时,(Ⅰ) β不能由321,,ααα线性表示;(Ⅱ) β可由321,,ααα唯一地线性表示, 并求出表示式;(Ⅲ) β可由321,,ααα线性表示, 但表示式不唯一, 并求出表示式.【分析】将β可否由321,,ααα线性表示的问题转化为线性方程组βαk αk αk =++332211是否有解的问题即易求解. 【详解】设有数,,,321k k k 使得βαk αk αk =++332211. (*) 记),,(321αααA =. 对矩阵),(βA 施以初等行变换, 有⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-+---+-=323032221111),(b a a b a βA ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---→000101111b a b a .(Ⅰ) 当0=a 时, 有⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---→10001001111),(b βA . 可知),()(βA r A r ≠. 故方程组(*)无解, β不能由321,,ααα线性表示. (Ⅱ) 当0≠a , 且b a ≠时, 有⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---→000101111),(b a b a βA ⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-→0100101011001a a 3),()(==βA r A r , 方程组(*)有唯一解：ak 111-=, a k 12=, 03=k ．此时β可由321,,ααα唯一地线性表示, 其表示式为 211)11(αaαa β+-=． (Ⅲ) 当0≠=b a 时, 对矩阵),(βA 施以初等行变换, 有⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---→000101111),(b a b a βA ⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡--→0000111011001a a ， 2),()(==βA r A r , 方程组(*)有无穷多解，其全部解为a k 111-=, c ak +=12, c k =3，其中c 为任意常数． β 可由321,,ααα线性表示, 但表示式不唯一, 其表示式为321)1()11(αc αc aαa β+++-=．【评注】本题属于常规题型, 曾考过两次(1991, 2000).(21) (本题满分13分) 设n 阶矩阵⎪⎪⎪⎪⎪⎭⎫⎝⎛=111ΛM M M ΛΛb b b bb b A . (Ⅰ) 求A 的特征值和特征向量;(Ⅱ) 求可逆矩阵P , 使得AP P 1-为对角矩阵.【分析】这是具体矩阵的特征值和特征向量的计算问题, 通常可由求解特征方程0||=-A E λ和齐次线性方程组0)(=-x A E λ来解决.【详解】 (Ⅰ) ο1当0≠b 时，111||---------=-λbbb λb b b λA E λΛM M M M ΛΛ＝1)]1(][)1(1[------n b λb n λ ,得A 的特征值为b n λ)1(11-+=，b λλn -===12Λ．对b n λ)1(11-+=，⎪⎪⎪⎪⎪⎭⎫⎝⎛---------=-b n b b b b n bb b bn A E λ)1()1()1(1ΛM M M ΛΛ→⎪⎪⎪⎪⎪⎭⎫⎝⎛---------)1(111)1(111)1(n n n ΛM M M ΛΛ →⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛------------0000111111111111ΛΛM M M M ΛΛn n n →⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛---------0000111111111111ΛΛM M MM ΛΛn n n→⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---000000001111ΛΛM M M M ΛΛn n n n n →⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛---0000110010101001ΛΛM M M MΛΛ解得Tξ)1,,1,1,1(1Λ=，所以A 的属于1λ的全部特征向量为 Tk ξk )1,,1,1,1(1Λ= (k 为任意不为零的常数)．对b λ-=12，⎪⎪⎪⎪⎪⎭⎫⎝⎛---------=-b b b b b b b b b A E λΛM M M ΛΛ2→⎪⎪⎪⎪⎪⎭⎫⎝⎛000000111ΛM M M ΛΛ 得基础解系为T ξ)0,,0,1,1(2Λ-=，T ξ)0,,1,0,1(3Λ-=，T n ξ)1,,0,0,1(,-=ΛΛ．故A 的属于2λ的全部特征向量为n n ξk ξk ξk +++Λ3322 (n k k k ,,,32Λ是不全为零的常数)．ο2 当0=b 时，n λλλλA E λ)1(1010001||-=---=-ΛM M M ΛΛ,特征值为11===n λλΛ，任意非零列向量均为特征向量．(Ⅱ) ο1当0≠b 时，A 有n 个线性无关的特征向量，令),,,(21n ξξξP Λ=，则⎪⎪⎪⎪⎪⎭⎫⎝⎛---+=-b b b n AP P 11)1(11Oο2 当0=b 时，E A =，对任意可逆矩阵P , 均有E AP P =-1．【评注】本题通过考查矩阵的特征值和特征向量而间接考查了行列式的计算, 齐次线性方程组的求解和矩阵的对角化等问题, 属于有一点综合性的试题. 另外,本题的解题思路是容易的, 只要注意矩阵中含有一个未知参数, 从而一般要讨论其不同取值情况. (22) (本题满分13分)设A ，B 为两个随机事件,且41)(=A P , 31)|(=AB P , 21)|(=B A P , 令 ⎩⎨⎧=不发生，，发生，A A X 0,1 ⎩⎨⎧=.0,1不发生，发生，B B Y求(Ⅰ) 二维随机变量),(Y X 的概率分布; (Ⅱ) X 与Y 的相关系数 XY ρ; (Ⅲ) 22Y X Z +=的概率分布.【分析】本题的关键是求出),(Y X 的概率分布，于是只要将二维随机变量),(Y X 的各取值对转化为随机事件A 和B 表示即可．【详解】 (Ⅰ) 因为 121)|()()(==A B P A P AB P ，于是 61)|()()(==B A P AB P B P ，则有 121)(}1,1{====AB P Y X P ， 61)()()(}0,1{=-====AB P A P B A P Y X P ， 121)()()(}1,0{=-====AB P B P B A P Y X P ， 32)]()()([1)(1)(}0,0{=-+-=⋃-=⋅===AB P B P A P B A P B A P Y X P ， ( 或 32121611211}0,0{=---===Y X P )，即),(Y X 的概率分布为：(Ⅱ) 方法一：因为 41)(==A P EX ，61)(==B P EY ，121)(=XY E ， 41)(2==A P EX ，61)(2==B P EY ，163)(22=-=EX EX DX ，165)(22=-=EY EY DY ，241)(),(=-=EXEY XY E Y X Cov ，所以X 与Y 的相关系数 1515151),(==⋅=DYDX Y X Cov ρXY ．方法二： X, Y 的概率分布分别为X 0 1 Y 0 1P 43 41 P 65 61 则61,41==EY EX ，163=DX ，DY=365, E(XY)=121,故 241)(),(=⋅-=EY EX XY E Y X Cov ，从而.1515),(=⋅=DYDX Y X Cov XY ρ(Ⅲ) Z 的可能取值为：0，1，2 ．32}0,0{}0{=====Y X P Z P ， 41}1,0{}0,1{}1{===+====Y X P Y X P Z P ， 121}1,1{}2{=====Y X P Z P ，即Z 的概率分布为：【评注】本题考查了二维离散随机变量联合概率分布，数字特征和二维离散随机变量函数的分布等计算问题，属于综合性题型 (23) (本题满分13分)设随机变量X 的分布函数为⎪⎩⎪⎨⎧≤>⎪⎭⎫ ⎝⎛-=，，，αx αx x αβαx F β0,1),,( 其中参数1,0>>βα. 设n X X X ,,,21Λ为来自总体X 的简单随机样本,(Ⅰ) 当1=α时, 求未知参数β的矩估计量; (Ⅱ) 当1=α时, 求未知参数β的最大似然估计量; (Ⅲ) 当2=β时, 求未知参数α的最大似然估计量.【分析】本题是一个常规题型, 只要注意求连续型总体未知参数的矩估计和最大似然估计都须已知密度函数, 从而先由分布函数求导得密度函数. 【详解】当1=α时, X 的概率密度为⎪⎩⎪⎨⎧≤>=+，，，101,),(1x x x ββx f β(Ⅰ) 由于⎰⎰+∞++∞∞--=⋅==11,1);(ββdx x βx dx βx xf EX β 令X ββ=-1, 解得 1-=X X β, 所以, 参数β的矩估计量为 1-=X Xβ.(Ⅱ) 对于总体X 的样本值n x x x ,,,21Λ, 似然函数为∏=+⎪⎩⎪⎨⎧=>==ni i βnni n i x x x x βαx f βL 1121.,0),,,2,1(1,)();()(其他ΛΛ当),,2,1(1n i x i Λ=>时, 0)(>βL , 取对数得 ∑=+-=ni ixββn βL 1ln )1(ln )(ln ,对β求导数，得∑=-=ni i x βn βd βL d 1ln )]([ln ，令0ln )]([ln 1=-=∑=ni i x βn βd βL d ，解得 ∑==ni ixnβ1ln ，于是β的最大似然估计量为∑==ni ixn1ln ˆβ．( Ⅲ) 当2=β时, X 的概率密度为⎪⎩⎪⎨⎧≤>=，，，αx αx x αβx f 0,2),(32对于总体X 的样本值n x x x ,,,21Λ, 似然函数为∏=⎪⎩⎪⎨⎧=>==ni i nnn i n i αx x x x ααx f βL 13212.,0),,,2,1(,)(2);()(其他ΛΛ当),,2,1(n i αx i Λ=>时, α越大，)(αL 越大, 即α的最大似然估计值为},,,m in{ˆ21n x x x αΛ=, 于是α的最大似然估计量为},,,m in{ˆ21n X X X αΛ=．。

2016年考研数学三真题及解析

2016年考研数学三真题及解析2016年考研数学（三）真题一、填空题：1－6小题，每小题4分，共24分. 把答案填在题中横线上.（1）()11lim ______.nn n n-→∞+⎛⎫= ⎪⎝⎭（2）设函数()f x 在2x =的某邻域内可导,且()()e f xf x '=，()21f =，则()2____.f '''=（3）设函数()f u 可微,且()102f '=,则()224z f xy =-在点(1,2)处的全微分()1,2d _____.z =（4）设矩阵2112A ⎛⎫= ⎪-⎝⎭，E 为2阶单位矩阵，矩阵B 满足2BA B E=+，则=B .（5）设随机变量X Y 与相互独立，且均服从区间[]0,3上的均匀分布，则{}{}max ,1P X Y ≤=_______. （6）设总体X 的概率密度为()()121,,,,2xnf x ex X X X -=-∞<<+∞L为总体X 的简单随机样本，其样本方差为2S ，则2____.ES=二、选择题：7－14小题，每小题4分，共32分. 每小题给出的四个选项中，只有一项符合题目要求，把所选项前的字母填在题后的括号内.（7）设函数()y f x =具有二阶导数，且()0,()0f x f x '''>>，x ∆为自变量x 在点0x 处的增量，d y y ∆与分别为()f x 在点0x 处对应的增量与微分，若0x ∆>，则(A) 0d y y<<∆. (B)0d y y<∆<.(C) d 0y y ∆<<. (D)d 0y y <∆< .[ ]（8）设函数()f x 在0x =处连续，且()22lim1h f h h →=，则(A) ()()000f f -'=且存在 (B)()()010f f -'=且存在(C)()()000f f +'=且存在(D)()()010f f +'=且存在 [ ] （9）若级数1n n a ∞=∑收敛，则级数(A) 1nn a ∞=∑收敛 . （B ）1(1)nnn a ∞=-∑收敛.(C) 11n n n a a ∞+=∑收敛. (D) 112nn n aa ∞+=+∑收敛.[ ]（10）设非齐次线性微分方程()()y P x y Q x '+=有两个不同的解12(),(),y x y x C为任意常数，则该方程的通解是（Ａ）[]12()()C y x y x -. （Ｂ）[]112()()()y x C y x y x +-. （Ｃ）[]12()()C y x y x +. （Ｄ）[]112()()()y x C y x y x ++[ ]（11）设(,)(,)f x y x y ϕ与均为可微函数，且(,)0yx y ϕ'≠，已知0(,)x y 是(,)f x y 在约束条件(,)0x y ϕ=下的一个极值点，下列选项正确的是(A) 若0(,)0xf x y '=，则0(,)0yf x y '=.(B) 若0(,)0xf x y '=，则0(,)0yf x y '≠.(C) 若0(,)0xf x y '≠，则0(,)0yf x y '=.(D)若00(,)0x f x y '≠，则00(,)0y f x y '≠.[ ]（12）设12,,,sαααL 均为n 维列向量，A 为m n ⨯矩阵，下列选项正确的是 (A) 若12,,,sαααL 线性相关，则12,,,sA A A αααL 线性相关.(B)若12,,,sαααL 线性相关，则12,,,sA A A αααL 线性无关.(C) 若12,,,sαααL 线性无关，则12,,,sA A A αααL 线性相关. (D) 若12,,,sαααL 线性无关，则12,,,sA A A αααL 线性无关.[ ]（13）设A 为3阶矩阵，将A 的第2行加到第1行得B ，再将B 的第1列的1-倍加到第2列得C ，记110010001P ⎛⎫ ⎪= ⎪⎪⎝⎭，则（Ａ）1C PAP-=. （Ｂ）1C PAP -=.（Ｃ）TC P AP=. （Ｄ）TC PAP =. ［］（14）设随机变量X 服从正态分布211(,)N μσ，Y 服从正态分布222(,)N μσ，且{}{}1211P X P Y μμ-<>-<则必有(A) 12σσ< (B) 12σσ>(C)12μμ< (D) 12μμ>[ ]三、解答题：15－23小题，共94分. 解答应写出文字说明、证明过程或演算步骤. （15）（本题满分7分）设()1sin,,0,01arctan xy y yf x y x y xy xπ-=->>+,求(Ⅰ) ()()lim ,y g x f x y →+∞=；(Ⅱ)()0lim x g x +→.（16）（本题满分7分）计算二重积分d Dx y，其中D 是由直线,1,0y x y x ===所围成的平面区域. （17）（本题满分10分）证明：当0a b π<<<时，sin 2cos sin 2cos b b b b a a a aππ++>++.（18）（本题满分8分）在xOy 坐标平面上，连续曲线L 过点()1,0M ，其上任意点()(),0P x y x ≠处的切线斜率与直线OP 的斜率之差等于ax（常数>0a ）. (Ⅰ) 求L 的方程；(Ⅱ) 当L 与直线y ax =所围成平面图形的面积为83时，确定a 的值.（19）（本题满分10分）求幂级数()()1211121n n n x n n -+∞=--∑的收敛域及和函数()s x .（20）（本题满分13分）设4维向量组()()()TTT1231,1,1,1,2,2,2,2,3,3,3,3,a a a ααα=+=+=+()T44,4,4,4a α=+，问a 为何值时1234,,,αααα线性相关?当1234,,,αααα线性相关时,求其一个极大线性无关组,并将其余向量用该极大线性无关组线性表出. （21）（本题满分13分）设3阶实对称矩阵A 的各行元素之和均为3,向量()()TT121,2,1,0,1,1αα=--=-是线性方程组0Ax =的两个解.(Ⅰ)求A 的特征值与特征向量； (Ⅱ)求正交矩阵Q 和对角矩阵Λ,使得TQ AQ =Λ；（Ⅲ）求A 及632A E ⎛⎫-⎪⎝⎭，其中E 为3阶单位矩阵.（22）（本题满分13分）设随机变量X 的概率密度为()1,1021,0240,X x f x x ⎧-<<⎪⎪⎪=≤<⎨⎪⎪⎪⎩　其他，令()2,,Y XF x y =为二维随机变量(,)X Y 的分布函数.(Ⅰ)求Y 的概率密度()Yf y ； (Ⅱ)Cov(,)X Y ；(Ⅲ)1,42F ⎛⎫- ⎪⎝⎭. （23）（本题满分13分）设总体X 的概率密度为(),01,;1,12,0,x f x x θθθ<<⎧⎪=-≤<⎨⎪⎩其他,其中θ是未知参数()01θ<<，12n,...,X X X 为来自总体X 的简单随机样本，记N 为样本值12,...,nx x x 中小于1的个数.（Ⅰ）求θ的矩估计；（Ⅱ）求θ的最大似然估计2006年考研数学（三）真题解析二、填空题：1－6小题，每小题4分，共24分. 把答案填在题中横线上.（1）()11lim 1.nn n n-→∞+⎛⎫= ⎪⎝⎭【分析】将其对数恒等化ln e NN =求解. 【详解】()(1)111ln lim (1)ln 1lim lim eennn n n n n n n n n n -→∞-++⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭→∞→∞+⎛⎫== ⎪⎝⎭，而数列{}(1)n -有界，1lim ln 0n n n →∞+⎛⎫= ⎪⎝⎭，所以1lim(1)ln 0n n n n →∞+⎛⎫-= ⎪⎝⎭. 故()101lim e 1nn n n -→∞+⎛⎫== ⎪⎝⎭.（2）设函数()f x 在2x =的某邻域内可导,且()()e f xf x '=，()21f =，则()322e .f '''=【分析】利用复合函数求导即可.【详解】由题设知，()()e f xf x '=，两边对x 求导得()()()2e()ef x f x f x f x '''==，两边再对x 求导得()()23()2e()2ef x f x f x f x ''''==，又()21f =，故 ()323(2)2e2e f f '''==.（3）设函数()f u 可微,且()102f '=,则()224z f xy =-在点(1,2)处的全微分()1,2d 4d 2d .z x y =-【分析】利用二元函数的全微分公式或微分形式不变性计算.【详解】方法一：因为22(1,2)(1,2)(4)84z f x y xx∂'=-⋅=∂，()22(1,2)(1,2)(4)22z f x y y y∂'=-⋅-=-∂，所以()()()1,21,21,2d d d 4d 2d z z zx y x y xy⎡⎤∂∂=+=-⎢⎥∂∂⎣⎦.方法二：对()224z f x y =-微分得()222222d (4)d(4)(4)8d 2d z f x y x y f x y x x y y ''=--=--，故 ()()1,2d (0)8d 2d 4d 2d zf x y x y'=-=-.（4）设矩阵2112A ⎛⎫=⎪-⎝⎭，E 为2阶单位矩阵，矩阵B 满足2BA B E=+，则=B 2 .【分析】将矩阵方程改写为AX B XA B AXB C ===或或的形式，再用方阵相乘的行列式性质进行计算即可.【详解】由题设，有 ()2B A E E -=于是有4B A E -=，而11211A E -==-，所以2B =.（5）设随机变量X Y 与相互独立，且均服从区间[]0,3上的均匀分布，则{}{}max ,1P X Y ≤=19. 【分析】利用X Y 与的独立性及分布计算. 【详解】由题设知，X Y 与具有相同的概率密度1,3()30,x f x ⎧≤≤⎪=⎨⎪⎩ 0 其他.则 {}{}{}max ,11,1P X Y P X Y ≤=≤≤{}{}11P X P Y =≤≤{}()2120111d 39P X x ⎛⎫=≤== ⎪⎝⎭⎰.【评注】本题属几何概型，也可如下计算，如下图：则 {}{}{}1max ,11,19S P X Y P X Y S≤=≤≤==阴.（6）设总体X 的概率密度为()()121,,,,2xnf x ex X X X -=-∞<<+∞L为总体X 的简单随机样本，其样本方差为2S ，则22.ES =【分析】利用样本方差的性质2ES DX=即可.【详解】因为()d e d 02xx EX xf x x x +∞+∞--∞-∞===⎰⎰，22222000()d e d e d e 2e d 2xx xx x EX x f x x x x x x x x+∞+∞+∞+∞---+∞--∞-∞====-+⎰⎰⎰⎰2e 2e d 2e 2xx xx x +∞-+∞--+∞=-+=-=⎰，所以()22202DX EX EX =-=-=，又因2S 是DX 的无偏估计量，所以22ES DX ==.二、选择题：7－14小题，每小题4分，共32分. 每小题给出的四个选项中，只有一项符合题目要求，把所选项前的字母填在题后的括号内.（7）设函数()y f x =具有二阶导数，且()0,()0f x f x '''>>，x ∆为自变量x 在点0x 处的增量，d y y ∆与分别为()f x 在点0x 处对应的增量与微分，若0x ∆>，则(A) 0d y y<<∆.(B)0d y y<∆<.(C)d 0y y ∆<<. (D)d 0y y <∆< . [ Ａ ]【分析】题设条件有明显的几何意义，用图示法求解.【详解】由()0,()0f x f x '''>>知，函数()f x 单调增加，曲线()y f x =凹向，作函数()y f x =的图形如右图所示，显然当x ∆>时，00d ()d ()0y y f x x f x x ''∆>==∆>，故应选(Ａ).（8）设函数()f x 在0x =处连续，且()22lim 1h f h h →=，则(A) ()()000f f -'=且存在 (B) ()()010f f -'=且存在(C)()()000f f +'=且存在 (D)()()010f f +'=且存在[ C ] 【分析】从()220lim1h f h h→=入手计算(0)f ，利用导数的左右导数定义判定(0),(0)f f -+''的存在性.【详解】由()22lim 1h f h h→=知，()2lim 0h f h →=.又因为()f x 在0x =处连续，则()20(0)lim ()lim 0x h f f x f h →→===.令2t h =，则()()220(0)1limlim (0)h t f h f t f f h t++→→-'===.所以(0)f +'存在，故本题选（C ）.（9）若级数1n n a ∞=∑收敛，则级数(A) 1nn a ∞=∑收敛 . （B ）1(1)nnn a ∞=-∑收敛.(C) 11n n n a a ∞+=∑收敛. (D) 112nn n aa ∞+=+∑收敛.[ Ｄ ]【分析】可以通过举反例及级数的性质来判定. 【详解】由1nn a ∞=∑收敛知11n n a ∞+=∑收敛，所以级数112nn n aa ∞+=+∑收敛，故应选(Ｄ). 或利用排除法：取1(1)nna n=-，则可排除选项（Ａ），（Ｂ）；取(1)nna =-.故（Ｄ）项正确.（10）设非齐次线性微分方程()()y P x y Q x '+=有两个不同的解12(),(),y x y x C为任意常数，则该方程的通解是（Ａ）[]12()()C y x y x -. （Ｂ）[]112()()()y x C y x y x +-.（Ｃ）[]12()()C y x y x +. （Ｄ）[]112()()()y x C y x y x ++ [ Ｂ ]【分析】利用一阶线性非齐次微分方程解的结构即可.【详解】由于12()()y x y x -是对应齐次线性微分方程()0y P x y '+=的非零解，所以它的通解是[]12()()Y C y x y x =-，故原方程的通解为[]1112()()()()y y x Y y x C y x y x =+=+-，故应选(Ｂ).【评注】本题属基本题型，考查一阶线性非齐次微分方程解的结构：*y y Y=+.其中*y 是所给一阶线性微分方程的特解，Y 是对应齐次微分方程的通解.（11）设(,)(,)f x y x y ϕ与均为可微函数，且(,)0yx y ϕ'≠，已知0(,)x y 是(,)f x y 在约束条件(,)0x y ϕ=下的一个极值点，下列选项正确的是(A) 若0(,)0xf x y '=，则0(,)0yf x y '=.(B) 若0(,)0xf x y '=，则0(,)0yf x y '≠.(C) 若0(,)0xf x y '≠，则0(,)0yf x y '=.(D)若00(,)0x f x y '≠，则00(,)0y f x y '≠.[ Ｄ ]【分析】利用拉格朗日函数(,,)(,)(,)F x y f x y x y λλϕ=+在000(,,)x y λ（0λ是对应0,x y 的参数λ的值）取到极值的必要条件即可.【详解】作拉格朗日函数(,,)(,)(,)F x y f x y x y λλϕ=+，并记对应0,x y 的参数λ的值为0λ，则000000(,,)0(,,)0x y F x y F x y λλ⎧'=⎪⎨'=⎪⎩，即0000000000(,)(,)0(,)(,)0x x y y f x y x y f x y x y λϕλϕ⎧''+=⎪⎨''+=⎪⎩ .消去0λ，得(,)(,)(,)(,)0xyyxf x y x y f x y x y ϕϕ''''-=,整理得000000001(,)(,)(,)(,)x y x y f x y f x y x y x y ϕϕ'''='.（因为(,)0yx y ϕ'≠），若0(,)0xf x y '≠，则0(,)0yf x y '≠.故选（Ｄ）.（12）设12,,,sαααL 均为n 维列向量，A 为m n ⨯矩阵，下列选项正确的是 (A)若12,,,sαααL 线性相关，则12,,,sA A A αααL 线性相关.(B) 若12,,,sαααL 线性相关，则12,,,sA A A αααL 线性无关.(C) 若12,,,sαααL 线性无关，则12,,,sA A A αααL 线性相关. (D) 若12,,,sαααL 线性无关，则12,,,sA A A αααL 线性无关.[ A ]【分析】本题考查向量组的线性相关性问题，利用定义或性质进行判定.【详解】记12(,,,)sB ααα=L ，则12(,,,)sA A A AB ααα=L .所以，若向量组12,,,sαααL 线性相关，则()r B s <，从而()()r AB r B s≤<，向量组12,,,sA A A αααL 也线性相关，故应选(Ａ).（13）设A 为3阶矩阵，将A 的第2行加到第1行得B ，再将B 的第1列的1-倍加到第2列得C ，记110010001P ⎛⎫ ⎪= ⎪⎪⎝⎭，则（Ａ）1C P AP-=. （Ｂ）1C PAP -=.（Ｃ）TC PAP=. （Ｄ）TC PAP =. ［Ｂ］【分析】利用矩阵的初等变换与初等矩阵的关系以及初等矩阵的性质可得. 【详解】由题设可得110110*********,010010010001001001001B A C B A --⎛⎫⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪=== ⎪ ⎪ ⎪ ⎪⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭ ，而1110010001P --⎛⎫ ⎪= ⎪⎪⎝⎭，则有1C PAP -=.故应选（Ｂ）.（14）设随机变量X 服从正态分布211(,)N μσ，Y 服从正态分布222(,)N μσ，且{}{}1211P X P Y μμ-<>-<则必有(A) 12σσ< (B) 12σσ>(C)12μμ< (D) 12μμ>[ A ]【分析】利用标准正态分布密度曲线的几何意义可得.【详解】由题设可得12112211X Y P P μμσσσσ⎧-⎫⎧-⎫<><⎨⎬⎨⎬⎩⎭⎩⎭，则12112121σσ⎛⎫⎛⎫Φ->Φ- ⎪ ⎪⎝⎭⎝⎭，即1211σσ⎛⎫⎛⎫Φ>Φ ⎪ ⎪⎝⎭⎝⎭. 其中()x Φ是标准正态分布的分布函数. 又()x Φ是单调不减函数，则1211σσ>，即12σσ<.故选(A).三、解答题：15－23小题，共94分. 解答应写出文字说明、证明过程或演算步骤.（15）（本题满分7分）设()1sin,,0,01arctan xy y yf x y x y xy xπ-=->>+,求(Ⅰ) ()()lim ,y g x f x y →+∞=；(Ⅱ)()0lim x g x +→.【分析】第(Ⅰ)问求极限时注意将x 作为常量求解，此问中含,0∞⋅∞∞型未定式极限；第(Ⅱ)问需利用第(Ⅰ)问的结果，含∞-∞未定式极限. 【详解】(Ⅰ)()()1sin lim ,lim 1arctan y y x y y y g x f x y xy x π→+∞→∞⎛⎫- ⎪⎪==-+ ⎪⎪⎝⎭sin 11111lim 1arctan arctan y x yx y x x x x y ππ→∞⎛⎫⎪ ⎪-⎪⎪-=-=-⎪ ⎪+ ⎪ ⎪ ⎪⎝⎭.(Ⅱ)()200011arctan lim lim lim arctan arctan x x x x x x x g x x x x xππ+++→→→--+⎛⎫=-= ⎪⎝⎭ （通分）22222000112arctan 2(1)1lim lim lim 22x x x x x x x x x x x x x xππππ+++→→→-+-+-+++====（16）（本题满分7分）计算二重积分d Dx y，其中D 是由直线,1,0y x y x ===所围成的平面区域.【分析】画出积分域，将二重积分化为累次积分即可.【详解】积分区域如右图.因为根号下的函数为关于x 的一次函数，“先x 后y”积分较容易，所以1220d d d d yDy xy x y y y xy x-=-⎰⎰⎰⎰()311222002122d d 339y y xy y y y y=--==⎰⎰（17）（本题满分10分）证明：当0a b π<<<时，sin 2cos sin 2cos b b b b a a a aππ++>++.【分析】利用“参数变易法”构造辅助函数，再利用函数的单调性证明.【详解】令()sin 2cos sin 2cos ,0f x x x x x a a a a a x b πππ=++---<≤≤<，则 ()sin cos 2sin cos sin f x x x x x x x x ππ'=+-+=-+，且()0f π'=.又()cos sin cos sin 0f x x x x x x x ''=--=-<，（0,sin 0x x x π<<>时），故当0a x b π<≤≤<时，()f x '单调减少，即()()0f x f π''>=，则()f x 单调增加，于是()()0f b f a >=，即sin 2cos sin 2cos b b b b a a a aππ++>++.（18）（本题满分8分）在xOy 坐标平面上，连续曲线L 过点()1,0M ，其上任意点()(),0P x y x ≠处的切线斜率与直线OP 的斜率之差等于ax （常数>0a ）. (Ⅰ) 求L 的方程；(Ⅱ) 当L 与直线y ax =所围成平面图形的面积为83时，确定a 的值.【分析】(Ⅰ)利用导数的几何意义建立微分方程，并求解；(Ⅱ)利用定积分计算平面图形的面积，确定参数.【详解】(Ⅰ) 设曲线L 的方程为()y f x =，则由题设可得yy ax x'-=，这是一阶线性微分方程，其中1(),()P x Q x axx=-=，代入通解公式得()11d d 2e e d x x x x y ax x C x ax C ax Cx -⎛⎫⎰⎰=+=+=+ ⎪⎝⎭⎰，又(1)0f =，所以C a =-. 故曲线L 的方程为2y ax ax =-(0)x ≠.(Ⅱ) L 与直线y ax =（>0a ）所围成平面图形如右图所示. 所以 ()22d D ax ax ax x ⎡⎤=--⎣⎦⎰()220482d 33a x x x a =-==⎰，故2a =.（19）（本题满分10分）求幂级数()()1211121n n n x n n -+∞=--∑的收敛域及和函数()s x .【分析】因为幂级数缺项，按函数项级数收敛域的求法计算；利用逐项求导或积分并结合已知函数的幂级数展开式计算和函数. 【详解】记121(1)()(21)n n n x u x n n -+-=-，则 2321121(1)()(1)(21)lim lim (1)()(21)n n n n n n n nx u x n n x x u x n n ++-+→∞→∞-++==--.所以当21,1xx <<即时，所给幂级数收敛；当1x >时，所给幂级数发散；当1x =±时，所给幂级数为1(1)(1),(21)(21)n nn n n n -----，均收敛，故所给幂级数的收敛域为[]1,1- 在()1,1-内，()12112111(1)(1)()22()(21)(21)2n n n nn n x x s x x xs x n n n n -+-∞∞==--===--∑∑，而12112211211(1)1(),()(1)211n n n n n n x s x s x x n x --∞∞--==-'''==-=-+∑∑，所以 111201()(0)()d d arctan 1xxs x s s t t t x t ''''-===+⎰⎰，又1(0)0s '=，于是1()arctan s x x'=.同理1110()(0)()d arctan d xxs x s s t t t t'-==⎰⎰()20201arctan d arctan ln 112xx t t t t x x x t =-=-++⎰，又 1(0)0s =，所以()211()arctan ln 12s x x x x =-+.故()22()2arctan ln 1s x x x x x =-+.()1,1x ∈-.由于所给幂级数在1x =±处都收敛，且()22()2arctan ln 1s x x x x x =-+在1x =± 处都连续，所以()s x 在1x =±成立，即()22()2arctan ln 1s x x x x x =-+，[]1,1x ∈-.（20）（本题满分13分）设4维向量组()()()TTT1231,1,1,1,2,2,2,2,3,3,3,3,a a a ααα=+=+=+()T44,4,4,4a α=+，问a 为何值时1234,,,αααα线性相关?当1234,,,αααα线性相关时,求其一个极大线性无关组,并将其余向量用该极大线性无关组线性表出.【分析】因为向量组中的向量个数和向量维数相同，所以用以向量为列向量的矩阵的行列式为零来确定参数a ；用初等变换求极大线性无关组.【详解】记以1234,,,αααα为列向量的矩阵为A ，则312341234(10)12341234a a A a a a a++==+++.于是当0,010A a a ===-即或时，1234,,,αααα线性相关.当0a =时，显然1α是一个极大线性无关组，且2131412,3,4αααααα===；当10a =-时，1α 2α 3α 4α9234183412741236A -⎛⎫ ⎪-⎪= ⎪- ⎪-⎝⎭，由于此时A 有三阶非零行列式9231834000127--=-≠-，所以123,,ααα为极大线性无关组，且123441230αααααααα+++==---，即.（21）（本题满分13分）设3阶实对称矩阵A 的各行元素之和均为3,向量()()TT121,2,1,0,1,1αα=--=-是线性方程组0Ax =的两个解.(Ⅰ) 求A 的特征值与特征向量； (Ⅱ) 求正交矩阵Q 和对角矩阵Λ,使得TQ AQ =Λ；（Ⅲ）求A 及632A E ⎛⎫-⎪⎝⎭，其中E 为3阶单位矩阵.【分析】由矩阵A 的各行元素之和均为3及矩阵乘法可得矩阵A 的一个特征值和对应的特征向量；由齐次线性方程组0Ax =有非零解可知A 必有零特征值，其非零解是0特征值所对应的特征向量.将A 的线性无关的特征向量正交化可得正交矩阵Q ；由TQAQ =Λ可得到A 和632A E ⎛⎫-⎪⎝⎭.【详解】 (Ⅰ) 因为矩阵A 的各行元素之和均为3，所以1311331131A ⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，则由特征值和特征向量的定义知，3λ=是矩阵A 的特征值，T(1,1,1)α=是对应的特征向量.对应3λ=的全部特征向量为k α，其中k 为不为零的常数. 又由题设知 120,0A A αα==，即11220,0A A αααα=⋅=⋅，而且12,αα线性无关，所以0λ=是矩阵A 的二重特征值，12,αα是其对应的特征向量，对应0λ=的全部特征向量为 1122k k αα+，其中12,k k 为不全为零的常数.(Ⅱ) 因为A 是实对称矩阵，所以α与12,αα正交，所以只需将12,αα正交.取 11βα=，()()21221111012,3120,61112αββαβββ⎛⎫-⎪-⎛⎫⎛⎫⎪- ⎪ ⎪=-=--= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭ ⎪⎝⎭.再将12,,αββ单位化，得1212312,,0ββαηηηαββ⎛⎛⎪====== ⎪ ⎪ ⎪ ⎪⎪ ⎪ ⎪⎝⎭ ⎪⎝⎭，令 []123,,Q ηηη=，则1TQQ -=，由A 是实对称矩阵必可相似对角化，得T 300Q AQ ⎡⎤⎢⎥==Λ⎢⎥⎢⎥⎣⎦. （Ⅲ）由(Ⅱ)知T 300Q AQ ⎡⎤⎢⎥==Λ⎢⎥⎢⎥⎣⎦，所以T 31110011101110A Q Q ⎛⎫⎪⎪⎛⎫⎛⎫⎪ ⎪ ⎪=Λ==⎪ ⎪ ⎪ ⎪ ⎪⎪ ⎝⎭⎝⎭⎪ ⎪ ⎪⎪⎝⎭⎭.666T T T 333222Q A E Q Q A E Q Q AQ E ⎡⎤⎛⎫⎛⎫⎛⎫-=-=- ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦6666633223333022203322E ⎛⎫⎛⎫⎡⎤⎛⎫ ⎪ ⎪⎢⎥ ⎪⎝⎭ ⎪⎛⎫⎢⎥ ⎪ ⎪⎛⎫⎛⎫ ⎪⎢⎥ ⎪ ⎪=-== ⎪ ⎪ ⎪⎢⎥ ⎪ ⎪⎝⎭⎝⎭ ⎪⎢⎥ ⎪ ⎪⎝⎭⎢⎥ ⎪⎛⎫ ⎪ ⎪⎢⎥ ⎪⎝⎭⎣⎦⎪⎝⎭⎝⎭，则666T 333222A E Q EQ E⎛⎫⎛⎫⎛⎫-== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.（22）（本题满分13分）设随机变量X 的概率密度为()1,1021,0240,X x f x x ⎧-<<⎪⎪⎪=≤<⎨⎪⎪⎪⎩　其他，令()2,,Y X F x y =为二维随机变量(,)X Y 的分布函数.(Ⅰ) 求Y 的概率密度()Yf y ；(Ⅱ) Cov(,)X Y ； (Ⅲ)1,42F ⎛⎫- ⎪⎝⎭.【分析】求一维随机变量函数的概率密度一般先求分布，然后求导得相应的概率密度或利用公式计算. 【详解】（I ）设Y 的分布函数为()YF y ，即2()()()Y F y P Y y P X y =≤=≤，则1) 当0y <时，()0YF y =；2) 当01y ≤<时，(2()()YF y P X y P X =<=<<001d 4x x =+=⎰3) 当14y ≤<时，(2()()1YF y P X y P X =<=-<<010111d d 242x x -=+=⎰. 4) 当4y ≥，()1YF y =.所以1()()40,Y Y y f y F y y <<⎪'==≤<⎪⎩其他.（II ） 22232Cov(,)Cov(,)()()X Y X X E X EX X EX EX EXEX ==--=-，而2101d d 244x x EX x x -=+=⎰⎰，2222105d d 246x x EX x x -=+=⎰⎰，33023107d d 248x x EX x x -=+=⎰⎰，所以 7152Cov(,)8463X Y =-⋅=.(Ⅲ)1,42F ⎛⎫- ⎪⎝⎭211,4,422P X Y P X X ⎛⎫⎛⎫=≤-≤=≤-≤ ⎪ ⎪⎝⎭⎝⎭11,22222P X X P X ⎛⎫⎛⎫=≤--≤≤=-≤≤- ⎪ ⎪⎝⎭⎝⎭12111d 24x --==⎰.2016年考研各科目专用题库复习和考试软件说明：本人已于2015年顺利通过了考研。

2016年考研数学三真题及答案解析

启航考研只为一次考上研
2016 考研数学三真题及超详细答案解析
天任启航考研
启航考研只为一次考上研天任启航考研
启航考研只为一次考上研天任启航考研
启航考研只为一次考上研天任启航考研
启航考研只为一次考上研天任启航考研
启航考研只为一次考上研天任启航考研
启航考研只为一次考上研
启航考研只为一次考上研天任启航考研
启航考研只为一次考上研天任启航考研
启航考研只航考研
启航考研只为一次考上研天任启航考研
启航考研只为一次考上研天任启航考研
启航考研只为一次考上研天任启航考研
启航考研只为一次考上研天任启航考研
启航考研只为一次考上研天任启航考研
启航考研只为一次考上研天任启航考研
启航考研只为一次考上研天任启航考研
启航考研只为一次考上研天任启航考研
P
天任启航考研

2016年考研数学三真题及解析

2016年考研数学（三）真题一、填空题：1－6小题，每小题4分，共24分. 把答案填在题中横线上. （1）()11lim ______.nn n n -→∞+⎛⎫=⎪⎝⎭（2）设函数()f x 在2x =的某邻域内可导,且()()e f x f x '=，()21f =，则()2____.f '''=（3）设函数()f u 可微,且()102f '=,则()224z f x y =-在点(1,2)处的全微分()1,2d _____.z =（4）设矩阵2112A ⎛⎫=⎪-⎝⎭，E 为2阶单位矩阵，矩阵B 满足2BA B E =+，则=B . （5）设随机变量X Y 与相互独立，且均服从区间[]0,3上的均匀分布，则{}{}max ,1P X Y ≤=_______. （6）设总体X 的概率密度为()()121,,,,2xn f x e x X X X -=-∞<<+∞为总体X 的简单随机样本，其样本方差为2S ，则2____.ES =二、选择题：7－14小题，每小题4分，共32分. 每小题给出的四个选项中，只有一项符合题目要求，把所选项前的字母填在题后的括号内.（7）设函数()y f x =具有二阶导数，且()0,()0f x f x '''>>，x ∆为自变量x 在点0x 处的增量，d y y ∆与分别为()f x 在点0x 处对应的增量与微分，若0x ∆>，则(A) 0d y y <<∆. (B) 0d y y <∆<.(C) d 0y y ∆<<. (D) d 0y y <∆< . [ ]（8）设函数()f x 在0x =处连续，且()22lim1h f h h→=，则(A) ()()000f f -'=且存在 (B) ()()010f f -'=且存在(C) ()()000f f +'=且存在 (D)()()010f f +'=且存在 [ ] （9）若级数1nn a∞=∑收敛，则级数(A)1nn a∞=∑收敛 . （B ）1(1)nn n a ∞=-∑收敛.(C)11n n n a a ∞+=∑收敛. (D)112n n n a a ∞+=+∑收敛. [ ]（10）设非齐次线性微分方程()()y P x y Q x '+=有两个不同的解12(),(),y x y x C 为任意常数，则该方程的通解是（Ａ）[]12()()C y x y x -. （Ｂ）[]112()()()y x C y x y x +-.（Ｃ）[]12()()C y x y x +. （Ｄ）[]112()()()y x C y x y x ++ [ ]（11）设(,)(,)f x y x y ϕ与均为可微函数，且(,)0y x y ϕ'≠，已知00(,)x y 是(,)f x y 在约束条件(,)0x y ϕ=下的一个极值点，下列选项正确的是(A) 若00(,)0x f x y '=，则00(,)0y f x y '=. (B) 若00(,)0x f x y '=，则00(,)0y f x y '≠. (C) 若00(,)0x f x y '≠，则00(,)0y f x y '=.(D) 若00(,)0x f x y '≠，则00(,)0y f x y '≠. [ ] （12）设12,,,s ααα均为n 维列向量，A 为m n ⨯矩阵，下列选项正确的是(A) 若12,,,s ααα线性相关，则12,,,s A A A ααα线性相关. (B) 若12,,,s ααα线性相关，则12,,,s A A A ααα线性无关. (C) 若12,,,s ααα线性无关，则12,,,s A A A ααα线性相关.(D) 若12,,,s ααα线性无关，则12,,,s A A A ααα线性无关. [ ]（13）设A 为3阶矩阵，将A 的第2行加到第1行得B ，再将B 的第1列的1-倍加到第2列得C ，记110010001P ⎛⎫⎪= ⎪ ⎪⎝⎭，则（Ａ）1C P AP -=. （Ｂ）1C PAP -=.（Ｃ）T C P AP =. （Ｄ）TC PAP =. ［］（14）设随机变量X 服从正态分布211(,)N μσ，Y 服从正态分布222(,)N μσ，且则必有(A) 12σσ< (B) 12σσ>(C) 12μμ< (D) 12μμ> [ ]三、解答题：15－23小题，共94分. 解答应写出文字说明、证明过程或演算步骤. （15）（本题满分7分）设()1sin,,0,01arctan xy y yf x y x y xy xπ-=->>+,求 (Ⅰ) ()()lim ,y g x f x y →+∞=；(Ⅱ) ()0lim x g x +→. （16）（本题满分7分）计算二重积分2d d Dy xy x y -⎰⎰，其中D 是由直线,1,0y x y x ===所围成的平面区域.（17）（本题满分10分）证明：当0a b π<<<时，sin 2cos sin 2cos b b b b a a a a ππ++>++.（18）（本题满分8分）在xOy 坐标平面上，连续曲线L 过点()1,0M ，其上任意点()(),0P x y x ≠处的切线斜率与直线OP 的斜率之差等于ax （常数>0a ）.(Ⅰ) 求L 的方程；(Ⅱ) 当L 与直线y ax =所围成平面图形的面积为83时，确定a 的值. （19）（本题满分10分）求幂级数()()1211121n n n x n n -+∞=--∑的收敛域及和函数()s x .（20）（本题满分13分）设4维向量组()()()TTT1231,1,1,1,2,2,2,2,3,3,3,3,a a a ααα=+=+=+()T44,4,4,4a α=+，问a 为何值时1234,,,αααα线性相关当1234,,,αααα线性相关时,求其一个极大线性无关组,并将其余向量用该极大线性无关组线性表出. （21）（本题满分13分）设3阶实对称矩阵A 的各行元素之和均为3,向量()()TT121,2,1,0,1,1αα=--=-是线性方程组0Ax =的两个解.(Ⅰ)求A 的特征值与特征向量；(Ⅱ)求正交矩阵Q 和对角矩阵Λ,使得TQ AQ =Λ；（Ⅲ）求A 及632A E ⎛⎫- ⎪⎝⎭，其中E 为3阶单位矩阵.（22）（本题满分13分）设随机变量X 的概率密度为()1,1021,0240,X x f x x ⎧-<<⎪⎪⎪=≤<⎨⎪⎪⎪⎩　其他，令()2,,Y X F x y =为二维随机变量(,)X Y 的分布函数. (Ⅰ)求Y 的概率密度()Y f y ； (Ⅱ)Cov(,)X Y ； (Ⅲ)1,42F ⎛⎫-⎪⎝⎭. （23）（本题满分13分）设总体X 的概率密度为其中θ是未知参数()01θ<<，12n ,...,X X X 为来自总体X 的简单随机样本，记N 为样本值12,...,n x x x 中小于1的个数.（Ⅰ）求θ的矩估计；（Ⅱ）求θ的最大似然估计2006年考研数学（三）真题解析二、填空题：1－6小题，每小题4分，共24分. 把答案填在题中横线上. （1）()11lim 1.nn n n -→∞+⎛⎫=⎪⎝⎭【分析】将其对数恒等化ln eNN =求解.【详解】()(1)111ln lim (1)ln 1lim lim eennn n n n n n n n n n -→∞-++⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭→∞→∞+⎛⎫== ⎪⎝⎭，而数列{}(1)n -有界，1lim ln 0n n n →∞+⎛⎫= ⎪⎝⎭，所以1lim(1)ln 0nn n n →∞+⎛⎫-= ⎪⎝⎭. 故 ()101lim e 1nn n n -→∞+⎛⎫==⎪⎝⎭.（2）设函数()f x 在2x =的某邻域内可导,且()()e f x f x '=，()21f =，则()322e .f '''=【分析】利用复合函数求导即可. 【详解】由题设知，()()ef x f x '=，两边对x 求导得()()()2e()ef x f x f x f x '''==，两边再对x 求导得 ()()23()2e()2ef x f x f x f x ''''==，又()21f =，故 ()323(2)2e2e f f '''==.（3）设函数()f u 可微,且()102f '=,则()224z f x y =-在点(1,2)处的全微分()1,2d 4d 2d .z x y =-【分析】利用二元函数的全微分公式或微分形式不变性计算. 【详解】方法一：因为22(1,2)(1,2)(4)84z f x y xx ∂'=-⋅=∂，()22(1,2)(1,2)(4)22z f x y y y∂'=-⋅-=-∂，所以 ()()()1,21,21,2d d d 4d 2d z z z x y x y xy⎡⎤∂∂=+=-⎢⎥∂∂⎣⎦. 方法二：对()224z f x y=-微分得()222222d (4)d(4)(4)8d 2d z f x y x y f x y x x y y ''=--=--，故 ()()1,2d (0)8d 2d 4d 2d z f x y x y '=-=-. （4）设矩阵2112A ⎛⎫=⎪-⎝⎭，E 为2阶单位矩阵，矩阵B 满足2BA B E =+，则=B 2 .【分析】将矩阵方程改写为AX B XA B AXB C ===或或的形式，再用方阵相乘的行列式性质进行计算即可.【详解】由题设，有于是有 4B A E -=，而11211A E -==-，所以2B =.（5）设随机变量X Y 与相互独立，且均服从区间[]0,3上的均匀分布，则{}{}max ,1P X Y ≤=19. 【分析】利用X Y 与的独立性及分布计算. 【详解】由题设知，X Y 与具有相同的概率密度1,3()30,x f x ⎧≤≤⎪=⎨⎪⎩ 0 其他.则 {}{}{}max ,11,1P X Y P X Y ≤=≤≤{}{}11P X P Y =≤≤{}()2120111d 39P X x ⎛⎫=≤== ⎪⎝⎭⎰. 【评注】本题属几何概型，也可如下计算，如下图：则 {}{}{}1max ,11,19S P X Y P X Y S ≤=≤≤==阴. （6）设总体X 的概率密度为()()121,,,,2xn f x e x X X X -=-∞<<+∞为总体X 的简单随机样本，其样本方差为2S ，则22.ES =【分析】利用样本方差的性质2ES DX =即可. 【详解】因为()d e d 02xx EX xf x x x +∞+∞--∞-∞===⎰⎰， 002e 2e d 2e 2xx xx x +∞-+∞--+∞=-+=-=⎰，所以 ()22202DX EX EX =-=-=，又因2S 是DX 的无偏估计量，所以 22ES DX ==.二、选择题：7－14小题，每小题4分，共32分. 每小题给出的四个选项中，只有一项符合题目要求，把所选项前的字母填在题后的括号内.（7）设函数()y f x =具有二阶导数，且()0,()0f x f x '''>>，x ∆为自变量x 在点0x 处的增量，d y y ∆与分别为()f x 在点0x 处对应的增量与微分，若0x ∆>，则(A) 0d y y <<∆. (B) 0d y y <∆<.(C) d 0y y ∆<<. (D) d 0y y <∆< .[ Ａ ]【分析】题设条件有明显的几何意义，用图示法求解.【详解】由()0,()0f x f x '''>>知，函数()f x 单调增加，曲线()y f x =凹向，作函数()y f x =的图形如右图所示，显然当0x ∆>时，00d ()d ()0y y f x x f x x ''∆>==∆>，故应选(Ａ).（8）设函数()f x 在0x =处连续，且()22lim1h f h h→=，则(A) ()()000f f -'=且存在 (B) ()()010f f -'=且存在 (C) ()()000f f +'=且存在 (D)()()010f f +'=且存在 [ C ] 【分析】从()22lim1h f h h→=入手计算(0)f ，利用导数的左右导数定义判定(0),(0)f f -+''的存在性. 【详解】由()22lim1h f h h→=知，()20lim 0h f h →=.又因为()f x 在0x =处连续，则()2(0)lim ()lim 0x h f f x f h→→===.令2t h =，则()()22(0)1limlim (0)h t f h f t f f h t++→→-'===.所以(0)f +'存在，故本题选（C ）. （9）若级数1nn a∞=∑收敛，则级数(A)1nn a∞=∑收敛 . （B ）1(1)nn n a ∞=-∑收敛.(C)11n n n a a ∞+=∑收敛. (D)112n n n a a ∞+=+∑收敛. [ Ｄ ] 【分析】可以通过举反例及级数的性质来判定. 【详解】由1n n a ∞=∑收敛知11n n a ∞+=∑收敛，所以级数112n n n a a ∞+=+∑收敛，故应选(Ｄ). 或利用排除法：取1(1)nn a n=-，则可排除选项（Ａ），（Ｂ）；取1(1)nn a n=-，则可排除选项（Ｃ）.故（Ｄ）项正确. （10）设非齐次线性微分方程()()y P x y Q x '+=有两个不同的解12(),(),y x y x C 为任意常数，则该方程的通解是（Ａ）[]12()()C y x y x -. （Ｂ）[]112()()()y x C y x y x +-.（Ｃ）[]12()()C y x y x +. （Ｄ）[]112()()()y x C y x y x ++ [ Ｂ ] 【分析】利用一阶线性非齐次微分方程解的结构即可.【详解】由于12()()y x y x -是对应齐次线性微分方程()0y P x y '+=的非零解，所以它的通解是[]12()()Y C y x y x =-，故原方程的通解为[]1112()()()()y y x Y y x C y x y x =+=+-，故应选(Ｂ).【评注】本题属基本题型，考查一阶线性非齐次微分方程解的结构：*y y Y =+.其中*y 是所给一阶线性微分方程的特解，Y 是对应齐次微分方程的通解.（11）设(,)(,)f x y x y ϕ与均为可微函数，且(,)0y x y ϕ'≠，已知00(,)x y 是(,)f x y 在约束条件(,)0x y ϕ=下的一个极值点，下列选项正确的是(A) 若00(,)0x f x y '=，则00(,)0y f x y '=. (B) 若00(,)0x f x y '=，则00(,)0y f x y '≠. (C) 若00(,)0x f x y '≠，则00(,)0y f x y '=.(D) 若00(,)0x f x y '≠，则00(,)0y f x y '≠. [ Ｄ ]【分析】利用拉格朗日函数(,,)(,)(,)F x y f x y x y λλϕ=+在000(,,)x y λ（0λ是对应00,x y 的参数λ的值）取到极值的必要条件即可.【详解】作拉格朗日函数(,,)(,)(,)F x y f x y x y λλϕ=+，并记对应00,x y 的参数λ的值为0λ，则000000(,,)0(,,)0x y F x y F x y λλ⎧'=⎪⎨'=⎪⎩，即0000000000(,)(,)0(,)(,)0x x y y f x y x y f x y x y λϕλϕ⎧''+=⎪⎨''+=⎪⎩ .消去0λ，得00000000(,)(,)(,)(,)0x y y x f x y x y f x y x y ϕϕ''''-=, 整理得 000000001(,)(,)(,)(,)x y x y f x y f x y x y x y ϕϕ'''='.（因为(,)0y x y ϕ'≠），若00(,)0x f x y '≠，则00(,)0y f x y '≠.故选（Ｄ）. （12）设12,,,s ααα均为n 维列向量，A 为m n ⨯矩阵，下列选项正确的是(A) 若12,,,s ααα线性相关，则12,,,s A A A ααα线性相关. (B) 若12,,,s ααα线性相关，则12,,,s A A A ααα线性无关. (C) 若12,,,s ααα线性无关，则12,,,s A A A ααα线性相关.(D) 若12,,,s ααα线性无关，则12,,,s A A A ααα线性无关. [ A ]【分析】本题考查向量组的线性相关性问题，利用定义或性质进行判定. 【详解】记12(,,,)s B ααα=，则12(,,,)s A A A AB ααα=.所以，若向量组12,,,s ααα线性相关，则()r B s <，从而()()r AB r B s ≤<，向量组12,,,s A A A ααα也线性相关，故应选(Ａ).（13）设A 为3阶矩阵，将A 的第2行加到第1行得B ，再将B 的第1列的1-倍加到第2列得C ，记110010001P ⎛⎫ ⎪= ⎪ ⎪⎝⎭，则（Ａ）1C P AP -=. （Ｂ）1C PAP -=.（Ｃ）TC P AP =. （Ｄ）TC PAP =. ［Ｂ］【分析】利用矩阵的初等变换与初等矩阵的关系以及初等矩阵的性质可得. 【详解】由题设可得11011011011010,010********1001001001B A C B A --⎛⎫⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪===⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭ ，而 1110010001P --⎛⎫⎪= ⎪ ⎪⎝⎭，则有1C PAP -=.故应选（Ｂ）.（14）设随机变量X 服从正态分布211(,)N μσ，Y 服从正态分布222(,)N μσ，且则必有(A) 12σσ< (B) 12σσ>(C) 12μμ< (D) 12μμ> [ A ] 【分析】利用标准正态分布密度曲线的几何意义可得.【详解】由题设可得12112211X Y P P μμσσσσ⎧-⎫⎧-⎫<><⎨⎬⎨⎬⎩⎭⎩⎭，则 12112121σσ⎛⎫⎛⎫Φ->Φ-⎪ ⎪⎝⎭⎝⎭，即1211σσ⎛⎫⎛⎫Φ>Φ ⎪ ⎪⎝⎭⎝⎭. 其中()x Φ是标准正态分布的分布函数. 又()x Φ是单调不减函数，则1211σσ>，即12σσ<.故选(A).三、解答题：15－23小题，共94分. 解答应写出文字说明、证明过程或演算步骤. （15）（本题满分7分）设()1sin,,0,01arctan xy y yf x y x y xy xπ-=->>+,求 (Ⅰ) ()()lim ,y g x f x y →+∞=；(Ⅱ) ()0lim x g x +→. 【分析】第(Ⅰ)问求极限时注意将x 作为常量求解，此问中含,0∞⋅∞∞型未定式极限；第(Ⅱ)问需利用第(Ⅰ)问的结果，含∞-∞未定式极限.【详解】(Ⅰ) ()()1sin lim ,lim 1arctan y y x y y y g x f x y xy x π→+∞→∞⎛⎫- ⎪⎪==-+⎪ ⎪⎝⎭sin 11111lim 1arctan arctan y x yxy x x x x y ππ→∞⎛⎫ ⎪ ⎪-⎪⎪-=-=-⎪ ⎪+ ⎪ ⎪ ⎪⎝⎭. (Ⅱ) ()200011arctan lim lim lim arctan arctan x x x x x x x g x x x x xππ+++→→→--+⎛⎫=-= ⎪⎝⎭ （通分）（16）（本题满分7分）计算二重积分2d d Dy xy x y -⎰⎰，其中D 是由直线,1,0y x y x ===所围成的平面区域.【分析】画出积分域，将二重积分化为累次积分即可.【详解】积分区域如右图.因为根号下的函数为关于x 的一次函数，“先x后y ”积分较容易，所以（17）（本题满分10分）证明：当0a b π<<<时，sin 2cos sin 2cos b b b b a a a a ππ++>++.【分析】利用“参数变易法”构造辅助函数，再利用函数的单调性证明. 【详解】令()sin 2cos sin 2cos ,0f x x x x x a a a a a x b πππ=++---<≤≤<，则 ()sin cos 2sin cos sin f x x x x x x x x ππ'=+-+=-+，且()0f π'=.又 ()cos sin cos sin 0f x x x x x x x ''=--=-<，（0,s i n 0x x x π<<>时），故当0a x b π<≤≤<时，()f x '单调减少，即()()0f x f π''>=，则()f x 单调增加，于是()()0f b f a >=，即sin 2cos sin 2cos b b b b a a a a ππ++>++.（18）（本题满分8分）在xOy 坐标平面上，连续曲线L 过点()1,0M ，其上任意点()(),0P x y x ≠处的切线斜率与直线OP 的斜率之差等于ax （常数>0a ）. (Ⅰ) 求L 的方程；(Ⅱ) 当L 与直线y ax =所围成平面图形的面积为83时，确定a 的值. 【分析】(Ⅰ)利用导数的几何意义建立微分方程，并求解；(Ⅱ)利用定积分计算平面图形的面积，确定参数. 【详解】(Ⅰ) 设曲线L 的方程为()y f x =，则由题设可得 y y ax x '-=，这是一阶线性微分方程，其中1(),()P x Q x ax x=-=，代入通解公式得 ()11d d 2e e d x x x x y ax x C x ax C ax Cx -⎛⎫⎰⎰=+=+=+ ⎪⎝⎭⎰，又(1)0f =，所以C a =-.故曲线L 的方程为 2y ax ax =-(0)x ≠.(Ⅱ) L 与直线y ax =（>0a ）所围成平面图形如右图所示. 所以 ()220482d 33ax x x a =-==⎰，故2a =.（19）（本题满分10分）求幂级数()()1211121n n n x n n -+∞=--∑的收敛域及和函数()s x .【分析】因为幂级数缺项，按函数项级数收敛域的求法计算；利用逐项求导或积分并结合已知函数的幂级数展开式计算和函数.【详解】记121(1)()(21)n n n x u x n n -+-=-，则2321121(1)()(1)(21)lim lim (1)()(21)n n n n n n n nx u x n n xx u x n n ++-+→∞→∞-++==--. 所以当21,1x x <<即时，所给幂级数收敛；当1x >时，所给幂级数发散；当1x =±时，所给幂级数为1(1)(1),(21)(21)n nn n n n -----，均收敛，故所给幂级数的收敛域为[]1,1-在()1,1-内，()12112111(1)(1)()22()(21)(21)2n n n nn n x x s x x xs x n n n n -+-∞∞==--===--∑∑，而 12112211211(1)1(),()(1)211n n n n n n x s x s x x n x --∞∞--==-'''==-=-+∑∑，所以 1112001()(0)()d d arctan 1xxs x s s t t t x t''''-===+⎰⎰，又1(0)0s '=，于是 1()arctan s x x '=.同理()20201arctan d arctan ln 112xx t t t t x x x t =-=-++⎰，又 1(0)0s =，所以 ()211()arctan ln 12s x x x x =-+.故 ()22()2arctan ln 1s x x x x x =-+.()1,1x ∈-.由于所给幂级数在1x =±处都收敛，且()22()2arctan ln 1s x x x x x =-+在1x =± 处都连续，所以()s x 在1x =±成立，即()22()2arctan ln 1s x x x x x =-+，[]1,1x ∈-. （20）（本题满分13分）设4维向量组()()()TTT1231,1,1,1,2,2,2,2,3,3,3,3,a a a ααα=+=+=+()T44,4,4,4a α=+，问a 为何值时1234,,,αααα线性相关当1234,,,αααα线性相关时,求其一个极大线性无关组,并将其余向量用该极大线性无关组线性表出.【分析】因为向量组中的向量个数和向量维数相同，所以用以向量为列向量的矩阵的行列式为零来确定参数a ；用初等变换求极大线性无关组.【详解】记以1234,,,αααα为列向量的矩阵为A ，则312341234(10)12341234aa A a a a a++==+++.于是当0,010A a a ===-即或时，1234,,,αααα线性相关.当0a =时，显然1α是一个极大线性无关组，且2131412,3,4αααααα===；当10a =-时，9234183412741236A -⎛⎫⎪-⎪= ⎪- ⎪-⎝⎭，由于此时A 有三阶非零行列式9231834000127--=-≠-，所以123,,ααα为极大线性无关组，且123441230αααααααα+++==---，即.（21）（本题满分13分）设3阶实对称矩阵A 的各行元素之和均为3,向量()()TT121,2,1,0,1,1αα=--=-是线性方程组0Ax =的两个解.(Ⅰ) 求A 的特征值与特征向量；(Ⅱ) 求正交矩阵Q 和对角矩阵Λ,使得TQ AQ =Λ；（Ⅲ）求A 及632A E ⎛⎫- ⎪⎝⎭，其中E 为3阶单位矩阵.【分析】由矩阵A 的各行元素之和均为3及矩阵乘法可得矩阵A 的一个特征值和对应的特征向量；由齐次线性方程组0Ax =有非零解可知A 必有零特征值，其非零解是0特征值所对应的特征向量.将A 的线性无关的特征向量正交化可得正交矩阵Q ；由TQ AQ =Λ可得到A 和632A E ⎛⎫- ⎪⎝⎭.【详解】 (Ⅰ) 因为矩阵A 的各行元素之和均为3，所以1311331131A ⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，则由特征值和特征向量的定义知，3λ=是矩阵A 的特征值，T(1,1,1)α=是对应的特征向量.对应3λ=的全部特征向量为k α，其中k 为不为零的常数.又由题设知 120,0A A αα==，即11220,0A A αααα=⋅=⋅，而且12,αα线性无关，所以0λ=是矩阵A 的二重特征值，12,αα是其对应的特征向量，对应0λ=的全部特征向量为 1122k k αα+，其中12,k k 为不全为零的常数.(Ⅱ) 因为A 是实对称矩阵，所以α与12,αα正交，所以只需将12,αα正交. 取 11βα=，()()21221111012,3120,61112αββαβββ⎛⎫-⎪-⎛⎫⎛⎫ ⎪- ⎪ ⎪=-=--= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭ ⎪⎝⎭.再将12,,αββ单位化，得121231211136212,,036111236ββαηηηαββ⎛⎫⎛⎫-⎛⎫ ⎪ ⎪- ⎪ ⎪⎪ ⎪ ⎪⎪====== ⎪⎪ ⎪ ⎪ ⎪ ⎪⎪ ⎪ ⎪ ⎪⎝⎭ ⎪ ⎪⎝⎭⎝⎭，令 []123,,Q ηηη=，则1T QQ -=，由A 是实对称矩阵必可相似对角化，得T300Q AQ ⎡⎤⎢⎥==Λ⎢⎥⎢⎥⎣⎦. （Ⅲ）由(Ⅱ)知 T300Q AQ ⎡⎤⎢⎥==Λ⎢⎥⎢⎥⎣⎦，所以T1111113623333111121210011136666011111111036222A QQ ⎛⎫⎛⎫-- ⎪⎪⎪⎪⎛⎫⎛⎫ ⎪⎪⎪ ⎪=Λ=--= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭ ⎪ ⎪--⎪ ⎪⎝⎭⎝⎭. 6666633223333022203322E ⎛⎫⎛⎫⎡⎤⎛⎫ ⎪ ⎪⎢⎥ ⎪⎝⎭ ⎪⎛⎫⎢⎥ ⎪ ⎪⎛⎫⎛⎫ ⎪⎢⎥ ⎪ ⎪=-== ⎪ ⎪ ⎪⎢⎥ ⎪ ⎪⎝⎭⎝⎭ ⎪⎢⎥ ⎪ ⎪⎝⎭⎢⎥ ⎪⎛⎫ ⎪ ⎪⎢⎥ ⎪⎝⎭⎣⎦⎪⎝⎭⎝⎭，则666T 333222A E Q EQ E ⎛⎫⎛⎫⎛⎫-== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.（22）（本题满分13分）设随机变量X 的概率密度为()1,1021,0240,X x f x x ⎧-<<⎪⎪⎪=≤<⎨⎪⎪⎪⎩　其他，令()2,,Y X F x y =为二维随机变量(,)X Y 的分布函数. (Ⅰ) 求Y 的概率密度()Y f y ； (Ⅱ) Cov(,)X Y ； (Ⅲ) 1,42F ⎛⎫-⎪⎝⎭. 【分析】求一维随机变量函数的概率密度一般先求分布，然后求导得相应的概率密度或利用公式计算.【详解】（I ）设Y 的分布函数为()Y F y ，即2()()()Y F y P Y y P X y =≤=≤，则1) 当0y <时，()0Y F y =；2) 当01y ≤<时， ()2()()Y F y P X y P y X y =<=-<<0113d d 244y y x x y -=+=⎰⎰. 3) 当14y ≤<时，()2()()1Y F y P X y P X y =<=-<<101111d d 2442y x x y -=+=+⎰⎰.4) 当4y ≥，()1Y F y =. 所以3,0181()(),1480,Y Y y y f y F y y y⎧<<⎪⎪⎪'==≤<⎨⎪⎪⎪⎩其他. （II ） 22232Cov(,)Cov(,)()()X Y X X E X EX X EX EX EXEX ==--=-，而 02101d d 244x x EX x x -=+=⎰⎰，22022105d d 246x x EX x x -=+=⎰⎰，33023107d d 248x x EX x x -=+=⎰⎰，所以 7152Cov(,)8463X Y =-⋅=. (Ⅲ) 1,42F ⎛⎫-⎪⎝⎭211,4,422P X Y P X X ⎛⎫⎛⎫=≤-≤=≤-≤ ⎪ ⎪⎝⎭⎝⎭12111d 24x --==⎰. 2016年考研各科目专用题库复习和考试软件说明：本人已于2015年顺利通过了考研。

2016考研数学三真题解析

边际收益为
dR dR dP 1 dR (1200 20 P)( ) 2 P 120 ，从而 dQ dP dQ 10 dQ
P 100
80 。
它的经济意义是需求量每提高 1 件，收益增加 80 万元。
5
（17）(本题满分 10 分) 设函数 f x

1
0
t 2 x 2 dt
2
0 1
0 0

1 2 1
______
【答案】： 2 3 4
4
-1 0 0 0 -1 0 = D4 【解析】：令 0 0 -1 4 3 2 +1
由展开定理地递推公式 D4 D3 4, D3 D2 3, D2 2 ，故
（A） J1 J 2 J 3 （B） J 3 J1 J 2 【答案】：（B）【解析】 D1，D2，D3 如图（C） J 2 J 3 J1 （D） J 2 J1 J 3

易知在 D1 D2 中 3 x y 0 ，在 D1 D3 中 3 x y 0 ，可知 J1 J 2，J1 J 3 ，故选 B （4）级数

（B） P A | B 0

（C） P A È B = 1
(
)
（ AB P B , P AB P B P AB 0 P B

可知 P B | A

P BA P A
dz 0 ,1 ______
【答案】：d z 1,0 d x d y 2 【解析】：由一阶微分形式不变性，
zdx ( x 1)dz 2 ydy 2 xf ( x z, y)dx x 2 f1' ( x z, y) dx dz x 2 f 2' ( x z, y)dy

2016年全国硕士研究生入学统一考试数学三考研真题答案凯程首发

一、选择题：1～8小题，每小题4分，共32分，下列每小题给出的四个选项中，只有一项符合题目要求的，请将所选项前的字母填在答题纸．．．指定位置上. （1）设函数()y f x =在(,)-∞+∞内连续，其导数如图所示，则（）（A ）函数有2个极值点，曲线()y f x =有2个拐点（B ）函数有2个极值点，曲线()y f x =有3个拐点（C ）函数有3个极值点，曲线()y f x =有1个拐点（D ）函数有3个极值点，曲线()y f x =有2个拐点【答案】（B ）【解析】【解析】由图像易知选B2、已知函数(,)x e f x y x y=-，则（A ）''0x y f f -= （B ）''0x y f f += （C ）''x y f f f -= （D ）''x y f f f += 【答案】（D ）【解析】()2(1)'x x e x y f x y --=- ()2'xy e f x y =-，所以''x y f f f +=（3）设(i ,,)ii D T ==⎰⎰123，其中{}(,),D x y x y =≤≤≤≤10101，{{}(,),,(,),D x y x y D x y x x y =≤≤≤≤=≤≤≤≤223010011，则（A ）T T T <<123（B ）T T T <<312 （C ）T T T <<231 （D ）T T T <<213【答案】B【解析】由积分区域的性质易知选B. （4）级数为sin()n n k ∞=-+∑1，（K 为常数）（A ）绝对收敛（B ）条件收敛（C ）发散（D ）收敛性与K 有关【答案】A【解析】由题目可得，sin())n n n n k n k ∞∞∞===+=+=∑111≤≤，由正项级数的比较判别法得，该级数绝对收敛。

(最新整理)2016年全国卷3理科数学试题及参考答案(WORD版)

2016年全国卷3理科数学试题及参考答案(WORD版)编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（2016年全国卷3理科数学试题及参考答案(WORD版)）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为2016年全国卷3理科数学试题及参考答案(WORD版)的全部内容。

绝密★启封并使用完毕前试题类型:新课标Ⅲ2016年普通高等学校招生全国统一考试理科数学本试卷分第I 卷（选择题)和第II 卷(非选择题)两部分，共24题，共150分,共4页。

考试结束后，将本试卷和答题卡一并交回。

注意事项：1.答题前，考生先将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在条形码区域内。

2.选择题必须使用2B 铅笔填涂;非选择题必须使用0。

5毫米黑字迹的签字笔书写，字体工整,笔迹清楚。

3。

请按照题号顺序在各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效.4。

作图可先用铅笔画出，确定后必须用黑色字迹的签字笔描黑.5.保持卡面清洁，不要折叠、不要弄破，不准使用涂改液、修正液、刮纸刀。

第I 卷一.选择题：本大题共12小题,每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的.(1）设集合，则S T ={}{}|(2)(3)0,|0S x x x T x x =--≥=>I A. B. C. D 。

[]2,3(][),23,-∞+∞ [)3,+∞(][)0,23,+∞ 【答案】D【解析】易得,，选D (][),23,S =-∞+∞ (][)0,23,S T ∴=+∞ 【考点】解一元二次不等式、交集y t，。

2016年考研数学三真题及答案

2016年考研数学三真题及答案【篇一：2016考研数学三真题(word版)】答题纸指定位置上。

（1）设函数y?f(x)在(??,??)内连续，其导函数的图形如图所示，则（）a.函数f(x)有2个极值点，曲线y?f(x)有2个拐点b.函数f(x)有2个极值点，曲线y?f(x)有3个拐点c.函数f(x)有3个极值点，曲线y?f(x)有1个拐点d.函数f(x)有3个极值点，曲线y?f(x)有2个拐点ex（2）已知函数f(x,y)?，则（） x?ya.fx??fy??0b.fx??fy??0c.fx???fy???fd.fx???fy???f（3）设jk?di(i?1,2,3)，其中d1??(x,y)0?x?1,0?y?1?，d2?(x,y)0?x?1,0?y?d3??(x,y)0?x?1,x2?y?1?则（）a.j1?j2?j3b.j3?j1?j2c.j2?j3?j1d.j2?j1?j3（4）级数为??n?1?（） n?k)（k为常数）a.绝对收敛b.条件收敛c.发散d.收敛性与k有关（5）设a,b是可逆矩阵，且a与b相似，则下列结论错误的是（） a.a与b相似1我们不鼓励考试期间核对答案，请在考试完毕后再看解析！ ttb.a与b相似c.a?a与b?b相似d.a?a与b?b相似222（6）设二次型f(x1,x2,x3)?a(x1?x2?x3)?2x1x2?2x2x3?2x1x3的正负惯性指数分别?1?1tt?1?1为1,2，则（）a.a?1b.a??2c.?2?a?1d.a?1或a??2（7）设a,b为两个随机变量，且0?p(a)?1,0?p(b)?1，如果p(ab)?1，则（） a.p(ba)?1 b.p(ab)?0c.p(a?b)?1d.p(ba)?1（8）设随机变量x与y相互独立，且x~n(1,2),y~n(1,4)，则d(xy)=（）a.6b.8c.14d.15二、填空题：9-14小题，每小题4分，共24分，请将答案写在答题纸指定位置上。