北师大版九年级上册第四章《相似三角形》复习课堂练习

合集下载

北师大版九年级数学上册第四章图形的相似4.4探索三角形相似的条件第3课时相似三角形的判定3同步练习及答案

第3课时相似三角形的判定3知识点由三边成比例判定两三角形相似图4－4－231．教材习题4.7第2题变式题如图4－4－23，每个小正方形的边长均为1，则下列图形(每个小正方形的边长均为1)中的三角形(阴影部分)与△ABC相似的是( )图4－4－242．已知AB＝12 cm，AC＝15 cm，BC＝21 cm，A1B1＝16 cm，B1C1＝28 cm，当A1C1＝________ cm时，△ABC∽△A1B1C1.3．已知△ABC的三边长分别为AB＝6 cm，BC＝7.5 cm，AC＝9 cm，△DEF的三边长分别为DE＝4 cm，EF＝5 cm，DF＝6 cm.求证：∠A＝∠D.4．已知△ABC的三边长分别为6 cm，7.5 cm，9 cm，△DEF的一边长为4 cm，当△DEF 的另两边长是下列哪一组时，这两个三角形相似( )A．2 cm，3 cm B．4 cm，5 cmC ．5 cm ，6 cmD ．6 cm ，7 cm图4－4－255．如图4－4－25，点A ，B ，C ，D 的坐标分别是(1，7)，(1，1)，(4，1)，(6，1)，若以C ，D ，E 为顶点的三角形与△ABC 相似，则点E 的坐标不可能是( )A ．(6，0)B ．(6，3)C ．(6，5)D ．(4，2)6．如图4－4－26，在△ABC 和△ADE 中，AB AD ＝BC DE ＝ACAE，点B ，D ，E 在一条直线上．求证：△ABD ∽△ACE .图4－4－267．如图4－4－27，在边长为1的小正方形组成的网格中，△ABC 和△DEF 的顶点都在格点上，P 1，P 2，P 3，P 4，P 5是△DEF 边上的5个格点，请按要求完成下列各题：(1)求证：△ABC 为直角三角形；(2)判断△ABC 和△DEF 是否相似，并说明理由；(3)画一个三角形，使它的三个顶点为P 1，P 2，P 3，P 4，P 5中的3个格点并且与△ABC 相似(要求：不写作法与证明)．图4－4－271．B [解析] 因为每个小正方形的边长均为1，所以已知的三角形的各边长分别为2，2，10，B 选项中的三角形三边长分别为1，2，5，三边与已知三角形的各边对应成比例，故两三角形相似．2．203．证明：∵AB DE ＝64＝32，BC EF ＝7.55＝32，AC DF ＝96＝32，∴AB DE ＝BC EF ＝ACDF，∴△ABC ∽△DEF ，∴∠A ＝∠D .4．C [解析] 设△DEF 的另两边的长分别为x cm ，y cm ，若△DEF 中为4 cm 长的边的对应边为6 cm ，则46＝x 7.5＝y9，解得x ＝5，y ＝6；若△DEF 中为4 cm 长的边的对应边为7.5 cm ，则47.5＝x 6＝y9，解得x ＝3.2，y ＝4.8；若△DEF 中为4 cm 长的边的对应边为9 cm ，则49＝x 6＝y 7.5，解得x ＝83，y ＝103.故选C.5．B6．证明：∵在△ABC 和△ADE 中，AB AD ＝BC DE ＝AC AE， ∴△ABC ∽△ADE ， ∴∠BAC ＝∠DAE ， ∴∠BAD ＝∠CAE . 又∵AB AD ＝AC AE，∴AB AC ＝AD AE， ∴△ABD ∽△ACE .7．解：(1)证明：∵AB 2＝20，AC 2＝5，BC 2＝25，∴AB2＋AC2＝BC2，∴△ABC为直角三角形，且∠BAC＝90°.(2)△ABC和△DEF相似．理由：由(1)中数据得AB＝2 5，AC＝5，BC＝5.由题意易知DE＝4 2，DF＝2 2，EF＝210，∴ABDE＝ACDF＝BCEF＝104，∴△ABC∽△DEF.(3)如图，连接P2P5，P2P4，P4P5.∵P2P5＝10，P2P4＝2，P4P5＝2 2，AB＝2 5，AC＝5，BC＝5，∴P2P5BC＝P4P5AB＝P2P4AC＝105，∴△ABC∽△P4P5P2.。

北师大版初中数学九年级上-册第四章相似三角形(复习)(共29张PPT)精选全文

归类探究
回归教材
中考预测
相似三角形及其应用
解析 ∵AD∶DB＝3∶5，
∴BD∶AB＝5∶8.
∵DE∥BC，
∴CE∶AC＝BD∶AB＝5∶8，
∵EF∥AB，
∴CF∶CB＝CE∶AC＝5∶8.
故选A.
考点聚焦
归类探究
回归教材
Байду номын сангаас中考预测
相似三角形及其应用
探究二相似三角形的性质及其应用
命题角度： 1. 利用相似三角形性质求角的度数或线段的长度； 2. 利用相似三角形性质探求比值关系．
例3 如图22－4，在平行四边形ABCD中，过点A作 AE⊥BC，垂足为E，连接DE，F为线段DE上一点，且 ∠AFE＝∠B. (1)求证：△ADF∽△DEC； (2)若AB＝8，AD＝6 ，AF＝4 ，求AE的长．
图22－4
考点聚焦
归类探究
回归教材
中考预测
相似三角形及其应用
考点聚焦
归类探究
回归教材
探究四位似命题角度： 1. 位似图形及位似中心定义； 2. 位似图形的性质应用； 3. 利用位似变换在网格纸里作图．
例 4 在平面直角坐标系中，已知点 E(－4，2)，F(－2，－2)，
以原点 O 为位似中心，相似比D为12，把△EFO 缩小，则点 E 的对应
点 E′的坐标是( )
A．(－2，1)
考点聚焦
归类探究
回归教材
中考预测
相似三角形及其应用
探究五相似三角形与圆
命题角度： 1. 圆中的相似计算； 2. 圆中的相似证明．例5 如图22－5，AB为⊙O的直径，C为⊙O上一点，AD 和过C点的直线互相垂直，垂足为D，且AC平分∠DAB. (1)求证：DC为⊙O的切线； (2)若⊙O的半径为3，AD＝4，求AC的长．

九年级数学上册第四章《图形的相似》4.5相似三角形判定定理的证明同步练习新版北师大版

5相似三角形判判断理的证明知识点 1证明相似三角形判判断理图 4－ 5－11．如图 4－ 5－ 1，在△ABC中，点D，E分别在AB，AC边上，DE∥BC，若AD＝ 1，BD＝DE2，则的值为()BC1111C. 4D.9A.2B.32．如图 4－5－ 2，在 ?ABCD中，AC与BD订交于点O，E 为OD的中点，连接AE并延长交 DC于点 F，则 DF∶ FC＝()A．1∶4 B ． 1∶3 C ．2∶3 D ．1∶ 2图 4－5－ 2图 4－5－33．2017·恩施州如图4－5－ 3，在△ABC中，DE∥BC，∠ADE＝∠EFC，AD∶BD＝5∶3，CF＝6，则 DE的长为()A．6 B ．8 C ．10 D ．124．用相似三角形的定义证明平行于三角形一边的直线和其余两边订交，所构成的三角形与原三角形相似．知识点 2相似三角形判断的综合应用5．如图 4－ 5－4，为了丈量一池塘的宽DE，在岸边找到一点C，测得 CD＝30 m，在 DC 的延长线上找到一点A，测得 AC＝5 m，过点 A作 AB∥ DE交 EC的延长线于点B，测得 AB＝6 m，则池塘的宽DE为()A． 25 m B ． 30 m C ． 36 m D ．40 m图 4－5－4图 4－5－ 56．如图 4－ 5－ 5，AB是斜靠在墙上的长梯，梯脚B距墙脚 1.6 m，梯上点 D距墙1.4 m，BD长0.55 m，该梯子的长是________．7．如图 4－ 5－6 所示，已知AD⊥BD， AE⊥BE，求证： AD· BC＝ AC· BE.图 4－ 5－68．如图 4－5－ 7，在正方形ABCD中， M为 BC上一点， F 是 AM的中点， EF⊥AM，垂足为 F，交 AD的延长线于点 E，交 DC于点 N.(1)求证：△ ABM∽△ EFA；(2) 若AB＝ 12，BM＝ 5，求DE的长．图 4－ 5－79．如图 4－ 5－ 8，△ABC中，点D，F在边AB上，点E在边AC上，假如D E∥ BC，EF∥CD，那么必定有()22A．DE＝AD·AE B ．AD＝AF·AB22C．AE＝AF·AD D ．AD＝AE·AC图 4－5－ 8图 4－ 5－910．如图 4－5－ 9，在边长为 9 的等边三角形ABC中，BD＝ 3，∠ADE＝ 60°，则AE的长为 ________．11．如图 4－ 5－ 10，已知AB∶AD＝BC∶DE＝AC∶AE，请猜想∠ABD与∠ACE的关系，并说明原由．图 4－5－1012．教材习题 4.9 第 3 题变式题如图4－ 5－ 11，在△ABC中，AC＝BC，点E，F在直线AB上，∠ ECF＝∠ A.2(1) 如图 4－ 5－11①，点E，F在AB上时，求证：AC＝ AF· BE；(2) 如图 4－ 5－11②，点E，F 在 AB及其延长线上，∠A＝60°， AB＝4， BE＝3，求 BF 的长．图 4－5－1113．如图 4－ 5－12，已知AB⊥DB于点B，CD⊥DB于点D，AB＝6，CD＝4，BD＝14，问：在 DB上能否存在点P，使得△ PCD与△ PAB相似？假如存在，央求出PD的长；假如不存在，请说明原由．图 4－5－12414．如图 4－ 5－ 13，已知直线l 的函数表达式为y＝－3x＋8，且 l 与 x 轴、 y 轴分别交于 A，B 两点，动点 Q从点 B开始在线段BA上以每秒2个单位长度的速度向点 A 挪动，同时动点 P 从点 A 开始在线段AO上以每秒1个单位长度的速度向点O挪动，设点 Q，P挪动的时间为 t 秒．(1)求点 A， B 的坐标；(2)当 t 为什么值时，以 A，P， Q为极点的三角形与△ AOB相似？(3)求出 (2) 中当以A，P，Q为极点的三角形与△AOB相似时线段PQ的长度．图 4－5－13详解1． B3． C [ 解析 ]由DE∥BC可得出∠ ADE＝∠ B，联合∠ ADE＝∠ EFC可得出∠ B＝∠ EFC，从而可得出BD∥ EF，联合 DE∥ BC可证出四边形BDEF为平行四边形，依据平行四边形的性8质可得出 DE＝ BF，由 DE∥BC可得出△ ADE∽△ ABC，依据相似三角形的性质可得出BC＝5DE，3再依据 CF＝ BC－ BF＝5DE＝6，因此 DE＝10.4．解：已知：如图，在△ABC中， DE∥ BC，并分别交AB， AC于点 D， E.求证：△ ADE与△ ABC相似．证明：∵ DE∥ BC，∴∠ ADE＝∠ B，∠ AED＝∠ C.过点 D作 DF∥ AC交 BC于点 F，又∵ DE∥ BC，∴四边形 DFCE是平行四边形，∴DE＝FC，FC DE AD∴＝＝，BC BC ABAD AE DE∴＝＝.AB AC BC而∠ A＝∠ A，∠ ADE＝∠ B，∠ AED＝∠ C，∴△ ADE∽△ ABC.5． C.7．证明：∵AD⊥BD，AE⊥BE，∴∠ ADC＝90°，∠ BEC＝90°.在△ ACD和△ BCE中，∵∠ ACD＝∠ BCE，∠ ADC＝∠ BEC，AD AC∴△ ACD∽△ BCE，∴＝，BE BC∴AD·BC＝ AC·BE.8．解： (1) 证明：∵四边形ABCD是正方形，∴∠ B＝90°， AD∥ BC，∴∠ AMB＝∠ EAF.又∵ EF⊥ AM，∴∠ AFE＝90°，∴∠ B＝∠ AFE，∴△ ABM∽△ EFA.(2)∵∠ B＝90°， AB＝12， BM＝5，∴ AM＝122＋52＝13， AD＝ AB＝12.1∵ F 是 AM的中点，∴ AF＝2AM＝6.5.∵△ ABM∽△ EFA，∴BM AM＝，FA EA513即＝，∴ EA＝，6.5 EA∴DE＝EA－ AD＝4.9.9． B10． 7.11．解：∠ABD＝∠ACE.原由以下：∵ AB∶AD＝ BC∶DE＝ AC∶AE，∴△ ABC∽△ ADE，∴∠ BAC＝∠ DAE，∴∠ BAD＝∠ CAE.又∵ AB∶ AD＝ AC∶ AE，即 AB∶ AC＝ AD∶ AE，∴△ BAD∽△ CAE，∴∠ ABD＝∠ ACE.12．解： (1) 证明：∵AC＝BC，∴∠ A＝∠ B.∵∠ BEC＝∠ ACE＋∠ A，∠ ACF＝∠ ACE＋∠ ECF，∠ ECF＝∠ A，∴∠ ACF＝∠ BEC，AC AF∴△ ACF∽△ BEC，∴＝，BE BC2∴ AC＝ AF· BE.(2)∵∠ A＝60°， AC＝ BC，∴△ ABC是等边三角形，∴∠ A＝∠ ABC＝∠ ACB＝60°＝∠ ECF，∴∠ ACE＝∠ FCB.又∵∠ ECB＝∠ ACB－∠ ACE，∠ F＝∠ ABC－∠ FCB，∴∠ ECB＝∠ F.又∵∠ ABC＝∠ A，∴△ ACF∽△ BEC，AC AF16，∴ ＝，∴ AF＝3BE BC∴ ＝－4＝ .BF AF AB 3 13．解：存在．①若△ PCD∽△ APB，则CD PD4PD＝，即＝，解得 PD＝2或 PD＝12；PB AB14－PD6②若△ PCD∽△ PAB，则CD PD4PD，解得 PD＝5.6.＝，即＝AB PB614－PD414．解： (1) 在y＝－x＋8中，当 x＝0时， y＝8；当 y＝0时， x＝6.故点 A的坐标为(6，0)，点 B 的坐标为(0，8)．(2) 在△AOB中，∠AOB＝90°，OA＝ 6，OB＝8，由勾股定理，得AB＝10.由题意易知BQ＝2t ， AQ＝10－2t ，AP＝ t .在△ AOB和△ AQP中，∠ BAO＝∠ PAQ，第一种状况：AQ AP当＝时，△ APQ∽△ AOB，AB AO10－ 2t t30即＝，解得 t ＝；10611第二种状况：AQ AP当＝时，△ AQP∽△ AOB，AO AB10－ 2t50即6＝10，解得 t ＝13.30 50故当 t 为11或13时，以 A，P， Q为极点的三角形与△AOB相似．(3)∵以 A， P，Q为极点的三角形与△ AOB相似，3030PQ 1140∴当 t ＝11时，8＝6，解得 PQ＝11；50当t ＝50PQ1340时，＝，解得＝ .13810PQ 134040故当以 A， P， Q为极点的三角形与△AOB相似时，线段PQ的长度是11或13.9。

北师大版九年级数学上册第四章《图形的相似》相似三角形的性质同步练习试题及答案 (3)

相似三角形周长和面积的性质——典型题专项训练知识点 1 有关周长的计算1．已知△ABC∽△A1B1C1，且AB＝4，A1B1＝6，则△ABC的周长和△A1B1C1的周长之比是( )A．9∶4 B．4∶9 C．2∶3 D．3∶2图4－7－102．如图4－7－10，在▱ABCD中，E是AD边上的中点，连接BE，并延长BE交CD的延长线于点F，则△EDF与△BCF的周长之比是( )A．1∶2 B．1∶3 C．1∶4 D．1∶53．如果△ABC∽△DEF，其相似比为3∶1，且△ABC的周长为27，那么△DEF的周长为( )A．9 B．18 C．27 D．814．如图4－7－11，在▱ABCD中，AB＝6，AD＝9，∠BAD的平分线交BC于点E，交DC 的延长线于点F，BG⊥AE于点G，BG＝4 2，求△FCE的周长．图4－7－11知识点 2 有关面积的计算5．已知△ABC∽△DEF，且相似比为1∶2，则△ABC与△DEF的面积比为( )A．1∶4 B．4∶1 C．1∶2 D．2∶1图4－7－126．如图4－7－12，在△ABC中，D是AB边上的一点，若∠ACD＝∠B，AD＝1，AC＝2，△ADC的面积为1，则△BCD的面积为( )A．1 B．2 C．3 D．47．教材例2变式题如图4－7－13，把△ABC沿AB边平移到△A′B′C′的位置，它们重叠部分(即图中阴影部分)的面积是△ABC面积的14，若AB＝2，则△ABC平移的距离是________．图4－7－13图4－7－148．如图4－7－14，在△ABC中，点D，E分别在AB，AC上，∠AED＝∠B，若AE＝2，△ADE的面积为4，四边形BCED的面积为5，则AB的长为________．9．如图4－7－15所示，在▱ABCD中，AE∶EB＝1∶2.(1)求△AEF与△CDF的周长的比；(2)若S△AEF＝6 cm2，求S△CDF.图4－7－1510．若两个相似三角形的面积之比为1∶4，则它们的周长之比为( )A．1∶2 B．1∶4 C．1∶5 D．1∶1611．如图4－7－16，DE是△ABC的中位线，延长DE至点F，使EF＝DE，连接CF，则S ∶S四边形BCED的值为( )△CEFA．1∶3 B．2∶3 C．1∶4 D．2∶54－7－164－7－1712．(教材综合与实践——制作视力表的应用)我们在制作视力表时发现，每个“E”形图的长和宽相等(即每个“E”形图近似于正方形)，如图4－7－17，小明在制作视力表时，测得l1＝14 cm，l2＝7 cm，他选择了一张面积为4 cm2的正方形卡纸，刚好可以剪得第②个小“E”形图．那么下面四张正方形卡纸中，能够刚好剪得第①个大“E”形图的是( ) A．面积为8 cm2的卡纸B．面积为16 cm2的卡纸C．面积为32 cm2的卡纸D．面积为64 cm2的卡纸13．如图4－7－18，在△ABC中，BC>AC，点D在BC上，且DC＝AC，∠ACB的平分线CF交AD于点F，E是AB的中点，连接EF.(1)求证：EF∥BC；(2)若四边形BDFE的面积为6，求△ABD的面积．图4－7－1814．如图4－7－19所示，M是△ABC内一点，过点M分别作三条直线平行于△ABC的各边，所形成的三个小三角形△1，△2，△3(图中阴影部分)的面积分别是4，9和49，求△ABC 的面积．图4－7－1915．某社区拟筹资金2000元，计划在一块上、下底长分别是10 m、20 m的梯形空地上种植花草．如图4－7－20，他们想在△AMD和△CMB地带种植单价为10元/m2的太阳花，当△AMD地带种满花后，已经花了500元，请你预算一下，若继续在△CMB地带种植同样的太阳花，资金是否够用，并说明理由．图4－7－2016．如图4－7－21，在△ABC中，AB＝5，BC＝3，CA＝4，PQ∥AB，点P在CA上(与点A，C不重合)，点Q在BC上．(1)当△PQC的面积与四边形PABQ的面积相等时，求CP的长．(2)当△PQC的周长与四边形PABQ的周长相等时，求CP的长．(3)试问：在AB上是否存在一点M，使得△PQM为等腰直角三角形？若存在，请求出PQ 的长；若不存在，请简要说明理由．图4－7－211．C 2.A3．A [解析] ∵△ABC∽△DEF，其相似比为3∶1，∴△ABC的周长△DEF的周长＝31，∴△DEF的周长＝13×27＝9.故选A.4．解：∵四边形ABCD是平行四边形，∴AB∥CD，AD∥BC，∴∠BAE＝∠F，∠EAD＝∠AEB.∵AE平分∠BAD，∴∠BAE＝∠EAD，∴∠BAE＝∠AEB，∴BE＝AB＝6，∴CE＝BC－BE＝3.∵∠AEB＝∠FEC，∠BAE＝∠F，∴△ABE∽△FCE，∴△ABE的周长△FCE的周长＝BECE＝2.∵BG⊥AE，∴AE＝2AG＝2 AB2－BG2＝4，∴△ABE的周长＝AB＋BE＋AE＝16，∴△FCE的周长＝12×△ABE的周长＝8.5．A6．C [解析] ∵∠ACD＝∠B，∠A＝∠A，∴△ACD∽△ABC，∴S△ACDS△ABC＝(ADAC)2＝14.∵S△ACD＝1，∴S△ABC＝4，∴S△BCD＝S△ABC－S△ACD＝3.7．1 [解析] 如图，∵把△ABC沿AB边平移到△A′B′C′的位置，∴AC∥A′C′，∴△ABC ∽△A′BD.∵S△ABC∶S△A′BD＝4，∴AB∶A′B＝2.∵AB＝2，∴A′B＝1，∴AA′＝2－1＝1.8．3 [解析] ∵∠AED＝∠B，∠A是公共角，∴△ADE∽△ACB，∴S△ADES△ACB＝(AEAB)2.∵△ADE的面积为4，四边形BCED的面积为5，∴△ABC的面积为9.∵AE＝2，∴49＝(2AB)2，解得AB＝3.9．解：(1)∵四边形ABCD是平行四边形，∴AB＝CD，AB∥CD，∴∠AEF＝∠CDF，∠FAE＝∠FCD，∴△AEF∽△CDF.∵AE∶EB＝1∶2，∴AE∶AB＝AE∶CD＝1∶3，∴△AEF与△CDF的周长的比为1∶3.(2)由(1)知，△AEF∽△CDF，相似比为1∶3，∴它们的面积比为1∶9.∵S△AEF＝6 cm2，∴S△CDF＝54 cm2.10．A 11.A12．B [解析] ∵每个“E”形图近似于正方形，∴P2D2∥P1D1，∴∠PP2D2＝∠PP1D1，∠P2D2P＝∠P1D1P，∴△PP2D2∽△PP1D1.∵l1＝14 cm，l2＝7 cm，∴P2D2∶P1D1＝1∶2.∵第②个小“E”形图是面积为4 cm2的正方形卡纸，∴第①个大“E”形图的面积＝4×4＝16(cm2)．故选B.13．解：(1)证明：∵DC＝AC，CF是∠ACB的平分线，∴CF是△ACD的中线，∴F是AD的中点．又∵E是AB的中点，∴EF∥BD，即EF∥BC.(2)由(1)知，EF∥BD，∴△AEF∽△ABD，∴S△AEFS△ABD＝\a\vs4\al\co1(\f(AEAB))2.又∵AE＝12AB，S△AEF＝S△ABD－S四边形BDFE＝S△ABD－6，∴S△ABD－6S△ABD＝\a\vs4\al\co1(\f(12))2，∴S△ABD＝8.14．解：根据题意，容易得到△1∽△2∽△3∽△ABC.因为△1、△2、△3的面积分别是4，9和49，所以它们之间的相似比为2∶3∶7，即BC 边被分成的三段从左到右的比为2∶7∶3，则△1与△ABC的相似比为2∶12＝1∶6，所以它们的面积比为1∶36，求得△ABC的面积是144.15．解：不够用．理由如下：在梯形ABCD中，∵AD∥BC，∴△AMD∽△CMB，∴S△AMDS△CMB＝(ADBC)2.∵AD＝10 m，BC＝20 m，∴S△AMDS△CMB＝(1020)2＝14.∵S△AMD＝500÷10＝50(m2)．∴S△CMB＝50×4＝200(m2)．还需要资金200×10＝2000(元)，而剩余资金为2000－500＝1500(元)<2000元，∴资金不够用．16．解：(1)∵PQ∥AB，∴△PQC∽△ABC.∵S△PQC＝S四边形PABQ，∴S△PQC∶S△ABC＝1∶2，∴CPCA＝12)＝2)2，∴CP＝2)2·CA＝2 2.(2)∵△PQC∽△ABC，∴CPCA＝CQCB＝PQAB，即CP4＝CQ3，∴CQ＝34CP.同理：PQ＝54CP，∴C△PQC＝CP＋PQ＋CQ＝CP＋54CP＋34CP＝3CP，C四边形PABQ＝PA＋AB＋BQ＋PQ＝4－CP＋AB＋3－CQ＋PQ＝4－CP＋5＋3－34CP＋54CP＝12－12CP.由C△PQC＝C四边形PABQ，得3CP＝12－12CP，∴72CP＝12，∴CP＝247.(3)存在．∵CA＝4，AB＝5，BC＝3，∴△ABC中AB边上的高为125.①如图(a)所示，当∠MPQ＝90°且PM＝PQ时，∵△CPQ∽△CAB，∴PQAB＝△CPQ中PQ上的高△CAB中AB上的高，∴PQ5＝125125，∴PQ＝6037；②当∠PQM＝90°时与①相同；③如图(b)所示，当∠PMQ＝90°且PM＝MQ时，过点M作ME⊥PQ，则ME＝12PQ，∴△CPQ中PQ上的高为125－ME＝125－12PQ.∵PQAB＝△CPQ中PQ上的高△CAB中AB上的高，∴PQ5＝1212125，∴PQ＝12049.综上可知，存在点M，使得△PQM为等腰直角三角形，此时PQ的长为6037或12049.相似三角形中特殊线段的性质——典型题专项训练知识点对应高、对应角平分线、对应中线的比1．已知△ABC∽△DEF，若△ABC与△DEF的相似比为34，则△ABC与△DEF对应角平分线的比为( )A.34B.43C.916D.1692．如图4－7－1，△ABC∽△A′B′C′，AD，BE分别是△ABC的高和中线，A′D′，B′E′分别是△A′B′C′的高和中线，且AD＝4，A′D′＝3，BE＝6，则B′E′的长为( )图4－7－1A.32B.52C.72D.923．已知△ABC∽△A′B′C′，AD和A′D′是它们的对应角平分线，已知AD＝8 cm，A′D′＝3 cm，则△ABC与△A′B′C′的对应高的比为________．4．已知△ABC∽△A′B′C′，BD和B′D′是它们的对应中线，已知ACA′C′＝32，B′D′＝4，则BD的长是________．5．如图4－7－2是一个照相机成像的示意图，如果底片AB宽40 mm，焦距是60 mm，求所拍摄的2 m外景物的宽CD.图4－7－26．已知△ABC∽△A′B′C′且相似比为13，△A′B′C′∽△A″B″C″且相似比为43，则△ABC与△A″B″C″的相似比为( )A.14B.94C.49D.94或497．如图4－7－3所示，某校宣传栏后面2 m处种了一排树，每隔2 m一棵，共种了6棵，小勇站在距宣传栏中间位置的垂直距离3 m处，正好看到这排树两端的树干，其余的4棵树均被挡住，那么宣传栏的长为________m．(不计宣传栏的厚度)4－7－3 4－7－48．如图4－7－4，矩形EFGH内接于△ABC，且边FG落在BC上，若AD⊥BC，BC＝3，AD ＝2，EF＝23EH，则EH的长为________．9．某高中学校为高一新生设计的学生板凳的正面示意图如图4－7－5所示．其中BA＝CD，BC＝20 cm，BC，EF平行于地面AD且到地面AD的距离分别为40 cm，8 cm，为使板凳两腿底端A，D之间的距离为50 cm，那么横梁EF应为多长？(材质及其厚度等暂忽略不计)图4－7－510．如图4－7－6，△ABC是一张锐角三角形的硬纸片，AD是边BC上的高，BC＝40 cm，AD＝30 cm，从这张硬纸片上剪下一个长HG是宽HE的2倍的矩形EFGH，使它的一边EF在BC上，顶点G，H分别在AC，AB上，AD与HG的交点为M.(1)求证：AMAD＝HGBC；(2)求矩形EFGH的周长．图4－7－611．如图4－7－7所示，有一侦察员在距敌方200 m的A处发现敌人的一座建筑物DE，但不知其高度，又不能靠近建筑物测量，机灵的侦察员将食指竖直举在右眼前，闭上左眼，并将食指前后移动，使食指恰好能将建筑物遮住．若此时眼睛到食指的距离约为40 cm，食指的长约为8 cm，你能根据上述条件计算出敌方建筑物DE的高度吗？请写出你的推理过程．图4－7－712．一块三角板的一条直角边AB的长为1.5 m，面积为1.5 m2，要把它加工成一个面积尽可能大的正方形桌面，甲、乙两名同学的加工方法如图4－7－8①②所示，请你用学过的知识说明哪名同学的加工方法更好．(加工损耗忽略不计，计算结果中的分数可保留)图4－7－813．从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形，如果分得的两个小三角形中一个为等腰三角形，另一个与原三角形相似，我们把这条线段叫做这个三角形的完美分割线．(1)如图4－7－9①，在△ABC中，CD为角平分线，∠A＝40°，∠B＝60°，求证：CD 是△ABC的完美分割线；(2)如图②，在△ABC中，AC＝2，BC＝2，CD是△ABC的完美分割线，且△ACD是以CD 为底边的等腰三角形，求完美分割线CD的长．图4－7－9详解1．A2．D [解析] ∵△ABC∽△A′B′C′，AD，BE分别是△ABC的高和中线，A′D′，B′E′分别是△A′B′C′的高和中线，∴ADA′D′＝BEB′E′.∵AD＝4，A′D′＝3，BE＝6，∴43＝6B′E′，解得B′E′＝92.3.834.65．解：由题意，可知△ABE∽△DCE，∴0.04CD＝0.062，解得CD＝43.答：所拍摄的2 m外景物的宽CD为43 m.6．C [解析] 设△ABC，△A′B′C′，△A″B″C″的一组对应边的长分别为x，y，z.∵△ABC∽△A′B′C′且相似比为13，△A′B′C′∽△A″B″C″且相似比为43，∴xy＝13，yz＝43，即x＝y3，z＝3y4，∴xz＝49，即△ABC与△A″B″C″的相似比为49.故选C.7．68．329．解：如图，过点C作CM∥BA，分别交EF，AD于点N，M，过点C作CP⊥AD，分别交EF，AD于点Q，P.由题意，得四边形ABCM是平行四边形，∴EN＝AM＝BC＝20 cm，∴MD＝AD－AM＝50－20＝30(cm)．由题意知CP＝40 cm，PQ＝8 cm，∴CQ＝32 cm.∵EF∥AD，∴△CNF∽△CMD，∴NFMD＝CQCP，即NF30＝3240，解得NF＝24(cm)．∴EF＝EN＋NF＝20＋24＝44(cm)．答：横梁EF应为44 cm.10．解：(1)证明：(证法一)∵四边形EFGH为矩形，∴EF∥GH，∴△AHG∽△ABC. ∵AD⊥BC，EF∥GH，∴AM⊥HG，∴AMAD＝HGBC；(证法二)∵四边形EFGH为矩形，∴EF∥GH，∴△AHG∽△ABC，△AHM∽△ABD，∴HGBC＝AHAB，AMAD＝AHAB，∴AMAD＝HGBC.(2)由(1)得AMAD＝HGBC.设HE＝x cm，则HG＝2x cm，∵AD⊥BC，∴DM＝HE，∴AM＝AD－DM＝AD－HE＝(30－x)cm.可得30－x30＝2x40，解得x＝12，2x＝24.故矩形EFGH的周长为2×(12＋24)＝72(cm)．11．解：如图，过点A作AG⊥BC于点G，并延长交DE于点F.∵BC∥DE，∴AF⊥DE，∠D＝∠ABC，∠AED＝∠ACB，∴△ADE∽△ABC，∴DEBC＝AFAG，∴DE＝AF·BCAG＝200×0.080.4＝40(m)．答：敌方建筑物DE的高度为40 m.12．解：由AB＝1.5 m，S△ABC＝1.5 m2，得BC＝2 m.在题图①中，设甲同学加工的正方形桌面的边长为x m.∵DE∥AB，∴Rt△CDE∽Rt△CBA，∴CDCB＝DEBA，即2－x2＝x1.5，解得x＝67；如图，在题图②中，过点B作BH⊥AC，交AC于点H，交DE于点P. AC＝AB2＋BC2＝1.52＋22＝2.5(m)，BH＝AB·BCAC＝1.5×22.5＝1.2(m)．设乙同学加工的正方形桌面的边长为y m.∵DE∥AC，∴△BDE∽△BAC，∴DEAC＝BPBH，即y2.5＝1.2－y1.2，解得y＝3037.∵67＝3035>3037，即x>y，∴x2>y2，∴甲同学的加工方法更好．13．解：(1)证明：∵∠A＝40°，∠B＝60°，∴∠ACB＝80°，∴△ABC不是等腰三角形．∵CD平分∠ACB，∴∠ACD＝∠BCD＝12∠ACB＝40°，∴∠ACD＝∠A＝40°，∴△ACD是等腰三角形．∵∠BCD＝∠A＝40°，∠CBD＝∠ABC，∴△BCD∽△BAC，∴CD是△ABC的完美分割线．(2)由题意得△BCD∽△BAC，∴BCBA＝BDBC.∵AC＝AD＝2，BC＝2，设BD＝x，则AB＝x＋2，∴2)x＋2＝x\r(2)，解得x＝－1±3，∵x＞0，∴BD＝x＝3－1.∵△BCD∽△BAC，∴CDAC＝BDBC.∵AC＝2，BC＝2，BD＝3－1，∴CD＝BD·ACBC＝3)－1\r(2)×2＝6－2.。

2023九年级数学上册第四章图形的相似相似三角形的判定课后练习二含解析新版北师大版

相似三角形的判定重难点易错点解析题一：题面：如图，平行四边形ABCD中，过点B的直线与对角线AC、边AD分别交于点E和F．过点E作EG∥BC，交AB于G，则图中相似三角形有（）．A．4对 B．5对 C．6对 D．7对金题精讲题一：题面：如图，在△ABC中，AB=5，AC=4，点D在边AB上，∠ACD=∠B，则AD的长为．题二：题面：在直角梯形ABCD中，AD∥BC，以AB为直径作圆O恰好与CD相切于E，连AC、BD相交于F，连EF．（1）求证：AB2=4AD•BC；（2）求证：EF∥BC．满分冲刺题一：题面：如图，在矩形ABCD 中，AB =4，AD =10，F 是AD 上一点，CF ⊥EF 于点F 交AB 于点E ， 12DC CF ．求AE 的长．题二：题面：如图，在正方形ABCD 中，F 是CD 上一点，AE ⊥AF ，点E 在CB 的延长线上，EF 交AB 于点G ．求证：DF •FC =BG •EC ．题三：题面：如图，已知边长为2的正方形ABCD 中，E 为CD 的中点，P 为BC 上的一点，问题：添加一个条件，使得△ABP 与以E 、C 、P 为顶点的三角形相似，共有几种添加方法？课后练习详解重难点易错点解析题一：答案：B．详解：根据平行四边形的性质，平行的性质和相似三角形的判定可得：△AGE∽△ABC，△BGE∽△BAF，△AEF∽△CEB，△ACB∽△CAD，△AGE∽△CDA，5对．故选B．金题精讲题一：答案：3.2．详解：∵∠ACD=∠B，∠A=∠A，∴△ABC∽△ACD．∴AD AC AC AB=．又∵AB=5，AC=4，∴445AD=，解得AD=3.2．题二：答案：AB2=4AD•BC；EF∥BC．详解：证明：（1）作DH⊥BC于H，如图，∵梯形ABCD为直角梯形，且AD∥BC，∴四边形ABHD为矩形，∴DH=AB，AD=BH，∴CH=CB AD，∵以AB为直径作圆O恰好与CD相切于E，∴DA、CB都是⊙O的切线，∴DE=DA，CE=CB，∴DC=DA+CB，在Rt△DHC中，DH2=DC2CH2，∴AB2=(AD+BC)2(BC AD)2，∴AB2=4AD•BC；（2）∵AD∥BC，∴△FDA∽△FBC，∴AD DF BC FB=，而DE=AD，EC=BC，∴DE DF EC FB=，∴EF∥BC．满分冲刺题一：答案：5232-．详解：∵四边形ABCD是矩形，∴∠A=∠D=90°，DC=AB=4，∵CF⊥EF，∴∠EFC=90°．∴∠AFE+∠DFC=90°，∵∠AEF+∠AFE=90°，∴∠AEF=∠DFC，∴△AEF∽△DFC．∴AE AF DF DC=，∵12DCCF=，DC=4，∴∠DFC=30°，∴443tan30tan30DCFD===︒︒，∴1043AF=-，∴5232AF FDAECD-==．题二：答案：DF•FC=BG•EC．详解：∵∠EAB+∠BAF=90°，∠DAF+∠BAF=90°，∴∠BAE=∠DAF，∴tan∠BAE=tan∠DAF，∵AB=AD，∴DF=BE，又∵AB∥CD，∴BE BG EC FC=，∴BE•FC=BG•EC，∴DF•FC=BG•EC．题三：答案：只有一种方法在BC上的一点使得BP=43．详解：如图设BP=x，若△ABP∽△ECP，得AB EC BP CP=，即212x x=-，解得x=43．若△PBA∽△ECP，得BP ECBA CP=，即122xx=-，化简得x22x+2=0，此方程无解，故不存在综上，只有一种方法在BC上的一点使得BP=43．（或延长AB至M，使BM=BA，连接EM，交BC与点P，则P就是符合条件的点）。

4.7 相似三角形的性质北师大版数学九年级上册堂堂练(含答案)

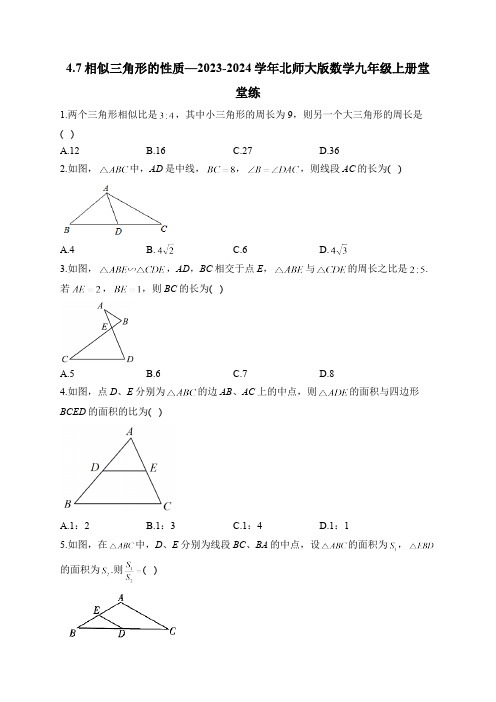
4.7相似三角形的性质—2023-2024学年北师大版数学九年级上册堂堂练1.两个三角形相似比是，其中小三角形的周长为9，则另一个大三角形的周长是( )A.12B.16C.27D.362.如图，中，AD是中线，，，则线段AC的长为( )A.4B.C.6D.3.如图，，AD，BC相交于点E，与的周长之比是.若，，则BC的长为( )A.5B.6C.7D.84.如图，点D、E分别为的边AB、AC上的中点，则的面积与四边形BCED的面积的比为( )A.1：2B.1：3C.1：4D.1：15.如图，在中，D、E分别为线段BC、BA的中点，设的面积为，的面积为.则( )A. B. C. D.6.两个相似三角形对应中线的比为2:3,周长的和是20,则这两个三角形的周长分别为_______.7.若两个相似三角形的面积之比为，则它们的对应角平分线之比为______________.8.如图，在矩形ABCD中，E为BC的中点，，垂足为F，，，求AE，DF的长.答案以及解析1.答案：A解析：解：两个三角形相似比是，两个三角形的周长之比是，其中小三角形的周长为9，另一个大三角形的周长是，故选A.2.答案：B解析：，AD是中线，，在和中，，，，，，；故选B.3.答案：B解析：，与的周长之比是，，，，，，故选B.4.答案：B解析：D、E分别为的边AB、AC上的中点，DE是的中位线，，，，的面积：的面积，的面积：四边形BCED的面积；故选B.5.答案：B解析：在中，D、E分别为线段BC、BA的中点，DE为的中位线，，，，，，即，故选：B.6.答案：8和12解析：这两个相似三角形对应中线的比为2:3,∴这两个相似三角形的周长比为2:3.设这两个三角形的周长分别为,则,解得.,即这两个三角形的周长分别为8和12.7.答案：解析：两个相似三角形的面积比为，它们的对应角平分线之比为. 8.答案：，解析：四边形ABCD是矩形，，，，又，，，E是BC的中点，，，，，解得：.。

北师大版数学九年级上册第四章第四节 4.4 第1课时相似三角形的定义及其判定定理1 同步练习(含答案)

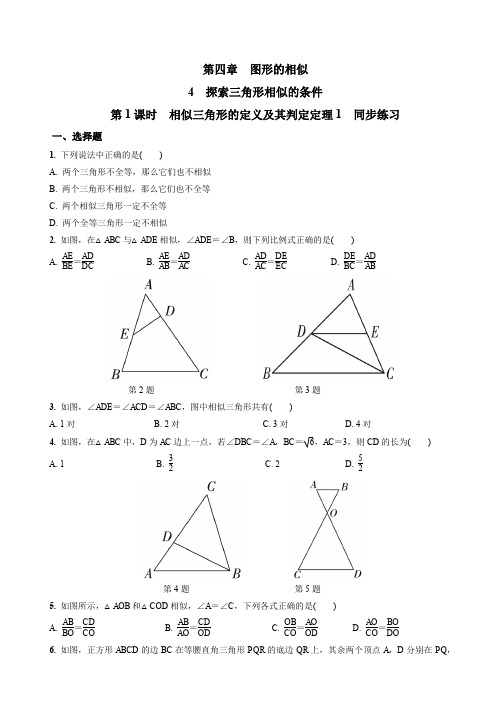
第四章图形的相似 4 探索三角形相似的条件第1课时相似三角形的定义及其判定定理1 同步练习一、选择题1. 下列说法中正确的是( )A. 两个三角形不全等，那么它们也不相似B. 两个三角形不相似，那么它们也不全等C. 两个相似三角形一定不全等D. 两个全等三角形一定不相似2. 如图，在△ABC 与△ADE 相似，∠ADE ＝∠B ，则下列比例式正确的是( ) A.AE BE ＝AD DC B. AE AB ＝AD AC C. AD AC ＝DE EC D. DE BC ＝AD AB第2题第3题3. 如图，∠ADE ＝∠ACD ＝∠ABC ，图中相似三角形共有( )A. 1对B. 2对C. 3对D. 4对4. 如图，在△ABC 中，D 为AC 边上一点，若∠DBC ＝∠A ，BC ＝6，AC ＝3，则CD 的长为( ) A. 1 B. 32 C. 2 D. 52第4题第5题5. 如图所示，△AOB 和△COD 相似，∠A ＝∠C ，下列各式正确的是( ) A.AB BO ＝CD CO B. AB AO ＝CD OD C. OB CO ＝AO OD D. AO CO ＝BODO6. 如图，正方形ABCD 的边BC 在等腰直角三角形PQR 的底边QR 上，其余两个顶点A ，D 分别在PQ ，PR 上，则P A ∶AQ 的值是( )A. 1∶2B. 1∶2C. 1∶3D. 2∶3第6题第7题7. 如图，在△ABC 中，∠B ＝90°，AB ＝6，BC ＝8，将△ABC 沿DE 折叠，使点C 落在AB 边上的C ′处，并且C ′D ∥BC ，则CD 的长是( )A.409 B. 509 C. 154 D. 2548. 如图，在△ABC 中，各边互不相等，点P 是AC 的中点，过点P 作一条直线，使截得的三角形与原三角形相似.这样的直线至多可作( )A. 1条B. 2条C. 3条D. 4条第8题第9题9. 如图，在△ABC 中，∠A ＝36°，AB ＝AC ，BD 是△ABC 的角平分线，则△ABC ∽ . 10. 如图，在边长为9的正三角形ABC 中，BD ＝3，∠ADE ＝60°，则AE 的长为 .11. 如图，已知▱ABCD 中，E 为AD 延长线上的一点，AD ＝23AE ，BE 交DC 于F ，指出图中各对相似三角形及其相似比.12. 如图，在梯形ABCD 中，AB ∥CD ，且AB ＝2CD ，E ，F 分别是AB ，BC 的中点.EF 与BD 相交于点M . (1)求证：△EDM ∽△FBM ； (2)若DB ＝9，求BM .13. 如图，在△ABC 中，∠ACB ＝90°，AC ＝BC ，P 是△ABC 内一点，且∠APB ＝∠APC ＝135°. (1)求证：△CP A ∽△APB ； (2)求PCPB的值.14. 在矩形ABCD 中，E 为CD 的中点，H 为BE 上的一点，EHBH＝3，连接CH 并延长交AB 于点G ，连接GE 并延长交AD 的延长线于点F .(1)求证：EC BG ＝EHBH ；(2)若∠CGF ＝90°时，求ABBC的值.15. 如图，在平面直角坐标系内，已知点A (0，6)，点B (8，0)，AB ＝10.动点P 从点A 开始在线段AO 上以每秒1个单位长度的速度向点O 移动，同时动点Q 从点B 开始在线段BA 上以每秒2个单位长度的速度向点A 移动，设点P ，Q 移动的时间为t 秒.(1)求直线AB 的函数表达式；(2)当t 为何值时，△APQ 与△AOB 相似，并求出此时点P 与点Q 的坐标.1. B2. D3. D4. C5. D6. B7. A8. D9. △BCD 10. 711. 解：△DEF ∽△CBF ，其相似比为21；△DEF ∽△AEB ，其相似比为31；△CBF ∽△AEB ，其相似比为32. 12. (1)证明：∵E 为AB 中点，∴EB ＝21AB ，∵CD ＝21AB ，∴EB ＝CD.又AB ∥CD ，∴四边形EBCD 为平行四边形，∴FB ∥DE .∴△EDM ∽△FBM .(2)解：由(1)知MD MB ＝DE FB ，由题意知，CB FB ＝DE FB ＝21，DB ＝9，故DM MB ＝21，MB ＋DM ＝9，得BM ＝3.13. (1)证明：∵∠ACB ＝90°，AC ＝BC ，∴∠CAB ＝∠CBA ＝45°.又∵∠APB ＝∠APC ＝135°，∴∠CAP ＋∠ACP＝45°，∴∠ACP ＝∠BAP ，∴△CP A ∽△APB .(2)解：由△CP A ∽△APB ，得PA PC ＝PB PA ＝AB AC .∵∠ACB ＝90°，AC ＝BC ，∴AB ＝AC ，∴PA PC ＝PB PA ＝21，∴PC ＝22P A ，PB ＝P A ，∴PB PC ＝PA PA ＝21.14. (1)证明：∵四边形ABCD 为矩形，∴AB ∥CD ，∴∠HBG ＝∠HEC ，∠HGB ＝∠HCE ，∴△BHG ∽EHC ，∴BG EC ＝BH EH ＝3.(2)解：∵∠A ＝∠CBG ＝90°，又∵∠CGF ＝90°，∴∠AGF ＋∠BGC ＝90°.又∵∠AGF ＋∠AFG ＝90°，∴∠BGC ＝∠AFG ，∴△AFG ∽△BGC ，∴BG AF ＝BC AG .由(1)知，BG EC ＝BH EH ＝3，∴BG ＝31EC ＝61CD ＝61AB ，∴AG ＝65AB .又∵△FDE ∽△F AG ，∴FA FD ＝AG DE ＝53，∴F A ＝25AD ＝25BC ，由BG AF ＝BC AG 得，AB 1＝BC AB ，∴BC2AB2＝18，∴BC AB＝3. 15. 解：(1)直线AB 的函数表达式为y ＝－43x ＋6.(2)由题意，知AP ＝t ，AQ ＝10－2t .可分两种情况讨论：①当∠APQ ＝∠AOB 时，有△APQ ∽△AOB ，此时t ＝1130，P (0，)，Q (，).②当∠AQP ＝∠AOB 时，有△APQ ∽△ABO ，此时t ＝1350，P (0，)，Q (，).。

2020-2021学年北师大版九年级上数学第四章第七节《相似三角形的性质》同步练习(有答案)

第7节相似三角形的性质一、选择题1、如果两个相似三角形对应边的比为 4∶5,那么它们对应中线的比是( )A. 2∶5B. 2∶5C. 4∶5D. 16∶252、若两个相似三角形对应中线的比为 3∶4,则它们对应角平分线的比是()A. 1∶16B. 16∶9C. 4∶3D. 3∶43、如图,在一斜边长为 30 cm 的直角三角形木板(即 Rt △ACB)中截取一个正方形 CDEF,点 D 在边 BC 上,点 E 在斜边 AB 上,点 F 在边 AC 上,若 AF ∶AC=1∶3,则这块木板截取正方形 CDEF 后,剩余部分的面积为( )A. 200 cm 2B. 170 cm 2C. 150 cm 2D. 100 cm 24、若两个相似三角形的面积之比为 4∶9,则它们对应角平分线之比为( ) A. 32 B. 23 C. 36 D. 26 5、如图,已知 D,E 分别是△ABC 的边 AB,AC 上的点,DE ∥BC,且 S △ADE ∶S 四边形DBCE =1∶8,那么AE ∶AC 等于( )A. 1∶9B. 1∶3C. 1∶8D. 1∶26、如图,在△ABC 中,AC=2,BC=4,D 为 BC 边上一点,且∠CAD=∠B.若△ADC 的面积为 a,则△ABD 的面积为( )A. 2aB. 25aC. 3aD. 27a 7、顺次连接三角形三边的中点,所构成的三角形与原三角形对应高的比是 .8、已知△ABC ∽△DEF,BG 、EH 分别是△ABC 和△DEF 的角平分线,BC=6 cm,EF=4 cm,BG=4.8 cm,则 EH= cm.9、若两个相似三角形对应中线的比是 2∶3,它们的周长之和为 15,则较小的三角形的周长为 .10、如图,平行于 BC 的直线 DE 把△ABC 分成的两部分面积相等,则ABAD = .11、如图,灯泡在圆桌的正上方,当距桌面 2 m 时,圆桌的影子的直径为 2.8 m,在仅仅改变圆桌的高度,其他条件不变的情况下,圆桌的桌面升高多少米,其影子的直径变为 3.2 m?12、如图,△ABC ∽△A'B'C',AD 、A'D'分别是这两个三角形的高,EF 、E'F'分别是这两个三角形的中位线, ''D A AD 与''F E EF 相等吗?为什么?13、如图,在△ABC 与△A'B'C'中,∠ABC=∠A'B'C',∠C=∠C',BG 和 B'G'分别是这两个三角形的角平分线,AM,A'M'分别是 BC,B'C'边上的中线,AN,A'N'分别是BC,B'C'边上的高,若AN ∶A'N'=5∶3,AM=10,B'G'=5,求 A'M',BG 的长.14、如图,已知△ABC ∽△ADE,AE=50,EC=30,问△ABC 与△ADE 的周长之比是多少?15、已知△ABC ∽△DEF, AB DE =32,△ABC 的周长是 12 cm,面积是 30 cm 2.求: (1)△DEF 的周长; (2)△DEF 的面积.16、在比例尺为 1∶10000 的地图上,有甲、乙两个相似的三角形区域,其周长分别为 10 cm 和15 cm.(1)求它们的面积比;(2)若在地图上量得甲三角形区域的面积为16 cm2,那么乙三角形区域的实际面积是多少?17、如图所示,中,点P 在BC 上,且BP∶PC=1∶3,连接AP,BD,交于点Q,S△BPQ=2 cm2.求:(1)△BPQ 与△DAQ 的周长比;(2)S△DAQ.答案2 1.C 2.D 3.D 4.A 5.B 6.C 7. 1∶2 8. 3.2 9. 6 10.2 11. 依题意,易证△ABC∽△ADE.12. 解析13. 解析14.解析∵AE=50,EC=30,∴AC=AE+EC=80.∵△ABC ∽△ADE,即△ABC 与△ADE 的周长之比是 8∶5.15.解析(1)∵△ABC 的周长是 12 cm,∴△DEF 的周长为 12×32=8(cm). (2)16.解析(1) ∵甲三角形区域的周长∶乙三角形区域的周长=10∶15=2∶3,（2）17.解析(1)因为四边形ABCD 为平行四边形,所以AD∥BC,AD=BC,所以∠QBP=∠QDA,∠QPB=∠QAD,所以△BPQ∽△DAQ.因为BP∶PC=1∶3,所以BP∶BC=1∶4,所以BP∶AD=1∶4,所以△BPQ 与△DAQ 的周长比为1∶4.(2)因为△BPQ∽△DAQ,。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

相似三角形-课堂练习+反馈提高
课堂练习
1.下列语句正确的是( )
A.在 △ABC 和△A′B′C′中,∠B=∠B′=90°,∠A=30°,∠C′=60°, 则△ABC 和△A′B′C′不相似;
B.在△ABC 和△A′B′C′中,AB=5,BC=7,AC=8,A′C ′=16,B′C′=14,A′B ′=10,则△ABC ∽△A′B′C′;
C.两个全等三角形不一定相似;
D.所有的菱形都相似
2.根据图中尺寸（AB ∥A ′B ′），那么物像长y （A ′B ′的长）与物长x （AB 的长）之间函数关系的图象大致是图中的（）
A B C D
3.如图，在正三角形ABC 中，D 、E 分别在AC 、AB
上，且
＝，AE ＝BE ，则有（）
（A ）△AED ∽△BED （B ）△AED ∽△CBD
（C ）△AED ∽△ABD （D ）△BAD ∽△BCD AC AD 3
1
( 3题 ) (4题)
4．已知：如图，∠ADE＝∠ACD＝∠ABC，图中相似三角形共有（）
（A）1对（B）2对（C）3对（D）4对
5.三角形三边之比为3:5:7,与它相似的三角形的最长边为21cm,则其余两边之和为( )
A.32cm
B.24cm
C.18cm
D.16cm
6. 已知⊿ABC∽⊿A′B′C′，且BC：B′C′=AC：A′C′，若AC=3，A′C′=1.8，则△A′B′C′与△ABC的相似比是（）。

A. 2:3
B. 3:2
C. 5:3
D. 3:5
7.下列条件中可以判定△ABC∽△A′B′C′的是（）
A.AB:AC＝A′B′:A′C′ B．AB:AC＝A′B′:A′C′，∠B=∠B′
C．AB:AC＝A′B′:A′C′，∠A=∠A′ D．AB:A′B′＝AC:A′C′
8. 已知一次函数y=2x+2与x轴y轴交于A、B两点，另一直线y=kx+3交x轴正半轴于E、交y轴于F点，如△AOB与E、F、O三点组成的三角形相似，那么k值为（）
A. 1.5
B. 6
C. 1.5或6
D. 以上都不对
9.已知一个三角形三边长是6cm，7.5cm，9cm，另一个三角形的三边是8cm，10cm，12cm，则这两个三角形（填相似或不相似）
10. 在1:25000000的中国政区图上，量得福州到北京的距离为6cm，则福州到北京的实际距离为 km。

11. 如图，平行四边形ABCD中，M是BC的中点，且AM=9，BD=12，AD=10，则该平行四边形的面积是_____________
12.四边形ABCD∽四边形A,B,C,D,, ∠A=70度，∠B,=108度，∠C,=92度则∠D=_______
13.在平行四边形ABCD中，AB=10，AD=6，E是AD的中点，在AB上取一点F，使⊿CBF∽⊿CDE，则BF的长为________.
14.如图所示,有一块呈三角形的草坪,其一边长为20m,在这个草坪的图纸上,若这条边的长为5cm, 其他两边的长都是3.5cm, 则该草坪其他两边的实际长度为_________.
15.在直角坐标中,已知点A(-2,0),B(0,4),C(0,3),过点C的直线交x轴于点D,使得以D,O,C为顶点的三角形与∽⊿AOB相似,这样的直线最多可以作____条.
16.已知AB是⊙O的直径，AB=12cm,CD是⊙O一条弦，它与AB交于点E，⊿ACE 与⊿BDE的面积之比为4:1,则AC：BD=_____.
17.已知：如图，在正方形ABCD中，P是BC上的点，且BP＝3PC，Q是CD的中点．求证：⊿ADQ∽⊿QCP．
18. ⊿AB C中,AD、CE是中线, ∠BAD=∠BCE,请猜想⊿ABC的形状,并证明.
作业
1.下列命题：①所有的等腰三角形都相似，②所有的等边三角形都相似，③所有的等腰直角三角形都相似，④所有的直角三角形都相似.其中，正确的是
( )
A.②③
B.②③④
C.③④
D.②④
2.两个相似菱形边长的比是1:4，那么它们的面积比是
( )
A ．1:2
B ．1:4
C ．1:8
D ．1:16
3.如图，点P 是△ABC 的边AB 上的一点，过点P 作直线（不与直线AB 重合）截△ABC ，使截得的三角形与原三角形相似.满足这样条件的直线最多有
( )
A.2条
B.3条
C.4条
D.5条
4.如图，E 是□ABCD 的边BC 延长线上的一点，连结AE 交CD 于F ，则图中共有相似三角形（）
A.1对
B.2对
C.3对
D.4对
5.两个相似三角形的一组对应边长分别为15和27，它们的周长之差为36，则较小三角形的周长是
.
6．若235x y y z +==，则______x y z x
++=. 7. 如图，A 、B 两间有一湖泊无法直接测距，已知AC=30m ，CD=24m,DE ∥AB,DE=16，则AB= ______ m.
8.如图，一张矩形报纸ABCD 的长为acm ，宽为bcm ，E 、F 分别是AB 、CD 的中点.将这张报纸沿着直线EF 对折，矩形AEFD 的长与宽之比等于矩形ABCD 的长和宽之经，则a:b 等于 .
9.如图，在□ABCD 中，E 是BC 中点，F 是BE 中点，AE 与DF 相交于H ，则ADH EFH S S ∆∆:=
10.如图，在矩形ABCD 中，AC 是对角线，E 是AC 的中点，过E 作MN 交AD 于M ，
交BC 于N ，⑴求证：AM=CN ；⑵若∠CEN=90°，EN:AB=2:3，EC=3，求BC 的长.。