实验三 无失真信源编码
合集下载
第四章：无失真信源编码
ε
ε
ε
ε
L[ H (S )+ε ] GL ε ξ= L <2 n nL
=2
−L[ logn−H (S )−ε ]
logn−H (S )−ε >0
① Lim p( A ) =1 ε L→ ∞
信源序列集合S
② H(P , P ,LPL ) →H(P LP ε ) 1 2 1 M n
信源熵
Aε
③ P = L= P ε = 1/ Mε 1 M
大概率事件熵
Aε
• 对于 A 有性质: 有性质 ε Lim p( A ) = 0 ε L→ ∞
由此可见， 由此可见，信源编码只需对信源中少数落入典型大概率事件的集合的符 号进行编码即可。 号进行编码即可。而对大多数属于非典型小概率事件集合中的信源符号 无需编码. 无需编码
H∞ ≅ 1.4bit
§4.2定长编码定理－4-进一步理解 4.2定长编码定理 定长编码定理－
解决方法： 解决方法：
考察： 字母个数为n 字母之间相关长度为L的英文信源， 考察： 字母个数为n，字母之间相关长度为L的英文信源，其可能的字母序列 但其中大部分字母序列是无意义的字母组合，而且随着L 总数为 L ；但其中大部分字母序列是无意义的字母组合，而且随着L n 的增加，这种无意义序列的总数越来越大。 的增加，这种无意义序列的总数越来越大。 进行联合编码，即对字母序列编码， 进行联合编码，即对字母序列编码，且只对哪些有意义的字母序列 方法： 方法： 编码，即需编码的字母序列的总数<< nL ,则平均每个信源符号所 编码，即需编码的字母序列的总数 则平均每个信源符号所 需的码符号个数可以大大减少，从而提高了传输效率。 需的码符号个数可以大大减少，从而提高了传输效率。 ！！但当 足够长后， 问题： 会引入一定的误差！！但当L足够长后 误差可以任意小。 问题： 会引入一定的误差！！但当 足够长后，误差可以任意小。
无失真信源编码
30/100
总结 对离散无记忆信源，给定 , 取 N N 0 ；那么对长度为N的信源序列，满足 下式的为典型序列，否则为非典型序列。
{x : Ni N pi , i 1, , q}
2 0 ，令 N 0 2
定理说明，当N足够大时，典型序列 x 的 的值接近信源的熵 对于有记忆的马氏源，定理5.2.1也成立
选择
，使得
log p
i 1
q
（5. 2. 5）
i
则式（5. 2. 3）成立。
27/100
下面证明定理的后半部分。设 x G 2 ， 根据（5.
2. 3）式，有
log p ( x ) H(X ) N
因为信源是无记忆的，所以 N 得到 log p ( x ) log p ( x i )
(5.2.3)
24/100
我们先证明（5. 2. 3）式。 设信源符号集 为 A {a1 , a 2 , a q } ， 各符号出现的概率分别为 p i ， x x1 x2 x N 为长度为 N 的序列，N 为 x 中符号 a i i 出现的次数。 将信源序列按下列原则分成两 ：G1、 G 2 ，其中， Ni G1 ： { x : pi , i 1, , q} （5. 2.4） N
q log p ( x ) N i log p i i 1
N(p
i 1
q
i
i ) log pi
NH ( X ) N i log pi
i 1
q
26/100
q log p ( x ) H ( X ) i log pi 所以 N i 1 q q log p ( x ) H ( X ) i log pi log pi N i 1 i 1
第三章-无失真信源编码（2）
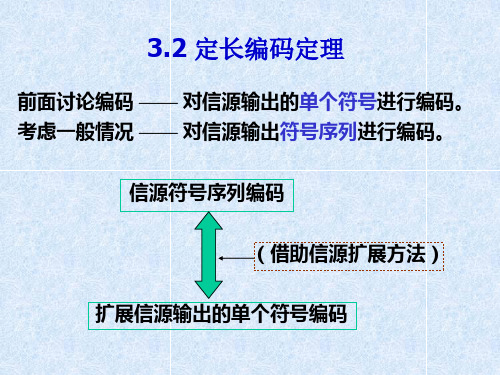
序列 x1x1 x1x2 x2x1 x2x2
序列概率 9/16 3/16 3/16 1/16
即时码 0 10 110 111
这个码的码字平均长度
lN
9 1
3 2
3 3
1 3 27
码元/ 信源序列
16 16 16 16 16
单个符号的平均码长
l
l
N
lN
27
码元 / 符号
N 2 32
编码效率
c
H(X)
例1：设有一简单DMS信源：
U
p
u1 1 2
u2 1 22
u3 1 23
u4 u5 u6 u7
111
1
24 25 26 26
用码元表X＝{0,1}对U的单个符号进行编码(N=1)，即对U
的单个符号进行2进制编码。
解：用X的两个码元对U的7个符号进行编码，单 个对应的定长码长：
l lN log q log 7 2.8 码元 / 符号 N log r log 2
j 1
log r
1 qN
r l j
ln 2
P(a j ) ln
j 1
P(aj )
1 qN
r l j
ln 2 j1 P(a j )( P(a j ) 1)
(ln z z 1)
qN
qN
rlj P(a j )
j 1
j 1
ln 2
11 0 (Kraft不等式和概率完备性质) ln 2
（2）根据信源的自信息量来选取与之对应的码长：
【说明】
霍夫曼编码是真正意义上的最佳编码，对给定的信源，平 均码长达到最小，编码效率最高，费诺编码次之，香农编码 效率最低。
无失真的信源编码.
0 1
0 1
这两种编码哪一种更好呢，我们来计算一下二者的码长。
第七节 霍夫曼编码——二进制哈夫曼编码
L1 P(si )li 0.4 1 0.2 2 0.2 3 0.1 4 0.1 4 2.2 L2 P(si )li 0.4 2 0.2 2 0.2 2 0.1 3 0.1 3 2.2
第七节 霍夫曼编码——二进制哈夫曼编码
例 设单符号离散无记忆信源如下，要求对信源编二进制 霍夫曼码。编码过程如下图（后页）。
x6 x7 x8 X x1 , x2 , x3 , x4 , x5 , P( X ) 0.4 0.18 0.1 0.1 0.07 0.06 0.05 0.04
x2 ,
,
xi ,
,
p( x2 ), ,
p( xi ), ,
xn , p( xn )
p( x ) 1
i 1 i
n
二进制香农码的编码步骤如下： 将信源符号按概率从大到小的顺序排列，为方便起见，令 p(x1)≥ p(x2)≥…≥ p(xn) 令p(x0)=0，用pa(xj)，j=i+1表示第i个码字的累加概率，则：
在图中读取码字的时候，一定要从后向前读，此时编出 来的码字才是可分离的异前置码。若从前向后读取码字， 则码字不可分离。
第七节 霍夫曼编码——二进制哈夫曼编码
第七节 霍夫曼编码——二进制哈夫曼编码
将上图左右颠倒过来重画一下，即可得到二进制哈夫曼码的码树。
第七节 霍夫曼编码——二进制哈夫曼编码
K 也不变，所以没有本质区别；
缩减信源时，若合并后的新符号概率与其他符号概率相等，从编码方 法上来说，这几个符号的次序可任意排列，编出的码都是正确的，但 得到的码字不相同。不同的编法得到的码字长度ki也不尽相同。
无失真的信源编码
费诺码也考虑了信源的统计特性，使经常出现 的信源符号能对应码长短的码字。
费诺码仍然是一种相当好的编码方法。 费诺编码方法同样适合于r元编码，只需每次
分成r组即可。
三种编码方式的比较
只有霍夫曼码必定是最佳码，霍夫曼码的平均 码长最小，信息传输率最大，编码效率最高， 但在实际使用时其设备较为复杂。
本章主要研究无失真信源编码的技术和方 法。从第5章香农第一定理已知，信源的 信息熵是信源进行无失真编码的理论极限 值。总能找到某种合适的编码方法使编码 后信源的信息传输率R’任意地逼近信源的 信息熵而不存在任何失真。在数据压缩技 术中无失真信源编码又常被称为熵编码。
从第二章的讨论可知，正是由于信源概率 分布的不均匀性，或者信源是有记忆的、 具有相关性，使信源中或多或少含有一定 的剩余度。只要寻找到去除相关性或者改 变概率分布不均匀的方法和手段，就能找 到熵编码的具体方法和实用码的结构。
二元霍夫曼码的特点
霍夫曼码的编码方法保证了概率大的符号对应 于短码，概率小的符号对应于长码，即pj>pk， lj>lk，而且短码得到充分利用。
每次缩减信源的最后两个码字总是最后一位码 元不同，前面各位码元相同（二元编码情况） 如表8.1和8.2所示。
每次缩减信源的最长两个码字有相同的码长 这三个特点保证了所得到的霍夫曼码一
霍夫曼编码的选择
霍夫曼编码方法得到的码并非是唯一的。 对于平均码长相等的霍夫曼码可以通过引进码
字长度偏离平均长度的方差选择判断。 在霍夫曼编码过程中，当缩减信源的概率分布
重新排列时，应使合并得来的概率和尽量处于 最高的位置，这样可以使得合并的元素重复编 码次数减少，使短码得到充分利用。
本章主要介绍霍夫曼编码。
费诺码仍然是一种相当好的编码方法。 费诺编码方法同样适合于r元编码，只需每次
分成r组即可。
三种编码方式的比较
只有霍夫曼码必定是最佳码，霍夫曼码的平均 码长最小，信息传输率最大，编码效率最高， 但在实际使用时其设备较为复杂。
本章主要研究无失真信源编码的技术和方 法。从第5章香农第一定理已知，信源的 信息熵是信源进行无失真编码的理论极限 值。总能找到某种合适的编码方法使编码 后信源的信息传输率R’任意地逼近信源的 信息熵而不存在任何失真。在数据压缩技 术中无失真信源编码又常被称为熵编码。
从第二章的讨论可知，正是由于信源概率 分布的不均匀性，或者信源是有记忆的、 具有相关性，使信源中或多或少含有一定 的剩余度。只要寻找到去除相关性或者改 变概率分布不均匀的方法和手段，就能找 到熵编码的具体方法和实用码的结构。
二元霍夫曼码的特点
霍夫曼码的编码方法保证了概率大的符号对应 于短码，概率小的符号对应于长码，即pj>pk， lj>lk，而且短码得到充分利用。
每次缩减信源的最后两个码字总是最后一位码 元不同，前面各位码元相同（二元编码情况） 如表8.1和8.2所示。
每次缩减信源的最长两个码字有相同的码长 这三个特点保证了所得到的霍夫曼码一
霍夫曼编码的选择
霍夫曼编码方法得到的码并非是唯一的。 对于平均码长相等的霍夫曼码可以通过引进码
字长度偏离平均长度的方差选择判断。 在霍夫曼编码过程中，当缩减信源的概率分布
重新排列时，应使合并得来的概率和尽量处于 最高的位置，这样可以使得合并的元素重复编 码次数减少，使短码得到充分利用。
本章主要介绍霍夫曼编码。
(信息论)第5章无失真信源编码
这就是说，每个英文电报符号至少要用5位二元符号进行 编码才能得到唯一可译码。 12
定长编码定理
定长信源编码定理讨论了编码的有关参数对译 码差错的限制关系
sq p s q
定理 5.3.1 设离散无记忆信源
S s1 P p s 1 p s 2 s2
的熵为H S ，其 N 次扩展信源为
S N 1 p 1 P
2 q p 2 p q
N N
现在用码符号集 X x1 , x2 ,, xr 对N次扩展信源 S N 进行长度为 l 的定长编码，对于 0, 0 ，只要满足
l H S N log r
则当 N 足够大时，译码错误概率为任意小，几乎可以实 现无失真编码。 反之，若满足
l H S 2 N log r
则不可能实现无失真编码。而当N足够大时，译码错误概 14 率近似等于1。
以上的定理5.3.1 和定理5.3.2实际上说明的是一个 问题，虽然该定理是在平稳无记忆离散信源的条件下 证明的，但它也同样适合于平稳有记忆信源，只要要 2 求有记忆信源的极限熵 H S 和极限方差 存在 即可。对于平稳有记忆信源，式(5.6)和式(5.7 ) 中 H S 应该为极限熵 H S 。
变长码(可变长度码)
2
奇异码：若码中所有码字都不相同，则称此码为非
奇异码。反之，称为奇异码。
同价码：每个码符号所占的传输时间都相同的码。定
长码中每个码字的传输时间相同。而变长码中的每个码 字的传输时间不一定相等。
表 5.1
信源符号si
信源符号出现概率 si p
定长编码定理
定长信源编码定理讨论了编码的有关参数对译 码差错的限制关系
sq p s q
定理 5.3.1 设离散无记忆信源
S s1 P p s 1 p s 2 s2
的熵为H S ，其 N 次扩展信源为
S N 1 p 1 P
2 q p 2 p q
N N
现在用码符号集 X x1 , x2 ,, xr 对N次扩展信源 S N 进行长度为 l 的定长编码，对于 0, 0 ，只要满足
l H S N log r
则当 N 足够大时，译码错误概率为任意小，几乎可以实 现无失真编码。 反之，若满足
l H S 2 N log r
则不可能实现无失真编码。而当N足够大时，译码错误概 14 率近似等于1。
以上的定理5.3.1 和定理5.3.2实际上说明的是一个 问题，虽然该定理是在平稳无记忆离散信源的条件下 证明的，但它也同样适合于平稳有记忆信源，只要要 2 求有记忆信源的极限熵 H S 和极限方差 存在 即可。对于平稳有记忆信源，式(5.6)和式(5.7 ) 中 H S 应该为极限熵 H S 。
变长码(可变长度码)
2
奇异码：若码中所有码字都不相同，则称此码为非
奇异码。反之，称为奇异码。
同价码：每个码符号所占的传输时间都相同的码。定
长码中每个码字的传输时间相同。而变长码中的每个码 字的传输时间不一定相等。
表 5.1
信源符号si
信源符号出现概率 si p
第3章 无失真信源编码--廖-2013-本科生讲解
表3-2中码3，收到“1”后就知道一个码字已经完结，无须 等待下一个符号抵达，所以无前缀码能够即时译码, 称之为 即时可译码，简称即时码。 而对于码 2 ，收到“ 1 ”后，并不能立即做出判决，就是 收到“10”也不能立即做出判决，则还要收到下面的码元才 能做出判决。所以非异字头码不能即时译码，称为 非即时 码，由于非异字头码的其中一些码字是另一些码字的延长， 故也称延长码。
无失真信源编码主要针对离散信源，连续信源在量化编 码的过程中必然会有量化失真，所以对连续信源只能近 似地再现信源的消息。
3.1.2 码的分类 信源编码可看成是从信源符号集到码符号集的一种映射，即将 信源符号集中的每个元素（可以是单符号，也可以是符号序列）映 射成一个长度为n的码字。对于同一个信源，编码方法是多种的。 【例 3.3】 用{u1 ，u2 ，u3，u4}表示信源的四个消息，码符号集为 {0,1}，表3-1列出了该信源的几种不同编码。 表3-1 同一信源的几种不同编码 信 源 消息 u1 u2 u3 u4 各消息 概率 q(u1) q(u2) q(u3) q(u4) 码1 00 11 10 11 码2 00 01 10 11 码3 0 1 00 11 码4 1 10 100 1000
一般，可以将码简单的分成如下几类：
1.二元码 若码符号集为 {0，1} ，则码字就是二元序列，称为二元码 , 二元码 通过二进制信道传输，这是数字通信和计算机通信中最常见的一种 码，表3-1列出的4种码都是二元码。 2.等长码 在一组码字集合C中的所有码字cm (m = 1,2, …,M)，其码长都相同， 码中所有码字的长度，都相同，则称这组码C为等长码，表3-1中列 出的码1、码2 就码长n = 2等长码。 3.变长码 若码字集合C中的所有码字cm (m = 1,2, …,M)，其码长不都相同，码 中的码字长短不一，称码C为变长码，表3-1中列出的码3、码4 就是 变长码。
第三章-无失真信源编码(1)
信源编码的主要任务就是减少冗余，提高编码效率。 信源编码的主要任务就是减少冗余，提高编码效率。 主要任务就是减少冗余 具体说，就是针对信源输出符号序列的统计特性， 具体说，就是针对信源输出符号序列的统计特性， 寻找一定的方法把信源输出符号序列变换为最短的码字序列。 寻找一定的方法把信源输出符号序列变换为最短的码字序列。
限失真信源编码－ 限失真信源编码－熵压缩编码
改变信源的熵。 改变信源的熵。 只能保证码元序列经译码后能按一定的失真容许度恢复 只能保证码元序列经译码后能按一定的失真容许度恢复 按一定的失真容许度 信源符号序列。 信源符号序列。 适用于连续信源或模拟信号（语音、图像信源）。 适用于连续信源或模拟信号（语音、图像信源）。 连续信源或模拟信号
{
3.1 码符号集中符号数 ＝2称为二元码，r＝3称为三元码 码符号集中符号数r＝ 称为二元码 ＝ 称为三元码 称为二元码， 3.2 若分组码中的码长都相同则称为等长码，否则称为变长码 若分组码中的码长都相同则称为等长码，
信源符号 信源符号出 现概率 码1 a1 a2 a3 a4 p(a1) p(a2) p(a3) p(a4) 00 01 10 11 码2 0 01 001 111 码表
f1 (u3 ) = w3 = 110, l3 = 3
1 1 1 1 l = ∑ P(ui )li = × 1 + × 2 + × 3 + × 3 = 1.75 (码元 / 符号) 2 4 8 8 i =1
【说明】 f1是定长编码； f2是变长编码，根据信源符号的概率的符号采用较 短的码字，不经常出现（概率小）的符号采用较长 的码字，因此平均码长就会缩短，是一种较好的编 码策略。
例如： 例如：U: {u1,u2,u3}; X:{0,1}; W: {w1=0, w2=10, w3=11}, 为唯一可译码。 为唯一可译码。 当接收码字序列为： 可以唯一地译为： 当接收码字序列为：10011001111 时，可以唯一地译为： w2,w1,w3,w1,w1,w3,w3; 如果码字集合为： 如果码字集合为：W:{w1=0,w2=01,w3=11} 则为非唯一可译码。 则为非唯一可译码。 当接收码字序列为： 可以译为： 当接收码字序列为：0011111101 时，可以译为：w1,w1(w2)……
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
实验三 无失真信源编码
一、[实验目的]
1、理解香农第一定理指出平均码长与信源之间的关系；
2、加深理解香农编码具有的重要的理论意义。
3、掌握霍夫曼编码的原理；
4、掌握霍夫曼编码的方法和步骤；
二、[实验环境]
windows XP,MATLAB 7
三、[实验原理]
香农第一定理：
设离散无记忆信源为
12 (1)
(2)....()S s s sq P p s p s p sq ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦
熵为H(S)，其N 次扩展信源为 12 (1)
(2)....()N q S p p p q P αααααα⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦ 熵为H(S N )。
码符号集X=（x1,x2,…,xr ）。
先对信源N S 进行编码，总可以找
到一种编码方法，构成惟一可以码，使S 中每个信源符号所需的平均码长满足： 1N L H S H S N N +>≥（）（）logr logr
当N →∞时 lim
()N r N L H S N
→∞= N L 是平均码长 1
()N q N i i i L p αλ==∑ i λ是i α对应的码字长度
四、[实验内容]
1、在给定离散无记忆信源
S
P s1 s2 s3 s4 1/8 5/16 7/16 1/8
=
条件下，实现二进制霍夫曼编码，求最后得到的码字并算出编码效率。
五、[实验过程]
每个实验项目包括：1)设计思路2)实验中出现的问题及解决方法；
某一离散信源概率分布：p=[1/2,1/4,1/8,1/16,1/16] 求信源的熵，并对该信源进行二元哈夫曼编码，得到码字和平均码长以及编码效率。
Matlab程序：
function [h,l]=huffman(p)
p=[1/2 1/4 1/8 1/16 1/16];
if length(find(p<0))~=0,
error('Not a prob.vector,there is negative component')
end
if abs (sum(p)-1)>10e-10
error('Input is not a prob.vector,the sun of the components is not equal to 1')
end
n=length(p);
q=p;
m=zeros(n-1,n);
for i=1:n-1
[q,l]=sort(q);
m(i,:)=[l(1:n-i+1),zeros(1,i-1)];
q=[q(1)+q(2),q(3:n),1];
end
for i=1:n-1
c(i,:)=blanks(n*n);
end
c(n-1,n)='0';
c(n-1,2*n)='1';
for i=2:n-1
c(n-i,1:n-1)=c(n-i+1,n*(find(m(n-i+1,:)==1))...
-(n-2):n*(find(m(n-i+1,:)==1)));
c(n-i,n)='0';
c(n-i,n+1:2*n-1)=c(n-i,1:n-1);
c(n-i,2*n)='1';
for j=1:i-1
c(n-i,(j+1)*n+1:(j+2)*n)=c(n-i+1,... n*(find(m(n-i+1,:)==j+1)-1)+1:n*find(m(n-i+1,:)==j+1));
end;
end
for i=1:n
h(i,1:n)=c(1,n*(find(m(1,:)==i)-1)+1:find(m(1,:)==i)*n);
l1(i)=length(find(abs(h(i,:))~=32));
end
l=sum(p.*l1)
运行结果为：l =
1.8750
ans =
1
01
001
0000
0001
六、[实验总结]。