湖北省孝感市中考数学模拟试卷(5月份)
湖北省孝感市数学中考模拟试卷
ABC 中考数学模拟试卷出卷人：孝南区祝站二中舒小军一.，精心选一选，相信自己的判断！（本题共12小题，每小题3分，共36分，在每小题给出的四个选项中只有一项是符合题目要求的，不涂、错涂或涂的代号超过一个，一律得0分）1.温度从-2°C 上升3°C 后是A ．1°CB ． -1°C C ．3°CD ．5°C2．以“和谐之旅”为主题北京奥运会火炬接力，传递总里程约为137000千米，这个数据用科学记数法可表示为（ ） A ．313.710⨯千米 B ．413.710⨯千米 C ．513.710⨯千米D ．613.710⨯千米3．一个三角形的两边长分别为3和7，且第三边长为整数，这样的三角形的周长最小值是A ．14B ．15C ．16D ．174．我市5月份某一周每天的最高气温统计如下：最高气温（℃） 28 29 30 31天 数 1 1 3 2则这组数据（最高气温）的众数与中位数分别是（ ）A ．29，30B ．30，29C ．30，30D ．30，315．均匀地向如图所示的容器注水，最后把容器注满．在注水过程中，能大致反映水面高度h 随时间t 变化的图象是（ ）6．一只蚂蚁在如图所示的树枝上寻找食物，假定蚂蚁在每个岔路口 都会随机地选择一条路径，则它获得食物的概率是（ ）A ． 1 2B ． 1 3C ． 1 4D ． 167．如图，△ABC 的三个顶点都在正方形网格的格点上， 则tan ∠A ＝（ ）A ． 6 5B ． 56C ．210 3 D ． 31020hhhht t t t OOOO注水ABCD8．如图，△AB C 内接于⊙O ，∠C= 45º，AB =4，则⊙O 的半径为A ．22B ．4C ．23D ．249、某个长方体主视图是边长为1cm 的正方形．沿这个正方形的对角线向垂直于正方形的方向将长方体切开，截面是一个正方形．那么这个长方体的俯视图是10. 二次函数2y ax bx c =++的图象如图所示，则一次函数ac bx y -=与反比例函数xcb a y +-=在同一坐标系内的图象大致为（ ）11．如图，圆锥的底面半径为5，母线长为20，一只蜘蛛从底面圆周上一点A出发沿圆锥的侧面爬行一周后回到点A 处的最短路程是（ ）A ．8B ．10 2C ．15 2D ．20 212．一个质点在第一象限及x 轴、y 轴上运动，在第一秒钟，它 从原点运动到(01)，，然后接着按图中箭头所示方向运动[即(00)(01)(11)(10)→→→→，，，，…]，且每秒移动一个单位， 那么第35秒时质点所在位置的坐标是（ ）第8题图ABCO 1- 1O xy（第10题图）yxO y xO yxO y x OA ．(40)，B ．(50)，C ．(05)，D ．(55)，二细心填一填，试自己的身手！（本大题共6小题，每小题3分，共18分，请将结果直接填写在答题卡相应位置上）13．反比例函数ky x=的图像过点(23)-，，则k = ．1 4．图1是四边形纸片ABCD ，其中∠B =120°，∠D =50°，若将其右下角向内折出△PCR如图2所示，恰使CP ∥AB ，RC ∥AD ，则∠C = °． ．15若关于x 的不等式⎩⎨⎧≤-<-1270x m x 的整数解共有4个，则m 的取值范围是16.用围棋子按下面的规律摆图形，则摆第n 个图形需要围棋子的枚数是 ．17．在实数范围内定义运算“☆”，其规则为：22a b a b =-☆， 则方程(43)13x =☆☆的解为x = ．18．四个全等的直角三角形围成一个大正方形，中间空出的部分是 一个小正方形，这样就组成了一个“赵爽弦图”（如图）．如果小正 方形面积为1，大正方形面积为25，直角三角形中较小的锐角为θ，那么sin θ= ．三、用心做一做，显显自己的能力！（本大题共7小题，满分66分，解答写在答题卡上19．(6分)解方程：013132=--+--xx x（第18题图）a c图120．(8分)某市为了节约生活用水，计划制定每位居民统一的月用水量标准，然后根据标准实行分段收费．为此，对居民上年度的月均用水量进行了抽样调查，并根据调查结果绘制了上年度月均用水量的频数分布直方图(图中分组含最低值，不含最高值)，请根据图中信息解答下列问题：(1)本次调查的居民人数为 人；(2)本次调查的居民月均用水量的中位数落在频数分布直方图中的第 小组内(从左至右)；(3)当地政府希望让85%左右居民的月均用水量低于制定的月用水量标准，根据上述调查结果，你认为月用水量标准(取整数)定为多少吨较为合适？21．(10分)『问题情境』勾股定理是一条古老的数学定理，它有多种证明方法，我国汉代数学家赵爽根据弦图，利用面积法进行了证明．著名数学家华罗庚曾提出把“数形关系”(勾股定理)带到其他星球，作为地球人与其他星球“人”进行第一次“谈话”的语言．『定理表述』请你根据图1中的直角三角形叙述勾股定理(用文字及符号语言叙述)．a cc b ab A BCD 图2『尝试证明』以图1中的直角三角形为基础，可以构造出以a 、b 为底，以a ＋b 为高的直角梯形(如图2)，请你利用图2，验证勾股定理．『知识拓展』利用图2中的直角梯形，我们可以证明a ＋bc ＜2．其证明步骤如下：∵BC ＝a ＋b ，AD ＝ ，又在直角梯形ABCD 中，BC AD (填大小关系)， 即 ． ∴a ＋bc＜2．22．(10分)关于x 的一元二次方程x 2―x ＋p ―1＝0有两实数根x 1、x 2．(1)求p 的取值范围；(2)[2＋x 1(1―x 2)][2＋x 2(1―x 1)]＝9，求p 的取值．23．（本题满分10分）如图，AB 为O e 的直径，PQ 切O e 于T ，AC PQ ⊥于C ，交O e 于D ． （1）求证：AT 平分BAC ∠；（5分） （2）若2AD =，TC =O e 的半径．（5分）24．(10分)X 市与W 市之间的城际铁路正在紧张有序地建设中．在建成通车前，进行了社会需求调查，得到一列火车一天往返次数m 与该列车每次拖挂车厢节数n 的部分数据如下：(1)请你根据上表数据，在三个函数模型：①y ＝kx ＋b (k 、b 为常数，k ≠0)；②y ＝ kx(k为常数，k ≠0)；③y ＝ax 2＋bx ＋c (a 、b 、c 为常数，a ≠0)中，选取一个适合的函数模型，求出的m 关于n 的函数关系式是m ＝ (不写n 的取值范围)； (2)结合你求出的函数，探究一列火车每次挂多少节车厢，一天往返多少次时，一天的设计运营人数Q 最多(每节车厢载客量设定为常数p )．（第23题图）A CBDEO xy225．(12分)如图，已知二次函数的图象顶点坐标为(2，0)，直线y＝x＋1与二次函数的图象交于A、B两点，其中点A在y轴上．(1)二次函数的解析式为y＝．(2)证明点(―m，2m―1)不在(1)中所求的二次函数的图象上．(3)C为线段AB的中点，过点C作CE⊥x轴于点E，CE与二次函数的图象交于点D．①y轴上存在点K，使以K、A、D、C为顶点的四边形是平行四边形，则点K的坐标是；②二次函数的图象上是否存在点P，使得S△POE＝2S△ABD？若存在，求出点P的坐标；若不存在，请说明理由．参考答案一、选择题：二、填空题：13.K＝-6 14.95° 15.6≤m＜7 16.2+3n （n为正整数） 17.x=±6 18.SinQ=3／51 2 3 4 5 6 7 8 9 10 11 12A CBC C B A AD B D B23．（1）证明：连接OT，e于T，Q切OPQOT PQ ∴⊥． 1分又AC PQ ⊥Q ，OT AC ∴∥TAC ATO ∴∠=∠ 3分 又OT OA =QATO OAT ∴∠=∠．OAT TAC ∴∠=∠，即AT 平分BAC ∠． ·················· 5分 （2）解：过点O 作OM AC ⊥于M ， ···················· 6分12ADAM MD ∴===．又90OTC ACT OMC ∠=∠=∠=o····················· 7分∴四边形OTCM 为矩形． ························· 8分3OM TC ∴==，∴在Rt AOM △中，22312AO OM AM =+=+=．即O e 的半径为2． ···························· 10分AB DOM （第23题图）。
湖北省孝感市2020年(春秋版)数学中考模拟试卷(5月)(I)卷
湖北省孝感市2020年（春秋版）数学中考模拟试卷（5月)（I）卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题；共24分)1. （2分）如果x、y互为倒数，那么“xy+3”的计算结果是（）A . 4B . 3C . 2D . 12. （2分） (2020八上·百色期末) 下列图形中，不是轴对称图形的是（）A .B .C .D .3. （2分） (2020七上·卫辉期末) 树叶上有许多气孔，在阳光下，这些气孔一面排出氧气和蒸腾水分，一面吸入二氧化碳，一个气孔在一秒钟内能吸入亿个二氧化碳分子，用科学记数法表示亿为（）A .B .C .D .4. （2分） (2019八下·雁江期中) 若分式的值为零，则x的取值为（）A . x≠3B . x≠－3C . x＝3D . x＝－35. （2分）同时投掷两枚硬币每次出现正面都向上的概率是（）A .B .C .D .6. （2分）如图，将△ABC绕点C按顺时针旋转60°得到△A′B′C，已知AC=6，BC=4，则线段AB扫过的图形的面积为（）A . πB . πC . 6πD . π7. （2分）(2018·开封模拟) 一组从小到大排列的数据：a，3，4，4，6(a为正整数)，唯一的众数是4，则该组数据的平均数是（）A . 3.6B . 3.8C . 3.6或3.8D . 4.28. （2分）(2018·南通) 下列计算中，正确的是（）A .B .C .D .9. （2分） (2016九上·无锡期末) 在Rt△ABC中,∠C=90°,若AC=2,BC=1,则tanA的值是（）A .B . 2C .D .10. （2分）把一个正方形的一边增加2cm，另一边增加1cm，所得的长方形的面积比正方形面积增加14cm2 ，那么原来正方形的边长是（）A . 3cmB . 5cmC . 4cmD . 6cm11. （2分）已知⊙O1、⊙O2的半径分别是2cm、4cm，若O1O2=6cm，则两圆的位置关系是（）A . 外切B . 相交C . 内切D . 外离12. （2分）二次函数y=x2-2x+3的对称轴为（）A . x=-2B . x=2C . x=1D . x=-1二、填空题 (共6题；共6分)13. （1分） (2016八下·固始期末) 已知是正整数，则实数n的最大值为________．14. （1分） (2017八上·忻城期中) 化简： ________15. （1分） (2019八下·广安期中) 已知a、b、c、d为四边形的四边长，a、c为对边，且满足a2+b2+c2+d2=2ac+2bd，则这个四边形一定是________形.16. （1分）(2019·吴兴模拟) 在平面直角坐标系中，将函数的图象绕坐标原点O顺时针旋转45°后，得到新曲线 .（1）如图①，已知点A(-1,a)，B(b,10)在函数的图象上，若 , 是A,B旋转后的对应点，连结 , ，则 =________；（2）如图②，曲线与直线相交于点M、N，则为________.17. （1分） (2019九上·海曙期末) 已知扇形的弧长为，半径为，则此扇形的圆心角为________度.18. （1分） (2017八下·钦州港期中) 如图，正方形ABCD的顶点C在直线a上，且点B，D到a的距离分别是1，2．则这个正方形的边长是________ 。
湖北省孝感市数学中考一模试卷(5月)
湖北省孝感市数学中考一模试卷（5月）姓名:________ 班级:________ 成绩:________一、单选题 (共10题；共20分)1. （2分） (2019七下·巴南月考) 下列运算正确的是（）A .B .C .D .2. （2分）正午时分，水平放置的正方形在地面上的投影是（）A . 正方形B . 长方形C . 平行四边形D . 菱形3. （2分）(2013·台州) 三门湾核电站的1号机组将于2013年的10月建成，其功率将达到1 250 000千瓦．其中1 250 000可用科学记数法表示为（）A . 125×104B . 12.5×105C . 1.25×106D . 0.125×1074. （2分） (2017八下·揭西期末) 下列图形是中心对称图形，但不是轴对称图形的是（）A .B .C .D .5. （2分） (2017八下·海淀期末) 如图，在△ 中, ，，边上的中线，那么的长是（）A .B .C .D .6. （2分）正多边形的中心角是36°，那么这个正多边形的边数是（）A . 10B . 8C . 6D . 57. （2分）反比例函数的图像在每个象限内，随的增大而减小，则的值可为（）A .B . 0C . 1D . 28. （2分）在一幅长为80cm，宽为50cm的矩形风景画的四周镶一条相同宽度的金色纸边，制成一幅矩形挂图，如图所示，如果要使整个挂图的面积是5400cm2 ，设金色纸边的宽为xcm，那么x满足的方程是（）A . (80+2x)(50+2x)=5400B . (80－x)(50－x)=5400C . (80+x)(50+x)=5400D . (80－2x)(50－2x)=54009. （2分）如图，已知△ABO的顶点A和AB边的中点C都在双曲线y=（x＞0）的一个分支上，点B在x轴上，CD⊥OB于D，则△AOC的面积为（）A . 2B . 3C . 4D .10. （2分）(2019·黄冈模拟) 如图，在平面直角坐标系中，四边形是菱形，点C的坐标为，，垂直于轴的直线从y轴出发，沿x轴正方向以每秒1个单位长度的速度向右平移，设直线与菱形的两边分别交于点M，N(点M在点N的上方)，若的面积为S，直线的运动时间为秒，则能大致反映S与的函数关系的图象是（）A .B .C .D .二、填空题 (共6题；共15分)11. （1分） (2018八上·番禺期末) 因式分解： ________．12. （10分） (2017七下·南陵竞赛) 已知在数轴l上，一动点Q从原点O出发，沿直线l以每秒钟2个单位长度的速度来回移动，其移动方式是先向右移动1个单位长度，再向左移动2个单位长度，又向右移动3个单位长度，再向左移动4个单位长度，又向右移动5个单位长度…（1）求出5秒钟后动点Q所处的位置；（2）如果在数轴l上还有一个定点A，且A与原点O相距20个单位长度，问：动点Q从原点出发，可能与点A重合吗？若能，则第一次与点A重合需多长时间？若不能，请说明理由．13. （1分）(2019·哈尔滨模拟) 不等式组的解集为________．14. （1分）如图，AB为半⊙O的直径，C为半圆弧的三等分点，过B，C两点的半⊙O的切线交于点P，若AB 的长是2a，则PA的长是________ ．15. （1分） (2019九上·湖州月考) 如图，抛物线（m为常数）交y轴于点A，与x 轴的一个交点在2和3之间，顶点为B.①抛物线与直线有且只有一个交点；②若点、点、点在该函数图象上，则；③将该抛物线向左平移2个单位，再向下平移2个单位，所得抛物线解析式为；④点A关于直线的对称点为C，点D、E分别在x轴和y轴上，当时，四边形BCDE周长的最小值为.其中正确判断的序号是________16. （1分）已知一次函数的图象经过（-1，2）和（-3，4），则这个一次函数的解析式为________.三、解答题 (共9题；共80分)17. （10分）(2017·邗江模拟)（1） +（）﹣1﹣2cos60°+（2﹣π）0（2）解不等式组．18. （5分）(2016·高邮模拟) 先化简，再求值：÷（m﹣1﹣），其中m=﹣3．19. （10分） (2019七上·洪泽期末) 如图，已知直线AB以及直线AB外一点P.按下述要求画图并填空：（1）①过点P画直线MN∥AB；②过点P画直线PC⊥AB，垂足为点；（2）量出点P到直线AB的距离约是多少cm（精确到0.1cm）20. （4分）有100名学生参加两次科技知识测试，条形图显示两次测试的分数分布情况．请你根据条形图提供的信息，回答下列问题（把答案填在题中横线上）：（1）两次测试最低分在第________次测试中；（2）第________次测试成绩较好；（3）第一次测试中，中位数在________分数段，第二次测试中，中位数在________分数段．21. （10分）(2017·商河模拟) 我国中东部地区雾霾天气趋于严重，环境治理已刻不容缓．我市某电器商场根据民众健康需要，代理销售某种家用空气净化器，其进价是200元/台．经过市场销售后发现：在一个月内，当售价是400元/台时，可售出200台，且售价每降低10元，就可多售出50台．若供货商规定这种空气净化器售价不能低于300元/台，代理销售商每月要完成不低于450台的销售任务．（1）试确定月销售量y（台）与售价x（元/台）之间的函数关系式；并求出自变量x的取值范围；（2）当售价x（元/台）定为多少时，商场每月销售这种空气净化器所获得的利润w（元）最大？最大利润是多少？22. （10分）如图，某市郊外景区内一条笔直的公路l经过A、B两个景点，景区管委会又开发了风景优美的景点C．经测量，C位于A的北偏东60°的方向上，C位于B的北偏东30°的方向上，且AB=10km．（1）求景点B与C的距离；（2）为了方便游客到景点C游玩，景区管委会准备由景点C向公路l修一条距离最短的公路，不考虑其他因素，求出这条最短公路的长．（结果保留根号）23. （10分） (2019·瑞安模拟) 如图，在▱ABCD中，E，F分别为边AB，CD的中点，BD是对角线.（1）求证：△ADE≌△CBF；（2）若∠ADB＝90°，AB＝6，求四边形BEDF的周长.24. （10分） (2018九上·新乡期末) 已知：如图，AB是⊙O的直径，BC是弦，∠B=30°，延长BA到D，使∠BDC=30°．（1）求证：DC是⊙O的切线；（2）若AB=2，求DC的长．25. （11分）(2018·淮安) 如图，在平面直角坐标系中，一次函数的图像与x轴和y轴分别相交于A、B两点．动点P从点A出发，在线段AO上以每秒3个单位长度的速度向点O作匀速运动，到达点O停止运动．点A关于点P的对称点为点Q，以线段PQ为边向上作正方形PQMN．设运动时间为t秒．（1）当t＝秒时，点Q的坐标是________；（2）在运动过程中，设正方形PQMN与△AOB重叠部分的面积为S，求S与t的函数表达式；（3）若正方形PQMN对角线的交点为T，请直接写出在运动过程中OT＋PT的最小值．参考答案一、单选题 (共10题；共20分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、二、填空题 (共6题；共15分)11-1、12-1、12-2、13-1、14-1、15-1、16-1、三、解答题 (共9题；共80分) 17-1、17-2、18-1、19-1、19-2、20-1、20-2、20-3、21-1、21-2、22-1、22-2、23-1、23-2、24-1、24-2、25-1、。
孝感市中考数学押题试卷(5月份)
孝感市中考数学押题试卷（5月份）姓名:________ 班级:________ 成绩:________一、选择题 (共10题；共20分)1. （2分）(2019·贺州) 某图书馆有图书约985000册，数据985000用科学记数法可表示为（）A . 985×103B . 98.5×104C . 9.85×105D . 0.985×1062. （2分） (2017七上·哈尔滨月考) 下列说法正确的有（）（1）-a一定是负数；（2）有理数分为正有理数和负有理数；（3）如果a大于b，那么a的倒数小于b的倒数；（4）几个有理数相乘，负因数的个数是奇数个时，积为负数；（5）符号不同的两个数互为相反数A . 0个B . 1个C . 2个D . 3个3. （2分） (2018八上·自贡期末) 在下列图形中，对称轴最多的是（）A . 等腰三角形B . 等边三角形C . 正方形D . 圆4. （2分） (2015七下·杭州期中) 下列计算正确的是（）A . a3•a4=a12B . （a3）4=a12C . （a2b）3=a5b3D . a3÷a4=a5. （2分） (2017九上·文安期末) 小伟掷一个质地均匀的正方体骰子，骰子的六个面上分别刻有1到6的点数．则向上的一面的点数大于4的概率为（）A .B .C .D .6. （2分）如图，AB∥CD，如果∠1是∠2的2倍，那么∠1等于（）A . 60°B . 90°C . 120°D . 150°7. （2分） (2017七下·莒县期末) 如图，小明在操场上从A点出发，沿直线前进10米后向左转40°，再沿直线前进10米后，又向左转40°，照这样走下去，他第一次回到出发地A点时，一共走了（）米．A . 70B . 80C . 90D . 1008. （2分） (2019八上·威海期末) 某次数学测试中，八年级一班平均分为80分，八年级二班的平均分为82分，下列说法错误的是（）A . 两个班的平均分为81分B . 两个班的平均分不可能高于82分C . 若一班的人数比二班多，则两个班的平均分低于81分D . 若两个班的人数相同，则两个班的平均分为81分9. （2分） (2015高三上·盘山期末) 如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为16cm2,则该半圆的半径为（）A . cmB . 9 cmC . cmD . cm10. （2分）(2017·开江模拟) 如图，正方形ABCD的边长为3cm，动点M从点B出发以3cm/s的速度沿着边BC﹣CD﹣DA运动，到达点A停止运动，另一动点N同时从点B出发，以1cm/s的速度沿着边BA向点A运动，到达点A停止运动，设点M运动时间为x（s），△AMN的面积为y（cm2），则y关于x的函数图象是（）A .B .C .D .二、填空题 (共6题；共6分)11. （1分）(2016·盐城) 当x=________时，分式的值为0．12. （1分）分解因式：12x2﹣3y2=________ .13. （1分）(2017·闵行模拟) 2016年3月完工的上海中心大厦是一座超高层地标式摩天大楼，其高度仅次于世界排名第一的阿联酋迪拜大厦，某人从距离地面高度263米的东方明珠球体观光层测得上海中心大厦顶部的仰角是22.3°．已知东方明珠与上海中心大厦的水平距离约为900米，那么上海中心大厦的高度约为________米（精确到1米）．（参考数据：sin22.3°≈0.38，cos22.3°≈0.93．tan22.3°≈0.41）14. （1分）如图，在△ABC中，AC=2，∠A=45°，tanB=，则BC的长为________．15. （1分） (2016八上·大悟期中) 用一块等边三角形的硬纸片（如图甲）做一个底面为等边三角形且高相等的无盖的盒子（边缝忽略不计，如图乙），在△ABC的每个顶点处各需剪掉一个四边形，其中四边形AMDN中，∠MDN 的度数为________16. （1分）⊙O的半径为3cm，B为⊙O外一点，OB交⊙O于点A，AB=OA，动点P从点A出发，以πcm/s的速度在⊙O上按逆时针方向运动一周回到点A立即停止．当点P运动的时间为________ s时，BP与⊙O相切．三、解答题 (共13题；共129分)17. （10分）(2017·济宁模拟) 计算下列各式（1）2cos45°+sin30°cos60°+cos30°（2） | ﹣5|+2cos30°+（）﹣1+（9﹣）0+ ．18. （5分）先化简，再求值：[﹣]+[1+]，其中a=， b=2．19. （5分）已知不等式 x﹣1＞x与x﹣2＞﹣mx的解集相同，求m的值．20. （5分）(2017·泾川模拟) 某工程队修建一条长1200米的道路，采用新的施工方式，工效提升了50%，结果提前4天完成任务．求这个工程队原计划每天修道路多少米．21. （10分）(2016·兖州模拟) 在平面直角坐标系xOy中，直线y=kx+b（k≠0）与双曲线y= 的一个交点为P（2，m），与x轴、y轴分别交于点A，B．（1）求m的值；（2）若PA=2AB，求k的值．22. （10分）已知关于x的一元二次方程：x2﹣（m﹣3）x﹣m=0．（1）试判断原方程根的情况；（2）若抛物线y=x2﹣（m﹣3）x﹣m与x轴交于A（x1，0），B（x2，0）两点，则A，B两点间的距离是否存在最大或最小值？若存在，求出这个值；若不存在，请说明理由．（友情提示：AB=|x2﹣x1|）23. （10分）如图,将▱ABCD沿过点A的直线l折叠,使点D落到AB边上的点D'处,直线l交CD边于点E,连接BE.（1）求证:四边形BCED'是平行四边形;（2）若BE平分∠AB C,求证:AB2=AE2+BE2.24. （15分）(2017·长沙模拟) 如图，在△ABC中，∠ABC=90°，以AB的中点O为圆心，OA为半径的圆交AC于点D，E是BC的中点，连接DE，OE．（1）判断DE与⊙O的位置关系，并说明理由；（2）求证：BC2=2CD•OE；（3）若cos∠BAD= ，BE= ，求OE的长．25. （12分）(2016·南平模拟) 2015年6月28日，“合福高铁”正式开通，对南平市的旅游产业带来了新的发展机遇．某旅行社抽样调查了2015年8月份该社接待来南平市若干个景点旅游的人数，并将调查结果绘制成如下两幅不完整的统计图表，请根据图表信息回答下列问题：景点频数（人数）频率九曲溪1160.29归宗岩0.25天成奇峡840.21溪源峡谷640.16华阳山360.09（1）此次共调查________人，（2）补全条形统计图；（3）由上表提供的数据可以制成扇形统计图，则“天成奇峡”所对扇形的圆心角为________°；（4）该旅行社预计今年8月份将要接待来以上景点的游客约2 500人，根据以上信息，请你估计去“九曲溪”的游客大约有多少人？26. （7分） (2016九上·宾县期中) 如图，直线y=﹣ x+1和抛物线y=x2+bx+c都经过点A（2，0）和点B（k，）（1） k的值是________；（2）求抛物线的解析式；（3）不等式x2+bx+c＞﹣ x+1的解集是________．27. （15分） (2016九上·西城期中) 在平面直角坐标系xOy中，抛物线y=mx2﹣8mx+16m﹣1（m＞0）与x 轴的交点分别为A（x1 ， 0），B（x2 ， 0）．（1）求证：抛物线总与x轴有两个不同的交点；（2）若AB=2，求此抛物线的解析式．（3）已知x轴上两点C（2，0），D（5，0），若抛物线y=mx2﹣8mx+16m﹣1（m＞0）与线段CD有交点，请写出m的取值范围．28. （15分） (2016九上·红桥期中) 在平面直角坐标系中，边长为2的正方形OABC的两顶点A、C分别在y 轴、x轴的正半轴上，点O在原点，现将正方形OABC绕O点顺时针旋转，当A点第一次落在直线y=x上时停止旋转，旋转过程中，AB边交直线y=x于点M，BC边交x轴于点N（如图）．（1）旋转过程中，当MN和AC平行时，求正方形OABC旋转的角度；（2）试证明旋转过程中，△MNO的边MN上的高为定值；（3）折△MBN的周长为p，在旋转过程中，p值是否发生变化？若发生变化，说明理由；若不发生变化，请给予证明，并求出p的值．29. （10分）(2019·北京) 在△ABC中，，分别是两边的中点，如果上的所有点都在△ABC的内部或边上，则称为△ABC的中内弧．例如，下图中是△ABC的一条中内弧．（1）如图，在Rt△ABC中，分别是的中点．画出△ABC的最长的中内弧，并直接写出此时的长；（2）在平面直角坐标系中，已知点，在△ABC中，分别是的中点．①若，求△ABC的中内弧所在圆的圆心的纵坐标的取值范围；②若在△ABC中存在一条中内弧，使得所在圆的圆心P在△A BC的内部或边上，直接写出t的取值范围．参考答案一、选择题 (共10题；共20分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、二、填空题 (共6题；共6分)11-1、12-1、13-1、14-1、15-1、16-1、三、解答题 (共13题；共129分)17-1、17-2、18-1、19-1、20-1、21-1、21-2、22-1、22-2、23-1、23-2、24-1、24-2、24-3、25-1、25-2、25-3、25-4、26-1、26-2、26-3、27-1、27-2、27-3、28-1、28-2、28-3、29-1、29-2、。
湖北省孝感市数学中考模拟试卷(5月)
湖北省孝感市数学中考模拟试卷（5月)姓名:________ 班级:________ 成绩:________一、单选题 (共12题；共24分)1. （2分） (2019七上·孝感月考) 下列说法正确的是（）A . 0 是最小的非负数B . 0 的倒数是0C . 0 表示没有D . 0 比－3 的绝对值大2. （2分） (2019八下·余姚期末) 下列图形是中心对称图形，但不是轴对称图形的是（）A .B .C .D .3. （2分） (2019七上·陇西期中) 国家提倡“低碳减排”，某公司计划在海边建风能发电站，电站年均发电量约为213000000度，若将数据213000000用科学记数法表示为（）A .B .C .D .4. （2分）若分式的值为零，则x的值为（）A . -1B . 1C . 0D . -1或15. （2分）(2013·宁波) 在一个不透明的布袋中装有3个白球和5个红球，它们除了颜色不同外，其余均相同．从中随机摸出一个球，摸到红球的概率是（）A .B .C .D .6. （2分） (2019九上·温岭月考) 下图是几种汽车轮毂的图案，图案绕中心旋转90°后能与原来的图案重合的是（）A .B .C .D .7. （2分）(2019·萧山模拟) 某景区在“五一”小长假期间，每天接待的旅客人数统计如下表.日期5月1日5月2日5月3日5月4日5月5日人数（万人）1.22 2.52 1.1表中表示人数的一组数据中，众数和中位数分别为（）A . 2.5万，2万B . 2.5万，2.5万C . 2万，2.5万D . 2万，2万8. （2分）下列运算正确的是（）A . a4•a2=a8B . 5a2b﹣3a2b=2C . （﹣2a2）3=﹣8a6D . a8÷a4=a29. （2分） (2016高一下·益阳期中) △ABC中，∠C=90°，BC=12，AB=13，那么sinA的值等于（）A .B .C .D .10. （2分）如图，AB⊥BC，AB＝10 cm，BC＝8 cm，一只蝉从C点沿CB方向以每秒1 cm的速度爬行，蝉开始爬行的同时，一只螳螂由A点沿AB方向以每秒2 cm的速度爬行，当螳螂和蝉爬行x秒后，它们分别到达了M，N 的位置，此时，△MNB的面积恰好为24 cm2，由题意可列方程（）A . 2x·x＝24B . (10－2x)(8－x)＝24C . (10－x)(8－2x)＝24D . (10－2x)(8－x)＝4811. （2分）已知两圆半径分别为7、3，圆心距为4，则这两圆的位置关系为（）A . 外离B . 内切C . 相交D . 内含12. （2分） (2018九上·绍兴期中) 向上发射一枚炮弹，经x秒后的高度为y公尺，且时间与高度关系为y=ax2+bx．若此炮弹在第7秒与第14秒时的高度相等，则在下列哪一个时间的高度是最高的？（）A . 第8秒B . 第10秒C . 第12秒D . 第15秒二、填空题 (共6题；共6分)13. （1分）(2012·南京) 使有意义的x的取值范围是________．14. （1分） (2015九下·义乌期中) 分解因式：x2+xy=________．15. （1分）已知△ABC的三边a,b,c满足a+b2+|c-6|+28=4 +10b,则△ABC的外接圆半径=________.16. （1分）已知抛物线y=ax2+bx经过点（﹣4，0），则这条抛物线的对称轴是________．17. （1分）(2016·西安模拟) 圆心角为120°，半径为6cm的扇形的弧长是________cm．18. （1分）(2019·沈阳) 如图，正方形ABCD的对角线AC上有一点E，且CE＝4AE，点F在DC的延长线上，连接EF，过点E作EG⊥EF，交CB的延长线于点G，连接GF并延长，交AC的延长线于点P，若AB＝5，CF＝2，则线段EP的长是________.三、解答题 (共8题；共69分)19. （5分） (2017九上·亳州期末) 计算：|﹣2|+2sin30°﹣（﹣）2+（tan45°）﹣1 ．20. （5分）(2017·微山模拟) 先化简，再求值：，其中．21. （7分）(2016·宁波) 如图，已知抛物线y=﹣x2+mx+3与x轴交于A，B两点，与y轴交于点C，点B的坐标为（3，0）（1）求m的值及抛物线的顶点坐标．（2）点P是抛物线对称轴l上的一个动点，当PA+PC的值最小时，求点P的坐标．22. （7分）(2017·微山模拟) 2017年3月23日，在世界杯预赛亚洲区12强赛A组6轮的较量中，中国足球队以1﹣0的比分战胜老对手韩国队晋级12强．某初中学校为了了解本校800名学生对本次比赛的关注程度，以便做好引导和教育工作，随机抽取了150名学生进行调查，按年级人数和关注程度，分别绘制了条形统计图（图1）和扇形统计图（图2）．（1）请你补全条形统计图，并求“特别关注”所在扇形的圆心角的度数；（2）求全校不关注本场比赛的学生大约有多少名？（3）在这次调查中，九年级共有两位男生和两位女生“不关注”本次比赛，现准备从四人中随机抽取两人进行座谈，请用列表法或画树状图的方法求出抽取的两人恰好是一男生和一女生的概率．23. （10分）(2017·肥城模拟) 如图，在直角坐标系中，⊙M经过原点O（0，0），点A（，0）与点B （0，﹣），点D在劣弧上，连接BD交x轴于点C，且∠COD=∠CBO．（1）求⊙M的半径；（2）求证：BD平分∠ABO；（3）在线段BD的延长线上找一点E，使得直线AE恰好为⊙M的切线，求此时点E的坐标．24. （10分） (2016九上·简阳期末) 某工程队修建一条总长为1860米的公路，在使用旧设备施工17天后，为尽快完成任务，工程队引进了新设备，从而将工作效率提高了50%，结果比原计划提前15天完成任务．（1）工程队在使用新设备后每天能修路多少米？（2）在使用旧设备和新设备工作效率不变的情况下，工程队计划使用旧设备m天，使用新设备n（16≤n≤26）天修建一条总长为1500米的公路，使用旧设备一天需花费16000元，使用新设备一天需花费25000元，当m、n分别为何值时，修建这条公路的总费用最少，并求出最少费用．25. （15分）(2018·南宁) 如图，抛物线y=ax2﹣5ax+c与坐标轴分别交于点A，C，E三点，其中A（﹣3，0），C（0，4），点B在x轴上，AC=BC，过点B作BD⊥x轴交抛物线于点D，点M，N分别是线段CO，BC上的动点，且CM=BN，连接MN，AM，AN．（1）求抛物线的解析式及点D的坐标；（2）当△CMN是直角三角形时，求点M的坐标；（3）试求出AM+AN的最小值．26. （10分）(2019·叶县模拟) 有两张完全重合的矩形纸片，将其中一张绕点A顺时针旋转90o后得到矩形AMEF(如图1)，连接BD，MF，若BD=16cm，∠ADB=30o.（1）试探究线段BD 与线段MF的数量关系和位置关系，并说明理由；（2）把△BCD 与△MEF 剪去，将△ABD绕点A顺时针旋转得△AB1D1，边AD1交FM 于点K(如图2)，设旋转角为β(0o＜β＜90o)，当△AFK 为等腰三角形时，求β的度数；（3）若将△AFM沿AB方向平移得到△A2F2M2(如图3)，F2M2与AD交于点P，A2M2与BD交于点N，当NP∥AB 时，求平移的距离.参考答案一、单选题 (共12题；共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共6题；共6分)13-1、14-1、15-1、16-1、17-1、18-1、三、解答题 (共8题；共69分)19-1、20-1、21-1、21-2、22-1、22-2、22-3、23-1、23-2、23-3、24-1、24-2、25-1、25-2、25-3、26-1、26-2、26-3、。
湖北孝感市2020年部分学校九年级5月调研考试数学试题(含答案)
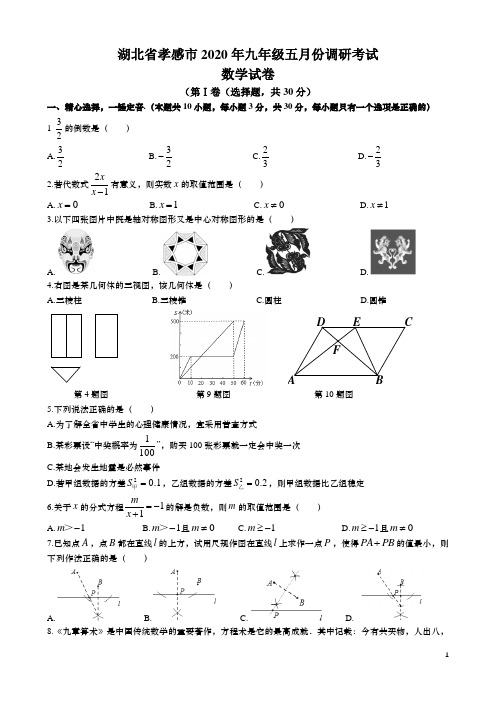
湖北省孝感市2020年九年级五月份调研考试数学试卷（第Ⅰ卷（选择题，共30分）一、精心选择，一锤定音.（本题共10小题，每小题3分，共30分，每小题只有一个选项是正确的）1-32的倒数是（ ） A.32 B.32- C.23 D.23- 2.若代数式21xx -有意义，则实数x 的取值范围是（ ）A.0x =B.1x =C.0x ≠D.1x ≠3.以下四张图片中既是轴对称图形又是中心对称图形的是（ ）A. B. C. D.4.右图是某几何体的三视图，该几何体是（ ）A.三棱柱B.三棱锥C.圆柱D.圆锥第4题图 第9题图 第10题图 5.下列说法正确的是（ ）A.为了解全省中学生的心理健康情况，宜采用普查方式B.某彩票设“中奖概率为1100”，购买100张彩票就一定会中奖一次 C.某地会发生地震是必然事件D.若甲组数据的方差20.1S =甲，乙组数据的方差20.2S =乙，则甲组数据比乙组稳定6.关于x 的分式方程11mx =-+的解是负数，则m 的取值范围是（ ） A.1m -＞ B.1m -＞且0m ≠ C.1m ≥- D.1m ≥-且0m ≠7.已知点A ，点B 都在直线l 的上方，试用尺规作图在直线l 上求作一点P ，使得PA PB +的值最小，则下列作法正确的是（ ）A. B. C. D.8.《九章算术》是中国传统数学的重要著作，方程术是它的最高成就．其中记载：今有共买物，人出八，FECD BA盈三；人出七，不足四，问人数、物价各几何？译文：今有人合伙购物，每人出8钱，会多3钱；每人出7钱，又会差4钱，问人数、物价各是多少？设合伙人数为x 人，物价为y 钱，以下列出的方程组正确的是（ ） A.8374y x y x -=⎧⎨-=⎩ B.8374y x x y -=⎧⎨-=⎩ C.8374x y y x -=⎧⎨-=⎩ D.8374x y x y -=⎧⎨-=⎩9.“龟兔赛跑”是同学们熟悉的寓言故事。
湖北省孝感市汉川市2024年中考模拟数学试题(含答案)
2024年九年级5月学业水平调研考试数学试卷（本试题卷共6页，满分120分，考试时间120分钟）☆祝考试顺刊☆注意事项：1.答卷前，考生务必将自己的姓名、准考证号填写在试卷和答题卡上，并将准考证号条形码粘贴在答题卡上指定位置。
2.选择题的作答：每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑。
写在试卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答：用黑色签字笔直接答在答题卡上对应的答题区域内，写在试卷、草稿纸和答题卡上的非答题区域均无效，作图一律用2B 铅笔或黑色签字笔。
一、选择题（本大题共10小题，每小题3分，共30分。
在每小题给出的四个选项中只有一项是符合题目要求的，不涂、错涂或涂的代号超过一个，一律得0分）1.若零下3摄氏度记为3-℃，则零上2摄氏度记为（）A.2-℃B.0℃ C.2℃ D.5℃2.如图，是一个正方体的平面展开图，把它折叠成正方体后，与“红”字面相对面上的字是（）A.基B.因C.传D.承3.2024年第一季度，中国经济交出了一份亮丽的成绩单，对外贸易增势良好，我国货物进出口总额为31133亿元，比上年同期增长21.4％.将数据“31133亿”用科学记数法表示正确的是（）A.113.113310⨯ B.1131.13310⨯ C.120.3113310⨯ D.123.113310⨯4.下列计算正确的是（）A.248a a a⋅= B.3332a a a -=C.()3236ab a b = D.()222a b a b +=+5.如图，在ABC △中，按以下步骤作图：①分别以点B 和C 为圆心，以大于12BC 的长为半径作弧，两弧相交于点M 和N ；②作直线MN 交边AB 于点E ，连接CE .若8BE =，则EC 的长为（）A.16B.12C.10D.86.如图是一款手推车的平面示意图，其中//AB CD ，130∠=︒，270∠=︒，则3∠的度数为（）A.50°B.40°C.30°D.20°7.下列事件，是必然事件的是（）A.通常加热到100℃，水沸腾B.经过有信号灯的路口，遇到红灯C.掷一次骰子，向上一面点数是6D.射击运动员射击一次，命中靶心8.如图，O 的直径AC 长为10，弦AD 长为6，ADC ∠的平分线交O 于点B ，连接AB ，BC ，则四边形ABCD 的周长为（）A.162+B.142+C.142+ D.249.观察下面两行数：1，5，11，19，29，…；1，3，6，10，15，….取每行数的第8个数，计算这两个数的和是（）A.147 B.126 C.107D.9210.如图，抛物线2y ax bx c =++（a ，b ，c 是常数，0a ≠）与x 轴交于A 、B 两点，顶点(),C m n .给出下列结论：①0abc >；②930a b c -+<；③若点11,2y ⎛⎫- ⎪⎝⎭，21,2y ⎛⎫ ⎪⎝⎭，33,2y ⎛⎫ ⎪⎝⎭在抛物线上，则213y y y <<；④当3n a=-时，以A ，B ，C 为顶点的三角形是等边三角形.其中正确结论的个数有（）A.4个B.3个C.2个D.1个二、填空题（本大题共5小题，每小题3分，共15分。
湖北省孝感市孝南区2022-2023学年九年级下学期5月月考数学试题(含答案)
孝南区2023年九年级5月质量监测数学试卷一、精心选一选（本大题共8小题，每小题3分，共24分，每小题只有一个选项是正确的）1．的相反数是（）A ．－2B ．2C ．D ．2．2021年12月9日，“天宫课堂”正式开课，我国航天员在中国空间站首次进行太空授课，本次授课结束时，网络在线观看人数累计超过14600000人次，把“14600000”用科学记数法表示为（ ）A ．B ．C ．D ．3．如图是由5个相同的正方体搭成的几何体，这个几何体的俯视图是（）A ．B ．C ．D ．4．下列运算中，正确的是（ ）A ．B ．C ．D ．5．某班准备从甲、乙、丙、丁四名同学中选一名最优秀的参加禁毒知识比赛，下表记录了四人3次选拔测试的相关数据：甲乙丙丁平均分95939594方差3.2 3.24.85.2根据表中数据，应该选择（ ）A ．甲B ．乙C ．丙D ．丁6．如图，将直角三角板放置在矩形纸片上，若，则的度数为（）2-12-1280.14610⨯71.4610⨯614.610⨯514610⨯2510a a a⋅=()222a b a b -=-22232a b a b a b -+=-()23636aa -=148∠=︒2∠A ．60°B ．52°C ．48°D ．42°7．如图，四边形ABCD 是的内接四边形，，，，，则AD 的长为（ ）A ．2B ．C ．D ．8．已知二次函数（，，为常数，）的部分图象如图所示，对称轴为直线，且与x 轴的一个交点在点和之间．下列四个结论：①；②若点、在此抛物线上，则；③；④对于任意实数m ，总有．其中正确的结论的个数是（）A ．1个B ．2个C ．3个D ．4个二、细心填一填（本大题共8小题，每小题3分，共24分）9．函数的自变量x 的取值范围是______．10．平面直角坐标系中，点关于y 轴的对称点的坐标是______．11．如图，航拍无人机从A 处测得一幢建筑物顶部B 的仰角为45°，测得底部C 的俯角为60°，此时航拍无人机与该建筑物的水平距离AD 为120m ，那么该建筑物的高度BC约为O e 90B ∠=︒120BCD ∠=︒2AB =1CD=432-2y ax bx c =++a b c 0a ≠1x =()1,0-()0,00abc <()13,C y-)2Dy 12y y >20a b c ++<()a b m am b +≥+y =()2,1P P '______m）．12．若一个直角三角形两条直角边的长分别是一元二次方程的两个实数根，则这个直角三角形斜边的长是______．13．如图，在中，尺规作图：以点A 为圆心，AB 的长为半径画弧交AD 于点F ，分别以点B ，F 为圆心，以大于的长为半径画弧交于点P ，作射线AP 交BC 与点E ，若，，则AE 的长为______．14．我国某型号运载火箭的整流罩的三视图如图所示，根据图中数据（单位：米）计算该整流罩的侧面积（单位：平方米）是______．15．《庄子·天下篇》记载“一尺之棰，日取其半，万世不竭”．如图，直线：与y 轴交于点A ，过点A 作x 轴的平行线交直线：于点，过点作y 轴的平行线交直线于点，以此类推，通过求，，，，…，由此得到______．1.732≈2640x x -+=ABCD Y 12BF 12BF =10AB =1l 112y x =+2l y x =1O 1O 1l 1A OA 11O A 22O A 33O A 20232023O A =16．如图，已知正方形ABCD 的边长为a ，点E 是AB 边上一动点，连接ED ，将ED 绕点E 顺时针旋转90°到EF ，连接DF ，CF ，则当之和取最小值时，的周长为______．（用含a 的代数式表示）三、用心做一做（本大题共8小题，共72分）17．（6分）先化简，再求值：，其中，．18．（8分）“绿水青山就是金山银山”，某村为了绿化荒山，计划在植树节当天种植柏树和杉树．经调查，购买1棵柏树比1棵杉树多50元，且花费900元购买杉树与花费1200元购买柏树的数量相同．（1）求柏树和杉树的单价各是多少元；（2）本次绿化荒山，需购买柏树和杉树共80棵，且柏树的棵数不少于杉树的2倍．为完成这次绿化任务，村里筹措了资金15000元，问该村完成这次绿化任务有几种方案？19．（8分）某校在开展“网络安全知识教育周”期间，在八年级中随机抽取了20名学生分成甲、乙两组，每组各10人，进行“网络安全”现场知识竞赛，把甲、乙两组的成绩进行整理分析（满分100分，竞赛得分用x 表示：为网络安全意识非常强，为网络安全意识强，为网路安全意识一般）．收集整理的数据制成如下两幅统计图：平均数中位数众数甲组a 8080乙组83bcDF CF +DCF △()()()()22322235xy x y x y y x y +-+--+x =1y =90100x ≤≤8090x ≤<80x <根据以上信息回答下列问题：（1）填空：______，______，______；（2）已知该校八年级有1000人，估计八年级网络安全意识非常强的人数一共是多少人？（3）现在准备从甲乙两组满分人数中抽取两名学生参加校际比赛，求抽取的两名同学恰好一人来自甲组，另一人来自乙组的概率．20．（9分）如图，以矩形ABCD 的边CD 为直径作，点E 是AB 的中点，连接CE 交于点F ，连接AF 并延长交BC 于点H ．（1）若连接AO ，试判断四边形AECO 的形状，并说明理由；（2）求证：AH 是的切线；（3）若，，求AH 的长．21．（9分）如图，直线与反比例函数的图象交于点，与x 轴交于点B ，平行于x 轴的直线交反比例函数的图象于点M ，交AB 于点N ，连接BM ．（1）求m 的值和反比例函数的解析式；（2）观察图象，直接写出当时不等式的解集；（3）直线沿y 轴方向平移，当n 为何值时，的面积最大？最大值是多少？a =b =c =O e O e O e 6AB =2CH =26y x =+()0ky k x=>(),8A m ()06y n n =<<0x >260kx x+->y n =BMN △22．（10分）某企业接到一批帽子生产任务，按要求在20天内完成，约定这批帽子的出厂价为每顶8元．为按时完成任务，该企业招收了新工人，设新工人小华第x 天生产的帽子数量为y 顶，y 与x 满足如下关系式：（1）小华第几天生产的帽子数量为220顶？（2）如图，设第x 天每顶帽子的成本是P 元，P 与x 之间的关系可用图中的函数图象来刻画．若小华第x 天创造的利润为w 元，求w 与x 之间的函数表达式，并求出第几天的利润最大？最大值是多少元？（3）设（2）小题中第m 天利润达到最大值，若要使第天的利润比第m 天的利润至少多49元，则第天每顶帽子至少应提价几元？23．（10分）【模型建立】（1）如图1，在等边中，点D 、E 分别在BC 、AC 边上，，求证：；【模型应用】（2）如图2，在中，，，于点D ，点E 在AC 边上，，点F 在DC 边上，，则的值为______；【模型拓展】（3）如图3，在钝角中，，点D 、E 分别在BC 、AC 边上，，若，，求DC 的长．()()200510100520x x y x x ≤≤⎧⎪=⎨+<≤⎪⎩()1m +()1m +ABC △60ADE ∠=︒AB CE BD DC ⋅=⋅Rt ABC △90BAC ∠=︒60B ∠=︒AD BC ⊥AE AD =60EFD ∠=︒CFDFABC △60ABC ∠=︒60DAE ADE ∠=∠=︒5AB =6CE =24．（12分）如图，抛物线与x 轴交于点A 、B ，与y 轴交于点C ，已知．（1）请直接写出：______；抛物线的解析式______；直线BC 的解析式______；______；（2）如图1，点P 是抛物线上位于直线BC 上方的一点，过点P 作BC 的垂线垂足为点G ，求线段PG 的最大值；（3）如图2，Q 为抛物线上一点，若，请求出点Q的坐标．()()22369y mx m x m =++-+()3,0B m =tan OCA ∠=45ACQ ∠=︒参考答案及评分标准一、选择题（3分×8=24分）题号12345678答案ABDCADBC二、选择题（3分×8=24分）9．10．11．32812．13．1614．12π15．16．三、解答题：17．解：原式当时，原式18．解：（1）设杉树的单价是x 元，则柏树的单价是元，依题意得：，解得：，经检验，是原方程的解，且符合题意，∴．答：柏树的单价是200元，杉树的单价是150元．（2）设购买柏树m 棵，则购买杉树棵，依题意得：，解得：．又∵m 为正整数，∴m 取54，55，56，57，58，59，60，∴该村完成这次绿化任务有7种方案．19．（1）838570（2）依题意得：（人），因此估计八年级网络安全意识非常强的人数一共是400人．（3）记甲组满分同学为A ，乙组满分同学为B 、C 画树状图为：所有等可能的情况为6种，符合条件的有4种．1x >()2,1-202312⎛⎫ ⎪⎝⎭)1a+22222412946106x xy y x y xy y xy =++-+--=x =1y =)6112==-()50x +900120050x x =+150x =150x =5015050200x +=+=()80m -()()2802001508915000m m m m ≥-⎧⎪⎨+-≤⎪⎩160603m ≤≤a =b =c =35100040020+⨯=故抽取两名同学恰好一人来自甲组，另一人来自乙组的概率为：20．（1）结论：四边形AECO 是平行四边形理由：∵四边形ABCD 是矩形 ∴， 又 ∴，∴四边形AECO 是平行四边形（2）由（1）得 ∴， 又 ∴则 又 ∴∴ 即 又OF 是的半径∴是的切线（3）由切线长定理可设，且 则 在中，由得得∴21．解：（1）∵直线经过点，∴，得 ∴，∵反比例函数经过点，∴，∴反比例函数的解析式为；（2）不等式的解集为；（3）由题意，点M 、N 的坐标为，，∵，∴4263P ==AB CD =AB CD ∥12AE AB =12CO CD =AE OC =AE OC ∥AO CE ∥14∠=∠23∠=∠OC OF =34∠=∠12∠=∠OD OF =OA OA =()SAS AOD AOF ≌△△90AFO ADO ∠=∠=︒OF AH ⊥O e AH O e AD AF x ==2HF CH ==2BH x =-2AH x =+Rt ABH △222AH BH AB =+()()222226x x +=-+92x =9132222AH x =+=+=26y x =+(),8A m 268m +=1m =()1,8A ()1,8A 8k =8y x=260kx x+->1x >8,M n n ⎛⎫⎪⎝⎭6,2n N n -⎛⎫ ⎪⎝⎭06n <<8602n n -->∴，∴时，的面积最大，最大值为22．（1）若 得 与不符，舍去当时，得 因此小华第12天生产帽子220顶（2）当时， 当时，①时， 当时，（元）②时， 当时，（元）③时， 当时，（元）综上所述：当时，W 有最大值，最大值为576元．（3）由（2）知：，则，设第15天提价元．当，则有 得故：第15天每顶帽子至少应提价0.2元23．（1）证明：∵是等边三角形，∴，∴．∵，∴，∴，()21186125322244BMN M n S MN y n n n -⎛⎫=⋅=⨯-=--+ ⎪⎝⎭△3n =BMN △25420220x =11x =05x ≤≤10100220x +=12x =010x ≤≤ 5.2P =1020x -≤0.1 4.2P x =+05x ≤≤()()88 5.22056W P y x x =-=-⨯=5x =280W =最大值510x <≤()()101008 5.228280W x x =+-=+10x =560W =最大值1020x <≤()()()21010080.1 4.214576W x x x =+-+=--+⎡⎤⎣⎦14x =576W =最大值14x =14m =115m +=a 15x =()()()()()81010080.1 4.2101002502.3W a p x a x x a =+-+=+-++=+⎡⎤⎣⎦()2502.357649a +-≥0.2a ≥ABC △60B C ∠=∠=︒180120ADB BAD B ∠+∠=︒-∠=︒60ADE ∠=︒180120ADB EDC ADE ∠+∠=︒-∠=︒BAD EDC ∠=∠∴，∴ ∴；（2）（3）解：在DC 上截取，连接EF ，如图，∵，∴为等边三角形，∴．∵，，由（1）知，∴，∴，∴．∵，∴，∴，∵，∴，∴，∴，∴，∵，∴．∴．24．解：（1） 3（2）如图1，过点P 作轴交BC 于点H ，设，则，∴，BAD CDE ∽△△AB BD CD EC=AB CE BD DC ⋅=⋅12CF DF =DF BA =60DAE ADE ∠=∠=︒ADE △AD DE =60ABC ∠=︒60ADE ∠=︒BAD EDF ∠=∠()BAD FDE SAS ≌△△60B EFD ∠=∠=︒120EFC ∠=︒60AED ∠=︒120DEC ∠=︒EFC DEC ∠=∠C C ∠=∠EFC DEC ∽△△EC CF DC EC =656CF CF =+25360CF CF +-=0CF >4CF =549DC DF CF =+=+=m =1-y =243x x -+-y =x -13PH y ∥()2,43P t t t -+-(),3H t t -()224333PH t t t t t =-+---=-+∵，∴，∵轴，∴ ∵∴，∴当时，PG（2）如图2，过点B 作交CQ 的延长线于点E ，过点E 作轴于点F ，则，∵，∴，∴，∵，∴，∴∴，又可知，∴， ∴ 由，得， ∴，∴，∴ ∴，又∴直线CE 的解析式为，联立方程组，解得：，，∴点Q 的坐标为．3OB OC ==45BCO CBO ∠=∠=︒PH y ∥45PHG ∠=︒90PGH ∠=︒()223sin 3sin 452PG PH PHG t t t ⎫=⋅∠=-+⨯︒=-⎪⎭32t =BE CB ⊥EF x ⊥90BFE CBE ∠=∠=︒45CBO ∠=︒45EBF ∠=︒BF EF BE ==45BCO ACQ ∠=∠=︒BCE OCA ∠=∠tan tan BCE OCA ∠=∠BE OA CB OC=()1,0A 1OA =()0,3C -3OC =3OB OC ==BC =13=BE =1BF EF ===314OF OB BF =+=+=()4,1E -()0,3C -132y x =-213243y x y x x ⎧=-⎪⎨⎪=-+-⎩1103x y =⎧⎨=-⎩227254x y ⎧=⎪⎪⎨⎪=-⎪⎩75,24⎛⎫- ⎪⎝⎭。
湖北省孝感市九年级5月学业水平模拟考试数学试卷
湖北省孝感市九年级5月学业水平模拟考试数学试卷姓名:________ 班级:________ 成绩:________一、单选题 (共14题；共24分)1. （2分）(2017·高邮模拟) 1不是﹣1的（）A . 相反数B . 绝对值C . 倒数D . 平方数2. （2分） (2017八下·山西期末) 若是完全平方式，则m的值是（）A . －1B . 7C . 7或－1D . 5或13. （2分）一根弹簧的原长为12 cm，它能挂的重量不能超过15 kg并且每挂重1kg就伸长1cm，写出挂重后的弹簧长度y（cm）与挂重x（kg）之间的函数关系式是（）A . y = x + 12（0＜x≤15）B . y = x + 12 （0≤x＜15）C . y = x + 12（0≤x≤15）D . y = x + 12 （0＜x＜15）4. （2分） (2018九上·鼎城期中) 如图，在Rt△ABC中，∠C＝90°，∠ABC＝60°，BD平分∠ABC，则的值为（）A .B . 3﹣C . 6﹣D .5. （2分）(2018·巴中) 在创建平安校园活动中，九年级一班举行了一次“安全知识竞赛”活动，第一小组6名同学的成绩（单位：分）分别是：87，91，93，87，97，96，下列关于这组数据说正确的是（）A . 中位数是90B . 平均数是90C . 众数是87D . 极差是96. （2分） (2018·东营模拟) 在平面坐标系中，正方形ABCD的位置如图所示，点A的坐标为（1，0），点D 的坐标为（0，2），延长CB交x轴于点A1 ，作正方形A1B1C1C，延长C1B1交x轴于点A2 ，作正方形A2B2C2C1,………按这样的规律进行下去，正方形A2018B2018C2018C2017的面积为（）A .B .C .D .7. （2分）如图，下列水平放置的几何体中，左视图不是长方形的是（）A .B .C .D .8. （2分）已知圆锥的底面半径为1cm，母线长为3cm，则其全面积为（）A . πB . 3πC . 4πD . 7π9. （1分）“银河1”计算机的计算速度为每秒384000000000，这个数字用科学记数法表示为________．10. （1分）把多项式3x3﹣6x2y+3xy2分解因式的结果是________．11. （1分）已知k＞0，且关于x的方程3kx2+12x+k+1=0有两个相等的实数根，那么k的值等于________.12. （2分）当时，双曲线y= 过点（，2 ）．13. （2分）(2017·槐荫模拟) 如图所示，四边形ABCD的四个顶点A、B、C、D的坐标分别为（﹣1，1）、（﹣1，﹣3）、（5，3）、（1，3），则其对称轴的函数表达式为________．14. （1分）在矩形ABCD中，AB=4，BC=3，点P在AB上．若将△D AP沿DP折叠，使点A落在矩形对角线上的A′处，则AP的长为________二、解答题 (共9题；共69分)15. （5分）(2018·广元) 计算：16. （5分）先化简再求值：当x= 时，求• ÷ 的值．17. （5分）(2017·兴庆模拟) 如图，在▱ABCD中，连接BD，在BD的延长线上取一点E，在DB的延长线上取一点F，使BF=DE，连接AF，CE．求证：AF∥CE．18. （2分） (2016七上·单县期末) 某校为了了解学生家长对孩子使用手机的态度情况，随机抽取部分学生家长进行问卷调查，发出问卷140份，每位学生家长1份，每份问卷仅表明一种态度，将回收的问卷进行整理（假设回收的问卷都有效），并绘制了如图两幅不完整的统计图．根据以上信息解答下列问题：（1）回收的问卷数为________份，“严加干涉”部分对应扇形的圆心角度数为________．（2）把条形统计图补充完整（3）若将“稍加询问”和“从来不管”视为“管理不严”，已知全校共1500名学生，请估计该校对孩子使用手机“管理不严”的家长大约有多少人？19. （10分）为弘扬“东亚文化”，某单位开展了“东亚文化之都”演讲比赛，在安排1位女选手和3位男选手的出场顺序时，采用随机抽签方式．（1）请直接写出第一位出场是女选手的概率；（2）请用画树状图或列表的方法表示第一、二位出场选手的所有等可能结果，并求出他们都是男选手的概率．20. （10分） (2017八下·禅城期末) 小明在学习了一次方程（组）、一元一次不等式和一次函数后，把相关知识归纳整理如下：一次函数与方程的关系：①一次函数的解析式就是一个二元一次方程；②点B的横坐标是方程①的解；③点C的坐标（x，y）中的x，y的值是方程组②的解一次函数与不等式的关系：①函数y=kx+b的函数值y小于0时，自变量x的取值范围就是不等式③的解集；②函数y=kx+b的函数值y大于0时，自变量x的取值范围就是不等式④的解集．（1）请根据以上方框中的内容在下面数学序号后写出相应的式子：①________；②________；③________；④________；（2）如果点C的坐标为（2，5），那么不等式kx+b≥k1x+b1的解集是________．21. （10分） (2017九上·上城期中) 如图（1）如图，是形内的高，是的外接圆⊙ 的直径．①求证：．②若，，，⊙ 的直径长．③如图，在边长为的小正方形组成的网格之中有一个格点三角形，请你从上面两小题中获得经验，直接写出此格点三角形的外接圆面积．（2）如图，是形外的高，若，，，（）题中②的结论是否还成立？成立与否都要说明理由．22. （2分）(2018·山西) 请阅读下列材料，并完成相应的任务：在数学中，利用图形在变化过程中的不变性质，常常可以找到解决问题的办法．著名美籍匈牙利数学家波利亚在他所著的《数学的发现》一书中有这样一个例子：请问如何在一个三角形ABC的AC和BC两边上分别取一点X和Y，使得AX=BY=XY．（如图）解决这个问题的操作步骤如下：第一步，在CA上作出一点D，使得CD=CB，连接BD．第二步，在CB上取一点Y'，作Y'Z'∥CA，交BD于点Z'，并在AB上取一点A'，使Z'A'=Y'Z'．第三步，过点A作AZ∥A'Z'，交BD于点Z．第四步，过点Z作ZY∥AC，交BC于点Y，再过点Y作YX∥ZA，交AC于点X．则有AX=BY=XY．下面是该结论的部分证明：证明：∵AZ∥A'Z'，∴∠BA'Z'=∠BAZ，又∵∠A'BZ'=∠ABZ．∴△BA'Z'～△BAZ．∴ ．同理可得．∴ ．∵Z'A'=Y'Z'，∴ZA=YZ．任务：（1）请根据上面的操作步骤及部分证明过程，判断四边形AXYZ的形状，并加以证明；（2）请再仔细阅读上面的操作步骤，在（1）的基础上完成AX=BY=XY的证明过程；（3）上述解决问题的过程中，通过作平行线把四边形BA'Z'Y'放大得到四边形BAZY，从而确定了点Z，Y的位置，这里运用了下面一种图形的变化是．A . 平移B . 旋转C . 轴对称D . 位似23. （20分）如图1所示，已知抛物线y=﹣x2+4x+5的顶点为D，与x轴交于A、B两点，与y轴交于C点，E为对称轴上的一点，连接CE，将线段CE绕点E按逆时针方向旋转90°后，点C的对应点C′恰好落在y轴上．（1）直接写出D点和E点的坐标；（2）点F为直线C′E与已知抛物线的一个交点，点H是抛物线上C与F之间的一个动点，若过点H作直线HG与y 轴平行，且与直线C′E交于点G，设点H的横坐标为m（0＜m＜4），那么当m为何值时，S△HGF：S△BGF=5：6？（3）图2所示的抛物线是由y=﹣x2+4x+5向右平移1个单位后得到的，点T（5，y）在抛物线上，点P是抛物线上O与T之间的任意一点，在线段OT上是否存在一点Q，使△PQT是等腰直角三角形？若存在，求出点Q的坐标；若不存在，请说明理由．参考答案一、单选题 (共14题；共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、13-1、14-1、二、解答题 (共9题；共69分)15-1、16-1、17-1、18-1、18-2、18-3、19-1、19-2、20-1、20-2、21-1、21-2、22-1、22-2、22-3、23-1、。
湖北孝感安陆市中考模拟数学考试卷(5月份)(解析版)(初三)中考模拟.doc
湖北孝感安陆市中考模拟数学考试卷（5月份）（解析版）（初三）中考模拟姓名:_____________ 年级:____________ 学号:______________题型选择题填空题简答题xx题xx题xx题总分得分一、xx题（每空xx 分，共xx分）l【答案】D【解析】试题分析：根据合并同类项，可判断A，根据同底数幂的乘法底数不变指数相加，可判断B，根据幂的乘方底数不变指数相乘，可判断C，根据同底数幂的除法底数不变指数相减，可判断D．A、不是同类项不能合并，故A错误；B、同底数幂的乘法底数不变指数相加，故B错误；C、幂的乘方底数不变指数相乘，故C错误；D、同底数幂的除法底数不变指数相减，故D正确；考点：(1)、同底数幂的除法；(2)、合并同类项；(3)、同底数幂的乘法；(4)、幂的乘方与积的乘方．【题文】下列几何体中，主视图相同的是（）A．①② B．①④ C．①③ D．②④【答案】C【解析】试题分析：分别找出四个几何体从正面看所得到的视图即可．①此几何体的主视图是矩形；②此几何体的主视图是等腰三角形；③此几何体的主视图是矩形；④此几何体的主视图是圆形；主视图相同的是①③考点：简单几何体的三视图．【题文】把不等式组的解集表示在数轴上，正确的是（）A． B．C． D．【答案】C【解析】评卷人得分试题分析：先求出不等式组的解集，再在数轴上表示出来即可．有①得：x＞﹣1；有②得：x≤1；所以不等式组的解集为：﹣1＜x≤1，在数轴上表示为：考点：(1)、在数轴上表示不等式的解集；(2)、解一元一次不等式组．【题文】如图，AB∥CD，CE平分∠BCD，∠DCE=18°，则∠B等于（）A．18° B．36° C．45° D．54°【答案】B【解析】试题分析：根据角平分线的定义求出∠BCD，再根据两直线平行，内错角相等可得∠B=∠BCD．∵CE平分∠BCD，∠DCE=18°，∴∠BCD=2∠DCE=2×18°=36°，∵AB∥CD，∴∠B=∠BCD=36°考点：平行线的性质．【题文】用配方法解方程x2﹣2x﹣5=0时，原方程应变形为（）A．（x+1）2=6 B．（x+2）2=9C．（x﹣1）2=6 D．（x﹣2）2=9【答案】C【解析】试题分析：配方法的一般步骤：(1)、把常数项移到等号的右边； (2)、把二次项的系数化为1；(3)、等式两边同时加上一次项系数一半的平方．由原方程移项，得 x2﹣2x=5，方程的两边同时加上一次项系数﹣2的一半的平方1，得 x2﹣2x+1=6∴（x﹣1）2=6．考点：解一元二次方程-配方法．【题文】某校8名学生参加了体育兴趣小组，他们被分成A、B两组进行训练，身高（单位：cm）如表所示：队员1队员2队员3队员4甲组176177175176乙组178175177174设两队队员身高的平均数依次为，，方差依次为s甲2，s乙2，则下列关系中完全正确的是（）A．甲=乙，S甲2＜S乙2B．甲=乙，S甲2＞S乙2C．甲＞乙，S甲2＜S乙2D．甲＞乙，S甲2＞S乙2【答案】A【解析】试题分析：根据平均数的定义分别计算甲乙的平均数，然后根据方差的计算公式分别计算甲乙的方差即可．考点：(1)、方差；(2)、算术平均数．【题文】估计介于（）A．0.4与0.5之间 B．0.5与0.6之间C．0.6与0.7之间 D．0.7与0.8之间【答案】C【解析】试题分析：先估算的范围，再进一步估算，即可解答．∵2.22=4.84，2.32=5.29，∴2.2＜＜2.3，∴0.6＜＜0.65．所以介于0.6与0.7之间．考点：估算无理数的大小．【题文】如图，四边形ABCD内接于⊙O，E为BC延长线上一点，∠A=50°，则∠DCE的度数为（）A．40° B．50° C．60° D．130°【答案】B【解析】试题分析：连接OB，OD，利用圆周角定理得到∠DOB=2∠A，∠DOB（大于平角的角）=2∠BCD，再由周角定义及等式的性质得到∠A与∠BCD互补，利用邻补角性质及同角的补角相等即可求出所求角的度数．连接OB，OD，∵∠DOB与∠A都对，∠DOB（大于平角的角）与∠BCD都对，∴∠DOB=2∠A，∠DOB（大于平角的角）=2∠BCD，∵∠DOB+∠DOB（大于平角的角）=360°，∴∠A+∠BCD=180°，∵∠DCE+∠BCD=180°，∴∠DCE=∠A=50°，考点：(1)、圆内接四边形的性质；(2)、圆周角定理．【题文】如图，在平面直角坐标系中，△OAB的边OA在x轴的正半轴上，OA=AB，边OB的中点C在双曲线y=上，将△OAB沿OB翻折后，点A的对应点A′，正好落在双曲线y=上，△OAB的面积为6，则k为（）A．1 B．2 C．3 D．4【答案】D【解析】试题分析：连接AA′，过点A′作A′E⊥x轴于点E，过点C作CF⊥x轴于点F，根据OA=AB结合翻折的特性可知∠A′BO=∠AOB，四边形OABA′为菱形，由中位线的性质结合平行线的性质可得出A′E=2CF，AE=2AF，再根据反比例函数系数k的几何意义和三角形面积公式即可得出OF=OA，S△OCF=×S△OAB=2，由此即可得出反比例系数k的值．连接AA′，过点A′作A′E⊥x轴于点E，过点C作CF⊥x轴于点F ，如图所示．∵OA=AB，∴∠AOB=∠ABO，由翻折的性质可知：∠A′BO=∠ABO，A′B=AB，A′O=AO，∴∠A′BO=∠AOB，四边形OABA′为菱形∴A′B∥OA．∵点C是线段OB的中点，A′E⊥x轴，CF⊥x轴，∴A′E=2CF，AE=2AF，又∵S△OA′E=S△OCF，∴OF=2OE，∴OE=EF=FA，∴OF=OA ．∵S△OAB=OA•A′E=6，S△OCF=OF•CF，∴S△OCF=×S△OAB=2．∵S△OCF=|k|=2，∴k=±4，∵反比例函数在第一象限有图象，∴k=4．考点：(1)、反比例函数系数k的几何意义；(2)、翻折变换（折叠问题）．【题文】化简：的结果是．【答案】【解析】试题分析：先进行二次根式的化简，然后合并同类二次根式即可．考点：二次根式的加减法．【题文】谷歌人工智能AlphaGo机器人与韩国棋手李世石的围棋挑战赛引起人们的广泛关注，人工智能完胜李世石，百度上搜索关键词“AlphaGo”，显示的搜索结果约为14100000条，将14100000用科学记数法表示应为．【答案】1.41×107【解析】试题分析：科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值是易错点，由于14100000有8位，所以可以确定n=8﹣1=7． 14100000=1.41×107考点：科学记数法—表示较大的数．【题文】如图，已知∠AOB=60°，点P在OA上，OP=8，点M、N在边OB上，PM=PN，若MN=2，则OM=．【答案】3【解析】试题分析：过P作PC垂直于MN，由等腰三角形三线合一性质得到MC=CN，求出MC的长，在直角三角形OPC 中，利用30度角所对的直角边等于斜边的一半求出OC的长，由OC﹣MC求出OM的长即可．过P作PC⊥MN，∵PM=PN，∴C为MN中点，即MC=NC=MN=1，在Rt△OPC中，∠AOB=60°，∴∠OPC=30°，∴OC=OP=4，则OM=OC﹣MC=4﹣1=3，考点：(1)、含30度角的直角三角形；(2)、等腰三角形的性质．【题文】已知，A，B为常数，则A+B的值为．【答案】1【解析】试题分析：先去分母整理得到（A﹣B）n+2A﹣1=0，再利用n任意使分式有意义的实数，所以A﹣B=0，2A ﹣1=0，然后求出A和B，再计算它们的和即可．取分母得1=A（n+2）﹣B•n，整理得（A﹣B）n+2A﹣1=0，根据题意得A﹣B=0，2A﹣1=0，解得A=B=，所以A+B=1．考点：分式的加减法．【题文】如图，正方形ABCD中，AB=4，E是BC的中点，点P是对角线AC上一动点，则PE+PB的最小值为．【答案】2【解析】试题分析：由于点B与点D关于AC对称，所以如果连接DE，交AC于点P，那PE+PB的值最小．在Rt△CDE 中，由勾股定理先计算出DE的长度，即为PE+PB的最小值．连接DE，交AC于点P，连接BD．∵点B与点D关于AC对称，∴DE的长即为PE+PB的最小值，∵AB=4，E是BC的中点，∴CE=2，在Rt△CDE中， DE=2．考点：(1)、轴对称-最短路线问题；(3)、正方形的性质．【题文】若m1，m2，…m2016是从0，1，2这三个数中取值的一列数，若m1+m2+…+m2016=1546，（m1﹣1）2+（m2﹣1）2+…+（m2016﹣1）2=1510，则在m1，m2，…m2016中，取值为2的个数为____．【答案】520【解析】试题分析：解决此题可以先设0有a个，1有b个，2有c个，根据据题意列出方程组求解即可．设0有a个，1有b个，2有c个，由题意得，解得，故取值为2的个数为502个考点：(1)、规律型：(2)、数字的变化类．【题文】先化简，再求值：（x﹣2）2﹣（2x+1）（2x+1）+4x（x+1），其中x=．【答案】7【解析】试题分析：首先利用完全平方公式以及单项式与多项式的乘法法则计算，然后去括号合并同类项即可化简，然后代入数值计算即可．试题解析：原式=（x2﹣4x+4）﹣（4x2﹣1）+（4x2+4x）=x2+5，当x=时，原式=（）2+5=7．考点：整式的混合运算—化简求值．【题文】已知，如图，直线AB与直线BC相交于点B，点D是直线BC上一点，直线DE∥AB，且点E到B，D 两点的距离相等．（1）用尺规作图作出点E；（不写作法，保留作图痕迹）（2）连接BE，求证：BD平分∠ABE．【答案】(1)答案见解析；(2)证明过程见解析【解析】试题分析：(1)、直接利用作一角等于已知角的作法结合线段垂直平分线的作法得出符合题意的图形；(2)、直接利用平行线的性质以及结合线段垂直平分线的性质得出答案．试题解析：(1)、如图所示：点E即为所求；(2)、∵DE∥AB，∴∠ABD=∠BDE，又∵EB=ED，∴∠EBD=∠EDB，∴∠ABD=∠EBD，即BD平分∠ABE．考点：(1)、作图—复杂作图；(2)、平行线的性质；(3)、线段垂直平分线的性质．【题文】已知关于x的方程x2﹣（k+1）x+k2+1=0有两个实数根．（1）求k的取值范围；（2）若抛物线y=x2﹣（k+1）x+k2+1与x轴交于A、B两点，点A、点B到原点O的距离分别为OA、OB ，且满足OA+OB﹣4OA•OB+5=0，求k的值．【答案】(1)、k≥；(2)、k=2.【解析】试题分析：(1)、由于关于x的一元二次方程x2﹣（2k+1）x+k2+2k=0有两个实数根，可知△≥0，据此进行计算即可； (2)、由根与系数的关系和已知条件得出关于k的方程，解方程即可．试题解析：(1)、∵原方程有两个实数根，∴△=（k+1）2﹣4（k2+1）≥0∴k2+2k+1﹣k2﹣4≥0，解得：k≥(2)、设A、B两点的坐标为A（x1，0）、B（x2，0）则x1、x2是方程x2﹣（k+1）x+k2+1=0的两根∵k≥，∴x1+x2=k+1＞0，x1•x2=k2+1＞0，∴x1＞0，x2＞0，∴OA+OB=|x1|+|x2|=x1+x2=k+1 OA•OB=|x1||x2|=4x1x2﹣5∴k+1=4（k2+1）﹣5，∴k2﹣k+2=0，∴k1=﹣1，k2=2，又∵k≥，∴k=2考点：抛物线与x轴的交点．【题文】如图，小明在大楼45米高（即PH=45米）的窗口P处进行观测，测得山坡上A处的俯角为15°，山脚B处的俯角为60°，已知该山坡的坡度i（即tan∠ABC）为1：，点P、H、B、C、A在同一个平面上，点H、B、C在同一条直线上，且PH⊥HC．（1）山坡坡脚（即∠ABC）的度数等于度；（2）求A、B两点间的距离．（结果精确到1米，参考数据：≈1.732）【答案】(1)、30°；(2)、52米【解析】试题分析：(1)、根据俯角以及坡度的定义即可求解；(2)、在直角△PHB中，根据三角函数即可求得PB的长，然后利用直角△PBA为等腰直角三角形，即可求解．试题解析：(1)、∵tan∠ABC=1：，∴∠ABC=30°；(2)、由题意得：∠PBH=60°，∵∠ABC=30°，∴∠ABP=90°，又∠APB=45°，∴△PAB为等腰直角三角形，在直角△PHB中，PB=30，在直角△PBA中，AB=PB=30≈52米．考点：(1)、解直角三角形的应用-仰角俯角问题；(2)、解直角三角形的应用-坡度坡角问题．【题文】小亮同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况，他从中随机调查了若干户居民的月均用水量（单位：t），并绘制了样本的频数分布表和频数分布直方图（如图）月均用水量（单位：t）频数百分比2≤x＜324%3≤x＜41224%4≤x＜5ab5≤x＜61020%6≤x＜7c12%7≤x＜836%8≤x＜924%（1）频数分布表中a=，b=．（填百分比），c=；补全频数分布直方图．（2）如果家庭月均用水量“大于或等于4t且小于7t”为中等用水量家庭，请你通过样本估计总体中的中等用水量家庭大约有户；（3）从月均用水量在2≤x＜3，8≤x＜9这两个范围内的样本家庭中任意抽取2个，请用列表法或画树状图求抽取出的2个家庭来自不同范围的概率．【答案】(1)、15.30%，6；(2)、279；(3)、．【解析】试题分析：(1)、根据第一组的频数是2，百分比是4%即可求得总人数，然后根据百分比的意义即可求出a ，b，c的值，进而可补全频数分布直方图；(2)、利用总户数540乘以对应的百分比即可求出总体中的中等用水量家庭的个数；(3)、在2≤x＜3范围的两户用a、b表示，8≤x＜9这两个范围内的两户用1，2表示，利用树状图法表示出所有可能的结果，然后利用概率公式求解试题解析：(1)、调查的总数是：2÷4%=50（户），则6≤x＜7部分调查的户数是：50×12%=6（户），即c=6则4≤x＜5的户数是：50﹣2﹣12﹣10﹣6﹣3﹣2=15（户），所占的百分比是：(15÷50)×100%=30%，即a=15，b=30%，补全频数分布直方图如图所示：(2)、中等用水量家庭大约有450×（30%+20%+12%）=279（户），(3)、在2≤x＜3范围的两户用a、b表示，8≤x＜9这两个范围内的两户用1，2表示．则抽取出的2个家庭来自不同范围的概率=．考点：(1)、列表法与树状图法；(2)、用样本估计总体；(3)、频数（率）分布表；(4)、频数（率）分布直方图．【题文】甲、乙两城市之间开通了动车组高速列车．已知每隔2h有一列速度相同的动车组列车从甲城开往乙城．如图，OA是第一列动车组列车离开甲城的路程s（km）与运行时间t（h）的函数图象，BC是一列从乙城开往甲城的普通快车距甲城的路程s（km）与运行时间t（h）的函数图象．请根据图中的信息，解答下列问题：（1）从图象看，普通快车发车时间比第一列动车组列车发车时间 1h（填”早”或”晚”），点B的纵坐标600的实际意义是；（2）请直接在图中画出第二列动车组列车离开甲城的路程s（km）与时间t（h）的函数图象；（3）若普通快车的速度为100km/h，①求第二列动车组列车出发多长时间后与普通快车相遇？②请直接写出这列普通快车在行驶途中与迎面而来的相邻两列动车组列车相遇的时间间隔．【答案】(1)、1h；甲、乙两城市之间的距离为600千米；(2)、答案见解析；(3)、①、2h；②、1.2h. 【解析】试题分析：(1)、根据图象中点B的实际意义即可得知；(2)、根据速度相同可知两直线平行，由间隔时间为2小时可知直线过（2，0），画出图象MN即可；(3)、①求出直线BC与直线MN的解析式，由解析式列出方程，解方程即可得相遇时间，继而可得答案；②求出直线BC与直线OA交点，即普通快车与第一辆动车相遇时间，由①可知相遇时间间隔．试题解析：(1)、由图可知，普通快车发车时间比第一列动车组列车发车时间晚1h；点B的纵坐标600的实际意义是：甲、乙两城市之间的距离为600千米；(2)、如图所示：(3)、①设直线MN的解析式为：S=k1t+b1，∵M（2，0），N（6，600），∴，解得：，∴S=150t﹣300；∵直线BC的解析式为：S=﹣100t+700，∴可得：150t﹣300=﹣100t+700，解得：t=4， 4﹣2=2．②根据题意，第一列动车组列车解析式为：y=150t，∴这列普通快车在行驶途中与迎面而来的相邻两列动车组列车相遇的时间间隔为：150t=﹣100t+700，解得：t=2.8， 4﹣2.8=1.2（小时）．考点：一次函数的应用．【题文】如图，A是以BC为直径的⊙O上的一点，AD⊥BC于点D，过点B作⊙O的切线，与CA的延长线相交于点E，点F是EB的中点，连结CF交AD于点G（1）求证：AF是⊙O的切线；（2）求证：AG=GD；（3）若FB=FG，且⊙O的半径长为3，求BD．【答案】(1)、证明过程见解析；(2)、证明过程见解析；(3)、2【解析】试题分析：(1)、要证AF是⊙O的切线，就是要证明∠FAO=90°，连接AB，根据BE是⊙O的切线和直角三角形的等量代换，就可得出结论；(2)、根据切线判定知道EB⊥BC，而AD⊥BC，从而可以确定AD∥BE，那么△BFC∽△DGC，又点F是EB的中点，就可得出结论；(3)、点F作FH⊥AD于点H，根据前两问的结论，利用三角形的相似性和勾股定理，可以求出BD的长度．试题解析：(1)、连结AB，∵BC是⊙O的直径，∴∠BAC=90°．∵F是斜边BE的中点，∴AF=FB=EF，∴∠FBA=∠FAB，又∵OA=OB，∴∠ABO=∠BAO∵BE是⊙O的切线，∴∠EBO=90°∵∠EBO=∠FBA+∠ABO=∠FAB+∠BAO=∠FAO=90°∴AF是⊙O的切线；(2)、∵BC是⊙O的直径，BE是⊙O的切线，∴EB⊥BC．又∵AD⊥BC，∴AD∥BE，∴△BFC∽△DGC，△FEC∽△GAC，∴=，=，∴=，∵F是斜边BE的中点，∴BF=EF，∴DG=AG；(3)、解：过点F作FH⊥AD于点H，∵BD⊥AD，FH⊥AD，∴FH∥BC．由(2)，知∠FBA=∠BAF，∴BF=AF．由已知，有BF=FG，∴AF=FG，即△AFG 是等腰三角形．∵FH⊥AD，∴AH=GH，∵DG=AG，∴DG=2HG，即=，∵FH∥BD，BF∥AD，∠FBD=90°，∴四边形BDHF是矩形，BD=FH，∵FH∥BC，易证△HFG∽△DCG，∴==，即===．∵⊙O的半径长为3，∴BC=6．∴==，解得BD=2．∴BD=FH=2．考点：切线的判定与性质．【题文】如图，抛物线y=ax2+bx+c（a≠0）与x轴、y轴分别交于点A（﹣1，0），B（3，0）、C（0，﹣3）三点．（1）直接写出抛物线的解析式；（2）点D（2，m）在第一象限的抛物线上，连接BC、BD，试问，在对称轴左侧的抛物线上是否存在一点P，满足∠PBC=∠DBC？如果存在，请求出点P点的坐标；如果不存在，请说明理由．（3）如图2，在（2）的条件下，将△BOC沿x轴正方向以每秒1个单位长度的速度向右平移，记平移后的三角形为△B′O′C′，在平移过程中，△B′O′C′与△BCD重叠的面积记为S，设平移的时间为t秒（0≤t≤3），试求S与t之间的函数关系式？【答案】(1)、y=x2﹣2x﹣3;(2)、P（﹣，﹣）；(3)、S=．【解析】试题分析：(1)、根据题意设抛物线交点式，待定系数法求解可得；(2)、求出点D坐标可得CD∥x轴，由B 、C坐标可得∠OCB=∠CBO=∠DCB=45°，继而证△CDB≌△CQB可得CQ=CD=2，即点Q的坐标，从而求得直线BP的解析式，设抛物线上的点P（n，n2﹣2n﹣3），代入直线BP解析式可求得n的值，可得答案；(3)、①点C′在CD上运动时，即0≤t≤2时，根据：S=S△BCD﹣S△CC″E﹣S△C″DF，求解即可；②点C ′在CD延长线上运动时，即2＜t≤3时，根据：S=S△GEB，求解可得．试题解析：(1)、根据题意设抛物线解析式为y=a（x+1）（x﹣3），将点C（0，﹣3）代入，得：﹣3a=﹣3，解得：a=1，∴y=（x+1）（x﹣3）=x2﹣2x﹣3，(2)、存在，将点D（2，m）代入抛物线解析式得：m=﹣3，∴D（2，﹣3），∵B（3，0），C（0，﹣3）∴OC=OB，∴∠OCB=∠CBO=45°，如图1，设BP交y轴于点Q，∵CD∥x轴，∴∠DCB=∠BCQ=45°∴△CDB≌△CQB（ASA）∴CQ=CD=2，∴点Q（0，﹣1），设直线BP：y=kx﹣1，点B（3，0）代入得：3k﹣1=0，∴k=，∴直线BP：y=x﹣1，设P的坐标为（n，n2﹣2n﹣3），代入y=x﹣1，得：n2﹣2n﹣3=n﹣1解得：n=﹣或n=3（舍去）当n=﹣时，n2﹣2n﹣3=﹣∴P（﹣，﹣）．(3)、∵B（3，0），C（0，﹣3），D（2，﹣3），∴求得直线BC：y=x﹣3，直线BD：y=3x﹣9，①当0≤t≤2时，如图2：∵由已知设C′（t，﹣3），B′（3+t，0）∴求得直线C′B′：y=（x﹣t）﹣3，再联立直线BD ：y=3x﹣9，求得F（，﹣t），∵∠DCB=45°∴C′E=t∴S=S△BCD﹣S△CC″E﹣S△C″DF=×2×3﹣×t×t﹣×（2﹣t）（3﹣t），整理得：S=﹣t2+3t（0≤t≤2）②当2＜t≤3时，如图3：∵由已知设G（t，3t﹣9），E（t，t﹣3）∴S=S△GEB=[（﹣3t+9）﹣（﹣t+3）]×（3﹣t）整理得：S=t2﹣6t+9（2＜t≤3），综上所述：S=．考点：二次函数综合题．。
湖北省孝感市2019-2020学年中考数学五模考试卷含解析
湖北省孝感市2019-2020学年中考数学五模考试卷一、选择题（本大题共12个小题，每小题4分，共48分．在每小题给出的四个选项中，只有一项是符合题目要求的．） 1．已知关于x 的方程2222x x a xx x x x+-+=--恰有一个实根，则满足条件的实数a 的值的个数为（ ） A ．1B ．2C ．3D ．42．如图，已知正五边形 ABCDE 内接于O e ，连结BD ，则ABD ∠的度数是（ ）A ．60︒B ．70︒C ．72︒D ．144︒3．中国古代人民很早就在生产生活中发现了许多有趣的数学问题，其中《孙子算经》中有个问题：今有三人共车，二车空；二人共车，九人步，问人与车各几何？这道题的意思是：今有若干人乘车，每三人乘一车，最终剩余2辆车，若每2人共乘一车，最终剩余9个人无车可乘，问有多少人，多少辆车？如果我们设有x 辆车，则可列方程（ ） A ．3(2)29x x -=+ B ．3(2)29x x +=- C ．9232x x -+= D ．9232x x +-=4．如图，四边形ABCD 是菱形，∠A=60°，AB=2，扇形BEF 的半径为2，圆心角为60°，则图中阴影部分的面积是（ ）A ．233πB ．233π-C ．3π-D ．3π5．计算25()77-+-的正确结果是（ ） A ．37B ．-37C ．1D ．﹣16．甲、乙、丙、丁四名射击运动员进行淘汰赛，在相同条件下，每人射击10次，甲、乙两人的成绩如图所示，丙、丁二人的成绩如表所示．欲淘汰一名运动员，从平均数和方差两个因素分析，应淘汰（ ）丙丁平均数8 8方差 1.2 1.8A．甲B．乙C．丙D．丁7．函数的自变量x的取值范围是（）A．x>1 B．x<1 C．x≤1D．x≥18．一、单选题如图中的小正方形边长都相等，若△MNP≌△MEQ，则点Q可能是图中的（）A．点A B．点B C．点C D．点D9．某小组5名同学在一周内参加家务劳动的时间如表所示，关于“劳动时间”的这组数据，以下说法正确的是（）动时间（小时） 3 3.5 4 4.5人数 1 1 2 1A．中位数是4，平均数是3.75 B．众数是4，平均数是3.75C．中位数是4，平均数是3.8 D．众数是2，平均数是3.810．如图，AB⊥BD，CD⊥BD，垂足分别为B、D，AC和BD相交于点E，EF⊥BD垂足为F．则下列结论错误的是（）A．B．C．D．11．下列所给函数中，y随x的增大而减小的是（）A．y=﹣x﹣1 B．y=2x2（x≥0）C．2yx=D．y=x+112．已知一组数据a，b，c的平均数为5，方差为4，那么数据a﹣2，b﹣2，c﹣2的平均数和方差分别是.（）A．3，2 B．3，4 C．5，2 D．5，4二、填空题：（本大题共6个小题，每小题4分，共24分．）13．如图，点A的坐标为（3，7），点B的坐标为（6，0），将△AOB绕点B按顺时针方向旋转一定的角度后得到△A′O′B，点A的对应点A′在x轴上，则点O′的坐标为_____．14．如图，在△ABC中，AB＝5，AC＝4，BC＝3，按以下步骤作图：①以A为圆心，任意长为半径作弧，分别交AB、AC于点M、N；②分别以点M、N为圆心，以大于12MN的长为半径作弧，两弧相交于点E；③作射线AE；④以同样的方法作射线BF，AE交BF于点O，连接OC，则OC＝________.15．如图，矩形ABCD的对角线BD经过的坐标原点，矩形的边分别平行于坐标轴，点C在反比例函数y=241k kx++的图象上，若点A的坐标为（﹣2，﹣3），则k的值为_____．16．如图，四边形ACDF 是正方形，CEA ∠和ABF ∠都是直角，且点,,E A B 三点共线，4AB =，则阴影部分的面积是__________．17．把16a 3﹣ab 2因式分解_____．18．如图，小阳发现电线杆AB 的影子落在土坡的坡面CD 和地面BC 上，量得8CD =，20BC =米，CD 与地面成30°角，且此时测得1米的影长为2米，则电线杆的高度为=__________米．三、解答题：（本大题共9个小题，共78分，解答应写出文字说明、证明过程或演算步骤．19．（6分）先化简，再求值：22144(1)1a a a a a-+-÷--，其中a 是方程a （a+1）＝0的解． 20．（6分）如图1，在四边形ABCD 中，AD ∥BC ，AB=CD=13，AD=11，BC=21，E 是BC 的中点，P 是AB 上的任意一点，连接PE ，将PE 绕点P 逆时针旋转90°得到PQ ． （1）如图2，过A 点，D 点作BC 的垂线，垂足分别为M ，N ，求sinB 的值； （2）若P 是AB 的中点，求点E 所经过的路径弧EQ 的长（结果保留π）； （3）若点Q 落在AB 或AD 边所在直线上，请直接写出BP 的长．21．（6分）为了解某校学生的课余兴趣爱好情况，某调查小组设计了“阅读”、“打球”、“书法”和“舞蹈”四个选项，用随机抽样的方法调查了该校部分学生的课余兴趣爱好情况（每个学生必须选一项且只能选一项），并根据调查结果绘制了如图统计图：根据统计图所提供的倍息，解答下列问题：（1）本次抽样调查中的学生人数是多少人；（2 ）补全条形统计图；（3）若该校共有2000名学生，请根据统计结果估计该校课余兴趣爱好为“打球”的学生人数；（4）现有爱好舞蹈的两名男生两名女生想参加舞蹈社，但只能选两名学生，请你用列表或画树状图的方法，求出正好选到一男一女的概率．22．（8分）已知：如图，在平面直角坐标系中，O为坐标原点，△OAB的顶点A、B的坐标分别是A（0，5），B（3，1），过点B画BC⊥AB交直线于点C，连结AC，以点A为圆心，AC为半径画弧交x轴负半轴于点D，连结AD、CD．（1）求证：△ABC≌△AOD．（2）设△ACD的面积为，求关于的函数关系式．（3）若四边形ABCD恰有一组对边平行，求的值．23．（8分）某景区在同一线路上顺次有三个景点A，B，C，甲、乙两名游客从景点A出发，甲步行到景点C；乙花20分钟时间排队后乘观光车先到景点B，在B处停留一段时间后，再步行到景点C．甲、乙两人离景点A的路程s（米）关于时间t（分钟）的函数图象如图所示．甲的速度是______米/分钟；当20≤t≤30时，求乙离景点A的路程s与t的函数表达式；乙出发后多长时间与甲在途中相遇？若当甲到达景点C时，乙与景点C的路程为360米，则乙从景点B步行到景点C的速度是多少？24．（10分）已知点E为正方形ABCD的边AD上一点，连接BE，过点C作CN⊥BE，垂足为M，交AB于点N．（1）求证：△ABE≌△BCN；（2）若N为AB的中点，求tan∠ABE．25．（10分）如图，已知抛物线经过原点o和x轴上一点A（4，0），抛物线顶点为E，它的对称轴与x 轴交于点D．直线y=﹣2x﹣1经过抛物线上一点B（﹣2，m）且与y轴交于点C，与抛物线的对称轴交于点F．（1）求m的值及该抛物线对应的解析式；（2）P（x，y）是抛物线上的一点，若S△ADP=S△ADC，求出所有符合条件的点P的坐标；（3）点Q是平面内任意一点，点M从点F出发，沿对称轴向上以每秒1个单位长度的速度匀速运动，设点M的运动时间为t秒，是否能使以Q、A、E、M四点为顶点的四边形是菱形．若能，请直接写出点M的运动时间t的值；若不能，请说明理由．26．（12分）某市政府大力支持大学生创业．李明在政府的扶持下投资销售一种进价为20元的护眼台灯．销售过程中发现，每月销售量Y（件）与销售单价x（元）之间的关系可近似的看作一次函数：y＝﹣10x+1．设李明每月获得利润为W（元），当销售单价定为多少元时，每月获得利润最大？根据物价部门规定，这种护眼台灯不得高于32元，如果李明想要每月获得的利润2000元，那么销售单价应定为多少元？27．（12分）如图，反比例函数y=kx（x＞0）的图象与一次函数y=2x的图象相交于点A，其横坐标为1．（1）求k的值；（1）点B为此反比例函数图象上一点，其纵坐标为2．过点B作CB∥OA，交x轴于点C，求点C的坐标．参考答案一、选择题（本大题共12个小题，每小题4分，共48分．在每小题给出的四个选项中，只有一项是符合题目要求的．）1．C【解析】【分析】先将原方程变形，转化为整式方程后得2x2-3x+（3-a）=1①．由于原方程只有一个实数根，因此，方程①的根有两种情况：（1）方程①有两个相等的实数根，此二等根使x（x-2）≠1；（2）方程①有两个不等的实数根，而其中一根使x（x-2）=1，另外一根使x（x-2）≠1．针对每一种情况，分别求出a的值及对应的原方程的根．【详解】去分母，将原方程两边同乘x（x﹣2），整理得2x2﹣3x+（3﹣a）=1．①方程①的根的情况有两种：（1）方程①有两个相等的实数根，即△=9﹣3×2（3﹣a）=1．解得a=238．当a=238时，解方程2x2﹣3x+（﹣72+3）=1，得x1=x2=34．（2）方程①有两个不等的实数根，而其中一根使原方程分母为零，即方程①有一个根为1或2．（i）当x=1时，代入①式得3﹣a=1，即a=3．当a=3时，解方程2x2﹣3x=1，x（2x﹣3）=1，x1=1或x2=1.4．而x 1=1是增根，即这时方程①的另一个根是x=1.4．它不使分母为零，确是原方程的唯一根． （ii ）当x=2时，代入①式，得2×3﹣2×3+（3﹣a ）=1，即a=5． 当a=5时，解方程2x 2﹣3x ﹣2=1，x 1=2，x 2=﹣12． x 1是增根，故x=﹣12为方程的唯一实根； 因此，若原分式方程只有一个实数根时，所求的a 的值分别是238，3，5共3个． 故选C ． 【点睛】考查了分式方程的解法及增根问题．由于原分式方程去分母后，得到一个含有字母的一元二次方程，所以要分情况进行讨论．理解分式方程产生增根的原因及一元二次方程解的情况从而正确进行分类是解题的关键． 2．C 【解析】 【分析】根据多边形内角和定理、正五边形的性质求出∠ABC 、CD=CB ，根据等腰三角形的性质求出∠CBD ，计算即可． 【详解】∵五边形ABCDE 为正五边形 ∴()1552180108ABC C ∠=∠=-⨯︒=︒ ∵CD CB = ∴181(8326)010CBD ∠=︒-︒=︒ ∴72ABD ABC CBD ∠=∠-∠=︒ 故选：C ． 【点睛】本题考查的是正多边形和圆、多边形的内角和定理，掌握正多边形和圆的关系、多边形内角和等于（n-2）×180°是解题的关键． 3．A 【解析】 【分析】根据每三人乘一车，最终剩余2辆车，每2人共乘一车，最终剩余1个人无车可乘，进而表示出总人数得出等式即可． 【详解】设有x 辆车，则可列方程：3（x-2）=2x+1． 故选：A ． 【点睛】此题主要考查了由实际问题抽象出一元一次方程，正确表示总人数是解题关键． 4．B 【解析】 【分析】根据菱形的性质得出△DAB 是等边三角形，进而利用全等三角形的判定得出△ABG ≌△DBH ，得出四边形GBHD 的面积等于△ABD 的面积，进而求出即可． 【详解】 连接BD ，∵四边形ABCD 是菱形，∠A=60°， ∴∠ADC=120°， ∴∠1=∠2=60°， ∴△DAB 是等边三角形， ∵AB=2，∴△ABD 3，∵扇形BEF 的半径为2，圆心角为60°， ∴∠4+∠5=60°，∠3+∠5=60°， ∴∠3=∠4，设AD 、BE 相交于点G ，设BF 、DC 相交于点H ， 在△ABG 和△DBH 中，2{34A AB BD ∠=∠=∠=∠， ∴△ABG ≌△DBH （ASA ），∴四边形GBHD 的面积等于△ABD 的面积，∴图中阴影部分的面积是：S 扇形EBF -S △ABD =26021233602π⨯-⨯=23π- 故选B ． 5．D 【解析】 【分析】根据有理数加法的运算方法，求出算式2577⎛⎫-+- ⎪⎝⎭的正确结果是多少即可． 【详解】 原式25 1.77⎛⎫=-+=- ⎪⎝⎭故选：D. 【点睛】此题主要考查了有理数的加法的运算方法，要熟练掌握，解答此题的关键是要明确：①同号相加，取相同符号，并把绝对值相加．②绝对值不等的异号加减，取绝对值较大的加 数符号，并用较大的绝对值减去较小的绝对值．互为相反数的两个数相加得1．③一个数同 1相加，仍得这个数． 6．D 【解析】 【分析】求出甲、乙的平均数、方差，再结合方差的意义即可判断． 【详解】x 甲=110（6+10+8+9+8+7+8+9+7+7）=8， 2S 甲=110 [（6-8）2+（10-8）2+（8-8）2+（9-8）2+（8-8）2+（7-8）2+（8-8）2+（9-8）2+（7-8）2+（7-8）2]=110×13 =1.3；x 乙=（7+10+7+7+9+8+7+9+9+7）=8，2S 乙=110[（7-8）2+（10-8）2+（7-8）2+（7-8）2+（9-8）2+（8-8）2+（7-8）2+（9-8）2+（9-8）2+（7-8）2]=110×12 =1.2；。
湖北省孝感市2019-2020学年中考数学五月模拟试卷含解析
湖北省孝感市2019-2020学年中考数学五月模拟试卷一、选择题（本大题共12个小题，每小题4分，共48分．在每小题给出的四个选项中，只有一项是符合题目要求的．）1．若数a，b在数轴上的位置如图示，则（）A．a+b＞0 B．ab＞0 C．a﹣b＞0 D．﹣a﹣b＞02．一个不透明的袋子里装着质地、大小都相同的3个红球和2个绿球，随机从中摸出一球，不再放回袋中，充分搅匀后再随机摸出一球．两次都摸到红球的概率是（）A．310B．925C．920D．353．如图，将一副三角板如此摆放，使得BO和CD平行，则∠AOD的度数为（）A．10°B．15°C．20°D．25°4．关于x的不等式2(1)4xa x＞＜-⎧⎨-⎩的解集为x＞3，那么a的取值范围为（）A．a＞3 B．a＜3 C．a≥3D．a≤35．如图，在△ABC中，∠B＝90°，AB＝3cm，BC＝6cm，动点P从点A开始沿AB向点B以1cm/s的速度移动，动点Q从点B开始沿BC向点C以2cm/s的速度移动，若P，Q两点分别从A，B两点同时出发，P点到达B点运动停止，则△PBQ的面积S随出发时间t的函数关系图象大致是（）A．B．C．D．6．2018的相反数是（）A．12018B．2018 C．-2018 D．12018-7．如图，△ABC为直角三角形，∠C=90°，BC=2cm，∠A=30°，四边形DEFG为矩形，3，EF=6cm，且点C、B、E、F在同一条直线上，点B与点E重合．Rt△ABC以每秒1cm的速度沿矩形DEFG 的边EF 向右平移，当点C 与点F 重合时停止．设Rt △ABC 与矩形DEFG 的重叠部分的面积为ycm 2，运动时间xs ．能反映ycm 2与xs 之间函数关系的大致图象是（ ）A ．B ．C ．D ．8．港珠澳大桥目前是全世界最长的跨海大桥，其主体工程“海中桥隧”全长35578米，数据35578用科学记数法表示为（ ） A ．35.578×103 B ．3.5578×104 C ．3.5578×105D ．0.35578×1059．如图，将矩形ABCD 沿EM 折叠，使顶点B 恰好落在CD 边的中点N 上．若AB=6，AD=9，则五边形ABMND 的周长为（ ）A ．28B ．26C ．25D ．2210．如图，AB 是O e 的直径，弦CD AB ⊥，CDB 30∠=o ，CD 23=，则阴影部分的面积为（ ）A ．2πB ．πC ．π3D ．2π 311．若3x ＞﹣3y ，则下列不等式中一定成立的是 （ ） A ．0x y +>B ．0x y ->C ．0x y +<D ．0x y -<12．如图，在△ABC 中，点D 在AB 边上，DE ∥BC ，与边AC 交于点E ，连结BE ，记△ADE ，△BCE 的面积分别为S 1，S 2，（ ）A ．若2AD ＞AB ，则3S 1＞2S 2 B ．若2AD ＞AB ，则3S 1＜2S 2C ．若2AD ＜AB ，则3S 1＞2S 2D ．若2AD ＜AB ，则3S 1＜2S 2二、填空题：（本大题共6个小题，每小题4分，共24分．） 13．已知⊙O 半径为1，A 、B 在⊙O 上，且2AB =，则AB 所对的圆周角为__o .14．如图，AC 是正五边形ABCDE 的一条对角线，则∠ACB ＝_____．15．若关于x 、y 的二元一次方程组2133x y m x y -=+⎧⎨+=⎩的解满足x ＋y ＞0，则m 的取值范围是____．16． “五一劳动节”，王老师将全班分成六个小组开展社会实践活动，活动结束后，随机抽取一个小组进行汇报展示．第五组被抽到的概率是___．17．将6本相同厚度的书叠起来，它们的高度是9厘米．如果将这样相同厚度的书叠起来的高度是42厘米，那么这些书有_____本． 18．计算：2﹣1+()22-=_____．三、解答题：（本大题共9个小题，共78分，解答应写出文字说明、证明过程或演算步骤．19．（6分）在ABC V 中，ABC 90o ∠=，BD 为AC 边上的中线，过点C 作CE BD ⊥于点E ，过点A 作BD 的平行线，交CE 的延长线于点F ，在AF 的延长线上截取FG BD =，连接BG ，DF ．()1求证：BD DF =；()2求证：四边形BDFG 为菱形； ()3若AG 5=，CF 7=，求四边形BDFG 的周长．20．（6分）（1）计算：2﹣212+（16）0+2sin60°．（2）先化简，再求值：（121x xx x---+）÷22121xx x-++，其中x=﹣1．21．（6分）如图，某校数学兴趣小组要测量大楼AB的高度，他们在点C处测得楼顶B的仰角为32°，再往大楼AB方向前进至点D处测得楼顶B的仰角为48°，CD＝96m，其中点A、D、C在同一直线上．求AD的长和大楼AB的高度（结果精确到2m）参考数据：sin48°≈2．74，cos48°≈2．67，tan48°≈2．22，3≈2．7322．（8分）据调查，超速行驶是引发交通事故的主要原因之一．小强用所学知识对一条笔直公路上的车辆进行测速，如图所示，观测点C到公路的距离CD=200m，检测路段的起点A位于点C的南偏东60°方向上，终点B位于点C的南偏东45°方向上．一辆轿车由东向西匀速行驶，测得此车由A处行驶到B处的时间为10s．问此车是否超过了该路段16m/s的限制速度？（观测点C离地面的距离忽略不计，参考数据：2≈1.41，3≈1.73）23．（8分）解方程21=122xx x---24．（10分）小明和小亮玩一个游戏：取三张大小、质地都相同的卡片，上面分别标有数字2、3、4（背面完全相同），现将标有数字的一面朝下．小明从中任意抽取一张，记下数字后放回洗匀，然后小亮从中任意抽取一张，计算小明和小亮抽得的两个数字之和．请你用画树状图或列表的方法，求出这两数和为6的概率．如果和为奇数，则小明胜；若和为偶数，则小亮胜．你认为这个游戏规则对双方公平吗？做出判断，并说明理由．25．（10分）如图，建筑物AB的高为6cm，在其正东方向有个通信塔CD，在它们之间的地面点M（B，M，D三点在一条直线上）处测得建筑物顶端A、塔项C的仰角分别为37°和60°，在A处测得塔顶C的仰角为30°，则通信塔CD的高度．（sin37°≈0.60，cos37°≈0.80，tan37°≈0.753，精确到0.1m）26．（12分）如图，AB 为⊙O 的直径，点D 、E 位于AB 两侧的半圆上，射线DC 切⊙O 于点D ，已知点E 是半圆弧AB 上的动点，点F 是射线DC 上的动点，连接DE 、AE ，DE 与AB 交于点P ，再连接FP 、FB ，且∠AED ＝45°． （1）求证：CD ∥AB ； （2）填空：①当∠DAE ＝ 时，四边形ADFP 是菱形； ②当∠DAE ＝ 时，四边形BFDP 是正方形．27．（12分）已知：如图，在半径为2的扇形AOB 中，90AOB ︒∠=°，点C 在半径OB 上，AC 的垂直平分线交OA 于点D ，交弧AB 于点E ，联结BE CD 、．（1）若C 是半径OB 中点，求OCD ∠的正弦值； （2）若E 是弧AB 的中点，求证：2•BE BO BC =；（3）联结CE ，当△DCE 是以CD 为腰的等腰三角形时，求CD 的长．参考答案一、选择题（本大题共12个小题，每小题4分，共48分．在每小题给出的四个选项中，只有一项是符合题目要求的．） 1．D 【解析】 【分析】首先根据有理数a ，b 在数轴上的位置判断出a 、b 两数的符号，从而确定答案． 【详解】由数轴可知：a ＜0＜b ，a<-1，0<b<1, 所以,A.a+b<0，故原选项错误； B. ab ＜0，故原选项错误； C.a-b<0，故原选项错误； D. 0a b -->,正确. 故选D ． 【点睛】本题考查了数轴及有理数的乘法，数轴上的数：右边的数总是大于左边的数，从而确定a ，b 的大小关系． 2．A 【解析】 【分析】列表或画树状图得出所有等可能的结果，找出两次都为红球的情况数，即可求出所求的概率： 【详解】 列表如下：∵所有等可能的情况数为20种，其中两次都为红球的情况有6种，∴63P2010==两次红，故选A.3．B【解析】【分析】根据题意可知，∠AOB=∠ABO=45°，∠DOC=30°，再根据平行线的性质即可解答【详解】根据题意可知∠AOB=∠ABO=45°，∠DOC=30°∵BO∥CD∴∠BOC=∠DCO=90°∴∠AOD=∠BOC-∠AOB-∠DOC=90°-45°-30°=15°故选B【点睛】此题考查三角形内角和，平行线的性质，解题关键在于利用平行线的性质得到角相等4．D【解析】分析：先解第一个不等式得到x＞3，由于不等式组的解集为x＞3，则利用同大取大可得到a的范围．详解：解不等式2（x-1）＞4，得：x＞3，解不等式a-x＜0，得：x＞a，∵不等式组的解集为x＞3，∴a≤3，故选D．点睛：本题考查了解一元一次不等式组：解一元一次不等式组时，一般先求出其中各不等式的解集，再求出这些解集的公共部分，利用数轴可以直观地表示不等式组的解集．解集的规律：同大取大；同小取小；大小小大中间找；大大小小找不到．5．C【解析】【分析】根据题意表示出△PBQ的面积S与t的关系式，进而得出答案．【详解】由题意可得：PB＝3﹣t，BQ＝2t，则△PBQ的面积S＝12PB•BQ＝12（3﹣t）×2t＝﹣t2+3t，故△PBQ的面积S随出发时间t的函数关系图象大致是二次函数图象，开口向下．故选C．【点睛】此题主要考查了动点问题的函数图象，正确得出函数关系式是解题关键．6．C【解析】【分析】根据只有符号不同的两个数互为相反数进行解答即可得.【详解】2018与-2018只有符号不同，由相反数的定义可得2018的相反数是-2018，故选C.【点睛】本题考查了相反数的定义，熟练掌握相反数的定义是解题的关键.7．A【解析】∵∠C=90°，BC=2cm，∠A=30°，∴AB=4，由勾股定理得：AC=23，∵四边形DEFG为矩形，∠C=90，∴DE=GF=23，∠C=∠DEF=90°，∴AC∥DE，此题有三种情况：（1）当0＜x＜2时，AB交DE于H，如图∵DE∥AC，∴EH BE AC BC=，223x=，解得：3x，所以y=12•3x•x=32x 2， ∵x 、y 之间是二次函数，所以所选答案C 错误，答案D 错误， ∵a=32＞0，开口向上； （2）当2≤x≤6时，如图，此时y=12×2×23=23， （3）当6＜x≤8时，如图，设△ABC 的面积是s 1，△FNB 的面积是s 2，BF=x ﹣6，与（1）类同，同法可求3﹣3 ∴y=s 1﹣s 2， =12×2×312×（x ﹣6）×3﹣3， =323﹣3， 30， ∴开口向下，所以答案A 正确，答案B 错误， 故选A ．点睛：本题考查函数的图象.在运动的过程中正确区分函数图象是解题的关键. 8．B 【解析】 【分析】科学计数法是a×10n ，且110a ≤<，n 为原数的整数位数减一．【详解】10，解：35578= 3.5578×4故选B．【点睛】本题主要考查的是利用科学计数法表示较大的数，属于基础题型．理解科学计数法的表示方法是解题的关键．9．A【解析】【分析】如图，运用矩形的性质首先证明CN=3，∠C=90°；运用翻折变换的性质证明BM=MN（设为λ），运用勾股定理列出关于λ的方程，求出λ，即可解决问题．【详解】如图，由题意得：BM=MN（设为λ），CN=DN=3；∵四边形ABCD为矩形，∴BC=AD=9，∠C=90°，MC=9-λ；由勾股定理得：λ2=（9-λ）2+32，解得：λ=5，∴五边形ABMND的周长=6+5+5+3+9=28，故选A．【点睛】该题主要考查了翻折变换的性质、矩形的性质、勾股定理等几何知识点及其应用问题；解题的关键是灵活运用翻折变换的性质、矩形的性质、勾股定理等几何知识点来分析、判断、推理或解答．10．D【解析】分析：连接OD，则根据垂径定理可得出CE=DE，继而将阴影部分的面积转化为扇形OBD的面积，代入扇形的面积公式求解即可．详解：连接OD,∵CD⊥AB，∴13,2CE DE CD === (垂径定理)， 故OCE ODE S S V V ，= 即可得阴影部分的面积等于扇形OBD 的面积，又∵30CDB ∠=︒，∴60COB ∠=o (圆周角定理)，∴OC=2，故S 扇形OBD=260π22π3603⨯=， 即阴影部分的面积为2π3. 故选D.点睛：考查圆周角定理，垂径定理，扇形面积的计算，熟记扇形的面积公式是解题的关键.11．A【解析】两边都除以3，得x ＞﹣y ，两边都加y ，得：x+y ＞0，故选A ．12．D【解析】【分析】根据题意判定△ADE ∽△ABC ，由相似三角形的面积之比等于相似比的平方解答．【详解】∵如图，在△ABC 中，DE ∥BC ，∴△ADE ∽△ABC ，∴2112BDE S AD SS S AB=++V （）， ∴若1AD ＞AB ，即12AD AB ＞时，11214BDE S S S S ++V ＞， 此时3S 1＞S 1+S △BDE ，而S 1+S △BDE ＜1S 1．但是不能确定3S 1与1S 1的大小，故选项A 不符合题意，选项B 不符合题意．若1AD ＜AB ，即12AD AB ＜时，11214BDE S S S S ++V ＜， 此时3S 1＜S 1+S △BDE ＜1S 1，故选项C 不符合题意，选项D 符合题意．故选D ．【点睛】考查了相似三角形的判定与性质，三角形相似的判定一直是中考考查的热点之一，在判定两个三角形相似时，应注意利用图形中已有的公共角、公共边等隐含条件，以充分发挥基本图形的作用，寻找相似三角形的一般方法是通过作平行线构造相似三角形．二、填空题：（本大题共6个小题，每小题4分，共24分．）13．45º或135º【解析】试题解析：如图所示，∵OC ⊥AB ，∴C 为AB 的中点,即1222AC BC AB === 在Rt △AOC 中,OA=1, 22AC = 根据勾股定理得：222OC OA AC =-=即OC=AC ， ∴△AOC 为等腰直角三角形，45AOC ∴∠=o ，同理45BOC ∠=o ，90AOB AOC BOC ∴∠=∠+∠=o ，∵∠AOB 与∠ADB 都对¶AB ,1452ADB AOB o ，∴∠=∠= ∵大角270AOB ∠=o ，135.AEB ∴∠=o 则弦AB 所对的圆周角为45o 或135.o 故答案为45或135.14．36°【解析】【分析】由正五边形的性质得出∠B=108°，AB=CB ，由等腰三角形的性质和三角形内角和定理即可得出结果．【详解】∵五边形ABCDE 是正五边形，∴∠B=108°，AB=CB ，∴∠ACB=（180°﹣108°）÷2=36°；故答案为36°．15．m>-1【解析】【分析】首先解关于x 和y 的方程组，利用m 表示出x+y ，代入x+y ＞0即可得到关于m 的不等式，求得m 的范围．【详解】解：2133x y m x y -=+⎧⎨+=⎩①②， ①+②得1x+1y ＝1m+4，则x+y ＝m+1，根据题意得m+1＞0，解得m ＞﹣1．故答案是：m ＞﹣1．【点睛】本题考查的是解二元一次方程组和解一元一次不等式，解答此题的关键是把m 当作已知数表示出x+y 的值，再得到关于m 的不等式．16．16【解析】【分析】根据概率是所求情况数与总情况数之比，可得答案．【详解】因为共有六个小组， 所以第五组被抽到的概率是16， 故答案为：16． 【点睛】本题考查了概率的知识．用到的知识点为：概率=所求情况数与总情况数之比．17．1．【解析】【分析】因为一本书的厚度是一定的，根据本数与书的高度成正比列比例式即可得到结论．【详解】设这些书有x 本， 由题意得，6942x =， 解得：x=1，答：这些书有1本．故答案为：1．【点睛】本题考查了比例的性质，正确的列出比例式是解题的关键．18．52【解析】根据负整指数幂的性质和二次根式的性质，可知12-=15222+=. 故答案为52. 三、解答题：（本大题共9个小题，共78分，解答应写出文字说明、证明过程或演算步骤．19．（1）证明见解析（2）证明见解析（3）1【分析】()1利用平行线的性质得到90CFA ∠=o ，再利用直角三角形斜边上的中线等于斜边的一半即可得证， ()2利用平行四边形的判定定理判定四边形BDFG 为平行四边形，再利用()1得结论即可得证， ()3设GF x =，则5AF x =-，利用菱形的性质和勾股定理得到CF 、AF 和AC 之间的关系，解出x 即可．【详解】()1证明：AG //BD Q ，CF BD ⊥，CF AG ∴⊥，又D Q 为AC 的中点，1DF AC 2∴=， 又1BD AC 2=Q ， BD DF ∴=，()2证明：BD//GF Q ，BD FG =，∴四边形BDFG 为平行四边形，又BD DF =Q ，∴四边形BDFG 为菱形，()3解：设GF x =，则AF 5x =-，AC 2x =，在Rt AFC V 中，222(2x)(5x)=+-，解得：1x 2=，216x (3=-舍去)， GF 2∴=，∴菱形BDFG 的周长为1．【点睛】本题考查了菱形的判定与性质直角三角形斜边上的中线，勾股定理等知识，正确掌握这些定义性质及判定并结合图形作答是解决本题的关键．20．（1）54-（2）20172018【解析】【分析】（1）根据负整数指数幂、二次根式、零指数幂和特殊角的三角函数值可以解答本题；（2）根据分式的减法和除法可以化简题目中的式子，然后将x 的值代入化简后的式子即可解答本题．解：（1）原式=14﹣2⨯=14﹣54; （2）原式=2(1)(1)(2)(+1)(1)21x x x x x x x x -+--⋅+- =22212(+1)(1)21x x x x x x x --+⋅+- =221(+1)(1)21x x x x x -⋅+- =+1x x， 当x=﹣1时，原式=2018+12018--=20172018． 【点睛】本题考查分式的化简求值、绝对值、零指数幂、负整数指数幂和特殊角的三角函数值，解答本题的关键是明确它们各自的计算方法．21．AD 的长约为225m ，大楼AB 的高约为226m【解析】【分析】首先设大楼AB 的高度为xm ，在Rt △ABC 中利用正切函数的定义可求得 ，然后根据∠ADB 的正切表示出AD 的长，又由CD=96m ，x 961.11-= ，解此方程即可求得答案． 【详解】解：设大楼AB 的高度为xm ，在Rt △ABC 中，∵∠C=32°，∠BAC=92°，∴AB AC=tan 30==o ，在Rt △ABD 中，AB tan ADB tan48AD ∠=︒=， ∴AB x AD =tan48 1.11=︒， ∵CD=AC-AD ，CD=96m ，x 961.11-= ， 解得：x≈226， ∴x 116AD 1051.11 1.11=≈≈ 答：大楼AB 的高度约为226m ，AD 的长约为225m ．本题考查解直角三角形的应用．要求学生能借助仰角构造直角三角形并解直角三角形，注意数形结合思想与方程思想的应用．22．此车没有超过了该路段16m/s 的限制速度．【解析】分析：根据直角三角形的性质和三角函数得出DB ，DA ，进而解答即可．详解：由题意得：∠DCA=60°，∠DCB=45°，在Rt △CDB 中，tan ∠DCB=1200DB DB DC ==， 解得：DB=200，在Rt △CDA 中，tan ∠DCA=200DA DA DC ==解得：∴AB=DA ﹣200≈146米， 轿车速度14614.61610AB v t ===<， 答：此车没有超过了该路段16m/s 的限制速度．点睛：本题考查了解直角三角形的应用﹣方向角问题，解答本题的关键是利用三角函数求出AD 与BD 的长度，难度一般．23．x=-1．【解析】【分析】【详解】解：方程两边同乘x-2，得2x=x-2+1解这个方程，得x= -1检验：x= -1时，x-2≠0∴原方程的解是x= -1首先去掉分母，观察可得最简公分母是（x ﹣2），方程两边乘最简公分母，可以把分式方程转化为整式方程求解，然后解一元一次方程，最后检验即可求解24． (1)列表见解析；（2）这个游戏规则对双方不公平．【解析】【分析】（1）首先根据题意列表，然后根据表求得所有等可能的结果与两数和为6的情况，再利用概率公式求解即可；（2）分别求出和为奇数、和为偶数的概率，即可得出游戏的公平性．（1）列表如下：由表可知，总共有9种结果，其中和为6的有3种，则这两数和为6的概率3193=； （2）这个游戏规则对双方不公平．理由如下：因为P （和为奇数）49=，P （和为偶数）59=，而4599≠，所以这个游戏规则对双方是不公平的． 【点睛】 本题考查了列表法求概率．注意树状图与列表法可以不重不漏的表示出所有等可能的情况．用到的知识点为：概率=所求情况数与总情况数之比．25．通信塔CD 的高度约为15.9cm ．【解析】【分析】过点A 作AE ⊥CD 于E ，设CE=xm ，解直角三角形求出AE ，解直角三角形求出BM 、DM ，即可得出关于x 的方程，求出方程的解即可．【详解】过点A 作AE ⊥CD 于E ，则四边形ABDE 是矩形，设CE=xcm ，在Rt △AEC 中，∠AEC=90°，∠CAE=30°，所以AE=330CE tan =︒， 在Rt △CDM 中，CD=CE+DE=CE+AB=（x+6）cm ，DM=()36603xCDtan+=︒cm，在Rt△ABM中，BM=63737ABtan tan=︒︒cm，∵AE=BD，∴()3663373xxtan+=+︒，解得：x=33+3，∴CD=CE+ED=3337tan︒+9≈15.9（cm），答：通信塔CD的高度约为15.9cm．【点睛】本题考查了解直角三角形，能通过解直角三角形求出AE、BM的长度是解此题的关键．26．（1）详见解析；（2）①67.5°；②90°．【解析】【分析】（1）要证明CD∥AB，只要证明∠ODF＝∠AOD即可，根据题目中的条件可以证明∠ODF＝∠AOD，从而可以解答本题；（2）①根据四边形ADFP是菱形和菱形的性质，可以求得∠DAE的度数；②根据四边形BFDP是正方形，可以求得∠DAE的度数．【详解】（1）证明：连接OD，如图所示，∵射线DC切⊙O于点D，∴OD⊥CD，即∠ODF＝90°，∵∠AED＝45°，∴∠AOD＝2∠AED＝90°，∴∠ODF＝∠AOD，∴CD∥AB；（2）①连接AF与DP交于点G，如图所示，∵四边形ADFP是菱形，∠AED＝45°，OA＝OD，∴AF⊥DP，∠AOD＝90°，∠DAG＝∠PAG，∴∠AGE＝90°，∠DAO＝45°，∴∠EAG＝45°，∠DAG＝∠PEG＝22.5°，∴∠EAD＝∠DAG+∠EAG＝22.5°+45°＝67.5°，故答案为：67.5°；②∵四边形BFDP是正方形，∴BF＝FD＝DP＝PB，∠DPB＝∠PBF＝∠BFD＝∠FDP＝90°，∴此时点P与点O重合，∴此时DE是直径，∴∠EAD＝90°，故答案为：90°．【点睛】本题考查菱形的判定与性质、切线的性质、正方形的判定，解答本题的关键是明确题意，找出所求问题需要的条件，利用菱形的性质和正方形的性质解答．27．（2）3sin CD5O∠=；（2）详见解析；（2）当DCEV是以CD为腰的等腰三角形时，CD的长为2或32．【解析】【分析】（2）先求出OC12=OB=2，设OD=x，得出CD=AD=OA﹣OD=2﹣x，根据勾股定理得：（2﹣x）2﹣x2=2求出x，即可得出结论；（2）先判断出¶¶AE BE=，进而得出∠CBE=∠BCE，再判断出△OBE∽△EBC，即可得出结论；（3）分两种情况：①当CD=CE时，判断出四边形ADCE是菱形，得出∠OCE=90°．在Rt△OCE中，OC2=OE2﹣CE2=4﹣a2．在Rt△COD中，OC2=CD2﹣OD2=a2﹣（2﹣a）2，建立方程求解即可；②当CD=DE时，判断出∠DAE=∠DEA，再判断出∠OAE=OEA，进而得出∠DEA=∠OEA，即：点D 和点O重合，即可得出结论．【详解】（2）∵C是半径OB中点，∴OC12=OB=2．∵DE是AC的垂直平分线，∴AD=CD．设OD=x，∴CD=AD=OA﹣OD=2﹣x．在Rt△OCD中，根据勾股定理得：（2﹣x）2﹣x2=2，∴x34=，∴CD54=，∴sin∠OCD35ODCD==；（2）如图2，连接AE，CE．∵DE是AC垂直平分线，∴AE=CE．∵E是弧AB的中点，∴¶¶AE BE=，∴AE=BE，∴BE=CE，∴∠CBE=∠BCE．连接OE，∴OE=OB，∴∠OBE=∠OEB，∴∠CBE=∠BCE=∠OEB．∵∠B=∠B，∴△OBE∽△EBC，∴BE OBBC BE=，∴BE2=BO•BC；（3）△DCE是以CD为腰的等腰三角形，分两种情况讨论：①当CD=CE时．∵DE是AC的垂直平分线，∴AD=CD，AE=CE，∴AD=CD=CE=AE，∴四边形ADCE是菱形，∴CE∥AD，∴∠OCE=90°，设菱形的边长为a，∴OD=OA﹣AD=2﹣a．在Rt△OCE中，OC2=OE2﹣CE2=4﹣a2．在Rt△COD中，OC2=CD2﹣OD2=a2﹣（2﹣a）2，∴4﹣a2=a2﹣（2﹣a）2，∴a=﹣23-2（舍）或a=232-；∴CD=232-；②当CD=DE时．∵DE是AC垂直平分线，∴AD=CD，∴AD=DE，∴∠DAE=∠DEA．连接OE，∴OA=OE，∴∠OAE=∠OEA，∴∠DEA=∠OEA，∴点D和点O重合，此时，点C和点B 重合，∴CD=2．综上所述：当△DCE是以CD为腰的等腰三角形时，CD的长为2或232-．【点睛】本题是圆的综合题，主要考查了勾股定理，线段垂直平分线的性质，菱形的判定和性质，锐角三角函数，作出辅助线是解答本题的关键．。
湖北省孝感市孝南区肖港初级中学九年级数学5月调研试题 新人教版
A ．B ． D ．C ． 主视方向21第2题图温馨提示：1．答题前，考生务必将自己所在学校、姓名、考号填写在答题卷上指定的位置．2．选择题选出答案后，把答案写在答题卷上对应题目的位置；非选择题的答案必须写在答题卷的指定位置，在本卷上答题无效．3．本试卷满分120分，考试时间120分钟． 一、精心选一选，相信自己的判断！（本大题共12小题，每小题3分，共36分．每小题给出的四个选项中只有一项是符合题目要求的，每一小题选对得3分，不选、选错或选出的代号超过一个的一律得0分） 1．3-的倒数是 A ．3-B ．3C ．13D ．13-2．左下图为主视方向的几何体，它的俯视图是3．如图，把一块含有30°角的直角三角板的两个顶点放在直 尺的对边上，如果∠1=20°，那么∠2的度数为 A ．20° B ．30° C ．40° D ．60°4．化简148312242÷-⨯+的结果是 A ．616+ B ．632+C ． 632++D ．64+5．如图，AD 为⊙O 的直径，作⊙O 的内接正三角形ABC ，甲、乙两人的作法分别是： 甲：1.作OD 的中垂线，交⊙O 于B ，C 两点，2.连接AB ，AC ，△ABC 即为所求的三角形． 乙：1.以D 为圆心，OD 长为半径作圆弧，交⊙O 于B ，C 两点. 2.连接AB ，BC ，CA ．△ABC 即为所求的三角形． 对于甲、乙两人的作法，可判断A.甲、乙均正确B.甲、乙均错误C.甲正确、乙错误D.甲错误、乙正确6．某班开展以“提倡勤俭节约，反对铺张浪费”为主题教育活动. 为了解学生每天使用零花钱的情况，小明随机调查了10名同学，结果如下表：每天使用零花钱（单位：元）0 2 3 4 5 人数12412关于这10名同学每天使用的零花钱，下列说法正确的是 A ．平均数是2.5B ．中位数是3C ．众数是2D ．方差是47．二次函数2y ax bx c =++的图象如图，则0y <时x 的取值范围是A ．1x <-B ．x ＞3C ．－1＜x ＜3D ．x ＜－1或x ＞38．如图所示，把一张矩形纸片对折，折痕为AB ，再把以AB 的中点O 为顶点的平角∠AOB 三等分，沿平角的三等分线折叠，将折叠后的图形剪出一个以O 为顶点的等腰三角形，那么剪出的等腰三角形全部展开第5题图第7题图平铺后得到的平面图形一定是A ．正三角形B ．正方形C ．正五边形D ．正六边形 9. 如图在△ABC 中，DE ∥BC ，AD =2，DB =4，DE =3，则BC 的长为A ．9B ．6C ．4D ．3 10．如图所示，△ABC 的顶点是正方形网格的格点，则sin A 的值为A.12B.55C.1010D.25511．如图，小正方形构成的网络中，半径为1的⊙O 的圆心O 在格点上，则图中阴影部分两个小扇形的面积之和为A.π41B.π21C. πD. π212．如图，平面直角坐标系中，⊙O 1过原点O ，且⊙O 1与⊙O 2相外切，圆心O 1与O 2在x 轴正半轴上，⊙O 1的半径O 1P 1、⊙O 2的半径O 2P 2都与x 轴垂直，且点P 1()11,x y 、P 2()22,x y 在反比例函数xy 1=（x >0）的图象上，则21y y +等于 A.22+B. 12-C. 221+D. 2 二、细心填一填，试试自己的身手！（本大题共6小题，每小题3分，满分18分） 13．使式子2-m 有意义的m 的取值范围是 ▲ ． 14.化简x yx y x y-=-- ▲ ． 15．如图，在平面直角坐标系中，将△ABC 绕点P 旋转180°得到△DEF ，则点P 的坐标为 ▲ ． 16．如图，已知△ABC 中，∠ABC =45°，AC =4，H 是高AD 和BE 的交点，则线段BH 的长度为____▲____. 第12题图第11题图OCB A第10题图B ACE D 第9题图HEC BA17．“上升数”是一个数中右边数字比左边数字大的自然数（如：34、568、2469等）．任取一个两位数，是“上升数”的概率是 ▲ ． 18．给出下列命题：命题1：直线x y =与双曲线x y 1=有一个交点是（1，1）； 命题2：直线x y 8=与双曲线x y 2=有一个交点是（21，4）；命题3：直线x y 27=与双曲线x y 3=有一个交点是（31，9）；命题4：直线x y 64=与双曲线x y 4=有一个交点是（41，16）；……请你阅读、观察上面命题，猜想并写出命题n （n 为正整数）： ▲ ． 三、用心做一做，显显自己的能力（本大题共7小题，满分66分）19．（满分6分）解不等式组⎪⎩⎪⎨⎧>+≥+231325x x x ，并写出不等式组的整数解．20．（满分8分）为了加强食品安全管理，有关部门对某大型超市的甲、乙两种品牌奶粉共抽取18罐进行检测，检测结果分成“优质”、“合格”、“不合格”三个等级，数据处理后制成以下折线统计图和扇形统计图．(1)说明甲、乙两种品牌奶粉各被抽取了多少罐用于检测？(2)在该超市购买一罐乙品牌奶粉，能买到“优质”等级的概率是多少？21. （满分10分）问题：如图1，a 、b 、c 、d 是同一平面内的一组等距平行线（相邻平行线间的距离为1）.画出一个正方形ABCD ，使它的顶点A 、B 、C 、D 分别在直线a 、b 、d 、c 上，并计算它的边长.图1 图2小明的思考过程：他利用图1中的等距平行线构造了33⨯的正方形网格，得到了辅助正方形第20题图EFGH，如图2所示, 再分别找到它的四条边的三等分点A、B、C、D，就可以画出一个满足题目要求的正方形.(1)请回答：图2中正方形ABCD的边长为▲ .(2)请参考小明的方法，解决下列问题：①请在图3的菱形网格（最小的菱形有一个内角为60︒，边长为1）中，画出一个等边△ABC，使它的顶点A、B、C落在格点上，且分别在直线a、b、c上；②求出①中△ABC的边长是__▲___.22．（满分10分）已知关于x的一元二次方程21(2)2602x m x m+-+-=．（1）求证：无论m取任何实数，方程都有两个实数根；（2）当3<m时，原方程的两实数根分别为1x、2x，且431121=-xx，求m的值.23．（满分10分）已知⊙O中，AC为直径，MA、MB分别切⊙O于点A、B．（1）如图①，若∠BAC=25°，求∠AMB的大小；（2）如图②，过点B作BD⊥AC于E，交⊙O于点D，若BD=MA，求∠AMB的大小．图3第23题图S ∕海里13 05 8 150t ∕小时34324．（满分10分）黄岩岛是我国南沙群岛的一个小岛，渔产丰富.一天某渔船离开港口前往该海域捕鱼.捕捞一段时间后，发现一外国舰艇进入我国水域向黄岩岛驶来，渔船向渔政部门报告，并立即返航.渔政船接到报告后，立即从该港口出发赶往黄岩岛.下图是渔政船及渔船与港口的距离s 和渔船离开港口的时间t 之间的函数图象.（假设渔船与渔政船沿同一航线航行）（1）写出渔船离港口的距离s 和它离开港口的时间t 的函数关系式：____▲______. （2）求渔船和渔政船相遇时，两船与黄岩岛的距离.（3）在渔政船驶往黄岩岛的过程中，渔船从港口出发经过___▲_____小时与渔政船相距30海里.25．（满分12分）如图1，在平面直角坐标系xOy 中，直线l ：34y x m =+与x 轴、y 轴分别交于点A 和点B (0，－1)，抛物线212y x bx c =++经过点B ，且与直线l 的另一个交点为C (4，n )． (1) 直接写出n 的值和抛物线的解析式： ▲ ;(2) 点D 在抛物线上，且点D 的横坐标为t （0< t <4）．DE ∥y 轴交直线l 于点E ，点F 在直线l 上，且四边形DFEG 为矩形（如图2）．①证明△OAB∽△FDE ；②若矩形DFEG 的周长为p ，求p 与t 的函数关系式以及p 的最大值；图1图2第24题图第25题图2013年5月九年级调考 数学试题参考答案13．m ≥2 14．1 15．（－1，－1） 16．4 17． 52 18．直线x n y 3=与双曲线x n y =有一个交点是（n1，2n ）. 第一节 解答题20. 解：（1）因为只有1罐奶粉不合格，所以这罐奶粉一定是甲种品牌.…………………………………2分甲种奶粉有1÷10%=10（罐），乙种奶粉有8（罐）…………………………………4分 （2）甲、乙两种品牌优质奶粉共抽10罐，其中乙种奶粉优质的有10-10×60%=4（罐） 在该超市购买一罐乙种品牌奶粉，能买到“优秀”等级的概率是0.5.…………………8分21．（1）5. ………………………3分 （2）①如图：(答案不唯一) ………………………7分②7 ………………………10分（2）解法一：∵1x 、2x 是21(2)2602x m x m +-+-=两实根，且3<m 不妨设21x x <，解得x 1=－2， x 2=6－2m ，……………………6分 又∵0)3(4)62(221<-=-=⋅m m x x ，∴01<x ，02>x∴由431121=-x x 得431112=-x x ∴4321261=+-m解得1=m ……………………8分23.解：（1）∵MA 切⊙O 于点A ，有∠MA C=90°…………………1分又∠BAC =25°∴∠MAB =∠MAC －∠BAC =25°…………………2分∵MA 、MB 切⊙O 于点A 、B ，∴MA =MB ,有∠MAB =∠MBA …………………3分∴∠AMB =180°－(∠MAB +∠MBA )=50°…………………5分(2)如图，连接AD 、AB ∵MA ⊥AC ，又BD ⊥AC∴MA ∥BD …………………6分又MA =BD∴四边形MADB 是平行四边形，有AD =BD ∵MA =MB∴四边形MADB 是菱形…………………8分又AC 为直径，AC ⊥BD ，得 AB =AD ∴△ABD 是等边三角形，有∠D =60°∴在菱形MADB 中∠AMB =∠D =60°…………………10分24．（1） 当0≤t ≤5时 s =30t当5＜t ≤8时 s =150当8＜t ≤13时 s =－30t +390 ……………………（3分）（2） 渔政船离港口的距离与渔船离开港口的时间的函数关系式设为s =kt +b⎪⎩⎪⎨⎧+=+=b k b k 33415080 ………………………………………………4分 解得： k =45 b =－360∴s =45t －360 ………………………………………………5分⎩⎨⎧+-=-=3903036045t s t s解得 t =10 s =90 渔船离黄岩岛距离为 150－90=60 （海里） ……………………………6分 (3) 9.6小时或10.4小时……………………………10分 25．解：（1）n =2………………………2分抛物线的解析式为215124y x x =--.………………………4分（2） ① ∵DE ∥y 轴， ∴∠OBA =∠FED .∵矩形DFEG 中，∠DFE =90°， ∴∠DFE =∠AOB =90°.∴△OAB ∽△FDE . ………………………7分 ②由① 知 △OAB ∽△FDE∴OA OB ABFD FE DE==. ∴45OA FD DE DE AB =⋅=，35OB FE DE DE AB =⋅=. …………………………………………9分∵直线l ：314y x =-与x 轴交于点A ，FyC E l。
2019届湖北孝感安陆市中考模拟数学试卷(5月份)【含答案及解析】
2019届湖北孝感安陆市中考模拟数学试卷（5月份）【含答案及解析】姓名___________ 班级____________ 分数__________题号一二三总分得分一、选择题1. 下面的数中，与﹣2的和为0的是（）A．2 B．﹣2 C． D．－2. 下列计算正确的是（）A．a2+a3=a5 B．a2?a3=a6C．（a2）3=a5 D．a5÷a2=a33. 下列几何体中，主视图相同的是（）A．①② B．①④ C．①③ D．②④4. 把不等式组的解集表示在数轴上，正确的是（）A． B．C． D．5. 如图，AB∥CD，CE平分∠BCD，∠DCE=18°，则∠Ｂ等于（）A．18° B．36° C．45° D．54°6. 用配方法解方程x2﹣2x﹣5=0时，原方程应变形为（）A．（x+1）2=6 B．（x+2）2=9C．（x﹣1）2=6 D．（x﹣2）2=97. 某校8名学生参加了体育兴趣小组，他们被分成A、B两组进行训练，身高（单位：cm）如表所示：8. 队员1队员2队员3队员4甲组176177175176乙组178175177174td9. 估计介于（）A．0.4与0.5之间 B．0.5与0.6之间C．0.6与0.7之间 D．0.7与0.8之间的度数为10. 如图，四边形ABCD内接于⊙O，E为BC延长线上一点，∠A=50°，则∠DCE（）A．40° B．50° C．60° D．130°的边OA在x轴的正半轴上，OA=AB，边OB的中点11. 如图，在平面直角坐标系中，△OABC在双曲线y=上，将△OAB沿OB翻折后，点A的对应点A′，正好落在双曲线y=上，△OAB的面积为6，则k为（）A．1 B．2 C．3 D．4二、填空题12. 化简：的结果是．13. 谷歌人工智能AlphaGo机器人与韩国棋手李世石的围棋挑战赛引起人们的广泛关注，人工智能完胜李世石，百度上搜索关键词“AlphaGo”，显示的搜索结果约为14100000条，将14100000用科学记数法表示应为．14. 如图，已知∠AOB=60°，点P在OA上，OP=8，点M、N在边OB上，PM=PN，若MN=2，则OM= ．15. 已知，A，B为常数，则A+B的值为．16. 如图，正方形ABCD中，AB=4，E是BC的中点，点P是对角线AC上一动点，则PE+PB 的最小值为．17. 若m1，m2，…m2016是从0，1，2这三个数中取值的一列数，若m1+m2+…+m2016=1546，（m1﹣1）2+（m2﹣1）2+…+（m2016﹣1）2=1510，则在m1，m2，…m2016中，取值为2的个数为____．三、解答题18. 先化简，再求值：（x﹣2）2﹣（2x+1）（2x+1）+4x（x+1），其中x=．19. 已知，如图，直线AB与直线BC相交于点B，点D是直线BC上一点，直线DE∥AB，且点E到B，D两点的距离相等．（1）用尺规作图作出点E；（不写作法，保留作图痕迹）（2）连接BE，求证：BD平分∠ABE．20. 已知关于x的方程x2﹣（k+1）x+k2+1=0有两个实数根．（1）求k的取值范围；（2）若抛物线y=x2﹣（k+1）x+k2+1与x轴交于A、B两点，点A、点B到原点O的距离分别为OA、OB，且满足OA+OB﹣4OA?OB+5=0，求k的值．21. 如图，小明在大楼45米高（即PH=45米）的窗口P处进行观测，测得山坡上A处的俯角为15°，山脚B处的俯角为60°，已知该山坡的坡度i（即tan∠ABC）为1：，点P、H、B、C、A在同一个平面上，点H、B、C在同一条直线上，且PH⊥HC．（1）山坡坡脚（即∠ABC）的度数等于度；（2）求A、B两点间的距离．（结果精确到1米，参考数据：≈1.732）22. 小亮同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况，他从中随机调查了若干户居民的月均用水量（单位：t），并绘制了样本的频数分布表和频数分布直方图（如图）23. 月均用水量（单位：t）频数百分比2≤x＜324% 3≤x＜41224% 4≤x＜5ab 5≤x＜61020% 6≤x＜7c12% 7≤x＜836% 8≤x＜924%td24. 甲、乙两城市之间开通了动车组高速列车．已知每隔2h有一列速度相同的动车组列车从甲城开往乙城．如图，OA是第一列动车组列车离开甲城的路程s（km）与运行时间t （h）的函数图象，BC是一列从乙城开往甲城的普通快车距甲城的路程s（km）与运行时间t（h）的函数图象．请根据图中的信息，解答下列问题：（1）从图象看，普通快车发车时间比第一列动车组列车发车时间 1h（填”早”或”晚”），点B的纵坐标600的实际意义是；（2）请直接在图中画出第二列动车组列车离开甲城的路程s（km）与时间t（h）的函数图象；（3）若普通快车的速度为100km/h，①求第二列动车组列车出发多长时间后与普通快车相遇？②请直接写出这列普通快车在行驶途中与迎面而来的相邻两列动车组列车相遇的时间间隔．于点D，过点B作⊙Ｏ的切线，与CA 25. 如图，A是以BC为直径的⊙Ｏ上的一点，AD⊥BC的延长线相交于点E，点F是EB的中点，连结CF交AD于点G（1）求证：AF是⊙Ｏ的切线；（2）求证：AG=GD；（3）若FB=FG，且⊙Ｏ的半径长为3，求BD．26. 如图，抛物线y=ax2+bx+c（a≠0）与x轴、y轴分别交于点A（﹣1，0），B（3，0）、C（0，﹣3）三点．（1）直接写出抛物线的解析式；（2）点D（2，m）在第一象限的抛物线上，连接BC、BD，试问，在对称轴左侧的抛物线上是否存在一点P，满足∠PBC=∠DBC？如果存在，请求出点P点的坐标；如果不存在，请说明理由．（3）如图2，在（2）的条件下，将△BOC沿x轴正方向以每秒1个单位长度的速度向右平移，记平移后的三角形为△B′O′C′，在平移过程中，△B′O′C′与△BCD重叠的面积记为S，设平移的时间为t秒（0≤t≤3），试求S与t之间的函数关系式？参考答案及解析第1题【答案】第2题【答案】第4题【答案】第5题【答案】第6题【答案】第8题【答案】第9题【答案】第11题【答案】第12题【答案】第13题【答案】第14题【答案】第15题【答案】第16题【答案】第17题【答案】第18题【答案】第19题【答案】第20题【答案】第21题【答案】第22题【答案】第23题【答案】第24题【答案】。
中考数学5月模拟试卷
2020年湖北省孝感市安陆市中考数学模拟试卷（5月份）一、精心选一选，相信自己的判断（共10小题，每小题3分，满分30分，在每小题给出的四个选项中只有一个是符合题目要求的，不涂、错涂或涂的代号超过一个，一律得0分）1．如图，数轴上有A，B，C，D四个点，其中表示2的相反数的点是（）A．点A B．点B C．点C D．点D2．2020年4月20日，天舟一号货运飞船在我国文昌航天发射场发射成功，进入距离地球393000米的预定轨道，将393000用科学记数法表示应为（）A．0.393×107B．3.93×105C．3.93×106D．393×1033．某物体的三视图如图，那么该物体形状可能是（）A．长方体B．圆锥 C．正方体D．圆柱4．《九章算术》是中国古代的数学专著，下面这道题是《九章算术》中第七章的一道题：“今有共买物，人出八，盈三；人出七，不足四，问人数、物价各几何？”译文：“几个人一起去购买某物品，如果每人出8钱，则多了3钱；如果每人出7钱，则少了4钱．问有多少人，物品的价格是多少？”设有x人，物品价格为y钱，可列方程组为（）A．B．C．D．5．如图，AB∥CD，直线EF分别交AB，CD于M，N两点，将一个含有45°角的直角三角尺按如图所示的方式摆放，若∠EMB=75°，则∠PNM等于（）A．15° B．25° C．30° D．45°6．在平面直角坐标系中，点P（﹣3，2）关于直线y=x对称点的坐标是（）A．（﹣3，﹣2）B．（3，2）C．（2，﹣3）D．（3，﹣2）7．某校合唱团有30名成员，下表是合唱团成员的年龄分布统计表：年龄（单位：岁）13 14 15 16频数（单位：名） 5 15 x 10﹣x对于不同的x，下列关于年龄的统计量不会发生改变的是（）A．平均数、中位数B．平均数、方差C．众数、中位数 D．众数、方差8．某商店在节日期间开展优惠促销活动：购买原价超过200元的商品，超过200元的部分可以享受打折优惠．若购买商品的实际付款金额y（单位：元）与商品原价x（单位：元）的函数关系的图象如图所示，则超过200元的部分可以享受的优惠是（）A．打八折B．打七折C．打六折D．打五折9．如图，已知AB、CD、EF都与BD垂直，垂足分别是B、D、F，且AB=1，CD=3，那么EF的长是（）A．B．C．D．10．如图所示，将若干个点摆成三角形图案，每条边（包括两个端点）有n（n是正整数且n＞1）个点，相应的图案中总的点数记为a n ，则++…+=（）A．B．C．D．二、细心填一填，试试自己的身手（本大题共6小题，每小题3分，共18分.请将结果直接填写在答题卡相应的位置上）11．方程x2﹣2=0的根是．12．某坡面的坡度是：1，则坡角α是度．13．如图所示，正六边形ABCDEF内接于⊙O，则∠ADF的度数为．14．一只不透明的袋子中装有红球和白球共30个，这些球除了颜色外都相同，校课外学习小组做摸球试验，将球搅匀后任意摸出一个球，记下颜色后放回、搅匀，通过多次重复试验，算得摸到红球的频率是20%，则袋中有个红球．15．如图，P是等边三角形ABC内一点，将线段AP绕点A顺时针旋转60°得到线段AQ，连接BQ．若PA=6，PB=8，PC=10，则四边形APBQ的面积为．16．已知二次函数y=ax2+bx+c的图象如图所示，给出下列结论：①abc＞0；②a﹣b+c＜0；③2a+b﹣c＜0；④4a+2b+c＞0，⑤若点（﹣，y1）和（，y2）在该图象上，则y1＞y2．其中正确的结论是（填入正确结论的序号）三、用心做一做，显显自己的能力（本大题共8小题，满分72分）17．（1）（﹣2）﹣1﹣|﹣|+（3.14﹣π）0+4cos45°（2）已知x2﹣2x﹣7=0，求（x﹣2）2+（x+3）（x﹣3）的值．18．解方程：．19．某校为更好地培养学生兴趣，开展“拓展课程走班选课”活动，随机抽查了部分学生，了解他们最喜爱的项目类型（分为书法、围棋、戏剧、国画共4类），并将统计结果绘制成如图不完整的频数分布表及频数分布直方图．最喜爱的传统文化项目类型频数分布表项目类型频数频率书法类18 a围棋类14 0.28喜剧类8 0.16国画类 b 0.20根据以上信息完成下列问题：（1）频数分布表中a= ，b= ；（2）补全频数分布直方图；（3）若全校共有学生1500名，估计该校最喜爱围棋的学生大约有多少人？20．去学校食堂就餐，经常会在一个买菜窗口前等待，经调查发现，同学的舒适度指数y与等时间x（分）之间满足反比例函数关系，如下表：等待时间x 1 2 5 10 20舒适度指数y 100 50 20 10 5已知学生等待时间不超过30分钟（1）求y与x的函数关系式，并写出自变量x的取值范围．（2）若等待时间8分钟时，求舒适度的值；（3）舒适度指数不低于10时，同学才会感到舒适．请说明，作为食堂的管理员，让每个在窗口买菜的同学最多等待多少时间？21．已知关于x的方程x2﹣（m+2）x+2m﹣1=0．（1）求证：此方程有两个不相等的实数根；（2）若抛物线y=x2﹣（m+2）x+2m﹣1=0与x轴有两个交点都在x轴正半轴上，求m的取值范围；（3）填空：若x2﹣（m+2）x+2m﹣1=0的两根都大于1，则m的取值范围是．22．如图，在平面直角坐标系中，⊙P经过y轴上一点C，与x轴分别相交于A、B两点，连接BP并延长分别交⊙P、y轴于点D、E，连接DC并延长交x轴于点F．若点F的坐标为（﹣1，0），点D的坐标为（1，6）．（1）求证：CD=CF；（2）判断⊙P与y轴的位置关系，并说明理由；（3）求直线BD的解析式．23．在△ABC中，AB=AC，∠BAC=90°，点D在射线BC上（与B、C两点不重合），以AD为边作正方形ADEF，使点E与点B在直线AD的异侧，射线BA与射线CF相交于点G．（1）若点D在线段BC上，如图1．①依题意补全图1；②判断BC与CG的数量关系与位置关系，并加以证明；（2）若点D在线段BC的延长线上，且G为CF中点，连接GE，AB=，则GE的长为，并简述求GE长的思路．24．如图，直线l：y=x﹣与x轴正半轴、y轴负半轴分别相交于A、C两点，抛物线y=x2+bx+c经过点B（﹣1，0）和点C．（1）填空：直接写出抛物线的解析式：；（2）已知点Q是抛物线y=x2+bx+c在第四象限内的一个动点．①如图，连接AQ、CQ，设点Q的横坐标为t，△AQC的面积为S，求S与t的函数关系式，并求出S的最大值；②连接BQ交AC于点D，连接BC，以BD为直径作⊙I，分别交BC、AB于点E、F，连接EF，求线段EF的最小值，并直接写出此时Q点的坐标．2020年湖北省孝感市安陆市中考数学模拟试卷（5月份）参考答案与试题解析一、精心选一选，相信自己的判断（共10小题，每小题3分，满分30分，在每小题给出的四个选项中只有一个是符合题目要求的，不涂、错涂或涂的代号超过一个，一律得0分）1．如图，数轴上有A，B，C，D四个点，其中表示2的相反数的点是（）A．点A B．点B C．点C D．点D【考点】14：相反数；13：数轴．【分析】相反数的定义：符号不同，绝对值相等的两个数叫互为相反数．根据定义，结合数轴进行分析．【解答】解：∵表示2的相反数的点，到原点的距离与2这点到原点的距离相等，并且与2分别位于原点的左右两侧，∴在A，B，C，D这四个点中满足以上条件的是A．故选A．2．2020年4月20日，天舟一号货运飞船在我国文昌航天发射场发射成功，进入距离地球393000米的预定轨道，将393000用科学记数法表示应为（）A．0.393×107B．3.93×105C．3.93×106D．393×103【考点】1I：科学记数法—表示较大的数．【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．【解答】解：将393000用科学记数法表示应为3.93×105．故选：B．3．某物体的三视图如图，那么该物体形状可能是（）A．长方体B．圆锥 C．正方体D．圆柱【考点】U3：由三视图判断几何体．【分析】根据正视图和左视图都是矩形，俯视图是圆，可以想象出只有圆柱符合这样的条件，因此物体的形状是圆柱．【解答】解：根据三视图的知识，正视图以及左视图都为矩形，俯视图是一个圆，易判断该几何体是圆柱．故选D．4．《九章算术》是中国古代的数学专著，下面这道题是《九章算术》中第七章的一道题：“今有共买物，人出八，盈三；人出七，不足四，问人数、物价各几何？”译文：“几个人一起去购买某物品，如果每人出8钱，则多了3钱；如果每人出7钱，则少了4钱．问有多少人，物品的价格是多少？”设有x人，物品价格为y钱，可列方程组为（）A．B．C．D．【考点】99：由实际问题抽象出二元一次方程组．【分析】设有x人，物品价值y钱，根据题意相等关系：①8×人数﹣3=物品价值，②7×人数+4=物品价值，据此可列方程组．【解答】解：设有x人，物品价格为y钱，根据题意，可列方程组：，故选：A．5．如图，AB∥CD，直线EF分别交AB，CD于M，N两点，将一个含有45°角的直角三角尺按如图所示的方式摆放，若∠EMB=75°，则∠PNM等于（）A．15° B．25° C．30° D．45°【考点】JA：平行线的性质．【分析】根据平行线的性质得到∠DNM=∠BME=75°，由等腰直角三角形的性质得到∠PND=45°，即可得到结论．【解答】解：∵AB∥CD，∴∠DNM=∠BME=75°，∵∠PND=45°，∴∠PNM=∠DNM﹣∠DNP=30°，故选：C．6．在平面直角坐标系中，点P（﹣3，2）关于直线y=x对称点的坐标是（）A．（﹣3，﹣2）B．（3，2）C．（2，﹣3）D．（3，﹣2）【考点】P6：坐标与图形变化﹣对称．【分析】作出图形，过点P作y轴的垂线与直线y=x相交，再过交点作x轴的垂线，然后根据线段垂直平分线上的点到两端点的距离相等求解即可．【解答】解：如图所示，点P（﹣3，2）关于直线y=x对称点的坐标是（3，﹣2）．故选D．7．某校合唱团有30名成员，下表是合唱团成员的年龄分布统计表：年龄（单位：岁）13 14 15 16频数（单位：名） 5 15 x 10﹣x对于不同的x，下列关于年龄的统计量不会发生改变的是（）A．平均数、中位数B．平均数、方差C．众数、中位数 D．众数、方差【考点】W7：方差；V7：频数（率）分布表；W2：加权平均数；W4：中位数；W5：众数．【分析】由频数分布表可知后两组的频数和为10，即可得知总人数，结合前两组的频数知出现次数最多的数据及第15、16个数据的平均数，可得答案．【解答】解：由表可知，年龄为15岁与年龄为16岁的频数和为x+10﹣x=10，则总人数为：5+15+10=30，故该组数据的众数为14岁，中位数为： =14岁，即对于不同的x，关于年龄的统计量不会发生改变的是众数和中位数；故选C．8．某商店在节日期间开展优惠促销活动：购买原价超过200元的商品，超过200元的部分可以享受打折优惠．若购买商品的实际付款金额y（单位：元）与商品原价x（单位：元）的函数关系的图象如图所示，则超过200元的部分可以享受的优惠是（）A．打八折B．打七折C．打六折D．打五折【考点】FH：一次函数的应用．【分析】设超过200元的部分可以享受的优惠是打n折，根据：实际付款金额=200+（商品原价﹣200）×，列出y关于x的函数关系式，由图象将x=500、y=410代入求解可得．【解答】解：设超过200元的部分可以享受的优惠是打n折，根据题意，得：y=200+（x﹣200）•，由图象可知，当x=500时，y=410，即：410=200+×，解得：n=7，∴超过200元的部分可以享受的优惠是打7折，故选：B．9．如图，已知AB、CD、EF都与BD垂直，垂足分别是B、D、F，且AB=1，CD=3，那么EF的长是（）A．B．C．D．【考点】S9：相似三角形的判定与性质．【分析】易证△DEF∽△DAB，△BEF∽△BCD，根据相似三角形的性质可得=， =，从而可得+=+=1．然后把AB=1，CD=3代入即可求出EF的值．【解答】解：∵AB、CD、EF都与BD垂直，∴AB∥CD∥EF，∴△DEF∽△DAB，△BEF∽△BCD，∴=， =，∴+=+==1．∵AB=1，CD=3，∴+=1，∴EF=．故选C．10．如图所示，将若干个点摆成三角形图案，每条边（包括两个端点）有n（n是正整数且n＞1）个点，相应的图案中总的点数记为a n ，则++…+=（）A．B．C．D．【考点】38：规律型：图形的变化类．【分析】根据图象规律得出通项公式a n=3n﹣3，根据数列{}的特点即可用列项法求其前n项和的公式，而++…+是前2020项的和，代入前n项和公式即可得答案．【解答】解：每个边上有n个点，把每个边上的点数相加得3n，这样角上的点数被重复计算了一次，故第n个图形的点数为3n﹣3，即a n=3n﹣3，令S n=++…+=++…+=，∴++…+=++…+=1﹣+﹣+…+﹣=，故选：B．二、细心填一填，试试自己的身手（本大题共6小题，每小题3分，共18分.请将结果直接填写在答题卡相应的位置上）11．方程x2﹣2=0的根是±．【考点】A5：解一元二次方程﹣直接开平方法．【分析】这个式子先移项，变成x2=2，从而把问题转化为求2的平方根，直接得出答案即可．【解答】解：移项得x2=2，∴x=±．故答案为：±．12．某坡面的坡度是：1，则坡角α是60 度．【考点】T9：解直角三角形的应用﹣坡度坡角问题．【分析】坡面的坡度就是坡角的正切值，已知角的正切值，即可求得角度．【解答】解：设坡角是α，则t anα=：1，则α=60°．故答案为：60．13．如图所示，正六边形ABCDEF内接于⊙O，则∠ADF的度数为30°．【考点】MM：正多边形和圆；L3：多边形内角与外角．【分析】连接OF，由多边形是正六边形可求出∠AOF的度数，再根据圆周角定理即可求出∠ADF的度数．【解答】解：连接OF，∵六边形ABCDEF是正六边形，∴∠AOF==60°，∴∠ADF=∠AOF=×60°=30°．故答案为：30°．14．一只不透明的袋子中装有红球和白球共30个，这些球除了颜色外都相同，校课外学习小组做摸球试验，将球搅匀后任意摸出一个球，记下颜色后放回、搅匀，通过多次重复试验，算得摸到红球的频率是20%，则袋中有 6 个红球．【考点】X8：利用频率估计概率．【分析】在同样条件下，大量反复试验时，随机事件发生的频率逐渐稳定在概率附近，可以从比例关系入手，列出方程求解．【解答】解：设袋中有x个红球．由题意可得： =20%，解得：x=6，故答案为：6．15．如图，P是等边三角形ABC内一点，将线段AP绕点A顺时针旋转60°得到线段AQ，连接BQ．若PA=6，PB=8，PC=10，则四边形APBQ的面积为24+9．【考点】R2：旋转的性质；KK：等边三角形的性质．【分析】连结PQ，如图，根据等边三角形的性质得∠BAC=60°，AB=AC，再根据旋转的性质得AP=PQ=6，∠PAQ=60°，则可判断△APQ为等边三角形，所以PQ=AP=6，接着证明△APC≌△ABQ得到PC=QB=10，然后利用勾股定理的逆定理证明△PBQ为直角三角形，再根据三角形面积公式，利用S四边形APBQ=S△BPQ+S△APQ进行计算．【解答】解：连结PQ，如图，∵△ABC为等边三角形，∴∠BAC=60°，AB=AC，∵线段AP绕点A顺时针旋转60°得到线段AQ，∴AP=PQ=6，∠PAQ=60°，∴△APQ为等边三角形，∴PQ=AP=6，∵∠CAP+∠BAP=60°，∠BAP+∠BAQ=60°，∴∠CAP=∠BAQ，在△APC和△ABQ中，，∴△APC≌△ABQ，∴PC=QB=10，在△BPQ中，∵PB2=82=64，PQ2=62，BQ2=102，而64+36=100，∴PB2+PQ2=BQ2，∴△PBQ为直角三角形，∠BPQ=90°，∴S四边形APBQ=S△BPQ+S△APQ=×6×8+×62=24+9．故答案为24+9．16．已知二次函数y=ax2+bx+c的图象如图所示，给出下列结论：①abc＞0；②a﹣b+c＜0；③2a+b﹣c＜0；④4a+2b+c＞0，⑤若点（﹣，y1）和（，y2）在该图象上，则y1＞y2．其中正确的结论是②③④（填入正确结论的序号）【考点】H4：二次函数图象与系数的关系．【分析】由二次函数的开口方向，对称轴x=1，以及二次函数与y的交点在x轴的上方，与x轴的交点的位置等条件来判断各结论的正误即可．【解答】解：∵抛物线开口向下，∴a＜0，∵对称轴在y轴右边，∴b＞0，∵抛物线与y轴的交点在x轴的上方，∴c＞0，∴abc＜0，故①错误；∵二次函数y=ax2+bx+c图象可知，当x=﹣1时，y＜0，∴a﹣b+c＜0，故②正确；∵二次函数图象的对称轴是直线x=1，c＞0，∴﹣=1，∴2a+b=0，∴2a+b＜c，∴2a+b﹣c＜0，故③正确；∵二次函数y=ax2+bx+c图象可知，当x=2时，y＞0，∴4a+2b+c＞0，故④正确；∵二次函数图象的对称轴是直线x=1，∴抛物线上x=﹣时的点与当x=时的点对称，∵x＞1，y随x的增大而减小，∴y1＜y2，故⑤错误；故答案为：②③④．三、用心做一做，显显自己的能力（本大题共8小题，满分72分）17．（1）（﹣2）﹣1﹣|﹣|+（3.14﹣π）0+4cos45°（2）已知x2﹣2x﹣7=0，求（x﹣2）2+（x+3）（x﹣3）的值．【考点】4J：整式的混合运算—化简求值；2C：实数的运算；6E：零指数幂；6F：负整数指数幂；T5：特殊角的三角函数值．【分析】（1）原式利用零指数幂、负整数指数幂法则，绝对值的代数意义，以及特殊角的三角函数值计算即可得到结果；（2）原式利用完全平方公式，平方差公式化简，去括号整理后，将已知等式变形后代入计算即可求出值．【解答】解：（1）原式=﹣﹣2+1+2=；（2）原式=x2﹣4x+4+x2﹣9=2x2﹣4x﹣5=2（x2﹣2x）﹣5，∵x2﹣2x﹣7=0，即x2﹣2x=7，∴原式=14﹣5=9．18．解方程：．【考点】B3：解分式方程．【分析】观察可得最简公分母是（x﹣1）（x+2），方程两边乘最简公分母，可以把分式方程转化为整式方程求解．【解答】解：方程两边都同乘以（x﹣1）（x+2），得x（x+2）﹣（x﹣1）（x+2）=3，化简，得x+2=3，解得：x=1．检验：把x=1代入（x﹣1）（x+2）=0．∴x=1不是原方程的解，原分式方程无解．19．某校为更好地培养学生兴趣，开展“拓展课程走班选课”活动，随机抽查了部分学生，了解他们最喜爱的项目类型（分为书法、围棋、戏剧、国画共4类），并将统计结果绘制成如图不完整的频数分布表及频数分布直方图．最喜爱的传统文化项目类型频数分布表项目类型频数频率书法类18 a围棋类14 0.28喜剧类8 0.16国画类 b 0.20根据以上信息完成下列问题：（1）频数分布表中a= 0.36 ，b= 10 ；（2）补全频数分布直方图；（3）若全校共有学生1500名，估计该校最喜爱围棋的学生大约有多少人？【考点】V8：频数（率）分布直方图；V5：用样本估计总体；V7：频数（率）分布表．【分析】（1）首先根据围棋类是14人，频率是0.28，据此即可求得总人数，然后利用18除以总人数即可求得a的值；用50乘以0.20求出b的值，即可解答；（2）根据b的值，画出直方图即可；（4）用总人数1500乘以喜爱围棋的学生频率即可求解；【解答】解：（1）14÷0.28=50（人），a=18÷50=0.36．b=50×0.20=10，故答案为0.36，10．（2）频数分布直方图，如图所示，（3）1500×0.28=420（人），答：若全校共有学生1500名，估计该校最喜爱围棋的学生大约有420人．20．去学校食堂就餐，经常会在一个买菜窗口前等待，经调查发现，同学的舒适度指数y与等时间x（分）之间满足反比例函数关系，如下表：等待时间x 1 2 5 10 20舒适度指数y 100 50 20 10 5已知学生等待时间不超过30分钟（1）求y与x的函数关系式，并写出自变量x的取值范围．（2）若等待时间8分钟时，求舒适度的值；（3）舒适度指数不低于10时，同学才会感到舒适．请说明，作为食堂的管理员，让每个在窗口买菜的同学最多等待多少时间？【考点】GA：反比例函数的应用．【分析】（1）观察表格发现：1×100=2×50=5×20，从而确定函数关系式y=，y代表舒适度指数，x （分）代表等待时间．（2）是已知x=8，代入函数解析式求得y．（3）是已知y≥10，就可以得到关于x的不等式求的x的范围．【解答】解：（1）观察表格发现：1×100=2×50=5×20=…，∴xy=100，∴y=（0＜x≤30）；（2）当x=8时，舒适度y==12.5；（3）舒适度指数不低于10时，由图象y≥10时，0＜x≤10所以作为食堂的管理员，让每个在窗口买菜的同学最多等待10分钟．21．已知关于x的方程x2﹣（m+2）x+2m﹣1=0．（1）求证：此方程有两个不相等的实数根；（2）若抛物线y=x2﹣（m+2）x+2m﹣1=0与x轴有两个交点都在x轴正半轴上，求m的取值范围；（3）填空：若x2﹣（m+2）x+2m﹣1=0的两根都大于1，则m的取值范围是m＞2 ．【考点】HA：抛物线与x轴的交点；H3：二次函数的性质．【分析】（1）表示出根的判别式，配方后得到根的判别式大于0，进而确定出方程总有两个不相等的实数根；（2）设抛物线y=x2﹣（m+2）x+2m﹣1=0与x轴两个交点的横坐标是x1，x2，根据两个交点都在x轴正半轴上得出x1+x2＞0，x1•x2＞0，利用根与系数的关系列出不等式组，求解即可；（3）设x2﹣（m+2）x+2m﹣1=0的两根是x1，x2，根据两根都大于1得出x1+x2＞2，（x1﹣1）（x2﹣1）＞0，根据根与系数的关系列出不等式组，求解即可．【解答】（1）证明：∵△=[﹣（m+2）]2﹣4（2m﹣1）=m2+4m+4﹣8m+4=m2﹣4m+8=（m﹣2）2+4，∵（m﹣2）2≥0，∴（m﹣2）2+4＞0，∴无论m取何实数时，此方程都有两个不相等的实数根；（2）解：设抛物线y=x2﹣（m+2）x+2m﹣1=0与x轴两个交点的横坐标是x1，x2，则x1+x2=m+2，x1•x2=2m﹣1．根据题意，得，解得m＞．即m的取值范围是m＞；（3）解：设x2﹣（m+2）x+2m﹣1=0的两根是x1，x2，则x1+x2=m+2，x1•x2=2m﹣1．根据题意，得，解得m＞2．故答案为m＞2．22．如图，在平面直角坐标系中，⊙P经过y轴上一点C，与x轴分别相交于A、B两点，连接BP并延长分别交⊙P、y轴于点D、E，连接DC并延长交x轴于点F．若点F的坐标为（﹣1，0），点D的坐标为（1，6）．（1）求证：CD=CF；（2）判断⊙P与y轴的位置关系，并说明理由；（3）求直线BD的解析式．【考点】MR：圆的综合题．【分析】（1）证△COF≌△CHD可得CD=CF；（2）连接PC，先由CD=CF、PD=PB知PC∥BF，结合BF⊥y轴知PC⊥y轴，即可得出结论；（3）连接AD，证BD=BF可得AD=OH=6、OA=DH=1，设BD=x，由BD2=AB2+AD2得x=10，从而知B（9，0），待定系数法求解可得．【解答】解：（1）如图，作DH⊥OE于点H，∴∠DHC=∠FOC=90°，∠DCH=∠FCO，∵D（1，6）、F（﹣1，0），∴DH=OF=1，在△COF和△CHD中，∵，∴△COF≌△CHD（AAS），∴CD=CF；（2）连接PC，∵CD=CF、PD=PB，∴PC为△BDF的中位线，∴PC∥BF，∵BF⊥y轴，∴PC⊥y轴，又PC为⊙P的半径，∴⊙P与y轴相切；（3）如图，连接AD，由（2）知BF=2PC，∵BD=2PC，∴BD=BF，∵BD是⊙P的直径，∴∠DAB=90°，∴AD=OH=6，OA=DH=1，设BD=x，则AB=x﹣2，由BD2=AB2+AD2得x2=（x﹣2）2+62，解得：x=10，∴OB=OA+AB=1+8=9，即B（9，0），设直线BD的解析式为y=kx+b，把B（9，0）、D（1，6）代入得，解得：，∴直线BD的解析式为y=﹣x+．23．在△ABC中，AB=AC，∠BAC=90°，点D在射线BC上（与B、C两点不重合），以AD为边作正方形ADEF，使点E与点B在直线AD的异侧，射线BA与射线CF相交于点G．（1）若点D在线段BC上，如图1．①依题意补全图1；②判断BC与CG的数量关系与位置关系，并加以证明；（2）若点D在线段BC的延长线上，且G为CF中点，连接GE，AB=，则GE的长为，并简述求GE长的思路．【考点】LO：四边形综合题．【分析】（1）①依题意补全图形，如图1所示，②判断出△BAD≌△CAF即可；（2）先判断出△BAD≌△CAF，得到BD=CF，BG⊥CF，得到直角三角形，利用勾股定理计算即可．【解答】（1）证明：①依题意补全图形，如图1所示，②BC⊥CG，BC=CG；∵∠BAC=90°，AB=AC，∴∠ABC=∠ACB=45°，∵四边形ADEF是正方形，∴AD=AF，∠DAF=90°，∵∠BAC=∠BAD+∠DAC=90°，∠DAF=∠CAF+∠DAC=90°，∴∠BAD=∠CAF，在△BAD和△CAF中，∴△BAD≌△CAF（SAS），∴∠ACF=∠ABD=45°，∴∠ACF+∠ACB=90°，∴BC⊥CG；∵点G是BA延长线上的点，BC=CG（2）如图2，∵∠BAC=90°，AB=AC，∴∠ABC=∠ACB=45°，∵四边形ADEF是正方形，∴AD=AF，∠DAF=90°，∵∠BAC=∠BAD﹣∠DAC=90°，∠DAF=∠CAF﹣∠DAC=90°，∴∠BAD=∠CAF，在△BAD和△CAF中，∴△BAD≌△CAF（SAS），∴∠ACF=∠ABD=45°，BD=CF，∴∠ACF+∠ACB=90°，∴BC⊥CF；∵AB=，BC=CD=CG=GF=2，∴在Rt△AGH中，根据勾股定理得，AG=，∴在Rt△AGH中，根据勾股定理的，DG=2，∵AD=，∴AH=，HG=，∴GI=AD﹣HG=，∴GE==故答案为．24．如图，直线l：y=x﹣与x轴正半轴、y轴负半轴分别相交于A、C两点，抛物线y=x2+bx+c经过点B（﹣1，0）和点C．（1）填空：直接写出抛物线的解析式：y=x2﹣x﹣；（2）已知点Q是抛物线y=x2+bx+c在第四象限内的一个动点．①如图，连接AQ、CQ，设点Q的横坐标为t，△AQC的面积为S，求S与t的函数关系式，并求出S的最大值；②连接BQ交AC于点D，连接BC，以BD为直径作⊙I，分别交BC、AB于点E、F，连接EF，求线段EF的最小值，并直接写出此时Q点的坐标．【考点】HF：二次函数综合题．【分析】解：（1）先利用一次函数解析式确定A（，0），C（0，﹣），然后把A点和C点坐标代入y=x2+bx+c得b、c的方程组，再解方程组求出b、c即可得到抛物线解析式为y=x2﹣x﹣；（2）①作QM∥y轴交直线AC于M，如图①，设Q（t， t2﹣t﹣），则M（t，t﹣），则用t 表示MQ得到MQ=﹣t2+t，再利用三角形面积公式和二次函数的性质求解；②连接OE、OF，作OH⊥EF于H，如图②，利用垂径定理得到EH=FH，再利用三角函数的定义求出∠OBC=60°，∠OAC=60°，AC=2OA=2，则△ABC为等边三角形，关键圆周角定理得到∠EIF=2∠EBF=120°，则∠IEH=30°，利用含30度的直角三角形三边的关系得到EH=IE，所以EF=2EH=IE=BD，于是可判定当BD⊥AC 时，即BD为等边△ABC的高时，BD的值最小，EF最小，由于此时BD=AC=，所以线段EF的最小值为，接下来求出直线BQ的解析式为y=﹣x﹣，然后通过解方程组得此时Q点的坐标．【解答】解：（1）当y=0时，x﹣=0，解得x=，则A（，0），当x=0时，y=x﹣=﹣，则C（0，﹣），把B（﹣1，0），C（0，﹣）代入y=x2+bx+c得，解得，所以抛物线解析式为y=x2﹣x﹣；故答案为y=x2﹣x﹣；（2）①作QM∥y轴交直线AC于M，如图①，设Q（t， t2﹣t﹣），则M（t，t﹣），∴MQ=t﹣﹣（t2﹣t﹣）=﹣t2+t，∴S=S△CMQ﹣S△AMQ=•MQ•1=﹣t2+t=﹣（t﹣1）2+，当t=1时，S有最大值；②连接OE、OF，作OH⊥EF于H，如图②，则EH=FH，在Rt△OBC中，∵tan∠OBC==，∴∠OBC=60°，同理可得∠OAC=60°，AC=2OA=2，∴△ABC为等边三角形，∵∠EIF=2∠EBF，∴∠EIF=120°，∴∠IEH=30°，在Rt△IEH中，∵cos∠IEH=，∴EH=IE，∴EF=2EH=IE，而IE=BD∴EF=BD，当BD的值最小时，EF的值最小，而当BD⊥AC时，即BD为等边△ABC的高时，BD的值最小，此时BD=AC=，∴线段EF的最小值为，∵∠QBA=30°，∴直线BQ与y轴的交点为（0，﹣），易得直线BQ的解析式为y=﹣x﹣，解方程组得或，∴此时Q点的坐标为（2，﹣）．2019-2020学年中考数学模拟试卷一、选择题（本大题共12个小题，每小题4分，共48分．在每小题给出的四个选项中，只有一项是符合题目要求的．）1．已知=2{=1xy是二元一次方程组+=8{=1mx nynx my-的解，则2m n-的算术平方根为（）A．±2 B．C．2 D．42．一个六边形的六个内角都是120°（如图），连续四条边的长依次为1，3，3，2，则这个六边形的周长是（）A．13 B．14 C．15 D．163．-2的倒数是（）A．-2 B．12-C．12D．24．在一次酒会上，每两人都只碰一次杯，如果一共碰杯55次，则参加酒会的人数为（）A．9人B．10人C．11人D．12人5．如图，将△ABC沿BC边上的中线AD平移到△A'B'C'的位置，已知△ABC的面积为9，阴影部分三角形的面积为1．若AA'=1，则A'D等于（）A．2 B．3 C．23D．326．如图，△OAB∽△OCD，OA：OC＝3：2，∠A＝α，∠C＝β，△OAB与△OCD的面积分别是S1和S2，△OAB与△OCD的周长分别是C1和C2，则下列等式一定成立的是()A．32OBCD=B．32αβ=C．1232SS=D．1232CC=7．世界上最小的开花结果植物是澳大利亚的出水浮萍，这种植物的果实像一个微小的无花果，质量只有0.0000000076克，将数0.0000000076用科学记数法表示为（）A．7.6×10﹣9B．7.6×10﹣8C．7.6×109D．7.6×1088．二次函数2y ax bx c=++的图象如图所示，则一次函数24y bx b ac=+-与反比例函数a b cyx++=在同一坐标系内的图象大致为( )A．B．C．D．9．如图，AC是⊙O的直径，弦BD⊥AO于E，连接BC，过点O作OF⊥BC于F，若BD=8cm，AE=2cm，则OF的长度是（）A．3cm B．6cm C．2.5cm D．5cm10．如图，已知在△ABC，AB＝AC．若以点B为圆心，BC长为半径画弧，交腰AC于点E，则下列结论一定正确的是（）A．AE＝EC B．AE＝BE C．∠EBC＝∠BAC D．∠EBC＝∠ABE11．把边长相等的正六边形ABCDEF和正五边形GHCDL的CD边重合，按照如图所示的方式叠放在一起，延长LG交AF于点P，则∠APG＝（）A．141°B．144°C．147°D．150°12．甲、乙两人同时分别从A，B两地沿同一条公路骑自行车到C地．已知A，C两地间的距离为110千米，B，C两地间的距离为100千米．甲骑自行车的平均速度比乙快2千米/时．结果两人同时到达C地．求两人的平均速度，为解决此问题，设乙骑自行车的平均速度为x千米/时．由题意列出方程．其中正确的是（）A．1101002x x=+B．1101002x x=+C．1101002x x=-D．1101002x x=-二、填空题：（本大题共6个小题，每小题4分，共24分．）13．已知关于x，y的二元一次方程组2321x y kx y+=⎧⎨+=-⎩的解互为相反数，则k的值是_________．14．如图：图象①②③均是以P0为圆心，1个单位长度为半径的扇形，将图形①②③分别沿东北，正南，西北方向同时平移，每次移动一个单位长度，第一次移动后图形①②③的圆心依次为P1P2P3，第二次移动后图形①②③的圆心依次为P4P5P6…，依此规律，P0P2018=_____个单位长度．15．如图，在△PAB中，PA＝PB，M、N、K分别是PA，PB，AB上的点，且AM＝BK，BN＝AK．若∠MKN ＝40°，则∠P的度数为___16．如图，△ABC中，AD是中线，AE是角平分线，CF⊥AE于F，AB=10，AC=6，则DF的长为__．17．若方程x2﹣2x﹣1＝0的两根分别为x1，x2，则x1+x2﹣x1x2的值为_____．18．将直角边长为5cm的等腰直角△ABC绕点A逆时针旋转15°后，得到△AB′C′，则图中阴影部分的面积是_____cm1．三、解答题：（本大题共9个小题，共78分，解答应写出文字说明、证明过程或演算步骤．19．（6分）列方程解应用题八年级学生去距学校10 km的博物馆参观，一部分学生骑自行车先走，过了20 min后，其余学生乘汽车出发，结果他们同时到达.已知汽车的速度是骑车学生速度的2倍，求骑车学生的速度.20．（6分）某工厂计划在规定时间内生产24000个零件，若每天比原计划多生产30个零件，则在规定时间内可以多生产300个零件．求原计划每天生产的零件个数和规定的天数．为了提前完成生产任务，工厂在安排原有工人按原计划正常生产的同时，引进5组机器人生产流水线共同参与零件生产，已知每组机器人生产流水线每天生产零件的个数比20个工人原计划每天生产的零件总数还多20%，按此测算，恰好提前两天完成24000个零件的生产任务，求原计划安排的工人人数．21．（6分）已知，如图，直线MN交⊙O于A，B两点，AC是直径，AD平分∠CAM交⊙O于D，过D作DE⊥MN于E．求证：DE是⊙O的切线；若DE=6cm，AE=3cm，求⊙O的半径．22．（8分）如图所示，AB是⊙O的一条弦，OD⊥AB，垂足为C，交⊙O于点D，点E在⊙O上．若∠AOD=52°，。
2023年湖北省孝感市云梦县中考数学模拟试卷(含答案解析)
2023年湖北省孝感市云梦县中考数学模拟试卷学校:___________姓名：___________班级：___________考号：___________一、单选题1．给出下列结论：①一个有理数的3倍大于这个有理数；②绝对值最小的整数是0；③规定了原点和单位长度的直线叫数轴；④如果a a =，那么0a >；⑤不是正数的数一定是负数．其中正确结论的个数为（）A ．1个B ．2个C ．3个D ．4个2．截至北京时间5月14日6时30分，全球累计确诊新冠肺炎病例超过435万例．用科学记数法表示435万是（）．A ．54.3510⨯B ．543.510⨯C ．70.43510⨯D ．64.3510⨯3．下列几何体中，主视图是圆的是（）A ．球B ．正方体C ．三棱锥D ．圆柱4．下列运算正确的是（）A ．326a a a ⋅=B ．5510a a a +=C ．()222a b a b +=+D ．()326a a =5．在物理实验课上，小明用弹簧称将铁块A 悬于盛有水的水槽中，然后匀速向上提起，直至铁块完全露出水面一定高度，则下图能反映弹簧称的读数y(单位N)与铁块被提起的高度x(单位cm)之间的函数关系的大致图象是【】A ．B ．C ．D ．6．下列调查中，适宜采用抽样调查的是()A ．对飞机零部件质量的调查B ．对全班45位同学身高的调查C ．对动车站客流量的调查D ．对全运会运动员使用兴奋剂的调查7．如图，BD 是ABC 的角平分线，DE 是BC 的垂直平分线，90,2A AD ∠=︒=，则CD 的长为（）A ．B ．6C ．5D ．48．以下列各组数据为边长，可以构成等腰三角形的是（）A ．1，1，2B ．1，1，3C ．2，2，1D ．2，2，5二、填空题9．观光塔是潍坊市区的标志性建筑.为测量其高度，如图，一人先在附近一楼房的底端Ａ点处观测观光塔顶端C 处的仰角是60°，然后爬到该楼房顶端B 点处观测观光塔底部D 处的俯角是30°，已知楼房高AB 约是45m ，根据以上观测数据可求观光塔的高CD 是______m.10．在函数12xy x=+中，自变量x 的取值范围是______．11．已知，正多边形的每个内角为150︒，则这个多边形的对角线共有______条．12．对于实数a ，b ，定义运算“*”：a*b=2()()a ab a b b a a b a⎧-≥⎪⎨-<⎪⎩例如3*1，因为3＞1，所以3*1=32﹣3×1=6．若x1，x2是一元二次方程x2﹣4=0的两个根，则x1*x2=_____．13．如图，有四张扑克牌，分别是红桃4，黑桃2，方块8，梅花6，它们的背面都相同，现将它们背面朝上洗匀后，从中任意摸出一张，记下牌面数字后放回，再将它们背面朝上洗匀，从中再任意摸出一张，记下牌面数字，则两次牌面数字都是4的倍数的概率是______．14．如图，在扇形CBA 中，∠ACB ＝90°，连接AB ，以BC 为直径作半圆，交AB 于点D ．若阴影部分的面积为（π﹣1），则阴影部分的周长为________．15．如图，在平面直角坐标系中，一颗棋子从点P 处开始跳动，第一次跳到点P 关于x 轴的对称点1P 处，接着跳到点1P 关于y 轴的对称点2P 处，第三次再跳到点2P 关于原点的对称点处，⋯，如此循环下去．当跳动第2009次时，棋子落点处的坐标是___________．16．如图，ABC 中，()60ABC AB AC ∠=︒<，D 为边AC 上的点，45ADB ∠=︒，AC =BD =AB 长是______．三、解答题17．计算：()()220.25-+-；(2)()()()2231x x x ----．18．为拓展学生视野，促进书本知识与生活实践的深度融合，某中学组织八年级全体学生开展研学活动．在此次活动中，若每名老师带队14名学生，则还剩10名学生没老师带；若每名老师带队15名学生，就有1名老师少带6名学生，现有甲、乙两种大型客车，它们的载客量和租金如表所示：客车类型甲型客车乙型客车载客量/（人/辆）3530租金/（元/辆）400320学校计划此次研学活动的租金总费用不超过3000元，且保证所有师生都有车坐，(1)参加此次研学活动的老师和学生各有多少人？(2)学校打算租甲型客车和乙型客车两种客车总共8辆车，学校共有几种租车方案？最少租车费用是多少？19．2022年5月，某市准备面向全市中学生举办“建设绿色生态家园”主题知识竞赛．为此，某校为筛选参赛选手，举办了“建设绿色生态家园”主题知识答题活动，并将随机抽取的部分学生的成绩划分为A ，B ，C ，D 四个等级，绘制了不完整的两种统计图：根据以上信息，回答下列问题：(1)计算成绩为B 等级的学生数，并把条形图补充完整；(2)求扇形统计图中m 的值；(3)求出扇形统计图中C 部分的圆心角的度数．20．如图，在锐角ABC 中，AC 是最短边；以AC 中点O 为圆心，12AC 长为半径作O ，交BC 于E ，过O 作∥OD BC 交O 于D ，连接AE 、AD 、DC ．(1)求证：D 是»AE 的中点；(2)求证：DAO B BAD ∠=∠+∠．21．某衬衣店将进价为30元的一种衬衣以40元售出，平均每月能售出600件，调查表明：这种衬衣售价每上涨1元，其销售量将减少10件．（1）写出月销售利润y （单位：元）与售价x （单位：元/件）之间的函数解析式．（2）当销售价定为45元时，计算月销售量和销售利润．（3）当销售价定为多少元时会获得最大利润？求出最大利润．22．如图在平面直角坐标系中，已知()0A a ，，()0B b ，，()1.52M --，，其中a 、b 满足()2130a b ++-=．(1)求ABM 的面积；(2)在x 轴上求一点P ，使得 AMP 的面积与ABM 的面积相等；(3)在y 轴上存在使BMP 的面积与ABM 的面积相等的P 点，请直接写出点P 的坐标．23．如图，抛物线22y ax bx =++经过点()()1040，，，A B -，与y 轴交于点C ．(1)求抛物线的解析式；(2)点D 为y 轴右侧抛物线上一点，是否存在点D ，使23ABC ABD S S =△△若存在，求出点D 的坐标；若不存在，请说明理由；(3)将直线BC 绕点B 顺时针旋转45°，与直线AC 交于点F ，直接写出BF 的长．参考答案：1．A【分析】根据数轴和绝对值的性质即可求解．【详解】解：①若一个有理数为负数，则这个有理数的3倍小于这个有理数，故①不正确；②绝对值最小的整数是0，故②正确；③规定了原点、正方向和单位长度的直线叫数轴，故③不正确；④如果a a =，那么0a ≥，故④不正确；⑤不是正数的数是负数或0，故⑤不正确；综上所述，正确的个数为1个，故选：A ．【点睛】本题考查了数轴的性质，用几何方法借助数轴来求解，非常直观，且不容易遗漏，体现了数形结合的优点．2．D【分析】科学记数法的表示形式为a×10n 的形式，其中1≤|a|＜10，n 为整数．确定n 的值时，要看把原数变成a 时，小数点移动了多少位，n 的绝对值与小数点移动的位数相同．当原数绝对值≥10时，n 是正数；当原数的绝对值＜1时，n 是负数．【详解】解：435万64350000 4.3510==⨯．故选D ．【点睛】此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n 的形式，其中1≤|a|＜10，n 为整数，表示时关键要正确确定a 的值以及n 的值．3．A【分析】根据主视图是从正面看，分别进行判断即可．【详解】解：A 、球的主视图是圆，故本选项符合题意；B 、正方体主视图是正方形，不是圆，故本选项不符合题意；C 、三棱锥的主视图不是圆，故本选项不符合题意；D 、圆柱的主视图是长方形，不是圆，故本选项不符合题意；故选：A ．【点睛】本题考查了几何体的三视图，解题关键是明确主视图、俯视图、左视图分别是从物体的正面、上面、左面看所得到的图形．4．D【分析】根据同底数幂的乘法法则，合并同类项法则，完全平方公式以及幂的乘方运算法则逐一判断即可．【详解】解：A 、3256a a a a ⋅=≠，故本选项不合题意；B 、555102a a a a +=≠，故本选项不合题意；C 、()222222a b a ab b a b +=++≠+，故本选项不合题意；D 、()326a a =，故本选项符合题意．故选：D ．【点睛】本题主要考查了同底数幂的乘法，合并同类项、完全平方公式以及幂的乘方，熟记相关公式和运算法则是解答本题的关键．5．C【详解】根据浮力的知识，铁块露出水面前读数y 不变，出水面后y 逐渐增大，离开水面后y 不变．因为小明用弹簧称将铁块A 悬于盛有水的水槽中，然后匀速向上提起，直至铁块完全露出水面一定高度．故选C ．6．C【分析】逐一对选项进行分析即可.【详解】A 选项中，对飞机零部件质量的调查,应该用普查，故该选项错误；B 选项中，对全班45位同学身高的调查，应该用普查，故该选项错误；C 选项中，对动车站客流量的调查，应该用抽样调查，故该选项正确；D 选项中，对全运会运动员使用兴奋剂的调查应该用普查，故该选项错误.故选C【点睛】本题主要考查了抽样调查和普查，掌握抽样调查和普查的区别是解题的关键.7．D【分析】根据线段垂直平分线的性质得到DB=DC ，根据角平分线的定义、三角形内角和定理求出∠C=∠DBC=∠ABD=30°，根据直角三角形的性质解答．【详解】∵ED 是BC 的垂直平分线，∴DB=DC ，∴∠C=∠DBC ，∵BD 是△ABC 的角平分线，∴∠ABD=∠DBC ，∵∠A=90°，∴∠C+∠ABC=90°，即∠C+∠ABD+∠DBC=90°，∴∠C=∠DBC=∠ABD=30°，∵DA ⊥BA ，DE ⊥BC ，∴DE=AD=2，∴CD=2ED=2AD=4，故选：D ．【点睛】本题考查的是线段垂直平分线的性质、直角三角形的性质，掌握线段垂直平分线上的点到线段两端点的距离相等是解题的关键．8．C【分析】利用等腰三角形有两条边相等以及三角形三边关系解决此题.【详解】解：1＋1＝2，不能构成三角形，A 项错误；1＋1＜3，不能构成三角形，B 项错误；2＋2＞1,2－2＜1，且有两条相等的边，能构成等腰三角形，C 项正确；2＋2＜5，不能构成三角形，D 项错误.故选C.【点睛】本题主要考查三角形三边关系以及等腰三角形的性质，熟练掌握这些基础知识点是解题的关键.9．135【详解】试题分析：根据题意可得：∠BDA=30°,∠DAC =60°,在Rt △ABD 中，因为AB=45m ，所以AD=m ，所以在Rt △ACD 中，CD=．考点：解直角三角形的应用．10．12x ≠-【分析】根据分式成立的条件求解即可．【详解】解：由题意可知：120x +≠，解得12x ≠-．故答案为：12x ≠-．【点睛】本题考查了求自变量的取值范围，分式成立的条件，掌握分母不能为零是解题关键．11．54【分析】先求出多边形每一个外角的度数，然后即可求出边数，再利用公式()132n n -代入数据计算即可．【详解】解：∵多边形的每个内角都等于150︒，∴多边形的每个外角都等于18015030︒-︒=︒，∴边数3603012n =︒÷︒=，∴对角线条数为()112123542⨯⨯-=．故答案是：54．【点睛】本题主要考查了多边形的外角与对角线的性质，求出边数是解题的关键，另外熟记从多边形的对角线的条数公式也很重要．12．8或﹣2【分析】先解方程，可求得方程的两根，再分两种情况分别代入所给中的运算计算即可．【详解】解方程x 2-4=0可得x=2或x=-2，当x 1=2，x 2=-2时，则x 1*x 2=22-2×（-2）=8，当x 1=-2，x 2=2时，则x 1*x 2=2--2-2（）=-2，故答案为8或-2．【点睛】本题为新定义题目，考查了实数的运算；根与系数的关系，正确理解题目中所给运算是解题的关键，注意分情况讨论．13．14##0.25【分析】先列表得出所有等可能结果，再从中找到符合条件的结果数，继而利用概率公式求解即可得出答案．【详解】解：列表如下24682()22，()42，()62，()82，4()24，()44，()64，()84，6()26，()46，()66，()86，8()28，()48，()68，()88，由表可知共有16种等可能结果，其中两次牌面数字都是4的倍数的有4种结果，∴两次牌面数字都是4的倍数的概率为41164=，故答案为：14．【点睛】本题考查了列表法与树状图法：通过列表法或树状图法展示所有等可能的结果求出n ，再从中选出符合事件A 或B 的结果数目m ，然后根据概率公式求出事件A 或B 的概率．14．22π+【分析】根据BC 为直径可知∠CDB ＝90°，在等腰直角三角形ABC 中，CD 垂直平分AB ，CD ＝DB ，D 为半圆的中点，设AC ＝BC ＝m ，则AB =，CD AD BD ＝＝，阴影部分的面积可以看作是扇形ACB 的面积与△ADC 的面积之差，据此求得直角三角形的边长，进而求得 AB 和 CD的长，进一步求得阴影部分的周长．【详解】解：设BC 的中点为O ，连接OD ，CD ，∵以BC 为直径作半圆，交AB 于点D ．∴CD ⊥AB ，∵AC ＝BC ，∠ACB ＝90°，∴AD ＝BD ，CD ＝12AB ，∴CD ＝BD ，∴ CDDB =，∵AD ＝BD ，CO ＝BO ，∴OD AC ∥，∴∠BOD ＝90°，设AC ＝BC ＝m ，则AB ，CD ＝AD ＝BD ＝2m ，∵阴影部分的面积为（π﹣1），∴22111422ADC ACB S S S m m ππ⎛⎫⋅⨯ ⎪ ⎪⎝⎭=阴影部分扇形﹣＝-＝﹣V ．∴2211144m m ππ﹣＝﹣，∴14m 2＝1，∴m ＝2，∴AC ＝BC ＝2，AB ＝OC ＝OB ＝1，∴ AB 的长为：902=180ππ⨯， BD 的长为：9011=1802ππ⨯，∴阴影部分的周长为：122222πππ+⨯++＝，故答案为：22π++．【点睛】本题考查了扇形的面积和弧长的计算，等腰直角三角形的性质，正确的作出辅助线是解题的关键．15．()32-，【分析】根据关于坐标轴以及原点对称的点的坐标的关系，以及循环的规律就可以得到棋子落点处的坐标．【详解】解：首先发现点P 的坐标是()32-，，第一次跳到点P 关于x 轴的对称点1P 处是()32--，，接着跳到点1P 关于y 轴的对称点2P 处是()32-，，第三次再跳到点2P 关于原点的对称点处是()32-，…，发现3次一循环．又200936692÷= ，当跳动第2009次时，棋子落点处的坐标是()32-，．故答案为：()32-，．【点睛】此类题应首先找到循环的规律，然后进行计算．熟悉：两个点若关于x 轴对称，则横坐标不变，纵坐标互为相反数；两个点若关于y 轴对称，则横坐标互为相反数，纵坐标不变；两个点若关于原点对称，则横坐标、纵坐标都是互为相反数．16【分析】如图，过点A 作AF BC ⊥于F ，过点B 作BE AC ⊥于E ．证明BDE △是等腰直角三角形，求出3BE =，设2AB x =，则BF x =．AF =，推出7BC x=，在Rt AFC △，利用勾股定理，构建方程求出x ，即可解决问题．【详解】解：如图，过点A 作AF BC ⊥于F ，过点B 作BE AC ⊥于E ．∴90BED AFB AFC ∠︒=∠=∠=，∵45ADB ∠=︒，∴BDE △是等腰直角三角形，∴32BE BD ==，∵11177322232ABC S AC BE BC AF =⋅⋅=⋅⋅=⨯⨯=△，设2AB x =，则BF x =，AF =，∴7BC x =，7CF x x=-，在Rt AFC △中，222AF CF AC +=，∴)22273x x ⎛⎫⎛⎫+-= ⎪ ⎪ ⎪⎝⎭⎝⎭，整理得，4212911470x x -+=，解得x =（负根已经舍弃），∴23x =∵AB AC <，∴AB =【点睛】本题考查等腰直角三角形的判定和性质，勾股定理以及解一元二次方程等知识，解题的关键是学会利用参数，构建方程解决问题，属于中考填空题中的压轴题．17．(1)0(2)1【分析】（1）分别根据算术平方根、乘方和零指数幂进行化简，再计算实数的加减即可；（2）先根据完全平方公式和多项式乘以多项式，再计算整式的加减即可．【详解】（1）原式341=-+0=；（2）原式()224443x x x x =-+--+224443x x x x =-+-+-1=．【点睛】本题考查了实数的混合运算，整式的混合运算，涉及求一个数的算术平方根，零指数幂，完全平方公式，多项式乘以多项式，熟练掌握各个运算法则是解题的关键．18．(1)参加此次研学活动的老师有16人，学生有234人．(2)学校共有4种租车方案，最少租车费用是2720元．【分析】（1）设参加此次研学活动的老师有x 人，学生有y 人，根据“若每名老师带队14名学生，则还剩10名学生没老师带；若每名老师带队15名学生，就有1名老师少带6名学生”列出二元一次方程组，求解即可；（2）设租甲型客车m 辆，则租乙型客车(8)m -辆，根据“学校打算租甲型客车和乙型客车两种客车总共8辆车，学校计划此次研学活动的租金总费用不超过3000元”列出一元一次不等式组，求出m 的范围，结合实际可得租车方案数，设租车总费用为w 元，即可得到w 与m 的函数关系式，再利用一次函数的性质即可得到答案．【详解】（1）设参加此次研学活动的老师有x 人，学生有y 人，由题意得1410156x y x y+=⎧⎨-=⎩解得16234x y =⎧⎨=⎩所以，参加此次研学活动的老师有16人，学生有234人．（2）设租甲型客车m 辆，则租乙型客车(8)m -辆，由题意得3530(8)23416400320(8)3000m m m m +-≥+⎧⎨+-≤⎩解得1252m ≤≤m 为正整数2,3,4,5m ∴=∴共有4种租车方案设租车总费用为w 元，由题意得400320(8)802560w m m m =+-=+w ∴的值随m 的增大而增大∴当2m =时，w 的值最小，最小为80225602720⨯+=元所以，学校共有4种租车方案，最少租车费用是2720元．【点睛】本题考查了二元一次方程组的应用，一元一次不等式组的应用以及一次函数的应用，正确理解题意，找准数量关系是解题的关键．19．(1)8人，条形图见解析(2)10(3)144︒【分析】（1）利用成绩为D 等级人数及所占百分数求出抽取的学生总数，再乘以成绩为B 等级人数所占的百分数即可求出成绩为B 等级的学生数；（2）用成绩为A 等级的人数除以抽取的学生总数，再乘以100即可求出m 的值；（3）用成绩为C 等级的人数除以抽取的学生总数，再乘以360度即为C 部分的圆心角的度数．【详解】（1）解：由题意知，成绩为D 等级的人数为12，所占百分比为30%，∴抽取的学生总数为：1230%40÷=（人），∴成绩为B 等级的学生数为：4020%8⨯=（人），补全后的条形图如下所示：（2）解：由题意知，成绩为A 等级的人数为4，抽取的学生总数为40，∴44010010m =复=．（3）解：由题意知，成绩为C 等级的人数为16，抽取的学生总数为40，∴C 部分的圆心角的度数1640360144=复�．【点睛】本题考查条形统计图与扇形统计图，解题的关键是将条形统计图与扇形统计图中表示的信息进行关联．20．(1)见解析(2)见解析【分析】（1）根据同弧或等弧所对的圆周角相等，可以证明该结论；（2）根据∥OD BC ，OD OA =，可以得到角的关系，然后通过转化就可以证明结论．【详解】（1）证明：∵由已知可得，∥OD BC ，OD OC =，∴ODC DCE ∠=∠，ODC OCD ∠=∠，∴OCD DCE ∠=∠，∴ AD DE=，即D 是»AE 的中点；（2）证明：延长AD 与BC 交于点G ，如图所示，∵∥OD BC ，OD OA =，∴ADO AGE ∠=∠，ADO DAO ∠=∠，∴AGE DAO ∠=∠，∵AGE B BAD ∠=∠+∠，∴DAO B BAD ∠=∠+∠．【点睛】本题考查圆周角定理，圆心角、弧、弦的关系、平行线的性质，三角形的外角与内角的关系，解题的关键是明确题意，找出所求结论需要的条件．21．（1）y=﹣10x2+1300x ﹣30000；（2）550件，8250元；（3）当x=65元，最大利润为12250元．【详解】试题分析：（1）根据每售价为x 元，由这种衬衣的售价每上涨1元，其销售量就减少10个，列出函数关系式即可；（2）销售价为45元，即上涨了5元，所以，代入即可得月销售量和销售利润；（3）用配方法求出二次函数的最大值即可．试题解析：（1）由题意可得：y=（x ﹣30）[600﹣10（x ﹣40）]=﹣10x 2+1300x ﹣30000；（2）当x=45时，600﹣10（x ﹣40）=550（件），y=﹣10×452+1300×45﹣30000=8250（元）；（3）y=﹣10x 2+1300x ﹣30000=﹣10（x ﹣65）2+12250，故当x=65（元），最大利润为12250元．【点睛】本题主要考查了二次函数的应用以及配方法求二次函数最值，得出y 与x 的函数关系是解题关键．22．(1)4ABM S = ；(2)()50P -，；(3)点P 的坐标为409⎛⎫ ⎪⎝⎭，或2809⎛⎫- ⎪⎝⎭，．【分析】（1）先根据非负性的性质求出a 、b 的值，再根据三角形面积公式求解即可；（2）设点()0P p ，，根据三角形面积公式进行求解即可得到答案；（3）设BM 交y 轴于点D ，设(0)P q ，，()0D d ，，先利用面积法求出43d =-．则403D ⎛⎫- ⎪⎝⎭，，再根据ABM BMP S S = ，得到()14||3 1.5423q ⎛⎫⎡⎤⨯--⨯--= ⎪⎣⎦⎝⎭，由此即可得到答案．【详解】（1）解：∵()2130a b ++-=，且|1|0a +≥，()230b -≥，∴10a +=，30b -=，∴1a =-，3b =，∴()10A -，，()30B ，，∴1142422ABM M S AB y =⋅=⨯⨯=△；（2）解：设点()0P p ，．由题意得11242AM P S p =⨯--⨯=△，∴3p =或5p =-．当3p =时， AMP 与ABM 重合，不合题意，舍去，∴点()50P -，；（3）解：如图②，设BM 交y 轴于点D ，设(0)P q ，，()0D d ，．∵()()1111()323 1.5()32222BOM B M C S OD x x OB y d ⎡⎤=⋅-=⋅-=⨯⨯=⨯--⨯-=⎣⎦△，∴43d =-．∴403D ⎛⎫- ⎪⎝⎭，．∵ABM BMP S S = ，∴1()42B M PD x x ⋅-=，∴()14||3 1.5423q ⎛⎫⎡⎤⨯--⨯--= ⎪⎣⎦⎝⎭，解得49q =或289-．∴点P 的坐标为409⎛⎫ ⎪⎝⎭，或2809⎛⎫- ⎪⎝⎭，．【点睛】本题主要考查了坐标与图形，三角形面积，绝对值方程，非负数的性质，解题的关在于能够熟练掌握非负数的性质，求出a 、b 的值．23．(1)213222y x x =-++(2)存在，点D 的坐标为：（1，3）或（2，3）或（5，-3）(3)【分析】（1）用待定系数法解答；（2）设D （x ，y ），根据题意及利用三角形面积列出方程，求出y 的值后代入抛物线的解析式即可解答（3）由勾股定理解得AC 的长，再根据勾股定理逆定理证明ABC 为直角三角形，设直线AC 与直线BE 交于点F ，过点F 作FM ⊥x 轴于点M ，由平行线分线段成比例解得FM 的长，求得点F 的坐标，最后根据两点间的距离公式解答．【详解】（1）解：把点()()1040，，，A B -代入抛物线22y ax bx =++得2016420a b a b -+=⎧⎨++=⎩1232a b ⎧=-⎪⎪∴⎨⎪=⎪⎩∴213222y x x =-++（2）由题意可知(0,2),(1,0),(4,0)C A B -5,2AB OC ∴==1152522ABC S AB OC ∴=⋅=⨯⨯= 23ABC ABD S S =△△315522ABD S ∴=⨯= 设D （x ，y ），11155222AB y y ∴⋅=⨯=3y ∴=当y =3时，由2132322x x -++=解得：1x =或2x =此时点D 的坐标为（1，3）或（2，3）；当y =-3时，由2132322x x -++=-解得：5x =或2x =-（舍去）此时点D 的坐标为（5，-3）；综上所述，点D 的坐标为：（1，3）或（2，3）或（5，-3）；（3）1,2,4,5AO OC OB AB ====2AC BC ∴==222AC BC AB ∴+=ABC ∴ 为直角三角形，即BC AC ⊥如图，设直线AC 与直线BE 交于点F ，过点F 作FM ⊥x 轴于点M ，由题意得，45FBC ∠=︒CF BC ∴==OC FMAO AC OM CF∴=1OM =2OC AC OM FM AF∴==2FM ∴=6FM ∴=答案第15页，共15页(2,6),(4,0)F B∴BF ∴==．【点睛】本题考查二次函数的图象上点的特征、待定系数法求二次函数解析式、勾股定理、平行线分线段成比例、两点间的距离公式等，关键是利用面积关系求出点D 的坐标．。
湖北省孝感市中考数学五模试卷
湖北省孝感市中考数学五模试卷姓名:________ 班级:________ 成绩:________一、选择题 (共10题；共20分)1. （2分）－2的相反数是（）A .B . －C . 2D . －22. （2分） (2018七上·鄞州期中) 港珠澳大桥于2018年10月24日正式通车，该工程总投资额为1269亿元，将1269亿用科学记数法表示为（）.A . 12.69×1010B . 1.269×1011C . 1.269×1012D . 0.1269×10133. （2分）(2014·福州) 下列计算正确的是（）A . x4•x4=x16B . （a3）2=a5C . （ab2）3=ab6D . a+2a=3a4. （2分）如图是一块带有圆形空洞和方形空洞的小木板，则下列物体中既可以堵住圆形空洞，又可以堵住方形空洞的是（）A .B .C .D .5. （2分） (2015七下·常州期中) 下列长度的三根木棒首尾相接，能做成三角形框架的是（）A . 13cm、7cm、5cmB . 5cm、7cm、3cmC . 7cm、5cm、12cmD . 5cm、15cm、9cm6. （2分） (2017八下·门头沟期末) 2022年将在北京—张家口举办冬季奥运会，北京将成为世界上第一个既举办夏季奥运会，又举办冬季奥运会的城市．某队要从两名选手中选取一名参加比赛，为此对这两名队员进行了五次测试，测试成绩如图所示：则下列说法中正确的是（）A . > ，应该选取B选手参加比赛；B . < ，应该选取A选手参加比赛；C . ≥ ，应该选取B选手参加比赛；D . ≤ ，应该选取A选手参加比赛.7. （2分）若关于x的一元二次方程（m﹣2）x2﹣2x+1=0有实根，则m的取值范围是（）A . m＜3B . m≤3C . m＜3且m≠2D . m≤3且m≠28. （2分）把抛物线的图象向右平移3个单位，再向下平移2个单位，所得图象的解析式为，则（）．A . 12B . 9C .D . 109. （2分）(2016·资阳) 如图，矩形ABCD与菱形EFGH的对角线均交于点O，且EG∥BC，将矩形折叠，使点C与点O重合，折痕MN恰好过点G若AB= ，EF=2，∠H=120°，则DN的长为（）A .B .C . ﹣D . 2 ﹣10. （2分）(2011·钦州) 函数y=ax﹣2（a≠0）与y=ax2（a≠0）在同一平面直角坐标系中的图象可能是（）A .B .C .D .二、填空题 (共8题；共8分)11. （1分）(2017·襄州模拟) 分解因式：m3﹣4m=________．12. （1分）(2017·罗平模拟) 函数y= 自变量的取值范围是________．13. （1分）(2017·江东模拟) 如图，△ABC是定圆O的内接三角形，AD为△ABC的高线，AE平分∠BAC交⊙O于E，交BC于G，连OE交BC于F，连OA，在下列结论中，①CE=2EF，②△ABG∽△AEC，③∠BAO=∠DAC，④为常量．其中正确的有________．14. （1分） (2015八下·灌阳期中) 已知菱形的两条对角线长分别是4和8，则菱形的面积为________．15. （1分）(2017·平顶山模拟) 如图，点A、B是函数y= 的图象上关于原点对称的任意两点，BC∥x轴，AC∥y轴，△ABC的面积为4，则k=________．16. （1分）(2016·绵阳) 如图，点O是边长为4 的等边△ABC的内心，将△OBC绕点O逆时针旋转30°得到△OB1C1 ， B1C1交BC于点D，B1C1交AC于点E，则DE=________．17. （1分）(2014·遵义) “今有邑，东西七里，南北九里，各开中门，出东门一十五里有木，问：出南门几何步而见木？”这段话摘自《九章算术》，意思是说：如图，矩形城池ABCD，东边城墙AB长9里，南边城墙AD 长7里，东门点E、南门点F分别是AB，AD的中点，EG⊥AB，FH⊥AD，EG=15里，HG经过A点，则FH=________里．18. （1分）如图，在△ABC中，∠B=∠C，∠BAD=34°，且∠ADE=∠AED，则∠CDE=________度．三、解答题 (共8题；共70分)19. （5分） (2018九上·于洪期末) 计算： .20. （5分） (2015八下·深圳期中) 先化简：，并从0，﹣1，2中选一个合适的数作为a的值代入求值．21. （5分） (2017七下·东莞期末) 学校为在汉语听写大赛中获得一、二等奖共30名学生购买奖品，其中一等奖奖品每份80元，二等奖奖品每份60元，共花费了2000元，获一等奖、二等奖的学生分别是多少？22. （10分） (2018九上·梁子湖期末) 已知函数与交于第一象限一点，轴于， .（1）求两个函数解析式；（2）求的面积.24. （10分） (2016九上·龙湾期中) 一个不透明的布袋里装有1个白球，3个红球，它们除颜色外其余都相同.（1）从中任意摸出1个球，记下颜色后放回，搅匀，再任意摸出1个球.求两次都摸出红球的概率（要求画树状图或列表）.（2）若加入若干个除颜色外完全相同的黑球后，从中任意摸出1个球，是红球的概率为，求加入的黑球有多少个？25. （10分）如图，AB与⊙O相切于点C，OA，OB分别交⊙O于点D，E，弧 .（1）求证：OA＝OB；（2）已知AB＝4 ，OA＝4，求阴影部分的面积．26. （15分）(2017·达州模拟) 如图，已知抛物线y= （x+2）（x﹣4）与x轴交于点A、B（点A位于点B的左侧），与y轴交于点C，CD∥x轴交抛物线于点D，M为抛物线的顶点．（1）求点A、B、C的坐标；（2）设动点N（﹣2，n），求使MN+BN的值最小时n的值；（3）P是抛物线上一点，请你探究：是否存在点P，使以P、A、B为顶点的三角形与△ABD相似（△PAB与△ABD不重合）？若存在，求出点P的坐标；若不存在，说明理由．参考答案一、选择题 (共10题；共20分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、二、填空题 (共8题；共8分)11-1、12-1、13-1、14-1、15-1、16-1、17-1、18-1、三、解答题 (共8题；共70分)19-1、20-1、21-1、22-1、22-2、24-1、24-2、25-1、25-2、26-1、26-2、。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
湖北省孝感市中考数学模拟试卷（5月份）
姓名:________ 班级:________ 成绩:________
一、选择题 (共10题；共20分)
1. （2分） (2017七上·黄冈期中) 下列说法正确的是（）
A . 若|a|=﹣a，则a＜0
B . 若a=b，m是有理数，则 =
C . 式子3xy2﹣4x3y+12是七次三项式
D . 若a＜0，ab＜0，则b＞0
2. （2分） m－n= ，则－3（n－m）=（）
A . －
B .
C .
D .
3. （2分）如果∠A和∠B是同旁内角，且∠A=60°，则∠B的度数是（）
A . 60°
B . 120°
C . 60°或120°
D . 不能确定
4. （2分） (2017七下·涪陵期末) 下列调查中，适宜采用普查方式的是（）
A . 调查涪陵电视台节目《晚间播报》的收视率
B . 调查涪陵市民对皮影表演艺术的喜爱程度
C . 调查涪陵城区居民对“武陵山大裂谷”的知晓率
D . 调查我国首艘宇宙飞船“天舟一号”的零部件质量
5. （2分） (2016八上·大悟期中) 如图，有A、B、C三个居民小区的位置成三角形，现决定在三个小区之间修建一个购物超市，使超市到三个小区的距离相等，则超市应建在（）
A . 在AC，BC两边高线的交点处
B . 在AC，BC两边中线的交点处
C . 在AC，BC两边垂直平分线的交点处
D . 在∠A，∠B两内角平分线的交点处
6. （2分） (2019八上·天台月考) 如图，在△ABC中，∠C=40 ° ，按图中虚线将∠C剪去后，∠1+∠2等于（）.
A . 140°
B . 210°
C . 220°
D . 320°
7. （2分）(2018·通辽) 已知⊙O的半径为10，圆心O到弦AB的距离为5，则弦AB所对的圆周角的度数是（）
A . 30°
B . 60°
C . 30°或150°
D . 60°或120°
8. （2分）如图，抛物线y=ax2+bx+c，OA=OC，下列关系中正确的是（）
A . ac+1=b
B . ab+1=c
C . bc+1=a
D .
9. （2分） (2018八上·义乌期中) 如图,将直角边AC=6cm，BC=8cm的直角△ABC纸片折叠，使点B与点A 重合，折痕为DE, 则CD等于（）
A .
B .
C .
D .
10. （2分） (2019八上·天河期末) 如图，在△ABC中，∠C＝90°，AB的垂直平分线交AB于D，交BC于E，连接AE，若CE＝5，AC＝12，且△ACE的周长为30，则BE的长是（）
A . 5
B . 10
C . 12
D . 13
二、填空题 (共6题；共7分)
11. （1分） (2018七上·湖州月考) 某颗粒物的直径是 0.000 002 5，把 0.000 002 5 用科学计数法表示为________．
12. （1分）如图所示，点A1、A2、A3在x轴上，且OA1=A1A2=A2A3 ，分别过点A1、A2、A3作y轴的平行线，与反比例函数y= （x＞0）的图象分别交于点B1、B2、B3 ，分别过点B1、B2、B3作x轴的平行线，分别与y轴交于点C1、C2、C3 ，连接OB1、OB2、OB3 ，那么图中阴影部分的面积之和为，则k的值为________．
13. （2分）已知∠α=72°，则∠α的余角是________，∠α的补角是________．
14. （1分） (2017七下·上饶期末) 二元一次方程组的解x，y的值相等，则k=________．
15. （1分） (2019九上·北碚期末) 如图，菱形OABC的一边OA在x轴的负半轴上，O是坐标原点，tan∠AOC=
，反比例函数y= 的图象经过点C，与AB交于点D，若△COD的面积为20，则k的值等于________.
16. （1分） (2018八上·深圳期中) 如图，度，，，且，AF平分交BC于F，若，，则线段AD的长为________．
三、解答题 (共9题；共94分)
17. （5分）先化简，再求值：，其中x=2．
18. （13分）(2018·灌南模拟) 州教育局为了解我州八年级学生参加社会实践活动情况，随机抽查了某县部分八年级学生第一学期参加社会实践活动的天数，并用得到的数据检测了两幅统计图，下面给出了两幅不完整的统计图（如图）
请根据图中提供的信息，回答下列问题：
（1） a=________%，并写出该扇形所对圆心角的度数为________，请补全条形图________．
（2）在这次抽样调查中，众数和中位数分别是多少？
（3）如果该县共有八年级学生2000人，请你估计“活动时间不少于7天”的学生人数大约有多少人？
19. （5分）我国明代数学家程大为曾提出过这样一个有趣的问题：有一个人赶着一群羊在前面走，另一个人牵着一只羊跟在后面．后面的人问赶羊的人说：“你这群羊有一百只吗？”赶羊的人回答：“我如果再得这么一群
羊，再得这么一群羊的一半，又得这群羊的四分之一，把你牵的羊也给我，我恰好有一百只．”请问这群羊有多少只？请设未知数，列出方程．
20. （15分）(2018·洪泽模拟) 如图，一次函数y=kx+b分别交y轴、x轴于C、D两点，与反比例函数y= （x＞0）的图象交于A（m，8），B（4，n）两点．
（1）求一次函数的解析式；
（2）根据图象直接写出kx+b﹣＜0的x的取值范围；
（3）求△AOB的面积．
21. （10分） (2017八上·高邑期末) 已知∠MAN=120°，AC平分∠MAN，点B、D分别在AN、AM上．
（1）如图1，若∠ABC=∠ADC=90°，请你探索线段AD、AB、AC之间的数量关系，并证明之；
（2）如图2，若∠ABC+∠ADC=180°，则（1）中的结论是否仍然成立？若成立，给出证明；若不成立，请说明理由．
22. （10分） (2017八下·东莞期末) 如图，在△ABC中，AB=13，BC=10，BC边上的中线AD=12.
（1）求证：AD⊥BC；
（2）求AC的长.
23. （15分） (2016七下·建瓯期末) 某文具商店销售功能相同的A，B两种品牌的计算器，购买2个A品牌和3个B品牌的计算器共需156元；购买3个A品牌和1个B品牌的计算器共需122元．
（1）求这两种品牌计算器的单价；
（2）学校开学前夕，该商店对这两种计算器开展了促销活动，具体办法如下：A品牌计算器按原价的八折销售，B品牌计算器5个以上超出部分按原价的七折销售．设购买x个A品牌的计算器需要y1元，购买x个B品牌的计算器需要y2元，若购买计算器的数量超过5个，分别用含x的式子表示出y1和y2；
（3）小明准备联系一部分同学集体购买同一品牌的计算器，若购买计算器的数量超过5个，请问购买哪种品牌的计算器更合算？说明理由．
24. （10分）(2013·资阳) 在一个边长为a（单位：cm）的正方形ABCD中，点E、M分别是线段AC，CD上的动点，连结DE并延长交正方形的边于点F，过点M作MN⊥DF于H，交AD于N．
（1）如图1，当点M与点C重合，求证：DF=MN；
（2）如图2，假设点M从点C出发，以1cm/s的速度沿CD向点D运动，点E同时从点A出发，以 cm/s 速度沿AC向点C运动，运动时间为t（t＞0）；
①判断命题“当点F是边AB中点时，则点M是边CD的三等分点”的真假，并说明理由．
②连结FM、FN，△MNF能否为等腰三角形？若能，请写出a，t之间的关系；若不能，请说明理由．
25. （11分）(2016·广东) 如图，在直角坐标系中，直线y=kx+1（k≠0）与双曲线y= （x＞0）相交于点P（1，m ）．
（1）求k的值；
（2）若点Q与点P关于直线y=x成轴对称，则点Q的坐标是Q（________）；
（3）若过P、Q二点的抛物线与y轴的交点为N（0，），求该抛物线的函数解析式，并求出抛物线的对称轴方程．
参考答案一、选择题 (共10题；共20分)
1-1、
2-1、
3-1、
4-1、
5-1、
6-1、
7-1、
8-1、
9-1、
10-1、
二、填空题 (共6题；共7分)
11-1、
12-1、
13-1、
14-1、
15-1、
16-1、
三、解答题 (共9题；共94分)
17-1、
18-1、
18-2、18-3、
19-1、
20-1、20-2、
20-3、
21-1、
21-2、22-1、
22-2、
23-1、
23-2、
23-3、
24-1、
25-1、25-2、
25-3、。