高中数学专题讲义-数学归纳法
高三数学精品课件： 数学归纳法
[主干知识·自主梳理] [考点分类·深度剖析] 课时作业
首页 上页 下页 尾页
考点三 归纳猜想证明 (核心考点——合作探究)
解析：(1)当 n＝1 时，由已知得 a1＝a21＋a11－1，a12＋2a1－2＝ 0.∴a1＝ 3－1(a1＞0)． 当 n＝2 时，由已知得 a1＋a2＝a22＋a12－1， 将 a1＝ 3－1 代入并整理得 a22＋2 3a2－2＝0. ∴a2＝ 5－ 3(a2＞0)．同理可得 a3＝ 7－ 5. 猜想 an＝ 2n＋1－ 2n－1(n∈N*)．
法的原理．
素养
2.能用数学归纳
☆
形成
法证明一些简单
的数学命题.
考查 主要通过数学归纳法证明问题，考查
角度 逻辑推理能力.
[主干知识·自主梳理] 重温教材 自查自纠
1．数学归纳法 证明一个与正整数 n 有关的命题，可按下列步骤进行： (1)(归纳奠基)证明当 n 取 第一个值 n0(n0∈N*)时命题成立． (2)(归纳递推)假设 n＝k(k≥n0，k∈N*)时命题成立，证明当 n＝k＋1 时命题也成立．
[主干知识·自主梳理] [考点分类·深度剖析] 课时作业
首页 上页 下页 尾页
考点二 证明不等式 (核心考点——合作探究)
当 n＝k＋1 时，左边＝k＋1 2＋k＋1 3＋…＋3k1＋3＝(k＋1 1＋k＋1 2 ＋k＋1 3＋…＋31k)＋3k1＋1＋3k1＋2＋3k1＋3－k＋1 1>56＋3k1＋3×3 －k＋1 1＝56， 所以当 n＝k＋1 时，命题也成立． 综合①②可知原命题成立．
[主干知识·自主梳理] [考点分类·深度剖析] 课时作业
首页 上页 下页 尾页
考点一 证明等式 (核心考点——合作探究)
高三数学总复习《数学归纳法》课件
k(2k+1),则当n=k+1时,
12-22+32-42+…+(2k-1)2-(2k)2+(2k+1)2 2 k 1
2
=-k(2k+1)+(2k+1) =-2k2-5k-3=-(k+1)(2k+3)
=-(k+1)
. 2 k 1
2
即当n=k+1时,等式也成立.
k 1 当n k 1时, 2 k 1 7 3 9
(2k 7) 3k 1 2 3k 1 9
k k 1 2 k 7 3 9 3 18 ( 3 1). 由于3k 1 1是2的倍数, 故18(3k 1 1)能被36整除,
下列命题总成立的是(
)
A.若f(3)≥9成立,则当k≥1时,均有f(k)≥k2成立 B.若f(5)≥25成立,则当k≤5时,均有f(k)≥k2成立 C.若f(7)<49成立,则当k≥8时,均有f(k)<k2成立 D.若f(4)=25成立,则当k≥4时,均有f(k)≥k2成立 答案:D
解析:若f(3)≥9,只能推出,当k≥3时f(k)>k2,所以A不正确;若
典例某数列的第一项为1,并且对所有的自然数n≥2,数列的前
n项积为n2. (1)写出这个数列的前五项; (2)写出这个数列的通项公式,并加以证明.
分析:根据数列前五项写出这个数列的通项公式,要注意观察
数列中各项与其序号变化的关系,归纳出构成数列的规律,同 时还要特别注意第一项与其他各项的差异,必要时可分段表 示,证明这个数列的通项公式可用数学归纳法.本题中要特别 注意第一个步骤的处理.
数学归纳法优质课件高中数学优质课件下载
数学归纳法优质课件高中数学优质课件一、教学内容本节课，我们将在高中数学教材第四章“数列与数学归纳法”中，深入学习数学归纳法。
具体内容涉及教材第2节，详细探讨数学归纳法基本原理、步骤及其在数列中应用。
二、教学目标1. 理解数学归纳法概念、原理和应用；2. 掌握数学归纳法证明步骤，并能运用其解决数列相关问题；3. 培养学生逻辑思维能力和推理能力。
三、教学难点与重点1. 教学难点：数学归纳法证明过程中，如何引导学生从特殊到一般，再由一般到特殊逻辑推理；2. 教学重点：数学归纳法证明步骤及其在数列中应用。
四、教具与学具准备1. 教具：PPT课件、黑板、粉笔；2. 学具：练习本、笔。
五、教学过程1. 实践情景引入：通过生活中实例，如“登楼梯问题”，引导学生思考如何用数学方法解决此类问题，从而引出数学归纳法；2. 例题讲解：讲解数学归纳法基本原理和步骤，结合具体例题，让学生直观地解数学归纳法在实际问题中应用；3. 随堂练习：让学生独立完成数列相关数学归纳法证明题，并及时给予指导和反馈；5. 课堂小结：让学生回顾本节课所学内容，巩固知识点。
六、板书设计1. 数学归纳法基本原理和步骤；2. 数列相关例题及解题过程；3. 课堂小结和课后作业。
七、作业设计1. 作业题目：（1）证明：1+3+5++(2n1)=n^2；（2）证明：1^2+2^2+3^2++n^2=n(n+1)(2n+1)/6。
答案：（1）略；（2）略。
2. 拓展延伸：让学生思考数学归纳法在其他数学领域（如不等式、函数等）应用。
八、课后反思及拓展延伸1. 反思：本节课学生对数学归纳法掌握情况，分析学生在证明过程中可能遇到问题，调整教学方法；2. 拓展延伸：引导学生探索数学归纳法在其他领域应用，培养学生创新思维和探究能力。
重点和难点解析在教学过程中，有几个细节是需要我重点关注。
实践情景引入方式对于激发学生学习兴趣至关重要。
例题讲解深度和广度直接影响到学生对数学归纳法理解程度。
高中数学讲义(人教A版选择性必修二)：第06讲 数学归纳法(教师版)
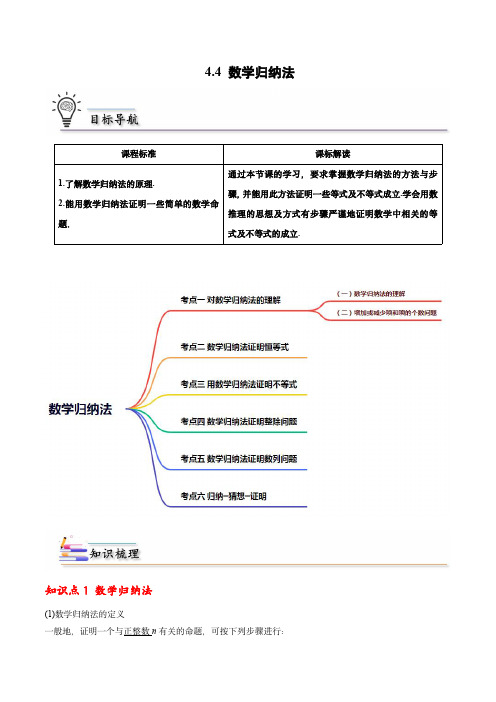
数学归纳法的三个关键点 (1)验证是基础：找准起点，奠基要稳，有些问题中验证的初始值不一定是 1. (2)递推是关键：数学归纳法的实质在于递推，要正确分析式子中项数的变化，弄清式子两边的构成规律． (3)利用假设是核心：在第二步证明 n＝k＋1 时，一定要利用归纳假设．
（一）数学归纳法的理解
【解析】当 n＝1 时，左边的最高次数为 1，
即最后一项为 a，左边是 1＋a，
故选：B.
【即学即练
2】（2022·全国·高二专题练习）用数学归纳法证明1
1
时，第
一步应验证不等式（ ）
A．1 1 2 2
B．1
1 2
1 3
2
C．1 1 1 3 23
A． k2 1 2
B． k2 1
C． k 12 k 2
D． k 12 2k 2
【解析】根据等式左边的特点，各数是先递增再递减，
由于 n k ，左边 12 22 ( k 1)2 k2 ( k 1)2 22 12 ,
n k 1时，左边 12 22 ( k 1)2 k2 ( k 1)2 k2 ( k 1)2 22 12 ，
4.4 数学归纳法
课程标准
课标解读
1.了解数学归纳法的原理. 2.能用数学归纳法证明一些简单的数学命 题．
通过本节课的学习，要求掌握数学归纳法的方法与步 骤，并能用此方法证明一些等式及不等式成立.学会用数 推理的思想及方式有步骤严谨地证明数学中相关的等 式及不等式的成立.
知识点 1 数学归纳法
(1)数学归纳法的定义 一般地，证明一个与正整数 n 有关的命题，可按下列步骤进行：
比较两式，从而等式左边应添加的式子是 (k 1)2 k 2 ，
故选： C ．
高中数学精品课件23数学归纳法1
高中数学精品课件2 3数学归纳法1一、教学内容本节课选自高中数学教材第二册第三章“数学归纳法”的第一课时。
详细内容包括数学归纳法的概念、原理和基本步骤，以及数学归纳法在实际问题中的应用。
二、教学目标1. 理解数学归纳法的概念，掌握数学归纳法的原理和基本步骤。
2. 能够运用数学归纳法解决一些简单的数学问题。
3. 培养学生的逻辑思维能力和归纳推理能力。
三、教学难点与重点教学难点：数学归纳法的证明过程，尤其是第二步的证明。
教学重点：数学归纳法的概念、原理和基本步骤。
四、教具与学具准备1. 教具：多媒体课件、黑板、粉笔。
2. 学具：教材、练习本、笔。
五、教学过程1. 导入：通过一个实践情景引入数学归纳法，如“如何计算一个台阶上到第n级台阶有多少种走法？”。
2. 基本概念：讲解数学归纳法的概念、原理和基本步骤。
3. 例题讲解：讲解一个典型的数学归纳法例题，如“证明1+2+3++n=n(n+1)/2”。
4. 随堂练习：让学生尝试解决一个类似的数学归纳法问题。
6. 应用拓展：讨论数学归纳法在实际问题中的应用，如数列求和、不等式证明等。
六、板书设计1. 数学归纳法（1）2. 内容：数学归纳法的概念、原理数学归纳法的基本步骤例题及解答随堂练习及答案七、作业设计1. 作业题目：（1）用数学归纳法证明：1^2+2^2+3^2++n^2=n(n+1)(2n+1)/6。
（2）已知数列{a_n}满足a_1=1，a_{n+1}=2a_n+1，用数学归纳法证明：a_n=2^n1。
2. 答案：见教材课后习题。
八、课后反思及拓展延伸1. 反思：本节课学生对数学归纳法的概念和证明步骤掌握情况，以及对例题和随堂练习的解决情况。
2. 拓展延伸：引导学生探索数学归纳法在更广泛领域中的应用，如组合数学、数论等。
重点和难点解析1. 教学难点：数学归纳法的证明过程，尤其是第二步的证明。
2. 例题讲解：讲解一个典型的数学归纳法例题。
3. 随堂练习：设计合适的随堂练习题，巩固学生对数学归纳法的理解。
2024年【新教材】高中数学课件之数学归纳法
2024年【新教材】高中数学课件之数学归纳法一、教学内容本节课选自2024年新教材高中数学必修二，主要围绕第六章第2节“数学归纳法”展开。
详细内容包括数学归纳法的定义、原理以及应用。
具体章节内容为：1. 数学归纳法的引入及基本概念2. 数学归纳法证明步骤与原理3. 数学归纳法在实际问题中的应用二、教学目标1. 理解数学归纳法的概念，掌握数学归纳法的基本步骤。
2. 能够运用数学归纳法证明简单的数学命题。
3. 了解数学归纳法在实际问题中的应用，提高解决问题的能力。
三、教学难点与重点教学难点：数学归纳法证明过程中步骤的严谨性。
教学重点：数学归纳法的基本概念、证明步骤及实际问题中的应用。
四、教具与学具准备1. 教具：PPT课件、黑板、粉笔。
2. 学具：练习本、笔。
五、教学过程1. 导入：通过一个实践情景（如：楼梯问题）引入数学归纳法的概念。
2. 新课讲解：a. 介绍数学归纳法的定义及基本原理。
b. 通过例题讲解数学归纳法证明步骤。
c. 分析数学归纳法在实际问题中的应用。
3. 随堂练习：让学生完成几道数学归纳法证明的题目，巩固所学知识。
4. 知识拓展：介绍数学归纳法在其他领域的应用，如计算机科学、经济学等。
六、板书设计1. 数学归纳法2. 定义：数学归纳法的概念3. 证明步骤：数学归纳法证明的基本步骤4. 应用示例：数学归纳法在实际问题中的应用七、作业设计1. 作业题目：a. 证明：1+3+5++(2n1)=n^2b. 证明：1^3+2^3+3^3++n^3=(1+2++n)^22. 答案：见课后附录。
八、课后反思及拓展延伸2. 拓展延伸：a. 让学生探讨数学归纳法在生活中的应用，提高学生运用数学知识解决问题的能力。
b. 引导学生了解数学归纳法在其他学科领域的应用，拓展知识视野。
重点和难点解析一、教学难点与重点1. 数学归纳法证明过程中步骤的严谨性。
2. 数学归纳法的基本概念、证明步骤及实际问题中的应用。
高中数学《数学归纳法》课件
证明：
1
（1）当n=1时，左边＝12＝1，右边＝
2
3
1
6
等式成立。
（2）假设当n=k时，等式成立，即
12 22 32 k 2 k(k 1)(2k 1) 6
那么： 左边=12+22+……+k2+(k+1)2
k(k 1)(2k 1) (k 1)2 6
❖ 设{pn}是一个与自然数相关的命题集合，如果 （1）证明起始命题p1(或p0)成立； （2）在假设pk成立的前提下，推出pk+1也成 立，那么可以断定。{pn}对一切正整数（或自 然数）成立，这种方法叫做数学归纳法。
引例1:已知数列{an}中， a1=1,an+1=an/(an+1),试求出a2,a3,a4并猜 想{an}的通项公式
k(k 1)(2k 1) 6(k 1)2
6 (k 1)(2k 2 7k 6)
6 (k 1)(k 2)(2k 3)
6
(k 1)(k 1) 12(k 1) 1 右边
6
即当n=k+1时等式也成立。 根据（1）和（2），可知命题
对任何n∈N＊都成立。
重点：两个步骤、一个结论； 注意：递推基础不可少，
故 n＝k＋1 时猜想也成立． 由①②可知，对 n≥2，n∈N*，有 an＝5×2n－2. 所以数列{an}的通项公式为 an＝55， ×n2＝ n－21，，n≥2.
Hale Waihona Puke 1 1 1 1 n .24 46 68
2n(2n 2) 4(n 1)
证明 （1）当n=1时，等式左边 1 1 , 24 8
等式右边 1 1, 所以等式成立. 4(11) 8
新教材高中数学第4章4.4数学归纳法课件苏教版选择性必修第一册
【解析】①当 n＝1 时，左边＝1，右边＝1×22 2＝1，等式成立．
②假设当 n＝kk∈N*，k≥1
时等式成立，即 13＋23＋33＋…＋k3＝[ k(k 1)]2 . 2
那么当 n＝k＋1 时，13＋23＋33＋…＋k3＋(k＋1)3＝[ k(k 1)]2 ＋(k＋1)3 2
＝(k＋1)2·k42＋k＋1
＝11× 11k+1+122k－1 ＋133×122k－1. 由归纳假设可知 11× 11k+1+122k－1 ＋133×122k－1 能被 133 整除，即11k＋2 ＋
122k＋1 能被 133 整除．所以 n＝k＋1 时结论也成立， 综上，由①②得，11n＋1 ＋122n－1能被 133 整除．
C．3k1＋1
D．3k1＋3
【解析】选 B.当 n＝k(k∈N*)时，所假设的不等式为 1 k＋1
＋1 k＋2
＋…＋31k
5 ≥6
，
当 n＝k＋1 时，要证明的不等式为 1 k＋2
＋1 k＋3
＋……＋31k
＋1 3k＋1
＋1 3k＋2
＋
1 3k＋3
5 ≥6
，
故需添加的项为 1 3k＋1
＋1 3k＋2
(n∈N*) .
【解析】①当 n＝1 时，11n＋1 ＋122n－1＝112＋12＝133 能被 133 整除，所以 n＝1 时结 论成立，
②假设当 n＝k(k∈N*) 时，11k＋1 ＋122k－1 能被 133 整除，
那么当 n＝k＋1 时，
11k＋2 ＋122k＋1 ＝11k＋1 ×11＋122k－1 ×122 ＝11k＋1 ×11＋122k－1 ×11－122k－1 ×11＋122k－1 ×122
高中数学人教版高二必修《归纳法》教育教学课件
注 意：
1、一定要用到归纳假设； 2、看清从k到k＋1中间的变化。
一、证明中需要注意的问题 (1)在第一步中的初始值不一定从1取起，证明时应根据具体情况而定.
例1:欲用数学归纳法证明2n>n2, 试问n的第一个取值应是多少?
答:对n=1,2,3,…,逐一尝试, 可知初始值为n=5.
例2.下面是某同学用数学归纳法证明命题
有几项？
f (k 1) 是什么,它比 f (k) 多出了多少，是首要问题。
小结:
1.与正整数有关的数学命题可以考虑用数学归纳法证明,但注 意不要滥用. 并非任何与正整数有关的命题都可以用它来证明。 如果命题没有“递推”关系，数学归纳法将会失去其效力。 2.掌握数学归纳法的实质与步骤 3. 数学归纳法的应用通常与数学的其他方法联系在一起的, 如比较法、放缩法、配凑法、分析法和综合法等.
数学归纳法
人
教
版
高
中
选
修
二
数学归纳法是一种证明与正整数有关的数学命题的重要方法.主要有两个步骤一个结论: （1）证明当n取第一个值n0（如 n0=1或2等）时结论正确 【归纳奠基】 （2）假设n=k(k≥n0,n∈N*)时结论正确，证明n=k+1时结论也正确【归纳递推】 （3）由（1）、（2）得出结论
数学归纳法-高中数学知识点讲解
数学归纳法
1．数学归纳法
【知识点的认识】
1．数学归纳法
一般地，当要证明一个命题对于不小于某正整数n0 的所有正整数n 都成立时，可以用以下两个步骤：
（1）证明当n＝n0 时命题成立；
（2）假设当n＝k（k∈N+，且k≥n0）时命题成立，证明n＝k+1 时命题也成立．
在完成了这两个步骤后，就可以断定命题对于不小于n0 的所有正整数都成立．这种证明方法称为数学归纳法．
2．用数学归纳法证明时，要分两个步骤，两者缺一不可．
（1）证明了第一步，就获得了递推的基础，但仅靠这一步还不能说明结论的正确性．
在这一步中，只需验证命题结论成立的最小的正整数就可以了，没有必要验证命题对几个正整数成立．
（2）证明了第二步，就获得了推理的依据．仅有第二步而没有第一步，则失去了递推的基础；而只有第一步而没有第二步，就可能得出不正确的结论，因为单靠第一步，我们无法递推下去，所以我们无法判断命题对n0+1，
n0+2，…，是否正确．
在第二步中，n＝k 命题成立，可以作为条件加以运用，而n＝k+1 时的情况则有待利用命题的已知条件，公理，定理，定义加以证明．
完成一，二步后，最后对命题做一个总的结论．
3．用数学归纳法证明恒等式的步骤及注意事项：
①明确初始值n0 并验证真假．（必不可少）
②“假设n＝k 时命题正确”并写出命题形式．
③分析“n＝k+1 时”命题是什么，并找出与“n＝k”时命题形式的差别．弄清左端应增加的项．
④明确等式左端变形目标，掌握恒等式变形常用的方法：乘法公式、因式分解、添拆项、配方等，并用上假设．
1/ 1。
高中数学选修2-2数学归纳法-【名师经典教学资料】
数学归纳法1、知识与技能(1)了解归纳法，理解数学归纳法的原理与实质，掌握数学归纳法证题的两个步骤。
(2)会证明简单的与正整数有关的命题。
2、过程与方法努力创设课堂愉悦的情境，使学生处于积极思考，大胆质疑的氛围，提高学生学习兴趣和课堂效率，让学生经历知识的构建过程，体会类比的数学思想。
3、情感态度价值观通过本节课的教学，使学生领悟数学思想和辩证唯物主义观点，激发学生学习热情，提高学生数学学习的兴趣，培养学生大胆猜想，小心求证的辩证思维素质，以及发现问题、提出问题的意见和数学交流能力。
教学重点、难点:教学重点：借助具体实例了解数学归纳法的基本思想，掌握它的基本步骤，运用它证明一些简单的与正整数n（n取无限多个值）有关的数学命题。
教学难点:(1)学生不易理解数学归纳法的思想实质，具体表现在不了解第二个步骤的作用，不易根据归纳假设作出证明。
(2)运用数学归纳法时，在“归纳递推”的步骤中发现具体问题的递推关系。
第2课时一、复习巩固数学归纳法的两个步骤二、实例应用例1、平面内有n 个圆，其中每两个圆都相交于两点，且无3个圆交于一点。
求证：这n 个圆将平面分成()22f n n n =-+个部分。
解析：当1n =时，一个圆将平面分成2个部分，()12f =，结论成立； 假设当n k =时，结论成立，即n 个圆将平面分成()22f k k k =-+个部分，当1n k =+时，第（k+1）个圆与前面k 个圆有2k 个交点，这2k 个交点将第（k+1）个圆分成2k 段，每段将各自所在区域一分为二，于是增加了2k个区域，所以k+1个圆将平面分成了()()12f k f k k +=+个部分，()()22212221(1)2f k k k k k k k k +=-++=++=+-++； 所以，当1n k =+时，结论成立。
综上所述，这n 个圆将平面分成()22f n n n =-+个部分。
例2、对于n N *∈，求证：()1211(2)n n x x +-+++，可被()233x x ++整除。
新教材高中数学第4章数列4.4数学归纳法课件新人教A版选择性必修第二册
2．结合探究问题 1，试给出一些常见的不等式放缩方法．
[提示] 在不等式证明时，我们可以使分母变大(小)，从而实现
数值变小(大)．如：
(1)
1＝ k
2 k＋
k>
2 k＋
k＋1＝2
k＋1－
kk∈N*，k>1，
1＝ k
2 k＋
k<
2 k＋
k－1＝2
k－
k－1k∈N*，k>1.
(2)k12<kk－1 1＝k－1 1－1k (k≥2)， k12>kk＋1 1＝1k－k＋1 1.
A．1
B．1＋a
C．1＋a＋a2
D．1＋a＋a2＋a3
C [当 n＝1 时，左边＝1＋a＋a1＋1＝1＋a＋a2，故 C 正确．]
3．用数学归纳法证明 1＋2＋3＋…＋(2n＋1)＝(n＋1)(2n＋1)时，
从“n＝k”到“n＝k＋1”，左边需增添的代数式是( )
A．(2k＋1)＋(2k＋2)
B．(2k－1)＋(2k＋1)
1 1×4
＋4×1 7
＋7×110
＋…
＋3k－213k＋1
＝3k＋k 1
，
则当 n＝k＋1 时，
1 1×4
＋4×1 7
＋7×110
＋…
＋3k－213k＋1
＋
1 [3k＋1－2][3k＋1＋1]
＝3k＋k 1 ＋3k＋113k＋4 ＝33kk＋2＋143kk＋＋14 ＝33kk＋＋113kk＋＋14 ＝3k＋k＋11＋1， 所以，当 n＝k＋1 时猜想也成立． 根据(1)和(2)，可知猜想对任意 n∈N*都成立．
4．已知 f (n)＝1＋12＋13＋…＋1n(n∈N*)，计算得 f (2)＝32，f (4) ＞2，f (8)＞52，f (16)＞3，f (32)＞72，由此推测，当 n＞2 时，有________．
人教版高中数学选择性必修2《数学归纳法》PPT课件
典例分析
例4 设为正实数，为大于1的正整数，若数列, + , ( + ) , … ，
+ − ， … 的前项和为 ，试比较 与的大小，并用数学归纳
法证明你的结论.
>
证明: (1)当 =2时， 不等式显然成立.
∗
(2)假设当 = ( ∈ 且>1时,不等式成立,即 >
的推理，证明n取所有正整数
都成立？
情景引入
我们先从多米诺骨牌游戏说起.码放
骨牌时,要保证任意相邻的两块骨牌,若
前一块骨牌倒下,则一定导致后块骨牌倒
下.这样,只要推倒第1块骨牌,就可导致
第2块骨牌倒下；而第2块骨牌倒下,就可
导致第3块骨牌倒下；…….总之,不论有
多少块骨牌,都能全部倒下.
探究新知
思考1：在这个游戏中，能使所有多米诺骨牌全部倒下的条件是什么？
高中数学
选择性必修第二册
RJ
RJA
4.4*数学归纳法
情景引入
我是
一毛
我是
二毛
我是
三毛
我不是
四毛！我
猜：
是小明！
四毛！
我是
谁？
不完全归纳： 从一类对象中的部分对象都具有某种性质推出
这类对象全体都具有这种性质的归纳推理方法
探究新知
问题1:口袋中有4个吃的东西，如何证明它们都是糖？
把研究对象一一都考察到，而推出结论的归纳法.
n＝k＋1
推出“当__________时命题也成立”．
只要完成这两个步骤，就可以断定命题对从n0开始的所有正整
数n都成立．
这种证明方法称为数学归纳法．
思考：数学归纳法的第一步n0的初始值是否一定为1?
数学归纳法-人教版高中数学
第03讲一数学归纳法知识图谱-数学归纳法数学归纳法的原理和步骤数学归纳法的应用第03讲成学归纳法错题回顾数学归纳法知识精讲一・数学归纳法原理设｛R｝是一个与正整数相关的命题的集合，如果①证明起始命题月成立；（2）在假设M成立的前提下，推出门也成立，那么可以断定，｛R｝对一切正整数成立.二・用数学归纳法证明命题的步骤1 .证明当力取第一个值％（例如乌=。
或其他正整数）时结论正确.2 .假设当久=机腥"才次）时结论正确（归纳假设）,证明当〃=卜1时结论正确.3 .对任何心忒时命题均正确.三点剖析_.注意事页1.证明了笫F，就获得了递推的基础，但仅靠这f还不能说明结论的晋遍性.在第一步中，考察结论成立的最小正整数就足够了，没有必要再考察几个正整数，即使命题对这几个正整数都成立.证明了策二步,就获得了递推的依据，但没有第F就失去了递推的基础.只有把第一步和第二步结合在一起，才能获得普遍性的结论.因此,完成了笫一步、笙二步后，还要做一个总的结论.2.在递推之前,M=k时结论是否成立是不确定的，因此用假设二字，这一步的实质是证明命题对X的正确性可以?!=阵1时的情况.有了这一步，联系第一步的结论（命题对汶=晃成立）,就可以知道命题对/・1也成立，进而再由第二步可知〃，即也成立…这样递推下去就可以知道对于所有不小于斗的正整数都成立.在这一步中，时命题成立，可以作为条件加以运用，而a时的情况则有待利用归纳假设、已知的定义、公式、定理加以证明，不能直接将处=上十】代入命题.二.方法点夜数学归纳法的应用1.用数学归纳法证明恒等式用数学归纳法证明恒等式时,首先要搞清等式两边的结构特点，注意由“Z到“=虹1“时等式两边项的变化情况，关键是如何将式子转化为与归纳假设结构相同的形式,以便使用归纳假设.特别是用数学归纳法证明三角恒等式时，要能熟练运用有关的三角知识,特别是一些三角公式，要密切关注两边三角式的结构特征，特别是"假设g*成立时，到M=也成立"的等式右边的形式，可将此时等式右边的式孑乍为要证的目标，使等式的左边通过三角公式的变换逐步向右边靠拢，最终达到两边完全一致.2.证明不等式用数学归纳法证明不等式的命题，远比证明恒等式困难得多，证明时要灵活运用不等式的性质.结合不等式证明的其他方法，明确“以=4+1"成立时的形式，抓住关键，理清思路，变换出符合形式的不等式.第二步的思路是:假设〃小时不等式成立，就是庭3,如果卜上1时不等式也成立,形式是,为了要证明②，可从式①再推出另一个不等式」之序，使得4二月•（或8=矿）.于是只要能证出gq,（或才I"）,则根据不等式的传递性可以得以上推理的关键是由①推出式③.至于在证明中究竟是使式③中的口|""4顼为好，还是B=为好，要根据实际条件来决定.3.证明几何问题用数学归纳法证明几何问题时，要注意结合几何图形的性质,在求由"7”到“1+1“增加的元素个数时，可以先用不完全归纳法找出其变化规律.4.证明数或式的整除问题用数学归纳法证明］余性问题必然会涉及数或式的整除性的知识，应适当复习・例如：①c\a^c\pa[②c\a,c b^c\(a-b\.题瞄井题模一数学归纳法的原理和步£例LL111用数学归纳法证明1+三+§+...+<n（neN+l n>l）时，笫一步应验证不等式（）111A、3 B.--1+2<21+2+3<211111C>~-D、亍三；1+2+3<31+2+3+4<3例1.2、11113用数学归纳法证明不等式” +L +〃十2>24的过程中，由推导k+1”时，不等式的左边增加了（）A--------------(&+l)+(k+l)、侬+1)+侬+1)丁#侬+1)(k+l)+(k+l)/+传+1). B、1FTID、以上都不对例1.3、某同学回答"用数学归纳法证明W qc+I e N」，，的过程如下：证明:(1)当卜1时，显然命题是正确的；(2)假设m"时，有般-Sk-L那么当”=卜1时，顼虹1).♦阵JF_3HJ好H4=优-1)-1,所以当”=技1时命题是正确的，由(1)(2)可知对于心匕命题都是正确的.以上证法是错误的,错误在于()A、从&到5的推理过程没有使用归b、归纳假设的写法不正确纳假设C、从*到的推理不严密D、”=1时，验证过程不具体题模二数学归纳法的应用例2.1、用数学归纳法证明：当心艾时，(1、2：-2乂3：｝+(3乂4：-4工5；-2M(2n*lf'=-?l(*l-rl)(4?2-r3j例2.2、已知伞3•求证:"-(H)(耳冲-矗H扃^一例2.3、平面内有芥个园都交于两点，其中每两个圆都交于两点，且无三个圆交于一点,求证：这刃个圆将平面分成*-刀-2个部分.例2.4、求证：，国=涉顷3,。
高中数学讲义：数学归纳法
数学归纳法一、基础知识：1、数学归纳法适用的范围：关于正整数n 的命题（例如数列，不等式，整除问题等），则可以考虑使用数学归纳法进行证明2、第一数学归纳法：通过假设n k =成立，再结合其它条件去证1n k =+成立即可。
证明的步骤如下：（1）归纳验证：验证0n n =（0n 是满足条件的最小整数）时，命题成立（2）归纳假设：假设()0,n k k n n N =³Î成立，证明当1n k =+时，命题也成立（3）归纳结论：得到结论：0,n n n N ³Î时，命题均成立3、第一归纳法要注意的地方：（1）数学归纳法所证命题不一定从1n =开始成立，可从任意一个正整数0n 开始，此时归纳验证从0n n =开始（2）归纳假设中，要注意0k n ³，保证递推的连续性（3）归纳假设中的n k =，命题成立，是证明1n k =+命题成立的重要条件。
在证明的过程中要注意寻找1n k =+与n k =的联系4、第二数学归纳法：在第一数学归纳法中有一个细节，就是在假设n k =命题成立时，可用的条件只有n k =，而不能默认其它n k £的时依然成立。
第二数学归纳法是对第一归纳法的补充，将归纳假设扩充为假设n k £，命题均成立，然后证明1n k =+命题成立。
可使用的条件要比第一归纳法多，证明的步骤如下：（1）归纳验证：验证0n n =（0n 是满足条件的最小整数）时，命题成立（2）归纳假设：假设()0,n k k n n N £³Î成立，证明当1n k =+时，命题也成立（3）归纳结论：得到结论：0,n n n N ³Î时，命题均成立二、典型例题例1：已知等比数列{}n a 的首项12a =，公比3q =，设n S 是它的前n 项和，求证：131n n S n S n++£思路：根据等比数列求和公式可化简所证不等式：321n n ³+，n k =时，不等式为321k k ³+；当1n k =+时，所证不等式为1323k k +³+，可明显看到n k =与1n k =+中，两个不等式的联系，从而想到利用数学归纳法进行证明证明：()11311n nn a q S q -==--，所证不等式为：1313131n n n n+-+£-()()()1313131n n n n +\-£+-1133331n n n n n n n ++Û×-£×+--321n n Û³+，下面用数学归纳法证明：（1）验证：1n =时，左边=右边，不等式成立（2）假设()1,n k k k N =³Î时，不等式成立，则1n k =+时，()()133332163211k k k k k +=׳+=+>++所以1n k =+时，不等式成立n N *\"Î，均有131n n S n S n++£小炼有话说：数学归纳法的证明过程，关键的地方在于寻找所证1n k =+与条件n k =之间的联系，一旦找到联系，则数学归纳法即可使用例2（2015，和平模拟）：已知数列{}n a 满足0n a >，其前n 项和1n S >，且()()112,6n n n S a a n N *=++Î（1）求数列{}n a 的通项公式（2）设21log 1n n b a æö=+ç÷èø，并记n T 为数列{}n b 的前n 项和，求证：233log ,2n n a T n N *+æö>Îç÷èø解：（1）2632n n n S a a =++①()21116322,n n n S a a n n N *---=++³Î②①-②可得：()222211116333n n n n n n n n n a a a a a a a a a ----=-+-Þ+=-0n a >Q 所以两边同除以1n n a a -+可得：13n n a a --={}n a \是公差为3的等差数列()131n a a n \=+-，在2632n n n S a a =++中令1n =可得：211116321S a a a =++Þ=（舍）或12a =31n a n \=-（2）思路：利用（1）可求出n b 和n T ，从而简化不等式可得：33633225312n n n +æö×××>ç÷-èøL ，若直接证明则需要进行放缩，难度较大。
高中必修二： 数学归纳法进阶讲义
1数学归纳法第一数学归纳法 设P(n)表示一个与自然数n有关的命题，若: (1)P(n0)(n0∈N)成立 (2)假设P(k)(k⩾n0)成立，可推出P(k+1)成立，则P(n)对一切自然数n⩾n0，n∈N时成立．第二类数学归纳法 设P(n)表示一个与自然数n有关的命题，若: (1)P(n0)(n0∈N)成立 (2)假设P(n)在n0⩽n⩽k时成立，由此可得P(k+1)成立，则P(n)对一切自然数n⩾n0都成立反向归纳法(倒推归纳法) 设P(n)表示一个与自然数n有关的命题，若: (1)P(n)对无限多个自然数n都成立 (2)假设P(k+1)成立，可推出P(k)也成立．跳跃数学归纳法第4讲【例1】证明：14+24+···+n4=n(n+1)(2n+1)(3n2+3n−1)30.【例2】设n为正整数，证明：1−12+13−14+···+12n−1−12n=1n+1+1n+2+···+12n.【例3】证明：在n⩾3时，2n可以表示成7x2+y2，其中x，y均为奇数．【例4】证明：任意等腰三角形可以分成n(n⩾3)个等腰三角形.第4讲【例5】证明：对所有的正整数n有√12+√22+√32+···+√n2<2【例6】数列F n+2=F n+1+F n，F1=1，F2=1，证明：F2n+1+F2n=F2n+1.2数学归纳法与数列【例7】设a0=1，a1=2，且n(n+1)a n+1=n(n−1)a n−(n−2)a n−1，n=1，2，3，···，求a0a1+a1a2+a2a3+···+a50a51．【例8】第4讲【例9】已知数列{a n}中，a1=1，a n+1a n−2n2(a n+1−a n)+1=0，求a n.【例10】a1=a2=1，a n+2=a2n+1+1a n，n=1，2，···，求证：对任意正整数n，a n都是整数．【例11】已知数列{a n}满足a0=1，a1=5及a n+2=2a2n+1−3a n+1−92a n，证明：所有的a n都是整数.【例12】设正数列a1，a2，···，a n，···满足a2n⩽a n−a n+1，n=1，2，3，···，求证：对任意n∈N∗，有a n<1n．第4讲【温馨提示】请将解题过程写在拍摄区。
数学归纳法完整版课件
数学归纳法完整版课件一、教学内容本节课将深入探讨数学归纳法，这是高中数学的一个重要部分。
教学内容基于教材第四章第四节“数学归纳法”，详细内容包括：1. 数学归纳法的定义与基本思想；2. 数学归纳法证明步骤；3. 数学归纳法在实际问题中的应用。
二、教学目标1. 理解数学归纳法的概念，掌握其基本步骤；2. 能够运用数学归纳法证明等式和不等式；3. 培养学生逻辑思维能力和解决实际问题的能力。
三、教学难点与重点重点：数学归纳法的定义、证明步骤及在实际问题中的应用。
难点：如何引导学生从具体问题中发现规律，并运用数学归纳法进行证明。
四、教具与学具准备1. 教具：PPT课件、黑板、粉笔；2. 学具：练习本、笔。
五、教学过程1. 实践情景引入（5分钟）利用PPT展示一个与数学归纳法相关的生活实例，引发学生思考，激发学习兴趣。
例：有一堆砖，第1块砖摞1厘米，以后每增加1块砖，摞的高度增加2厘米。
求第n块砖摞的高度。
2. 知识讲解（10分钟）详细讲解数学归纳法的定义、证明步骤，通过例题解释如何运用数学归纳法。
例题：证明1+2+3++n = n(n+1)/2。
3. 随堂练习（10分钟）让学生独立完成练习题，巩固所学知识。
练习题：证明2+4+6++2n = n(n+1)。
4. 互动讨论（5分钟）邀请几名学生分享解题思路，共同讨论解决方法。
六、板书设计1. 板书左侧：数学归纳法的定义与证明步骤；2. 板书右侧：例题及解题过程。
七、作业设计1. 作业题目：证明1^3+2^3+3^3++n^3 = (1+2++n)^2。
答案：数学归纳法证明如下：（1）当n=1时，等式成立；（2）假设当n=k时，等式成立，即1^3+2^3++k^3 = (1+2++k)^2；（3）当n=k+1时，等式左侧为1^3+2^3++k^3+(k+1)^3，根据归纳假设，等于(1+2++k)^2+(k+1)^3；（4）将(1+2++k)^2+(k+1)^3展开，得到(1+2++k+k+1)^2，即(1+2++n)^2，等式成立。
2024年高中数学课件44数学归纳法
2024年高中数学课件44数学归纳法一、教学内容本节课选自高中数学教材必修五第三章第四节“数学归纳法”，内容包括数学归纳法的定义、原理以及应用。
具体涉及教材第44页的例1、例2及课后习题。
二、教学目标1. 理解数学归纳法的定义，掌握数学归纳法的步骤。
2. 学会运用数学归纳法证明等式和不等式。
3. 提高学生的逻辑思维能力和解决问题的能力。
三、教学难点与重点重点：数学归纳法的定义和步骤，以及如何运用数学归纳法进行证明。
难点：理解数学归纳法的原理，以及如何将问题转化为数学归纳法适用的形式。
四、教具与学具准备1. 教具：多媒体教学设备、黑板、粉笔。
2. 学具：教材、笔记本、练习本。
五、教学过程1. 引入：通过一个实践情景（如：爬楼梯问题），引导学生思考如何证明一个与自然数有关的命题对所有自然数都成立。
2. 讲解：介绍数学归纳法的定义和步骤，讲解例1和例2，解释如何运用数学归纳法进行证明。
3. 举例：给出一个具体的数学归纳法证明实例，让学生跟随老师一起完成证明过程。
4. 练习：布置随堂练习，让学生独立完成，巩固所学知识。
5. 讲解：针对学生的疑问和错误，进行讲解和指导。
六、板书设计1. 数学归纳法2. 定义：数学归纳法的定义3. 步骤：数学归纳法的步骤4. 例题：例1、例25. 练习：随堂练习题目七、作业设计1. 作业题目：（1）运用数学归纳法证明：1+3+5++(2n1)=n^2。
（2）运用数学归纳法证明：对于任意自然数n，有C(n,0)+C(n,1)++C(n,n)=2^n。
2. 答案：见附录。
八、课后反思及拓展延伸1. 反思：本节课学生对于数学归纳法的理解和运用程度，以及教学过程中的优点和不足。
2. 拓展延伸：（1）了解数学归纳法在数学竞赛中的应用。
（2）探索数学归纳法在其他领域（如：计算机科学）的应用。
（3）引导学生思考数学归纳法与完全归纳法、构造法等证明方法的关系和区别。
附录：作业答案：1. 证明：1+3+5++(2n1)=n^2。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
题型一：数学归纳法基础【例1】已知n 为正偶数，用数学归纳法证明111111112()2341242n n n n-+-++=+++-++时，若已假设2(≥=k k n 为偶数）时命题为真，则还需要用归纳假设再证 （ ）A ．1+=k n 时等式成立B ．2+=k n 时等式成立C ．22+=k n 时等式成立D ．)2(2+=k n 时等式成立【例2】已知n 是正偶数，用数学归纳法证明时，若已假设n=k （2≥k 且为偶数）时命题为真，，则还需证明（ ）A.n=k+1时命题成立B. n=k+2时命题成立C. n=2k+2时命题成立D. n=2（k+2）时命题成立【例3】某个命题与正整数n 有关，如果当)(+∈=N k k n 时命题成立，那么可推得当1+=k n 时命题也成立. 现已知当7=n 时该命题不成立，那么可推得（ ）A ．当n=6时该命题不成立B ．当n=6时该命题成立C ．当n=8时该命题不成立D ．当n=8时该命题成立【例4】利用数学归纳法证明“*),12(312)()2)(1(N n n n n n n n ∈-⨯⋅⋅⋅⨯⨯⨯=+⋅⋅⋅++ ”时，从“k n =”变到“1+=k n ”时，左边应增乘的因式是 （ ） A 12+k B112++k k C 1)22)(12(+++k k k D 132++k k【例5】用数学归纳法证明),1(11122*+∈≠--=++++N n a aa a a a n n，在验证n=1时，典例分析板块三.数学归纳法左边计算所得的式子是（ ）A. 1B.a +1C.21a a ++D. 421a a a +++【例6】用数学归纳法证明n n n n n 2)()2)(1(=+++ ))(12(31*∈+⋅⋅⋅⋅N n n ，从“k到k+1”左端需乘的代数式是（ ） A.2k+1 B.)12(2+k C.112++k k D.132++k k【例7】用数学归纳法证明：1+21+31+)1,(,121>∈<-+*n N n n n 时，在第二步证明从n=k 到n=k+1成立时，左边增加的项数是（ ） A.k 2 B.12-k C.12-k D.12+k【例8】设)1()2()1()(-++++=n f f f n n f ，用数学归纳法证明“)()1()2()1(n nf n f f f n =-++++ ”时，第一步要证的等式是【例9】用数学归纳法证明“)12(212)()2)(1(-⋅⋅⋅⋅=+++n n n n n n ”（+∈N n ）时，从 “n k =到1n k =+”时，左边应增添的式子是__ __。
【例10】用数学归纳法证明不等式241312111>++++++n n n n 的过程中，由k 推导到k+1时，不等式左边增加的式子是【例11】是否存在常数c b a ,,是等式22222421(1)2(2)()n n n n n an bn c ⋅-+⋅-+⋅⋅⋅+⋅-=++对一切)*N n ∈成立？证明你的结论。
题型二：证明整除问题【例12】若存在正整数m ，使得)(93)72()(*∈+-=N n n n f n 能被m 整除，则m =【例13】证明：)(,)3(1*∈+-N n x n 能被2+x 整除【例14】已知数列{}n a 满足1201a a ==，，当*n ∈N 时，21n n n a a a ++=+．求证：数列{}n a 的第41(*)m m +∈N 项能被3整除．【例15】 用数学归纳法证明：731(*)n n n +-∈N 能被9整除．【例16】设n 是任意正整数，求证：35n n +能被6整除．【例17】用数学归纳法证明：对于一切正整数n ，227433n n --能被264整除．【例18】2n (n ≥4且n ∈N *)个正数排成一个n 行n 列的数阵：第1列第2列第3列 …… 第n 列第1行 11a 12a 13a …… 1n a 第2行 21a 22a 23a…… 2n a…… …… …… …… …… …… 第n 行 1n a 2n a 3n a …… nn a 其中ik a (1≤i ≤n ，1≤k ≤n ，且i ，k ∈N )表示该数阵中位于第i 行第k 列的数.已知该数阵每一行的数成等差数列，每一列的数成公比为2的等比数列，且23a =8，34a =20. (Ⅰ)求11a 和ik a ；(Ⅱ)设12(1)3(2)1n n n n n A a a a a --=++++，证明：当n 为3的倍数时，(n A n +)能被21整除.题型三：证明恒等式与不等式【例19】证明不等式111123212n n++++>-……（n N *∈）【例20】用数学归纳法证明：*n N ∈，22211131 (2321)nn n ++++≥+.【例21】证明：*n ∈N ，111111111......234212122n n n n n-+-++-=+++-++.【例22】用数学归纳法证明：221111tan tan tan cot cot (*)22222222n n n n m m n αααααα+++=-≠∈∈Z N π，，．【例23】是否存在常数a 、b 、c ，使等式)(12)1()1(32212222c bn an n n n n +++=+++⋅+⋅ 对一切正整数n 都成立？证明你的结论【例24】在数列}{n a 中，nnn a a a x a -+==+11,tan 11， （1）写出,,21a a 3a ；（2）求数列}{n a 的通项公式【例25】用数学归纳法证明：222111arctanarctan arctanarctan (*)212221nn n n +++=∈⋅⋅⋅+N【例26】用数学归纳法证明：（Ⅰ）)12(2)1()12)(12(532311222++=+-++⋅+⋅n n n n n n ； （Ⅱ） n n ≤-+++++1214131211 ；【例27】对于2n ≥的自然数，证明：21n >+【例28】已知01a <<，求证：对任意大于1的自然数n ，21()1nna a n a a->-．题型四：数列中的数学归纳法【例29】设12,,...n a a a 均为正数，且12...1n a a a +++=，求证：当n ≥2的时候，22212...n a a a +++≥1n【例30】已知数列{}n a 中，11,02n n n na S a a =+->，求数列{}n a 的通项公式.【例31】在数列{}(*)n a n ∈N 中，11a =，n S 是它的前n 项和，当2n ≥时，12n n n a S S -，，成等比数列，求数列的通项公式．【例32】设整数数列{}n a 满足11a =，212a =，320a =，且32122n n n n a a a a +++=+-．证明：任意正整数n ， 114n n a a ++是一个整数的平方．【例33】由正实数组成的数列{}n a 满足：2112n n n a a a n +-=≤，，，．证明：对任意*n ∈N ，都有1n a n<．【例34】实数数列{}n a 定义如下114(1)12n n n a t a a a n t +==-=∈R ，，，，，已知20090a = ⑴证明：对任意*n ∈N ，01n a ≤≤；⑵问有多少个不同的t ，使得20090a =．【例35】两个实数数列{}n x 、{}n y 满足：11tan 3x y π==，1112n n n x y y n ++==+=，，证明：1n >时，23n n x y <<．【例36】在数列{}n a 中，若它的前n 项和1(*)n n S na n =-∈N ． ⑴计算1234a a a a ，，，的值；⑵猜想n a 的表达式，并用数学归纳法证明你的结论．【例37】已知函数3()(1)1x f x x x +=≠-+，设数列{}n a 满足11a =，1()n n a f a +=，数列{}n b 满足n n b a =-，n *∈N．用数学归纳法证明n b【例38】设数列1a ，2a ，…n a …中的每一项都不为0．证明：{}n a 为等差数列的充分必要条件是：对任何n ∈N ，都有1223111111n n n na a a a a a a a +++++=．题型五：其他类型题【例39】已知函数))((*N n n f ∈，满足条件：①2)2(=f ；② )()()(y f x f y x f ⋅=⋅；③ *)(N n f ∈；④当y x >时，有)()(y f x f >. (1) 求)1(f ，)3(f 的值；(2) 由)1(f ，)2(f ，)3(f 的值，猜想)(n f 的解析式； (3) 证明你猜想的)(n f 的解析式的正确性.【例40】数列{}n a ，2111,23()n n a a a n n n N *+==-+∈（Ⅰ）是否存在常数λ，μ使得数列{}2n a n n λμ++是等比数列，若存在求μλ、 的值，若不存在，说明理由。
（Ⅱ）设 112n n n b a n -=+-，123n n S b b b b =++++求证：2n ≥时，65(1)(21)3n n S n n <<++【例41】已知数列{}n a 满足：10a =，21221,12,2n n n n a n n a a -+⎧⎪⎪=⎨++⎪⎪⎩为偶数为奇数，2,3,4,n =．（Ⅰ）求567,,a a a 的值； （Ⅱ）设212n n na b -=，试求数列{}n b 的通项公式；（Ⅲ）对于任意的正整数n ，试讨论n a 与1n a +的大小关系．。