高考数学 思维导图素材 三角函数
三角函数的思维导图(中)-1
因为:sinA = a/c,cscA = c/a; 所以:sinA*cscA
=( a/c)*( c/a) =1
让学习更容易
版本
文件名称
三角函数-思维导图(中)-1
日期
2.1.3.2 第二个是 cosA*secA = 1。这个是很容易推导,推导如下。
第 5页 共 7页
V1.0 2020-02-05
因为:cosA = b/c,secA = c/b; 所以:cosA*secA
第 7页 共 7页
V1.0 2020-02-05
让学习更容易
因为:cscA=c/a, cotA=b/a 又: c^2-b^2=a^2 所以:(cscA)^2-(cotA)^2
=(c/a)^2-(b/a)^2 =(c^2-b^2)/a^2 =a^2/b^2 =1。 2.1.1.4 总结,三角函数的平方关系,无非是使用勾股定理推导出来而已。
让学习更容易
版本
文件名称
让学习更容易
版本
文件名称
三角函数-思维导图anα cot(π+α)=cotα
公式三:任意角α与-α的三角函数值之间的关系 sin(-α)=-sinα cos(-α)=cosα tan(-α)=-tanα cot(-α)=-cotα
公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系 sin(π-α)=sinα cos(π-α)=-cosα tan(π-α)=-tanα cot(π-α)=-cotα
因为:secA=c/b, tanA=a/b 又: c^2-a^2=b^2 所以:(secA)^2-(tanA)^2
=(c/b)^2-(a/b)^2 =(c^2-a^2)/b^2 =b^2/b^2 =1。 同样地,我们记住勾股定理,就能简单快速推导道 1+(tanA)^2 = (secA)^2。 2.1.1.3 第三个是 1+(cota)^2 = (csca)^2。其它道理是相通的,还是这个三角形,还是使用勾股 定理,推导此公式。
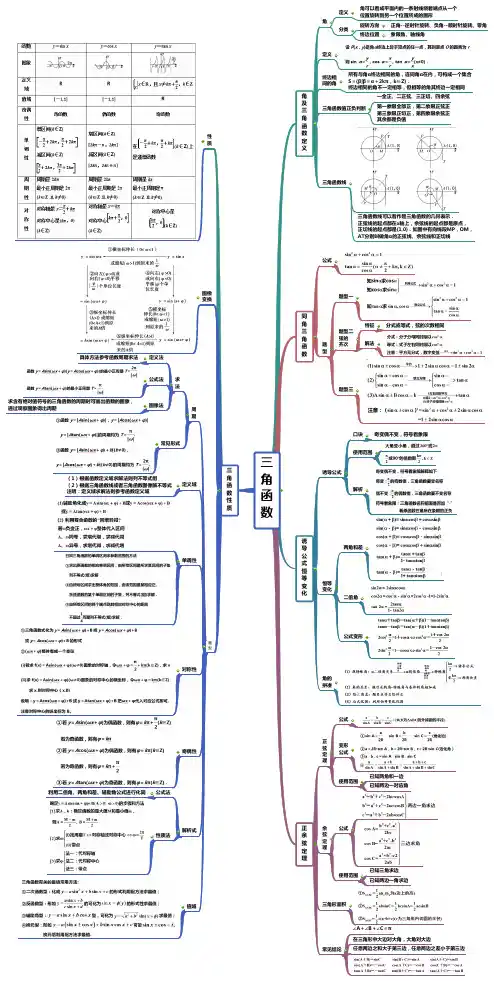
三角函数-高考数学复习思维导图(人教版)
所有与角α终边相同的角,连同角α在内,可构成一个集合特征
解法
分式或等式,弦的次数相同
奇变偶不变,符号看象限
求含有绝对值符号的三角函数的周期时可画出函数的图象,通过观察图象得出周期
(1)根据函数定义域求解法则列不等式组
(2)根据三角函数线或者三角函数图像解不等式公式法
利用二倍角、两角和差、辅助角公式进行化简
已知两角和一边已知两边一对应角
已知三角求边已知两边一角求边
A +∠
B +∠
C =π
在三角形中大边对大角,大角对大边。
三角函数有关知识结构图
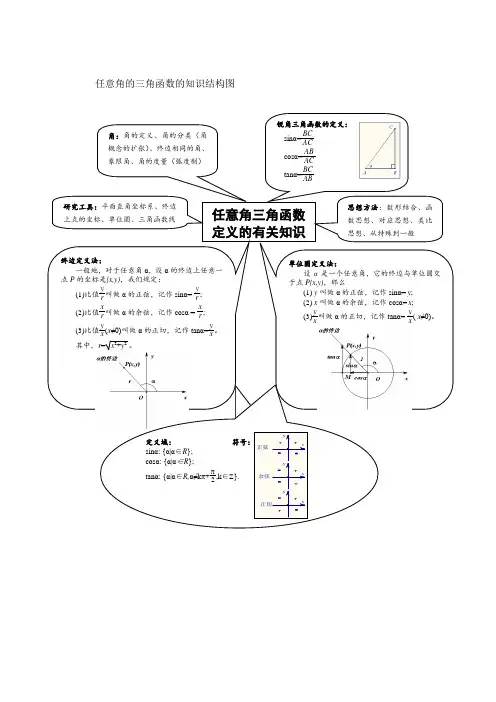
任意角三角函数
定义的有关知识
角:角的定义、角的分类(角概念的扩张)、终边相同的角、象限角、角的度量(弧度制)
锐角三角函数的定义:
sin α=BC AC
cos α=AB AC
tan α=BC AB
研究工具:平面直角坐标系、终边
上点的坐标、单位圆、三角函数线 思想方法:数形结合、函数思想、对应思想、类比思想、从特殊到一般
终边定义法:
一般地,对于任意角α,设α的终边上任意一点P 的坐标是(x,y),我们规定:
(1)比值 y r 叫做α的正弦,记作sin α= y r
;
(2)比值 x r 叫做α的余弦,记作cos α = x r ;
(3)比值 y x (x ≠0)叫做α的正切,记作tan α= y
x 。
其中,r =x 2+y 2 。
单位圆定义法:
设α是一个任意角,它的终边与单位圆交于点P(x,y),那么
(1) y 叫做α的正弦,记作sin α= y ; (2) x 叫做α的余弦,记作cos α= x ; (3) y x 叫做α的正切,记作tan α= y
x
( x ≠0)。
定义域: 符号:
sin α: {α|α∈R };
cos α: {α|α∈R };
tan α: {α|α∈R,α≠k π+π
2
,k ∈Z}.
任意角的三角函数的知识结构图
y x
y x
y x 正切
余弦+
+-
-
+
+----++正弦。
湘教版必修第二册三角恒等变换思维导图

湘教版必修第二册三角恒等变换思维导图
三角函数恒等变换不但在三角函数式的化简、求值和证明三角恒等式中经常用到,而且.由于通过三角换元可将某些代数问题化归为三角问题;立体几何中的诸多位置关系以其交角来刻画,最后又以三角问题反映出来。
由于参数方程的建立,又可将解析几何中的曲线问题归结为三角问题.因此,三角恒等变换在整个高中数学中涉及面广.是常见的解题“工具”。
三角函数恒等变换在整个高中数学应用广泛,在掌握三角函数恒等变换之前,要在脑中有张“全局图”,是十分有必要的。
三角函数的基本关系式的总结。
所谓的平方关系,就是本质是勾股定理在三角函数里的另外表现。
三角函数的商关系,无非就是直角三角形各个边的比例关系。
三角函数的倒数关系,也是同样道理。
我们也可以用图四的关系图,更加直观理解他们的关系。
上图为三角函数恒等变换的思维导图。
三角函数-精品思维导图

三角函数的思维导图一:概述三角函数是数学中属于初等函数中的超越函数的函数。
它们的本质是任何角的集合与一个比值的集合的变量之间的映射。
通常的三角函数是在平面直角坐标系中定义的。
其定义域为整个实数域。
三角函数公式看似很多、很复杂,但只要掌握了三角函数的本质及内部规律,就会发现三角函数各个公式之间有强大的联系。
而掌握三角函数的内部规律及本质也是学好三角函数的关键所在。
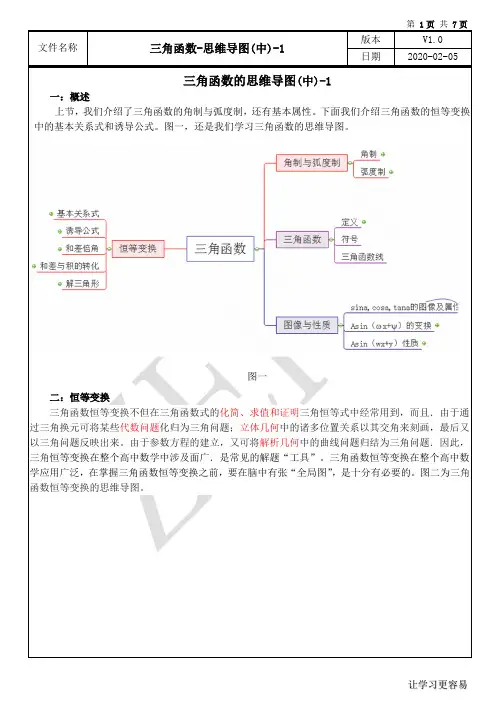
下面是通过思维导图的方式,将这些内部规律和联系表现出现,方便学习者掌握三角函数。
图一为学习三角函数的主要分支。
我们从下列分支,一个一个分支开始学习。
图一二:角度与弧度制2.1我们知道,常见的度量方法有角度制与弧度制两种。
什么是角度制?所谓角度制,就是将圆周 360 等分,其中 1 份所对应的圆心角定义为 1 度,记作1°。
并将 1度的 1/60 定义为 1 分,记作 1';将 1 分的 1/60 定义为 1 秒,记作 1"。
换言之,1°=60',1'=60"。
图二是角度制的示意图。
2.2而弧度制则是根据圆心角、弧长、半径之间的数量关系而引入的。
当弧长等于半径时,弧所对应的圆心角为 1 弧度,记作 1rad。
正角度弧度数是一个正数,负角度弧度数是一个负数,零角度弧度数。
半径为r的圆的圆心角α所对的弧度长为l,那么角α的弧度数的绝对值是 | α | = l / r。
图二2.3角度制与弧度制的换算,数字表达式和图示表示如下所示。
2.4图四为角制和弧度制的思维导图。
图四角度制与弧度制数字表达式: 360 o = 2π rad 180 o = π rad1 o =(π / 180)rad ≈ 0.01745 rad 1 rad =(180 /π)o ≈ 57.30 o α 度的角 = α ·(π / 180)rad角度制与弧度制图示表示:三:三角函数基本属性3.1 三角函数的定义。
