基于MATLAB的数字模拟仿真..
基于matlab的数字基带传输系统仿真实验设计

基于matlab的数字基带传输系统仿真实验设
计
数字基带传输系统仿真实验设计
一、实验目的
1.了解数字基带传输系统的基本结构和原理;
2.通过Matlab仿真来研究数字基带传输系统的性能特点;
3.实际操作,掌握Matlab对数字信号处理的基本方法。
二、实验内容
1.设计数字基带传输系统的仿真模型,包括信源、调制器、信道、解调器、接收端等模块;
2.模拟实现数字信号的采样、量化、编码等过程;
3.采用常用的调制方式,如BPSK、QPSK、16QAM等,进行调制处理,并观察不同调制方式下的信噪比和误码率的关系;
4.在传输过程中引入噪声,观察噪声对信号传输质量的影响;
5.实现误码率的计算和信噪比的测量;
6.结合实际情况,设计合适的信号处理算法,提高数字基带传输系统的性能。
三、实验步骤
1.根据实验要求,设计数字基带传输系统的仿真模型,包括信源、调制器、信道、解调器、接收端等模块;
2.实现数字信号的采样、量化、编码等处理过程;
3.采用常用的调制方式(如BPSK、QPSK、16QAM等),进行信号调制处理;
4.在传输过程中引入噪声,并观察噪声对信号传输质量的影响;
5.实现误码率的计算和信噪比的测量;
6.根据实验结果,设计合适的信号处理算法,提高数字基带传输系统的性能。
四、实验结果
1.实验结果应包括调制方式、误码率、信噪比等参数;
2.根据实验结果,评估数字基带传输系统的性能,提出改善方法。
五、实验总结
1.总结数字基带传输系统的基本结构和原理;
2.分析数字基带传输系统的性能特点,包括误码率、信噪比等;
3.掌握Matlab对数字信号处理的基本方法。
基于MATLAB模拟调制系统的仿真设计

基于MATLAB模拟调制系统的仿真设计调制是无线通信系统中的重要环节,主要用于在传输信号过程中对信号进行编码和解码,以实现信号的传输和接收。
MATLAB作为一种强大的数学仿真工具,可以方便地进行调制系统的仿真设计。
调制系统一般包括三个主要部分:调制器、信道和解调器。
调制器负责将发送信号进行编码,以适应信道传输的需求;信道主要是指无线信号在传输过程中的传播环境,会受到各种影响,如多径效应、噪声等;解调器对接收到的信号进行解码,恢复出原始信号。
在MATLAB中,可以利用其信号处理、通信和仿真工具箱来进行调制系统的仿真设计。
以下是一个基于MATLAB的调制系统的仿真设计流程:1.确定调制方式:首先确定要使用的调制方式,比如常见的调制方式有调幅(AM)、调频(FM)、相位调制(PM)等。
根据需求选择合适的调制方式。
2.信号生成:使用MATLAB的信号处理工具箱生成原始信号。
可以选择不同的函数生成不同的信号,如正弦信号、方波信号、高斯脉冲等。
3.调制器设计:根据选择的调制方式,设计相应的调制器。
比如对于AM调制,可以通过将原始信号与载波进行乘法运算来实现;对于FM调制,可以通过改变载波频率的方式来实现。
在MATLAB中,可以使用相关函数来实现这些调制方式。
4.信号传输:将调制后的信号传输到信道中。
可以在仿真中模拟不同的信道情况,如加入噪声、多径效应等。
MATLAB提供了相关函数来模拟这些信道效应。
5.解调器设计:设计相应的解调器以恢复原始信号。
解调器的设计与调制器的设计相对应。
在MATLAB中,可以使用相关函数来实现解调器。
6.信号分析:对仿真结果进行分析。
可以通过绘制波形图、功率谱密度图等来观察信号在传输过程中的变化。
除了上述基本的仿真设计流程外,还可以在仿真过程中加入其他功能,如信号压缩、信号变换等。
MATLAB提供了大量的工具箱,可以方便地实现这些功能。
总之,基于MATLAB的调制系统仿真设计可以方便地模拟调制系统的工作过程,以及对不同信道效应的影响。
MATLAB和数字仿真.

4、人在回路仿真-必须实时运行
5、软件在回路仿真-大部分情况下要拟仿真:采用数学模型,在模拟计算机上进行的 实验研究。50年代 •描述连续物理系统的动态过程比较自然、逼真,具有 仿真速度快、失真小、结果可靠的优点,但受元器件性 能影响,仿真精度较低,对计算机控制系统的仿真较困 难,自动化程度低。 •模拟计算机的核心是运算部分,它由我们熟知的“模 拟运算放大器”为主要部件所构成。 2、数字仿真:采用数学模型,在数字计算机上借助于 数值计算方法所进行的仿真实验。60年代
1.4 仿真技术的发展趋势
1、硬件方面:基于多CPU并行处理技术的全数字仿真 将有效提高仿真系统的速度,大大增强数字仿真的 实时性。 2、应用软件方面:直接面向用户的数字仿真软件不断 推陈出新,各种专家系统与智能化技术将更深入地 应用于仿真软件开发之中,使得在人机界面、结果 输出、综合评判等方面达到更理想的境界。
3、快捷 • 提高设计效率:比如电路设计,服装设计等等。 4、具有优化设计和预测的特殊功能 • 对一些真实系统进行结构和参数的优化设计是非常 困难的,这时仿真可以发挥它特殊的优化设计功能。 • 在非工程系统中(如社会、管理、经济等系统), 由于其规模及复杂程度巨大,直接实验几乎不可能, 这时通过仿真技术的应用可以获得对系统的某种超 前认识。
但是这样一个开发流程总是欠缺和工程实现的 有效连接,系统级的设计产物无法和硬件产品直接 挂钩。工程师无法直接应用 MATLAB/Simulink 的宝 贵资源。为了改善设计流程中的这一缺陷, MATLAB 产品体系中加入了连接工程实现的桥梁 — 实时代码生成工具 Real-Time Workshop ( RTW )。 RTW 使用户可以直接将 Simulink 框图模型转化为实 时标准 C 代码,进而为快速原型系统、半物理仿真 系统或者产品提供设计输入。
通信原理基于matlab的计算机仿真

通信原理基于matlab的计算机仿真通信原理基于matlab的计算机仿真已经成为通信领域中一项重要的研究工具。
此类仿真软件通过模拟现实情形,能够极大地加快通信设备的开发进程,并且可以帮助工程师进行实验,发现并解决通讯中可能存在的问题。
同时,matlab的通信仿真功能也成为了相关教材和教学实验的首选,许多大学,尤其是通信工程专业的学生要通过matlab的仿真来更好地理解通信原理和通信设备的工作原理。
由于matlab的专业性,无论是对于传输介质的模型计算,还是信号的传输过程的计算仿真,都非常适合。
通信原理的matlab仿真可以有效地帮助工程师分析各种信号,包括模拟信号、数字信号及混合信号。
这种仿真可用于计算机网络、通信系统设计以及无线通信和移动通信等领域。
在matlab中,通信原理的仿真重点是信号的传输与接收。
目前,通信设备主要采用数字信号的传输方式,而matlab中也能够实现该方式的仿真。
通过模拟数字信号的传输过程,可以帮助工程师分析此类信号在不同媒介下的传输效果。
所以,在进行数字信号的仿真时,matlab会考虑到以下几个因素:1.噪声在数字通信中,噪声是一个常见的问题。
因此,在matlab 的仿真中也要考虑到噪声的影响因素。
matlab能够对噪声进行建模,模拟各种环境下的噪声对数字信号的影响程度。
2.数据传输速率数据传输速率也会影响数字信号的仿真结果。
matlab可以模拟数字信号传输的速率以及不同速率下的传输效果。
3.差错率差错率也是数字信号传输中的一个显著因素,matlab在通信原理仿真中也会进行模拟。
除数字信号外,模拟信号的仿真也是通信原理仿真领域的一项重要工作。
在matlab的仿真中,通常对模拟信号的传输和接收会更加复杂。
通信原理的matlab仿真的一个重要应用就是误码率和比特误差率测试。
误码率和比特误差率都是评估数字信号传输质量的指标。
通信系统的设计旨在在受到最小干扰时保持误差率的最小化。
基于MATLAB的模拟信号数字化系统的研究与仿真

基于MATLAB的模拟信号数字化系统的研究与仿真摘要本文研究的主要内容是《通信原理》仿真实验平台的设计与实现---模拟信号数字化Matlab软件仿真。
若信源输出的是模拟信号,如电话传送的话音信号,模拟摄像机输出的图像信号等,若使其在数字信道中传输,必须在发送端将模拟信号转换成数字信号,即进行A/D变换,在接收端则要进行D/A变换。
模拟信号数字化由抽样、量化、编码三部分组成。
由于数字信号的传送具有稳定性好,可靠性高,方便传送和传送等诸多优点,使得被广泛应用到各种技术中。
不仅如此,Matlab仿真软件是常用的工具之一,可用于通信系统的设计和仿真。
在科研教学方面发挥着重要的作用。
Matlab有诸多优点,编程简单、操作容易、处理数据迅速等。
本文主要阐述的是模拟信号数字化的理论基础和实现方法。
利用Matlab提供的可视化工具建立了数字化系统的仿真模型,详细讲述了抽样、量化、编码的设计,并指出了在仿真建模中要注意的问题。
在给定的仿真条件下,运行了仿真程序,得到了预期的仿真结果。
关键词:Matlab、模拟信号数字化、仿真绪论1837年,莫尔斯完成了电报系统,此系统于1844年在华盛顿和巴尔迪摩尔之间试运营,这可认为是电信或者远程通信,也就是数字通信的开始。
数字化可从脉冲编码调制开始说起。
1937年里夫提出用脉冲编码调制对语声信号编码,这种方法优点很多。
例如易于加密,不像模拟传输那样有噪声积累等。
但在当代代价太大,无法实用化;在第二次世界大战期间,美军曾开发并使用24路PCM系统,取得优良的保密效果。
但在商业上应用还要等到20世纪70年代。
才能取代当时普遍采用的载波系统。
我国70代初期决定采用30路的一次群标准,80年代初步引入商用,并开始了通信数字化的方向。
数字化的另一个动向是计算机通信的发展。
随着计算机能力的强大,并日益被利用,计算机之间的信息共享成为进一步扩大其效能的必需。
60年代对此进行了很多研究,其结果表现在1972年投入使用的阿巴网。
毕业设计(论文)基于matlab的数字基带通信系统仿真
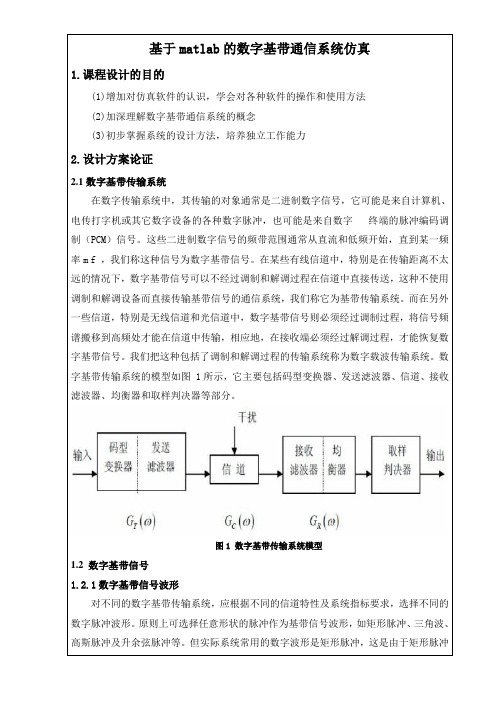
基于matlab的数字基带通信系统仿真1.课程设计的目的(1)增加对仿真软件的认识,学会对各种软件的操作和使用方法(2)加深理解数字基带通信系统的概念(3)初步掌握系统的设计方法,培养独立工作能力2.设计方案论证2.1数字基带传输系统在数字传输系统中,其传输的对象通常是二进制数字信号,它可能是来自计算机、电传打字机或其它数字设备的各种数字脉冲,也可能是来自数字终端的脉冲编码调制(PCM)信号。
这些二进制数字信号的频带范围通常从直流和低频开始,直到某一频率m f ,我们称这种信号为数字基带信号。
在某些有线信道中,特别是在传输距离不太远的情况下,数字基带信号可以不经过调制和解调过程在信道中直接传送,这种不使用调制和解调设备而直接传输基带信号的通信系统,我们称它为基带传输系统。
而在另外一些信道,特别是无线信道和光信道中,数字基带信号则必须经过调制过程,将信号频谱搬移到高频处才能在信道中传输,相应地,在接收端必须经过解调过程,才能恢复数字基带信号。
我们把这种包括了调制和解调过程的传输系统称为数字载波传输系统。
数字基带传输系统的模型如图 1所示,它主要包括码型变换器、发送滤波器、信道、接收滤波器、均衡器和取样判决器等部分。
图1 数字基带传输系统模型1.2 数字基带信号1.2.1数字基带信号波形对不同的数字基带传输系统,应根据不同的信道特性及系统指标要求,选择不同的数字脉冲波形。
原则上可选择任意形状的脉冲作为基带信号波形,如矩形脉冲、三角波、高斯脉冲及升余弦脉冲等。
但实际系统常用的数字波形是矩形脉冲,这是由于矩形脉冲纤数字传输系统中的线路传输码型。
此外,CMI 码和曼彻斯特码一样都是将一位二进制码用一组两位二进制码表示,因此称其为1B2B 码。
(5)4B/3T 码4B/3T 码是1B/1T 码的改进型它把4 个二进制码元变换为3个三进制码元。
显然,在相同信息速率的条件下,4B/3T 码的码元传输速率要比1B/1T 码的低,因而提高了系统的传输效率。
基于MATLAB模拟调制系统的仿真设计
基于MATLAB模拟调制系统的仿真设计摘要:本文基于MATLAB平台,通过建立调制系统的仿真模型,实现了对调制系统的仿真设计。
首先对调制系统的基本原理进行了介绍,然后建立了调制系统的数学模型。
接着使用MATLAB对模型进行了仿真分析,包括调制信号的产生、载波信号的产生、调制信号与载波信号的混合调制、调制后的信号的传输等过程。
最后,通过仿真结果的分析,对调制系统的性能进行了评估,并提出了优化方案。
本文的研究对于调制系统的设计和优化具有一定的参考意义。
关键词:调制系统;MATLAB仿真;混合调制;性能评估;优化方案一、引言调制是无线通信中的一项基本技术,通过将信息信号与载波信号进行合成,使信息信号能够被传输到远距离的通信接收端。
调制系统是实现调制技术的关键,其性能直接影响到通信系统的可靠性和传输质量。
因此,对调制系统的研究和优化具有重要的意义。
二、调制系统的基本原理调制系统的基本原理是将信息信号经过调制器与载波信号进行混合调制,形成调制后的信号。
调制过程中,需要考虑到载波频率、调制信号幅度、调制信号频率等参数的选择。
常见的调制方式有幅度调制(AM)、频率调制(FM)、相位调制(PM)等。
三、调制系统的数学模型调制系统的数学模型是根据调制原理建立的,一般可表示为:$s(t) = A_c \cdot (1 + m \cdot \cos(f_m \cdot t)) \cdot\cos(f_c \cdot t)$其中,$s(t)$表示调制后的信号,$A_c$为载波幅度,$m$为调制系数,$f_m$为调制信号频率,$f_c$为载波频率。
四、MATLAB仿真设计4.1调制信号的产生通过MATLAB生成调制信号,并将其绘制出来,以便后续的仿真分析。
4.2载波信号的产生通过MATLAB生成载波信号,并将其绘制出来,以便后续的仿真分析。
4.3调制信号与载波信号的混合调制将调制信号与载波信号进行混合调制,并将调制后的信号绘制出来,以便后续的仿真分析。
基于MATLAB的数字基带通信系统仿真
北京邮电大学世纪学院毕业设计(论文)题目基于Matlab的数字基带通信系统仿真学号学生姓名专业名称通信与信息工程所在系(院) 通信与信息工程系指导教师年月日北京邮电大学世纪学院毕业设计(论文)任务书备注1、由指导教师撰写,可根据长度加页,一式三份,教务处、系(院)各留存一份,发给学生一份,任务完成后附在论文内;2、凡审核不通过的任务书,请重新申报。
题目数字基带传输系统的仿真摘要本论文主要研究了数字信号的基带传输的基本概念及数字信号基带传输的传输过程和如何用MATLAB软件仿真设计数字基带传输系统。
本文首先介绍了MATLAB仿真软件。
然后介绍了本课题的理论依据,包括数字通信,数字基带传输系统的组成及数字基带信号的传输过程。
接着介绍了数字基带传输系统的特性包括数字PAM信号功率普密度及常用线路码型,并通过比较最终选择双极性不归零码。
之后介绍了数字基带信号的最佳接收的条件以及如何通过示波器观察基带信号的波形。
最后按照仿真过程基本步骤用MATLAB的仿真工具实现了数字基带传输系统的仿真过程,对系统进行了分析。
关键词数字基带传输系统 MATLAB 计算机仿真Title Digital Base Band Transmission System SimulationAbstractThis paper mainly studies the baseband transmission of digital signal and the basic concept of baseband transmission of digital signal in the transmission process and how to use MATLAB software to design and Simulation of digital baseband transmission system. This paper first introduces MATLAB simulation software. Then introduces the theoretical basis, including digital communication, digital baseband transmission system and digital baseband signal transmission process. Then it introduces the characteristics of digital baseband transmission system includes the digital PAM signal power spectrum density and commonly used line code, and through the comparison of the final choice of bipolar nrz. After introducing the digital baseband signal received by the best conditions and how the baseband signal waveform oscilloscope observation. Finally, in accordance with the basic steps of simulation process using MATLAB simulation tool to achieve the digital baseband transmission system simulation process, has carried on the system analysis.Keywords Digital Base Band Transmission System Computer simulation1.序论 (1)1.1 数字基带传输系统概述 (1)2. MATLAB基本知识 (4)2.1 MATLAB简介 (4)2.2 MATLAB特点 (4)2.3 MATLAB优势 (5)2.4 MATLAB常用函数 (7)2.5 MATLAB常用工具箱 (8)3.数字基带传输系统的简介 (10)3.1 研究意义 (10)3.2数字基带传输系统 (10)3.2.1 基带传输系统简介 (10)3.2.2 基带传输系统结构图 (11)3.2.3 基带传输过程 (11)4.综合研究基带传输系统的特性 (13)4.1数字PAM信号 (13)4.2数字PAM信号功率谱密度 (14)4.2.1单极性不归零码(NRZ) (14)4.2.2 双极性不归零码 (15)4.2.3 单极性归零码(RZ) (15)4.2.4双极性归零码 (16)4.2.5差分码(相对码) (17)4.3常用线路码型 (18)4.3.1 AMI码 (19)4.3.2 HDB3码 (19)4.3.3 CMI码 (20)4.3.4 数字双向码 (20)4.4数字基带信号的最佳接收 (20)4.5带限系统下的基带信号 (21)4.5.1 抽样点无码间干扰的基带成型 (21)4.5.2 升余弦滚降系统 (21)4.5.3 最佳基带系统 (21)4.5.4 基带信号眼图 (22)4.6 部分响应系统 (24)5.基带传输系统的设计及仿真 (25)5.1随机信号的产生 (26)5.1.1 高斯噪声的产生 (26)5.1.2 随机码序列的产生 (26)5.1.3 产生数字基带信号的一般方法 (26)5.1.4 NRZ及RZ信号的产生 (27)5.1.5 眼图 (28)5.2 误码率 (28)5.2.1取样判决 (28)5.2.2 误码率测量 (28)5.4 实验结果 (29)6.通信系统发展前景 (31)6.1 3G技术 ...................................................................................................... 错误!未定义书签。
基于MATLAB的模拟信号数字化系统的研究与仿真
脉冲编码调制(PCM)原理:
图 1-9 脉冲编码调制示意图
PCM 系统的原理方框图如下图所示,同种,输入的模拟信号 m(t)经抽样、量化、
编码后变换成数字信号,经心道传送到接收端的译码器,由译码器还原出抽样值,再经过
定理内容:抽样定理在时域上可以表述为:对于一个频带限制在(0,fH)Hz 内的时间 连续信号 f(t),如果以 Ts≤1/(2fH)秒间隔对其进行等间隔抽样,则 f(t)将被所得到的 抽样值完全确定。模拟信号的抽样过程如下图。
图 1-2 模拟信号抽样的过程示意图
下图分析可知模拟信号抽样过程中各个信号的波形与频谱。
模拟信号数字化系统的研究与仿真
5
通信原理课程设计
图 1-4 两种情况下的抽样信号频谱分析
应该注意的一点是:抽样频率并不是越高越好。只要能满足抽样频率大于奈奎斯特频 率,并留有一定的防卫带即可。
1.1.2 带通信号的抽样定理
实际中遇到的许多信号时带通型信号,模拟信号的频道限制在 fL~fH 之间,fL 为信号 最低频率,fH 为最高频率。而且当 fH>B,其中 B=fH-fL 时,该信号通常被成为带通型信号, 其中 B 为带通信号的频带。
对于带通信号,如果采用低通抽样定理的抽样速率 fs≥2fh,对频率限制在 fL 与 fH 之间 的带通型信号抽样,肯定能满足频谱不混叠的要求,如图所示。
模拟信号数字化系统的研究与仿真
6
通信原理课程设计
图 1-5 带通信号的抽样频谱
定理内容:一个带通信号 f(t),其频率限制在 fL 与 fH 之间,带宽为 B=fh-fl,如果 最小抽样速率 fs=2fh/n,n 是一个不超过 fh/B 的最大整数,那么 f(t)就可以完全由抽 样值确定。 下面两种情况说明:
现代控制系统分析与设计——基于matlab的仿真与实现
现代控制系统分析与设计——基于matlab的仿真与实现随着社会经济的发展,现代控制理论对于促进技术进步有着巨大的贡献。
随着现代控制技术的发展,设计现代控制系统的重要性也随之增加。
本文的主要目的是分析和设计基于matlab的现代控制系统,并进行仿真和实现。
现代控制系统涉及多种理论,比如微分方程,线性系统理论,数字滤波,信号处理等等。
而matlab是一款非常便捷的工具,可以帮助我们更有效率的分析和设计现代控制系统。
首先,matlab可以用来帮助我们研究现代控制系统的特性和性能,可以实现过程模拟,帮助我们定义控制系统的模型,进而确定系统的参数,以此设计更有效的控制系统。
此外,matlab还可以进行提示性程序和实际应用程序的构建,可以用来实现现代控制系统的仿真。
仿真可以帮助我们更好地理解现代控制系统的工作原理和特性,因此,matlab可以用作控制系统的重要设计工具。
另外,matlab的可视化界面可以帮助我们实现更直观的仿真,它可以提供更多的可视化效果,以便实现对控制系统特性和性能的详细分析和研究。
最后,matlab也可以用来实现现代控制系统的实际实施,利用matlab来实现控制系统,不仅可以增加开发效率,更重要的是可以增加系统稳定性和可靠性。
综上所述,matlab可以用来分析和设计现代控制系统,实现仿
真和实施,这一切都有助于提高我们的现代控制系统设计的效率和水平,从而大大提高了我们的社会生活和工作效率。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基于MATLAB的数字模拟仿真摘要:本文阐述了计算机模拟仿真在解决实际问题时的重要性,并较为系统的介绍了使用计算机仿真的原理及方法。
对于计算机模拟仿真的三大类方法:蒙特卡罗法、连续系统模拟和离散事件系统模拟,在本文中均给出了与之对应的实例及基于MATLAB模拟仿真的相关程序,并通过实例深入的分析了计算机模拟解决实际问题的优势及不足。
关键词:计算机模拟;仿真原理;数学模型;蒙特卡罗法;连续系统模拟;离散事件系统模拟在实际问题中,我们通常会面对一些带随机因素的复杂系统,用分析方法建模常常需要作许多简化假设,这样进行处理过后的模型与我们面临的实际问题可能相差很远,以致求解得到答案根本无法应用,这时,计算机模拟几乎成为唯一的选择。
本文通过对计算机模拟仿真进行系统地介绍,寻求利用模拟仿真来解决问题的一般方法,并深入探讨了这些方法的长处和不足。
我们定义一些具有特定的功能、相互之间以一定的规律联系的对象所组成的总体为一个系统,模拟就是利用物理的、数学的模型以系统为问题解决对象,来类比、模仿现实系统及其演变过程,以寻求过程规律的一种方法。
模拟的基本思想是建立一个实验的模型,这个模型包含所研究系统的主要特点,这样做的目的就是通过对这个实验模型的运行,获得所要研究系统的必要信息。
另外,系统的运行离不开算法,仿真算法是将系统模型转换成仿真模型的一类算法,在数字仿真模型中起核心和关键作用。
1、所谓计算机仿真计算机仿真是利用计算机对一个实际系统的结构和行为进行动态演示,以评价或预测该系统的行为效果。
它是解决较复杂的实际问题的一条有效途径。
针对一个确定的系统,根据运行的相似原理,利用计算机来逼真模仿研究对象(研究对象可以是真实的系统,也可以是设想中的系统),计算机仿真是将研究对象进行数学描述,建模编程,且在计算机中运行实现。
对比于物理模拟通常花费较大、周期较长,且在物理模型上改变系统结构和系数都较困难的诸多缺陷,计算机模拟不怕破坏、易修改、可重用,有更强的系统适应能力。
但是计算机模拟也有缺陷,比如受限于系统建模技术,即系统数学模型不易建立、程序调试复杂等。
计算机仿真可以用于研制产品或设计系统的全过程中,包括方案论证、技术指标确定、设计分析、生产制造、试验测试、维护训练、故障处理等各个阶段。
2、计算机仿真的目的对于一个系统,是否选择进行计算机模拟的问题,基于判断计算机模拟与非计算机模拟方法孰优孰劣的问题。
归纳以下运用计算机模拟的情况:(1)在一个实际系统还没有建立起来之前,要对系统的行为或结果进行分析研究时,计算机仿真是一种行之有效的方法。
(2)在有些真实系统上做实验会影响系统的正常运行,这时进行计算机模拟就是为了避免给实际系统带来不必要的损失。
如在生产中任意改变工艺参数可能会导致废品,在经济活动中随意将一个决策付诸行动可能会引起经济混乱。
(3)当人是系统的一部分时,他的行为往往会影响实验的效果,这时运用系统进行仿真研究,就是为了排除人的主观因素的影响。
(4)在实际系统上做实验时,由于系统误差和偶然误差的存在,对实验结果的好坏我们很难作出正确的判断,这时运用计算机模拟,就可以保证每次操作的条件相同,排除误差。
(5)有些系统一旦建立起来之后就无法复原,利用计算机模拟可重复性的这一优势,可以获得显著的经济效益。
例如要投资建立一个大型企业,要分析它建成之后的经济效益和社会效益,不能用建立起来试试看的办法,因为建成后就无法回到原来的状态了。
3、计算机仿真的分类计算机模拟分为动态模拟和静态模拟,数值分析中的蒙特卡罗法就是典型的静态模拟,动态模拟可以分为连续系统模拟和离散事件系统模拟。
连续系统模拟研究系统的状态随时间连续变化的情况,在解决实际问题时,一般要建立微分方程模型,先确定系统的连续状态变化量,然后将它在时间上进行适当的离散量化处理,并由此模拟系统的运行状态。
而离散事件系统模拟讨论的是系统状态只在一些离散时间点上,由于随机时间的推进而发生变化,其问题解决模型一般用流程图或网络来表示。
注:连续系统模拟中虽然有时也考虑一些随机作用,但经常还是把它当作确定性问题去考虑,而在离散事件系统模拟中事件的出现和系统状态变量几乎总都是随机的。
但是,值得注意的一点是,在这两种系统模拟中时间具有重要作用,我们都是要观察系统在时间过程中的变化。
4、计算机仿真的原理事实告诉我们,现实世界充满不确定性,我们所研究的现实对象往往难以摆脱随机因素的影响。
要使我们的数学模型能够较真实地刻画实际对象,必须面对这个现实。
概率论是用数学的思想和方法处理和研究随机现象的一个有效的工具。
但有时它还难以用来处理复杂系统中的随机性。
而我们运用计算机来模拟随机现象的方法基于随机数,它经常应用于复杂系统的动态仿真的研究当中。
仿真模型是处理复杂系统中随机性的计算机模型,也是使用计算机研究和解决实际问题的一条重要途径。
对随机现象进行模拟,实质上要给出随机变量的模拟,也就是说利用计算机随机地产生一系列数值(称为随机数),它们的出现要服从一定的概率分布。
目前,经常使用的是按照在实际应用中用哪种随机数生成法,要针对具体的系统做出与之相适应的选择。
(1)当研究对象视为大量相互独立的随机变量之和,且其中每一种变量对总和的影响都很小时,可以认为该对象服从正态分布。
(2)考试分数的偏差、射击命中点与目标的偏差、人的身高、体重等,都可近似看成服从正态分布。
(3)排队服务系统中顾客到达率为常数时的到达间隔、故障率为常数时零件的寿命都服从指数分布。
指数分布在排队论、可靠性分析中有广泛应用。
(4)涉及到排队系统、产品检验、天文、物理等领域时可用到泊松分布。
5、计算机仿真的方法5.1解决计算机模拟的一般步骤:进行计算机仿真一般要进过四个步骤:系统分析,模型构造,运行与改进和输出结果[]1。
图中A 表示系统分析,B 表示模型构造,C 表示运行与改进,D 表示输出结果第一步:系统分析,明确目标。
就是要明确问题和提出总体方案。
首先要把被仿真系统的内容表达清楚,弄清仿真的目的,然后选择描述这些目标的主要环节和状态变量,明确定义所研究问题的范围、边界和初始条件,并充分估计初始条件对系统主要性能的影响。
第二步:模型构造、采集数据。
包括建立模型、收集数据、编写程序、程序验证和模型确认等。
建立模型就是选择合适的仿真方法,如时间步长法、事件表法等,确定系统的初始状态, 设计整个系统的仿真流程。
最后选择合适的通用语言或仿真语言编写、调试程序。
第三步:模型的运行与改进。
首先确定一些具体的运行方案,如初始条件、参数、步长、重复次数等,然后输入数据,运行程序,直到符合实际系统的要求及精度为止。
第四步:模型输出、统计分析。
包括提供文件的清单,记录重要的中间结果,输出格式要有利于用户了解整个仿真过程,分析和使用仿真结果。
D 图4-1:仿真步骤流程5.2针对不同的模拟方法举例5.2.1基于随机数来进行计算机模拟的蒙特卡罗法(Random simulation )蒙特卡罗法属于实验数学的一个分支,它利用随机数进行统计试验,以求得的统计特征值(如均值、概率等)作为待解决问题的数值解。
而在这一过程中所作的统计试验称为蒙特卡罗法。
蒙特卡罗法的基本思想原理是首先建立一个概率模型,使所求问题的解正好是该模型的参数或其他有关的特征量。
然后通过模拟、统计,即多次随机抽样实验,统计出某事件发生的百分比。
只要实验次数很大,该百分比便近似于事件发生的概率。
而这实际上也就是概率的统计定义。
5.2.1.1蒙特卡罗法的原理这里引用资料[]2,根据车比雪夫定理,设1X ,2X ,, ,n X 是相独立的随机变量序列,它们服从相同的分布,且有有限的数学期望a 和方差 ,则1X ,2X ,, ,n X 的算术平均值当时∞→n 按概率1收敛于a ,即对于任意0>ε有:111lim =⎭⎬⎫⎩⎨⎧<-∑=∞→εn i i n a x n P 由中心极限定理得到:⎰∑∞+∞--=∞→=⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧≤-dt e a x n P t n i i n 212211lim πεσ 即当n 很大时,σa x n ni i -∑=11近似服从标准正态分布。
5.2.1.2蒙特卡罗法的实例应用这里应用蒙特卡洛法解决最古老但又不失经典的例子——浦丰(Buffon)投针问题。
问题重述:若干条相互平行线间的距离为d ,针的长度为l ,将针投出后其与平行线相交的概率为P ,求出其概率。
模型建立:通过计算可知针与平行线相交的概率为:πd l 2=P其中d 为平行线间距离,l 为针的长度,其中d l <,将针投n 次,若有m 次与平行线相交,则可用n m 作为P 的近似值。
由此可计算出π的近似值为:m d nl 2≈π 注:要使结果更加准确就需使n 尽量大一些编程求解:设x 是一随机变量,它服从区间[]d 0,上的均匀分布。
同理,ϕ是服从区间[]π,0上的均匀分布。
按照某种抽样法,产生随机变量的可能值,例如进行n 次抽样,得到样本值()i i x ϕ,,其中n 2,1i ,, =,统计出满足不等式:()d lsin x i i ≥+ϕ的次数()n <m m 然后利用MATLAB7.0进行进行计算机编程模拟(程序见附录一)。
当取1=l ,2=d10000=n 时,模拟得到:概率3185.0=P ,圆周率1397.3=π 这与真实值已经很接近了。
5.2.2基于离散时间点上的离散型随机变量的模拟(Discrete system )离散系统是指系统状态只在有限的时间点或可数的时间点上有随机事件发生的系统,在这些点上发生的离散事件改变了系统的状态,并假设系统状态的变化是在该时间点上瞬时完成的,即离散事件是瞬时出现的。
5.2.2.1离散型随机变量模拟的原理设离散随机变量X 的可能值为{}i x ,相应的概率为i i p x X P ==)(,,,2,1 =i 设()00=p,()∑==ni i n p p1,,,2,1 =n 将)(n p 作为分点,把区间()1,0分为一系列小区间()()()n n p p ,1-。
设Y 是()1,0上均匀随机变量,则有:()()()n n p Y p P ≤<-1=()()1--n n p p =n p =()n x x P =, ,2,1=n因此可以用随机变量Y 落在内的情况来模拟离散的随机变量X 的取值情况。
5.2.2.2离散型随机变量模拟的实例应用在离散型随机变量模拟所解决的问题中,排队系统是一类很常见又非常重要的问题,且这类问题广泛存在于银行、医院、超市等现实生活中的领域。
由一个或多个服务台和一些等待服务的顾客组成的离散时间系统称为排队系统。
这里列举一个简单的排队系统问题,并从中了解离散型随机变量模拟的思想方法。
