土力学天然地基承载力
土力学天然地基承载力
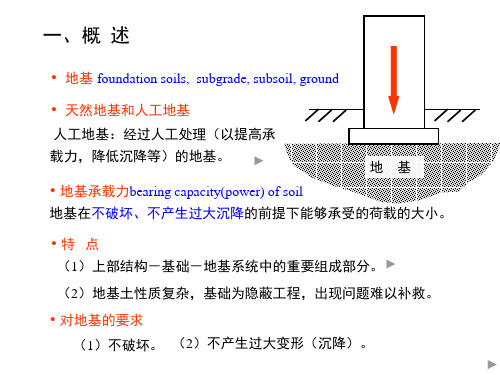
Nc (Nq 1) cot
缺陷：基础置于砂土地基表面（c=0，H=0）时
地基极限承载力为0
地基破坏的模型试验
2. Prandtl-Vesic公式
地基土的自重所对应的极限承载力为
pk
1 2
1
b
N
则埋深为H、粘聚力为c、内摩擦角为φ的地基的极限承载力为
式中
pk pk pk
Nc
c
Nq 2
基底
III
土体移动方向
90 剪切破坏面（滑移面）
对数螺旋线 r=r0 exp( tan )
I：主动区 II：过渡区 III：被动区 均处于极限平衡（破坏）状态
破坏面夹角为 90
• 极限承载力 pk Nq 2 H Nc c Prandtl-Reissner公式
Nq
tan2 (45
) exp( tan)
二、地基的典型破坏形态
1. 整体剪切破坏 general shear
剪切破坏面与地面连通，形成圆弧滑面，地基土从侧面挤出。
密实砂土或硬粘土
临塑荷载 pa
pk 极限荷载
p
S p－S 曲线是地基土变形、破坏的宏观反映。
2. 局部剪切破坏 local shear
破坏面未延伸到地表，地表微微隆起。
中密砂土或一般粘性土 或基础埋深较大时
Meyerhof (50年代) Hansen (60年代)
Vesic (70年代)
1. Prandtl-Reissner地基极限承载力计算公式
Prandtl (1920)建立地基无自重、基础置于地表地基的极限承载力 Reissner (1924)将基础两侧土作为荷载施加于地基，建立承载力计算 公式。
浅谈浅基础地基承载力的确定
浅谈浅基础地基承载力的确定摘要：地基承载力是土力学的三大经典问题之一。
天然地基承载力是岩土工程勘察文件中不可缺少的一个内容，也是天然地基浅基础设计的基本依据。
在承受基础以及上部建筑物的所有荷载作用下，地基中的应力状态会发生改变。
一方面附加应力引起地基内土体变形，导致建筑物沉降，另一方面，当土中一点的某一面上的剪应力等于该点地基土的抗剪强度时，该点就达到极限平衡，发生剪切破坏。
在确定地基承载力时，必须满足上述两个条件，即变形与强度两个指标同时满足规范允许值，才能达到规范对建筑物地基承载力的要求。
关键词：地基承载力；原位试验；临塑荷载；临界荷载；极限承载力；静止侧压力系数。
1.1 浅基础地基承载力概述地基承载力问题是土力学中的一个重要的研究课题，其目的是为了掌握地基的承载规律，发挥地基的承载能力，通过合理确定地基承载力确保地基不致因荷载作用而发生剪切破坏，产生过大变形而影响建筑物或土工建筑物的正常使用。
为此，地基基础设计一般都限制基底压力最大不超过地基容许承载力。
地基承载力计算方法的合理确定，对工程的经济性和安全性影响极大。
在规范中涉猎了五个不同的承载力概念：地基容许承载力、地基承载力基本值、地基承载力标准值、地基承载力设计值和地基承载力特征值。
地基容许承载力（[f]）：在保证地基稳定性和建筑物的沉降量不超过容许值的的条件下，地基土体所能承受的最大压力；地基承载力基本值（f0):根据土的室内试验或原位测试物理力学指标的平均值,按经验公式计算或查经验表格得到，相当于标准基础宽度和深度时的地基容许承载力值；地基承载力标准值（fk）：考虑了土性指标变异影响后，相当于标准基础宽度和埋深时地基容许承载力代表值，可通过承载力基本值乘以回归修正系数得到，也可通过野外鉴别结果、标准贯入试验、轻便触探试验锤击数查表获得；地基承载力设计值(f)：地基承载力标准值经基础宽度和埋深修正后的值，或直接用地基强度指标按承载力理论公式计算得到的地基承载力。
地基承载力
p1/ 4
(c ctg d b / 4) d 244 .1kPa ctg / 2
(2)地下水位上升时，地下水位以下土的重度用有效重度
sat w 11.0kN / m3
1.5 19 0.5 11 17.0kN / m3 2 (c ctg 0 d / 4) b 0 d 225 .7kPa ctg / 2
普朗特尔理论的极限承载力理论解
pu cNc 承载力系数 2 0 式中： N c ctg [exp( tan ) tan (45 / 2) 1]
当基础有埋深d 时 式中： P
pu cNc 0 dNq
N q exp( tan ) tan 2 (45 0 / 2)
二、临塑荷载pcr和临界荷载 (d c ctg ) 当zmax＝0，地基所 p d ctg 2 能承受的基底附加 压力为临塑荷载 (c ctg d b / 4) p d 中心荷载 ctg / 2 塑性区开展深度在 某一范围内所对应 (c ctg d b / 3) p d 偏心荷载 的荷载为临界荷载 ctg / 2
pu 0.6bN 0 dNq 1.2cNc 重庆交通大学河海学院 岩土与地质工程系
23
三、汉森极限承载力理论
对于均质地基、基础底面完全光滑，受中心倾斜荷载作用
汉森公式
pu 1/ 2bN S d i g b 0 dNq Sq d qiq g qbq cNc Sc dcic g cbc
24
按理论公式确定地基容许承载力
地基的容许承载力 将上述各公式算出的极限承载力Pu，除以安 全系数Fs，即得到地基的容许承载力
天然地基承载力与地基强度—按设计规范确定地基承载力(土力学课件)
(2)各类岩土地基基本承载力表中的数值允许内插；
(3)原位测试方法及成果的应用，可参照国家和铁道部
有关标准的规定。
1、岩石地基的基本承载力
岩石类别
确定因素：
节理间距
节理发育情况
查表
（见规范）
例
30<35<60,硬质岩
节理很发育
节理发育
节理不发育
密实程度
土名
湿度
稍 松 稍 密 中 密
密
实
砾砂、粗砂
与湿度无关
200
370
430
550
中砂
与湿度无关
150
330
370
450
稍湿或潮湿
100
230
270
350
饱 和
-
190
210
300
稍湿或潮湿
-
190
210
300
饱 和
-
90
110
200
细砂
粉砂
某砂样,粒径大于0.25mm的颗粒含量超过全重的50%
《铁路桥涵地基和基础设计规范》
确定地基基本承载力
（TB10002.5-2005）
《铁路桥涵地基和基础设计规范》
一、地基土基本承载力的确定
地基土基本承载力0 指地质简单的一般桥涵地基，当基础
的宽度b≤2m，埋置深度小于h≤3m时地基的承载力。
二、规范规定
(1)当基础宽度b(m)，对于矩形基础为短边宽度，对于
(1) 基础宽度b，对于矩形基础为短边宽度，对于圆形或正多
边形基础为F1/2（ F为基础的底面积）。
(2)各类岩土地基基本承载力表中的数值允许内插；
土力学-第六章土压力、地基承载力和土坡稳定
土楔在三力作用下，静力平衡
E 1 2 h Ka 2
滑裂面是任意给定的，不同滑裂面得 到一系列土压力E，E是q的函数，E 的最大值Emax，即为墙背的主动土压 力Ea，所对应的滑动面即是最危险滑 动面
1 2 Ea h 2 cos 2 ( ) sin( )sin( ) 2 cos cos( ) 1 cos( ) cos( )
36.6kPa
paB下 1h1K a 2 2c2 K a 2＝ .2kPa － 4 paC ( 1h1 2 h2 ) K a 2 2c2 K a 2 36.6kPa
＝ 主动土压力合力 Ea 10.4 2 / 2 (4.2 36.6) 3 / 2 71.6kN / m
hKp ＋2c√Kp
1.粘性土被动土压力强度不存在负侧压力区 2.合力大小为分布图形的面积，即梯形分布图形面积 3.合力作用点在梯形形心
hp
四、例题分析 【例】有一挡土墙，高6米，墙背直立、光滑，墙后填土
面水平。填土为粘性土，其重度、内摩擦角、粘聚力如下 图所示 ，求主动土压力及其作用点，并绘出主动土压力 分布图
pa zKa 2c K a
pa zK a
h
hKa
1.无粘性土主动土压力强度与z成正比，沿墙高呈三角形分布 2.合力大小为分布图形的面积，即三角形面积 3.合力作用点在三角形形心，即作用在离墙底h/3处
h/3
Ea
(1/ 2)h2 Ka
当c＞0, 粘性土
pa zKa 2c K a
z0 ≤0说明不存在负侧压力区，
2.成层填土情况（以无粘性土为例）
h1
h2 h3
A B
土压力、地基承载力
必须注意，在图中所 示的土压力分布图只 表示其大小，而不代 编辑ppt 表其作用方向。
3)墙背对土楔体的反力E，与它大小相等、方向相反 的作用力就是墙背上的土压力。反力E的方向必与墙 背的法线N2成δ角。当土楔下滑时，墙对土楔的阻力 是向上，故反力E必在N2的下侧。
E1 2H 2c co 2 o s s s)i(cn o )( s s)i(sn i n ( ))(
压力通过梯形压力分布图的形心。
Ep1 2H2Kp2cHKp
编辑ppt
3.4 几种情况下的土压力计算
3.4.1 填土面有均布荷载
a）连续均布荷载q
方法：将均布荷载换算成当量的土重，当量的土层
厚度（虚构） hq/ ;
由均布荷载q换算成虚构填土高h,产生的土压力按 墙高为h+H计算。
b）填土面和墙背倾斜
编辑ppt
—土压力与土坡稳定性—
土坡可分为天然土坡和人工土坡，由于人工开挖 和不利的自然因素，土坡可能发生整体滑动而失稳。 土坡的滑塌常造成严重的工程事故，并危及人身安 全。因此对影响工程安全的天然边坡或人工边坡都 应进行边坡的稳定性验算，对不稳定边坡宜采取必 要的工程措施予以加固。对于某些人工边坡，如高 层建筑深基坑周缘、人工堆填土边缘，由于空间限 制使边坡角设计很陡，临空面附近的土体会沿着直 线面或弧形面下滑，因此必须预先采用挡土墙等结 构物以平衡土坡的侧向压力，我们把这种压力称为 土压力。土压力的计算是对人工土坡进行支挡结构 设计的前提。
φ--墙后填土的内摩擦角（度）；
α--墙背的倾斜角（度），俯斜时取正号，仰斜
为负号；
β--墙后填土面的倾角（度）；
δ--土对挡土墙背的摩擦角根据墙背填土的内摩
擦角φ查表确定。
地基土的承载力
地基土的承载力地基土的承载力是指地基土在不破坏的情况下能承受的最大荷载。
在土力学中，承载力是一个重要的概念，通常用来设计建筑物、路基、桥梁等工程结构的基础。
在地基设计中，了解地基土的承载力是至关重要的。
本文将介绍地基土承载力的基本概念、影响因素和计算方法。
承载力的定义地基土的承载力是指土体在无限趋近于极限状态时，土体内产生的抗力，也就是它所能承受的最大荷载。
承载力的计算是地基设计的重要环节，它直接关系到工程结构的安全性和可靠性。
影响因素1.土的类型不同类型的土壤有着不同的物理、化学和力学性质。
因此，不同类型的土壤对于荷载的承受能力也有着不同的影响。
比如，黏性土和粘性土的黏聚力和内摩擦角相对较大，其承载能力也相对较高。
2.土体密度土体的密度是指单位体积土壤中的含水量和固体颗粒的体积之比。
土体密度的大小直接影响到土的承载能力，一般来说，土体密度越大，它的承载能力就越高。
3.底部条件底部条件是指地基土与固体底面的接触情况和底部土壤本身的性质，对于地基土的承载能力也有着重要的影响。
一些底部条件比较差的情况，如泥淖地或淤泥地，他们的承载能力就相对较低。
4.荷载类型和荷载方式地基土承载能力的大小也直接与荷载类型和荷载方式有关。
对于不同的荷载类型，如静载和动荷载，承载能力计算的方法也不尽相同。
同样的，不同方向的荷载也会对地基土的承载能力产生影响。
比如侧向荷载，它的承载能力通常要低于竖直荷载。
承载力的计算承载力的计算通常可以使用理论和实验两种方法。
根据土力学原理，可以通过计算土壤中抗剪强度的大小来确定其承载能力。
这种方法成为理论方法。
另外，通过实验方法也可以对地基土的承载能力进行估算。
在理论计算中，可以根据土壤的类型、密度和底部条件等因素来确定土壤的抗剪强度大小。
然后通过计算出在不同荷载情况下土壤中的剪应力大小，来进一步计算出地基土的承载力。
在实验室中，可以通过模拟地基荷载的情况，进行试验来测定土壤的承载能力。
土力学讲课第六章地基土承载力
例题分析
有一条形基础，宽度 b = 3m ，埋深 h = 1m ，地基土内摩擦角 j =30 °，黏聚力 c =20kPa ，天然重度 =18kN/m 3 。试求：
（ a ）地基临塑荷载； （ b ）当极限平衡区最大深度达到 0.3 b 时的均布荷载数值。 解
：
（ a ）计算公式：
（b）临界荷载：
（1）原位测试
（1） 静载荷试验
fa=fak+b(b-3)+dm(d-0.5)
fak :静载荷试验确定的承载力-特征值（标准值） fa ：深宽修正后的承载力特征值（设计值）
（2）承载力公式法：
fa=Mbb+Md md+Mcck fa :承载力特征值（设计值）
——相当与
p1/4=NB /2+Nq d+Ncc
时，有：
化简后，得到：
p
0.3b
=333.8kPa
总结上节课的内容 极限承载力理论界和半理论解 1 Prantl解 假设和滑裂面形状 2 太沙基解，一般解形式 3 极限承载力的影响因素 , c, ，D, B,
pu
B
2
N cNc qNq
B
p 实际地面 D I 45o－/2 III II E F
• 合力= 1， 3 • 设k0 =1.0 • 弹性区的合力：
图6.5 条形均布荷载作用下地基主应力
p D (a)无埋置深度 (b)有埋置深度 1,3 ( 0 sin 0 ) ( D z ) （ 1）
允许地基中有一定的塑性区，作为设计承载力
--考察地基中塑性区的发展
D
D
I区：朗肯主动区
垂直应力pu为大主应力，
地基承载力原理
地基承载力原理
地基承载力原理是指建筑物在地基上受力时，通过地基的承载和传递，使地基能够承受和传递建筑物的重力和其他荷载。
地基承载力原理是土力学中的基础理论之一。
在建筑物施工过程中，地基承载力原理起着重要的作用。
建筑物的重力和其他荷载会通过建筑结构传递到地基上，地基将这些荷载承受并向地下分散。
地基的承载力是指地基能够承受的最大荷载。
地基承载力的大小与地基的类型、土壤的性质、地基的深度等因素有关。
不同类型的地基，如浅基础、深基础、桩基等，其承载力的计算方法也有所不同。
土壤的性质对地基承载力有直接影响。
不同种类的土壤具有不同的承载力，如黏土、砂土、砾石等。
土壤的密实程度、含水量以及土壤颗粒的大小和形状都会影响地基的承载力。
地基的深度也是影响地基承载力的关键因素。
通常情况下，地基的承载力随着地基的深度增加而增加。
这是因为地基深入地下后，能够承受的土体体积增加，从而增加了承载力。
为了确保建筑物的安全和稳定，需要对地基承载力进行合理的计算和评估。
通过合理设计地基的面积、深度和类型，可以确保地基能够承受建筑物的荷载，并稳定地传递到地下。
这样可以防止地基荷载过大导致地基沉降或破坏，从而保证建筑物的使用寿命和安全性。
总之，地基承载力原理是建筑物施工过程中不可忽视的重要原理。
通过合理设计和计算地基的承载力，可以保证建筑物的安全和稳定。
土力学与地基基础地基承载力的确定
f ak
分为浅层平板和深 层平板载荷试验
2) 试验装置
3) 测试方法及步骤
4) 试验数据整理 5) 按载荷试验成果确定地基承载力特征 值 ⑴ 当p~s曲线上有比例界限时，取其比例界限所对应的 荷载值
po f ak
⑵ 当极限荷载小于比例极 限荷载值的2倍时，取其极 限荷载值的一半
f ak ps
△ d
f a M bb M d md M cCk
b
b
例题 某粘土地基上的基 础尺寸及埋深如右 图所示 试按强度理论公式计 算地基承载力特征值 分析
16.5kN / m3
地下水位
1 .8 m
2 .0 m
0 .6 m
sat 18.5kN / m 3 k 26.5o
2) 修正公式
f a f ak b b 3 d m d 0.5
修正后的地基承 载力特征值 地基承载力 特征值
注意： ⑴ 基础埋深范围内的土的重度要 加权平均，持力层在地下水位下要 取有效重度。
基础宽度和埋深的地基 承载力修正系数
⑵ b＜3m按3m取值，b＞6m按6m取值。
例：某基础底面尺寸为 3.0*4.8m，其它结构与 地基资料如右图所示：
2 .0 m
17.2kN / m3 16.6kN / m3
人工填土 粉土
0 .8 m 1 .2 m
试确定持力层地基承载 力特征值的修正值 分析：
18.7kN / m3
I L 0.5, e 0.83 f ak 176kPa
ck 5kPa
f a M bb M d md M cCk
m?
7.4.4 经验方法确定地基承载力 大量工程实践中，人们总结了一些 实用的确定地基承载力的方法，用 来综合确定地基承载力。 7.4.4.1 间接原位测试的方法
(完整版)地基承载力检测
地基承载力如何检测1、平板荷载试验：适用于各类土、软质岩和风化岩体。
平板荷载试验平板荷载试验是一项使用最早、应用最广泛的原位试验方法，该试验是在一定尺寸的刚性承压板上分级施加荷载，观测各级荷载作用下天然地基土随压力和变形的原位试验，它可用于：根据荷载-沉降关系线(曲线)确定地基力的承载力；设计土的变形模量；估算土的不排水抗剪强度及极限填土高度。
平板荷载试验适用于地表浅层地基，特别适用于各种填土、含碎石的土类。
由于试验比较直观、简单，因此多年来应用广泛，但本方法的使用有以下局限性：平板荷载试验的影响深度范围不超过两倍承压板宽度(或直径)，故只能了解地表浅层地基土的特性；承压板的尺寸比实际基础小，在刚性板边缘产生塑性区的开展，更易造成地基的破坏，使预估的承载力偏低。
荷载平板试验是在地表进行的，没有埋置深度所存在的超载，也会降低承载力；应用时应考虑荷载试验的加载速率较实际工程快得多，对透水性较差的软粘土，其变形状况与实际有较大的差异，由此确定的参数也有很大的差异；小尺寸刚性承压板下土中的应力状态极复杂，由此推求的变形模量只能是近似的。
1 荷载板2千斤顶3加长杆4调节丝杆5球铰座 6 手动液压泵7 油压表8 测桥9 百分表10仪表支架11测桥支撑座图1 平板荷载仪组成示意图2、螺旋板荷载试验：适用于软土、一般粘性土、粉土及砂类土。
试验方法螺旋板载荷试验是将一螺旋型的承压板用人力或机械旋入地面以下的预定深度，通过传力杆向螺旋形承压板施加压力，测定承压板的下沉量，其深度可达10-15米，可测求地基土的压缩模量、固结系数、承载力等指标。
试验时应按如下步骤进行：1.1 在所需进行试验的位置进行钻孔，当钻至试验深度上20-30cm处，停止钻进，清除孔底受压或受扰动土层。
1.2 将螺旋板连接在传力杆上旋入土层，螺旋板入土时，应按每转一圈下入一个螺距进行操作，减少对土的扰动。
螺旋板与土层的接触面应加工光滑，可使对土体的扰动大大减少。
(完整版)地基承载力
第十章 地基承载力第一节 概述地基随建筑物荷载的作用后，内部应力发生变化，表现在两方面：一种是由于地基土在建筑物荷载作用下产生压缩变形，引起基础过大的沉降量或沉降差，使上部结构倾斜，造成建筑物沉降；另一种是由于建筑物的荷载过大，超过了基础下持力层土所能承受荷载的能力而使地基产生滑动破坏。
因此在设计建筑物基础时，必须满足下列条件： 地基： 强度——承载力——容许承载力变形——变形量（沉降量）——容许沉降量一、几个名词1、地基承载力：指地基土单位面积上所能随荷载的能力。
地基承载力问题属于地基的强度和稳定问题。
2、容许承载力：指同时兼顾地基强度、稳定性和变形要求这两个条件时的承载力。
它是一个变量，是和建筑物允许变形值密切联系在一起。
3、地基承载力标准值：是根据野外鉴别结果确定的承载力值。
包括：标贯试验、静力触探、旁压及其它原位测试得到的值。
4、地基承载力基本值：是根据室内物理、力学指标平均值，查表确定的承载力值，包括载荷试验得到的值）。
通常0f f f k ψ=5、极限承载力：指地基即将丧失稳定性时的承载力。
二、地基承载力确定的途径 目前确定方法有：1．根据原位试验确定：载荷试验、标准贯入、静力触探等。
每种试验都有一定的适用条件。
2．根据地基承载力的理论公式确定。
3．根据《建筑地基基础设计规范》确定。
根据大量测试资料和建筑经验，通过统计分析，总结出各种类型的土在某种条件下的容许承载力，查表。
一般：一级建筑物：载荷试验，理论公式及原位测试确定f ；二级建筑物：规范查出，原位测试；尚应结合理论公式； 三级建筑物：邻近建筑经验。
三、确定地基承载力应考虑的因素地基承载力不仅决定于地基的性质，还受到以下影响因素的制约。
1．基础形状的影响：在用极限荷载理论公式计算地基承载力时是按条形基础考虑的，对于非条形基础应考虑形状不同地基承载的影响。
2．荷载倾斜与偏心的影响：在用理论公式计算地基承载力时，均是按中心受荷考虑的，但荷载的倾斜荷偏心对地基承载力是有影响的。
天然基础的地基承载力限值
天然基础的地基承载力限值一、概述天然基础的地基承载力是指地基在承受建筑物或其他结构物荷载时，不发生剪切破坏、沉降变形或倾覆失稳的最大荷载值。
为了确保建筑物的安全与稳定，必须对地基承载力进行合理的设计和控制。
本篇文档将围绕影响天然基础的地基承载力限值的因素展开讨论，主要涉及基础材料强度、基础埋置深度、地基土质条件、基础面积与形状、地下水条件、环境因素、荷载特性以及相邻基础影响等方面。
二、基础材料强度基础材料的强度对地基承载力有着直接的影响。
混凝土、钢材等基础材料的强度越高，其承载能力越强。
在设计基础时，应充分考虑材料的强度，并根据工程需求选择合适的材料。
三、基础埋置深度基础的埋置深度也会影响其承载能力。
一般来说，埋置深度越大，基础对土体的支撑作用越强，地基承载力也会相应提高。
因此，在确定基础埋置深度时，应充分考虑地质条件、地下水状况等因素。
四、地基土质条件地基土质条件是决定地基承载力的关键因素。
不同土质的承载能力差异很大，如砂土、黏土、岩石等。
因此，在建筑物选址和设计基础时，应对地基土质进行详细的勘察和评估。
五、基础面积与形状基础的面积和形状也会影响其承载能力。
较大的基础底面积能够更好地分散建筑物荷载，提高地基承载力。
同时，合理的基础形状也能优化应力分布，增强基础的稳定性。
六、地下水条件地下水对地基承载力具有重要影响。
地下水位过高会使土体软化，降低承载能力；地下水位过低则可能导致土体收缩开裂，影响基础的稳定性。
因此，在设计和施工过程中应充分考虑地下水条件。
七、环境因素环境因素如气候变化、地震等也会对地基承载力产生影响。
气候变化可能引起土体的热胀冷缩，从而影响基础的稳定性；地震则可能引起地基的震陷、液化等现象，降低承载能力。
因此，在建筑物设计和施工过程中应充分考虑环境因素的影响。
八、荷载特性建筑物的荷载特性也会影响地基承载力。
不同的建筑物类型、结构形式和功能需求产生的荷载不同，对地基的承载能力要求也不同。
《土质学与土力学》第9章 地基承载力
Nanjing University of Technology
太沙基极限承载力理论
当基础放在无粘性土(c＝0)的表面上(D＝0)时，地基的承载力将等于零， 这显然是不合理。这种不合理现象的出现，主要是将士当作无重量介质(＝ 0)所造成的。为了弥补这一缺陷，许多学者在普朗德尔的基础上作了修正和 发展，使承载力公式逐步得到完善。
太沙基极限承载力公式：
pu
1 BN 2
r
0 DN
q
cN
c
( 3 ) tan
Nq
e 2 cos
2
2 ( 45 0
)
2
N c ( N q 1) cot
不 排 水 饱 和 软 粘 土 地 基 ， u=0 ， Nq=1,Nc=2p/3+1。此时地基极限承载力为：
pu q5.7c
Nanjing University of Technology
Nanjing University of Technology
P～S关系曲线
P～S曲线特征
当基础荷载较小时，基底压力P与沉降S基
本上成直线关系(oa)。属于线弹性变形阶段。 当荷载增加到某一数值时，在基础边缘处
的土开始发生剪切破坏．随着荷载的增加，剪 切破坏区(或称塑性变形区)逐渐扩大。这时压 力与沉降之间成曲线关系(ab)，属于弹塑性变形 阶段。
所以
2=/2-
塑性区的最大发展深度Zmax
Z m ap x 0 D (c o 2 t) tca n 0D
基底压力的一般形式：
p c o tZ m a ( 1 xc o t) 0 D c (c o c t o )t
2
2
2
Nanjing University of Technology
地基容许承载力与承载力特征值
地基容许承载力的确定方法地基的容许承载力是单位面积上容许的最大压力;容许承载的基本要素是：地基土性质；地基土生成条件；建筑物的结构特征;极限承载力是能承受的最大荷载;将极限承载力除以一定的安全系数,才能作为地基的容许承载力;浆砌片石挡墙地基承载力达不到设计要求时,将基础改为砼基础是为了增加挡墙的整体性.这也只能是相差不大时才行.一般来说要深挖直至达到要求.如果深挖不行只有扩大基础,降低压强.或者改为其它方案从现场施工的角度来讲地基,地基可分为天然地基、人工地基;地基就是基础下面承压的;天然地基是不需要人加固的天然土层,其节约工程造价;人工地基：经过人工处理或改良的地基;当土层的状况较好,承载力较强时可以采用天然地基；而在地质状况不佳的条件下,如坡地、沙地或淤泥地质,或虽然土层质地较好,但上部荷载过大时,为使地基具有足够的承载能力,则要采用人工加固地基,即人工地基地基容许承载力与承载力特征值所有建筑物和土工建筑物地基基础设计时,均应满足地基承载力和变形的要求,对经常受水平荷载作用的高层建筑高耸结构、高路堤和挡土墙以及建造在斜坡上或边坡附近的建筑物,尚应验算地基稳定性;通常地基计算时,首先应限制基底压力小于等于地基容许承载力或地基承载力特征值设计值 ,以便确定基础的埋置深度和底面尺寸,然后验算地基变形,必要时验算地基稳定性;地基容许承载力是指地基稳定有足够安全度的承载能力,也即地基极限承载力除以一安全系数,此即定值法确定的地基承载力；同时必须验算地基变形不超过允许变形值;地基承载力特征值是指地基稳定有保证可靠度的承载能力,它作为随机变量是以概率理论为基础的,分项系数表达的极限状态设计法确定的地基承载力；同时也要验算地基变形不超过允许变形值;因此,地基容许承载力或地基承载力特征值的定义是在保证地基稳定的条件下,使建筑物基础沉降的计算值不超过允许值的地基承载力;地基容许承载力:定值设计方法承载力特征值:极限状态设计法按定值设计方法计算时,基底压力P不得超过修正后的地基容许承载力.按极限状态设计法计算时,基底压力P不得超过修正后的承载力特征值;理论公式确定地基承载力均为修正后的地基容许承载力和承载力特征值.原位法和规范法确定地基承载力未包含基础埋深和宽度两个因素理论公式法确定地基承载力特征值在国标建筑地基基础设计规范 GB50007 中采用地基临塑荷载 P 1/4 的修正公式：b: 大于6m,按6m考虑,对于砂土小于3m,按3m考虑基本承载力与承载力特征值勤有什么关系.许多公式中出现承载力特征值而未出现基本承载力,基本承载力主要用来衡量什么的承载力基本值与承载力的标准值,是一对,属于89规范中的术语,指按土试指标或测试指标确定的承载力值,叫承载力基本值,经过统计修正以后就叫承载力标准值了;不过这套名词对于岩土工程界来说,非常不适合,不象结构专业中研究的工程材料一样,可以确定其标准值,地质体的标准值是很难确定,或者说是根本就不存在了;从这个角度来看,承载力标准值的说法,应该是前一版规范中的一个最大错误了;现行的2001版规范中就修正了这个错误,改称为承载力特征值,即表述地质体一个特征状态的数值,并不具有严格的数学含义,与77规范中的容许允许承载力是基本一致的,等于是现行规范又回到了过去的77规范体系中来了;1.天然地基的承载力标准值,按下列方法和步骤分别予以确定：①由静载试验得出的地基承载力基本值,经数理统计后可作为地基承载力的标准值采用;②由土的抗剪强度指标的标准值φk和ck,经过式的计算,所得结果即为地基承载力标准值；③按确定地基承载力标准值适用于一般多层建筑④由现场抗剪强度试验确定地基承载力标准值;2. 地基承载力的使用对于一级建筑物,地基承载力的标准值应按第一、二款或第一、二、四款综合确定;对于一级建筑物的初步设计和二级建筑物的施工图设计,可由第二款,结合共它几种方法综合取值;一般多层建筑可由第三款查表法选定;浅谈地基承载力特征值的确定地基承载力直接影响建筑物的安全和正常使用;因而在选用确定承载力方法时,应本着准确而又合理的方法综合确定,做到即安全可靠,有经济合理;关键词：地基承载力；特征值；确定1概述;建筑物因地基问题引起的破坏主要有两种：一由于建筑物荷载过大,超过了持力层所能承受的能力,而使地基产生滑动破坏；二是由于外荷载作用产生的压缩变形,引起基础过大的沉降量或沉降差,使上部结构倾斜、开裂毁坏;因此,在确定地基承载力时,除应保证地记得强度和稳定性,还应保证建筑物的沉降量和不均匀沉降;其确定复杂,影响因素极多,如地基土的特性,外荷载,基础的形式,埋深以及地下水等都将影响承载力的大小;2地基承载力的概念;所谓的地基承载力就是指地基所能承受荷载的能力;在不同的状态下,地基具有不同的承载力,如极限承载力,临塑承载力等;在设计建筑物基础时,为了保证建筑物的安全和正常使用,既保证地基稳定性不受破坏,而且具有一定的安全度,同时还应满足建筑物的变形要求即正常使用状态,常将基底压力限制在某一允许的范围之内,该容许值即地记的容许承载力,常以P表示;建筑地基基础设计规范GBTJ-89用承载力标准值取代了习惯用的容许承载力P,而现行的建筑地基基础设计规范GB5007-2002采用地基承载力特征值fak表示,正常使用极限状态计算时的地基承载力,其涵义是发挥正常使用功能时所允许采用的抗拉设计值;影响地基承载力特征值的因素较多,它不仅与地基的形成条件和性质有关,而且与基础的结构类型、荷载大小及施工深度等因素密切相关;4地基承载力方法的确定原则;地基承载力直接影响建筑物的安全和正常使用;因而在选用确定承载力方法时,应本着准确而又合理的方法综合确定,做到即安全可靠,有经济合理;第五节天然地基的容许承载力天然地基的容许承载力是天然地基所能承受建筑物基础作用在地基单位面积上容许的最大压力;在这个压力下,地基的强度和变形都满足设计的要求,建筑物安全和正常使用不会受到不利的影响;确定地基的容许承载的基本要素是：1地基土性质；2地基土生成条件；3建筑物的结构特征;一、按限制塑性变形区的范围来确定地基的容许承载力二、根据极限承载力确定地基容许承载力三、按地基规范承载力表确定地基容许承载力在饱和软粘土和砂、砾等粗粒土中,取原状土样困难;为避免取原状土样,地基容许承载力的另一种确定方法就是用原位试验;主要方法有下列几种：一载荷试验通常将试验测得的p－s曲线上的极限荷载pu 除以安全系数,或取临塑荷载pcr作为地基承载力的基本值;每层土的试验数就不少于3个,取各个试验结果的平均值作为承载力的标准值,再经过基础的宽度和深度的修正后就得到地基承载力的设计值;二静力触探试验静力触探试验时测得将探头贯入土中时所受的阻力Ps,用下列诸式确定地基承载力的设计值;1．梅耶霍夫公式式中：Ps--静力触探试验的贯入阻力kPa；B--基础宽度m；D--基础埋深m;2．国内建议公式式中：Ps的单位为kg/cm2,式8－32的标准值fk再用公式8－30修正后即得到承载力的设计值;三标准贯入试验标准贯入试验根据试验测得的标准贯入击数,用下列方法评价地基的承载力：1．GBJ7－89规范由,确定地基土的承载力标准值;2．太沙基和皮克公式太沙基和皮克在控制建筑物总沉降不超过25mm的前提下,建议根据标准贯入击数用下列公式求地基的容许承载力;显然,因为对沉降量控制很严格,所以上式将给出过于安全的结果;3．梅耶霍夫公式以上公式中,f以kg/cm2为单位,埋置深度D和基础宽度B均以m为单位;四旁压试验根据旁压试验测得的p-V曲线可以确定旁压器深度处周围土体的横向水平向极限承载力puh ;考虑地基土体的不等向性,把用旁压试验测得的横向极限承载力puh经过修正,并除以安全系数Fs后,才能作为地基承载力的设计值f,有式中：p--试验高程处的静止土压力；q--基础埋置深度处的侧面荷载；K--与土的性质、基础形状和埋深有关的系数;天然地基的容许承载力的确定方法可参见;表8－3 碎石土承载力标准值kPa注：①表中数值适用于骨架颗粒空隙全部由中砂、粗砂或硬塑、坚硬状态的粘性土或稍湿的粉土充填；②当粗颗粒为中等风化或强风化时,可按其风化程度适当降低承载力,当颗粒间呈半胶结状态时,可适当提高承载力;本表格来自建筑地基基础设计规范GBJ7-89表8－4 粉土承载力基本值kPa注：①有括号者仅供内插用；②折算系数ζ为0；③在湖、塘、沟、谷与河漫滩地段新近沉积的粉土,其工程性质一般较差,应根据当地实践经验取值;表8－5 粘性土承载力基本值kPa注：①有括号者仅供内插用；②折算系数ζ为；③在湖、塘、沟、谷与河漫滩地段新近沉积的粘性土,其工程性能一般较差；第四及其以前沉积的老粘性土,其工程性能通常较好,这些土均应根据当纪晚更新世Q3地实践经验取值;注：对于内陆淤泥和淤泥质土,可参照使用;表8－7 红粘土承载力基本值kPa注：①本表仅适用于定义范围内的红粘土；②折算系数ζ为;注：①本表只适用于堆填时间超过10年的粘性土以及超过5年的粉土；②表8－9 砂土承载力标准值kPa表8－10 粘性土承载力标准值kPa注：N指锤重为10kg的轻便触探试验贯入击数;10表8-12 素填土承载力标准值kPa注：本表只适用于粘性土与粉土组成的素填土;表8－13 承载力修正系数注：①强风化的岩石,可参照所风化形成的相应土类取值；②Sr 为土的饱和度,Sr≤,稍湿；＜Sr≤,很湿；Sr＞,饱和;例题8－4地基为均匀中砂,容重γ＝m3,条形基础宽度B＝,埋深D＝,基底下滑裂面范围内土的平均标准贯入击数=20,静力触探试验的贯入阻力Ps=3500kPa,试估算地基土的容许承载力;解：1.根据标准贯入击数=20,求地基的容许承载力1用规范承载力表查,求承载力标准值按式8－30求承载力设计值2太沙基公式8－333用梅耶霍夫公式8－34根据三种方法计算结果,GBJ7－89规范与梅耶霍夫公式比较接近,太沙基公式偏低很多,因为它对沉降量控制很严格;2.根据贯入阻力ps,求地基容许承载力1用梅耶霍夫公式8－312国内建议公式按式8－30,求承载力设计值根据上述两公式计算结果相差不是很大;综合以上结果,除太沙基公式因对沉降要求比较严格,故承载力偏低外,其它计算公式、结果比较接近;综合考虑,地基承载力可取为300kN/m2;本人从事地基承载力研究多年,做过多年平板载荷试验,系统地做过：不同宽度,埋深的平板载荷试验;主编过铁路桥规地基承载力表及有关条文,和周镜院士等主编地基承载力试验文集铁道出版社1978,对桥规地基可靠度进行过研究;对地基承载力进行了多年的思考：深感当今土力学教课书和有关地基承载力的多种规范需要更新;本人四十余年研究,有几点认识：1 在土力学教课书中,不论是太沙基的地基公式按强度指标计算地基再除以安全系数确定地基容许承载力,还是其它各种三项地基承载力公式,包括规范中的,是不可信的,列在规范中也不可信的,不要再研究了;2现行地基规范取消了地基承载力表,是很对的,但不彻底;3按变形确定地基容许承载力概念清楚,最可取,上海孙更生先生的见解是对的,最有成就,是国内许多先行者的代表;详见孙更生、郑大同主编的“软土地基与地下工程”4建议按触探土力学的方法用连续的触探指标计算变形确定地基容许承载力;。
天然地基承载力和变形的关系
天然地基承载力和变形的关系引言：天然地基承载力和变形是土力学中重要的研究内容，它们直接影响着土地的稳定性和工程结构的安全性。
本文将从理论和实践两个方面，探讨天然地基承载力和变形之间的关系。
一、天然地基承载力的定义和影响因素天然地基承载力是指土壤能够承受的最大荷载。
它受到土壤类型、土层厚度、土壤密度、含水量、孔隙度等因素的影响。
不同类型的土壤具有不同的承载力，例如，黏土的承载力相对较高，而砂土的承载力相对较低。
二、天然地基变形的定义和分类天然地基变形是指土壤在受力作用下发生的形变。
按照变形形态的不同，可以将天然地基变形分为弹性变形和塑性变形。
弹性变形是指土壤在受力作用下发生的可恢复的形变，而塑性变形是指土壤在受力作用下发生的不可恢复的形变。
三、天然地基承载力与变形的关系天然地基承载力和变形之间存在着密切的关系。
一方面，较高的承载力意味着土壤能够承受更大的荷载，从而减小了土壤的变形。
另一方面，较大的变形可能会导致土壤的承载力下降，从而影响工程结构的安全性。
四、天然地基承载力与变形的影响因素天然地基承载力和变形的影响因素是相互关联的。
首先，土壤类型是影响承载力和变形的重要因素。
不同类型的土壤具有不同的物理性质和力学特性，因此其承载力和变形也存在差异。
其次，土壤含水量对承载力和变形有着显著影响。
过高或过低的含水量都会导致土壤的力学性质发生变化，进而影响承载力和变形。
此外，孔隙度和土层厚度等因素也会对承载力和变形产生影响。
五、天然地基承载力与变形的测试方法为了准确评估天然地基的承载力和变形情况，需要进行相应的测试。
常用的测试方法包括静载试验、动力触探试验和现场观测等。
静载试验通过加载荷载并记录土壤变形情况，来评估土壤的承载力和变形。
动力触探试验则通过触探钻杆的击打次数和阻力来判断土层的承载力和变形特性。
现场观测包括对工程结构的变形和沉降情况进行实时监测，以评估天然地基的变形情况。
六、天然地基承载力和变形的工程应用天然地基承载力和变形的研究对于工程设计和施工具有重要意义。
地基承载力
地基承载力地基在变形容许和维系稳定的前提下，单位面积所能承受荷载的能力。
通俗点说，就是地基所能承受的安全荷载。
（1）地基承载力：地基所能承受荷载的能力。
（2）地基容许承载力：保证满足地基稳定性的要求与地基变形不超过允许值，地基单位面积上所能承受的荷载。
（3）地基承载力基本值：按标准方法试验，未经数理统计处理的数据。
可由土的物理性质指标查规范得出的承载力。
（4）地基承载力标准值：在正常情况下，可能出现承载力最小值，系按标准方法试验，并经数理统计处理得出的数据。
可由野外鉴别结果和动力触探试验的锤击数直接查规范承载力表确定，也可根据承载力基本值乘以回归修正系数即得。
（5）地基承载力设计值：地基在保证稳定性的条件下，满足建筑物基础沉降要求的所能承受荷载的能力。
可由塑性荷载直接，也可由极限荷载除以安全系数得到，或由地基承载力标准值经过基础宽度和埋深修正后确定。
（6）地基承载力的特征值：正常使用极限状态计算时的地基承载力。
即在发挥正常使用功能时地基所允许采用抗力的设计值。
它是以概率理论为基础，也是在保证地基稳定的条件下，使建筑物基础沉降计算值不超过允许值的地基承载力。
在设计建筑物基础时，各行业使用《规范》不同，地基容许承载力、地基承载力设计值与特征值在概念上有所不同，但在使用含义上相当地基容许承载力简介各种土木工程在整个使用年限内都要求地基稳定，要求地基不致因承载力不足、渗流破坏而失去稳定性，也不致因变形过大而影响正常使用。
地基承载力是指地基承担荷载的能力。
在荷载作用下，地基要产生变形。
随着荷载的增大，地基变形逐渐增大，初始阶段地基尚处在弹性平衡状态，具有安全承载能力。
当荷载增大到地基中开始出现某点，或小区域内各点某一截面上的剪应力达到土的抗剪强度时，该点或小区域内各点就剪切破坏而处在极限平衡状态，土中应力将发生重分布。
这种小范围的剪切破坏区，称为塑性区。
地基小范围的极限平衡状态大都可以恢复到弹性平衡状态，地基尚能趋于稳定，仍具有安全的承载能力。
《土质学与土力学》 10 地基承载力
土质学与土力学 10 地基承载力《土质学与土力学》第十章 地基承载力第一节 概述地基随建筑物荷载的作用后，内部应力发生变化，表现在两方面：一种是由于地基土在建筑物荷载作用下产生压缩变形，引起基础过大的沉降量或沉降差，使上部结构倾斜，造成建筑物沉降；另一种是由于建筑物的荷载过大，超过了基础下持力层土所能承受荷载的能力而使地基产生滑动破坏。
因此在设计建筑物基础时，必须满足下列条件： 地基： 强度——承载力——容许承载力变形——变形量（沉降量）——容许沉降量一、几个名词1、地基承载力：指地基土单位面积上所能随荷载的能力。
地基承载力问题属于地基的强度和稳定问题。
2、容许承载力：指同时兼顾地基强度、稳定性和变形要求这两个条件时的承载力。
它是一个变量，是和建筑物允许变形值密切联系在一起。
3、地基承载力标准值：是根据野外鉴别结果确定的承载力值。
包括：标贯试验、静力触探、旁压及其它原位测试得到的值。
4、地基承载力基本值：是根据室内物理、力学指标平均值，查表确定的承载力值，包括载荷试验得到的值）。
通常0f f f k ψ=5、极限承载力：指地基即将丧失稳定性时的承载力。
二、地基承载力确定的途径 目前确定方法有：1．根据原位试验确定：载荷试验、标准贯入、静力触探等。
每种试验都有一定的适用条件。
2．根据地基承载力的理论公式确定。
3．根据《建筑地基基础设计规范》确定。
根据大量测试资料和建筑经验，通过统计分析，总结出各种类型的土在某种条件下的容许承载力，查表。
一般：一级建筑物：载荷试验，理论公式及原位测试确定f ；一级建筑物：规范查出，原位测试；尚应结合理论公式； 一级建筑物：邻近建筑经验。
三、确定地基承载力应考虑的因素地基承载力不仅决定于地基的性质，还受到以下影响因素的制约。
1．基础形状的影响：在用极限荷载理论公式计算地基承载力时是按条形基础考虑的，对于非条形基础应考虑形状不同地基承载的影响。
2．荷载倾斜与偏心的影响：在用理论公式计算地基承载力时，均是按中心受荷考虑的，但荷载的倾斜荷偏心对地基承载力是有影响的。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
由 MB 0
推导出：
a
pk N q q0 N c c
C
pk Nq H Nc c
Nq
tan2 (45o
) exp(
2
tan )
B
a
r0 r
p p
E′
c ds r r0 exp( tan ) f
Nc (Nq 1) cot
地基土的自重所对应的极限承载力为
pk
1 2
1
b
3、滑裂土体自重所产生的摩擦抗力。
该抗力的大小，除决定于土的重度γ和内摩擦角φ以外， 还决定于滑裂土体的体积，因而，地基的极限承载力随 着基础宽度b的增加而线性增加。
地基极限承载力的其它极限平衡法
• Terzaghi 公式
基础底面粗糙
破坏区
弹性区
破坏区
破坏区
破坏区
• Meyerhof 公式
计入基底以上土的抗剪强度，适用于埋深较大的基础。 在斜坡、成层土地基上时的承载力计算。
N
N 2(Nq 1) tan
则埋深为H、粘聚力为c、内摩擦角为φ的地基的极限承载力为
pk pk pk
式中
Nc
c
Nq 2 H
基底
12基底1b N
Prandtl-Vesic公式
以上
以下
Nq
tan2 (45o
) exp(
2
tan )
Nc (Nq 1) cot
N 2(Nq 1) tan
2
1
3
2
cos 2
2
3
1
xz
1
3
2
s in 2
z , zx
极限平衡条件
1
12（1-
）=
3
12（1+
3）sin +
c cos
x
23
1
z
x 0(1 sin cos 2 ) c cos cos 2
z
0 (1 sin
cos
2 )
c cos
cos
2
xz 0 sin sin2 c cos sin2
Vesic提出
N q，Nc，N 是 关 于的 函 数 ， 称 为 承 载 力 系数 可查表6－1
承载力的适用条件：
pk
Nc
c
Nq 2
H
1 2
1b
N
该公式只适用于中心垂直荷载作用下的条形基础，当 基础形状改变，荷载出现偏心或倾斜，地基的极限荷 载将发生变化。
经验修正法
pk
c ic
பைடு நூலகம்
c
Nc
q0
iq
q
Nq
• Hansen 公式
中心倾斜荷载、基础性状的影响等。
• Vesic公式
地基土压缩性的影响。 整体剪切破坏计算公式向局部、冲切破坏的推广。
算例分析
粘性土地基上条形基础的宽度b 2m，基础埋置深
度H 1.5m,地基土的天然容重＝17.6kN / m3 ,粘聚 力c 10kPa,摩擦角＝200，按照Pr andtl Vesic方法
求解地基极限承载力。
解：
pk
Nc
c
Nq 2
H
1 2
1b
N
Nq
tan2 (45o
) exp(
2
tan )
Nq tan2(45 10) exp( tan20) 7.328
Prandtl-Vesic近似公式的基本假设：
2、先假设 0，c 0，q0 H 0 ，基底光滑，由此计算出
此时地基的极限压力 pk 。 3、再假设 0，c＝0，q0 0 ，由此计算出此时地基的极限压力 pk
对于一般地基， 0，c 0，q0 0 ，此时极限压力
的计算，可以用 pk pk pk 。
1 2
1b
ir
r
N
c，q，r — 为 形 状 修 正 系 数 ； 可查表6－2
ic，iq，ir — 为 荷 载 倾 斜 修 正 系 数 ；
地基极限承载力理论公式的含义
pk
Nc
c
Nq 2
H
1 2
1b
N
地基的极限承载力公式由三个部分组成：
1、滑裂面上粘聚力c所产生的抗力；
2、基底两侧均布荷载 q0 产生的抗力； 3、滑裂土体自重所产生的摩擦抗力。
1、滑裂面上粘聚力c所产生的抗力；
该抗力的大小，首先决定于土的内摩擦角φ和粘聚力c， 其次决定于滑裂面的形状和长度。
对于砂性土c=0，基础的埋深对承载力起着重要的作用，如果基础 埋深太浅，则地基的承载力会显著下降。
2、基底两侧均布荷载 q0 产生的抗力； 该抗力的大小，除决定于土的重度γ和内摩擦角φ，还决 定于基础埋深H。
地基极限承载力的理论解 及规范法确定地基承载力
一、浅基础地基极限承载力的理论解 二、规范法确定地基承载力
一、浅基础地基极限承载力的理论解
地基极限承载力
地基极限承载力ultimate bearing capacity :是地基破坏前所能承受的最
大基底压力。
地基极限承载力的确定方法
理论方法 现场试验 经验公式法
其 中 0 ( 1 3 ) / 2
将上述应力分量相对于x、z取微分，再代入静力平衡方程，得：
(1
sin
cos 2 )
0
x
sin
s in 2
0
z
2
0
s
in
2
z
cos 2
x
0
(1
sin
cos 2 )
0
z
sin
s in 2
0
x
2
0
s
in
2
z
cos 2
x
上述方程为 0, 变量的非线性偏微分方程，其解析解的求 解是非常困难的。
浅基础地基极限承载力理论解的简化计算
简化计算方法一般是先假定地基破坏图式，再根据静力 平衡原理求得地基极限荷载，也称为极限平衡法。
2、浅基础地基极限承载力的Prandtl-Vesic近似解
Prandtl-Vesic近似公式的基本假设： 1、假设浅基础地基的破坏模式如下图：
pk
45o
2
q0 2H
I 区主动区
垂直应力pk为大主应力，与水平方向夹角 45φ 2。
A
a pk (1 sin ) pi sin
pk
B
a
C
=pk
III区被动区 B
竖直方向为小主应力，
与小主应力方向夹角452
p
q0=H
D′
E′
3= H
1
p q0 (1 sin ) pi sin
Ⅱ过度区
Ⅱ区所以外力处于静力平衡状态， 各外力对B点的力矩之和为0。
III
II
I
45o 2
r0 r II
III
土体移动方向
90o 剪切破坏面（滑移面）
I：主动区 II：过渡区 III：被动区 均处于极限平衡（破坏）状态
对数螺旋线 r=r0 exp( tan )
破坏面夹角为 90o
地基破坏的模型试验
2、浅基础地基极限承载力的Prandtl-Vesic近似解
1、浅基础地基极限承载力的理论精确解
对于浅基础地基极限承载力的理论精确解可根据： 极限平衡条件和力的平衡微分方程求解。
平面应变问题的静力平衡微分方程
x xz 0
x z
zx z
x z
z
x
z xz
x
平面应力状态
主应力与应力分量的关系
x , xz
x
1
3
2
1
3
2
cos
2
z
1
3