气体分子运动论和热力学基础之奥托循环图
气体分子运动论和热力学基础之奥托循环图

THANKS FOR WATCHING
感谢您的观看
等温过程
在等温过程中,气体吸收热量而 温度保持不变。在奥托循环图中, 等温过程用水平线表示。
等压过程
在等压过程中,气体压力保持不 变而吸收或释放热量。在奥托循 环图中,等压过程用斜线表示。
绝热过程
在绝热过程中,气体既不吸收也 不释放热量,温度和压力都发生 变化。在奥托循环图中,绝热过 程用垂直线表示。
新型燃烧技术
研究新型的燃烧技术,如催化燃烧、等离子体燃 烧等,以提高燃烧效率和降低污染物排放。
新型热能转换技术
研究新型的热能转换技术,如热电转换、热光转 换等,以提高热能转换效率和降低能耗。
3
新型工质选择
研究新型的工质选择,如氢气、氨气等,以提高 工质的热力学效率和降低环境影响。
05 结论与展望
总结气体分子运动论和奥托循环图的重要性和应用价值
奥托循环图在发动机设计中的应用
发动机效率分析
奥托循环图可以用于分析发动机在不 同工况下的效率,帮助工程师优化设 计,提高发动机的燃油经济性和动力 性能。
燃烧过程模拟
通过奥托循环图,可以模拟发动机的 燃烧过程,了解燃烧室内温度、压力 、气体组分等参数的变化,为燃烧系 统的改进提供依据。
奥托循环图在能源利用领域的应用
环保工程
在环保工程中,奥托循环图可以用于分析废气处理、气体排放等过程的性能, 为污染控制和治理提供支持。
04 奥托循环图的优化与改进
提高奥托循环图的效率
01
优化燃烧过程
通过改进燃烧室设计,提高燃料 的燃烧效率,减少未完全燃烧的 物质,从而提高热能转换效率。
02
优化热能转换
03
优化工质选择
第08章气体动理论优秀课件

V0
M M mol
Vmol
其中: M 为气体的总质量;
Mmol 为气体的摩尔质量。
PV P0V0 M P0Vmol
T
T0
M mol T0
3.理想气体状态方程的变形
理想气体状态方程:PVRT M RT Mm ol
PRTNART
V VNA
N V
RT NA
nkT
NA为阿伏加德罗常数, NA6.022 12 03
国际单位:绝对温标 T 开,k
T t 2.7 13 5
常用单位:摄氏温标 t 度, C
4.摩尔数 M M mol
单位:摩尔,mol
气体质量 摩尔质量
5.普适气体恒量 R
R 8 .3J1 m - 1 k o - 1 l
P0 1.01325105 Pa
标准状态: T0 273.15 K
Vmol 22.4103 m3
常缓慢,以至于过程中
p
的每一个中间状态都近
似于平衡态。
准静态过程的过程曲线 可以用p -V 图来描述, 图上的每一点都表示系 统的一个平衡态。
p
( pA,VA,TA )
( pC,VC,TC )
( pB,VB,TB )
O
V
确定平衡态的宏观性质的量称为状态参量。
系统状态的描述
宏观量称为状态参量,(如体积,温度,压强)可直接测量 微观量(如分子的质量,位置,速度)无法直接测量
国际单位:牛顿/米2,帕(Pa)
常用单位:大气压(atm) 1 at 1 m .0 1 1 5 P 3 0a
2.体积 V----气体分子活动的空间体积。
从几何角度描写气体状态的物理量。
对于理想气体分子大小不计,分子活动的空间体积 就是容器的体积。
奥拓循环的实际过程

1
1 7
0.4
55%
实际上汽油机的效率只有25%左右。
卡诺循环
(4)排气过程 开放排气口,使气体压强突然降为大 气压,这过程近似于一个等体过程(图中过程eb), 然后再由飞轮的惯性带动活塞,使之从右向左移动, 排出废气,这是个等压过程(图中过程ba)。 严格地说,上述内燃机进行的过程不能看作是 个循环过程。因为过程进行中,最初的工作物为燃 料及空气。后经燃烧,工作物变为二氧化碳,水汽 等废气,从气缸向外排出不再回复到初始状态。但 因内燃机作功主要是在p-V图上bcdeb这一封闭曲线 所代表的过程中,为了分析与计算的方便,我们可 换用空气作为工作物,经历bcedb这个循环,而把它 叫做空气奥托循环。
卡诺循环
气体主要在循环的等体过程cd中吸热(相当于 在爆炸中产生的热),而在等体过程eb中放热(相 当于随废气而排出的热),设气体的质量为M,摩 尔质量为Mmol,摩尔定体热容为Cv,则在等体过程 cd中,气体吸取的热量Q1为:
M Q1 Cv Td Tc M mol
而在等体过程eb中放出的热量应为
p
d
c
p0 a
e b
O
V1
V2 V
卡诺循环
(2)压缩过程 活塞自右向左移动,将已吸入气 缸内的混合气体加以压缩,使之体积减小,温度升 高,压强增大。由于压缩较快,气缸散热较慢,可 看作一绝热过程(图中过程bc)
(3)爆炸、作功过程 在上述高温压缩气体中, 用电火花或其他方式引起燃烧爆炸,气体压强随之 骤增,由于爆炸时间短促,活塞在这一瞬间移动的 距离极小,这近似是个等体过程(图中过程cd)。 这一巨大的压强把活塞向右推动而作功,同时压强 也随着气体的膨胀而降低,爆炸后的作功过程可看 成一绝热过程(图中过程de)。
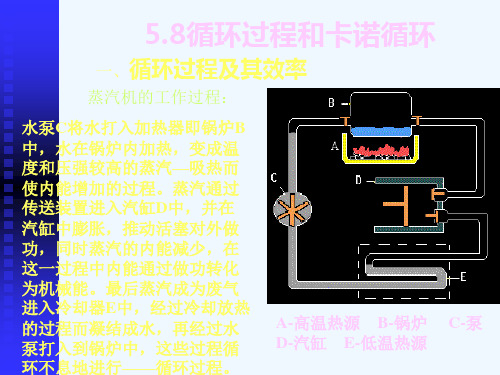
新热力学基础4循环过程和卡诺循环
,
本题有几种解题思路: 1.利用理想气体状态方程和以 Cp、 Cv表达的热量公式,求 循环过程吸收的热量Q1和放出的热量Q2,然后用 求 解. 2.用 求解,式中A为P--V 图上过程曲线包围的 面积. 3.利用过程方程分别求出a、b、c、d各态的温度及摩尔数,再 利用Cp、Cv表述的热量公式求出Q1及Q2,最后求效率。
将证明在同样两个温度T1和T2之间工作 的各种工质的卡诺循环的效率都由上式给定,而 且是实际热机可能效率的最大值。 应为理想气体温标所定义的温度。 可证明,当用热力学温标表示两个热源的温度时, 因为T1和T2是在求理想气体热量时引进的, 卡诺循环的效率的表示仍为上式。
讨论: (1)要完成一次卡诺循环必须有高温和低温两个热源(有时分 别叫做热源与冷源); (2)卡诺循环的效率只与两个热源的温度有关,高温热源的温 度愈高,低温热源的温度愈低, 卡诺循环的效率愈大,也就是说当两热源的温度差愈大,从高温热 源所吸取的热量Q1 的利用价值愈大; (3)卡诺循环的效率总是小于1的(除非T。=0 K)。
h =
工质对外做的净功
A
=
从高温热源吸的热
Q = 1- Q Q 11
2
1
卡诺循环
1824年卡诺(法国工程师1796-1832)提出了一个 能体现热机循环基本特征的理想循环。后人称之 卡诺循环。 本节讨论以理想气体为工质的卡诺循环。 由4个准静态过程(两个等温、两个绝热)组成。
卡诺循环是在两个温度恒定的热源(一个高温热源,一个低温热源) 之间工作的循环过程。 在整个循环中,工作物质和高温热源或低温热源交换能量,没有散 热漏气等因素存在, 卡诺循环是由两个平衡的等温过程和两个平衡的绝热过程组成。
理想的柴油内燃机循环过程由debc的绝热过程方程恒量得由等压过程cd有引入绝热压缩比rvbvc定压膨胀比vdvc由式最后得到21bevcdpttcqttcq??????一定量的理想气体经历如图所示的循环过程
奥托循环

1.达到奥托循环:内可逆定容加热理想循环又称奥托循环,基于这种循环而制造的煤气机和汽油机是最早的活塞式内燃机3.饱和状态:假设容器空间没有其他气体,随着容器空间中的水蒸气分子逐渐增多,液面上的蒸汽压力也逐渐增大,水蒸气的压力愈大,密度愈大,水蒸气的分子与液面碰撞愈频繁,变为水分子的水蒸气分子数也愈多。
到一定状态时,这两种方向相反的过程就会达到动态平衡。
此时,两种过程仍在不断进行,但宏观结果是状态不再改变。
这种液相和气相处于动态平衡的状态称为饱和状态。
4饱和蒸汽:处于饱和状态的蒸汽称为饱和蒸汽,液体称为饱和液体5此时,气液的温度相同,称为饱和温度,用Ts表示。
6蒸汽的压力称为饱和压力,用Ps表示7饱和蒸汽压方程::9闭口系统:一个热力系统如果和外界只有能力交换而无物质交换,则该系统称为闭口系统,.(又称闭口系)如图1-5b中内燃机气缸内气体为系统,即为闭口系统。
闭口系统内的质量保持恒定不变,所以闭口系统又叫控制质量。
开口系统:如果热力系统和外界不仅有能量交换而且有物质交换,则该系统叫做开口系统(又称开口系)10比热容:为了计算气体状态变化过程中的的吸(或放)热量,引入了比热容。
物体温度升高1K(或1℃)所需热量称为质量热容,又称比热容,单位J/(kg.K),用c表示,其定义式为11:热力设备中工质往往是在接近压力不变或体积不变的条件下吸热或放热的,因此定压过程和定容过程的比热容最常用,它们称为比定压热容(也称质量定压热容)和比定容热容(也称质量定容热容)分别以Cp和Cy表示。
12:比热容比:13:比湿度:定义1kg干空气所带有的水蒸气质量为含湿量(又称比湿度),以d表示,习惯上表示为kg(水蒸气)/kg(干空气),即14:比体积:单位质量物质所占的体积称为比体积,即15:标准状态下的燃烧热和生成热分别为标准燃烧焓和标准生成焓,分别用16:为计算△G,与标准生成焓一样,规定在1标准大气压298.15K下,由单质生成1mol化合物时,自由焓的变化量为该化合物的标准生成自由焓,或标准吉布斯函数,用符号表示,并规定稳定单质或元素的标准生成自由焓为零。
气体分子运动论和热力学基础之卡诺循环图

基本概念
温度、压力、体积、热量、功等。
热力学第一定律
能量守恒定律在热现象中的应用,表 示为Q=ΔU。
热力学第二定律
揭示了热现象中自然过程的方向性, 表示为W≥-ΔQ。
卡诺循环的热力学过程
等温吸热过程
等温放热过程
气体从温度为T1的高温热源吸热,温度不 变,对外界做功。
气体对外界做功,温度不变,将热量放给 温度为T2的低温热源。
卡诺循环图通过图形的方式,直观地展示了气体分子在热机 工作过程中的状态变化和能量转换过程,有助于深入理解热 力学的原理和应用。
卡诺循环图的重要性
卡诺循环图是热力学中一个核心的理论模型,对于理解热 力学的基本原理、热机的效率以及能源利用等问题具有重 要意义。
通过卡诺循环图,人们可以直观地了解热机的工作过程和 效率,为改进和优化热机设计提供理论支持。同时,卡诺 循环图也是研究和开发新型热机的重要工具,有助于推动 能源科学和技术的发展。
分子运动论的基本概念
分子
组成物质的最小单位,具有质 量、动量和速度等物理属性。
分子的平均自由程
分子在连续两次碰撞之间所走的 平均距离,与气体分子的速度和 气体分子的碰撞频率有关。
分子的平均动能
分子由于热运动而具有的动能 ,与温度有关。
分子的分布函数
描述分子在空间中分布的概率函 数,可以用来计算分子的空间分
03
卡诺循环图介绍
卡诺循环图定义
卡诺循环图是表示卡诺循环过程的示 意图,由四个等温过程和两个等熵过 程组成。
它揭示了理想热机的效率与工作物质 和热源温度之间的关系。
卡诺循环图的组成
等温吸热过程
气体从高温热源吸收热量,对外界做功。
等熵吸热过程
8.10气体分子运动论和热力学基础之狄塞尔循环图

c dQ 2 a
V1 V2
V0
V
{范例8.10} 狄塞尔循环图
Td − Ta Q2 η =− 1 1− = Q1 γ (Tc − Tb )
k1 = V0/V1 = 15, k2 = V0/V2 = 5。
根据理想气体绝热过程的体积与温度的 关系Vγ-1T = C,对于绝热过程a→b可得 即 Ta = Tb / k1
γ −1
TaV0γ −1 = TbV1γ −1
p b Q1 c dQ 2 a V1 V2 V0 V
即
Td = Tc / k2
γ −1
γ −1 γ −1 对于绝热过程c→d可得 TdV0 = TcV2
γ Tc / k2 −1 − Tb / k1γ −1 因此循环 η = 1 − 效率为 γ (Tc − Tb )
{范例8.10} 狄塞尔循环图
狄塞尔柴油机进行的循环如图近似表示。设工作物质为双 原子理想气体,a→b和c→d为绝热过程,b→c是等压过程, d→a为等容过程。绝热压缩比k1 = V0/V1 = 15,绝热膨胀比 k2 = V0/V2 = 5,求循环效率和循环一周对外所做的功。 [解析]假设理想气体的质量为M,摩尔质量为μ。 a→b和c→d为绝热过程,不吸热也不放热。 Q1 b→c是等压吸热过程,Q M C (T − T ) p = 1 b µ p c b 所吸收的热量为 d→a是等容放热过程, Q M C (T − T ) = 2 µ V d a 所放出的热量为 因此循环效率为 其中γ = Cp/CV。
第八章结束 湖南大学物电院 周群益老师谢谢您的使用!
V1 V2
V0
V
由于绝热压 缩比V0/V1 = 15很大,所 以b点的相对 体积很小, 压强很大。
奥托循环效率推导1-r

奥托循环效率推导1-r摘要:1.奥托循环简介2.奥托循环效率的定义3.奥托循环效率的推导过程4.1-r 的含义及其对奥托循环效率的影响5.结论正文:一、奥托循环简介奥托循环,又称为四冲程循环,是一种内燃机工作原理。
它由四个冲程组成:吸气、压缩、燃烧和排气。
在这个循环中,燃料和空气混合后在气缸内燃烧产生高温高压气体,使活塞做往复运动,从而转化为机械能,驱动发动机工作。
二、奥托循环效率的定义奥托循环效率是指内燃机在一个完整的工作循环中,有效功与燃料燃烧产生的热量的比值。
有效功是指发动机输出的净功,即扣除了机械摩擦损失和散热损失后的功。
效率越高,说明内燃机的能量转化越充分,动力性能越好。
三、奥托循环效率的推导过程根据热力学第一定律,能量守恒,内燃机在一个工作循环中吸收的热量等于放出的热量与做功的和。
设燃料的热值为q,质量为m,气缸容积为V,活塞行程为S,燃烧室温度为T,则吸收的热量Q=mqT。
根据气体状态方程,pV=nRT,可得热量Q=nRT,其中n 为燃料的摩尔数,R 为气体常数。
因此,Q=m/M·R·T,其中M 为燃料的摩尔质量。
有效功W=p2V-p1V,其中p1 为吸气时的气压,p2 为排气时的气压。
根据气体状态方程,pV=nRT,可得p=nRT/V,代入有效功公式得W=m/M·R·T·(V/T-V/T),化简得W=m/M·R·T·ΔV/T。
所以,奥托循环效率η=W/Q=(m/M·R·T·ΔV/T)/(m/M·R·T)=ΔV/T。
四、1-r 的含义及其对奥托循环效率的影响在奥托循环中,1-r 代表的是排气门开启程度。
当1-r=1 时,排气门完全关闭,排气冲程的气体流动阻力最小,排气效率最高,但可能导致燃烧室内的废气排放过多,影响燃烧效率。
当1-r=0 时,排气门完全打开,排气冲程的气体流动阻力最大,排气效率最低,但可以保证燃烧室内的废气排放最少,燃烧效率最高。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
在绝热压缩比不变 的情况下,不论等 容增压比如何变化, 气体循环效率都不 变,但是对外做的 功会发生改变。
如果等容增压 比为2,则循 环效率仍为 54.1%,循环 一周对外所做 的相对功变为 2.94A0。
{范例8.9} 奥托循环图
M M Ta Td Ta Td CV (Tc Tb ), Q2 CV (Td Ta ) , Q1 p Tb Tc Tb Tc c
b→c是等容过程, 压强与温度成正比
Tc pc kp Tb pb
d→a也是等容过程, pd Td Tc k p pa Ta Tb 利用前一公式可得
Q1 b
dQ
a
2
O V 2 可见:d→a的等容减压比等于b→c的等容增压比。
V1 V
气体从高温热源 Q1 M CV Tb ( Tc 1) M CV Ta kV 1 (k p 1) 对于一定气 体,绝热压 Tb 吸收的热量为 缩比越大, 气体向低温热源 Q2 M CV Ta (Td 1) M CV Ta (k p 1) 等容增压比 Ta 放出的热量为 越大,气体 对外所做的 气体循环一周 A Q1 Q2 M CV Ta (kV 1 1)(k p 1) 功越多。 所做的功为
M b→c是等容吸热过程, Q1 CV (Tc Tb ) 所吸收的热量为
c
Q1 b dQ a
2
d→a是等容放热过程, Q2 M CV (Td Ta ) 所放出的热量为 因此循环效率为
T T Q 1 2 1 d a . Q1 Tc .9} 奥托循环图
理想气体绝热过程的体积-温度方程为 Ta (Vb ) 1 (V2 ) 1 ( 1 ) 1 Tb Va V1 kV Vγ-1T = C,对于绝热过程a→b可得 对于绝热过 Td (Vc ) 1 (V2 ) 1 ( 1 ) 1 V1 kV 程c→d可得 Tc Vd
{范例8.9} 奥托循环图
在燃烧汽油的四冲程内燃机中进行的循环叫奥托循环, 可用图近似表示。设工作物质为双原子理想气体,a→b 和c→d为绝热过程,b→c和d→a为等容过程。体积的绝 热压缩比为kV = V1/V2 = 7,等容增压比为kp = pc/pb = 3, 求循环效率和循环一周的功。精确绘制奥托循环图。 [解析]假设理想气体的质量为M,摩尔质量为μ。双原子 气体分子的自由度为i = 5,比热容比为γ = 1 + 2/i = 1.4。 a→b和c→d为绝热过程,不吸热也不放热。 p
气体经过等 容增压,c点 压强就达到 pc = 45.7pa。
再经过绝热压缩, d点的压强为pd = 3pa,这是因为从 d点到a点的等容 减压比等于从b点 到c点的等容增压 比。 这个奥托循环的效率达到54.1%, 循环一周对外做的功为5.89A0。
利用压缩比可求得b 点的体积Vb = Va/7 = 0.14Va,经过绝热压 缩,b点的压强为pb = 15.2pa。
Ta Td Ta Td 所以 Tb Tc Tb Tc
p
c
这里用了 分比定理。
Q1 b
O V 2
dQ
a
2
循环效 1 Ta 1 (V2 ) 1 1 ( 1 ) 1 Tb V1 kV 率为
V1 V 这是理想 的情形, 实际效率 只有25% 左右。
可见:循环效率只与绝热压缩比有关,与等容压 强比无关;绝热压缩比越大,循环效率就越高。 提高压缩比可提高循环效率,但是由于汽油的 燃点比较低,压缩比的提高受到一定的限制。 将数值代入可得效率为η = 1 – (1/7)0.4 = 54.1%。
