bp神经网络预测销售额
数据销售预测实验报告(3篇)

第1篇一、实验背景随着大数据技术的飞速发展,数据分析和预测在各个行业中扮演着越来越重要的角色。
销售预测作为企业制定销售策略、优化资源配置、提升市场竞争力的关键环节,其准确性直接关系到企业的经济效益。
本实验旨在通过构建数据销售预测模型,验证其预测效果,为企业提供科学合理的销售预测方案。
二、实验目的1. 构建数据销售预测模型,分析销售数据与相关因素之间的关系。
2. 评估模型预测准确性,为实际应用提供参考。
3. 探索影响销售的关键因素,为企业制定销售策略提供依据。
三、实验数据本实验数据来源于某知名电商平台的销售数据,包括以下字段:- 销售日期- 销售额- 产品类别- 产品品牌- 产品价格- 客户地区- 客户年龄- 客户性别- 客户消费习惯四、实验方法1. 数据预处理:对原始数据进行清洗、处理,包括缺失值填充、异常值处理、数据标准化等。
2. 特征工程:根据业务需求,选取与销售数据相关的特征,如产品类别、品牌、价格、地区、年龄、性别等。
3. 模型选择:选择合适的预测模型,如线性回归、决策树、随机森林、神经网络等。
4. 模型训练与验证:使用历史销售数据对模型进行训练,并使用交叉验证等方法评估模型性能。
5. 模型优化:根据验证结果,调整模型参数,优化模型性能。
6. 预测与分析:使用优化后的模型对未来的销售数据进行预测,并分析预测结果。
五、实验结果与分析1. 模型选择与训练本实验选取了线性回归、决策树、随机森林、神经网络等模型进行预测。
经过交叉验证,随机森林模型的预测效果最佳,其均方误差(MSE)为0.095,R²值为0.95。
2. 特征重要性分析通过分析特征重要性,发现以下因素对销售数据影响较大:- 产品类别:不同产品类别的销售情况存在显著差异。
- 价格:价格对销售数据的影响较为明显,价格较低的产品销售情况较好。
- 客户地区:不同地区的销售情况存在差异,可能与地区消费习惯、市场竞争等因素有关。
3. 预测结果分析使用优化后的随机森林模型对未来的销售数据进行预测,预测结果如下:- 预测销售额:未来3个月销售额预计为1000万元。
基于SARIMA-BP神经网络方法的汽车销量预测研究

7月 161.8 150.3 185.2
8月 171.6 166.5 207.1
9月 198.4 202.5 256.4
10 月 198.7 222.2 265.0
11 月 209.1 250.9 293.9
12 月 241.0 278.6 305.7
模型,其表达式为:
(8)
式中, 为 季 节回归 量, 为 季 节回归 阶 数,
的预测要求。提出了一种SARIMA-BP神经网络预测方法,利用SARIMA方法对时间序列的线性部分进行建模,利用BP神经网络方法对时
间序列的非线性部分进行建模。仿真结果表明,SARIMA-BP神经网络方法比单一模型的预测准确率更高。
关键词:时间序列 灰色关联分析法 SARIMA-BP神经网络方法
中图分类号:F714
针对汽车销量数据中包含的线性特征和非线性特征,本文提 出了一种基于SARIMA-BP神经网络的预测方法,利用BP神经网络 自学习能力强的特征实现对非线性动态变化的自适应调控,通过 神经网络的非线性函数逼近和收敛优势保证了预测的精度和稳 定性。
强的特点,应用灰色关联分析法对其进行筛选。
汽车销量序列为
,影响因素的
表1 销量影响因素筛选
关联度 0.9125 0.8729 0.8543
影响因素 购置7869 0.7523
1 汽车销量影响因素的选取 当前影响汽车销量的因素[6]归纳起来大体有以下几种(:1)社
会因素,如人均可支配收入、道路基础设施建设(;2)国家政策,如 购置税补贴、限购政策等(;3)价格因素,如燃油价格、汽车售价等; (4)技术因素,如汽车用料质量、制造工艺等。
灰色关联分析法[7]主要通过对系统特征序列进行数据分析, 得出相关因素的曲线形状相似度,依据灰色关联度的大小判断因 素的影响程度。针对汽车销量影响因素呈现出多样化且关联性较
BP神经网络算法预测销量高低

BP神经⽹络算法预测销量⾼低 理论以前写过:,这⾥根据天⽓、是否周末、有⽆促销的情况,来预测销量情况。
function [ matrix,attributes ] = bp_preprocess( inputfile )%% BP神经⽹络算法数据预处理,把字符串转换为0,1编码% inputfile: 输⼊数据⽂件;% output:转换后的0,1矩阵;% attributes: 属性和Label;%%读取数据[~,txt]=xlsread(inputfile);attributes=txt(1,2:end);data = txt(2:end,2:end);%%针对每列数据进⾏转换[rows,cols] = size(data);matrix = zeros(rows,cols);for j=1:colsmatrix(:,j) = cellfun(@trans2onefalse,data(:,j));endendfunction flag = trans2onefalse(data)if strcmp(data,'坏') ||strcmp(data,'否')...||strcmp(data,'低')flag =0;return ;endflag =1;end%%使⽤BP神经⽹络算法预测销量⾼低clear ;%参数初始化inputfile = '../data/sales_data.xls'; %销量及其他属性数据%%数据预处理disp('正在进⾏数据预处理...'); [matrix,~] = bp_preprocess(inputfile); %%输⼊数据变换input = matrix(:,1:end-1);target = matrix(:,end);input=input';target=target';target=full(ind2vec(target+1));%%新建BP神经⽹络,并设置参数% net = feedforwardnet(10);net = patternnet(10);net.trainParam.epochs=1000;net.trainParam.show=25;net.trainParam.showCommandLine=0; net.trainParam.showWindow=1; net.trainParam.goal=0;net.trainParam.time=inf;net.trainParam.min_grad=1e-6; net.trainParam.max_fail=5;net.performFcn='mse';%训练神经⽹络模型net= train(net,input,target);disp('BP神经⽹络训练完成!');%%使⽤训练好的BP神经⽹络进⾏预测y= sim(net,input);plotconfusion(target,y);disp('销量预测完成!'); 可以看出,检测样本为34个,预测正确的个数为26,预测准确率为76.5%,预测准确率较低,是由于神经⽹络预测时需要较多的样本,是在此预测数据较少造成的。
BP神经网络的应用
x2
w1 w2
xk
wk wn
net
传输函数 f ( )
y f ( net )
输出端y
xn
输入端
1.2.3 BP神经网络模型
(2)使用S型激活函数时BP网络输入与输出关系 输入 net x1w1 x2 w2 ... xn wn b 1 输出 y f (net ) 1 e net 1 1 输出的导数 f '(net ) y (1 y ) - net net 2 1 e (1 e ) 根据S型激活函数的图形可 知,对神经网络进行训练, 应该将net的值尽量控制在 收敛比较快的范围内.
从训练情况可以看出,在误差值比较大的时候训练就 停止了,将输入p带入训练后的矩阵,发现输出结果与t很 不一致,说明这里找不到分类的规律。
Jean Gabriel Ganascia
Ricard Gavalda Melinda T. Gervasio Attilio Giordana Paul W. Goldberg Diana Gordon Jonathan Gratch
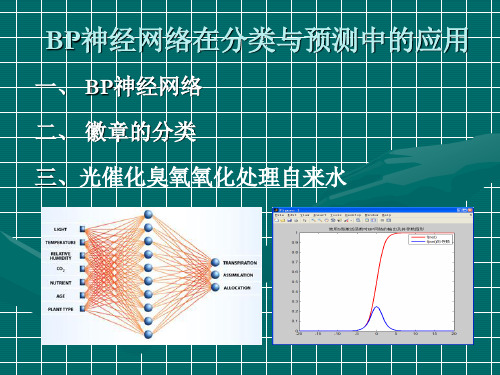
BP神经网络在分类与预测中的应用
二、徽章的分类
14名未参加会议的代表 徽章 代表姓名 徽章 代表姓名 ? Merrick L. Furst ? Jean Gabriel Ganascia ? William Gasarch ? Ricard Gavalda ? Yolanda Gil ? Melinda T. Gervasio ? David Gillman ? Attilio Giordana ? Kate Goelz ? Paul W. Goldberg ? Sally Goldman ? Diana Gordon ? Geoffrey Gordon ? Jonathan Gratch 徽章问题的背景
BP神经网络预测模型及应用

B P神经网络预测模型及应用(总5页)-CAL-FENGHAI.-(YICAI)-Company One1-CAL-本页仅作为文档封面,使用请直接删除B P神经网络预测模型及应用摘要采用BP神经网络的原理,建立神经网络的预测模型,并利用建立的人工神经网络训练并预测车辆的销售量,最后得出合理的评价和预测结果。
【关键词】神经网络模型预测应用1 BP神经网络预测模型1.1 BP神经网络基本理论人工神经网络是基于模仿生物大脑的结构和功能而构成的一种信息处理系统。
该网络由许多神经元组成,每个神经元可以有多个输入,但只有一个输出,各神经元之间不同的连接方式构成了不同的神经网络模型,BP网为其中之一,它又被称为多层前馈神经网络。
1.2 BP神经网络预测模型(1)初始化,给各连接权值(wij,vi)及阐值(θi)赋予随机值,确定网络结构,即输入单元、中间层单元以及输出层单元的个数;通过计算机仿真确定各系数。
在进行BP网络设计前,一般应从网络的层数、每层中的神经元个数、初始值以及学习方法等方面进行考虑,BP 网络由输入层、隐含层和输出层组成。
隐含层神经元个数由以下经验公式计算:(1)式中:s为隐层节点数,m为输入层节点数,n为输出层节点数,h为正整数,一般取3―7. BP网络采用了有一定阈值特性的、连续可微的sigmoid函数作为神经元的激发函数。
采用的s型函数为:(2)式中:s为隐层节点数,m为输入层节点数,n为输出层节点数,h为正整数,一般取3―7.计算值需经四舍五入取整。
(2)当网络的结构和训练数据确定后,误差函数主要受激励函数的影响,尽管从理论分析中得到比的收敛速度快,但是也存在着不足之处。
当网络收敛到一定程度或者是已经收敛而条件又有变化的时候,过于灵敏的反映会使得系统产生震荡,难于收敛。
因此,对激励函数进行进一步改进,当权值wij(k)的修正值Δwij(k)Δwij(k+1)<0时,,其中a为大于零小于1的常数。
基于BP神经网络的农作物销售量预测-以贵州省威宁县荞酥为例

基于 BP神经网络的农作物销售量预测-以贵州省威宁县荞酥为例【摘要】电商库存补单是电商资金运转的一大难题,科学的补充订单和解决库存深度问题能加强电商供应链体系建设,帮助电商加速资金流动,减少库存压力,降低存储成本。
本文针对传统的农产品销量预测模型方法的难点和新时代背景下农产品预测市场的需求,根据气候、时间、价格和质量、销售区域五个因素,利用LM算法优化了bp神经网络,并对贵州省威宁县荞酥的未来几天农产品销量建立了相应的网络模型,进行预测实验。
结果表明该模型的预测精度较为准确,可以进行预测实验。
关键词:bp神经网络机器学习销量预测 LM算法荞酥0 引言随着我国乡村特色农业振兴战略的实施,使用“互联网+”等利用科技方法指导农业生产的方法成为了未来的发展方向。
基于以上背景,本文引入了一种bp神经网络对每个产品的平均销售额数据进行了预测,bp神经网络相较于其他各种传统销售预测分析方法而言,具有强大的非线性,自动的学习和独立有组织的预测能力。
在本文中,使用Levenberg-Marquardt算法对bp神经网络进行优化,本算法的性能相较于传统bp神经网络的梯度下降算法性能要提升很多,可以显著提高预测的速度以及精度。
1 bp神经网络原理1.1.bp神经网络原理简介bp神经网络最早是被Rumelhart和McClelland于1986年前被提出的。
bp模型神经网络的主要设计思想其实就是包含了两个组成部分,它们的主要目标分别是:产生信号的前向信息传递与产生误差后向信号传播。
通过不断地更新调整整个网络的资源授权值,使网络的最终输出尽可能无限接近于期望输出,使得最终达到训练的目的。
1.bp神经网络模型建立1.bp神经网络结构参数选择在设计BP神经网络时,需要考虑的因素有很多,其中主要的是网络的层数、每层神经元的个数和学习速率。
本实验选择三级结构,其中五个输入,隐含层为六个节点来进行训练,并在实验过程中不断调整学习率。
基于BP神经网络的上市物流公司业绩预测模型

中 图分 类 号
Pr e di c t i o n Mo de l o f Li s t e d Lo g i s t i c s Co mp a ny
Re g a r d i n g t h e d a t a o f f i r s t 2 3 l i s t e d l o g i s t i c s c o mp a n i e s i n 2 0 1 0 a s t h e r e s e a r c h o b j e c t , t h e B P a l g o r i t h m i s a d o p t e d t o e s t a b —
’ 0 ∞
( 5 )
其 中, 叩 是研 究 时 的速 率 ; 叩 >0
对 于负 向指标 , 标 准化 后 的隶属 函数 是 :
F , 一1 一( A, 一B j m i n ) / ( C, Ⅱ Ⅲ 一B )
是 回传 的错误 信号 :
一 一
在这 个 函数里 , F 是 指标 , A, 是额定值 , B 是 指 标 的最小 值 , C , 是 它 的最大 值 , . 是预 估指 数 。
即B P神 经 网络 , 这 是 目前应 用 最 广 泛 的 神经 网络 之一 , 同 时它也 是 一 种 带 隐蔽 层 的多 层 前 馈 网络 。 本 文 的思路 和方 法 就 源 自于 _ 8 卅 这 几 份 研究 著 作 :
4 )确 认 网络 的输 出节 点数 K 这里 得到 网 络 的 输 出结 果 只 是 业 绩 评估 方 面 的一个 指 数认 证 系数 , 所 以得 出节 点 数 K 是 1 。 2 . 4 B P神经 网络 的计 算过 程
基于神经网络系统的智能穿戴设备销售的预测研究

文章编号:2095-6835(2022)16-0084-04基于神经网络系统的智能穿戴设备销售的预测研究杨柳青青(武汉理工大学经济学院,湖北武汉430070)摘要:智能产品近年来发展势头大涨,这很大一部分受益于电商平台的崛起和消费升级,在智能产品爆发式增长的同时,其业绩增长变得越来越困难。
随着科学技术的迅速发展,人工神经网络技术在现代发展中逐渐成熟。
通过建立神经网络模型对时间序列进行预测,并对未来智能产品的销售进行了预测。
主要以BP神经网络为主,以遗传算法为辅来搭建基于BP神经网络的销售预测系统;然后从智能产品的崛起出发,根据目前智能产品存在的问题,并结合神经网络预测系统和大数据技术对智能产品营销策略提出相应的建议,对未来智能产品市场进行展望。
关键词:遗传算法;神经网络;智能产品;销售预测中图分类号:TN912.34文献标志码:A DOI:10.15913/ki.kjycx.2022.16.0261研究背景1.1智能穿戴设备市场的崛起早在20世纪60年代,智能穿戴设备的思想和雏形就已出现,直到20世纪80年代真正可以穿戴的智能设备才开始出现在社会大众眼前。
智能穿戴设备是运用穿戴技术对用户的身体状况、睡眠状况、运动状况等进行监测。
目前,随着科学技术的进步,智能穿戴设备市场正在逐步崛起,已有不少学者开始研究智能穿戴设备在智慧养老领域、智能健身、防疫预警等方面的应用。
智能穿戴设备的代表产品有Apple Watch 苹果智能手表、华为智能手表、小米手环等,截至2016年,全球智能设备市场的规模已达60亿元。
随着当今社会逐渐智能化,智能穿戴设备的种类越来越丰富,人们对智能穿戴设备也有了更高的追求,其将极大地影响人们的生活方式。
从传统时代到互联网时代,消费者行为模式[1]经历了从AIDMA(用户在购买商品前的心理过程)到AISAS(用户在社会化媒体上产生购买行为前后的过程)的转变。
到了移动网络时代,消费者的行为特征往往符合AISAS模式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一,说明
对销售额进行bp神经网络预测,销售额如表1
其中前17月数据用作训练样本,来预测第18个月的数据,然后利用前18个月的数据来预测第19个月的数据,以此来预测全部月份的数据,并最终给出真实值与预测值之间的误差
二,程序
程序包括两部分,main.m为主程序,NNetwork.m为训练及预测程序,NNetwork输入为真实数据,输出为预测数据。
程序如下
main程序
clear all %清除变量空间
clc %清除命令窗口所有数据
close all %关闭所有figure窗口
% 数据,前17组为训练数据
t=[124.2 117.1 108.4 102.8 99.2 98.6 100.4 100. 99.4 101.2 103.9 101.8 101.5 104.8 105.9 99.3 103.3 113.2 116.5 117.1 116.9 115.8]; %%原始数据(数据的观测值)
n=1; %每次预测个数
for i=17:21
s=t(1:i);
[a, anew]=NNetwork(s,n); %调用神经网络预测程序
disp(['预测的第',num2str(i+1),'个值为']);
anew %预测值
pred=a(1,:) ;
pred(end+1)=anew; %加上预测值新数据
end
%画图部分
figure
xx=1:i+1;
plot(xx,pred,'r-*',xx,t,'k--+');
legend('预测值','实际值');
xlabel('点数');
ylabel('数据');
figure
s=abs(pred-t)./t*100;
plot(xx,s,'b-*');
xlabel('点数');
ylabel('误差比例(%)');
disp('实际值的标准差为')
std(t) %求标准差
disp('预测值的标准差为')
std(pred)
NNetwork程序如下
function [a, anew]=NNetwork(x,n)
% x为神经网络训练数组
% n为预测数据的个数
p=1:length(x); %%数据的个数
warning off
%数据归一化
[pn,minp,maxp,tn,mint,maxt]=premnmx(p,x);
%BP网络训练
net=newff([-1,1],[5,1],{'tansig','tansig','purelin'},'traingdx'); net.trainParam.show=1000; %每1000轮回显示一次结果net.trainParam.Lr=0.05; %学习速率为0.05
net.trainParam.epochs=5000; %循环5000次
net.trainParam.goal=1e-6; %均方误差
net=train(net,pn,tn); %训练
an=sim(net,pn); %神经网络仿真
a=postmnmx(an,mint,maxt); %还原仿真得到的数据,反归一化%对新数据进行预测
xx=1:length(x);
pnew=[length(xx):length(xx)+n];%预测数据
pnewn=tramnmx(pnew,minp,maxp);%新数据归一化
anewn=sim(net,pnewn);
anew=postmnmx(anewn,mint,maxt);%还原得到预测值
anew=anew(2);
三,程序运行截图
运行main.m文件,结果如图
并给出真实值与预测值的标准差
真是值与预测值的对比曲线及误差比例曲线如图。
