Matlab数学实验1 简单函数曲线
Matlab数学实验1简单函数曲线解读

>> plot(x,cos(x),’bd-.’); 可以只指定其中某几个 >> plot(x,cos(x),’k*-’); 排列顺序任意
蓝色、点划线 离散点为菱形
黑色、实线 离散点用星号
线型
- 实线 : 虚线 -. 点划线 -- 间断线
点标记
.点 o 小圆圈 x 叉子符 + 加号 * 星号 s 方格 d 菱形 ^ 朝上三角 v 朝下三角 > 朝右三角 < 朝左三角 p 五角星 h 六角星
所得图形如下所示:
ezpolar是简易极坐标作图命令。也可以把上面的输入改为: ezpolar(‘3*cos(3*t)’),运行此程序也可得到上面的图形。
课堂上机练习
1. 作出函数y tan x和y cot x的图形观察其周期性和变化趋势。
2. 在区间[1,1]内画出函数y sin 1 的图形。 x
颜色
y 黄色 m 棕色 c 青色 r 红色 g 绿色 b 蓝色 w 白色 k 黑色
[0,2 ]
作图命令: x=linspace(0,2*pi,30); y=sin(x); z=cos(x); plot(x,y,'r',x,z,'go');
注:linspace是Matlab中的一个指令,linspace(x1,x2,N)用 于产生x1,x2之间的N点行矢量。其中x1、x2、N分别为起始值、 终止值、元素个数。若缺省N,默认点数为100 。
ezplot(‘f(x,y)’)
f (x, y) 0 在区间 2 x 2 ,2 y 2 上的图形
ezplot(‘f’,’g’,[a,b])
x f (t), y g(t) 在区间 a t b 上的图形
实验一matlab环境语法及数学运算(验证性实验-2课时)

实验一Matlab环境语法及数学运算(验证性实验-2课时)一、实验目的:1、熟悉matlab软件的环境语法及简单的数学运算;2、能熟练运用matlab软件进行简单的数学运算;二、实验设备PC机,配置:PIII450/内存128M/显卡TNT32M/硬盘10G以上。
局域网、MATLAB7.0环境、投影仪三、实验原理MATLAB环境是一种为数值计算、数据分析和图形显示服务的交互式的环境。
MATLAB有3种窗口,即:命令窗口(The Command Window)、m-文件编辑窗口(The Edit Window)和图形窗口(The Figure Window),而Simulink另外又有Simulink 模型编辑窗口。
1.命令窗口(The Command Window)当MATLAB启动后,出现的最大的窗口就是命令窗口。
用户可以在提示符“>>”后面输入交互的命令,这些命令就立即被执行。
在MATLAB中,一连串命令可以放置在一个文件中,不必把它们直接在命令窗口内输入。
在命令窗口中输入该文件名,这一连串命令就被执行了。
因为这样的文件都是以“.m”为后缀,所以称为m-文件。
2.m-文件编辑窗口(The Edit Window)我们可以用m-文件编辑窗口来产生新的m-文件,或者编辑已经存在的m-文件。
在MATLAB主界面上选择菜单“File/New/M-file”就打开了一个新的m-文件编辑窗口;选择菜单“File/Open”就可以打开一个已经存在的m-文件,并且可以在这个窗口中编辑这个m-文件。
四、实验内容:1、帮助命令使用 help 命令,查找 sqrt(开方)函数的使用方法;2、矩阵运算(1)矩阵的乘法已知 A=[1 2;3 4]; B=[5 6;7 8];求 A^2*B(2)矩阵除法已知 A=[1 2 3;4 5 6;7 8 9];B=[1 0 0;0 2 0;0 0 3];A\B,A/B(3)矩阵的转置及共轭转置已知 A=[5+i,2-i,1;6*i,4,9-i];求 A.', A'(4)使用冒号选出指定元素已知: A=[1 2 3;4 5 6;7 8 9];求 A 中第 3 行前 2 个元素;A 中所有列第 2,3 行的元素;A 中第 3 列前 2 个元素为:3、多项式求多项式 p(x) = x3 + 2x+ 4的根4、基本绘图命令(1)绘制余弦曲线 y=cos(t),t∈[0,2π](2)在同一坐标系中绘制余弦曲线 y=cos(t-0.25)和正弦曲线 y=sin(t-0.5),t∈[0,2π]5、基本绘图控制绘制[0,4π]区间上的 x1=10sint 曲线,并要求:(1)线形为点划线、颜色为红色、数据点标记为加号;(2)坐标轴控制:显示范围、刻度线、比例、网络线(3)标注控制:坐标轴名称、标题、相应文本;五、实验步骤1、帮助命令使用 help 命令,查找 sqrt(开方)函数的使用方法;SQRT Square root.SQRT(X) is the square root of the elements of X. Complexresults are produced if X is not positive.See also sqrtm.Overloaded functions or methods (ones with the same name in other directories) help sym/sqrt.mReference page in Help browserdoc sqrt2、矩阵运算(1)矩阵的乘法已知 A=[1 2;3 4]; B=[5 6;7 8];求 A^2*BA^2*B =105 122229 266(2)矩阵除法已知 A=[1 2 3;4 5 6;7 8 9];B=[1 0 0;0 2 0;0 0 3];A\B,A/BWarning: Matrix is close to singular or badly scaled.Results may be inaccurate. RCOND = 1.541976e-018.A\B =1.0e+016 *-0.4504 1.8014 -1.35110.9007 -3.6029 2.7022-0.4504 1.8014 -1.3511A/B =1.0000 1.0000 1.00004.0000 2.5000 2.00007.0000 4.0000 3.0000(3)矩阵的转置及共轭转置已知 A=[5+i,2-i,1;6*i,4,9-i];求 A.', A'A.'=5.0000 + 1.0000i 0 +6.0000i2.0000 - 1.0000i 4.00001.0000 9.0000 - 1.0000iA’ =5.0000 - 1.0000i 0 -6.0000i2.0000 + 1.0000i 4.00001.0000 9.0000 + 1.0000i(4)使用冒号选出指定元素已知: A=[1 2 3;4 5 6;7 8 9];求 A 中第 3 行前 2 个元素;A 中所有列第 2,3 行的元素;A 中第 3 列前 2 个元素为:A(3,1:2) =7 8A(2:3,:) =4 5 67 8 9A(1:2,3) =363、多项式求多项式 p(x) = x3 + 2x+ 4的根p=[1 0 2 4];roots(p)ans =0.5898 + 1.7445i0.5898 - 1.7445i-1.17954、基本绘图命令(1)绘制余弦曲线 y=cos(t),t∈[0,2π]t=0:pi/100:2*pi;y=cos(t);plot(t,y)(2)在同一坐标系中绘制余弦曲线 y=cos(t-0.25)和正弦曲线 y=sin(t-0.5),t∈[0,2π]t=0:pi/100:2*pi;y1=cos(t-0.25);y2=sin(t-0.5);plot(t,y1,t,y2)5、基本绘图控制绘制[0,4π]区间上的 x1=10sint 曲线,并要求:(1)线形为点划线、颜色为红色、数据点标记为加号;(2)坐标轴控制:显示范围、刻度线、比例、网络线(3)标注控制:坐标轴名称、标题、相应文本;程序:t=0:pi/100:4*pi;x1=10*sin(t);plot(t,x1,'r-.+')title('t from 0 to 4{\pi}')xlabel('Variable t')ylabel('Variable x1')grid ontext(2,5,'曲线x1=10*sin(t)')legend('x1')六、实验要求利用所学知识,完成上述各项实验内容,并将实验过程和实验步骤和结果写在报告中。
数学实验(MATLAB)课后习题答案
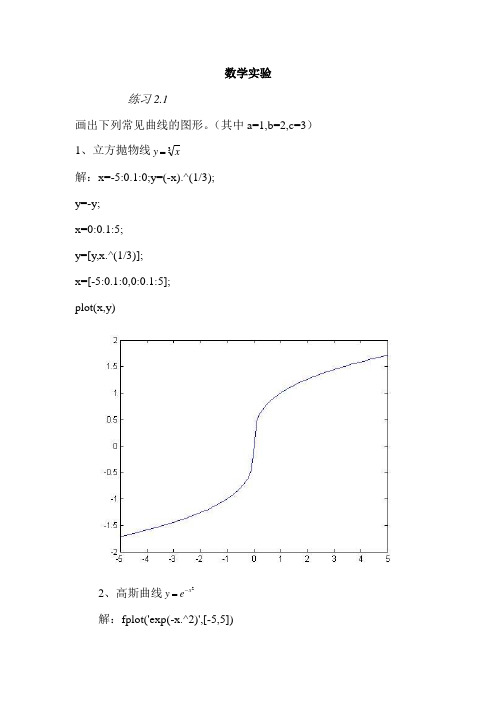
数学实验练习2.1画出下列常见曲线的图形。
(其中a=1,b=2,c=3)1、立方抛物线3xy=解:x=-5:0.1:0;y=(-x).^(1/3);y=-y;x=0:0.1:5;y=[y,x.^(1/3)];x=[-5:0.1:0,0:0.1:5];plot(x,y)2、高斯曲线2x e=y-解:fplot('exp(-x.^2)',[-5,5])3、笛卡儿曲线)3(13,1333222axy y x t at y t at x =++=+=解:ezplot('x.^3+y.^3-3*x*y',[-5,5])xyx.3+y.3-3 x y = 0或t=-5:0.1:5; x=3*t./(1+t.^2); y=3*t.^2./(1+t.^2); plot(x,y)4、蔓叶线)(1,1322322xa x y t at y t at x -=+=+=解:ezplot('y.^2-x.^3/(1-x)',[-5,5])xyy.2-x.3/(1-x) = 0或t=-5:0.1:5; x=t.^2./(1+t.^2); y=t.^3./(1+t.^2); plot(x,y)5、摆线)cos 1(),sin (t b y t t a x -=-= 解:t=0:0.1:2*pi;x=t-sin(t); y=2*(1-cos(t)); plot(x,y)6、星形线)(sin ,cos 32323233a y x t a y t a x =+== 解:t=0:0.1:2*pi; x=cos(t).^3; y=sin(t).^3;plot(x,y)或ezplot('x.^(2/3)+y.^(2/3)-1',[-1,1])xyx.2/3+y.2/3-1 = 07、螺旋线ct z t b y t a x ===,sin ,cos 解:t=0:0.1:2*pi; x=cos(t); y=2*sin(t); z=3*t; plot3(x,y,z) grid on8、阿基米德螺线θa r = 解:x =0:0.1:2*pi; r=x; polar(x,r)902701809、对数螺线θa e r = 解:x =0:0.1:2*pi; r=exp(x); polar(x,r)90270180010、双纽线))()((2cos 22222222y x a y x a r -=+=θ 解:x=0:0.1:2*pi; r=sqrt(cos(2*x)); polar(x,r)90270或ezplot('(x.^2+y.^2).^2-(x.^2-y.^2)',[-1,1]) grid onxy(x.2+y.2).2-(x.2-y.2) = 011、双纽线)2)((2sin 222222xy a y x a r =+=θ 解:x=0:0.1:2*pi; r=sqrt(sin(2*x)); polar(x,r)90270或ezplot('(x.^2+y.^2).^2-2*x*y',[-1,1]) grid onxy(x.2+y.2).2-2 x y = 012、心形线)cos 1(θ+=a r 解:x =0:0.1:2*pi; r=1+cos(x); polar(x,r)90270练习2.21、求出下列极限值。
高等数学:MATLAB实验

MATLAB实验
2.fplot绘图命令 fplot绘图命令专门用于绘制一元函数曲线,格式为:
fplot('fun',[a,b]) 用于绘制区间[a,b]上的函数y=fun的图像.
MATLAB实验 【实验内容】
MATLAB实验
由此可知,函数在点x=3处的二阶导数为6,所以f(3)=3为 极小值;函数在点x= 1处的二阶导数为-6,所以f(1)=7为极大值.
MATLAB实验
例12-10 假设某种商品的需求量q 是单价p(单位:元)的函 数q=12000-80p,商 品的总成本C 是需求量q 的函数 C=25000+50q.每单位商品需要纳税2元,试求使销售 利润达 到最大的商品单价和最大利润额.
MATLAB实验
MATLAB实验
MATLAB实验
MATLAB实验
MATLAB实验
MATLAB实验
MATLAB实验
MATLAB实验
MATLAB实验 实验九 用 MATLAB求解二重积分
【实验目的】 熟悉LAB中的int命令,会用int命令求解简单的二重积分.
MATLAB实验
【实验M步A骤T】 由于二重积分可以化成二次积分来进行计算,因此只要
MATLAB实验
MATLAB实验
MATLAB实验
MATLAB实验
MATLAB实验
实验七 应用 MATLAB绘制三维曲线图
【实验目的】 (1)熟悉 MATLAB软件的绘图功能; (2)熟悉常见空间曲线的作图方法.
【实验要求】 (1)掌握 MATLAB中绘图命令plot3和 mesh的使用; (2)会用plot3和 mesh函数绘制出某区间的三维曲线,线型
MATLAB数学实验报告1

MATLAB数学实验报告1Matlab数学实验报告⼀、实验⽬的通过以下四组实验,熟悉MATLAB的编程技巧,学会运⽤MATLAB的⼀些主要功能、命令,通过建⽴数学模型解决理论或实际问题。
了解诸如分岔、混沌等概念、学会建⽴Malthu模型和Logistic 模型、懂得最⼩⼆乘法、线性规划等基本思想。
⼆、实验内容2.1实验题⽬⼀2.1.1实验问题Feigenbaum曾对超越函数y=λsin(πx)(λ为⾮负实数)进⾏了分岔与混沌的研究,试进⾏迭代格式x k+1=λsin(πx k),做出相应的Feigenbaum图2.1.2程序设计clear;clf;axis([0,4,0,4]);hold onfor r=0:0.3:3.9x=[0.1];for i=2:150x(i)=r*sin(3.14*x(i-1));endpause(0.5)for i=101:150plot(r,x(i),'k.');endtext(r-0.1,max(x(101:150))+0.05,['\it{r}=',num2str(r)]) end加密迭代后clear;clf;axis([0,4,0,4]);hold onfor r=0:0.005:3.9x=[0.1];for i=2:150x(i)=r*sin(3.14*x(i-1));endpause(0.1)for i=101:150plot(r,x(i),'k.');endend运⾏后得到Feigenbaum图2.2实验题⽬⼆2.2.1实验问题某农夫有⼀个半径10⽶的圆形⽜栏,长满了草。
他要将⼀头⽜拴在⽜栏边界的桩栏上,但只让⽜吃到⼀半草,问拴⽜⿐⼦的绳⼦应为多长?2.2.2问题分析如图所⽰,E为圆ABD的圆⼼,AB为拴⽜的绳⼦,圆ABD为草场,区域ABCD为⽜能到达的区域。
问题要求区域ABCD等于圆ABC的⼀半,可以设BC等于x,只要求出∠a和∠b就能求出所求⾯积。
《数学实验》实验报告——用MATLAB绘制sin曲线
试验步骤(根据问题分析及试验目的所计划的试验步骤):
(1)设计实验程序,程序如下:
(2)试运行实验程序,逐步修改程序。
试验过程(含详细试验步骤、程序清单及异常情况记录等)
(1)将编写的程序在软件中试运行;
(2)逐步修改指令,排除出现的各种异常情况;
(3)运行结果如下:
结果分析:
运行的结果能达到实验的目的和要求,通过在同一幅图上的(-pi,pi)区间,可绘制出用0.5的间隔的sinx的红色曲线,用0.1的间隔的sin(x+0.5)的绿色曲线,用0.01的间隔的sin(x+1)的蓝色曲线,并给图的x和y轴添加标注。
x1=-pi:0.5:pi
y1=sin(x1);
x2=-pi:0.1:pi
y2=sin(x2+0.5);
x3=-pi:0.01:pi
y3=sin(x3+1);
plot(x1,y1,'r',x2,y2,'g',x3,y3,'b')
xlabel('x1,x2,x3')
ylabel('sin(x1),sin(x2+0.5),sin(x3+1)')
有的工具绘制起来比较繁琐所达到的结果也不尽如人意所以就需要寻找一种比较容易操作及效果比较好的工具来完成sin曲线的绘实验报告
班级
****
学号
****
姓名
matlab 拟合曲线 计算峰面积

matlab 拟合曲线计算峰面积Matlab拟合曲线计算峰面积Matlab是一种强大的数值计算软件,广泛应用于工程、科学和数学领域。
其中拟合曲线是Matlab的一个重要功能,可以用来处理实验数据并计算峰面积。
本文将介绍如何使用Matlab进行拟合曲线并计算峰面积。
一、数据导入与预处理首先,将实验数据导入Matlab。
可以通过直接复制粘贴数据、导入文本文件或使用Matlab内置函数读取数据文件。
在导入数据之后,我们可以对数据进行必要的预处理,例如去除噪声、平滑数据或调整数据格式。
二、选择合适的拟合函数根据实验数据的特征和目标,选择一个合适的拟合函数。
Matlab提供了多种内置的拟合函数,例如多项式、指数、对数、高斯函数等。
如果内置函数无法满足需求,也可以定义自己的拟合函数。
三、进行曲线拟合使用Matlab的拟合函数进行曲线拟合。
具体的拟合过程可以参考Matlab的文档或拟合函数的说明。
一般情况下,我们需要提供初始拟合参数和拟合范围,并设置拟合的精度和迭代次数。
拟合结束后,可以得到最佳拟合曲线的参数。
四、绘制拟合曲线根据得到的最佳拟合参数,绘制拟合曲线。
可以使用Matlab提供的绘图功能,将原始数据和拟合曲线在同一个坐标系下进行绘制。
通过可视化比较,我们可以判断拟合曲线的准确性,并做进一步的调整。
五、计算峰面积计算峰面积是基于拟合曲线的。
在Matlab中,可以通过计算拟合曲线下的积分来得到峰面积。
具体方法是使用Matlab的积分函数,将拟合曲线作为输入函数进行积分。
积分范围可以根据实际情况进行设置。
六、结果分析与优化根据计算得到的峰面积,进行结果分析与优化。
可以与其他实验数据进行对比,评估拟合曲线的准确性和峰面积的可信度。
如果需要对拟合精度进行优化,可以调整拟合函数的参数或采用其他更复杂的拟合模型。
七、应用拓展除了计算峰面积,Matlab还可以应用于其他拟合曲线相关的问题。
例如,可以进行峰值识别、波形拟合、数据拟合等,以满足不同实验需求。
matlab平台上函数单调性与凹凸性判定的数学实验

matlab平台上函数单调性与凹凸性判定的数学
实验
简要描述
本文主要介绍利用matlab平台上函数单调性凹凸性的判定实验。
实验开始先介绍一元函数的单调性与凹凸性,单调性是指函数图像在一条直线上单方向增加或减少的性质,可以分为函数的单调递增、函数的单调递减;凹凸是指函数图像的增减性质由单调性变为凹凸,是指抛物线型或非抛物线型驼峰状,即有凹中凸性质。
然后,用matlab程序建模,判定单调性与凹凸性数学函数,并用matlab函数fplot和ezplot绘制函数图像。
最后进行仿真实验,设计函数y=x3/2+2,使用fplot绘图,求导及凹凸性,即求导dy/dx=1.5x0.5.此函数在x>0时增加,x=0时为极值,为凹凸函数。
综上所述,本次实验以matlab 为实验平台,以一元函数的单调性和凹凸性为主要分析内容,采用matlab函数fplot和ezplot 绘制图像,仿真求函数单调性与凹凸性,让我们理解函数单调性、凹凸性质。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
点标记
.点 o 小圆圈 x 叉子符 + 加号 * 星号 s 方格 d 菱形 ^ 朝上三角 v 朝下三角 > 朝右三角 < 朝左三角 p 五角星 h 六角星
颜色
y 黄色 m 棕色 c 青色 r 红色 g 绿色 b 蓝色 w 白色 k 黑色
[0,2 ]
作图命令: x=linspace(0,2*pi,30); y=sin(x); z=cos(x); plot(x,y,'r',x,z,'go');
ezplot(‘f(x,y)’)
f (x, y) 0 在区间 2 x 2 ,2 y 2 上的图形
ezplot(‘f’,’g’,[a,b])
x f (t), y g(t) 在区间 a t b 上的图形
例3:ezplot('sin(x)')
ezplot('sin(x)',[-pi,pi])
0.8
0.6
0.4
0.2
0
-0.2
-0.4
-0.6
-0.8
-1
0
1
2
3
4
5
6
7
标题
title(’text’)
例:>> x=[0:0.1:4*pi];
>> y=cos(x); >> plot(x,y); >> title('y=cos(x)的函数图像')
可以指定文本的属性 title('text', 'Property1', value1, ' Property2', value2, ...)
axis([-1,1,-2,2])
3、解:程序代码: >> t=linspace(0,2*pi,100); plot(cos(t).*cos(5*t),sin(t).*cos(3*t));
1、也可以这样编程序代码: syms x ss=0.05; x2=[0:0.001:((pi/2)-ss)]; x3=[((pi/2)+ss):0.001:pi+pi/2-ss]; x4=[pi+pi/2+ss:0.001:2*pi]; y=tan(x); plot(x2,subs(y,x2),x3,subs(y,x3), x4,subs(y,x4),[0 2*pi],[0 0])
Matlab 作图
1、Matlab作图原理:
Matlab是通过描点、连线来实现的,故画一 个曲线图形之前,必须先取得该图形上的一系列的 点的坐标(即横坐标和纵坐标),然后将该点集的 坐标传给Matlab函数画图.
2、Matlab作图命令: (1)plot(x,y, string)
图形属性
x,y是向量,分别表示点集的横坐标和纵坐标
Matlab——简单二维作图
一、实验目的: 1.了解基本初等函数及图形特征,会用
Matlab图形命令画图; 2.会画复合函数、参数函数、隐函数及极
坐标下函数的图形。 3. 能在同一个坐标系内画出多个函数的
图形
二、实验要求: 熟悉Matlab图形命令plot,ezplot,polar及
其用法。
三、实验内容:
3.
画出参数方程xy
cost sin5 3ex log3(3 x)在区间[2,2]上的图形特征。
1、:程序代码: >> x=linspace(0,2*pi,600);
t=sin(x)./(cos(x)+eps); plot(x,t);title('tan(x)');axis ([0,2*pi,-50,50]);
plot(x,y)--画实线 plot(x,y1,s1,x,y2,s2,……,x,yn,sn)
--将多条线画在一起
Matlab 作图
例1. 画出 y=sin(x) 在 [0,2 ]上的图像。
Matlab作图步骤:
给出离散点列: x=[0:pi/10:2*pi]
计算函数值: y=sin(x) 画图:用 matlab 二维绘图命令 plot 作出函数图形
所得图形如下所示:
ezpolar是简易极坐标作图命令。也可以把上面的输入改为: ezpolar(‘3*cos(3*t)’),运行此程序也可得到上面的图形。
课堂上机练习
1. 作出函数y tan x和y cot x的图形观察其周期性和变化趋势。
2. 在区间[1,1]内画出函数y sin 1 的图形。 x
如何画出 y=sin(x) 在 [0, 2*pi] 上的图像?
普通手工作图思路:
找点: x=0, pi/4, pi/2, 3*pi/4, pi, … 计算函数值:
y=sin(0), sin(pi/4), sin(pi/2), … 描点:在坐标系中画出这些离散点 用直线或曲线连接这些点,得到函数的大致图形
4、解:程序代码: >> x=linspace(-2,2,10000); y=x.^5+3*exp(x)+log(3-x)/log(3);
plot(x,y);
plot(x,y)
作图命令:
x=[0:pi/10:2*pi]; y=sin(x); plot(x,y)
点和线的基本属性
plot(x,y,’string’)
其中 string 是用 单引号 括起来的字符串,用来指定图 形的属性(点、线的形状和颜色)
>> x=[0:0.2:2*pi];
红色、虚线、 离散点用加号
(2)二维曲线绘图: ezplot
ezplot即Easy to use function plotter,是一个易 用的一元函数绘图函数 。特别是在绘制参数函数和 隐函数的图像时,ezplot要比plot更方便。因为plot绘 制图形时要指定自变量的范围,而ezplot无需数据准 备,直接绘出图形。
解 输入命令
ezplot('exp(x)+sin(x*y)',[-2,0.5,0,2])
(3)极坐标方程绘图命令: polar
如果想用利用曲线的极坐标方程作图,可使用 polar命令,其基本形式是:
polar(theta,rho)
例如曲线的极坐标方程为: 3cos3 ,要作出
它的图形,应输入:
theta=0:0.1:2*pi; >> rho=3*cos(3*theta); >> polar(theta,rho)
Property: linewidth, markersize, fontsize, fontweight, fontname, color …
坐标轴标注 xlabel(’text’) 或 ylabel(’text’)
例:
>> x=[0:0.1:4*pi];
y=cos(x);
plot(x,y); title('y=cos(x)的函数图像','color','r'); >> xlabel('x轴'); >> ylabel('y轴')
x=linspace(0,2*pi,100); ct=cos(x)./(sin(x)+eps); plot(x,ct);title('cot(x)');axis ([0,2*pi,-50,50]);
2、解:程序代码: >> x=linspace(-1,1,10000);
y=sin(1./x); plot(x,y);
注:linspace是Matlab中的一个指令,linspace(x1,x2,N)用 于产生x1,x2之间的N点行矢量。其中x1、x2、N分别为起始值、 终止值、元素个数。若缺省N,默认点数为100 。
该命令运行结果如下图所示:
在[0,2 ]用红线画sin(x),用绿圈画cos(x),结果所示:
1
例4. 在 [0, ] 上画y=sin(x)的图形
解 输入命令
ezplot('sin(x)',[0,pi])
例5.
在[0,2
]上画出星形线
y x
cos3 s in 3
t的图形。 t
解 输入命令
ezplot('cos(t)^3','sin(t)^3',[0,2*pi])
例6. 在[2, 0.5],[0, 2]上画出隐函数ex +sin(xy)=0的图形。
>> plot(x,cos(x));
>> plot(x,cos(x),’r+:’); 属性可以全部指定,也
>> plot(x,cos(x),’bd-.’); 可以只指定其中某几个 >> plot(x,cos(x),’k*-’); 排列顺序任意
蓝色、点划线 离散点为菱形
黑色、实线 离散点用星号
线型
- 实线 : 虚线 -. 点划线 -- 间断线
ezplot的调用格式:
ezplot(‘f’,[a,b])
绘制 f f(x) 在区间 a x b 上的图形
ezplot(‘f’)
缺省的绘图区间为 [-2, 2]
绘制 f f(x) 在区间 2 x 2 上的图形
ezplot(‘f(x,y)’,[a,b,c,d])
f (x, y) 0 在区间 a x b,c y d 上的图形
